A 3D real-scale, biomimetic and biohybrid model of the blood-brain barrier fabricated through two-photon lithography

Abstract

The investigation of the crossing of exogenous substances through the blood-brain barrier (BBB) is object of intensive research in biomedicine, and one of the main obstacles for reliable in vitro evaluations is represented by the difficulties at the base of developing realistic models of the barrier, that could resemble as most accurately as possible the in vivo environment. Here, for the first time, a 1:1 scale, biomimetic and biohybrid BBB model is proposed, developed by taking advantage of an innovative submicrometric-resolution 3D printing technique, namely two-photon lithography. Microtubes inspired to the brain capillaries were fabricated and used as scaffolds for the co-culturing of endothelial-like bEnd.3 and U87 glioblastoma cells. The constructs show the maturation of tight junctions, good performances in terms of hindering dextran diffusion through the barrier with respect to the microfluidic system without cells, and a satisfactory trans-endothelial electrical resistance (75 ± 2 Ω cm²), which is comparable to that observed in the literature with bEnd.3 monolayer-based models. Moreover, a mathematical model has been developed, that assisted both the design of the 3D microfluidic chip and its characterization. Overall, these results show the effective formation of a bioinspired cellular barrier based on microtubes reproducing brain microcapillaries to scale. This system will be exploited as a realistic in vitro model for the investigation of BBB crossing of nanomaterials and drugs, envisaging therapeutic and diagnostic applications for several brain pathologies, including brain cancer.

Incidence of central nervous systems (CNS) disorders is still rising despite the significant improvement in the understanding of their pathological mechanisms, and many new drugs, even if virtually able to treat these disorders, have not yet been clinically investigated because of their inability to cross the blood-brain barrier (BBB) and to enter into the brain compartment.^[1–3]

The elaboration of reliable in vitro models of the BBB is extremely relevant both for investigating the development of neurovascular disorders^[4–6] and for performing high-throughput screening of drug delivery through the BBB, and thus to treat CNS disorders.^[7] Furthermore, the possibility to mimic as most faithfully as possible in vitro the structure and the functionality of the neurovascular system could allow to rigorously study the BBB crossing without the use of in vivo models, thus limiting important ethical concerns.^[8] Finally, the accessibility of the in vitro models consents to finely tune different microenvironmental conditions and to easily quantify the biophysical effects of experimental treatments.^[9–10] For all these reasons, great efforts have been put forward the development of realistic in vitro models of the BBB, from simple two-dimensional (2D) models (for a comprehensive review the reader is referred to Cecchelli et al.^[7] and to Wilhelm et al.^[11]), to 2D microfluidic chips,^[12–14] up to arriving to more complex biomimetic three-dimensional (3D) systems.^[15–17] Here, we present for the first time a dynamic 3D biohybrid model of the BBB able to reproduce at 1:1 scale the capillaries of the neurovascular system. In order to mimic the function/structure of the brain microvessels, which are characterized by a size of about 10 μm, we exploited an advanced 3D microfabrication technique, namely two-photon lithography (TPL). This biohybrid BBB consists of porous tubular structures, each of them scaffolding a biological barrier of endothelial cells connected by tight junctions, with the aim of recapitulating the typical 3D tubular structure and the micrometric size of the brain capillaries.

The main components of the envisaged BBB physical model had to mimic brain microcapillaries: we considered tubes having 10 μm average diameter,^[18,19] encasing a liquid flow having around 1 mm s ^-1 average speed^[20,21] (assuming a water-like working fluid as discussed below, the associated Reynolds number is on the order of 10^-2). Moreover, on the surface of each tube, we assumed a regular pattern of circular orifices (hereafter called pores) allowing for mass transport towards the external environment (as functional to the investigation of BBB crossing by selected species transported along with the flow in the microcapillaries).

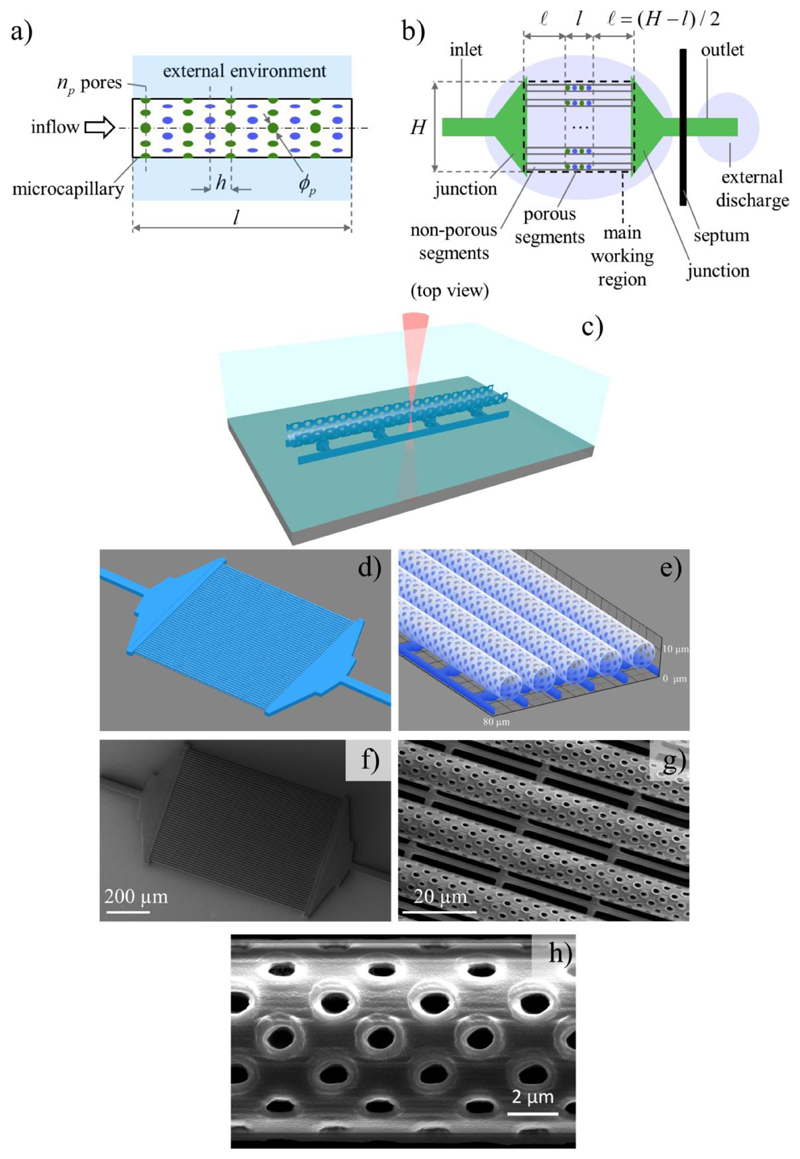
With reference to the schematic in Figure 1a, in order to ice-break chip design we assumed: ϕ_p = 1 μm as pore diameter; the pores to lie on cross-sectional planes uniformly distributed along the tube axis with pitch h = 2.5 μm; n_p = 8 pores uniformly distributed on each corresponding cross-section, with subsequent cross-sections being angularly shifted by π/n_p rad to enhance pore density. We considered n_t = 50 tubes to be fed in parallel, for two practical reasons: not to operate the circuit with exceedingly low inlet flow rates, and to enhance detection capabilities thanks to redundancy.

Figure 1.

Bioinspired microfluidic system design and microfabrication. a) Schematic of the porous tube (mimicking a microcapillary) that simultaneously scaffolds the cells and allows for species transport towards the external environment. b) Schematic (top view) of the microfluidic chip devised to operate multiple porous tubes in parallel. c) Scheme depicting the two-photon lithography fabrication of the microfluidic system with porous tubular-shaped microcapillaries. d) Design of the microfluidic system consisting of the microcapillaries arranged in parallel and connected to the inflow and the outflow reservoirs. e) High magnification of the designed porous microcapillaries. Representative scanning electron microscopy images f) of the obtained microfluidic chip, g) of the tubes, and h) of the pores, highlighting the high reproducibility and resolution of the fabrication technique.

We correspondingly defined an inlet and an outlet structure (channels), as well as junction structures to reach the main working region comprising the porous tube segments, framed by size-matching non-porous tube segments conceived as inflow and outflow guides. A corresponding schematic is shown in Figure 1b. The outlet was assumed to reach an external discharge region, namely a liquid domain similar to that one external to the tubes yet kept separate from the latter by a solid septum. At that design stage we tentatively set H = 800 μm as characteristic size for the main working region (essentially to keep fabrication times manageable), whereas the length l of the porous tube segments was still to be defined. This microfluidic system has been fabricated by exploiting the TPL, a high-resolution photolithographic technique which allows for the 3D fabrication of nanostructured scaffolds,^[22] owing to the phenomenon of the two-photon polymerization of dedicated photoresists (Figure 1c).

In Figure 1d, it is possible to appreciate the geometric model of the whole microfluidic system, while a magnification of the porous microcapillaries characterized by a 10 μm diameter is shown in Figure 1e. Scanning electron microscopy (SEM) of the obtained microfluidic chip and of the porous microtubes are instead respectively reported in Figure 1f and Figure 1g. These scans reveal the high reproducibility and accuracy of the TPL approach, which allows polymerizing structures faithfully reproducing the 3D model. A high magnification SEM image of the pores is shown in Figure 1h, from which we have evaluated an average pore diameter of about 1 μm (1.05 ± 0.08 μm): the low standard deviation of this measurement quantitatively confirms the high reliability and reproducibility of the TPL technique.

Further details of the structure design and fabrication are reported as Supporting Information (Figure S1-S3). Although 1 μm pores were adopted for all the experiments presented in this work, we also demonstrated the possibility to finely tune the pore diameter (Supporting Information, Figure S4) for the fabrication of different future prototypes.

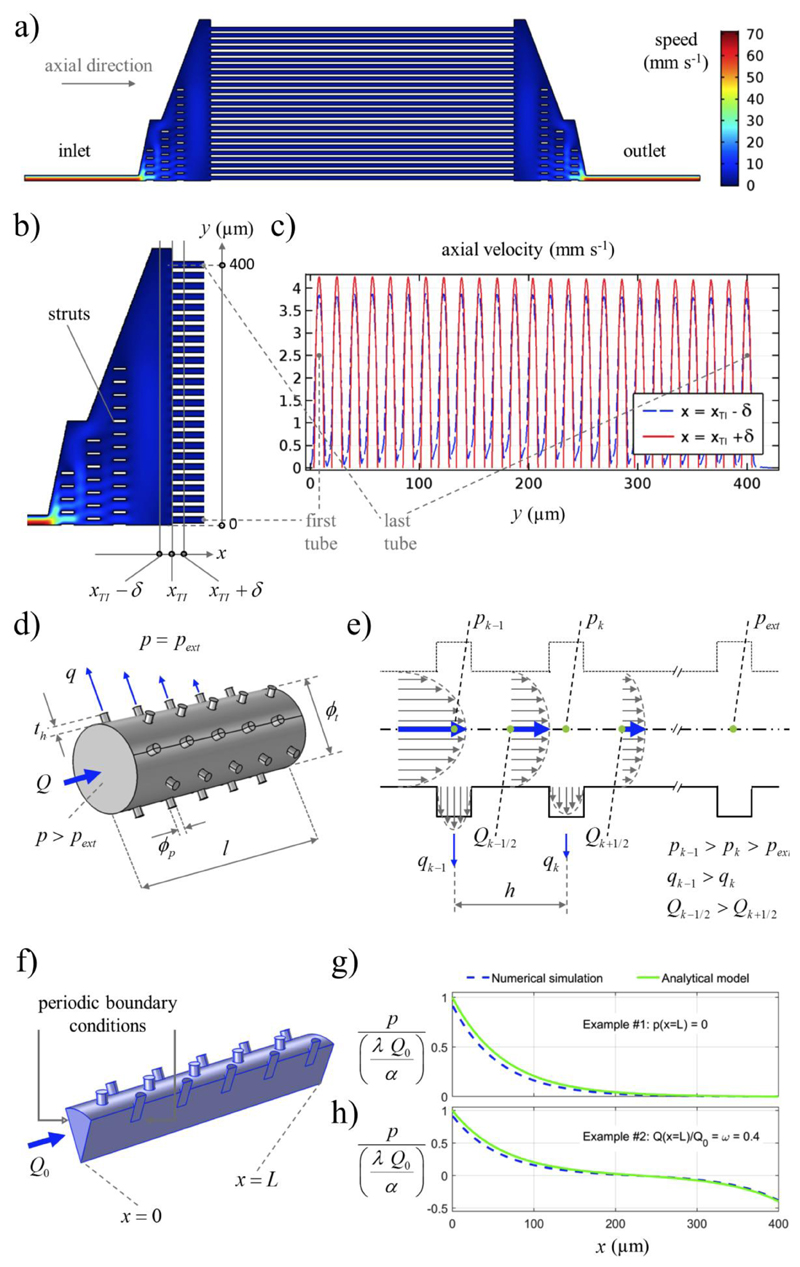
Concerning the model-based design of our system, we adequately substantiated the assumption of flows occurring in parallel through numerical simulations (Figures 2a-c). Specifically, Figure 2a and 2b are the intensity plots related to the fluid speed; Figure 2b shows that the struts locally affect the flow filed, yet in correspondence to the microcapillaries inlet section (denoted by abscissa x_T1) the flow is uniform. This is further remarked by Figure 2c that express the axial velocity profiles obtained through cut-sections immediately before and after (distance δ = 0.01 μm) the considered inlet section. The details of the numerical simulations are reported in Supporting Information.

Figure 2.

Modeling of the microfluidic system. a) Intensity plot of the fluid speed numerically computed on a simplified 2D geometry (half domain, by symmetry). b) Detail showing the struts supporting the junctions, and the considered cut-sections (δ = 0.01 μm). c) Axial velocity trends on the cut-sections: their uniformity shows that the considered geometry permits to operate the microcapillaries in parallel, as desired. d) Schematic of the porous tube fluid domain. Both the core and the spillage flow rates are indicated (only some spillages, for simplicity), together with relevant geometrical and physical entities. e) Schematic (sagittal cut-section) of the tube indicating, in particular, the axial pressure damping due to viscosity: after a characteristic length, pressure difference is dissipated so that spillage becomes negligible. We estimated such a characteristic length by introducing an analytical model, and we exploited that estimate to also set the length of the porous tube. f) Schematic of the fluid domain (relevant portion, by symmetry) used in the 3D numerical simulations carried out to assess the accuracy of the analytical model. g, h) Illustrative results showing that the analytical solution approximates the numerical one accurately enough for our purposes; both the solutions reported in Equation 5 and Equation 6 are considered, respectively in g) and h), for completeness. Explicitly accounting for relevant physical entities, the analytical solution provides a useful tool to evolve and optimize chip design.

Based on preliminary fabrication tests, we adopted ϕ_t = 9.5 μm and t_h = 1 μm for the tube inner diameter and thickness, respectively. We then addressed the determination of l based on the following arguments. In the absence of pores, one expects the flow to approximately conform to the classical Poiseuille flow (at least far enough from the tube end-sections), expressed by the following equation:^[23]

$$\begin{array}{ccc}Q=-\alpha p^{\prime },& & with\alpha \equiv \frac{\pi {\left(\frac{{\varphi }_t}{2}\right)}^4}{8\mu }\end{array},$$ (1)

where Q and p respectively denote flow rate (along the tube) and pressure, μ indicates fluid viscosity, and prime hereafter denotes differentiation with respect to the axial space coordinate. For the Poiseuille solution the pressure gradient is constant: pressure linearly decreases along the tube axial direction due to viscous effects. Considering the pores, however, a stronger decrease in pressure can be hypothesized, due to the spillage potentially occurring at any pores. Moreover, the higher the (local) pressure is, the higher the spilling flow rate should be (for a given pore geometry). Indeed, for the Stokes flow through a cylindrical orifice with diameter ϕ_p and length t_h, this is confirmed by the following analytical solution:^[24]

$$q=\beta (p-p_{ext}),with\beta \equiv \frac{{\left(\frac{{\varphi }_p}{2}\right)}^3}{\mu (\frac{16t_h}{\pi {\varphi }_p}+3)},$$ (2)

where q and p - p_ext denote spillage flow rate and pressure difference (internal versus external), respectively. The considered fluid-dynamic problem is sketched in Figure 2d and Figure 2e. In the latter subfigure, in particular, Poiseuille-like parabolic velocity profiles are used to depict the spillage potentially occurring when the pore diameter is sensibly smaller than the tube diameter and the pores are enough distant from one another for the corresponding spillages to be “mutually independent” (this approximation seemed to be reasonable in our case). Consistently, after some characteristic length over which the pressure difference is fully dissipated by viscous effects, the spillage is expected to be negligible (here we are tacitly assuming that the outlet boundary conditions are such that the flow can evolve according to the described dynamics; this is not a limiting assumption as clarified below). We decided to estimate the aforementioned characteristic length in order to assign l. Indeed, leveraging the underlying fluid dynamics at the considered design stage seemed to be a valid strategy per se, and it could effectively simplify some experimental steps including negative controls. For instance, with reference to Figure 1b, when the pores are not covered by cells (and by assuming l on the order of the said characteristic length), the inflow should exit almost completely through the pores (i.e., the flow reaching the external discharge should be negligible). Conversely, in correspondence of a perfect cell covering, the liquid volume outside the porous segment should remain unperturbed and the whole inflow should reach the external discharge.

In order to estimate the aforementioned characteristic length, we introduced a mathematical model. We deliberately aimed at obtaining explicit analytical expressions in order to foster model-based chip design. With reference to the schematic in Figures 2d-e, we selected Q and p as problem unknowns, and we assumed p_ext = 0, being the pressure defined up to a constant for the considered incompressible-fluid flow.^[23] Considering any two of the subsequent sections indexed by k in Figures 2e, mass conservation implied Q_k+1/2 - Q_k-1/2 = -n_p q_k (since q was meant to describe the flow rate through a single pore). For ease of model derivation, we assumed the pitch h to be small compared to the sought characteristic length (working assumption), and we consistently considered the unknowns as (well-behave) continuous functions of the axial space coordinate only (we were looking for a stationary solution). Based on this approximation, the aforementioned mass balance could be locally approximated by hQ’ = -n_p q. Moreover, we assumed Equation 1 to describe the momentum balance (formally the same as for Poiseuille), yet the pressure gradient was allowed to vary (different from Poiseuille). Finally, we assumed a given flow rate Q₀ at the tube inlet, in view of the targeted experimental conditions. Representing the axial coordinate by x, with x =0 and x = L respectively denoting the inlet and the outlet section of the porous tube, we thus considered the following problem:

$$\{\begin{array}{c}h{Q}^{\prime }=-n_{p}q\\ Q=-\alpha p^{\prime }\\ q=\beta p\\ Q(x=0)=Q_0\end{array},$$ (3)

with α and β defined in Equation 1 and Equation 2, respectively. Equation 3 can be recast as follows:

$$\{\begin{array}{c}{p}^{″}={\lambda }^{-2}p\\ Q=-\alpha p^{\prime }\\ Q(x=0)=Q_0\end{array},with{\lambda }^2\equiv \frac{\alpha h}{\beta n_p}=\left(\frac{{\varphi }_t^{4}h}{{\varphi }_p^3}\right)\left(\frac{\pi }{16n_p}\right)\left(\frac{16}{\pi }\frac{t_h}{{\varphi }_p}+3\right),$$ (4)

where λ immediately provides an intrinsic physical length scale for the considered trends. Recalling the relevant parameter values introduced so far (i.e., ϕ_p = 1 μm, h = 2.5 μm, n_p = 8, ϕ_t = 9.5 μm and t_h = 1 μm), one gets λ = 63.6 μm.

To close and solve the differential problem stated in Equation 4 we considered two illustrative cases, both associated with outlet boundary conditions of practical interest for the experiments. For the first case we assumed p(x = L) =0; the corresponding solution reads:

$$\{\begin{array}{c}p=\left(\frac{\lambda Q_0}{\alpha }\right)\frac{\text{exp}(\widehat{L}-\widehat{x})-\text{exp}(\widehat{x}-\widehat{L})}{\text{exp}(\widehat{L})+\text{exp}(-\widehat{L})}\\ Q=Q_0\frac{\text{exp}(\widehat{L}-\widehat{x})+\text{exp}(\widehat{x}-\widehat{L})}{\text{exp}(\widehat{L})+\text{exp}(-\widehat{L})}\end{array},\text{with}\widehat{x}\equiv \frac{x}{\lambda }(\text{and}\widehat{L}\equiv \frac{L}{\lambda }).$$ (5)

For the second case we assumed Q(x = L) = ωQ₀, where ω denotes a (chosen) control parameter; the corresponding solution reads:

$$\{\begin{array}{c}p=\left(\frac{\lambda Q_0}{\alpha }\right)\frac{[\text{exp}(\widehat{L}-\widehat{x})+\text{exp}(\widehat{x}-\widehat{L})]-\omega [\text{exp}(\widehat{x})-\text{exp}(-\widehat{x})]}{\text{exp}(\widehat{L})-\text{exp}(-\widehat{L})}\\ Q=Q_0\frac{[\text{exp}(\widehat{L}-\widehat{x})-\text{exp}(\widehat{x}-\widehat{L})]+\omega [\text{exp}(\widehat{x})-\text{exp}(-\widehat{x})]}{\text{exp}(\widehat{L})-\text{exp}(-\widehat{L})}\end{array}.$$ (6)

The explicit solution provided by Equation 5 corresponds to the experimental conditions actually considered in our study, since both the external discharge fluid domain and that one outside the porous tube (cf. Figure 1b) were kept at the atmospheric pressure during our tests. The explicit solution provided by Equation 6 corresponds to complementary experimental conditions that extend those considered in the current study.

We assessed the obtained continuous solution (with respect to the discrete spillage problem) through numerical simulations (Figure 2f-h): details of the numerical simulations are reported as Supporting Information.

Based on the considered results, the analytical solution suitably predicted the relevant pressure and flow rate trends, for both outlet conditions. Therefore, we finalized the chip design by choosing l =400 μm, since this was also consistent with the previously adopted value of H. For completeness, let us remark that we experimentally verified the predicted flow behavior; for instance, we fully confirmed that no detectable flow reached the external discharge domain when performing negative control experiments.

Let us remark that, through the developed model, we identified an intrinsic physical length scale (λ), and we obtained analytical expressions (primarily the λ expression in Equation 4) that can be effectively used to optimize chip design. We know that model accuracy would be enhanced for h ≪ λ, whereas it could be spoiled when ϕ_p is too large compared to ϕ_t (while the sensitivity to the relative magnitude between h and ϕ_p is less straightforward).

Nonetheless, the model could be effectively used to further explore and optimize the design workspace, since the obtained analytical expressions are physically-based and computationally inexpensive. As example, we could investigate additional values for ϕ_p, h and t_h. The chosen value of ϕ_p, for instance, was simultaneously large enough to allow for relevant drug molecules to potentially exit the tube and small enough for the pores to be suitably covered by the considered cells. Smaller pore diameters, leading in particular to finer pore patterns, could be of interest as well. Moreover, the proposed model could be extended so as to also consider different cross-sectional shapes for the pores, even if it could be more challenging to accurately model β (besides α) for non-circular cross-sections. To conclude, we introduced a model-based design approach that can be used to evolve and refine chip design beyond the current study and results.

After fabricating the microfluidic system based on the aforementioned model, we proceeded to cultivate bEnd.3 endothelial cells around the porous microcapillaries in order to develop the in vitro biohybrid BBB and to test its transendothelial electrical resistance (TEER) and its permeability to dextran under dynamic conditions. bEnd.3 cell monolayer represents a convenient and widely exploited BBB model, especially for testing the paracellular route of transport (for more details please refer to Supplementary Information).

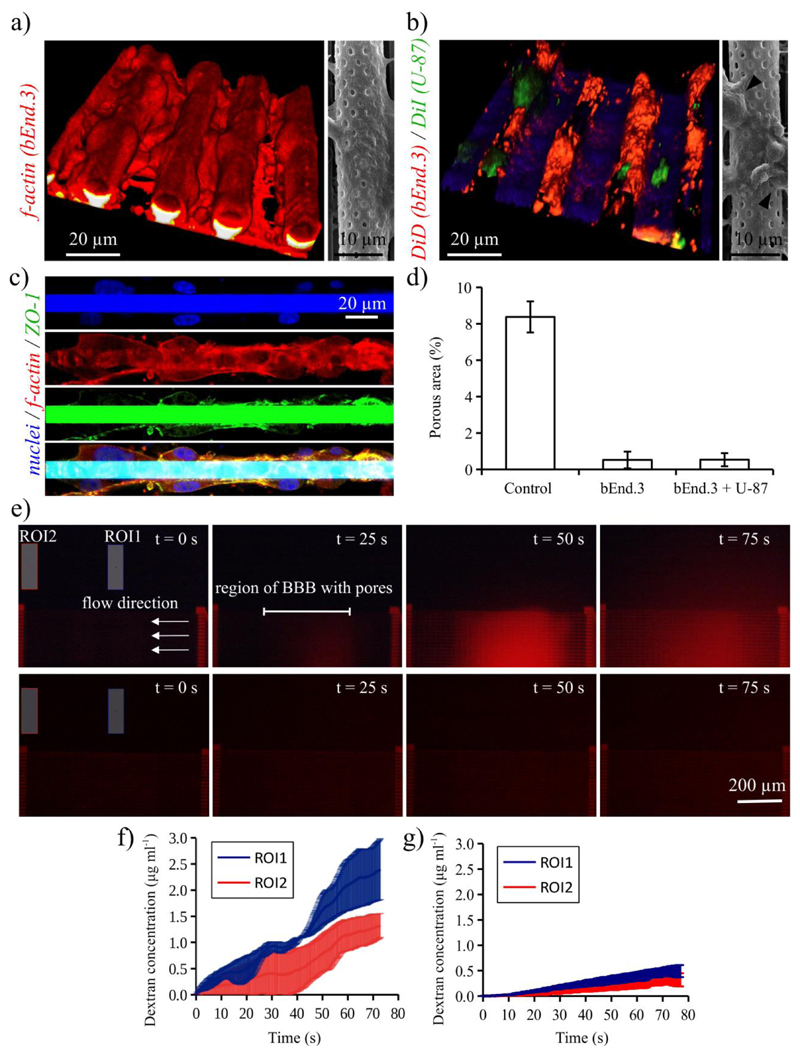
In the left image of Figure 3a, we report the confocal laser scanning microscopy (CLSM) 3D rendering of bEnd.3 cells stained with TRITC-phalloidin (f-actin in red). From the 3D imaging, it is possible to appreciate as the bEnd.3 cells are able to efficiently cover the tubular structures after 3 days of culture. In the right image of Figure 3a, the high magnification SEM imaging of the biohybrid system is reported: this representative scan qualitatively reveals the almost complete covering of the pores by the endothelial cells.

Figure 3.

Dynamic 3D real scale bio-hybrid blood-brain barrier model. a) In the left image, the 3D rendering of confocal laser scanning microscopy (CLSM) showing bEnd.3 cells (f-actin in red) cultured covering the porous tubes of the microfluidic system; the right image shows a high magnification SEM image. b) Co-culture of endothelial-like bEnd.3 and human glioblastoma U-87 cells on the porous tubes of the microfluidic system; in the left image, the CLSM of bEnd.3 and U-87 cell membranes (shown in red and in green, respectively) and, in the right image, SEM image with black arrows indicating U-87 cells. c) Immunofluorescence staining against zonula occludens-1 (ZO-1), revealing a high expression of this marker (ZO-1 in green, f-actin in red and nuclei in blue). d) Quantitative evaluation of the porous area (%) of the microcapillaries without cells and after the culture / co-culture. e) Fluorescence time-lapse images of the fluorescent dextran pumped in the microfluidic system without cells (images on top) and on the bio-hybrid system with bEnd.3 cells (images on bottom) and acquired at time t = 0, 25, 50 and 75 s. The extratubular concentration of the fluorescent dextran was monitored during time-lapse fluorescence imaging in two region of interest (ROI1 and ROI2). The extratubular dextran concentrations over time in ROI1 and ROI2 for the microcapillaries without cells and covered by bEnd.3 cells are reported in f) and g), respectively.

The proposed biohybrid system is envisaged to perform, in future experiments, high-throughput investigations on the BBB crossing efficiency of different anti-tumoral drugs (either plain or associated to nanocarriers). For this reason, we verified the possibility to obtain co-culture of human glioblastoma cancer cells on the scaffolds. CLSM of the co-culture, where plasma membranes of bEnd.3 and of U-87 cells are respectively stained in red and in green and corresponding SEM scan are reported in Figure 3b. U-87 cells resulted able to grow on the biohybrid BBB model and can be morphologically identified because of their round shape (black arrows in the SEM image).

The efficient maturation of the tight junctions was verified with an immunofluorescence staining against zonula occludens-1 (ZO-1), which reveals a high expression of this marker (ZO-1 in green, f-actin in red and nuclei in blue, Figure 3c). The 3D localization of the nuclei is reported in Supporting Information (Video S1) and reveals as bEnd.3 cells are positioned all around the microcapillaries.

The quantitative evaluation of the porous area (%) of the microcapillaries without cells and after the cell culture or co-culture was performed by analyzing low magnification SEM images (Supplementary Information, Figure S5), and the obtained results are reported in Figure 3d. The percentage of porous area projection in the microcapillaries without cells corresponds to 8.3 ± 0.9 %, and it is significantly higher with respect to that found after bEnd.3 (0.52 ± 0.5 %) or bEnd.3/U-87 co-culture (0.54 ± 0.4 %).

The investigation of dextran diffusion through microcapillaries was carried out both on the microfluidic chip without cells and on the biohybrid system with bEnd.3 cells by pumping from the inlet a 40 μg ml^-1 of fluorescent dextran in phenol red-free cell culture medium at 50 μl h^-1. Considering that the microfluidic chip is constituted by 50 microcapillaries arranged in parallel, the flow in each microcapillary is 1 μl h^-1 (corresponding to an average speed of 3.5 mm s^-1 for a tube diameter of 10 μm), a value comparable to that one of cerebral microcapillaries.^[20,21] The concentration of the fluorescent dextran was monitored during time lapse fluorescence imaging in two regions of interest (ROI) of the extratubular area (ROI1 and ROI2, respectively located near and far from the porous segment and indicated with blue and red colors in Figures 3e-g). Different time points of the fluorescence time lapse imaging (recorded at time t = 0, 25, 50 and 75 s) are shown in Figure 3e for the microfluidic system without (upper images) and with the cultured cells (lower images). The dextran concentrations over the time in ROI1 and ROI2 are derived from the average fluorescence intensity through a calibration curve (Figure S6a) and are reported in Figure 3f for the microcapillaries without cells and in Figure 3g for the microcapillaries covered by bEnd.3 cells.

The concentration of the dextran in the extratubular medium (0.49 ± 0.11 μg ml^-1 for ROI1 and 0.32 ± 0.12 μg ml^-1 for ROI2; t = 75 s) in case of cultured cells is remarkably lower with respect to the case of plain porous microcapillaries (2.41 ± 0.58 μg ml^-1 for ROI1 and 1.33 ± 0.23 μg ml^-1 for ROI2; t = 75 s), thus confirming as bEnd.3 cells successfully developed a 3D biological barrier around the microcapillaries. The average fluorescence intensity of ROI1 is higher with respect to that of ROI2 in both the experimental conditions, thus indicating that the fluorescent dextran is permeating from the porous segment and then diffusing in the surrounding areas.

Spectrofluorimetric analyses of the dextran concentration after 4 minutes of experiment in the extratubular medium (1.27 ± 0.03 μg ml^-1 for microcapillaries without cells and 0.28 ± 0.05 μg ml^-1 for the biohybrid system) and in the outflow reservoir (0.02 ± 0.01 μg ml^-1 for microcapillaries without cells, and 0.77 ± 0.01 μg ml^-1 for the biohybrid system) further showed the functional efficacy of the biological barrier. Indeed, in the case of the experiment without cells, the dextran was found only in the extratubular compartment, while, in the case of the biohybrid system, almost all of the dextran was transported through the microcapillaries to the outflow reservoir. This result experimentally corroborates the predictivity of our analytical model. The dextran concentration in the latter analyses has been derived from the calibration curve reported in Figure S6b.

The bEnd.3 cell covering the microtubular vessels not only induced a remarkably decrease of dextran permeability, yet also the TEER significantly increased (75 ± 2 Ω cm²) with respect to the microfluidic system without cells (15 ± 5 Ω cm²). These values are comparable with those observed on bEnd.3 monolayer-based 2D BBB models, which typically are in the range of 30-140 Ω cm².^[25–27] Models characterized by similar values of TEER, despite still significantly lower than those in vivo,^[28] are successfully adopted for the investigation of drug / nanoparticle transport across the BBB.^[25,27] Notwithstanding, future experiments can be devoted to increase the TEER and to decrease the dextran permeability, for example by co-culturing endothelial-like cells with astrocytes,^[29] treating bEnd.3 cells with astrocyte conditioned-medium^[30] or with specific molecules (e.g., hydrocortisone^[31]), and applying shear stress^[32,33].

The TEER of the bEnd.3 monolayer remains stable after 5 days of culture (71 ± 10 Ω cm²), thus indicating preserved cell viability and functionality of the BBB model. This is qualitatively confirmed by confocal imaging: a representative acquisition is reported in Supplementary Information (Figure S7), and shows as the bEnd.3 cells are still viable and completely interfaced to the microcapillaries after 5 days of culture.

The proposed biomimetic dynamic 3D system, characterized by microcapillary diameter size and fluid flows similar to the in vivo physiological situations, represents a potential improvement of other models already well-established in the literature, since it will allow to reliably reproduce the physiological environment and to accurately estimate the amount of drugs / nanomaterial-associated compounds delivered through a modular length of the system. Moreover, the cell behavior drastically change from 2D to 3D in vitro models, the latter ones allowing more physiologically relevant information and predictive data to be obtained.^[34] Our work can be considered a further step in this direction, by providing a new reliable platform where the role of different molecules on the development of the 3D functional barrier can be investigated.

Concluding, we modeled, fabricated and characterized for the first time a prototype of 3D 1:1 scale biohybrid BBB. The high resolution and reproducibility of the TPL technique will allow to finely tune different parameters (e.g., pore and microcapillary diameter, pore density, porous segment length, etc.) in order to refine our system and adapt it to model blood vessels of different sizes and morphologies. Future studies will be dedicated to investigate the permeability of different compounds / anticancer agents, even in their free form or associated with nanomaterials, through the BBB model, and possibly ad hoc modified or functionalized, respectively, in order to efficiently reach the barrier. Moreover, owing to the reverse engineering approach, the architecture of brain microvasculature in physiologic healthy and non-healthy conditions (for example, in case of brain tumors) can be reconstructed through 3D CLSM and then reproduced through TPL. These future investigations will allow to faithfully mimic in vitro the 3D neurovasculature of different pathological conditions, and to perform high-throughput studies in which a variety of drug treatments / therapeutic approaches may be tested.

Supplementary Material

Supporting Information is available from the Wiley Online Library or from the author.