Propensity score methods to control for confounding in observational cohort studies: a statistical primer and application to endoscopy research

Abstract

Background and Aims

Confounding is a major concern in nonexperimental studies of endoscopic interventions and can lead to biased estimates of the effects of treatment. Propensity score methods, which are commonly used in the pharmacoepidemiology literature, can effectively control for baseline confounding by balancing measured baseline confounders and risk factors and creating comparable populations of treated and untreated patients.

Methods

We propose the following 5-step checklist to guide the use and evaluation of propensity score methods: (1) select covariates; (2) assess covariate balance in risk factors before propensity score implementation; (3) estimate and implement the propensity score in the study cohort; (4) re-assess covariate balance in risk factors after propensity score implementation; and (5) critically evaluate differences between matched and unmatched patients after propensity score implementation. We then apply this checklist to an endoscopy example using a study cohort of 411 adults with newly diagnosed eosinophilic esophagitis (EoE), some of whom were treated with esophageal dilation.

Results

We identified 156 patients, aged 18 and older, who were treated with esophageal dilation, and 255 patients who were nondilated. We successfully matched 148 (95%) dilated patients to nondilated patients who had a propensity score within 0.1, based on patient age, sex, race, self-reported food allergy, and presence of narrowing at baseline endoscopy. Crude imbalances were observed before propensity score matching in several baseline covariates, including age, sex, and narrowing; however, propensity score matching was successful in achieving balance across all measured covariates.

Conclusions

We provide an introduction to propensity score methods, including a straightforward checklist for implementing propensity score methods in nonexperimental studies of treatment effectiveness. Moreover, we demonstrate the advantage of using the typical patient characteristics table as a simple but effective diagnostic tool for evaluating the success of propensity score methods in an applied example of esophageal dilation in EoE.

INTRODUCTION

Confounding can occur when there are imbalances in baseline covariates that affect the outcome of interest, and constitutes a major threat to the validity of treatment effect estimates in nonexperimental studies.¹ Insufficient control for such imbalances leads to biased estimates of the treatment effects (ie, the association between a clinical treatment or intervention and an outcome of interest).² Randomized clinical trials inherently balance baseline covariates, thereby avoiding systematic confounding (Figure 1). In observational cohort studies, however, confounding becomes a major concern. Due to the lack of randomization, patients with specific risk factors for an outcome of interest can be systematically channeled either toward or away from a specific treatment modality.^3,4

FIGURE 1. Visualization of Basic Confounding Triangle and Role of Randomization and Propensity Score Methods to Control for Confounding.

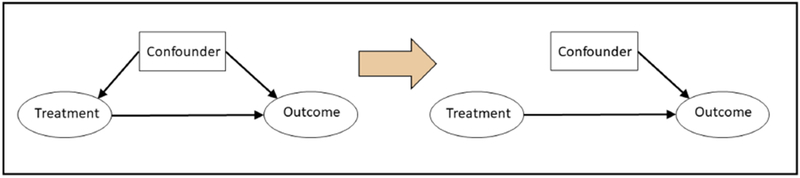
The figure on the left illustrates the relationship between a treatment, confounder, and outcome, where a confounder is any baseline characteristic that affects both the treatment and the outcome of interest (left). If the confounder is not balanced at baseline between treatment groups, the resulting estimate of the treatment effect will be biased.

Randomization and propensity score methods both aim to control for confounding by removing the relationship between confounders and treatment assignment (right). This eliminates imbalances in measured baseline characteristics between treatment groups, leading to an unbiased estimate.

Propensity score methods, widely used to control for confounding in observational studies with dichotomous treatment modalities, mimic the intended effects of randomization by balancing measured baseline covariates across treatment groups (Figure 1).⁵ Formally defined as a patient’s predicted probability, or propensity, of receiving the treatment under study, given his or her measured baseline characteristics and comorbidities,⁶ the propensity score combines many patient characteristics into a single, easy-to-apply summary score that can be used for confounding control. All propensity score methods aim to generate comparable study populations of treated and untreated patients, where risk factors for the outcome of interest are balanced at baseline and differences in outcome risk can be attributed to the effect of treatment alone.^7–9

The following primer offers a 5-step checklist for implementing and diagnosing the success and shortcomings of propensity score methods in observational cohort studies, using a real-world data example on esophageal dilation for treatment of eosinophilic esophagitis (EoE). We describe how to use the typical patient characteristics table to assess balance of patient characteristics across treatment groups before and after propensity score implementation, as an effective tool to diagnose the success of propensity score implementation and identify the presence of residual confounding. Finally, we describe common pitfalls encountered in the implementation and evaluation of propensity score methods. This checklist serves as a practical tool for investigators, reviewers, and readers who are seeking to gain a deeper understanding of propensity score methods encountered in the endoscopy literature or use propensity score methods in their own nonexperimental research.

METHODS

The proposed checklist (Figure 2) is comprised of the following steps: (1) select covariates; (2) assess covariate balance in risk factors before propensity score implementation; (3) estimate and implement the propensity score in the study cohort; (4) re-assess covariate balance in risk factors after propensity score implementation; and (5) critically evaluate differences between matched and unmatched patients after propensity score implementation.

FIGURE 2. Checklist for Implementing and Diagnosing Propensity Score (PS) Methods.

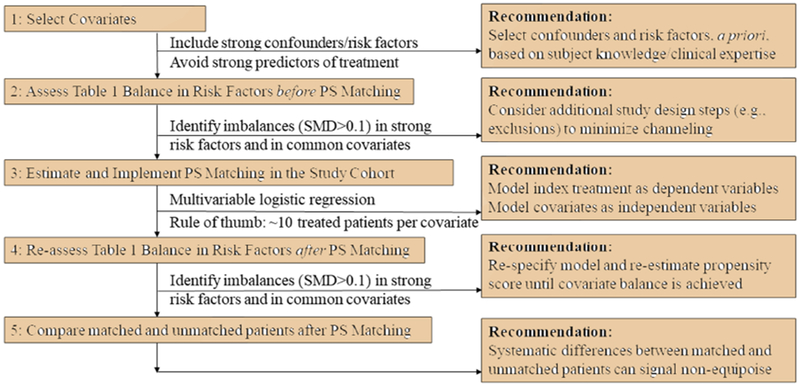
Note: the standardized mean difference (SMD) is calculated as the difference between two means or proportions, divided by the pooled standard deviation. The SMD is advantageous over the p-value in that it quantifies the degree of imbalance and is not sensitive to sample size.

We applied this propensity score checklist to a cohort study of 781 EoE cases collected through the University of North Carolina EoE Clinicopathological Database, who either did or did not undergo treatment with esophageal dilation. The database has been described in detail elsewhere.^10–12. Briefly, the database contains patients of all ages with newly diagnosed EoE. Patients were required to meet consensus diagnostic guidelines for EoE (≥15 eosinophils in at least 1 high-power field (eos/hpf), plus at least 1 typical symptom of esophageal dysfunction, namely dysphagia, food impaction, heartburn, or feeding intolerance), and did not respond to proton-pump inhibitor treatment.^13,14

Step 1: Select Covariates

The propensity score is a single score that summarizes an individual patient’s predicted probability of receiving the study treatment, based on his or her unique combination of measured baseline covariates. As such, the propensity score varies based on the specific combination of covariates that are selected, and the choice of the covariate set can have a meaningful downstream impact on the bias and precision of the estimated treatment effect.¹⁵ The propensity score literature has come to consensus on 2 guiding principles for the covariate selection process: (1) all covariates believed to affect the risk for the outcome should be included in the propensity score model; and (2) covariates that are related to the treatment only but are not risk factors for the outcome should not be included in the propensity score model.^15–17 Including covariates that affect the risk for the outcome, which include both confounders and independent risk factors for the outcome, removes bias. Inclusion of strong predictors of treatment reduces the precision (ie, results in larger standard errors) of the treatment effect estimate and should therefore be avoided if these predictors of treatment do not also affect the risk for the outcome (ie, are not confounders). Finally, inclusion of covariates with weak prognostic potential for the outcome is still recommended,^18,19 but application of this approach may be limited depending on the number of treated patients available for study.^19,20 If using logistic regression to estimate the propensity score, a general rule of thumb is to allow roughly 6 to 10 treated patients per covariate included.^20–23

Ideally, the relationships among treatment, covariates, and outcome should be determined a priori based on subject matter knowledge and clinical experience,^15,24 although empirical evidence may be used to augment pre-existing knowledge.^25,26 Purely data-driven techniques, such as stepwise regression and use of c-statistics or AUC (area under the curve), are generally discouraged as the sole basis for variable selection.^24,27 One empirical approach developed in pharmacoepidemiology is the use of high-dimensional propensity score methods in administrative healthcare databases, which uses semiautomated methods to identify the optimal set of adjustment covariates from a large pool of candidate risk factors.^28,29 However, we again emphasize the value of subject matter knowledge to critically appraise the output of such high dimensional methods to avoid including covariates that are only related to the treatment but not to the outcome. This can result in bias amplification, especially in situations when outcomes are uncommon.^30,31

Investigators should also decide, a priori, whether to model covariates in categorical or continuous form. If using categories for continuous covariates, we recommend using clinically meaningful thresholds (eg, BMI <18.5, 18.5-<25, 25-<30, 30+) over percentile-based approaches (eg, quartiles). For continuous variables, if the relationship between covariate and treatment is believed to be non-linear, we recommend supplementing first-order terms (eg, age) by adding quadratic or even cubic terms (eg, age² + age³) to allow more flexible fitting of the data. Interaction terms and log transformations should also be considered to improve model fit.

Step 2: Assess Covariate Balance in Risk Factors before Propensity Score Implementation

It is important to carefully identify and examine imbalances in covariates in the population before implementing the propensity score. The typical patient characteristics table is a useful tool for identifying these imbalances. We commonly quantify imbalances using the standardized mean difference (SMD),³² which measures the degree of difference between 2 means or proportions. The SMD is calculated as the difference between two means or proportions, divided by the pooled standard deviation. Although other options are available,³³ the SMD is advantageous over the P value in that it estimates the magnitude of the difference and is not sensitive to sample size. We typically calculate a separate SMD for each individual covariate, which enables us to assess the potential for confounding by each covariate based on the difference in that covariate between treatment groups, as well as the strength of the relationship between that covariate and the outcome.

Large imbalances (eg, SMD>0.1)³⁴ in strong risk factors for the outcome, or if multiple risk factors are more common among treated patients, can signal the presence of systematic channeling of patients into one treatment group or another based on those risk factors. This can introduce a strong source of bias that may be difficult to address through propensity score methods alone. In such cases, investigators may want to consider excluding patients with risk factors that may channel patients toward, or away from, treatment, in order to minimize bias in the analysis population. In the EoE example, because patients under age 18 are typically contraindicated for esophageal dilation and are therefore nondilated, it may be prudent to exclude those patients and focus the analysis in an adult population.

Step 3: Estimate and Implement Propensity Score in the Study Cohort

Once appropriate covariates are selected for the propensity score model, a number of options are available to estimate the score itself. The most common approach is multivariable logistic regression, with the treatment as the dependent variable and the covariate set as independent variables.^9,35,36 Other methods, including classification and regression tree and neural networks, are available but less commonly used.^36–38 The coefficients from this regression are then used to estimate the propensity score for each patient based on his or her specific combination of covariates. The resulting propensity score estimates, therefore, reflect each patient’s unique covariate pattern. Treated and untreated patients with the same estimated propensity score will tend to have the same covariate pattern.

The estimated propensity score can then be applied to address confounding in a number of ways. Here, we focus on application via individual (1:1) matching using the estimated propensity score, one of the most common implementation approaches, which aims to generate a group of untreated patients who are directly comparable to those who are treated.^36,39 By matching untreated patients to treated patients with the same or similar range (often referred to as a “caliper”) of propensity scores, we create 2 comparable groups of patients who are equally likely to have received either treatment modality based on their measured covariates. This cohort construction strategy allows us to address the study question: “What outcomes would we have observed had all treated patients in the study instead not received the treatment?”^40–43 In the case that more than 2 treatment modalities are under investigation, we recommend performing separate propensity score estimation and matching in reference to a single index group whose treatment contrast is of interest. When comparing multiple treatment groups, authors and readers should be aware of the specific treatment contrasts presented because these can have a meaningful influence on the types of clinical conclusions that can be inferred.⁴⁴ The same principle applies to analyses in subgroups of patients; when performing subgroup analyses, we recommend performing separate propensity score estimation and matching within each patient subgroup.

Step 4: Assess Covariate Balance in Risk Factors after Propensity Score Implementation

We can use similar strategies as introduced in Step 2 for using the typical patient characteristics table to assess balance in covariates after propensity score matching. In particular, strong risk factors that remain imbalanced (SMD>0.1) between treatment groups after propensity score matching are a particular source of concern because of residual confounding. Therefore, subject matter expertise is needed to interpret any remaining imbalances in covariates after propensity score matching.

We highlight here the iterative nature of the propensity score modeling process; in situations with remaining covariate imbalances, the propensity score needs to be re-specified and re-estimated until strong risk factors are fully balanced to ensure adequate control of measured covariates. This refinement of the propensity score must be conducted before analyzing outcomes to avoid potential concerns about “fishing” for statistically significant results. However, relatively unbiased treatment effect estimates can still be obtained if minor imbalances remain only in covariates that are not believed to be strong risk factors for the outcome. Authors, reviewers, and readers should rely on a combination of subject matter knowledge and empirical evidence to determine whether or not post-propensity score matching imbalances in measured covariates are likely to introduce substantial bias in the estimated treatment effect, and take steps to refine the propensity score model as needed. This “transparency” with respect to the performance of statistical confounding control is one of the major advantages of the propensity score.⁷

Step 5: Critically Evaluate Differences between Matched and Unmatched Patients after Propensity Score Matching

In conducting propensity score matching, there often exists a group of treated patients that have no observed counterpart among the untreated population, due to extremely high propensity score values (commonly termed the nonoverlapping “tails” of the propensity score distribution). These individuals (Figure 3, Panel 3) often represent patients with an absolute indication for treatment, ie, who are not eligible for “no treatment,” such as adults with EoE who have long durations of symptoms before diagnosis and/or present with severe strictures. It is obvious that we will not be able to estimate a treatment effect in these patients and they will be dropped from a propensity score matched analysis. Specific problems can arise, particularly in the following situations: (1) loss of a large proportion of the treated population (eg, >10%) after matching; (2) substantial changes in covariate distribution of the treated group after matching; and (3) treatment effects are expected to vary by those measured characteristics. When specific groups of patients are systematically dropped from analysis during matching, we lose the ability to estimate a treatment effect in those patient subgroups. Authors and readers need to pay careful attention to how the population changes before and after propensity score matching to avoid overgeneralization of treatment effect results.

FIGURE 3. Distributions of estimated propensity scores (PS) for patients treated with balloon dilation versus nondilation.

This figure presents the distribution of estimated propensity scores among a study cohort of 411 adults with newly diagnosed eosinophilic esophagitis, 156 of whom received esophageal dilation (blue line) and 255 of whom did not (red line). The propensity score represents each patient’s predicted probability, or propensity, of being dilated, given his or her measured baseline characteristics and comorbidities.

RESULTS

We illustrate the use of the propensity score checklist in the study population described above, of EoE patients who did and did not undergo esophageal dilation. For this exercise, we focus on covariate balance and therefore do not include a specific outcome of interest. We assume, however, that the covariates presented are risk factors for an outcome of interest (eg, EoE symptom reduction). We initially identified 177 patients who were treated with dilation, and 597 patients who were not dilated. Seven patients were missing dilation data and were excluded from subsequent analyses.

Step 1: Select Covariates

We analyzed the following available covariates: age, sex, race, food allergy, and presence of narrowing. Presence of stricture was considered as a candidate covariate, but was removed from the propensity score model because the presence of esophageal stricture is a strong indication for dilation. In practice, we recommend excluding patients with strong indications (or contraindications) for treatment in whom there is no real choice or equipoise among treatments compared. For example, in the present analysis, over 75% of treated patients reported presence of stricture at baseline compared with only 6% in untreated patients. However, because the primary aim of the present analysis was to demonstrate the ability of propensity score methods to balance dilated and nondilated cohorts on a set of measured covariates, we decided to leave those patients in the analysis for practical purposes, to ensure sufficient study sample to demonstrate the propensity score process. Table 1 presents the characteristics of these patients, both before and after propensity score matching. We chose to model all covariates in categorical form, with age (0-9, 10-17, 18-29, 30-39, 40+) (modeled as dummy variables, using patients aged 18-29 as the reference group), and sex (female, male), race (white, non-white), food allergy (yes/no), and narrowing (yes/no) modeled as binary variables.

TABLE 1.

Characteristics of Eosinophilic Esophagitis Patients with and without Esophageal Dilation, Before and After Propensity Score (PS) Matching

Characteristic	PANEL 1: BEFORE PS Matching					PANEL 2: BEFORE PS Matching1 AGE ≥ 18					PANEL 3: AFTER PS Matching2,3 AGE ≥ 18
	Dilation (n=177)		No Dilation (n=597)		SMD6	Dilation (n=156)		No Dilation (n=255)		SMD	Dilation (n=148)		No Dilation (n=148)		SMD
Age, mean (SD)	38.5 (14.9)		23.0 (18.0)			40.6 (14.2)		39.4 (13.4)			40.8 (14.4)		40.0 (13.3)
Age Category
0-9	0	0%	168	28%	0.88	---	---	---	---	---	---	---	---	---	---
10-17	10	6%	155	26%	0.58	---	---	---	---	---	---	---	---	---	---
18-29	50	28%	75	13%	0.40	44	28%	69	27%	0.03	42	28%	40	27%	0.03
30-39	38	21%	76	13%	0.23	36	23%	71	28%	0.11	33	22%	39	26%	0.09
40 +	79	45%	123	21%	0.53	76	49%	115	45%	0.07	73	49%	69	47%	0.05
Sex
Female	61	34%	193	32%	0.05	54	35%	109	43%	0.17	52	35%	57	39%	0.07
Male	116	66%	404	68%	0.05	102	65%	146	57%	0.17	96	65%	91	61%	0.07
Race
White	147	83%	470	79%	0.11	140	90%	235	92%	0.08	138	93%	140	95%	0.06
Non-White4	12	7%	54	9%	0.08	16	10%	20	8%	0.08	10	7%	8	5%	0.06
Missing/Unknown	17	10%	68	11%	0.06	---	---	---	---	---	---	---	---	---	---
Covariates
Food Allergy	39	22%	166	28%	0.13	33	21%	51	20%	0.03	29	20%	29	20%	0.00
Narrowing5	74	42%	48	8%	0.85	65	42%	38	15%	0.62	60	41%	59	40%	0.01

^1.Excluding patients with missing/unknown race

^2.Propensity score estimated using age at biopsy (18-29 (reference), 30-39, 40+), sex (female, male), race (white, non-white), self-reported food allergy (yes/no), and presence of narrowing (yes/no)

^3.1:1 matching on estimated propensity score, with replacement, using caliper of 0.1

^4.Black, Hispanic, Asian, Native American, other

^5.In the University of North Carolina EoE Clinicopathological Database database, “narrowing” referred to findings where a longer segment of esophagus had a smaller caliber than normal. This was distinct from esophageal “stricture,” which was defined as a focal constriction of the esophageal lumen. Patients could have narrowing without a focal stricture, a focal stricture without narrowing, or both present at the same time. As these findings were felt to be distinct, both were recorded separately.

^6.The standardized mean difference (SMD) was calculated as the difference between two means or proportions, divided by the pooled standard deviation.

Overall, patients were aged 0 to 82, with mean (SD) age of 26.5 (18.5) years, and were predominantly male (67%) and white (80%). Approximately 29% of EoE patients reported a history of food allergy, and narrowing was found in 16% of patients. Forty-four patients (12 dilated, 32 nondilated) were missing data on race and were subsequently excluded from analysis.

Step 2: Assess Covariate Balance in Risk Factors before Propensity Score Implementation

Before propensity score matching, we observed notable differences in measured covariates between patients who were and were not dilated (Table 1, Panel 1). A lower proportion of dilated patients reported having a food allergy (22% vs 28%), whereas much higher proportions of dilated patients had observed narrowing (42% vs 8%). Additionally, dilated patients were much older compared with nondilated patients (mean age, 38.5 vs 23.0, respectively). Only 6% of dilated patients were under the age of 18, compared with 54% of nondilated patients. This stark difference signaled the potential for treatment channeling and nonequipoise due to age because younger children with EoE rarely required dilation. To address this source of channeling, we restricted the study cohort to patients aged 18 and older (Table 1, Panel 2), which improved crude covariate balance between treatment groups. Remaining imbalances were deemed manageable using propensity score methods. After restriction, 156 dilated patients and 255 nondilated patients remained in the study cohort (Table 1, Panel 2).

Step 3: Estimate and Implement Propensity Score in the Study Cohort

We estimated the propensity score for each patient using multivariable logistic regression. As previously described, the model was designed with dilation status (yes/no) as the dependent variable, and with age (18-29, 30-39, 40+), sex (female, male), race (white, nonwhite), food allergy (yes/no), and narrowing (yes/no) as independent variables. Figure 3 presents the distributions of estimated propensity scores in both the dilated and non-dilated groups. Individual matching (1:1, with replacement) was then performed using the estimated propensity score and a caliper of 0.1. We were unable to find nondilated matches for 8 dilated patients, resulting in 148 matched pairs (Table 1, Panel 3).

We performed a sensitivity analysis sampling propensity-matched controls (nondilated patients) without replacement, which resulted in matches for 123 (79%) dilated patients. However, characteristics of matched dilated patients were largely similar to those observed in the main analysis (sampling with replacement).

Step 4: Assess Covariate Balance in Risk Factors after Propensity Score Implementation

Characteristics between dilated patients and their matched, nondilated controls, were well-balanced after propensity score matching (Table 1, Panel 3), with all covariate SMDs <0.1. Propensity score matching was particularly effective in balancing proportions of patients with food allergy and narrowing (SMD«0).

Step 5: Critically Evaluate Differences between Matched and Unmatched Patients after Propensity Score Matching

As previously noted, nondilated matches could be identified for 148 (95%) out of 156 dilated patients. Compared with matched dilated patients (Table 2), the 8 dilated patients who were unmatched were slightly younger (mean age, unmatched vs matched, 37.0 vs 40.8), with higher proportions of male (75% vs 65%) and nonwhite (75% vs 7%) patients, and higher proportions of patients with food allergy (50% vs 20%) and narrowing (63% vs 41%).

TABLE 2.

Comparison of matched versus unmatched patients treated with esophageal dilation

Characteristic	Matched (n=148)		Unmatched (n=8)		SMD
Age, mean (SD)	40.8 (14.4)		37.0 (9.6)
Age Category
18-29	42	28%	2	25%	0.08
30-39	33	22%	3	38%	0.34
40 +	73	49%	3	38%	0.24
Sex
Female	52	35%	2	25%	0.22
Male	96	65%	6	75%	0.22
Race
White	138	93%	2	25%	1.93
Non-White	10	7%	6	75%	1.93
Covariates
Food Allergy	29	20%	4	50%	0.67
Narrowing	60	41%	5	63%	0.45

DISCUSSION

We introduce a 5-step checklist for implementing and interpreting propensity score methods in observational cohort studies and illustrate the use of this checklist using an endoscopy example. We provide advice on how to (1) select covariates; (2) diagnose crude covariate balance using Table 1; (3) estimate and implement propensity score matching; (4) re-assess matched covariate balance using Table 1; and (5) critically evaluate differences between matched and unmatched patients after propensity score matching. In particular, we demonstrate that propensity score matching was effective in removing baseline imbalances in measured covariates, thereby controlling for measured confounding between patients treated with esophageal dilation and those who were not.

Propensity score methods have been used widely in comparative effectiveness research and pharmacoepidemiology^{7,19,36,45–49} and can be viewed in part as an extension of more “traditional” methods used to control for confounding, such as matching and stratification. By summarizing a large set of patient characteristics into a single score, the propensity score offers a more efficient and effective method for performing matching and stratification. Propensity score methods can additionally be combined with these “traditional” methods to further improve confounding control. For example, in the presence of overwhelming risk factors (eg, age, sex), investigators may consider first matching directly on those risk factors, then applying propensity score methods to further resolve or improve remaining imbalances in measured covariates between treatment cohorts.⁵⁰

The “Table 1” diagnostic has been demonstrated to be a transparent and effective means to judge the success of propensity score implementation.⁷ Additional diagnostic and sensitivity analyses are available; for example, we can assess propensity score distributions among treated and untreated populations,⁵¹ and “trim” (remove) patients in the left and right tails of the propensity score distribution to reduce the potential for confounding at the extremes of the propensity score distribution.⁸ We can also vary the size of the propensity score matching caliper, which has been extensively explored and can influence the success of the propensity score matching process.^32,52–54 Finally, as we demonstrate, it is important to compare treated patients who are matched with those who are not matched to assess whether specific groups of treated patients are systematically dropped from analysis during matching. Matching with replacement, which we used in our analysis, can help to alleviate this issue by allowing each untreated patient to be matched to multiple treated patients. This approach tends to minimize the potential to drop treated patients due to lack of available matches and yields increased overall sample size compared with matching without replacement. We can then account for any “over-representation” of untreated patients who are matched twice or more in the analysis by using a “robust” standard error estimator, which is available in most statistical analysis packages.

Alternative methods have been developed and applied to broaden the use of propensity score methods in different research settings. In addition to individual matching using the propensity score, investigators have the option to stratify the analysis by the propensity score. This technique enables the estimation of treatment effects within subgroups of patients with specific “propensity” for treatment.^6,55 In our EoE example, this could have allowed us to assess the effect of dilation separately among patients who were more likely, or less likely, to have been indicated for dilation. The propensity score can also be used directly as an adjustment variable in subsequent outcome models,⁵⁶ although this approach is generally discouraged because it does not lend itself to a causal interpretation for a specific target population and requires 2 correctly specified models instead of only 1. Finally, a common propensity score method is based on re-weighting cohorts using the estimated propensity score (ie, “inverse probability weighting”). These weighting methods have their roots in sampling weights and are described in greater detail elsewhere.^36,57–61 In short, weighting aims to create 2 hypothetical “pseudo-populations” that are identical and mirror a target population of patients, and then simulates what would happen if one pseudopopulation was treated and the other was not. Weighting methods are especially useful when the treatment effect varies across measured covariates, in which case they allow us to estimate treatment effects in specific defined study populations. Weighting also tends to exclude fewer treated patients from the analysis; whereas matching automatically excludes patients in regions of nonoverlapping propensity scores, weighting retains these patients in the study population and simply down-weights them in the final analysis. Note that the same “Table 1” diagnostics used in our matched example can be used to evaluate covariate balance in weighted populations.

There are a number of strengths attributed to propensity score methods. First, successful propensity score implementation balances measured covariates between a group of treated and untreated patients; although this mimics the intended effects of randomization, it only removes the effects of measured confounders whereas randomization can be expected to remove all confounding. Second, the propensity score is a summary score that can capture an immense amount of information and is straightforward to estimate and implement, allowing for the control of a large number of confounding factors while minimizing standard errors. These precision benefits are particularly notable in studies in which the outcome is rare, but a reasonable number of treated and untreated patients are available.^20,62 Third, by creating exchangeable populations of patients with balanced risk factors for the outcome, propensity score methods allow for the estimation of causal contrasts in analytic populations of treated and untreated patients. As we have demonstrated, this exchangeability can be easily diagnosed using “Table 1” by comparing the balance of measured covariates between treated and untreated patients both before and after propensity score matching.

We also share some limitations of propensity score methods. First, because the propensity score is a summary of measured covariates, it cannot eliminate unmeasured confounding, a major drawback of observational studies. As a result, we highlight the importance of prespecifying important risk factors for the outcome and striving to ensure accurate and complete measurement of those factors. Furthermore, we highlight the importance of study design to minimize the potential for strong covariate imbalances by excluding patients with strong indications (eg, stricture) and contraindications (eg, age <18) for a single treatment modality. Pharmacoepidemiology studies often restrict study populations to patients with similar indications for treatment by comparing 2 treatments with the same indication (“active comparators”),⁶³ rather than comparing treatment against no treatment. If investigators can identify a study population in which measured risk factors do not predict treatment choice (ie, no crude imbalances in measured risk factors before propensity score implementation), it is often more plausible to assume that we have also minimized the potential for confounding by unmeasured risk factors. Second, like randomization, propensity score methods account for confounding by baseline characteristics only, but do not control for time-varying confounding that occurs after start of follow-up. Third, the success of propensity score methods to control for confounding can be sensitive to misspecification and misinterpretation of the propensity score model, as well as to the presence of missing data in measured covariates. Multiple imputation methods^64–66 have been developed and demonstrated to be effective in addressing the latter issue, and the former can be improved through careful prespecification and iterative refinement of the propensity score model. Finally, we acknowledge that the accuracy of propensity score estimation and implementation can be limited in the setting of rare treatments, where a large proportion of untreated patients are often disregarded and data on patterns related to treatment modality can be sparse and imprecise. However, other methods including disease risk scores⁶⁷ and fine propensity score stratification approaches⁵⁵ are available for confounding control in these settings.

CONCLUSION

Propensity score methods are an effective means to control for baseline confounding by balancing important risk factors among treatment groups at the start of follow-up. Estimating the propensity score for a study sample is straightforward using multivariable logistic regression. Covariate balance and success of propensity score methods can be easily diagnosed and refined using the common “Table 1” of patient characteristics that is ubiquitous in scientific literature. Propensity score-matched populations can be used to obtain unbiased estimates of the effect of a treatment on the study population.

Acronyms and Abbreviations

EoE

eosinophilic esophagitis

AUC

area under the curve

BMI

body mass index

SMD

standardized mean difference