Solubility of β-Ca₃(PO₄)₂ in the System Ca(OH)₂-H₃PO₄-H₂O at 5, 15, 25, and 37 °C

Abstract

Solubility isotherms of beta-tricalcium phosphate, β-Ca(PO₄)₂, prepared by heating mixtures of CaCO₃ and CaHPO₄ above 800 °C, were determined in the ternary system Ca(OH)₂-H₃PO₄-H₂O at 5, 15, 25, and 37 °C in the pH range 6.0–7.5 by equilibration with dilute H₃PO₄ solutions. The results indicate that β-Ca₃(PO₄)₂ has a negative thermal coefficient of solubility. The solubility product, K_s, was determined as a function of temperature by a generalized least-squares procedure; the resulting equation is

$$\text{log}{K}_s=-45723.26/T+287.4536-0.546763T;$$

the values of K_s and its dispersion at 25 and 37 °C are 1.20(0.056), and 0.283(0.011) × 10⁻²⁹. Thermodynamic functions for the dissolution of the salt at the four experimental temperatures are reported.

When treated as an adjustable constant, the Ca/P ratio in these β-Ca₃(PO₄)₂ solutions was found to have the value 1.514(0.010), confirming that the stoichiometry of the high temperature form of this salt is correctly indicated by the above formula.

The computed isotherms at 25 °C for several calcium phosphates are compared; it is shown that β-Ca₃(PO₄)₂ is, next to Ca₅(PO₄)₃OH, the most stable at pH’s above 6.36. The singular points of the β-Ca₃(PO₄)₂ isotherm with those of CaHPO₄ · 2H₂O and CaHPO₄ are at pH’s 5.88 and 6.36, respectively.

1. Introduction

Whitlockite, a mineral related to β-Ca₃(PO₄)₂ (beta-tricalcium phosphate), is an important constituent of dental calculus [1, 2]¹ and may occur in carious lesions [3, 4, 5] and calcified aortas [6]. The formation and stability of whitlockite seem to be enhanced by the presence of cations smaller than Ca²⁺, such as Fe²⁺ and Mg²⁺ [7]. There appears to be a structural difference between material prepared at a high temperature (referred to here as β-Ca₃(PO₄)₂) and that which is formed in an aqueous environment (whitlockite) [7]. Information on the solubility of either form of this salt in the ternary system Ca(OH)₂-H₃PO₄-H₂O has hitherto been lacking. Preliminary reports on the solubility at 25 °C [8], and at 5, 15, and 37 °C [9] of the high temperature product have been presented earlier. We report here the consolidated results and refined calculations at these four temperatures. The experimental data were treated by the generalized least squares procedure described in earlier publications [10, 11, 12], taking into account the formation of ion pairs.

2. Materials and Methods

2.1. Preparation of β-Ca₃(PO₄)₂

The starting materials used were calcium carbonate (reagent grade) and dicalcium phosphate (CaHPO₄), the preparation of which has been described in detail [13]. Mixtures of these salts were suspended in ethanol, homogenized, filtered, and dried for a day or longer at approximately 1000 °C. After cooling, the product was examined microscopically and analyzed. The process was repeated after adjustment of the composition by an incremental addition of the appropriate salt or of aq. Ca(OH)₂. When the composition was satisfactory (molar Ca/P ratio = 1.50) the product was converted to the high temperature form (α-Ca₃(PO₄)₂) by heating to 1150 to 1200 °C; this treatment removed inhomogeneities noted by microscopic examination. Finally the product was reconverted to the β-form by prolonged heating at 800 to 950 °C. The final preparation consisted of aggregates of rounded grains ranging from 7 to 50 μm in diameter. The percentage of phosphorus present as pyrophosphate was at most 0.30. X-ray powder diffraction patterns confirmed that the bulk of the material was β-Ca₃(PO₄)₂, with a few barely detectable peaks that could be attributed to α-(Ca)₃(PO₄)₂.

2.2. Analyses

The methods for the measurement of pH, calcium and phosphorus (as orthophosphate) have been described in earlier publications [12, 13]. Phosphorus as pyrophosphate was determined by the method of Gee and Dietz [14].

2.3. Equilibrations

Batch equilibration was employed. Glass-stoppered 200 ml bottles containing 2–3 g of β-Ca₃(PO₄)₂ were half filled with phosphoric acid solutions of known concentrations while flushing with a stream of N₂; after sealing the stoppers with paraffin, the bottles were rotated end-over-end in a water bath held to within 0.1 degree of the selected temperature for periods ranging from 2–3 weeks. Samples were passed through millipore filters before analysis. Final equilibration runs were made only after preliminary “washing” runs were made under the same conditions. This procedure was used to ascertain the behavior of the systems and in particular to check on possible changes in the solid during prolonged exposure to the acid solutions. No significant changes in composition or form of the solid were detected in any of the systems included in the final equilibrations.

3. Calculations

The methods and procedures used for calculating solubility products and ion pair association constants by generalized least squares have been described previously [12]. In what follows only the modifications and specifications pertinent to the case of β-Ca₃(PO₄)₂ are given in detail. Curly brackets will be used to denote equation, section, and table numbers used in the previous paper [12]. In this work the purpose of the calculations was to obtain the “true” solubility product, K_s, of β-Ca₃(PO₄)₂ as a function of temperature, and to compute the adjusted values of the observations. The values for the association constants of the ion pairs [CaHPO₄]° and [CaH₂PO₄]⁺, K_x and K_y respectively, were taken from the earlier work (table {12}). The weighted sum of squares of residuals of four observations per system (concentration of total calcium, Ca, and total phosphorus, P, initial phosphoric acid concentration, P₀, and pH) was minimized subject to three condition functions: saturation with respect to β-Ca₃(PO₄)₂, congruent dissolution of this salt, and electroneutrality.² Separate adjustments were first made at each temperature to establish the trend of the variation in K_s, and to check the appropriateness of the weight assignments. A final run was made with the combined data, in which K_s was computed by the least squares estimation of the coefficients A_j in the expression ln K_s = A₁/T + A₂ + A₃T, with T the temperature in Kelvins (eq. {16}).

Table 12.

Results of preliminary calculations

°C	Number of functions (r)	Number of points (N)	f c	Sd × 104	Ks × 1029
5	a3	8	23	1.02	0.970
15	3	7	20	0.944	1.69
25	3	9	26	.936	1.19
37	b2	11	21	.996	0.283

^aSaturation, electroneutrality and congruent dissolution.

^bSaturation and congruent dissolution.

^cDegrees of Freedom =Nr − 1.

^dStandard deviation.

3.1. Balance Equations, Solubility Product, and Activity Coefficients

The equations of mass balance are given by eqs {1} to {4}. Activity coefficients and ionic strength are defined in eqs {10} and {11a}. (Only the Debye-Hückel (D. – H.) type coefficients are used in this report.) The ionic activity product is defined for β-Ca₃(PO₄)₂ as

$$K_{\text{TC}}={\left({\text{Ca}}^{2+}\right)}^3{\left({\text{PO}}^{3-}\right)}^2,$$ (1)

where the first factor (activity of ionic calcium) and the second (activity of orthophosphate ion) are defined as follows:

$$\left({\text{Ca}}^{2+}\right)=(\text{Ca}-\tau )/{\text{g}}_{\text{Ca}}$$ (2a)

$$\left({\text{PO}}_4^{3-}\right)=(\text{P}-\tau )k_3/\left({\text{H}}^{+}\right)N.$$ (2b)

The quantities g_Ca, k₃, and N are defined in the equations of [12] already referred to; (H⁺) = 10^−pH, and τ is the sum of ion pair concentrations, eq {8}. The apparent solubility product, $K_{\text{TC}}^{\prime }$, was calculated taking τ to be zero.

3.2. Condition Functions, Parameters, and Standard Deviation

As mentioned above, each system was required to satisfy three (two at 37 °C) conditions. The electroneutrality condition is given by eq {14}. The other two conditions are defined here as:

(1) Saturation with respect to β-Ca₃(PO₄)₂

$${\left({\text{Ca}}^{2+}\right)}^3{\left({\text{PO}}_4^{3-}\right)}^2-K_s=0,$$ (3)

where the activities are given by eqs (2a) and (2b); (2) Congruent dissolution of β-Ca₃(PO₄)₂

$$\text{Ca}/\left(\text{P}-{\text{P}}_0\right)-R=0,$$ (4)

where R is the expected value of the ratio, 3/2.

Since the ion pair association constants were not subject to adjustment in these calculations, the number of constants is just one (K_s); the number of adjustable parameters (p) is one or three corresponding to separate (ln K_s = A₂) or combined (ln K_s = A₁/T + A₂ + A₃T) data adjustments, respectively. (See sec. {3.5b}.) The standard deviation is given by eq {22}, with the degrees of freedom, Nr-p, in that equation replaced by Σ_tN_tr_t-p. Here N_t and r_t are the number of systems and condition functions, respectively, at temperature t.

4. Results

4.1. Solubility and Solubility Product

The compositions of saturated β-Ca₃(PO₄)₂ solutions at 5, 15, 25, and 37 °C are summarized in tables 1 through 4. Congruent dissolution is indicated by the smallness of the variation in the Ca:(P−P₀) ratio about the expected value 1.5. Column 5 exhibits the values of the apparent solubility product, $K_{\text{TC}}^{\prime }$ (no ion pairs assumed); there is no discernible trend towards a minimum, in contrast to $K_{\text{DC}}^{\prime }$ for CaHPO₄ · 2H₂O [12]. Its lower solubility, which reduces the concentrations of the ion pairs, along with the restricted range of pH values available for the β–Ca₃(PO₄)₂ data, make it difficult to establish the existence of a minimum. The values of K_TC as computed with the unadjusted data and appropriate values of the ion pair concentrations, eq (1), are shown in the last column of the tables as $K_{\text{TC}}^0$.

Table 1.

Solubility of β-tricalcium phosphate at 5 °C Unadjusted quantities

Initial Acid P0 M ×103	Composition of equil. Solns.			$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	$K_{\text{TC}}^{\prime }$ × 1029	$K_{\text{TC}}^{\circ }$ ×1029
	pH	Ca M ×103	P M×103
0.197	7.230	0.338	0.410	1.59	1.13	0.86
.590	6.776	.712	1.057	1.52	1.88	1.35
.590	6.758	.684	1.033	1.54	1.40	1.02
.986	6.567	1.032	1.666	1.52	2.25	1.60
.788	6.584	0.834	1.344	1.50	0.97	0.72
1.38	6.353	1.29	2.26	1.47	1.21	.88
1.66	6.300	1.54	2.65	1.56	1.66	1.20
1.66	6.291	1.52	2.66	1.52	1.49	1.08

Table 4.

Solubility of β-tricalcium phosphate at 37 °C Unadjusted quantities

Initial Acid Po M × 103	Composition of equil. solns.			$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	$K_{\text{TC}}^{\prime }$ × 1029	$K_{\text{TC}}^{\circ }$ ×1029
	pH	Ca M × 103	P M × I03
0.197	6.909	0.226	0.340	1.58	0.295	0.253
.197	6.891	.243	.351	1.58	.335	.287
.392	6.612	.371	.625	1.59	.378	.322
.590	6.414	.499	.903	1.59	.344	.293
.590	6.405	.507	.931	1.49	.352	.300
.788	6.249	.670	1.262	1.41	.360	.308
.986	6.146	.799	1.533	1.46	.347	.298
.986	6.136	.794	1.527	1.47	.311	.267
1.38	5.993	1.05	2.06	1.54	.329	.283
1.66	5.894	1.26	2.47	1.56	.315	.272
1.66	5.889	1.25	2.51	1.47	.309	.267

Table 2.

Solubility of β-tricalcium phosphate at 15 °C Unadjusted quantities

Initial Acid P0 M ×103	Composition of equil. solns.			$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	<$K_{\text{TC}}^{\prime }$ × 1029	$K_{\text{TC}}^{\circ }$ ×1029
	pH	Ca M ×103	P M ×103
0.205	7.251	0.336	0.421	1.56	2.96	2.44
.415	6.896	.537	.759	1.56	2.69	2.20
.829	6.564	.859	1.377	1.57	2.22	1.81
.829	6.558	.843	. 1.362	1.58	1.96	1.61
1.04	6.460	1.04	1.68	1.62	2.32	1.89
1.04	6.458	1.08	1.72	1.59	2.60	2.11
2.07	6.081	1.79	3.22	1.56	1.29	1.07

Table 3.

Solubility of β-tricalcium phosphate at 25 °C Unadjusted quantities

Initial Acid Po M ×103	Composition of equil. solns.			$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	$K_{\text{TC}}^{\prime }$×1029	$K_{\text{TC}}^{\circ }$ ×1029
	pH	Ca M ×103	P M × l03
0.110	7.391	0.199	0.229	1.67	1.11	0.97
.200	7.063	.295	.397	1.50	1.09	.95
.816	6.455	.795	1.346	1.50	1.56	1.33
.816	6.443	.809	1.338	1.55	1.47	1.25
.816	6.430	.793	1.330	1.54	1.23	1.06
1.21	6.305	1.06	1.88	1.58	1.80	1.52
1.60	6.177	1.36	2.48	1.55	1.98	1.68
2.03	6.031	1.69	3.16	1.50	1.57	1.34
2.29	5.974	1.88	3.52	1.53	1.52	1.29

Tables 5 through 8 summarize the data adjustments as found for the combined data. The ionic strength, μ, is shown in column 5. The last two columns of these tables illustrate the effectiveness of the adjustment procedure. The Ca:(P−P₀) ratios have the expected value of 1.5. The adjusted values of K_TC at temperature T in the last column are in every case the same (to five digits or better) as the value of the constant K_s given by the adjustment for that temperature. To a sufficient approximation,

$$\text{log}{K}_s=-45723.26/T+287.4536-0.546763T.$$ (5)

Values of log K_s and K_s, and their standard errors at the four temperatures are exhibited in table 9. (The standard error of the adjustment is discussed in section 5.1.)

Table 5.

Solubility of β-tricalcium phosphate at 5 °C Adjusted quantities

Initial Acid Po M ×103	Composition of equil. solns			μ ×103	$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	KTc × 1029
	pH	Ca M × I03	P M × I03
0.203(3)a	7.267(10)	0.321(4)	0.417(6)	1.11	1.50	0.972
.597(9)	6.754(9)	.674(8)	1.046(15)	2.13	1.50	.972
.591(9)	6.758(9)	.670(8)	1.038(15)	2.11	1.50	.972
.982(15)	6.521(9)	.989(13)	1.642(24)	3.01	1.50	.972
.798(12)	6.618(9)	.840(11)	1.358(19)	2.59	1.50	.972
1.383(21)	6.361(9)	1.308(17)	2:255(32)	3.90	1.50	.972
1.642(25)	6.280(9)	1.513(20)	2.651 38)	4.47	1.50	.972
1.645(25)	6.280(9)	1.515(20)	2.655(38)	4.48	1.50	.972

^aStandard errors in the last digit(s) calculated by eq {26}.

Table 8.

Solubility of β-tricalcium phosphate at 37 °C Adjusted quantities

Initial Acid Po M ×103	Composition of equil. solns.			μ ×103	$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	KTC×1029
	pH	Ca M ×103	P M ×103
0.195(2)	6.924(7)	0.225(3)	0.345(2)	0.792	1.50	0.283
.196(2)	6.891(7)	.240(3)	.356(2)	.823	1.50	.283
.389(3)	6.599(7)	.365(5)	.632(4)	1.22	1.50	.283
.585(5)	6.411(7)	.494(6)	.914(6)	1.61	1.50	.283
.591(5)	6.398(6)	.507(6)	.928(6)	1.64	1.50	.283
.794(7)	6.239(6)	.675(8)	1.244(8)	2.12	1.50	.283
.989(8)	6.140(6)	.801(10)	1.524(9)	2.51	1.50	.283
.989(8)	6.142(6)	.799(10)	1.521(9)	2.50	1.50	.283
1.377(11)	5.993(6)	1.041(13)	2.071(13)	3.24	1.50	.283
1.648(14)	5.898(6)	1.252(16)	2.482(15)	3.85	1.50	.283
1.661(14)	5.895(6)	1.259(16)	2.500(15)	3.87	1.50	.283

Table 9.

Temperature dependence of the solubility product

log Ks = −45723.26/T+ 287.4536 −.546763T [eq(5)]
°C	logKs + 29	Ks× 1029
5	−0.0121 a(0.026)	0.972 (0.059)
15	0.2251 (0.020)	1.679 (0.076)
25	0.0796 (0.020)	1.201 (0.056)
37	−0.5481 (0.016)	0.283 (0.01l)

^aStandard error.

Table 6.

Solubility of β-tricalcium phosphate at 15 °C Adjusted quantities

Initial Acid Po M ×103	Composition of equil. solns.			μ ×103	$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	KTC × 1029
	pH	Ca M × 103	P M ×103
0.204(3)	7.216(9)	0.320(6)	0.417(6)	1.13	1.50	1.68
.415(7)	6.876(9)	.513(6)	.758(10)	1.72	1.50	1.68
.823(13)	6.557(8)	.848(10)	1.389(20)	2.69	1.50	1.68
.819(13)	6.560(8)	.844(10)	1.382(19)	2.68	1.50	1.68
1.030(16)	6.452(8)	1.012(13)	1.705(24)	3.16	1.50	1.68
1.045(16)	6.456(8)	1.024(13)	1.727(24)	3.20	1.50	1.68
2.074(31)	6.124(8)	1.825(24)	3.290(46)	5.49	1.50	1.68

Table 7.

Solubility of β-tricalcium phosphate at 25 °C Adjusted quantities

Initial Acid Po M × l03	Composition of equil. solns.			μ ×103	$\frac{\text{Ca}}{\text{P}-{\text{P}}_0}$	KTC×1029
	pH	Ca M ×103	P M ×103
0.108(2)	7.412(10)	0.198(2)	0.240(3)	0.728	1.50	1.20
.203(2)	7.093(9)	.297(3)	.401(5)	1.04	1.50	1.20
.810(12)	6.442(8)	.797(10)	1.341(19)	2.53	1.50	1.20
.813(12)	6.440(8)	.800(10)	1.347(19)	2.53	1.50	1.20
.812(12)	6.441(8)	.799(10)	1.344(19)	2.53	1.50	1.20
1.166(18)	6.271(8)	1.074(14)	1.882(27)	3.33	1.50	1.20
1.550(23)	6.136(8)	1.371(18)	2.464(36)	4.19	1.50	1.20
2.001(30)	6.015(8)	1.717(23)	3.146(45)	5.19	1.50	1.20
2.249(33)	5.960(8)	1.907(26)	3.521(51)	5.74	1.50	1.20

The temperature dependence of the solubility product is illustrated in figure 1, where the smooth curve was obtained with the use of eq (5). The values of K_s from preliminary independent adjustments at the four temperatures (table 12) are plotted and are practically identical with the values in table 9. The 95 percent confidence intervals (horizontal lines) were computed at each temperature from the standard errors in table 9. The K_TC values plotted in the figure as experimental points are those listed in column 6 of tables 1 through 4. (The values of K_TC at 37 °C, covering the narrow range (0.25 to 0.32) × 10²⁹, have been omitted for clarity.)

Figure 1.

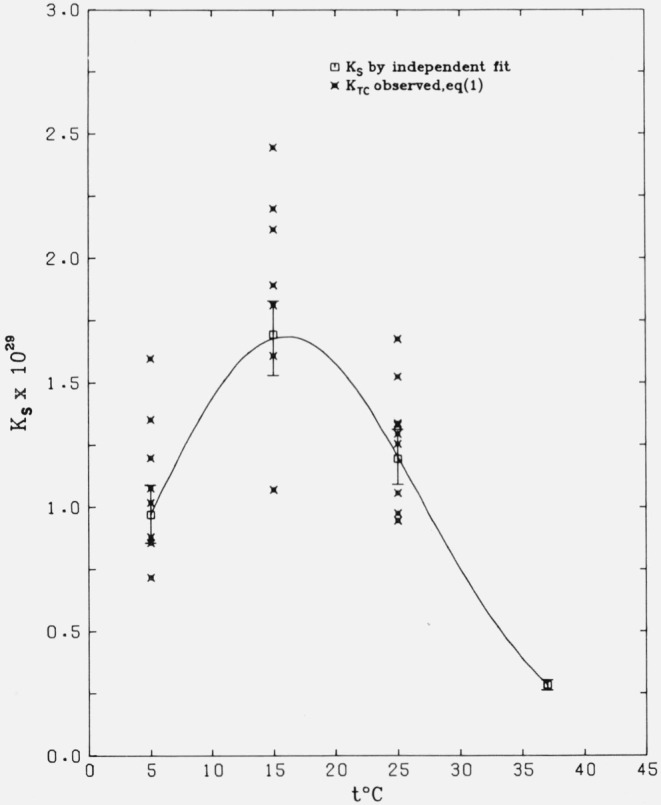
Temperature dependence (eq (5)) of the solubility product of β-Ca₃(PO₄)₂.

Points are the “experimental” values. See text. The 95 percent confidence intervals are shown as vertical lines.

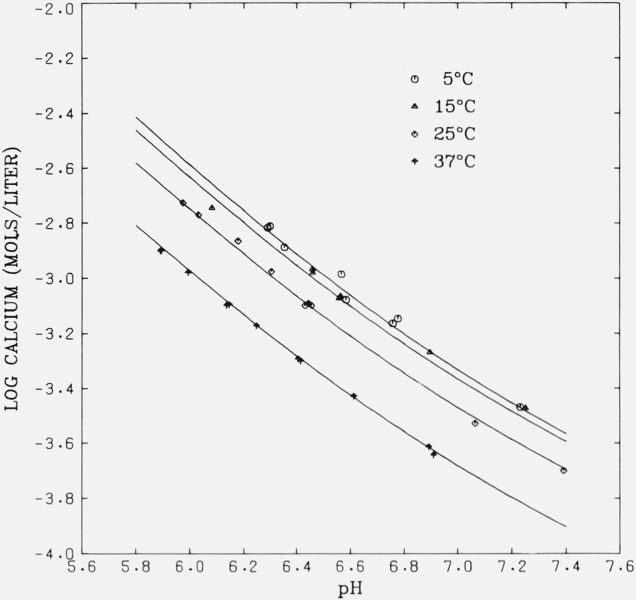
Figure 2 shows the solubility isotherms for β-Ca₃(PO₄)₂ in terms of log (total calcium concentration) as a function of pH. The smooth curves were obtained in a separate calculation using appropriate values of K_s (table 9), K_x and K_y (table {12}), and a sequence of pH values (arbitrary) covering the range of interest. The adjusted values of Ca and pH, tables 5–8, are a subset on the curves but are not indicated. All of the experimental points (tables 1–4) are plotted in the figure. It is evident from the relative positions of the curves, in spite of some ambiguity in the data for 15 °C, that the solubility of this salt decreases with increasing temperature; in this respect its behavior resembles that of CaHPO₄ · 2H₂O [12] and CaHPO₄ [13].

Figure 2.

Calculated isotherms of β-Ca₃(PO₄)₂ at 5, 15, 25, and 37 °C.

Points represent experimental data.

4.2. Ion Pairs

Table 10 gives the concentrations at 25 °C of the ion pairs [CaHPO₄]° and [CaH₂PO₄]⁺ as found by the adjustment. The percentage of bound calcium (sum of pair conc. × 100/total calcium concentration) is also shown. The values for the other temperatures are similar. Two points may be noted in reference to the earlier results from [12]. The concentrations of both pairs remain very small relative to the total calcium concentration over the range of observed pH. The maximum bound calcium was 8 percent (5 °C) in contrast to a figure of over 20 percent for the more soluble salt, CaHPO₄ · 2H₂O. An attempt to estimate the values of the association constants K_x and K_y in the adjustment of the β-Ca₃(PO₄)₂ data was not successful under these conditions. Secondly, in contrast to the pH-independent values of the concentration X° of [CaHPO₄]° expected and found for solutions saturated with respect to the solids CaHPO₄ · 2H₂O [12] and CaHPO₄ [13], the values reported here are pH-variable as indicated in table 10. This variation is predictable, since the pH-independence of X° is a consequence of the pH-invariance of the “true” activity product (Ca²⁺) (HPO₄²⁻) in solutions saturated with CaHPO₄ · 2H₂O or CaHPO₄ (eq {6}); on the contrary, this product is pH-variable in saturated solutions of β-Ca₃(PO₄)₂.

Table 10.

Concentration of ion pairs and bound calcium at 25 °C

pH	$\left[{\text{CaHPO}}_4^0\right]$ M ×103	$\left[{\text{CaH}}_{\text{2}}{\text{PO}}_4^{+}\right]$ M ×103	l00τa/Ca
7.412	0.0058	0.0001	2.95
7.093	.0100	.0003	3.46
6.442	.0284	.0034	3.99
6.440	.0285	.0034	3.99
6.441	.0284	.0034	3.99
6.271	.0368	.0066	4.04
6.136	.0451	.0111	4.10
6.015	.0539	.0177	4.17
5.960	.0584	.0219	4.21

^aτ is sum of ion pair concentrations.

4.3. Thermodynamic Quantities

The dissolution of β – Ca₃(PO₄)₂ is described by the reaction

$${\text{Ca}}_3{\left({\text{PO}}_4\right)}_2=3{\text{Ca}}^{2+}+2P{O}_4^{3-}.$$ (6)

The quantities ΔG°, ΔS°, ΔH° and their associated standard errors³ were calculated for this reaction from eq (5) for log K_s following the procedure of eqs {27–29}. The results are tabulated in table 11.

Table 11.

Thermodynamic quantities

°C	Δ G° kcala/mol	ΔH° kcal/mol	ΔS° cal/mol · K
5	36.9	15.7	−76.5
	b (0.03)	(1.4)	(5.0)
15	37.9	1.5	−127
	(.03)	(.7)	(2)
25	39.4	−13.2	−177
	(.03)	(.5)	(1)
37	41.9	−31.4	−237
	(.02)	(1.4)	(4)

^a1 kcal = 4184.0 joules.

^bStandard error.

5. Discussion

5.1. Standard Deviation. Weights and Goodness of Fit

The adequacy of the adjustment results was examined by several criteria. Three of them are discussed here and the remainder in the following section. In the first place the exploratory adjustments for the four temperature sets were utilized to check for uniformity of the estimated standard deviation (s, eq {22}) among the sets. The results for these runs (using the final weights described below) are summarized in table 12. Secondly, assuming the correctness of the physical model, the x² statistic with f degrees of freedom (sec. 3.2) was used to judge the overall adequacy of the weights assignments. Since the expected value of x² = f, and the test value of ${\chi }^2=\left(s^2/s_0^2\right)f$, where s₀ = 1 × 10⁻⁴ is the estimate of s used in defining the weights (eq {12}), a poor assignment of errors will yield a value of s that may differ markedly from s₀; that is, the hypothesis χ² = f would be rejected. In view of the variability in the initial K_TC values (fig. 1) at 5, 15, and 25 °C, the weights at these temperatures were computed from the following errors assigned to the observables: Ca, 3.5 percent; P (and P₀), 2.5 percent; pH, 0.020 (absolute). The (smaller) errors assigned to the 37 °C data were the same as those used for CaHPO₄ · 2H₂O [12]. With this assignment of weights, s² for the final adjustment of the combined data has the value 0.938 × 10⁻⁸, with f = 3 × (8+ 7 + 9) + 2 × 11 − 3 = 91. Since the critical values of ${\chi }_{91}^2$ (95%), 66.5 and 119.3, bracket the value of f, the assigned weights may be considered reasonable, and a 95 percent confidence interval for s² is (0.73 < s² < 1.31) × 10⁻⁸. The corresponding values of s and its dispersion [15] are 0.968 × 10⁻⁴ and 0.072 × 10⁻⁴; the confidence interval for s is (0.86 < s < 1.14) × 10⁻⁴.

An additional check was made by adopting an alternative model: the combined data were adjusted with ion pairs assumed absent and weights as described above. As might be anticipated from the very low ion pair concentrations listed in table 10, the resulting standard deviation of 1.06 × 10⁻⁴ hardly differs from the value reported above, 0.968 × 10⁻⁴. However, the residuals at 5° and 15 °C showed considerably less randomness in the distribution of signs, and somewhat larger magnitudes, with this alternative model. The data are best described by the ion pair model.

5.2. Solubility Isotherms

The experimental design underlying the data reported herein was intended to assure the attainment of equilibrium of solutions of variable initial phosphoric acid concentration with solid β-Ca₃(PO₄)₂ of known purity. The three condition functions adopted for the adjustment assume (i) equilibrium (saturation), (ii) congruent dissolution, (i.e., dissolution, without the formation of extraneous solid phases) and (iii) electroneutrality (i.e., all charged species accounted for). If this model correctly describes the data, and if the errors are random, the experimental points plotted as in figure 2 should be close to the computed isotherms and show a random scatter about the curves. This implies that at each temperature the relative residuals (residual/observed value) should be small (< 0.03) and have a random distribution of signs. Alternatively, the standardized residuals (not reported) were computed and, with a few exceptions, satisfy these criteria. A glance at figure 2 shows that most of the exceptions with respect to size occur in the 15 °C data. In addition, these experimental points seem to define a curve that is somewhat skewed with respect to the computed 15 °C curve. It is possible that the saturation condition was not satisfied at some of these points.

The data for 37 °C presented a different problem. In spite of the unusually narrow range of initial K_TC values, the attempt to adjust these data using all three condition functions gave an unsatisfactory value of s and uniformly large and negative relative residuals for calcium. Examination of the initial electroneutrality values showed them to be almost uniformly negative and larger in magnitude by a factor of at least 10 than the values computed at the other temperatures. The reason for this is obscure. Two possible explanations are (1) systematic errors in the analysis for calcium and (2) the presence of a foreign ion of positive charge. Considering the experimental procedures and the fact that the solid β-Ca₃(PO₄)₂ at all four temperatures was from the same batch of material, the second possibility seems very unlikely. In any event, the omission of the electroneutrality condition produced acceptable numerical results which were confirmed in the following manner. An adjustment (not reported) was made with the 37 °C data excluded; the adjusted values of K_s, 0.970, 1.694, and 1.193 × 10⁻²⁹ at 5, 15, and 25 °C, respectively, are very close to those reported in table 9 for these temperatures. The corresponding equation for log K_s, similar to eq (5), predicts the value 0.267 × 10⁻²⁹ for K_s at 37 °C, in good agreement with that found for the 37 °C data alone (table 12).

5.3. Stoichiometric Composition of β-Ca₃(PO₄)₂

It has been suggested [16, 17] that the Ca/P ratio in whitlockite may be 10/7 rather than 3/2. Inspection of tables 1–4 shows that the value of 10/7 lies well below most of the listed Ca:(P − P₀) ratios. Wallace and Brown [18] have shown by the pyrolysis of calcium orthophosphates that the ratio in whitlockite-like materials prepared at high temperatures is very close to 3/2. A recalculation of their results, using weights derived from their published standard errors, yielded a weighted mean ratio of 1.500, standard error of the mean, 0.011, and a 95 percent confidence interval on 14 degrees of freedom, 1.476 < Ca/P < 1.524. In order to further test the value of the ratio, using the solubility data of this paper, an additional adjustment was run, in which the ratio R in eq (4) was treated as an additional adjustable constant. The result was $\widehat{R}=1.514$, $\sigma \left\{\widehat{R}\right\}=0.010$, and s² = 0.926 × 10⁻⁸ (90 degrees of freedom), which is very close to the value, 0.938 × 10⁻⁸ found above (sec. 5.1). Using the t statistic, both R = 3/2 and R = 10/7 were tested at the 95 percent level against $\widehat{R}$; the hypothesis R = 10/7 was easily rejected, whereas R = 3/2 was acceptable. These results confirm the chemical findings of Wallace and Brown [18] and the crystal structure analysis [7, 19] of the thermally prepared form of this salt. The latter showed that the apparent anomaly in the unit-cell contents is explained by the fact that one of the calcium sites is only one-half occupied.

5.4. Comparison With Reported Data

We are unaware of any previous attempts to determine the solubility product of well-characterized β-Ca₃(PO₄)₂. Bjerrum’s compilation [20] contains several references [21–24], all but one of which pertain to work done long before the chemistry of the sparingly soluble calcium phosphates was well understood. In particular, preparations described as Ca₃(PO₄)₂ very probably contained the less soluble salt, Ca₅(PO₄)₃OH (hydroxyapatite). A more recent report [24] gives 2.0 × 10⁻²⁹ as the value of the solubility product [Ca²⁺]³[PO₄³⁻]² at circa 20 °C; no details on the material employed are available to us. From the thermochemical data published by the National Bureau of Standards [25, 26, 27], including a standard heat of formation at 25 °C for β-Ca₃(PO₄)₂ equal to −928.5 kcal/mol, we derive the unreasonably small value K_TC (25 °C) = 2.0 × 10⁻³³. The uncertainty in a solubility product derived from a variety of thermochemical data is known to be considerable and the direct measurement of solubility of well-characterized material as reported here may be expected to yield a value of K_TC subject to much less uncertainty.

5.5. Chemical Significance

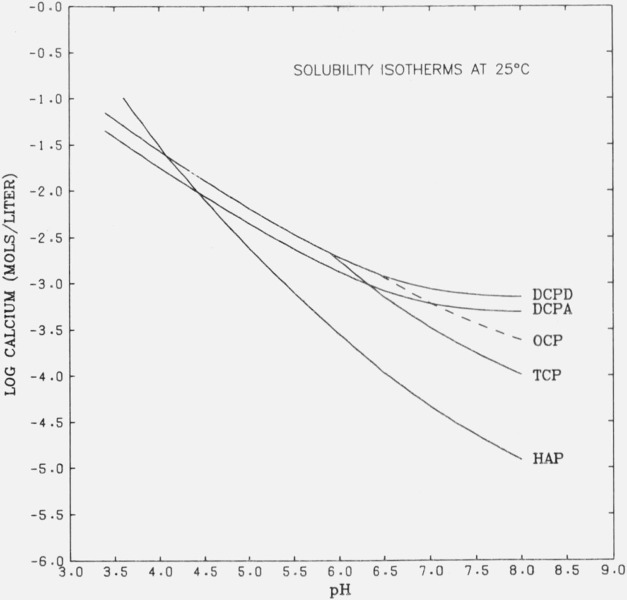
Isotherms for the data at 25 °C of several calcium phosphates in the ternary system are plotted in figure 3. It can be seen that β-Ca₃(PO₄)₂ is second only to Ca₅(PO₄)₃OH in stability at pH’s above 6.36. The calculated pH’s of the singular points at 25 °C for β-Ca₃(PO₄)₂ with CaHPO₄ · 2H₂O and CaHPO₄ are 5.88 and 6.36, respectively.

Figure 3.

Calculated isotherms at 25 °C illustrating the relative stability of several calcium phosphates.

DCPD, CaHPO₄ · 2H₂O [12]; DCPA, CaHPO₄ [13]; OCP, ${\text{Ca}}_4{\left({\text{PO}}_4\right)}_3\text{H}\cdot 2\frac{1}{2}{\text{H}}_2\text{O}$ [28]; TCP, β-Ca₃(PO₄)₂; HAP, Ca₅(PO₄)₃OH [29].′

In view of the indication that small cations such as Mg²⁺ and Fe²⁺ stabilize whitlockite and β-Ca₃(PO₄)₂, it seems reasonable to expect that under certain aqueous conditions the stability of these compounds may be even greater than revealed by our results for pure β-Ca₃(PO₄)₂.