Crystallization of Random Copolymers

Abstract

A theory of crystallization is formulated for random copolymers which crystallize with the non-crystallizable co-units incorporated into the crystalline lattice as defects. The appropriate melting point equation and other associated thermodynamic properties are derived for this model as a function of crystal thickness and comonomer concentration. The formation of lamellar type morphology is assumed to be a kinetically determined phenomena and nucleation theory is utilized accordingly. The isothermal lamella thickness is predicted to increase in a definitive manner as the noncrystallizable comonomer concentration X increases, while the associated isothermal growth rate is predicted to decrease. The variation of lamella thickness with X when the copolymer is quenched or cooled at a uniform rate is also qualitatively predicted. Under these conditions lamella thickness decreases with increasing X, which is in accord with previous experimental observations on random copolymers of tetrafluoroethylene and hexafluoropropylene as well as other random copolymers. Theory also suggests how the surface free energy parameters σ_e and σ can be determined from isothermal crystallization experiments for a series of random copolymers of varying composition.

1. Introduction

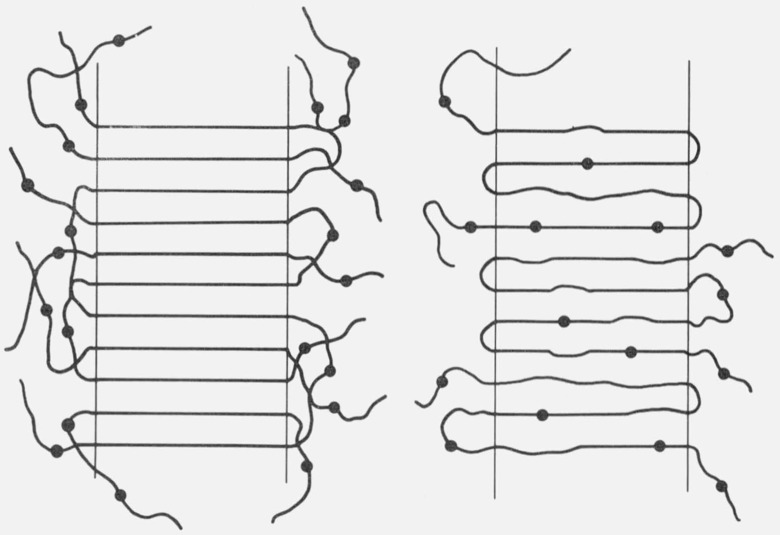
A random copolymer can potentially crystallize in two extreme ways. It can form a two-phase system in which the crystalline phase is composed entirely of A units and is in equilibrium with a mixed amorphous phase of A units and noncrystallizable comonomer B units (comonomer exclusion). Alternatively, the copolymer may form a two phase system in which the crystalline phase is a solid solution of A and B units; the comonomer B units produce defects in the crystalline A lattice and both phases have the same composition (comonomer inclusion). The question arises as to which state is more characteristic of the experimentally observed crystalline state. One can try to answer this question by invoking thermodynamics: if the observed state is a true thermodynamic state, then we need only determine the state of lowest free energy. Figure 1 schematically illustrates the two models.

Figure 1. Two extreme representations of lamellar random copolymer crystals, the exclusion model (left) and inclusion model (right).

In Flory’s theory of copolymer crystallization [1]¹ it is tacitly assumed that the state of lowest free energy is the two phase system where the comonomer B units are excluded from the crystal. However, on a priori grounds, there is no reason to believe that the exclusion model is thermodynamically more stable than the inclusion model. Moreover, the question as to which state is more stable is largely academic because the observed state probably corresponds to a meta-stable state determined by kinetic factors. This is certainly the case in homopolymer crystallization. Thick crystals are thermodynamically more stable than thin lamellar crystals with high surface to volume ratios; nevertheless, metastable lamellar morphology develops under the usual kinetic conditions of homopolymer crystallization.

Real copolymer crystals may exhibit a morphology intermediate to the two extremes in figure 1. In the present paper, a simple theory for random copolymer crystallization is formulated which adopts the view that lamella crystalline morphology is kinetically determined and that the inclusion model is more characteristic of the crystalline state. A preliminary account of this theory has been given previously [2].

In section 2 melting temperature relationships are derived as a function of copolymer composition and crystal thickness. The heats of fusion associated with the two models are also considered. In section 3 an elementary kinetic theory of crystallization is formulated and in section 4 the conclusions of the study are briefly outlined.

2. Thermodynamics

2.1. Equilibrium Melting Point

Melting point equations have previously been derived for the exclusion [1] and inclusion [3], [4] models. What follows is an alternative derivation of the equilibrium melting point for the inclusion model. First, we enumerate the assumptions upon which the derivation rests:

1. The heat of fusion ΔH and the entropy of fusion ΔS are independent of temperature; $\text{Δ}H\left(T\right)=\text{Δ}H\left(T_m^0\right)$ and $\text{Δ}S\left(T\right)=\text{Δ}S\left(T_m^0\right)=\text{Δ}H\left(T_m^0\right)/T_m^0$ where $T_m^0$ is the equilibrium melting point of the homopolymer.

2. Compositional changes do not affect the entropy of fusion; if X is the mole fraction of B co-units in the copolymers, then $\mathrm{\Delta }S\left(T,X\right)=\mathrm{\Delta }S\left(T,0\right)=\mathrm{\Delta }S(T_m^0)$.

3. The heat of fusion is a simple linear function of the number of comonomer units that enter the crystal:

   $$\text{Δ}H\left(T,X\right)=\mathrm{\Delta }H\left(T_m^0\right)-X\mathrm{\Delta }{H}_d$$ (1)

   where ΔH_d is the heat of transition (an excess enthalpy) associated with the formation of a defect in the crystalline lattice, ΔH_d ⩾ 0.

Assumption 1 is the usual and simplest approximation employed in determining the bulk free energy difference between melt and crystal; an analysis of the error inherent in this approximation has been made [5]. Assumption 2 is a good approximation if the composition of the crystal and melt are identical. Moreover, a sizable fraction of the entropy of fusion is configurational entropy (estimated to be about 75% for polyethylene [6]) which should be relatively insensitive to compositional changes. Assumption 3 is valid when comonomer defects in the crystal are isolated (low concentrations required) so that they do not interact.

When a copolymer crystal, free of nonequilibrium defects and surface effects, is in equilibrium with the melt, the melting temperature $T_m^0$ is given by

$$T_m^0\left(X\right)=\frac{\text{Δ}H\left(T_m^0,\left(X\right)\right)}{\text{Δ}S\left(T_m^0,\left(X\right)\right)}$$ (2a)

Utilization of the previously mentioned assumptions then yields

$$T_m^0\left(X\right)=\left[\frac{\text{Δ}H\left(T_m^0,X\right)}{\text{Δ}H\left(T_m^0\right)}\right]T_m^0=\left(1-AX\right)T_m^0$$ (2b)

where $A\equiv \mathrm{\Delta }{H}_d/\mathrm{\Delta }H(T_m^0)$.

2.2. Melting Temperature of Lamellar Crystals

Small crystals with high surface to volume ratios will melt at temperatures below the equilibrium melting temperature $T_m^0$. Denoting by ΔG the bulk free energy difference between copolymer crystal and melt, a thin lamellar crystal of thickness l is in equilibrium with the melt when [5]

$$\text{Δ}G-\text{2}{\sigma }_e/l=0$$ (3)

where σ_e is the surface free energy of the basal plane of the lamellar crystal. For $T\le T_m^0$ the bulk free energy difference ΔG(T, X) is given by

$$\text{Δ}G\left(T,X\right)=\text{Δ}H\left(T,X\right)-T\text{Δ}S\left(T,X\right)$$ (4a)

and thus from assumption 2 and eqs (1) and (2)

$$\text{Δ}G\left(T,X\right)=\text{Δ}H\left(T_m^0\right)\left(T_m^0\left(X\right)-T\right)/T_m^0$$ (4b)

Combining eqs (2b), (3), and (4b), the following equation for the melting temperature T_m(l) of a lamellar copolymer crystal obtains:

$$T_m\left(l\right)=\left\{1-\frac{2{\sigma }_e}{\text{Δ}H\left(T_m^0\right)}\left(\text{l/}l\right)-AX\right\}{T}_m^0$$ (5)

Notice that eq (5) reduces to eq (2b) for large l, as it should.

Equation (5) is slightly different in functional form than the melting point equation first derived by Eby [3], [4] for solid solution copolymer crystals. In addition to the assumptions mentioned above, there is an unnecessary series expansion; the effect of comonomer concentration and finite crystal thickness on the melting temperature is evaluated to first order (higher order corrections which are small are ignored). The present derivation has avoided the use of series expansions and thus the melting point depression $\left(T_m^0-T_m\right)$ is predicted to be slightly larger by a factor $T_m^0/T_m$ than the original Eby equation. However, refitting² the data of [4] yielded constants which agreed within the limits of error with the former ones and which did not alter the conclusions in [4].

As mentioned previously, Flory [1] assumes that the copolymer crystal is composed entirely of A units; B co-units are excluded and remain in an amorphous phase. The melting point depression is caused by the fact that preferential ordering of the copolymer chains is required for crystallization (an entropy effect) whereas in the present case, the melting point depression is caused by the defective heat of fusion that accompanies the crystallization (an enthalpy effect). For a random copolymer and low comonomer concentrations, the Flory equation reduces to

$$T_m\simeq \left(1-A\prime X\right)T_m^0$$ (6)

where $A^{\prime }=R{T}_{.m}/\mathrm{\Delta }H(T_m^0)$. Comparison of eq (6) with eq (2b) shows that they are identical in form except that RT_m has replaced ΔH_d in eq (2b) – a manifestation of the different effects considered (entropy versus enthalpy). Although Flory did not consider the effect of crystal size on the melting temperature, such an effect is obtainable from his theory [see eq (14) of ref. [1]]. The resulting equation is similar to eq (5) which implies that melting temperature data taken as a function of copolymer composition and crystal thickness cannot distinguish between the comonomer exclusion and inclusion crystal models.

2.3. Heats of Fusion

Crystallinity studies (density or x-ray) combined with calorimetric studies can, in principle, determine which model is more appropriate. By assuming that enthalpy effects are additive it can be shown in a straightforward fashion that the observed heat of fusion ΔH* for the inclusion model is given by

$$\text{Δ}H*/\text{χ=Δ}H-X\text{Δ}{H}_d-2\text{Δ}{H}_e/l$$ (7)

where χ is the degree of crystallinity and ΔH_e is the excess enthalpy associated with forming the basal surfaces of the lamellar crystal. However, for the exclusion model, we have

$$\text{Δ}H*/\text{χ=Δ}H-2\text{Δ}{H}_e/l$$ (8)

Note that for the exclusion model ΔH*/χ is independent of the co-unit concentration X whereas it is linearly dependent on X for the inclusion model.

3. Kinetics

3.1. Lamella Thickness

When nucleation theory is applied to the crystallization of linear chain molecules, the theoretical crystal thickness l* is given by [7]

$$l*=l_c+\delta l$$ (9)

where l_c = 2σ_e/ΔG is the critical crystal thickness and δl is a small additive term (usually about 10 Å) which is a weak function of termperature in the usual crystallization temperature range. Crystal thicknesses less than l_c are thermodynamically unstable.

The experimentally observed crystal thickness l_obs may differ from l* because crystals may thicken with time [8], In general,

$$l_{\text{obs}}=l_c+C\left(T\right)$$ (10)

where C(T) includes δl plus any thickening that may occur at the crystallization temperature T. Of course, C(T) is also a function of time, but it will be assumed throughout that we are dealing with the long time (or an isochronal) value of C(T). The thermodynamic driving force ΔG for the crystallization of a random copolymer is given by eq (4b); thus

$$l_{\text{obs}}=\frac{2{\sigma }_e{T}_m^0}{\text{Δ}H\left(T_m^0\right)\left(T_m^0\left(X\right)-T\right)}+C\left(T\right)$$ (11)

If σ_e is independent of the comonomer concentration X, then

$$l_{\text{obs}}=l_c^0\left[\text{l+}\frac{T_m^0-T_m^0\left(X\right)}{T_m^0\left(X\right)-T}\right]+C\left(T\right)$$ (12)

or if C(T) is independent of X,

$$=l_{\text{obs}}^0+l_c^0\left[\frac{T_m^0-T_m^0\left(X\right)}{T_m^0\left(X\right)-T}\right]=l_{\text{obs}}^0+l_c^{0}f\left(X,T\right)$$ (13)

where the superscript 0 on l_obs and l_c indicates that these quantities refer to the homopolymer; from eq (2b) we have

$$f\left(X,T\right)=AX/\left[\left(1-T/T_m^0\right)-AX\right]$$ (14)

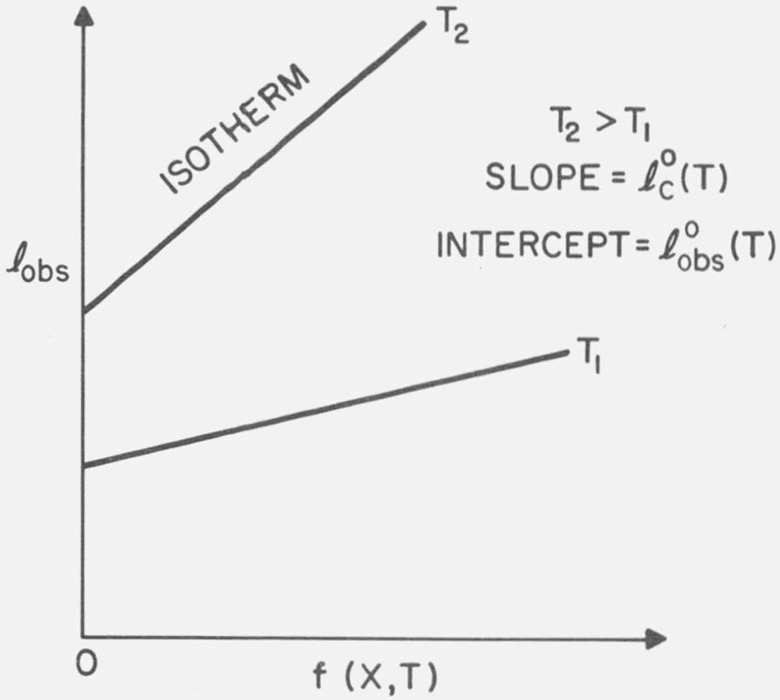
Note that f(X, T) increases monotonically with both X and T; that is, ∂f/∂T > 0 and ∂f/∂X > 0. Therefore, eqs (13) and (14) show that isothermal plots of l_obs, say at T₁, against f (X, T₁) are linear with intercept $l_{\text{obs}}^0\left(T_1\right)$ and positive slope $l_c^0\left(T_1\right)$. Random copolymers of various comonomer concentrations crystallized at the same temperature should form crystals with thicknesses that increase with increasing comonomer concentration (see fig. 2). For low concentrations we have

$$f\left(X,T\right)=\left(\frac{A{T}_m^0}{T_m^0-T}\right)X$$ (15)

and thus, isothermal plots of l_obs against X are initially linear with a positive slope equal to $l_c^0\left(T_1\right)A{T}_m^0/\left(T_m^0-T\right)$.

Figure 2. Variation of theoretical, isothermal lamellar thickness with the comonomer concentration X.

The variable f(X, T) plotted along the abscissa increases monotonically with X and is proportional to X for small X.

The derivation of eq (13) from eq (12) assumed that the thickening that occurs at the crystallization temperature T was independent of the comonomer concentration X. A better approximation is

$${\frac{\partial C}{\partial X}|}_T=\text{constant}$$ (16)

In general

$$C\left(T,X\right)=C\left(T,0\right)+{\frac{\partial C}{\partial X}|}_{T}X+{\frac{{\partial }^{2}C}{\partial X^2}|}_T\frac{X^2}{2!}+\mathrm{\dots }$$ (17)

but when eq (16) holds, eq (13) becomes

$$l_{\text{obs}}=l_{\text{obs}}^0+l_c^{0}f\left(X,T\right)+{\frac{\partial C}{\partial X}|}_{T}X$$ (18)

Even if approximation (16) is not strictly true, eq (18) will hold approximately when second and higher order terms in eq (17) are small compared to the first order term.

The equilibrium theory of Flory [1] for the exclusion model also predicts that crystallite thicknesses increase with increasing X for a random copolymer. At first this result for the exclusion model seems unreasonable because long uninterrupted sequence lengths of crystallizable units are decreasing with increasing X. However, in the Flory theory a compensating decrease in crystallinity accompanies the increase in crystallite thickness. Thus, both the exclusion and inclusion models (equilibrium and kinetic theories, respectively) predict that the isothermal crystal thickness increases with increasing concentration of the non-crystallizable co-unit.

3.2. Nucleation and Crystal Growth

In the simplest approximation, the nucleation rate S of a coherent surface nucleus is given by [7–9]

$$S=S_0\text{exp}\left(-\text{Δ}G*/RT\right)\text{exp}\left(-2\sigma l_c/RT\right)$$ (19a)

where S₀ is a constant, ΔG* is the activation free energy for the transport of a polymer segment across the melt-crystal interface and σ is the lateral surface free energy of the lamellar polymer crystal. For nucleation controlled crystal growth, the lateral growth rate of a copolymer crystal is proportional to S [7, 10]. Therefore, since $l_c=l_c^0\left[1+f\left(X,T\right)\right]$ from eq (12), we have

$$\text{ln}S+\text{Δ}G*/RT=-2\sigma l_c^0\left[\text{l}+f\left(X,T\right)\right]/RT+\text{ln}{S}_0$$ (19b)

Equation (19b) suggests that isothermal plots of In S + ΔG*/RT against f(X, T) are linear with a negative slope equal to $2\sigma l_c^0/RT$ (see fig. 3). In principle, the homopolymer critical thickness value $l_c^0$ can be obtained from isothermal crystallization experiments (crystal thickness measurements required) by using

Figure 3. A schematic for the variation of the theoretical nucleation rate with temperature and composition.

The line labeled X₁ indicates how the nucleation rate might vary when quenching a copolymer with composition X₁ from a high to low temperature. Most of the crystallization will occur over a narrow range of temperature of average temperature T₁. A second copolymer with composition X₂ (X₂ > X₁) will crystallize during similar quenching with an average temperature T₂ which is less thanT₁.

eqs (13) or (18); thus, the surface free energy parameter σ can be determined from eq (19b) by measuring isothermal growth (nucleation) rates. The other surface free energy parameter σ_e is obtained, of course, from the relation

$$l_c^0=2{\sigma }_e/\text{Δ}{G}^0=2{\sigma }_e{T}_m^0/\text{Δ}H\left(T_m^0\right)\left(T_m^0-T\right)$$ (20)

If we ignore for the moment the presence of ΔG* in eq (19), then two copolymers, one with comonomer concentration X₁ and the other with a higher concentration X₂, will grow at approximately the same rate if $T_m^0\left(X_1\right)-T_1=T_m^0\left(X_2\right)-T_2$; that is, S(X₁, T₁) ≃ S(X₂, T₂) at equal undercoolings. Since X₂ > X₁, $T_m^0\left(X_2\right)<T_m^0\left(X_1\right)$ by eq (2b) and, therefore, T₂ < T₁. To obtain the same crystallization rates as X increases requires lower absolute temperatures.

Now the temperature coefficient of ΔG* is negative (S decreases with decreasing T) and the effect of diffusional transport is to lower even farther the temperature (T₂) required to obtain equal growth rates. Usually a WLF type of free energy is employed for ΔG*:

$$\text{Δ}{G}_{\text{WLF}}^{*}/RT=C_1/\left(C_2+T-T_g\right)$$ (21)

where C₁ and C₂ are positive constants and T_g is the glass transition temperature of the polymer [8, 9].

Experimentally, it has been observed that the crystal thickness of tetrafluoroethylene and hexafluoropropylene random copolymers [3] as well as other random copolymers [11, 12] tends to decrease as comonomer concentration X increases in apparent contradiction to the results of section 3.1. However, some of these copolymer crystals were prepared under rapid cooling conditions (quenching of thin films of melt in ice water [13]) or at uniform cooling rates. During cooling most of the crystal growth will occur over a small temperature interval; say the average temperature in this interval is T₁ for a copolymer of concentration X₁. If a second copolymer of higher concentration X₂ is quenched in the same way, then the average temperature T₂ of the temperature interval where most crystal growth occurs will be lower than T₁ for reasons discussed above (see fig. 3). In the absence of diffusional transport effects, the two copolymers would crystallize approximately at the same effective undercooling and thus, we might expect crystal thicknesses to be independent of comonomer concentration. However, the transport term tends to reduce T₂ causing the effective undercooling of the second sample of higher concentration X₂ to be greater than the first. Higher effective undercoolings would cause a decrease in lamellar thickness.

The argument that the transport term $\mathrm{\Delta }{G}_{\text{WLF}}^{*}$ causes the effective undercooling for equal growth rates to increase as the co-unit concentration X increases assumes that T_g is independent of X. What is the situation if T_g varies with X? If T_g increases with X the argument is strengthened; if T_g decreases with X, a more careful analysis is required to determine whether or not the argument is valid. In the appendix such an analysis is carried out and the conditions for which the argument is still valid are defined.

For the tetrafluoroethylene-hexafluoropropylene random copolymers, annealing studies [14] have shown that the rate of annealing is determined by the undercooling $\left(T_m^0\left(X\right)-T_{\text{anneal}}\right)$; i.e., the crystal thickness of copolymers with different concentrations will thicken approximately at the same rate at equal undercoolings. The rate of annealing decreases exponentially as $\left(T_m^0\left(X\right)-T_{\text{anneal}}\right)$ increases. Thus, if diffusional transport increases the effective undercooling at which crystal growth occurs, as has been argued, then the contribution that crystal thickening makes to the observed crystal thickness decreases as X increases.

In summary for experiments where the copolymer is quenched or cooled at a uniform rate, diffusional transport effects can cause the effective undercooling at which crystallization occurs to increase as the non-crystallizable co-unit concentration X increases. Higher undercoolings cause both terms in eq (10) for the observed crystal thickness to decrease with increasing X.

4. Conclusions

The main conclusions of this theoretical study are summarized below:

1. Both the inclusion and exclusion models predict a depression of the crystalline melting point. For the inclusion model the melting point depression is caused by a defective heat of fusion that accompanies the crystallization, whereas for the exclusion model, the depression is caused by the fact that preferential ordering of the copolymer chains is required for crystallization which raises the entropy of fusion. However, careful crystallinity studies combined with calorimetric determinations of heats of fusion can ascertain which model is more appropriate for a given random copolymer system.

2. The kinetically determined, isothermal lamella thickness is predicted to increase while the growth rate decreases with increasing concentration X of the noncrystallizable comonomer. Flory’s equilibrium theory for the exclusion model also predicts that the crystal thickness increases with X and thus, both theories are qualitatively equivalent in this respect. This aspect of the theory has yet to be tested experimentally.

3. Qualitatively, the crystal thickness is predicted to decrease with increasing X when the copolymers are crystallized by quenching or cooling at a uniform rate. This is in accord with existing experimental evidence.

4. The surface free energy parameters σ_e and σ can be determined from isothermal crystallization experiments by measuring crystal growth rates and thicknesses as a function of copolymer composition. This method is unlike the usual method employed for homopolymer crystal growth studies where temperature is a variable.

5. The kinetic theory of crystallization formulated herein is applicable, in principle, to any model. Both inclusion and exclusion models or any intermediate model will depress the equilibrium melting point $T_m^0$ of the homopolymer to some new equilibrium value $T_m^0\left(X\right)$. Since the kinetics of crystallization ultimately depend on thermodynamic quantities, in particular $T_m^0$ and $T_m^0\left(X\right)$, all models will qualitatively affect the kinetics in the same manner. The fundamental quantity which enters the kinetic theory is

   $$\left(T_m^0-\left(T_m^0\right)\left(X\right)\right)/\left(T_m^0\left(X\right)-T\right)$$

   For the inclusion model this quantity depends on composition (X) in a specific way and is defined as f(X, T) in this paper. However, it has been shown that for low concentrations of the noncrystallizable co-unit, both inclusion and exclusion models yield equivalent expressions for $T_m^0\left(X\right)$ [see eqs (2b) and (6)]. It seems reasonable, therefore, to conjecture that in the limit of low concentrations the functional form of f (X, T) is correct for all molecular models of the crystalline state.

5. Appendix. Variations in $\mathrm{\Delta }{G}_{WLF}^{*}$ With Composition and Temperature

In the main text it was argued that diffusional transport effects can result in higher effective undercoolings for copolymers of higher concentration (X) when quenching on cooling at a uniform rate. The argument assumes that T_g either is unaffected or increases as X increases. If ∂T_g/∂X is negative the argument must be qualified. For this purpose the variations in $\mathrm{\Delta }{G}_{\text{WLF}}^{*}/RT$ with respect to composition and temperature are calculated below.

Let $Z=\mathrm{\Delta }{G}_{\text{WLF}}^{*}/RT$, then from eq. (21), we have

$$\left|\frac{\partial \text{ln}Z}{\partial T}\right|=\frac{1}{C_2+T-T_g}$$

and

$$\left|\frac{\partial \text{ln}Z}{\partial X}\right|=\frac{\partial T_g/\partial X}{C_2+T-T_g}$$

If ∂T_g/∂X is negative the argument will be valid if the change in Z between the two crystallization temperatures, $T_1-T_2=T_m^0\left(X_1\right)-T_m^0\left(X_2\right)$, exceeds the change in Z with concentration. To a first approximation this condition can be expressed as

$$\left|\frac{\partial \text{ln}Z}{\partial T}\right|\left[T_m^0\left(X_1\right)-T_m^0\left(X_2\right)\right]>\left|\frac{\partial \text{ln}Z}{\partial X}\right|\left[X_2-X_1\right]$$

or

$$-\frac{\partial T_g}{\partial X}<\frac{T_m^0\left(X_1\right)-T_m^0\left(X_2\right)}{X_2-X_1}$$

From eq (2b), we have

$$-\frac{\partial T_g}{\partial X}<A{T}_m^0$$

For example, A = 1.4 and $T_m^0=612K$ for the tetrafluoroethylene-hexafluoropropylene random copolymers and thus, the argument is valid if T_g decreases at a rate less than 8 K for a 1 percent change in composition.