Refractive Indices of Fused Silica at Low Temperatures

Abstract

The refractive indices of a commercial fused silica specimen were determined at ten wavelengths from 404.7 to 667.8 nm over the temperature range from −200 to +20 °C. The data are needed for the design of optical systems for space applications where the extremes of temperature are encountered. Values of the thermal coefficient of refractive index were found to be positive and varied from about 9 × 10⁻⁶/°C at room temperature to 3 × 10⁻⁶/°C at liquid nitrogen temperature. The data also showed that there is an increase in dispersion with increasing temperature. These results bear out the predictions of the theory for the thermo-optic behavior of solids.

1. Introduction

Data on the refractive indices of fused silica at low temperatures are needed in the design of optical systems for space applications. A survey of the literature shows that Rinne [1, 2]¹ made measurements to −160 °C for four spectral lines of helium radiation. He used the classic minimum deviation method with a prism of fused silica and a goniometer which read to 2 s. The data are reported to 5 significant figure’s. Austin and Pierce [3] have reported on refractive indices to −200 °C for one spectral line of helium at 587.6 nm. These authors used an optical interference method in which change in optical path length was measured, and the change in refractive index from an initial value was calculated; the technique requires data on linear thermal expansion. This method makes it possible to obtain index data to 6 significant figures.

The source of the fused silica was not specified in either of the above investigations. In the present study, it was desired to obtain data on commerical fused silica, Corning Code 7940,² from +20 to −200°C for 10 wavelengths from 404.7 to 667.8 nm.

Fused silica is an interesting material for study, because it is known from earlier work that the change of refractive index with temperature, dn/dT, is very large, being about 9 × 10⁻⁶/°C at room temperature, [3] whereas for most optical crown glasses it is about 2 or 3 × 10⁻⁶/°C [4,5]. On the other hand, the coefficient of thermal expansion is extremely low, being about 0.5 × 10⁻⁶/°C [6, 7] while most optical glasses have values on the order of 8 to 10 × 10⁻⁶/°C [4]. There is, therefore, a large value of dn/dT for fused silica which cannot be attributed to change in volume.

2. Experimental Method

The interference method employed by Austin and Pierce [3] offers the attractive feature of high precision of measurement. There is the additional feature that, since the specimen employed is small, thermal gradients constitute less of a problem. Moreover, a continuous record of change in optical path length may be obtained by using a continuously recording camera. For these several reasons it was decided to use this basic method with some amplifications to permit the photographing of fringe shifts for several spectral lines simultaneously.

In the optical interference method the specimen in the form of a plate with flat, polished faces constitutes the interferometer. When this plate is viewed in reflection using collimated, monochromatic light, a pattern of localized, Fizeau-type interference fringes may be seen at the top surface. For a specimen of thickness, t, and refractive index, n, the fringe number N is given by

$$N\lambda =2tn.$$ (1)

A change in temperature, T, will cause a shift in the fringe pattern, because of changes in t and n. By differentiating (1) and rearranging it is found that

$$\frac{\Delta n}{\Delta T}=\frac{\Delta N\lambda }{2t\Delta T}-\frac{n\Delta t}{t\Delta T}.$$ (2)

For a given temperature interval, ΔT, a measurement of the number of fringes that pass a fixed reference mark and the change in thickness, together with data on the initial index and thickness, permit the calculation of Δn.

The shift in interference fringes was recorded photographically on high speed film, using an optical system similar to the one described by Saunders [8]. It has been found that the proper adjustment of a prism in Saunders’ apparatus permits the recording of fringe shifts for several spectral lines on the same film [9]. In the present investigation four spectral lines of helium, 471.3, 501.6, 587.6 and 667.8 nm were recorded on one film, four spectral lines of cadmium, 467.8, 480.0, 508.6, and 643.8 nm were recorded on a second and two lines of mercury, 404.7 and 435.8 nm were recorded on a third.

The fused silica specimen was about 0.3 cm in thickness. This specimen was half-silvered on the front surface and fully silvered on the back surface in order to increase the brightness in the image plane.

The specimen was enclosed in a cryostat, in which liquid nitrogen was used to effect the reduction in temperature; this apparatus has been described [10]. In the present experiment, liquid nitrogen was added, a little at a time, and, after each addition, a waiting period of about one-half hour was allowed for a quasi-equilibrium condition to obtain. The temperature was measured at each plateau with a potentiometer and a calibrated copper-constantan thermocouple. Calculations showed that the sensitivity of measurement was 0.02 °C at room temperature and 0.5 °C at the lowest temperatures. In each run, eight to twelve temperature intervals provided data points from +20 to about −192°C.

3. Results and Discussion

The experiments involved only measurement of changes in optical path, and initial values of refractive index at 20 °C for the various spectral lines were those reported by Malitson [11]. The small corrections for the change in length, Δt, were taken from the data of Scheel and Heuse [6] which are recommended by Sosman in his compendium on silica [7], With this information plus the measured values of ΔN, it was possible to calculate Δn for each temperature interval. It was estimated that shifts could be measured to one-tenth of an interference fringe, and calculations showed that this meant that the sensitivity of measurement was about ±2 × 10⁻⁵ in Δn.

The calculated values of Δn were then fitted by computer to a cubic equation, and values of Δn at temperature intervals of 10 °C were printed out from +20 to −200 °C. These increments were added to the initial values of refractive index, and the results which refer to air at 20 °C are shown in table 1. The standard deviation of each value of the original data was within ±1 × 10⁻⁵.

Table 1.

Refractive index of fused silica, Corning Code 7940, as a function of temperature and wavelength

Temp °C╲λ, nm	667.8 He	643.8 Cd	587.6 He	508.6 Cd	501.6 He	480.0 Cd	471.3 He	467.8 Cd	435.8 Hg	404.7 Hg
+ 20	1.45607	1.45670	1.45846	1.46186	1.46224	1.46350	1.46406	1.46429	1.46669	1.46962
+ 10	1.45599	1.45663	1.45838	1.46177	1.46215	1.46431	1.46398	1.46420	1.46661	1.46953
0	1.45590	1.45655	1.45829	1.46169	1.46206	1.46332	1.46389	1.46412	1.46653	1.46944
−10	1.45582	1.45647	1.45821	1.46161	1.46198	1.46323	1.46381	1.46403	1.46645	1.46935
−20	1.45573	1.45639	1.45813	1.46152	1.46189	1.46315	1.46372	1.46395	1.46637	1.46926
−30	1.45565	1.45631	1.45805	1.46144	1.46181	1.46306	1.46364	1.46386	1.46629	1.46918
−40	1.45557	1.45623	1.45797	1.46136	1.46173	1.46298	1.46356	1.46378	1.46620	1.46909
−50	1.45550	1.45615	1.45789	1.46128	1.46165	1.46290	1.46347	1.46370	1.46612	1.46901
−60	1.45542	1.45607	1.45781	1.46120	1.46157	1.46282	1.46340	1.46362	1.46604	1.46892
−70	1.45535	1.45600	1.45774	1.46112	1.46150	1.46275	1.46332	1.46354	1.46597	1.46884
−80	1.45528	1.45592	1.45767	1.46105	1.46143	1.46267	1.46324	1.46347	1.46589	1.46876
−90	1.45521	1.45585	1.45760	1.46098	1.46136	1.46260	1.46317	1.46340	1.46581	1.46869
−100	1.45514	1.45578	1.45753	1.46091	1.46129	1.46254	1.46310	1.46333	1.46574	1.46862
−110	1.45508	1.45571	1.45747	1.46085	1.46123	1.46247	1.46304	1.46326	1.46567	1.46855
−120	1.45503	1.45565	1.45741	1.46079	1.46116	1.46241	1.46297	1.46320	1.46561	1.46848
−130	1.45497	1.45560	1.45736	1.46073	1.46111	1.46236	1.46291	1.46314	1.46555	1.46842
−140	1.45492	1.45554	1.45731	1.46068	1.46105	1.46231	1.46286	1.46309	1.46549	1.46837
−150	1.45488	1.45550	1.45726	1.46063	1.46100	1.46226	1.46281	1.46304	1.46544	1.46832
−160	1.45484	1/5546	1.45722	1.46059	1.46095	1:46222	1.46276	1.46300	1.46539	1.46828
−170	1.45480	1.45543	1.45719	1.46055	1.46091	1.46218	1.46272	1.46297	1.46535	1.46824
−180	1.45477	1.45541	1.45716	1.46052	1.46087	1.46215	1.46269	1.46294	1.46531	1.46821
−190	1.45475	1.45540	1.45713	1.46049	1.46084	1.46212	1.46266	1.46291	1.46528	1.46818
−200	1.45473	1.45539	1.45711	1.46047	1.46081	1.46210	1.46264	1.46289	1.46525	1.46816

The initial values of refractive index used in the present study differed from those of the earlier investigators, but it is still possible to make a comparison of the changes in refractive index between two specified temperatures. The temperatures, 18 and −160 °C were selected because Rinne [1, 2] reports his data at these points, and Austin and Pierce [3] give an equation from which these values may be obtained. In the present study, values at 18 °C were found from the computer run although they are not given in table 1. The differences in refractive index are shown in table 2 for the four wavelengths used by Rinne and the single wavelength employed by Austin and Pierce. Considering that the sensitivity of measurement of the interference method is ±2 × 10⁻⁵, the difference of 4 × 10⁻⁵ for the two values of Δn at 587.6 nm (data of Austin and Pierce versus data of the present study) seems reasonable. Rinne’s data are of lesser precision, but, recognizing this, the agreement between the sets of data appears to be good.

Table 2.

Change in refractive index, −Δn × 10⁴, for fused silica for the temperature interval from +18 to −160 °C

λ, nm	667.8	587.6	501.6	471.3
Present study	12.1	12.2	12.7	12.8
Austin and Pierce		11.8
Rinne	10	11	12	14

It should be noted that the data obtained here bear out the phenomenological theory for the thermal change in the refractive index of solids which has been developed by Ramachandran [12, 5, 13]. According to this theory, dn/dT in a solid depends upon (1) a change in the number of dispersion centers and (2) a variation in the dispersion frequencies. This variation in the dispersion frequencies, in turn, shows a dependence upon volume change as the solid expands as well as an effect due purely to temperature.

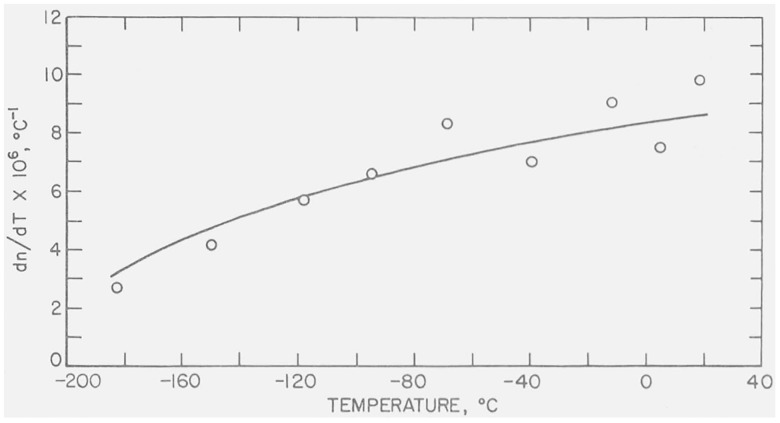
From data on commercial glasses [5] and fused silica [13], Ramachandran has inferred that the variation of the dispersion frequencies in these materials is essentially independent of change in volume and is almost solely dependent on temperature change itself. This is very apparent in the case of vitreous silica where the thermal expansion is extremely small, and the shift in the fundamental dispersion frequency accounts almost entirely for the observed changes in dn/dT. Values of dn/dT for the spectral line of 587.6 nm are shown as a function of temperature in figure 1. It can be seen in the figure that dn/dT decreases continuously to the lowest temperatures investigated, even though there is a maximum in the density of fused silica at about −80 °C [6, 7].

Figure 1. Temperature variation of dn/dT for fused silica at the helium spectral line of 587.6 nm.

The curve represents smoothed data taken from the computer run. The points represent values of Δn/ΔT calculated from the experimental data between two adjacent values of temperature and plotted at the mid-point.

The theory also predicts that the magnitude of the temperature shift of the fundamental absorption band decreases with fall of temperature, and probably vanishes at low temperatures. In fused silica this is manifested in the variation of dn/dT with temperature as shown in figure 1. For several commercial optical glasses, Molby [4] has found that refractive index versus temperature data exhibit a minimum at some reduced temperature. The commercial glasses have an appreciable thermal expansion (in contrast to fused silica) with an accompanying contribution to dn/dT that is always negative because of the lessening in the number of dispersion centers. The data on the optical glasses may be explained by the reduced contribution to dn/dT by the temperature shift of the fundamental absorption band at low temperatures.

Ramachandran has pointed out that the shift of fundamental absorption band with increasing temperature is toward longer wavelengths, so that there is an increase in dispersion. This is borne out by the data for fused silica shown in table 1, by subtracting the value of the refractive index for the spectral line of 667.8 nm from that at 404.7 nm, comparison shows that the differences are 0.01343 and 0.01355 at −200 and + 20 °C, respectively.