Measurements of Absolute Values in Biochemical Fluorescence Spectroscopy

Abstract

Fluorescence spectroscopy is an important tool of the biochemist studying the structure and interactions of proteins and nucleic acids. The four basic quantities to measure accurately are: 1. spectra (corrected excitation and emission), 2. quantum yields (Q), 3. fluorescence decay characteristics, and 4. polarization. Commercially available instruments, with little modification, can be used to obtain these measurements, but the biochemist in this field is very dependent on the accuracy of measurements of substances he uses as standards. Confusion arises from disagreement between reported values for standards which may be used to calibrate a detector system to obtain quantum yields, or to set up lifetime and polarization photometers. For instance, the protein chemist is fond of using tryptophan and quinine as quantum yield standards, but Q for tryptophan has been variously reported as 0.13 and 0.20, and Q values for quinine bisulfate range from 0.4 to 0.7. The biochemist should also be aware of the problems inherent in the use of commerically available instruments in absolute measurements, as well as the special complications arising in complex biochemical systems where the fluorescence is heterogeneous.

I. Introduction

A. Applications of Fluorescence Spectroscopy in Biochemistry

Within the last dozen years, biochemists have generally become aware of the value of fluorescence spectroscopy as a tool for the study of macromolecules such as proteins and nucleic acids. The marked increase in the use of fluorescence during recent years has also been due to improvements in instrumentation and techniques. Before discussing the types of measurements which are needed, let us consider some of the applications of fluorescence spectroscopy in physical biochemistry:

1. Obtaining Information on the Size and Shape of Macromolecules.

In 1952, Weber [1, 2]¹ pointed out that the polarization of fluorescence of dyes attached to proteins could be used to give information on rotational relaxation times. These times were an estimate of the Brownian motion occurring during the lifetime of the excited state; hence, information was obtained concerning the size and shape of the proteins. The equation derived by Weber [1] to correlate the degree of polarization, P, with the fluorescence decay time τ, and the relaxation time ρ_h, was based on similar equations originally formulated by Perrin [3] and Levshin [4] for simple organic fluorophors:

$$\frac{1}{P}-\frac{1}{3}=\left(\frac{1}{P_0}-\frac{1}{3}\right)\left(1+\frac{3\tau }{{\rho }_h}\right)$$ (1)

where P₀ is the limiting polarization. Because the quantity τ/ρ_h is proportional to the ratio T/η (T, absolute temperature; η viscosity), a “Perrin plot” of $1\overline{P}-1/3$ versus T/η obtained from polarization data with protein-dye conjugates at different temperatures and/or viscosities, contains all the information needed to calculate the rotational relaxation time of the molecule, provided the lifetime can be measured. Polarization data are also useful for following conformational changes such as unfolding or dissociation of a protein. Such events can frequently be monitored by no other known techniques [5]. Note that utilization of eq (1) requires both polarization and lifetime determinations.

2. Study of Binding Equilibria

The interaction of proteins with small ligands is a key function of proteins comprising certain physiological systems. This is especially true in the case of enzymes, proteins with catalytic properties. Some of these ligands, such as coenzymes like reduced nicotinamide adenine dinucleotide (NADH) are naturally fluorescent, and the binding of the ligands is accompanied by a large (typically, 2- to 5-fold) enhancement of the quantum yield, alteration of the emission spectrum, and an increase in the polarization of fluorescence. Other ligands such as flavin coenzymes are quenched on binding to proteins. Also, Velick [6] showed that the ultraviolet fluorescence of proteins is often quenched on binding of certain ligands. Any or all of these changes in fluorescence parameters are useful in obtaining the stoichiometry and association constants of the binding.

3. Elucidation of the Nature of Binding Sites

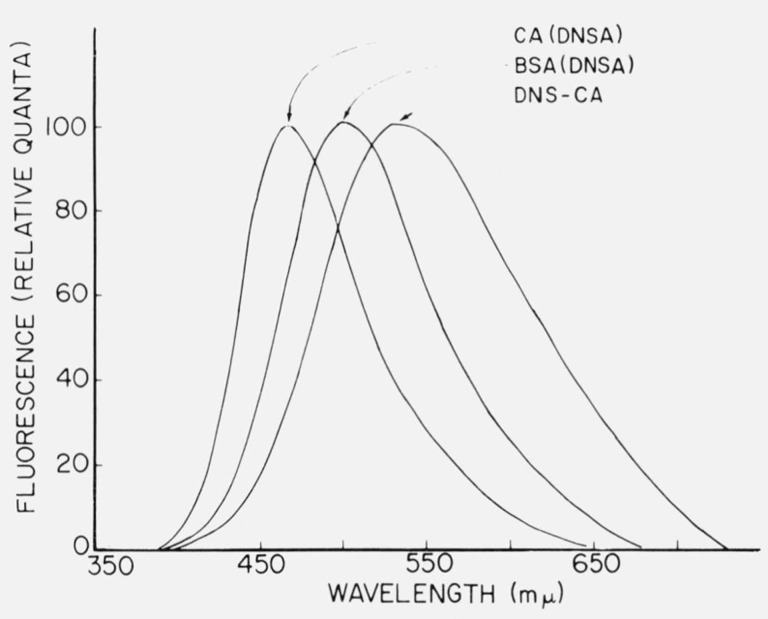
The dielectric properties of different areas on proteins differ markedly; such differences can be signalled by the fluorescence behavior of fluorescent ligands bound to these areas. Dyes which have been useful in this regard have been dubbed “fluorescent probes”. The Stokes shift and quantum yield of bound fluorescent probes have been used to estimate the microscopic dielectric constant of binding sites in proteins. An example of how the nature of the binding site affects fluorescence is given in figure 1. The l-dimethylaminonapthalene-5-sulfonyl (DNS) group has emission properties which make it useful for a variety of fluorescence studies, including polarization. When DNS is used as a probe, a high quantum yield and a small Stokes shift is indicative of a nonpolar environment. Absorbed onto the active site of the enzyme, carbonic anhydrase, DNS in the form of the sulfonamide has a smaller Stokes shift than it does when adsorbed to BSA (bovine serum albumin) or attached covalently to the enzyme (fig. 1).

Figure 1.

Corrected emission spectra of proteins containing the 1-dimethylamino-naphthalene-5-sulfonyl (DNS) group. CA(DNSA) and BSA(DNSA) are adsorbates of carbonic anhydrase and bovine serum albumin containing 1-dimethylamino-naphthalene-5-sulfonamide, and DNS-CA is a conjugate prepared by reacting carbonic anhydrase with DNS chloride. The curves are normalized to the same height. From Chen and Kernohan [7].

4. Study of the Environment Near Tryptophan and Tyrosine Residues in Proteins

Since it was discovered in the late 1950’s that proteins have an ultraviolet fluorescence due to aromatic amino acids, much has been learned about the types of molecules or groups on a protein which can influence such fluorescence. The spectrum of tryptophanyl fluorescence is an indicator of the polarity of the environment near the emitting group. Changes in intrinsic fluorescence can be used to follow conformational changes or binding. Intrinsic fluorescence is a useful optical parameter for kinetic studies, including rapid reactions followed by stopped-flow or perturbation methods.

5. Determination of Intermolecular Distances by Energy Transfer

The radiationless transfer of energy from an excited chromophore to an acceptor molecule via a dipoledipole resonance mechanism has been shown to occur in many intances. The theory of such energy transfer was studied by Förster [8] who developed a method for estimating the distance between donor and acceptor moieties based on their spectroscopic properties and the degree of energy transfer. Fluorometry is the best method for studying energy transfer, because this process is manifested by a quenching of the fluorescence of the donor and/or a sensitized fluorescence of the aceptor. A common example is that of a dye attached to a protein: the distance between the dye and the tryptophan residues may be estimated by the energy transfer from tryptophan to dye.

6. Study of the Orientation of Molecules Attached to Asymmetrical Macromolecules

By the use of polarized excitation, it is possible to obtain information on the orientation of ligands on a larger molecule. Using polarized photoselection, Lerman [9] determined that certain mutagenic dyes were attached with their planes perpendicular to the axis of deoxyribonucleic acid (DNA) molecules; this was the basis for his theory that mutagens intracalate between DNA base pairs. The orientation of dyes attached to proteins can similarly be studied by polarization measurements [10, 11]. The lack of a unique orientation of a dye fixed on a protein can also be detected. Such would be the case if dyes were attached in a random manner, or if a dye were attached to a flexible segment of the macromolecule.

7. Study of Changes in Conformation of Macromolecules

This is perhaps the most important use of fluorescence spectroscopy in biochemistry at present, and is accomplished by following changes in intrinsic fluorescence parameters as well as the fluorescence of attached groups. Such changes sometimes cannot be followed by other optical methods, and fluorescence becomes the method of choice, especially for kinetic studies.

B. The Parallel Development of Fluorescence Spectroscopy and Instrumentation

From the preceding section, one can see that biochemical fluorescence spectroscopy requires the measurement of a variety of parameters: excitation and emission spectra, quantum yields, lifetimes, and polarization. The needs of biochemists often exceed those of individual physicists or physical chemists, although in biological fields investigators frequently are considerably less knowledgeable concerning instrumentation than physical scientists and are not qualified to construct their own instruments. However, commercially available instrumentation has improved and often has incorporated the best features of laboratory-built devices described in the literature. It is now possible to measure all of the above fluorescence parameters with available instrumentation. The development of such instrumentation has played an important role in the evolution of fluorescence techniques.

Following the description by Bowman et al. [12] in 1955 of the first spectrofluorometer, several instruments based on their design were produced commercially. Such instruments contain, basically, a xenon arc lamp, a sample compartment, two monochromators, and a photodetector system. The principal innovations by Bowman et al. were the introduction of the xenon arc as a source of energy continuum for fluorescence excitation, and the incorporation of two monochromators for excitation and emission. In this country, at least half a dozen spectrofluorometers of this type are marketed. There are probably thousands of these spectrofluorometers in use. They may serve as a basic tool for fluorescence spectroscopy and are of modest cost.

More sophisticated instruments are now available for determining spectra which have been designed to compensate for variations of exciting energy and photodetector response. These instruments generally cost 3 or 4 times as much as an uncompensated spectrofluorometer.

Polarization measurements have been made on light scattering photometers, filter fluorometers, and spectroflurometers [12]. Although specific instruments for fluorescence polarimetry do not seem to be generally used, the modification of other available instrumentation for such purposes poses no great problem. Even in the field of lifetime measurements there are commercial instruments available for the purpose. The TRW Instruments 75A (El Segundo, California)² fluorescence decay apparatus and the ORTEC Model 9200 fluorescence spectrometer are the first instruments for determining lifetimes, which were previously accessible only to those with considerable engineering skill.

II. Measurement of Fluorescence Parameters

A. Definition of the Term “Absolute”

The term “absolute” as used here refers to a property of a substance rather than its measurement. For example, the absolute quantum yield of a substance is the ratio of the photons emitted to the number of photons absorbed, in contrast to the relative quantum yield, the number of photons emitted by one substance as compared with another under specified conditions. Confusion may arise, because the phrase “absolute quantum yield” has been used by some workers to denote the quantum yield which has been measured by an “absolute” method; i.e., a method not requiring the use of a reference standard of known quantum yield. Absolute measurements are frequently required in certain bilogical fields like bioluminescence, but will not be treated here.

1. Excitation and Emission Spectra.

a. Definition.—

The true, or absolute, fluorescence emission spectrum of a substance is a plot showing the relative number of photons emitted at different wavelengths; i.e., dq/dλ versus λ, where q represents the total number of photons emitted and λ is the wavelength. Alternatively, the same information can be plotted on a frequency scale, dq/dν versus ν in cm⁻¹. For simple organic compounds the emission spectrum is generally independent of the excitation wavelength, but for complex systems there is no single absolute emission spectrum since the emission may vary continuously with exciting light energy.

The excitation spectrum is a plot of the relative number of photons emitted at a given wavelength as a function of the exciting wavelength. The true, or corrected, excitation spectrum is compensated for any variations of excitation energy with wavelength. The corrected excitation spectrum is expected to coincide with the absorption spectrum in simple compounds, but this relationship may not hold in large biochemical systems.

b. Need for Corrected Spectra.—

Absolute fluorescence spectra would be useful for comparing results from different laboratories and have long been advocated [14] as being the most suitable form of data presentation. Expensive spectrofluorometers are available for automatic recording of absolute fluorescence spectra. However, many uncorrected spectra are published even today, and some case can be made for continued use of uncorrected data. Thus, when the main point of a study is simply to show changes in fluorescence characteristics, there is little reason to take trouble to correct the spectra. The thousands of spectrofluorometers in use are equipped with similar gratings and photomultiplier tubes, so that uncorrected spectra from one laboratory can, in fact, be used for comparison with results from another laboratory.

Absolute spectra are more informative, are required for quantum yield determinations, and are necessary for calculations of natural lifetimes or energy transfer distances. Nonetheless, one can confidently predict continued use of uncorrected spectra in the literature.

c. Calibration of Lamp Output and Detector Response.–

Since most biochemists utilize uncompensated spectrofluorometers, it should be pointed out that procedures for calibrating these instruments have been published, e.g. [5, 15, 16]. The main steps involve (a) Calibration and alignment of the monochromators with a line source such as a mercury pen lamp, (b) Calibration of the exciting source with a fluorescent screen solution, such as Rhodamine B or some other dye, and (c) Calibration of the detector response by comparing the recorded signal from a standard lamp with its known output.

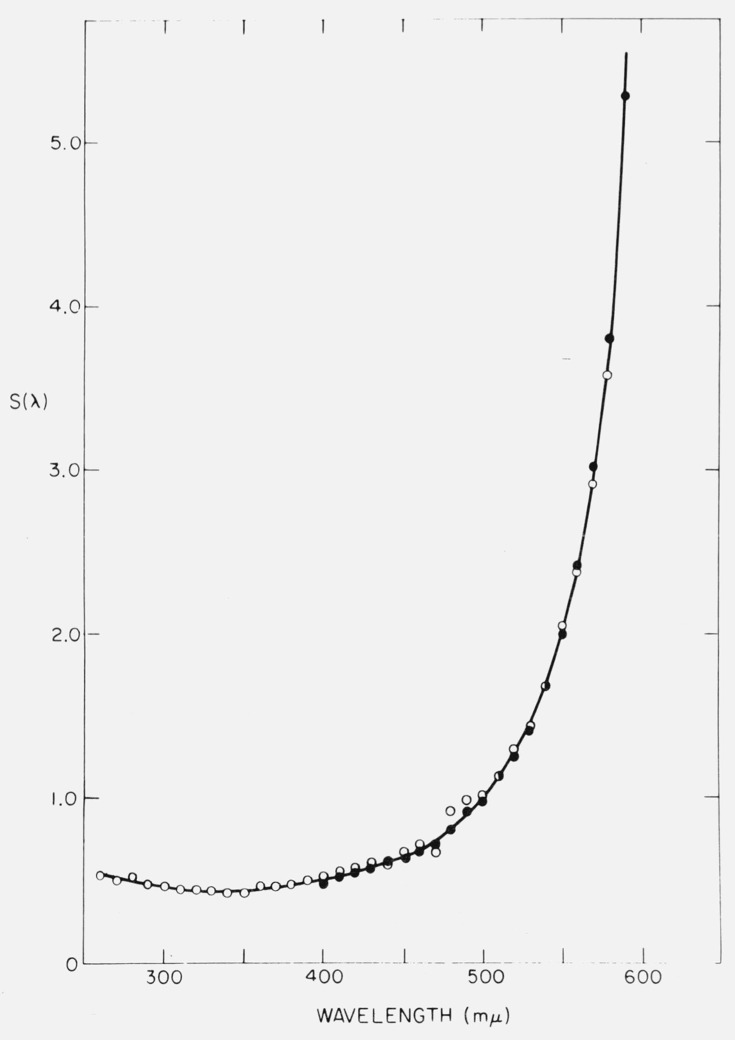
An example of a detector response calibration curve is given in figure 2. The response of an RCA 1P28 Photomultiplier in an Aminco-Bowman spectrofluorometer fitted with a grating blazed for maximum response at 300 nm seems to be quite linear in the region from 290 nm to 400 nm. The detector system thus delivers “absolute” emission spectra for substances like proteins which emit in this range. By choosing suitable gratings and phototubes, it is sometimes possible to obtain linear response in regions of visible fluorescence as well, thus avoiding the need for point-by-point correction of spectra.

Figure 2.

Detector calibration curve for Aminco-Bowman Spectrofluorometer fitted with 1P28 phototube and a grating blazed at 300 nm. Filled circles: data obtained with a National Bureau of Standards tungsten filament lamp. Open circles: data obtained with calibrated xenon arc lamp. S(λ) is a function of the reciprocal of the sensitivity. From Chen [16]

The accuracy of detector calibration depends on such factors as the photometric accuracy of the system and the accuracy of the standard lamp calibration. Lee and Seliger [17] have considered at length all the possible errors involved in absolute calibrations of detector systems. Their interest was principally the determination of chemiluminescent quantum yields, and it was necessary to know the relation between the number of photons and the detector response. In contrast, the determination of true emission spectra require that the relative detector response at different wavelengths be specified. Hence, the uncertainty in Lee and Seliger’s absolute calibrations, ±4.5 percent, is an upper limit in the more usual calibrations.

Calibration of spectrofluorometers by the use of “standard spectra” of well-known substances has been advocated [18]. In theory this would be a very convenient method. Comparison of the apparent excitation spectrum of a simple compound could be made with its absorption spectrum to yield the correction factors for lamp output. The method eliminates the need for a front-surface illumination attachment [15], which is needed for calibrations using the fluorescent screen method. Comparing absorption and emission spectra has the disadvantage that the same dispersion generally cannot be used in the absorption and fluorescence spectrometers. Other disadvantages make the comparison-of-spectra method less desirable than the fluorescent screen method. The latter results in a continuous plot of photon output versus wavelength compared with the discontinuous plot obtained by spectral comparison. Also, several absorption spectra are required to achieve a desired optical density at regions of maxima and minima, and several fluorescence excitation spectra at different gain settings will be needed as well.

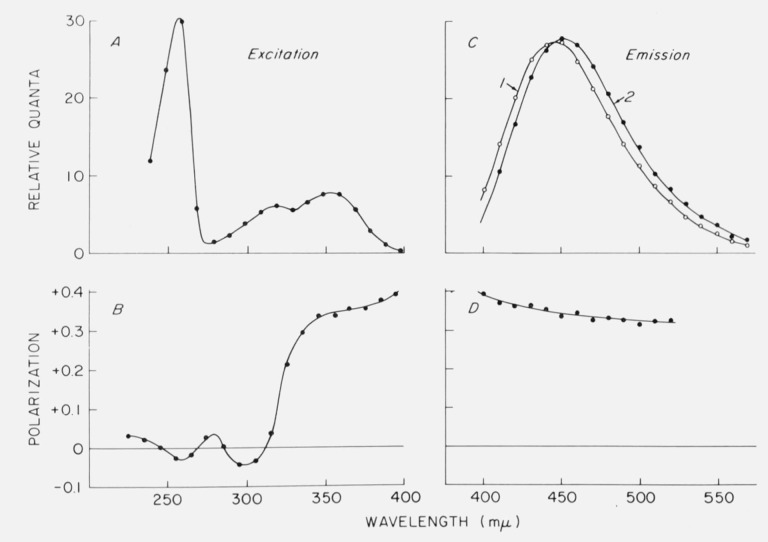
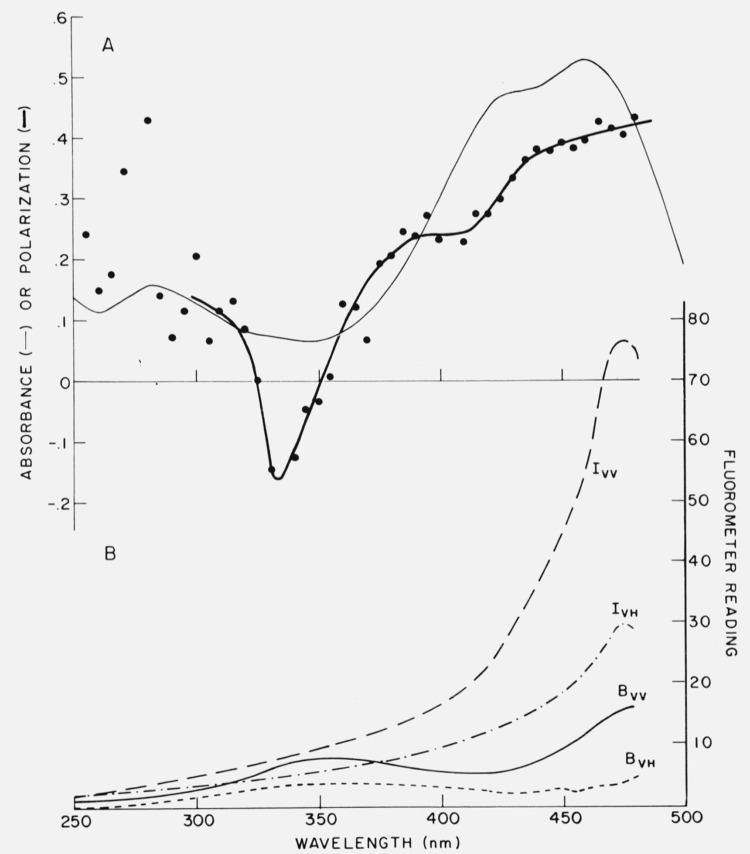
The use of “standard spectra” to calibrate the detector response is becoming common practice as more corrected spectra are published. Unfortunately, the reliability of any given published spectrum is unknown, and it would perhaps be helpful if some spectra were certified by a committee of experts. In the past, there have been many discrepancies in published emission spectra of quinine [19], although more recent spectra seem to agree closely [20–23] and could be used for detector calibration. One complication which we pointed out several years ago is that the emission spectrum of quinine shows a red shift when excited in the long wavelength edge of the absorption band [21]. This effect is shown in figure 3. The emission shift has been postulated by Fletcher [22] to be related to photoselection of quinine molecules with slightly different conformations. Other compounds also show this effect [21, 22, 24], which may involve what Fletcher calls rotatable auxochromes such as the methoxy group at the 6-position of the quinoline nucleus in quinine. At low temperatures, emission spectral shifts also occur due to the presence of different solvation states [25]. However, the spectrum of quinine under usual conditions of excitation should be suitable for a standard.

Figure 3.

Fluorescence and polarization spectra of quinine in glycerol containing 0.1 N H₂SO₄ at 8 °C A. Excitation spectrum. B. Fluorescence polarization spectrum obtained with varied exciting wavelength and emission monochromator set at 450 nm. C. Corrected emission spectra obtained with excitation at 340 nm (curve 1) and 390 nm (curve 2). D. Variation of polarization in the emission band with constant excitation at 340 nm. From Chen [21].

2. Quantum Yield Measurements

a. The Comparative Method of Determination.—

In biochemistry, the quantum yield is most often obtained by comparison with a quantum yield standard. A spectrofluorometer is required, and the yield is calculated from the relation

$$\frac{Q_x}{Q_{st}}=\frac{F_x}{F_{st}}\times \frac{A_{st}}{A_x}\times \frac{{\varphi }_{st}}{{\varphi }_x}\times \frac{n_{st}^2}{n_x^2}$$ (2)

where Q is the quantum yield, F is the area under the corrected emission spectrum, A is the optical absorbance at the exciting wavelength, ϕ is the relative photon output of the light source at that wavelength, and n is the refractive index. The subscripts x and st refer to the unknown and standard.

b. Factors Affecting the Accuracy.—

1. Accuracy of the emission detector response calibration.

Any errors present may have little effect on the quantum yield calculations if the spectra of the standard and unknown are similar. One should not use fluorescein as a standard to determine quantum yields of ultraviolet fluorescence, for example.

2. “Bookkeeping” errors.

Anyone who has attempted to perform quantum yield determinations must surely be impressed by the large number of factors which have to be inserted into the final calculations. Aside from the terms in eq (2), one must also remember that the photometer sensitivity may have been set at different values for standard and unknown, and the sensitivity scale may need recalibration. The absorbance, A, is usually read for concentrated solutions which then are diluted by some factor which renders self absorption unlikely in the fluorescence measurement; the dilution factor must be inserted. One can suspect that some of the large errors which have appeared in the literature are due to deficiencies in bookkeeping.

3. Determination of the absorbance.

Although it would seem a simple matter to determine the absorbance of the test substances, errors arise because the wavelength calibrations of the spectrofluorometer and the spectrophotometer may be slightly incorrect. Excitation then may occur at a wavelength different from that at which the absorbance was measured. The bandwidth of the monochromators also are usually different, and the amount of error from this discrepancy depends on the spectral characteristics of the compounds. We have found that our average deviations for quantum yield determinations have been smaller when the unknown and standard are each excited at the peak of their long wavelength absorption bands. With this method, one never need worry about slight monochromator alignment errors which would produce large errors in regions of sharply changing absorption.

4. Source output calibration.

If sample and unknown are excited at the same wavelength, the term ϕ_st/ϕ_x of eq (2) reduces to one. However, since different wavelengths are usually used, some error may intrude. The lamp calibration curve for the xenon arc [16] is fairly smooth from 230–400 nm. In this region, if the exciting wavelengths for x and st are not too wide, one would not expect much error to be introduced if there is slight inaccuracy in the knowledge of the exciting wavelengths. Between 400 nm and 520 nm, however, there are some strong peaks in the xenon arc output. In this region, perhaps it would be best to use the same wavelength to excite both standard and unknown. The calibration curve itself might be erroneous due to factors such as impurities in the fluorescent screen substance. This may be checked by using several different screens, or by determining if the calibration curve allows for corrected excitation spectra which match the absorption spectra.

5. Polarization effects.

In protein and nucleic acid fluorescence studies, the emission is frequently polarized due to the large size of the molecules. The resulting emission anisotropy can introduce an error into the quantum yield calculations even when unpolarized excitation is used, since even here, in instruments utilizing right-angle viewing geometry, the fluorescence is polarized. A number of papers have considered this problem [26–29]. Taking the worst possible case, Paoletti and Le Pecq [29] have estimated that a 15 percent error could occur in relative quantum yield measurements. However, an error this large could only occur with a sample showing maximum polarization in an instrument having large polarization artifacts, and where the fluorescence of standard and unknown were compared at individual emission wavelengths. Since the actual conditions for quantum yield assays are normally quite different, the errors are usually neglected, and indeed have never emerged as a great problem.

6. Accuracy of the value of the fluorescence standard.

a. Characteristics of quinine fluorescence.

Recent reviews [30, 31] have pointed out the surprising discrepancies in reported quantum yields which exist in the literature and the controversy over the values of several well-known quantum yield standards. The most common standard is quinine in aqueous sulfuric acid solutions. An absolute yield of 0.55 for quinine in 1.0 N H₂SO₄ was reported by Melhuish [32, 33] as well as by Windsor and Dawson [30]. These workers employed absolute methods for the determination. A value of 0.58 for quinine in 0.1 N H₂SO₄ was reported by Eastman [34] using a technique which was probably less accurate. The report by Drobnik and Yearghers [35] that quinine probably had a yield of less than 0.4 must be dismissed, since Fletcher [36] was unable to duplicate their experiment and found a discrepancy of a factor of 6 in their reported Q for 2-aminopurine. Windsor and Dawson [30] pointed out that there were already literature reports that quinine yield was dependent on the concentration of sulfuric acid. Many investigators, including ourselves, were guilty of using 0.546 for the yield of quinine in 0.1 N H₂SO₄ rather than 1.0 N acid. We find that the quantum yield actually is 6 percent lower in the more dilute acid, so a yield of 0.51 should be used. The reason for the dependence of yield on acid concentration is not clear, but it must be an excited state phenomenon since we have been unable to demonstrate any significant change in absorption spectrum for quinine dissolved in 10 N H₂SO₄ compared with 0.1 N H₂SO₄.

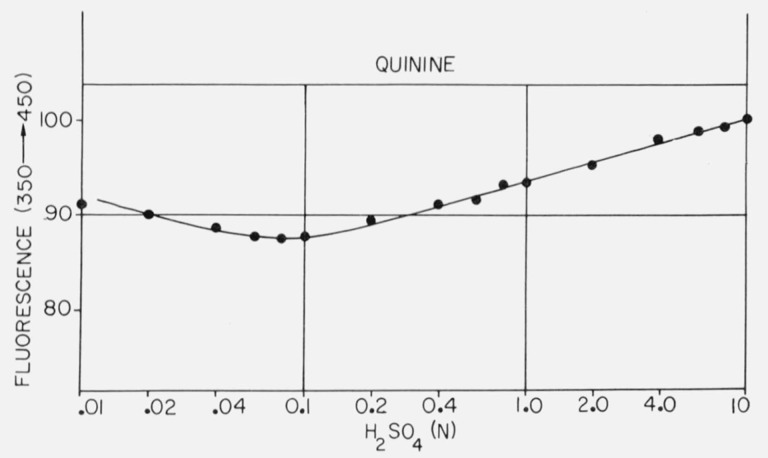
Figure 4 shows the titration of quinine which has a midpoint at about pH 4.3 by absorption measurements. The optical density-pH titration curve shows the normal flattening at both ends, but the titration by fluorescence shows a slight continuing rise in the acid region, although the midpoint of the titration curve is the same. Figure 5 shows the variation of quinine fluorescence yield with sulfuric acid concentration. Several features may provide a clue as to the processes involved here. The fluorescence increases almost linearly from 0.1 N to 10 N H₂SO₄, although there is no change in absorption. However, we have also noted that SO₄⁼ is a quencher of quinine fluorescence, although Stern-Volmer kinetics were not obtained. Thus the rise in quinine yield at high acid concentrations would be even larger except for the presence of sulfate ion. The slight increase in quinine yield at low acid concentration is reproducible and may be due to the lower concentration of sulfate ion.

Figure 4.

Titration of quinine monitored by fluorescence at 450 nm (---) or by optical density at 360 nm (—).

Figure 5.

Effect of H₂SO₄ concentration on the fluorescence of quinine excited at 350 nm and monitored at 450 nm.

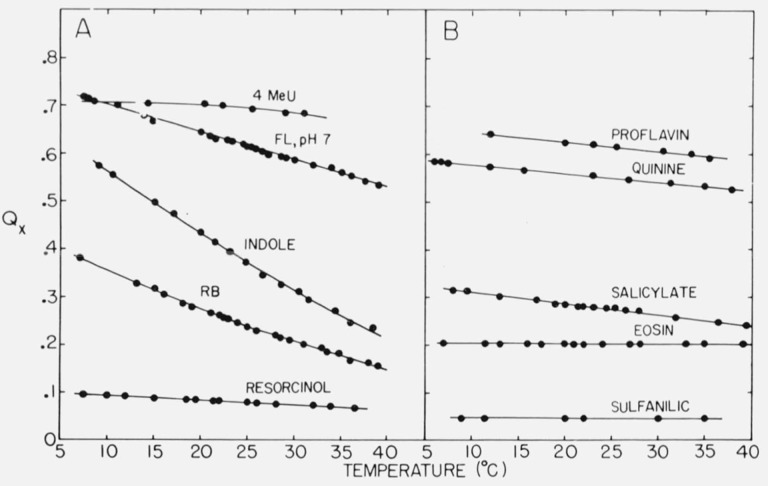
Quinine is a good quantum yield standard for biochemical studies for several reasons. It is used in aqueous solutions. There is little overlap of absorption and emission spectra. The quantum yield is high. The material is obtained in pure form readily and is stable in acid solutions for months. There is little structure in the absorption spectrum and none in the emission spectrum, so high resolution equipment is not needed. The temperature dependence of the yield is relatively small. Figure 6 shows the temperature dependence of the yields of some compounds which might be useful as standards.

Figure 6.

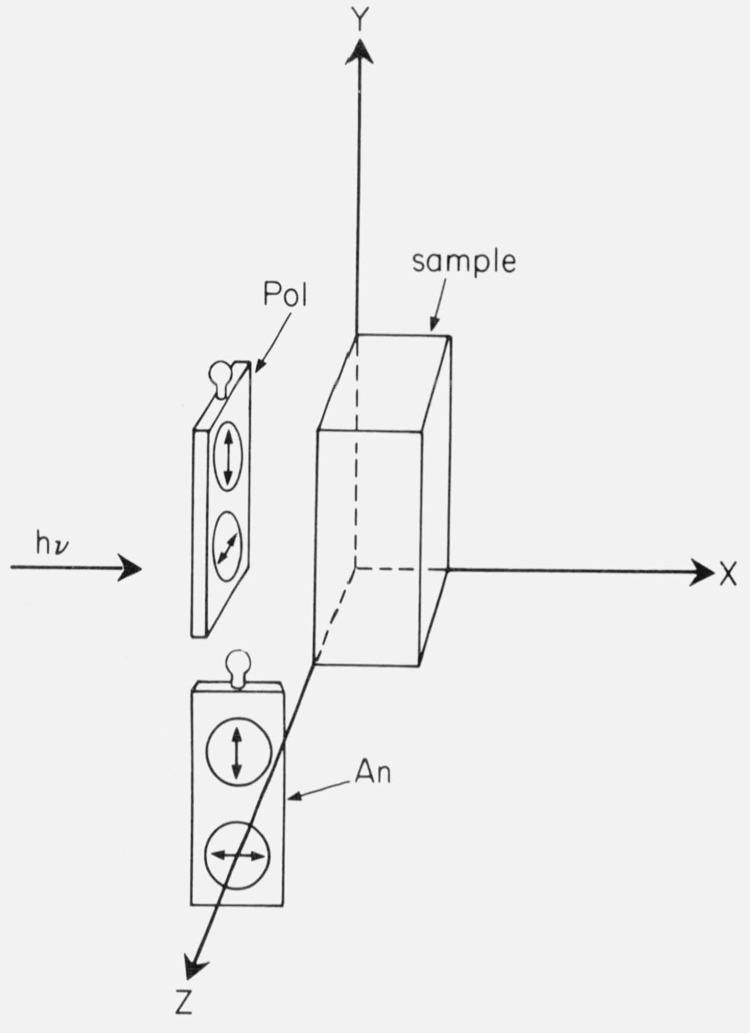
Recommended arrangement of polarizers in the Aminco-Bowman spectrofluorometer. The polarizers (Pol) and analyzers (An) are in sliding filter holders. From Chen and Bowman [13].

It is interesting that Rusakowicz and Testa [37] obtained a quantum yield of 0.46 for quinine in 0.1 N H₂SO₄ when comparing it with 9,10-diphenylanthracene, assumed to have a yield of 1.0 in cyclohexane. This value approaches Windsor and Dawson’s value of 0.50 [30] and a value of 0.51 which we now favor. The value of 0.46 is fairly good since a very large refractive index correction (17%) was needed for comparing cyclohexane and water solutions. Nevertheless, there is no compelling reason to favor use of 0.46 rather than 0.51 as the yield for quinine in 0.1 N H₂SO₄.

The commonly accepted value for the quantum yield of quinine has also been challenged recently by Scott et al. [23], who claim that the yield in 0.1 N sulfuric acid is 0.70 ± 0.02. This value was determined from a comparison of measured lifetime with calculated natural lifetime, assuming the relation Q = τ/τ_nat. This approach must be questioned, since the calculated natural lifetimes based on equations such as those of Forster [38] or Strickler and Berg [39] are quite approximate. Both Ware and Baldwin [40] and Birks and Dyson [41] noted the discrepancy between the measured and calculated lifetimes of quinine and have proposed explanations for this. The value of 0.70 must be too high, because many studies have used 0.55 as the value for quinine and have obtained values near unity for other compounds by comparison with quinine. Substitution of 0.70 for 0.55 would result in many quantum yields of greater than unity.

b. Controversy over the quantum yield of tryptophan.

The most common quantum yield standard used in biochemistry for the ultraviolet region is tryptophan, because it has an emission which matches closely the tryptophanyl fluorescence of proteins. Here, too, there has been controversy over the quantum yield. Shore and Pardee [42] estimated Q to be 0.09, but used a rather crude method involving a spectrophotometer modified for fluorometry with filters. Teale and Weber [43] subsequently reported a value of 0.20, which has since been widely used. We reported that the value should be 0.13 [44] based on comparison with quinine in 0.1 N H₂SO₄ assumed (incorrectly) to have a yield of 0.55. Our value for tryptophan Q should be revised downward to 0.12 in view of the lower yield of quinine, 0.51. Also using quinine as a standard, Børresen [45] and Bridges and Williams [46] obtained tryptophan yields of 0.11 and 0.15. Eisinger [47] determined the tryptophan quantum yield to be 0.14 based on comparison with p-terphenyl, whose yield was 0.87. If Eisinger’s data are correct, there can be no doubt that the value of 0.20 is much too high, for then the quantum yield of p-terphenyl would greatly exceed unity. We have convinced ourselves that 0.20 is, in fact, too high by similar comparisons with 9,10-diphenylanthracene and 2-aminopyridine (2AMP) which have very high quantum yields and have been recommended as standards [37, 48]. This simple experiment is recommended to anyone still in doubt concerning the quantum yield of tryptophan. While absolute measurements of quantum yield are difficult, relative quantum yields can easily be carried out with a precision of 5 percent. Therefore, if a standard with a supposed quantum yield of 1.0 is used, it is easy to determine an upper limit for the yield of any given unknown. Q determined in this way may be the real quantum yield, or, if the standard’s Q turns out to be less than 1.0, some smaller value.

c. Other useful standards.

Some quantum yields which have been measured in the author’s laboratory are listed in table 1. Several values are at variance with those reported recently from Testa’s laboratory [37, 48, 49]: 1. The yield of 2AMP is found to be 0.73 rather than 0.60. 2. The yield of 2AMP is found to be 6, rather than 13, times that of tryptophan. 3. A value of 0.55 for quinine in 1 N H₂SO₄ is consistent with our relative measurements, and is slightly higher than would be expected from the value of 0.46 reported for quinine in 0.1 N H₂SO₄.

Table 1.

Quantum yields of some possible standards

Compound	Q	Standard, Qst
2-Aminopyridine, 0.1 N H2SO4	*0.74	9,10-diphenylanthraoene, 1.0
Do	.73	tryptophan, 0.12
Do	.74	quinine, 1 N H2SO4, 0.55
Trytophan, water	*.12	9,10-diphenylanthracene, 1.0
Do	.12	quinine, 1 N H2SO4, 0.55
l-dimethylaminonaphthalene-5-sulfonate, 0.1 M NaHCO3	.34	Do.
4Methylumbelliferone, 0.01 M NaOH	.64	Do.
4-Methylumbelliferone, 0.01 M HCl	.65	Do.
5-Hydroxyindole (serotonin), pH 7.4	.23	Do.
Tyrosine, water	.13	Do.
Phenylalanine, water	.022	Do.
Phenol, water	.13	Do.
l-dimethylaminonaphthalene-5-sulfonamide, pH 7.4	.051	Do.

All values were obtained by the author with the Aminco-Bowman spectrofluorometer and a Gary Model 11S spectrophotometer, except for those marked (*). The latter were determined with a Turner Model 210 spectrofluorometer. The author is indebted to Dr. H. Edelhoch for the use of this instrument.

Tryptophan with a quantum yield of 0.12 seems to be the best standard for protein quantum yields. The idea of using a protein as a quantum yield standard has occurred to us. However, when testing different commercial preparations of serum albumin, the most widely available protein in pure form, we have found wide variations in yield. Fresh tryptophan solutions are more suitable; solutions are not stable for more than one day.

There are, of course, many other compounds which might be suitable for standards, but the problem is to find compounds which have been examined in many different laboratories which agree on the quantum yield values. Fluorescein in aqueous base has frequently been used with a yield of 0.85 [cf. 50], and this is an excellent standard if the unknown has similar spectra. Biochemists will most often require aqueous standard solutions, since their samples are usually in water. The correction factor for refractive index differences between a given solvent and water may be quite large (+ 17% for cyclohexane solutions, for example). The correction factor is only approximate for the actual geometry existing in a given spectrofluorometer, and should be avoided wherever possible.

d. On the “certification” of quantum yield standards.

In spite of our own confidence in the quantum yield data in table 1, we recognize that acceptance of compounds as standards comes only after agreement is reached between a number of reliable laboratories. Several studies have supported the values listed for tryptophan, 1-dimethylaminonaphthalene-5-sulfonate, quinine, 9,10-diphenylanthracene, and other compounds. Although a caveat has been issued [31] against the use of tryptophan as a standard, because of the controversy over its yield, a careful review of the data show that tryptophan Q is as well known as that of quinine. The use of quantum yield values for compounds over which controversy has not yet developed, because they have not been adequately investigated, seems irrational. The dearth of accepted quantum yield values is well brought out by the review of Demas and Crosby [31]. Perhaps one solution would be to carry out a cooperative study between several laboratories on a number of standards. This might speed the “certification” of standards.

3. Polarization Measurements

a. Definitions.—

The degree of fluorescence polarization, P, is defined by

$$P=\frac{I_V-I_H}{I_V+I_H}.$$

If a fluorometer utilizes right-angle geometry, I_V and I_H refer to the intensities measured with the analyzer oriented normal and parallel to the direction of excitation. Fluorescence polarization is observed when the excitation is either polarized or unpolarized, provided that observation of the fluorescence is normal to the direction of excitation. If polarization observed with excitation polarized vertically (i.e., parallel to the orientation of the analyzer when measuring I_V) is p_p, the polarization observed with unpolarized, or natural, excitation, p_n, is given by

$$p_p=\frac{2p_n}{1+p_n}.$$

Most studies are carried out with polarized excitation because the absolute values of the polarization are higher (− 1/3 ⩽ p_p ⩽ + 1/2) than with natural light (− 1/7 ⩽ p_n ⩽ +1/3). Perhaps the main reason for utilizing natural light is to obtain greater excitation intensities.

b. Measurement of polarization.—

If a light-scattering photometer is adapted for polarization of fluorescence measurements, one is generally limited to excitation with certain mercury lines, and both excitation and emission are selected by filters. The use of a spectrofluorometer results in greater flexibility. There seem to be no commercially available instruments designed primarily for fluorescence polarimetry, but polarizing attachments are offered by makers of light-scattering photometers and spectrofluorometers.

c. Artifacts in polarization measurements.—

1. Defective collimation.

The definition of P given above is based on the assumption that the exciting and emitted rays are perfectly collimated. In long path-length instruments, such a condition is nearly achieved. However, we have found that some simple filter fluorometers are quite unsuited for polarization measurements because the lamp is large and placed close to the sample, and the photodetector is also adjacent to the sample chamber. Large lenses which collect the fluorescence emitted at large angles to the axis connecting the sample and the photodetector may also invalidate the polarization data.

2. Polarizer defects.

These can be several types. Azumi and McGlynn [51] found that improperly fabricated Glan prisms rotated the beam of light as the prisms were turned from one orientation to the other. Errors in mounting can cause the ordinary (unpolarized) ray to pass to the sample, or the polarizers may be set at some angle to the desired orientation. Some film polarizers may have incomplete polarization, especially at short wavelengths. Most polaroid film polarizers do not seem to be light-fast and will rapidly bleach when exposed to a high intensity source. However, some light-fast film polarizers of large aperture are available [13]. A convenient arrangement for spectrofluorometers is to use such filters in the exciting beam, and polaroid analyzers before the photodetector, as shown in figure 7. This arrangement has been used by many workers with good results.

Figure 7.

Variation of the quantum yield, Q_x, of some compounds with temperature. Abbreviations: 4 MeU, 4-methylumbelliferone; FL, fluorescein; RB, Rhodamine B.

3. Spurious polarization introduced by the instrument.

Light reflected from surfaces in a grating monochromator instrument becomes partly polarized, and such polarization must be corrected. In the exciting beam, this partial polarization is best rendered completely polarized; i.e., p_p rather than p_n is measured, especially in spectrofluorometers. The polarization introduced by the emission monochromator is wavelength dependent and related to variations in efficiency of the grating (“grating anomalies”). This artifact may be corrected by first determining the relative response of the detector system at any wavelength to horizontally and vertically polarized light. The grating correction factor, G, is obtained by observing a source of unpolarized light with the analyzer in the vertical and horizontal positions. A fluorescent sample can act as such a source if excited with horizontally polarized light. Polarization is then determined from

$$P=\frac{I_{VV}-G{I}_{VH}}{I_{VV}+G{I}_{VH}}$$

where G = I_HV/I_HH, and the subscripts refer to the orientations of the polarizer and analyzer.

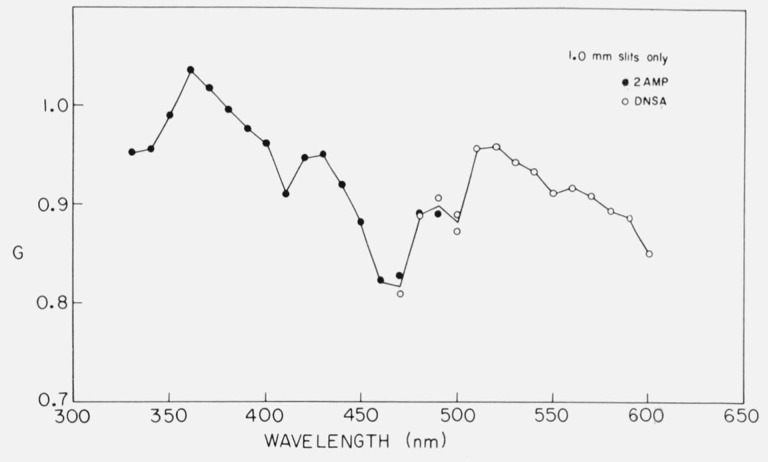
G should depend only on the wavelength setting of the emission monochromator. For this reason, a calibration curve may be obtained with one or two highly fluorescent solutions and may be applied to measurements on other substances. The monochromator bandwidth should affect the G factor, but in our tests, the available bandwidths made very little difference in G [52]. Figure 8 shows the G factor calibration obtained with a spectrofluorometer. Although G could be measured for each sample, some solutions have very low fluorescence yield, and there may be large blank corrections required in determining I_HV and I_HH. A calibration curve obtained under better conditions is preferable. One of the interesting features of figure 8 is that G varies sharply with wavelength. Some authors [51] have suggested that G declines monotonically with wavelength, but this is clearly not the case.

Figure 8.

Dependence of the grating factor, G, with emission setting; i.e., calibration curve for G. The samples used were 10⁻⁴ M 2AMP in 0.1 N H₂SO₄ excited at 285 nm, and 10⁻³ M DNSA (1-dimethylaminonaphthalene-5-sulfonamide) in 50 percent ethanol, excited at 330 nm. G was calculated from I_HV/I_HH. From Chen [52].

4. Contributions from blanks.

Like other measurements involving fluorescence intensity, polarization measurements should be rigorously corrected for blank contributions. If the G factor is known from prior calibration, polarization measurements still require four measured values: I_VV and I_VH for sample and blank. The magnitude of the blank relative to the sample signal can be large, as shown in figure 9 for the example involving bilirubin. Q for bilirubin bound to albumin is less than 0.01, and there is a background fluorescence due to impurities on albumin. There are relatively few instances where the blank can be neglected completely. Such might be the case of high quantum yield dyes dissolved in glycerol. A number of “automatic” fluorescence polarimeters have been described [53–55] in which I_VH and I_VV are measured simultaneously and ratioed electronically to give a function proportional to P. However, the common failing of these instruments is an inability to correct for the blank.

Figure 9.

Example showing significance of blanks in polarization measurements. In A are shown the absorption (light line) and polarization spectrum (heavy line and points) of bilirubin bound to rabbit serum albumin. The polarization was calculated, using G = 0.960, from the data of Part B, which gives the apparent excitation spectra of the sample (I) and blank (B). Subscripts refer to orientation of the polarizer and analyzer. The emission was monitored at 520 nm. From Chen [52].

5. Scattering.

If scatter signal reaches the detector, the polarization will be anomalously high. Scatter can be corrected with a suitable blank, but such blanks may not be available. For example, in obtaining the polarization of the intrinsic emission from a protein, the blank should have the same light-scattering properties without being fluorescent. In turbid solutions, scatter may indirectly lower the observed fluorescence by causing the excitation to appear to reach the sample from many directions due to multiple reflections. For the most accurate measurements, the solutions should be clarified by centrifugation or filtration.

6. Depolarization by radiative energy transfer.

In concentrated solutions of substances with considerable overlap of their absorption and emission spectra, depolarization can result from secondary fluorescence which has been excited by self-absorption of radiation. The effect can be detected by the increase in P upon dilution, and can be minimized by the use of small path length cells. Dyes with high absorption coefficients, like fluorescein and Rhodamine B, have been reported to exhibit concentration depolarization in solutions as dilute as 4 × 10⁻⁶ M [56].

d. Standards for Polarization.—

Standards for fluorescence polarimetry would be helpful to evaluate the performance of a given instrument, but such well-defined standards do not appear to exist. There are considerable variations in reported polarization values for given solutions. The variations are as great as in the area of reported quantum yield values. In the absence of such standards, it is necessary to be certain that the apparatus registers zero polarization for nonviscous solutions of compounds with long lifetimes. Anthracene or other aromatic hydrocarbons in ethanol or cyclohexane may serve this purpose. At the other end of the scale, a sample having nearly the theoretical maximum polarization of 0.5 is desirable. An instrument could read zero for the polarization of a nonviscous solution, but might well give erroneously low polarizations for viscous solutions. Alkaline fluorescein, or Rhodamine B, in glycerol were reported to have polarizations between 0.4 and 0.5 and are therefore often used to test the performance of fluorescence polarimeters. The polarizations reported by various workers are given in table 2. Note that there is considerable variation in these values. The best agreement is for Rhodamine B excited at 546 nm: the P values are 0.45 ± 0.01. Poor agreement is found for the values of polarization of Rhodamine B excited at 366 nm.

Table 2.

Polarizations of dilute dye solutions in glycerol

Sample	Exciting wavelength (nm)	P	Reference
Fluorescein	366	0.28	Chen and Bowman [13]
Do	366	.424	Price at al. [57]
Do	430–520	.477±0.01	Chen and Bowman [13]
Do	436	.440	Weber [56]
Do	436	.446	Price et al. [57]
Do	436	.4922	Szalay et al. [58]
Rhodamine B	366	−0.17	Chen and Bowman [13]
Do	366	−.0655	Weber [56]
Do	366	−.091	Price et al. [57]
Do	366	−.17	Kaye[59]
Do	436	−.020	Chen and Bowman [13]
Do	436	−.0244	Weber [56]
Do	436	0.0	Price et al. [57]
Do	436	−0.03	Kaye [59]
Do	546	0.462	Chen and Bowman [13]
Do	546	.444	Weber [56]
Do	546	.441	Price et al. [57]
Do	546	.462	Singleterry and Weinberger [27]
Do	546	.44	Kaye [59]

Useful polarization standards should have polarization which is independent of the emission wavelength. We have found this to be the case for Rhodamine B, fluorescein, and other compounds. However, we found [21] that quinine polarization decreases with wavelength in the emission band (fig. 3).

In many biochemical systems, the emission arises from several fluorophors such as dyes or tryptophans in different parts of a single protein. The polarization therefore depends on both the exciting and emission wavelengths. Much of the early work on the polarization of dye conjugates was obtained with fluorometers where the emission was isolated by a cut-off filter. Such data cannot be duplicated on a spectrofluorometer which detects only a segment of the emission band.

4. Fluorescence Lifetimes.

The fluorescence decay time, or lifetime, τ, is defined by I = I₀e^−t/τ where I₀ is the fluorescence intensity at time t = 0 following a delta function exciting pulse, and I is the intensity at subsequent time t. The lifetime is thus the time required for decay of the fluorescence to a value of I₀/e.

The decay times of organic molecules in solution which are of interest to biochemists lie in the range of 0.1 to 100 ns. The accurate measurement of such short times requires complex electronic equipment, but there have been many recent advances in this field. There were no commercially produced instruments for the measurement of τ until 1966. However, numerous laboratory-built instruments had been designed and described. The features of such instruments have been reviewed by Birks and Munro [60].

Two basic types of instrument have been employed. (a) Phase and modulation fluorometers. Here the sample is excited by light which is sinusoidally modulated at megacycle frequencies. The fluorescence thus also fluctuates at these frequencies, but lags behind the excitation by a certain time which is detected electrically as a phase shift with reference to the exciting light. From the phase shift, one can calculate the lifetime value if fluorescence is assumed to decay as a single exponential. The fluorescence decay is also manifested as a decrease in the degree of modulation, and the lifetime can be obtained from this parameter quite apart from the electrical phase shift. Müller et al. [61] reported that a phase fluorometer could be constructed wholly from commercially available components. Spencer and Weber [62] have also constructed a modern phase and modulation fluorometer. Both of these instruments are said to have a very high time resolution, of the order of 0.02 nsec. Therefore, the accuracy of lifetime measurements can be said to exceed the accuracy of absolute determinations of quantum yield. No phase fluorometers have ever been marketed. (b) Nanosecond pulse instruments. By repetitively exciting a sample with a short pulse of light, it is possible to obtain directly, with the aid of a fast oscilloscope, the curve of the fluorescence decay. Ideally, the light flash should be infinitely short; the observed fluorescence should then decay exponentially. Practically, lamp pulses have a finite duration with widths at half maximum intensity of 1 to 10 ns, and the pulse shape may be irregular. The fluorescence decay is also a complex function from which the lifetime must be extracted by any of several mathematical procedures. Advances in lamp design and the use of mode-locked lasers with picosecond pulses may in the future avoid the need for such manipulations, since the excitation will be much shorter than the fluorescence.

The two instruments which are currently available from commercial sources for lifetime determinations are both based on the nanosecond pulse method. In 1966, TRW Instruments introduced a decay time apparatus consisting of a nanosecond fluorometer with a “decay time computer” and requiring a dual-gun oscilloscope. One gun of the oscilloscope was used to display the signal from the sample chamber, while the other channel was connected to the computer, which in turn consisted of a variable waveform signal generator and an analog circuit. The computer was used to compare the shapes of the waveforms derived from the lamp pulse and from a fluorescent sample. The difference between the waveforms was analyzed by the computer to give the corresponding decay time directly. The instrument has been described in some detail [63, 64], is still available, and can be fitted with different kinds of lamps for excitation at different wavelengths. Although originally designed for long lifetimes such as those associated with solid laser materials, the instrument was shown to be capable of measuring lifetimes less than 2 ns [65].

Recently, ORTEC, Inc. (Oak Ridge, Tenn.) has produced a nanosecond pulse instrument based on the so-called single photon counting principle. The important feature of the system is the method used to detect and record the signal from the sample chamber. The low intensity, very fast, nanosecond flash lamp is made weaker still by attenuators so that for each repetitive pulse, no more than one photon which leaves the fluorescent sample causes a response in the photo-detector. By timing the interval between the flash and the arrival of the photon at the detector, a histogram of counts versus time is built up and stored in a multichannel analyzer. After sufficient counts have been accumulated, the curve can be displayed on an oscilloscope or digitized for computer analysis. The advantage of the system is the extreme sensitivity, the good time resolution, the use of a lamp, which because of its low output can be made very fast, and then recording the actual undistorted decay. The system theoretically can be used to determine multiple lifetimes present in the fluorescence.

Lifetime measurements by any of the instruments mentioned require only a single standard, namely, a reflecting or scattering substance serving as a standard with τ = 0. No comparison with substances of known lifetimes is needed, so each lifetime measurement is, in fact, an absolute determination. There are now several compilations of lifetimes which can be used by investigators to test the accuracy of their instruments [60, 66].

Some lifetimes of fluorescence standards are listed in table 3. Many developers of lifetime instruments have examined fluorescein in aqueous base, and a lifetime of 4.5 ± 0.3 ns agrees with most of the values listed. Curiously, the value of 3.83 ns was obtained by Müller et al. [61] with an instrument estimated to be accurate to 0.02 ns. Several values for quinine lifetime have been reported and are listed in table 3. In 1.0 N H₂SO₄ the lifetime of quinine obtained by averaging the tabulated data is 19.9 ns with an average deviation of 0.5 ns or 2.5 percent. The agreement for this compound is as impressive as any listed by Birks and Munro [60], so quinine is probably the best lifetime standard now available.

Table 3.

Lifetimes of some fluorescence standards

Sample	Lifetime (ns)	Reference
Quinine, 0.1 N H2SO4	19.5	Weber [67]
Quinine, 1.0 N H2SO4	19.2	Berlman [66]
Do	19.4	Ware and Baldwin [40]
Do	20.1	Birks and Dyson [41]
Do	20.5	Metcalf, cited in [41]
Quinine, 10.0 N H2SO4	21.8	Present work
Quinine, 1.07 N H2SO4.	20.4	Do.
Quinine, 0.1 N H2SO4	19.0	Present work, also [65]
Quinine, 0.2 M Tris-NO3̄ pH 8…	17.2	Do.
Fluorescein, dilute NaOH or KOH.	4.62	Ware and Baldwin [40]
Do	4.6	Szymanowski [68]
Do	4.6	Metcalf [69]
Do	4.8	Bennett [70]
Do	4.8	Brody[73]
Do	4.8	Kirchhoff[74]
Do	4.8	Maercks [75]
Do	4.5	Bailey and Rollefson [71]
Do	4.5	Chen et al. [65]
Do	4.2	Weber [67]
Do	4.0	Brewer et al. [72]
Do	4.0	Strickler and Berg [39]
Do	3.83	Müller et al. [6]
9,10-Diphenylanthracene, cyclohexane, not de-aerated.	6.7	Present work
9,10-Diphenylanthracene, cyclohexane, de-aerated.	9.35	Berlman [66]
Do	10.0	Amata et al. [76]
2-Aminopyridine,0.1 yVH2SO4…	12.7	Present work
1-Dimethylaminonaphthalene-5-sulfonate, 0.1 M NaHCO3.	13.8	Chen et al. [65]
Do	13.6	Föirster and Rokos [77]

However, some caution is required in the use of quinine, because we have now found that not only the quantum yield, but the lifetime too, is dependent on the concentration of sulfuric acid (table 3) present.

III. Summary and Conclusions

In biochemistry, many of the same principles for measuring absolute fluorescence parameters are used which are employed in any other area of physical chemistry. Perhaps the only differences are the general use of aqueous solutions, the greater need for commercially available instrumentation, and the diverse types of measurement needed. The range and quality of available instruments have improved. There are still many problems regarding standards to be used for quantum yields, polarization, and spectra. Quinine, the universal standard, has been shown to undergo changes in emission spectrum, quantum yield, polarization, and lifetime depending on factors such as the wavelength of excitation and the sulfuric acid concentration. To determine what the “true” values are for a given compound, further reporting of such values is to be encouraged. It is suggested that collaborative efforts might speed up the “certification” of values for fluorescence standards.