Abstract
Measurements of the heat capacity and relative enthalpy were made on aluminum carbide (Al4C3) from 15 to 1173 °K. The thermodynamic properties were calculated up to 2000 °K from the data by judicious extrapolation above 1173 °K. In conjunction with the heat-of-formation data on Al4C3 obtained by King and Armstrong and by Mah, second- and third-law analyses have been made of the thermodynamics of several high-temperature vapor-equilibrium reactions involving Al4C3.
1. Introduction
The results of heat-capacity and enthalpy measurements on aluminum carbide, Al4C3, in the range 15 to 1173 °K presented in this paper have been obtained in connection with a research program at the National Bureau of Standards to provide accurate thermodynamic and related data on the “light” elements and their compounds. No heat-capacity measurements on Al4C3 have been previously published, except for the relative enthalpy measurements in the range 273 to 693 °K by Satoh [1]1 on a sample that contained only 74.74 percent Al4C3, the impurities being 23.43 and 1.83 percent Al2O3 and SiO2, respectively. The work reported by Satoh is based on measurements at only three temperatures in the above temperature range.
Aluminum carbide, Al4C3, is a yellow rhombohedral crystal of space group with a = 8.53 Å and α= 22°28′ [2]. Each carbon atom is surrounded by aluminum atoms and the shortest C—C distance is 3.16 Å [2], indicating that the carbon atoms are not bonded to one another. There are two structurally different carbon atoms, and the C—Al distance ranges from 1.90 to 2.22 Å. One of the carbon structures has six aluminum atoms at 2.17Å, and the other has one aluminum atom at 1.90 Å, three at 1.94 Å, and one at 2.22 Å. On hydrolysis, Al4C3 yields methane. Other aluminum carbides that have been reported are Al2(C2)3 [3] and Al3C [4]. The carbide Al2(C2)3, made by reacting acetylene with aluminum at 450 to 500 °C, yields acetylene on hydrolysis [3]. The carbide Al3C, observed in the Al—Al2O3—Al4C3 phase investigations reported by Baur and Brunner [4], should yield CH4 on hydrolysis.
2. Sample
The measurements of the low-temperature heat capacity and the high-temperature relative enthalpy were made on the same aluminum carbide sample kindly supplied by the Aluminum. Company of America, ALCOA Research Laboratories, through the courtesy of George Long. The material had been prepared by heating a stoichiometric mixture of aluminum powder and lampblack in an atmosphere of argon to 1800 °C. Qualitative spectrochemical analyses were made on representative specimens of the sample by the Spectrochemistry Section of the National Bureau of Standards. The results are summarized in table 1.
Table 1. Spectrochemical analysis of the sample of aluminum carbide (Al4C3).
| Element | % | Element | % | Element | % |
|---|---|---|---|---|---|
| Ag | −(?) | Hf | — | Sb | — |
| Al | >10 | Hg | — | Sc | — |
| As | — | In | — | Si | 0.01 −0.1 |
| Au | — | Ir | — | Sn | — |
| B | — | La | — | Sr | — |
| Ba | — | Mg | 0.001 −0.01 | Ta | — |
| Be | — | Mn | 0. 0001–0.001 | Te | — |
| Bi | — | Mo | — | Th | — |
| Ca | 0.0001−0.001 | Nb | — | Ti | 0.001−0.01 |
| Cd | — | Ni | 0.001 −0.01 | TI | — |
| Ce | — | Os | — | U | — |
| Co | — | P | — | V | 0.01 −0.1 |
| Cr | 0.001 −0.01 (?) | Pb | — | W | — |
| Cu | 0.001 −0.01 | Pd | — | Y | — |
| Fe | 0.1 −1.0 | Pt | — | Zn | — |
| Ga | — | Rh | — | Zr | 0.001−0.01 |
| Ge | — | Ru | — |
— : Not detected.
Chemical analyses were performed by Rolf A. Paulson of the Applied Analytical Research Section of the National Bureau of Standards. These results are given in table 2. Specimens 1 and 2 were sampled from the original Al4C3 preparation as received. Specimen 3 was sampled from that portion of the Al4C3 preparation on which the low-temperature heat-capacity measurements had been completed. The percentage Al4C3 was determined by dissolving a sample in hot sulfuric acid. The evolved gases, taken to be CH4 and H2, were burned and the combustion products collected. The amount of CO2 collected was converted to Al4C3 and the excess H2O over that attributable to CH4 was reckoned to have been formed from H2 released from the acid by free aluminum and iron. The insoluble residue from the hot sulfuric acid treatment was taken to be free carbon. Aliquot portions of the sulfuric acid solution were analyzed for total aluminum as Al2O3 by precipitating Al(OH)3 with ammonium hydroxide and igniting to Al2O3. The excess of aluminum over that attributable to Al4C3, free aluminum metal, and AlN was assumed to be Al2O3 in the original sample. The iron, determined in specimen 3 only, was analyzed colorimetrically using the thiocyanate-complex method on an aliquot portion of the sulfuric acid solution. The percentage AlN was determined by the Kjeldahl method on separate samples of the Al4C3 preparation.
Table 2. Chemical analysis of the sample of aluminum carbide (Al4C3).
| Component | Percentage by weight | ||
|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | |
| Al4C3 | 94.9 | 94.8 | 94.8 |
| Free Al | 1.2 | 1.3 | 1.0 |
| Free C | 0.9 | 0.7 | 1.0 |
| AlN | 1.4 | 13 | 1.3 |
| Al2O3 | 2.0 | 2.0 | 2.2 |
| Free Fe | 0.06 | ||
| Total | 100.4 | 100.1 | 100.36 |
The results of the chemical analysis agree with the usual composition found (of about 95% Al4C3) in samples prepared by the same method [5]. The small discrepancies in the analyses can be attributed to either uncertainties in the analytical methods or small inhornogeneities in the sample. The approximate summation of the analyses to 100 percent is an indication of the reliability of the analytical methods used. E. E. Hughes of the Applied Analytical Research Section, National Bureau of Standards, analyzed the gases generated by the action of an acid on the Al4C3 sample and found no acetylene or methylacetylene, indicating that Al2(C2)3 was not present in the Al4C3 preparation. No effort was made to determine whether Al3C was present.
M. v. Stackelberg et al. [6, 7] reported the conditions for formation and the crystal structure of the compound Al5C3N (Al4C3.AlN). The results of the heat-capacity measurements presented in this paper were processed assuming that the nitrogen found in the chemical analysis came from AIN mixed with Al4C3.
For the analysis of high-temperature relative-enthalpy measurements the average of the chemical analyses obtained in specimens 1 and 2 was normalized to yield 100 percent total analysis. The iron content, the chemical analysis for which was not made in specimens 1 and 2, was considered too small to contribute significantly to the results of the experimental data. In the processing of the heat-capacity data obtained at low temperatures, the chemical analysis obtained on specimen 3 was used, after normalizing to give a total analysis of 100 percent.
The corrections for the impurities were made assuming that the relative enthalpies were additive. The contributions from Al, Al2O3, and AlN impurities were adjusted in accordance with the tabular values of thermodynamic functions obtained through the analysis of the literature data in connection with the light element research program [8]. The values for C were based mostly on the measurements of De Sorbo and Tyler [9]. The corrections for Fe were obtained primarily from the heat-capacity data reported by Simon and Swain [10] and by Kelley [11].
3. Low-Temperature Calorimetry
3.1. Apparatus and Method
The low-temperature heat-capacity measurements were made from about 18 to 380 °K in an adiabatic calorimeter similar in design to that described previously [12]. The calorimeter vessel, which was filled with sample as described in section 3.2 and sealed by means of a specially designed gold-gasket closure [13], was suspended within the adiabatic shield system by means of a Nylon string instead of the filling tube shown in the above reference. The adiabatic shield was controlled automatically by means of a combination of electronic and electromechanical equipment. Details of the design of the calorimeter used, its operation, and the automatic adiabatic control system will be described in a later publication.
The platinum resistance thermometer used in the measurements was calibrated in accordance with the International Practical Temperature Scale of 1948 [14]. The temperatures in degrees Kelvin (°K) were obtained by adding 273.15 deg to the temperatures in degrees Celsius (°C). Below 90 °K, the thermometer was calibrated on the NBS-1955 provisional scale which is numerically 0.01 deg lower than the former NBS-1939 provisional scale [15]. The resistance measurements were made by means of a Mueller bridge and a high sensitivity galvanometer to the nearest 0.00001 Ω. The temperatures were calculated from the resistance by inverse interpolation in a table of resistance given as a function of the temperature at closely spaced regular intervals.
The electrical power introduced into the calorimeter heater (100 Ω of constantan wire) was measured by means of a Wenner potentiometer in conjunction with a volt box, standard resistor, and saturated standard cells. A constant-current power supply stable to 10 ppm or better was used to facilitate the power measurements. The duration of each heating interval was measured by means of a high precision interval timer operated on 60-cycle frequency standard provided at the National Bureau of Standards. The 60-cycle frequency standard is based on a 100 kHz quartz oscillator which is stable to 0.5 ppm. The estimated uncertainty in the readings of the interval timer was not greater than ±0.01 sec for any heating period, none of which was less than 2 min in these experiments.
3.2. Results
A sample of 153.8063 g mass was poured into the calorimeter vessel in a controlled-atmosphere box filled with argon gas (dew-point of −50 °C). At the same time, samples of the Al4C3 were sealed in test tubes under dry argon gas for chemical analysis. The calorimeter vessel plus the sample was evacuated and purged with dry helium gas several times. Finally, helium gas at a pressure of 5.8 cm Hg was sealed in the container with the sample. After completion of the measurements the calorimeter vessel was opened in the controlled-atmosphere box and additional samples taken for chemical analysis. As mentioned earlier, the analysis of the low-temperature heat data was based on the chemical analysis of the sample on which the measurements had been made (chemical analysis of specimen 3).
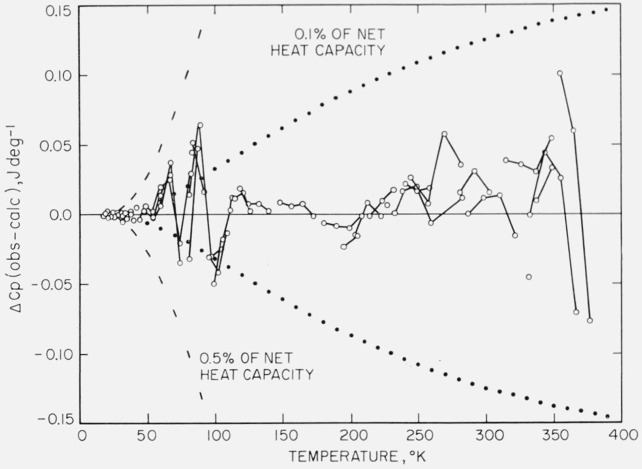
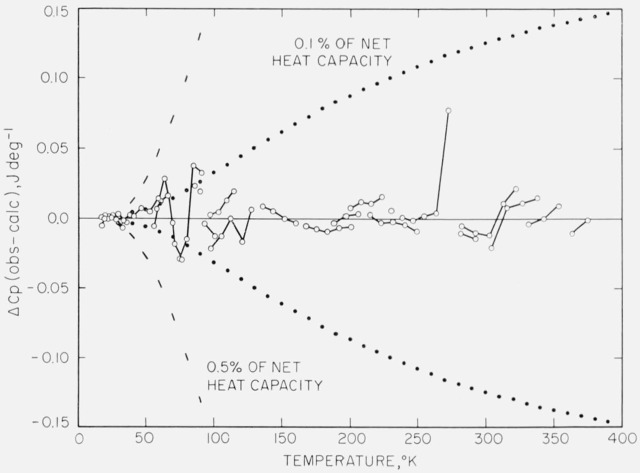
On the calorimeter vessel plus the sample (“gross”), 14 runs totaling 108 heat-capacity determinations were made and on the empty vessel (“tare”), 11 runs totaling 87 determinations were made. The experimental data of each of these two sets of measurements were fitted to empirical equations over selected, partially overlapping temperature intervals by the method of least squares using a digital computer. (A “set” of measurements consists of the observations of energy increments and the corresponding temperatures from about 18 to 380 °K on the empty vessel or on the vessel with sample. Measurements made during a given condition are classified as a “run” within the “set”.) The empirical equations consisted of polynomials, the positive powers of temperature up to 4 being used below the inflection point in the heat capacity and powers from −4 to +4 in the region of the inflection point and above. Details of the computer routines used will be described in a later publication. Briefly, the overlapping equations for each set were joined at temperatures of the most favorable combinations of values of heat capacity and its first and second derivatives. The values of heat capacity obtained at regularly spaced integral temperatures by this process were smoothed by a 9-point cubic smoothing code [16] on the computer. (For the two sets of heat data obtained between 18 and 380 °K, a smooth function is defined and restricted to the following properties: (a) continuous derivatives, (b) monotonic increasing with not more than two inflection points, and (c) sigmoidal configuration of the heat-capacity curve.) The deviations of the observations of each set of measurements from the final smoothed values are shown in figures 1 and 2.
Figure 1. Deviations of the heat-capacity measurements on sample plus calorimeter vessel.
Figure 2. Deviations of the heat-capacity measurements on the empty calorimeter vessel.
The net values of heat capacity, obtained by differencing the above smoothed gross and tare values at corresponding temperatures, were corrected for the impurities and the helium exchange gas and again smoothed on the computer wherever necessary. These values were then converted to molal units using atomic weights based on carbon-12 [17]. A Debye heat-capacity function, fitted to the smoothed values at the lower temperatures, was used to obtain the values from 0 to 18 °K.
A consideration was given at this point regarding the use of a table of thermodynamic functions. Although the joule is a more fundamental unit of energy and its use is preferred, most scientists who use tables of thermodynamic functions are accustomed to the calorie as an energy unit. The values of heat capacity were converted, therefore, to the unit cal deg−1 mol−1 using the relation: 1 defined calorie = 4.1840 J. These values of heat capacity from 0 to 390 °K were later combined with the high-temperature heat data (see sec. 5) and the thermodynamic functions from 0 to 1200 °K (table 5) obtained in terms of the defined calorie. The hope is that eventually the joule would be the common energy unit in all scientific work. The thermodynamic functions of table 5 are, therefore, repeated in the appendix in terms of the joule.
Table 5. Thermodynamic functions for aluminum carbide (Al4C3) solid phase.
Gram molecular weight=143.9594 g, T deg K=t deg C+273.15
| T | ||||||
|---|---|---|---|---|---|---|
| °K | Cal deg−1 mol−1 | Cal mol−1 | Cal deg−1 mol−1 | Cal deg−1 mol−1 | Cal mol−1 | Cal deg−1 mol−1 |
| 0.00 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5.00 | .001 | .001 | .000 | .000 | .000 | .000 |
| 10.00 | .005 | .012 | .001 | .002 | .004 | .000 |
| 15.00 | .017 | .062 | .004 | .006 | .021 | .001 |
| 20.00 | .041 | .195 | .010 | .013 | .065 | .003 |
| 25.00 | .095 | .520 | .021 | .027 | .162 | .006 |
| 30.00 | .188 | 1.207 | .040 | .052 | .355 | .012 |
| 35.00 | .334 | 2.486 | .071 | .091 | .707 | .020 |
| 40.00 | .549 | 4.667 | .117 | .149 | 1.299 | .032 |
| 45.00 | .833 | 8.094 | .180 | .230 | 2.236 | .050 |
| 50.00 | 1.183 | 13.106 | .262 | .335 | 3.636 | .073 |
| 55.00 | 1.603 | 20.042 | .364 | .467 | 5.628 | .102 |
| 60.00 | 2.083 | 29.236 | .487 | .626 | 8.350 | .139 |
| 65.00 | 2.612 | 40.956 | .630 | .814 | 11.939 | .184 |
| 70.00 | 3.191 | 55.444 | .792 | 1.028 | 16.532 | .236 |
| 75.00 | 3.801 | 72.910 | .972 | 1.269 | 22.265 | .297 |
| 80.00 | 4.437 | 93.495 | 1.169 | 1.534 | 29.264 | .366 |
| 85.00 | 5.089 | 117.31 | 1.380 | 1.823 | 37.648 | .443 |
| 90.00 | 5.753 | 144.41 | 1.605 | 2.133 | 47.529 | .528 |
| 95.00 | 6.424 | 174.85 | 1.841 | 2.462 | 59.007 | .621 |
| 100.00 | 7.099 | 208.66 | 2.087 | 2,808 | 72.175 | .722 |
| 105.00 | 7.776 | 245.84 | 2.341 | 3.171 | 87.117 | .830 |
| 110.00 | 8.456 | 286.42 | 2.604 | 3.549 | 103.91 | .945 |
| 115.00 | 9.138 | 330.41 | 2.873 | 3.939 | 122.62 | 1.066 |
| 120.00 | 9.819 | 377.80 | 3.148 | 4.343 | 143.32 | 1.194 |
| 125.00 | 10.499 | 428.60 | 3.429 | 4.757 | 166.07 | 1.329 |
| 130.00 | 11.175 | 482.79 | 3.714 | 5.182 | 190.92 | 1.469 |
| 135.00 | 11.843 | 540.34 | 4.002 | 5.617 | 217.91 | 1.614 |
| 140.00 | 12.503 | 601.21 | 4.294 | 6.059 | 247.10 | 1.765 |
| 145.00 | 13.154 | 665.35 | 4.589 | 6.509 | 278.51 | 1.921 |
| 150.00 | 13.795 | 732.73 | 4.885 | 6.966 | 312.20 | 2.081 |
| 155.00 | 14.427 | 803.29 | 5.183 | 7.429 | 348.19 | 2.246 |
| 160.00 | 15.048 | 876.98 | 5.481 | 7.897 | 386.50 | 2.416 |
| 165.00 | 15.658 | 953.75 | 5.780 | 8.369 | 427.16 | 2.589 |
| 170.00 | 16.258 | 1033.5 | 6.080 | 8.846 | 470.20 | 2.766 |
| 175.00 | 16.846 | 1116.3 | 6.379 | 9.325 | 515.62 | 2.946 |
| 180.00 | 17.424 | 1202.0 | 6.678 | 9.808 | 563.46 | 3.130 |
| 185.90 | 17.991 | 1290.5 | 6.976 | 10.293 | 613.71 | 3.317 |
| 190.00 | 18.546 | 1381.9 | 7.273 | 10.780 | 666.39 | 3.507 |
| 195.00 | 19.090 | 1476.0 | 7.569 | 11.269 | 721.51 | 3.700 |
| 200.00 | 19.622 | 1572.8 | 7.864 | 11.759 | 779.08 | 3.895 |
| 205.00 | 20.141 | 1672.2 | 8.157 | 12.250 | 839.11 | 4.093 |
| 210.00 | 20.649 | 1774.2 | 8.448 | 12.742 | 901.59 | 4.293 |
| 215.00 | 21.144 | 1878.6 | 8.738 | 13.233 | 966.52 | 4.495 |
| 220.00 | 21.628 | 1985.6 | 9.025 | 13.725 | 1033.9 | 4.700 |
| 225.00 | 22.101 | 2094.9 | 9.311 | 14.216 | 1103.8 | 4.906 |
| 230.00 | 22.564 | 2206.6 | 9.594 | 14.707 | 1176.1 | 5.113 |
| 235.00 | 23.016 | 2320.5 | 9.875 | 15.197 | 1250.8 | 5.323 |
| 240.00 | 23.459 | 2436.7 | 10.153 | 15.687 | 1328.1 | 5.534 |
| 245.00 | 23.893 | 2555.1 | 10.429 | 16.175 | 1407.7 | 5.746 |
| 250.00 | 24.317 | 2675.6 | 10.703 | 16.662 | 1489.8 | 5.959 |
| 255.00 | 24.732 | 2798.3 | 10.974 | 17.147 | 1574.3 | 6.174 |
| 260.00 | 25.136 | 2922.9 | 11.242 | 17.632 | 1661.3 | 6.389 |
| 265.00 | 25.530 | 3049.6 | 11.508 | 18.114 | 1750.6 | 6.606 |
| 270.00 | 25.914 | 3178.2 | 11.771 | 18.595 | 1842.4 | 6.824 |
| 273.15 | 26.151 | 3260.2 | 11.936 | 18.897 | 1901.5 | 6.961 |
| 275.00 | 26.288 | 3308.7 | 12.032 | 19.074 | 1936.6 | 7.042 |
| 280.00 | 26.651 | 3441.1 | 12.290 | 19.551 | 2033.1 | 7.261 |
| 285.00 | 27.005 | 3575.2 | 12.545 | 20.026 | 2132.1 | 7.481 |
| 290.00 | 27.351 | 3711.1 | 12.797 | 20.498 | 2233.4 | 7.701 |
| 295.00 | 27.695 | 3848.7 | 13.047 | 20.969 | 2337.1 | 7.922 |
| 298.15 | 27.909 | 3936.3 | 13.202 | 21.264 | 2403.6 | 8.062 |
| 300.00 | 28.035 | 3988.1 | 13.294 | 21.437 | 2443.1 | 8.144 |
| 310.00 | 28.694 | 4271.7 | 13.780 | 22.367 | 2662.1 | 8.587 |
| 320.00 | 29.314 | 4561.8 | 14.256 | 23.288 | 2890.4 | 9.032 |
| 330.00 | 29.894 | 4857.9 | 14.721 | 24.199 | 3127.8 | 9.478 |
| 340.00 | 30.439 | 5159.6 | 15.175 | 25.100 | 3374.3 | 9.925 |
| 350.00 | 30.952 | 5466.5 | 15.619 | 25.990 | 3629.8 | 10.371 |
| 360.00 | 31.435 | 5778.5 | 16.051 | 26.868 | 3894.1 | 10.817 |
| 370.00 | 31.893 | 6095.2 | 16.473 | 27.736 | 4167.1 | 11.262 |
| 373.15 | 32.032 | 6195.8 | 16.604 | 28.007 | 4254.9 | 11.403 |
| 380.00 | 32.324 | 6416.3 | 16.885 | 28.592 | 4448.8 | 11.707 |
| 390.00 | 32.726 | 6741.6 | 17.286 | 29.437 | 4738.9 | 12.151 |
| 400.00 | 33.104 | 7070.7 | 17.677 | 30.270 | 5037.5 | 12.594 |
| 425.00 | 33.973 | 7909.4 | 18.610 | 32.304 | 5819.8 | 13.694 |
| 450.00 | 34.746 | 8768.6 | 19.486 | 34.268 | 6652.1 | 14.782 |
| 475.00 | 35.439 | 9646.0 | 20.307 | 36.166 | 7532.7 | 15.858 |
| 500.00 | 36.064 | 10540. | 21.080 | 38.000 | 8459.9 | 16.920 |
| 550.00 | 37.145 | 12371. | 22.493 | 41.489 | 10448. | 18.996 |
| 600.00 | 38.050 | 14252. | 23.753 | 44.761 | 12605. | 21.009 |
| 650.00 | 38.818 | 16174. | 24.883 | 47.838 | 14921. | 22.955 |
| 700.00 | 39.479 | 18132. | 25.902 | 50.739 | 17386. | 24.837 |
| 750.00 | 40.055 | 20120. | 26.827 | 53.483 | 19992. | 26.656 |
| 800.00 | 40.561 | 22136. | 27.670 | 56.085 | 22732. | 28.415 |
| 850.00 | 41.010 | 24175. | 28.442 | 58.558 | 25599. | 30.116 |
| 900.00 | 41.411 | 26236. | 29.151 | 60.913 | 28586. | 31.762 |
| 950.00 | 41.772 | 28316. | 29.806 | 63.162 | 31688. | 33.356 |
| 1000.00 | 42.099 | 30413. | 30.413 | 65.313 | 34900. | 34.900 |
| 1050.00 | 42.396 | 32525. | 30.976 | 67.374 | 38218. | 36.398 |
| 1100.00 | 42.669 | 34652. | 31.502 | 69.353 | 41636. | 37.851 |
| 1150.00 | 42.919 | 36792. | 31.993 | 71.255 | 4.5152. | 39.263 |
| 1200.00 | 43.150 | 38944. | 32.453 | 73.087 | 48761. | 40.634 |
| 1250.00 | 43.364 | 41106. | 32.885 | 74.853 | 52460. | 41.968 |
| 1300.00 | 43.563 | 43280. | 33.292 | 76.557 | 56245. | 43.265 |
| 1350.00 | 43.748 | 45463. | 33.676 | 78.205 | 60114. | 44.529 |
| 1400.00 | 43.922 | 47654. | 34.039 | 79.799 | 64065. | 45.760 |
| 1450.00 | 44.085 | 49855. | 34.382 | 81.343 | 68093. | 46.961 |
| 1500.00 | 44.239 | 52063. | 34.708 | 82.841 | 72198. | 48.132 |
| 1550.00 | 44.384 | 54278. | 35.018 | 84.294 | 76377. | 49.275 |
| 1600.00 | 44.521 | 56501. | 35.313 | 85.705 | 80627. | 50.392 |
| 1650.00 | 44.651 | 58730. | 35.594 | 87.077 | 84947. | 51.483 |
| 1700.00 | 44.774 | 60966. | 35.862 | 88.412 | 89334. | 52.549 |
| 1750.00 | 44.892 | 63208. | 36.119 | 89.711 | 93787. | 53.593 |
| 1800.00 | 45.004 | 65455. | 36.364 | 90.978 | 98305. | 54.614 |
| 1850.00 | 45.111 | 67708. | 36.599 | 92.212 | 102884. | 55.613 |
| 1900.00 | 45.213 | 69966. | 36.824 | 93.416 | 107525. | 56.592 |
| 1950.00 | 45.311 | 72229. | 37.041 | 94.592 | 112226. | 57.552 |
| 2000.00 | 45.406 | 74497. | 37.249 | 95.741 | 116984. | 58.492 |
is the enthalpy of the solid at 0 °K and 1 atm pressure.
Heat-capacity determinations usually require two series of measurements, one on the sample plus the calorimeter vessel and the other on the empty vessel. By conducting the two series of measurements under as identical conditions as possible, certain errors that occur equally in both measurements may be canceled in the final processing of the data. The data from both series of measurements are most useful in certain applications, such as in the numerical evaluation of the precision and accuracy of the original observations, in the correlation of the temperature scale, etc. These data are, however, not directly useful where the heat capacity of the substance is needed for the comparison of the precision and accuracy of measurements with other laboratories. The method used in processing the experimental data as outlined above yields the final smoothed values of heat capacity and the relation of these values with the original observations is linked through a somewhat tortuous path.
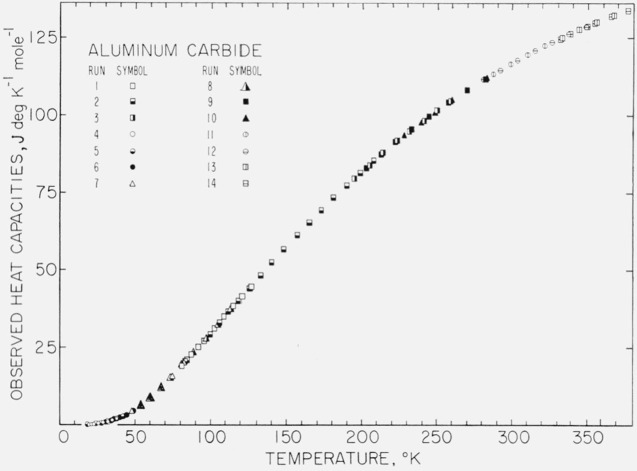
To meet the requirements for evaluating the precision of the observation and for comparing the results with other laboratories a “compromised” list of experimental data is given in table 3. The values of “observed molal heat capacity” given in the units of J deg−1 mol−1 in table 3 were obtained by subtracting the smoothed tare heat capacity from the gross heat capacity at the observed temperatures (midtemperatures of the enthalpy increments). The tare heat capacities at the corresponding temperatures were obtained by interpolation in the table of smoothed tare heat capacities mentioned earlier. Corrections have been made for the impurities and for the helium gas. Curvature corrections were made wherever significant. These observed molal heat capacities are plotted in figure 3.
Table 3. Observed heat capacity of aluminum carbide (Al4C3).
Gram molecular weight = 143.9594 g, T deg K=t deg C +273.15
| T | CP |
|---|---|
| RUN 1 | |
| °K | J deq−1 mol−1 |
| 80.9304 | 19.039 |
| 87.5349 | 22.750 |
| 95.5198 | 27.145 |
| 102.6529 | 31.166 |
| 109.1860 | 34.903 |
| 115.2630 | 38.389 |
| 120.9611 | 41.644 |
| 126.3603 | 44.702 |
| RUN 2 | |
| 83.3668 | 20.442 |
| 83.7841 | 20.682 |
| 92.0007 | 25.212 |
| 99.2987 | 29.260 |
| 105.9164 | 33.041 |
| 112.1039 | 36.581 |
| 118.3925 | 40.182 |
| 125.2915 | 44.100 |
| 132.5943 | 48.216 |
| 140.0859 | 52.360 |
| 148.2666 | 56.796 |
| 156.8223 | 61.313 |
| 165.0743 | 65.555 |
| 173.0867 | 69.543 |
| 181.1510 | 73.440 |
| 189.9219 | 77.545 |
| 199.0012 | 81.640 |
| RUN 3 | |
| 208.2596 | 85.650 |
| 194.8391 | 79.768 |
| 204.7784 | 84.152 |
| 214.3612 | 88.195 |
| 223.6167 | 91.931 |
| 232.5986 | 95.409 |
| 241.3449 | 98.662 |
| 250.2226 | 101.831 |
| 259.2433 | 104.929 |
| RUN 4 | |
| 19.4395 | 0.154 |
| 21.2826 | 0.214 |
| 23.1934 | 0.298 |
| 26.1223 | 0.468 |
| 28.9497 | 0.690 |
| 31.8285 | 0.978 |
| 34.7029 | 1.356 |
| 37.9361 | 1.897 |
| RUN 5 | |
| 18.3556 | 0.125 |
| 20.5917 | 0.194 |
| 22.9086 | 0.286 |
| 25.3911 | 0.425 |
| 28.2211 | 0.628 |
| 31.0744 | 0.900 |
| 34.2214 | 1.292 |
| 38.0580 | 1.925 |
| 42.2987 | 2.823 |
| RUN 6 | |
| 32.2736 | 1.037 |
| 35.9656 | 1.554 |
| 39.9007 | 2.283 |
| 44.3825 | 3.329 |
| 48.7699 | 4.578 |
| 53.7296 | 6.250 |
| 60.1927 | 8.834 |
| 67.1891 | 12.007 |
| RUN 7 | |
| 47.9512 | 4.334 |
| 53.8036 | 6.274 |
| 60.2681 | 8.859 |
| 67.1238 | 11.979 |
| 74.4382 | 15.603 |
| 82.5811 | 20.002 |
| RUN 8 | |
| 53.6690 | 6.221 |
| 59.9095 | 8.700 |
| 67.0407 | 11.949 |
| 73.8189 | 15.264 |
| 80.9261 | 19.085 |
| 88.8040 | 23.473 |
| 96.7037 | 27.812 |
| 104.9602 | 32.491 |
| 113.3395 | 37.293 |
| RUN 9 | |
| 202,6976 | 83.252 |
| 212.7334 | 87.532 |
| 222.8071 | 91.600 |
| 233.1927 | 95.614 |
| 244.9902 | 99.979 |
| 257.7564 | 104.411 |
| 270.1210 | 108.507 |
| 282.1421 | 112.178 |
| RUN 10 | |
| 228.2582 | 93.736 |
| 238.8640 | 97.746 |
| 249.4063 | 101.545 |
| 260.0404 | 105.168 |
| 282.9258 | 112.385 |
| RUN 11 | |
| 287.5948 | 113.747 |
| 299.1951 | 117.040 |
| 310.6701 | 120.112 |
| 322.1925 | 122.999 |
| RUN 12 | |
| 280.8853 | 111.785 |
| 291.7646 | 114.978 |
| 303.4013 | 118.188 |
| 314.9180 | 121.232 |
| 326.3407 | 124.053 |
| 337.6879 | 126.647 |
| 348.8494 | 129.087 |
| RUN 13 | |
| 332.8417 | 125.529 |
| 344.3231 | 128.107 |
| 355.7442 | 130.520 |
| 367.1535 | 132.793 |
| RUN 14 | |
| 332.3944 | 125.383 |
| 338.2360 | 126.747 |
| 349.3925 | 129.181 |
| 354.7007 | 130.379 |
| 365.6101 | 132.607 |
| 376.3752 | 134.648 |
Figure 3. Observed values of the molal heat capacity of aluminum carbide.
4. High-Temperature Relative Enthalpy Measurements
4.1. Method and Apparatus
The relative enthalpy measurements were made from 273 to 1173 °K (0 to 900 °C) by the “drop” method using a Bunsen ice calorimeter. Details of the method have been described previously [18]. Briefly, the method involved suspending the samples sealed in a container (for the present measurements the container consisted mostly of the alloy Ni(80%) —Cr(20%)) in a furnace. When a constant, known temperature is attained, the container and its contents are dropped, with nearly free fall, into a Bunsen ice calorimeter in which is determined the heat evolved by the container plus sample in cooling to 273.15 °K. In order to account for the enthalpy of the container and the heat lost during the drop, a similar experiment is made with the empty container at the same furnace temperature. The difference between the two values of heat evolved in the ice calorimeter is a measure of the enthalpy change of the sample between 273.15 °K and the temperature in the furnace.
In the furnace used the sample is surrounded by a silver pipe 25 cm long and of 1.3 cm wall thickness, in order to minimize the temperature gradients around the sample and thus improve the accuracy of measuring its temperatures. Customarily, the temperature of this furnace (and hence that of the sample) is measured by a calibrated platinum resistance thermometer (precision, ±0.002 deg) from 0 to 600 °C and by a calibrated Pt—Pt−10 percent Rh thermocouple (precision, ±0.01 deg) at all temperatures. The routine simultaneous measurement by both instruments at and below 600 °C ensures that the thermocouple readings are consistent with the thermometer readings, which are more accurate. Unfortunately, shortly before the measurements on Al4C3 were begun, the thermometer suffered an accident and it was consequently necessary to use the thermocouple alone at all the temperatures.
Just before the measurements of the relative enthalpy of Al4C3, similar measurements were carried out on a sample of Calorimetry-Conference standard sample of α-Al2O3 in a silver container (six at 400, two at 600, and two at 700 °C), in order to check the overall accuracy. Compared with the smoothed values published earlier by the Bureau and recently slightly corrected [19], the mean enthalpies of the Al2O3 found at these three temperatures were respectively +0.02 ±0.06, —0.01 ±0.01, and −0.02 ±0.01 percent higher. (The stated tolerances represent the standard deviations of the means.)
4.2. Results
All the high-temperature heat measurements were made on the same sample of aluminum carbide. The same identical container was used both with and without the sample, in order to preclude possible small differences in the relative enthalpy per unit mass of different specimens of the container alloy. The results of the enthalpy measurements are summarized in table 4. The second and third columns give, in chronological order for each furnace temperature, the heats found in individual measurements on the container with sample and on the empty container, respectively. The values given have been corrected for small unavoidable differences in mass of the various parts of the container, and for the contribution of the impurities to the heats measured. The largest part of the latter correction above 873.15 °K, about −8 cal for the sample measured, was for the heat of fusion of the free aluminum present, and largely eliminated a small hump in a plot against temperature of the uncorrected net enthalpy of the sample near the melting point of this element, 932 °K.
Table 4. High-temperature enthalpy measurements on aluminum carbide (Al4C3).
| Furnace temperature |
Individual heat measurementsa | HT–H273.15 of Al4C3b | ||
|---|---|---|---|---|
| Sample + container | Container only | Mean observed | Obs.-calcd., eq (1)c | |
| °K | cal | cal | cal mol−1 | cal mol−1 |
| 373.2 | 285.0 | 149.6 | 2939d | −8 |
| 286.3 | 150.4 | |||
| 287.3 | 150.6 | |||
| 151.1 | ||||
| 473.2 | 600.4 | (306.8)e | 6305 | −27 |
| 602.4 | 310.1 | |||
| 601.8 | 309.8 | |||
| 311.1 | ||||
| 310.2 | ||||
| 573.2 | 936.9 | 475.2 | 9994 | +6 |
| 936.7 | 475.5 | |||
| 938.2 | ||||
| 936.8 | ||||
| 936.7 | ||||
| 936.7 | ||||
| 673.2 | 1289.7 | 648.0 | 13877 | +49 |
| 1288.9 | 647.9 | |||
| 1288.3 | ||||
| 773.2 | 1648.0 | 826.8 | 17794 | −8 |
| 1648.6 | 825.9 | |||
| 873.2 | 2021.1 | 1009.6 | 21883 | +4 |
| 2020.1 | 1009.9 | |||
| 973.2 | 2405.4 | 1205.9 | 25980 | −56 |
| 2406.0 | 1205.3 | |||
| 1073.2 | 2808.8 | 1409.1 | 30289 | +29 |
| 2807.7f | 1409.1 | |||
| 1173.2 | 3213.1f | 1615.6 | 34543 | +5 |
| 3210.4f | 1617.4 | |||
| 1614.5 | ||||
| 1616.9 | ||||
With all corrections applied, including those for the impurities in the sample. Sample mass=6.650 g.
Molecular weight of Al4C3=143.959.
The final values of (HT—H273.15) (table 5) are smaller than those calculated from eq (1) by 11.5 cal mol−1 at 373.15 °K and by 10 cal mol−1 at each of the other temperatures in table 4.
The value found from the measurements with the adiabatic calorimeter is 2933.0 cal mol−1.
Omitted from the mean because of inferior precision.
In these measurements 0.003 g of the sample had been removed, but these values have been corrected to a basis of the 6.650 g of sample present in the other measurements in this column.
Obviously no individual measurement in the third column of table 4 is uniquely associated with one in the second column. For each furnace temperature the difference between the averages for the two columns gives the mean observed net relative enthalpy of aluminum carbide shown on a mole basis in the fourth column. Using the method of least squares, these values (equally weighted) were used to determine the constants of the following empirical equation for Al4C3:
| (1) |
(For consistency, the equation has more significant figures than the precision of the observations.) The deviations of the mean observed values from eq (1) are given in the last column. The final values of enthalpy from 373 to 1173 °K, relative to 273 °K (table 5) are consistently lower than eq (1) by 10 cal mol−1, an amount which is within the precision of the high-temperature measurements.
The heat measurements on the empty container were not smoothed separately because their temperature variation possesses an irregularity reflecting a well-known transition in the alloy 80 percent Ni−20 percent Cr in this temperature range.
5. Comparison of the Low- and High-Temperature Heat Data and the Calculation of Thermodynamic Functions
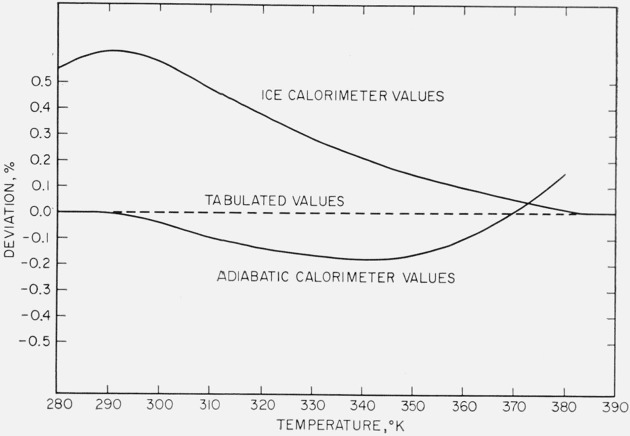
The low-temperature heat-capacity data overlap the high-temperature relative-enthalpy data in the range 273.15 to 380 °K. Numerical integration of the smoothed values of the low-temperature heat-capacity yielded 2933 cal mol−1 for the enthalpy change between 273.15 and 373.15 °K. The high-temperature relative enthalpy measurements (see table 4) give an average value of 2939 cal mol−1 and the enthalpy equation (eq (1)) gives 2947 cal mol−1 for this temperature interval. The smoothed values of heat capacity from the low-temperature measurements were merged with the values of heat capacity calculated from the relative enthalpy equation (eq (1)) in a manner such that the resultant enthalpy change from 273.15 to 373.15 °K would be about the average of the mean values determined by the two methods. After a process of adjusting and smoothing, the final values of heat capacity that were obtained yielded 2936 cal mol−1 for the enthalpy change of this temperature interval. In figure 4, the final selected values of heat capacity are compared with those from the low-temperature measurements and from the enthalpy equation (eq (1)) in the interval 270 to 390 °K.
Figure 4. Comparison of the final selected values of heat capacity (table 5) with those of the low-temperature measurements and those derived from the enthalpy equation (eq (1)).
The relative-enthalpy equation (eq (1)) was used to extrapolate the thermodynamic properties up to 2000 °K. The equation is of a form generally used for high-temperature heat capacities and is “well behaved” in terms of the configuration of the heat-capacity curve and the derivatives up to 2000 °K and higher. The various thermodynamic properties between 0 and 2000 °K given in table 5 were calculated from the heat capacities, using the standard thermodynamic relations [18], by numerical methods on the IBM 7094 computer.
Initially the various high-temperature vapor-equilibrium data involving Al4C3 were analyzed in order to obtain a guide for extrapolating the calorimetric data above 1200 °K. The entropy of Al4C3 was calculated from the ΔS° of the equilibrium reactions in which the of the components was assumed to be zero. After consideration of the uncertainties in the values of S° calculated from the vapor-equilibrium data, the extrapolated values of eq (1) was found to be within the estimated uncertainties. Equation (1) was, therefore, used in the extrapolation. The details of this comparison and the subsequent refinements in the calculation, in which the of the components are considered, are discussed in the following section (sec. 6).
6. Comparison of the Calorimetric and Vapor-Equilibrium Data
The calorimetric data obtained on Al4C3 and the results of extrapolating the thermodynamic properties to 2000 °K have been compared with vapor-equilibrium data on reactions involving Al4C3. Intercomparisons were made of the results of thermodynamic analyses by three methods that are ordinarily used, depending upon the thermodynamic data available. The values of S° of Al4C3 and ΔH° and ΔS° of the various reactions that were obtained are intercompared. Vapor pressures calculated from calorimetric data are compared graphically with the observed values.
In method I the vapor-pressure data only were used, in which is assumed for the reactions. Whenever the vapor-pressure equation only was given, the ΔS° of the reaction was calculated from the relations:
| (2) |
and
| (3) |
where n is the net number of moles of gaseous species produced in the reaction as written and R is the molal gas constant. When numerical values of the vapor pressure were given, the relation
| (4) |
was used and ΔH° and ΔS° obtained by the least squares method. Whenever both equation and numerical values were given, the values obtained through the least-squares analysis were selected for the comparison. The corresponding values of S° of Al4C3 were calculated, using the tables of thermodynamic properties recently issued from the National Bureau of Standards [8] containing values for the other substances in the reactions.
In method II, the ΔH° and ΔS° of the vapor equilibrium reactions were calculated taking into consideration the of the components of the reaction involved. For Al4C3 the thermodynamic properties given in table 5 were used and for the other substances several of the appropriate sources of thermodynamic properties were used [8,20]. The calculations of method II were carried out using a method suggested by Prosen [21] and illustrated by Otto [22]. Margrave [23] reported a similar method. The method involves the relation:
| (5) |
where
| (6) |
and the symbol * indicates the temperature at which the ΔH° and ΔS° are to be determined. For these calculations the temperature * was selected for purposes of the comparison at about the mid-temperature of the range of vapor-equilibrium data (at which the calculations of ΔH° and ΔS° were made assuming ). The equilibrium constant K was taken to be the observed pressures of the gaseous species involved, raised to the appropriate power. The values of and were obtained by the least squares method.
In method III, the values of ΔH° and ΔS° of the reaction were calculated using the thermochemical and thermodynamic data on the components of the reactions [8, 20, 24, 25, 26]. For Al4C3, Mah [25] reported −53.4±2.0 kcal mol−1 for the heat of formation (298 °K) from combustion measurements on Al4C3 involving the reaction:
| (7) |
(Henceforth, any thermodynamic property at T °K will be symbolized, for example, by ΔH° (T °K), and 298.15 °K will be abbreviated to 298 °K.) More recently King and Armstrong [26] obtained (298 °K) = −49.7 ±1.2 kcal mol−1 from combustion measurements on a portion of the same Al4C3 preparation on which the present calorimetric results are being reported. Negligible amounts of δ—Al2O3 were found in the combustion products by Mah [25], but the experiments of King and Armstrong [26] showed from 50 to 75 percent δ—Al2O3 which was corrected for the heat of transition to the α form. The somewhat purer sample used by Mah may be the reason for the negligible amounts of δ—Al2O3 found in her experiments [27]. If α—Al2O3 only were assumed to have been formed in the combustion reaction, the measurements of King and Armstrong [26] would yield . The earlier combustion measurements of Roth and colleagues [28, 29, 30] yield kcal mol−1 when the recent thermochemical data [8, 24] are applied to their reported heat of reaction (−1036.7 ±6.2 kcal mol−1 for eq (7). The value −49.7 ±1.2 kcal mol,−1 obtained by King and Armstrong [26], was used in the calculations by method III. In the comparison of the vapor pressures of the various equilibrium reactions the value −53.4 ±2.0 kcal mol−1 obtained by Mah [25] was used also.
Table 6 shows the comparison of the calorimetric values of S° of Al4C3 with those calculated from the various vapor-equilibrium reactions assuming (method I) and when the values of of the reactions were considered (method II). The comparison of the values of ΔH° and ΔS° of the vapor-equilibrium reaction obtained from vapor-pressure (methods I and II) and calorimetric (method III) data is given in table 7. (Hereafter, the methods of calculation used to obtain the various thermodynamic quantities will be identified by the Roman numerals indicated above.)
Table 6. Comparison of the entropy of aluminum carbide (Al4C3) obtained from the calorimetric measurements with those calculated from vapor-equilibrium data.
| Source | System or reaction | Temperature range | Tcmpcrature of S° |
|||
|---|---|---|---|---|---|---|
| Assuming |
from thermal data | Calorimetric data |
||||
| °K | °K | e.u.a | e.u.a | e.u.a.b | ||
| Meschi and Searcy [31] | Al4C3(c)=4Al(g)+3C(c) | 1500–1800 | 1650 | 99.8 | 99.5 | 87.1 |
| Prescott and Hineke [36] | 4AlN(c)+3C(c)=Al4C3(c) + 2N2(g) |
1774–1909 | 1850 | 97.5 | 97.4 | 92.2 |
| Prescott and Hineke [37] | 2 Al203(c)+9C(c) = Al4C3(c) + 6CO(g) | 1967–2293 | 2150 | 90.0 | 84.6 | 99.0 |
| Brunner [38] | 2Al203(c)+9C(c) = Al4Ca(c) + 6CO(g) | 1853–2253 | 2100 | 58.0 | 57.3 | 98.0 |
| Grjotheim et al., [41] | 8MgO(c)+Al4C3(c) = 2MgAl2O4(c)+3C(c) +6Mg(g) | 1324–1452 | 1400 | 74.9 | 74.8 | 79.8 |
e.u. = cal deg−1mol−1.
Obtained from table 5.
Table 7. Comparison of the thermodynamics of vapor-equilibrium reactions of table 6 calculated by various methods.
| Reference | T | Calculations from vapor-equilibrium data | Calculations from calorimetric data | Difference (method II—calorimetric data) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method I assuming ΔCp=0 | Method II ΔCp from calorimetric data | |||||||||
| °K | kcal mol−1 | cal deg−1 mol−1 | kcal mol−1 | cal deg−1mol−1 | kcal mol−1 | cal deg−1mol−1 | kcal mol−1 | kcal mol−1 | kcal mol−1 | |
| Meschi and Searcy [31] | 1650 | 345.2±27.3a | 117.5±16.4a | 345.6±27.3a | 117.8±16.4a | 351.1±2.1b,c | 130.2±0.3 | −5.5 | −20.5 | +15.0 |
| Prescott and Hincke [36] | 1850 | 257.4±14.9 | 92.6±8.0 | 257.2±14.9 | 92.5±8.0 | 250.3±1.7 | 87.3±0.3 | +6.9 | +9.6 | −2.7 |
| Prescott and Hincke [37] | 2150 | 535.6±88.0 | 239.8±41.5 | 535.0±87.8 | 239.6±41.4 | 566.8±7.2 | 248.9±0.7 | −31.8 | −20.0 | −11.8 |
| Brunner [38] | 2100 | 467.6±3.4 | 209.4±1.7 | 466.1±3.4 | 208.7±1.6 | 567.6±7.2 | 249.3±0.7 | −101.5 | −85.3 | −16.2 |
| Grjotheim et al., [41] | 1400 | 297.2±6.5 | 172.4±4.7 | 297.2±6.5 | 172.3±4.7 | 301.3±4.7 | 167.5±0.3 | −4.1 | +6.7 | −10.8 |
These figures following the ± symbols are standard deviations defined for the values of ΔH° by:
These figures following the ± symbols were obtained from the relation where ϵi is the estimated uncertainty of the calorimetric data used.
These values of ΔH° are based on the (298 °K) for Al4C3 reported by King and Armstrong [26].
The thermochemical and thermodynamic data were used to calculate the vapor pressure of the gaseous species of the vapor-equilibrium data. The activity coefficients of the components were assumed to be unity. The log10p (observed or vapor-pressure equation obtained from least-square analysis) and log10p (vapor pressures calculated from calorimetric data) are plotted in figure 5 for comparison.
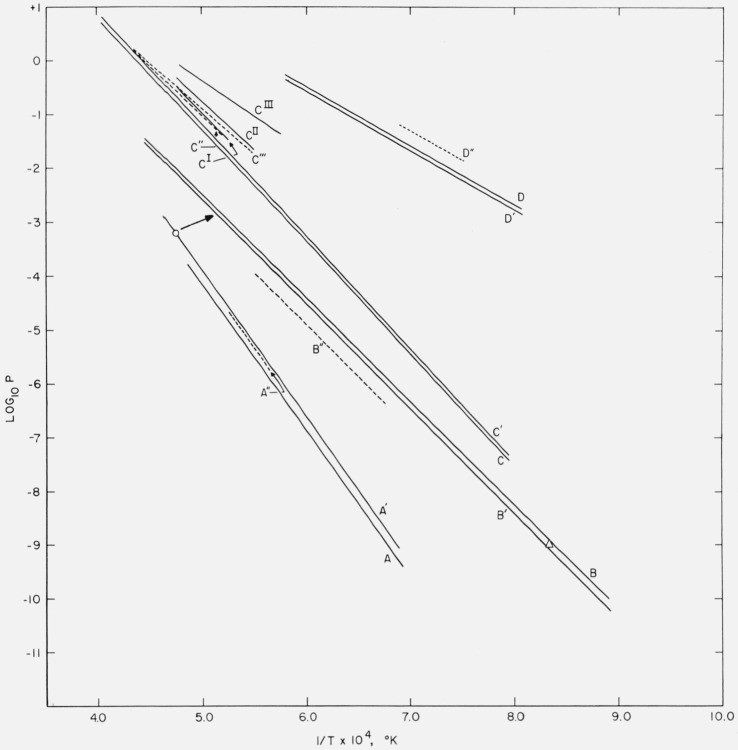
Figure 5. Comparison of vapor pressures (log10 P versus 1/T) calculated from heat of formation and thermodynamic data with published values obtained in high-temperature equilibrium measurements.
(a) 4AlN(c) + 3C(c) → Al4C3(c) + 2N2(g): A and A′ calculation from thermal data,* A′′ = Prescott and Hincke [36].
(b) Al4C3(c) → 4Al(g) + 3C(c): B and B′ = calculation from thermal data,* B′′ = Meschi and Searcy [31], ○ = Chupka et al. [34], Δ = Campbell [35].
(c) 2Al2O3(c) + 9C(c) = Al4C3(c) + 6CO(g): C and C′ calculation from thermal data,*
C′′ = Prescott and Hincke [37], C′′′ = Brunner [38].
CI = Al4O4C(c) + 6C(c) → Al4C3(c) + 4CO(g): Cox and Pidgeon [40].
CII = 2Al2O3(c) + 3C(c) → Al4O4C(c) + 2CO(g): [40].
CIII = Al2O3(c) + 3C(c) → Al2OC(c) + 2CO(g): [40].
(d) 8MgO(c) + Al4C3(c) → 2MgAl2O4(c) + 3C(c) + 6Mg(g): D and D′ = calculation from thermal data, D′′ = Grjotheim et al. [41].
The simplest vapor-equilibrium reaction analyzed is the dissociation of Al4C3:
| (8) |
Meschi and Searcy [31] measured the vapor pressure of aluminum in the above reaction in the region from 1500 to 1800 °K by means of the Knudsen effusion method and by a torsion method. They reported for the reaction ΔH° (1600 °K) = 356 ±12 kcal mol−1 based on the vapor-pressure equation obtained from two of the runs by the torsion method. The values of ΔH° from each of the above two runs differed by 20 kcal mol−1. The values of ΔH° and ΔS° for the reaction (eq (8)) were evaluated at 1650 °K, the midtemperature of the experimental range, using method I with the numerical data between 1600 and 1700 °K given only for the Knudsen effusion method. The results using method II are based on the same numerical values. (Meschi and Searcy [31] show a large number of observations in their plot but report only seven numerical values. The analysis is based on these seven values, which are unfortunately closely spaced in temperature and yield a poorer precision figure than that obtained by Meschi and Searcy using a larger number of observations.)
Earlier, Ruff and Jellinek [32] investigated the vapor equilibrium of the Al-C system and found as much as 14 percent of carbon in the gaseous products at 2543 °K. Zeeman [33] reported an analysis of the spectrum of AlC produced at 2423 °K in a graphite resistance furnace containing aluminum. On the other hand, a mass spectrometric analysis of the gaseous products from Al4C3 dissociation at 2100 °K by Chupka et al. [34] showed insufficient amounts of gaseous Al-C compounds to account for the large amounts of carbon found by Ruff and Jellinek [32]. Chupka et al. [34] found no molecular species of the formula AlC treated by Zeeman [33]. The measurements of Ruff and Jellinek probably contained CO from oxygen contamination. Therefore, their results are not compared in tables 6 and 7.
The comparison of the vapor pressures of the Al4C3 dissociation equilibrium (fig. 5, curves B) shows that the observed values B′′ [31] and those calculated from the calorimetric data B, B′ are displaced very nearly parallel from each other. The close agreement (about 1.5%) of the values of ΔH° given in table 7 conforms with the agreement in the “slopes” of the vapor pressures. The displacement of the vapor-pressure curves is related to the deviations in the values of ΔS°. Thus
| (9) |
and δΔG°=—nRTδ In p, where n is the number of moles of the gas involved in the equilibrium and R is the molal gas constant. If δΔH°=0, then δΔS°= nRδ In p.
The single vapor-pressure value reported for the Al4C3 dissociation by Chupka et al. [34] is shown (fig. 5) to be over an order of magnitude lower than the calculated curve. Campbell [35] reported ΔG° (1193 °K) = 35.8 kcal mol−1 for the reaction:
| (10) |
calculated from the activity coefficient obtained from the measurement of the vapor pressure of aluminum monofluoride over the Al4C3-Al-C system and over pure aluminum at 1193 °K (920 °C). The value plotted in figure 5 was obtained after converting to the basis of aluminum vapor [8]. The agreement is fortuitously very close.
Prescott and Hincke [36] investigated the equilibrium reaction between aluminium carbide and nitrogen
| (11) |
in the region 1774 to 1909 °K. The Al4C3 sample was prepared by heating pellets of finely divided aluminum metal and graphite as high as 1880 °K. These pellets were mixed in stoichiometric proportion plus 10 percent excess of graphite. The equilibrium pressures were determined from time-pressure measurements obtained by means of a McLeod gage. M. v. Stackelberg et al. [6, 7] reported an intermediate compound, Al5C3N, similar in appearance and properties to Al4C3, and pointed out that the equilibrium reaction investigated by Prescott and Hincke [36] possibly involved instead:
| (12) |
or
| (13) |
depending upon the degree of nitridation of Al4C3 to AlN. Since no thermodynamic data are available on Al5C3N, the comparison is based on the reaction given by eq (11). Methods I and II were applied with the numerical values of vapor pressures reported by Prescott and Hincke [36].
If ΔG°<0 for the reaction
| (14) |
then ΔG° (eq (12))>ΔG° (eq (11)) and the observed vapor pressures according to eq (12) should be lower than those calculated from the thermal data for eq (11). On the other hand, ΔG° (eq (13))<ΔG° (eq (11)) so that the observed vapor pressures according to eq (13) should be higher than the calculated values based on eq (11). The plot of figure 5, curves A, shows that the observed vapor-pressures A” lie midway between the calculated values A′ and A (eq (11)) based on the heat of formation obtained by Mah [25] and by King and Armstrong [26], respectively. The agreement is shown to be reasonably good, so that ΔG° of the reaction represented by eq (14) is probably close to zero or compensating effects exist. (If the compound Al5C3N were considered a mixture, the reactions represented by eqs (12) and (13) reduce to eq (11).)
In an earlier investigation, Prescott and Hincke [37] reported vapor-equilibrium measurements on the reaction between aluminum oxide and carbon in the region 1967 to 2293 °K
| (15) |
Calculations applying methods I and II were made with the numerical values that were reported.
Brunner [38] also investigated the equilibria of the Al2O3-C reaction in the region 1853 to 2253 °K. The numerical values reported by Brunner are considerably more precise than those reported by Prescott and Hincke [37] for the reaction. Table 5 was extrapolated slightly above 2000 °K in order to compare the results reported by Prescott and Hincke [37] and by Brunner [38].
The divergent vapor-pressure values reported by various investigators for the Al2O3-C reaction (see fig. 5, curves C) may be partially explained, depending upon the equilibrium reaction, on the basis of formation of aluminum oxycarbides. According to the phase diagram investigations reported by Foster, Long, and Hunter [27] and the survey of existing data on the Al-O-C system by Motzfeldt [39], Al2O3 and Al4C3 can not coexist at equilibrium. The equilibrium investigated by Prescott and Hincke [37] could be
| (16) |
or
| (17) |
instead of the reaction represented by eq (15). At the upper temperatures (above 2100 °K) liquid phases may have been present. If ΔG°<0 for the formation of the oxycarbides,
| (18) |
or
| (19) |
then the equilibrium represented by eq (17) should yield higher vapor pressures than those calculated according to eq (15). For eq (16), the relative values of vapor pressure with respect to eq (15) will depend on the relative values of of the oxycarbides. Another equilibrium reaction possible, according to the phase diagram [27, 39], is
| (20) |
but for this reaction the observed vapor pressure should be lower than those calculated for eq (15). Prescott and Hincke [37] used an “excess” of Al2O3; the reactions given by eqs (16), (17), and (20) are possible depending upon the “excess”. Brunner [38], on the other hand, used stoichiometric amounts of Al2O3 and C corresponding to eq (15) and his results are even higher than those of Prescott and Hincke [37].
Recently, Cox and Pidgeon [40] using a differential thermal analysis method reported results on the equilibrium reactions represented by eq (17),
| (21) |
and
| (22) |
The measurements were made on each of three samples having Al2O3 to C molal ratios of 2:3, 2:6, and 2:9. Vapor-pressure equations of the form given by eq (4) were obtained by fitting the experimental data, corresponding to reactions represented by eqs (17), (21), and (22), respectively, by the method of least squares. (The numerical values, which were absent in the original paper, were kindly supplied by the authors.) These equations, plotted in figure 5, show that the vapor pressures observed by Cox and Pidgeon [40] are considerably higher than those calculated for the reaction given by eq (15). The vapor pressures corresponding to reaction (22) are fairly close to the values reported by Prescott and Hincke [37]; the values for reaction (17) join at the lower temperatures with those obtained by Brunner [38]. The values for reaction (21) are higher than any of the other vapor pressures plotted for the Al-O-C system. Actually, of the three reactions reported by Cox and Pidgeon [40], only the reaction given by eq (17) is possible according to the phase diagrams [27, 39].
Recently, Grjotheim, Herstad, and Johannessen [41] reported vapor-equilibrium investigations by means of the transpiration method of the reaction:
| (23) |
in the range 1325 to 1450 °K. The observed vapor pressures are higher than the calculated values on the average by a factor of 2 (fig. 5, curves D), which corresponds to δΔG0 (1400 °K) of about 12 kcal for the reaction given in eq (23). The uncertainty in the calorimetric data is considerably lower than 12 kcal and it is unlikely that the vapor-pressure measurements are in error by a factor of 2. The values of ΔH° (table 7) agree, however, within about 1.3 percent.
The comparisons of the results of thermodynamic analysis of high temperature vapor-equilibrium reactions show that the ΔH° of the reactions calculated from calorimetric data and by the second-law method using vapor-pressure data can agree within a few percent or better and within about the uncertainity of the calorimetric data. The vapor pressures and, therefore, the ΔG° of the reactions show systematic differences that are, in some cases, greater than the uncertainties in the calorimetric data or in the vapor-pressure determination. These differences are reflected in the values of δΔG° of table 7≈δ log p of figure 5. These differences can be attributed partially to the deviations from unity of the activity coefficients of the components of the equilibrium reaction or the reactions being different from those as written. Also, because of the finite time involved in the experiments, possible kinetic effects can contribute to the deviations. For the second-law values of ΔH°, the standard deviation figures depend on the precision of the measurements and on the temperature distribution of observations. In method I, any departure from linearity of the log p versus 1/T relation increases the standard deviation figure. Wide divergences in ΔH° and ΔS° were found in the Al-O-C system; the need for further work on the system is indicated.
In the vapor-equilibrium reactions that were analyzed, the results obtained using method I and II were essentially the same, since in method I the ΔS° and ΔH° were evaluated at the mean temperature of the range of measurements (as should always be done) and also since the term given by eq (6) is small. In other equilibria or for wider ranges, this term may become important and should be used whenever a value or estimate of is available.
Acknowledgments
The authors are indebted to Willis R. Thurber for all the measurements on the sample with the “drop” calorimeter, and to Rolf A. Paulson of the Analysis and Purification Section of the National Bureau of Standards for the chemical analyses on the samples. The processing of the heat measurements would not have been possible without the chemical analysis. The gift of the Al4C3 sample from the Aluminum Company of America, ALCOA Research Laboratories, through the courtesy of George Long, is gratefully acknowledged.
This work was sponsored by the Advanced Research Projects Agency, Department of Defense, under ARPA Ordcr No. 20.
Appendix. Thermodynamic functions for aluminum carbide (Al4C3) solid phase.
Gram molecular weight = 143.9594 g, T deg K=t deg C+273.15
| T | ||||||
|---|---|---|---|---|---|---|
| °K | J deg−1 mol−1 | J mol−1 | J deg−1 mol−1 | J deg−1 mol−1 | J mol−1 | J deg−1 mol−1 |
| 0.00 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5.00 | .003 | .003 | .001 | .001 | .001 | .000 |
| 10.00 | .020 | .051 | .005 | .007 | .017 | .002 |
| 15.00 | .069 | .259 | .017 | .023 | .086 | .006 |
| 20.00 | .170 | .817 | .041 | .054 | .272 | .014 |
| 25.00 | .397 | 2.177 | .087 | .114 | .679 | .027 |
| 30.00 | .786 | 5.052 | .168 | .218 | 1.488 | .050 |
| 35.00 | 1.398 | 10.402 | .297 | .382 | 2.958 | .085 |
| 40.00 | 2.299 | 19.525 | .488 | .624 | 5.436 | .136 |
| 45.00 | 3.484 | 33.866 | .753 | .960 | 9.356 | .208 |
| 50.00 | 4.950 | 54.838 | 1.097 | 1.401 | 15.215 | .304 |
| 55.00 | 6.707 | 83.854 | 1.525 | 1.953 | 23.551 | .428 |
| 60.00 | 8.716 | 122.33 | 2.039 | 2.621 | 34.937 | .582 |
| 65.00 | 10.929 | 171.36 | 2.636 | 3.405 | 49.954 | .769 |
| 70.00 | 13.351 | 231.98 | 3.314 | 4.302 | 69.175 | .988 |
| 75.00 | 15.902 | 305.05 | 4.067 | 5.310 | 93.159 | 1.242 |
| 80.00 | 18.564 | 391.18 | 4.890 | 6.420 | 122.44 | 1.531 |
| 85.00 | 21.294 | 490.81 | 5.774 | 7.627 | 157.52 | 1.853 |
| 90.00 | 24.073 | 604.21 | 6.713 | 8.923 | 198.86 | 2.210 |
| 95.00 | 26.878 | 731.57 | 7.701 | 10.300 | 246.89 | 2.599 |
| 100.00 | 29.702 | 873.02 | 8.730 | 11.750 | 301.98 | 3.020 |
| 105.00 | 32.537 | 1028.6 | 9.796 | 13.268 | 364.50 | 3.471 |
| 110.00 | 35.381 | 1198.4 | 10.895 | 14.847 | 434.76 | 3.952 |
| 115.00 | 38.232 | 1382.4 | 12.021 | 16.483 | 513.06 | 4.461 |
| 120.00 | 41.085 | 1580.7 | 13.173 | 18.170 | 599.67 | 4.997 |
| 125.00 | 43.929 | 1793.3 | 14.346 | 19.905 | 694.84 | 5.559 |
| 130.00 | 46.755 | 2020.0 | 15.538 | 21.683 | 798.80 | 6.145 |
| 135.00 | 49.552 | 2260.8 | 16.746 | 23.500 | 911.74 | 6.754 |
| 140.00 | 52.314 | 2515.4 | 17.967 | 25.352 | 1033.9 | 7.385 |
| 145.00 | 55.037 | 2783.8 | 19.199 | 27.236 | 1165.3 | 8.037 |
| 150.00 | 57.719 | 3065.8 | 20.438 | 29.147 | 1306.3 | 8.708 |
| 155.00 | 60.361 | 3361.0 | 21.684 | 31.083 | 1456.8 | 9.399 |
| 160.00 | 62.959 | 3669.3 | 22.933 | 33.040 | 1617.1 | 10.107 |
| 165.00 | 65.513 | 3990.5 | 24.185 | 35.017 | 1787.3 | 10.832 |
| 170.00 | 68.022 | 4324.3 | 25.437 | 37.010 | 1967.3 | 11.572 |
| 175.00 | 70.485 | 4670.6 | 26.689 | 39.017 | 2157.4 | 12.328 |
| 180.00 | 72.902 | 5029.1 | 27.940 | 41.037 | 2357.5 | 13.097 |
| 185.00 | 75.273 | 5399.6 | 29.187 | 43.067 | 2567.8 | 13.880 |
| 190.00 | 77.598 | 5781.8 | 30.430 | 45.105 | 2788.2 | 14.675 |
| 195.00 | 79.873 | 6175.5 | 31.669 | 47.150 | 3018.8 | 15.481 |
| 200.00 | 82.098 | 6580.4 | 32.902 | 49.201 | 3259.7 | 16.298 |
| 205.00 | 84.271 | 6996.4 | 34.129 | 51.255 | 3510.8 | 17.126 |
| 210.00 | 86.394 | 7423.0 | 35.348 | 53.311 | 3772.2 | 17.963 |
| 215.00 | 88.466 | 7860.2 | 36.559 | 55.368 | 4043.9 | 18.809 |
| 220.00 | 90.492 | 8307.6 | 37.762 | 57.425 | 4325.9 | 19.663 |
| 225.00 | 92.471 | 8765.1 | 38.956 | 59.481 | 4618.2 | 20.525 |
| 230.00 | 94.407 | 9232.3 | 40.140 | 61.535 | 4920.7 | 21.394 |
| 235.00 | 96.300 | 9709.1 | 41.315 | 63.586 | 5233.5 | 22.270 |
| 240.00 | 98.154 | 10195. | 42.480 | 65.632 | 5556.6 | 23.152 |
| 245.00 | 99.968 | 10691. | 43.635 | 67.675 | 5889.9 | 24.040 |
| 250.00 | 101.74 | 11195. | 44.779 | 69.713 | 6233.3 | 24.933 |
| 255.00 | 103.48 | 11708. | 45.913 | 71.745 | 6587.0 | 25.831 |
| 260.00 | 105.17 | 12230. | 47.037 | 73.770 | 6950.8 | 26.734 |
| 265.00 | 106.82 | 12760. | 48.149 | 75.789 | 7324.7 | 27.640 |
| 270.00 | 108.42 | 13298. | 49.251 | 77.801 | 7708.6 | 28.551 |
| 273.15 | 109.42 | 13641. | 49.939 | 79.064 | 7955.7 | 29.126 |
| 275.00 | 109.99 | 13844. | 50.341 | 79.805 | 8102.7 | 29.464 |
| 280.00 | 111.51 | 14397. | 51.419 | 81.800 | 8506.7 | 30.381 |
| 285.00 | 112.99 | 14959. | 52.487 | 83.787 | 8920.6 | 31.301 |
| 290.00 | 114.44 | 15527. | 53.542 | 85.765 | 9344.5 | 32.223 |
| 295.00 | 115.87 | 16103. | 54.587 | 87.733 | 9778.3 | 33.147 |
| 298.15 | 116.77 | 16469. | 55.239 | 88.969 | 10057. | 33.730 |
| 300.00 | 117.30 | 16686. | 55.620 | 89.693 | 10222. | 34.073 |
| 310.00 | 120.06 | 17873. | 57.655 | 93.584 | 11138. | 35.930 |
| 320.00 | 122.65 | 19087. | 59.646 | 97.437 | 12093. | 37.792 |
| 330.00 | 125.08 | 20325. | 61.592 | 101.25 | 13087. | 39.657 |
| 340.00 | 127.36 | 21588. | 63.493 | 105.02 | 14118. | 41.524 |
| 350.00 | 129.50 | 22872. | 65.349 | 108.74 | 15187. | 43.392 |
| 360.00 | 131.53 | 24177. | 67.159 | 112.42 | 16293. | 45.258 |
| 370.00 | 133.44 | 25502. | 68.925 | 116.05 | 17435. | 47.122 |
| 373.15 | 134.02 | 25923. | 69.472 | 117.18 | 17803. | 47.709 |
| 380.00 | 135.24 | 26846. | 70.647 | 119.63 | 18614. | 48.983 |
| 390.00 | 136.93 | 28207. | 72.325 | 123.16 | 19828. | 50.840 |
| 400.00 | 138.51 | 29584. | 73.960 | 126.65 | 21077. | 52.692 |
| 425.00 | 142.14 | 33093. | 77.866 | 135.16 | 24350. | 57.294 |
| 450.00 | 145.38 | 36688. | 81.528 | 143.38 | 27832. | 61.850 |
| 475.00 | 148.28 | 40359. | 84.966 | 151.32 | 31517. | 66.351 |
| 500.00 | 150.89 | 44099. | 88.198 | 158.99 | 35396. | 70.792 |
| 550.00 | 155.42 | 51760. | 94.110 | 173.59 | 43715. | 79.481 |
| 600.00 | 159.20 | 59629. | 99.381 | 187.28 | 52740. | 87.900 |
| 650.00 | 162.42 | 67671. | 104.11 | 200.15 | 62429. | 96.045 |
| 700.00 | 165.18 | 75863. | 108.38 | 212.29 | 72743. | 103.92 |
| 750.00 | 167.59 | 84183. | 112.24 | 223.77 | 83647. | 111.53 |
| 800.00 | 169.71 | 92617. | 115.77 | 234.66 | 95111. | 118.89 |
| 850.00 | 171.59 | 101150. | 119.00 | 245.01 | 107104. | 126.01 |
| 900.00 | 173.26 | 109772. | 121.97 | 254.86 | 119603. | 132.89 |
| 950.00 | 174.77 | 118474. | 124.71 | 264.27 | 132583. | 139.56 |
| 1000.00 | 176.14 | 127247. | 127.25 | 273.27 | 146023. | 146.02 |
| 1050.00 | 177.39 | 136086. | 129.61 | 281.89 | 159904. | 152.29 |
| 1100.00 | 178.53 | 144984. | 131.80 | 290.17 | 174207. | 158.37 |
| 1150.00 | 179.57 | 153937. | 133.86 | 298.13 | 188916. | 164.27 |
| 1200.00 | 180.54 | 162940. | 135.78 | 305.80 | 204015. | 170.01 |
| 1250.00 | 181.43 | 171989. | 137.59 | 313.18 | 219491. | 175.59 |
| 1300.00 | 182.27 | 181082. | 139.29 | 320.32 | 235329. | 181.02 |
| 1350.00 | 183.04 | 190215. | 140.90 | 327.21 | 251518. | 186.31 |
| 1400.00 | 183.77 | 199386. | 142.42 | 333.88 | 268047. | 191.46 |
| 1450.00 | 184.45 | 208592. | 143.86 | 340.34 | 284903. | 196.48 |
| 1500.00 | 185.10 | 217830. | 145.22 | 346.61 | 302077. | 201.38 |
| 1550.00 | 185.70 | 227101. | 146.52 | 352.68 | 319560. | 206.17 |
| 1600.00 | 186.28 | 236400. | 147.75 | 358.59 | 337343. | 210.84 |
| 1650.00 | 186.82 | 245728. | 148.93 | 364.33 | 355417. | 215.40 |
| 1700.00 | 187.34 | 255082. | 150.05 | 369.91 | 373773. | 219.87 |
| 1750.00 | 187.83 | 264461. | 151.12 | 375.35 | 392406. | 224.23 |
| 1800.00 | 188.30 | 273864. | 152.15 | 380.65 | 411306. | 228.50 |
| 1850.00 | 188.74 | 283290. | 153.13 | 385.82 | 430468. | 232.69 |
| 1900.00 | 189.17 | 292738. | 154.07 | 390.85 | 449886. | 236.78 |
| 1950.00 | 189.58 | 302207. | 154.98 | 395.77 | 469552. | 240.80 |
| 2000.00 | 189.98 | 311696. | 155.85 | 400.58 | 489461. | 244.73 |
is the enthalpy of the solid at 0 °K and 1 atm pressure.
Footnotes
7. References
- [1].Satoh S., Sci Papers Inst. Phys. Chem. Research (Tokyo) 34, 50 (1938). [Google Scholar]
- [2].Stackelberg M. v. and Schnorrenberg E., Z. physik. Chem. B27, 37 (1934). [Google Scholar]
- [3].Durand J. F., Bull. Soc. Chim. 35, 1141 (1924). [Google Scholar]
- [4].Baur E. and Brunner R., Z. Elektrochem. 40, 154 (1934). [Google Scholar]
- [5].Long George, private communication, June 21, 1960. [Google Scholar]
- [6].Stackelberg M. v., Schnorrenberg E., Paulus R., and Spiess K. F., Z. physik. Chem. A175, 127 (1935). [Google Scholar]
- [7].Stackelberg M. v.and Spiess K. F., Z. physik. Chem. A175, 140 (1935). [Google Scholar]
- [8].Preliminary Report on the Thermodynamic Properties of Selected Light-Element and Some Related Compounds, National Bureau of Standards Report No. 6928, July 1, 1960.
- [9].DeSorbo W. and Tyler W. W., J. Chem. Phys. 21, 1660 (1953). [Google Scholar]
- [10].Simon F. and Swain R. C., Z. physikal. Chem. 28B, 189 (1935). [Google Scholar]
- [11].Kelley K. K., J. Chem. Phys. 11, 16 (1943). [Google Scholar]
- [12].Scott R. B., Meyers C. H., Rands R. D. Jr., Brickwedde F. G., and Bekkedahl N., J. Res. NBS 35, 39 (1945) RP 1661. [Google Scholar]
- [13].Furukawa G. T., Reilly M. L., and Piccirelli J. H., J. Res. NBS 68A (Phys. and Chem.) No. 4, 381 (1964). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Stimson H. F., Res J.. NBS 65A (Phys. and Chem.) No. 3, 139 (1961). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hoge H. J. and Brickwedde F. G., J. Res. NBS 22, 351 (1939) RP1188. [Google Scholar]
- [16].Whittaker E. T. and Robinson G., The Calculus of Observations. A Treatise on Numerical Mathematics, pp. 285–316, 4th ed. (Blackie and Sons, London, 1944). [Google Scholar]
- [17].IUPAC revises atomic weight values, Chem. Eng. News 39, 42 (1961). [Google Scholar]
- [18].Furukawa G. T., Douglas T. B., McCoskey R. E., and Ginnings D. C., J. Res. NBS 57, 67 (1956) RP2694. [Google Scholar]
- [19].Ginnings D. C., J. Phys. Chem. 67, 1917 (1963). [Google Scholar]
- [20].Hilsenrath J., Beckett C. W., Benedict W. S., Fano L., Hoge H. J., Masi J. F., Nuttall R. L., Touloukian Y. S., and Woolley H. W., Tables of thermal properties of gases, NBS Circ. 564, November 1, 1955. [Google Scholar]
- [21].Prosen E. J., private communication. [Google Scholar]
- [22].Otto E. M., J. Electrochem. Soc. 111, 88 (1964). [Google Scholar]
- [23].Margrave J. L., J. Phys. Chem. 64, 288 (1960). [Google Scholar]
- [24].JANAF Thermochemical Data, The Dow Chemical Company, Thermal Laboratory, Midland, Mich. [Google Scholar]
- [25].Mah A. D., Bureau of Mines RI 6415, 1964. [Google Scholar]
- [26].King R. C. and Armstrong G. T., J. Res. NBS 68A, (Phys. and Chem.) No. 6, 661 (1964). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Foster L. M., Long G., and Hunter M. S., J. Am. Ceram. Soc. 39, 1 (1956). [Google Scholar]
- [28].Meichsner A. and Roth W. A., Z. Elektrochem. 40, 19 (1934). [Google Scholar]
- [29].Roth W. A., Wolf U. and Fritz O., Z. Electrochem. 46, 42 (1940). [Google Scholar]
- [30].Roth W. A., Z. Elektrochem. 48, 267 (1942). [Google Scholar]
- [31].Meschi D. J. and Searcy A. W., J. Phys. Chem. 63, 1175 (1959). [Google Scholar]
- [32].Ruff O. and Jellinek E., Z. anorg. allgem. Chem. 97, 312 (1916). [Google Scholar]
- [33].Zeeman P. B., Can. J. Phys. 32, 9 (1954). [Google Scholar]
- [34].Chupka W. A., Berkowitz J., Giese C. F., and Inghram M; G., J. Phys. Chem. 62, 611 (1958). [Google Scholar]
- [35].Campbell C. S., Met. Soc. Conf. 7, 412 (1961). [Google Scholar]
- [36].Prescott C. H. Jr., and Hincke W. B., J. Am. Chem. Soc. 50, 3228 (1928). [Google Scholar]
- [37].Prescott C. H. Jr., and Hincke W. B., J. Am. Chem. Soc. 49, 2753 (1927). [Google Scholar]
- [38].Brunner R., Z. Elektrochem. 38, 55 (1932). [Google Scholar]
- [39].Motzfeldt K., Tek. Ukeblad. 109, 1137 (1962). [Google Scholar]
- [40].Cox J. H. and Pidgeon L. M., Can. J. Chem. 41, 671 (1963). [Google Scholar]
- [41].Grjotheim K., Herstad O., and Stahl-Johannessen K., Z. anorg. allgem. Chem. 328, 267 (1964). [Google Scholar]
- [42].Natrella M. G., Experimental statistics, (National Bureau of Standards Handbook, No. 91), U.S. Government Printing Office, Washington, D.C., 20402, 1963. [Google Scholar]