Abstract
Some precise measurements of the vapor pressure of liquid water at seven temperatures in the range 25 to 100 °C were reported recently by H. F. Stimson of NBS. These measurements have an estimated standard deviation of 20 ppm or less, except at 25 °C where the estimated standard deviation is 44 ppm. We have derived a formula which yields computed values of vapor pressure agreeing with Stimson’s measurements to within 7 ppm.
We integrated the Clausius-Clapeyron equation using the accurate calorimetric data of Osborne, Stimson, and Ginnings and the Goff and Gratch formulations for the virial coefficients of water vapor to obtain an equation that has a rational basis. This equation was then adjusted to bring it into closer accord with Stimson’s pressure measurements. Two tables are given of the vapor pressure, expressed in pascals, as a function of temperature at 0.1-deg intervals over the range 0 to 100 °C, one on the International Practical Temperature Scale of 1948 and the other on the International Practical Temperature Scale of 1968.
Keywords: Clausius-Clapeyron equation, saturation vapor pressure over water, vapor pressure, vapor pressure of water, water vapor, steam, virial coefficients
1. Introduction
In establishing and maintaining humidity standards, in calibrating hygrometers, and in making precision humidity measurements, an accurate equation for the vapor pressure of water is essential. Such an equation also plays a vital role in steam power technology. It is important in the fields of meteorology and air conditioning where precise calculations relating to the water vapor content of atmospheric air are often made. It is employed in chemical thermodynamics, where the vapor pressure of the pure water substance is used as a reference standard in calibrating boiling point apparatus, in comparative vapor pressure measurements, in ebulliometry and in evaluating vapor pressure data of organic liquids.
It has been the practice at NBS to use the Goff and Gratch vapor pressure formulation [1]1 in all work pertaining to hygrometry. Recently, H. F. Stimson [2] published the results of some precise measurements of the vapor pressure of water at seven temperatures from 25 to 100 °C. These vapor pressures, obtained with the steam boiler and precision manometer used at NBS in the 1940’s to calibrate standard platinum resistance thermometers [3], have an estimated standard deviation of 20 ppm or less except at 25 °C where the estimated standard deviation is 44 ppm. Although vapor pressures calculated using the Goff and Gratch formulation are in reasonably good accord with Stimson’s measurements, differing at most, at 25 °C, by 95 ppm, we concluded that it would be desirable to have a formulation that was in closer agreement with Stimson’s measurements, preferably within the estimated uncertainty of the latter. The purpose of this paper is to present such a formulation. We shall limit our considerations to temperatures 0 to 100 °C.
2. Derivation
We start with a modified version of the Clausius-Clapeyron equation [4]
| (1) |
where p is the pressure of the saturated vapor, v is the specific volume of the saturated vapor, T is the absolute thermodynamic temperature, γ is an experimentally measured ealorimetric quantity, and dp/dT is the derivative of the vapor pressure with respect to the absolute thermodynamic temperature. The quantity γ [4] is the heat supplied to water to evaporate a unit mass of water isothermally and withdraw its vapor from the calorimeter. It differs from the latent heat of vaporization, L, by a small quantity, β, that is,
| (2) |
where
| (3) |
and v’ is the specific volume of the saturated liquid. The quantity β may be pictured as the heat necessary to vaporize water to fill the space no longer filled with liquid in the γ experiment.
The virial equation of state for water vapor, expressed as a power series in p,
| (4) |
when substituted into eq (1) yields
| (5) |
where
| (6) |
Z is the compressibility factor, R is the gas constant for water vapor, B’ is the second pressure-series virial coefficient, and C’ is the third pressure-series virial coefficient. For temperatures up to 100 °C, fourth and higher virial coefficients affect Z by less than 12 ppm and therefore will be neglected.
Performing some simple mathematical manipulations and integrations, eq (5) becomes
| (7) |
where p0 and p correspond to vapor pressures at temperatures T0 and T, respectively. The first integral on the right-hand side of the equation provides the major contribution to the vapor pressure. The second integral on the right-hand side of the equation accounts for the deviation of water vapor from ideal gas behavior.
We shall show later that the quantity γ can be represented with high precision by the polynomial equation
| (8) |
which, when substituted into the first integral on the right-hand side of eq (7) yields
| (9) |
Equation (9) reduces to
| (10) |
where
| (11) |
The derivation of eq (10) is similar in some respects to that of Goff and Gratch [5, 6].
In 1939, Osborne, Stimson and Ginnings [7] reported weighted mean values of γ from 0 to 200 °C based on precise calorimetric measurements in the range 0 to 100 °C and on similar measurements made in the same laboratory during 1930–32 in the range 50 to 270 °C [8] and in 1937 in the range 100 to 374 °C [9]. We fitted eq (8) to these weighted means by the method of least squares, retaining the units international joules per gram for γ and temperature t in degrees C based on the International Temperature Scale of 1927 (ITS–27) but letting the absolute temperature T48 = t + 273.15. In our range of interest, 0 to 100 °C, t has the same numerical value on the International Temperature Scale of 1927 (ITS–27) [10], the International Temperature Scale of 1948 (ITS–48) [11], and the International Practical Temperature Scale of 1948 (IPTS–48) [12]. Therefore, we will use t interchangeably on these scales as may prove convenient. However, the absolute temperature T48, due to the choice of 273.15 conforms to IPTS–48. The coefficients of eq (8) have the following numerical values: a = 3.4660697 × 103, b = −5.6067899, c= 1.0963233 × 10−2, and d = −1.2366148 × 10−5. The residual standard deviation2 is 0.231 international joules per gram, about 1 part in 10,000.
Virial coefficients for steam are usually derived from p-v-t measurements [13, 14, 15, 16]. Unfortunately, there are no p-v-t measurements for steam (water vapor) in the range 0 to 100 °C.
The early experiments of Knoblauch, Linde and Klebe [17], which were performed at temperatures from 100 to 180 °C, are suspect because of the static method used which leads to systematic errors due to the adsorption of water vapor on the walls of the container [13]. The experiments of Keyes, Smith, and Gerry [13], made by a continuous flow-method, cover the range 195 to 460 °C. These, too, are suspect below the critical temperature because of possible adsorption effects [16]. Other investigators have provided data at higher temperatures and pressures. It is possible to extrapolate the virial coefficients obtained at higher temperatures to lower temperatures [13, 14], but such extrapolations do not give values with the requisite accuracy for our purpose. Alternately, calorimetric data can be employed to obtain enthalpy coefficients, which, when integrated with respect to temperature, yield virial coefficients. This procedure was employed by Goff and Gratch [5, 6], who used the 38 to 125 °C throttling experiment data of Collins and Keyes [18] and the γ data of Osborne, Stimson and Ginnings [7] to derive second and third pressure-series virial coefficients valid for the range 0 to 100 °C [5, 6, 19]. Because the Goff and Gratch empirical relationships for the pressure-series virial coefficients are based on experimental data in the range of temperatures of interest to us, and because, of the various virial coefficients we tried, the Goff and Gratch virial coefficients yielded values of vapor pressure in closest agreement with Stimson’s experimental values, we chose to use them. We converted the Goff and Gratch relationships [19] to SI units compatible with eqs (4) and (6) to obtain
| (12) |
and
| (13) |
where B’ is in units of reciprocal pressure, 1/pascal,3 C’ is in units of the square of the reciprocal pressure, (1/pascal)2, and T48 is based on IPTS–48. The equations as derived by Goff and Gratch presumably were in terms of absolute temperature on ITS–27. Over the range 0 to 100 °C, the errors arising in B’ C’, Z, and Z−1 from using T48 without conversion are negligible. The Clausius-Clapeyron equation is an exact thermodynamic expression in which T is the absolute thermodynamic temperature. It therefore follows that the temperature T in eq (10), which was derived from the Clausius-Clapeyron equation, is also the absolute thermodynamic temperature. We will assume that T48 is a reasonably close approximation to the absolute thermodynamic temperature T and reserve for later discussion the reasons for this assumption. We inserted into eq (10) the coefficients of eq (8) on the basis of T48, and the virial coefficients given by eqs (12) and (13) as functions of T48. We selected as lower limits of integration for substitution into eqs (10) and (11) the pressure p0= 101325.0 pascals, which is one standard atmosphere, and the temperature T0 = 373.15 K, which is the absolute temperature assigned to the steam point at one standard atmosphere on T48. The gas constant for water vapor, R, is 0.46151 joules per gram kelvin and was derived from the NAS–NRC recommended value [20] of 8.3143 joules per mol kelvin for the universal gas constant and 18.01534 grams for the molar mass of water vapor on the unified carbon-12 scale. The units of the quantity γ were made consistent with R by the conversion factor 1 international joule = 1.000165 (absolute) joule [21]. After inserting the appropriate constants and conversion factor, eq (10) becomes
| (14) |
where A0 = −7.51152 × 103, A1= 85.0869143, A2 = 2.3759056 × 10−2, A3 = −1.399697 × 10−5 B = −12.150799, C = −2.1671578, p is expressed in pascals, T48 = t48+ 273.15 in kelvins, and t48 is in degrees Celsius on IPTS–48.
Because eq (14) is implicit in p we calculated p by iteration, numerically evaluating the integral at 1/4-deg intervals by means of the trapezoidal rule [22]. Iteration at each interval was terminated when successive values of p differed by less than one ppm. Evaluating the integral at 1/4-deg intervals was considered satisfactory. A check calculation at 80 °C showed that decreasing the interval to 0.025 deg produced a change in p of much less than one ppm from that obtained using 1/4-deg intervals.
The calculation of p by eq (14) is best accomplished with the aid of a high-speed digital computer. For desk-type calculations, an explicit equation without the integral is desirable. Equation (14) was converted into such an explicit form. A polynomial of the fourth degree was fitted, by the method of least squares, to numerical values of the integral at 1-deg intervals from 0 to 100 °C to give
| (15) |
where D0 = −5.2075843 × 10−2, D1 = −5.769527 × 10−5, D2 = 3.2537152 × 10−6, D3, = −1.6189993 × 10−8, and D4 = 2.381486 × l0−11. Substituting eq (15) into eq (14), integrating the left-hand side of eq (14), and combining terms yielded
| (16) |
The coefficients are listed in table 1.
Table 1.
Coefficients to vapor pressure equations on IPTS–48
|
Eq (16) n = 5 |
Eq (17) n = 5 |
Eq (18a) n = 2 |
Eq (18b) n = 3 |
Eq (18c) n = 4 |
|
|---|---|---|---|---|---|
| E0 | −7.51152 × 103 | −7.51152 × 103 | −7.2465822 × 103 | −6.7777203 × 103 | −7.7847207 × 103 |
| E1 | 9.65609269 × 101 | 9.65389644 × 101 | 7.7641232 × 101 | 5.44,09359 × 101 | 1.1670432 × 102 |
| E2 | 2.3701361 × 10−2 | 2.3998970 × 10−2 | 5.7447142 × 10−3 | −8.0404143 × 10−3 | 5.1177435 × 10−2 |
| E3 | −1.0145982 × 10−5 | −1.1654551 × 10−5 | 7.1544503 × 10−6 | −5.438695 × 10−5 | |
| E4 | −1.6189993 × 10−8 | −1.2810336 × 10−8 | 3.189024 × 10−8 | ||
| E5 | 2.3816486 × 10−11 | 2.0998405 × 10−11 | |||
| B | −1.2150799 × 101 | −1.2150799 × 101 | −8.2470402 | −3.8358214 | −1.6463576 × 101 |
On plotting the very small differences between In p given by eq (16) and Stimson’s measurements as a function of temperature, we observed that the course of the curve was smooth. A polynomial of the fourth degree was fitted to this difference curve. By adding the corresponding coefficients of like powers in T48 to eq (16) we obtained
| (17) |
which is identical to eq (16), except that the numerical values of the coefficients E1 through E5 are slightly different. The coefficients are listed in table 1.
We investigated the feasibility of simplifying eq (17). Numerous formulas have been proposed for empirically representing the functional relationship between vapor pressure and temperature [23, 24, 25, 26]. A procedure often followed is to select the formula with the least number of terms that not only best fits the vapor pressure data but also yields derivatives that are smooth and regular. We chose the equation
| (18) |
because it is analogous in form to our derived eq (17) and fitted it for 2 ⪙ n ⪙ 4 by the method of least squares to values of vapor pressure generated at 1-deg intervals from 0 to 100 °C by eq (17). The coefficients are listed in table 1. For convenience in identifying the several versions of eq (18), each has been designated with a letter a through c corresponding to n = 2, 3, and 4, respectively.
3. Results
The measurements made at the Physikalisch-Technische Reichsanstalt by Holborn and Henning [27] in 1908 from 50 to 200 °C and by Scheel and Heuse [28] in 1910 from 0 to 50 °C have, until now, constituted the major sources of data for the vapor pressure of water in the 0 to 100 °C range. In 1919, PTR published revised values of the vapor pressure [29] and these have served as the input data for many empirical formulations [30, 31].
The steam point has been used as one of the defining fixed points for the several successive practical temperatures scales that have been adopted internationally [10, 11, 12, 32]. Because of this, the vapor pressure near the steam point has been investigated in great detail [33, 34, 35, 36, 37, 38]. Most of these measurements were made over narrow temperature spans around 100 °C. The largest temperature range, 73 to 130 °C, was covered in 1939 by Moser and Zmaczynski [37] who used both a static and a dynamic method in their determinations. Beattie and Blaisdell in 1937 [36] and Michels, Blaisse, Ten Seldam and Wouters in 1943 [38] limited their observations to several degrees below and above 100 °C.
Douslin and McCullough in 1963 [39] and Douslin in 1970 [40], using an inclined dead-weight piston gage, made vapor pressure measurements from 0 to 20 °C.
The above series of measurements, plus the measurements of Stimson, comprise the most important determinations covering the 0 to 100 °C span.
We compared our formulation with these experimental data and with other formulations in order to obtain a general perspective on the degree of accord achieved. However, because of the high precision and internal consistency of the Stimson measurements we judged the efficacy of our vapor pressure equations primarily on their agreement with the Stimson data.
3.1. Comparisons With Stimson’s Measurements
Differences in vapor pressure between Stimson’s measurements and eqs (14), (16), (17), and (18) are given in table 2. The standard deviation of Stimson’s values are also shown. Equation (14) yields values which agree with Stimson’s measurements to within one standard deviation of the latter, except at 50 and 80 °C where the agreement is within two standard deviations. The maximum difference is 32 ppm and occurs at 25 °C. The conversion of eq (14), an implicit equation, to eq (16), an explicit equation, has little effect on the differences. Equation (17), which was obtained by making a minor adjustment to the coefficients of eq (16), is in closer accord with Stimson’s measurements. The maximum difference is 7 ppm. Of the three variants of eq (18), which are least square fits to values generated by eq (17), eqs (18b) and (18c) are in excellent agreement with Stimson’s measurements, differing at most by 9 ppm. The differences for eq (18a) are larger, becoming as great as 52 ppm at 100 °C. There does not appear to be any reason for choosing any one equation from eqs (17), (18b), and (18c) on the basis of the difference between calculated vapor pressures and Stimson’s measurements.
Table 2.
Comparison between calculated vapor pressures and Stimson’s measurements on IPTS–48
| Temperature IPTS-48 | Stimson’s measurements | Eq (14) |
Eq (16) n = 5 |
Eq (17) n = 5 |
Eq (18a) n = 2 |
Eq (18b) n = 4 |
Eq (18c) n = 4 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vapor pressure | Standard deviation | ||||||||||||||
| °C | pascals | pascals | ppm | pascal | ppm | pascal | ppm | pascal | ppm | pascal | ppm | pascal | ppm | pascal | ppm |
| 25 | 3167.0 | 0.14 | 44 | + 0.1 | + 32 | + 0.1 | + 32 | 0.0 | 0 | 0.0 | 0 | 0.0 | 0 | 0.0 | 0 |
| 40 | 7377.27 | .15 | 20 | +.11 | + 15 | +.08 | + 11 | −.05 | −7 | −.14 | −19 | −.02 | −3 | −.07 | −9 |
| 50 | 12338.30 | .18 | 15 | + .22 | + 18 | + .18 | + 14 | + .09 | + 7 | −.15 | −12 | + .10 | + 8 | + .05 | + 4 |
| 60 | 19924.22 | .16 | 8 | −.15 | − 8 | − .17 | − | − .12 | −6 | − .33 | −17 | − .13 | −7 | − .18 | −9 |
| 70 | 31166.15 | .22 | 7 | − .20 | − 6 | − .20 | − | + .15 | + 5 | + .40 | + 12 | + .16 | + 5 | + .05 | + 2 |
| 80 | 47363.9 | .52 | 11 | − .7 | −15 | − .9 | −19 | − .2 | −4 | + .9 | + 19 | 0.0 | 0 | − .4 | −8 |
| 100 | 101325.0 | 1.59 | 16 | + .1 | + 1 | + .2 | + 2 | 0.0 | 0 | −5.3 | −52 | − .5 | −5 | − .4 | −4 |
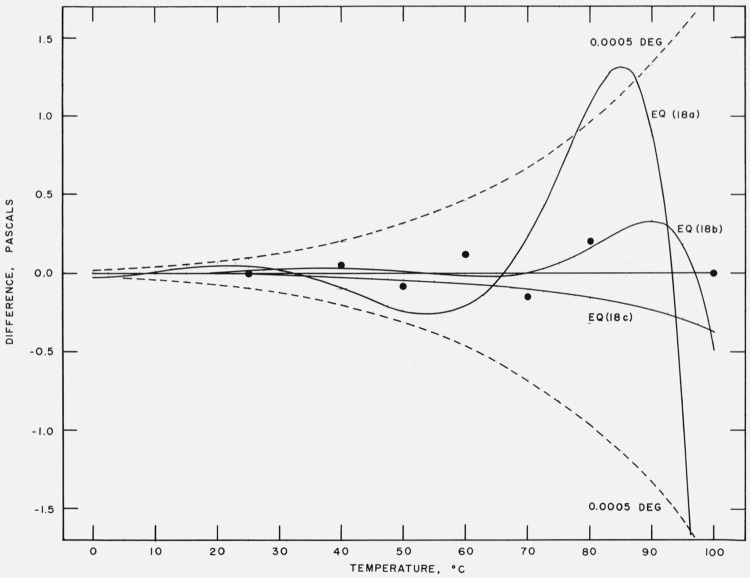
Using eq (17) as a base line, differences between eqs (18a) through (18c) and eq (17) were computed and plotted in pascals on figure 1 and in ppm on figure 2. The differences between Stimson’s measurements and eq (17) are also shown. As n decreases from 4 to 2 the differences increase. Equation (18c) deviates systematically from eq (17) by 3 ppm. The differences between eq (18b) and (17) and eqs (18a) and (17) show oscillatory patterns; they do not exceed 9 ppm for eq (18b) but reach 52 ppm for (18a). Equations (18c) and (18b) offer a reduction in terms without a significant loss in accuracy. If a lower order of accuracy is acceptable, then eq (18a) could be used. In our opinion, eq (17) is preferable because it has a thermodynamic origin and, therefore, may inspire more confidence for interpolation and extrapolation. However, eq (17) has seven terms and where a simpler formula is desired, eq (18b), with five terms, would be our choice.
Figure 1. Comparison of equations.
Vapor pressure difference [other–eq (17)] in pascals between eqs (18a), (18b), and (18c) and eq (17). Vapor pressure difference between Stimson’s measurements and eq (17) shown by solid circles. Dashed lines are difference curves for a temperature deviation of ± 0.0005 deg.
Figure 2. Comparison of equations.
Relative vapor pressure difference in ppm between eqs (18a), (18b), and (18c) and eq (17). Relative vapor pressure difference between Stimson’s measurements and eq (17) shown by solid circles. Dashed lines are difference curves for a temperature deviation of ± 0.0005 deg.
3.2. Comparisons With Douslin’s Measurements
Douslin [39, 40] has made two sets of vapor pressure measurements over liquid water at temperatures below 25 °C using an inclined-piston dead-weight pressure gage.4 The earlier measurements are as much as 4 pascals (30 microns) higher at some temperatures which Douslin attributed to incomplete degassing of his water sample in the earlier work. In the later work, the measurements were made in two series, Series I with the piston unweighted and Series II with the piston weighted. The two series overlap in temperature. We have compared Douslin’s later measurements [40] with eq (17). The differences are given in table 3. Douslin’s vapor pressures, measured on IPTS–68, were adjusted to IPTS–48 for this comparison. He reported that his estimated maximum systematic error varied from 0.32 pascal at 0 °C to 0.81 pascal at 20 °C, or, in relative terms, from 520 to 350 ppm. There is a systematic difference between Douslin’s measurements and our calculations, his observed values deviating from our computed values by two to three times his estimated maximum systematic error. It must be emphasized that eq (17) was adjusted to fit Stimson’s measurements in the range 25 to 100 °C and that our calculations below 25 °C are therefore, in part, extrapolations and may not necessarily fit other experimental measurements with comparable accuracy.
Table 3.
Comparison between calculated vapor pressures and Douslin’s measurements on IPTS–48
| Temperature IPTS-48 | Douslin’s Adjusted Measurements | Vapor Pressure Difference Douslin — Eq (17) |
|||
|---|---|---|---|---|---|
| Vapor pressure | Maximum systematic error | ||||
| °C | pascals | pascals | ppm | pascals | ppm |
| Series I | |||||
| 0 | a611.5 | 0.32 | 520 | + 0.7 | + 1140 |
| 0.01 | 612.2 | .33 | 540 | + 1.0 | + 1630 |
| 1 | 657.4 | .35 | 530 | + 0.8 | + 1220 |
| 2 | 706.2 | .35 | 490 | + 0.7 | + 990 |
| 3 | 758.6 | .36 | 470 | + 1.1 | + 1450 |
| 4 | 813.7 | .37 | 460 | + 0.8 | + 980 |
| 5 | 873.0 | .39 | 440 | + 1.1 | + 1260 |
| 7.5 | 1037.2 | .43 | 410 | + 1.0 | + 960 |
| 10 | 1228.8 | .45 | 370 | + 1.6 | + 1300 |
| 15 | 1706.1 | .57 | 340 | + 1.7 | + 1000 |
| Series II | |||||
| 7.5 | 1036.8 | 0.43 | 410 | + 0.6 | + 580 |
| 12.5 | 1448.2 | .61 | 420 | −0.4 | −280 |
| 17.5 | 2000.1 | .73 | 370 | + 1.1 | + 550 |
| 20 | 2338.7 | .81 | 350 | + 1.4 | + 600 |
Metastable state; vapor pressure with respect to supercooled water.
3.3. Comparisons at the Ice and Triple Points
In table 4 we have compared several Physikalisch-Technische Reichsanstalt measurements of vapor pressure at 0 °C [28, 41, 42], Prytz’s measurement at the triple point [43], and steam table values at both the ice and triple points [16, 44, 48] with corresponding values calculated with eq (17). It may be noted that the ice and triple points should not be subject to any temperature scale uncertainty as may be the case at other temperatures with data from the early 1900’s. To complete the tabulation, Douslin’s values at 0° and 0.01 °C [40] are repeated here.
Table 4.
Ice point and triple point vapor pressures comparisons
| Source | Reference | Ice point, 0° | Triple point, 0.01 °C | ||||
|---|---|---|---|---|---|---|---|
| Vapor pressurea | Difference Other-Eq (17) |
Vapor pressure | Difference Other-Eq (17) |
||||
| Eq (7) | pascal 610.75 | pascal | ppm | pascal 611.20 | pascal | ppm | |
| Experimental Measurements | |||||||
| Thiesen and Scheel (1900) | [41] | 610.46 | −0.29 | − 480 | |||
| Scheel and Heuse (1909) | [42] | 610.46 | −0.29 | − 480 | |||
| Scheel and Heuse (1910) | [28] | 610.11 | −0.64 | −1050 | |||
| Prytz (1931) | [43] | 611.52 | + 0.32 | + 530 | |||
| Douslin (1970) | [40] | 611.5 | + 0.75 | + 1200 | 612.2 | + 1.0 | + 1640 |
| Steam Tables | |||||||
| IST (1963) | [44] | 610.8 | + 0.05 | + 80 | 611.2 | 0.0 | 0 |
| NEL (1964) | [44] | 610.7 | −0.05 | − 80 | 611.2 | 0.0 | 0 |
| IFC (1967) | [48] | 610.8 | + 0.05 | + 80 | 611.2 | 0.0 | 0 |
| Keenan, Keyes, et al. (1969) | [16] | 610.8 | + 0.05 | + 80 | 611.3 | + 0.1 | + 160 |
Metastable state; vapor pressure with respect to supercooled water.
At 0 °C, the PTR data are lower and Douslin’s measurement is higher than our calculated value. At the triple point, Prytz’s and Douslin’s measurements are higher than our calculated value. We are in very good agreement with the steam table values.
3.4. Comparisons at and below the Steam Point
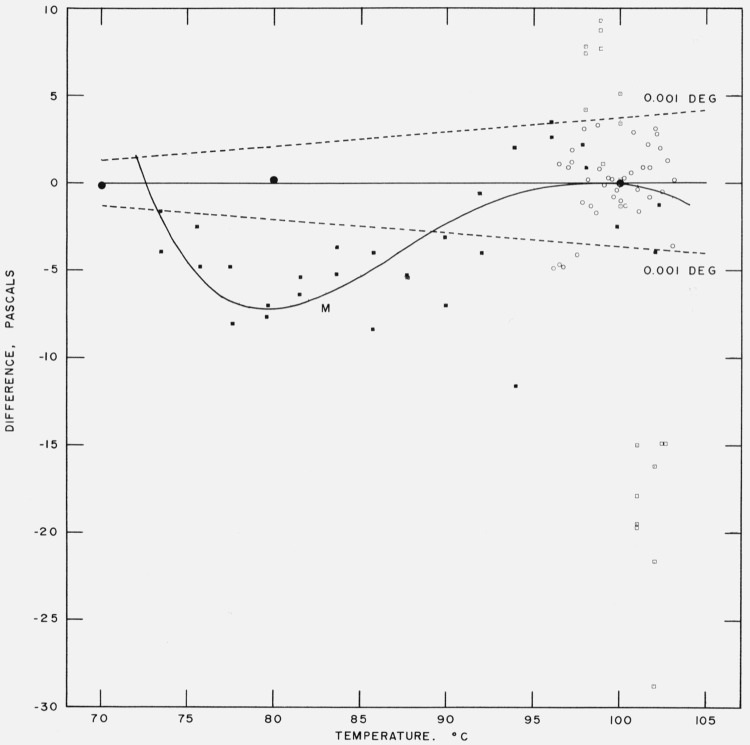
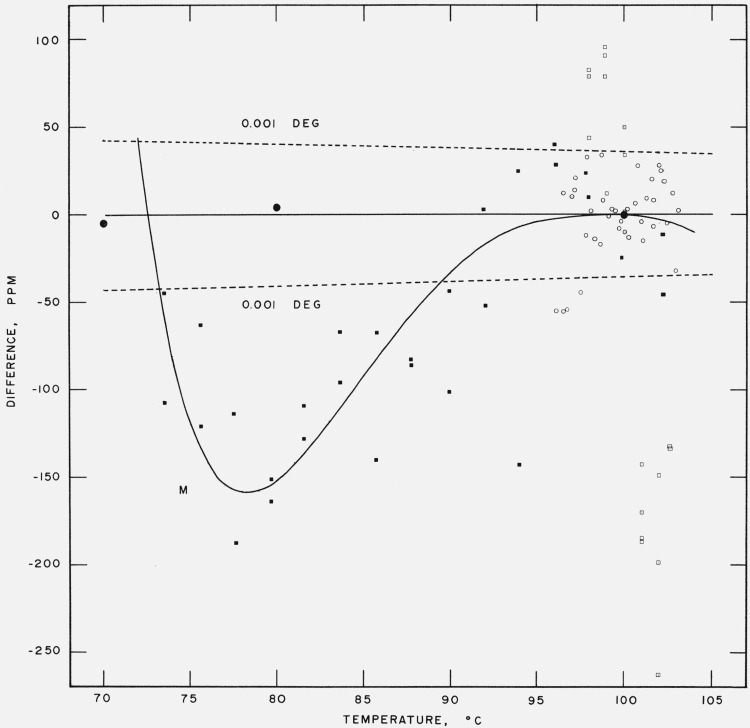
We have compared the Moser and Zmaczynski data [37],5 the Beattie and Blaisdell data [36], and the Michels, Blaisse, Ten Seldam and Wouters data [38] with eq (17). This is shown as a plot of vapor pressure differences, in pascals, in figure 3 and as a plot of relative vapor pressure differences, in ppm, in figure 4. Moser and Zmaczynski fitted their data to a polynomial equation of the fourth degree in temperature. We, therefore, have included a curve of the differences between the Moser and Zmaczynski equation and eq (17). There is a varying negative difference between the Moser and Zmaczynski data and eq (17), reaching a maximum at 78 °C of −8 pascals (−190 ppm). The Beattie and Blaisdell data cover only the very narrow temperature range of 96 to 103 °C. The differences appear to be random with respect to sign and magnitude. The residual standard deviation (based on n-7 degrees of freedom where 7 is the number of coefficients in eq (17)) is 1.55 pascals (17 ppm). The Michels et al. data extend from 98 to 102.6 °C. The differences vary linearly with temperature from about + 9.3 pascals (+100 ppm) at 98 °C to about −27.7 pascals (−260 ppm) at 102.6 °C.
Figure 3. Comparison with experimental data at and below the steam point.
Vapor pressure difference [measurement – eq (17)] in pascals between measurement and eq (17).
● Stimson
■ Moser and Zmaczynski
○ Beattie and Blaisdell
□ Michels, Blaisse, Ten Seldam and Wouters
M Moser and Zmaczynski equation
Dashed lines are difference curves for a temperature deviation of ± 0.001 deg.
Figure 4. Comparison with experimental data at and below the steam point.
Relative vapor pressure difference in ppm between measurement and eq (17).
● Stimson
■ Moser and Zmaczynski ○ Beattie and Blaisdell
□ Michels, Blaisse, Ten Seldam and Wouters M Moser and Zmaczynski equation
Dashed lines are difference curves for a temperature deviation of ±0.001 deg.
3.5. Comparisons With Other Formulations
There have been numerous attempts to formulate vapor pressure equations for the pure water substance. Some of the equations are based on theoretical considerations, others are empirical. Since Sonntag [45] has summarized the extensive literature on the vapor pressure of water, we will not attempt to repeat it here. However, we will compare vapor pressures computed from several formulas which are in current use with vapor pressures computed from eq (17) over the range 0 to 100 °C. We have chosen for this purpose the equations due to Gerry [44, 46], Goff and Gratch [1], American Petroleum Institute [47], 1967 IFC [48], Bridgeman and Aldrich [49], and Gibson and Bruges [50].
The Gerry equation is an empirical formula derived from Physikalisch-Technische Reichsanstalt data. It was adopted by the Third International Conference on Steam Tables in 1934 [51] and has been used in successive formulations of the International Skeleton Tables.
The Goff and Gratch equation is based on integration of the Clausius-Clapeyron equation. It was adopted in 1947 by the Twelfth Conference of Directors of the International Meteorological Organization and by the Joint International Committee on Psychrometric Data in 1949 [19]. Tables of vapor pressure were published in the ASHRAE Guide [52] and in the Smithsonian Meteorological Tables [53]. Goff transposed this equation from the absolute ITS–48 to the absolute IPTS–48 [1] in which form it was adopted by the World Meteorological Organization [54]. It is this latter version which we use for our comparison.
The American Petroleum Institute Research Project 44 values of vapor pressure were calculated from the Antoine equation using several sets of constants, each set valid for a narrow range of temperatures. These constants were derived by fitting the Antoine equation to vapor pressures obtained from the Osborne and Meyers formulation [31] to which were added the “Cragoe-Stimson” corrections. The latter were obtained from vapor pressure measurements made at NBS in 1942 which had received limited private circulation but had remained unpublished until 1967 [50]. These 1942 measurements, augmented by a more extensive series of measurements made during the years 1947 through 1949, were finally published in 1969 by Stimson [2].
At the Sixth International Conference on the Properties of Steam an International Formulation Committee (IFC) was established to develop for use with computers a thermodynamically consistent formulation of the properties of steam within the tolerances of the International Skeleton Table of 1963. The result was the 1967 IFC Formulation for Industrial Use. Values of vapor pressure calculated using the vapor pressure equation given by the 1967 IFC are tabulated in the 1967 ASME Steam Tables [48].
In 1964, Bridgeman and Aldrich published an equation and tables of vapor pressure for water. Keenan et al. [16] used the Bridgeman and Aldrich values to derive an alternate equation. We used the logarithm of the vapor pressure given by Bridgeman and Aldrich in their tables [49] and converted this to vapor pressure.
Gibson and Bruges [50] derived two empirical vapor pressure equations using Chebyshev polynomials. One equation, which we will designate by a, reproduces the entries in table 1 of the 1964 NEL Steam Tables [44] which, in turn, are derived from the Gerry equation [44, 46], for 0 to 100 °C and from the Osborne and Meyers formulation [31] above 100 °C. The second equation, which we will designate by b, is based on APIRP–44 values [47] between 0 and 100 °C, and on the Osborne and Meyers formulation above 100 °C.
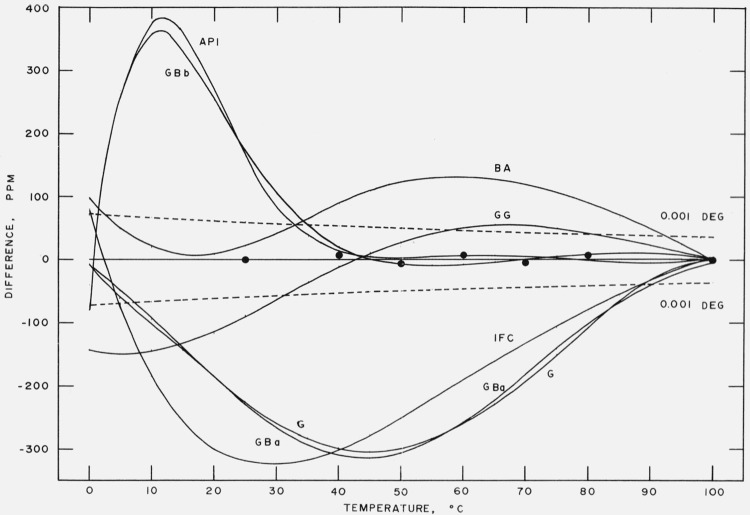
We have calculated the differences in vapor pressure between each of the above formulations and eq (17) and plotted these in pascals on figure 5 and in ppm on figure 6. Also included on these figures are the differences between Stimson’s measurements and eq (17). These figures show the degree of accord of the several formulations with eq (17) as well as with the Stimson vapor pressures.
Figure 5. Comparison with other formulations.
Vapor pressure difference [other–eq (17)] in pascals between other formulations and eq (17).
API American Petroleum Institute Research Project 44
BA Bridgeman and Aldrich
G Gerry
GBa Gibson and Bruges, eq (a)
GBb Gibson and Bruges, eq (b)
GG Goff and Gratch
IFG International Formulation Committee
Dashed lines are differences curves for a temperature deviation of ± 0.001 deg.
Figure 6. Comparison with other formulations.
Relative vapor pressure difference in ppm between other formulations and eq (17).
API Ameriean Petroleum Institute Research Project 44.
BA Bridgeman and Aldrieh
G Gerry
GBa Gibson and Bruges, eq (a)
GBb Gibson and Bruges, eq (b)
GG Goff and Gratch
IFC International Formulation Committee
Dashed lines are difference curves for a temperature deviation of ± 0.001 deg.
3.6. Conversion to IPTS-68
In 1968 the International Practical Temperature Scale of 1968 (IPTS-68) was adopted [32] as a replacement for IPTS-48. We have converted eq (17) from IPTS-48 to IPTS-68. Let the difference between these two scales be designated by μ, that is,
| (19) |
Douglas [55] has shown that from 0 to 630.74 °C, μ is given by
| (20) |
where
| (21) |
and t68 is in Celsius degrees on IPTS-68. Expanding eq (20) into a polynomial, converting t68 to T68, where T68 = t68 + 273.15, and neglecting higher order terms in T68, we obtain
| (22) |
where α0 = 1.1314914, α1= −9.9294171 × 10−3, α2 = 3.0306087 × 10−5 α3 = −3.9043313 × 10−8 and α4 = 1.7044968 × 10−11. Equations (19) and (22) are now substituted into eq (17) which, after appropriate algebraic manipulations, and neglecting higher order terms in μ, becomes
| (23) |
where F0 = −8.49922 × 103, F1 = −7.4231865 × 103, F2 = 96.1635147, F3 = 2.4917646 × 10−2, F4 = −1.3160119 × 10−5 F5 = −1.1460454 × 10−8, F6 = 2.1701289 × 10−11, F7 = −3.610258 × 10−15, F8 = 3.8504519 × 10−18, F9 = −1.4317 × 10−21, and B = −12.150799.
In the range 0 to 100 °C, the numerical values of temperature on IPTS-48 are larger than on IPTS-68. Therefore, at the same numerical values of temperature, the corresponding vapor pressures are smaller on IPTS-48. For example, at t48 = 50 °C, the vapor pressure, calculated by eq (17), is 12338.39 pascals whereas at t68 = 50 °C, the vapor pressure, calculated by eq (23), is 12344.73 pascals.
We investigated the feasibility of simplifying eq (23). We fitted the equation
| (24) |
for 2 ⪙ n ⪙ 4 by the method of least squares to values of vapor pressure generated at 1-deg intervals from 0 to 100 °C by eq (23). The results are comparable to that obtained for T48. We, therefore, only present the results for n = 3 where the largest difference between eqs (23) and (24) is 8 ppm. The coefficients are as follows: G0 = −6898.2434, G1 = 59.38385, G2 = − 5.797662 × 10−3, G3 = 6.2223854 × 10−6, and H = − 4.7406885. Equation (24) on IPTS-68 with these coefficients is equivalent to eq (18b) on IPTS-48.
3.7. Tabulations
Using eqs (17) and (23) we computed vapor pressure in pascals, as a function of temperature, in degrees Celsuis, at 0.1-deg intervals, from 0 to 100 °C, These computed values are given in table 5 on IPTS-48 and in table 6 on IPTS-68.
Table 5.
Saturation vapor pressure over water (IPTS-48)
| Temperature deg C | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| pascals | pascals | pascals | pascals | pascals | pascals | pascals | pascals | pascals | pascals | |
| 0 | a610.752 | 615.205 | 619.686 | 624.196 | 628.736 | 633.304 | 637.902 | 642.529 | 647.187 | 651.874 |
| 1 | 656.591 | 661.338 | 666.116 | 670.924 | 675.763 | 680.633 | 685.534 | 690.466 | 695.429 | 700.425 |
| 2 | 705.451 | 710.510 | 715.601 | 720.724 | 725.879 | 731.068 | 736.289 | 741.542 | 746.829 | 752.150 |
| 3 | 757.504 | 762.891 | 768.313 | 773.768 | 779.258 | 784.782 | 790.341 | 795.934 | 801.563 | 807.227 |
| 4 | 812.926 | 818.660 | 824.431 | 830.237 | 836.079 | 841.958 | 847.873 | 853.825 | 859.814 | 865.840 |
| 5 | 871.903 | 878.004 | 884.142 | 890.318 | 896.533 | 902.785 | 909.076 | 915.406 | 921.775 | 928.183 |
| 6 | 934.630 | 941.117 | 947.643 | 954.209 | 960.816 | 967.462 | 974.150 | 980.878 | 987.647 | 994.457 |
| 7 | 1001.31 | 1008.20 | 1015.14 | 1022.11 | 1029.13 | 1036.20 | 1043.30 | 1050.45 | 1057.64 | 1064.87 |
| 8 | 1072.15 | 1079.47 | 1086.84 | 1094.25 | 1101.70 | 1109.20 | 1116.75 | 1124.34 | 1131.97 | 1139.65 |
| 9 | 1147.38 | 1155.15 | 1162.97 | 1170.83 | 1178.75 | 1186.71 | 1194.71 | 1202.77 | 1210.87 | 1219.02 |
| 10 | 1227.22 | 1235.46 | 1243.76 | 1252.10 | 1260.50 | 1268.94 | 1277.43 | 1285.98 | 1294.57 | 1303.22 |
| 11 | 1311.91 | 1320.66 | 1329.45 | 1338.30 | 1347.20 | 1356.15 | 1365.16 | 1374.22 | 1383.33 | 1392.49 |
| 12 | 1401.71 | 1410.98 | 1420.30 | 1429.68 | 1439.11 | 1448.60 | 1458.14 | 1467.74 | 1477.39 | 1487.10 |
| 13 | 1496.87 | 1506.69 | 1516.57 | 1526.50 | 1536.49 | 1546.54 | 1556.65 | 1566.81 | 1577.04 | 1587.32 |
| 14 | 1597.66 | 1608.06 | 1618.52 | 1629.04 | 1639.62 | 1650.25 | 1660.95 | 1671.72 | 1682.54 | 1693.42 |
| 15 | 1704.37 | 1715.37 | 1726.44 | 1737.57 | 1748.77 | 1760.03 | 1771.35 | 1782.74 | 1794.19 | 1805.70 |
| 16 | 1817.28 | 1828.92 | 1840.63 | 1852.41 | 1864.25 | 1876.16 | 1888.13 | 1900.18 | 1912.28 | 1924.46 |
| 17 | 1936.70 | 1949–02 | 1961.40 | 1973.85 | 1986.37 | 1998.96 | 2011.62 | 2024.34 | 2037.14 | 2050.01 |
| 18 | 2062.96 | 2075.97 | 2089.05 | 2102.21 | 2115.44 | 2128.74 | 2142.12 | 2155.57 | 2169.09 | 2182.69 |
| 19 | 2196.36 | 2210.11 | 2223.93 | 2237.83 | 2251.80 | 2265.85 | 2279.98 | 2294.18 | 2308.47 | 2322.83 |
| 20 | 2337-26 | 2351.78 | 2366.37 | 2381.05 | 2395.80 | 2410.63 | 2425.55 | 2440.54 | 2455.62 | 2470.77 |
| 21 | 2486.01 | 2501.33 | 2516.73 | 2532.22 | 2547.79 | 2563.44 | 2579.18 | 2595.00 | 2610.90 | 2626.90 |
| 22 | 2642.97 | 2659.13 | 2675.38 | 2691.72 | 2708.14 | 2724.65 | 2741.25 | 2757.94 | 2774.71 | 2791.57 |
| 23 | 2808.53 | 2825.57 | 2842.70 | 2859.93 | 2877.24 | 2894.65 | 2912.15 | 2929.74 | 2947.42 | 2965.20 |
| 24 | 2983.07 | 3001.03 | 3019.09 | 3037.24 | 3055.49 | 3073.84 | 3092.28 | 3110.81 | 3129.44 | 3148.17 |
| 25 | 3167.00 | 3185.93 | 3204.95 | 3224.08 | 3243.30 | 3262.62 | 3282.05 | 3301.57 | 3321.20 | 3340.92 |
| 26 | 3360.75 | 3380.68 | 3400.72 | 3420.86 | 3441.10 | 3461.44 | 3481.90 | 3502.45 | 3523.11 | 3543.88 |
| 27 | 3564.75 | 3585.74 | 3606.82 | 3628.02 | 3649.33 | 3670.74 | 3692.26 | 3713.90 | 3735.64 | 3757.49 |
| 28 | 3779.46 | 3801.54 | 3823.73 | 3846.03 | 3868.44 | 3890.97 | 3913.61 | 3936.37 | 3959.24 | 3982.23 |
| 29 | 4005.33 | 4028.56 | 4051.89 | 4075.35 | 4098.92 | 4122.61 | 4146.42 | 4170.35 | 4194.40 | 4218.57 |
| 30 | 4242.86 | 4267.28 | 4291.81 | 4316.47 | 4341.25 | 4366.15 | 4391.18 | 4416.33 | 4441.61 | 4467.01 |
| 31 | 4492.54 | 4518.20 | 4543.98 | 4569.89 | 4595.93 | 4622.10 | 4648.40 | 4674.82 | 4701.38 | 4728.07 |
| 32 | 4754.89 | 4781.84 | 4808.93 | 4836.14 | 4863.49 | 4890.98 | 4918.60 | 4946.35 | 4974.24 | 5002.27 |
| 33 | 5030.44 | 5058.74 | 5087.18 | 5115.76 | 5144.47 | 5173.33 | 5202.33 | 5231.47 | 5260.74 | 5290.17 |
| 34 | 5319.73 | 5349.44 | 5379.29 | 5409.28 | 5439.42 | 5469.71 | 5500.14 | 5530.72 | 5561.45 | 5592.32 |
| 35 | 5623.34 | 5654.51 | 5685.83 | 5717.30 | 5748.92 | 5780.69 | 5812.62 | 5844.70 | 5876.93 | 5909.31 |
| 36 | 5941.85 | 5974.54 | 6007.39 | 6040.40 | 6073.56 | 6106.88 | 6140.36 | 6173.99 | 6207.79 | 6241.75 |
| 37 | 6275.86 | 6310.14 | 6344.58 | 6379.18 | 6413.95 | 6448.87 | 6483.97 | 6519.23 | 6554.65 | 6590.24 |
| 38 | 6626.00 | 6661.92 | 6698.02 | 6734.28 | 6770.71 | 6807.31 | 6844.08 | 6881.03 | 6918.15 | 6955.44 |
| 39 | 6992.90 | 7030.54 | 7068.35 | 7106.34 | 7144.50 | 7182.84 | 7221.36 | 7260.06 | 7298.93 | 7337.99 |
| 40 | 7377.22 | 7416.64 | 7456.24 | 7496.02 | 7535.98 | 7576.13 | 7616.46 | 7656.98 | 7697.68 | 7738.57 |
| 41 | 7779.65 | 7820.92 | 7862.37 | 7904.01 | 7945.85 | 7987.87 | 8030.09 | 8072.50 | 8115.10 | 8157.89 |
| 42 | 8200.88 | 8244.07 | 8287.45 | 8331.02 | 8374.80 | 8418.77 | 8462.94 | 8507.31 | 8551.89 | 8596.66 |
| 43 | 8641.63 | 8686.81 | 8732.19 | 8777.78 | 8823.57 | 8869.56 | 8915.76 | 8962.17 | 9008.79 | 9055.61 |
| 44 | 9102.65 | 9149.89 | 9197.35 | 9245.02 | 9292.90 | 9340.99 | 9389.30 | 9437.82 | 9486.56 | 9535.51 |
| 45 | 9584.69 | 9634.08 | 9683.68 | 9733.51 | 9783.56 | 9833.83 | 9884.32 | 9935.04 | 9985.98 | 10037.14 |
| 46 | 10088.53 | 10140.14 | 0191.99 | 10244.06 | 0296.35 | 0348.88 | 0401.64 | 10454.63 | 10507.85 | 10561.30 |
| 47 | 10614.98 | 10668.91 | 0723.06 | 10777.45 | 0832.08 | 0886.95 | 0942.05 | 10997.40 | 11052.98 | 11108.81 |
| 48 | 11164.88 | 11221.19 | II277.74 | 11334.54 | 1391.58 | 1448.88 | 1506.41 | 11564.20 | 11622.23 | 11680.52 |
| 49 | 11739.05 | 11797.84 | 1856.88 | 11916.17 | 1975.72 | 2035.52 | 2095.58 | 12155.89 | 12216.47 | 12277.30 |
| 50 | 12338.39 | 12399.74 | 2461.35 | 2523.23 | 2585.37 | 2647.77 | 2710.44 | 12773.37 | 12836.57 | 12900.04 |
| 51 | 12963.77 | 13027.78 | 3092.06 | 3156.61 | 3221.43 | 3286.52 | 3351.89 | 13417.54 | 13483.46 | 13549.66 |
| 52 | 13616.13 | 13682.89 | 3749.92 | 3817.24 | 3884.84 | 3952.72 | 4020.88 | 14089.33 | 14158.07 | 14227.09 |
| 53 | 14296.40 | 14366.00 | 4435.89 | 4506.07 | 4576.54 | 4647.30 | 4718.36 | 14789.71 | 14861.36 | 14933.31 |
| 54 | 15005.55 | 5078.09 | 5150.93 | 5224.07 | 5297.51 | 5371.26 | 5445.31 | 15519.66 | 15594.32 | 15669.29 |
| 55 | 15744.56 | 15820.15 | 5896.04 | 5972.25 | 6048.76 | 6125.59 | 6202.73 | 16280.19 | 16357.97 | 16436.06 |
| 56 | 16514.47 | 16593.19 | 6672.24 | 6751.61 | 6831.31 | 6911.32 | 6991.66 | 17072.33 | 17153.32 | 17234.64 |
| 57 | 17316.29 | 17398.27 | 7480.58 | 7563.22 | 7646.20 | 7729.51 | 7813.15 | 17897.13 | 17981.45 | 18066.11 |
| 58 | 18151.11 | 18236.45 | 8322.12 | 8408.15 | 8494.51 | 8581.23 | 8668.29 | 18755.69 | 18843.45 | 18931.55 |
| 59 | 19020.01 | 9108.81 | 9197.97 | 9287.49 | 9377.36 | 9467.58 | 9558.17 | 19649.11 | 19740.41 | 19832.08 |
| 60 | 19924.10 | 20016.49 | 20109.25 | 20202.37 | 20295.86 | 20389.71 | 20483.93 | 20578.53 | 20673.50 | 20768.83 |
| 61 | 20864.55 | 20960.64 | 21057.10 | 21153.94 | 21251.16 | 21348.76 | 21446.74 | 21545.11 | 21643.86 | 21742.99 |
| 62 | 21842.51 | 21942.41 | 22042.70 | 22143.39 | 22244.46 | 22345.93 | 22447.79 | 22550.04 | 22652.69 | 22755.73 |
| 63 | 22859.18 | 22963.02 | 23067.27 | 23171.91 | 23276.96 | 23382.41 | 23488.27 | 23594.54 | 23701.21 | 23808.29 |
| 64 | 23915.79 | 24023.69 | 24132.01 | 24240.75 | 24349.90 | 24459.46 | 24569.45 | 24679.85 | 24790.67 | 24901.92 |
| 65 | 25013.59 | 25125.69 | 25238.21 | 25351.15 | 25464.53 | 25578.34 | 25692.58 | 25807.25 | 25922.35 | 26037.89 |
| 66 | 26153.87 | 26270.28 | 26387.13 | 26504.43 | 26622.16 | 26740.34 | 26858.96 | 26978.03 | 27097.54 | 27217.51 |
| 67 | 27337.92 | 27458.79 | 27580.10 | 27701.88 | 27824.10 | 27946.79 | 28069.93 | 28193.53 | 28317.59 | 28442.11 |
| 68 | 28567.10 | 28692.55 | 28818.47 | 28944.85 | 29071.71 | 29199.03 | 29326.83 | 29455.10 | 29583.84 | 29713.06 |
| 69 | 29842.76 | 29972.94 | 30103.59 | 30234.73 | 30366.35 | 30498.46 | 30631.05 | 30764.13 | 30897.70 | 31031.76 |
| 70 | 31166.31 | 31301.35 | 31436.89 | 31572.92 | 31709.45 | 31846.48 | 31984.01 | 32122.04 | 32260.57 | 32399.61 |
| 71 | 32539.16 | 32679.21 | 32819.77 | 32960.84 | 33102.43 | 33244.53 | 33387.14 | 33530.27 | 33673.92 | 33818.08 |
| 72 | 33962.77 | 34107.98 | 34253.72 | 34399.98 | 34546.76 | 34694.08 | 34841.92 | 34990.30 | 35139.21 | 35288.65 |
| 73 | 35438.63 | 35589.15 | 35740.21 | 35891.80 | 36043.94 | 36196.63 | 36349.86 | 36503.63 | 36657.95 | 36812.83 |
| 74 | 36968.25 | 37124.23 | 37280.77 | 37437.85 | 37595.50 | 37753.71 | 37912.47 | 38071.80 | 38231.70 | 38392.16 |
| 75 | 38553.18 | 38714.78 | 38876.94 | 39039.68 | 39202.99 | 39366.88 | 39531.34 | 39696.38 | 39862.01 | 40028.21 |
| 76 | 40195.00 | 40362.37 | 40530.33 | 40698.87 | 40868.01 | 41037.73 | 41208.06 | 41378.97 | 41550.48 | 41722.59 |
| 77 | 41895.30 | 42068.61 | 42242.52 | 42417.04 | 42592.16 | 42767.90 | 42944.24 | 43121.19 | 43298.76 | 43476.94 |
| 78 | 43655.73 | 43835.15 | 44015.18 | 44195.84 | 44377.11 | 44559.02 | 44741.55 | 44924.71 | 45108.49 | 45292.91 |
| 79 | 45477.96 | 45663.65 | 45849.98 | 46036.94 | 46224.54 | 46412.79 | 46601.67 | 46791.21 | 46981.39 | 47172.22 |
| 80 | 47363.70 | 47555.83 | 47748.62 | 47942.06 | 48136.16 | 48330.92 | 48526.34 | 48722.42 | 48919.17 | 49116.58 |
| 81 | 49314.67 | 49513.42 | 49712.84 | 49912.94 | 50113.71 | 50315.16 | 50517.29 | 50720.10 | 50923.59 | 51127.77 |
| 82 | 51332.63 | 51538.18 | 51744.43 | 51951.36 | 52158.98 | 52367.30 | 52576.32 | 52786.04 | 52996.46 | 53207.58 |
| 83 | 53419.40 | 53631.93 | 53845.17 | 54059.12 | 54273.78 | 54489.16 | 54705.25 | 54922.05 | 55139.58 | 55357.83 |
| 84 | 55576.80 | 55796.50 | 56016.92 | 56238.07 | 56459.95 | 56682.57 | 56905.92 | 57130.00 | 57354.82 | 57580.39 |
| 85 | 57806.69 | 58033.74 | 58261,54 | 58490.08 | 58719.37 | 58949.42 | 59180.21 | 59411.77 | 59644.08 | 59877.15 |
| 86 | 60110.98 | 60345.57 | 60580.93 | 60817.06 | 61053.95 | 61291.62 | 61530.06 | 61769.27 | 62009.26 | 62250.03 |
| 87 | 62491.58 | 62733.92 | 62977.04 | 63220.94 | 63465.64 | 63711.12 | 63957.40 | 64204.47 | 64452.34 | 64701.01 |
| 88 | 64950.48 | 65200.75 | 65451.82 | 65703.71 | 65956.40 | 66209.90 | 66464.22 | 66719.35 | 66975.30 | 67232.06 |
| 89 | 67489.65 | 67748.06 | 68007.30 | 68267.36 | 68528.26 | 68789.98 | 69052.54 | 69315.93 | 69580.16 | 69845.23 |
| 90 | 70111.14 | 70377.90 | 70645.50 | 70913.95 | 71183.25 | 71453.40 | 71724.41 | 71996.27 | 72268.99 | 72542.57 |
| 91 | 72817.02 | 73092.33 | 73368.50 | 73645.55 | 73923.46 | 74202.25 | 74481.92 | 74762.46 | 75043.88 | 75326.18 |
| 92 | 75609.37 | 75893.44 | 76178.41 | 76464.26 | 76751.00 | 77038.64 | 77327.18 | 77616.62 | 77906.95 | 78198.19 |
| 93 | 78490.34 | 78783.39 | 79077.36 | 79372.24 | 79668.03 | 79964.73 | 80262.36 | 80560.91 | 80860.38 | 81160.77 |
| 94 | 81462.10 | 81764.35 | 82067.53 | 82371.65 | 82676.71 | 82982.71 | 83289.64 | 83597.52 | 83906.35 | 84216.12 |
| 95 | 84526.84 | 84838.51 | 85151.14 | 85464.73 | 85779.28 | 86094.78 | 86411.25 | 86728.69 | 87047.09 | 87366.47 |
| 96 | 87686.81 | 88008.13 | 88330.43 | 88653.71 | 88977.97 | 89303.22 | 89629.45 | 89956.67 | 90284.88 | 90614.09 |
| 97 | 90944.29 | 91275.49 | 91607.69 | 91940.89 | 92275.10 | 92610.31 | 92946.53 | 93283.77 | 93622.02 | 93961.29 |
| 98 | 94301.58 | 94642.88 | 94985.22 | 95328.58 | 95672.96 | 96018.38 | 96364.83 | 96712.32 | 97060.85 | 97410.41 |
| 99 | 97761.02 | 98112.68 | 98465.38 | 98819.13 | 99173.94 | 99529.80 | 99886.71 | 100244.69 | 100603.73 | 100963.83 |
| 100 | 101325.01 |
Metastable state; vapor pressure with respect to supercooled water.
Table 6.
Saturation vapor pressure over water (IPTS–68)
| Temperature deg C | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| pascals | pascals | pascals | pascals | pascals | pascals | pascals | pascals | pascals | pascals | |
| 0 | a610.752 | 615.207 | 619.690 | 624.203 | 628.744 | 633.315 | 637.916 | 642.545 | 647.205 | 651.894 |
| 1 | 656.614 | 661.364 | 666.144 | 670.955 | 675.796 | 680.669 | 685.572 | 690.507 | 695.473 | 700.471 |
| 2 | 705.500 | 710.562 | 715.655 | 720.781 | 725.939 | 731.130 | 736.354 | 741.611 | 746.901 | 752.224 |
| 3 | 757.581 | 762.971 | 768.396 | 773.854 | 779.347 | 784.874 | 790.436 | 796.033 | 801.664 | 807.331 |
| 4 | 813.034 | 818.771 | 824.545 | 830.355 | 836.200 | 842.082 | 848.001 | 853.956 | 859.948 | 865.978 |
| 5 | 872.045 | 878.149 | 884.291 | 890.470 | 896.688 | 902.945 | 909.239 | 915.573 | 921.945 | 928.357 |
| 6 | 934.808 | 941.298 | 947.828 | 954.399 | 961.009 | 967.660 | 974.351 | 981.083 | 987.856 | 994.670 |
| 7 | 1001.53 | 1008.42 | 1015.36 | 1022.34 | 1029.37 | 1036.43 | 1043.54 | 1050.70 | 1057.89 | 1065.13 |
| 8 | 1072.41 | 1079.74 | 1087.11 | 1094.52 | 1101.98 | 1109.48 | 1117.03 | 1124.63 | 1132.27 | 1139.95 |
| 9 | 1147.68 | 1155.46 | 1163.28 | 1171.15 | 1179.07 | 1187.04 | 1195.05 | 1203.11 | 1211.21 | 1219.37 |
| 10 | 1227.57 | 1235.83 | 1244.13 | 1252.48 | 1260.88 | 1269.32 | 1277.82 | 1286.37 | 1294.97 | 1303.62 |
| 11 | 1312.32 | 1321.07 | 1329.87 | 1338.73 | 1347.63 | 1356.59 | 1365.60 | 1374.67 | 1383.78 | 1392.95 |
| 12 | 1402.17 | 1411.45 | 1420.78 | 1430.16 | 1439.60 | 1449.10 | 1458.64 | 1468.25 | 1477.91 | 1487.62 |
| 13 | 1497.39 | 1507.22 | 1517.11 | 1527.05 | 1537.04 | 1547.10 | 1557.21 | 1567.39 | 1577.62 | 1587.90 |
| 14 | 1598.25 | 1608.66 | 1619.12 | 1629.65 | 1640.24 | 1650.88 | 1661.59 | 1672.36 | 1683.18 | 1694.08 |
| 15 | 1705.03 | 1716.04 | 1727.12 | 1738.26 | 1749.46 | 1760.73 | 1772.06 | 1783.45 | 1794.91 | 1806.43 |
| 16 | 1818.01 | 1829.67 | 1841.38 | 1853.17 | 1865.02 | 1876.93 | 1888.91 | 1900.96 | 1913.08 | 1925.27 |
| 17 | 1937.52 | 1949.84 | 1962.23 | 1974.69 | 1987.21 | 1999.81 | 2012.48 | 2025.21 | 2038.02 | 2050.90 |
| 18 | 2063.85 | 2076.87 | 2089.97 | 2103.13 | 2116.37 | 2129.68 | 2143.07 | 2156.53 | 2170.06 | 2183.66 |
| 19 | 2197.34 | 2211.10 | 2224.93 | 2238.84 | 2252.82 | 2266.88 | 2281.02 | 2295.23 | 2309.52 | 2323.89 |
| 20 | 2338.34 | 2352.86 | 2367.47 | 2382.15 | 2396.91 | 2411.76 | 2426.68 | 2441.68 | 2456.77 | 2471.93 |
| 21 | 2487.18 | 2502.51 | 2517.93 | 2533.42 | 2549.00 | 2564.66 | 2580.41 | 2596.24 | 2612.16 | 2628.16 |
| 22 | 2644.25 | 2660.42 | 2676.68 | 2693.02 | 2709.46 | 2725.98 | 2742.59 | 2759.28 | 2776.07 | 2792.94 |
| 23 | 2809.91 | 2826.96 | 2844.11 | 2861.34 | 2878.67 | 2896.09 | 2913.60 | 2931.20 | 2948.89 | 2966.68 |
| 24 | 2984.56 | 3002.54 | 3020.61 | 3038.77 | 3057.03 | 3075.39 | 3093.84 | 3112.39 | 3131.03 | 3149.78 |
| 25 | 3168.62 | 3187.55 | 3206.59 | 3225.73 | 3244.96 | 3264.30 | 3283.73 | 3303.27 | 3322.91 | 3342.65 |
| 26 | 3362.49 | 3382.43 | 3402.48 | 3422.63 | 3442.89 | 3463.24 | 3483.71 | 3504.28 | 3524.95 | 3545.73 |
| 27 | 3566.62 | 3587.62 | 3608.72 | 3629.93 | 3651.25 | 3672.67 | 3694.21 | 3715.86 | 3737.61 | 3759.48 |
| 28 | 3781.46 | 3803.55 | 3825.75 | 3848.07 | 3870.50 | 3893.04 | 3915.70 | 3938.47 | 3961.36 | 3984.36 |
| 29 | 4007.48 | 4030.71 | 4054.06 | 4077.53 | 4101.12 | 4124.83 | 4148.65 | 4172.59 | 4196.66 | 4220.84 |
| 30 | 4245.15 | 4269.58 | 4294.13 | 4318.80 | 4343.60 | 4368.52 | 4393.56 | 4418.73 | 4444.02 | 4469.44 |
| 31 | 4494.98 | 4520.65 | 4546.45 | 4572.38 | 4598.43 | 4624.62 | 4650.93 | 4677.37 | 4703.95 | 4730.65 |
| 32 | 4757.49 | 4784.46 | 4811.56 | 4838.79 | 4866.16 | 4893.66 | 4921.29 | 4949.07 | 4976.97 | 5005.02 |
| 33 | 5033.20 | 5061.52 | 5089.97 | 5118.57 | 5147.30 | 5176.17 | 5205.19 | 5234.34 | 5263.64 | 5293.08 |
| 34 | 5322.66 | 5352.39 | 5382.25 | 5412.27 | 5442.42 | 5472.73 | 5503.18 | 5533.77 | 5564.52 | 5595.41 |
| 35 | 5626.45 | 5657.63 | 5688.97 | 5720.46 | 5752.10 | 5783.89 | 5815.83 | 5847.93 | 5880.18 | 5912.58 |
| 36 | 5945.14 | 5977.85 | 6010.72 | 6043.74 | 6076.92 | 6110.26 | 6143.75 | 6177.41 | 6211.22 | 6245.20 |
| 37 | 6279.33 | 6313.63 | 6348.09 | 6382.71 | 6417.50 | 6452.44 | 6487.56 | 6522.83 | 6558.28 | 6593.89 |
| 38 | 6629.66 | 6665.61 | 6701.72 | 6738.00 | 6774.45 | 6811.08 | 6847.87 | 6884.83 | 6921.97 | 6959.28 |
| 39 | 6996.76 | 7034.42 | 7072.25 | 7110.26 | 7148.44 | 7186.80 | 7225.34 | 7264.06 | 7302.96 | 7342.03 |
| 40 | 7381.29 | 7420.73 | 7460.35 | 7500.15 | 7540.13 | 7580.30 | 7620.65 | 7661.19 | 7701.92 | 7742.83 |
| 41 | 7783.92 | 7825.21 | 7866.69 | 7908.35 | 7950.21 | 7992.25 | 8034.49 | 8076.92 | 8119.54 | 8162.36 |
| 42 | 8205.37 | 8248.57 | 8291.98 | 8335.58 | 8379.37 | 8423.37 | 8467.56 | 8511.95 | 8556.55 | 8601.34 |
| 43 | 8646.34 | 8691.54 | 8736.94 | 8782.55 | 8828.36 | 8874.38 | 8920.60 | 8967.03 | 9013.67 | 9060.52 |
| 44 | 9107.58 | 9154.84 | 9202.32 | 9250.01 | 9297.92 | 9346.03 | 9394.36 | 9442.91 | 9491.67 | 9540.65 |
| 45 | 9589.84 | 9639.25 | 9688.89 | 9738.74 | 9788.81 | 9839.10 | 9889.62 | 9940.36 | 9991.32 | 10042.50 |
| 46 | 10093.92 | 10145.55 | 10197.42 | 10249.51 | 10301.83 | 10354.38 | 10407.16 | 10460.18 | 10513.42 | 10566.90 |
| 47 | 10620.61 | 10674.55 | 10728.73 | 10783.15 | 10837.80 | 10892.69 | 10947.82 | 11003.19 | 11058.79 | 11114.64 |
| 48 | 11170.74 | 11227.07 | 11283.65 | 11340.47 | 11397.54 | 11454.86 | 11512.42 | 11570.23 | 11628.29 | 11686.60 |
| 49 | 11745.15 | 11803.97 | 11863.03 | 11922.35 | 11981.92 | 12041.74 | 12101.83 | 12162.17 | 12222.76 | 12283.62 |
| 50 | 12344.73 | 12406.11 | 12467.75 | 12529.65 | 12591.81 | 12654.24 | 12716.93 | 12779.89 | 12843.11 | 12906.61 |
| 51 | 12970.37 | 13034.40 | 13098.70 | 13163.27 | 13228.12 | 13293.24 | 13358.63 | 13424.30 | 13490.25 | 13556.47 |
| 52 | 13622.97 | 13689.75 | 13756.81 | 13824.15 | 13891.78 | 13959.68 | 14027.87 | 14096.35 | 14165.11 | 14234.16 |
| 53 | 14303.49 | 14373.12 | 14443.03 | 14513.23 | 14583.73 | 14654.52 | 14725.60 | 14796.98 | 14868.65 | 14940.62 |
| 54 | 15012.89 | 15085.45 | 15158.32 | 15231.49 | 15304.96 | 15378.73 | 15452.80 | 15527.18 | 15601.86 | 15676.86 |
| 55 | 15752.16 | 15827.76 | 15903.68 | 15979.91 | 16056.45 | 16133.31 | 16210.47 | 16287.96 | 16365.76 | 16443.87 |
| 56 | 16522.31 | 16601.06 | 16680.13 | 16759.53 | 16839.25 | 16919.29 | 16999.65 | 17080.34 | 17161.36 | 17242.71 |
| 57 | 17324.38 | 17406.39 | 17488.72 | 17571.39 | 17654.39 | 17737.72 | 17821.39 | 17905.40 | 17989.74 | 18074.42 |
| 58 | 18159.44 | 18244.81 | 18330.51 | 18416.56 | 18502.95 | 18589.69 | 18676.77 | 18764.20 | 18851.98 | 18940.11 |
| 59 | 19028.59 | 19117.42 | 19206.60 | 19296.14 | 19386.04 | 19476.29 | 19566.90 | 19657.86 | 19749.19 | 19840.88 |
| 60 | 19932.93 | 20025.34 | 20118.12 | 20211.26 | 20304.77 | 20398.65 | 20492.90 | 20587.52 | 20682.51 | 20777.87 |
| 61 | 20873.61 | 20969.72 | 21066.21 | 21163.07 | 21260.32 | 21357.94 | 21455.95 | 21554.33 | 21653.10 | 21752.26 |
| 62 | 21851.80 | 21951.73 | 22052.04 | 22152.75 | 22253.85 | 22355.33 | 22457.21 | 22559.49 | 22662.16 | 22765.23 |
| 63 | 22868.70 | 22972.56 | 23076.83 | 23181.50 | 23286.57 | 23392.04 | 23497.92 | 23604.21 | 23710.91 | 23818.01 |
| 64 | 23925.53 | 24033.45 | 24141.79 | 24250.55 | 24359.72 | 24469.31 | 24579.31 | 24689.74 | 24800.58 | 24911.85 |
| 65 | 25023.54 | 25135.66 | 25248.20 | 25361.17 | 25474.56 | 25588.39 | 25702.65 | 25817.34 | 25932.46 | 26048.02 |
| 66 | 26164.02 | 26280.45 | 26397.32 | 26514.64 | 26632.39 | 26750.59 | 26869.23 | 26988.32 | 27107.85 | 27227.83 |
| 67 | 27348.27 | 27469.15 | 27590.48 | 27712.27 | 27834.52 | 27957.22 | 28080.38 | 28204.00 | 28328.08 | 28452.62 |
| 68 | 28577.62 | 28703.09 | 28829.03 | 28955.43 | 29082.30 | 29209.64 | 29337.46 | 29465.74 | 29594.50 | 29723.74 |
| 69 | 29853.45 | 29983.65 | 30114.32 | 30245.47 | 30377.11 | 30509.23 | 30641.84 | 30774.93 | 30908.51 | 31042.59 |
| 70 | 31177.15 | 31312.21 | 31447.76 | 31583.81 | 31720.35 | 31857.39 | 31994.94 | 32132.98 | 32271.53 | 32410.58 |
| 71 | 32550.14 | 32690.21 | 32830.78 | 32971.87 | 33113.46 | 33255.57 | 33398.20 | 33541.34 | 33685.00 | 33829.18 |
| 72 | 33973.88 | 34119.10 | 34264.84 | 34411.11 | 34557.91 | 34705.24 | 34853.09 | 35001.48 | 35150.40 | 35299.85 |
| 73 | 35449.84 | 35600.37 | 35751.43 | 35903.04 | 36055.19 | 36207.88 | 36361.12 | 36514.90 | 36669.23 | 36824.11 |
| 74 | 36979.55 | 37135.53 | 37292.07 | 37449.17 | 37606.82 | 37765.03 | 37923.81 | 38083.14 | 38243.04 | 38403.51 |
| 75 | 38564.54 | 38726.14 | 38888.31 | 39051.05 | 39214.37 | 39378.26 | 39542.72 | 39707.77 | 39873.39 | 40039.60 |
| 76 | 40206.39 | 40373.76 | 40541.73 | 40710.27 | 40879.41 | 41049.14 | 41219.46 | 41390.38 | 41561.89 | 41734.00 |
| 77 | 41906.71 | 42080.02 | 42253.93 | 42428.45 | 42603.57 | 42779.30 | 42955.64. | 43132.59 | 43310.16 | 43488.34 |
| 78 | 43667.13 | 43846.54 | 44026.57 | 44207.22 | 44388.50 | 44570.40 | 44752.92 | 44936.08 | 45119.86 | 45304.27 |
| 79 | 45489.32 | 45675.00 | 45861.32 | 46048.28 | 46235.87 | 46424.11 | 46612.99 | 46802.52 | 46992.69 | 47183.51 |
| 80 | 47374.98 | 47567.l1 | 47759.89 | 47953.32 | 48147.41 | 48342.16 | 48537.57 | 48733.64 | 48930.38 | 49127.78 |
| 81 | 49325.85 | 49524.59 | 49724.00 | 49924.09 | 50124.85 | 50326.28 | 50528.40 | 50731.19 | 50934.67 | 51138.83 |
| 82 | 51343.68 | 51549.22 | 51755.44 | 51962.36 | 52169.97 | 52378.27 | 52587.27 | 52796.97 | 53007.37 | 53218.47 |
| 83 | 53430.28 | 53642.79 | 53856.01 | 54069.94 | 54284.58 | 54499.93 | 54716.00 | 54932.78 | 55150.29 | 55368.51 |
| 84 | 55587.46 | 55807.14 | 56027.53 | 56248.66 | 56470.52 | 56693.11 | 56916.43 | 57140.49 | 57365.29 | 57590.82 |
| 85 | 57817.10 | 58044.12 | 58271.89 | 58500.41 | 58729.67 | 58959.68 | 59190.45 | 59421.97 | 59654.25 | 59887.29 |
| 86 | 60121.09 | 60355.65 | 60590.98 | 60827.07 | 61063.94 | 61301.57 | 61539.97 | 61779.15 | 62019.11 | 62259.84 |
| 87 | 62501.36 | 62743.65 | 62986.73 | 63230.60 | 63475.26 | 63720.70 | 63966.94 | 64213.98 | 64461.80 | 64710.43 |
| 88 | 64959.86 | 65210.09 | 65461.12 | 65712.96 | 65965.61 | 66219.07 | 66473.34 | 66728.43 | 66984.33 | 67241.05 |
| 89 | 67498.60 | 67756.96 | 68016.15 | 68276.16 | 68537.01 | 68798.68 | 69061.19 | 69324.53 | 69588.71 | 69853.73 |
| 90 | 70119.59 | 70386.30 | 70653.85 | 70922.24 | 71191.49 | 71461.58 | 71732.54 | 72004.34 | 72277.01 | 72550.53 |
| 91 | 72824.92 | 73100.17 | 73376.29 | 73653.27 | 73931.13 | 74209.86 | 74489.46 | 74769.94 | 75051.30 | 75333.54 |
| 92 | 75616.66 | 75900.67 | 76185.57 | 76471.36 | 76758.04 | 77045.61 | 77334.08 | 77623.45 | 77913.72 | 78204.89 |
| 93 | 78496.96 | 78789.95 | 79083.84 | 79378.65 | 79674.36 | 79971.00 | 80268.55 | 80567.02 | 80866.42 | 81166.74 |
| 94 | 81467.99 | 81770.16 | 82073.27 | 82377.31 | 82682.29 | 82988.20 | 83295.06 | 83602.86 | 83911.60 | 84221.29 |
| 95 | 84531.93 | 84843.52 | 85156.07 | 85469.57 | 85784.03 | 86099.44 | 86415.83 | 86733.17 | 87051.49 | 87370.77 |
| 96 | 87691.03 | 88012.26 | 88334.47 | 88657.66 | 88981.82 | 89306.97 | 89633.11 | 89960.24 | 90288.35 | 90617.46 |
| 97 | 90947.56 | 91278.66 | 91610.76 | 91943.86 | 92277.97 | 92613.08 | 92949.20 | 93286.34 | 93624.48 | 93963.65 |
| 98 | 94303.83 | 94645.03 | 94987.26 | 95330.51 | 95674.79 | 96020.09 | 96366.43 | 96713.81 | 97062.22 | 97411.68 |
| 99 | 97762.17 | 98113.71 | 98466.30 | 98819.94 | 99174.62 | 99530.37 | 99887.16 | 100245.02 | 100603.94 | 100963.92 |
| 100 | 101324.97 |
Metastable state; vapor pressure with respect to supercooled water.
4. Discussion
4.1. Thermodynamic Temperature
IPTS–68 was adopted as a replacement for IPTS–48 on the basis, at least in part, that it approached the thermodynamic temperature scale to within the uncertainty of the latter. Presumably, therefore, the conversion of γ and of B’ and C’ from IPTS–48 to IPTS–68, and the substitution of these quantities into eqs (10) and (11) should yield a solution giving vapor pressure on IPTS–68. This is not the case. The conversion of γ from IPTS–48 to IPTS–68 introduces a maximum change in γ, which occurs at 50 °C, of about 0.04 joules per gram, a quantity which has negligible effect on p. Similarly, B’ and C’, and consequently p, are affected insignificantly by the change in temperature scales. The lower limits of integration, p0 and T0, remain identical on the two scales. Thus, when temperature scale changes in γ, B’ and C’ are made, eq (10) still leads to a formulation that yields vapor pressures in substantial agreement with Stimson’s vapor pressures on IPTS–48 and not on IPTS–68. The inference from these results is that IPTS–48 may be a closer approximation to the thermodynamic temperature scale in the range 0 to 100 °C than IPTS–68. It is for this reason that we based our derivation on IPTS–48 rather than IPTS–68.
4.2. Error Analysis
It is of interest to estimate the uncertainty in calculating p arising from estimated errors in γ, Z, R, T, and T0, using the Clausius-Clapeyron equation. For purposes of this error analysis, we shall derive a simplified vapor pressure equation and we shall assume that all variables are independent. Equation (5) serves as a convenient starting point for this analysis:
| (5) |
The calorimetric quantity γ varies from 2500 to 2257 j/g as t increases from 0 to 100 °C. As an approximation let γ be equal to 2400 j/g and constant. The compressibility factor Z varies from 0.9995 to 0.9845 over the same temperature range. Let Z be approximated by unity. Under these conditions, the integration of eq (5) yields
| (25) |
| (26) |
Differentiating p with respect to each parameter, replacing the differentials by finite increments, and dividing each side by p, we obtain
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
If we let the finite increments represent estimated errors in their respective parameters, then these equations permit us to calculate the corresponding estimated relative error in pressure Since p0 and T0 are the assigned steam point values of pressure and temperature on IPTS-48, and since our derivation was made on this scale, it will be assumed that both p0 and T0 have zero error. The estimated error in γ will be taken as 0.23 j/g, the residual standard deviation of the least square fit of eq (8) to the Osborne, Stimson, and Ginnings data. The estimated error in R, the specific gas constant for water vapor, arises from the estimated errors in the universal molar gas constant and in the molecular weight of water. According to Bain [44], the error limit in R, defined as three times the standard deviation, is 7 × 10−5 j/gK. We will use the standard deviation as our estimate of error in R, i.e., 2.3 × l0−5 j/gK. Goff [19] has assigned tolerances to the Goff and Gratch virial coefficients which he set at twice the probable error. We have converted his tolerances to standard deviations, and computed, as the equivalent estimated error in Z, the quantity 2 × 10−4, valid from 0 to 100 °C. The absolute temperature T enters into eq (26) as the independent variable so that it is subject neither to experimental nor scale error. Experimental and scale errors in T affect γ and the virial coefficients; however, these temperature errors show up and are contained in the assigned estimated errors in γ and Z.
A summary of the relative errors in p due to the estimated errors in γ, R, and Z is given in table 7. Assuming that the estimated errors in γ, R, and Z are systematic, then the total estimated error in p is at most the arithmetic sum of the estimated errors in p due to Δγ, ΔR, and ΔZ, respectively. This error analysis sets the outer bounds, that is, the estimated maximum error, that might occur in the calculation of p.
Table 7.
Estimated uncertainty in thermodynamic computation of vapor pressure
| Temperature t |
Estimated relative error in vapor pressure due to estimated uncertainties in |
Estimated maximum error in vapor pressure |
|||
|---|---|---|---|---|---|
| γ | R | Z | |||
| °C | ppm | ppm | ppm | ppm | pascals |
| 0 | 490 | 254 | 1021 | 1765 | 1.08 |
| 10 | 426 | 221 | 887 | 1534 | 1.88 |
| 20 | 366 | 190 | 761 | 1317 | 3.08 |
| 30 | 310 | 161 | 644 | 1115 | 4.73 |
| 40 | 257 | 133 | 535 | 925 | 6.82 |
| 50 | 208 | 108 | 432 | 748 | 9.23 |
| 60 | 161 | 83 | 335 | 579 | 11.54 |
| 70 | 117 | 61 | 244 | 422 | 13.15 |
| 80 | 76 | 39 | 158 | 273 | 12.93 |
| 90 | 37 | 19 | 77 | 133 | 9.32 |
| 100 | 0 | 0 | 0 | 0 | 0 |
The deviations of our formulation from Stimson’s data may be taken as a measure of the actual error in the calculation of vapor pressure. Therefore, one would expect these deviations to be comparable to the estimated maximum errors in the calculation of p, but they are two orders of magnitude smaller. It is possible that the estimates of uncertainty assigned to γ, R, and Z may be conservative leading to estimated maximum errors in p that are too large. It is also possible that the systematic errors in γ, R, and Z tend to compensate each other whereas we assumed that these are additive. Finally, the Goff and Gratch virial coefficients, which we used to compute Z, are not completely independent parameters. Goff and Gratch derived these virial coefficients using vapor pressure data, first in computing enthalpy coefficients from calorimetric data, that is, from γ, and second, in evaluating the constants of integration that result from integrating enthalpy coefficients to obtain virial coefficients. The effect of this procedure is that the virial coefficients are partially dependent on, and self-consistent with, p and γ. Although the Cragoe-Stimson measurements were available to Goff and Gratch [6], apparently these were used only for comparison with their vapor pressure equation and not for deriving virial coefficients. On the other hand, the Gerry equation [7], the Osborne and Meyers formulation [31] and the Moser and Zmaczynski vapor pressure measurements [37] were used directly or indirectly.
We have employed virial coefficients due to Keyes [56] and to Czuha as given by Bain [44] and obtained equations which predict vapor pressures significantly different from Stimson’s measurements, but well within our estimated maximum error. We ascribe, in part, the close concordance of our formulation with Stimson’s measurements to our use of the Goff and Gratch virial coefficients.
It is clear that if the parameters γ, R, and Z were completely independent, then they must be known to an accuracy that is 1 to 2 orders of magnitude better than they are now known if thermodynamic calculations of vapor pressure are to have an uncertainty comparable to Stimson’s measurements. Therefore, our formulation should not be taken as a corroboration from completely independent thermodynamic data of Stimson’s vapor pressure measurements; rather it should be viewed as a smoothing function that has a theoretical basis. This is particularly true of eq (17) which was adjusted to fit Stimson’s measurements. However, it is evident that there is a high level of thermodynamic consistency among the parameters p, γ, and Z.
5. Conclusions
The feasibility of computing the vapor pressure of water to a high order of accuracy by a smoothing function that has a rational basis has been demonstrated. Calculated vapor pressures agree with the very precise measurements of Stimson to within 7 ppm from 25 to 100 °C.
At the ice point the PTR data is in reasonable accord with the value calculated from eq (17); at the triple point and ice point, steam table values are very close to our calculated values. Prytz’s triple point measurement is 0.3 pascal (490 ppm) higher than our calculated value.
It should be noted that the triple point, the most stable condition of the pure water substance, which serves as a defining fixed point on the thermodynamic temperature scale and is reproducible in temperature to a very high order of accuracy, has a comparatively inexactly known saturation pressure. A definitive determination of the vapor pressure at the triple point is needed.
Douslin’s measurements from 0 to 20 °C are systematically higher than our calculations by 0.6 to 1.7 pascals, roughly of the order of 2 to 3 times his estimated maximum systematic error.
The Moser and Zmaczynski data from 73 to 100 °C are systematically lower than the values predicted by eq (17) whereas the Beattie and Blaisdell data, which only encompass the range 96 to 103 °C, deviate randomly about our curve with an estimated residual standard deviation of 1.55 pascals (17 ppm).
Equation (17) has seven terms, and where a simpler equation is desired, eq (18b) with five terms can be used with little degradation in the accuracy of the computed values. Equation (24) with n = 3 on IPTS–68 is equivalent to eq (18b) on IPTS–48.
Footnotes
Figures in brackets indicate the literature references at the end of this paper.
The residual standard deviation is given by where ri is the difference between the weighted mean and the corresponding computed value, n is the number of fitted points, n − 4 is the number of degrees of freedom and 4 is the number of coefficients in eq (8).
1 pascal = 1 newton/m2= 10−5 bar= 10−2 mb = 7.50062 × 10−3 mm Hg.
We wish to thank Dr. D. R. Douslin for permission to quote from his second paper prior to publication.
The Moser and Zmaczynski data extend over the temperature range 73 to 130 °C. We have limited our consideration of these data to the temperature span 73 to 103 °C, the upper end corresponding to the highest temperature of the Beattie and Blaisdell data.
6. References
- [1].Goff J. A., Saturation pressure of water on the new kelvin scale, Humidity and Moisture, Arnold Wexler, Editor-in-chief, vol. 3 (Reinhold Publishing Corporation, New York, 1965) p. 289. [Google Scholar]
- [2].Stimson H. F., Some precise measurements of the vapor pressure of water in the range from 25 to 100 °C, J. Res. Nat. Bur. Stand. (U.S.), 73A (Phys. and Chem.) No. 4, 493–496 (September–October 1969). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Stimson H. F., Precision resistance thermometry and fixed points Temperature, Its Measurement and Control in Science and Industry, Vol. 2, American Institute of Physics Symposium, 1939. (New York City, Reinhold Publishing Co.) [Google Scholar]
- [4].Osborne Nathan S., Calorimetry of a fluid, J. Res. Nat. Bur. Stand. (U.S.), 4, 609–629 (1930)RP168. [Google Scholar]
- [5].Goff J. A. and Gratch S., Thermodynamic properties of moist air. Heating, Piping and Air Conditioning, ASHVE Journal Section 17, 334 (1945). [Google Scholar]
- [6].Goff John A. and Gratch S., Low-pressure properties of water from −160 to 212 F, Trans. ASHVE 52, 95 (1946). [Google Scholar]
- [7].Osborne N. S., Stimson H. F., and Ginnings D. C., Measurements of heat capacity and heat of vaporization of water in the range 0° to 100 °C, J. Res. Nat. Bur. Stand. (U.S.), 23, 197–260 (1939)RP1228. [Google Scholar]
- [8].Fiock E. F. and Ginnings D. C., Heat of vaporization of water at 50°, 70°, and 90 °C, J. Res. Nat. Bur. Stand. (U.S.), 8,321–324 (1932)RP416. [Google Scholar]
- [9].Osborne N. S., Stimson H. F., and Ginnings D. C., Calorimetric determination of the thermodynamic properties of saturated water in both the liquid and gaseous states from 100° to 374 °C, J. Res. Nat. Bur. Stand. (U.S.), 18, 389–447 (1937)RP983. [Google Scholar]
- [10].Burgess G. K., The international temperature scale, J. Res. Nat. Bur. Stand. (U.S.), 1, 635–640 (1928)RP22. [Google Scholar]
- [11].Stimson H. F., International temperature scale of 1948, J. Res. Nat. Bur. Stand. (U.S.), 42, 209–217 (1949)RP1962. [DOI] [PubMed] [Google Scholar]
- [12].Stimson H. F., International practical temperature scale of 1948. Text revision of 1960, J. Res. Nat. Bur. Stand. (U.S.), 65A (Phys. and Chem.), No. 3, 139–145 (May–June 1961). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Keyes F. G., Smith L. B., and Gerry H. T., The specific volume of steam in the saturated and superheated condition together with derived values of the enthalpy, entropy, heat capacity and Joule Thompson coefficients. Proc. Am. Acad. Arts Sci. 70, 319 (1936). [Google Scholar]
- [14].Keyes F. G., The consistency of the thermodynamic data for water substance vapor phase to 550 °C, J. Chem. Phys. 17, 923 (1949). [Google Scholar]
- [15].Keyes F. G., The 1957 status of steam properties, Trans. ASME 80, 555 (1958). [Google Scholar]
- [16].Keenan J. H., Keyes F. G., Hill P. G., and Moore J. G., Steam Tables (John Wiley and Sons, Inc., New York, 1969). [Google Scholar]
- [17].Knoblauch O., Linde R. and Klebe H., Die thermischen Eigenshaften des gesättigen und des überhitzten Wasserdampfes zwischen 100° und 180 °C, Mittheilung über Forschungsarbeiten d. Ver. d. Ing. 21, 33 (1905). [Google Scholar]
- [18].Collins S. C., and Keyes F. G., The heat capacity and pressure variation of the enthalpy for steam from 38° to 125 °C. Proc. Am. Acad. Arts. Sci. 72, 283 (1938). [Google Scholar]
- [19].Goff J. A., Standardization of thermodynamic properties of moist air-final report of the Working Subcommittee, International Joint Committee on Psychrometric Data, ASHVE J. Section, Heating, Piping and Air Conditioning 55, 118 (1949). [Google Scholar]
- [20].New values for the physical constants, Nat. Bur. Stand. (U.S.), Tech. News Bull. 47 (10) 175 (1963). [Google Scholar]
- [21].ASTM Metric Practice Guide, Nat. Bur. Stand. (U.S.), Handb. 102, 49 pages (1967). [Google Scholar]
- [22].Abramowitz M., and Stegun I. A., Handbook of Mathematical Functions, Nat. Bur. Stand. (U.S.), Appl. Math. Ser. 55, 885 (June 1964). [Google Scholar]
- [23].Partington J. R., An Advanced Treastise on Physical Chemistry, vol. 2 (Longman, London, 1951). [Google Scholar]
- [24].Miller D. G., Estimating vapor pressures – a comparison of equations, Ind. Eng. Chem. 56, 46 (1964). [Google Scholar]
- [25].Ambrose D., Councell J. F., and Davenport A. J., The use of Chebyshev polynomials for the representation of vapour pressures between the triple point and the critical point. J. Chem. Thermo. 2, 283 (1970). [Google Scholar]
- [26].Goodwin R. D., Nonanalytic vapor pressure equation with data for nitrogen and oxygen. J. Res. Nat. Bur. Stand. (U.S.), 73A, (Phys. and Chem.) No, 5, 487–491 (September–October 1969). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Holborn L., and Henning F. Über das Platinthermometer und den Sättigungsdruck des Wasserdampfes zwischen 50 and 200°, Ann. Physik. IV, 26, 54 (1908). [Google Scholar]
- [28].Scheel K., and Heuse W. Bestimmung des Sättigungsdruckes von Wasserdampf zwischen 0 und + 50°, Ann. Physik. IV 31, 715 (1910). [Google Scholar]
- [29].Holborn L., Scheel K., and Henning F., Wärmetabellen (Vieweg and Sohn, 1919). [Google Scholar]
- [30].Smith L. B., Keyes F. G., and Gerry H. T., The vapor pressure of water, Proc. Am. Acad. Arts and Sci.69, 137 (1934). [Google Scholar]
- [31].Osborne N. S., and Meyers C. H., A formula and tables for the pressure of saturated water vapor in the range 0 to 374 °C, J. Res. Nat. Bur. Stand. (U.S.), 13, 1–20 (1934)RP691. [Google Scholar]
- [32].The International Practical Temperature Scale of 1968, Metrologia 5, 35 (1969). [Google Scholar]
- [33].Volet Ch., La température d’ébullition d’eau d’après les experiences de P. Chappuis, Travaux et Mémoires du Bureau international des Poids et Measures 18, 11 (1929). [Google Scholar]
- [34].Zmaczynski A., and Bonhoure A., La température d’ébullition de l’eau en fonction de la pression, J. Phys. et Rad. (VII) 1, 285, (1930). [Google Scholar]
- [35].Moser H., Eine statische Methode für präzise Dampfdruckmessungen bei höheren Temperaturen und ihre Anwendung zur Sicherung des Hundertpunktes der Temperaturskala, Ann. Phys. (5) 14, 790 (1932). [Google Scholar]
- [36].Beattie J. A. and Blaisdell B. E., An experimental study of the absolute temperature scale. III. The reproducibility of the steam point. The effect of pressure on the steam point, Proc. Am. Acad. Arts Sci. 71, 361 (1937). [Google Scholar]
- [37].Moser H. and Zmaczynski A. Sättigungsdruck von Wasserdampf Zwischen 73 und 130°, Physik. Zeits 40, 221 (1939). [Google Scholar]
- [38].Michels A., Blaisse B., Ten Seldam C. A. and Wouters H. M., The vapour pressure of water in the neighborhood of 100 °C. Physica 10, 613 (1943). [Google Scholar]
- [39].Douslin D. R. and McCullough J. P., An inclined-piston deadweight pressure gage, U.S. Bureau of Mines Rept. of Investigation No. 6149 (1963). [Google Scholar]
- [40].Douslin D. R., Vapor pressure of water from −2.5 to 20 °C, J. Chem. Thermodynamics, in press. [Google Scholar]
- [41].Thiesen M. and Scheel K., Bestimmung der Spannkraft des gesättigen Wasserdampfes bei Temperaturen zwischen −12° und +25°, Wiss. Abh. physik-techn. Reichsanst. 3, 71 (1900). [Google Scholar]
- [42].Scheel K. and Heuse W., Bestimmung des Sättigungsdruckes von Wasserdampf unter 0°, Ann. Physik. 29, 729 (1909). [Google Scholar]
- [43].Prytz K., Manomètre a contact optique et son emploi pour la determination du triple point d’eau, Mathematisk-fysike meddelelser Danske Videnskabernes Selskab, Copenhagen 11, No. 2 (1931). [Google Scholar]
- [44].Bain R. W., N.E.L. Steam Tables, 1964, Her Majesty’s Stationery Office, Edinburgh, 1964. [Google Scholar]
- [45].Sonntag D., Hygrometrie, pp. 91–102 (Akademie-Verlag, Berlin, 1966–1968). [Google Scholar]
- [46].Osborne N. S., Stimson H. F. and Ginnings D. C., Thermal properties of saturated water and steam, J. Res. Nat. Bur. Stand. (U.S.), 23, 261–270 (1939) RP1229. [Google Scholar]
- [47].APIRP 44 Table 2–l–(1.01)-k, American Petroleum Institute Research Project 44, Texas A and M University, Chemical Thermodynamics Properties Center, Dept. of Chem., College Station, Texas: (1964). [Google Scholar]
- [48].Meyer C. A., McClintock R. B., Silvestri G. J., and Spencer R. C. Jr. 1967. ASME Steam Tables, American Soc. Mech. Eng., New York. [Google Scholar]
- [49].Bridgeman O. C., and Aldrich E. W., Vapor pressure tables for water, Trans ASME. J. Heat Transfer Series C–D 86, 279 (1964). [Google Scholar]
- [50].Gibson M. R. and Bruges E. A., New equations for the thermodynamic properties of saturated water in both the liquid and vapor phases, J. Mech. Eng. Science 9, 24 (1967). [Google Scholar]
- [51].The Third International Conference on Steam Tables, Mech. Eng. 57, 710 (1935). [Google Scholar]
- [52].ASHRAE Guide and Data Book, Fundamentals and Equipment. 1961, 1965 and 1966, American Society of Heating Refrigerating and Air Conditioning Engineers, Inc., New York. [Google Scholar]
- [53].List R. J., Smithsonian Meteorological Tables, Sixth revised edition, Smithsonian Institution, Washington: (1951). [Google Scholar]
- [54].Resolution 19, IV Congress, World Meteorological Organization, 1963.
- [55].Douglas T. B. Conversion of existing calorimetrically determined thermodynamic properties to the basis of the International Practical Temperature Scale of 1968. J. Res. Nat. Bur. Stand. (U.S.), 73A (Phys. and Chem), No. 5, 451–470 (September–October 1969). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Keyes F. G. The thermodynamic properties of water substance 0 to 150 °C. J. Chem. Phys. 15, 602 (1947). [Google Scholar]