The estimated change in the level and distribution of PM_2.5-attributable health impacts in the United States: 2005–2014

Abstract

Background:

Photochemical modeling can predict the level and distribution of pollutant concentrations over time, but is resource-intensive. Partly for this reason, there are few studies exploring the multi-year trajectory of the historical change in fine particle (PM_2.5) levels and associated health impacts in the U.S.

Objectives:

We used a unique dataset of Community Multi-Scale Air Quality (CMAQ) model simulations performed for a subset of years over a decade-long period fused with observations to estimate the change in ambient levels of PM_2.5 across the contiguous U.S. We also quantified the change in PM_2.5-attributable health risks and characterized the level of risk inequality over this period.

Methods:

We estimated annual mean PM_2.5 concentrations in 2005, 2011 and 2014. Using log-linear and logistic concentration-response coefficients we estimated changes in the numbers of deaths, hospital admissions and other morbidity outcomes. Calculating the Gini coefficient and Atkinson Index, we characterized the extent to which PM_2.5 attributable risks were shared equally across the population or instead concentrated among certain subgroups.

Results:

In 2005 the estimated fraction of deaths due to PM_2.5 was 6.1%. This estimated value falls to 4.6% by 2014. Every portion of the contiguous U.S. experiences a decline in the risk of PM-related premature death over the 10-year period. As measured by the Gini coefficient and Atkinson index, the level of PM mortality risk is shared more equally in 2014 than in 2005 among all subgroups.

Conclusions:

Between 2005 and 2014, the level of PM_2.5 concentrations fall, and the risk of premature death, declined and became more equitably distributed across the U.S. population.

1. Introduction

Abundant evidence indicates that the ambient levels of common air pollutants including fine particles, ground-level ozone, carbon monoxide, lead, sulfur dioxide and nitrogen dioxide have fallen nationwide over the past 40 years (Hubbell et al., 2009; Kim et al., 2015; US EPA, 2010). A rich and growing literature has linked the monitored decline in pollution levels to measurable improvements in public health. Air pollution intervention studies have reported fewer deaths and acute illnesses due to abrupt short-term improvements to air quality (Clancy et al., 2002; Pope, 1989). Other studies have observed increases in life expectancy at birth due to declining fine particle levels across multiple years (Correia et al., 2013; Pope et al., 2009). These and other epidemiological studies, combined with controlled human exposure and toxicological studies, provide a substantial body of evidence that the long-term downward secular trend in air pollution has yielded substantial benefits to human health in the United States (US EPA, 2009).

Air pollution risk assessments build upon the literature above by applying concentration-response relationships derived from epidemiological studies to quantify counts of adverse effects; these estimates provide insight to the scope and magnitude of the human health impacts of changes in air pollution over space and time (Anenberg et al., 2009; Caiazzo et al., 2013; Levy et al., 2010). Indeed, decision makers often evaluate the merits of air quality policies on the basis of these estimates—either policies they are formulating or those instituted in the past (Chestnut and Mills, 2005; Fann et al., 2017; Fann et al., 2013a; Hubbell et al., 2009; Wesson et al., 2010).

While the network of air quality monitors in the U.S. is extensive, it is spatially and temporally incomplete. By contrast, photochemical air quality models can predict concentrations over a very broad geographic area, when appropriately specified. Risk assessments drawing upon model-predicted air quality changes often do so for a “snapshot” in time or for a limited number of years; this is due in part to the significant resources often needed to simulate multiple years of air quality levels using a photochemical air quality model (Berman et al., 2012; Fann et al., 2013a; Fann and Risley, 2011a). In part for this reason, there is a relative paucity of risk assessments in the literature featuring a time series of historical air quality surfaces (Fann et al., 2018; Fann et al., 2011b; Wesson et al., 2010). Simulating air quality changes associated with emission changes in a single year, or a discrete number of years, limits the scope of technical and policy questions that can be addressed—the most obvious one being, how does air quality change in the years subsequent to those simulated by the model? To what extent does air quality continue to improve, and among what populations?

In this article, we attempt to address this gap in the literature by drawing upon a time-series of chemical transport model scenarios to quantify changes in concentrations, exposure and risk across a multi-year period. We use a dataset of Community Multi-Scale Air Quality (CMAQ) model predicted concentrations fused with observations of fine particles over the contiguous U.S. for the years 2005, 2011, and 2014; these years reflect the best available U.S. EPA-performed model simulations over a decade-long period. We seek to build upon the air pollution health risk assessment literature by leveraging this unique air quality modeling dataset to help answer the following questions: (1) how does the burden to public health associated with PM_2.5 change between 2005 and 2014?; (2) to what extent do subpopulations at greatest risk of air pollution health impacts benefit from these changes?; and (3) does estimated air pollution risk become more equitably distributed over this period?

2. Methods

2.1. Estimating changes in PM_2.5 concentrations in 2005, 2011 and 2014

We draw upon previously published estimates of PM_2.5 concentrations for the year 2005 that are documented elsewhere (Fann et al., 2012b). In brief, that analysis employed the Community Multiscale Air Quality (CMAQ) model version 4.7 and the U.S. EPA 2005 modeling platform to predict PM_2.5 concentrations at a 12 km by 12 km grid scale. Using a technique we describe further below, that analysis spatially fused the CMAQ model predictions with monitored concentrations.

To develop spatial fields of PM_2.5 concentrations for the years 2011 and 2014, simulations were performed with the CMAQ model (Byun and Schere, 2006). The CMAQ modeling domain covered the contiguous U.S. and parts of surrounding areas with 12-km horizontal grid resolution. Chemical boundary conditions were based on 2° × 2.5° resolution global simulations with the GEOS-Chem model (Bey et al., 2001). Gas-phase chemistry was simulated with the Carbon Bond 2005 (CB05) chemical mechanism for 2011 and CB6r3 for 2014. Surface exchange of NH₃ was simulated with CMAQ’s bidirectional exchange parameterization (Bash et al., 2013). The 2011 and 2014 CMAQ simulations have been described previously and model performance was considered acceptable based on detailed evaluation using national air monitoring data and consideration of performance from other recent modeling applications (Simon et al., 2012; U.S. EPA, 2018a; USEPA, 2015).

Meteorological fields used in the air quality simulations were based on the Weather Research and Forecasting (WRF) Advanced Research WRF (ARW) core (Otte and Pleim, 2010; Skamarock et al., 2008) model. WRF simulations were based on 12-km horizontal resolution and 35 vertical layers. Key physics options used include the Pleim-Xiu land surface model, Morrison two-moment microphysics, Kain-Fritz cumulus parameterization with the moisture-advection trigger, and the rapid radiative transfer model for general circulation models (RRTMG) longwave and shortwave radiation scheme (Iacono et al., 2008; Ma and Tan, 2009; Mlawer et al., 1997; Morrison et al., 2009; Pleim and Xiu, 2003).

Emission files used in the CMAQ simulations were developed with the Sparse Matrix Operator Kernel for Emissions (SMOKE) model (Houyoux et al., 2000; USEPA, 2015). Anthropogenic emissions were largely based on the 2011 National Emission Inventory (NEI) version 1 for the 2011 simulation and version 1 of the 2014 NEI for the 2014 simulation. Point source emissions from electric generation units (EGUs) were based on continuous emission monitoring (CEM) data when possible. Onroad mobile source emissions were generally based on the Motor Vehicle Emission Simulator (MOVES; www.epa.gov/moves) model, although onroad emissions in California were based on the EMFAC (www.arb.ca.gov/emfac/) model. The SMARTFIRE2 modeling system (www.airfire.org/smartfire) was used to develop emissions for prescribed burning and wildfires. Biogenic emissions were based on Biogenic Emission Information System (BEIS) version 3.14 (Bash et al., 2016). Lightning NO and sea-spray emissions were simulated within CMAQ (Allen et al., 2012; Kelly et al., 2010).

Emissions from fires and biogenic sources were year-specific for the 2005, 2011 and 2014 cases. Overall, projected national NO_x emissions were 36% lower for 2011 than for 2005, national SO₂ emissions were 57% lower for 2011 than for 2005, and primary PM_2.5 emissions were 4% higher for 2011 than for 2005. The apparent increase in total primary PM_2.5 emissions between 2005 and 2011 was largely a result of year specific wildfire emissions. The wildfire emissions in 2011 were ~80% higher (more than 900,000 t per year higher) than the 2005 emissions. This not only has a large impact on the national emissions totals, but also causes large local and regional impacts on the estimated annual average PM_2.5 concentrations in areas that were most heavily impacted by fires in the years examined. There were also additional emissions reductions that occurred beyond 2011. Compared with the 2005 case, national emissions for 2014 were 45% lower for NO_x, 69% lower for SO₂, and 8% lower for PM_2.5.

PM_2.5 spatial fields used to estimate health impacts below were developed by combining PM_2.5 information from national air monitoring networks and CMAQ model predictions. The data fusion was done to leverage the accuracy of the observations and the spatial and temporal coverage of the CMAQ modeling. Data fusion was performed using EPA’s Software for Model Attainment Test (SMAT) according to a “fused” Voronoi neighbor averaging (VNA) interpolation approach that has been described previously (Abt, 2012, 2007; Fann et al., 2012a; Wang et al., 2015). Briefly, VNA interpolation of monitored concentrations to a prediction point involves calculating an inverse-distance-squared weighted average concentration from values measured at monitors in neighboring Voronoi polygons (Fann et al., 2012c). The data fusion approach is implemented in this framework by applying VNA interpolation to monitored concentrations that have been scaled by the ratio of the CMAQ concentration in the grid cell containing the prediction point to the CMAQ concentration in the grid cell containing the monitor. Observations used for the 2005, 2011, and 2014 data fusion were from PM_2.5 measurements at Federal Reference Monitor (FRM) and Interagency Monitoring for Protection of Visual Environments (IMPROVE) sites. The monitored PM_2.5 species concentrations were from the Chemical Speciation Network (CSN) and IMPROVE monitoring sites (Solomon et al., 2014).

2.2. Estimating counts of air pollution-attributable human health impacts

This analysis employs a health impact function to quantify the number of PM_2.5 related premature deaths and illnesses in each year. The health impact functions we applied in this analysis incorporated four input parameters: (1) an effect coefficient (or, beta parameter) from a published air pollution epidemiology study; (2) a count of the population affected; (3) the air quality concentration to which the population is exposed; (4) a baseline rate of death or disease among this population. We applied a separate health impact function for each PM_2.5 health endpoint we quantified. We quantified health outcomes for each of the years noted above and updated the previously published 2005 analysis to apply the concentration-response parameters applied in this analysis for the years 2011 and 2014. To automate the procedure for calculating health impacts we used the BenMAP-CE software program (Sacks et al., 2018; U.S. EPA, 2018b). We quantified PM_2.5-related health outcomes including premature death, respiratory hospital admissions, cardiovascular hospital admissions, emergency department visits for asthma, upper respiratory symptoms, lower respiratory symptoms, days of work lost, days of school lost, cases of aggravated asthma, and cases of acute respiratory symptoms.

Using the health impact function for PM_2.5-related deaths as an example, we specify the input parameters below. In Eq. (1), we estimated the number of PM_2.5-related total deaths (y_ij) for adults in each county j (j = 1,…,J where J is the total number of counties) during a specific year i (i = 2005, 2011, 2014) as

$$\begin{array}{l}{y}_{ij}={\Sigma }_a{y}_{ija}\\ y_{ija}=m{0}_{ija}\times (e^{\beta ·C}{}_{ik}-1)\times P_{ika},\end{array}$$ (1)

where β is a beta coefficient for all-cause mortality in adults associated with annual average exposure to PM_2.5, m_0ija is the baseline all-cause death rate for adults in county j in year i stratified in 10-year age (a) bins, C_ik is annual mean PM_2.5 concentration in air quality grid cell k in year i, and P_ika is the number of adult residents in air quality grid cell k in year i stratified into 5-year age bins. This health impact function returns a count of the number of PM_2.5-related deaths occurring in each county due to annual mean PM_2.5 concentration in each year i.

For this health impact function we derived a long-term mortality β coefficient from a Hazard Ratio (HR) reported in the most recent extended analysis of the American Cancer Society (ACS) cohort (ages 30 and older) (HR 1.06; 95% CI: 1.04, 1.08 per 10 μg/m³ increase in annual average PM_2.5 concentrations, adjusted for all individual-level and ecologic covariates) (Krewski et al., 2009) (Table 1). Though a large, and growing, number of long-term epidemiological studies report HR for PM_2.5, we selected an HR from Krewski et al. because it: (1) reflects a large and nationally representative cohort; (2) is broadly cited and applied extensively in PM_2.5 risk assessments, thus making the results easier to compare with those reported elsewhere in the literature.

Table 1.

Distribution of CMAQ model predicted PM_2.5 concentrations and population-weighted PM_2.5 levels in 2005, 2011 and 2014.

Year	Annual average PM2.5 (μg/m3)										National population-weighted annual average PM2.5
	Number of cells	Min	Percentile					Max	Mean	SD
			10%	25%	50%	75%	90%
2005	97416	0.97	2.85	3.89	5.4	8.17	11.24	59.73	6.25	3.15	10.98
2011	86000	0.91	2.65	3.44	4.87	7.31	8.99	50.62	5.45	2.5	8.92
2014	83591	0.94	2.79	3.67	4.87	6.63	7.99	34.46	5.22	2.1	8.35

We defined m_0ija as the county-level age-stratified all-cause death rates from the Centers for Disease Control Wide-ranging Online Data for Epidemiologic Research database (Centers for Disease Control and Prevention, 2016). To account for the improved longevity of the population over time, we projected these death rates to future years using a life table reported by the U.S. Census Bureau (U.S. EPA, 2018b); more details regarding procedure can be found in the Supplemental Materials (Table S-1 and S-2). We defined the baseline incidence rates for the morbidity endpoints using rates of hospital admissions, emergency department visits and other outcomes for the year 2014. We defined P_ika using age-stratified population data from the U.S. Census Bureau. We projected year 2000 Census population counts to the year 2005 and 2010 Census population counts to the years 2011 and 2014 using demographic forecasts from the Woods & Poole company (Woods and Poole, 2012).

The health impact function combines data that are expressed at different spatial scales. When calculating the function, the BenMAP-CE program assigns the death rates, stored at the county level, to the 12 km by 12 km air quality modeling grid cell. For example, when two or more counties overlap with a 12 km by 12 km cell, the program calculates the percentage of each county that overlaps with that cell. The program then calculates an average of the incidence rates, weighted according to the percentage overlap, and assigns this rate to the 12 km cell. This new 12 km by 12 km incidence rate is next used by the program in the health impact function.

We performed a Monte Carlo simulation to sample from the standard error reported in the epidemiological study for each beta coefficient, which allowed us to construct an error distribution of estimated PM_2.5 and ozone-related effects. We estimated total numbers of premature deaths and illnesses in the continental U.S. for each year by summing the county-specific estimates, and report the sums of the 2.5th and 97.5th percentiles of the Monte Carlo distributions as 95% confidence intervals.

When calculating Eq. (1) we assume that the association between the pollutant and each health outcome is log-linear over the entire range of PM_2.5 exposure, with no level below which PM_2.5 would not increase the risk of death (Schwartz et al., 2008; US EPA, 2009). The lowest measured level of the Krewski et al. (2009) study is 5.8 μg/m³ and thus we extrapolated the portion of the curve below this level. Previous analyses suggest that the fraction of the U.S. population exposed to concentrations below this level is less than 10% (U.S. EPA, 2015, 2013, 2011). The β coefficient for each PM_2.5 mortality and morbidity endpoint can be found in the Supplemental materials (Table S-3). Effect coefficients and baseline incidence rates for the full suite of PM_2.5 endpoints can be found in the Supplemental materials (Table S-4).

We calculated the fraction of all deaths due to PM_2.5 in each county j and year i using the following function:

$$A{F}_{ij}=\frac{y_{ij}}{{\Sigma }_{a}m{o}_{ija}\times P_{ija}}$$ (2)

where y_ij is the estimated number of air pollution deaths in county j in year i, m_0ija is the age-stratified baseline death rate, and, P_ija is the age-stratified population, respectively, in county j in year i.

We calculated the population-weighted annual mean concentration for all counties combined (C_i) in year i as

$$C_i=\frac{{\Sigma }^j{C}_{ij}\times P_{ij}}{P_i}$$ (3)

where C_ij is the county-average PM_2.5 concentration in county j in year i, P_ij is the population in county j in year i, and P_i is the total population over all counties combined in year i.

2.3. Assessing the change in air pollution risk among susceptible and vulnerable populations

The air pollution epidemiology, controlled human exposure and toxicology literature indicates that some population subgroups may be at greater risk to air pollution effects than the general population (Fann et al., 2011b; Levy et al., 2002; Pope and Dockery, 2006; Sacks et al., 2011). This elevated risk can be described in terms of population susceptibility and vulnerability (American Lung Association, 2001; Levy et al., 2002). For the purposes of this manuscript, we define “susceptible” as populations whose baseline health status is compromised. We select all-cause county-level death rates as a proxy for this variable for two reasons: (1) we quantify air pollution-related deaths relatively to a baseline rate of death and thus, other things being equal, locations experiencing a higher death rate will see a greater number of air pollution-attributable deaths; (2) rates of age-stratified rates of death are available for each county in the U.S. We use “vulnerable” to refer to non-health factors such socioeconomic status that affect how a population subgroup responds to an air pollution episode. We select education attainment as a proxy for this variable because populations with a lower level of education attained may be at elevated risk of PM-related premature death (Krewski et al., 2009). With respect to education attained, Krewski and colleagues observed a greater HR for those with less than a grade twelve education, noting that while “…reasons for this finding are unknown, it was suggested that level of education attainment may likely indicate the effects of complex and multifactorial socioeconomic processes on mortality or may reflect disproportionate pollution exposures.” Thus, we viewed education attained as a reasonable indicator of population vulnerability. This approach to defining susceptible and vulnerable populations is generally consistent with one demonstrated elsewhere in the literature (Fann et al., 2011c; Harper et al., 2013; Levy et al., 2002).

We define the location of vulnerable populations by identifying the percentage of populations in each U.S. County who have achieved less than a high school education in the year 2005 (Supplemental Figs. S-1 and S-2). We plot the spatial distribution of this variable, and select among the counties that are at the 50th, 75th and 90th percentile of this distribution. We define the location of susceptible populations by identifying the all-cause death rate among populations aged 65 and older for each U.S. County in the year 2005. We again plot the spatial distribution of this variable, selecting among the counties that are at the 50th, 75th and 90th percentile of this distribution.

As our primary measure of risk inequality for the exposure and risk projections, we calculated Atkinson Indices (AI). As applied here, AI is a measure of risk inequality ranging from zero to one, with higher values indicating greater inequality. Previous literature identifies the AI as the most appropriate inequality indicator for health benefits analyses, due in part to its decomposable nature, which allows us to calculate within-and between-group inequalities (Levy et al., 2006). Within-group inequality can be conceptualized as the amount of inequality that would remain if there were no differences in the level of risk between groups. Conversely, between-group inequality would be the remaining inequality if the risk levels within groups were made equal (Elbers et al., 2005). In addition to providing subgroup decomposability, the AI also satisfies the Pigou-Dalton transfer principle, whereby the index decreases when risk is redistributed from high-risk to low-risk populations. (Levy et al., 2006). In order to capture a range of sensitivities, we calculate the change in inequality related to three exposure and risk metrics: (1) estimated changes in PM_2.5 exposures, (2) counts of PM_2.5 related premature deaths, and (3) the fraction of all deaths due to PM_2.5.

The AI is calculated as follows:

$$AI=1-{\left[\frac{1}{n}\sum _{i=1}^n{\left[\frac{x_i}{\overline{x}}\right]}^{1-\epsilon }\right]}^{\frac{1}{1-\epsilon }}$$ (4)

where n is the total population, x_i is the risk for individual i, $\overline{x}$ is the mean risk, and ε is a sensitivity parameter with a range from 0 to infinity. Given the origin of the AI as a measure of income inequality, ε has a counterintuitive interpretation for risk inequality. Traditionally, as ε increases, the AI places more weight on the lowest income groups (De Maio, 2007). In contrast, for our analysis, a higher ε places more weight on the low end of the risk distribution. Consistent with past analyses on health risk inequality, we select an ε of 0.75 for our primary analysis, and also calculate an upper-bound AI with an ε of 3 (Fann et al., 2011b; Levy et al., 2007, 2006). In addition to an overall AI, we use Lasso de la Vega and Urrutia’s factorial decomposition equation to calculate within- and between-group inequalities for the previously defined vulnerable and susceptible populations (Casilda et al., 2003).

We conduct a sensitivity analysis using the Gini coefficient as an additional inequality metric to compare to the AI (Dorfman, 1979). The Gini coefficient also satisfies the Pigou-Dalton transfer principle, but is not subgroup decomposable. Therefore, Gini coefficients are calculated to estimate risk inequalities in the population at-large, but do not reflect any within- or between-group differences among the vulnerable and susceptible populations. The Gini coefficient is defined as:

$$Gini=\frac{\frac{1}{n^2}{\sum }_{i=1}^n{\sum }_{j=1}^n\left|x_i-x_j\right|}{2\mu }$$ (5)

where n is the total population, x_i is the risk for individual i, x_j is the risk for individual j, and μ is the average risk in the population. In addition to reporting absolute AIs and Gini coefficients for each of the air quality model years, we also calculate the percent change relative to 2005 to demonstrate the change in risk inequalities across time.

3. Results

3.1. Estimated change in PM_2.5 related mortality and morbidity

The overall level of model-predicted PM_2.5 concentrations decline between 2005 and 2014 (Table 1). The model estimated level of annual mean PM_2.5 concentrations declines from 6.25 μg/m³ in 2005–5.22 for 2014. The standard deviation of 12 km predicted concentrations in PM_2.5 declines over time, suggesting that the predicted levels of these pollutants are less dispersed and more equitably distributed. The average level at which the U.S. population is exposed to these pollutants also falls. The model-predicted population-weighted annual mean concentration falls by about a third (from 10.98 to 8.35).

The estimated number of PM_2.5-related deaths is about 150,000 in the year 2005 (Table 2). We estimate that this value fell to about 124,000 in the year 2011 and 121,000 in the year 2014; over this period, the U.S. population increased by approximately 22 million people, or about 7.1%. As a fraction of total all-cause deaths, the percentage share of PM-attributable mortality declines from 6.1% in 2005 to 4.6% in 2014, a fall of about a third.

Table 2.

PM_2.5-related premature deaths and the percentage of all deaths due to PM_2.5 in 2005, 2011 and 2014.

Year	Estimated numbers of premature deaths attributable to PM2.5 (95% confidence interval)a	Percentage of total deaths attributable to PM2.5
2005	150,000 (100,000–200,000)	6.1%
2011	124,000 (84,000–160,000)	5%
2014	121,000 (83,000–160,000)	4.6%

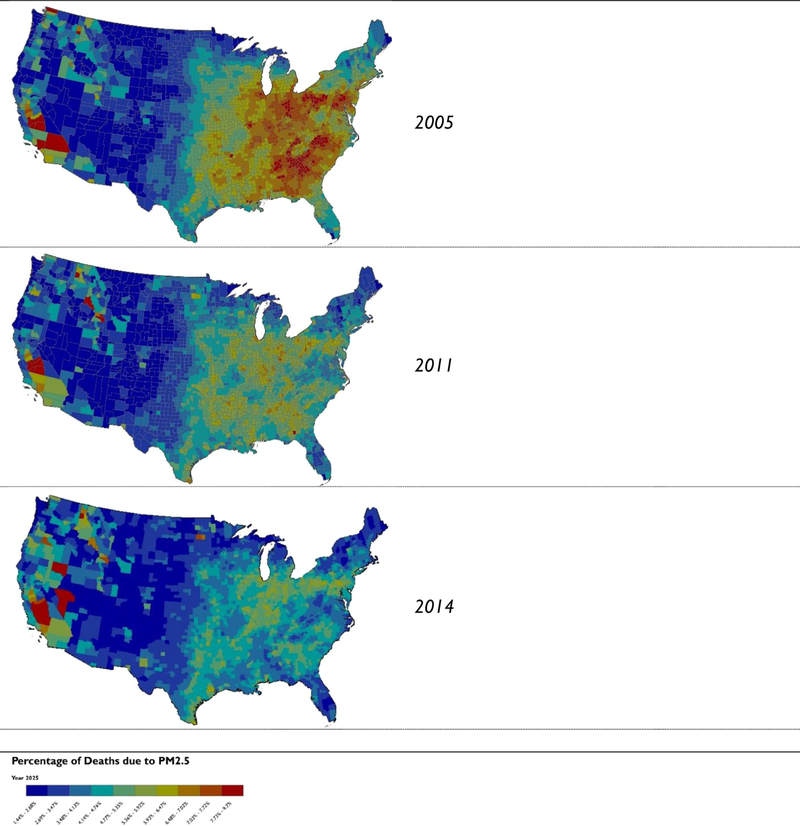
We find that in 2005 the PM_2.5 mortality burden is estimated to be greatest among counties in the Eastern United States and in Southern California (Fig. 1). The PM_2.5 mortality burden falls in most areas of the country by 2014, with some exceptions in western areas with greater wildfire activity and winter meteorological stagnation in 2014. We array the fraction of deaths due to PM_2.5 at the county level as a cumulative distribution function (CDF) for each model year (Fig. 2) and find that the burden falls in each year. We estimate the largest reduction in the mortality burden to occur between 2005 and 2011, with a smaller decline between 2011 and the 2014 emissions case.

Fig. 1.

Percentage of Total Deaths Due to PM_2.5 in U.S. Counties: 2005, 2011 and 2014.

Fig. 2.

Cumulative Percentage of Total Deaths Due to PM_2.5 in U.S. Counties: 2005, 2011 and 2014.

We estimate additional morbidity outcomes, including hundreds of millions of cases of acute respiratory symptoms, tens of millions of cases of exacerbated asthma and days of work and school lost due to poor air quality, millions of cases of upper and lower respiratory symptoms, hundreds of thousands of cases of non-fatal heart attacks and acute bronchitis and tens of thousands of hospital and emergency department visits (Table 3). These morbidity effects, including non-fatal heart attacks, respiratory and cardiovascular hospital admissions, cases of exacerbated asthma, and lost work days, remain roughly constant over the multi-year modeling period.

Table 3.

Estimated PM_2.5-related Morbidity Effects in 2005, 2011 and 2014.

	2005	2011	2014
PM-related effects
Non-fatal heart attacks	125,000 (33,000–200,000)	116,000 (31,000–190,000)	110,000 (28,000–170,000)
Cardiovascular Hospital Admissions	44,000 (20,000–79,000)	40,000 (18,000–72,000)	29,000 (13,000–52,000)
Respiratory hospital admissions	35,000 (−10,000–67,000)	32,000 (−9000–59,000)	27,000 (−8300–52,000)
Emergency Room Visits for Asthma	77,000 (−30,000–160,000)	64,000 (−25,000–130,000)	68,000 (−26,000–140,000)
Exacerbated Asthma	11,500,000 (−300,000–78,000,000)	9,400,000 (−240,000–65,000,000)	8800,000 (−220,000–62,000,000)
Lower Respiratory Symptoms	2700,000 (1100,000–4,00,000)	2200,000 (890,000–3,400,000)	2100,000 (840,000–3,200,000)
Upper Respiratory Symptoms	4300,000 (780,000–7,700,000)	3,500,000 (630,000–6,200,000)	3200,000 (590,000–5,800,000)
Acute Respiratory Symptoms	110,000,000 (91,000,000–130,000,000)	97,000,000 (79,000,000–110,000,000)	92,000,000 (76,000,000–110,000,000)
Lost Work Days	19,000,000 (16,000,000–22,000,000)	17,000,000 (14,000,000–19,000,000)	16,000,000 (13,000,000–18,000,000)
Acute Bronchitis	200,000 (−57,000–380,000)	170,000 (−45,000–330,000)	160,000 (−43,000–310,000)

3.2. Estimated change in exposure and risk inequality

The estimated Atkinson Index (AI) coefficient, which we use to express the extent to which exposure and risk are equitably distributed across the population, declines between 2005 and 2014 when applied to the estimated changes in PM_2.5 exposures, counts of PM_2.5 related premature deaths and the fraction of all deaths due to PM_2.5. Between 2005 and 2014, the AI for the incidence of PM_2.5 related mortality falls by about 7%, while the AI for PM_2.5 exposures and the fraction of all deaths attributable to PM_2.5 each decline by nearly 34% (Table 4). The estimated Gini coefficient values show a similar trend, falling by about 4% for the incidence of PM-related deaths between 2005 and 2011 and about 20% for the attributable fraction and PM_2.5 exposures during this same timeframe (Table 5).

Table 4.

Atkinson index values for changes in exposure, incidence of PM-related mortality and the fraction of deaths due to PM2.5 in 2005, 2011 and 2014 (ε = 0.75).

Year	Exposure		Incidence		Attributable Fraction
	Atkinson	Percent Change	Atkinson	Percent Change	Atkinson	Percent Change
2005	0.026842	-	0.574953	-	0.025323	-
2011	0.018761	− 30.1%	0. 548466	− 4.6%	0.017802	− 29.7%
2014	0.017753	− 33.9%	0.536328	− 6.7%	0.016786	− 33.7%

Table 5.

Gini coefficients for changes in exposure, incidence of PM-related mortality and the fraction of deaths due to PM2.5 in 2005, 2011 and 2014.

Year	Exposure		Incidence		Attributable Fraction
	Gini	Percent Change	Gini	Percent Change	Gini	Percent Change
2005	0.144	-	0.704	-	0.140	-
2011	0.121	− 16.3%	0.685	− 2.8%	0.117	− 16%
2014	0.118	− 18.5%	0.677	− 3.78%	0.114	− 18.3%

In the interest of brevity, we present a subset of the AI sensitivity analyses, focusing on within and between group inequality in the fraction of all deaths due to PM_2.5 (Table 6); a full suite of sensitivity analyses may be found in the Supplemental materials (Table S-3–S-5). The less-than-grade-12 subgroup, whom we defined to be most vulnerable to air pollution, sees a reduction in both the between-group and within-group level of risk inequality over time. This result implies that risk is more equitably distributed among populations within this subgroup and is also more similar to the risks experienced by the rest of the population. The results are similar for the mortality subgroup, where the between and within AI falls between 2005 and 2011, again implying that mortality risks among this subgroup are becoming more equitably distributed within the group and between this group and the broader population.

Table 6.

Atkinson sensitivity results: within and between group comparisons for the attributable fraction results in 2005, 2011, 2014 and 2018 (ε = 0.75).

Year	Education Subgroup				Mortality Subgroup
	Within	Between	Within (percent change)	Between (percent change)	Within	Between	Within (percent change)	Between (percent change)
2005	0.0239675	0.0014062	-	-	0.0252418	8.28E–05	-	-
2011	0.0171927	0.0006837	− 28.3%	− 54.3%	0.0175628	0.0001048	− 29.9%	29.5%
2014	0.0160011	0.0008229	− 33.2%	− 41.5%	0.0167861	2.03E–05	− 33.5%	− 99.8%

4. Discussion

The overall health burden associated with PM_2.5 in the United States has declined over time and the implementation of local, state and federal air quality policies is likely to further this trend into the future (Fann et al., 2013a, 2013b; Hubbell et al., 2009). That the estimated counts of PM-related deaths fall over time is noteworthy, given both the concurrent increase in the overall size of the U.S. population and the shift in the age distribution toward older populations who are more susceptible to air pollution-related adverse effects. Put differently, the estimated burden falls even as the pool of individuals at greatest risk of PM-related death increases. This outcome is a direct result of the precipitous decline in fine particle levels across the contiguous United States, particularly in regions that have historically experienced among the highest levels of PM_2.5, including the upper Midwest, the southeast and parts of California.

While our analysis does not identify the specific contributions of individual local, state and federal policies to the PM_2.5 reductions, it is reasonable to infer that a host of national-scale air quality management policies controlling particle pollution are at least partly responsible (Fann et al., 2013a, 2013b; Hubbell et al., 2009). By the year 2014 the estimated level of PM_2.5-attributable risk falls and becomes more equitably distributed over space and by population subgroup, implying that the remaining PM_2.5 concentrations and risks are spatially attenuated. Future analyses may wish to perform fine-scale modeling to characterize distributions of exposure and risk at higher resolution, given that the 12 km by 12 km modeling may mask near-field heterogeneity in fine particle concentrations.

The total counts of PM-attributable deaths estimated in the year 2005, the earliest year in this analysis, compare favorably to those estimated elsewhere in the literature (Caiazzo et al., 2013; Fann et al., 2011a; Fann and Risley, 2011b). The estimated number of PM-related morbidity effects, including hospital admissions and emergency department visits, differ slightly from those reported by Fann and colleagues in their 2011 analysis. Here we estimate a slightly larger number of PM-attributable premature deaths, due in part to using a different estimate of baseline deaths and by calculating air pollution deaths for the full range of exposures. These differences are due to the fact that this analysis uses a different suite of health impact functions, population projections and baseline rates of hospital and emergency department visit rates than the 2011 analysis.

In addition to the estimated decline in the overall health burden associated with PM_2.5, the assessment of risk inequality indicates that PM_2.5-related risks have become more equitably distributed across the population. Local, state and federal policies have historically aimed to reduce PM_2.5 concentrations where they were most elevated—which tended to be in urban locations. Thus, reducing concentrations in urban areas may also have flattened the distribution of PM_2.5 concentrations and risk—thus reducing overall inequality. Put differently, air quality has over time improved in a way that directly benefited populations at greatest risk. These results further suggest that the PM_2.5-related risks will continue to be more equitably shared across the population in the future. Notably, the pattern of observed decrements in risk inequality were robust to the choice of inequality metric and/or risk metric. Regardless of the employed risk metric, AI and Gini coefficients estimated that the largest reductions in risk inequality relative to 2005 occurred in 2011, with continued decreases in 2014.

The interpretability of the decomposed AI results describing the within- and between-group inequality for vulnerable and susceptible populations is less clear. The results suggest that nearly all of the observed risk inequality is occurring within groups. However, this may be an artifact of the decomposed AI equations. Specifically, while between-group inequality is calculated relative to total inequality, Elbers et al. (2005) argue that there is no realistic scenario where the inequality measured between two or more groups would account for all of the inequality in a given population. As such, the authors note that “it is not surprising that one rarely observes a high share of between-group inequality” (Elbers et al., 2005). Therefore, the observed between-group inequality for the vulnerable and susceptible populations may be artificially low due to the relative size of the groups and risk distributions therein. Additionally, this could have resulted in unstable between-group inequality estimates, which may account for the lack of a clear pattern establishing how the inequality between vulnerable and susceptible subgroups and the population at-large is estimated to change relative to the baseline year.

The results of this assessment are subject to important limitations and uncertainties that affect the interpretability of the results. First, each element of the analytical approach is itself subject to uncertainties. For example, the air quality model-simulated ambient concentrations for 2005, 2011, and 2014 reflect historical changes in emissions, meteorology, and boundary conditions; any errors in these model inputs are propagated through the air quality model.

A second source of uncertainty relates to the health impact assessment. While we accounted for changes in the size and distribution of the U.S. population over time and the change in the baseline rate of death, we fixed the morbidity rates used to quantify endpoints including hospital admissions and emergency department visits to a single year. Evidence suggests that rates of cardiovascular-related health outcomes is declining over time; this implies that our estimates of air pollution-related cardiovascular outcomes may be overstated, given that we quantify these effects relative to a baseline rate of disease. We also limited our analysis to a relatively small set of air pollution outcomes. More recent evidence suggests that PM_2.5 exposure is associated with both metabolic, neurological and cerebrovascular effects which we do not explore in this assessment.

There are additional uncertainties regarding the use of the AI to quantify risk inequality. Notably, the AI includes an explicit inequality aversion parameter that weights the inequality estimate relative to where differences in risk occur across the distribution (Harper et al., 2013). As discussed previously, the AI sensitivity parameter has a somewhat counterintuitive interpretation when applied to risk inequality, with a higher parameter value resulting in greater weight placed on differences in the lower end of the distribution (i.e., those with lower risk). Consequently, the choice of different sensitivity parameters can lead to substantial differences in the AI. In an attempt to account for the implicit subjectivity in choosing a sensitivity parameter, we calculated an upper bound AI using a higher sensitivity parameter. The AI values calculated using the higher sensitivity parameter were much higher than those calculated using our primary parameter, but the direction of the changes remained consistent over time. We also calculated Gini coefficients to provide a measure of risk inequality that does not implement an explicit inequality aversion parameter. Again, the estimated changes in inequality over time were directionally consistent with those estimated using the AI. Therefore, despite the uncertainty introduced by the subjectivity of the sensitivity parameter, the observed directionality of the changes in inequality remained robust across alternative parameter values and inequality measures. The distributional analysis also considers changes in the distribution of premature death. The distribution of other non-mortality endpoints, particularly among children, may differ. Future work may wish to address this limitation. Finally, this analysis employs 12 km by 12 km predictions which will not full account for near-field variability in PM concentrations.

Notwithstanding the uncertainties and limitations above, this analysis provides additional evidence that particle levels are falling through the year 2014 and public health is improving. This manuscript also provides new evidence that falling PM_2.5 levels, and associated risks, are becoming more equitably distributed over time and are benefiting those populations most susceptible and vulnerable to poor air quality.