Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2019 Aug 13;5(8):1468–1474. doi: 10.1021/acscentsci.9b00590

Predicting Kinase Inhibitor Resistance: Physics-Based and Data-Driven Approaches

Matteo Aldeghi 1,*, Vytautas Gapsys 1, Bert L de Groot 1,*
PMCID: PMC6716344  PMID: 31482130

Abstract

graphic file with name oc9b00590_0004.jpg

Resistance to small molecule drugs often emerges in cancer cells, viruses, and bacteria as a result of the evolutionary pressure exerted by the therapy. Protein mutations that directly impair drug binding are frequently involved in resistance, and the ability to anticipate these mutations would be beneficial in drug development and clinical practice. Here, we evaluate the ability of three distinct computational methods to predict ligand binding affinity changes upon protein mutation for the cancer target Abl kinase. These structure-based approaches rely on first-principle statistical mechanics, mixed physics- and knowledge-based potentials, and machine learning, and were able to estimate binding affinity changes and identify resistant mutations with remarkable accuracy. We expect that these complementary approaches will enable the routine prediction of resistance-causing mutations in a variety of other target proteins.

Short abstract

Physics-based and data-driven computational approaches accurately predict the effect of protein mutation on inhibitor binding and identify resistance-causing mutations in human Abl kinase.

Introduction

Drug resistance is one of the chief challenges to be overcome in the development of robust anticancer and antimicrobial therapies. While resistance can emerge via multiple mechanisms, such as increased drug efflux or activation of alternative signaling pathways, it is often caused by protein mutations directly impacting drug binding.1,2 Anticipating these resistance-causing mutations is of interest for personalized medicine, as it would inform treatment decisions based on the patient’s genotype3,4 and aid the development of combination therapies. It would also benefit drug development by allowing the parallel exploration of inhibitors with different resistance profiles. While large-scale experimentation is feasible,5 it is neither cheap nor convenient, and accurate computer predictions mitigate the need for systematic experimentation.

Protein kinases are among the most exploited drug targets, with 48 inhibitors approved to date in the United States.6 The majority of these inhibitors target tyrosine kinases,6 which play a critical role in the modulation of growth factor signaling.7,8 Hence, tyrosine kinase inhibitors (TKIs) are employed against a number of malignancies, like chronic myelogenous leukemia (CML) and nonsmall-cell lung cancer.7,8 In particular, TKIs targeting the human kinase Abl are the first-line therapy for the treatment of CML.9 However, susceptibility to resistance requires continued development of new-generation inhibitors.8 For instance, in nonsmall-cell lung cancer, acquired resistance inevitably occurs within 1–2 years of starting the therapy.10 In CML, more than 25% of patients switch TKI due to intolerance or resistance,11 the latter being most often caused by mutations in Abl.8 Because kinases display a long tail of rare and uncharacterized mutations,12 the sensitivity of many clinically identified kinase mutants to TKI treatment is often unknown. Thus, rapid and accurate computational approaches could impact clinical decision-making by providing oncologists with a first indication of whether the observed mutation is likely to cause resistance to certain inhibitors.

Here, we show how both physics-based and data-driven computational approaches can be used to accurately estimate the change in affinity of TKIs for the human kinase Abl caused by single-point mutations. To test the different methodologies, we used a data set of 144 Abl:TKI affinity changes (ΔΔG) across 8 TKIs caused by 31 Abl mutations (Figure 1), which was compiled by Hauser et al.12 using publicly available cell viability IC50 data. The computational approaches tested were based on (i) molecular dynamics (MD) simulations13 with a nonequilibrium free energy calculation protocol;14−16 (ii) Rosetta, a modeling program that uses mixed physics- and knowledge-based potentials;17,18 and (iii) machine learning (ML).19 For completeness, we discuss our results also in light of those obtained by Hauser et al.12 with the OPLS3 force field20 and a MD-based approach similar to ours (Table 1).

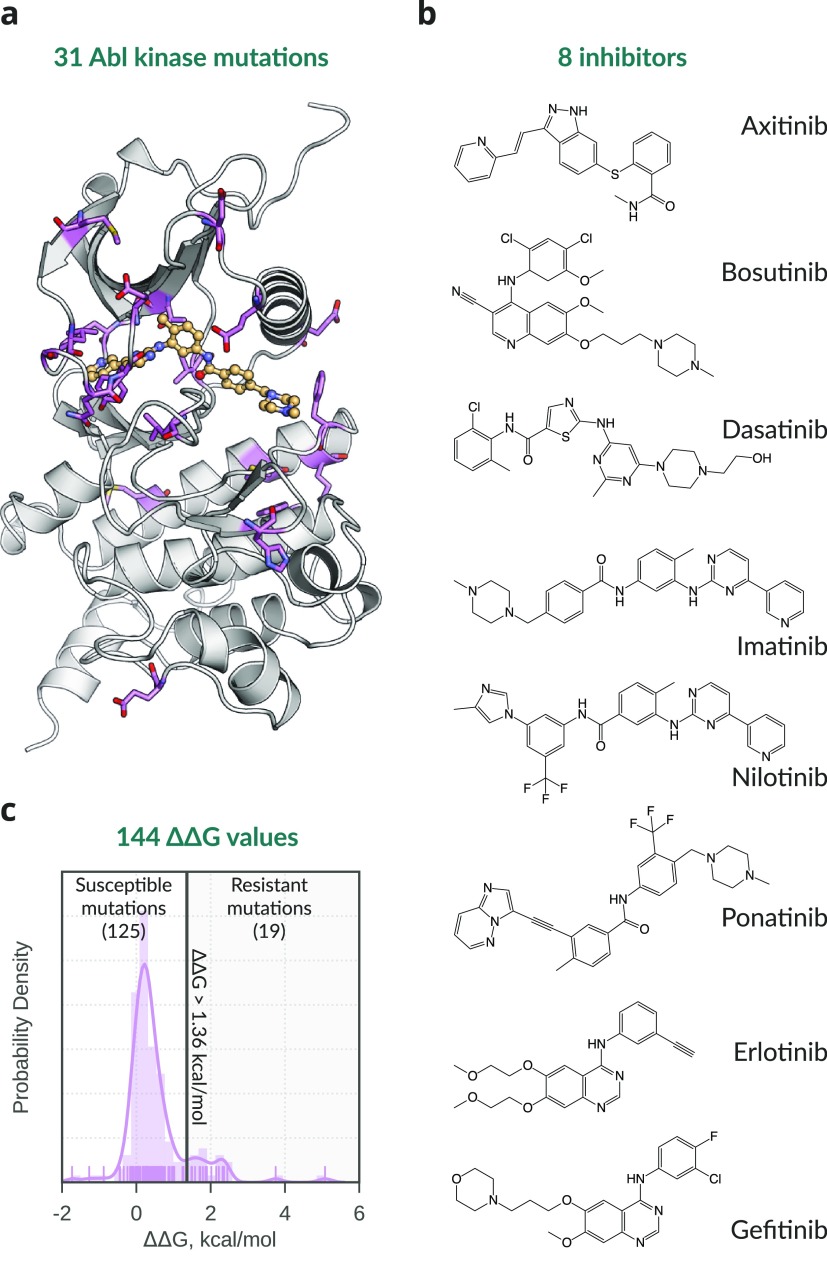
Figure 1.

Figure 1

Open in a new tab

Data set of Abl kinase mutations and associated TKI affinity changes (ΔΔG) studied. (a) Structure of human Abl kinase (PDB-ID 1OPJ) with imatinib (light orange) bound. Mutated wild-type residues are shown as violet sticks. (b) Name and chemical structure of the 8 TKIs studied. (c) Distribution of the 144 experimental ΔΔG values. The line at ΔΔG = 1.36 kcal/mol separates mutations defined as resistant from susceptible.

Table 1. Summary of the Approaches Used, Their Performance, and Computational Costa.

      Approximate cost per ΔΔG estimate
 Performance
Abbreviation Method Force field or scoring function Hardware Compute hours RMSE (kcal/mol) Pearson AUPRC
OP3 Molecular Dynamics OPLS3b 1 GPUc 72g 1.070.891.25 0.490.190.69 0.560.320.76
C22 Molecular Dynamics Charmm22* and CGenFF v 3.0.1 10 CPUd cores and 1 GPUe 59 1.030.851.21 0.240.010.44 0.250.120.48
A99 Molecular Dynamics Amber99sb*-ILDN and GAFF v 2.1 10 CPUd cores and 1 GPUe 59 0.910.771.05 0.440.240.59 0.560.320.77
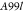Inline graphic Molecular Dynamics Amber99sb*-ILDN and GAFF v 2.1 10 CPUd cores and 1 GPUe 98g 0.910.741.09 0.420.200.59 0.510.270.75
R15 Rosetta REF15 1 CPUf core 32 0.720.600.83 0.670.450.81 0.530.290.74
R16 Rosetta βNOV16 1 CPUf core 32 0.830.700.96 0.590.350.74 0.390.180.60
ML1 Machine Learning n/a 1 CPUf core 0.02 0.870.681.06 0.12-0.040.29 0.200.100.39
ML2 Machine Learning n/a 1 CPUf core 0.02 0.680.550.80 0.570.340.72 0.470.250.68
Open in a new tab
a

For the performance measures, the point estimates from the original samples and their 95% bootstrapped confidence intervals are shown (xlowerupper). RMSE: root-mean-square error; AUPRC: area under the precision-recall curve.

b

Data for the MD calculations with the OPLS3 force field refer to and were taken from Hauser et al.12

c

Nvidia (Pascal architecture).

d

Intel Xeon E5-2630 v 4.

e

Nvidia GeForce GTX 1080 Titan.

f

Intel Xeon (Broadwell architecture).

g

Time for charge-conserving mutations. For charge-changing mutations the simulation time is double.

Results and Discussion

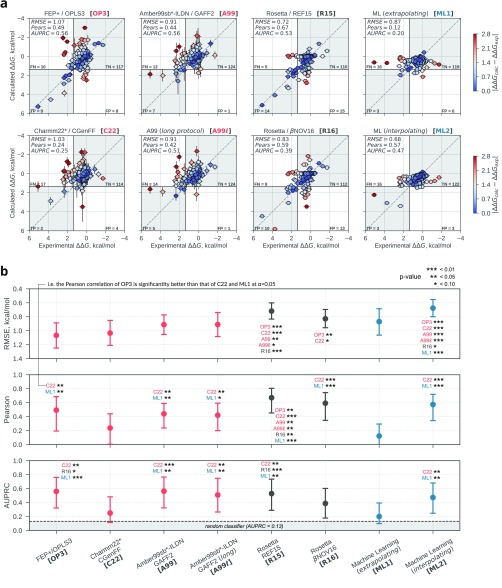
The performance of all calculations was assessed by the root-mean-square error (RMSE) between calculated and experimentally measured ΔΔG values, the Pearson correlation coefficient (r), and the area under the precision recall curve (AUPRC).21 The latter measures the ability to classify mutations as resistant or susceptible. In particular, precision measures which fraction of mutations classified as resistant are actually resistant, whereas recall measures which fraction of resistant mutations are correctly classified as resistant. Consistent with previous work,12 resistant mutations were defined as those causing more than a 10-fold drop in affinity (ΔΔGexp > 1.36 kcal/mol). On this data set, given the fraction of resistant mutations (Figure 1c), a random classifier would return an AUPRC of 0.13.

First, we estimated changes in TKI affinity with an approach based on the first-principles of statistical mechanics. MD simulations were used to sample the isothermal–isobaric ensemble while a specific residue was “alchemically” mutated14 into another one. From the nonequilibrium work required to transform the residue, it is possible to recover the equilibrium free energy difference22,23 and, using a suitable thermodynamic cycle (Figure S1), a rigorous estimate of ΔΔG. We tested multiple force fields, and, on this data set, Amber force fields performed better than Charmm (Figure S2, Table S1); halogen bond modeling did not improve the Charmm results (Figure S3). For simplicity, we discuss only the results obtained with the best-performing Amber (A99)24−27 and Charmm (C22)28−31 force fields (Table 1). The performance of A99 was comparable to that of OP3 (Figure 2),12 which was obtained by Hauser et al.12 with the FEP+ program by Schrödinger Inc. and the recently optimized proprietary OPLS3 force field.20 C22 performed significantly worse than A99 and OP3 in terms of correlation and classification ability. Surprisingly, combining force fields in a consensus approach (considering half of the simulations for each parent force field) did not generally improve the results (Figure S4). It is conceivable that, on this data set, the benefits of the additional sampling obtained with one force field outweighs those expected by combining multiple force fields.16 We also did not observe a dependence of the accuracy of the calculation on the net charge change of the system upon mutation (Figure S5).

Figure 2.

Figure 2

Open in a new tab

Accuracy of the ΔΔG estimates. (a) Scatter plots of experimental versus calculated ΔΔG values. The identity is shown as a dashed gray line. The four quadrants indicate the location of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) according to the definition of resistant and susceptible mutations used (resistant if ΔΔGexp > 1.36 kcal/mol, susceptible otherwise)12 and an equivalent cutoff (1.36 kcal/mol) for the calculated ΔΔG values. Each ΔΔG estimate is color-coded according to its absolute error with respect to the experimental ΔΔG value; at 300 K, an error of 1.4 kcal/mol corresponds to a ∼10-fold error in Kd change, and an error of 2.8 kcal/mol to a ∼100-fold error in Kd change. (b) Summary of the performance of the ΔΔG estimates across approaches in terms of RMSE, Pearson correlation, and AUPRC; point estimates from the original samples and 95% bootstrapped confidence intervals are shown (SI Methods). Differences at three levels of significance are reported using labels within the chart: e.g., a “C22**” label above the RMSE mark of OP3 indicates that the RMSE of OP3 is significantly lower (i.e., better agreement with experiment) than that of C22 at α = 0.05.

While our free energy protocol used a total of 216 ns of MD per ΔΔG estimate,16 OP3 used 720 ns for charge-changing mutations, and 360 ns for charge-conserving ones.12 We thus also tested a more expensive protocol 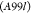Inline graphic, which matched exactly the simulation time invested by OP3. 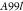Inline graphic improved upon the uncertainty (Figure S6), but not upon the accuracy (Figure 2), of the A99 estimates. Lower uncertainty is expected when more calculation repeats are used as in this case. On the other hand, accuracy is not necessarily proportional to the length of the simulations, as longer simulations allow for better sampling but also larger deviation from the experimentally determined structure in a potentially artificial fashion. Overall, this rigorous physics-based approach returned accurate ΔΔG estimates (e.g., for A99, RMSE = 0.91 kcal/mol, r = 0.44, and AUPRC = 0.56) and was able to discriminate between resistant and susceptible mutants well. However, a strong dependence of the results on the force field was observed. In addition, compared to the approaches discussed later, the MD based calculations required considerable computational resources (∼2.5 days on 10 CPU cores and one GPU per ΔΔG estimate).

As an approach that is neither rigorously physics-based nor purely statistical, we tested a recently proposed Rosetta protocol18 that was found to perform well also on protein–ligand binding.16 This method samples multiple conformations of wild-type and mutant proteins with a Monte Carlo algorithm and estimates ΔΔG with the all-atom Rosetta energy function,17 a mixed knowledge- and physics-based potential, by averaging over the generated wild-type and mutant ensembles. We found this approach (R15) to be highly accurate on this data set (Figure 2)—with low absolute errors (RMSE = 0.72 kcal/mol), strong correlation (r = 0.67), and good classification performance (AUPRC = 0.53)—while requiring only moderate computational resources (∼32 h on a single CPU core per ΔΔG estimate). In addition to the standard REF15 scoring function, we tested the βNOV16 function (R16), which returned slightly worse results than R15 for this system (Figure 2). As had been noticed before,16 here too, complementing Rosetta with the MD results via simple averaging generally resulted in enhanced performance (Figure S7). For instance, combining A99 and R15, we obtained a particularly strong consensus estimate (Figure S8) with RMSE = 0.62 kcal/mol, r = 0.71, and AUPRC = 0.61. This can be attributed to the complementary performance of the two approaches: while the MD based calculations showed better precision performance and a lower number of false positives, Rosetta displayed better recall and a lower number of false negatives (Table S2, Figure 2).

As a purely data-driven approach, we employed extremely randomized regression trees,19 a ML technique that uses ensembles of decision trees similarly to random forest. As input features, we used terms derived from the crystallographic protein–ligand structures (e.g., hydrogen bonds, nonpolar contacts, residue-ligand distance), ligand and residue physicochemical properties, and fast empirical scoring functions.32−34 However, the way information from these sources is transformed to produce a ΔΔG estimate does not rely on any specific physical model. The technical details of the ML model construction are provided in the SI Methods. An advantage of this statistical approach is speed: once the necessary input features have been computed, a ΔΔG estimate can be obtained in seconds.

The ML model was trained and validated on a subset of the Platinum database,35 and then tested on the TKI data set. The training/validation set contained 484 point-mutations with associated ΔΔG values across 84 proteins and 143 ligands. We computed a total of 128 features, and then used a greedy algorithm to select any number of features, up to 40, which minimized the mean-squared error of 10-fold cross-validation. The folds were built such that each of them would contain a unique set of proteins not present in the other folds. This procedure identified an optimal set of 29 features (Data S3). After training, the model was tested on the TKI data set (ML1 in Figure 2). Given no tyrosine kinase was present in the training set, we effectively assessed whether the model could extrapolate to this protein target. ML1 performed well in terms of RMSE (0.87 kcal/mol) but was not significantly better than random in terms of correlation and classification ability (r = 0.12-0.040.29, AUPRC = 0.200.10), and was overall comparable to the MD results obtained with the Charmm force fields (Figure 2, Table S1). These results are similar to those obtained with another ML model36 based on Gaussian process regression (Figure S9).

Given that ML is expected to perform best when trained on the most relevant data,37 we asked whether the model performance would improve when trained on tyrosine kinase mutations only. In this case, we effectively assessed the interpolative ability of the model, as it was trained and tested on the TKI data set (ML2). To do this, we used 8-fold nested cross-validation. At each iteration, the model selected a subset of the 128 features via 7-fold cross validation with 7 inhibitors and was then tested on the eighth. This was done 8 times to obtain predictions for all TKIs and thus all entries in the data set. ML2 accurately estimated ΔΔG values and could discriminate well between resistant and susceptible mutations (RMSE = 0.68 kcal/mol, r = 0.57, AUPRC = 0.47).

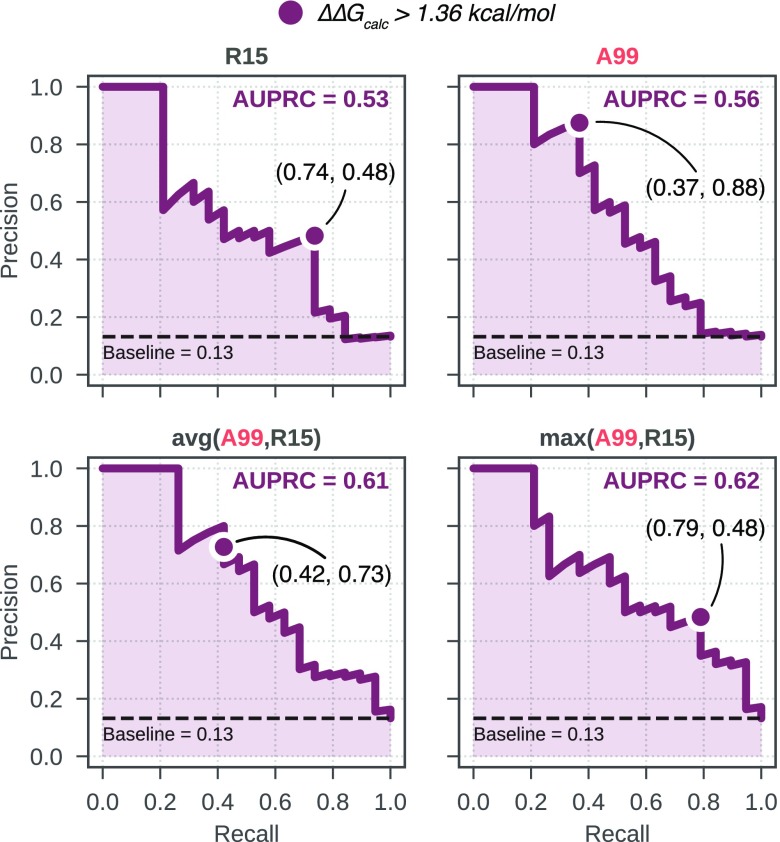
If the objective is only to identify resistant mutations38 rather than assessing their impact on ligand binding quantitatively, then AUPRC is the most relevant performance measure to examine. In this regard, MD based calculations with the OPLS3 or Amber99 force fields (OP3, A99, 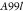Inline graphic), and Rosetta with the REF15 scoring function (R15) provided the best performance (Figure 3, Figure S10). Furthermore, in this scenario, one is likely willing to accept a larger fraction of false positives if this means recovering more resistant mutations. Thus, a suitable consensus strategy is to select the most positive ΔΔG estimate among those available to maximize the recall (at the expense of precision) at a given threshold (Figure S11). Using this approach with A99 and R15 returns an AUPRC of 0.62 and, at the conventional threshold of ΔΔGcalc > 1.36 kcal/mol, a recall of 0.79 and a precision of 0.48 (Figure 3; Table S2). This means that about half of the mutations classified as resistant are in fact resistant, and 79% of the resistant mutations in the data set have been identified.

Figure 3.

Figure 3

Open in a new tab

Precision recall curves for selected approaches. A99 and R15 have been combined to give two consensus results: in “avg(A99,R15)”, the results of A99 and R15 have been averaged; in “max(A99,R15)”, for each mutation, the most positive ΔΔG estimate among A99 and R15 was selected. The curve for a random estimator is shown as a dashed black line (baseline with AUPRC of 0.13). The precision and recall corresponding to the conventional threshold of ΔΔGcalc > 1.36 kcal/mol is reported and marked by a circle on the curves.

From the results presented, it emerges that the latest computational approaches, from physics-based to data-driven ones, are able to predict TKI affinity changes upon Abl mutation and identify resistance-causing mutations. However, the different methods have different strengths and weaknesses. The MD-based calculations achieved a remarkable performance considering that force field parameters are based on fundamental physical properties of organic molecules (e.g., quantum mechanical energies and electrostatic potentials, liquid densities, and enthalpies of vaporization), rather than binding affinities directly. This, together with the rigorous statistical mechanical treatment, might lie at the basis of the demonstrated generalizability16,39 of the approach across protein–ligand systems. The downside is the comparably higher computational cost required to obtain precise ΔΔG estimates. On the other hand, ML predictions proved accurate only when the binding affinities for Abl:TKI were used directly for training. With this information, however, a ΔΔG estimate could be generated in a matter of seconds to minutes on a single CPU core, with most of the time spent collecting the necessary structure-based features. Thus, the optimal approach choice in a prospective scenario will depend on the amount of prior information available for the system of interest, the nature of the study (a large-scale scan versus an in-depth study of a few mutations), as well as the computational resources at hand. That being said, we found that Rosetta struck a good balance between accuracy, generalizability, and computational cost. Similar to MD, this approach considers an ensemble of protein–ligand conformations,18 and its scoring function is based on simple physical and structural properties of organic molecules and biomolecules,17 so that it does not require binding affinities to the system of interest for training. In addition, approximations such as the use of implicit solvation and a more limited conformational sampling result in a moderate computational cost.

Conclusion

In summary, we have shown how fundamentally different structure-based approaches are able to predict TKI resistance to similar or better accuracy than reported thus far. Taking advantage of multiple techniques in a consensus fashion resulted in remarkable accuracy and tuning of the classification performance. These results suggest that a diverse set of computational approaches, each with its own strengths and weaknesses, is now available for the reliable estimate of resistance-causing protein mutations. It is our hope that the availability of multiple complementary approaches will enable the routine prediction of resistance-causing mutations across many other protein targets.

Acknowledgments

M.A. was supported by a Postdoctoral Research Fellowship of the Alexander von Humboldt Foundation. V.G. was supported by the BioExcel CoE (www.bioexcel.eu), a project funded by the European Union (Contract H2020-EINFRA-2015-1-675728).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00590.

  • Methods, including supporting figures and data tables (PDF)

  • Data S1: detailed information on the data set and numerical results for all calculations (XLSX)

  • Data S2: input files pertaining to the molecular-dynamics-based free energy calculations and Rosetta calculations (ZIP)

  • Data S3: input files and Jupyter notebooks used for the training and testing of the machine learning model. Available at https://doi.org/10.5281/zenodo.3350897

The authors declare no competing financial interest.

Supplementary Material

oc9b00590_si_001.pdf (6.8MB, pdf)
oc9b00590_si_002.xlsx (45.6KB, xlsx)
oc9b00590_si_003.zip (1.5MB, zip)

References

  1. Lovly C. M.; Shaw A. T. Molecular Pathways: Resistance to Kinase Inhibitors and Implications for Therapeutic Strategies. Clin. Cancer Res. 2014, 20 (9), 2249–2256. 10.1158/1078-0432.CCR-13-1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Housman G.; Byler S.; Heerboth S.; Lapinska K.; Longacre M.; Snyder N.; Sarkar S. Drug Resistance in Cancer: An Overview. Cancers 2014, 6 (3), 1769–1792. 10.3390/cancers6031769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Zehir A.; Benayed R.; Shah R. H.; Syed A.; Middha S.; Kim H. R.; Srinivasan P.; Gao J.; Chakravarty D.; Devlin S. M.; Hellmann M. D.; Barron D. A.; Schram A. M.; Hameed M.; Dogan S.; Ross D. S.; Hechtman J. F.; DeLair D. F.; Yao J. J.; Mandelker D. L.; Cheng D. T.; Chandramohan R.; Mohanty A. S.; Ptashkin R. N.; Jayakumaran G.; Prasad M.; Syed M. H.; Rema A. B.; Liu Z. Y.; Nafa K.; Borsu L.; Sadowska J.; Casanova J.; Bacares R.; Kiecka I. J.; Razumova A.; Son J. B.; Stewart L.; Baldi T.; Mullaney K. A.; Al-Ahmadie H.; Vakiani E.; Abeshouse A. A.; Penson A. V.; Jonsson P.; Camacho N.; Chang M. T.; Won H. H.; Gross B. E.; Kundra R.; Heins Z. J.; Chen H. W.; Phillips S.; Zhang H.; Wang J.; Ochoa A.; Wills J.; Eubank M.; Thomas S. B.; Gardos S. M.; Reales D. N.; Galle J.; Durany R.; Cambria R.; Abida W.; Cercek A.; Feldman D. R.; Gounder M. M.; Hakimi A. A.; Harding J. J.; Iyer G.; Janjigian Y. Y.; Jordan E. J.; Kelly C. M.; Lowery M. A.; Morris L. G. T.; Omuro A. M.; Raj N.; Razavi P.; Shoushtari A. N.; Shukla N.; Soumerai T. E.; Varghese A. M.; Yaeger R.; Coleman J.; Bochner B.; Riely G. J.; Saltz L. B.; Scher H. I.; Sabbatini P. J.; Robson M. E.; Klimstra D. S.; Taylor B. S.; Baselga J.; Schultz N.; Hyman D. M.; Arcila M. E.; Solit D. B.; Ladanyi M.; Berger M. F. Mutational Landscape of Metastatic Cancer Revealed from Prospective Clinical Sequencing of 10,000 Patients. Nat. Med. 2017, 23 (6), 703–713. 10.1038/nm.4333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Fowler P. W.; Cole K.; Gordon N. C.; Kearns A. M.; Llewelyn M. J.; Peto T. E. A.; Crook D. W.; Walker A. S. Robust Prediction of Resistance to Trimethoprim in Staphylococcus Aureus. Cell Chem. Biol. 2018, 25 (3), 339–349. 10.1016/j.chembiol.2017.12.009. [DOI] [PubMed] [Google Scholar]
  5. Melnikov A.; Rogov P.; Wang L.; Gnirke A.; Mikkelsen T. S. Comprehensive Mutational Scanning of a Kinase in Vivo Reveals Substrate-Dependent Fitness Landscapes. Nucleic Acids Res. 2014, 42 (14), e112 10.1093/nar/gku511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Roskoski R. Properties of FDA-Approved Small Molecule Protein Kinase Inhibitors. Pharmacol. Res. 2019, 144, 19–50. 10.1016/j.phrs.2019.03.006. [DOI] [PubMed] [Google Scholar]
  7. Bhullar K. S.; Lagarón N. O.; McGowan E. M.; Parmar I.; Jha A.; Hubbard B. P.; Rupasinghe H. P. V. Kinase-Targeted Cancer Therapies: Progress, Challenges and Future Directions. Mol. Cancer 2018, 17 (1), 1–20. 10.1186/s12943-018-0804-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Arora A.; Scholar E. M. Role of Tyrosine Kinase Inhibitors in Cancer Therapy. J. Pharmacol. Exp. Ther. 2005, 315 (3), 971–979. 10.1124/jpet.105.084145. [DOI] [PubMed] [Google Scholar]
  9. Jiao Q.; Bi L.; Ren Y.; Song S.; Wang Q.; Wang Y. S. Advances in Studies of Tyrosine Kinase Inhibitors and Their Acquired Resistance. Mol. Cancer 2018, 17 (1), 1–12. 10.1186/s12943-018-0801-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Camidge D. R.; Pao W.; Sequist L. V. Acquired Resistance to TKIs in Solid Tumours: Learning from Lung Cancer. Nat. Rev. Clin. Oncol. 2014, 11, 473. 10.1038/nrclinonc.2014.104. [DOI] [PubMed] [Google Scholar]
  11. Patel A. B.; O’Hare T.; Deininger M. W. Mechanisms of Resistance to ABL Kinase Inhibition in Chronic Myeloid Leukemia and the Development of Next Generation ABL Kinase Inhibitors. Hematol. Oncol. Clin. North Am. 2017, 31 (4), 589–612. 10.1016/j.hoc.2017.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hauser K.; Negron C.; Albanese S. K.; Ray S.; Steinbrecher T.; Abel R.; Chodera J. D.; Wang L. Predicting Resistance of Clinical Abl Mutations to Targeted Kinase Inhibitors Using Alchemical Free-Energy Calculations. Commun. Biol. 2018, 1 (1), 70. 10.1038/s42003-018-0075-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. Software X 2015, 2, 1–7. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  14. Gapsys V.; Michielssens S.; Seeliger D.; de Groot B. L. Pmx: Automated Protein Structure and Topology Generation for Alchemical Perturbations. J. Comput. Chem. 2015, 36 (5), 348–354. 10.1002/jcc.23804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gapsys V.; Michielssens S.; Seeliger D.; de Groot B. L. Accurate and Rigorous Prediction of the Changes in Protein Free Energies in a Large-Scale Mutation Scan. Angew. Chem., Int. Ed. 2016, 55 (26), 7364–7368. 10.1002/anie.201510054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Aldeghi M.; Gapsys V.; de Groot B. L. Accurate Estimation of Ligand Binding Affinity Changes upon Protein Mutation. ACS Cent. Sci. 2018, 4 (12), 1708–1718. 10.1021/acscentsci.8b00717. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Alford R. F.; Leaver-Fay A.; Jeliazkov J. R.; O’Meara M. J.; DiMaio F. P.; Park H.; Shapovalov M. V.; Renfrew P. D.; Mulligan V. K.; Kappel K.; Labonte J. W.; Pacella M. S.; Bonneau R.; Bradley P.; Dunbrack R. L.; Das R.; Baker D.; Kuhlman B.; Kortemme T.; Gray J. J. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J. Chem. Theory Comput. 2017, 13 (6), 3031–3048. 10.1021/acs.jctc.7b00125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Barlow K. A.; Ó Conchúir S.; Thompson S.; Suresh P.; Lucas J. E.; Heinonen M.; Kortemme T. Flex DdG: Rosetta Ensemble-Based Estimation of Changes in Protein-Protein Binding Affinity upon Mutation. J. Phys. Chem. B 2018, 122 (21), 5389–5399. 10.1021/acs.jpcb.7b11367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Geurts P.; Ernst D.; Wehenkel L. Extremely Randomized Trees. Mach. Learn. 2006, 63 (1), 3–42. 10.1007/s10994-006-6226-1. [DOI] [Google Scholar]
  20. Harder E.; Damm W.; Maple J.; Wu C.; Reboul M.; Xiang J. Y.; Wang L.; Lupyan D.; Dahlgren M. K.; Knight J. L.; Kaus J. W.; Cerutti D. S.; Krilov G.; Jorgensen W. L.; Abel R.; Friesner R. A. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput. 2016, 12 (1), 281–296. 10.1021/acs.jctc.5b00864. [DOI] [PubMed] [Google Scholar]
  21. Saito T.; Rehmsmeier M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS One 2015, 10 (3), e0118432 10.1371/journal.pone.0118432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jarzynski C. Equilibrium Free-Energy Differences from Nonequilibrium Measurements: A Master-Equation Approach. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1997, 56 (5), 5018–5035. 10.1103/PhysRevE.56.5018. [DOI] [Google Scholar]
  23. Crooks G. E. Entropy Production Fluctuation Theorem and the Nonequilibrium Work Relation for Free Energy Differences. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1999, 60 (3), 2721–2726. 10.1103/PhysRevE.60.2721. [DOI] [PubMed] [Google Scholar]
  24. Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins: Struct., Funct., Genet. 2006, 65 (3), 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Best R. B.; Hummer G. Optimized Molecular Dynamics Force Fields Applied to the Helix-Coil Transition of Polypeptides. J. Phys. Chem. B 2009, 113 (26), 9004–9015. 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Improved Side-Chain Torsion Potentials for the Amber Ff99SB Protein Force Field. Proteins: Struct., Funct., Genet. 2010, 78 (8), 1950–1958. 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25 (9), 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  28. MacKerell a D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiórkiewicz-Kuczera J.; Yin D.; Karplus M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102 (18), 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  29. Mackerell A. D.; Feig M.; Brooks C. L. Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of Gas-Phase Quantum Mechanics in Reproducing Protein Conformational Distributions in Molecular Dynamics Simulation. J. Comput. Chem. 2004, 25 (11), 1400–1415. 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
  30. Piana S.; Lindorff-Larsen K.; Shaw D. E. How Robust Are Protein Folding Simulations with Respect to Force Field Parameterization?. Biophys. J. 2011, 100 (9), L47–L49. 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; MacKerell A. D. CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2009, 31 (4), 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Salentin S.; Schreiber S.; Haupt V. J.; Schroeder M.; Adasme M. F. PLIP: Fully Automated Protein-Ligand Interaction Profiler. Nucleic Acids Res. 2015, 43 (W1), W443–W447. 10.1093/nar/gkv315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Trott O.; Olson A. J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2009, 31 (2), 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wang C.; Zhang Y. Improving Scoring-Docking-Screening Powers of Protein-Ligand Scoring Functions Using Random Forest. J. Comput. Chem. 2017, 38 (3), 169–177. 10.1002/jcc.24667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pires D. E. V.; Blundell T. L.; Ascher D. B. Platinum: A Database of Experimentally Measured Effects of Mutations on Structurally Defined Protein-Ligand Complexes. Nucleic Acids Res. 2015, 43 (D1), D387–D391. 10.1093/nar/gku966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pires D. E. V.; Blundell T. L.; Ascher D. B. MCSM-Lig: Quantifying the Effects of Mutations on Protein-Small Molecule Affinity in Genetic Disease and Emergence of Drug Resistance. Sci. Rep. 2016, 6 (1), 29575. 10.1038/srep29575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ross G. A.; Morris G.; Biggin P. One Size Does Not Fit All: The Limits of Structure-Based Models in Drug Discovery. J. Chem. Theory Comput. 2013, 9, 4266–4274. 10.1021/ct4004228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Carter J.; Walker T. M.; Walker A. S.; Whitfield M.; Peto T. E. A.; Crook D. W.; Fowler P. W. Prediction of Pyrazinamide Resistance in Mycobacterium Tuberculosis Using Structure-Based Machine Learning Approaches. Bio Rxiv 2019, 518142. 10.2139/ssrn.3391941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Cournia Z.; Allen B.; Sherman W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model. 2017, 57 (12), 2911–2937. 10.1021/acs.jcim.7b00564. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc9b00590_si_001.pdf (6.8MB, pdf)
oc9b00590_si_002.xlsx (45.6KB, xlsx)
oc9b00590_si_003.zip (1.5MB, zip)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES