Abstract
Purpose:
Many outcomes derived from electronic health records (EHR) are not only imperfect but may suffer from exposure-dependent differential misclassification due to variability in the quality and availability of EHR data across exposure groups. The objective of this study was to quantify the inflation of type I error rates that can result from differential outcome misclassification.
Methods:
We used data on gold-standard and EHR-derived second breast cancers in a cohort of women with a prior breast cancer diagnosis from 1993–2006 enrolled in Kaiser Permanente Washington. We simulated an exposure that was independent of the true outcome status. A surrogate outcome was then simulated with varying sensitivity and specificity according to exposure status. We estimated the type I error rate for a test of association relating this exposure to the surrogate outcome, while varying outcome sensitivity and specificity in exposed individuals.
Results:
Type I error rates were substantially inflated above the nominal level (5%) for even modest departures from non-differential misclassification. Holding sensitivity in exposed and unexposed groups at 85%, a difference in specificity of 10% between the exposed and unexposed (80% vs 90%) resulted in a 36% type I error rate. Type I error was inflated more by differential specificity than sensitivity.
Conclusions:
Differential outcome misclassification may induce spurious findings. Researchers using EHR-derived outcomes should use misclassification-adjusted methods whenever possible or conduct sensitivity analyses to investigate the possibility of false-positive findings, especially for exposures that may be related to the accuracy of outcome ascertainment.
Keywords: electronic health record, misclassification, outcome, phenotype, validation
Introduction
Electronic health records (EHR) have become an important data source for investigating adverse outcomes associated with pharmacologic exposures. However, EHR-derived data are imperfect, and many recent studies have drawn attention to multiple challenges of working with this data source1–3. One challenge of working with EHR data is the lack of gold-standard information on patient outcomes. It is well known that non-differential outcome misclassification, in which sensitivity and specificity of the surrogate outcome are unrelated to the true exposure status, tends to bias results towards the null4. However, if misclassification is differential, bias can be towards or away from the null5,6. Differential misclassification of outcomes with respect to exposure status may be common in EHR-based studies investigating pharmacologic exposures because patients receiving treatments of interest may access the health care system more frequently, leading to richer EHR data and possibly more sensitive and/or less specific outcome ascertainment for these patients7.
EHR-based studies are frequently used for hypothesis generation and identification of novel risk factors. A key concern for findings from such studies is lack of reproducibility8–11. For EHR-based discovery, outcome misclassification is a key contributor to irreproducibility12. Using data from the eMERGE study, we previously quantified the loss of power attributable to outcome misclassification13. However, spurious associations induced by outcome misclassification are also an important contributor to lack of reproducibility.
We have previously developed and validated an EHR-based algorithm for identifying second breast cancers in women with a personal history of breast cancer14,15. An EHR-derived second breast cancer measure can be paired with pharmacologic exposures derived from prescription or drug dispensing databases to identify medications that may increase or decrease the risk of a second breast cancer. Using the previously developed EHR-based algorithm, we conducted statistical simulation studies to investigate bias in association parameter estimates due to differential outcome misclassification. We found that, when misclassification of second breast cancers was non-differential, parameter estimates were only minimally biased. However, under differential misclassification bias became relatively severe16.
The objective of this paper was to extend our previous investigation on bias due to differential misclassification in EHR-derived outcomes to quantify the magnitude of type I error resulting from exposure-dependent differential misclassification. Quantifying type I error is important in the context of EHR-based pharmacoepidemiologic studies because it provides a measure of the frequency of false-positive findings that may result from this type of measurement error. The results from this investigation can improve understanding of the lack of reproducibility of some EHR-derived findings.
Methods
The BRAVA Study of Second Breast Cancers
We used data from the BRAVA study, an investigation of second breast cancer algorithm development that incorporated a subset of patients from a larger, prior study17. BRAVA data come from Kaiser Permanente Washington (KPWA), a large integrated health care system in Washington-state. We included women enrolled in KPWA with a primary stage I – IIB invasive breast cancer diagnosis between 1993 and 2006. Patient demographics, primary breast cancer characteristics, co-morbidities, and medication exposures were extracted from the KPWA virtual data warehouse and manual chart abstraction. Dates of second breast cancers were manually abstracted from patient records and extracted from a tumor registry to provide gold-standard outcome information. In addition, a “high specificity algorithm” for second breast cancer events15 was applied to structured EHR data to obtain an algorithm-derived second breast cancer indicator. Estimated sensitivity and specificity for this algorithm were 89% and 99%, respectively15. The BRAVA study was reviewed and approved by the Kaiser Permanente Washington Institutional Review Board.
Simulation Study
The objective of simulation studies was to estimate the frequency of false-positive findings (i.e., type I errors) that is induced when a surrogate outcome subject to differential misclassification is used rather than the gold-standard outcome. Simulations used BRAVA data on second breast cancers and patient characteristics combined with a simulated, hypothetical medication exposure that does not affect second breast cancer risk. We used data from BRAVA on a binary gold-standard outcome (second breast cancers, D), a binary surrogate outcome (algorithm-derived second breast cancers, S), and patient risk factors (X). We then simulated a binary exposure (E), which was independent of true second breast cancer status but associated with the sensitivity and specificity of the surrogate outcome. E represents a novel exposure suspected of increasing second breast cancer risk such as a medication.
Differential misclassification was induced by defining different accuracy measures for the surrogate S conditional on the exposure level E. Specifically, for j, k=0, 1, we define exposure-dependent accuracy measures (i.e., sensitivity and specificity) as ajk = P(S = 1|D = j, E = k) with D=0 indicating no second breast cancer and 1 indicating a second breast cancer diagnosis, and E=0 for no exposure and 1 for exposure. Differential misclassification was defined as aj0 ≠ aj1, for j=0, 1.
In simulation studies, we used values for S and D observed in the BRAVA data and simulated E from a Bernoulli distribution with probability given by the following equation. Specifically, under the independence of outcome and exposure, the probability of E =1 conditional on S and D is given by
where j = 0, 1.
We set the marginal prevalence of exposure, P(E=1), to 0.2. We fixed a10, sensitivity in the unexposed group, at 0.85 and a00, 1-specificity in the unexposed group, at 0.1. We then varied sensitivity and 1-specificity in the exposed group, a11 and a01, across a range of values. We repeated the process of simulating the exposure variable E 1000 times for each combination of a11 and a01.
The target of inference was the odds ratio for the association between D and E, adjusted for patient risk factors X. However, we assume that in the context of an EHR-based study only information on S is available rather than D and therefore estimate the association between S and E adjusted for X. Although E was simulated independent of X, we adjusted for X in all analyses to mirror common practice in pharmacoepidemiologic studies of adjusting for variables known to be strongly associated with the outcome of interest. In settings where the association of these factors with the exposure of interest is uncertain, they are typically included in regression models to address the possibility of confounding.
Additional simulation studies using simulated true and surrogate disease outcomes, as opposed to observed values in the BRAVA cohort, in addition to simulated exposures allowed us to investigate a broad range of values for outcome prevalence as well as sensitivity and specificity in the unexposed group. As results were similar, we present only analyses using outcomes from BRAVA data combined with simulated exposures. The additional simulations are available in the Online Methods Supplement.
Statistical analysis
Using BRAVA data on S and X combined with simulated exposure data (E), we estimated the association between E and S using multivariable logistic regression. Logistic regression models adjusted for simulated exposure, E, and variables in X: age (continuous), year at diagnosis (categorical), primary breast cancer stage (categorical), and estrogen and progesterone receptor (ER, PR) status (categorical). For each model, we used the p-value based on the Wald statistic for the odds ratio (OR) associated with E to determine whether to accept or reject the null hypothesis, using a threshold for statistical significance of 0.05. For each combination of a01 and a11, we computed the proportion of simulations in which we rejected the null hypothesis. Since, in all settings, E was simulated to be independent of D, this proportion estimated the type I error. Using a significance threshold of 0.05, 5% of simulations would result in rejected null hypotheses if there were no type I error inflation.
Results
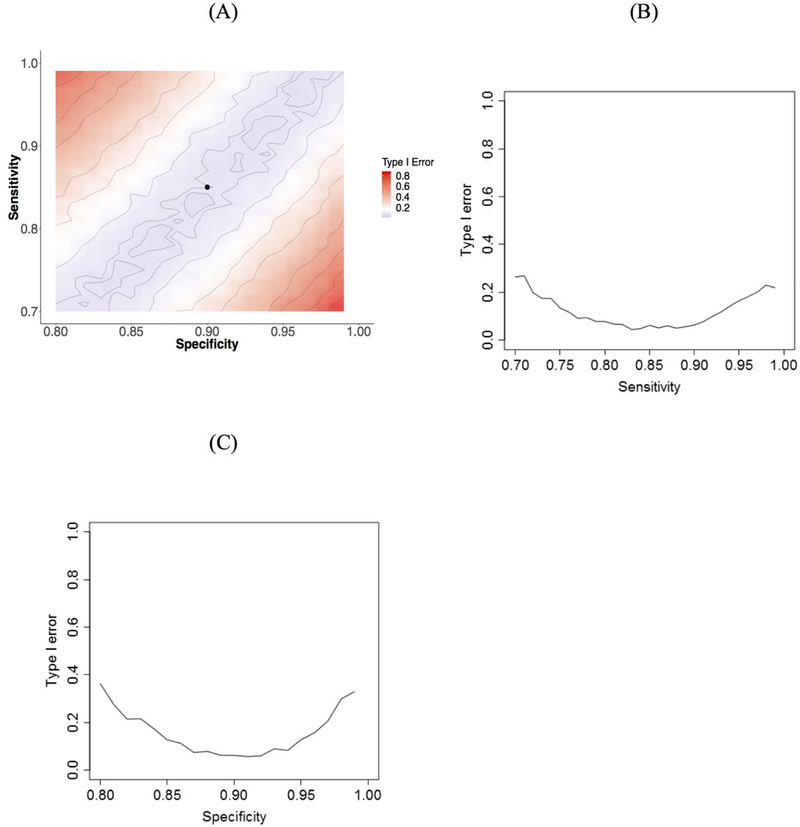
Our simulations used data on 3,152 women included in the BRAVA study (Table 1). In this sample, 407 patients were observed to experience a second breast cancer during study follow-up based on tumor registry and manual abstraction of patients’ medical records. Thus, the prevalence of second breast cancer events in the BRAVA dataset, P(D = 1), in this cohort was 0.129. Adjusted logistic regression models for the association between a simulated, independent exposure and second breast cancer status exhibited substantial inflation of the type I error rate as both sensitivity and specificity of the surrogate second breast cancer measure for exposed individuals deviated from their values in unexposed individuals (Figure 1). When sensitivity and specificity were the same in exposed and unexposed individuals (non-differential misclassification), type I error was 0.05. Holding specificity equal in exposed and unexposed individuals, when sensitivity was 10% higher in exposed individuals compared to unexposed (i.e., 0.95 vs 0.85) the type I error rate increased to 17%. Similarly, holding sensitivity equal between the two groups, a 10% decrease in specificity between exposed and unexposed individuals (i.e., 0.80 vs 0.90) resulted in a type I error rate of 36%.
Table 1.
Summary statistics for the BRAVA cohort used in simulation studies. Descriptive statistics for this cohort have been previously presented9 and are reused by permission of Oxford University Press.
| Characteristic | Overall (N = 3152) |
Women with no second breast cancer (N = 2745) |
Women with second breast cancer (N = 407) |
|---|---|---|---|
| Age (years), mean (SD) | 62.8 (13.3) | 63.1 (13.2) | 60.8 (13.9) |
| Year of primary diagnosis, N (%) | |||
| 1993 – 1995 | 578 (18.3) | 469 (17.1) | 109 (26.8) |
| 1996 – 1999 | 993 (31.5) | 846 (30.8) | 147 (36.1) |
| 2000 – 2003 | 971 (30.8) | 861 (31.4) | 110 (27.0) |
| 2004 – 2006 | 610 (19.4) | 569 (20.7) | 41 (10.1) |
| Primary breast cancer stage, N (%) | |||
| Local | 2479 (78.6) | 2200 (80.1) | 279 (68.6) |
| Regional | 673 (21.4) | 545 (19.9) | 128 (31.4) |
| ER/PR status, N (%) | |||
| ER positive | 2459 (78.0) | 2177 (79.3) | 282 (69.3) |
| Both ER and PR negative | 462 (14.7) | 364 (13.3) | 98 (24.1) |
| Other | 231 (7.3) | 204 (7.4) | 27 (6.6) |
SD: standard deviation; ER: estrogen receptor; PR: progesterone receptor
Figure 1.
Color coded contour plot of type I error as a function of sensitivity and specificity in exposed individuals (A), plot of type I error rate versus sensitivity in the exposed (B), and plot of type I error rate versus specificity in the exposed (C) using outcome and covariate data from BRAVA with simulated exposure data. In the contour plot (A), the black dot indicates sensitivity and specificity in the unexposed group. In the sensitivity plot (B), specificity in the exposed group is fixed at the value for the unexposed group (0.9) and in the specificity plot (C), sensitivity in the exposed group is fixed at the value for the unexposed group (0.85).
Discussion
Our analysis found that, in the context of an investigation of second breast cancers using EHR-derived outcomes subject to misclassification, type I error was substantially inflated above the nominal level when outcome misclassification was differential with respect to exposure. Even for an outcome with marginally good sensitivity and specificity, differences in accuracy between exposed and unexposed individuals frequently induced a spurious association between outcome and exposure. Results were particularly sensitive to differential specificity, with type I error increasing to very high levels for even small differences in specificity between exposed and unexposed individuals.
Differential misclassification is likely to be common in many settings using health care data, particularly those investigating medication exposures. Because classification accuracy is dependent on the intensity and type of interaction a patient has with the health care system, exposures that tend to result in more frequent contact with the health care system or that are correlated with health care seeking behavior are likely to exhibit differential misclassification. Previously, we found that differential misclassification induced notable bias in effect estimates in the setting of second breast cancers14,16. Based on our results, type I error rates for naïve analyses of such exposures will also be substantially inflated.
This study has several strengths. Notably, we used real EHR-derived data on second breast cancers including a previously validated EHR-based outcome measure and a chart review-validated gold-standard outcome to inform our simulations. A simulation approach is ideal for characterizing type I error because it provides a setting in which we know, by design, that the gold-standard outcome and exposure are not associated. Any observed association is therefore certain to be spurious. By coupling simulated exposure data with real EHR data we are able to ensure that all other elements of the data distribution are realistic and reflect a real-world setting.
Limitations of our study include use of data from a single health care system and disease setting. However, our results in terms of differential misclassification and the magnitude of induced type I error are likely generalizable to other settings. Type I error is sample size dependent. Therefore, our results based on a cohort of approximately 3,000 patients represent a lower bound on the inflation of type I rates relative to larger studies. Additionally, while this work highlights the sensitivity of type I error rates to differential misclassification, we have not investigated the ability of statistical approaches for misclassification to correct this type I error inflation.
In conclusion, we found that differential misclassification in EHR-derived outcomes can lead to substantially inflated type I error rates and, consequently, false-positive findings. Our investigation highlights the importance of using validated outcomes with good operating characteristics, conducting appropriate sensitivity analyses, and using misclassification-adjusted analytic approaches to reduce the risk of identifying spurious relationships.
Supplementary Material
Key points:
Exposure-dependent differential outcome misclassification may occur in pharmacoepidemiologic studies using EHR-derived outcomes in which exposures are related to the frequency or intensity of interaction with the health care system.
Differential outcome misclassification leads to substantial inflation of the type I error rate.
Type I error inflation due to differential outcome misclassification is particularly severe when outcome specificity differs between exposed and unexposed individuals.
Exposure-stratified estimates of outcome operating characteristics and misclassification adjusted analytic methods are needed to reduce the risk of spurious findings.
Acknowledgments
Research reported in this paper was supported by the National Institutes of Health under award numbers R01CA120562, R01CA09377, R01LM012607, R01AI130460, and R21CA143242 and the American Cancer Society under award number CRTG-03–024-01-CCE. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
This work has not been posted or presented previously.
References
- 1.Weiskopf NG, Weng C. Methods and dimensions of electronic health record data quality assessment: enabling reuse for clinical research. Journal of the American Medical Informatics Association : JAMIA 2013;20:144–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wells BJ, Chagin KM, Nowacki AS, Kattan MW. Strategies for handling missing data in electronic health record derived data. EGEMS (Wash DC) 2013;1:1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Weiskopf NG, Hripcsak G, Swaminathan S, Weng CH. Defining and measuring completeness of electronic health records for secondary use. J Biomed Inform 2013;46:830–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Neuhaus JM. Bias and efficiency loss due to misclassified responses in binary regression. Biometrika 1999;86:843–55. [Google Scholar]
- 5.Magder LS, Hughes JP. Logistic regression when the outcome is measured with uncertainty. American journal of epidemiology 1997;146:195–203. [DOI] [PubMed] [Google Scholar]
- 6.Neuhaus JM. Analysis of clustered and longitudinal binary data subject to response misclassification. Biometrics 2002;58:675–83. [DOI] [PubMed] [Google Scholar]
- 7.Cox E, Martin BC, Van Staa T, Garbe E, Siebert U, Johnson ML. Good research practices for comparative effectiveness research: approaches to mitigate bias and confounding in the design of nonrandomized studies of treatment effects using secondary data sources: the International Society for Pharmacoeconomics and Outcomes Research Good Research Practices for Retrospective Database Analysis Task Force Report--Part II. Value in health : the journal of the International Society for Pharmacoeconomics and Outcomes Research 2009;12:1053–61. [DOI] [PubMed] [Google Scholar]
- 8.Schuemie MJ, Hripcsak G, Ryan PB, Madigan D, Suchard MA. Robust empirical calibration of p-values using observational data. Stat Med 2016;35:3883–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schuemie MJ, Ryan PB, DuMouchel W, Suchard MA, Madigan D. Interpreting observational studies: why empirical calibration is needed to correct p-values. Stat Med 2014;33:209–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gruber S, Tchetgen Tchetgen E. Limitations of empirical calibration of p-values using observational data. Stat Med 2016;35:3869–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Springate DA, Kontopantelis E, Ashcroft DM, et al. ClinicalCodes: An Online Clinical Codes Repository to Improve the Validity and Reproducibility of Research Using Electronic Medical Records. Plos One 2014;9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Manuel DG, Rosella LC, Stukel TA. Importance of accurately identifying disease in studies using electronic health records. BMJ 2010;341:c4226. [DOI] [PubMed] [Google Scholar]
- 13.Duan R, Cao M, Wu Y, et al. An Empirical Study for Impacts of Measurement Errors on EHR based Association Studies. AMIA Annu Symp Proc 2016;2016:1764–73. [PMC free article] [PubMed] [Google Scholar]
- 14.Chubak J, Onega T, Zhu W, Buist DS, Hubbard RA. An Electronic Health Record-based Algorithm to Ascertain the Date of Second Breast Cancer Events. Medical care 2017;55:e81–e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chubak J, Yu O, Pocobelli G, et al. Administrative data algorithms to identify second breast cancer events following early-stage invasive breast cancer. J Natl Cancer Inst 2012;104:931–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hubbard R, Harton J, Zhu W, Wang L, Chubak J. Methods for time to event analyses using imperfect electronic health records-derived endpoints. In: Chen D-G, Jin Z, Li G, Li Y, Liu A, Zhao Y, eds. New Advances in Statistics and Data Science: Springer; 2017. [Google Scholar]
- 17.Boudreau DM, Yu O, Chubak J, et al. Comparative safety of cardiovascular medication use and breast cancer outcomes among women with early stage breast cancer. Breast cancer research and treatment 2014;144:405–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.