Abstract
In the present work, an optimization method called Particle Swarm Optimization (PSO) was applied to study the kinetics of alkali-catalyzed rapeseed oil transesterification, using methanol, in a batch process.
The validation of the PSO program was realized using numerical and experimental data from literature. The PSO method resulted in a 4 times lower error compared to classic methods used in the domain, which showed its efficiency and strength.
After validation, an experimental study was led on the transesterification of rapeseed oil and methanol in a batch process using KOH as catalyst (1wt/wt %) with a methanol:oil molar ratio of 6:1 at 45 °C, 55 °C and 65 °C respectively. Then, PSO was used in order to determine the reaction rate constants () of the reversible 3-steps of transesterification mechanism as well as the kinetic parameters (activation energy Ea and pre-exponential factor A).
Then, the kinetic model was used in order to investigate the effects of methanol: oil molar ratio variation (3:1, 4:1, 5:1, 6:1, 8:1, 12:1) on rate constants, yield and conversion rate at 65 °C.
The results of the simulation showed a perfect agreement with experimental results.
Keywords: Chemical engineering, Kinetic study, Particle swarm optimization, Transesterification reaction
1. Introduction
The consumption and production of biodiesel continue to increase worldwide. Biodiesel being a source of green and renewable energy, it is considered as an alternative fuel to conventional diesel oil [1].
The synthesis of biodiesel from oil can be performed by several methods such as thermochemistry [2, 3] i.e. esterification and transesterification via catalytic or non-catalytic pathways [4, 5, 6, 7]. Alkali-catalyzed transesterification is the most commonly used and consists in reacting a triglyceride molecule with three molecules of alcohol to produce three molecules of methyl ester, known as biodiesel, and one molecule of glycerol [8, 9].
The catalytic transesterification reaction follows a three-stepped reaction scheme, as illustrated in Fig. 1. During the first, step the decomposition of triglycerides (TG) to diglycerides (DG) occurs with a formation of one methyl ester, the second one transforms diglycerides to monoglycerides (MG) and methyl ester, and the last step is the decomposition of monoglycerides into glycerol and methyl ester [10].
Fig. 1.
Scheme for stepwise transesterification reaction.
In order to determine the kinetic parameters of the reaction (activation energy and pre-exponential factor), a kinetic study is required. This study is essential to design and upscale facilities to industrial level.
Several researches on the kinetics of homogeneous and heterogeneous catalysis of transesterification have been carried out using different raw materials and synthesis methods [11, 12, 13, 14, 15]. Ramezani et al. [16] studied parameters affecting the transesterification reaction of castor oil in order to optimize its yield and used their results to adjust a kinetic correlation using the pseudo-first order hypothesis.
Hanny et al. [15] proposed a kinetic model for the estimation of hydroxide-catalyzed methanolysis reaction of mixture of Jatropha curcas–waste food oil that contains 1%wt of free fatty acids (FFA) in a batch reactor at 50 °C, a mixing speed of 900 rpm, a methanol:oil molar ratio of 6:1, and 1%wt KOH. The developed model takes into account the side effects of saponification of glycerides, esters and free fatty acids (FFA). Karmee et al. [17] studied the transesterification of MG extracted from crude Pongamia oil with methanol and KOH catalyst. Their results revealed that the reaction follows a second-order, reversible kinetic model where the rate constants increase with temperature while reverse rate constants decrease.
In general, the treatment of experimental results for the determination of kinetic and energetic parameters can be carried out by different methods, i.e. iterative, linear and differential equations. Janajreh et al. [18] and Leevijit et al. [19] used least-square regression technique to solve linear equations system in order to find the best fit of the transesterification's rate constants. One of the difficulties of curve adjustment in non-linear problems is that multiple solutions can fit the results, while in reality, only one solution is correct. The reason behind that is that the least sum of the squared errors represents a local minimum rather than an overall minimum. The choice of initial estimates for the parameters also plays an important role in the curve's fit trajectory to a local minimum [19, 20].
Other methods such as Monte Carlo simulation was adopted by Bashiri et al. [1] to study the catalytic transesterification kinetics of soybean oil, methanol and NaOH. On the other hand, Issariyakul et al. [10] used regression and differential equation solvers based on the 4th and 5th orders Runge-Kutta to determine the values of the rate constants of the catalytic transesterification of mustard and palm oils.
Particle Swarm Optimization (PSO), one of the latest metaheuristics that applies the population-based stochastic optimization technique, was originally developed by Kennedy & Eberhart [21].
The particle swarm optimisation (PSO) method has been used in several fields (chemical, thermal). This algorithm is a powerful and stochastic scalable computation method that can be used to find the global optimum in a complex search space. It is easier to implement and has faster convergence than other scalable methods, such as genetic algorithm (GA), insofar as it does not use any evolutionary operator, such as crossbreeding and mutation. In addition, the PSO is robust and requires fewer parameters and computing memory [22], well suited for solving non-linear and non-convex systems. Compared to other optimization methods, the PSO is more efficient, requiring fewer functions and gives faster convergence and better results, it is a population-based algorithm, it can be parallelized efficiently in order to reduce the computing time [23, 24, 25, 26]. The methods used in the kinetics of transesterification reaction, like the linear equation and iterative methods depend on the initial solution and a convergence towards non-optimum solutions is highly probable.
For the best knowledge of authors, this method has never been used to study the kinetics of transesterification, although its powerful algorithm. For this purpose, the PSO method was applied, in the present work, for the determination of the kinetic parameters (Ea, A, n) of the transesterification reaction in 3 reversible steps based on experimental results. The biodiesel considered in this study was prepared from rapeseed oil.
2. Materials and methods
2.1. Raw materials
The raw material used in the experiments is commercial rapeseed oil. Its fatty acid composition is shown in Table 1.
Table 1.
Characteristics of rapeseed oil.
| Properties | |
| Viscosity | 28.7 mPas (45 °C) |
| 22.8 mPas (55 °C) | |
| 17.1 mPas (65 °C) | |
| Dansity | 0.850 kg/l |
| Acid number | 1.10 mgKOH/g |
| Water content | nd |
| Composition | |
| Fatty acid | Content (% wt/wt) |
| Oleic (18:1) | 60 |
| Linoleic (18:2) | 22 |
| Linolenic (18:3) | 8.4 |
| Palmitic (16:0) | 4.2 |
| Gondoic (20:1) | 2.1 |
| Stearic (18:0) | 1.6 |
| Arachidic (20:0) | 0.4 |
| Euric (22:1) | 0.5 |
| Behenic (22:0) | 0.3 |
| Palmitoleic (16:1) | 0.1 |
| Ecosadiensic (20:1) | 0.1 |
The reagents selected for this study are: commercial methanol with a purity of 98% purchased from Prolabo Chemicals and commercial potassium hydroxide having a purity of 85%, purchased from Acros.
In order to stop the transesterification reaction within samples, hydrochloric acid 1N and tetrahydrofuran (THF) purchased from Pprolabo and Aacros respectively, were used.
The standard solutions used for GC-FID calibration and for the determination of free and total glycerine according to ASTMD 6584 were:
triolein, diolein, monolein, glycerin as standards and 1,2,4-butantriol, 1,2, 3-tridecanol glycerol (tricaprine) as internal standards 1 and 2 respectively and N-methyl-N- (trimethylsilyl) trifluoroacetamide (MSTFA) were purchased from Sigma Aldrich
2.2. Experimental methodology
The experimental study was carried out in a batch reactor (Fig. 2) using a 500 ml flask (1), filled with reagents (oil, alcohol, and catalyst). The reactor was sealed with rubber stoppers, to prevent evaporation of methanol, and immersed in a thermostatic water-bath (2). Stirring is applied using a magnetic rod and an agitator (3).
Fig. 2.
Experimental setup.
Initially, 200 g of oil are poured in the flask and heated to the desired reaction temperature (45, 55, 65 °C), while the rotational speed of the mixer was fixed to 600 rpm. At the same time, a mixture of methanol and KOH is prepared using an alcohol: oil molar ratio of (6:1) and 1wt % of KOH catalyst, before being mixed with the oil. The molar ratio (6:1) and the amount of catalyst at 1wt % of oil, were chosen based on earlier studies [9].
In order to determine the evolution of the reaction and the composition of chemical species in the mixture, 5 ml samples were taken at different times of the reaction (1, 2, 3, 4, 5, 6, 8, 10, 15, 25, 35, 45, 55, 65, 90 and 120 min), and poured on an ice cooled mixture of 1 ml of 1 N hydrochloric acid and 5 ml of tetrahydrofuran in order to stop the reaction. The hydrochloric acid was used to neutralize the catalyst and KCl, produced during reaction, precipitates in the bottom. A centrifugation step follows to separate the aqueous phase from organic phase, the latter will be stored at -20 °C before analysis [27].
Collected samples were analysed using an Agilent 7820A type gas chromatograph coupled with a flame ionization detector (GC-FID) to determine the concentrations of TG, MG, DG and GL. The column contains 5% phenylpolydimethylsiloxane (15 m × 0.32 mm, film thickness 0.1 μm). The operating conditions are summarized in Table 2. The apparatus was calibrated according to ASTM D 6584 before analysis.
Table 2.
Operating conditions for Glycerides detection.
| Injector | ||
| Cool on column injection | ||
| Sample size | 1 μl | |
| Column temperature program | ||
| Initial temperature | 50 °C | hold 1 min |
| Rate 1 | 15 °C/min to 180 °C | |
| Rate 2 | 7 °C/min to 230 °C | |
| Rate 3 | 30 °C/min to 380 °C | hold 10 min |
| Detector | ||
| Type | Flame ionization | |
| Temperature | 380 °C | |
| Carrier gas | ||
| Type | helium | Measured at 50 °C |
| Flow rate | 3 ml/min | |
The fatty acid methyl esters profile was analysed using the Perkin Elmer CLARUS 600 mass spectrometer coupled to a gas chromatograph and flame ionization detector (GCMS-FID). An Agilent SLB-5MS column (30 m × 0.250 mm, film thickness 0.25 μm) was used. The operating conditions are summarized in Table 3.
Table 3.
Operating conditions for methyl esters analysis.
| Injector | ||
| Cool on column injection | ||
| Sample size | 1μl | |
| Column temperature program | ||
| Initial temperature | 70 °C | hold 1 min |
| Rate 1 | 12 °C/min to 180 °C | |
| Rate 2 | 7 °C/min to 240 °C | |
| Rate 3 | 12 °C/min to 330 °C | hold 6.76 min |
| Detector | ||
| type | Flame ionization | |
| temperature | 380 °C | |
| Carrier gas | ||
| Type | helium | Measured at 50 °C |
| Flow rate | 1 ml/min | |
2.3. Kinetic model
2.3.1. Mechanism of reaction
The global catalytic transesterification reaction is modelled by a series of 3 reversible reactions as presented in eqs. (1), (2), (3) [20]. To simplify the representation, the molar concentrations of TG, DG, MG, ME, GL and AL species will be designated as C1, C2, C3, C4, C5 and C6 respectively.
| (1) |
| (2) |
| (3) |
The rate of each reaction is given by a first order ordinary differential equation (ODE). The system of ODEs is written in the form of Eq. (4).
| (4) |
With:
The estimation of the rate constants kj, is based on the resolution of the ODEs. The results thus obtained will be compared with the experimental data of the transesterification under constant temperatures. The optimization of the estimation of the constants kj is carried out using PSO, known for its robustness, its precision and its speed. The six rate constants (k1 to k6) are estimated by minimizing the following objective function:
| (5) |
where N is the number of analysed samples. is the molar concentration of species i, determined experimentally at the time tk. The concentration of alcohol (C6) was not measured experimentally. It will be determined by deduction. and are the maximum and minimum values respectively. is the molar concentration of specie i, at the time tk, calculated after each estimation of the rate constants kj.
2.3.2. PSO method
PSO method is a stochastic optimization approach, which maintains a swarm of J candidate solutions. Each candidate solution Sj is, in turn, a population of I particles xi,j. Each particle is animated with a velocity vi,j. The global swarm, composed of particles xi,j, can be represented graphically in Fig. 3 by circular crowns (I) of radii and .
Fig. 3.
Instant distribution of swarm particles.
Each particle xi, j is defined by its position vector Ri, j and its instantaneous speed vi, j. The best candidate solution (Sj, best) of the swarm, which optimizes the objective function of the problem, is identified and saved as the best global system solution (Gbest).
The particles, whose positions (xi, j) and velocities (vi, j) are initially generated randomly, are "transported" through the space of the ith circular crown, searching a better position. Updating the positions of particles consists in determining the position of the particle (xi, j) at the instant (t + 1) as a function of its position at the time (t). It is modelled by the following formula:
| (6) |
This new position is adjusted by the updated stochastic speed , which is given by the following formula:
| (7) |
where ; and .The updated speed at the time (t + 1) depends on its current speed , the best position recorded by the particle itself and the position of the particle constituting the best solution among its neighbourhood . Fig. 4 shows position (Eq. (6)) and velocity (Eq. (7)) updates of the particle .
Fig. 4.
Updates of the velocity and position of the particle j of the swarm i.
In addition, in Eq. (7), and ; where c1 and c2 are respectively the cognitive and the social acceleration constants while and are random numbers between 0 and 1.
The population is evaluated by the fitness function. In most cases, greater individual's fitness value indicates the individual's higher ability to adapt to the environment. Here, the fitness value is the error between experimental and calculated concentration (Eq. (5)). The best solution is obtained when smallest total error is reached.
The pseudocode of PSO algorithm is presented in Fig. 5. It shows that for each iteration, the swarm, as well as the positions and the speeds of particles, are initialized. The best position seen by the particle itself (Pbest) and the particle occupying the best position in the swarm (Gbest) will also be updated.
Fig. 5.
Pseudocode of PSO algorithm.
The convergence of the calculations is ensured by setting tolerance between the value of the objective function computed at the current iteration (t) and the iteration (t-200). Iterations stop if the tolerance is less than 10−12 or the maximum number of iterations (iter) is reached [28].
Taking into account the unknown final iteration value on one hand, and the need to iterate on the whole interval of inertia weight on the other hand, the current value is calculated at each iteration using the following sinusoidal equation:
| (8) |
The PSO stability and the convergence of the system towards an equilibrium point are ensured only if the following conditions are satisfied [23, 29].
| (9) |
Furthermore, empirical results have shown that a constant inertia ω = 0.7298 and an acceleration coefficient c1 = c2 = 1.49618 provide good convergence in the resolution and optimization of systems proven in the literature and our system [30, 31].
Tables 4 and 5: summarize the various parameters of PSO, used to estimate the rate constants and the kinetic triplets.
Table 4.
Limit values [xmin, i, xmax, i] particle positions in swarms.
| ith parameters | ki [mol.s−1] | Ln(Ai) | Ei[J.mol-1.K−1] | ni |
|---|---|---|---|---|
| 1st parameters | [0.01,10] | [1.27.10−6, 786164.20] | [-120.103, 120.103] | [0.5, 10] |
| 2nd parameters | [0.01,10] | [1.27.10−6, 786164.20] | [-120.103, 120.103] | [0.5, 10] |
| 3th parameters | [0.01,10] | [1.27.10−6, 786164.20] | [-120.103, 120.103] | [0.5, 10] |
| 4th parameters | [0.01,10] | [1.27.10−6, 786164.20] | [-120.103, 120.103] | [0.5, 10] |
| 5th parameters | [0.01,10] | [1.27.10−6, 786164.20] | [-120.103, 120.103] | [0.5, 10] |
| 6th parameters | [0.01,10] | [1.27.10−6, 786164.20] | [-120.103, 120.103] | [0.5, 10] |
| Iterations (iter) | 1500 | 3000 | ||
| Populations (J) | 1000 | 200 | ||
| Parameters (I) | 6 | 3 | ||
Table 5.
PSO program parameters.
| C1 | C2 | ωmin | ωmax | vmax,i |
|---|---|---|---|---|
| 1.49618 | 1.49618 | 0.5 | 0.9 | 0.2*(xmax,i - xmin,i) |
2.3.3. Estimation of kinetic parameters
As noticed previously, the estimation of the rate constants kj, is based on the resolution of the previous ODEs (Eq. (4)). Two steps are hence considered.
Step 1
The concentrations of species are calculated by discretizing the ODEs of Eq. (4) using the Runge-Kutta method of order 4 (RK-4). The resolution is initiated by the initial solution , which is derived from the experiment. It is equal to for triglyceride (C1), 6*for alcohol (C6) and zero for the other species (C2 to C5).
Step 2
The rate constants of different reactions were determined at different temperatures (Tm). The evolution of each constant as a function of temperature (kj (T)) serves as a datum point to estimate again the kinetic triplet of each reaction (Aj, Ej et nj).
Several studies have shown that the rate constant of a chemical reaction is modelled using Arrhenius law. In this study, it will be modelled by the modified Arrhenius law, given by the following formula [20]:
| (10) |
Similarly, the kinetic triplet of each reaction, namely the pre-exponential factor (Aj), the activation energy (Ej) and the degree (nj), will also be estimated using the PSO method, by minimizing the following objective function:
| (11) |
M is the number of temperature levels (three in this study) at which the constants kj have been determined. is the rate constant of the jth reaction, determined precisely at the temperature Tm (step 1). is the rate constant of the jth reaction, calculated at the temperature Tm using Eq. (10), after each estimation of the kinetic triplet Aj, Ej et nj.
3. Results and discussion
3.1. Validation of PSO algorithm
In order to validate the PSO calculation algorithm, it was applied to determine the transesterification kinetics based on the experimental work of Noureddini et al. [26]. The calculated kinetic parameters were compared to the simulated results reported by Bashiri et al. [1]. These authors have adopted the Monte Carlo method to model the transesterification reaction based on experimental results of Noureddini et al. [26]. Table 6 shows a comparison between K values determined by PSO method (present work) and those calculated by Bashiri et al. [1]. A slight difference can be observed for K1 and K6, however significant variations are noticed for K2, K4 and K5, which appears clearly in the deviation with respect to experimental data [26].
Table 6.
The kinetic parameters of methanolysis of soybean oil in presence of NaOH.
On the Fig. 6 are represented the calculated concentrations, by PSO (present work) and Monte Carlo (Bashiri et al. [1]) methods, of glycerol (Fig. 6a) and methyl ester (Fig. 6b). The calculated values are compared to the experimental results [26]. It is clear that values obtained with PSO method are closer to the experimental concentrations.
Fig. 6.
Comparison of the calculated concentrations (present work, Bashiri et al. [1]) with the experimental values [26]. (a) Glycerol; (b) Methyl ester.
The error estimated by the objective function (5) was less than 1% while this error is about 3 % for [1]. This result shows the robustness of the PSO method for optimization and the convergence of the rate constants values which reflects a perfect concordance of the numerical results with the experimental ones.
The optimization of these parameters makes it possible to size the chemical reactor with high accuracy. For this, the use of an optimizer allows to size the reactor with fewer errors. The larger the error, the more oversized the reactor will be, which will affect the investment, maintenance and energy costs spent during the reaction [32].
3.2. Application of PSO method to rapeseed oil transesterification
In this section, PSO method is used to estimate the kinetic and energetic parameters of the transesterification reaction of rapeseed oil, performed in this study. Transesterification experiments were carried out according to the procedure and operating conditions presented previously (§ 2.2). Table 7 presents the kinetic parameters determined for the three considered temperatures, namely, 45, 55 and 65 °C. In this study the best fit was found with n = 1 for the modified Arrhenius law.
Table 7.
The kinetic parameters of rapeseed oil transesterification in presence of KOH.
| Steps | K (L/mol.min) |
A (L/mol.min) | Ea (kJ/mol) | ||
|---|---|---|---|---|---|
| 45 °C | 55 °C | 65 °C | |||
| 0.0772 | 0.1129 | 0.2497 | 6.12 × 105 | 57.800 | |
| 0.1850 | 0.0928 | 0.0586 | 2.13 × 10−13 | 57.472 | |
| 0.07103 | 0.1038 | 0.1912 | 5.88 × 103 | 45.476 | |
| 0.1098 | 0.0778 | 0.0744 | 8.40 × 106 | 21.942 | |
| 0.107315 | 0.1216 | 0.2197 | 1.44 × 102 | 34.708 | |
| 0.00942 | 0.0065 | 0.00171 | 6.62 × 103 | 5.358 | |
Figs. 7 and 8 show the evolution of calculated concentrations of TG, MG, DG, GL and ME in comparison with experimental results at 45 and 65 °C respectively. We can observe a good agreement between simulated values by PSO method and experimental ones. The relative error is about 0.05% for all the species calculated using the objective function (Eq. (5)).
Fig. 7.
Experimental and simulated data of triglyceride (TG: ▲), monoglyceride (MG: *), diglyceride (DG: ♦), glycerol (GL: ■) and methyl ester (ME:•) concentrations during reaction. (KOH: 1wt%, temperature: 45 °C, rate of stirring: 600 rpm).
Fig. 8.
Experimental and simulated data of triglyceride (TG: ▲), monoglyceride (MG: *), diglyceride (DG: ♦), glycerol (GL: ■) and methyl ester (ME:•) concentration during reaction. (KOH 1wt%, temperature 65 °C, rate of stirring 600 rpm).
It can be noticed that the evolutions of ME and GL follow a sigmoidal curve shapes (Figs. 7 and 8). This behaviour is explained by a slow reaction rate followed by a sudden increase before slowing down again at the end of reaction. In fact, the first step is a slow phase which is controlled by mass transfer between the two immiscible phases (oil and alcohol) while the second one is fast and controlled chemically, where the reaction medium is homogeneous. The last step is a slow equilibrium regime during the completion of the reaction where a two-phase system (biodiesel and glycerol) is established again [20].
In addition, the amount of DG and MG increases in the 5 min following the beginning of reaction then it decreases until equilibrium. On the other hand, the concentration of TG decreases rapidly until equilibrium. The temperature increase enhances the transesterification reaction and shortens the conversion time. The results show that conversion rate reaches an asymptote after respectively 35, 45 and 55 min at 65, 55 and 45 °C, respectively. Furthermore, the Figs. 7 and 8) show a perfect concordance between the experimental and simulated data. Consequently, the mechanism with 3 steps coupled to Arrhenius law kinetics simulates transesterification reaction of rapeseed oil with high accuracy.
3.3. Effect of operating conditions
3.3.1. Effect of temperature on the reaction
The effect of temperature on the transesterification rate of rapeseed oil in the presence of KOH was studied. Different temperatures were selected (25 °C, 35 °C, 45 °C, 55 °C and 65 °C) to approximate this effect on yield. Fig. 9 represents the simulation of the effect of temperature on the concentration of the methyl ester. The initial data entry was [TG]0 = 0.74 mol/l, [CH3OH]0 = 6 [TG]0 and 1wt% KOH.
Fig. 9.
Temperature effect on the concentration of methyl ester with time (KOH 1wt%, rate of stirring 600 rpm).
The simulation was carried out by calculating the constants at temperatures ranging from 25 to 65 °C with a step of 10 °C using modified Arrhenius equation (Eq. (10) and Table 7).
The maximum yield of methyl ester (99.9%) was reached after 2 hours of reaction at 65 °C. The yield is calculated using Eq. (12).
Temperature has a direct influence on the advancement of the reaction through the Arrhenius law rate constants (Eq. (10)). When the temperature increases, the conversion rate of oil into methyl esters increases (Table 8).
| (12) |
Where:
Table 8.
The simulation results of transesterification of rapeseed oil in presence of KOH at different temperatures.
| Temperature | Yield (%) |
|||
|---|---|---|---|---|
| 3 (min) | 10 (min) | 30 (min) | 60 (min) | |
| 25 °C | 4 | 18 | 27 | 36 |
| 35 °C | 11 | 35 | 47 | 53 |
| 45 °C | 15 | 48 | 59 | 67 |
| 55 °C | 24 | 59 | 77 | 86 |
| 65 °C | 27 | 80 | 97 | 99 |
, and are initial mole numbers of TG, DG, and MG. at t = 0 min , and are the instantaneous mole numbers of TG, DG, and MG at the moment t of the reaction. The equation becomes
| (13) |
3.3.2. Effect of oil to methanol feed ratio on the reaction
Regarding the alcohol: oil molar ratio, its effect was examined based on the reaction mechanism determined previously. Theoretically, the transesterification reaction requires three moles of methanol to convert one mole of triglycerides to methyl ester. Since the reaction is carried out in three reversible stages, to favour and increase the conversion rate by the Chatelier principle, an excess of alcohol must be added to the reaction mixture.
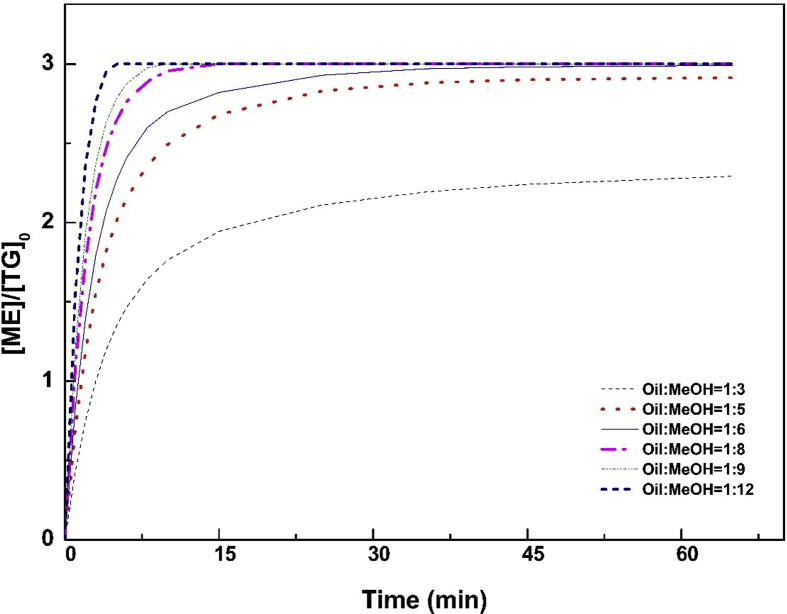
As it can be seen from Fig. 10. The simulation of the effect of methanol on the rate of reaction was realised with initial data input [TG]0 = 0.74 mol/l, [CH3OH] = 6*[TG]0 and 1wt% of KOH at 65 °C. The yield of ME after 60 minutes increases proportionally with the increase of alcohol excess.
Fig. 10.
Effect of molar ratio on the conversion of methyl ester (KOH 1%.wt, temperature 65 °C, rate of stirring 600 rpm).
For methanol: oil ratios higher than 6:1, the increase of yield, after 1 h of reaction, is insignificant. For example, by doubling this ratio, the yield increases only by 0.14%. Moreover, the presence of excess alcohol makes the separation of the methyl ester-glycerine phases more difficult. Based on this observation. The methanol to oil ratio of 6:1 was adopted as optimal (see Table 9).
Table 9.
The simulation results of transesterification of rapeseed oil in presence of KOH at different oil to methanol feed ratios.
| Oil: MeOH | yield |
|||
|---|---|---|---|---|
| 3 (min) | 10 (min) | 30 (min) | 60 (min) | |
| 1:3 | 14.17 | 48.86 | 70.35 | 76.40 |
| 1:5 | 23.08 | 71.76818 | 94.25455 | 97.04 |
| 1:6 | 27.40 | 80.23182 | 97.57727 | 99.65 |
| 1:8 | 35.80 | 91.99 | 99.04 | 99.85 |
| 1:9 | 39.80 | 95.85 | 99.5 | 99.90 |
| 1:12 | 51.30 | 99.80 | 99.99 | 99.99 |
The simulation of the molar ratio effect makes it possible to optimize the amount of alcohol and the reaction time. The optimum amount of alcohol is (1: 6) for a reaction time of 60 min in order to have a conversion rate equal to 99 %.
4. Conclusions
In this work, a modified particle swarm optimization method (PSO) was applied to determine the transesterification kinetics of rapeseed oil with methanol in the presence of 1 wt% KOH catalyst.
The validation of the PSO program was performed by comparing obtained results with published numerical and experimental data. The calculated error was 4 times lower than that obtained by Monte Carlo method.
The use of the PSO program as optimizer allows a perfect fit with the experimental data, with estimation errors lower than 0.05%. This error margin allows a precise dimensioning of the transesterification reactor
The evolution of the concentration of chemical species during transesterification reaction was predicted by the proposed 3-steps kinetic model.
The study of temperature influence on the rate constants showed that they tend to increase for the direct reactions and to decrease for the reverse ones. The maximum yield of ME and the conversion rate of TG were recorded at a temperature of 65 °C.
The mechanism and kinetic parameters for a temperature of 65 °C were used in the simulation of the influence of the molar ratio on the transesterification reaction rate. The optimum ratio of methanol: oil was 6:1 which gave a 99% conversion.
Declarations
Author contribution statement
Mohamed Kadi: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Naïm Akkouche: Analyzed and interpreted the data.
Sary Awad, Khaled Loubar: Conceived and designed the experiments; Analyzed and interpreted the data.
Mohand Tazerout: Conceived and designed the experiments.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Bashiri H., Pourbeiram N. Biodiesel production through transesterification of soybean oil: a kinetic Monte Carlo study. J. Mol. Liq. 2016;223:10–15. [Google Scholar]
- 2.Ito T., Sakurai Y., Kakuta Y., Sugano M., Hirano K. Biodiesel production from waste animal fats using pyrolysis method. Fuel Process. Technol. 2012;94:47–52. [Google Scholar]
- 3.Abdelfattah M.S.H., Abu-Elyazeed O.S.M., Abd El mawla E., Abdelazeem M.A. On biodiesels from castor raw oil using catalytic pyrolysis. Energy. 2018;143:950–960. [Google Scholar]
- 4.Liu Y., Tu Q., Knothe G., Lu M. Direct transesterification of spent coffee grounds for biodiesel production. Fuel. 2017;199:157–161. [Google Scholar]
- 5.Marso T.M.M., Kalpage C.S., Udugala-Ganehenege M.Y. Metal modified graphene oxide composite catalyst for the production of biodiesel via pre-esterification of Calophyllum inophyllum oil. Fuel. 2017;199:47–64. [Google Scholar]
- 6.de Luna M.D.G., Cuasay J.L., Tolosa N.C., Chung T.W. Transesterification of soybean oil using a novel heterogeneous base catalyst: synthesis and characterization of Na-pumice catalyst, optimization of transesterification conditions, studies on reaction kinetics and catalyst reusability. Fuel. 2017;209:246–253. [Google Scholar]
- 7.Yunus N.B.M., Roslan N.A.B., Yee C.S., Abidin S.Z. Esterification of free fatty acid in used cooking oil using gelular exchange resin as catalysts. Proc. Eng. 2016;148:1274–1281. [Google Scholar]
- 8.Stojković I.J., Stamenković O.S., Povrenović D.S., Veljković V.B. Purification technologies for crude biodiesel obtained by alkali-catalyzed transesterification. Renew. Sustain. Energy Rev. 2014;32:1–15. [Google Scholar]
- 9.Rashid U., Anwar F. Production of biodiesel through optimized alkaline-catalyzed transesterification of rapeseed oil. Fuel. 2008;87:265–273. [Google Scholar]
- 10.Issariyakul T., Dalai A.K. Comparative kinetics of transesterification for biodiesel production from palm oil and mustard oil. Can. J. Chem. Eng. 2012;90:342–350. [Google Scholar]
- 11.Kanda L.R.S., Corazza M.L., Zatta L., Wypych F. Kinetics evaluation of the ethyl esterification of long chain fatty acids using commercial montmorillonite K10 as catalyst. Fuel. 2017;193:265–274. [Google Scholar]
- 12.Ma Y., Wang Q., Sun X., Wu C., Gao Z. Kinetics studies of biodiesel production from waste cooking oil using FeCl3-modified resin as heterogeneous catalyst. Renew. Energy. 2017;107:522–530. [Google Scholar]
- 13.Ye W., Gao Y., Ding H., Liu M., Liu S., Han X. Kinetics of transesterification of palm oil under conventional heating and microwave irradiation, using CaO as heterogeneous catalyst. Fuel. 2016;180:574–579. [Google Scholar]
- 14.Li Y., Du W., Dai L., Liu D. Kinetic study on free lipase NS81006-catalyzed biodiesel production from soybean oil. J. Mol. Catal. B Enzym. 2015;121 [Google Scholar]
- 15.Berchmans H.J., Morishita K., Takarada T. Kinetic study of hydroxide-catalyzed methanolysis of Jatropha curcas-waste food oil mixture for biodiesel production. Fuel. 2013;104:46–52. [Google Scholar]
- 16.Ramezani K., Rowshanzamir S., Eikani M.H. Castor oil transesterification reaction: a kinetic study and optimization of parameters. Energy. 2010;35:4142–4148. [Google Scholar]
- 17.Karmee S.K., Mahesh P., Ravi R., Chadha A. Kinetic study of the base-catalyzed transesterification of monoglycerides from pongamia oil. J. Am. Oil Chem. Soc. 2004;81:425–430. [Google Scholar]
- 18.Janajreh I., Elsamad T., Aljaberi A., Diouri M. Transesterification of waste cooking oil: kinetic study and reactive flow analysis. Energy Proc. 2015;75:547–553. [Google Scholar]
- 19.Leevijit T. A second order kinetics of palm oil transesterification. Sustain. Energy. 2004;025:277–281. [Google Scholar]
- 20.Noureddini H., Zhu D. Kinetics of transesterification of soybean oil. J. Am. Oil Chem. Soc. 1997;74:1457–1463. [Google Scholar]
- 21.Kennedy J., Eberhart R. 1995. Particle Swarm Optimization; pp. 1942–1948. [Google Scholar]
- 22.Guner A.R., Sevkli M. 2008. A Discrete Particle Swarm Optimization Algorithm for Uncapacitated Facility Location Problem 2008. [Google Scholar]
- 23.Guo Z., Chen L., Chen W. Chemical engineering research and design estimation of kinetic parameters from adiabatic calorimetric data by a hybrid particle swarm optimization method. Chem Eng Res Des. 2017;122:273–279. [Google Scholar]
- 24.Liu P., Liu J. Multi-leader PSO (MLPSO): a new PSO variant for solving global optimization problems. Appl. Soft Comput. J. 2017;61:256–263. [Google Scholar]
- 25.Yang J., Lu L., Ouyang W., Gou Y., Chen Y., Ma H. Estimation of kinetic parameters of an anaerobic digestion model using particle swarm optimization. Biochem. Eng. J. 2017;120:25–32. [Google Scholar]
- 26.Xu L., Jiang Y., Wang L. Thermal decomposition of rape straw: pyrolysis modeling and kinetic study via particle swarm optimization. Energy Convers. Manag. 2017;146:124–133. [Google Scholar]
- 27.Meher L.C., Vidya Sagar D., Naik S.N. Technical aspects of biodiesel production by transesterification - a review. Renew. Sustain. Energy Rev. 2006;10:248–268. [Google Scholar]
- 28.Hoang T.T., Cho M.Y., Alam M.N., Vu Q.T. A novel differential particle swarm optimization for parameter selection of support vector machines for monitoring metal-oxide surge arrester conditions. Swarm Evol. Comput. 2017;38:120–126. [Google Scholar]
- 29.Perez R.E., Behdinan K. Particle swarm approach for structural design optimization. Comput. Struct. 2007;85:1579–1588. [Google Scholar]
- 30.Bergh F. Van Den, Engelbrecht A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006;176:937–971. [Google Scholar]
- 31.Eberhart R.C., Shi Y. Comparing inertia weights and constriction factors in particle swarm. Optimization. 2000;1:84–88. [Google Scholar]
- 32.Enscp I., Nationale É., Chimie S De. 2019. Réacteurs Chimiques - Technologie Réacteurs Chimiques; p. 33. [Google Scholar]