Preload Sensitivity with TORVAD Counterpulse Support Prevents Suction and Overpumping

Abstract

Purpose:

This study compares preload sensitivity of continuous flow (CF) VAD support to counterpulsation using the Windmill toroidal VAD (TORVAD). The TORVAD is a two-piston rotary pump that ejects 30 ml in early diastole, which increases cardiac output while preserving aortic valve flow.

Methods:

Preload sensitivity was compared for CF vs TORVAD counterpulse support using two lumped parameter models of the cardiovascular system: 1) an open-loop model of the systemic circulation was used to obtain ventricular function curves by isolating the systemic circulation and prescribing preload and afterload boundary conditions, and 2) a closed-loop model was used to test the physiological response to changes in pulmonary vascular resistance, systemic vascular resistance, heart rate, inotropic state, and blood volume. In the open-loop model, ventricular function curves (cardiac output vs left ventricular preload) are used to assess preload sensitivity. In the closed-loop model, left ventricular end systolic volume is used to assess the risk of left ventricular suction.

Results:

At low preloads of 5 mmHg, CF support overpumps the circulation compared to TORVAD counterpulse support (cardiac output of 3.3 L/min for the healthy heart, 4.7 with CF support, and 3.5 with TORVAD counterpulse support) and has much less sensitivity than counterpulse support (0.342 L/min/mmHg for the healthy heart, 0.092 with CF support, and 0.306 with TORVAD counterpulse support). In the closed-loop model, when PVR is increased beyond 0.035 mmHg s/ml, CF support overpumps the circulation and causes ventricular suction events, but TORVAD counterpulse support maintains sufficient ventricular volume and does not cause suction.

Conclusions:

Counterpulse support with the TORVAD preserves aortic valve flow and provides physiological sensitivity across all preload conditions. This should prevent overpumping and minimize the risk of suction.

INTRODUCTION

Ventricular assist devices (VADs) are implanted to restore the cardiac output deficiency in patients with end-stage congestive heart failure when pharmaceutical approaches have been exhausted or when donor hearts for transplantation are not available. Adoption of this technology has increased rapidly over the last decade, but VAD implant rates have begun to plateau in recent years due to the persistence of major adverse events such as bleeding, infection, stroke, and right heart failure(l). Virtually all implanted VADs are continuous flow (CF) devices, either axial flow pumps like the Abbott HeartMate II (HMII) or centrifugal flow pumps like the Medtronic HVAD and Abbott HeartMate 3 (1). While the primary purpose of a VAD is to increase cardiac output, VADs should also ideally restore a physiological response to metabolic demand which can vary throughout the day depending on the patient’s activity level or physiological status.

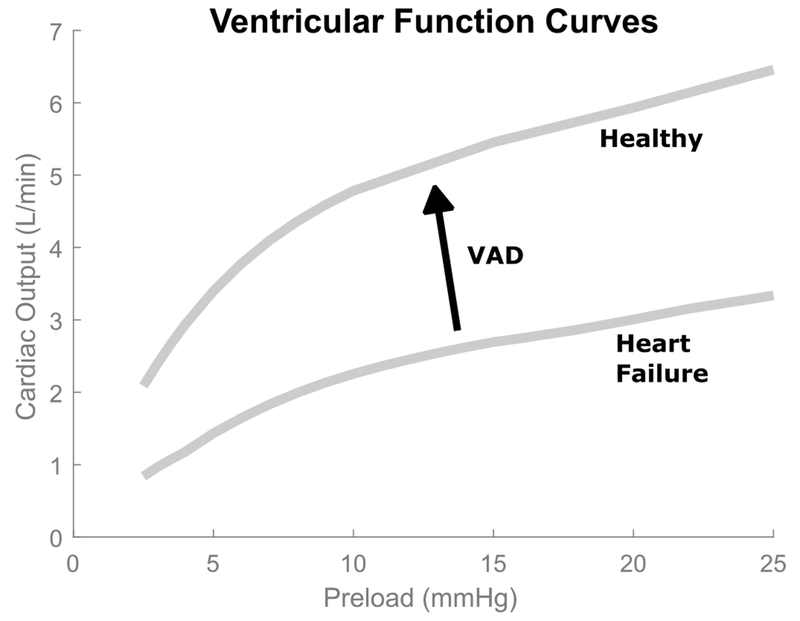
The cardiovascular system has many complex passive and active autoregulatory pathways for cardiac output (2). Of particular interest in this study is the Starling response whereby the ventricle adjusts cardiac output in response to changes in ventricular preload (3). In Starling’s seminal work on ventricular autoregulation in intact hearts (4), he studied the relationship between cardiac output and ventricular preload using excised canine hearts, and produced the first so-called Starling curves that demonstrated a highly nonlinear relationship between ventricular preload and cardiac output (see Figure 1). In heart failure, cardiac output decreases. Ventricular assist devices increase cardiac output but they should also ideally preserve the nonlinear Starling response.

Figure 1.

Ventricular function curves illustrate the nonlinear relationship between cardiac output and left ventricular preload. In heart failure, cardiac output (CO) is decreased. Ventricular assist devices (VADs) are implanted to boost CO. Ideally, they would also restore the nonlinear CO response to ventricular preload.

Continuous flow devices are well known to be insensitive to ventricular preload. It has been estimated that CF devices have 30-50% the preload sensitivity compared to a healthy heart (5,6). This creates impaired autoregulation of cardiac output that is significantly altered and non-physiological (7). Left-to-right flow balancing issues and left ventricular overpumping can quickly lead to suction events, ventricular septal wall deviations, pulmonary edema, tricuspid valvular regurgitation, arrhythmias, and if sustained, aortic valve leaflet fusion, right heart dysfunction, and ultimately right heart failure in 10-30% of patients (8,9). These conditions create a difficult clinical balancing act involving control of systemic vascular resistance and intravascular fluid volume with vasodilator and inotropic medications in an attempt to adjust left ventricular output and reduce ventricular suction events and maintain viable right ventricular function (10).

This study compares preload sensitivity of CF support to counterpulsation using the Windmill toroidal VAD (TORVAD). The TORVAD is a positive-displacement pump that produces 30 ml ejections by independently controlling two pistons within a toroidal pump chamber (11). The device is synchronized to the cardiac cycle using an integrated electrocardiogram (ECG) lead to detect ventricular depolarization (12). The primary operating mode of the TORVAD is a synchronous counterpulse in early diastole, which increases cardiac output while preserving aortic valve flow and provides ventricular unloading comparable to CF devices (12). The TORVAD flow rate in synchronous mode is a function of heart rate alone and is not itself sensitive to preload or afterload, but the preserved aortic valve flow that results from counterpulse support is generated by remaining left ventricular function, which is physiologically sensitive to changes in ventricular preload and afterload. Understanding how the positive displacement TORVAD ejection and the left ventricle work together by quantifying the combined response to preload and comparing it to the current standard of care is the purpose of this paper.

METHODS

Lumped parameter models of the cardiovascular system are routinely used to simulate the hemodynamics that result from VAD support (13). The models have few terms, which makes parameterization relatively straightforward. Additionally, models consist of simple ordinary differential equations, so they can be solved very quickly, which allows many different variations in physiologic properties or levels of assist to be modeled.

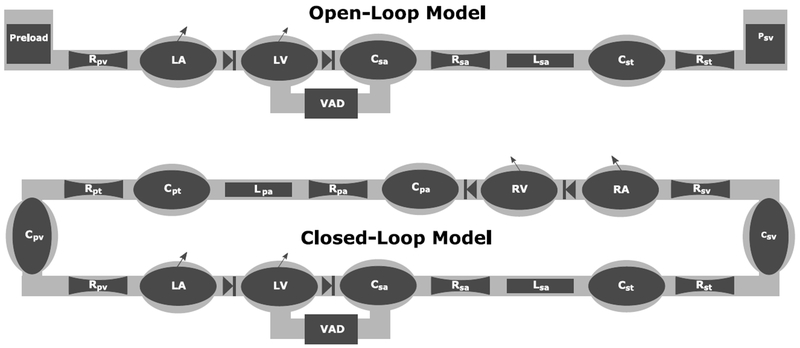
Two models were used to study the Starling response of the cardiovascular system with CF and TORVAD synchronous counterpulsation. First, an open-loop simulation of the systemic circulation was used to obtain ventricular function curves by isolating the systemic circulation and directly prescribing preload and afterload boundary conditions. Second, a closed-loop simulation that includes the pulmonary circulation was used to study the hemodynamic effects and risk of suction caused by changes to pulmonary vascular resistance, systemic vascular resistance, heart rate, inotropic state, and blood volume. These model schematics are illustrated in Figure 2. A previously validated lumped parameter model was used as a framework (12,14). Details of the model are described in the Appendix.

Figure 2.

Schematic representations of the open-loop and closed-loop cardiovascular system models. The open-loop model directly prescribes the preload and afterload boundary conditions. The closed-loop model is used to study specific conditions such as high pulmonary vascular resistance. The systemic circulation includes left atrium (LA), left ventricular (LV), systemic arteries (sa), systemic arterial tree (st), and systemic veins (sv). The pulmonary circulation includes the right atrium (RA), right ventricle (RV), pulmonary arteries (pa), pulmonary artery tree (pt), and pulmonary vein (pv). The model consists of various compliant (C), resistive (R), and inertial (L) elements. Additional details can be found in previous publications (12,14).

Four different conditions were modeled: healthy, heart failure, heart failure with CF support, and heart failure with TORVAD synchronous counterpulsation. Cardiovascular parameters such as vessel compliance and resistance are provided in the Appendix and previous publications (12,14). Baseline hemodynamics and parameters are shown in Table 1. The continuous flow device was modeled using pressure flow curves for the HMII at 9,000 rotations per minute (rpm). How dynamics caused by the cannula fluid inertance and viscous resistance were also incorporated (12). The TORVAD flow was generated using a prescribed sinusoidal flow rate pulse with a 30 ml stroke volume and with an ejection time of 300 ms in early diastole (12). Early diastole was chosen as the primary operating mode of the device because it maximizes aortic valve flow while providing full support.

Table 1.

Baseline hemodynamic parameters for four simulation conditions: healthy, heart failure (HF), heart failure with continuous flow (CF) support modeled as an axial flow pump at 9,000 rpm, and heart failure with 30 ml TORVAD counterpulse support. Note that the cardiac output increases from 3.8 to 5.3 L/min with both CF and TORVAD support, even though the VAD flow rate is 4.9 L/min for the CF device and only 2.7 L/min for the TORVAD counterpulse device. This is because counterpulse support preserves 2.6 L/min of aortic valve flow by ventricular contraction, while the CF device pumps during systole and therefore diminishes aortic valve flow to 0.4 L/min.

	HR	CO	QVAD	QAO	MAP	LVESV	SW	SVR	PVR
Condition		L/min	L/min	L/min	mmhg	ml	mmHg ml	mmHg s/ml	mmHg s /ml
Healthy	70	5.6	-	5.6	90	92	7768	0.895	0.045
Heart Failure (HF)	90	3.8	-	3.8	70	182	2682	1.010	0.045
HF+CF (9kpm)	90	5.3	4.9	0.4	75	157	2008	0.760	0.045
HF+TORVAD Counterpulse	90	5.3	2.7	2.6	75	164	1859	0.760	0.045

HR heart rate, CO cardiac output, QVAD ventricular assist device mean flow rate, QAO mean flow rate through the aortic valve, MAP mean arterial pressure, LVESV left ventricular end systolic volume, SW stroke work, SVR systemic vascular resistance, PVR pulmonary vascular resistance

For the open-loop simulation, the model was simplified to the systemic circulation only, which was defined to include the pulmonary veins, left atria and ventricle and valves, and the systemic arterial tree consisting of the larger elastic vessels, smaller arterioles, and capillaries. The pulmonary circulation was removed for this simulation, not because its function and response are unimportant, but rather to eliminate it as an additional variable so that the entire possible range of right-sided conditions (for example, elevated pulmonary vascular resistance, right heart failure, or pulmonary edema) could be studied by changing the boundary conditions of the left-sided model.

Ventricular function curves were obtained by varying the preload pressure in the open-loop model from 2 to 25 mmHg in 0.5 mmHg increments at constant afterload resistance listed in Table 1. At each preload pressure, the model was simulated until cycle-to-cycle flows and pressures converged. Once the model stabilized, flow rates were averaged over the final cardiac cycle to assess the metrics of cardiac output, VAD flow, and aortic valve flow.

For the closed-loop simulation, the pulmonary circulation was included so that changes in pulmonary vascular resistance (PVR), systemic vascular resistance (SVR), heart rate (HR), inotropic state, and blood volume could be studied to observe the response with different modalities of ventricular support. Changes in PVR are of particular interest because elevated PVR is common in VAD patients (15) and can also occur during postural changes or the Valsalva maneuver (16,17), and changes in PVR are used in cardiovascular modeling to test the propensity of ventricular suction with VAD support (18–20).

In the closed-loop configuration, each of the four parameters were independently varied from baseline values. Pulmonary vascular resistance was adjusted from 0.02 to 0.50 mmHg s/ml by modifying the resistance of the pulmonary vascular tree (R_pt). Systemic vascular resistance was adjusted from 0.2 to 1.4 mmHg s/ml by changing the resistance of the systemic vascular tree (R_st). Heart rate was adjusted from 40 to 140 beats per minute (bpm) by modifying the RR interval of the simulation. Inotropic state was adjusted from 50% to 150% of the baseline ventricular elastance by scaling the active elastance (E_m) of both left and right ventricular. Finally, blood volume was adjusted by adding and removing up to 750 ml blood volume from the closed loop simulation. All four cardiovascular and support conditions were modeled (healthy, heart failure, CF, and TORVAD counterpulse support). Twenty-five simulations were run for each parameter that was varied using values that were spaced equally between the minimum and maximum described above. For each simulation, the parameter was changed and then the simulation was run until the cycle-to-cycle pressures and flows converged. The primary purpose of this study was to assess whether overpumping occurred for the different types of support. This was assessed by ventricular suction, which was defined as left ventricular volumes less than 15 ml, which is the approximate volume when the ventricular walls could start to be drawn inward past the diameter of the protruding inflow tip. Cardiac output (CO), mean arterial pressure (MAP), and left ventricular end systolic volume (LVESV) were recorded after each simulation converged.

RESULTS

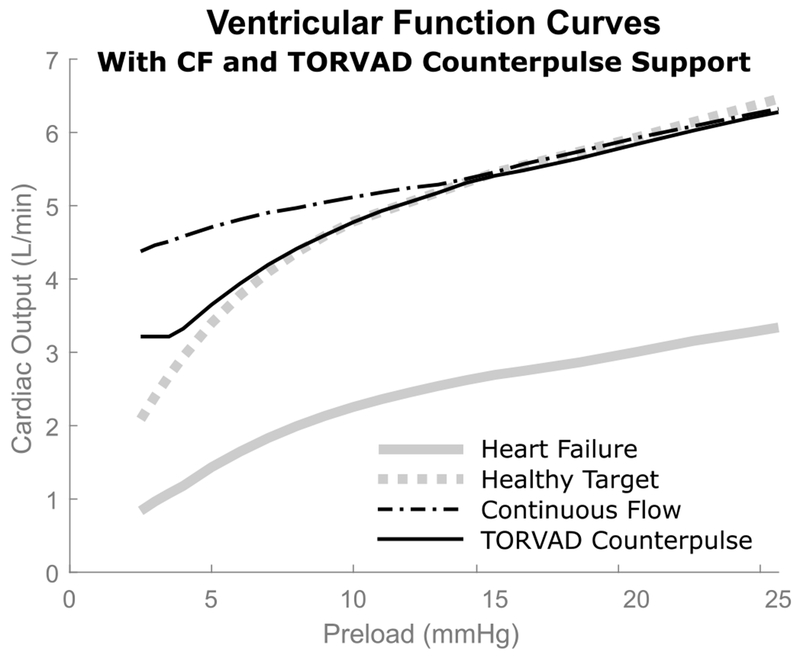
Ventricular function curves are used to quantify the relationship between cardiac output and left ventricular preload at a constant afterload resistance. All four conditions are displayed in Figure 3: healthy; heart failure; heart failure with CF support; and heart failure with TORVAD synchronous counterpulsation. The solid gray line represents the cardiac output response to changes in preload for heart failure and the dashed gray line represents the healthy condition and also provides an ideal target for VAD support. Both the CF device and TORVAD counterpulse support provided a substantial increase in cardiac output, but had different sensitivities depending on preload. Preload sensitivity is quantified by the slope of a tangent line of the ventricular function curve at a specific preload, and is expressed in terms of the change in cardiac output (L/min) per change in pressure (mmHg). Preload sensitivities for all four conditions at preloads of 5, 10, and 20 mmHg are listed in Table 2.

Figure 3.

Simulated ventricular function curves from the open-loop cardiovascular system model with continuous flow (CF) support and TORVAD counterpulse support. As expected, both VADs boost cardiac output back to healthy levels, but the CF device overpumps the circulation at low preloads compared to a normal healthy response. TORVAD counterpulse support does not overpump at low preloads, but follows the healthy nonlinear response.

Table 2.

Preload sensitivity and cardiac output from the open-loop model simulation, reported at three different preload pressures (5, 10, and 20 mmHg) and for all four different conditions simulated (healthy, heart failure, heart failure with continuous flow (CF) support at 9,000 rpm, and heart failure with 30ml TORVAD counterpulse support).

	Preload sensitivity L/min/mmHg			Cardiac Output L/min
	Preload pressure mmHg			Preload pressure mmHg
Condition	20	10	5	20	10	5
Healthy	.084	.170	.342	5.9	4.7	3.3
Heart Failure (HF)	.068	.116	.265	3	2.2	1.4
HF + CF (9kpm)	.083	.080	.086	5.9	5.1	4.7
HF + TORVAD Counterpulse	.086	.156	.306	5.8	4.7	3.5

At higher preloads of 20 mmHg, both modalities of support provide similar cardiac outputs compared to the healthy heart (5.9 L/min for the healthy heart, 3.0 for heart failure, 5.9 with CF support, and 5.8 with TORVAD counterpulse support) and provide physiological responses to ventricular preload in terms of preload sensitivities (0.084 L/min/mmHg for the healthy heart, 0.068 for heart failure, 0.083 with CF support, and 0.086 with TORVAD counterpulse support). As preload decreases, the cardiac outputs and preload sensitivities of the different pumping modalities start to diverge. At nominal preloads of 10 mmHg, the cardiac outputs are still fairly similar (4.7 L/min for the healthy heart, 2.2 for heart failure, 5.1 with CF support, and 4.7 with TORVAD counterpulse support) but the sensitivity with TORVAD support increases to match the healthy heart while the preload sensitivity with CF support does not adjust (0.170 L/min/mmHg for the healthy heart, 0.116 for heart failure, 0.080 with CF support, and 0.156 with TORVAD counterpulse support). At low preloads of 5 mmHg, the CF device overpumps the circulation compared to the healthy heart and TORVAD support (3.3 L/min for the healthy heart, 1.4 for heart failure, 4.7 with CF support, and 3.5 with TORVAD counterpulse support) and the difference in preload sensitivity between the modalities becomes even more pronounced (0.342 L/min/mmHg for the healthy heart, 0.265 for heart failure, 0.092 with CF support, and 0.306 with TORVAD counterpulse support). These CF sensitivities compare well to other published sensitivity values for the HMII in the literature, for example 0.095 L/min/mmHg reported by Khalil, et al (ref) and 0.09 reported by Salamonsen, et al (5).

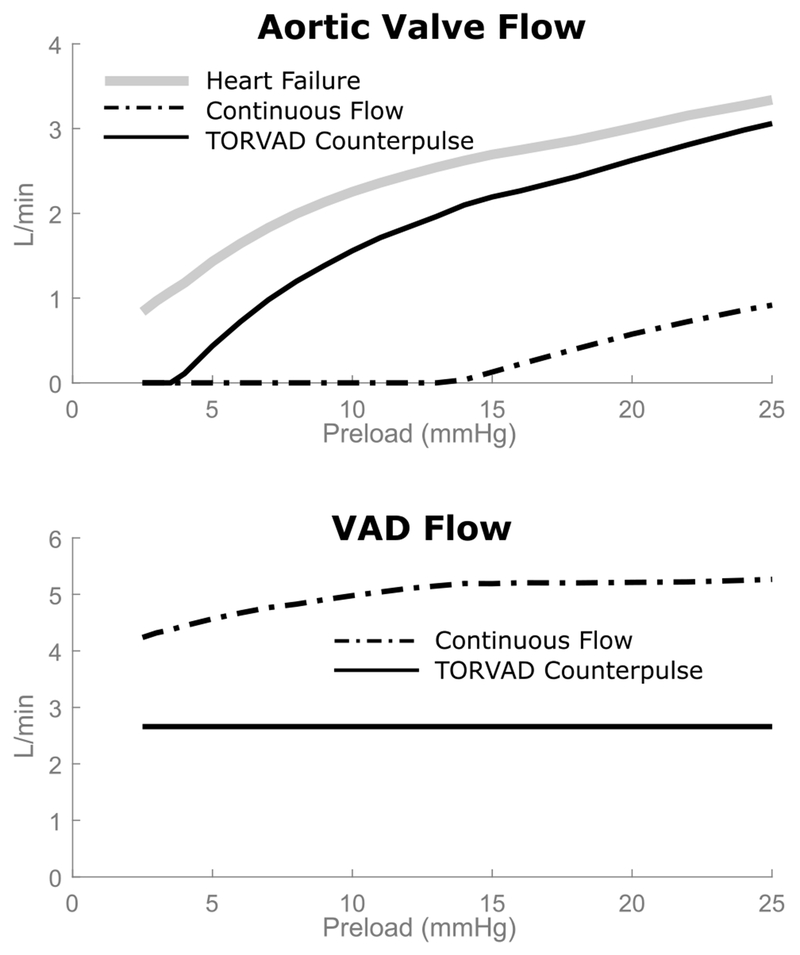
This difference in cardiac output and preload sensitivity for the different modalities of support can be explained by the relationship between aortic valve flow and VAD flow, which is shown in Figure 4. With TORVAD counterpulse support, aortic valve flow is preserved because the VAD temporarily pauses pumping and allows the ventricle to contract in systole, and then the VAD provides an early diastolic counterpulse to boost cardiac output (12). The preserved aortic valve flow is physiologically sensitive to preload, so cardiac output is automatically adjusted. This is demonstrated by the ventricular function curve with TORVAD support, which is almost a direct offset from the healthy heart failure curve. The TORVAD is positive displacement, so it provides a cardiac output offset to the ventricular function curve while allowing the native heart function and eject blood through the aortic valve to control the shape of the ventricular function curve. Continuous flow devices pump throughout the cardiac cycle, effectively shunting flow during systole so that the majority if not all of the cardiac output goes through the device, which is not able to provide an inherent physiological response to preload (5). As a result, as preload pressure drops, the CF VAD provides too much flow compared to the failing or even healthy heart.

Figure 4.

Aortic valve flow and VAD flow as a function of ventricular preload. With TORVAD counterpulse support, much of the native flow through the aortic valve is maintained. It is this flow that remains physiologically sensitive to preload changes and produces the nonlinear response seen in Figure 3. For CF support, aortic valve flow is significantly diminished and becomes zero at moderate preloads at which point the VAD takes over the entire cardiac output, which does not have physiological sensitivity to preload and causes overpumping at low preloads.

Baseline results for the closed-loop model with the initial SVR, PVR, and HR settings are provided in Table 1. From baseline heart failure, both CF and TORVAD counterpulse support boost cardiac output from 3.8 to 5.3 L/min, but the TORVAD does so with only half the VAD flow (2.7 for the TORVAD compared to 4.9 L/min for CF). This is because counterpulse support preserves more aortic valve flow (2.6 L/min with TORVAD compare to 0.4 L/min with CF). Ventricular unloading can be assessed for these different support modalities with left ventricular stroke work (LVSW), which is calculated as the area of the LV pressure-volume loop and represents the work done by the ventricle during one cardiac cycle. Both modalities of support reduce stroke work from 2,682 mmHg ml in heart failure (down to 1,859 with TORVAD support and 2,008 with CF support). The difference and clinical significance between these two may be negligible, but is highlighted here because this may be somewhat counterintuitive given that the ventricle ejects more blood through the aortic valve with TORVAD counterpulse support. These results demonstrate that the TORVAD provides comparable unloading in terms of LVSW with only half the VAD flow compared to CF support. This is because the ventricle is still contracting and doing the work of ejecting blood with CF support except that it pumps through the VAD rather than through the aortic valve.

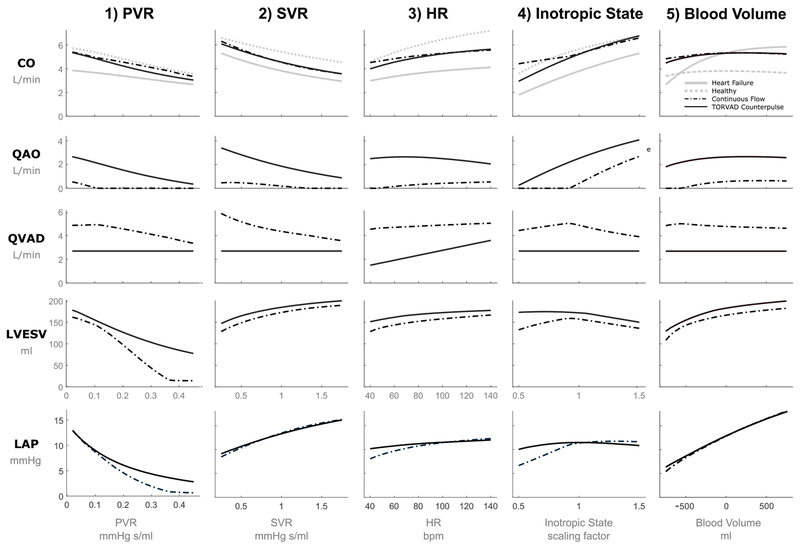
Results of PVR, SVR, HR, inotropic variation, and blood volume are shown in Figure 5. Mean cardiac output, aortic valve flow, VAD flow, left ventricular end systolic volume, and left atrial pressure are shown as a function of the varied parameters (PVR, SVR, HR, percent inotropic change, and blood volume change). Of particular interest are the PVR results, which demonstrate the most difference between the different types of support. As PVR increases, cardiac output with CF support remains higher than cardiac output with TORVAD counterpulse support, as a result left ventricular suction (defined as left ventricular volume less than 15 ml) begins to occur when PVR is greater than 0.35 mmHg s/ml. This finding is confirmed by similar studies that experienced suction at a PVR of 0.375 mmHg s/ml (21).

Figure 5.

Cardiac output (CO), aortic valve flow rate (QAO), VAD flow rate (QVAD), left ventricular end systolic volume (LVESV), and mean left atrial pressure (LAP) for CF and TORVAD counterpulse support for changes in (1) PVR pulmonary vascular resistance (PVR), (2) systemic vascular resistance (SVR), (3) heart rate (HR), (4) inotropic state, and (5) blood volume. Healthy and heart failure cardiac output values are also displayed for comparison.

The results of SVR, HR, inotropic state, and blood volume in Figure 5 all have similar results in terms of cardiac output, and demonstrate that the response to changes in SVR and blood volume is fairly similar for the both CF and TORVAD counterpulse support and that both appear to be offsets from the heart failure curve. For low HR, inotropic state, and blood volume, CO is higher and LVESV is lower with CF support compared to TORVAD support, but never enough to cause left ventricular suction in these simulations.

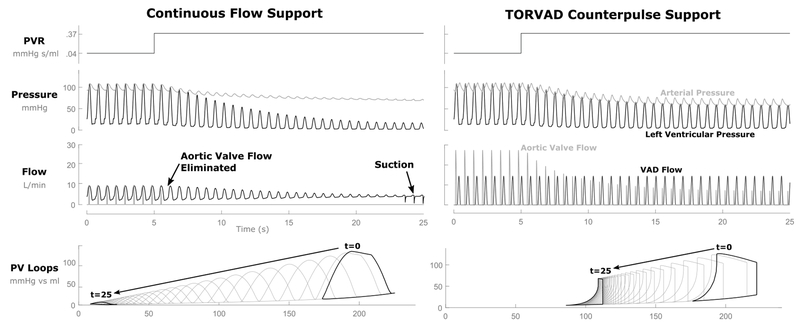
Figure 6 shows arterial and left ventricular pressure curves, aortic and VAD flow curves, and left ventricular pressure-volume loops for the closed-loop simulation with CF and TORVAD counterpulse support after a step change in PVR from 0.04 to 0.37 mmHg s/ml at 5 seconds on the plot. This simulation is included to provide an example of how changes in PVR alter hemodynamics and shift the left ventricular PV loops. With CF support, the small amount of aortic valve flow that was present before the PVR increase very quickly dropped to zero as the VAD flow took over the entire CO. Left ventricular volume continued to drop significantly and with it the pressure the ventricle was able to generate. Eventually, suction events began to occur as the ventricular volume reached a critical minimum. With TORVAD counterpulse support, native aortic valve flow was preserved, allowing the left ventricle to provide a large margin of adjustment to CO when the preload dropped after the PVR increase. This reduction in CO demonstrates that the ventricle is not overpumped and no suction events occur.

Figure 6.

Hemodynamics (pressure and flow) and pressure-volume (PV) loop responses to a step-change in pulmonary vascular resistance in the closed-loop simulation. When pulmonary vascular resistance is increased from 1 to 2 Wood units, the continuous flow overpumps the circulation resulting in low ventricular volumes and ventricular suction events. TORVAD counterpulse support preserves aortic valve flow that physiologically responds to the change in preload, which reduces cardiac output and prevents overpumping.

DISCUSSION

Passive autoregulation of cardiac output by the left ventricle is critical for maintaining a healthy response to physiological feedback. Ventricular preload varies throughout the day depending on the patient’s physical activity, volume status, or pathological state (2). Continuous flow devices are set to a constant rotational speed by the clinician at periodic follow-up visits, but cannot automatically adjust flow throughout the day in response to physiological need.

Continuous flow VADs pump throughout the cardiac cycle. The highest VAD flow rate is during systole because blood that would normally be ejected by the left ventricle through the aortic valve is instead shunted through the VAD to the point where the aortic valve only opens sporadically or often not at all (10). This can result in aortic valve commissural fusion, aortic insufficiency, and outflow tract and aortic root thrombus in CF VAD recipients (22,23). Additionally, when aortic valve flow is diminished and the entirety of the CO is taken over by the CF device, preload sensitivity significantly deviates from the normal response at low preloads, which can lead to overpumping. Active physiological control methods have been proposed that would modulate flow based on various feedback mechanisms to overcome this deficiency, but these methods have not yet been implemented in clinical practice (24,25). Many of these algorithms specifically try to recreate the Starling response using indwelling pressure transducers to measure preload and adjust pump flow to follow prescribed ventricular function curves (5,26). Some indwelling pressure sensors can be prone to thrombus formation and long term drift, which compromise accurate measurements, and long-term reliable solutions have not yet emerged (24). Others have proposed estimation of preload using pump metrics such as the differential pump pressure or the pulsatility index to drive a Starling-like control (17,27,28). However, these methods also require indwelling sensors or rely on pump-derived estimations of pressure and flow that are prone to inaccuracies outside of steady-state conditions or due to viscosity variation.

Synchronous counterpulsation with the TORVAD device preserves native aortic valve flow. By operating the pump in this mode, the TORVAD briefly ceases to pump blood in systole allowing the ventricle to eject normally through the aortic valve. By preserving native aortic flow with counterpulse support, patency of the native aortic valve is maintained and the autoregulatory aspect of the heart is preserved in the native aortic valve flow, thereby restoring the physiologic preload sensitivity of the cardiovascular system. Pumping in this way prevents suction from occurring at low preloads, which would prevent septal wall shift and could reduce the risk of progression to right heart failure. Synchronous counterpulsation might be considered a form of both active and passive control. It’s active in the sense that pump ejections are synchronized to the cardiac cycle such that the pump flow rate automatically changes based on the heart rate and the pump ejection occurs during diastole, but passive in the sense that cardiac output responds to preload due to the preservation of the native aortic ejection without the need for additional pressure sensors or pump flow rate changes.

One limitation of TORVAD counterpulse support is that preload sensitivity depends on the remaining preload response of the failing ventricle. The TORVAD has a fixed 30 ml stroke volume that is insensitive to changes in preload. It is only by preserving aortic valve flow with counterpulsation that a physiological response to preload remains. If ventricular function were to significantly deteriorate, then the TORVAD may need to operate asynchronously to take over the entire CO. Similarly, if ventricular function improves, then the TORVAD ejection could be adjusted to a different time in the cardiac cycle, or the pump could eject every other heart beat.

Salamonsen, et al., specified three requirements for Starling-like control (27): (a) preload sensitivity should be comparable to that of the left ventricle; (b) it should be maximal at low preloads and fall nonlinearly and become negligible at high preloads; and (c) the amplitude of the Starling curve should scale to compensate for metabolic requirements during exercise or stress. The results demonstrated here for TORVAD counterpulse support satisfy the first two requirements. While preload sensitivity has been considered one of the most important aspect of regulating cardiac output, afterload, heart rate, and inotropic state are also important regulating mechanisms (2,3).The results of the closed-loop model in Figure 5 show that the response to changes in SVR is fairly similar for both CF and TORVAD counterpulse support. Both appear to be offsets from the heart failure curve and have the same general shape of the compared to the healthy or failure curves. This may seem to be in contrast to claims that CF devices have three to four times the afterload sensitivity of the healthy heart (5,6), but the referenced study did not account for the increased preload that can also occur with increased afterload. As CO drops, preload increases, which makes ventricular contractions stronger. Similar responses are also shown for increased heart rate and inotropic state compared to the healthy and failing heart, at least in terms of the general shape of the curves. There is a greater difference between the modalities of support as HR and inotropic state decrease where CF support produces more cardiac output than with TORVAD support, but these may not be clinically significant.

One of the limitations of this study is that SVR, PVR, HR, inotropic state, and blood volume were individually varied in the closed-loop study. This was done to isolate their effect from one another, but in reality they may vary simultaneously, along with other unaccounted for parameters such as vascular tone. A multivariable analysis may be helpful to answer these questions and motivates future work.

CONCLUSION

Preload sensitivity is an important feedback mechanism for cardiac output autoregulation in response to metabolic demand, which varies from activity level, fluid volume, or pathological status. Continuous flow devices are less sensitive to preload compared to the normal healthy heart, especially at low preloads where they overpump the system. Counterpulse support with the TORVAD preserves aortic valve flow, provides physiological sensitivity across all preload conditions, and reduces the risk of suction at low preload pressures. This should prevent overpumping and minimize the risk of suction and septal wall shift.

Appendix

Brief details of the cardiovascular system lumped parameter are provided here. This model is based on previously published work (12,14). Lumped parameter models of the systemic and pulmonary vessels contain two energy storage elements (representing vessel compliance C and fluid inertance L), and one passive elements (representing viscous fluid resistance R).

Energy storage elements can be represented by differential equations, which can be integrated over time to simulate the dynamics of the cardiovascular system. The equation for the rate of change of pressure (P) is a function of the compliance (C) and the flow in (Q_i) and out (Q_o) of the vessel.

$$\stackrel{.}{P}=\frac{Q_i-Q_o}{C}$$

When fluid inertance elements are present in the model, the differential equation for flow in the element (Q) is a function of the viscous resistance (R), inertance of the fluid in the tube (L), and the pressure at the inlet (P_i) and outlet (P_o).

$$\stackrel{.}{Q}=\frac{P_i-P_o-\mathrm{RQ}}{L}$$

When inertial effects are neglected and there is only a passive resistive between two independent pressures, the flow becomes a dependent variable.

$$Q=\frac{P_i-P_o}{\text{R}}$$

The volume in the atria and ventricles are modeled following the conservation of mass principle.

$$\stackrel{.}{V}=Q_i-Q_o$$

And the heart valves are represented as ideal diodes with a nonlinear orifice model,

$$Q=\{\begin{array}{cc}\sqrt{P_i-P_o}{/}_{\text{R}}& P_i>P_o\\ 0& P_i\le P_o\end{array}$$

Pressure in the atria and ventricle are defined by active and passive pressures, which are functions of volume that are modulated by the normalized time varying elastance function e(t) (29,30).

$$P=\left[1-e\left(t\right)\right]P_P\left(V\right)+e\left(t\right)P_a\left(V\right)$$

The passive pressure (P_p) is also known as the end diastolic pressure volume relationship (EDPVR) and represents the passive elastance of the ventricle during diastole when the ventricle is not contracting and has been modeled several ways. Some studies have opted for a simple linear relationship described by a minimum ventricular elastance, which is clearly not physiologic but may suffice for simulation studies over a very limited range of ventricular preloads (31,32). Logarithmic models have also been proposed to define an initial stiffness at the unstressed volume as well as an asymptotic maximum volume determined by the pericardium and cardiac cytoskeleton (33,34). Most computational models in the literature use exponential relationship (35,36). Exponential coefficients are derived from passive filling curves obtained from excised hearts of human and animals. These curves have been shown to represent the nonlinear aspect of filling relatively well and account for increased stiffness at higher filling volumes.

The approach taken in this study makes use of principles from all models above by superimposing an exponential and linear function (37).

$$P_p=S_0\left[r(V-V_0)+(1-r)\frac{e^{\alpha (V-V_0)}-1}{\alpha }\right]$$

In this way, one extra term is added to the typical exponential model so that the stiffness (S₀) at the unstressed volume (V₀) can be controlled as it is done in the logarithmic model. This can be seen by determining the slope of the curve by evaluating the derivative with respect to volume at the unstressed volume.

$$S_0=\frac{\partial P_p}{\partial V}|{}_{V=V_0}$$

To parameterize the passive pressure, the exponential constant (α) is defined as well as the stiffness (S₀) at the unstressed volume. Then a single operating point through which the passive pressure curve should pass is defined (P_op and V_op). From these, the coefficient r can be found by

$$r=\frac{\frac{P_{op}\alpha }{S_0}-e^{\alpha \left(V_{op}-V_0\right)}+1}{\alpha \left(V_{op}-V_0\right)-e^{\alpha \left(V_{op}-V_0\right)}+1}$$

Table A1 provides values for healthy and heart failure conditions.

The active pressure (P_a) is also known as the end systolic pressure volume relationship (ESPVR) and is assumed to be a linear function of volume with a maximum elastance E_m

$$P_a=E_m\left(V-V_0\right)$$

The model is parameterized for healthy and heart failure conditions using values described in previous publications (12,14). The ordinary differential equations (ODEs) that represent the time rate of change of the energy storage elements in the model are numerically integrated using an ODE solver in Matlab.

Table Al.

Passive pressure (EDPVR) parameters for healthy and heart failure conditions. An operating pressure-volume pair (V_op and P_op) through which the passive pressure curve should pass is defined, as well as the stiffness at the unstressed volume (s), and the exponential coefficient (α). From these, the other dependent coefficients (β and γ) can be calculated.

Parameter	Healthy	Heart Failure
α (1/ml)	0.025	0.020
s (mmHg/ml)	0.050	0.045
Vop (ml)	120	230
Pop (mmHg)	10	25