Graphene-like monolayer monoxides and monochlorides

Significance

Since the discovery of graphene in 2004, 2D materials have sparked tremendous interest due to their fascinating optical, mechanical, and electronic properties, and their potential in catalysis, optoelectronic devices, energy storage, and conversion. After experimental and theoretical studies mainly focused on atomically thin nanomaterials with layered structures, the whole family of 2D materials is almost complete, and recently few new graphene-like materials were reported. Here, we report the discovery of graphene-like mononitrides, monoxides, monochlorides, and monoselenide monolayers, which have shown high dynamic, thermal, kinetic, and mechanic stabilities.

Abstract

Two-dimensional monolayer materials, with thicknesses of up to several atoms, can be obtained from almost every layer-structured material. It is believed that the catalogs of known 2D materials are almost complete, with fewer new graphene-like materials being discovered. Here, we report 2D graphene-like monolayers from monoxides such as BeO, MgO, CaO, SrO, BaO, and rock-salt structured monochlorides such as LiCl, and NaCl using first-principle calculations. Two-dimensional materials containing d-orbital atoms such as HfO, CdO, and AgCl are predicted. Adopting the same strategy, 2D graphene-like monolayers from mononitrides such as scandium nitride (ScN) and monoselenides such as cadmium selenide (CdSe) are discovered. Stress engineering is found to help stabilize 2D monolayers, through canceling the imaginary frequency of phonon dispersion relation. These 2D monolayers show high dynamic, thermal, kinetic, and mechanic stabilities due to atomic hybridization, and electronic delocalization.

Two-dimensional materials have sparked tremendous interest due to their structural, optical, mechanical, and electronic properties, and potential applications in areas such as catalysis, photonics, energy storage, and sensing devices. Since the discovery of graphene in 2004 by Novoselov and Geim (1), much attention has been paid to the design of 2D materials both experimentally and theoretically. Via functionalization, many derivatives of graphene have been extensively explored in order to tune the band gap, such as graphene oxide, graphane (2), fluorographene (3), and chlorographene (4). Other group IV based materials, such as silicene, germanene, and stanine have also progressed from theoretical predictions (5, 6) to experimental observations (7–9), exhibiting electronic characteristics similar to graphene. The synthesis of phosphorene, a monolayer of phosphorus, has opened up a new field of group V based 2D monolayer materials (10). Since the report (11) of molybdenum disulphide (MoS₂) devices with switching on/off ratios of >10⁸ and room-temperature single-layer mobility of at least 200 cm²V⁻¹⋅s⁻¹, studies into MoS₂ monolayers have increased and aroused a great interest in the entire 2D chalcogenide family (12).

As these studies have progressed, 2D monolayers with one or several atomic thicknesses can be obtained from almost every layered material. For instance, Coleman et al. (13) showed that layered compounds such as MoS₂, WS₂, MoSe₂, MoTe₂, TaSe₂, NbSe₂, NiTe₂, BN, and Bi₂Te₃ could be efficiently dispersed in common solvents and deposited as individual flakes or formed into films. Nicolosi et al. (14) reviewed the liquid exfoliation of layered materials, including graphite, h-BN, transition-metal dichalcogenides, transition-metal trichalcogenides, layered metal halides (MoCl₂, CrCl₃, PbCl₄ etc.), layered oxides (Ti_xO_y, V₂O₅, MoO₃, FeOCl, etc.), III–VI layered semiconductors (GaSe, InSe), layered zirconium phosphates and phosphonates, clays, and ternary transition-metal carbides and nitrides. However, from an experimental point of view, the study of 2D monolayers requires synthesis using chemical fabrication methods, and detailed characterization techniques such as X-ray diffraction, high-resolution transmission electron microscopy, atomic force microscopy, Raman spectroscopy, and scanning tunneling microscopy, making it heavily time-consuming to undertake a systematic study for a large number of candidate materials. Lebègue et al. (15) used the efficiency of density-functional theory to reveal the electronic and magnetic structures of possible new 2D materials. At present, almost every potential layered material that exists in the Inorganic Crystal Structure Database has been investigated, including each combination of 2D dichalcogenides such as ZrS₂, WTe₂, PdSe₂, and other nondichalcogenides layered compounds such as PbIF, Cu₂S, FeS, FeBr₃, and KC₆FeO₃N₃ (15). Kamal et al. (16) studied binary XY systems consisting of equal numbers of group IV and VI elements in puckered, buckled, and planar arrangements, by employing electronic structure calculations based on density-functional theory.

Arising from the numerous reviews and studies on the subject, a complete family of 2D materials has been established with few new materials being reported. Tan et al. (17) summarized the state-of-the-art progress of ultrathin 2D nanomaterials, with a particular emphasis on their recent advances. In this work, we report graphene-like monolayer monoxides such as MgO, BaO, and monochlorides such as NaCl. These materials usually have a rock-salt-like structure with a space group of $Fm\overline{3}m$ in Hermann–Mauguin notation. Seen from the lattice structure of NaCl in Fig. 1A, each of the 2 atom forms a separate face-centered cubic lattice, with the 2 lattices interpenetrating to form a 3D checkerboard pattern. However, there are few existing reports of 2D monolayers of NaCl and other rock-salt-like materials. Herein, by employing first-principle calculations, we report on stable graphene-like monoxides and their related structural and electronic properties.

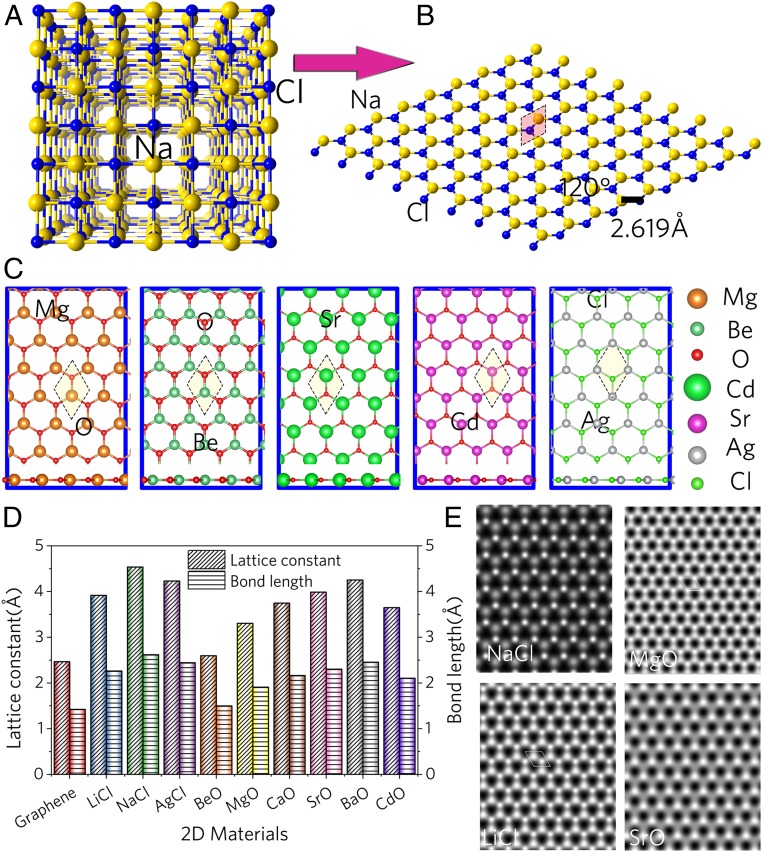
Fig. 1.

(A) Rock-salt lattice structure of bulk NaCl. (B) Planar view of a 2D NaCl monolayer. (C) Planar and side views of 2D MgO, BeO, SrO, CdO, and AgCl monolayers. (D) Lattice constants and bond lengths of 2D materials, as compared to graphene. (E) The simulated STM images of NaCl, MgO, LiCl, and SrO 2D monolayers.

The rock-salt-like binary compounds were filtered out and screened from the structure database. We then focused on common materials with fewer or no d orbitals, such as MgO, NaCl, and BaO. By using a particle swarm structural search and first-principle calculations based on both density-functional theory (DFT) and density functional perturbation theory (DFPT), we predicted graphene-like monolayers with high stability. Details of the theoretical computation can be found in SI Appendix, Methods. Fig. 1 B and C show schematic models of these monoxides and other compounds. All these materials maintain a graphene-like structure within a 1-atom-thickness planar hex-coordinate lattice. Fig. 1D shows the bond length and lattice parameters of these 2D materials. The comparison of lattice parameters of 2D monolayers with 3D bulks is listed in SI Appendix, Tables S1 and S2 The length of the Na–Cl bond in the 2D NaCl monolayer is shorter than that (2.820 Å) in rock-salt NaCl. The length of the Ba–O bond in the 2D BaO monolayer is 2.457 Å, while the length of MgO is 1.908 Å. Next, the simulated scanning tunneling microscopy (STM) images of the optimized 2D monolayers were shown in Fig. 1E and SI Appendix, Fig. S3, based on the Tersoff and Hamann approximation (18) at constant height mode used to mimic the experimental setup (19). The simulated STM images of 2D NaCl, MgO, LiCl, and SrO monolayers show the symmetrical honeycomb structure, which is similar to the structure of graphene. The simulated STM images of discovered 2D BaO, AgCl, HfO, BeO, and CdO monolayers are shown in SI Appendix, Fig. S3. The simulated STM images of 2D BaO sheets, 2D AgCl sheets, and 2D CdO sheets show surfaces with a hexagonal pattern, while the simulated STM images of 2D BeO sheets and 2D HfO sheets reveal surfaces with triangular patterns.

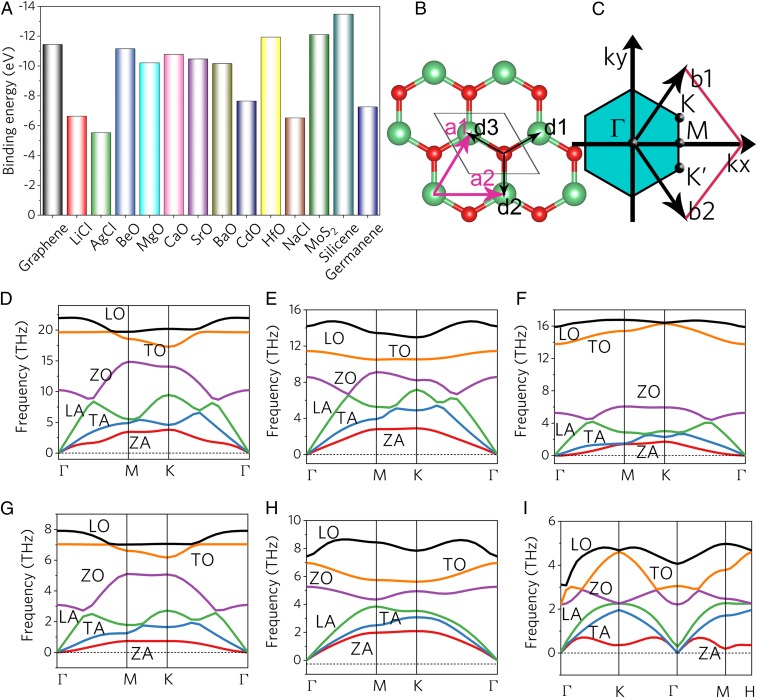
To evaluate the stability of this structure, binding energies (E_b) were calculated using the formula E_b = E_AB − E_A − E_B, where E_AB, E_A, and E_B are the respective energies of the 2D monolayer compound AB and their constituent atoms A and B. The calculated binding energies of these 2D materials are shown in Fig. 2A, together with that of graphene, silicone, germanene, and MoS₂ for comparison. All of the calculated binding energies are negative, revealing that all these 2D monolayer compounds are energetically stable. Moreover, the energies of the 2D monolayers are comparative to that of graphene, MoS₂, and germanene. This implies that the predicted 2D sheets could be experimentally synthesized. The mechanical stability was evaluated by calculating the elastic constant. For these 2D materials, the calculated elastic constants satisfy this Born stability criterion for the hexagonal system (20). Details of the elastic constant can be found in SI Appendix, Tables S4 and S5. The kinetic stability of the presented 2D materials can be characterized by calculating the phonon dispersion using DFPT methods along the high-symmetry lines in the Brillouin zone, as shown in Fig. 2. Similar to graphene (21–23), these 2D monolayers have 6 phonon branches: out-of-plane acoustic (ZA) and out-of-plane optical (ZO) phonons, where Z indicates that the displacement vector is along the z axis; transverse acoustic (TA), transverse optical (TO), longitudinal acoustic (LA), and longitudinal optical (LO) phonons, which correspond to vibrations within the 2D plane. All frequencies are positive, with no appearance of imaginary phonon modes, indicating that the graphene-like monoxides and monochlorides are thermodynamic stable.

Fig. 2.

(A) Binding energies of predicted 2D materials compared to graphene, germanene, MoS₂, and silicone. (B) Graphene-like honeycomb lattice from 2 interpenetrating triangular lattices (a1 and a2 are the primitive vectors). (C) Brillouin zone corresponding to a planar hexagonal lattice with high symmetry k points. The Dirac cones are located at the K and K′ points for graphene. (D–I) Phonon dispersion relations of (D) 2D MgO monolayers, (E) 2D CaO monolayer, (F) 2D CdO monolayer, (G) 2D NaCl monolayer, (H) 2D LiCl monolayer, and (I) 2D AgCl monolayer.

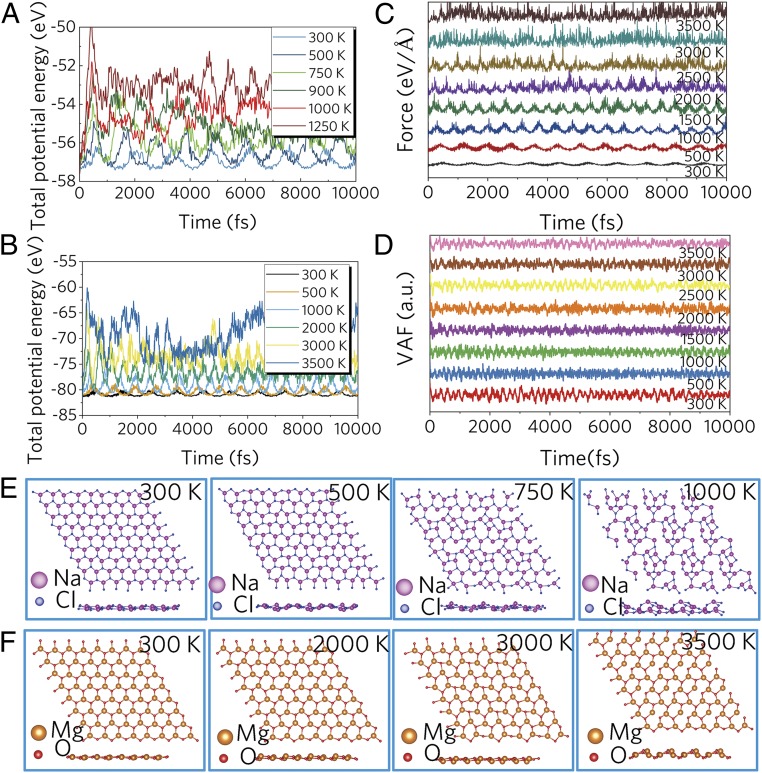
In order to examine the thermal stability of these 2D monolayers, we performed ab initio molecular dynamics (AIMD) simulations as shown in Fig. 3. A 3 × 3 × 1 supercell for each 2D monolayer was built to reduce the lattice translational constraints at various temperatures in the range of 300∼3,500 K. Fluctuations of total potential energy for the 2D MgO and NaCl monolayers at different temperatures during AIMD simulation are shown in Fig. 3 and SI Appendix, Figs. S11–S13. All of the atoms in the 2D monolayers only slightly vibrate around their equilibrium positions after annealing at 300 K for 10 ps, indicating that all these materials are stable at room temperature. For the 2D MgO monolayer, average values of the total potential energy remain nearly constant during the entire simulation in the temperature range from 300 to 3,000 K, confirming that this monolayer is thermally stable at 3,000 K. Similarly, the 2D SrO monolayer is thermally stable at 2,000 K, while the 2D NaCl monolayer is thermally stable at 500 K. Snapshots of structures calculated by AIMD at different temperatures are shown in Fig. 3 D–F. The planar hexacoordinate motifs were well-maintained at room temperature for the 2D MgO, SrO, and NaCl monolayers. At 3,500 K, some bonds in the 2D MgO monolayer had broken, but the system still held together as a whole. For the case of SrO, the atoms fluctuate significantly, and the system shows reconstruction at 2,500 K, implying that the 2D hexacoordinate motifs were broken. At 1,000 K, by 10 ps, the 2D NaCl monolayer starts to melt. These results suggest that these 2D monolayers have excellent thermal stability and can maintain structural integrity and planar geometry.

Fig. 3.

Fluctuation of the total potential energy of (A) 2D NaCl monolayer and (B) 2D MgO monolayer; (C) forces and (D) velocity autocorrelation function of a 2D MgO monolayer for 10 ps at different temperatures during AIMD simulation. Snapshots of (E) 2D MgO monolayers and (F) 2D NaCl monolayers at different temperatures, by top view (Top) and side view (Bottom).

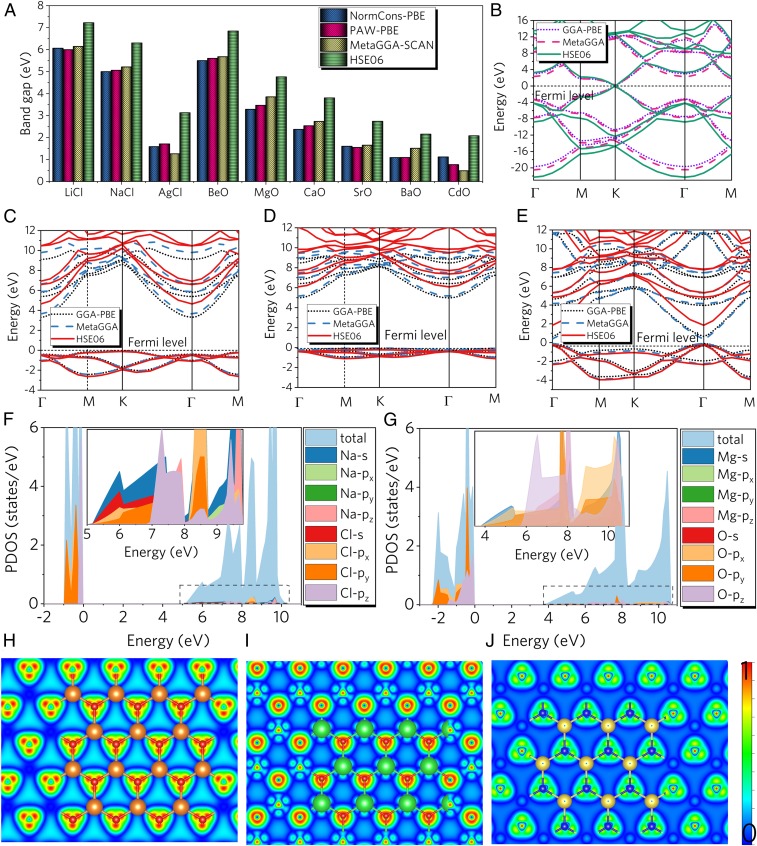
To gain further insights into the chemical bonding and the stabilization mechanisms of these graphene-like monolayer monoxides and monochlorides, we calculated the differential charge density, electronic band structure, and electronic density of states (DOS) as shown in Fig. 4. For comparison, we also calculated the band structure of graphene using similar methods as shown in Fig. 4B. Graphene shows typical Dirac band character, which is in agreement with previous research (24–26). Fig. 4 C–E show the band structure of MgO, NaCl, and CdO 2D monolayers, respectively. Band structures for the other 2D monolayers can be found in SI Appendix, Fig. S14, together with the comparison of band gap with experimental values in SI Appendix, Table S3. Note that generalized gradient approximation (GGA) calculations tend to underestimate the band gaps of semiconducting materials. Therefore, band structures were calculated by using the GGA Perdew-Burke-Ernzerhof revised for solids (PBEsol) with both projector-augmented wave (PAW) pseudopotential and norm-conserving pseudopotential, strongly constrained appropriately normed (SCAN) meta-GGA, Heyd−Scuseria−Ernzerhof functional (HSE06) exchange functional, and norm-conserving pseudopotential. As seen in Fig. 4A, the calculated band gaps using GGA-PBEsol are in accordance with the band gaps using SCAN. Within the SCAN meta-GGA exchange functional, the band structure is slightly improved, yet greater improvement is achieved using the HSE06 hybrid functional as seen in Fig. 4 C–E. Both MgO and NaCl 2D monolayers have an indirect band gap of 4.8 and 6.3 eV at the HSE06 level, respectively. Two-dimensional CdO monolayers are direct band gap semiconductors, with a band gap of 2.5 eV at HSE06 level (0.85 eV at the PBE level) at the Γ point. The computed partial density of states (PDOSs) of the predicted 2D materials was also analyzed. The representative PDOS for 2D MgO and NaCl are plotted in Fig. 4. For the case of the 2D NaCl monolayer, the valence band maximum (VBM) is mainly determined by the Cl-p orbitals, together with a small contribution from the Na-s orbitals. The conduction band minimum (CBM) is determined by the Na-s, Cl-s, Cl-p_x, and Cl-p_y orbitals, with the Cl-p_z orbital contributing to a higher conduction band. Similarly, for the case of the 2D MgO monolayer, the VBM is mainly determined by the O-p orbitals, together with a small contribution of Mg-s orbitals. The CBM is determined by the Mg-s, O-s, O-p_x, and O-p_y orbitals, with the O-p_z orbital contributing to the higher conduction band. For the case of CdO shown in SI Appendix, Fig. S15, VBM is mainly determined by the O-2p orbitals, together with contributions from the Cd-d and Cd-p orbitals. The CBM at around 2 eV is determined by the Cd-s and O-s orbitals. These are crucial in stabilizing the planar hexagonal-coordinated 2D framework in terms of passivating out-of-plane bonds. To get a deeper insight into the nature and stability of the bonding in our 2D monolayers, we further analyzed the deformation electron density distribution. Isosurface plots of the deformation electronic density of 2D MgO, 2D NaCl, and 2D CdO monolayers are shown in SI Appendix, Fig. S4 H–J. The charge transfer occurs primarily from the metal atom to the more highly electronegative oxygen or chlorine atoms. On the basis of Bader charge analysis, we found that each Mg atom in a 2D MgO sheet transfers 1.618 e to the adjacent O atoms, which denotes a considerable ionization of Mg atoms and electron donation to oxygen. Similarly, Cl atoms capture 0.853 e from each Na atom in the 2D NaCl sheet, suggesting electron donation to Cl atoms. This electron transfer leads to stabilization of the 2D monolayer sheets. Further details of the Bader charge analysis can be found in SI Appendix, Table S6, together with Mulliken population analysis showing similar electron transfer. Total charge density analysis of the 2D MgO (NaCl) monolayers shows that electrons are distributed around the oxygen (or chlorine) atoms and the triangular-sphere–shaped O-p_x (Cl-p_x) and O-p_y (Cl-p_y) orbitals have the largest deformation, spreading along the Mg–O (Na–Cl) bonds. For the 2D CdO monolayer, the appreciable concentration of electron density along the Cd-O contacts indicates typical characteristics of covalent compounds. Next, we further analyzed the electron localization function (ELF) (27). The values of ELF, which can range from 0 to 1, indicate the degree of localization of electrons. For the top and side view in SI Appendix, Figs. S16–S18, the O-p and Cl-p orbitals shown in green (ELF = 0.50) imply heavily delocalized features. The blue contours around the metal atoms (ELF = 0.00) indicate the electron deficiency of metal atoms in the 2D monolayer, which agrees with the deformation electron density and Bader charge analysis.

Fig. 4.

(A) Band gaps calculated using norm-conserving PBE, PAW-PBE, MetaGGA-SCAN, and HSE06 exchange functionals. (B–E) Band structure of graphene, 2D MgO, 2D NaCl, and 2D CdO monolayers calculated using PAW-PBE, MetaGGA-SCAN, and HSE06 exchange functionals. PDOS of (F) 2D NaCl monolayer and (G) 2D MgO monolayer. (Inset) Enlarged PDOS. Isosurface plots of deformation electronic density of (H) 2D MgO monolayer, (I) 2D NaCl monolayer, and (J) 2D CdO monolayer. Charge accumulation and depletion regions are shown in red and blue, respectively.

After considering our theoretical predictions and simulations, these graphene-like monoxides and monochloride monolayers are found stable, suggesting the possibility of experimental fabrication in an ambient environment. In a structural lattice, the corresponding bulk materials are nonlayered, and hold a face-centered cubic symmetry with the point group $Fm\overline{3}m$. This indicates that a 2D graphene-like monolayer could be obtained from the rock-salt-like bulks. To address this issue, other 2D materials, including mononitrides such as scandium nitride (ScN) and monoselenides such as cadmium selenide (CdSe), are further calculated and predicted as shown in SI Appendix. Bulk ScN and CdSe both have a rock-salt-like structure. The predicted 2D ScN monolayer is stable without any negative frequency, while the phonon dispersion of the 2D CdSe monolayer shows a metastable character due to the negative frequency. This negative frequency can be converted to positive by considering the effects of external stress, as shown in SI Appendix, Fig. S10, indicating that ambient stresses can help stabilize 2D CdSe monolayers.

Methods

Candidate structures were searched using a particle-swarm optimization method within an evolutionary algorithm, as implemented in CALYPSO code (28, 29). First-principle calculations of predicted 2D materials were performed by VASP (30, 31) and CASTEP code (32). SCAN meta-GGA functional, and HSE06 screened hybrid functional (33, 34) were employed to improve the band structure. Phonon dispersion calculations and AIMD simulations were performed to evaluate the kinetic stability and thermal stability (35–37). Detailed methods are provided in the SI Appendix.