In Vivo Characterization of the Deformation of the Human Optic Nerve Head Using Optical Coherence Tomography and Digital Volume Correlation

Abstract

We developed a method to measure the 3-dimensional (3D) strain field in the optic nerve head (ONH) in vivo between two intraocular pressures (IOP). Radial optical coherence tomography (OCT) scans were taken of the ONH of 5 eyes from 5 glaucoma patients before and after IOP-lowering surgery and from 5 eyes from 3 glaucoma suspect patients before and after raising IOP by wearing tight-fitting swimming goggles. Scans taken at higher and lower IOP were compared using a custom digital volume correlation (DVC) algorithm to calculate strains in the anterior lamina cribrosa (ALC), retina, and choroid. Changes in anterior lamina depth (ALD) relative to Bruch’s membrane were also analyzed. Average displacement error was estimated to be subpixel and strain errors were smaller than 0.37%. Suturelysis decreased IOP by 9–20 mmHg and decreased compressive anterior-posterior strain E_zz in the ALC by 0.76% (p = 0.002,n = 5). Goggle-wearing increased IOP by 3–4 mmHg and produced compressive E_zz in the ALC (−0.32%, p = 0.001,n = 5). Greater IOP decrease was associated with greater ALD change (p = 0.047,n = 10) and greater strains in the ALC (E_zz: p = 0.002,n = 10). A deepening of ALD was associated with lower IOP and greater ALC strains (p ≤ 0.045,n = 10). A DVC-based method to measure strains from OCT images caused by IOP changes as small as 2.3 mmHg provides preliminary evidence that ALD is shallower and ALC strains are less compressive at higher IOP and that ALD change is associated with ALC strains.

1. Introduction

Glaucoma is the second leading cause of blindness worldwide after cataract [1] and is characterized by the progressive dysfunction and death of the retinal ganglion cells (RGCs) whose axons are injured at the optic nerve head (ONH). RGC axons travel through the ONH via a connective tissue structure known as the lamina cribrosa (LC) before entering the optic nerve. Glaucoma is associated with remodeling of the LC and surrounding sclera. As RGC axons are lost, the rim of the optic disc becomes thinner and the apparent cup of the ONH widens and deepens [2–6]. Remodeling of the LC during glaucoma includes posterior migration of the beams of the LC, increased bowing and thinning of the LC, and an increase in the optic disc area [7]. The pores of the superior and inferior human LC are larger and have lower connective tissue density [8], and pressure-induced strains in these regions have been measured to be greater [9]. Previous experiments in both human and monkey eyes observed an association between regions with a higher degree of RGC axon loss and these regions of lower LC connective tissue density [8, 10, 11]. Recent studies by our group and others have used volume imaging and image correlation methods to map the pressure-induced deformation of the ONH in post mortem eyes, and have revealed heterogeneous strain fields with localized regions of large strains reaching 10% [9, 12–16]. These regional differences match the greater susceptibility to glaucoma damage for axons passing through the ONH poles [9]. This suggests that at least one major pathogenetic mechanism of glaucoma is based on the mechanical features of the LC.

The level of IOP is an important risk factor that is strongly associated with the prevalence and severity of optic nerve axon damage in open-angle glaucoma [17–20]. Higher IOP is associated with increased glaucoma prevalence and axon damage [21–23] and lowering IOP has been shown to slow the progression of the disease [24, 25]. However, nearly half of patients with open angle glaucoma have normal IOP and the majority of patients with high IOP (ocular hypertensives) do not develop glaucoma [19, 26–28]. Variations in the IOP-induced strain response of the LC may explain why some eyes with normal IOP develop glaucoma damage and why IOP lowering is effective at slowing the progression of the disease. Regions of low connective tissue density may be more susceptible to RGC injury from the larger strains experienced at these sites in response to IOP as measured ex vivo; however, the ONH strain response measured ex vivo may not be representative of the behavior in vivo.

A common approach to analyze ONH deformation in vivo has been to segment ONH structures in optical coherence tomography (OCT) images and to measure IOP-induced changes in the position and shape of the LC anterior surface relative to Bruch’s membrane opening (BMO) [29–35]. We found that the change in the anterior lamina border depth (ALD) after IOP decrease by the suturelysis procedure after trabeculectomy [33] could be either anterior (into the eye) or posterior (out of the eye). The direction and degree of movement were significantly related to the degree of glaucoma damage. Furthermore, for the same amount of IOP change, eyes with a lower baseline IOP experienced greater LC depth change than eyes at higher IOP, as would be expected for a stiffening stress response typical of collagenous tissues. In addition, regions of the ONH with more normal nerve fiber layer thickness had greater LC depth change with IOP lowering. These results suggest that the motion of the anterior lamina surface may be a biomechanical marker for degree of glaucoma injury and susceptibility. However, changes in LC anterior depth alone may not reflect LC strains. Modeling studies show that the LC anterior surface can move anteriorly or posteriorly in response to an IOP change, depending on the relative stiffness of the LC compared to the sclera [36, 37]. Moreover, the motion of the LC anterior surface alone does not indicate the strain state, i.e., whether the tissue is experiencing tension, compression or shear.

Girard et al. [38, 39] developed a DVC method to analyze spectral domain (SD)-OCT B-scans of the ONH taken within 21 days before and 50 days after trabeculectomy surgery. They segmented the tissues of the ONH and reported a significant strain relief in the visible LC volume with IOP lowering. Strain relief was greater in eyes with severe visual field loss. The investigators also applied the method to study the ONH deformation caused by acute IOP elevation by ophthalmodynamometer indentation on the sclera in normal, ocular hypertensive, and glaucoma subjects [40]. They found that LC strains induced by indentation were significantly smaller in ocular hypertensives compared to normals, but they did not find significant differences in the strain response of normal and glaucoma eyes.

There are a number of challenges to measuring strain accurately by DVC analysis of OCT images of the ONH. Image contrast decreases and noise increases with depth and commercial OCT machines can only image 200–300 μm below the anterior LC border. Overlying blood vessels block the view of the LC in some regions and ONH tissues can move during imaging [39] due to blood vessel pulsation and eye motion. Rigid body motions are automatically corrected by some commercial OCT machines, but these phenomena can still result in changes in illumination and local ONH deformation, which contribute to positional uncertainty in image volumes taken over longer periods of time. Girard and coworkers imaged eyes at the same IOP sequentially and calculated an average effective strain error of 1.07% [38].

To address some of these challenges, we have developed a DVC method [9, 15, 16] to analyze radial OCT scans of the ONH before and after IOP change to measure strains in the LC volume and changes in ALD. We developed a protocol for image post-processing to enhance contrast and reduce noise, which improves DVC accuracy. We applied the DVC method to calculate ONH strains in glaucoma patients and glaucoma suspect patients after IOP change by laser suturelysis and by wearing tight fitting goggles [41]. The strains in the LC were analyzed for variations with region, effects of IOP change, and association with the motion of the anterior LC border.

2. Methods

2.1. Experimental Subjects

Eight patients of the Wilmer Glaucoma Center of Excellence, who have undergone standard diagnostic testing for glaucoma during prior examinations, underwent SD-OCT imaging (Spectralis, Heidelberg Engineering, Heidelberg, Germany) before and after laser suturelysis in the post-operative period after trabeculectomy glaucoma surgery, and before and after short-term wearing of tight-fitting swimming goggles without lenses [41]. OCT scans before and after IOP change were performed on the same day for both the suturelysis and goggle wearing group. For the goggle group, OCT scans were taken after the patients wore the goggles for 15 minutes. IOP was measured using an ICare tonometer (ICare Finland Oy, Espoo, Finland), and was recorded as the average of two mean measurements of 6 IOPs each. We imaged the ONH of 5 eyes from 5 glaucoma patients, ages 63–83 (70.6 ± 7.6), with an average IOP reduction of 15.2 ± 4.1 mmHg (9–20 mmHg) after suturelysis and 5 eyes from 3 patients, ages 52–77 (65.8±12.7), with an average IOP increase of 2.8±1.6 mmHg (0–4 mmHg) caused by wearing goggles. Among the suturelysis patients, 1 had moderate glaucoma damage and 4 had mild damage as measured by HFA2i 24–2 visual field tests (Carl Zeiss Meditec, Inc., Dublin, CA, USA). The 3 goggle-wearing patients had normal visual fields (Tab. 1). This study was approved by the Institutional Review Board of the Johns Hopkins School of Medicine on April 22, 2017. Written, informed consent was obtained from patients prior to imaging.

Table 1:

Glaucoma patients recruited for SD-OCT imaging before and after laser suturelysis and wearing tight-fitting goggles, showing demographics information and visual field index (VFI).

Eye ID	Gender	Age (yr)	Race	Eye	VFI	IOP Change	High IOP	Low IOP
Eye 1L	Male	67	Caucasian	Left	93%	Suturelysis	24 mmHg	10 mmHg
Eye 2L	Male	68	Caucasian	Left	45%	Suturelysis	38 mmHg	18 mmHg
Eye 3R	Female	72	Caucasian	Right	97%	Suturelysis	29 mmHg	13 mmHg
Eye 4L	Male	83	Caucasian	Left	91%	Suturelysis	21 mmHg	4 mmHg
Eye 5L	Female	63	Caucasian	Left	92%	Suturelysis	20 mmHg	11 mmHg
Eye 6L	Female	77	Caucasian	Left	99%	Goggles	17 mmHg	14 mmHg
Eye 7R	Female	74	Caucasian	Right	100%	Goggles	22 mmHg	18 mmHg
Eye 7L	Female	74	Caucasian	Left	100%	Goggles	24 mmHg	21 mmHg
Eye 8R	Male	52	Caucasian	Right	100%	Goggles	23 mmHg	19 mmHg
Eye 8L	Male	52	Caucasian	Left	100%	Goggles	20 mmHg	20 mmHg

2.2. OCT Imaging

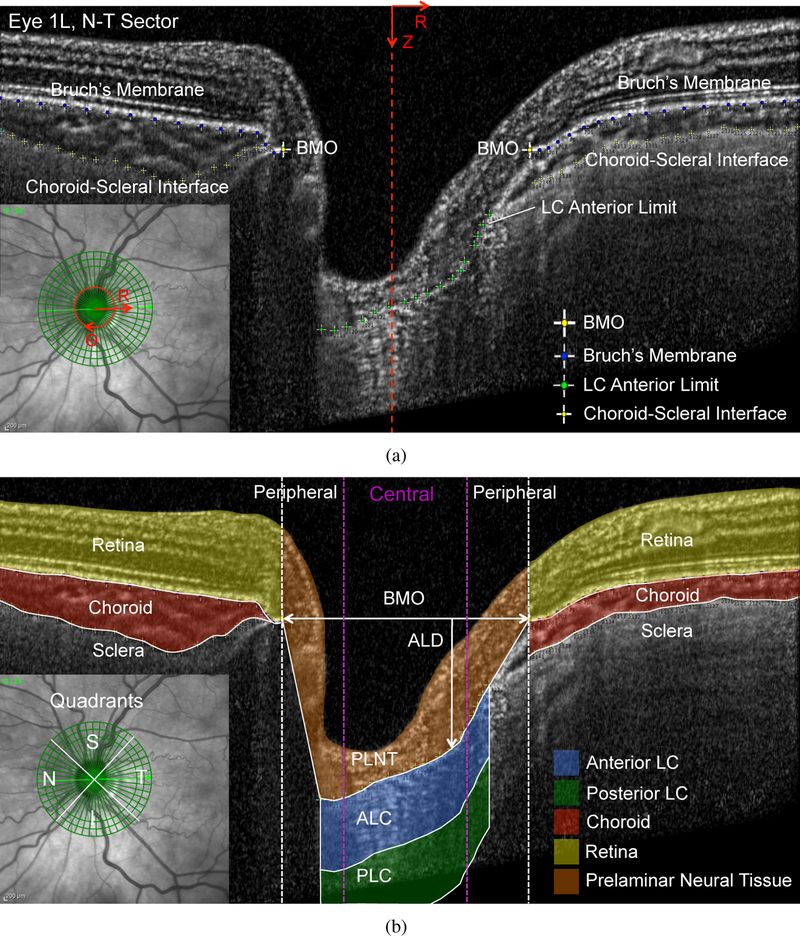
Patients were imaged 2–3 times at each IOP, with 30 seconds between image volumes. Each image volume consisted of 24 high-resolution radial SD-OCT scans centered about the ONH. The first scan was taken along an orientation perpendicular to the axis connecting the center of Bruch’s membrane opening and the fovea, and subsequent scans were taken every 7.5° clockwise in the circumferential direction (Fig. 1a). Successive image volumes were registered automatically to the orientation of the first image volume by the Spectralis software. Each radial scan had a resolution of 768 × 495 pixels in the (R,Z) plane, and was obtained from the average of 25 B-scans, with 768 A-scans per B scan. The acquisition time for the image volume was estimated to be 20 seconds, with some variation based on patient motion. Images were acquired in enhanced depth imaging mode to capture the choroid and parts of the sclera and LC. The resolution in the anterior-posterior (Z) direction was 3.87 μm/pixel, and the resolution in the radial (R) varied from 5.62 to 6.17 μm/pixel (mean ± standard deviation = 5.86 ± 0.23 μm/pixel) based on the optical magnification used for each eye. The scaling factors were recorded for each image volume and the images were exported as a series of de-identified images, which contained both the OCT image and a retinal map showing the orientation of the scan relative to the ONH (Fig. 1a).

Figure 1:

Contrast enhancement of scan 12 (nasal-temporal) for Eye 1L: a) original scan with retinal image showing scan location, b) contrast enhancement by CLAHE, c) noise reduction by Gamma correction.

2.3. Image post-processing

Amongst the image volumes acquired at each IOP, the volumes with the best focus, contrast, and lowest noise (Fig. 1a) were selected and imported into FIJI [42] for post-processing. The contrast was enhanced using piecewise contrast limited adaptive histogram equalization (CLAHE function, blocksize: 14, slope: 3.5, Fig. 1b) and the signal to noise ratio was reduced using the Gamma function and a Gamma correction of 1.75 (Fig. 1c) (Supplemental Sec. S1). We have previously demonstrated the efficacy of noise reduction and CLAHE contrast enhancement in improving DVC correlation [9].

2.4. Manual Segmentation of the tissue structures

The post-processed image volumes were imported into MATLAB (R2015b, Mathworks, Natick, MA, US) and reconstructed into a 768 × 495 × 24 three-dimensional matrix of 8-bit intensity values corresponding to the (R,Z,Θ) pixel positions. Each image was cropped to remove 13 pixels on the left and right side and 35 pixels on the bottom (posterior) edge of each image, as these areas were dark and contained imaging distortions. The volume was then resampled to a size of 371 × 360 × 48 pixels, by cutting each image down the middle in the R dimension, so that R = 0 corresponded to the center of the ONH in each image, Z = 0 corresponded to the top of each image, and Θ = 0 corresponded to the inferior-superior or 6–12 clock hour, with 7.5°or 0.25 clock hours between each consecutive image (Fig. 2a).

Figure 2:

a) Defining the (R,Z,Θ) orientations and manual marking of Bruch’s membrane, choroid-scleral interface, BMO, and LC anterior limit for scan 24 (superior-inferior) of Eye 4L, which has a fully visible anterior LC limit. b) The resulting segmentation of the ALC, PLC, PLNT, retina, choroid, sclera, and the central and peripheral ONH. The lines — denote tissue boundaries determined by manual segmentation, - - the radial position of the BMO points, and the radial position dividing the central and peripheral ALC.

Structural features within the image volume at the baseline IOP before IOP change by suturelysis or goggle-wearing were manually marked within FIJI to segment the tissues of the ONH. The posterior edge of Bruch’s membrane and the choroid-scleral limit were marked, where visible, on the 24 radial scans by points spaced every 15–25 pixels (Fig. 2a). Bruch’s membrane opening (BMO) was marked with 2 points in each scan. The visible portions of the LC anterior border were marked by points spaced every 10–20 pixels in each scan (Fig. 2a). The (R,Z,Θ) pixel positions of the marked points were then imported into MATLAB. The points of Bruch’s membrane on the left and right side of each scan were fit to a 5th order polynomial (MATLAB function polyfit), and used to segment the retina and the choroid (Fig. 2b). The points marked on the choroid-scleral interface were fit to a 6th order polynomial and used to segment the choroid and sclera. The anterior LC border has an irregular shape that varied significantly among eyes. A piecewise linear interpolation of the points marking the anterior LC border was used to divide the prelaminar neural tissue (PLNT) from the LC. There was no distinct posterior limit of the LC (identified histologically as the initial myelination of axons) that was visible in most of the OCT volumes. Thus, the anterior LC (ALC) region was defined in each scan from the anterior LC border to 250 μm posterior to the border (Fig. 2b). When there was tissue identified posterior to the ALC, the posterior LC (PLC) region was defined as the region from the posterior border of the ALC to 250 μm posterior to the ALC (Fig. 2b). The 250 μm thicknesses selected to segment the ALC and PLC was based on average histological measurements of the human LC thickness [43]. When the anterior LC border was not visible across the entire zone underlying BMO, we delimited the PLNT by drawing a straight line from the end of visible anterior LC border to the BMO (Fig. 3b). The LC was not assessed posterior to these regions because the location of the LC limit was unclear.

Figure 3:

a) Defining the (R,Z,Θ) orientations and manual marking of Bruch’s membrane, choroid-scleral interface, BMO, and LC anterior limit for scan 12 (nasal-temporal) of Eye 1L, which has a partially occluded anterior LC limit. b) The resulting segmentation of the ALC, PLC, PLNT, retina, choroid, sclera, and the central and peripheral ONH. The lines — denote tissue boundaries determined by manual segmentation, - - the radial position of the BMO points, and the radial position dividing the central and peripheral ALC.

The BMO width was defined in each scan as the length of a line connecting the BMO points. The anterior LC depth (ALD) was calculated as the vertical distance from the BMO line to the LC anterior limit (Fig. 4). The PLNT, ALC, and PLC regions were divided into central and peripheral regions, such that each occupied 50% of the BMO width as shown in in Figures 2b and 3b.

Figure 4:

Illustration of ALD and BMO width calculation in sector scan 24 (superior-inferior) for Eye 4L: a) the marked BMO and LC anterior limit at high and low IOP and b) ALD calculation and change from high to low IOP. Changes are exaggerated for emphasis.

2.5. Digital volume correlation of ONH displacements

The Fast-Iterative DVC algorithm was developed by Bar-Kochba et al. [44] to analyze rectangular image volumes and to calculate the deformation field by correlating the image intensity patterns of a deformed image volume to the reference volume. The algorithm initially uses a large subset size and coarse spacing for image correlation, then iteratively refines the subset size and spacing to achieve higher spatial resolution and displacement accuracy. We modified the algorithm to analyze the cylindrical volume formed by the 24 radial OCT scans and calculate the displacement fields in the R (U_R), Z (U_Z), and Θ (U_Θ) directions between images acquired at an initial (baseline) IOP and at a subsequent (deformed) IOP. For suturelysis patients, the reference images were the higher pressure (before surgery) images. For the patients who wore goggles, the reference images were the lower pressure (before goggles) images. The cylindrical volume formed by the 24 radial OCT scans was converted to a rectangular image volume by first padding the boundaries of the radial scan in Z and R with zeros. At R = 0, the signal from the opposing side of each scan (Fig. 2a, 3a) was used to pad the boundary instead of zeros so as to enable displacement correlation up to the centerline. At Θ = 0 and 2π, the signal from scans across the boundary was similarly used to pad the volume so as to enable continuous displacement correlation up to these boundaries. A starting subset size of 128 × 128 × 32 pixels and a coarse calculation spacing of 32 × 32 × 8 pixels in (R, Z, Θ) ) was selected for the first iteration and the spacing and size was refined in 5 successive iterations to a final subset size of 48 × 48 × 16 pixels and spacing of 1 × 1 × 1, or every pixel. The cross-correlation coefficient and components of the displacement field (U_R, U_Z, U_Θ) in microns were exported for subsequent analysis of strains and errors.

2.6. Displacement post-processing and strain calculations

The DVC displacement correlation error in each eye was estimated by applying a rigid body motion of 10 μm in Z and a uniform strain of 2% tension in R and 2% compression in Z to each reference volume, then applying DVC to calculate the resulting displacement field compared to the applied displacement field (Supplemental Section S2.2). We also estimated the baseline positional error due to factors such as patient motion and venous pulsation at a constant IOP by correlating 2 of the duplicate image volumes acquired at the same IOP with DVC (Supplemental Sec. S2.1). The DVC correlation and baseline displacement errors, and the strain error fields resulting from them, were summarized using 4 metrics: bias (average error), uncertainty (standard deviation of error), absolute average error (average magnitude of error), and absolute uncertainty (standard deviation of error magnitude) as shown in Supplemental Sections S2.1–S2.3.

We developed the following sequence of filters to remove regions with poor DVC correlation, high displacement errors, and displacement outliers. The specifications of the displacement filters, such as the threshold and subset size, were selected by varying the settings within each algorithm and investigating the effect on the DVC displacement and strain error fields. The settings selected reduced the average absolute displacement errors to less than 0.25 pixel.

We first applied a DVC correlation filter that removed regions with a DVC correlation coefficient below 0.055. Regions with a low cross-correlation coefficient corresponded to dark or oversaturated areas of low contrast (Supplemental Sec. S1.1). Displacement calculations within 32 pixels of the left and right edges of the image and within 25 pixels of the bottom (posterior edge) of the image were also removed because these border regions typically exhibited poor DVC correlation. A displacement error filter was applied to remove regions where the U_Z or U_R DVC correlation error exceeded 5 μm. We further removed displacement outliers where U_R or U_Z displacement was 10 μm or greater than the average displacement within an 8 pixel radius (98 × 66 μm R, Z neighborhood). A 2D Gaussian filter was applied to smooth the U_R and U_Z displacement fields and fill in small holes in the R–Z plane. A 1D Gaussian filter was applied to smooth the U_Θ displacements through all 48 slices at each R, Z pixel. Gaussian filters were designed to preserve average gradients and displacement magnitudes but to smooth sharp spikes in the displacement fields (Supplemental Sec. S1.2).

To calculate the displacement gradients with respect to R and Z at a given point, the displacements U_R, U_Z, and U_Θ, in a 71×71 pixel R–Z neighborhood were fit to a plane. To calculate the displacement gradients with respect to the Θ direction, a 4th-order polynomial function was fit to the displacement components at each pixel (R,Z) through all 48 radial scans in the Q direction, with the radial scans 1, 2, 47, and 48 on the edges of the Θ = 0 and 2π boundary repeated twice to enforce continuity of the fit at the boundary. This combination of local fitting in the R – Z plane and global fitting in Θ yielded the lowest DVC correlation strain errors in a pilot study. To prevent the calculation of strains outside of tissue boundaries and in areas of poor correlation, displacement gradients were only calculated at pixels that met the following criteria:

1. 80% or more of the points in the 5 × 5 pixel neighborhood surrounding the pixel must have displacement correlation,

2. if displacement correlation existed at the pixel, 25% or more of the points within the 71 × 71 pixel R–Z neighborhood and 48 pixel Θ neighborhood must have displacement correlation,

3. if displacement correlation did not exist at the pixel, 50% or more of the points within the 71 × 71 pixel R – Z neighborhood must be correlated to allow for interpolation of the gradients with respect to R and Z.

The cylindrical components of the Green-Lagrange strain tensor were calculated from the displacement gradients at each pixel as,

$$\begin{gathered} E_{rr}=\frac{\partial U_R}{\partial R}+\frac{1}{2}\left[{\left(\frac{\partial U_R}{\partial R}\right)}^2+{\left(\frac{\partial U_{\Theta }}{\partial R}\right)}^2+{\left(\frac{\partial U_Z}{\partial R}\right)}^2\right], \\ {E}_{zz}=\frac{\partial U_Z}{\partial Z}+\frac{1}{2}\left[{\left(\frac{\partial U_R}{\partial Z}\right)}^2+{\left(\frac{\partial U_{\Theta }}{\partial Z}\right)}^2+{\left(\frac{\partial U_Z}{\partial Z}\right)}^2\right], \\ {E}_{rz}=\frac{1}{2}\left[\frac{\partial U_R}{\partial Z}+\frac{\partial U_Z}{\partial R}+\frac{\partial U_Z}{\partial R}\frac{\partial U_Z}{\partial Z}+\frac{\partial U_{\Theta }}{\partial R}\frac{\partial U_{\Theta }}{\partial Z}+\frac{\partial U_Z}{\partial R}\frac{\partial U_Z}{\partial Z}\right], \\ {E}_{\theta \theta }=\frac{U_r}{R}+\frac{1}{R}\frac{\partial U_{\Theta }}{\partial \Theta }+\frac{1}{2}\left[\frac{1}{R^2}{\left(\frac{\partial U_Z}{\partial \Theta }\right)}^2+{\left(\frac{1}{R}\frac{\partial U_R}{\partial \Theta }-\frac{U_{\Theta }}{R}\right)}^2+{\left(\frac{1}{R}\frac{\partial U_{\Theta }}{\partial \Theta }+\frac{U_R}{R}\right)}^2\right], \\ {E}_{\theta r}=\frac{1}{2}\left[\frac{\partial U_{\Theta }}{\partial R}+\frac{1}{R}\left(\frac{\partial U_R}{\partial \Theta }+\frac{\partial U_R}{\partial \Theta }\frac{\partial U_R}{\partial R}+\frac{\partial U_Z}{\partial \Theta }\frac{\partial U_Z}{\partial R}+\frac{\partial U_{\Theta }}{\partial \Theta }\frac{\partial U_{\Theta }}{\partial R}+U_R\frac{\partial U_{\Theta }}{\partial R}-U_{\Theta }\frac{\partial U_R}{\partial R}-U_{\Theta }\right)\right], \\ {E}_{\theta z}=\frac{1}{2}\left[\frac{\partial U_{\Theta }}{\partial Z}+\frac{1}{R}\left(\frac{\partial U_Z}{\partial \Theta }+\frac{\partial U_Z}{\partial \Theta }\frac{\partial U_Z}{\partial Z}+\frac{\partial U_R}{\partial \Theta }\frac{\partial U_R}{\partial Z}+\frac{\partial U_{\Theta }}{\partial \Theta }\frac{\partial U_{\Theta }}{\partial Z}+U_R\frac{\partial U_{\Theta }}{\partial Z}-U_{\Theta }\frac{\partial U_R}{\partial Z}\right)\right]. \end{gathered}$$ (1)

The strain components E_rr, E_zz, and E_rz were used to calculate the maximum principal strain E_max, minimum principal strain E_min, and the maximum shear strain Γ_max in the R–Z plane within each image as,

$$\begin{gathered} E_{max}=\frac{E_{rr}+E_{zz}}{2}+\sqrt{{\left(\frac{E_{rr}-E_{zz}}{2}\right)}^2+E_{rz}{}^2}, \\ {E}_{min}=\frac{E_{rr}+E_{zz}}{2}-\sqrt{{\left(\frac{E_{rr}-E_{zz}}{2}\right)}^2+E_{rz}{}^2}, \\ {\mathrm{\Gamma }}_{max}=\sqrt{{\left(\frac{E_{rr}-E_{zz}}{2}\right)}^2+E_{rz}{}^2}. \end{gathered}$$ (2)

Principal strains were calculated in the R–Z plane rather than in 3D because the displacement resolution in Θ decreased with the radial distance and was lower on average than the displacement resolution in R and Z.

2.7. Statistics

The strain measures E_rr, E_zz, E_θθ, E_max, E_min, and Γ_max in both the suturelysis and goggle eyes were averaged within the ALC, PLNT, retina, choroid, and sclera tissues within the ONH and within the central and peripheral ONH regions as described in Section 2.4. Statistical analyses were performed using the MATLAB statistics and machine learning toolbox (version R2015a). We analyzed: 1) differences in the outcomes between the tissues of the ONH; 2) differences in the outcomes in the central and peripheral ALC; 3) associations between the average ALC strain outcomes, ALD change, IOP change, and IOP change as a percentage of the higher IOP value.

When reporting strain for goggle and suturelysis groups separately, the initial pressure state (before alteration by surgery or goggles) was used as the reference. Thus, strain in suturelysis eyes signifies the decrease in strain with IOP lowering. Strain in the goggle eyes is from the increase in pressure from tight-fitting goggles pressing on the orbit of the eye. For statistical tests 2 and 3 the groups were combined by reversing the sign of strain and ALD change in the goggle eyes, thus ALD change and strain outcomes correspond to a lowering of IOP from a higher IOP reference in these analyses for both groups. This will allow the strains from the 2 groups to be analyzed together for associations with ALD and IOP change, increasing the range of IOP change and baseline IOPs investigated. We reversed the sign of the strains for the goggle group rather than rerunning the DVC analysis using the high pressure images as the reference state for simplicity. The difference between these two methods are small because the strains in the ONH are small.

For analysis of data with more than one measurement per eye, e.g. the comparison of strains between ONH tissues and between the central and peripheral ONH, a repeated measures model and repeated anova (fitrm, ranova) was used, which took into the account the correlation between measurements within the same eye. Pairwise comparisons, mean differences, and 95% confidence intervals were obtained afterward from the model with the MATLAB function multcompare. A one-sample student’s T-test (ttest) was used to determine if regional strain measures and ALD change were significantly different than zero on average across all specimens. For analysis of data with one measurement per eye, e.g. the correlation between the average strain in the ALC and IOP change, a linear model (fitlm, anovan) was used. Clustering of eyes from the same donor and age, race, and sex were not accounted for in these models due to the small sample size. Comparisons were considered significant if the p-value from each model was less than 0.05.

3. Results

DVC correlation within the LC depended on visibility in the OCT scans, which varied with the thickness and the morphology of blood vessels in the overlying neural tissue. For the 5 suturelysis eyes, we were able to calculate strain in 63% of the ALC volume, 83% of the central ALC volume and 42% of the peripheral ALC volume. For the 5 goggle eyes, which had thicker neural tissues above the LC, we were able to calculate strain in 52% of the ALC volume, 67% of the central ALC volume and 37% of the peripheral ALC volume. DVC correlation within the PLC was poor, and less than 10% on average, so strains were not analyzed within this region.

Average displacement errors were estimated to be less than 1/4 pixel and average strain errors less than 0.37%. Average absolute displacement error was less than 1.3 μm in R, 0.8 μm in Z, and 2.3 μm in Θ. Average absolute strain error was less than 0.37% for E_rr, 0.35% for E_zz, 0.26% for E_rz, and 0.29% for E_θθ. Average displacement uncertainty (standard deviation of error) was less than 1.6 μm in R, 0.8 μm in Z, and 2.6 μm in Θ. Average strain uncertainty was less than 0.47% for E_rr, 0.31% for E_zz, 0.33% for E_rz, and 0.39% for E_θθ (Suppemental Sec. S2.3).

3.1. IOP-induced strains in the ONH

In the 5 suturelysis eyes, IOP decreased by 9–20 mmHg (15.2±4.1 mmHg), resulting in significant positive E_zz strain (Fig. 8a–e) and significant maximum principal strain E_max and maximum shear strain Γ_max in the tissues of the ONH (Fig. 6a). E_zz strain was 0.763±0.240% in the ALC (p = 0.0021), 0.826±0.516% in the PLNT (p = 0.0232), and 2.396±1.815% in the choroid (p = 0.0418) (Fig. 5a). ALD also increased significantly by 3.71 ± 1.90 μm on average (p = 0.0121, Supplemental Tab. S3). The average radial strain E_rr (−0.170±0.339%), circumferential strain E_θθ (−0.404±0.745%), and shear strain components E_rz, E_θr, E_θz were not statistically greater than zero in the ALC (Fig. 6a). The 3 ONH with smaller ALD at baseline (< 400 μm) had negative average E_rr (−0.306 ± 0.193%) and E_θθ (−0.892 ± 0.413%) in the ALC (Tab. Supplemental Tab. S3), which would be consistent with a contraction in LC diameter with IOP lowering (Fig. 7a). The 2 ONH with larger ALD at baseline (> 450 μm) had on average positive E_rr (0.034±0.498%) and E_θθ (0.328 ± 0.413%) in the ALC (Tab. Supplemental Tab. S3), which indicated an expansion in LC diameter with IOP lowering.

Figure 8:

E_zz strains within the I-S sector of each eye after IOP alteration. E_zz at the lower IOP for suturelysis patients: a) Eye 1L (24–10 mmHg), b) Eye 2L (38–18 mmHg), c) Eye 3R (29–13 mmHg), d) Eye 4L (21–4 mmHg), and e) Eye 5L (20–11 mmHg). E_zz at the higher IOP for goggle wearing patients: f) Eye 6L (14–17 mmHg), g) Eye 7R (18–22 mmHg), h) Eye 7L (21–24 mmHg), i) Eye 8R (19–23 mmHg), and j) Eye 8L (20–20 mmHg). The lines — denote tissue boundaries determined by manual segmentation and - - the radial position of the BMO points

Figure 6:

Comparison of the strain outcomes in the ALC a) after IOP-lowering via suturelysis and b) after IOP increase from wearing goggles, showing the p-values for strain outcomes significantly different than zero (*). Both groups experienced significant maximum principal strain E_max and maximum shear strain Γ_max. E_zz strain was positive in the suturelysis group, which indicates that the tissue experienced less compression at the lower pressure, and negative in the goggle group, indicating greater compression at the higher pressure.

Figure 5:

Comparison of E_zz strain in the tissues of the ONH a) after IOP-lowering via suturelysis and b) after IOP increase from wearing goggles, showing the p-values for strain outcomes significantly different than zero (*). E_zz was significantly different than zero in both groups.

Figure 7:

Strains within the ONH of Eye 2L after IOP lowering from 38 to 18 mmHg from suturelysis. The left column shows strain outcomes overlaid on scan 1 (inferior-superior, 180°–0°) at the lower IOP. The right hand column shows the thickness averaged ALC strains plotted on the reconstruction of the anterior LC surface at the lower IOP. a) E_rr within I-S sector , b) E_rr within ALC, c) E_zz within I-S sector, d) E_zz within ALC, e) E_max within I-S sector, f) E_max within ALC, g) Γ_max within I-S sector, h) G_max within ALC. The lines — denote tissue boundaries determined by 17 manual segmentation, - - the radial position of the BMO points, and the radial position dividing the central and peripheral ALC. Note that DVC correlation within some images covered only part of the region within the marked boundaries of the choroid.

In the 5 goggle eyes, IOP increased by 0–4 mmHg (2.8±1.6 mmHg), which generated compressive E_zz strain in the ALC (Fig. 8f–j). Average E_zz strain was −0.319 ± 0.077% in the ALC (p = 0.0007) and − 0.275±0.268% in the PLNT (p = 0.0834) (Fig. 5b). ALD change was near zero on average (−0.503 ± 1.892 μm), decreasing in 3 eyes, increasing in one eye, and remaining unchanged in one eye (average magnitude: 1.6±0.9 μm, Supplemental Tab. S3). Average E_rr, E_θθ, E_rz, E_θr, E_θz strains in all ONH tissues were not statistically greater than zero (Fig. 6b, Supplemental Tab. S3).

In the following sections, ALD change and strain outcomes in the ALC will be reported for an IOP difference between higher and lower for both the suturelysis and goggle groups. This will allow the strains from the 2 groups to be analyzed together for associations with ALD and IOP change.

3.2. Regional strain variations in the anterior LC

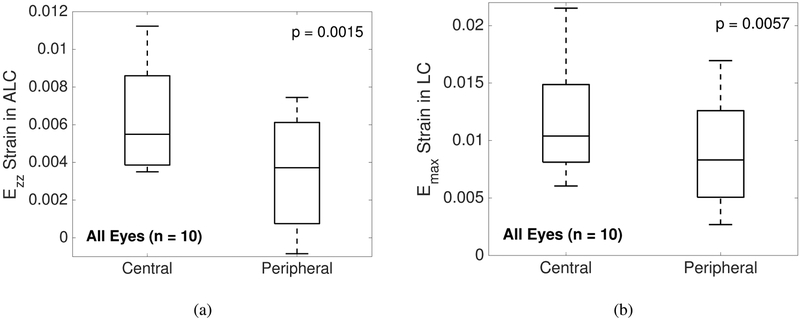
The central ALC had significantly greater E_zz (p = 0.0016,n = 10) and E_max (p = 0.0057,n = 10) than the peripheral ALC (Tab. 2, Fig. 9). There were no significant differences in average ALD change or Γ_max between the central and peripheral ALC.

Table 2:

Comparison of average strain outcomes and ALD change in the central and peripheral ALC regions. The central ALC had greater average E_zz and E_max strains compared to the peripheral ALC in both suturelysis and goggle eyes (p < 0.006,n = 10).

Sample Size	Outcomes in Anterior LC	Central Average	Peripheral Average	Mean Difference Central - Peripheral (95% CI)	p-value repeated anova
Suturelysis (n=5)	ALD Change (μm)	3.732±1.864	3.543±2.018	0.189 (−0.856, 1.233)	0.6421
	Ezz Strain (10−2)	0.888±0.211	0.490±0.308	0.398 (0.138, 0.657)	0.0131
	Emax Strain (10−2)	1.367±0.480	1.212±0.332	0.155 (−0.124, 0.433)	0.1977
	Γmax Strain (10−2)	1.078±0.493	0.945±0.342	0.134 (−0.311, 0.578)	0.4512
Goggles (n=5)	ALD Change (μm)	0.597±1.957	0.356±1.967	0.241 (−0.890, 1.372)	0.5858
	Ezz Strain (10−2)	0.387±0.025	0.188±0.199	0.199 (−0.019, 0.416)	0.0641
	Emax Strain (10−2)	0.895±0.369	0.529±0.220	0.365 (0.121, 0.610)	0.0143
	Γmax Strain (10−2)	0.669±0.253	0.557±0.176	0.112 (−0.152, 0.376)	0.3031
All Eyes (n=10)	ALD Change (μm)	2.164±2.445	1.949±2.520	0.108 (−0.367, 0.583)	0.6189
	Ezz Strain (10−2)	0.638±0.300	0.339±0.291	0.298 (0.148, 0.448)	0.0015
	Emax Strain (10−2)	1.131±0.474	0.871 ±0.447	0.260 (0.097, 0.423)	0.0057
	Γmax Strain (10−2)	0.874±0.428	0.751±0.328	0.123 (−0.076, 0.322)	0.1954

Figure 9:

Comparison of the average a) E_zz and b) E_max in the central and peripheral ALC regions for all eyes (n = 10). Both strain outcomes were greater in the central ALC compared to the peripheral ALC (p ¡ 0.01).

3.3. Variations in LC deformation with IOP

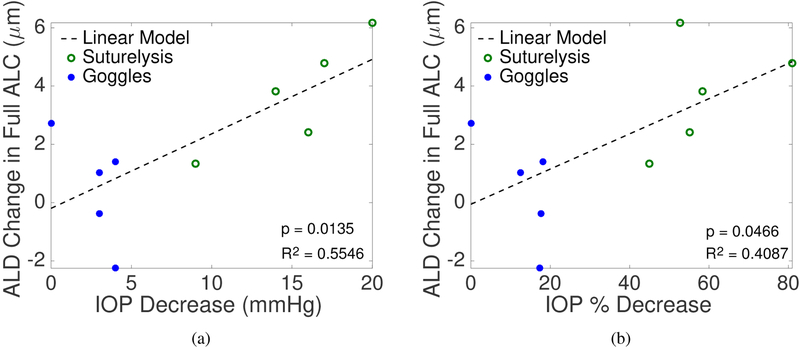
We applied linear regression models to investigate associations between the ALC strains, ALD change, and IOP change. On average, a larger E_zz was obtained for a greater decrease in IOP in the ALC (p = 0.0228,n = 10, Fig. 10a) and central ALC (p = 0.0040,n = 10). This means that on average, a larger decrease in IOP produced a larger decrease in the compressive strains experienced by the ALC. A larger E_max (p = 0.0085,n = 10, Fig. 10c) and Γ_max (p = 0.0110,n = 10, Fig. 10e) were obtained in the peripheral ALC for larger IOP decrease (Tab. 3). We also analyzed for association of IOP as a percentage of the higher IOP value to account for differences in the range of IOP. The linear regression for the percent IOP change had a higher correlation coefficient and lower p-value than the association with absolute IOP change (Tab.3), which suggests that the ALC exhibits a nonlinear pressure-strain response. A larger E_zz was associated with a higher percentage of IOP decrease in the ALC (p = 0.0024,n = 10, Fig. 10b) and in the central ALC (p = 0.0001,n = 10). Likewise a larger E_max (p = 0.0017,n = 10, Fig. 10d) and Γ_max (p = 0.0126,n = 10, Fig. 10f) was obtained for a larger percent IOP decrease in the peripheral ALC.

Figure 10:

Variation in the strain outcomes with the change in IOP showing: a) E_zz in the ALC increasing with larger IOP decrease and b) larger percentage IOP decrease relative to the higher IOP; c) E_max in the peripheral ALC increasing with larger IOP decrease and d) larger percentage IOP decrease relative to the higher IOP; e) Γ_max in the peripheral ALC increasing with larger IOP decrease and f) larger percentage IOP decrease relative to the higher IOP.

Table 3:

Linear models were used to investigate the correlation of IOP decrease (mmHg) and percent IOP decrease (%) with average E_zz, E_max, and Γ_max strains within the full, central, and peripheral ALC. Bolded p-values represent significant correlations. There was a significant positive correlation between IOP decrease and average ALD change in the LC (p = 0.0135), and a significant positive correlation between percent IOP decrease and average E_max within the peripheral ALC (p = 0.0017), average Γ_max within the peripheral ALC (p = 0.0126), and average E_zz (p = 0.0001) in the central ALC. IOP decrease correlated similarly with strains, but with less significance.

Linear correlation: LC deformation and IOP	LC Region	Mean change per 10 mmHg IOP decrease (95% CI)	R2	p-value (linear model)	Mean change per 10% IOP decrease (95% CI)	R2	p-value (linear model)
ALD Change (μm)	Full	2.556 (0.689 4.424)	0.555	0.0135	0.604 (0.012 1.197)	0.409	0.0466
	Central	2.493 (0.594 4.392)	0.534	0.0164	0.560 (−0.055 1.175)	0.355	0.0691
	Peripheral	2.547 (0.568 4.525)	0.524	0.0179	0.642 (0.050 1.233)	0.439	0.0368
Ezz Strain (10−2)	Full	0.284 (0.051 0.516)	0.497	0.0228	0.093 (0.044 0.142)	0.704	0.0024
	Central	0.341 (0.144 0.538)	0.666	0.0040	0.106 (0.070 0.142)	0.850	0.0001
	Peripheral	0.153 (−0.155 0.460)	0.141	0.2852	0.066 (−0.008 0.140)	0.345	0.0744
Emax Strain (10−2)	Full	0.371 (−0.039 0.780)	0.353	0.0702	0.121 (0.022 0.220)	0.497	0.0228
	Central	0.317 (−0.157 0.791)	0.229	0.1615	0.111 (−0.006 0.229)	0.374	0.0604
	Peripheral	0.484 (0.161 0.806)	0.600	0.0085	0.147 (0.073 0.220)	0.726	0.0017
Γmax Strain (10−2)	Full	0.287 (−0.045 0.619)	0.331	0.0817	0.093 (0.011 0.175)	0.458	0.0316
	Central	0.276 (−0.156 0.708)	0.214	0.1786	0.101 (−0.004 0.207)	0.381	0.0574
	Peripheral	0.347 (0.104 0.591)	0.576	0.0110	0.094 (0.026 0.163)	0.561	0.0126

A larger IOP decrease caused the anterior LC surface to move more posteriorly relative to BMO and resulted in a greater average ALD change in the central (p = 0.0164), peripheral (p = 0.0179), and full LC (p = 0.0135,n = 10, Fig. 11a). ALD change was significantly related both to degree of IOP change and percent IOP decrease relative to the higher IOP (Tab. 3, Fig. 11).

Figure 11:

Variation in the ALD change with the change in IOP showing: a) ALD deepening with larger IOP decrease and b) larger percentage IOP decrease relative to the higher IOP.

3.4. Variations in LC strains with ALD

We next evaluated the association between ALC strains and ALD change (Tab. 4). For the full ALC, E_max and Γ_max were significantly greater with greater ALD change (p ≤ 0.0448,n = 10). In the central ALC, ALD change significantly increased with increasing E_zz (p = 0.0489,n = 10, Fig. 12a) and E_max (p = 0.0457,n = 10). In the peripheral ALC, ALD change significantly increased with increasing E_max (p = 0.0391,n = 10) and Γ_max (p = 0.0161,n = 10, Fig. 12c).

Table 4:

Linear models were used to investigate the correlation of average ALD change and average E_zz, E_max, and Γ_max strains within the full, central, and peripheral ALC. Bolded p-values represent significant correlations. ALD change had a significant positive correlation with average Γ_max strain within the peripheral ALC (p = 0.0161), E_zz strain within the central ALC (p = 0.0489), and E_max strain within the central (p = 0.0457) and peripheral (p = 0.0391) ALC.

Linear Correlation: Strain and ALD Change	LC Region	Mean strain per 1 μm ALD change (95% CI)	R2	p-value (linear model)
Ezz Strain (10−2)	Full	0.068 (−0.009 0.146)	0.341	0.0764
	Central	0.078 (0.000 0.155)	0.402	0.0489
	Peripheral	0.043 (−0.044 0.131)	0.138	0.2897
Emax Strain (10−2)	Full	0.126 (0.020 0.233)	0.484	0.0255
	Central	0.124 (0.003 0.246)	0.411	0.0457
	Peripheral	0.117 (0.007 0.226)	0.432	0.0391
Γmax Strain (10−2)	Full	0.093 (0.003 0.184)	0.414	0.0448
	Central	0.088 (−0.035 0.212)	0.255	0.1365
	Peripheral	0.095 (0.023 0.168)	0.536	0.0161

Figure 12:

Variation in the strain outcomes with the change in ALD showing: a) E_zz in the central ALC increasing with deepening ALD, b) E_max strain in the full ALC increasing with deepening ALD, and c) Γ_max in the peripheral ALC increasing with deepening ALD.

4. Discussion

We developed a method to estimate LC strain by analyzing deformation of the ONH in radial OCT scans in vivo before and after IOP changes. The radial scans are centered on the ONH and provide high spatial resolution imaging of the LC volume, using significantly fewer images than horizontal scans. Furthermore, the limiting entry points to the ONH, the ends of Bruch’s membrane, are seen well on either side of every radial image, as compared to horizontal scans which often cannot analyze the upper and lower poles of the ONH using this landmark. Because fewer images are necessary for this analysis, imaging time is faster and there is less DVC correlation error caused by eye motion. The Spectralis software accounts for rigid body motion of the eye during scanning, but it cannot account for the strains induced by eye motion. Thus, longer imaging times result in more spatial uncertainty in the imaged volume. We developed a series of post-processing steps to filter out regions of poor displacement correlation and high displacement errors to further decrease the average baseline positional and strain errors.

Girard et al. [38, 39] reported a DVC method to analyze OCT volumes, composed of horizontal B-scans of the ONH taken before and after trabeculectomy. They reported a reduction in effective strain, which was defined by the authors in [39], after IOP-lowering surgery in the LC volume. Their illustrations suggest that the portion of images identified as LC was much larger than that selected here. The authors estimated an average effective strain error of 1.07% from consecutive OCT scans at the same IOP [39]. We used a similar method to estimate baseline errors, and determined that the mean absolute displacement and strain errors were < 2.3 μm (1/4 pixel in R,Z,Θ) and 0.37% respectively. Beotra and coworkers [39] measured average effective strains in the LC of 6.08 ± 3.31% for primary open-angle glaucoma subjects and 4.05 ± 2.40% for primary angle-closure glaucoma subjects with brief ophthalmodynamometry-induced IOP elevations of 18 ± 4 mmHg to 36 ± 5 mmHg. For comparison, we calculated an average effective strain of 2.78 ± 1.10% in the LC for an IOP decrease of 26 ± 7 mmHg to 11 ± 5 mmHg for our 5 suturelysis patients using the strain definition provided by Beotra et al.

Prior studies that measured ALD movement in vivo after IOP-lowering surgery as a surrogate for LC strain used OCT images acquired either within 2 minutes or weeks apart. Beotra et al. [40] imaged the ONH after less than 2 minutes of ophthalmodynamometer scleral indentation, during which the viscoelastic ONH response may not have fully equilibrated, leading to ALD changes of only −2.80 ± 3.59 μm for primary open-angle glaucoma subjects. Likewise, Agoumi et al. measured ALD changes ≤ 10 μm after brief ophthalmodynamometer indentation [31]. In the present series, the suturelysis-induced, ALD change ranged from 1.3–6.2 μm. The positive ALD change indicated that IOP decrease caused the average anterior LC surface to move posteriorly. In our previous study of ALD change after suturelysis, mean ALD change was 47 ± 142 μm and mean absolute ALD change was 112 ± 90 μm, with some LC moving anteriorly and some posteriorly, depending upon the degree of glaucoma damage [33]. Clearly, the direction of ALD movement is likely to be influenced not only by the direction of IOP change, but by the combined action of scleral and LC strain. However, in our original report, some eyes were imaged on the same day and some were imaged weeks apart. In the present study, to avoid the confounding effects of remodeling, we performed all imaging on the same day as IOP change, but not in as short a time frame as the ophthalmodynamometry studies. This is likely to permit fuller immediate strain change, but will avoid tissue remodeling that would occur over weeks. While each study approach has value in determining the tissue response, the spacing between images needs to be accounted in evaluating such strain data.

In addition to the length of time between images, the amount of IOP change and, potentially, the range within which IOP change occurred [33], are important variables determining measured strain. While more data are needed to evaluate these associations, with mean IOP lowering by suturelysis of 15.2 ± 4.1 mmHg, average anterior-posterior strains of E_zz = 0.6–1.0% and ALD changes of 1.3–6.2 μm were induced in the ALC. Goggle-wearing changed IOP by a smaller amount (mean = 2.8 ± 1.6 mmHg), inducing ALD change from −2.3 to 2.7 μm and compressive anterior-posterior LC strains of 0.3–0.4%. Even with such small IOP changes, average E_zz strains and ALD change magnitudes were larger than zero and of the same order as the estimated DVC displacement and strain errors in the Z direction of 0.72 μm and 0.34% respectively. Thus, our method can measure LC deformation even for small IOP changes. More recently, we have achieved IOP increase up to 15 mmHg by tightening the goggle fit. Wearing tight-fitting goggles without lenses is a promising method for inducing short-term IOP changes to measure LC biomechanics with imaging.

The method presented here allows for regional strain comparisons within the LC. In these initial eyes, LC strains exhibited large regional variation. E_zz and E_max strains were larger in the central LC compared to the peripheral LC, perhaps due to variation in LC microstructure and shape. The central LC beams are generally arranged perpendicular to the OCT image axis, while those of the peripheral LC curve significantly upwards to join the sclera, an effect that will be exaggerated in more damaged glaucoma eyes. Interestingly, the DVC strain maps showed that an increase in IOP placed the central LC in compression, but could induce tension in the peripheral LC. The presence of regions of compressive and tensile strains in the peripheral LC caused the average E_zz strain to be lower than in the central LC.

It is interesting to compare LC strains measured in post mortem eyes with those from in vivo imaging methods. While we previously conducted an ex vivo inflation test of the human ONH, the calculated strains were only accurate near the posterior surface of the LC and anterior-posterior strain could not be accurately assessed [9]. Coudrillier et al. measured the strain in the ex vivo porcine ONH between 6 and 30 mmHg [13] and reported accurate anterior-posterior strains as of 22.1 ± 2.0% on average, which were larger than the strains measured in the plane of the laminar beams (the radial-circumferential plane). While this study also measured greater average anterior-posterior strains, the magnitude of the strains was smaller. This could be because of differences between species or between the ex vivo and in vivo models. In addition to lacking blood flow and having potential autolytic change in cellular structure, the optic nerves were cut flush to the sclera in the ex vivo inflation tests, which may result in a more compliant LC inflation response and larger anterior-posterior strains. Moreover, strains were measured in the ex vivo experiments from a lower baseline IOP, where the LC exhibits a more compliant inflation response than at higher IOP. Ocular tissues exhibit significant creep in response to changes in IOP, which varies between eyes but is reduced after equilibration at a constant pressure ex vivo [9]. It will be interesting to perform controlled in vivo imaging over short-term periods to assess the creep in the living eye.

In this study we showed that ALD change was significantly associated with IOP change and also with E_zz, E_max, and Γ_max strains in the ALC. Vianna et al. [45] showed a significant association between choroidal thickness and the measurement of ALD referenced to the BMO and proposed that changes in choroidal thickness may also influence the calculation of ALD change referenced to the BMO. While we acknowledge that choroidal thickness also changes with IOP, the significant narrowing of the choroid near the ONH, at the point where it joins the end of Bruch’s membrane, means that the movement of the BMO relative to the choroidal thickness change, as measured under the fovea, is small. This can be visually confirmed in Eye 4L where the choroid narrows at the BMO (Fig. 2b) and ALD changes near both BMO endpoints were near-zero (Fig. 4b). If ALD changes were dominated by choroid thickness changes, we would instead expect to see large ALD changes at the BMO endpoints. However, in rarer cases where the choroid remains thick underneath the BMO (Figure 3b, temporal side), choroid thickness changes may have a greater influence the motion of the BMO and thus ALD change. Vianna et al. [45] suggested using the choroidal-scleral interface as a reference plane to address this potential confounding factor, but we have found that the ability to indicate the choroidal-scleral interface has much higher variability than the specification of BMO end points, which is nearly 99% reproducible and 99% in agreement with human observers’ manual markings [46]. For these reasons, and the fact that the choroid usually narrows significantly at the BMO, we think that the continued use of a BMO reference plane is justified, though we acknowledge that some investigators have shown value in the use of alternative reference planes.

There are several limitations to this study that warrant further discussion. This pilot study had a small sample size, and IOP changes in the goggle eyes were clustered over a small range. The clustering of the data for the goggle-wearing group about a small IOP change range will be expanded in further work. Radial SD-OCT imaging with the present instrumentation has non-ideal contrast and resolution for DVC analysis. The spacing between scans in Q varies linearly with the distance in R in radial sections, and consequently, the cylindrical voxels are more asymmetric than in rectangular volume imaging methods. While the spacing between images was small (< 18 μm) within the average BMO width in this study (1545 μm), it can be as high as 50 μm on the edge of the images where retina, choroid, and scleral strains are analyzed. Consequently, E_θθ, E_θr, and E_θz strains have lower resolution in these tissues. Contrast in Z also fades with depth, and, while we were able to study much of the zone 250 μm posterior to the anterior LC border, the zone posterior to this, which grades into the myelinated optic nerve, is not visible. Likewise, the posterior border of the sclera is most often indistinct, so that scleral strains could only be estimated by selecting an arbitrary thickness with acceptable correlation. The brightness and noise content overall varied significantly between successive image volumes. To address these issues, we used contrast enhancement to equalize the brightness of features between different IOP and gamma correction to reduce the brightness of noise in the background. These image processing methods greatly improved DVC performance. In some eyes, thicker prelaminar neural tissues and retinal blood vessels obscure parts of the LC, which reduces data on the peripheral LC and differentially affects regional assessments. The percentage of the anterior LC with displacement correlation within the acceptable error range (Central: 40 – 99%, Peripheral: 17 – 80%) and the area of correlation within the scans (Central: 2.0 – 4.7 mm², Peripheral: 0.8 – 3.9 mm²) varied significantly among eyes. The peripheral LC exhibited the largest variation in morphology, orientation, correlation area, and average strain, and these differences should be characterized in future studies to further analyze the strain response. This study used a Gaussian displacement smoothing filter, a displacement fitting window of 71×71 pixels in the R–Z plane, and a 4th order polynomial to fit displacements in Θ to calculate strains. Filters were sized to be wider than blood vessel shadows and other dark artifacts in the images, reducing the error these features introduced into the calculated strain field. These methods smoothed local sharp peaks in the strain field, but improved the accuracy of regional strain calculations in correlation error tests to less than 0.37%. In comparison, local strain calculation methods with no Gaussian filtering resulted in average strain errors in excess of 1%, mainly because of poor correlation near blood vessel shadows and on the surface of the retina.

5. Conclusions

We developed a volume correlation method to analyze radial OCT scans of the ONH in patients before and after IOP changes to measure the 3D deformation of the human ONH. The main findings of the work is that:

1. We developed a system of error filters that reduced the average absolute error in strain calculations to less than 0.37% and anterior-posterior and radial displacement calculations to less than 1.25 micron. This resolution is of the same order as the average magnitude of ALD change 1.6 μm and E_zz 0.32% for IOP changes of 0–4 mmHg applied by wearing tight-fitting swimming goggles.

2. Decreasing IOP produced a reduction in the compressive E_zz strain in the LC and a small but significant average posterior motion of the anterior LC depth.

3. LC strains and ALD change increased with a larger decrease in IOP.

4. ALD moved more posteriorly for a larger reduction in the compressive E_zz strain in the LC.