Abstract
Valve interstitial cells (VIC) are the primary cell type residing within heart valve tissues. In many valve pathologies, VICs become activated and will subsequently profoundly remodel the valve tissue extracellular matrix (ECM). A primary indicator of VIC activation is the upregulation of α–smooth muscle actin (αSMA) fibers, which in turn increase VIC contractility. Thus, contractile state reflects VIC activation and ECM biosynthesis levels. In general, cell contraction studies have largely utilized two-dimensional substrates, which are a vastly different micro mechanical environment than exist in the 3D native leaflet tissue. To address this limitation, hydrogels have been a popular choice for studying cells in a three–dimensional environment due to their tunable properties and optical transparency, which allows for direct cell visualization. In the present study, we extended the use of hydrogels to study the active contractile behavior of VICs. Aortic VICs (AVIC) were encapsulated within poly(ethylene glycol) (PEG) hydrogels and were subjected to flexural–deformation tests to assess the state of AVIC contraction. Using a finite element model of the experimental setup, we determined the effective shear modulus μ of the constructs. An increase in μ resulting from AVIC active contraction was observed. Results further indicated that AVIC contraction had a more pronounced effect on μ in softer gels (72 ± 21% increase in μ within 2.5 kPa gels) and was dependent upon the availability of adhesion sites (0.5 – 1 mM CRGDS). The transparency of the gel allowed us to image AVICs directly within the hydrogel, where we observed a time-dependent decrease in volume (time constant τ = 3.04 min) when the AVICs were induced into a hypertensive state. Our results indicated that AVIC contraction was regulated by both the intrinsic (unseeded) gel stiffness and the CRGDS peptide concentrations. This finding suggests that AVIC contractile state can be profoundly modulated through their local micro environment using modifiable PEG gels in a 3D micromechanical-emulating environment. Moving forward, this approach has the potential to be used towards delineating normal and diseased VIC biomechanical properties using highly tunable PEG biomaterials.
Keywords: heart valve interstitial cell, mechanobiology, cell–material interactions, beam bending, poly (ethylene glycol) hydrogel, cell contraction
1. Introduction
Heart valves are complex, multi-layered structures that ensure coordinated, unidirectional blood flow within the heart, and are uniquely adapted to their local environment. For example, the left ventricle is a mechanically demanding environment, and thus the residing mitral and aortic valves (MV and AV, respectively) have thicker and stiffer valve leaflets than their right-side counterparts, the tricuspid and pulmonary valves, respectively [1]. The complex microstructure of valve leaflets produces anisotropic, layer-specific mechanical responses [2, 3].
Valve interstitial cells (VIC) reside within the mechanically demanding environment of heart valve leaflet tissues, which undergo large, rapid planar deformations throughout the cardiac cycle [4]. Tissue–level stresses and deformations also provide critical stimuli that regulates the biosynthesis of extracellular matrix (ECM) proteins by mechanically induced signal transduction to VICs [5]. VICs can take on various potential phenotypes including quiescent, activated, and osteoblastic. In response to growth or pathological cues, VICs become activated and increase intracellular assembly of alpha–smooth muscle actin (α–SMA) which increases cellular contractility and aids in wound closure. In addition, activated VICs, driven by a disturbance in the homeostatic stress state of the valve, can remodel and synthesize new ECM components [6].
Previous work suggests that in response to micro environmental differences, aortic VICs (AVIC) and mitral VICs (MVIC) are stiffer and more activated than pulmonary VICs (PVIC) and tricuspid VICs (TVIC) [7, 8]. This peculiar left–right side differences between VICs can be attributed to differences in loading, embryological origin, and extracellular matrix (ECM) composition [9]. Such differences may lay the basis for age related formation of calcium nodules into the AV, which can alter the ECM and mechanics of the AV and compromise valve function [10]. Moreover, due to the intimate connection between VICs and local tissue microenvironment, understanding the influence of the surrounding ECM on VICs is critical to understanding valve disease.
The importance of studying VIC mechanobiology within different mechanical and biochemical environments is highlighted by valve diseases, such as calcific aortic valve disease [11] and myxomatous mitral valve disease [12]. Both of these diseases alter the mechanical and biochemical composition of the valve, leading to altered loading patterns onto the underlying VIC population. This in turn leads to altered cell deformation and subsequently effects VIC activation and collagen deposition [5]. The ECM remodeling activity of VICs have the potential to then initiate a positive feedback loop between altered valve mechanics and VIC biosynthesis which furthers the progression of valve disease. Thus, understanding the influence of the surrounding ECM on VICs is critical to understanding valve disease.
Despite the important biosynthetic role that VICs play in regulating valve tissue structure and function, little is known about VIC mechanobiology within the actual complex native 3D micro–environment. To date, VIC mechanical properties have primarily been studied ex–vivo using 2D techniques such as traction force microscopy [13], two–dimensional cantilever experiments [14], and micro-patterned island arrays [15]. Despite the valuable knowledge gained from these studies, the 2D substrate environment is very different to the native 3D valve leaflet and does not replicate the complexity of the 3D responses. Previously, Ayoub et al. used focused ion beam scanning electron microscopy to investigate the 3D VIC micro–environment and reported that VICs maintain intimate contact with complex collagen networks and both sheet–like lamellar and circumferentially oriented elastin networks [2]. The level of complexity observed within the native VIC miroenvironement is challenging to emulate using 2D substrates. In addition, imposing physiological and three-dimensional loading conditions is a major challenge. [16].
This situation has led us and others to study VIC mechanical responses directly within the native tissue environment [17–19]. Previously, Kershaw et al. reported that AVIC contraction directly contributes to tissue–level force generation using uniaxial testing methods [18]. Subsequently, Merryman et al. conducted bending tests on excised samples of AV leaflet tissue under different levels of AVIC contraction and demonstrated that AVIC contraction increases layer specific tissue–level stiffness [17]. To extrapolate how the mechanical contributions of AVICs affect tissue–level stiffness, Buchanan et al. developed a morphologically faithful down–scale finite element (FE) based model of the native AV leaflet tissue [20]. They determined that AVIC contraction strength, stress fiber orientation, and connectivity to ECM are the major factors that govern AVIC ability to modulate tissue stiffness [20]. The model also predicted that AVICs were 75% less connected within the ventricularis layer of the AV than in the fibrosa layer and that AVICs generate greater forces in 3D than in 2D due to an increase in attachment sites.
Although these native tissue studies led to new insights into VIC-ECM function, the ability to modify native tissues to probe VIC-ECM interactions remains very limited, nor do they lend themselves to direct VIC visualization. Our previous combined experimental–computational methods used for native tissues [20] highlights both the benefits of this approach and the need for an alternative platform to study VICs in 3D which allow for direct modulation of cellular mechanical function.
In response to these limitations, synthetic hydrogels have been used to study cells in 3D [21, 22]. These 3D matrices mimic the native environment more closely than 2D substrates and allow for staining and visualization throughout the 3D sample using fluorescence microscopy. In addition, manipulating hydrogel composition enables the investigation of a wide range of applications including the study of stem cell differentiation [23], cell traction forces [24], and cancer biology [25]. Functionalizing poly (ethylene glycol) (PEG) molecules with norbornene groups allows for the incorporation of peptide sequences with cysteine residues within the hydrogel structure. In previous work, norbornene–functionalized PEG has been used to form hydrogel matrices with MMP-degradable peptide crosslinks and with Cys-Arg-Gly-Asp-Ser (CRGDS) adhesive peptide sequences incorporated into the structure to allow for cellular attachment [22]. These hydrogels have been used extensively to study how material properties affect mesenchymal stem cell viability [26] and differentiation [27] as well as aortic valve interstitial cell (AVIC) biological function [21, 22, 28].
In the present study, we extended the use of PEG hydrogels to study AVIC contraction within tissue mimicking 3D environments. As demonstrated in our native tissue studies [17], flexure is a physiologically relevant form of deformation in the AV and is extremely sensitive to small changes in tissue or biomaterial stiffness. It is thus ideal to study the effects of VIC contraction using tissue level epxeriments of VICs embedded in PEG hydrogels. Through this experimental configuration, we set out to study how changes in hydrogel stiffness and adhesive ligand density affect AVIC contraction. We adapted our previous beam–bending FE model of the aortic valve [29] to capture the bending response of AVIC seeded hydrogels (AVIC–hydrogels) by modeling the AVIC–hydrogels using a Neo–Hookean material model. From this, we determined the effective shear modulus μ as a means to compare the macroscale stiffness of the AVIC–hydrogels under different cellular contractile states and hydrogel compositions. We then assessed AVIC contractile state within stiffness modulated and CRGDS modulated PEG hydrogels. Furthermore, we exploited the transparent optical properties of the hydrogels to directly visualize AVIC stress fiber networks using two–photon microscopy. Using this system, we are able to uniquely probe the kinetics of AVIC active contraction and quantify the associated volume loss. We demonstrate that AVIC contraction directly affects the effective shear modulus of AVIC–hydrogel constructs and we demonstrate the basic feasiblity of the hydrogel system to serve as a viable tool to be used in future VIC mechanobiological studies.
2. Materials and methods
2.1. AVIC extraction and culture
Whole porcine hearts were obtained from a local abattoir and AVICs were extracted as previously reported [30]. Briefly, the aortic valve leaflets were excised and rinsed with Earle’s Balanced Salt Solution (EBSS, Thermo Fisher Scientific) before incubation within collagenase solution (0.75 mg/ml in EBSS, Thermo Fisher Scientific) at standard conditions (37°C, 5% CO2) for 30 minutes. The initial collagenase digestion was used to remove the vascular endothelial cell layer and the solution was discarded. The leaflets were then placed in a fresh collagenase solution and incubated for 60 minutes. After the incubation period, the solution was vortexed to dislodge the AVICs from the leaflets. The solution was then filtered using a 100 μm cell strainer and centrifuged. The AVICs were resuspended and cultured in growth media (Medium 199, 15% fetal bovine serum (FBS), 2% pen-step, 0.4% fungizone, all Thermo Fisher Scientific) and AVICs with passage numbers 2–4 were used for experimentation.
2.2. AVIC-hydrogel fabrication
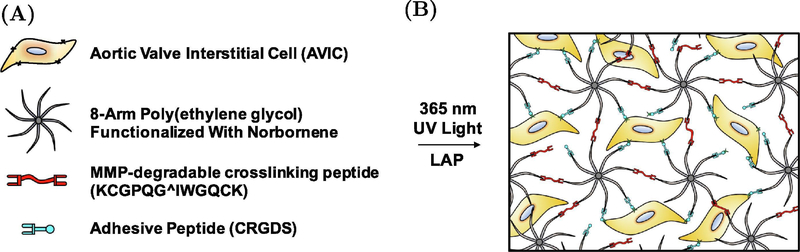
AVICs were suspended at 10 million cells/ml in a hydrogel pre-polymer solution containing 8–arm, 40 kDA PEG-norbornene (Jenkem), MMP-degradable crosslinking peptides (Bachem), CRGDS adhesive peptides (Bachem), lithium phenyl- 2,4,6 - trimethylbenzolphosphinate (LAP) photoinitiator (Sigma-aldrich), and PBS (Sigma-Aldrich) (Fig. 1A & 1B). The solution was pipetted into a silicone mold (10 × 5 × 1 mm) that was placed firmly on top of a siliconized glass slide and was polymerized underneath UV light (365 nm, ~2.5 mW/cm2) for 3 minutes. The hydrogel Young’s modulus (E) was altered for this study by adjusting the concentration of the crosslinker and the thiol:ene ratio of the polymer solution to produce hydrogels with modulus of 2.5, 5, and 10 kPa. The hydrogel moduli used in this study were chosen to represent culture environments that are soft, medium, and stiff and fall within distinct ranges that have been previously shown to elicit different AVIC biological responses [21, 28]. In the stiffness modulated gels, the CRGDS concentration was maintained at 1 mM to ensure proper attachment to the hydrogel [22]. A separate set of 10 kPa gels with altered CRGDS concentrations were fabricated (0 mM CRGDS and 0.5 mM CRGDS) to study the dependence of AVIC active contraction on CRGDS concentration, independent of hydrogel moduli. Data acquired from the 10 kPa gels from the stiffness modulated hydrogels (containing 1 mM CRGDS) was also used for comparison to the CRGDS concentration modulated gels. The composition of each unique hydrogel group is detailed in supplemental tables 1 & 2. AVIC-hydrogels were incubated for 24 hours in growth medium (15% FBS, Thermo Fisher Scientific) after fabrication and were then switched to starvation medium (1% FBS) to limit cellular proliferation. The starvation media was then changed after 3 days of culture. The AVIC-hydrogels were incubated for a total of 5 days before being subjected to experimentation.
Figure 1:
Composition of test samples. (A) Components of hydrogel precursor solution prior to polymerization. Specific concentrations of each component for every hydrogel group can be found in supplemental tables 1 & 2. (B) Schematic of AVIC-hydrogel internal architecture.
2.3. Mechanical Evaluation
2.3.1. Experimental protocol
The dimensions of each AVIC-hydrogel were measured before mechanical testing (Fig. 2A). Sections of teflon tubing were attached along the width of the AVIC-hydrogels using small amounts of cyanoacrylate glue to allow for attachment to the testing apparatus and red-tracking beads were placed along the length of the testing specimens (Fig. 2B). One side of the AVIC-hydrogel was attached to a moving post (via the section of teflon tubing) and the other side was attached to a bending bar of known stiffness. A reference rod was used to note the start position of the test and the “zero–force” position of the bending bar. A linear actuator displaced the left side of the testing specimen towards the bending bar, causing the bending bar to displace and for the sample to deflect downwards. A CCD camera was used to image the sample during testing and the positions of the red-tracking beads were recorded and used to compute the change in curvature (Δκ) of the test specimen. Each AVIC-hydrogel specimen (approximately 10 mm in length) was tested to a maximum Δκ of 0.3 mm−1 for a total of three times (under normal, hypertensive, and non-contractile conditions). First the sample was allowed to incubate for 10 minutes in phenyl red free DMEM (5 mM KCl, normal treatment) before being subjected to end-loading, flexural deformations (flex-testing). After that, the testing solution was switched to KCl supplemented phenyl-red free DMEM (90 mM KCl, hypertensive treatment) and the sample was tested again after 10 minutes of incubation. Lastly, the testing solution was exchanged for 70% methanol (non-contractile treatment) to stop cellular activate contraction through eliciting cell death and the sample was tested a final time after 10 minutes within the non-contractile solution.
Figure 2:
Mechanical testing set–up. (A) AVIC-hydrogel after 5 days of incubation. (B) Representative AVIC-hydrogel undergoing end-loading, flexural deformation testing.
2.3.2. Experimental Calculations
From the experimental data, the bending moment (M) was calculated as follows
| (1) |
where P is the axial force exerted on the test specimen calculated from the displacement and known stiffness of the bending bar and Y is the vertical deflection of the center marker (Fig. 2B). The second moment of inertia (I) is calculated from the dimensions of the test specimen as
| (2) |
The centroids of the red-tracking beads were fit to a fourth-order polynomial (y) and used to calculate the curvature (κ) of the test specimen using the following equation
| (3) |
A custom written LabView VI performed all calculations and reported the moment (M/I) and change in curvature (Δκ = κ−κ0) of the sample throughout the duration of the test. The net level of force generated in the specimen by resulting bending deformations was thus expressed as M/I at a chosen level of curvature change Δκ or end-displacement.
2.4. Finite–element simulation of the AVIC–hydrogel beam bending experiment
We observed that the AVIC–hydrogels behaved as isotropic, hyperelastic materials whose moment-curvature responses were consistently non-linear. To this end, we formulated a FE model that simulated the AVIC–hydrogel bending experiment, similar to the model developed by Buchanan et al. for the AV [29], to determine the effective mechanical properties of the gel. Specifically, the FE model was developed within FEniCS [31] and modeled the AVIC-hydrogel samples using a nearly incompressible Neo–Hookean material model implemented with tetrahedral hybrid elements via the following strain energy density function
| (4) |
where μ and λ are the shear modulus and the first Lamé parameter, respectively, I1 is the first invariant of the Right Cauchy-Green deformation tensor (I1 = tr(C) where C = FTF and F is the deformation gradient tensor), and J is the Jacobian (J = det(F)). The hydrogel was assumed to be nearly incompressible (a Possion’s ratio (ν) of 0.499 in the small strain limit). Note that for the nearly incompressible case (i.e. λ >> μ) the finite element method is prone to kinematic locking [32, 33]. To avoid locking, we use a mixed formulation where the pressure–like value (p) defined in the constitutive relation is an independent variable in addition to the displacement field. By simultaneously solving for displacement and p in a mixed finite element formulation, the kinematic locking was avoided. As we assume near incompressibility and a Neo–Hookean constitutive model, the shear modulus (μ) was the only tunable parameter in the model. The first Lamé parameter (λ) is simply computed from μ and ν as , using a small strain analogy.
The dimensions of the mesh are set to match the dimensions of the test specimens. A sufficiently refined mesh, as determined form a mesh independence study (Supplemental Fig. 1), consisted of 2400 tetrahedral hybrid elements containing quadratically interpolated displacement degrees of freedom and linearly interpolated pressure degrees of freedom (13608 total degrees of freedom). The mesh was fixed to two pin-constraints along the width of the geometry. The initial curvature of the AVIC–hydrogel specimen during testing was imposed on the simulated geometry before the bending simulations were run. To accomplish this, an arbitrary initial body force was applied onto the simulated hydrogel, which caused the hydrogel to deflect. Then, the left pin constraint was subjected to small horizontal displacements until the horizontal component of the body force on the right pin constraint decreased to zero (consistent with what was done experimentally to establish a “zero–force” position). Then, the simulated initial curvature of the mesh was computed using the spatial locations of five evenly spaced nodes along the length of the geometry and Eq. 3. This value was compared to the experimental initial curvature value and the process was iterated until an acceptable match between and was established.
After the appropriate body force was determined, the simulation of the experiment was conducted. The value of μ was determined by minimizing the difference between experimental results and simulation results obtained via the finite element method. Equation 4 serves as the strain energy density function that governs the mechanical behavior (i.e. stress–strain response) of the AVIC-hydrogel specimen within FEniCS. An initial guess for μ was input and the left pin constraint was subjected to small incremental displacements toward the fixed right pin constraint. For direct comparison to the experimental setup, a moment M at each incremental displacement was calculated by multiplying the force acting on the right pin joint with the vertical displacement of the center of the bending face of the simulated geometry. In this manner, M vs displacement (moment–displacement) plots were generated from the FE simulations and compared directly to the experimental data. The Broyden-Fletcher-Goldfarb-Shanno gradient descent algorithm (from the Python package scipy.optimize) was used to find the value of μ that produced the best-fit line as determined from least-squares regression. Once the best fit was determined, the resulting modulus μ was recorded. Simulations were run for all contractile levels (normal, hypertensive, non-contractile) in each hydrogel composition (n=5 for all compositions). Values for μ are reported as mean ± SEM.
2.5. Immunostaining
AVIC-hydrogels were fixed in 10% formalin for thirty minutes and then washed with PBS. The samples were then permeabilized with PBS-Tween (PBST, 0.05 wt% Tween 20 in PBS, Sigma-Aldrich) at room temperature for 1 hour. After that, non-specific binding was blocked with 1% bovine serum albumin (BSA, Sigma-Aldrich) in PBST for an additional hour. Primary antibodies (mouse anti-αSMA, mouse anti-αV β3 integrin, all Abcam ) in 1% BSA solution were all added at a 1:200 dilution (5 μg per ml) and the samples were incubated at 4°C overnight. The samples were washed 3 X 1h with PBS before addition of the secondary antibody solution (goat anti-mouse AlexaFluor 488 (1:300, 6.66 μg per ml, Life Technologies), NucBlue™ Fixed Cell ReadyProbes™ Reagent (DAPI, 2 drops per ml, Invitrogen), Phalloidin-Tetramethylrhodamine B isothiocyanate (stain for filamentous actin (f-actin), 1:300, 50 μg per ml, Sigma-Aldrich) and incubated at 4°C overnight before being washed 3 X 1h with PBS and imaged underneath a Bruker Ultima IV two-photon microscope (20x water immersion lens). At least 3 image stacks were obtained for every AVIC-hydrogel specimen with dimensions of 256 × 256 × 50 μm at 1 μm spacing.
2.6. AVIC volumetric measurements
It is a well established phenomenon that cells can modulate their intracellular volume, which can be highly dependent upon cell phenotype amoung other variables. [34]. Herein, we were specifically interested in assessing AVIC volumetric changes from the normal state to the chemically-induced hypercontractile state. AVIC seeded hydrogels with a functional modulus (E) of 2.5 kPa were stained with calcein AM and ethidium homodimer (EthD-1) (both ThermoFisher Scientific) per the manufacturer’s instructions. Three gel samples were imaged in total. The samples were incubated in a working solution containing 2 μM calcein AM and 4 μM EthD-1 for 45 minutes. The samples were then treated with a hypertensive solution to induce active contraction before being imaged with a Zeiss LSM inverted confocal microscope using a 40×, 1.4 numerical aperture (NA), oil-immersion objective lens (Zeiss) equipped with an environmental chamber, keeping the samples at 37°C throughout the imaging process. We obtained z-stacks encompassing entire cells every three minutes. A 213 × 213 × 39 μm volume (voxel dimensions: 0.42 × 0.42 × 1 μm ) was obtained from each gel and multiple cells were captured within the volume. The z-stacks were obtained at a step size of 1 μm in the z-direction and frame averaging (4 frames per image) was implemented to reduce random noise. The spatial and temporal resolution chosen allowed for fast image acquisition (approximately 2 min and 30 s per z-stack) while reducing the effects of phototoxicity and photobleaching.
Only live cells (staining positive for only calcein AM throughout the entire imaging process) were included in the cellular volume analysis. A custom Matlab script was used to estimate cellular volume. First, the images were subjected to a photobleach correction algorithm [35]. Then the images were subjected to a consistent threshold and pixels with positive calcein AM fluorescence were summed across all planes. This value was then multiplied by the pixel area and step size of the z-stack to arrive at a final cellular volume. We observed that the volume of the cells decreased exponentially and therefore the data was fit to the following modified exponential decay equation
| (5) |
where v is the volume at time t, v0 is the initial normalized volume (i.e. 1), and vf is the final normalized volume. The first term of Eq. 5 represents the exponential reduction of the cellular volume with respect to time and the second term enforces that the limit of Eq. 5 as t approaches ∞ becomes vf. A time constant (τ) was determined using the curve–fitting tool in Matlab.
2.7. Statistical Methods
Data was presented as ± standard error mean (SEM). A repeated measure, two–way analysis of variance (ANOVA) was performed on the absolute values of μ for both the stiffness and CRGDS concentration modulated gels. For the percent change values, a repeated measure, two–way ANOVA was performed with the non-contractile case serving as the control group. A repeated measure, one–way ANOVA was performed on the values at maximum displacement between all treatment groups for all hydrogel compositions. p–values < 0.05 were regarded as statistically significant. All statistical analysis was performed using SigmaPlot (San Jose, CA, USA). n=5 for all AVIC–hydrogel flexural deformation testing groups and n = 3 for the AVIC volumetric measurement experiments.
3. Results
3.1. Finite element model captures the flexural response of the AVIC–hydrogel specimens
The FE model (Fig. 3) was able to accurately reproduce the non–linear moment–displacement response for the unseeded hydrogel material as well as the AVIC seeded hydrogels that were stiffness moduluated (Fig. 4 & 5) and CRGDS modulated (Fig. 6 & 7) across all cell contractile levels. The mean r2 value for the fit was above 0.90 for all hydrogel groups (supplemental tables 3 & 4). From the simulations, μ was outputted and reported as mean ± SEM (Fig. 5A & 7A). It was observed that the μ values of the AVIC–hydrogel constructs increased when the cells were in a hypertensive state and decreased when the cells were in a non-contractile state across all hydrogel stiffness groups (Fig. 5). Within the CRGDS concentration modulated hydrogels, μ increased with respect to cell contraction and decreased in the absence of cell contraction in the 0.5 and 1 mM CRGDS groups whereas no change was observed with hydrogels containing 0 mM of CRGDS peptides (Fig. 7).
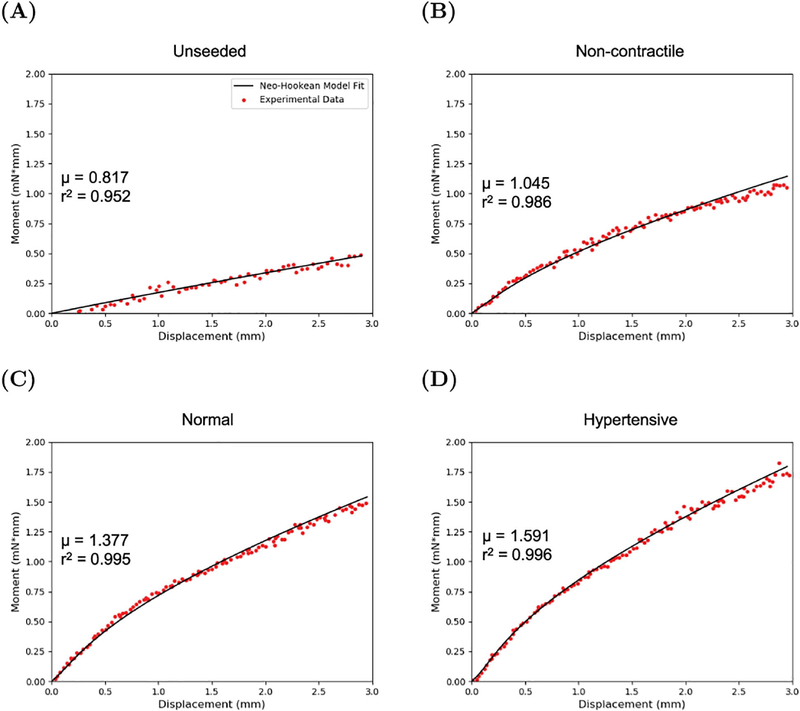
Figure 3:
Representative Neo-Hookean material model fit to the moment-displacement data of an (A) unseeded 5 kPa hydrogel and a 5 kPa AVIC–hydrogel specimen under (B) non-contractile (70 % methanol), (C) normal (5 mM KCl), and (D) hypertensive (90 mM KCl) conditions.
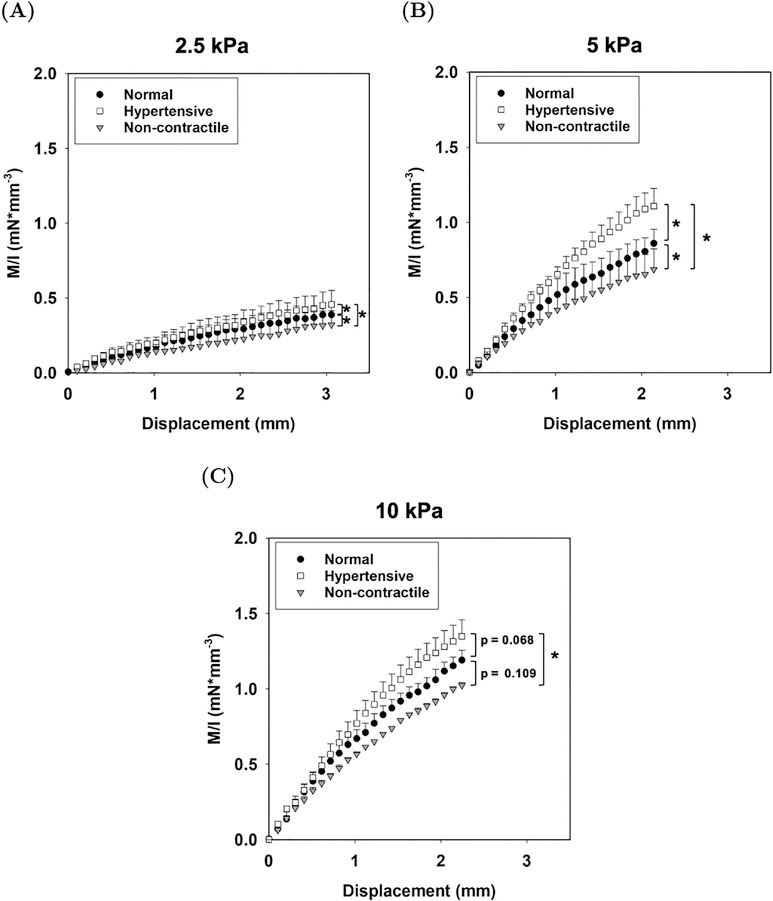
Figure 4:
Averaged experimental moment–displacement responses for (A) 2.5, (B) 5, and (C) 10 kPa AVIC-hydrogels under normal, hypertensive, and non-contractile conditions. An asterisk (*) denotes that there is a statistically significant difference between the values at maximum displacement (p–value < 0.05).
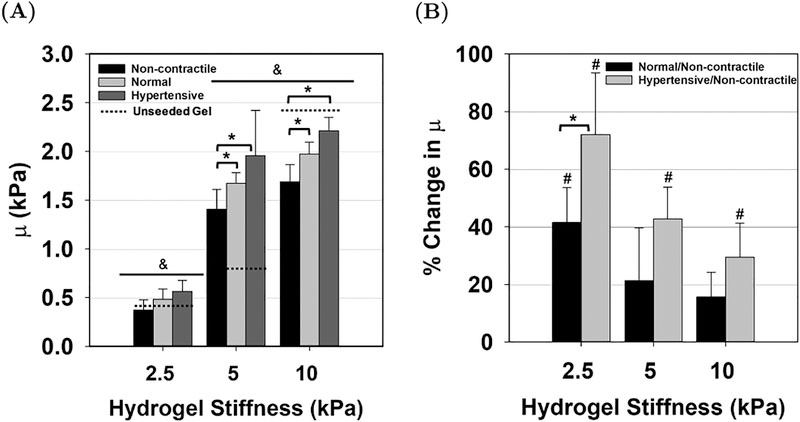
Figure 5:
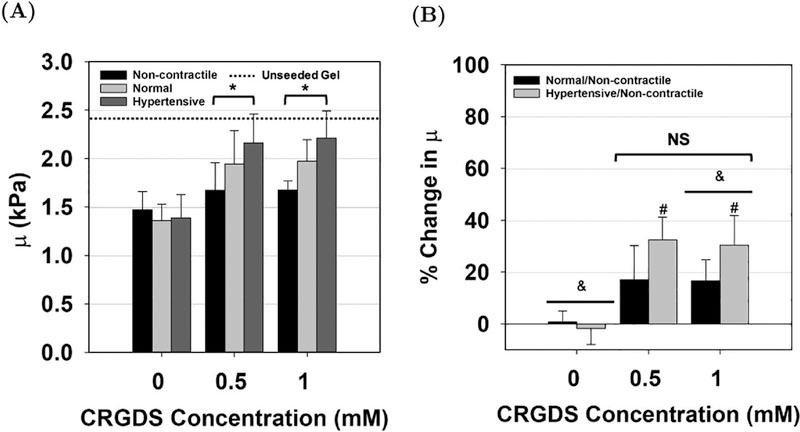
(A) Shear modulus μ determined from the FE simulations for each hydrogel stiffness group. An asterisk (*) denotes statistically significant differences (p-value < 0.05) between the contractile levels and the ampersand symbol (&) denotes statistically significant differences between hydrogel stiffness groups. (B) Percent change of the normal and hypertensive μ from the non-contractile condition. An asterisk (*) denotes statistically significant differences between the contractile levels and a pound symbol (#) denotes statistically significant differences from the control (non-contractile/non-contractile).
Figure 6:
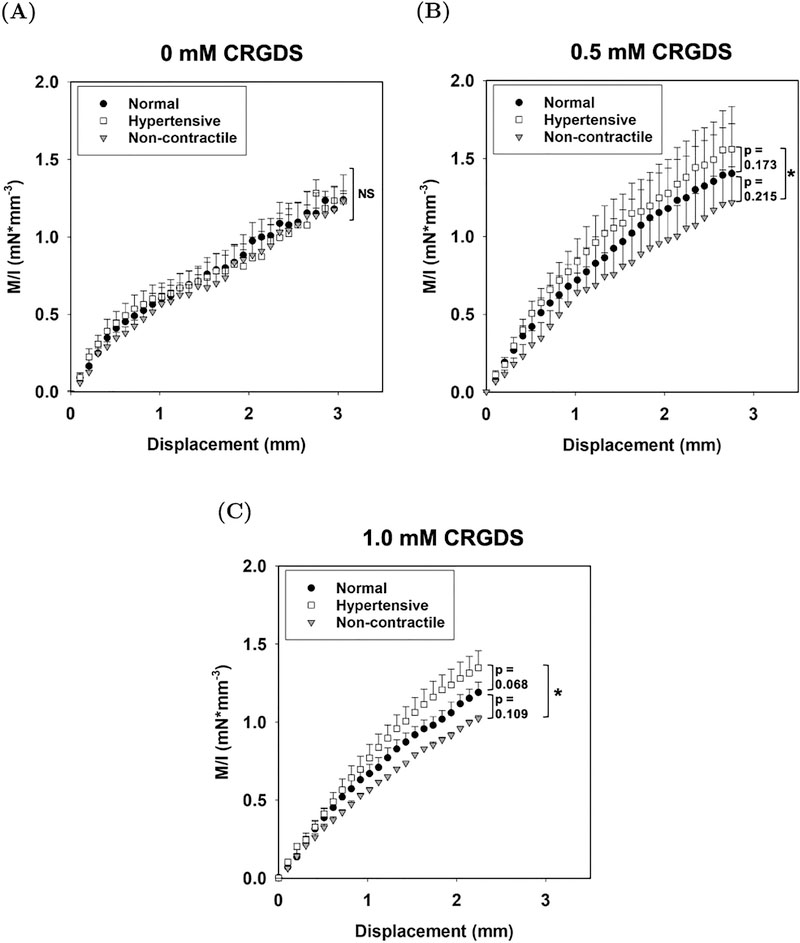
Averaged experimental moment–displacement responses for (A) 0, (B) 0.5, and (C) 1 mM CRGDS hydrogels under normal, hypertensive, and non-contractile conditions. An asterisk (*) denotes that there is a statistically significant difference between the values at maximum displacement (p–value < 0.05).
Figure 7:
(A) Material parameter μ determined from the FE model for AVIC-hydrogels containing 0, 0.5, and 1 mM of CRGDS peptide. An asterisk (*) denotes statistically significant differences (p-value < 0.05) between the contractile levels. (B) The percent change from the non-contractile μ to the normal and hypertensive μ for various CRGDS concentrated AVIC-hydrogels. No significant difference was found between the 0.5 and 1.0 mM CRGDS groups. An ampersand symbol (&) denotes statistically significant differences between the CRGDS concentration groups whereas a pound symbol (#) denotes statistically significant difference from the control (non-contractile/non-contractile).
3.2. AVIC response to hydrogel modulus
We observed higher M/I values at the maximum displacement after treating the samples with the hypertensive solution and lower M/I values after treatment with the non-contractile solution as compared to the normal condition among all hydrogel stiffness groups (Fig. 4). The differences in M/I at the maximum displacement values were statistically significant between the normal, hypertensive, and non–contractile treatments within 2.5 kPa and 5 kPa hydrogels (Fig. 4A & 4B). In the 10 kPa group, there was only a significant difference between the hypertensive and non-contractile conditions (Fig. 4C). Higher stiffness hydrogels showed higher M/I values and clear distinction between the different treatment conditions was observed in the M/I vs displacement plots across all stiffness groups (Fig. 4). Further analysis of the moment–displacement responses showed an increase in μ between the normal and non-contractile state and between the hypertensive and normal state for all hydrogel stiffnesses (Fig. 5A). Results show that the effects of AVIC basal contraction within the normal state (basal tonus) accounted for an average increase of 42 ± 12% in μ in the 2.5 kPa group, a 21 ± 18% increase in the 5 kPa group, and only a 16 ± 9% increase in the 10 kPa group (Fig. 5B). The hypertensive treatment resulted in a total of 72 ± 21% increase in μ from the non-contractile state in the 2.5 kPa group, an increase of 43 ± 11% in the 5 kPa group, and an increase of 29 ± 12% in the 10 kPa groups (Fig. 5B). The shear modulus of cell–seeded 2.5 and 5 kPa AVIC–hydrogel samples were either equivalent or above the shear modulus of the unseeded gel. In the 10 kPa case, the cell–seeded hydrogel samples were less stiff than the unseeded gel.
3.3. AVIC contraction response with varying levels of CRGDS
Adjusting the CRGDS concentration within the AVIC-hydrogel constructs altered cellular active contraction response. From the mechanical evaluation of the specimens, we observed statistically significant differences in moment values at the maximum displacement between the hypertensive and non-contractile conditions among hydrogels containing 0.5 and 1 mM of CRGDS adhesive peptides (Fig. 6B & 6C). This distinction is lost among hydrogels containing 0 mM CRGDS (Fig. 6A).
We observed an increase in μ from the non-contractile state to the normal state and from the normal state to the hypertensive state in both the 0.5 and 1.0 mM CRGDS hydrogel groups, whereas no change was observed in the 0 mM CRGDS group (Fig. 7A). The percent change in μ from the non-contractile state to both the hypertensive and the normal state was computed for every CRGDS concentration level (Fig. 7B). No increase in μ was observed after treatment with the hypertensive solution among hydrogels containing 0 mM of CRGDS. There was approximately a 17 ± 13% increase in μ from the non-contractile condition to the normal condition in hydrogels containing 0.5 mM of CRGDS and a 32 ± 9% increase in μ when active contraction was induced with the hypertensive treatment. In the 1 mM CRGDS group, there was a 17 ± 8% increase in μ from the non-contractile to the normal condition and a 30 ± 11% increase when the AVICs were in a hypertensive state. There appeared to be no drastic differences in the effects of cell contraction on the percent change of the hydrogel bending stiffness between the 0.5 mM and 1.0 mM CRGDS groups. Futhermore, the cell–seeded, CRGDS peptide concentration modulated AVIC–hydrogel specimens were found to be less stiff than the unseeded gel.
3.4. Visualization of AVIC intracellular structures
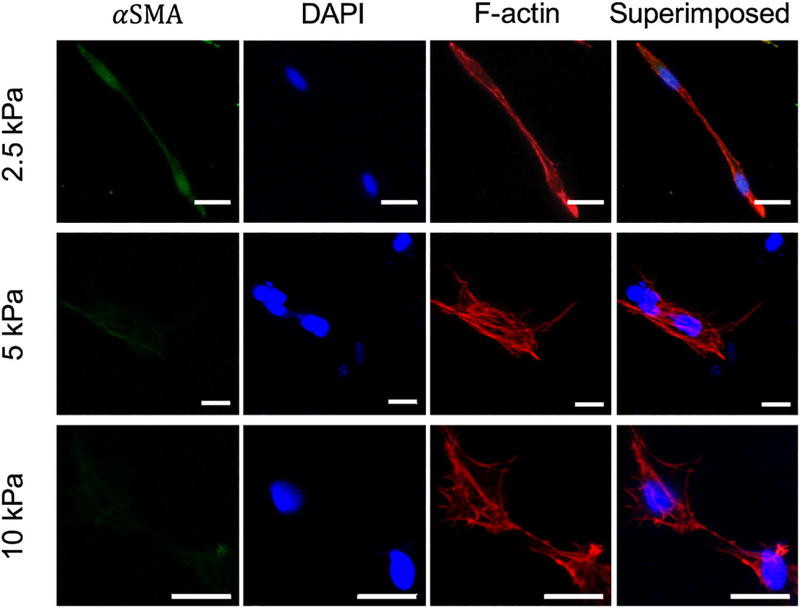
F-actin and α-SMA stress fibers were stained and imaged within 2.5, 5, and 10 kPa hydrogels (Fig. 8). The presence of α-SMA stress fibers is a hallmark of AVIC activation. It was observed that within 2.5 kPa gels, AVICs qualitatively expressed more α-SMA overall than when encapsulated within 5 and 10 kPa gels (Fig. 8). In addition, AVICs were more elongated, consistent with previous studies using low modulus gels [22]. Across all gel moduli, it was observed that AVICs formed complex f-actin structures and established multiple points of contact with the surrounding hydrogel environment.
Figure 8:
Alpha-smooth muscle actin (green), nuclear (blue), and f-actin (red) staining of AVICs within 2.5, 5, and 10 kPa hydrogels (scale bar = 20μm).
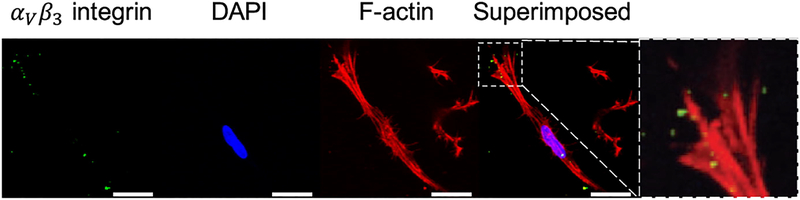
The co-localization of αV β3 integrins with f-actin stress fibers was captured using immunostaining techniques (Fig. 9). After 5 days of culture, we observe that AVICs establish and maintain attachment within the hydrogel matrices. The inset depicts the co-localization of a cluster of integrins at the edge of the cell, likely signifying a focal adhesion.
Figure 9:
αV β3 integrin (green), nuclear (blue), and f-actin (red) stains of AVICs within 2.5 kPa hydrogels (scale bar=20 μm.)
3.5. Kinetics of AVIC active contraction: AVIC volumetric measurements
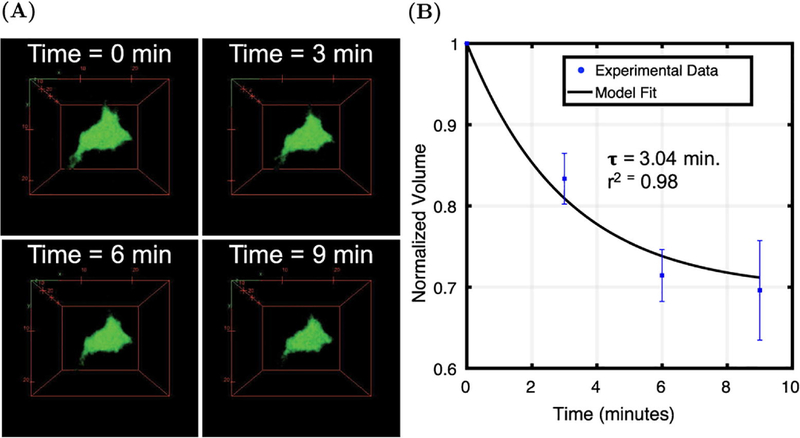
The changes in cellular volume associated with KCl induced active contraction was quantified using confocal microscopy. We were able to obtain consistent z-stacks encompassing the same cells throughout the entire time series experiment (Fig. 10A). We found that AVICs reduced in cellular volume following treatment with a hypertensive solution (Fig. 10B) and numerically determined that τ = 3.04 minutes through fitting the data to Eq. 5. The model showed good agreement with the experimental data (r2 = 0.98). We observed that AVIC volume reduced approximately 30 ± 6% after 9 minutes within a hypertensive solution.
Figure 10:
AVIC contraction kinetic study within 2.5 kPa gels. (A) Volumetric renderings of AVICs at time = 0, 3, 6, and 9 minutes after treatment with a hypertensive solution (90 mM KCl). (B) Time series AVIC volumetric measurements after stimulation with 90 mM KCl (n = 3).
4. Discussion
4.1. Summary and major findings
The flexural deformation mode approach used in this study was shown to be a suitable, sensitive, and repeatable method for assessing AVIC contraction within hydrogel specimens. In the present work, we assessed the effective or bulk shear modulus μ of the gel with and without the contracting AVICs, as well as with and without CRGDS peptides, which control integrin-mediated AVIC-Gel attachments. Thus the effective value of μ represents the total effects of the gel intrinsic modulus, AVIC passive mechanical properties, and AVIC contractile forces. In Fig. 5 we show how AVIC contraction increases μ, but also that this effect is relatively reduced as the intrinsic gel modulus increases from 2.5 to 10 kPa. Similarly, in Fig. 7 we show how CRGDS concentration affected the AVIC contractile contributions to μ. Taken together, these results show how both the intrinsic (unseeded) gel stiffness and the CRGDS peptide concentration both modulate how AVIC contraction affects the effective μ. Moreover, μ is a sensitive indicator to AVIC contractile state.
4.2. Material model
The FE model was able to faithfully reproduce the experimental moment–displacement data across all hydrogel groups and cell contraction states very well (average r2 > 0.90) (supplementary tables 3 & 4). The representative model fits to the non-contractile, normal, and hypertensive states in Fig. 3 showed that a simple Neo-Hookean material model faithfully reproduced the non-linear moment–displacement relation of the AVIC–hydrogels undergoing a bending deformation. Using a nearly incompressible Neo-Hookean material model for this purpose is well suited and produces accurate simulations of the mechanical testing experiment through use of only one parameter, μ.
4.3. AVIC mechanical responses to hydrogel moduli
There was a significant difference in M/I values at maximum displacement between all contractile levels in the 2.5 and 5 kPa hydrogel groups, suggesting that AVIC contraction directly affects the macro stiffness of the AVIC–hydrogel constructs (Fig. 4A & 4B). However, in the 10 kPa group, there was only a statistically significant difference between the M/I values at displacement between the hypertensive and non-contractile conditions (Fig. 4C). This is possibly attributed to a decrease in cell activation and viability within higher stiffness gels that reduce the net effect of AVIC contraction [21].
Significant differences in the absolute value of μ was observed between the 2.5 kPa group and the 5 and 10 kPa groups (Fig. 5A, p–value = 0.003 and 0.006 respectively). This is to be expected owing to the larger amounts of MMP–degradable peptide crosslinkers incorporated into the structure of 5 and 10 kPa hydrogels. Interestingly, there was no significant difference between the 5 and 10 kPa hydrogel groups. As reported previously by others [21], this is possibly explained by a larger percentage of AVICs expressing α–SMA and increased AVIC viability within the 5 kPa group compared to the 10 kPa group that increases the contribution of AVIC contraction on the macro–level AVIC–hydrogel construct stiffness. We hypothesize that an increase in AVIC contribution influences the 5 kPa AVIC–hydrogel to behave mechanically similar to the 10 kPa AVIC–hydrogel.
Significant differences in μ between the non-contractile and normal states and between the non-contractile and hypertensive states were observed within the 5 kPa and 10 kPa stiffness groups (Fig. 5A). No significant differences were observed between the contractile states within the 2.5 kPa group. As seen in Fig. 5B, when the individual specimens are normalized to themselves (repeated measures), it is revealed that the largest percent change in μ is observed within the 2.5 kPa group. This result suggests that although there is a higher variation in absolute μ between the samples in the 2.5 kPa group, the effect of AVIC contraction on the macro stiffness of the AVIC–hydrogel construct is consistent and the greatest within this group.
The effects of AVIC contraction within the hypertensive state resulted in a statistically significant increase in the percent change of μ from the non-contractile state across all hydrogel stiffness groups (Fig. 5B). However, only in the 2.5 kPa group was there a significant difference in the percent change of μ between the normal and non-contractile state (identified with # symbol) and between the percent change of the normal/non-contractile and hypertensive/non-contractile state (identified with * symbol). This may be due to the increased presence of α–SMA fiber networks in AVICs seeded in lower moduli gels as observed in this study (Fig. 8) and others [21]. It has been previously reported that ~42 ± 6% of VICs seeded within soft gels (0.24 kPa) express organized stress fiber networks containing α–SMA compared to only ~2.5 ± 0.1% of VICs expressing α–SMA in higher stiffness gels (13 kPa) [21]. It has also been previously shown that the fraction of activated AVICs increase in lower moduli gels and thus AVIC contraction increases as well [21, 28]. This potentially contributes to the increase in percent change in μ that we observe within the 2.5 kPa group. Additionally, it has been shown that a higher fraction of VICs remain viable in lower modulus gels than in higher modulus gels [21] and this, compounded with higher VIC activation, can potentially explain the drastic increase in the percent change in μ within the 2.5 kPa group that is absent within the 5 and 10 kPa group.
We observed that the largest percent change in μ from the non-contractile state to the normal state (42 ± 12% increase) within the 2.5 kPa group (Fig. 5B). This is less than what has been reported for the average change in effective stiffness in native AV leaflet tissues under similar conditions (~76%) [17]. In addition, a maximum of 72 ± 21% increase in μ from the non-contractile state to the hypertensive state was observed in the gel system whereas an average of ~130% increase in effective stiffness was observed in AV leaflet tissues under similar conditions [17]. This suggests that the effects of the cell basal tonus and contraction maybe reduced within the PEG gels. This may be a result of differences in cellular milieus between native tissues and synthetic hydrogel environments. In native tissues, AVICs present various α and β subunit integrin combinations, suggesting that AVICs bind to a number of different ECM components including fibronectin and different types of collagen and laminin [36]. In contrast, within the PEG gels, AVICs gradually up-regulate αV β3 integrins to bind to CRGDS, an adhesive peptide sequence found in fibronectin (Fig. 9) [22]. The reduction of ECM components available for adhesion and structure possibly explains the reduction in the net effect of AVIC basal tonus and contraction in synthetic environments.
We found that the VIC–seeded 2.5 and 5 kPa hydrogels were either just as stiff or stiffer than the unseeded hydrogel. Interestingly, in the 10 kPa hydrogel group we found that the cell–seeded samples were softer than the unseeded hydrogel. This may be due to the reduced effects of cell contraction on the resulting macro–level stiffness of the constructs in this group due to the higher intrinsic stiffness of the gel (10 kPa) which has been shown to reduce the fraction of activated VICs [21]. This can potentially cause the cell–seeded gel to be softer than the unseeded gel owing to the less activated cell population that effectively reduces the total volume fraction of the hydrogel material as previously reported [37]. In softer gels, it is possible that the mechanical contributions of AVIC contraction influences the AVIC seeded hydrogels to be comparable or stiffer than the unseeded material.
4.4. AVIC active contraction is dependent upon CRGDS concentration
CRGDS adhesion peptides serve as connection sites between AVICs and the hydrogel matrix. Intuitively, for AVICs to deform the hydrogel material and have an effect on the resulting μ, adequate connection must be present between AVICs and the micro-environment. To test this hypothesis, we altered the concentration of CRGDS within the constructs and assessed the ability of AVICs to contract within them. From flexural deformation tests, we observed statistically significant differences in moment values at maximum displacement between the non-contractile state and the hypertensive state among hydrogels containing 0.5 mM and 1 mM of CRGDS (Fig. 6B & 6C). There was no significant difference between the moment values at maximum displacement in the absence of CRGDS peptide sequences (Fig. 6A). Through model fitting of the moment–displacement plots, it was observed that there was a statistically significant increase in μ between the non-contractile state and the hypertensive state with hydrogels containing 0.5 and 1 mM of CRGDS (p-values = 0.003 and 0.001 respectively, Fig. 7A). No significant differences were found within the 0 mM CRGDS group. This result indicates that CRGDS concentration is a major component governing the translation of AVIC contraction onto the macro–level hydrogel stiffness and confirms that our mechanical evaluation technique can detect this.
Within the 1 mM group, μ significantly increased (p–value = 0.004) by 30 ± 11% due to the hypertensive treatment, suggesting that adequate AVIC-ECM coupling is established which allows for AVICs to modulate the stiffness of the hydrogel environment. We also observed an increase in μ from the non-contractile state to the normal state (17 ± 8%), suggesting that a basal tonus is present within 1 mM CRGDS hydrogels, although this difference was found to be not statistically significant (p-value = 0.06) (Fig. 7B). Similar trends within the 1.0 mM CRGDS group were found within the 0.5 mM CRGDS group. However, only the 1 mM CRGDS group percent change in μ was significantly greater than the 0 mM CRGDS group (p–value = 0.041, Fig. 7B). The 0 mM CRGDS group showed no change in μ with respect to the chemical treatments. When taken together, these results suggest that AVIC active contraction is highly dependent upon the presence of an adhesion ligand and that the contractile activity of AVICs is similar in the presence of 0.5 mM and 1.0 mM of CRGDS.
Previous studies have shown that AVICs seeded within hydrogels containing varying amounts of CRGDS (0 – 2000 mM) all show good cell viability up to 10 days after the initial encapsulation [22, 28]. These studies report increases in the fraction of activated VICs (via assessment of α–SMA expression), increases in the aspect ratio of VICs, and an increase in expression of αvβ3 integrins (known to bind to the RGD sequence) with respect to increasing CRGDS concentration. Therefore, we believe that the differences in material properties that we observed between the CRGDS modulated gels arise from the compounded effects of increased VIC activation, elongation, and expression of αvβ3 integrins within hydrogels containing a higher concentration of CRGDS. We found that the cell–seeded, CRGDS modulated gels were softer than the unseeded hydrogel. Similar to the explanation provided for the same observation in the hydrogel moduli groups (Section 4.3), this may be due to the reduced effects of cell contraction on the resulting macro–level stiffness of the constructs due to the higher intrinsic stiffness of the gel (10 kPa) [21].
4.5. AVIC morphology, stress-fiber formation, and integrin binding within PEG gels
Integrins and stress-fibers (αSMA and f-actin) are key components in regulating cell-structure interactions. Previous work has shown that AVICs bind to the CRGDS adhesive sequence through the αV β3 integrin [22]. Imaging these components allows us to obtain a better understanding of the processes underlying how AVICs bind to the hydrogel structure and alter the gel mechanics. Using immunostaining techniques, we were able to visualize AVICs directly within the hydrogel matrices (Fig. 8). We note that AVICs became more elongated within softer hydrogels, which is consistent with previous studies reporting as much as 70% decrease in aspect ratio from soft to stiff hydrogels [21]. However, it is not clear if this morphology difference is a result of the hydrogel stiffness or stress-relaxation properties. Chaudhuri et al. reported that stem cells seeded within hydrogels with faster relaxation times became more elongated than within hydrogels with slower relaxation times, independent of hydrogel stiffness [23]. With the current hydrogel chemistry used in this study, the stiffness and stress-relaxation properties are coupled and tunable through adjusting the concentration of MMP-degradable crosslinks, which does not allow us to uniquely study the effects of these two parameters separately. However, it is clear that the mechanics of the culture environment plays a large role in regulating AVIC shape, which has been shown previously to be a key regulator of AVIC contraction at the population [14] and the single cell level [15]. Tandon et al. report that when AVICs were cultured within thin micropatterned protein lines (10 μm wide), this led to increased cell and nuclear aspect ratios as compared to AVICs seeded within wider lines (80 μm wide) [14]. In addition, it was reported that AVICs seeded onto thinner lines (and thus having more elongated morphologies) produced the maximum contractile stress and the maximum basal tonus that was observed. These observations align well with our report of VICs being more elongated (Fig. 8) and thus more contractile (Fig. 5B) within the 2.5 kPa gel group. Interestingly, Tandon et al. report no significant differences in α–SMA expression between the thin and wide patterned groups suggesting that cell shape modulates cell contractility independent of cell phenotype [14]. Future work is needed to fully elucidate the underyling mechanisms of how cell shape effects the contractile behavior of AVICs.
From our observations, we observed that AVICs more substantially expressed α–SMA within 2.5 kPa gels, suggesting that they are more activated (Fig. 8). Previous studies have quantified this and report that VICs within softer gels (0.24 kPa) contain ~80% more α–SMA mRNA than VICs seeded within stiffer gels (12 kPa) [21]. A potential explanation for the increase in AVIC activation within lower moduli gels could be related to environmental pressure influencing AVICs to remodel their environment in an attempt to return to a homeostatic stress state. This perhaps may not be present in higher stiffness gels because the cellular milieu closer matches that of the native homeostatic stress state.
It is known that AVICs establish adequate adhesion within the hydrogel environment through αV β3 integrin binding onto CRGDS peptide sequences (Fig. 9). From our mechanical testing results (Fig. 6 & 7), we conclude that this cell-hydrogel interface is crucial for AVIC contraction. A previous study by Benton et al. showed that 80–100% of VICs stained positive for the αvβ3 integrin when cultured in the presence of 1–2 mM CRGDS after 6 days [22]. Interestingly, this study also showed that after 10 days, VICs seeded within hydrogels containing no CRGDS stained positive for αvβ3 integrins. This is possibly a result of binding onto cell–secreted ECM. In future work, it may be useful to use techniques such as second harmonic generation to assess ECM production within the hydrogels in order to assess the availability of alternative adhesion sites. However, both our imaging and mechanical testing results (Fig. 7 & 9) indicate that AVIC binding to CRGDS via αV β3 integrins is potentially a major regulator of AVIC contraction within a 5 day culture period.
4.6. Insights into AVIC active contraction kinetics
Using confocal microscopy, we observed a decrease in AVIC volume after treatment with a hypertensive solution (Fig. 10A & 10B). Cells are generally regarded as being nearly incompressible [38–40], with cell contractile forces insufficient to change the cell volume. A possible explanation is the efflux of water caused by cellular contraction as previously reported [41]. Guo et al. concluded that the reduction in volume can possibly be explained by activation of ion channels through contractile tension of the cytoskeleton which in turn regulates the amount of intercellular water and essentially cell volume [41]. They observed no decrease in volume when ion channels and certain ATP-dependent processes were inhibited. Although more work is needed to investigate the underlying processes, it is clear that AVIC active contraction has a large effect on cellular volume and is a possible mechanism for volume regulation. The use of PEG gels to investigate AVIC contraction kinetics demonstrate a unique advantage to using synthetic hydrogels over native tissues in studying cell mechanics. Imaging experiments as such would not be practical or perhaps even possible with native tissues; specifically, time-series imaging of AVICs within native tissue presents a major challenge.
4.7. AVIC response within hydrogels vs native tissues
The native flexural properties of the AV have been previously reported [17, 29] to have an effective shear modulus of ~100 kPa. However, the flexural response of the native AV leaflet is dependent upon the direction of flexure because the fibrosa and the ventriculars layers behave differently in tension than in compression. Specifically, Buchanan et al. found that it requires a total of 4 moduli to capture the bi–directional flexural behavior of the native AV leaflet [29]. Therefore, it is important to note that native tissues cannot be described by a Neo–Hookean material model (i.e. single moduli), as they have complex 3D structures and exhibit non-linear, anisotropic mechanical behaviors under finite (large) deformations. Thus, it is not possible to precisely imitate native tissue with the gel used in this study nor any single phase material regardless of its specific mechanical behaviors. Rather, the hydrogel system serves as an excellent and tunable tool in the study of VICs in 3D environments that can elucidate many of their critical mechanobiological responses.
In this study, we did not test the AVIC-hydrogels under multiaxial loading, as the gel is isotropic. The hydrogel system does not recapitulate the complexity and layer-specific ECM components present in the native valve, eliminating the need to assess the bending response of the constructs in both directions. However, from our testing approach of the AVIC-hydrogels, we were able to reproduce similar phenomenon as observed in native tissues. Specifically, the contraction of AVICs within the hydrogel constructs had a detectable effect on overall bending stiffness. However, the effects were much reduced. In the native AV, Merryman et al. observed an increase of 130% in bending stiffness in the “with curvature” direction from the non-contractile tissue state to the hypertensive state [17]. In the hydrogel system, we observed a maximum of only 72 ± 21% (2.5 kPa group). This difference can possibly be attributed to the loss of complexity, compared to native tissue, within the hydrogel system.
4.8. Limitations
While being able to reproduce many of the VIC-ECM connection features, the PEG gel used in this study is not a fibrous system and therefore cannot mimic the local AVIC micro environment exactly and thus disallows a collective preferred direction of the encapsulated AVIC population. However, this can be mediated in the future with the application of uniaxial constraints [42], incorporation of highly tunable polymeric fibers [43, 44], or stretch [45] using our established tissue strip bioreactor system to direct cellular alignment [5]. An increase in cellular alignment should help the collective contraction of AVICs to be more pronounced, and thus measurable, on the macro level. Within the literature [21] and through our experimental observations, we note that cellular viability reduces substantially within higher moduli gels (5 and 10 kPa). We hypothesize that this is due to the hindered ability of the AVICs to spread within the stiffer environment. In this study, we aimed to investigate AVIC response in a holistic manner and chose to include the 5 and 10 kPa hydrogel groups. If desired in the future, techniques like dynamic stiffening can be used to study AVICs in higher stiffness gels without compromising cellular viability [21]. In addition, future work will focus on developing high–confidence methods to quantify the presence of cellular components in–situ to more accurately identify cell phenotype within the hydrogel system.
4.9. Conclusions
The tunable properties of the synthetic PEG hydrogels make it a very effective and attractive tool for AVIC mechanobiology studies. In the present study, we demonstrated that AVIC contraction increases the overall bending response of the hydrogel constructs, similar to what has been found with native AVs. The consistency of this phenomenon provides confidence that the hydrogel system is a suitable and realistic 3D platform to study the mechanics of AVICs. In addition, the optical properties of the hydrogel offer an experimental advantage over native tissues in assessing the stress fiber networks of AVICs directly. Future experimental work will focus on utilizing the hydrogel system to perform long-term mechanobiology experiments using our established bioreactors to study healthy and diseased AVICs. The ability to choose the cell source that will be seeded and studied also opens up the possibility of performing high-throughput experiments using human AVICs. Furthermore, the incorporation of alternative adhesion peptides and whole proteins within the intricate structure of the PEG gel and how this affects AVIC mechanics can be explored in the future. The use of simulation allowed for a convenient material parameter to compare between the hydrogel groups and contractile states. Future work will focus on establishing a down-scale model for the AVIC-hydrogel constructs to further explain the macro-level results using built-in AVIC inclusions with tunable parameters like contractility level, stress-fiber orientation, and connectivity to the surrounding ECM.
Supplementary Material
5. Acknowledgments
We would like to thank Drs. Rachel Buchanan and Daniel P. Howsmon for their insightful discussions, Yen-Yu Chen for assistance with conducting the experiments, and Christian Gil for assistance with instrumentation. All images were acquired through the Core Facilities and Center for Biomedical Research Support at the University of Texas at Austin and through the Department of Biomedical Engineering at the University of Texas at Austin. Funding was provided for this work by the National Science Foundation Graduate Research Fellowship Program [grant number DGE-1610403] to AK and by the National Institutes of Health [grant number R01 HL–119297, HL–073021, and HL–142504] to MSS and [grant number R01 HL–132353] to KSA.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
6. References
- [1].Pham T, Sulejmani F, Shin E, Wang D, Sun W, Quantification and comparison of the mechanical properties of four human cardiac valves, Acta Biomaterialia 54 (2017) 345–355. doi: 10.1016/j.actbio.2017.03.026. [DOI] [PubMed] [Google Scholar]
- [2].Ayoub S, Tsai KC, Khalighi AH, Sacks MS, The three-dimensional microenvironment of the mitral valve: Insights into the effects of physiological loads, Cellular and Molecular Bioengineering 11 (2018) 291–306. doi: 10.1007/s12195-018-0529-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Rego BV, Sacks MS, A functionally graded material model for the transmural stress distribution of the aortic valve leaflet., Journal of biomechanics 54 (2017) 88–95. doi: 10.1016/j.jbiomech.2017.01.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Lee C-H, Zhang W, Feaver K, Gorman RC, Gorman JH, Sacks MS, On the in vivo function of the mitral heart valve leaflet: insights into tissue-interstitial cell biomechanical coupling., Biomechanics and modeling in mechanobiology 16 (2017) 1613–1632. doi: 10.1007/s10237-017-0908-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Ayoub S, Lee C-H, Driesbaugh KH, Anselmo W, Hughes CT, Ferrari G, Gorman RC, Gorman JH, Sacks MS, Regulation of valve interstitial cell homeostasis by mechanical deformation: implications for heart valve disease and surgical repair., Journal of the Royal Society, Interface 14. doi: 10.1098/rsif.2017.0580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Rego BV, Wells SM, Lee C-H, Sacks MS, Mitral valve leaflet remodelling during pregnancy: insights into cell-mediated recovery of tissue homeostasis., Journal of the Royal Society, Interface 13 (125). doi: 10.1098/rsif.2016.0709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Merryman WD, Liao J, Parekh A, Candiello JE, Lin H, Sacks MS, Differences in tissue-remodeling potential of aortic and pulmonary heart valve interstitial cells, Tissue Eng 13 (9) (2007) 2281–9. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=17596117 [DOI] [PubMed] [Google Scholar]
- [8].Merryman WD, Youn I, Lukoff HD, Krueger PM, Guilak F, Hopkins RA, Sacks MS, Correlation between heart valve interstitial cell stiffness and transvalvular pressure: implications for collagen biosynthesis, Am J Physiol Heart Circ Physiol 290 (1) (2006) H224–31. [DOI] [PubMed] [Google Scholar]
- [9].Sacks MS, Merryman WD, Schmidt DE, On the biomechanics of heart valve function, J Biomech 42 (12) (2009) 1804–24. doi: 10.1016/j.jbiomech.2009.05.015. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=19540499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Cloyd KL, El-Hamamsy I, Boonrungsiman S, Hedegaard M, Gentleman E, Sarathchandra P, Colazzo F, Gentleman MM, Yacoub MH, Chester AH, Stevens MM, Characterization of porcine aortic valvular interstitial cell ‘calcified’ nodules, PLoS One 7 (10) (2012) e48154. doi: 10.1371/journal.pone.0048154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Yip CY, Simmons CA, The aortic valve microenvironment and its role in calcific aortic valve disease, Cardiovasc Pathol 20 (3) (2011) 177–82. doi: 10.1016/j.carpath.2010.12.001. URL http://www.ncbi.nlm.nih.gov/pubmed/21256052 [DOI] [PubMed] [Google Scholar]
- [12].Mills WR, Barber JE, Ratliff NB, Cosgrove DM 3rd, Vesely I, Griffin BP, Biomechanical and echocardiographic characterization of flail mitral leaflet due to myxomatous disease: further evidence for early surgical intervention, Am Heart J 148 (1) (2004) 144–50. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15215804 [DOI] [PubMed] [Google Scholar]
- [13].Cirka H, Monterosso M, Diamantides N, Favreau J, Wen Q, Billiar K, Active Traction Force Response to Long-Term Cyclic Stretch Is Dependent on Cell Pre-stress, Biophys J 110 (8) (2016) 1845–57. doi: 10.1016/j.bpj.2016.02.036. URL http://www.ncbi.nlm.nih.gov/pubmed/27119644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Tandon I, Razavi A, Ravishankar P, Walker A, Sturdivant NM, Lam NT, Wolchok JC, Balachandran K, Valve interstitial cell shape modulates cell contractility independent of cell phenotype, Journal of Biomechanicsl 49 (2016) 3289–3297. doi: 10.1016/j.jbiomech.2016.08.013. [DOI] [PubMed] [Google Scholar]
- [15].Lam NT, Muldoon TJ, Quinn KP, Rajaram N, Balachandran K, Valve interstitial cell contractile strength and metabolic state are dependent on its shape, Integrative Biology (8) (2016) 1079–1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Mabry KM, Payne SZ, Anseth KS, Microarray analyses to quantify advantages of 2d and 3d hydrogel culture systems in maintaining the native valvular interstitial cell phenotype, Biomaterials 74 (2016) 31–41. doi: 10.1016/j.biomaterials.2015.09.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Merryman WD, Huang HYS, Schoen FJ, Sacks MS, The effects of cellular contraction on aortic valve leaflet flexural stiffness, J Biomech 39 (1) (2006) 88–96. [DOI] [PubMed] [Google Scholar]
- [18].Kershaw JD, Misfeld M, Sievers HH, Yacoub MH, Chester AH, Specific regional and directional contractile responses of aortic cusp tissue, J Heart Valve Dis 13 (5) (2004) 798–803. URL http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15473483 [PubMed] [Google Scholar]
- [19].Stephens E, Durst C, Swanson J, Grande-Allen K, Ingels N, Miller D, Functional Coupling of Valvular Interstitial Cells and Collagen Via 21 Integrins in the Mitral Leaflet, Cell Mol Bioeng (2010) 1–10 doi: 10.1007/s12195-010-0139-6. URL 10.1007/s12195-010-0139-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Khang A, Buchanan RM, Ayoub S, Rego BV, Lee C-H, Ferrari G, Anseth KS, Sacks MS, Mechanobiology of the heart valve interstitial cell: Simulation, experiment, and discovery, in: Mechanobiology in Health and Disease, Elsevier, 2018, pp. 249–283. doi: 10.1016/b978-0-12-812952-4.00008-8. [DOI] [Google Scholar]
- [21].Mabry KM, Lawrence RL, Anseth KS, Dynamic stiffening of poly(ethylene glycol)-based hydrogels to direct valvular interstitial cell phenotype in a three-dimensional environment, Biomaterials 49 (2015) 47–56. doi: 10.1016/j.biomaterials.2015.01.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Benton JA, Fairbanks BD, Anseth KS, Characterization of valvular interstitial cell function in three dimensional matrix metalloproteinase degradable PEG hydrogels, Biomaterials 30 (34) (2009) 6593–603. doi: 10.1016/j.biomaterials.2009.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Chauduri O, Gu L, Klumpers D, Darnell M, Bencherif SA, Weaver JC, Huebsch N, Lee H, Lippens E, Duda GN, Mooney DJ, Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nature Materials 15 (2016) 326–336. doi: 10.1038/nmat4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Legant WR, Miller JS, Blakely BL, Cohen DM, Genin GM, Chen CS, Measurement of mechanical tractions exerted by cells in three-dimensional matrices, Nature Methods 7 (12) (2010) 969–971. doi: 10.1038/nmeth.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Park KM, Lewis D, Gerecht S, Bioinspired hydrogels to engineer cancer microenvironments, Annual Review of Biomedical Engineering 19 (2017) 109–133. doi: 10.1146/annurev-bioeng-071516-044619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Salinas CN, Anseth KS, The influence of the rgd peptide motif and its contextual presentation in peg gels on human mesenchymal stem cell viability, Journal of Tissue Engineering and Regenerative Medicine 2 (2008) 296–304. doi: 10.1002/term.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Salinas CN, Anseth KS, The enhancement of chondrogenic differentiation of human mesenchymal stem cells by enzymatically regulated rgd functionalities, Biomaterials 29 (2008) 2370–2377. doi: 10.1016/j.biomaterials.2008.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Mabry KM, Schroeder ME, Payne SZ, Anseth KS, Three-dimensional high-throughput cell encapsulation platform to study changes in cell-matrix interactions, Applied Materials & Intefaces 8 (2016) 21914–21922. doi: 10.1021/acsami.5b11359. [DOI] [PubMed] [Google Scholar]
- [29].Buchanan RM, Sacks MS , Interlayer micromechanics of the aortic heart valve leaflet, Biomech Model Mechanobioldoi: 10.1007/s10237-013-0536-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Johnson CM, Hanson MN, Helgeson SC, Porcine cardiac valvular subendothelial cells in culture: Cell isolation and growth characteristics, Journal of Molecular and Cellular Cardiology 19 (1987) 1185–1193. doi: 10.1016/S0022-2828(87)80529-1. [DOI] [PubMed] [Google Scholar]
- [31].Alnæs MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN, The fenics project version 1.5, Archive of Numerical Software 3 (100). doi: 10.11588/ans.2015.100.20553. [DOI] [Google Scholar]
- [32].Hughes T, The finite element method: linear static and dynamic finite element analysis, Dover Publications, 2000. URL http://books.google.com/books?id=yarmSc7ULRsC [Google Scholar]
- [33].Wriggers P, Nonlinear Finite Element Methods, Springer Berlin Heidelberg, 2008. URL https://www.ebook.de/de/product/19292615/peter_wriggers_nonlinear_finite_element_methods.html [Google Scholar]
- [34].Jester JV, Brown A, adn Pappa D, Vasiliou V, Myofibroblast differentiation modulates keratocyte crystallin protein expression, concentration, and cellular light scattering, Investigative Ophthalmology & Visual Science 53 (2) (2012) 770–778. doi: 10.1167/iovs.11-9092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Vicente NB, Zamboni JED, Adur JF, Paravini EV, Casco VH, Photobleaching correction in fluorescence microscopy images, Journal of Physics: Conference Series 90 (1–8). doi: 10.1088/1742-6596/90/1/012068. [DOI] [Google Scholar]
- [36].Latif N, Sarathchandra P, Taylor P, Antoniw J, Yacoub M, Molecules mediating cell-ECM and cell-cell communication in human heart valves, Cell Biochemistry and Biophysics 43 (2) (2005) 275–287. doi: 10.1385/CBB:43:2:275. [DOI] [PubMed] [Google Scholar]
- [37].Durst CA, Cuchiara MP, Mansfield EG, West JL, Grande-Allen KJ, Flexural characterization of cell encapsulated PEGDA hydrogels with applications for tissue engineered heart valves, Acta Biomaterialia 7 (6) (2011) 2467–2476. doi: 10.1016/j.actbio.2011.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Trickey WR, Baaijens FP, Laursen TA, Alexopoulos LG, Guilak F, Determination of the Poisson’s ratio of the cell: recovery properties of chondrocytes after release from complete micropipette aspiration, J Biomech 39 (1) (2006) 78–87. doi: 10.1016/j.jbiomech.2004.11.006. [DOI] [PubMed] [Google Scholar]
- [39].Ofek G, Natoli RM, Athanasiou KA, In situ mechanical properties of the chondrocyte cytoplasm and nucleus, J Biomech 42 (7) (2009) 873–7. doi: 10.1016/j.jbiomech.2009.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Jones WR, Ting-Beall HP, Lee GM, Kelley SS, Hochmuth RM, Guilak F, Alterations in the Young’s modulus and volumetric properties of chondrocytes isolated from normal and osteoarthritic human cartilage, J Biomech 32 (2) (1999) 119–27. [DOI] [PubMed] [Google Scholar]
- [41].Guo M, Pegoraro AF, Mao A, Zhou EH, Arany PR, Han Y, Burnette DT, Jensen MH, Kasza KE, Moore JR, Mackintosh FC, Fredberg JJ, Mooney DJ, Lippincott-Schwartz J, Weitz DA, Cell volume change through water efflux impacts cell stiffness and stem cell fate, PNAS 114. doi: 10.1073/pnas.1705179114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Puperi DS, Kishan A, Punske ZE, Wu Y, Cosgriff-Hernandez E, West JL, Grande-Allen KJ, Electrospun polyurethane and hydrogel composite scaffolds as biomechanical mimics for aortic valve tissue engineering, ACS Biomaterials Science and Engineering 2 (2016) 1546–1558. doi: 10.1021/acsbiomaterials.6b00309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Khang A, Ravishankar P, Krishnaswamy A, Anderson P, Cone S, Liu Z, Qian X, Balachandran K, Engineering anisotropic biphasic janus-type polymer nanofiber scaffold networks via centrifugal jet spinning, J Biomed Mater Res Part B 105 (2017) 2455–2464. [DOI] [PubMed] [Google Scholar]
- [44].Ravishankar P, Khang A, Laredo M, Balachandran K, Using dimensionless numbers to predict centrifugal jet spun nanofiber morphology, Journal of Nanomaterials. [Google Scholar]
- [45].Lam NT, Lam H, Sturdivant NM, Balachandran K, Fabrication of a matrigel-collagen semi-interpenetrating scaffold for use in dynamic valve interstitial cell culture, Biomedical Materials 12 (2017) 045013. doi: 10.1088/1748-605X/aa71be. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.