Coupling Dynamics and Evolutionary Information with Structure to Identify Protein Regulatory and Functional Binding Sites

Abstract

Binding sites in proteins can be either specifically functional binding sites (active sites) that bind specific substrates with high affinity or regulatory binding sites (allosteric sites), that modulate the activity of functional binding sites through effector molecules. Owing to their significance in determining protein function, the identification of protein functional and regulatory binding sites is widely acknowledged as an important biological problem. In this work, we present a novel binding site prediction method, AR-Pred (Active and Regulatory site Prediction), which supplements protein geometry, evolutionary and physicochemical features with information about protein dynamics to predict putative active and allosteric site residues. Since the intrinsic dynamics of globular proteins plays an essential role in controlling binding events, we find it to be an important feature for the identification of protein binding sites. We train and validate our predictive models on multiple balanced training and validation sets with random forest machine learning and obtain an ensemble of discrete models for each prediction type. Our models for active site prediction yield a median AUC of 91% and MCC of 0.68, whereas the less well-defined allosteric sites are predicted at a lower level with a median AUC of 80% and MCC of 0.48. When tested on an independent set of proteins, our models for active site prediction show comparable performance to two existing methods and gains compared to two others, while the allosteric site models show gains when tested against three existing prediction methods. AR-Pred is available as a free downloadable package at https://github.com/sambitmishra0628/AR-PRED_source.

Introduction

Many globular proteins are enzymes that catalyze chemical reactions on bound substrates with the whole protein facilitating the reaction by lowering energy barriers¹. The catalytic efficiency can be regulated by environmental factors such as temperature and pH and, importantly, often also by the binding of effectors or allosteric modulators. Such interactions with other molecules are a key regulatory aspect of proteins in general, and this type of regulation relates closely to their functions. Consequently, the identification of possible binding sites is of vital importance. It is a useful step in the process of annotating proteins for function and is a widely acknowledged problem.

Proteins exhibit a broad spectrum of ligand and macromolecule binding sites². Metalloproteins have metal ion cofactor binding sites, molecular chaperones like GROEL can bind to other proteins, DNA binding sites are found in helicases and topoisomerases, while proteases bind to targeted peptides. Specifically, ligand binding sites in most enzymes can be broadly classified into two categories: a functional binding site or active site where the substrate binds in order to undergo chemical modification,³ and a regulatory binding site or allosteric site where, binding of an effector molecule can regulate and control the activity of the protein. ⁴ The active site may be classified into the substrate binding site comprising all residues that interact with the substrate and a more limited catalytic site, comprising only those residues directly taking part in the chemical reaction. In this study, we use the term active site to refer inclusively to include both sub-categories.

A protein’s active site is comprised of a group of residues, often in a deep pocket and even sometimes at an interface between subunits, and in some cases the site is accessible through a network of channels.⁵ Proteins also frequently undergo transitions between different conformations that can control access to the active site. The structural architecture and the physicochemical nature of the residues in the active site are evolutionarily conserved or changed across different species, to retain the specific function of the protein or to modify it. Active sites constitute the functional binding sites of enzymes and play a key role in defining an enzyme’s function. Deletion of residues at or near the active site can result in total loss of function. While an enzyme’s active site defines directly its biological activity, allosteric or regulatory sites control such activity remotely. Residues constituting such sites are commonly localized at cavities on a protein surface and are typically more accessible to ligands than are the residues in active sites. Protein allostery is a fundamental biological mechanism through which binding of a ligand molecule at a site remote to the functional site in an enzyme results in changes to the shape or dynamics of the functional site, either activating or inactivating the enzyme’s activity.⁶ Such allosteric processes facilitate communication between distant sites in proteins. Allostery is key for signal transduction: the receptors on the surface of cells use it to transmit signals from the exterior to the interior of the cell.⁷ Abnormalities in allosteric regulation have also been linked to several human diseases such as cancer and Alzheimer’s.⁸ Allosteric drugs represent a major effort in pharmaceuticals contrasting with to drugs/inhibitors targeted to active sites.^{9, 10} Because allosteric residues are subject to lower evolutionary pressure compared to orthosteric residues, they are often not conserved across all phyla and have the advantage of being highly specific. Hence, allosteric drugs targeting a pathogen have a lower risk of interfering with host proteins. They also have the potential to activate as well as inhibit the target protein and can be used together with drugs that target active site residues.

Several computational methods already exist for the prediction of ligand binding sites in proteins. These computational approaches are either template-based, utilizing homologous structures with known binding sites or geometry-based, using structural geometry to detect binding site pockets. Also, some methods are energy-based and rank putative ligand binding sites by their computed interaction energies with hypothetical ligands.¹¹ Specific methods also exist for the prediction of functional sites (active sites). The Fuzzy Oil Drop model by Brylinski and co-workers¹² evaluates irregularities in the hydrophobicity distribution of residues in a protein and assigns functional importance to regions having high irregularities. Ondrechen et al. developed a computational method that calculates theoretical microscopic titration curves (THEMATICS) and showed that residues exhibiting anomalies in their predicted titration curves occur at active sites.^{13, 14} A more sophisticated method POOL was later developed that uses electrostatic and geometric properties derived from protein structures in addition to sequence conservation and features from THEMATICS to assign likelihood estimates for residues as part of the active site^{15, 16}. Capra et al. developed ConCavity which combines evolutionary sequence conservation with geometric features obtained from pocket finding algorithms to predict active site residues.¹⁷ Another method that predicts active site pockets is AADS that uses geometric information on cavities in addition to physico-chemical properties of residues.¹⁸ Some methods have implemented genetic algorithms, which use structural information as well as sequence and network based properties in combination with machine learning to identify active site residues.^{19, 20} More recently, protein dynamics was also used as a predictor for active sites. Glantz-Gashai and co-workers revealed that normal modes can expose active sites, and they used changes in solvent accessibilities to predict active site residues.²¹

Numerous initiatives have also been taken to identify allosteric sites. The ASD database includes a diverse set of proteins with known allosteric residues. The identifications of allosteric sites for the proteins in this database are based on experimental methods which include disulfide trapping, high-throughput screening and fragment-based screening.²² There have also been different approaches that use sequence and structural information to make predictions of allosteric sites in proteins. Lockless and Ranganathan used statistical coupling analysis (SCA) to identify networks of coevolving residues for protein families and later, used these to identify potential allosteric sites and pathways.²³ Allosite is a structure-based machine learning predictor that uses the physicochemical properties of pockets predicted by FPocket as descriptors to train a support vector machine (SVM) model and make predictions of allosteric pockets.²⁴ AlloPred uses normal mode perturbations on different pockets in a protein to identify the pockets whose perturbation induces maximum flexibility changes for the catalytic residues.²⁵ A similar method that uses normal modes to simulate the effect of ligand binding on protein flexibility is used in the protein allosteric and regulatory sites (PARS) server.²⁶ This server tags those pockets in a protein as allosteric that induce maximum flexibility changes in the protein upon ligand binding. SPACER is another prediction tool that combines normal modes with dynamics and uses ‘binding leverage’ to locate potential sites in proteins where ligand binding can trigger a population shift affecting the conformational state of the protein.²⁷

The dynamic nature of proteins is a critical element that can control function by transient reorganization of enzyme active sites²⁸ and their regulatory behavior by a shift in conformational dynamics upon effector binding.⁷ In addition, protein dynamics is thought to play a pivotal role in the evolution of novel function²⁹. Collectively these studies suggest that supplementing information on protein dynamics with structural and evolutionary features within a machine learning scheme can lead to improved predictions of ligand binding residues, both for active site and allosteric residues, which is the underlying premise for the present work. To test this hypothesis, we use the dataset compiled by Greener and Sternberg²⁵ used for AlloPred, since it includes information about both allosteric and active site residues and develop predictive models for both active and allosteric sites. In our models, we include features that describe the dynamic behavior of residues in a protein molecule by using elastic network models.^{30, 31} Previous studies showed that these simple models can efficiently capture the functional dynamics of proteins^{32, 33} and that the global dynamics derived with ENMs shows strong overlap with the motions from atomistic molecular dynamic simulations.^{34, 35} Some of these dynamical features include mean-square fluctuations of residues and the resilience of residues to external perturbations given by dynamic flexibility index.³⁶ For prediction of allosteric residues, we specifically consider the shortest dynamically correlated path between a given residue and the active site residues and the effect of perturbing the active site residues on a given residue. In addition, we also model a protein structure as a network where each node is a residue and the edge between a pair of nodes is weighted by the extent of dynamic correlation between them, following which we calculate network centrality features for each residue. We supplement dynamical features with structure-based features such as solvent accessibilities, amino acid physicochemical properties like hydrophobicity and evolutionary conservation.

Our results suggest that while residue conservation is a more important predictor for active site residues, features describing protein geometry and the extent of dynamic correlation with active site are the key identifiers for allosteric site residues. Our study also reports that properties defining the chemical nature of residues, such as hydrophobicity, are more important for the identification of active site residues than allosteric sites, demonstrating the importance of chemical specificity for residues at active sites. Allosteric residues, however, are a consequence of a protein’s geometry and intrinsic dynamics; their location is driven by the extent of dynamic control over the active site. We compare against four existing methods with the test set of proteins and find that our predictions of active sites having comparable performance to POOL and ConCavity and outperforming two - Fuzzy Oil Drop and AADS. Our models for allostery however, outperform all three methods compared - AlloPred, AlloSitePro and Spacer. Our study thus, verifies the importance of incorporating residue-level dynamical information into predictive models for ligand binding sites.

Methods

Dataset

In accord with our aim to develop predictive models for both allosteric and active site residues, we use the dataset of protein structures compiled by Greener and Sternberg²⁵ for AlloPred that contains information on both allosteric and active site residues. The authors obtained information about allosteric residues from ASBench and used the Catalytic Site Atlas and UniProt in addition to ASBench to identify active site residues. The training and testing datasets provided there include a total of 119 proteins.

Dataset processing

We split the multimeric proteins in our dataset into their individual chains. This results in a total of 173 separate protein chains. We then retain those chains identified as both allosteric and catalytic residues, leaving 165 protein chains (from the 105 proteins). For the same set, we calculate all the features as described in the next section. For some structures, we encountered errors during feature calculations. For example, calculations for evolutionary conservation gave errors in the presence of non-standard amino acids and in some cases, solvent accessibility and secondary structure calculations couldn’t be performed for all residues for some proteins. We discard these structures and our final dataset contains 144 protein monomers.

Features

For each protein, we calculate features at the residue-level; we represent each residue as a vector of different features. Based on how they were calculated and what aspect of a protein they represent, these features can be broadly grouped into four categories: a. features based on amino acid physicochemical properties, b. features describing the rate of residue evolution, c. features from protein structure geometry, and d. features describing protein dynamics. Table 1 provides a list of features considered under each category and below is given a brief description of the features used.

Table 1.

Summary of features in each of the 4 categories

Feature Category	Feature Name
Amino acid physico-chemical nature	1. Residue type (based on side chain charge and polarity) 2. Residue identity (20 standard amino acids) 3. Kyte-Doolittle hydropathy index
Protein Geometry	1. Solvent accessibility 2. Secondary structure 3. Pocket residues 4. Node centralities calculated using unweighted amino-acid contact map (cutoff distance 13Å) 5. Node centralities calculated using weighted amino-acid contact map (edges weighted by distance between residue Cα-atoms) 6. Node centralities calculated by transforming the 3-dimensional protein structure into a 2-dimensional amino-acid potential matrix (using the Betancourt-Thirumalai contact potentials)
Amino acid evolution	Conservation scores
Protein dynamics	1. Mean-squared fluctuations 2. Dynamic Flexibility Index 3. Active site perturbation response (only for allosteric residue prediction) 4. Shortest dynamically-correlated path to active site residues (only for allosteric residue prediction)

Residue type

We classify residues based on their hydrophobicity and charge into three classes similar to the approach taken by Petrova et al.³⁷

Class 1: His, Arg, Lys, Glu and Asp (charged residues)

Class 2: Gln, Thr, Ser, Asn, Cys, Tyr and Trp (polar residues)

Class 3: Gly, Phe, Leu, Met, Ala, Ile, Pro and Val (hydrophobic residues)

Residue identity

We label each of the 20 amino acids (A, R, N, D, C, E, Q, G, H, I, L, K, M, F, P, S, T, W, Y and V) separately.

Solvent accessibility

We perform calculations for solvent accessibility using Naccess³⁸ with default parameters. For each residue, Naccess reports a total of 10 absolute and relative accessibility values, all of which are included in our feature set. (Details are in Supporting Information.)

Secondary structure

We use the DSSP program³⁹ to assign the secondary structures in a consistent way. DSSP assigns a single letter code (H, S, G, T, E, B, I, -) to each residue corresponding to the secondary structure type.

Mean square fluctuations

We use the Anisotropic Network Model (ANM), a type of Elastic Network Model (ENM) to calculate the residue-level fluctuations.³⁰ We model each protein as a coarse-grained elastic network by representing its N residues by their respective C^α atoms and connecting all pairs of residues with harmonic springs. The potential energy of this system under equilibrium is given as

$$V=\frac{1}{2}\Delta R^{T}H\Delta R$$ (1)

Here, ΔR is the vector of changes in positions for all residues, ΔR^T is its transpose and H is the 3N by 3N-dimensional Hessian matrix obtained from the second derivatives of the potential function. We vary the strength of the springs γ between residue pairs i and jby the inverse of their separation distance (d_ij), given by the following equation⁴⁰.

$$\gamma ={\left(\frac{1}{d_{ij}}\right)}^2$$ (2)

Upon diagonalization, the Hessian matrix yields 3N-6 normal modes (V) and eigenvalues (λ) corresponding to the non-rigid body fluctuation dynamics of the protein. We calculate the mean-square fluctuations (MSF) of residues in a protein using these 3N-6 eigenvalues and eigenvectors with the following equation

$$<\mathrm{\Delta }{R}_i^2>={\sum }_{j=1}^{3N-6}\frac{1}{{\lambda }_j}{\sum }_{i=3k-2}^{3k}{V}_{ji}^2,k\in [1,N]$$ (3)

Hydropathy index

We use the Kyte-Doolittle hydropathy scale⁴¹ to represent residue hydrophobicities.

Dynamic flexibility index (DFI)

From linear response theory, the response vector to an external perturbation in a protein structure such as binding of a ligand can be obtained from

$$\mathrm{\Delta }{R}_{3N\times 1}=H_{3N\times 3N}^{-1}{F}_{3N\times 1}$$ (4)

Here, ΔR is a 3N dimensional response vector giving the positional displacement of each atom in X, Y and Z, F is a 3N dimensional force vector and H^‒1 is the 3N by 3N-dimensional pseudoinverse of the Hessian matrix calculated using the 3N-6 non-rigid body eigenvectors as follows

$$H^{-1}={\sum }_{i=1}^{3N-6}{\lambda }_i^{-1}{V}_i{V}_i^T$$ (5)

A response matrix A can then be created using response vectors as follows.

$$A=\left[\begin{array}{ccc}(\left|\mathrm{\Delta }{R}^1\right|& \left|\mathrm{\Delta }{R}^2\right|\left|\mathrm{\Delta }{R}^3\right|\cdots & \left|\mathrm{\Delta }{R}^N\right|{)}_1\\ (\left|\mathrm{\Delta }{R}^1\right|& \left|\mathrm{\Delta }{R}^2\right|\left|\mathrm{\Delta }{R}^3\right|& \left|\mathrm{\Delta }{R}^N\right|{)}_2\\ ⋮& \ddots & ⋮\\ (\left|\mathrm{\Delta }{R}^1\right|& \cdots & \left|\mathrm{\Delta }{R}^N\right|{)}_N\end{array}\right]$$ (6)

Each row in such a matrix is the average response of all residues upon perturbing a given residue i. The metric dynamic flexibility index (DFI) for a residue j is then calculated as

$$DF{I}_j=\frac{S_j}{\left({\sum }_{j=1}^N{S}_j\right)},where{S}_j={\sum }_{i=1}^N{A}_{ij}$$ (7)

Dynamic flexibility index^{36, 42} estimates the resilience of a given residue position to perturbations at all positions within the 3-D structure of the protein. Sites with low DFI, such as hinges, are more resilient to perturbations and are hence, dynamically more stable than sites having high values of DFI. DFI also measures the significance of each position’s contribution to the global functional dynamics of the protein. We perform calculations of DFI for each protein and obtain the indices for each residue using the method described by Gerek et al. ³⁶

Active site perturbation response (only for allosteric predictors)

The active site perturbation response is a measure of the effect of perturbations on the functional binding site (active site) on other residues. Residues which show higher fluctuation responses upon perturbation of the active site are often associated with allosteric signal transmission. We calculate the active site perturbation response as described by Kumar et al⁴² For the calculation of this feature, identifying the active site residues is essential.

Residue conservation scores

For each protein, we extract the sequence from the PDB file and then search for homologous sequences using BLAST⁴³ (with default parameters) against the non-redundant protein sequence database with an e-value cutoff of 0.01, percentage identity in the range of ≥ 35% and ≤ 95% and query coverage of 80%. To filter out duplicates, we use CD-Hit⁴⁴ and cluster the initial set of homologs at 95% sequence identity and then select only the representative sequences from each cluster. We perform a multiple sequence alignment (MSA) with Clustal Omega⁴⁵ with default parameters on a randomly selected set of 150 representative homologs for each protein. Using Rate4Site⁴⁶ with its default parameters for the evolutionary model (JTT) and rate inference method (Bayesian), we then calculate the conservation scores for each protein from its respective MSA file. Rate4Site reports the extent of conservation at a position as a z-score, with a lower score indicating stronger conservation.

Network centralities

We render each protein structure as a coarse-grained network whose nodes are residue represented by their C^α atoms. The edges are weighted or unweighted depending on the type of network. For each network, we calculate the node betweenness, closeness, degree, eigen and page rank centralities. In the following text, we summarize the networks and their properties used in this study. Further details of how the centrality was calculated are given in the Supporting Information.

1. Network based on distance cutoff. A protein is modeled as a coarse-grained system by representing individual residues by their C^α atoms and by adding edges between residue pairs which are within a distance cutoff of 13Å. The choice for this distance cutoff is based on a preliminary analysis in which we explore cutoffs of 10–15 Å and observe, for the same subset of features, the predictive performances to be all similar (Fig. S3). We thus proceed by arbitrarily considering 13Å as the cutoff.

2. Distance weighted network. The edge between a residue pair is weighted by spatial proximity – in this case the distance between the C^α atoms. Such a network can be regarded as an interaction strength network – edges between spatially close residues are given higher weights than edges between distant residues.

3. Network weighted by the correlation of inter-residue dynamics. The edges are weighted by the extent of dynamic correlation between the residue pairs.

4. Network weighted by the interaction energy. The edges between residue C^α atoms are weighted by their interaction strengths obtained by using the Betancourt and Thirumalai (BT) contact potential⁴⁷. We convert energies in the BT potential matrix into positive scores by calculating their Boltzmann factors. Thus, more favorable interacting pairs (lower interaction energies) have larger weights.

Pocket residues

We use Fpocket⁴⁸ to predict cavities or pockets from atom positions in protein structures and identify the residues that are located in pockets. Fpocket uses alpha spheres and Voronoi tessellations to identify pockets in a protein. It considers a residue to be part of a pocket if any of the residue atoms are at a distance equal to the radius of an alpha sphere in the pocket.

Shortest path to catalytic residues (only for allosteric predictors)

Upon binding of effectors, allosteric residues transmit signals to functional binding sites through allosteric signaling pathways – chains of residues connecting between the regulatory and the active site. For identification of residues involved in effector binding, one of the features that we also consider is the shortest dynamically correlated path between a given residue and the active site. Our underlying hypothesis is that potential effector binding residues will have shorter paths that are more dynamically correlated than other residues.

By considering a protein as a system of C^α atoms with residues connected by Hookean springs with stiffness varying inversely with the square of the distance (Eq. 2), we obtain the dynamic correlation c_ij between residues (Eq. 6) and transform it into a dissimilarity matrix D (Eq. 7).

$$c_{ij}=\frac{trace{H}_{ij}^{-1}}{\sqrt{trace{H}_{ii}^{-1}trace{H}_{jj}^{-1}}}$$ (8)

$$D_{ij}=1-c_{ij}$$ (9)

The protein is modeled as a network with each residue pair within 13 Å being connected by an edge whose weight is the distance-transformed correlation in dynamics obtained with Eq. 9. With such a network formulation, we use Dijkstra’s algorithm⁴⁹ to calculate the shortest path between a given residue and any of the active site residues. In addition, we also consider the median shortest path from a given residue to all active site residues. It should be noted that for the calculation of this feature, prior knowledge of active site residues is required.

Training, validation and test datasets

Figure 1 illustrates the overall workflow of AR-Pred and highlights the number of positive and negative labels in the training, validation and test data. Tables S1 and S2 report the proteins considered in the datasets for allosteric and active site models, respectively. Details regarding the datasets are provided in the Supporting Information.

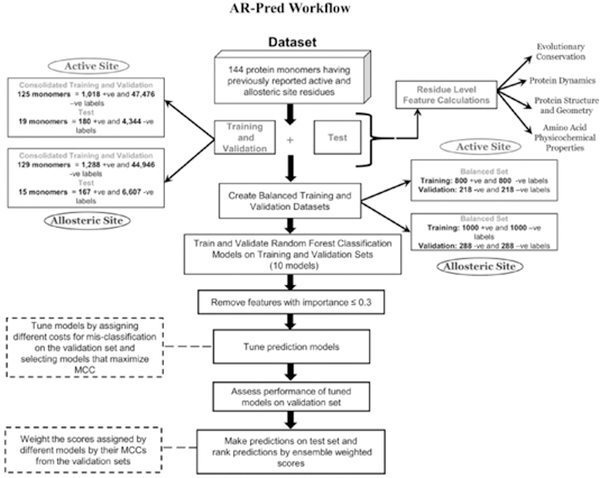
Figure 1.

AR-Pred Workflow with the observed protocol followed. The training and test data were created from a benchmark set of 144 protein monomers. Ten random forest models were created for each prediction class (active and allosteric site), each trained and validated on a separate balanced dataset. All ten models from each class are used to make predictions on the test set. Predictions made by each model are weighted with the model’s Matthew’s Correlation Coefficient.

Machine learning models

We use the TreeBagger module (https://www.mathworks.com/help/stats/treebagger.html) in Matlab, an implementation of the random forest algorithm, to develop separate predictive models for allosteric and active site residues. For each type, we first train the algorithm with each of the 10 balanced training sets and then verify performance on the corresponding validation set. Thus, we have 10 models each trained using a different dataset. Our random forest implementation uses 100 trees and a minimum of 2 leaves at each node. To optimize the performance of each model we also include misclassification costs (penalty for false negatives and false positives) in our model with a cost matrix. Using a brute force approach, we verify the classification performance using different cost combinations for false positives and false negatives in the range of 0.1 to 1 in steps of 0.1 and select the combination that maximizes the Matthews correlation coefficient (MCC) for a given model. Including such costs in each model improves slightly the performance as shown in Fig. S4 and S5.

Feature selection

We exclude all features found to have feature importance below 0.3. The notations used for the features and their descriptions are provided in Table 2.

Table 2.

Notations for selected features and their descriptions

Feature Notation	Feature Description
AA IDENTITY	Identity of each amino acid (from the 20 amino acid types)
AA TYPE	Amino acid type based on hydrophobicity, polarity and charge
ACTIVESITE PERTURBATION RESPONSE	Response of a given residue upon perturbing residues in the active site
ASA (ABS/REL) POLAR	Absolute or relative solvent accessibility for all oxygen and nitrogen atoms in a residue side chain
ASA (ABS/REL) NONPOLAR	Absolute or relative solvent accessibility for all non-oxygen and nitrogen atoms in a residue side chain
ASA (ABS/REL) ALLATOM	Absolute or relative solvent accessibility for all atoms in a residue
ASA (ABS/REL) SIDECHAIN	Absolute or relative solvent accessibility for all side-chain atoms in a residue
ASA (ABS/REL) MAINCHAIN	Absolute or relative solvent accessibility for all main-chain atoms in a residue
BETWEENNESS D13	Residue betweenness centrality for unweighted network (dist cutoff 13Å)
BETWEENNESS CORR NET DIST TRANSFORMED	Residue betweenness centrality for network having edges weighted by distance-transformed dynamic correlations
BETWEENNESS BT POT	Residue betweenness centrality for network having edges weighted by the Betancourt-Thirumalai (BT) potential
CONSERVATION SCORE	Extent of conservation for a residue
CLOSENESS_D13	Residue closeness centrality for unweighted network (dist cutoff 13Å)
CLOSENESS INT STNGT MAT	Residue closeness centrality for network with edges weighted by inverse distance between residues
CLOSENESS CORR NET DIST TRANSFORMED	Residue closeness centrality for network having edges weighted by distance-transformed dynamic correlations
CLOSENESS BT POT	Residue closeness centrality for network having edges weighted by the Betancourt- Thirumalai (BT) potential
DFI	Dynamic flexibility index
DEGREE D13	Residue degree centrality for unweighted network (dist cutoff 13Å)
DEGREE INT STNGT MAT	Residue degree centrality for network with edges weighted by inverse distance between residues
DEGREE CORR NET DIST TRANSFORMED	Residue degree centrality for network having edges weighted by distance-transformed dynamic correlations
DEGREE BT POT	Residue degree centrality for network having edges weighted by the Betancourt-Thirumalai (BT) potential
EIGEN D13	Residue eigen centrality for unweighted network (dist cutoff 13Å)
EIGEN INT STNGT MAT	Residue eigen centrality for network with edges weighted by inverse distance between residues
EIGEN CORR NET DIST TRANSFORMED	Residue eigen centrality for network having edges weighted by distance-transformed dynamic correlations
EIGEN BT PT	Residue eigen centrality for network having edges weighted by the Betancourt-Thirumalai (BT) potential
ISPOCKETRESIDUE	Binary feature indicating whether a residue is part of a pocket or not
KD HYDROPHOBICITY	Residue hydrophobicity based on the Kyte-Doolittle hydrophobicity scale
MSF	Residue mean square fluctuation
MEDIAN SHORTEST PATH TO ACTIVESITE RES	Median value of all shortest paths from a given residue to any of the active site residues
PAGERANK D13	Residue page rank centrality for unweighted network (dcutoff 13Å)
PAGERANK INTSTNGTMAT	Residue page rank centrality for network with edges weighted by inverse distance between residues
PAGERANK CORR NET DIST TRANSFORMED	Residue page rank centrality for network having edges weighted by distance-transformed dynamic correlations
PAGERANK BT POT	Residue page rank centrality for network having edges weighted by the Betancourt-Thirumalai (BT) potential
SEC STRUCT	Secondary structure notation for a residue
SHORTEST PATH TO ACTIVESITE RES	Shortest dynamically correlated path from a given residue to any of the active site residues

Model performance evaluation

We evaluate the performance of our models by using the standard metrics in Table 3.

Table 3.

Metrics used to evaluate the performance of machine learned models

Metric Name/Notation	Description
Area under curve (AUC)	The area under curve for the receiver operating characteristics curve for different values of true positive rates and false positive rates.
Sensitivity	$\frac{TP}{TP+FN}$
Specificity	$\frac{TN}{TN+FP}$
Precision	$\frac{TP}{TP+FP}$
False negative rate (FNR)	$\frac{FN}{FN+TP}$
False positive rate (FPR)	$\frac{FP}{FP+TN}$
Accuracy	$\frac{TP+TN}{TP+TN+FP+FN}$
F1 score	$\frac{2TP}{2TP+FP+FN}$
Matthews correlation coefficient	$\frac{TP\ast TN-FP\ast FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$

TP: True positive, FP: False positive, TN: True negative, FN: False negative

Prediction on test dataset

We weight the probability score assigned to each residue for a given model by its MCC for its corresponding validation set and then obtain a cumulative weighted score for each residue in a protein from the ensemble of 10 models with the following equation

$$Scor{e}_{weighted}^i={\sum }_{N=1}^{10}MC{C}_N{S}_N^i$$ (10)

Here, MCC_N is the MCC of the Nth model and $S_N^i$ is the score of the i^th residue assigned by the Nth model. We use this formulation of weighted scores on the models trained for allostery and on those trained for active site detection to identify the most probable allosteric and active site residues, respectively.

Results and Discussion

We use a previously compiled dataset that was used by Greener and Sternberg for the allosteric prediction tool, AlloPred²⁵. The compiled dataset has information on both allosteric and active site residues and thus provides the basis for a scheme to predict both allosteric and active site residues. In our approach, we compile a diverse set of features based on amino acid physicochemical properties, evolutionary conservation, protein structural geometry and supplement them with features that relate to the dynamical nature of the proteins. Since dynamics is critical for maintaining the functional and regulatory roles in proteins, we are presuming that including such information will improve the detection of residues important for regulation or substrate modification.

Our goal is to develop prediction models for active and allosteric site residues using a common subset of features. We are calling our method AR-Pred. To this end, we first calculate the features described in Methods for all proteins in the dataset and exclude proteins for which any of the features could not be calculated. For multimeric proteins in our dataset, feature calculations were performed on each subunit after splitting the multimer into its separate subunits, resulting in a feature vector of size M (M is the number of features) for each residue. A single protein having N residues can thus be described by an N by M matrix of features. Next, we divide the dataset of protein structures into distinct training, validation and test sets based on the distribution of the number of active site and allosteric residues (Fig. S1 and Fig. S2). For each prediction class (active site and allosteric), we create 10 balanced training and validation sets. We train a random forest classification model on each training set and verify its performance on the respective validation set. Consequently, we have 10 models trained and validated for each prediction class. We use this ensemble of 10 models to make predictions for the test sets. Details concerning the creation of training, validation and test datasets are provided in Supporting Information.

The prediction models for active sites and allostery collectively constitute AR-Pred. First, we compare the performances for AR-Pred’s active site and allosteric prediction models for their respective validation sets. Second, we focus on the features which were important determinants of the models’ performance. Third, we predict allosteric and active site residues on the test data, verify the extent of randomness in AR-Pred’s predictions and compare our predictions with other methods. Fourth, we inspect the predictions made by the allosteric models on one of the test proteins to identify false positives. Finally, we consider one protein common to the test data sets of active sites and allostery to verify the localization of predicted active and allosteric site residues and show a connection between the intrinsic dynamics of these sites.

Performance of validation sets

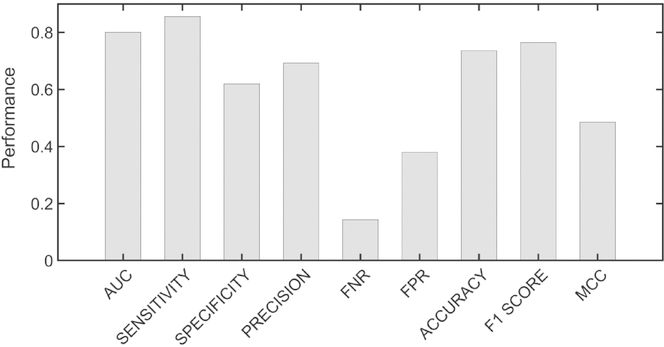
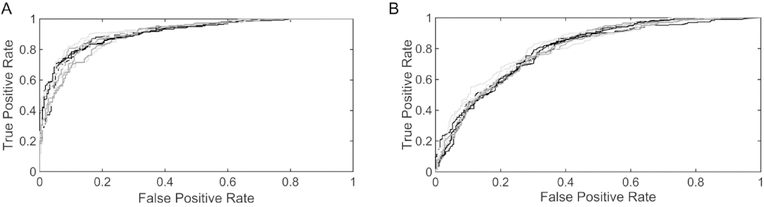
Figures 2 and 3 show the resulting metrics for the average performance of the 10 models on the validation data set for the active sites and the allosteric sites, respectively. It is seen that the average performance of the models for active sites is better than for allosteric sites. The performance for each of the 10 models for active and allosteric sites is given in Fig. S6 and S7, respectively. It is interesting to note a greater inter-model variation in sensitivity and specificity for allosteric sites than for active sites. The models for allostery also exhibit higher variance for false positive rate (FPR) than the models for active sites. Both indicate that predicting active sites is more reliable than predicting allosteric residues. The receiver operating characteristic (ROC) curves for active site and allosteric models in Fig. 4A and Fig. 4B, respectively clearly show the better performance for active sites than for allosteric sites, with the area under the curve (AUC) for active sites being substantially higher than for allosteric sites.

Figure 2.

Metrics for the performance of active site models. Median metrics calculated across the ten models for active site prediction. The metrics were calculated on the validation set corresponding to each model.

Figure 3.

Metrics for the performance of allosteric site models. Median metrics calculated for the ten models for allosteric site prediction. Calculations were performed as for the metrics of the active site models.

Figure 4.

Receiver Operating Characteristics (ROC) Area Under Curve (AUC). AUCs for active site models (A) vs allosteric models (B). Clearly the active site predictions are significantly better than the allosteric site predictions, possibly because the prior assignments of allosteric sites are more uncertain.

At first this suggests that the predictive nature of our models for allosteric sites is less significant and is more random than the models for active site, however one must consider that active sites are substantially better known and have been investigated more exhaustively in comparison with allosteric sites. Active sites have long been exploited as popular drug targets by pharmaceutical industries and thus, their identification is supported by a plethora of experimental evidence. There have been relatively fewer studies on allostery which may indicate that many allosteric sites in proteins remain unknown, explaining the variance between allosteric site models.

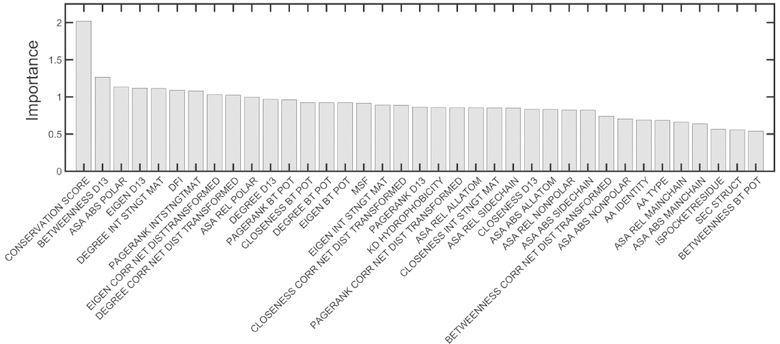
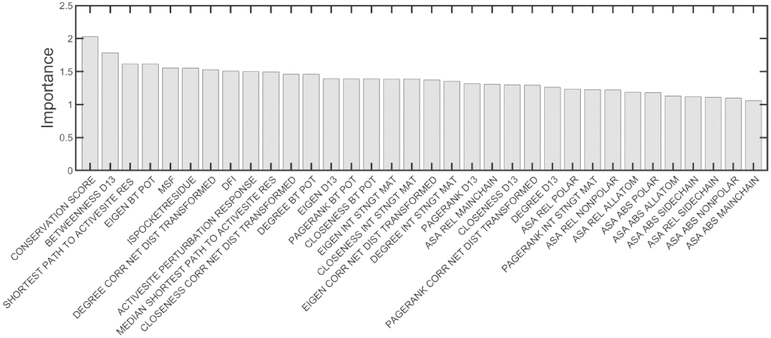
Feature importance

The feature importance for the two classes of predictions is shown in Figs. 5 and 6. For both the models of active site and allosteric site predictions, residue conservation score is the most important feature. However, it is significantly more important for active site than for allosteric site detection, as indicated by the remarkably large difference between the importance of conservation in comparison with the other features. We also notice that the residue node betweenness centralities obtained by representing proteins as unweighted networks and adding edges between residues within 13 Å are rated as the second most important feature for both allosteric and active site residues. More importantly we observe features related to the residue-level dynamics ranked within the top 10 important features for both prediction types. It is seen that for both predictors, the resilience of residues to external perturbations described by the dynamic flexibility index (DFI) is also listed in the top 10 most important features. However, the extent of residue mobility described by mean-square fluctuations (MSF) is a more important factor for allosteric sites than for active sites. Besides, features describing the extent of coupling with the active sites such as the shortest dynamically correlated path to the active sites and the dynamic response upon perturbing the active sites are also important determinants for allostery, as might be expected. These results also suggest that solvent accessibility is more important for determining active site residues than for allosteric residues, indicating a strong preference of residues in active sites for their extent of solvent accessibility. Also, features relating to the physicochemical properties of amino acids such as amino acid hydrophobicity and secondary structures are important predictors for the active site residues and occur in Fig. 5 but are not present in Fig. 6 and do not seem to contribute significantly towards allosteric site detection.

Figure 5.

Assignments of importance of various input factors for the active site models. The median feature importance calculated across the 10 models for active site prediction are shown. The features are ordered by their importance.

Figure 6.

Assignments of importance of the various input factors for the allosteric site models. The median feature importance calculated across the 10 models for the allosteric site predictions are shown. The features are ordered by their importance.

Predictions on test datasets

Active site prediction

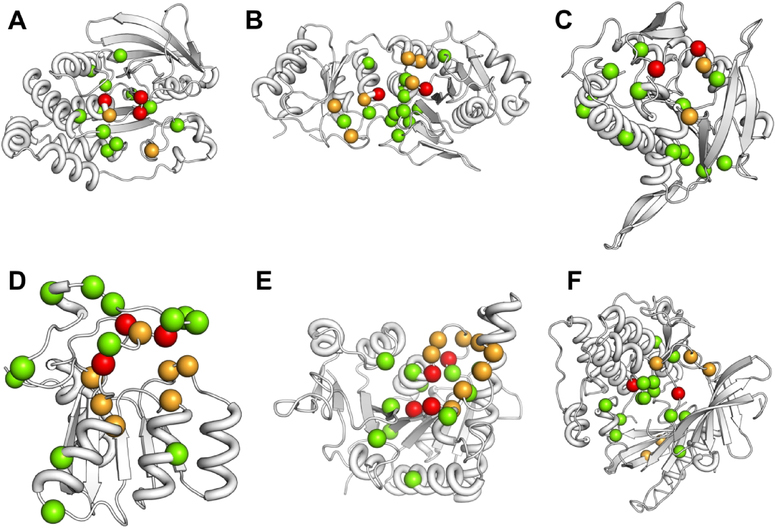
We have mapped out the predictions for active site residues from AR-Pred and compare them with the known active sites for 6 proteins in the test dataset. We rank residues by their weighted probability scores and for each protein we show only the top 15 residues. In Fig. 7, the predicted true positives are shown as red spheres, with remaining known active site residues orange, and the excess predicted ones in green. It is seen from this figure that in the predicted pool of residues, at least 2 residues are true positives in all 6 cases, while in two cases (A and D) there are 3 true positives and 4 true positives in E. For 4 of the cases, the top 15 predicted residues are localized in the vicinity of the known active sites (Fig. 7 A, B, E and F) while, in two cases (Fig. 7 C and D) the predicted residues are more scattered.

Figure 7.

Predictions on active sites for six proteins. Top 15 predicted residues for active sites are shown. The reported active sites are colored orange, the predicted true positives as red and the putative active sites predicted are shown as green spheres. The proteins for which these predictions are shown: A. Protein tyrosine phosphatase 1B (PDB 1T49, chain A), B. L-Asparaginase I (PDB 2HIM, chain A), C. Uracil phosphoribosyltransferase (PDB 1JLR, chain A), D. Deoxycytidylate deaminase (PDB 2HVW, chain A), E. UMP Kinase (PDB 2V4Y, chain A), F. AKT 1 (PDB 3O96, chain A).

To test whether the predictions are random, we perform two tests. First, for all proteins in the test data, we consider the shortest distance between the heavy atoms of the top 15 predicted residues and any of the known active site residues and plot their distribution. Second, we perform 50 iterations of random residue selection by picking 15 residues randomly from each protein. For each iteration, we compare the distribution of the shortest distances between the heavy atoms of the randomly sampled residues and any of the known active site residues with the distribution of distances for the top 15 predicted active sites in each protein. Such an analysis should tell us how closely clustered the predicted active site residues are around the known active site residues and the extent of randomness in the locations of the predicted active site residues. Results are shown in Figs. S8 and S9, respectively. In Fig. S9, we observe the highest peak near 2.5Å and the distribution has a negative gradient at 5Å suggesting that the predicted residues are nearer the known ones. Fig. S9 suggests that the predictions are not random since the peaks are much sharper for the predicted residues (red) and at shorter distances than for the random ones (blue). It is also worth noting that there is a second smaller peak for the predicted residues, around 20Å, suggesting a bimodal distribution of the shortest distances and possible alternative functional binding sites for a given protein.

Allosteric site predictions

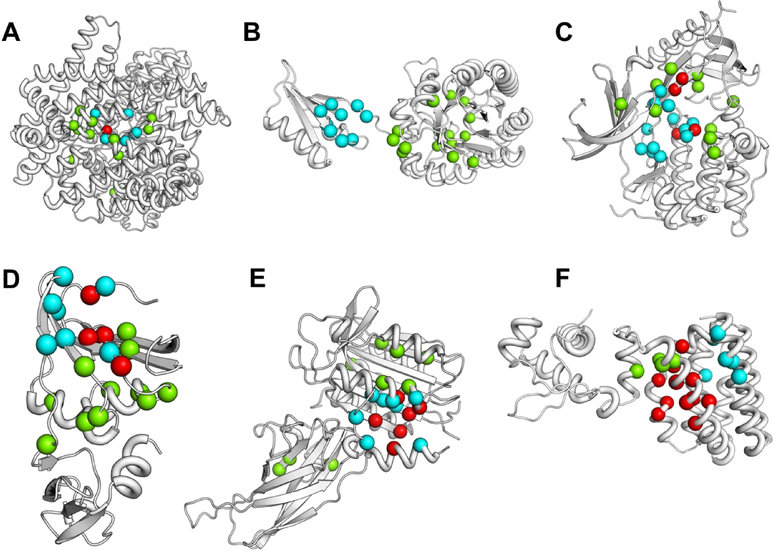
In Fig. 8, we have mapped the predicted allosteric residues by AR-Pred onto the structures of 6 proteins (showing cyan colored spheres for known allosteric residues, green for predicted and red for predicted true positives). It is seen that in five out of the 6 cases (Fig. 8 A, C, D, E and F) the predicted residues are tightly clustered around the known ones. We also observe a higher number of true positives for the allosteric predictions: a maximum of 11 residues are true positives out of the top 15 (Fig. 8F). One of the six proteins (Fig. 8B) shows nearly a complete mismatch between the predicted and known allosteric residues. The protein is DAH7PS from Thermotoga maritima (PDB 3PG9) which is involved in the shikimate pathway, essential for the synthesis of aromatic amino acids. We further verify the significance of the predicted residues for this protein and investigate whether they might constitute potential allosteric pathways. DAH7PS has two domains - an N-terminal regulatory domain and a C-terminal catalytic domain (Fig. S10) and catalyzes the condensation between the substrates phosphoenolpyruvate (PEP) and D-erythrose 4-phosphate (E4P) to form 3-deoxy-D-arabino-heptulosonate 7-phosphate (DAH7P). It is known to be regulated by tyrosine which binds to the regulatory domain and reduces affinity for both substrates.⁵⁰ Upon binding, tyrosine induces a displacement in the position of the β2-α2 loop in the catalytic domain (colored in violet in Fig. S10). In Fig. S11 (A, B, C, D, E and F), we have mapped the predictions for the top 5, 10, 15, 20, 30 and 40 allosteric residues. It is worth noting that one of the top 5 predicted residues (Fig. S11A) is located on the β2-α2 loop of the catalytic domain. We observe that with an increasing number of predicted residues, more residues are predicted on the linker connecting the regulatory and catalytic domains and on the β2-α2 loop. Also, in the top 40 predicted residues (Fig. S11F), 3 residues are located on the regulatory domain of which, 2 are true positives. Figure S11F also appears to describe two putative allosteric pathways (red and blue arrows) between the opposite ends of the protein from the regulatory domain a to the β2-α2 loop of the catalytic domain. It is seen that the two pathways are on either side of the active site (shown as orange spheres). Interestingly, some of the predicted residues are in vicinity of the active site residues. Since a protein’s dynamic nature introduces the possibility of multiple allosteric pathways, these residues may be part of such pathways to control activity or even the dynamics of the active site.

Figure 8.

Visualization of the allosteric site predictions on six proteins. The top 15 residues predicted for allosteric sits are shown for the 6 proteins in the corresponding test dataset. Previously reported allosteric sites are shown in cyan, the predicted true positives in red and the putative predicted sites as green spheres. The proteins considered are: A. Phosphoenolpyruvate carboxylase (PDB 1FIY, chain A), B. DAH7P synthase (PDB 3PG9, chain F), C. AKT 1 (PDB 3O96, chain A), D. Aspartate transcarbamoylase (PDB 2BE9, chain B), E. MALT1 (4I1R, chain A), F. FadR (1H9G, chain A).

To verify the extent of randomness in our predictions for allosteric residues, we perform an analysis similar to that above for the predicted active site residues: a) we probe the distribution of the shortest Euclidean distances between the heavy atoms of the predicted residues and any of the true allosteric residues, and b) we compare the distributions of the shortest distances for the predicted residues against a pool of randomly selected residues. In Fig. S12, we plot the distribution of the shortest distances for the top 15 predicted residues for all proteins in the allosteric test data and it shows that there is a single maximum with the peak close to 6 Å. This suggests that a major fraction of the predicted residues is tightly clustered around the experimentally verified residues. However, as shown for DAH7PS some predicted residues constitute allosteric pathways that have differing characteristics that may also be important. Such residues can be located away from the effector binding site and can skew the distribution plot. Fig. S13 compares the distributions of the shortest distances for the top 15 predicted allosteric residues in all proteins for 15 randomly chosen residues. The comparison is carried out for 50 iterations. It is clearly seen that in all iterations, the predicted residues are associated with sharper peaks at shorter distances than in the randomly chosen cases, further confirming that these predictions are not random.

Comparisons with existing methods

Active site predictions

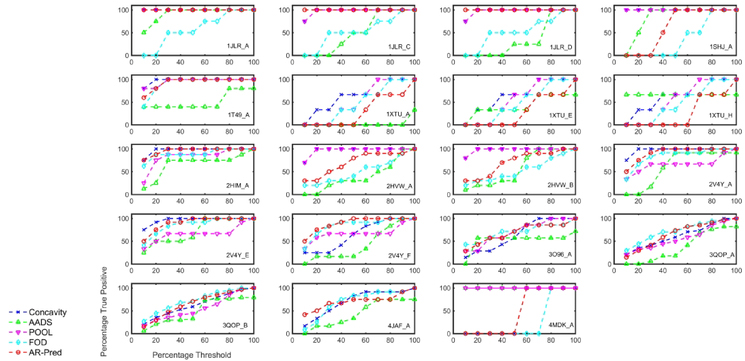
We compare AR-Pred’s predictions for active sites with the results from four other methods: Concavity,¹⁷ AADS,¹⁸ POOL,¹⁵ and FOD.¹² For each method, we rank the predictions by their scores and, in Fig. 9, plot the percentage of true positives predicted (ordinate) for a certain percentage of the ranked predictions (abscissa), referred to here as percentage threshold. Our aim is to systematically compare the percentage of predicted true positives below a percentage threshold for each of these methods against our results. Three out of the four methods (Concavity, POOL and FOD) assign scores to residues in a protein based on their propensity for being active site residues. However, AADS predicts active site pockets, where each pocket contains multiple residues. To make comparisons with such pocket-based methods, we rank residues based on the rank of their pocket. Thus, all residues in a given pocket are assigned the same rank. Then, we filter residues which appear in multiple pockets by considering them only as part of the higher ranked pocket and consider the pool of residues in every threshold percent to identify the number of predicted true positives.

Figure 9.

Comparison of the AR-Pred’s predicted active sites with predictions from other methods for 19 proteins. Prediction comparisons are made between the AR-Pred’s active site predictions and four other methods (Concavity, AADS, POOL and FOD) for each protein in the test data. On the X-axis we have the percentage of predictions considered as a threshold and plot the percentage of true positives predicted under a certain threshold by each method.

Results are shown for each individual protein in the test dataset in Fig. 9, comparing the prediction performance of AR-Pred (red curve) with the above-mentioned methods. When considering the percentage of true positives in the top 10 percent of the predicted residues, AR-Pred outperforms FOD in 11 out of the 19 cases and AADS in 14 out of 19 cases and we observe a similar performance for 5 and 3 proteins, respectively. At the same threshold, we perform better than Concavity in 5 cases and show similar performance in 6 cases. In the case of POOL, we have results only for 18 out of the 19 cases (4JAF gave errors). We see similar performance for POOL as for Concavity, with 6 cases of improved performance and 5 cases of similar performance. When considering a threshold of the top 30 percent of the predicted residues, our method performs better than Concavity and POOL in 4 and 6 cases, respectively and we observe similar performances in 7 and 8 cases, respectively. Upon comparing with FOD and AADS, at 30 percent threshold, we perform better in 9 and 12 cases and observe similar performance in 8 and 3 cases, respectively. Table 4 shows the percentage of proteins from the test data for which our method predicts the same or higher numbers of true positives than the four other methods at various threshold percentages. AR-Pred shows at least similar or better performance compared to Concavity, AADS, POOL and FOD for a median 57.9%, 79.0%, 66.7% and 84.2% of the test proteins, respectively for the thresholds of 10–50 percent of the predictions. These results clearly indicate that including protein-dynamics information together with the physiochemical, structural and evolutionary features, leads to the improved detection of active site residues.

Table 4. AR-Pred performance compared with other active site prediction methods.

The percentage of proteins for which AR-Pred predicts the same or a larger number of true positive active site residues relative to the other methods is tabulated. The calculations are reported for different percent thresholds that consider the top 10, 20, 30, 40 and 50 percent of predictions.

Threshold Percent╲Method	Concavity	AADS	POOL	FOD
10	57.9	89.5	61.1	84.2
20	36.8	73.7	72.2	89.5
30	57.9	79.0	77.8	89.5
40	63.2	79.0	61.1	63.2
50	68.4	84.2	66.7	79.0
Median	57.9	79.0	66.7	84.2

Allosteric site predictions

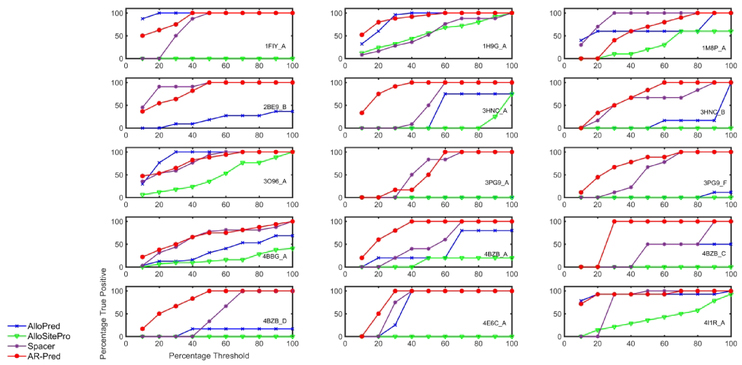
We compare the predictive power of our method with three existing methods: AlloPred,²⁵ AlloSitePro,⁵¹ and SPACER.²⁷ AlloPred is the source of the dataset we have used to develop our prediction models. AlloSitePro is an upgraded implementation of AlloSite.²⁴ SPACER uses binding leverage, the ability of a binding site to couple with the intrinsic motions of a protein to identify potential allosteric sites and makes predictions at the residue-level; whereas, both AlloPred and AlloSitePro predict pockets. To perform comparisons, we follow the same procedure as above for the active site prediction models. Results are shown in Fig. 10. With a threshold of 10 percent of the predicted residues, we observe gains in true positives against AlloPred, AlloSite and SPACER for 8, 9 and 9 proteins and similar performances for 4, 5 and 4 proteins, respectively. In 7 cases, our method performs better than all the three other methods, at the 10 % threshold. Table 5 shows the percentage of proteins in the test data for which our method shows better or comparable true positive rates for different threshold percentages. When compared to AlloPred, AlloSitePro and SPACER, our method gives comparable or better predictions for a median of 80, 93.3 and 86. 7 percent of the test files, respectively. These results confirm our underlying premise – that including dynamics information with other features leads to improvements in the prediction of allosteric residues.

Figure 10.

Comparison of the AR-Pred’s allosteric site predictions with other methods for 15 proteins. We compare the prediction performance for our allosteric predictions (AR-Pred) against those from three other methods (AlloSite, AlloPred and SPACER) for each protein in the test data. The abscissa and ordinates have same descriptions as in Fig. 9.

Table 5. AR-Pred performance compared with other allosteric site prediction methods.

The percentage of proteins for which AR-Pred predicts the same or a larger number of true positive allosteric site residues relative to the other methods is tabulated. The calculations are performed at different percentile thresholds for the top 10, 20, 30, 40 and 50 percent of the predictions.

Threshold Percent╲Method	AlloPred	AlloSitePro	SPACER
10	80.0	93.3	86.7
20	80.0	93.3	86.7
30	73.3	93.3	86.7
40	86.7	93.3	80.0
50	86.7	93.3	66.7
Median	80.0	93.3	86.7

Inspection of false positives in allosteric predictions

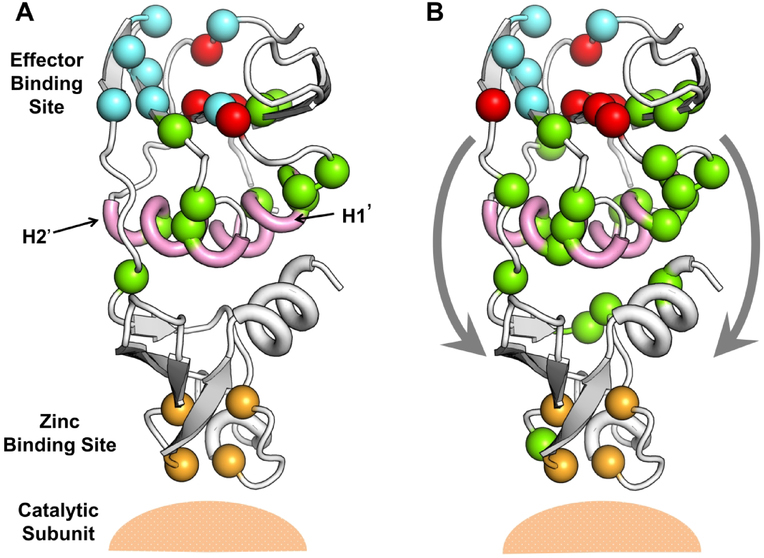
The protein aspartate transcarbamoylase (ATCase) from Sulfolobus acidocaldarius ATCase plays a vital role in the pyrimidine biosynthesis pathway, catalyzing the carbamoylation of the α-amino group of L-aspartate by carbamoyl phosphate and forming N-carbamoyl-L-aspartate and orthophosphate. It is a heteromeric structure comprised of two chains, catalytic and regulatory.⁵² While the catalytic chain comprises aspartate and carbamoyl phosphate binding domains, the allosteric chain has the allosteric domain which binds to regulators and zinc binding domains, which makes contact with the catalytic subunits. We consider the regulatory chain of the enzyme (PDB 2BE9, chain F) and the predictions made for the allosteric residues. In Fig. 11 we show the top 15 (Fig. 11A) and top 30 (Fig. 11B) allosteric residues predicted for this protein. Previously, Vos et. al.⁵³ compared the crystal structures for the CTP (allosteric regulator) bound and unbound structures for the Sulfolobus acidocaldarius ATCase and observed changes to the conformation of the bound form relative to the unbound form. Based on these observations, the authors proposed two allosteric pathways that transmit the effector binding signal to the catalytic subunits. We have shown the direction of these pathways with arrows in Fig. 11B. The H1’ and H2’ helices (shown in pink) show conformational deformations upon effector binding and hence, are considered critical for the allosteric signal transmission. For the top 15 predicted allosteric residues (Fig. 11A), we have 4 true positives (red spheres) while, 6 predicted residues lie on the H1’ and H2’ helices. Upon considering the top 30 predicted allosteric residues, we observe an increase in the number of residues on the two helices. It is interesting to note that the predicted residues align closely to the two proposed pathways and one of the residues in the pathways (Fig. 11B) is near the catalytic subunit. Such residues may be regarded as “sink” or “terminal” residues in an allosteric pathway in which the “source” is the effector binding site.

Figure 11.

Potential allosteric pathways for aspartate transcarbamoylase (PDB 2BE9). Predictions made with AR-Pred’s allosteric model for the top 15 allosteric residues (A) and top 30 allosteric residues (B) are shown. The two helices previously proposed to play a key role in transmitting allosteric signal from the effector binding site to the catalytic site are colored in pink. The zinc binding site is shown in orange. The reported allosteric residues are colored in cyan, the predicted true positives in red and the putative allosteric residues predicted by AR-Pred are shown as green spheres. The two proposed pathways are described in (B) by the two arrows.

Overlaps between allosteric and active site residue predictions

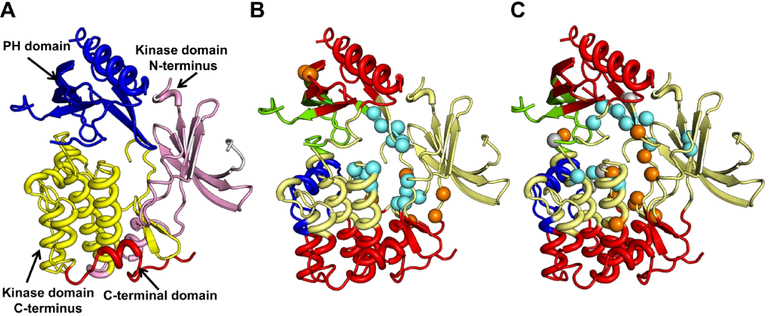
One of the proteins common to our allosteric and active site test structures is AKT1, a human serine/threonine AGC protein kinase (PDB 3O96) associated with the PI3K/AKT and other signaling pathways. AKT1 contains an N-terminal PH domain, inter-domain linker, a kinase domain and a C-terminal domain often referred to as the C-terminal hydrophobic motif (Fig. 12A). The PH domain binds phosphatidylinositide and directs the translocation of the protein from cytosol to the plasma membrane. The kinase domain contains the catalytic site responsible for phosphorylation and binds ATP.⁵⁴ We use this protein structure to visualize the agreement between the predicted and known allosteric and active site residues. By dividing the proteins into cohesive units that move as rigid bodies,⁵⁵ we also learn about the localization of the predicted residues with respect to these structural domains. First, we divide the protein into dynamic cohesive units, also referred to as dynamic communities. To do this, we reduce the protein using a coarse-grained C^α representation and calculate the inverse Hessian for the elastic potential of the system using the first 20 low frequency normal modes with Eq. 5. Next, we calculate the correlation between residue-dynamics and express the inter-residue correlation matrix as a dissimilarity matrix using equations 8 and 9, respectively. Then, we identify dynamical structural blocks using the method described by Danon,⁵⁶ dividing the protein into four distinct dynamic communities.

Figure 12.

AKT 1 (PDB 3O96) domains, communities and predictions. (A) The three major domains of AKT 1 are shown. The kinase domain is split into its respective N and C-terminus domains and these four parts are shown in different colors. Experimentally reported (B) and top 15 AR-Pred predicted (C) allosteric and active site residues are shown. The protein backbone is colored based on its division into the computed four dynamic communities. Regions in the same color show highly correlated motions, indicating these are the rigid elements in the protein’s dynamics. The allosteric residues are in cyan, the active site residues in orange. In the predictions made by AR-Pred, residues which were predicted both as allosteric and active sites are shown in gray.

Figures 12B and 12C compare the known active and allosteric site residues (B) with the top 15 predictions made by our models (C). From the computed dynamic communities, it is seen that the kinase domain is similarly divided into two communities - red and yellow (Fig. 12 B and C). The rigid unit in the C-terminus of the kinase domain (in red at the bottom) shows dynamic coordination with the PH domain at the top, together forming one community. 4 out of the top 15 predicted allosteric residues coincide with the known ones, while we see an overlap of 2 residues at the active site. A strikingly common feature shared between the predicted and true allosteric residues is their location on the same dynamic communities, suggesting that both the predicted and known sites are highly correlated in their dynamics. It is even more interesting to notice that some of the predicted active site residues are reported to be allosteric. On closer observation, we find some of these residues are neighbors to residues that form the active site. This could make their feature profile very similar to that of the active site residues, making it hard for our models to distinguish between them. This suggests that a residue’s functional classification is strongly influenced by its neighboring residues. Terminal or sink residues in an allosteric pathway, which are proximate to the active site, may not strictly be only allosteric but could also be involved in the active site. Their physicochemical, structural and dynamical properties may strongly correlate with active sites, even presenting them as potential functional binding sites. Based on these criteria, a strict classification of residues as allosteric or active site may not always be feasible owing to the influence of neighboring residues. This raises a few intriguing questions: could sharing a similar feature profile with active site residues introduce a constraint on a residue’s evolution? It is also interesting to consider whether some of these residues might eventually evolve and be transformed into active site residues.

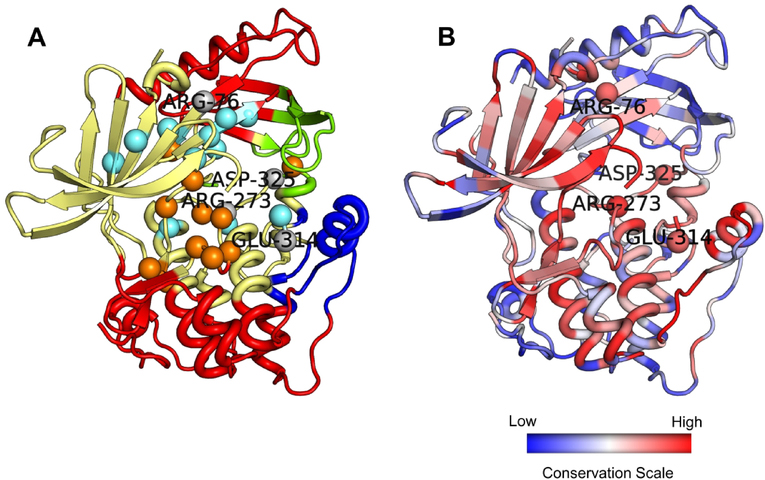
Our model predicts four residues (shown in gray spheres) as both allosteric and active site residues (Fig 12C and 13A). Two of these residues are located on the boundary of a pair of dynamic communities. We hypothesize that these residues are examples of cases where, a strict classification scheme is not applicable. These residues may be classified into either category. Previous studies have shown that active sites of the proteasome can allosterically regulate each other’s activity.⁵⁷ Other studies have indicated the presence of intrasteric control⁵⁸ directed at active sites, in which a short peptide, mimicking the substrate in the vicinity of the active site, binds and regulates the activity of the active site.⁵⁹ Such studies suggest that active sites could self-regulate their activity which, in a sense, is clearly related to allostery. The residues which our model predicts to be both functional and regulatory sites could then possibly be identified as self-regulating residues. Owing to their location at the boundaries between dynamic communities, they could also play a key role of allosteric signal transmission between the communities. We further confirm the functional importance of these residues by showing their evolutionary conservation in Fig 13B, which confirms that these residues have strong conservation. More importantly, three of these residues, Arg76, Asp325 and Glu314 have not been reported earlier as either active site or allosteric residues. Our method is thus, capable of predicting novel putative binding sites which, in principle, should be functionally significant owing to their strong conservation patterns.

Figure 13.

Overlap between allosteric and active site residue predictions. (A) Four residues predicted by AR-Pred to be both allosteric and active site are shown in gray and labelled. The coloring scheme is same as in Fig. 12. (B) The protein is colored by its evolutionary conservation, with the color scale varying from blue to red – least conserved to most conserved.

Conclusions

We have developed discrete machine learning models using the random forest approach to predict allosteric and active site residues. Our prediction models for allostery and active site detection use a common subset of features, which broadly include amino acid physicochemical properties, protein structure geometry, residue conservation and intrinsic dynamics of the protein structure. Instead of making predictions from a single model, we have used an ensemble approach to make predictions. In such an approach, we make multiple models for each prediction class, each model is trained and validated on a separate training-validation set and then predictions are made using each model. Residue-level scores assigned by each model are weighted by the model’s MCC and from this we calculate a weighted-ensemble score for each residue that relates to its probability of being an allosteric or active site residue. When compared to existing methods, our implementation makes predictions at the residue level by assigning them weighted probability scores. Such an implementation is useful, especially in the field of protein engineering by providing candidate residues whose mutations could possibly alter a protein’s activity.

When assessed on the test dataset, our models for active site detection show comparable performance to two existing methods and gains against two others. Our models for allostery however, show superior performance over three of the existing methods. It is worth noting that including information on the residue dynamics in addition to other properties appears to be the origin of this significant gain in performance. However, our test datasets for allostery and active site prediction have only a small number of proteins, 15 and 19 respectively, but there are two points in support of the present approach. First, since our models make predictions at the residue-level, having a larger set of residues in the test dataset is a more important consideration than the number of proteins. A number of existing methods identify pockets and then, rank them based on their propensity of being active or allosteric binding pockets.^{18, 25, 26, 60–62} Because proteins have fewer pockets than residues, these methods have been tested on datasets having diverse numbers of proteins. On the contrary, our models consider the total number of residues in the allosteric and active site test data sets where we have 167 allosteric, 6607 non-allosteric, 180 active site and 4344 non-active site residues. Second, since our aim is to develop separate models for the predictions of active and allosteric site residues, our required dataset needs to have labels for both allosteric and active site residues, and the number of such annotations is limited.

Our study shows for an example that there can be considerable overlap between the feature profiles of active and allosteric site residues and hence, our models predict certain allosteric residues to be active site residues and vice-versa. Residues that are terminal along an allosteric pathway often lie in close spatial proximity to the active site. Hence, their physicochemical, structural and dynamical characteristics can closely resemble those of the active site residues. Besides, previous studies have also suggested that active sites may be allosterically coupled with one another. Based on these observations, a rigid classification of residues into allosteric and functional classes would, in some cases, be inappropriate.