Abstract
In order to handle complex tasks in hard-to-reach environments, small-scale robots have to possess suitable dexterous and untethered control capabilities. The fabrication and manipulation of soft, small-scale grippers complying to these requirements is now made possible by advances in material science and robotics. In this paper, we use soft, small-scale grippers to demonstrate pick-and-place tasks. The precise remote control is obtained by altering both the magnetic field gradient and the temperature in the workspace. This allows us to regulate the position and grasping configuration of the soft thermally-responsive hydrogel-nanoparticle composite magnetic grippers. The magnetic closed-loop control achieves precise localization with an average region-of-convergence of the gripper of 0.12±0.05 mm. The micro-sized payload can be placed with a positioning error of 0.57±0.33 mm. The soft grippers move with an average velocity of 0.72±0.13 mm/s without a micro-sized payload, and at 1.09±0.07 mm/s with a micro-sized payload.
I. Introduction
The ability of untethered, small-scale robots to handle nontrivial tasks has been demonstrated in a broad variety of applications, such as manipulation, assembly and microactuation [1]–[3]. However, traditional small robots are often passive with no shape-changing capabilities. This results in limited dexterity that restricts the complexity of achievable tasks. In contrast, robots with gripping capabilities provide significant advantages in achieving complex tasks. Small-scale grippers have enabled a wide set of applications, like precise micro-assembly, minimally invasive surgery, genetics, cell manipulation and mechanical characterization [4]–[7]. For instance, Gultepe et al. demonstrated the feasibility of an in vivo biopsy of the porcine bile duct using thermally-responsive grippers [8]. Ichikawa et al. demonstrated the enucleation of bovine oocytes using untethered millimeter-scale grippers [6].
In the aforementioned studies, the small size of the grippers has been exploited to perform tasks that would otherwise be unfeasible with traditional techniques. Nonetheless, at least four main challenges need to be overcome before untethered grippers can be broadly used in biomedical applications; (1) Further miniaturization of the grippers combined with untethered operation has to be achieved.(2) Precise closed-loop control of motion and grasping of the grippers has to be realized. (3) The grippers have to reliably manipulate micro-sized objects. (4) The grippers have to be fabricated using biocompatible materials and operate in a manner that poses no risk to humans.
Size reduction and untethered actuation are critical to enable maneuverability of small-scale grippers in hard-to-reach environments. Conventional robotic approaches with electrical motors and actuators do not allow for significant miniaturization of the electronic components and on-board batteries. Hence, the use of wirelessly powered self-folding robots have drawn interest and shown promising results [9]–[15]. A family of prominent self-folding structures are composed of hydrogels. Hydrogels have several attractive properties of relevance to untethered small robots. Many can be constructed with biocompatible and even biodegradable polymer chains or cross-linkers making them attractive for biomedical applications. They can function in aqueous media of relevance to biology and medicine. Their soft and squishy nature allows them to mimic the touch and feel of biological and even human appendages. Finally, they can be photopatterned into definite shapes so that they can change their shape on swelling and shrinkage [16].
A. Related Work
In this paper, self-folding is achieved by constraining the swelling of the hydrogel using a stiff polymer (SU-8). As previously demonstrated this combination of a stiff polymer with a reversibly swelling hydrogel can be used to create microtools with significant strength and applicability for grasping applications. In a related study, Breger et al. doped the polymer with magnetic nanoparticles to demonstrate open-loop control of soft grippers [17]. We utilize similarly designed grippers to realize closed-loop control and obtain levels of precision and reliability that are not achievable in open-loop. Closed-loop control of hydrogel grippers have also been reported by Fusco et al. [11], [12]. The main differences between [11], [12] and our study are: a) The previously reported grippers in [11], [12] were not magnetic themselves, so magnetic motion control was only possible when they gripped onto a magnetic object. (b) Previously near-IR radiation was used to heat the grippers whereas here we use a Peltier element. (c) The numerical results and analysis of the closed-loop motion control and pick-and-place tasks were not reported. Consequently, the accuracy of previously reported tasks remains unclear.
B. Contribution
In this study, we demonstrate and analyze the performance of loaded and unloaded grippers that can be precisely localized and positioned in two-dimensional space using closed-loop motion control. We exploit the self-folding properties of the hydrogel to endow temperature control and regulate the configuration of the grippers. Finally, through the synergy of magnetic and temperature control, we demonstrate the capability of grippers to execute pick-and-place of micro-sized objects.
The paper is organized as follows: Section II presents the electromagnetic system, fabrication process and characterization of the soft grippers. Section II-C describes the used tracking and control techniques. Section IV presents and discusses the experimental results. Finally, Section V concludes and provides directions for future work.
II. Experimental Setup
In this section, the magnetic and thermal systems are described. Subsequently, we illustrate the fabrication process of the gripper and the techniques applied for their magnetic and thermal characterization.
A. Magnetic and Thermal Systems
Our magnetic system consists of six orthogonally oriented electromagnets surrounding a Petri dish with an attached Peltier element (Fig. 1) [18]. The electromagnets are controlled using a proportional-integral-derivative (PID) controller [19]. Each electromagnet is powered by an Elmo Whistle 1/60 servo controller (Elmo Motion Control, Petach-Tikva, Israel). A color camera (Point Grey Research Inc., Richmond, Canada) and a microscope (Mitutoyo, Kawasaki, Japan) are used to track the grippers. The system can generate magnetic fields with maximum magnitude of 15 mT with 60 mT/m gradients. These magnetic fields are safe in clinical applications, where fields of up to 1.5 T are used daily in magnetic resonance imaging.
Fig. 1.
Top: Photographs of the electromagnetic and thermal systems used to control the soft grippers. The system consists of 6 orthogonally-configured coils, and a Peltier element. The electromagnetic coils have a cutoff frequency of 70 Hz and a maximum current rating of 1 A. The system generates a maximum magnetic field and magnetic field gradient of 15 mT and 60 mT/m, respectively. Bottom: Snapshots showing the gripper grasping a micro-sized bead. The scale bar is 0.8 mm.
A Peltier element is used to regulate the temperature of the water where the soft grippers are floating. The element is attached below the Petri dish with conductive double-sided tape and controls its temperature by conduction. An Arduino Uno (Arduino, Ivrea, Italy) micro-controller powers and controls the Peltier element using Proportional-Derivative (PD) control [19]. The PD temperature controller is able to achieve a steady-state error of about 1°C and can heat the water at an average rate of 10°C/min. A commercial thermometric probe is used in the PD control loop.
B. Fabrication of Grippers
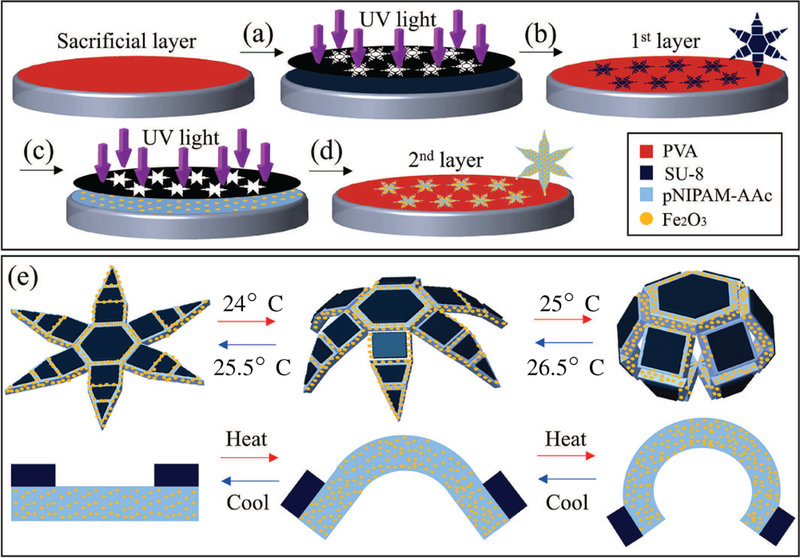
In order to fabricate the segmented SU-8/continuous poly-N-isopropylacrylamide (pNIPAM-AAc) bilayer grippers, a 90% hydrolyzed polyvinyl alcohol (PVA) sacrificial layer is spin coated onto a silicon (Si) wafer and then baked at 115°C for 5 minutes (Fig. 2). SU-8 is then spin coated on the PVA at 2000 rpm followed by a pre-bake process at 70°C for 1 minute, 115°C for 3 minutes, and 70°C for 1 minute. The 21μm-thick SU-8 film is then photopatterned using a photomask and exposed to 180 mJ/cm2 ultraviolet (UV) light (365 nm) to initiate crosslinking. Further, post-baking is carried out at 70°C for 1 minutes, 115°C for 3 minutes, and 70°C for 1 minute. Uncrosslinked portions of the SU-8 are removed using a commercial SU-8 developer for 1 minute and then washed with acetone for 1 second and isopropyl alcohol (IPA) for 10 seconds before being dried with compressed air. In order to make the 34μm-thick magnetic second layer of pNIPAM-AAc, 5% w/w biocompatible iron (III) oxide (Fe2O3, Sigma-Aldrich, St. Louis, USA) 50 nm nanoparticles are incorporated into the pNIPAM-AAc stock solution [17]. The obtained pNIPAM-AAc solution including Fe2O3 is patterned on the previously photopatterned SU-8 segments using a second dark field mask and aligned in non-contact mode using spacers. Once deposited and aligned, pNIPAM-AAc is exposed to 40 mJ/cm2 UV light to initiate crosslinking. A wash in acetone and IPA is used to remove uncrosslinked pNIPAM-AAc before drying using compressed air. Finally, the wafer is immersed in DI water overnight to completely dissolve the PVA sacrificial layer. When fully opened, the grippers have an hexagram shape with a tip-to-tip dimension of 4 mm. When fully closed, the grippers have the shape of a sphere with an approximately 0.4 mm radius.
Fig. 2.
A schematic of the fabrication process of the soft grippers: (a) SU-8 is spin-coated on a polyvinyl alcohol (PVA) sacrificial layer. (b) The SU-8 film is photopatterned and exposed to ultraviolet (UV) light. (c) A 95% poly-N-isopropylacrylamide (pNIPAM-AAc) and 5% biocompatible Fe2O3 layer is deposited on the SU-8 layer. (d) The coated surface is photopatterned and exposed to UV light to obtain segmented, multi-fingered, bilayer grippers with rigid phalanges and flexible joints. (e) Schematic images of the untethered grippers in open and closed (grasping) configurations. Also shown is a side-view of a single hinge.
C. Magnetic Characterization of Grippers
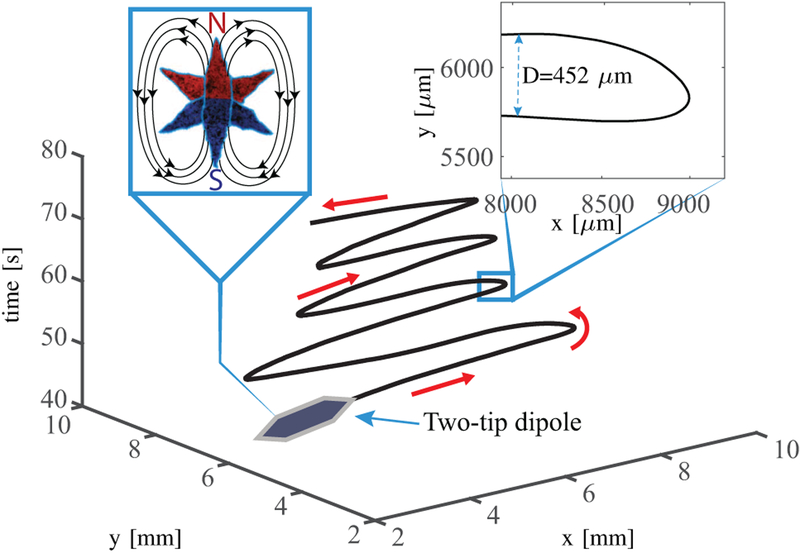
We characterize the grippers resulting from this fabrication process evaluating their magnetic dipole moment and thermal behavior (Sec. II-D). The magnetic dipole moment of the grippers is required for modeling purposes (Sec. III-A). In order to evaluate mg, the grippers are assumed to have a uniform Fe2O3 distribution. We divide the six-tip gripper in three pairs of counterposed two-tip dipoles. The magnetic dipole moments of the latter ones can be superposed to obtain mg (Fig.3). The magnitude of mtips is experimentally measured using the U-turn technique, after removing four tips from the gripper to obtain a two-tips dipole [20]. The two-tip dipole align along the magnetic field lines, reversing the field direction cause them to perform a U-turn whose diameter (D) is given by
| (1) |
where is linear velocity of the dipole, and α is its rotational drag coefficient. We calculate the value of α to be 2.2×10−11 Am2sT approximating the two-tip dipole by a cylinder [21]. In order to determine the magnetic dipole moment, we apply uniform magnetic fields of 3.5 mT. The fields are reversed to initiate the U-turn. The experiment is repeated 20 times. The average U-turn diameter and velocity are 0.19±0.05 mm and 0.73±0.13 mm/s, respectively. Using (1) we obtain |mtips| =3.5×10−8 Am2. The direction of mtips is determined using where is the magnetic pole strength and is the vector separating the two poles [22]. Finally, the magnetic dipole moment of the gripper is computed as the superposition of three rotated two-tip dipoles. The magnitude of mg results 7×10−8 Am2 while its orientation with respect to the gripper is represented in Fig. 3. We note that the adopted technique overestimates the magnetic dipole moment of the central overlapping part. However, this section is assumed to have a negligible effect on the overall magnetic dipole moment due to its small d.
Fig. 3.
Schematic of the trajectory of the two-tip dipole during the U-turn experiments for magnetic characterization. Left inset: A graphical representation of the magnetic dipole moment of the soft gripper as a superposition of the magnetic dipole moments of its two-tip dipoles.
D. Thermal Characterization
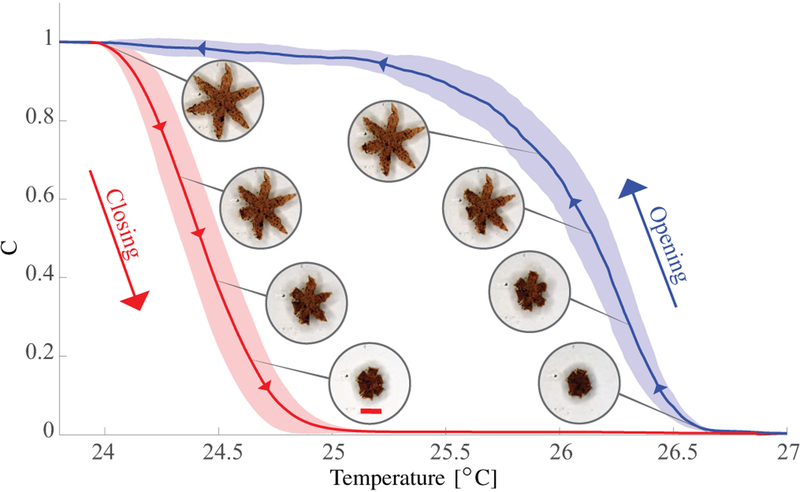
We also characterize the thermal response of the grip-pers. For this purpose, the temperature of the water was increased until the gripper was fully closed, and then decreased to room temperature. During this procedure, the gripper changes its configuration from star-shaped to spherical, and back (Fig. 4). Therefore, we use the diameter of the gripper to evaluate its configuration (Sec. III-B). Five successive opening and closing cycles were analyzed for three different grippers. The results are shown in Fig. 4. The grippers on average completely opened at temperatures below 24°C and fully closed above 27°C. However, we noticed a variance of these boundaries depending on the temperature dynamics. Open grippers closed at lower temperatures than the ones at which closed grippers opened. We attribute this behavior to the heating rate being higher than the cooling rate.
Fig. 4.
Results of the opening and closing characterization of the soft grippers (15 experimental trials): The red and blue lines show the average configuration of the grippers when they are heated and cooled, respectively. The corresponding shaded areas depict the standard deviations. The coefficient C is an indicator of the configuration of the grippers and varies from 1 (for an open configuration) to 0 (for a closed configuration). The value is computed as , where D(T) is the diameter of the contour of the gripper at temperature T, Dclosed and Dopen are the diameter values for the completely closed and open gripper, respectively. The scale bar is 0.8 mm.
III. Tracking and Control
This section presents the modeling and control of our setup. Also the tracking procedure for position extraction and prediction is commented upon.
A. Modeling and Control
Magnetic-based wireless control techniques are used for the motion control of grippers. These are based on the ability to map the currents at the electromagnets into the electromagnetic forces exerted on the grippers using,
| (2) |
where F are the electromagnetic forces acting on the soft gripper, and are the magnetic field produced by the electromagnets and their currents, respectively, and is the actuation matrix, which maps the input currents into magnetic forces [23]. The forces are then regulated using a two-input, three-output Multi-Input Multi-Output (MIMO) PID controller. The two inputs of the regulator are the x− and y−coordinates of the gripper. The output F is subsequently mapped into I using the pseudo-inverse of Λ(mmg, P) [24].
The computation of the force-current map (Λ) requires the knowledge of B(P) and mmg. The B(P) of our setup has been evaluated in previous studies, using a finite elements model analysis, and successively verified using a calibrated three-axis Hall magnetometer [25]. The value of mmg is estimated in Sec. II-C, the tracking procedure to obtain P is presented in Sec. III-B.
B. Tracking
The tracking process is composed of two steps. The first step aims at extracting the gripper contour from the input image, and is presented in Fig. 5. The points of this contour are subsequently mapped to the imaginary plane at the beginning of the successive step. The selected equation for this mapping is zn = xn + iyn for n = 0, 1, …, N where N is the number of the re-sampled contour points, xn and yn are the coordinates of the n-th re-sampled point, and i is the imaginary number [26]. We use this uniform sampled complex representation to calculate the Discrete Fourier Transform (DFT) coefficients by,
| (3) |
where goes from −15 to 16. The DFT coefficients provide us the position, scale and orientation of the gripper [26]. In order to increase noise rejection, we ignore all the contours that are not 6-fold symmetric by only tracking objects that satisfy the following conditions [27]:
| (4) |
| (5) |
where Zk are normalized Fourier descriptors. Furthermore, we set a threshold constraint on the ratio between contour and area of the contour. This value must be between 0.5 and 1 in order to avoid erroneous tracking of other 6-fold symmetric objects.
Fig. 5.
Flowchart illustrating the steps in the contour-extraction process for the soft grippers. (a) Input image from the microscope in Red-Green-Blue (RGB) colorspace. (b) The input is converted to Hue-Saturation-Value (HSV) color representation to separate chrominance from luminance and achieve glare robustness. (c) The image binarized using a Gaussian-window threshold after the application of a median filter. (d) The extracted contour of the gripper. The scale bar is 0.8 mm.
For the purpose of dealing with uncertainties in the tracking, we implemented a standard Kalman filter [28]. The Kalman filter provides a one-step ahead estimation of positions and velocities, using current positions and control-input. The process noise is assumed to be a random variable with a Gaussian distribution N(0, Q), being an empirically determined covariance matrix.
IV. Results
In this section, we evaluate the performance and capabilities of the grippers. First motion control experiments are performed. Following these experiments, through the cooperation of motion and temperature closed-loop control, we assess the performance and capabilities of the grippers in pick-and-place tasks.
A. Motion Control of Grippers
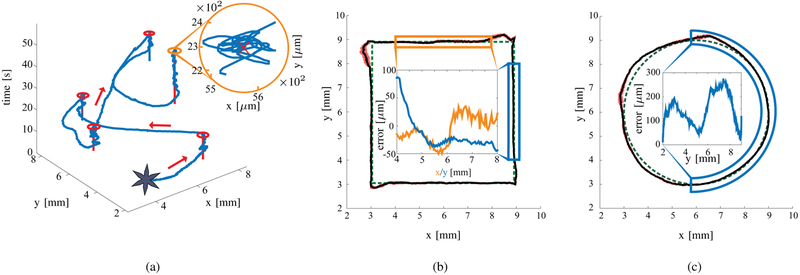
In these experiments, we evaluate the closed-loop control of soft grippers during point-to-point control and tracking of circular and square paths (Fig. 6). The experiments are performed both when the grippers are unloaded, and loaded with a 500 μm diameter polystyrene bead (Polysciences, Warrington, USA) (micro-sized non-magnetic payload). The circular path has a radius of 3 mm. The square path has sides of 6 mm. In order to verify the statistical reliability of the results, we perform 50 experimental trials for each task, using 10 different grippers without the micro-sized payload. The experimental results are tabulated in Table I. The grippers without micro-sized payload move with an average velocity and positioning error of 0.72±0.13 mm/s and 0.11±0.1 mm, respectively. Please refer to the accompanying video for the experiments.
Fig. 6.
Representative closed-loop motion control experimental results of a gripper. (a) An example of point-to-point motion control experiments. The red lines represents the setpoint, the blue line the trajectory of the gripper, and the red circles the Region of Convergence (ROC). (b) and (c) depict the trajectory following experiments. The green dashed path represents the reference trajectory, the black line shows the path of the gripper, and the red area represents the standard deviation for the corresponding point among all the experiments. The insets show the positioning error in the highlighted parts of the trajectories. Please refer to the accompanying video for the experiments.
TABLE I.
Experimental motion control results of soft grippers for point-to-point, circular and square trajectories. The average speeds and Euclidean-norm of average positioning error are reported with the respective standard deviation (150 and 15 experimental trials are conducted for grippers without and with the micro-sized non-magnetic payload, respectively).
| Grippers without micro-sized payload | Grippers with micro-sized payload | |||
|---|---|---|---|---|
| Experiment | Average speed | Error | Average speed | Error |
| Point to point | 0.8±0.1 mm/s | 0.12±0.05 mm | 1.1 ±0.06 mm/s | 0.23±0.04 mm |
| Circular | 0.62±0.13 mm/s | 0.12±0.09 mm | 1.08 ±0.04 mm/s | 0.17±0.12 mm |
| Square | 0.73±0.11 mm/s | 0.09±0.1 mm | 1.08±0.04 mm/s | 0.13±0.12 mm |
The average positioning error for the 150 experimental trials is 3% of the body length of the gripper. The error never reaches values above 5.5% of the gripper body length and such errors only occur during sharp turns, when the magnetic dipole moment of the gripper and the magnetic field are the least aligned, resulting in a weaker magnetic force (2).
In order to determine whether the performance difference among different grippers can be considered statistically negligible, we performed a Two One-Sided T-test (TOST) [29]. The tests revealed statistical equivalence, with 90% interval confidence, suggesting that all soft grippers behave similarly. Consequently, the number of experimental trials of motion control experiments of grippers with the micro-sized payload was reduced to 15 trials. These experiments followed the previously presented methodology and the results are tabulated in Table I. The grippers with the micro-sized payload moved 52% faster than grippers without the micro-sized payload, with an average velocity and positioning error of 1.09±0.07 mm/s and 0.17±0.23 mm, respectively. We attribute this increase in speed to the compact folded spherical-shape of the closed cargo loaded gripper which reduces the shear forces with the water and the side-walls of the dish.
B. Pick-and-Place Tasks
In this section, we highlight the ability of grippers to perform pick-and-place tasks. A gripper is positioned above a 500 μm spherical plastic bead. Once the position is reached, the temperature is raised to 40°C. This causes the gripper to close, and grasp the bead. Therefore, the micro-sized payload is captured within the gripper and can be dragged to the desired dropping location. The releasing procedure is activated by decreasing the temperature below 25°C. The experiment is repeated five times with an average positioning error of the bead of 0.57±0.33 mm. The micro-sized payload is transported for 1.5 cm with an average velocity of 1.09±0.07 mm/s. Please refer to the accompanying video for the experiments.
V. Conclusions and Future Work
In this paper, we characterize soft, self-folding grippers and analyze their capabilities and performance. Moreover, we demonstrate their ability to pick-and-place micro-scale objects. The gripper can be localized and follow trajectories with average positioning errors of 0.03 body lengths and speeds of 0.2 body lengths per second. Pick-and-place tasks are completed at average velocity of 1.09±0.07 mm/s and positioning error of the micro-sized object of 0.57 mm.
The experiments are enabled via two significant advances in materials science and robotics which include, (1) The fabrication of reversible soft-actuating grippers that harness mechanical energy and shape change from swelling; hence, they do not need wires, batteries or external power sources for actuation. (2) The ability to control the local temperature and magnetic field in a closed-loop with high accuracy.
As part of future work, grippers will be controlled in three-dimensional space. Furthermore, fully-autonomous pick-and-place of irregularly shaped objects will be studied. Moreover, advanced control techniques (e.g., cascade control) will be used to optimize the tracking of more intricate paths. Also, the Fe2O3 pattern of the grippers will be exploited in order to utilize the presented system in clinically-relevant applications using medical imaging systems.
ACKNOWLEDGMENT
This research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation programme (Grant Agreement #638428 - project ROBOTAR: Robot-Assisted Flexible Needle Steering for Targeted Delivery of Magnetic Agents).
The research reported in this publication was also supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (NIH) under Award Number R01EB017742. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Contributor Information
Federico Ongaro, Surgical Robotics Laboratory, Department of Biomechanical Engineering, MIRA-Institute for Biomedical Technology and Technical Medicine, University of Twente, The Netherlands..
ChangKyu Yoon, Department of Materials Science and Engineering, Johns Hopkins University, Baltimore, USA..
Frank van den Brink, Surgical Robotics Laboratory, Department of Biomechanical Engineering, MIRA-Institute for Biomedical Technology and Technical Medicine, University of Twente, The Netherlands..
Momen Abayazid, Surgical Robotics Laboratory, Department of Biomechanical Engineering, MIRA-Institute for Biomedical Technology and Technical Medicine, University of Twente, The Netherlands..
Seung Hyun Oh, Department of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, USA..
David H. Gracias, Department of Materials Science and Engineering, Johns Hopkins University, Baltimore, USA. Department of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, USA.
Sarthak Misra, Surgical Robotics Laboratory, Department of Biomechanical Engineering, MIRA-Institute for Biomedical Technology and Technical Medicine, University of Twente, The Netherlands.; Department of Biomedical Engineering, University of Groningen and University Medical Centre Groningen, The Netherlands.
References
- [1].Martel S and Mohammad M, “Using a swarm of self-propelled natural microrobots in the form of flagellated bacteria to perform complex micro-assembly tasks,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pp. 500–505, Alaska, USA, May 2010. [Google Scholar]
- [2].Tottori S, Zhang L, Qiu F, Krawczyk KK, Franco-Obregón A, and Nelson BJ, “Magnetic helical micromachines: fabrication, controlled swimming, and cargo transport,” Advanced materials, vol. 24, no. 6, pp. 811–816, 2012. [DOI] [PubMed] [Google Scholar]
- [3].Sitti M, Ceylan H, Hu W, Giltinan J, Turan M, Yim S, and Diller E, “Biomedical applications of untethered mobile milli/microrobots,” Proceedings of the IEEE, vol. 103, no. 2, pp. 205–224, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Randhawa JS, Leong TG, Bassik N, Benson BR, Jochmans MT, and Gracias DH, “Pick-and-place using chemically actuated microgrippers,” Journal of the American Chemical Society, vol. 130, no. 51, pp. 17 238–17 239, 2008. [DOI] [PubMed] [Google Scholar]
- [5].Diller E and Sitti M, “Three-dimensional programmable assembly by untethered magnetic robotic micro-grippers,” Advanced Functional Materials, vol. 24, no. 28, pp. 4397–4404, 2014. [Google Scholar]
- [6].Ichikawa A, Sakuma S, Arai F., and Akagi S, “Untethered micro-robot with gripping mechanism for on-chip cell surgery utilizing outer magnetic force,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pp. 3795–3800, Hong Kong, China, May 2014. [Google Scholar]
- [7].Malachowski K, Jamal M, Jin Q, Polat B, Morris CJ, and Gracias DH, “Self-folding single cell grippers,” Nano Letters, vol. 14, no. 7, pp. 4164–4170, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Gultepe E, Randhawa JS, Kadam S, Yamanaka S, Selaru FM,Shin EJ, Kalloo AN, and Gracias DH, “Biopsy with thermally-responsive untethered microtools,” Advanced Materials, vol. 25, no. 4, pp. 514–519, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Randhawa JS, Laflin KE, Seelam N, and Gracias DH, “Microchemomechanical systems,” Advanced Functional Materials, vol. 21, no. 13, pp. 2395–2410, 2011. [Google Scholar]
- [10].Malachowski K, Breger J, Kwag HR, Wang MO, Fisher JP, Selaru FM, and Gracias DH, “Stimuli-responsive theragrippers for chemomechanical controlled release,” Angewandte Chemie, vol. 126, no. 31, pp. 8183–8187, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Fusco S, Sakar MS, Kennedy S, Peters C, Bottani R, Starsich F, Mao A, Sotiriou GA, Pané S, Pratsinis SE et al. , “An integrated microrobotic platform for on-demand, targeted therapeutic interventions,” Advanced Materials, vol. 26, no. 6, pp. 952–957, 2014. [DOI] [PubMed] [Google Scholar]
- [12].Fusco S, Sakar MS, Kennedy S, Peters C, Pane S, Mooney D, and Nelson BJ, “Self-folding mobile microrobots for biomedical applications,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pp. 3777–3782, Hong Kong, China, 2014. [Google Scholar]
- [13].Kuo JC, Huang HW, Tung SW, and Yang YJ, “A hydrogel-based intravascular microgripper manipulated using magnetic fields,” Sensors and Actuators A: Physical, vol. 211, pp. 121–130, 2014. [Google Scholar]
- [14].Miyashita S, Guitron S, Ludersdorfer M, Sung CR, and Rus D, “Untethered miniature origami robot that self-folds, walks, swims, and degrades,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pp. 1490–1496, Seattle, WA, USA, May 2015. [Google Scholar]
- [15].Li H, Go G, Ko SY, Park J-O, and Park S, “Magnetic actuated ph-responsive hydrogel-based soft micro-robot for targeted drug delivery,” Smart Materials and Structures, vol. 25, no. 2, p. 027001, 2016. [Google Scholar]
- [16].Gracias DH, “Stimuli responsive self-folding using thin polymer films,” Current Opinion in Chemical Engineering, vol. 2, no. 1, pp. 112–119, 2013. [Google Scholar]
- [17].Breger JC, Yoon C, Xiao R, Kwag HR, Wang MO, Fisher JP, Nguyen TD, and Gracias DH, “Self-folding thermo-magnetically responsive soft microgrippers,” ACS Applied Materials & Interfaces, vol. 7, no. 5, pp. 3398–3405, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Sanchez A, Sadek YM, Khalil ISM, and Misra S, “Mobimag: A compact device for medical research using wireless control of magnetic microrobots,” in Proceedings of the Design of Medical Devices Conference-Europe, pp. 100–101, Delft, Netherlands, October 2014. [Google Scholar]
- [19].Franklin GF, Powell JD, and Emami-Naeini A, “Feedback control of dynamics systems,” Addison-Wesley, Reading, MA, 1994. [Google Scholar]
- [20].Bahaj AS, James PAB, and Moeschler FD, “An alternative method for the estimation of the magnetic moment of non-spherical magnetotactic bacteria,” IEEE Transactions on Magnetics, vol. 32, no. 5, pp. 5133–5135, 1996. [Google Scholar]
- [21].Chemla YR, Grossman HL, Lee TS, Clarke J, Adamkiewicz M, and Buchanan BB, “A new study of bacterial motion: superconducting quantum interference device microscopy of magnetotactic bacteria,” Biophysical Journal, vol. 76, no. 6, pp. 3323–3330, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Brown WF, “Magnetostatic principles,” in Ferromagnetism. North-Holland Amsterdam, 1962. [Google Scholar]
- [23].Khalil ISM and Misra S, “Control characteristics of magneto-tactic bacteria: Magnetospirillum Magnetotacticum strain MS-1 and Magnetospirillum Magneticum strain AMB-1,” IEEE Transactions on Magnetics, vol. 50, no. 4, pp. 1–11, 2014. [Google Scholar]
- [24].Khalil ISM, Abelmann L, and Misra S, “Magnetic-based motion control of paramagnetic microparticles with disturbance compensation,” IEEE Transactions on Magnetics, vol. 50, no. 10, pp. 1–10, 2014. [Google Scholar]
- [25].Sanchez A, Magdanz V, Schmidt OG, and Misra S, “Magnetic control of self-propelled microjets under ultrasound image guidance,” in Proceedings of the IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, pp. 169–174, Sao Paulo, Brazil, August 2014. [Google Scholar]
- [26].Van der Heijden F, Image based measurement systems: object recognition and parameter estimation. John Wiley & Sons Ltd, 1994. [Google Scholar]
- [27].He M, “The faber polynomials for m-fold symmetric domains,” Journal of Computational and Applied Mathematics, vol. 54, no. 3, pp. 313–324, 1994. [Google Scholar]
- [28].Belanger PR, Dobrovolny P, Helmy A, and Zhang X, “Estimation of angular velocity and acceleration from shaft-encoder measurements,” The International Journal of Robotics Research, vol. 17, no. 11, pp. 1225–1233, 1998. [Google Scholar]
- [29].Limentani GB, Ringo MC, Ye F, Bergquist ML, and Mc-Sorley EO, “Beyond the t-test: statistical equivalence testing,” Analytical Chemistry, vol. 77, no. 11, pp. 221–226, 2005. [DOI] [PubMed] [Google Scholar]