The Validity of Resting Metabolic Rate-Prediction Equations and Reliability of Measured RMR in Female Athletes

Abstract

The aim of the current study was to; 1) assess the test-retest reliability of an indirect calorimetry analyzer (Parvo Medics TrueOne), and 2) compare measured RMR with three RMR-predictive (pRMR) equations in female athletes. In part one, 12 recreationally-exercising women (mean ± SD; age 27.5 ± 12.3 y) performed two RMR assessments, on separate days, utilising the Parvo Medics TrueOne analyser. In part two, 25 recreationally-exercising women to sub-elite athletes (mean ± SD; age 30.1 ± 10.2 y) underwent an RMR assessment using the Parvo Medics TrueOne analyser, which was compared to three calculated pRMR equations (Harris-Benedict (H-B), Mifflin-St Jeor (M), World Health Organisation (WHO)). eTest-retest reliability for the TrueOne analyser was deemed acceptable (CV = 5.3%, ICC = 0.92). The validity of pRMR when compared to measured RMR showed low levels of agreement in all 3 predictive equations (M: CV = 21.4%, TEE = 269 kcal.day⁻¹, r = 0.16, WHO: CV = 21.5%, TEE = 270 kcal.day⁻¹, r = 0.13 H-B: CV = 21.6%, TEE = 270 kcal.day⁻¹, r = 0.13). The Parvo Medics TrueOne analyser is a reliable tool for measuring RMR. Caution should be taken when using pRMR equations in female athletes as they do not take into account the likely differences in fat free mass in these populations.

INTRODUCTION

The measurement of energy metabolism has been shown to correlate with energy availability, menstrual function, and bone mineral density in female athletes (8). Disturbances in energy balance resulting in a state of energy deficiency can compromise overall health status (20) and may have a negative impact on sport performance in athletic populations (17). Accurate identification of energy deficiency typically involves the measurement of resting metabolic rate (RMR) often in conjunction with hormonal profiling (9) and energy balance monitoring (4), Given that RMR is a commonly used assessment tool (8, 18, 22) for the identification of energy deficiency in athletes, the accuracy and reliability of the assessment is critical.

RMR measured by indirect calorimetry provides information at rest by measuring the volume of oxygen consumption (VO₂), volume of carbon dioxide production (VCO₂), and respiratory exchange ratios (RER = VCO₂/VO₂). RMR values can then be used in combination with hormonal profile and energy balance measures to formulate an overall picture of energy availability. Energy availability is a delicate balance between energy in and energy out, thus the validity and reliability of RMR measurement tools is crucial. The Parvo Medics TrueOne analyser (TrueOne 2400, Parvo Medics, Sandy UT) is often used in sport science laboratory settings to measure RMR as it has been reported to be a valid measurement tool for assessing RMR against the Deltatrac II (VIASYS Healthcare, Inc., SensorMedics, Yorba Linda, CA) (7) and the Douglas Bag system (26) in male recreational and elite athletic populations. However, the test-retest reliability of the TrueOne in recreationally-trained female athletic populations is yet to be determined.

The use of pRMR equations is extensive in metabolic research literature as these equations are inexpensive and easy to administer. However, the validity of the pRMR equations come into question when deviating from the original population from which they were developed (3). For example, the three most frequently used pRMR equations are the Harris-Benedict, the Mifflin-St Jeor and the World Health Organisation (WHO) equations. The Harris-Benedict equation was developed and validated in the early 1900’s. For the validation, 136 male (age: 27 ± 9 y) and 103 female participants (age: 31 ± 14 y) took part in the initial study (12). The Mifflin-St Jeor equation was derived from a sample of 498 (female n = 247, male n = 251) average-weight (f = 54.9 ± 4.5 kg, m = 68.5 ± 5.8 kg), overweight (f = 63.7 ± 5.5 kg, m = 80.2 ± 7.5 kg), obese (f = 76.2 ± 6.6 kg, m = 92.2 ± 7.3 kg), and severely obese (f = 89.4 ± 11.0 kg, m = 108.7 ± 13.1 kg) individuals aged 19 to 78 years (45 ± 14 y). The World Health Organisation (WHO) equations were developed using data mostly derived from young European military and police recruits, including 2,279 men and 247 women with 45% of Italian descent. Caution must be taken when generalizing the findings from these original validation studies to wider population groups, especially athlete samples. Given that athletes have greater muscle mass/fat free mass, and therefore an increase in metabolic cost, RMR will be greater than in those with less muscle mass. Therefore, RMR could potentially be underestimated. While all three RMR-prediction equations have been studied extensively for both their validity and reliability, across a range of populations, with varying results, the equations have yet to be validated against measured RMR values in a recreationally trained female-athlete population.

The aim of the current study was to determine the reliability of the Parvo Medics TrueOne indirect calorimetry analyser for measuring RMR in a recreationally active female population. A secondary aim of the study was to assess the validity of three pRMR equations relative to the measured RMR values in both recreationally active female athletes and sub-elite female athletes. We hypothesize that the pRMR equations will underestimate RMR values in the sub-elite athletes, due to the fact that highly-trained female athletes are likely to have larger muscle mass and fat free mass than the populations where the equations were originally validated.

METHODS

Participants

Part one (measured RMR) included 12 recreationally-trained females and Part two (measured RMR and predicted RMR) involved 25 female athletes (recreationally-trained and sub-elite). All participants volunteered to take part and their physical characteristics and demographics are shown in Table 1. Criteria for inclusion as a recreationally-trained female comprised of being free of any illness or injury and a minimum exercise requirement of at least 3 hr.wk⁻¹. Inclusion criteria for the sub-elite population compromised of being free of any illness or injury, be currently regularly training ( > 10hr.wk⁻¹), and of having represented New Zealand in their given sport in the last 3 years. All participants provided informed written consent and the study received ethical approval from the University of Waikato Human Research Ethics Committee.

Table 1.

Participant characteristics.

Variable	Recreational Athletes (n = 12)	Sub-Elite Athletes (n = 13)
Age (y)	27.5 ± 12.3	32.5 ± 7.4
Height (cm)	169.3 ± 7.3	167.9 ± 7.8
Body Mass (kg)	69.0 ± 9.4	60.9 ± 6.7
Body Mass Index	24 ± 3	22 ± 2
Weekly Exercise Duration (hr.wk−1)	8.0 ± 3.6	16.0 ± 4.0*

Note. Recreational athletes were involved in Part One and Part Two of the study, while Sub-Elite Athletes were only involved in Part Two of the study. Data shown as means ± SD.

^*indicates significant difference between groups (p < 0.05).

Protocol

The current study was split into two parts. For Part I, on two separate occasions, 12 recreationally trained female athletes participated in a test-retest reliability study, performing RMR measurements in our laboratory, with each trial separated by a minimum of 24 h and a maximum of 5 days.

Part II of the study included 25 female athletes (recreational to sub-elite) performing one RMR assessment using the Parvo Medics TrueOne analyser. The measured RMR was then compared to three pRMR equations (Harris-Benedict, Mifflin St-Jeor and World Health Organisation).

Measured RMR was conducted using the ‘RMR’ function on the TrueOne metabolic analyser (TrueOne 2400, Parvo Medics, Sandy UT). On the morning of the assessments, participants arrived at the laboratory for their scheduled lab appointment (between 0600 and 0830 h) following an overnight fast of > 10 h, with participants refraining from caffeine and alcohol intake > 24 h prior to testing. Participants were instructed to sleep 8 h the night before testing and recorded their 24 h dietary intake prior to the first trial to be replicated prior to the second trial (for Part 1). Participants were also asked to refrain from exercise in the 24 h leading up to each RMR assessment. Both trials were performed at the same time of day to control for any diurnal variation.

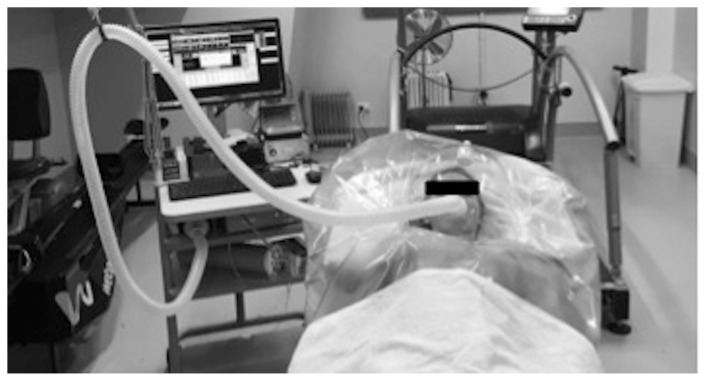
Participants were to arrive at the laboratory in a relaxed and rested state and were instructed to perform minimal activity between waking and arrival to the RMR testing session. Upon arrival to the laboratory participants height (cm) and body mass (kg; in minimal clothing) were measured before a 5-min passive rest period prior to the RMR assessment. (6). Participants were asked to relax and lie supine on a bed with the head rest set at an incline of 45° during the 20-min assessment period, but to maintain alertness with eyes open. The canopy (Figure 1) was then placed over the head, shoulders and upper chest of the participant to reduce contaminant air entering or expired air escaping during measurement. Flow rate was established at 28 to 30 ml.min⁻¹ within the first 4 min of the assessment as per manufacturer’s instructions. Expired air was sampled every 15 s. Data was averaged over 30 s and the participants file was exported in Microsoft Excel format for subsequent calculation of RMR (kcal.day⁻¹) via the Weir formula (25). RMR was calculated using the average of the final minute of each 5-min segment of the assessment (4 to 5, 9 to 10, 14 to 15 and 19 to 20 min).

Figure 1.

The resting metabolic rate (RMR) assessment setup with the Parvo Medics TrueOne indirect calorimetry analyzer.

Three RMR-prediction (pRMR) equations were calculated in the current study for comparison to the measured RMR value. The timeframe with the highest level of reliability during the RMR assessment (e.g. 0–5, 5–10, 10–15, 15–20 min) was used for comparison to the pRMR equations. All pRMR equations listed have been described elsewhere (11, 12, 16, 19, 21).

The Harris Benedict equation was calculated as follows:

$$\text{RMR}=655+(9.6\times \text{BM})+(1.7\times \text{H})-(4.4\times \text{A})$$ Eq. 1)

The Mifflin-St Jeor equation was calculated as follows:

$$\text{RMR}=(9.99\times \text{BM})+(6.25\times \text{H})-(4.92\times \text{A})-161$$ Eq. 2)

The World Health Organisation equation was calculated as follows:

$$\text{RMR}=(13.3\times \text{BM}+334\times (\text{H}/100))+35$$ Eq. 3)

Where BM = body mass (kg), H = height (cm) and A = age (y)

Statistical Analysis

All data is presented as mean ± SD unless stated otherwise. Statistical significance was set at p < 0.05. Comparison of the pRMR with measured RMR assessment was achieved using a Students’ paired t-test, Pearson product-moment correlation analysis, 95% limits of agreement (LOA), mean bias (%) and typical error of estimate (TEE). While correlation analysis indicates the degree to which two variables are associated, it does not necessarily indicate the extent to which values agree or disagree. To overcome this limitation, the approach of quantifying the level of agreement between the methods measuring the same parameter (in this case RMR) was employed (1, 2). The mean difference between methods (2 standard deviations or 95% of a normally distributed population) was determined. The TEE and mean bias between methods was determined using an excel spreadsheet (14), with the TEE expressed both in raw units and as a coefficient of variation (CV) percentage. The magnitude of correlation between the predicted and actual RMR values was assessed with the following thresholds: < 0.1, trivial; < 0.1–0.3, small; < 0.3–0.5, moderate; < 0.5–0.7, large; < 0.7–0.9, very large; and < 0.9–1.0, almost perfect. Test-retest reliability data was analysed using an Excel spreadsheet for reliability (15). TEE and overall reliability of RMR is presented as CV% and as an absolute value (kcal.day⁻¹) along with intra-class correlation coefficients (ICC’s) and upper and lower 90% confidence intervals (CI).

RESULTS

RMR was observed as an almost perfect agreement between trials 1 and 2 for the 15–20 min timeframe of the test (Table 1). RMR measures were less reliable in the 0–15 min timeframes, with CV’s ranging from 7.0–11.1% (Table 2).

Table 2.

Test-retest reliability outcomes for resting metabolic rate (RMR).

Variable	RMR (kcal.day−1) (Mean ± SD)	Mean bias (kcal.day−1) (90% CI)	Range of mean difference (kcal.day−1) (± 2SD)	TEE (kcal.day−1) (90% CI)	CV% (90% CI)	Correlation (r) (90% CI)
Measured RMR	1452 ± 267	-	-	-	-	-
Harris-Benedict	1438 ± 113	−14 (−108 – 80)	−554 – 526	270 (218 – 358)	21.6 (17.1 – 29.5)	0.13 (−0.22 – 0.45)
Mifflin-St Jeor	1392 ± 140	−61 (−157 – 36)	−611 – 490	269 (217 – 356)	21.4 (17.0 – 29.4)	0.16 (−0.19 – 0.47)
World Health Organisation	1460 ± 133	7 (−89 – 104)	−544 – 559	270 (218 – 358)	21.5 (17.1 – 29.5)	0.13 (−0.21 – 0.45)

Note. Expressed as typical error of estimate (TEE), coefficient of variation (CV%) and Intra-class correlation coefficient (ICC).

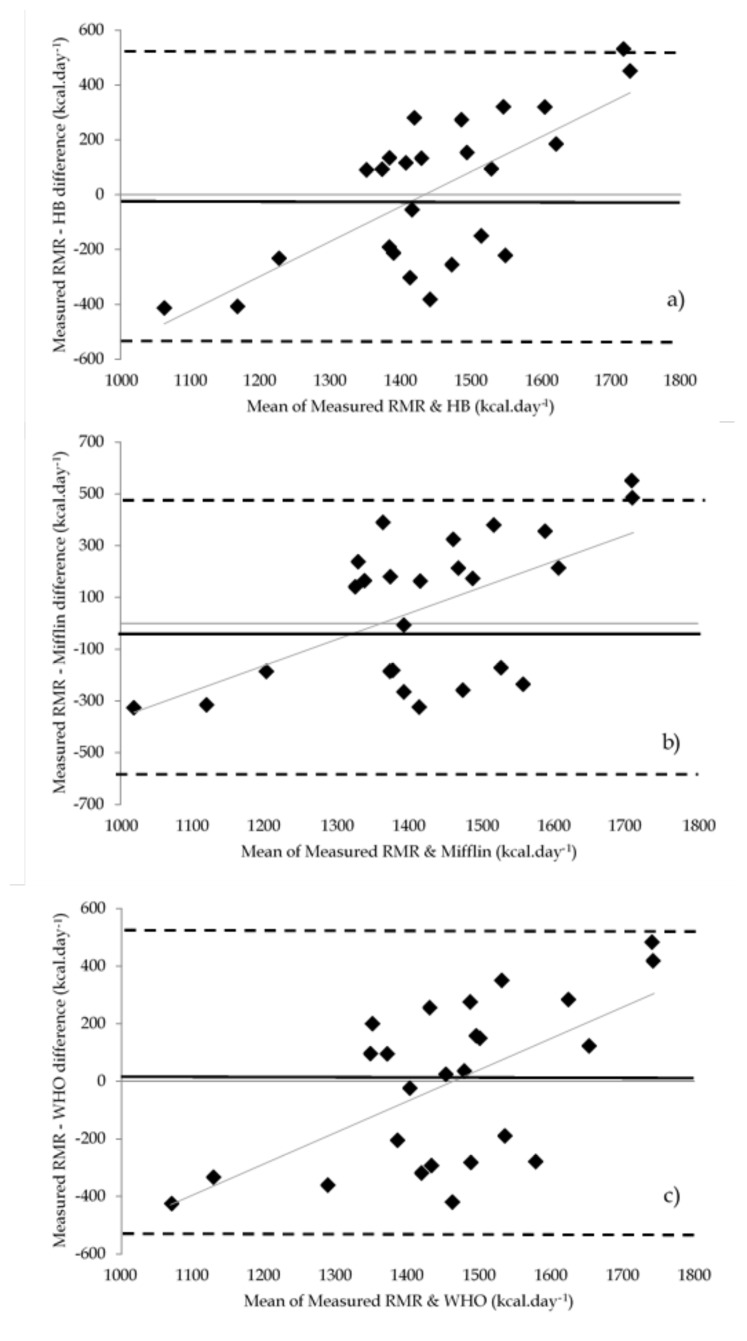
The validity of all three predictive equations when compared to measured RMR was questionable, with low levels of agreement. Results are shown in Table 3. Mifflin-St Jeor showed only a small level of agreement, followed closely by the WHO equation and the Harris-Benedict (Table 3). Bland-Altman plots for agreement between the three predictive equations and measured RMR are shown in Figure 2.

Table 3.

Comparison of measured RMR and three RMR-prediction equations in all female athletes (recreational to sub-elite).

Variable	RMR (kcal.day−1)		TEE (kcal.day−1) (90% CI)	CV% (90% CI)	ICC (90% CI)
	Trial 1 (Mean ± SD)	Trial 2 (Mean ± SD)
5-min	1332 ± 243	1253 ± 227	143 (107 – 222)	10.5 (7.8 – 16.8)	0.66 (0.27 – 0.86)
10-min	1227 ± 175	1307 ± 192	88 (66 – 137)	7.0 (5.2 – 11.1)	0.80 (0.53 – 0.93)
15-min	1216 ± 229	1273 ± 222	126 (94 – 196)	11.1 (8.2 – 17.7)	0.73 (0.38 – 0.89)
20-min	1244 ± 207	1285 ± 194	62 (42 – 96)	5.3 (3.9 – 8.3)	0.92 (0.80 – 0.97)

Note. Mean bias, range of mean difference (95% limits of agreement or ± 2SD) typical error of estimate (TEE – raw and CV%) and Pearson’s correlation coefficient (r) between methods.

^#represents significant difference when compared to Measured RMR (p < 0.01).

Figure 2.

The level of agreement plots (Bland-Altman) showing ± 95% limits of agreement (represented as dashed lines) between the measured RMR and each of the RMR prediction equation values in all female athletes (recreational to sub-elite): a) RMR vs. Harris-Benedict (HB); b) RMR vs. Mifflin-St Jeor (Mifflin); c) RMR vs. World Health Organisation (WHO). Solid black line represents the difference between methods. Gray line represents linear line of best fit

Data was then separated for training status effect of two groups: recreationally trained female athletes (n = 12) and; sub-elite female athletes (n = 13). Results are presented in Table 4. Between groups there was a significant difference in measured RMR values (p < 0.01). In recreationally trained female athletes, the equation that showed the highest agreement to measured RMR was the Mifflin-St Jeor equation, followed by the WHO equation and then the Harris-Benedict (Table 2). In sub-elite female athletes, the equation that showed the highest agreement to measured RMR was the Mifflin-St Jeor, followed the WHO and the Harris-Benedict (Table 4).

Table 4.

Comparison of measured RMR and three RMR-prediction equations in sub-elite athletes and recreational athletes.

Variables	RMR (kcal.day−1) (Mean ± SD)		Mean bias (kcal.day−1) (90% CI)		TEE (kcal.day−1) (90%CI)		CV% (90% CI)		Correlation (r) (90% CI)
	Sub-Elite	Recreational	Sub-Elite	Recreational	Sub-Elite	Recreational	Sub-Elite	Recreational	Sub-Elite	Recreational
Measured RMR	1629 ± 189*	1260 ± 195*	-	-	-	-	-	-	-	-
Harris-Benedict	1391 ± 81#	1484 ± 128#	−234 (−305 – −163)	224 (144 – 304)	139 (104 – 216)	162 (120 – 259)	8.5 (6.3 – 13.5)	14.5 (10.5 – 24.0)	0.71 (0.35 – 0.89)	0.61 (0.16 – 0.85)
Mifflin-St Jeor	1366 ± 102#	1451 ± 155#	−293 (−358 – −228)	191 (117 – 265)	131 (98 – 203)	148 (109 – 236)	8.1 (6.0 – 12.9)	12.9 (9.4 – 21.3)	0.75 (0.42 – 0.90)	0.69 (0.30 – 0.89)
World Health Organization	1405 ± 102#	1518 ± 141#	−224 (−291 – −157)	258 (184 – 332)	138 (103 – 213)	150 (111 – 239)	8.5 (6.3 – 13.5)	13.0 (9.5 – 21.5)	0.72 (0.37 – 0.89)	0.68 (0.28 – 0.88)

Note. Typical error of estimate (TEE – raw and CV%) and Pearson’s correlation coefficient (r) between methods.

^#represents significant difference when compared to Measured RMR (p < 0.01).

^*represents significant difference between groups (p < 0.01).

DISCUSSION

The current study assessed the reliability of the Parvo Medics TrueOne analyser as a method of indirect calorimetry for assessing RMR in a recreationally-trained female athlete population. The study also compared measured RMR values to those obtained through three commonly used pRMR equations in 25 sub-elite female athletes. The main findings of this study are: a) the Parvo Medics TrueOne analyzer resulted in almost perfect levels of test-retest reliability and; b) the three pRMR equations analysed in the present study overestimated the RMR in the recreationally trained female athlete cohort, however, in the sub-elite population of female athletes, the predictive equations underestimated RMR and showed a higher correlation. This finding related to the underestimation of RMR in the sub-elite population confirms our original hypothesis, that the equations do not take into account the likely higher fat free mass/muscle mass in highly-trained athletes.

The test-retest reliability of the Parvo Medics TrueOne analyzer for measuring RMR in the current study is in agreement with previous studies; Woods and colleagues (26) reported a test-retest reliability CV of ~6.5 % for the same analyzer in a mixed population of male and female endurance athletes. Woods et al. (26) employed an onsite protocol to minimize the influence of activities of daily living, such as rising from bed, dressing and transport to the laboratory (e.g. participants performed RMR measures on waking). While this was not performed, and is a potential limitation to the current study, it is interesting to note that our study resulted in higher levels of reliability. This may be related to the differences in protocol used (e.g. mouthpiece in exercise mode vs. canopy/hood in RMR mode); or potentially, the studied population all being exercisers and a more uniform cohort (mixed vs. single sex only). It is difficult to ascertain the training status of the participants in the Woods et al. study, as they are described as participants 18–40 years old with a minimum training history of two years in their chosen sport. This makes any comparison between participants in their study and the current study somewhat speculative. Similar to the current study, Cooper et al. (7) reported a CV of 4.8% for test-retest reliability of the Parvo Medics TrueOne analyzer when tested on two male and 11 female participants (43 ± 8 years). Cooper et al. (7) also compared five other metabolic cart systems in the measurement of RMR and concluded that the Parvo Medics TrueOne analyzer was the most valid instrument alongside the Vmax system.

Compher et al. (6) recommends that a CV < 10% is sufficient for the measurement of resting energy status. Based on this recommendation, the pRMR equations used in the current study were inappropriate for estimating RMR in the female recreational athletes, however, in sub-elite female athletes, the equations were valid in estimating RMR. Results from the recreational female athletes in our study produced CV’s of between 12.9–14.0% when compared to our indirect calorimetry analyser, with all three equations over-predicting RMR values. The Mifflin-St Jeor equation was the closest predictive value, with a CV of 12.9% and a mean bias of 191 kcal.day⁻¹.

The pRMR equations underestimated RMR by 131–139 kcal.day⁻¹ in the sub-elite female athletes. The current findings align with observations of Flack, et al. (10), which indicated that as fat free mass increased, the predictive equations further underestimated RMR which may explain the underestimation in our sub-elite female athlete population. Although fat-free mass was not measured in the current study, it is assumed, due to the vast literature on body composition and female athletes, that a greater percentage of body mass is of lean muscle in the current cohort.

Hasson, et al. (13) also observed an underestimation using the Mifflin-St Jeor equation when participants were classified as within a normal weight range in both males and females. In other research by Bullough, et al. (5) it has been reported that people who expend large amounts of energy and also match this expenditure with large amounts of energy intake were shown to have an elevated RMR. Conversely, RMR is reduced when large amounts of energy is expended and energy intake is decreased. Tremblay, et al. (23) also demonstrated this relationship of low energy intake suppressing overall RMR. This could explain the significant difference in measured RMR between our recreationally-exercising females and sub-elite female athletes however we did not measure energy intake or expenditure in either population. With this knowledge, it should be noted that pRMR equations do not take into account energy intake or expenditure, which may contribute to the high variance between different populations using the equations.

A common element of all three prediction equations utilized for comparison in this study is the lack of physical activity (24). The Harris-Benedict equation was developed and validated using predominantly white participants (136 male and 103 female) of an average build and body mass (11). The Mifflin-St Jeor equation was derived from a sample of 498 average-weight, overweight, obese, and severely obese individuals ages 19 to 78 (19), and the WHO equation was mostly derived from young European military and police recruits, including 2,279 men and 247 women with 45% of Italian descent (16). It is known that greater levels of physical activity increase energy expenditure and lean mass, factors which have been shown to effect RMR; thus, the importance of testing the validity of these well-established equations in cohorts of varying physical activity levels, as demonstrated by the cohorts of the current study.

The Parvo Medics TrueOne analyser is a reliable tool for measuring RMR in recreationally trained female athletes, However, the over-prediction of RMR derived from pRMR equations in recreationally trained female athletes, when compared to measured RMR values, is a factor to consider when investigating energy balance and energy availability. As is the under-estimation of RMR in a sub-elite athlete cohort. As RMR is a tool used in the competitive sporting environment to determine energy availability and subsequent prevention of relative energy deficiency in sport (RED-S); caution when using pRMR equations in sub-elite female athletes is warranted. Future research should aim to develop athlete-specific calculations, or corrections to existing calculations, for predicting RMR in both male and female athletes. These calculations should take into account the higher muscle mass that is often seen in these populations.