Absolute and Relative pK_a Predictions via a DFT Approach Applied to the SAMPL6 Blind Challenge

Abstract

In this work, quantum mechanical methods were used to predict the microscopic and macroscopic pK_a values for a set of 24 molecules as a part of the SAMPL6 blind challenge. The SMD solvation model was employed with M06–2X and different basis sets to evaluate three pK_a calculation schemes (direct, vertical, and adiabatic). The adiabatic scheme is the most accurate approach (RMSE=1.40 pK_a units) and has high correlation (R²=0.93), with respect to experiment. This approach can be improved by applying a linear correction to yield and RMSE of 0.73 pK_a units. Additionally, we consider including explicit solvent representation and multiple lower-energy conformations to improve the predictions for outliers. Adding three water molecules explicitly can reduce the error by 2 to 4 pK_a units, with respect to experiment, whereas including multiple local minima conformations does not necessarily improve the pK_a prediction.

Introduction

The use of in silico modelling in rational design has become a popular and valuable tool in current research and development for agricultural, environmental, and pharmaceutical applications, as a multifaceted technique capable of providing rapid understanding to in situ phenomena that may be difficult to measure or study[1]. Computer-aided modeling is advantageous for forecasting how a molecule may react in different environments and is heavily utilized for virtual screening and lead optimization in drug discovery as a provisional method for physicochemical and biophysical characterization, including solubility, ionization, lipophilicity, etc. While there are many computational high-throughput models for predicting physicochemical properties, challenges persist for predictions of how molecules ionize in solution. The acid dissociation constant (K_a) or its corresponding logarithmic constant (pK_a), is a quantitative measure of the strength of an acid in solution in the context of acid-base reactions related to the free energy ($\text{Δ}{G}_{\text{aq}}$) of an acid losing a proton.

$$\text{p}{K}_a=\frac{\text{Δ}{G}_{\text{aq}}}{RT\ln \left(10\right)}$$ (1)

Many methods for predicting pK_a have been designed, spanning across electronic structure theory, molecular mechanics, and machine learning approaches[2–4]. Popular QSAR-style methods have been implemented in software packages, such as ADMET Predictor (S+pK_a method[5]), Epik[6], pK_a Prospector[7], and ACD/pK_a Percepta Platform[8]. While these empirical methods can provide instantaneous predictions, inaccuracies arise for large and flexible molecules in which steric effects and microstate conformations surpass the Hammett-Taft approach[9].

A variety of semi-empirical and quantum chemical approaches have been developed—varying by not only the level of theory, but also by the solvation model and the reaction scheme[10–13]. For semi-empirical approaches, Jensen et al. considered several combinations of semi-empirical methods and implicit solvation models to predict the pK_a of 48 druglike molecules using a relative scheme [14]. From the evaluation of 6 semi-empirical methods, the AM1 and PM3 methods provided predictions within 1.4–1.6 pH units. Another study comparing the semi-empirical approaches with ab initio methods for predicting pK_a values for a set of molecules containing a variety of ionizable groups, including alcohols and carboxylic acids, shows that PM6-based methods can provide predictions close to the accuracy of CBS-4B3/SMD [15].

Various ab initio methods, including CBS[16], Gaussian-n[17–20] and ccCA[21], have been applied with continuum solvation models to predict pK_a values and are reported to predict pK_a values as low as 0.5 pK_a units from experiment, however, most of these approaches have only been employed on small molecule datasets [14, 15, 22–26]. Although wavefunction-based methods and composite ab initio methods provide high levels of accuracy, for larger molecules they are less attractive due to the computational expense, hence the interest in exploiting more approximate methods, such as electronic density-based approaches.

Density functional theory (DFT) methods are popular as they have been applied to an array of chemical applications, achieving desired accuracies for a broad range of gas phase reactions and properties [27, 28]. There are many DFT functionals and extensive assessments which illustrate that different functionals perform better for specific properties[29]. For calculations in the solution phase, DFT functionals are often used with implicit continuum models, such as CPCM[30], COSMO[31], and SMD[32] models, which are optimized for usage with modest levels of theory (smaller basis sets). Several studies employing hybrid functionals—including B3LYP, B97–1, BMK, B98, M06, and M06–2X—with the SMD model have shown that the M06–2X functional provides more accurate predictions than other functionals considered for main group element calculations, which would be expected as the SMD model was parametrized using M05–2X[26, 33]. The combination of M06–2X density functional and SMD model has been used in a recent pK_a study[15], which yielded mean unsigned error of 0.9, 0.4, and 0.5 pK_a units respectively for carboxylic acids, aliphatic amines, and thiols. While different groups are evaluating their methods on different datasets, it is difficult to compare the various approaches. SAMPL blind challenges provide a unique platform for designing novel approaches and assessing current methods. The need for appropriate methods for predicting of pK_a was highlighted in the previous SAMPL5 challenge for predicting partition coefficients, as the ionization and tautomerization states differed in the cyclohexane and water phase. The SAMPL6 pK_a challenge entails the prediction of microscopic and macroscopic pK_a values divided into three sub-challenges: 1) the prediction of microscopic pK_a values of associated microstates; 2) the prediction of microstate population as a function of pH ranging from 2 to 12; and 3) the macroscopic pK_a. The dataset is composed of 24 drug-like fragments, each containing multiple ionization and tautomeric states.

In this work for the SAMPL6 challenge, we explored several unique approaches to predict microscopic and macroscopic pK_a values. Absolute pK_a values were predicted using three different calculation schemes: the direct scheme, the vertical scheme, and the adiabatic scheme. We consider multiple tactics in efforts to achieve more accurate predictions. For each scheme, we tried to improve the accuracy by (1) single point energy corrections utilizing larger basis sets; (2) including multiple conformations per microstate in the pK_a calculation; (3) including explicit water molecules to stabilize neutral and charged microstates; (4) applying a linear correction to the calculated pK_a values.

Methods

A source of error in pK_a calculations arises from the reaction scheme used to approximate the solution phase free energy (ΔG_aq). For a generic acid (HA) in water, the equilibrium of acid dissociation reaction (K_a) can be written symbolically as

$$\begin{gathered} \text{HA}+{\text{H}}_2\text{O}\rightleftharpoons {\text{A}}^{-}+{\text{H}}_3{\text{O}}^{+}; \\ {K}_a=\frac{\left[{\text{A}}^{-}\right]\left[{\text{H}}_3{\text{O}}^{+}\right]}{\left[\text{HA}\right]\left[{\text{H}}_2\text{O}\right]} \end{gathered}$$ (2)

which expresses the proton transfer from the acid to yield its conjugate base (A^-) and hydronium (H₃O⁺). For this expression, the direct thermodynamic cycle (Figure 1) is used for calculating absolute pK_a values. In concentrated aqueous solutions, the expression can be simplified to the dissociation of an acid into its conjugate base (Cycle B). Previous studies comparing thermodynamic cycles with continuum solvation models highlight that the simplified expression, Cycle B, tends to be more accurate than Cycle A[24]. In Cycle A, the solution phase free energy is computed using the gas phase ($\text{Δ}{G}_{\text{gas}}$) and solvation free energies ($\text{Δ}{G}_{\text{S}}$). The solvation free energy of the proton, $\text{Δ}{G}_{\text{S}}^{*}$ $\left({\text{H}}^{+}\right)$, used is −265.9 kcal/mol[34] includes the standard state correction from 1 atm to 1 M. The proton gas phase free energy ($G_{\text{gas}}^{\text{°}}({\text{H}}^{+})=-6.28$ kcal/mol) comes from the Sackur-Tetrode equation[35].

Figure 1.

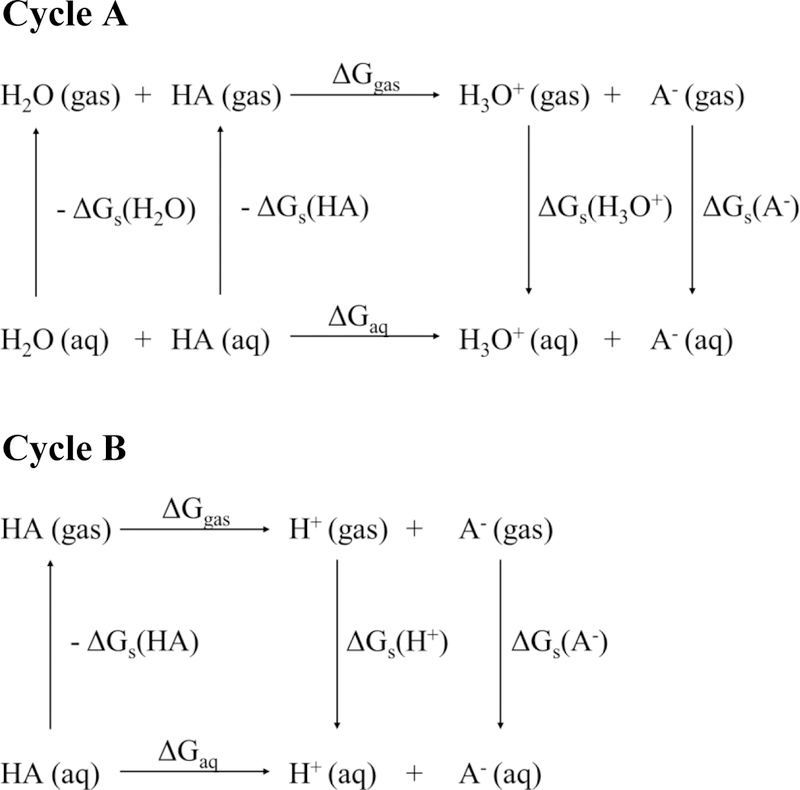
Thermodynamic cycles used for pK_a calculation schemes.

$$\text{Δ}{G}_{\text{aq}}=\text{Δ}{G}_{\text{gas}}+\text{ΔΔ}{G}_{\text{S}}$$ (3a)

$$\text{Δ}{G}_{\text{gas}}^{*}=G_{\text{gas}}^{°}\left({\text{H}}^{+}\right)+G_{\text{gas}}^{°}\left({\text{A}}^{-}\right)-G_{\text{gas}}^{°}\left(\text{HA}\right)+RT\text{ln}\left(\frac{RT}{P}\right)$$ (3b)

$$\text{Δ}{G}_{\text{S}}^{*}=\text{Δ}{G}_{\text{S}}^{°}\left({\text{H}}^{+}\right)+\text{Δ}{G}_{\text{S}}^{°}\left({\text{A}}^{-}\right)-\text{Δ}{G}_{\text{S}}^{°}\left(\text{HA}\right)$$ (3c)

Here, we use a superscript “°” to denote the condition of 1 atm, and “*” to denote the condition of 1 M.

Calculation Schemes

In this challenge, three different schemes are used to compute the free energy foreach microstate pair. The notations ${\mathbf{R}}_{\mathbf{\text{g}}}$ and ${\mathbf{R}}_{\mathbf{\text{l}}}$ correspond to stationary points obtained from gas phase and solution phase optimizations, respectively[36].

Scheme D: Direct scheme

The direct scheme (noted Scheme D) determines the solution phase free energy without use of thermodynamic cycle.

$$G^{\text{D}}=E_{\left(\text{aq}\right)}\left({\mathbf{R}}_{\mathbf{l}}\right)+G_{\left(\text{aq}\right)}^{\text{corr}}\left({\mathbf{R}}_{\mathbf{l}}\right)$$ (4)

In this scheme, the reaction free energy is determined by solution phase geometries. Thermal corrections to the free energy $G^{\text{corr}}$ are added to the total energy to approximate $\text{Δ}{G}_{(\text{aq})}$. To note, all energy terms of the direct scheme are computed within the implicit solvent model. The approximation made in the direct scheme is that gas phase contributions are not needed, i.e. geometries.

In contrast, the vertical scheme (Scheme V) uses the gas phase geometry and assumes that free energy of the solute relaxing in solution phase is negligible.

Scheme V: Vertical scheme

$$G^{\text{V}}=E_{\left(\text{g}\right)}\left({\mathbf{R}}_{\mathbf{g}}\right)+G_{\left(\text{g}\right)}^{\text{corr}}\left({\mathbf{R}}_{\mathbf{g}}\right)+\text{Δ}{G}_{\text{S}}\left({\mathbf{R}}_{\mathbf{g}}\right)$$ (5a)

$$\text{Δ}{G}_{\text{S}}=E_{\text{aq}}\left({\mathbf{R}}_{\mathbf{g}}\right)-E_{\text{g}}\left({\mathbf{R}}_{\mathbf{g}}\right)$$ (5b)

In this expression, $\text{Δ}{G}_{\text{aq}}$ is calculated using the gas phase free energy and the solvation free energy ($\text{Δ}{G}_{\text{S}}$), which is the difference between the gas phase and solution phase total energies. Here, $E_{(\text{aq})}$ is determined by employing the continuum solvation approach on the gas phase structure. Thermal corrections to the gas phase free energy $G_{(\text{g})}^{\text{corr}}$ are used in this representation, as it is assumed that the thermal contributions in both phases are similar.

Scheme A: Adiabatic scheme

The adiabatic scheme (Scheme A) considers both the gas and solution phase geometries.

$${\text{G}}^{\text{A}}=E_{\left(\text{g}\right)}\left({\mathbf{R}}_{\mathbf{g}}\right)+G_{\left(\text{g}\right)}^{\text{corr}}+\text{Δ}{G}_S$$ (6a)

$$\text{Δ}{G}_{\text{S}}=E_{\text{aq}}\left({\mathbf{R}}_{\mathbf{l}}\right)-E_{\text{g}}\left({\mathbf{R}}_{\mathbf{g}}\right)$$ (6b)

This scheme differs from the vertical scheme by the total energy contributions from the solute relaxed in solution, hence $E_{(\text{aq})}$ is determined by optimizing the molecule in solution phase. The difference between the thermal contributions in gas phase and solution phase (relaxed) can be approximated by the difference in the adiabatic and direct scheme ($\Delta \Delta G_{\text{(D}\to \text{A)}}^{\text{corr}}=\Delta G_{{}^{{{}_{\text{g}}}_{\text{as}}}}^{{{}^{\text{c}}}^{\text{orr}}}-\Delta G_{aq}^{corr};\Delta G^{\text{D}\to \text{A}}=G^{\text{A}}-G^{\text{D}}$)

Conventionally, thermodynamic cycle is used to calculate the solution phase free energy when using continuum solvation models. The primary reason is that continuum solvation models are generally parameterized to produce accurate solvation free energies using lower levels of theory (HF or DFT with double-$\zeta$ quality basis sets); however, by using thermodynamic cycle the solution phase free energy can be determined at different levels of theory.

Inspired by the work of J. Ho[37], we consider modifications of each scheme in hopes to obtain more accurate energetics by including single point energy corrections (augmented by “$+S$”) using larger basis sets (denoted by a superscript, $\text{H}$). In the D+S Scheme, the total energy term in aqueous solution $E_{\text{aq}}$ is replaced with the total energy obtained with a larger basis set.

$$G^{\left(\text{D}+\text{S}\right)}=E_{\left(\text{aq}\right)}^{\text{H}}\left({\mathbf{R}}_{\mathbf{l}}\right)+G_{\left(\text{aq}\right)}^{\text{corr}}\left({\mathbf{R}}_{\mathbf{l}}\right)$$ (7)

For the vertical and adiabatic schemes, the solvation free energies ($\text{Δ}{G}_S$) are calculated with larger basis sets,

$$G^{\text{thermodynamic}\text{cycle}}=E_{\left(\text{g}\right)}\left({\mathbf{R}}_{\mathbf{g}}\right)+G_{\left(\text{g}\right)}^{\text{corr}}\left({\mathbf{R}}_{\mathbf{g}}\right)+\text{Δ}{G}_{\text{S}}^{\text{H}}\left({\mathbf{R}}_{\mathbf{g}}\right)$$ (8a)

$$\text{Δ}{G}_{\text{S}}^{\text{H}}=E_{\text{aq}}^{\text{H}}\left({\mathbf{R}}_{\mathbf{x}}\right)-E_{\text{g}}^{\text{H}}\left({\mathbf{R}}_{\mathbf{g}}\right),\text{x}=\text{l}\text{when}\text{scheme}\text{A},\text{x}=\text{g}\text{when}\text{scheme}\text{V}$$ (8b)

As both approaches use thermodynamic cycle, the V+S scheme and A+S schemes differ by the geometry $({\mathbf{R}}_{\mathbf{x}})$ in which the aqueous phase total energies are determined.

$$G^{\left(\text{A}+\text{S}\right)}-{\text{G}}^{\left(\text{V}+\text{S}\right)}=E_{\text{aq}}^{\text{H}}\left({\mathbf{R}}_{\mathbf{l}}\right)-E_{\text{aq}}^{\text{H}}\left({\mathbf{R}}_{\mathbf{g}}\right)$$ (9)

Microstate populations as a function of pH

To predict the fractional microstate populations at different pH values, we consider the following reactions from n charged microstate to m charged microstate (m < n),

$${({\text{H}}_n\text{A})}^{n+}\stackrel{K_a(n|m)}{\to }{({\text{H}}_m\text{A})}^{m+}+(n-m){\text{H}}^{+}$$

while the equilibrium constant is

$$K_a\left(n\text{|}m\right)\equiv \frac{\left[{({\text{H}}_m\text{A})}^{m+}\right]{\left[{\text{H}}^{+}\right]}^{\left(n-m\right)}}{\left[{({\text{H}}_n\text{A})}^{n+}\right]}$$ (10a)

and

$$K_a\left(n\text{|}m\right)=e^{-\frac{G\left(m\right)+\left(n-m\right)G\left({\text{H}}^{+}\right)-G\left(n\right)}{kT}}$$ (10b)

Therefore,

$$\frac{\left[{({\text{H}}_m\text{A})}^{m+}\right]{\left[{\text{H}}^{+}\right]}^{\left(n-m\right)}}{\left[{({\text{H}}_n\text{A})}^{n+}\right]}=e^{-\frac{G\left(m\right)+\left(n-m\right)G\left({\text{H}}^{+}\right)-G\left(n\right)}{kT}}$$ (11)

After applying the variable separation approach, we arrive at

$$\frac{\left[{({\text{H}}_m\text{A})}^{m+}\right]}{{\left[{\text{H}}^{+}\right]}^m{e}^{-\frac{G\left(m\right)-mG\left({\text{H}}^{+}\right)}{kT}}}=\frac{\left[{({\text{H}}_n\text{A})}^{n+}\right]}{{\left[{\text{H}}^{+}\right]}^n{e}^{-\frac{G\left(n\right)-nG\left({\text{H}}^{+}\right)}{kT}}}\equiv \frac{\left[{({\text{H}}_n\text{A})}^{n+}\right]}{Q\left(n\right)}$$ (12)

$Q(n)$ is the partition function at specified pH value and defined as

$$Q\left(n\right)\equiv {\left[{\text{H}}^{+}\right]}^n{e}^{-\frac{G\left(n\right)-nG\left({\text{H}}^{+}\right)}{kT}}$$ (13)

Therefore, the partition function for microstate A with charge n_A is

$$Q_A\left(n_A\right)=e^{-\frac{G_A\left(n_A\right)-n_{A}G\left({\text{H}}^{+}\right)}{kT}-n_A\ln \left(10\right)\text{pH}}$$ (14)

Note that this partition function also holds when n_A < 0.

The population for microstate A with charge n_A is obtained as

$$P_A\left(n_A\right)=\frac{Q_A\left(n_A\right)}{{\sum }_{X=\cdots ,A,\cdots }{Q}_X\left(n_X\right)}$$ (15)

Macroscopic pK_a values

To compute the macroscopic pK_a values, we can use the conclusion from the derivation of the microstate population, so we have

$$\begin{array}{l}{K}_a^{\text{Macro}}\left(n+1\text{|}n\right)=\frac{\left[{\text{H}}^{+}\right]P\left(n\right)}{P\left(n+1\right)}\\ =\frac{\left[{\text{H}}^{+}\right]{\sum }_X{Q}_X\left(n_X\right){\delta }_{n,n_X}}{{\sum }_X{Q}_X\left(n_X\right){\delta }_{\left(n+1\right),n_X}}\\ =\frac{e^{-\frac{G\left({\text{H}}^{+}\right)}{kT}}{\sum }_X{e}^{-\frac{G_X\left(n_X\right)}{kT}}{\delta }_{n,n_X}}{{\sum }_X{e}^{-\frac{G_X\left(n_X\right)}{kT}}{\delta }_{\left(n+1\right),n_X}}\end{array}$$ (16)

Here ${\delta }_{i,j}$ is the Kronecker delta and then the macroscopic $p{K}_a$ between the microstates with a charge of n+1 and the microstates with a charge of n is

$$\begin{array}{l}\text{p}{K}_a^{\text{Macro}}\left(n+1\text{|}n\right)=-\log \frac{e^{-\frac{G\left({\text{H}}^{+}\right)}{kT}}{\sum }_X{e}^{-\frac{G_X\left(n_X\right)}{kT}}{\delta }_{n,n_X}}{{\sum }_X{e}^{-\frac{G_X\left(n_X\right)}{kT}}{\delta }_{\left(n+1\right),n_X}}\\ =-\log \frac{{\sum }_X{e}^{-\frac{G_X\left(n_X\right)}{kT}}{\delta }_{n,n_X}}{{\sum }_X{e}^{-\frac{G_X\left(n_X\right)}{kT}}{\delta }_{\left(n+1\right),n_X}}+\frac{G\left({\text{H}}^{+}\right)}{kT\text{ln}10}\end{array}$$ (17)

QM Calculations

The initial structures of the 352 microstates were generated from the SMILES strings provided by the SAMPL6 pK_a challenge using Open Babel 2.4.1[38]. Gas phase and solution phase geometry optimizations were performed using the M06–2X density functional[39]. As charged and uncharged species are represented in the molecule set, the 6–31G(d) basis set[32] are used for cationic species whereas additional diffuse functions (6–31+G(d)[40]) are included for the anionic microstates. All QM optimizations were performed with “tight” wave function and geometry convergence criteria, by using an “ultrafine” numerical quadrature as required by M06–2X functional.

To maintain consistency of the basis sets between microstate reaction pairs, duplicate calculations are carried out for neutral species using each basis set (Table 2).

Table 2.

Basis sets selection per sub-challenge.

	6–31+G(d)/6–311++G(d,p)	6–31G(d)/6–311G(d,p)
Type I	Anionic species in the pair	Cationic species in the pair
Type II	$\text{p}H>p{K}_a^{\text{Macro}}(-1|0)$	$\text{p}H<p{K}_a^{\text{Macro}}(-1|0)$
Type III	Between anions or anion/neutral	Between cations or cation/neutral

Frequencies were examined to confirm stationary points and scaled by 0.9465 and 0.9500 for methods using the 6–31G(d) and 6–31+G(d) basis sets, respectively[41]. Additional single point energy calculations for each microstate are performed using M06–2X in conjunction with 6–311G(d,p) and 6–311++G(d,p) to serve as corrections to the respective double-$\zeta$ basis sets. Solution phase geometry optimizations and single point calculations were carried out using the SMD implicit solvation model[42]. All calculations were performed in Gaussian 16 (Rev. A.03) [43] using an Ultrafine integration grid. To improve conformational sampling, two different algorithms were considered. Per microstate, ten low-energy conformers were stochastically and systematically generated using the MOE software and compared against the optimized structures of each microstate. For microstates in which there was a large difference in the conformation, the new conformers were subjected to the aforementioned workflow.

Results & Discussion

Our method of using two basis sets is similar to the method using mixed basis set where the diffuse functions are added at the reactive center to allow improved modeling of negative ions [44]. We do not adopt using mixed basis sets because the excess electron is assumed to be delocalized over the entire molecule instead of the deprotonated atom.

Errors in pK_a calculations arise from the reaction scheme in which the aqueous free energy is approximated. In this challenge, we considered several approaches for predicting absolute pK_a values that differ by how free energy contributions in gas phase and solution phase are determined. Our submissions for Type I, Type II, and Type III predictions, per scheme, are listed in Table 1. To note, the calculated pK_a values are reported without standard error of the mean (SEM).

Table 1.

SAMPL6 submission IDs for our approaches.

Scheme	D	D+S	V	A	A+S
Type I	wexjs	w4z0e	arcko	wcvnu	ko8yx
Type II	t28dq	z0ima	yzx8f	gt0oq	i5m8f
Type III	y75vj	xikp8	5byn6	w4iyd	ryzue

Direct Scheme

In the direct scheme, the aqueous free energy is determined only by solution phase calculations, avoiding thermodynamic cycle. This is an attractive approach as it requires only two calculations (of each microstate pair) and would already account for solvent-induced effects since the geometries are optimized in the solution phase. From the results shown in Table 2, overall, the direct approach predicts pK_a values within a mean absolute deviation (MAD) of 1.36 pK_a units from the experiment. Some of the major outliers include SM01, SM06, SM14, SM23. SM18 and SM23 are suffering from the hydrogen bonding effect. These molecules can form stronger hydrogen bonding with their functional group (Phenol hydroxyl group or Aniline amino group) which is related to the macroscopic pK_a, while other molecules can also suffer from the hydrogen bonding but less significantly because the hydrogen bonds being formed is much weaker. Some of these conformations were biased because the implicit solvation model cannot describe the hydrogen bonding effectively.

A previous study comparing the accuracy of the direct scheme with a low (MP2) and high (G3) level of theory, reported that use of a higher-level of theory improves the MAD with respect to experiment for carboxylic, inorganic, and cationic acids using the direct scheme from 0.4 to 0.9 pK_a units [39]. Rather than using a different method, we consider improving the quality of the basis set to represent a better level of theory for this challenge. In most cases, adding additional basis functions yields poorer predictions, as great as 5.0 pKa units away from the direct scheme. This excludes SM04, SM07, SM20, SM22, and SM24, as we see that using a larger basis set yields predictions of an average of 0.5 pK_a units closer to experiment (1.3 pK_a units difference for SM20).

Vertical Scheme

The vertical scheme utilizes gas phase geometries and thermodynamic cycle to approximate the free energy of solvation. By contrasting the direct and vertical scheme, the difference in the gas phase contribution and solution phase contribution to the solvation free energy is highlighted. Overall, the vertical scheme provides overestimations of the pK_a, yielding a MAE of 1.74 pK_a units. To note, this is greater than the MAE of the direct method (This corresponds to a difference of 0.38 pK_a units or 0.5 kcal/mol free energy difference distributed in the difference of the geometries). Compared to the direct scheme, the vertical scheme overestimates the pK_a for SM06 and SM09. This poorer performance of the vertical scheme is surprising because this approach is common to the methods in which continuum solvation models are parameterized.

As the vertical scheme assumes the gas phase geometry, it works well for the small or rigid molecules (e.g. SM02, SM05, SM09, etc.), and we consider using larger basis sets for the solvation free energy term (Equation (3c)). In most cases, the inclusion of triple-$\zeta$ basis sets improves the predictions by an average of 0.1 to 0.2 pK_a units with respect to experiment. Cases in which the trend does not follow (in which the larger basis set yields predictions greater than that predicted using smaller basis sets), occur for polyprotic molecules, such as SM15 and SM22.

Adiabatic Scheme

Considering both optimized gas phase and solution phase structures is hypothesized to provide more accurate pK_a predictions as it includes the energetic compensation for relaxing in solvent. Using the adiabatic scheme, this yields pK_a values with a MAE of 1.26 pK_a units. Comparing the two thermodynamic cycle-based approaches, the adiabatic scheme provides more accurate pK_a than the vertical scheme for (64%) of the molecules. This highlights that the structures determined in both gas phase and solution phase are significant for determining pK_a values.

Similar to the direct and vertical schemes, we examine how using a larger basis set impacts the solvation free energy. The results indicate that using a triple-$\zeta$-level basis set on the solvation free energy term improves the pK_a predictions by an average of 0.2 pK_a units.

Comparison of the Schemes

Overall, the results in Table 3 illustrate a hierarchy of the different reaction schemes. Contrasting the three schemes, pK_a values determined via the direct scheme and adiabatic scheme are closer to experiment than those predicted using the vertical scheme. However, this relationship only holds to the level of theory employed for each reaction scheme (in this case, using M06–2X with a double-$\zeta$ level basis set). When applying a larger basis set to the solvation free energy calculation, the adiabatic and vertical scheme have less error (MAE is 1.10 and 1.48, respectively) with respect to experiment than the direct scheme (MAE is 1.95). The reason is that a more accurate solvation free energy can be obtained by using a larger basis set.

Table 3.

Absolute macroscopic pK_a values via the direct (D), vertical (V), and adiabatic (A) schemes.

Molecule	Experiment	Scheme
ID	pKa	D	D+S	V	V+S	A	A+S
SM01	9.53 ± 0.01	12.53	14.51	13.41	13.11	12.03	11.78
SM02	5.03 ± 0.01	5.12	4.60	4.24	4.66	4.27	4.67
SM03	7.02 ± 0.01	7.39	8.66	8.32	8.17	7.46	7.30
SM04	6.02 ± 0.01	6.40	5.86	7.54	7.71	6.78	6.89
SM05	4.59 ± 0.01	3.28	2.56	4.85	4.97	2.42	2.38
SM06	3.03 ± 0.04	0.66	−0.06	0.32	0.48	1.17	1.38
SM06a	11.74 ± 0.01	15.33	16.65	16.92	16.75	14.56	14.60
SM07	6.08 ± 0.01	7.19	6.61	7.01	7.17	6.35	6.42
SM08	4.22 ± 0.01	4.34	6.29	5.83	5.77	3.33	3.33
SM09	5.37 ± 0.01	5.31	4.80	4.89	5.08	5.10	5.31
SM10	9.02 ± 0.01	9.53	10.75	7.69	7.62	8.00	8.00
SM11	3.89 ± 0.01	2.60	2.37	2.99	3.29	2.90	3.16
SM12	5.28 ± 0.01	4.74	4.25	4.46	4.67	4.48	4.69
SM13	5.77 ± 0.01	4.69	4.19	5.47	5.62	5.58	5.66
SM14	2.58 ± 0.01	−1.07	−1.67	−0.37	−0.26	−0.43	−0.13
SM14a	5.30 ± 0.01	4.91	4.42	4.64	4.84	5.09	5.20
SM15	4.70 ± 0.01	3.74	3.23	3.57	3.73	3.79	3.94
SM15a	8.94 ± 0.01	11.02	13.07	11.80	11.39	10.73	10.38
SM16	5.37 ± 0.01	3.60	3.30	3.62	3.80	4.49	4.79
SM16a	10.65 ± 0.01	12.35	13.32	12.45	12.27	11.71	11.41
SM17	3.16 ± 0.01	1.38	1.28	1.51	1.55	2.17	2.39
SM18	2.15 ± 0.02	1.84	1.27	2.04	2.27	2.28	2.58
SM18a	9.58 ± 0.03	10.11	11.73	11.29	11.21	10.76	10.68
SM18b	11.02 ± 0.04	13.78	14.62	13.04	13.05	15.21	15.02
SM19	9.56 ± 0.02	10.41	11.69	11.87	11.80	10.09	10.14
SM20	5.70 ± 0.03	3.84	5.17	5.14	5.26	3.99	4.35
SM21	4.10 ± 0.01	1.87	1.36	1.65	2.14	1.99	2.55
SM22	2.40 ± 0.02	3.19	2.66	3.00	2.82	3.03	2.83
SM22a	7.43 ± 0.01	9.30	9.90	9.89	9.79	9.03	8.73
SM23	5.45 ± 0.01	3.08	2.85	2.69	2.95	5.75	5.99
SM24	2.60 ± 0.01	3.55	2.97	2.85	2.99	3.74	3.36
MSE		−0.08	0.16	0.24	0.30	0.04	0.07
MAE		1.36	1.95	1.61	1.48	1.26	1.10
MaxD		3.59	4.98	5.18	5.01	4.19	4.00
RMSE		1.70	2.38	1.98	1.85	1.55	1.40
R2		0.92	0.91	0.89	0.90	0.92	0.93

^apK_a,2

^bpK_a,3

Our submission to the SAMPL6 challenge (Table 1), did not include the standard state correction (which made a difference in 1.39 pK_a units) and also used another value for the free energy of solvation of a proton not recommended (a difference of 0.22 pK_a units); this has been corrected. These results are encouraging as the pK_a predictions via the adiabatic and direct schemes correlate well with experiment, having a correlation coefficient greater than 0.9.

To confirm if the approach predicts the proper chemistry, we evaluate the different schemes on a small subset of molecules that share a similar scaffold, differing by electron donation or withdrawing groups. The molecules SM02, SM04, SM07, SM09, SM12, and SM13 share the 4-Aminoquinazoline scaffold. Ranked by acidity, SM02, SM12, and SM09 differ by substituents on the phenyl ring spanning a variance of 0.35 pK_a units. The direct schemes are unable to properly determine the trend, as the predictions indicate that SM12 is more acidic than SM02 (SM12 is a Ph-Cl whereas SM02 is a Ph-CF3). In contrast, the vertical schemes rank the acidities of SM02 and SM12 correctly, however, overestimate the acidity of the SM09. This is believed to be a result of an issue with the gas phase geometry. That means using unrelaxed geometry cannot obtain accurate solvation free energy when the molecule is flexible and has different conformations in different phases. SM13 has a larger pK_a and is different as it contains electronic donating groups on the quinazoline as opposed to the amino group. The direct and vertical scheme overestimate the acidity relative to SM02, SM12, and SM09. The difference between SM04 and SM07 is small quantitatively and qualitatively (0.04 pK_a units). Interestingly, only the direct scheme was able to properly rank the acidities for these molecules. We also compare the microscopic pK_a values with respect to experiment for these molecules and observe the same trends (Table S6).

Room for Improvement

Aside of the chosen level of theory employed, another source of error arises from the lack of explicit interactions between the solute and water, which are not accounted for in continuum solvation models. For example, functional groups such as alcohol and phenols, the ionic state may be stabilized in solution by hydrogen bonding. Including explicit water molecules with continuum solvation models, also termed microsolvation or cluster-continuum modeling, has been shown to improve pK_a predictions for such issues[45]. In general, this could result in overestimation or underestimation of pK_a values for acids and bases.

For example, the pK_a for molecules SM01, SM15, and SM22, which may undergo deprotonation at the phenol group, are overestimated by 1.3–5.0 pK_a units. As a proof of concept, we try to improve pK_a predictions for SM01 by adding water molecules near the hydroxyl group. Adding one water molecule improves the prediction of the pK_a by an average of 1.3 pK_a units (Figure 3). By saturating the hydroxyl group with 3 water molecules, the pK_a improves by an average of 3.0 pK_a units (Table S3).

Figure 3.

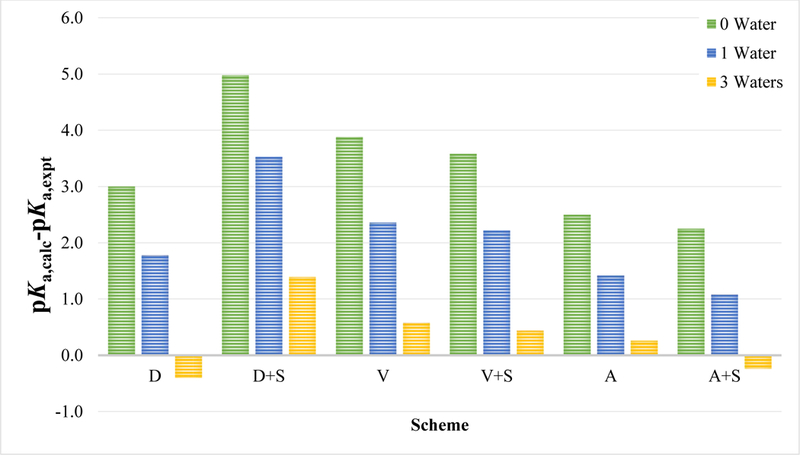
Effect of microsolvation on pK_a calculations schemes for SM01.

Relative Schemes

When employing the different calculation schemes for this challenge, we only considered predicting absolute pK_a values as opposed to relative pK_a values. Relative schemes for calculating pK_a use empirical parameters to scale or offset the solute phase free energy.

$$\text{p}{K}_a=A\frac{\Delta G_{\text{aq}}}{RT\ln 10}+B$$ (18)

Using a relative scheme as an offset (A=1) to the free energy entails identifying and applying (subjectively) good reference models, which relies on chemical intuition. As this challenge includes 620 unique acid-base pairs, identifying the proper reference models proved difficult the molecules had multiple protonation sites. Alternatively, a linear regression fit can be applied to the calculated solution free energy to correct for systematic errors (e.g. concentration of water, proton solvation free energy). As this is a popular approach for calculating pK_a[45, 46], we consider applying a linear regression correction to each scheme. To determine the parameters A and B, two training sets, consisting of 63 acid reactions (Table S2) and 56 bases (Table S3), were used. The linear fitting parameters determined for each scheme can be found in the Supporting Information (Table S4). For each scheme, while applying a linear regression fit does not improve the correlation ($\text{Δ}{R}^2=\pm 0.01$), this approach does improve the pK_a predictions, with a lower MAE and RMSE than the respective absolute calculation pK_a schemes (Table 4).

Table 4.

Comparison of linear regression fit macroscopic pK_a values via direct (D), vertical (V), and adiabatic (A) schemes with experiment.

Molecule ID	pKa Expt.	D	D+S	V	V+S	A	A+S
SM01	9.53 ± 0.01	9.79	9.89	8.96	10.07	9.75	9.73
SM02	5.03 ± 0.01	5.50	5.41	5.55	5.21	4.96	5.16
SM03	7.02 ± 0.01	7.12	6.81	6.76	7.39	7.35	7.36
SM04	6.02 ± 0.01	6.29	6.21	7.00	7.11	6.53	6.57
SM05	4.59 ± 0.01	4.35	4.12	5.84	5.41	3.81	3.71
SM06	3.03 ± 0.04	2.73	2.46	2.59	2.62	3.04	3.08
SM06a	11.74 ± 0.01	11.26	11.01	11.89	11.94	11.08	11.22
SM07	6.08 ± 0.01	6.79	6.68	7.08	6.77	6.26	6.27
SM08	4.22 ± 0.01	5.52	5.56	5.22	6.30	5.17	5.25
SM09	5.37 ± 0.01	5.62	5.53	5.38	5.47	5.48	5.57
SM10	9.02 ± 0.01	8.23	7.91	6.56	7.25	7.63	7.72
SM11	3.89 ± 0.01	3.93	4.00	4.52	4.36	4.11	4.20
SM12	5.28 ± 0.01	5.26	5.19	5.54	5.22	5.09	5.18
SM13	5.77 ± 0.01	5.23	5.15	5.74	5.81	5.78	5.79
SM14	2.58 ± 0.01	1.65	1.44	2.16	2.16	2.04	2.13
SM14a	5.30 ± 0.01	5.37	5.30	5.23	5.33	5.48	5.50
SM15	4.70 ± 0.01	4.64	4.54	4.98	4.64	4.66	4.70
SM15a	8.94 ± 0.01	9.00	9.13	8.05	9.18	9.07	8.99
SM16	5.37 ± 0.01	4.55	4.58	4.97	4.68	5.10	5.24
SM16a	10.65 ± 0.01	9.70	9.26	8.95	9.64	9.58	9.53
SM17	3.16 ± 0.01	3.17	3.31	3.5	3.28	3.66	3.72
SM18	2.15 ± 0.02	3.46	3.30	4.22	3.73	3.72	3.84
SM18a	9.58 ± 0.03	8.53	8.42	8.13	9.09	9.08	9.14
SM18b	11.02 ± 0.04	10.44	9.94	9.08	10.04	11.42	11.44
SM19	9.56 ± 0.02	8.68	8.40	8.68	9.40	8.73	8.86
SM20	5.70 ± 0.03	5.26	4.98	5.37	6.03	5.52	5.79
SM21	4.10 ± 0.01	3.48	3.36	4.05	3.65	3.55	3.82
SM22	2.40 ± 0.02	4.30	4.18	4.43	4.07	4.19	4.00
SM22a	7.43 ± 0.01	8.11	7.46	7.83	8.36	8.17	8.11
SM23	5.45 ± 0.01	4.23	4.30	4.33	4.15	5.88	6.00
SM24	2.60 ± 0.01	4.47	4.43	4.27	4.18	4.56	4.37
MSE		−0.04	−0.18	−0.06	0.17	0.11	0.15
MAE		0.64	0.71	0.90	0.67	0.57	0.54
MaxD		1.90	1.83	2.46	2.08	1.96	1.77
RMSE		0.82	0.89	1.11	0.89	0.76	0.73
R2		0.91	0.90	0.85	0.90	0.93	0.93

^apK_a2

^bpK_a3

We believe the issue that the slope of the experimental pK_a vs calculated pK_a is not the expected value of 1 is due to the hydrogen bonding effects. Since the hydrogen bonding can stabilize the charged species having little effect to the neutral species, the pK_a values for the bases are usually underestimated while those for the acids are usually overestimated without explicitly considering the hydrogen bonds between the solvent and the solute. The slope can approach the expected value of 1 by including explicit waters[45].

Multiple Minima Consideration

All pK_a values have been determined using one conformation per microstate pair. The molecules within the SAMPL6 pK_a data set are not rigid (excluding SM01 and SM22) and can adopt multiple conformations that satisfy local minima. To probe if the exclusion of multiple minima as a source of error in our pK_a calculations, we generate 6 to 32 different conformations for each microstate of SM06 and re-calculate the macroscopic pK_a by sequentially including the lowest energy conformations per microstate. As shown in Table 5, including multiple minima has little impact to the pK_a prediction (0.1 to 0.6 pK_a units). By applying the linear regression fit, the pK_a predictions are closer to experiment using one conformation per microstate. Including additional conformations per microstate yields a maximum difference of 0.3 pK_a unit (Table S5).

Table 5.

Macroscopic pK_a values of SM06 determined as a function by microstate conformations.^a

No. Conf.b	pKa1						pKa2
	D	D+S	V	V+S	A	A+S	D	D+S	V	V+S	A	A+S
1	0.66	−0.06	0.32	0.48	1.17	1.38	15.33	16.65	16.92	16.75	14.56	14.60
3	0.67	−0.01	0.30	0.47	1.17	1.37	15.49	16.83	17.21	17.05	14.89	14.96
5	0.63	−0.03	0.23	0.40	1.17	1.42	15.52	16.92	17.31	17.16	15.00	15.09
7	0.61	−0.05	0.30	0.46	1.19	1.46	15.55	16.96	17.39	17.25	15.09	15.16
9	0.60	−0.05	0.30	0.46	1.19	1.48	15.55	16.96	17.39	17.29	15.08	15.19
11	0.62	−0.03	0.30	0.46	1.19	1.48	15.55	16.96	17.39	17.29	15.09	15.20
13	0.63	−0.02	0.30	0.46	1.19	1.48	15.55	16.96	17.40	17.29	15.09	15.20
15	0.63	−0.02	0.30	0.46	1.19	1.48	15.55	16.96	17.40	17.29	15.09	15.20
Range	0.07	0.05	0.09	0.08	0.02	0.11	0.22	0.31	0.48	0.54	0.53	0.60

^aThe experimental pK_a values of SM06 are 3.03 and 11.74 for pK_a1 and pK_a2, respectively.

^bNumber of conformations used per microstate to calculate the microscopic pK_a.

Conclusion

In this study, three calculations schemes were used to predict the pK_a of molecules in the SAMPL6 challenge. The adiabatic scheme yields more accurate pK_a predictions than the direct and vertical schemes. Using a larger basis set with the adiabatic scheme yields the best results of among the other schemes, yielding an RMSE of 1.40 pK_a. A combination of popular and inexpensive methods (M06–2X/Pople basis sets (6–31G(d)/6–311G(d,p) or 6–31+G(d)/6–311++G(d,p))//SMD) is being used in our approach, which means that our approach can be carried out in most popular software packages. Without additional parameterization, we have a very encouraging result with a RMSE of 1.40 and R² of 0.93 by using different basis sets for different charged species. However, if linear correction is applied, we can improve our results to achieve a RMSE of 0.73 and R² of 0.94. Our approach can be further improved since there are still multiple sources of error from the current method, basis set, and solvation model. In the future, we will try using different methods, basis sets, and solvation models in our approach to find out the best combination.

Figure 2.

Structures of the 24 molecules in the SAMPL6 pK_a challenge.