Network Effects in Blau Space: Imputing Social Context from Survey Data

Abstract

We develop a method of imputing ego network characteristics for respondents in probability samples of individuals. This imputed network uses the homophily principle to estimate certain properties of a respondent’s core discussion network in the absence of actual network data. These properties measure the potential exposure of respondents to the attitudes, values, beliefs, etc. of their (likely) network alters. We use American National Election Survey data (2016 ANES) to demonstrate that the imputed network features show substantial effects on individual level measures, such as political attitudes and beliefs. In some cases, the imputed network variable substantially reduces the effects of standard socio-demographic variables like age and education. We argue that the imputed network variable captures many of the aspects of social context that have been at the core of sociological analysis for decades.

Introduction

The problem of representing social context has been a core issue for sociologists ever since Durkheim’s (1951 [1897]) seminal work on suicide. Durkheim’s great contribution was to show that features of the social environment affected the rates of individual behavior, even when that individual behavior was intensely personal. In some ways, the great project initiated by Durkheim has been sidetracked by the massive wave of survey research that has inundated sociology since its initiation during World War II (e.g., Stouffer et al. 1949). Since institutional support for survey analysis began in the mid twentieth century, there has been a push to build ever more complex statistical models of atomized individual behavior based on probability samples in social surveys. Largely as a result of the importation of regression techniques and econometric methods pioneered by Blalock (1972), Duncan (1966), and others, survey analysis has become the dominant mode of quantitative analysis for sociologists. These regression techniques allow sociologists to efficiently model aggregate features of society using survey data. But, the details of social context are lost when a probability sample removes the person from the matrix of connections that make up the social world at the level of individual experience (Barton 1968). In the last few decades, there has been growing attention to quantitative models of social context in the form of social network analysis, which attends to the connections among individuals and other social entities such as groups, organizations, associations, and so forth (Wasserman and Faust 1994; Butts 2008).

It was not until Erbring and Young’s (1979) seminal paper that we began to recognize a potential flaw of the regression models of social experience that are now standard in the social sciences: the error terms in those regressions are autocorrelated because individual observations are statistically dependent (see also Friedkin 1990). The basic idea is that social interaction creates dependencies in the data, as individuals in the study may be exposed to similar flows of information and influences. This fact, a version of Galton’s Problem (e.g., Naroll 1961), poses threats to survey analysis because the omission of the sources of these correlations can cause bias in the parameter estimates and their standard errors. The social structure of relationships that connect individuals to one another create the correlations and regressions that the standard approach models. We argue that this social structure, reflecting the flows of information from individual to individual, is actually in the residuals of most of the standard models.

The structural relations that connect individuals to one another are only tangentially captured by the standard methods of survey analysis. Years of education, for example, gets at exposure to a general institutional form (Kingston et al. 2003; Werfhorst and Mijs. 2010); occupational prestige proxies position in the division of labor (Hauser and Warren 1997); years of age get indirectly at life experience, period and cohort (Yang 2008; Bell 2014). But the actual map of connections among persons that carry the flows of information and influence have been difficult to capture because of the very nature of a probability sample, which sacrifices local detail for wide coverage. The problem posed for survey research by the lack of information on this communication map is that behind every regression result in which an independent variable seems to predict an attribute is the possibility that people have acquired the attribute through social transmission. We contend that one of the core assumptions of sociology, that social context creates individuals, is fundamentally ignored by the standard methods applied to survey analysis.

In short, we need to rule out the possibility that people have acquired an attribute through interaction with other people who have that attribute, before we can even begin to interpret the effects of conventional independent variables. Recent work on networks and culture offer similar arguments. For example, DellaPosta, Shi and Macy (2015) use simulation to explore the dangers of interpreting traditional regression models. Building on the work of McPherson (1983; 2004), they show how correlations between demographic characteristics, like age or education, and other outcomes, like consumption patterns, can arise simply based on diffusion processes (see also Mark 2004). Actors in the simulation change their behaviors and attitudes over time as they are influenced by others around them. Disproportionately, actors are influenced by people with similar demographic characteristics as themselves (as people tend to interact with similar others), meaning that everyone with a given level of education (for example) will have similar consumption patterns, political attitudes, and the like. This influence process leads to strong correlations between demographic characteristics, like age or education, and other outcomes (like political attitudes), even in cases where no causal relationship exists (see also Suh, Shi and Brashears 2017).

This paper introduces a method that integrates the statistical models of survey analysis with a simple model of societal context.¹ The basic idea is to impute the social context of respondents in cases where no network data are available. The method allows survey researchers to estimate the exposure of respondents to any important social attribute, from political attitudes to health behaviors to organizational memberships. This makes it possible to estimate the coefficients for independent variables, like age and education, while controlling for the exposure of sampled respondents to the attitudes, values, beliefs, etc. of their (likely) friends or confidants. We begin by describing the image of social structure underlying this model.

Social Structure from the Ground Up

We begin with the assumption that information flows from person to person in society. As Carley (1991) suggests, this is the fundamental description of social morphology which underlies the institutional, associational, and interactive structure that we observe as society. The flow of information across the network of connections can be most conveniently thought of in terms of a simple graph, with N persons as points and the L lines of the graph representing the connections. This model can be represented mathematically with an N by N adjacency matrix, with a zero in the i, j position representing the absence of a tie between person i and person j, and a 1 indicating a tie. Of course, the representation of information flow as a binary characteristic is itself a gross oversimplification of what is a very high dimensional set of human relations (e.g., see adams, Moody and Morris 2013; Gondal and McLean 2013; Smith and Papachristos 2016 for analyses with multiple relations). For instance, distinguishing the information flow between husband and wife versus that between bank teller and customer is likely to be of great relevance to most sociological concerns. Each of these different kinds of relationships generates a distinct matrix: one for marriage, friendship, barter, neighbor, and so on. Thus, in reality we have a large number of matrices, each of size N by N. For example, setting N equal to the size of the U.S. would give us a model encompassing all the information flow for the country.

In theory, a researcher blessed with this set of matrices could adjust any regression (on that population) for contagion effects: estimating the effect of education, age, etc. on their outcome of interest, all while controlling for the complex network structure representing the flow of information between actors. Thus, in an ideal setting, a researcher could control for the probability, or potential, for social transmission on the outcome of interest, showing how likely two individuals in the study are to be exposed to similar influences.

Unfortunately, it is often impossible to measure the full set of matrices that describe the flow of information in a population (Smith and Burow 2018). A researcher interested in the entire U.S population, for example, would need multiple matrices of millions of nodes. This is generally prohibitive. Of course, this is the primary reason that researchers sample, to avoid collecting a census on a large population. We thus need to find some way of parsing this system that does not require complete information on each of the entries in all these matrices. Fortunately, some simplifications are at hand.

The Homophily Principle

One of the most reliable findings in social science (McPherson et al. 2001) is the observation that people who are similar are more likely to associate than people who are different (see also Smith, McPherson and Smith-Lovin 2014). Friends, kin, business associates, casual acquaintances, and most contacts are likely to be similar in their background characteristics. We live in geographic areas filled with people like us (Iceland and Nelson 2008); we work in homogeneous settings (Tomaskovic-Devey et al. 2006); we go to school with others like us (Mouw and Entwisle 2006); we marry people from similar backgrounds (Rosenfeld 20008; Choi and Tienda 2017). The probability that we will have social contact with someone else declines with their social difference from us, and this is called the homophily principle (Blau 1977; McPherson 2004). When we use the term homophily we are referring to an aggregate tendency for individuals to interact with similar others. This aggregate tendency towards homophily is created by a number of processes. Opportunity structures, differences in resources and preferences combine to create homophilous networks, and we focus on the aggregate level of homophily created by all of these processes (see McPherson et al. 2001 or Smith et al. 2014 for a more detailed discussion).

The homophily principle does not, of course, imply that we never meet others unlike us. On the contrary, since there are many more people in society unlike us than similar to us, we may well spend a lot of time with dissimilar others (Blau, Beeker, Fitzpatrick 1984; Schaefer 2010). But, relative to the number of available others to have contact with, we always spend a disproportionate amount of time with those like us.

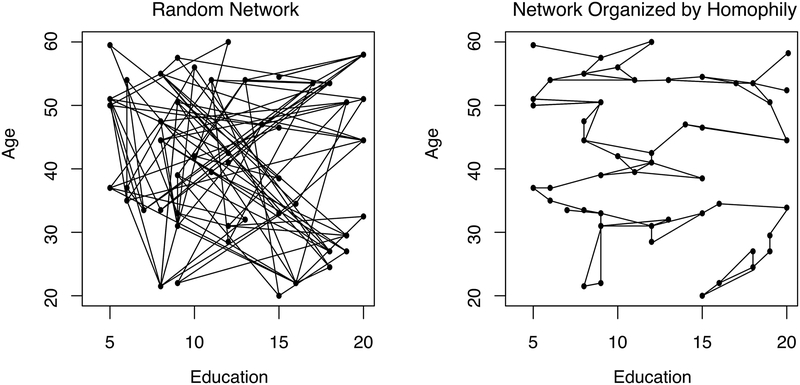
Figure 1 makes this homophily principle concrete. Figure 1 is based on a two dimensional space, consisting of age and education. We call the multidimensional social space generated by the socio-demographic variables Blau space, after Peter Blau (1977) who was the first to systematically theorize these relations (see McPherson and Ranger-Moore 1991 for a discussion). The points in the two dimensional space are people, and the lines connecting the points are contacts between people. The contacts could consist of any kind of information flow: money, conversation, material artifacts, sexual intercourse, or any other kind of social tie. There are two panels. The first represents a random network, where pairs of actors are randomly connected. The second panel has the same basic features as the first panel (with actors in the same locations and the total number of ties held fixed), but the ties are now formed based on the homophily principle; where ties are less likely to form if two people differ in terms of age and education.

Figure 1.

Example Networks in Two Dimensional Blau Space

The important message from the figure is that homophily localizes the flow of information through the system. As a message is passed from one actor to another, distance is traversed in years of education or years of age. In the random network, information flows easily across the demographic space, as ties exist between distant regions of Blau space. The homophily-based network is very different, as there are few direct ties between distant demographic regions. We can see in Figure 1 that the greater the Blau distance, the greater the number of intervening links between any two potential partners, making it unlikely that individuals will be exposed to information from distant regions of Blau space. In this way, great Blau (social) distance hinders the coordination of activities, the development of common viewpoints, common membership in groups, and a host of other joint social entities (McPherson 1983, McPherson and Ranger-Moore 1991, McPherson et al 1992, Popielarz and McPherson 1995, Mark 1998, McPherson and Rotolo 1996).

In short, niches form in Blau space: where information flows over social ties and people tend to form social ties with similar others. Individuals with similar demographic characteristics are thus likely to join the same groups, espouse similar attitudes, consume the same products, and so on. The idea that diffusion can create niches in Blau space implicitly underlies a number of recent, influential articles, ranging from studies on political polarization to social inequality to cultural consumption (e.g., Baldassarri and Bearman 2007; DiMaggio and Garip 2011; Centola 2015).

Homophily occurs quite generally in all modern times and places (McPherson et al. 2001). There are a few significant exceptions, usually produced by biology: we marry across sexes, our children and parents differ in age from us, and so forth. But, taken broadly, the homophily principle applies to all social dimensions and across time and space. We use the great generality of this result as a building block.

Homophily as a Predictor of Network Ties

The fact that homophily affects virtually every type of relationship in virtually every social dimension allows us to use social (i.e., Blau) distance as a proxy for those ties, drastically simplifying the problem of measurement created by the adjacency matrices discussed above. In essence, the homophily principle simplifies the set of adjacency matrices (based on the full population and multiple relations) to a single matrix of social distances which captures important systematic aspects about the flow of information in a population (see also Smith 2017).

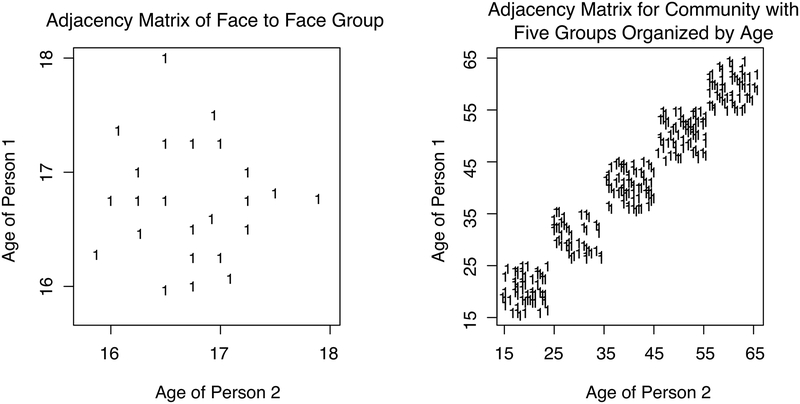
How does homophily simplify a very complicated inferential problem? The answer is that while the homophily principle is a general property of social networks, its effects are typically a direct function of the size of the system being studied (as is the concentration of power-Mayhew and Levinger 1976). Figure 2 illustrates this property. The first panel of the figure shows a typical pattern of network ties in a small group, such as a classroom or a social gathering (e.g., McFarland et al. 2014). The ones in the figure indicate that person i and person j have a social connection, with the figure indicating the age of each person in the dyad. In this restricted setting, the socio-demographic characteristics which form the basis of Blau’s theory of social association do not vary much. Social groups tend to be homogenous, or at least more homogenous than the population at-large (McPherson 1983; McPherson and Smith-Lovin 1987; McPherson et al 1992).² Since the groups are constituted by individuals who have relatively low social distance from one another, the variance in social distance will be low and the homophily effect will be suppressed inside the group. In this case, all individuals in the group are young, making it hard for age-based social clusters to emerge. Older kids are more likely to be friends with older kids, but the effect is comparatively weak. The strongest divide, between kids and adults, is completely missed.

Figure 2.

Effect of Homophily on Network Ties at Different Scales

At a larger scale, for instance, the level of a community, the homophily effect will explain much more of the structure of social ties, since the variables which make up the Blau dimensions vary a great deal more in the general population than in the subgroups formed through social association. In our example, this means considering a population with a wider age distribution. We see this in the second panel, which includes both younger and older individuals. For illustration purposes, we offer an example where age is strongly mapped onto group membership and people only form ties within groups. The result is that people will tend to interact with people of a similar age, making age similarity an excellent predictor of a social tie. For example, the divide between young and old becomes clear with this more birds-eye view of the social system.

At the level of a whole country or even the earth itself, the homophily effect is essentially the only source of structure detectable, assuming we consider geography a Blau dimension (Butts et al. 2012). The vast majority of social connections occur among those nearby in geographic, socio-demographic space. Thus, the homophily principle structures social associations almost completely at the largest scale of social systems.

The scale effect of homophily (becoming more important as system size increases) is important because this makes it possible to rely heavily on homophily as a way of imputing what interactions patterns are likely to look like. Thus, because homophily structures large-scale social systems so completely, we can proxy what transmissions processes are occurring in our data; i.e., that two people close in Blau space are vastly more likely to be influenced by similar flows of information than two people who are far in Blau space. The question is how to incorporate these contagion effects (between people close in Blau space) into a traditional regression framework, even when no network data are available. We offer a broad overview of the approach before turning to the more technical details.

Broad Overview of Approach

The approach has four basic steps. First, we take ego network data from a known probability sample of the U.S. (Burt 1984; Marsden 1987). Ego network data are based on an independent, random sample of the population. The survey will contain information about ego, the respondent, as well as their alters, the people that ego has close connections with (friendship, discuss important matters, etc.). The survey will include demographic information, like gender, age, and education, for both the respondent and their named alters.

Second, we estimate the strength of homophily using the ego network data from step 1. The model answers a crucial question: How strong is the tendency for people to interact with people who are similar to themselves? For example, how likely are two people to interact if they match on all demographic characteristics (two women with PhDs) compared to two people who are very different demographically (a women with a PhD and a man with a high school degree)? The coefficients in the model capture how much the probability of interaction goes down as distance in social space (between actors) goes up.

Third, we take the estimated model from step 2 and use the coefficients to predict the probability of interaction between any two people in a different, focal dataset, one where no network data (ego network or otherwise) exists. We assume that this second dataset constitutes typical survey data, where respondents are independently sampled and no information about their network connections is available. Thus, step 3 is an act of out of sample prediction: where we predict the probability of interaction between all respondents based on a model estimated from a completely different data source (the ego network data from step 1).

Fourth, we estimate a spatial autocorrelation model, using the predicted probabilities of interaction from step 3 as inputs (Doreian 1981; Anselin 1988; Mizruchi and Neuman 2008). Here, we assume that a researcher is interested in modeling an outcome, like attitudes or behaviors, as a function of a series of independent variables, like education, age, etc. We also assume that we are using the dataset from step 3, which has no network information on the respondents.³ We run a spatial model that controls for the (imputed) social context of the respondents. The model is based on the homophily principle. Two people close in social space will have higher probabilities of interaction, and are thus more likely to be influenced by similar flows of information (as they are comparatively close in the true, unobserved network). The spatial model adjusts for this inferred autocorrelation, arriving at coefficients for education, age, etc., while controlling for diffusion effects in social space — where people in the same region of social space are likely to take on similar attitudes, beliefs and behaviors (McPherson 2004; DellaPosta et al. 2015).

Note that a researcher would only strictly need to do steps 3–4 in their analysis, as steps 1–2 are performed independently of any particular study. In this paper, we discuss how the base model in step 2 is estimated, but in practice, a researcher could take the results presented here and apply them directly in their own analysis. Alternatively, a researcher could do all 4 steps, using ego network data appropriate for their population of interest. For example, it would be necessary to redo steps 1–2 for studies interested in populations outside the U.S.

Details of the Approach: Imputing Social Structure

Step 1: Sampling Ego Networks

In step 1, we gather ego network data from a known data source. It is typically not feasible to measure network properties directly for all individuals in a large system such as the United States, since that would require a census of all the ties between hundreds of millions of people. Recognizing this fact early on, researchers developed network sampling techniques which allow standard survey methods to get at important network properties without the necessity of exhausting the population. These network sampling methods (Granovetter 1976) have resulted in studies of networks in the United States (Burt 1984) and internationally (Hollinger and Haller 1990). In essence, the method involves getting information on the local social network ties (the ego network) of respondents in a standard probability survey of individuals. These ego networks allow inferences about general properties of the whole system, such as the average number of network ties, the density of ties, and so forth (Marsden 1987; Moore 1990; McPherson et al 2006; Smith 2012). The primary source of information on networks in the United States comes from the General Social Survey (GSS), which has periodically gathered information on a representative sample of adults since 1972. The first national network sampling effort occurred in 1985, was partially replicated in 1987, and fully replicated in 2004 (McPherson et al 2006). Respondents were asked to report on up to five of the contacts with which they discuss important matters (Burt 1984, Marsden 1987).

We use the 1985 and 2004 GSS ego network data as a means of estimating the effect of homophily on the probability of interaction between two people (see step 2 for details). The GSS ego network data include detailed information on up to 5 network alters (defined as core discussion partners) for each respondent. Most crucially for this paper, the respondents reported on the age, race, sex, religion, and education of their alters. Respondents also answered analogous questions about themselves. We thus know the race, age, etc. of each respondent and their discussion partners.

The GSS ego network data have a number of ideal properties. Most clearly, the data are a nationally representative sample of social networks of the U.S. population; this is the exact data necessary for the proposed approach, which will ultimately try and impute social context on another data source based on the estimates of the ego network data. It is necessary that the original data be representative of the U.S. population. Similarly, the GSS has fairly standard measures of key demographic characteristics, making it easier to apply the results to another dataset (which is likely to have similar kinds of measures). Other kinds of data, including socio-centric network data, offer rich, detailed information, but are generally circumscribed to particular subpopulations, often bounded by geography or institutional walls. This makes them less than ideal options when the goal is to estimate the probability of interaction for the U.S. as a whole, and then use those estimates in subsequent analyses on different datasets. The GSS data are also ideal as they capture a relation that moves beyond the most intimate tie of marriage (or cohabitation), which is more typically collected (e.g., Rosenfeld 2008; Torche 2010; Schwartz 2013). We are thus able to capture a range of social contacts that extend further into a person’s social network.

There are also a number of potential drawbacks that come with the GSS ego network data.⁴ Probably the most important measurement constraint is the fact that relying on individuals to recover information about their network contacts introduces many issues of memory and context (Marin 2004; Almquist 2012). Given the large volume of people that most individuals come into contact within the course of even a single day, the prospect of recovering meaningful information on even a small fraction of contacts is daunting. Recognition of this fundamental problem has led most research on ego networks to recover the most important contacts; in the GSS case, those people the respondent discusses important matters with. The value of allowing the respondent to define important is that the instrument does not assume anything about the respondent or the region of the surrounding network. The difficulty, of course, is that we do not know much about the actual ties. Some work has been done in unpacking the important matters relation (Bearman and Parigi 2004; Byungkyu and Bearman 2017), but we are still in great ignorance about what these ties really mean. Clearly, the method is biased toward the ties of greatest salience to the respondent, but the extent of this selective bias is not well understood, nor is the relationship between the revealed ties and the rest of the contacts in the respondent’s social network. Thus, while ego network data capture weaker relationships than marriage or cohabitation, they still tend toward relatively strong ties. Future work could extend the approach by employing data on weaker ties.

Similarly, the GSS name generator is quite general and may not always match the substantive case of interest. For example, if we thought that the outcome of interest rested on discussing political topics, we may want to employ a network relation capturing the people the respondents discusses politics with. The GSS data do not work perfectly here as one could discuss important matters with a close confidant but not consider politics an important matter (Bearman and Parigi 2004). If the patterning of homophily was drastically different between political discussion and more general discussion, the estimated model could be inaccurate. In such cases, a researcher could employ alternative data to estimate the initial homophily model. The 2008 ANES data, for example, has ego network data based on the ‘discuss politics with’ name generator. The data are limited to three alters, which is a drawback, but is otherwise analogous to the GSS data. In our own analysis, we employ the GSS data for the main results and include supplementary results based on the 2008 ANES. We thus offer a robustness check, to see how sensitive the results are to choice of ego network data.

Step 2: Estimating Strength of Homophily from Ego Network Data

In step 2, we use the ego network data from step 1 to estimate the strength of homophily in core discussion networks. The outcome of interest is the existence/non-existence of a social tie between actors (do actor i and actor j discuss important matters?). The independent variables represent the socio-demographic distance between actors (are i and j the same gender?). We estimate the model using all demographic dimensions available in the ego network data: in this case age, education, gender, race and religion. See Smith et al. 2014 for details.

We use a modified version of the case-control method to estimate the strength of homophily. A case-control model is ideal for our purpose because it makes it easier to estimate the predicted probability of interaction between two actors. Alternative models, such a log-linear models, make this is a difficult task. A case-control model also has the advantage of easily incorporating multiple predictors into the model, making it possible to condition the probability of interaction on multiple social dimensions (Smith et al. 2014).

The case-control method is a standard approach in epidemiological research. The method is designed to study rare conditions (e.g., a disease state) that are challenging to capture through random sampling (Breslow and Day 1980). Case-control models compare the observed cases, those with the condition, to the controls, those without the condition, on some exposure or preexisting condition of interest (e.g., exercise or diet) (Hosmer and Lemeshow 1989). Cases that possess the given condition are combined with cases collected independently, which do not possess the condition, and logistic regression analysis proceeds as though the entire dataset were sampled under the same regime (Allison 1999; King and Zeng 2001). The case-control method is thus a version of logistic regression applied to data sampled on the dependent variable (Prentice and Pyke 1979; Pregibon 1984).

The case-control method is ideal for ego network data. Ego network data capture the rare condition of interest, a confiding relationship between two individuals. Ego network data thus sample on the dependent variable, rather than randomly sampling from all dyads (or pairs of people who may or may not be tied together). We proceed by comparing the cases, pairs with a confiding relationship, to the controls, pairs with no confiding relationship. The ‘preexisting condition’ is the socio-demographic distance between each person in the pair.

Sampling Ties and Non-ties: Cases and Controls

We begin by demonstrating how a probability sample of individuals can yield a sample of network ties. The ego network approach is a blend of the probability methods of survey analysis and network imagery. Here, we treat the set of ties that we recover from the General Social Survey (between respondents and their confidants) as a representative sample of the ties that existed among people in the United States circa 1985 and 2004. This forms the case portion.

The control portion of our case-control model comes from the set of non-ties between the sampled respondents from the GSS. Respondents in the GSS name up to 5 alters, but there is little reason to believe that other respondents (from the sample) are included in those named alters. The model thus uses the non-ties found between randomly selected GSS respondents to construct the control portion of the sample. This amounts to a probability sample of the possible, but non-existing, ties among U.S. residents. The control sample is formed by constructing non-ties between each pair of respondents, by year; formally, respondents (restricted to those respondents with at least one tie) are randomly paired together, based on population weights. This is analogous to traditional log-linear models, which analyze marriage rates relative to random mixing in the population (Blossfeld 2008).

The Case Control Model

We use the constructed case and control samples to model the effect of socio-demographic distance on the probability of a confiding tie. The control portion of the sample (i.e., the respondent-respondent pairings) constitutes the non-ties, while the case portion of the sample (i.e., the respondent-alter connections in the GSS network module) constitutes the ties. We combine the two samples, case and control, to form a case-control dataset and perform a logistic regression (Breslow and Day 1980; Hosmer and Lemesow 1989). We regress the presence of a confiding tie on the socio-demographic distance between paired individuals. We use the variables education age, race sex and religion to define socio-demographic distance within each pair. Education and age are measured as years, while race, sex and religion are categorical variables.⁵ Socio-demographic distance is measured as match/no match for race, religion and sex (i.e., are the two people in the pair a different race? 0 if no; 1 if yes) and is measured as the absolute difference for age and education (how many years apart are the two people in the pair, in terms of age or education?). We regress the vector of observed zeros and ones (1=tie; 0= no tie) in the combined sample upon the observed socio-demographic distances to estimate the homophily patterns:

$$\text{ln}\left(\frac{p\left(ti{e}_{ij}\right)}{1-p\left(ti{e}_{ij}\right)}\right)={\beta }_0+{\beta }_1*RaceDif{f}_{ij}+{\beta }_2*ReligionDif{f}_{ij}+{\beta }_3*SexDif{f}_{ij}+{\beta }_4*AgeDif{f}_{ij}+{\beta }_5*EducDif{f}_{ij}+{\beta }_6*Yea{r}_{ij}$$ (1)

where β₁ is the logistic regression parameter corresponding to the racial difference between i and j, β₂ corresponds to the religious difference and so on. The results are presented in Table 1. Table 1 includes two models, one with the base effects of the socio-demographic distances and one where the effects of socio-demographic distance are allowed to vary by year (between 1985 and 2004). As would be expected for measures of homophily, all the effects of the Blau dimensions are negative, indicating a decreasing probability of contact with increasing socio-demographic distance. See Smith et al. (2014) for a full discussion of the results.^6,7

Table 1.

Case-Control Logistic Regression Predicting a Confiding Relationship based on GSS Ego Network Data, 1985 and 2004

Variables	Model 1	Model 2
Intercept	−14.456***	−14.519***
	(.048)	(.057)
Different Race	−1.819***	−1.959***
	(.077)	(.117)
Different Religion	−1.362***	−1.27***
	(.044)	(.060)
Different Sex	−.317***	−.373***
	(.025)	(.033)
Education Difference	−.049***	−.047***
	(.002)	(.002)
Age Difference	−.173***	−.157***
	(.009)	(.012)
Different Race		.264
		(.155)
Different Religion		−.215*
		(.092)
Different Sex		.144**
		(.05)
Education Difference		−.005
		(.003)
Age Difference		−.044*
		(.020)
Year	−.179***	−.052
	(.047)	(.089)
N (respondents)	3001	3001
N (dyads)	1139161	1139161

Note: Standard errors in parentheses.

The standard errors are calculated using bootstrap estimates. The standard errors are equal to the standard deviation of the coefficients across 1000 iterations and are thus not dependent on the number of dyads. For each iteration, we take a random sample of respondents from each year and rerun the case control logistic regression.

Step 3 Estimating Probability of Interaction between all Respondents in Second Dataset

In step 3, we take the estimated coefficients from step 2 and apply them to a different dataset (i.e., not the 1985 and 2004 GSS). This is the focal dataset from the perspective of the researcher, or the dataset that the regression of interest is based on. In our example below, the focal dataset is the 2016 American National Election Study (ANES). We take this focal dataset and calculate the predicted probability of a tie between any two individuals in the sample. We estimate the probability of contact between individuals as conditioned by their distance in Blau space. Each respondent in the sample is paired with all other respondents in the sample, creating (n × n)/2 pairs, where n is the number of respondents. For each ij pair, we take the socio-demographic characteristics of person i and contrast them to the socio-demographic characteristics of person j, in terms of education, age, race, religion, and gender (is person i the same gender as person j?). This yields the analogous Blau distance variables used in step 2 (RaceDiff, ReligionDiff, etc.). We then calculate the probability of interaction between person i and person j, based on their socio-demographic differences, as well as the coefficients from step 2. This is repeated for all pairs. Formally:

$$p\left(ti{e}_{ij}\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_1*RaceDif{f}_{ij}+{\beta }_2*ReligionDif{f}_{ij}+{\beta }_3*SexDif{f}_{ij}+{\beta }_4*AgeDif{f}_{ij}+{\beta }_5*EducDif{f}_{ij}\right)}}$$ (2)

The estimates from equation (2) are assembled into an n by n matrix, defined as P.⁸ This matrix has elements that express the fitted chance of each respondent in having a tie with each other respondent. In essence, this P matrix stands in for the N by N matrix discussed in the introductory section, by focusing on the direct transmission of information through core discussion networks, which are embedded in those larger networks.

Step 4 Spatial Model

In step 4, we use the P matrix inferred in step 3 to estimate a spatial effects regression model. The spatial regression models an outcome of interest, like political attitudes, as a function of demographic characteristics (and other independent variables) and the political attitudes of ‘neighboring’ respondents. This makes it possible to condition the coefficients for demographic characteristics, like age and education, on the social context, controlling for the likely attributes (e.g., attitudes) of the respondent’s network alters.

The model is estimated based on the focal dataset, as well as the matrix of probabilities from step 3. The matrix of probabilities, P, is first transformed into a row stochastic matrix, defined as W, to conform to the requirements of the spatial regression model. The W matrix is thus the row-conditioned P matrix, where each entry is divided by the sum of the row. Each entry in this row conditioned matrix, W, is proportional to the fitted probability that the i-th respondent shares a core network tie with the j-th respondent. By making it row conditioned, we calculate the proportional probability, or weight, for respondent i to interact with someone like respondent j. Higher weights suggest that respondent i is exposed to information and influences from people like respondent j.

It is important to recognize that the probability of two respondents knowing each other is small.⁹ Thus, we are not claiming to have captured the particular people that respondent i has social connections with; rather, the values in the W matrix reflect the types of people that i is likely to know. A respondent will have the highest weights with respondents that have similar characteristics as themselves, and lower, but non-zero, weights with respondents who differ on race, education, etc. This reflects the idea that information flow should occur most readily between nearby regions in social space, and is less likely, but not impossible, between distant regions. Similarly, some dimensions in social space may be more salient than others; so that two respondents who differ on one dimension (say education) may still have high weights, as long as they match on other salient dimensions, like race.

The W matrix is then used to infer the social context of each respondent, in terms of the outcome of interest. The outcome of interest is defined as Y. This could be political attitudes, health behaviors, etc. For each respondent, the entries in W capture the kinds of people they are likely to know (and be similar to), with higher values indicating higher weights. Y captures the variable of interest for each respondent. By multiplying W by Y, we get the values for Y that each respondent is most likely to be surrounded by.

Formally, the W matrix is multiplied by the vector of Y values of the respondents, yielding a vector equal to WY. WY is proportional to the probability that ego will discuss important matters with individuals possessing attribute Y. In essence, the entries in WY describe the social context of each respondent. We term this computed product WY the imputed network of the respondent. If Y is continuous, then WY is the mean value of Y among ego’s potential (or imputed) network alters. With this in hand, we form the spatial regression model:

$$Y_i=\mathit{\eta }{\mathit{X}}_i+\Delta {(\mathit{W}Y)}_i+{\text{ε}}_i$$ (3)

Where Y_i represents the outcome of interest, ηX_i represents the effects of other independent variables (like age or education), Δ is the effect of spatial distance in Blau space, and ε_i is a stochastic disturbance term (Anselin 1988).

A very important characteristic of equation (3) is that it is a special case of the equilibrium distribution of the network social influence model (French 1956; Friedkin 1998). This fact implies that we can view the parameters in (3) as representing a cross-sectional snapshot of a dynamic process in which local opinions, beliefs, etc. are equilibrated through social interaction in local networks (compare with Friedkin 1998, Chapter 2). The local mechanisms of contagion of information through network ties are translated into a homophilous landscape by the W matrix, which then transforms the distribution of that information into a predicted social environment for each respondent in WY. The Δ coefficient is a single parameter that summarizes the dependence of the respondent’s value of Y on the social environment.

On the Problem of Selection

We have largely discussed the model in terms of homophily and contagion, where information, attitudes, etc. flow over ties highly concentrated in Blau space. It is also important to consider the role of selection in network formation and its relationship to the proposed model. With selection effects, individuals form relationships with partners who have similar behaviors and attitudes as themselves, thus creating the correlations between ego and alter on the attribute of interest. If selection were the only network process operating, then we would not need to worry about adjusting our regression models for contagion effects (as the attribute was acquired prior to interaction). Our own view is that even in strong cases of selection, contagion is still likely to operate. Here, actors form ties with similar others on the attribute of interest; the network then acts as a kind of echo chamber, sustaining and amplifying the initially shared attribute (i.e., setting the standard for what is considered normal). For example, two conservatives may become friends and help support each other’s conservative attitudes.

More generally, we suggest that our model offers a different take on the problem of influence and selection. It is less about estimating peer influence, and more about trying to specify a new baseline model to compare typical models against. The focus is thus on the demographic variables themselves; where the question is whether the effects of age or education are real, above what we expect based on network processes. We are now in a position to explore an example of our analysis.

Empirical Example: Political Attitudes in the U.S.

The empirical example focuses on political attitudes. The relationship between demographic variables, like age, education or race/ethnicity, and political attitudes constitutes one of the core problems of survey research. Hundreds of studies have asked if more educated people are more tolerant, more liberal, support certain policies, etc. (e.g., Jackman and Muha 1984; Farley et al. 1994; Stubager 2008). A common idea is that the process of education inculcates the individual with values that promote certain dispositions that are more tolerant of other groups (e.g., Schuman et al. 1997). Similarly, a common argument is that education serves to expand one’s horizons and reasoning capability, allowing for political leanings that are more global, less ‘emotional’ and thus, on the whole, run towards the liberal side (see Wodtke 2012 for a summary). We test this hypothesis while adjusting for potential contagion effects in the data. We suggest that individuals will be liberal (tolerant, etc.) when they interact with liberal (tolerant, etc.) others, and will be conservative when they interact with conservative others. By taking this into account, we arrive at an estimate for the effect of education on attitudes, net of the contagion effects of being surrounded by people who are liberal/conservative.

Our analysis will consider analogous arguments about gender, religion, race/ethnicity and age. For example, we might expect older individuals to have different (e.g., more conservative) political leanings than younger individuals (Campbell and Strate 1981; Alwin and Krosnick 1991). But how much of the differences across age groups are driven by the different social contexts that younger/older individuals inhabit? The basic idea is to estimate models predicting attitudes as a function of demographic variables, while controlling for the imputed social context.

Data

The data come from the 2016 ANES. The ANES is a nationally representative survey designed to capture the political attitudes, voting behaviors and party identification of the U.S. We utilize the pre-election survey. The ANES also includes detailed demographic information. In our case the focus is on age, education, race, religion and gender. Note that the data do not include ego network information. We deliberately select a dataset without ego network data in order to make clear how the approach could be applied in practice; i.e., that a researcher could control for the imputed social context of each respondent, even when ego network data are not directly available.

Dependent Variables

Our case study includes three different dependent variables, representing different kinds of political ideology measures. The first is a scale capturing negative/positive feelings about the Democratic Party. The scale ranges from 0 to 100 with 0 corresponding to negative feelings and 100 corresponding to positive feelings about the Democratic Party. The second outcome of interest is a scale variable capturing how much the respondent agrees with government support for African Americans. The question asked respondents to place themselves on a 7-point scale, with 1 indicating that “Blacks should help themselves” and 7 indicating that the government should “help Blacks”.¹⁰ The third variable is also a 7-point scale, capturing general support for defense spending. A value of 1 corresponds to low support (“government should decrease defense spending”) and a value of 7 corresponds to high support (“government should increase defense spending”).

Independent Variables

We include terms in the model for education, age, gender, race/ethnicity and religion. This makes it possible to see which demographic variables are affected by including the social context variable. It also offers a stringent test of the approach, making sure that the imputed contextual variable is not a simple summation of the demographic variables, but, instead, offers information above the inclusion of each term separately in the model.

Education is measured as an ordinal variable, with values ranging from no schooling to doctorate degree. We recode this variable to adhere (as closely as possible) to the years of school associated with the selected grade or degree. Thus, an individual with a high school degree is coded as 12 years, a college degree as 16 and so on. Age is measured simply as years, while gender is measured as a binary variable: male/female. Race/ethnicity includes categories for white, black, Hispanic, Asian, Native American and other. Religion includes categories for Protestant, Catholic, Jewish, other and none. White serves as the reference category for race while Protestant serves as the reference for religion.

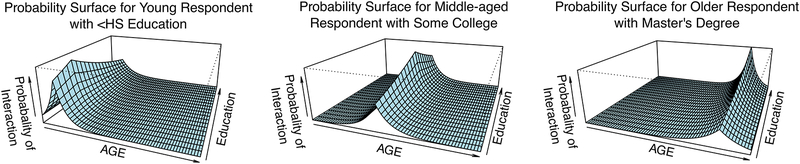
We also use this demographic information (on all five variables) to construct the P matrix, showing the probability of interaction between respondents. We take the age, education, etc. of each respondent, and contrast that to the age, education, etc. of each other respondent. We then use equation (2) to predict the probability of interaction between each person in the ANES¹¹. The P matrix is then used to form the W matrix, the row-conditioned (or relative) matrix of probabilities. To give some insight into the form of the regression results, Figure 3 presents the fitted estimates for three hypothetical individuals, with varying values of age and education (ranging from a young respondent with <HS to an older respondent with a PhD). The figure captures the probability of interaction between the hypothetical person and potential alters with varying characteristics of age and education. The probability surface declines in every direction from the hypothetical respondent, with the decline steepest in the age dimension. This figure illustrates visually the effects of the homophily principle in Blau space; that is, each individual occupies a locus that forms a peak in the rate of association. The declining probability of contact with increasing Blau distance shapes the kind of information that each person will be exposed to through their networks. Information from distant regions of Blau space is attenuated by the steep decline in the probability of transmission, while the noise from the immediate social environment is at once loud and redundant. These two processes combine to reinforce local homogeneity in social circles, while systematically allowing heterogeneity of information across socially distant habitats.

Figure 3.

Probability of Interaction between Hypothetical Respondents and Potential Alters at Different Distances in Blau Space

Model

Our model takes the form of equation (3), with a spatial effects model for each dependent variable. For example, for the democrat likability scale:

$${\text{EgoDemocratScale}}_{\text{i}}={\eta }_0+{\eta }_1{\text{*Education}}_{\text{i}}+{\eta }_2{\text{*Age}}_{\text{i}}+{\eta }_3{\text{*Female}}_{\text{i}}+{\eta }_4*{\text{Black}}_{\text{i}}+{\eta }_5*{\text{Hispanic}}_{\text{i}}+{\eta }_6{\text{*Asian}}_{\text{i}}+{\eta }_7{\text{*NativeAmerican}}_{\text{i}}+{\eta }_8{\text{*OtherRace}}_{\text{i}}+{\eta }_9{\text{*Catholic}}_{\text{i}}+{\eta }_{10}{\text{*Jewish}}_{\text{i}}+{\eta }_{11}*{\text{None}}_{\text{i}}+{\eta }_{12}*{\text{OtherReligion}}_{\text{i}}+\Delta \text{*}{\left(W\text{*AlterDemocratScale}\right)}_i+{\text{ ε}}_i$$ (4)

Where Δ is the network effects regression coefficient, W is the n by n matrix of row-conditioned tie probabilities, η₁ is the effect of years of education, η₂ is the effect of years of age, etc., and ε_i is a stochastic error term.

Note that democrat scale appears on both sides of the equation, but we are not predicting ego’s political leanings from ego’s political leanings; instead, we are predicting ego’s feelings about the Democratic Party from the weighted average of ego’s projected network alters, and their characteristics. The i, i entry in the W matrix is set equal to zero; the self-weight of the respondent is zero in equations (3) and (4). Thus, while Y appears on both sides of equations (3) and (4), we are not predicting Y from itself, since the self-weight has been eliminated. In the expression Δ*(W*AlterDemocratScale)_i, only the attitudes of a respondent’s imputed network alters affects ego’s attitude, here feelings about the Democratic Party. The Δ coefficient parameterizes the effect of having network alters possessing a liberal attitude, and the η coefficients evaluate the effect of years of education, gender age, etc., taking into account the network effects contained in W*DemocratScale.

Results

Table 2 presents the results for our three dependent variables. There are two models for each outcome of interest. The first model only includes the demographic variables while the second model is the full model, including the demographic variables and the control for social context.

Table 2.

Spatial Model Results for Three Political Variables in 2016 ANES

	Democrat Scale		Assistance to African Americans		Support for Defense Spending
Variables	Model 1	Model 2	Model 1	Model 2	Model 1	Model 2
Intercept	34.913***	1.121	2.224***	−.580***	5.321***	1.440*
	(3.051)	(6.400)	(0.204)	(0.335)	(0.176)	(0.579)
Age	−0.011	0.017	−0.007***	−0.003	0.016***	0.010***
	(0.027)	(0.027)	(0.002)	(0.002)	(0.002)	(0.002)
Education	0.478**	0.389*	0.087***	0.069***	−0.09***	−0.068***
	(0.18)	(0.180)	(0.012)	(0.012)	(0.01)	(0.010)
Female (reference=Male)	−6.624***	−4.798***	−0.219***	−0.157**	−0.01	0.013
	(0.915)	(0.960)	(0.061)	(0.061)	(0.052)	(0.052)
Race/Ethnicity (Reference=White)
Black	34.247***	22.875***	1.988***	1.246***	−0.376***	−0.260**
	(1.582)	(2.281)	(0.106)	(0.115)	(0.096)	(0.096)
Hispanic	17.061***	10.389***	1.086***	0.661***	−0.173	−0.114
	(1.617)	(1.893)	(0.111)	(0.114)	(0.094)	(0.094)
Asian	8.382**	4.570	0.158	−0.058	−0.397**	−0.305*
	(2.657)	(2.710)	(0.179)	(0.178)	(0.151)	(0.151)
Native American	16.542**	12.662*	0.986*	0.735	0.448	0.477
	(6.1)	(6.106)	(0.43)	(0.428)	(0.362)	(0.361)
Other Race	9.531***	5.476*	0.637***	0.354*	0.115	0.140
	(2.366)	(2.430)	(0.156)	(0.156)	(0.138)	(0.137)
Religion (Reference=Protestant)
Catholic	6.787***	3.955***	0.13	0.041	−0.115	−0.024
	(1.169)	(1.237)	(0.078)	(0.078)	(0.066)	(0.067)
Jewish	17.099***	13.966***	0.997***	0.792***	−0.687***	−0.495**
	(3.221)	(3.238)	(0.216)	(0.215)	(0.177)	(0.178)
None	13.293***	8.811***	0.759***	0.458***	−1.061***	−0.674***
	(1.345)	(1.455)	(0.089)	(0.090)	(0.075)	(0.092)
Other Religion	5.421**	3.246	0.398**	0.256	−0.531***	−0.356**
	(2.016)	(2.032)	(0.135)	(0.135)	(0.115)	(0.117)
Spatial Parameter		0.800***		0.909***		0.812***
		(0.125)		(0.060)		(0.120)
AIC	35324.529	35316.967	13309.671	13289.557	11905.142	11897.590
N	3723	3723	3349	3349	3278	3278

We begin with the political thermometer variable, showing how respondents relate to the Democratic Party (0–100, with 100 being more favorable). In general, Model 1 indicates that those with higher education have more positive feelings towards the Democrats, while women and white individuals have lower ratings. For example, black individuals have reported scores 34.25 points above that of white individuals, controlling for gender, age, religion and education. We also see that Protestants tend to have lower attachment to the Democratic Party, with lower ratings than Catholics and Jews, as well as individuals who claim no religion and other religion.

Model 2 adds the spatial term to the base model, controlling for the imputed social context of each respondent. The inclusion of the social context term affects the results in important ways.¹² Most clearly, some of the effects that are significant in Model 1 are no longer significant once we control for social context. For example, in Model 1, we see that the Asian coefficient is 8.38 and is significant. Controlling for social context, the coefficient reduces to 4.57, a 45 percent drop, and is no longer statistically significant. Thus, from Model 1, we would conclude that Asian individuals report more favorable attitudes about the Democratic Party (controlling for the other demographic variables). Once we account for the social context of our respondents, we see that Asian respondents and white respondents are not necessarily different in their political leanings. Thus, the gap in political attitudes seen in Model 1 is driven by differences in social context between whites and Asians, with Asians more likely to be surrounded by people who are favorable to the Democratic Party. We see a similar story with religion, where those in the Other category (i.e., Hindu, Muslim, etc.), report more favorable feelings toward the Democrat Party than Protestants. This effect is significant in Model 1 but disappears once we control for social context, with the coefficient decreasing by about 40% between the two models.

More generally, almost all of the coefficients are affected by the inclusion of the social context term. Across the board, the coefficients drop in magnitude, with smaller effects in Model 2 than in Model 1. For example, the coefficient on Catholic, while still significant, drops in magnitude by 40% (6.78 to 3.95), suggesting that 40 percent of the difference between Catholics and Protestants can be explained by differences in social context. Similarly, we see the coefficient on none, comparing those with no religion to Protestants, drop by 34 percent. Or, looking at race/ethnicity, the coefficient on Hispanic drops by 40 percent between the two models, while the coefficient on black drops by 33 percent. The education coefficient is also reduced between the models, with a drop of about 20 percent.

The spatial term itself is significant and positive, suggesting that respondents who are surrounded by people who like the Democratic Party are also more likely to like the Democratic Party. The magnitude of this effect is quite large. Consider two cases: one where the respondent is surrounded by people who hate the Democrats; and one where the respondent is surrounded by people who love the Democrats. Assume the first respondent has alters with a mean value of 40 on the Democrat Scale, while the second has alters with a mean value of 70. We would predict a 24-point increase in the respondent’s reported liking of the Democrat Party. Note that this effect is net of the other demographic characteristics. To put this in perspective, the magnitude of the effect is larger than the effect for education, gender, race, religion, etc. For example, increasing education across the entire range of values (i.e. 20 years) is associated with an 8-point increase in liking the Democrats. Individuals in very different social worlds are likely to have very different political leanings, and this effect can trump differences based on demographic characteristics.

The results are similar for our two other outcomes of interest, black assistance and defense spending. The black assistance model predicts support for the government offering assistance to blacks. The base model only contains the demographic variables. It is clear from Model 1 that younger, better educated individuals tend to support government assistance. For example, the coefficient on age is negative and significant. Model 2 includes the social context term. Again, there are large consequences for controlling for (imputed) social context. Most striking, the coefficient on age decreases by 57 percent between the two models and is no longer significant. Thus, controlling for the likely attitudes of those around the respondents, there is no statistically discernable difference between younger and older individuals. It is not simply that being older makes you more conservative: being older means you are more likely to be surrounded by conservative opinions, which in turn, shapes your own opinions. Similarly, the coefficients on Native American and other religion are no longer significant, once we control for social context. More generally, the coefficients drop substantially (even when the coefficient is still significant) with the inclusion of the social context term; this ranges from over a 100 percent drop (the Asian coefficient) to a 20 percent drop (for education). For example, there is a 40 percent decrease in the coefficient for Hispanic and a 37 percent decrease in the coefficient on black. This means that much of the racial differences in political opinion, here about government assistance, is explained by the differing social contexts in which white, black and Hispanic individuals are likely to find themselves; with black and Hispanic individuals less likely to be surrounded by conservative voices.

Again, we see that the spatial coefficient itself is positive and significant, suggesting that individuals surrounded by positive attitudes about government support also have positive attitudes about government support. The magnitude of this effect is large, on par or larger than with the more traditional demographic variables. For example, moving a respondent from an average social context (with a mean value of 4) to a more liberal one (with a mean value of 6) increases their predicted score by a value of 1.8. This is considerably larger than the expected change associated with a 75-year increase in age or a 20-year decrease in education.

The results for defense spending are largely similar (although no coefficient goes from significant to insignificant between the two models) and we do not offer a separate discussion of these results. See Table 2 for the full regression models. Overall, there is evidence that the imputed social environment in Blau space can help explain individual attitudes in the U. S. population. Without controlling for social context, we run the risk of overestimating and misinterpreting the effect of demographic variables on our outcome of interest.

Sensitivity Analysis: Conceptual and Statistical

The results thus far suggest the utility of imputing the social context of independently sampled respondents. But should this model always ‘work’? What about cases where the dependent variable does not have a niche? That is, when the dependent variable is either more or less randomly distributed across Blau space (c.f., McPherson and Ranger-Moore 1991; Mark 1998), or when its distribution is lumpy or clearly multimodal.

We explore this scenario by running the model on additional variable in the ANES. Table A1 presents the analogous results to Table 2 (OLS compared to spatial model) for two variables: one capturing attitudes about health insurance and the other capturing attitudes about guaranteed incomes. For example, the health insurance question asks respondents if they thought the government should provide medical insurance (running from 1 to 7, 1 being pro government medical insurance). These two variables reflect attitudes about more specific kinds of polices. Such attitudes are likely to be more heterogeneously distributed across social space, as even those who have the same general political leanings may hold different policy views. A muddy picture in social space, without well-defined niches, should yields weak results in the spatial model. Looking at Table A1, we can see that these outcomes do, in fact, represent weak cases. The coefficient on the spatial term is not significant in either model, while adding the spatial term does not improve the fit. The standard error for the spatial term is also quite high in both models. This all suggests that the spatial term adds little new information above the linear combination of the demographic variables, as we would expect with outcomes that do not have clearly defined niches in social space. This result is suggestive (albeit not conclusive) that the underlying assumptions of the model are being mirrored in the results.

In the spirit of further skepticism for our approach, we have explored several avenues of attack on this model. First, we did Monte Carlo studies assigning random Blau distances to the cases in our analysis.¹³ The resulting distribution of spatial parameters is centered on zero, as one would expect if the model is actually operating as we intend. Second, we explored the statistical properties of our estimator under a variety of assumptions about the statistical dependencies that arise in network analysis. For instance, we modeled a randomly chosen alter, rather than use all of the reported alters, with substantively similar results. We split the sample into two random halves, and estimated the values in the P matrix from the first set, and applied this matrix to the second set, with similar results. We experimented with various versions of eliminating kin relations entirely, with including and excluding spouses, and so forth. The resulting spatial models were robust, in that they all lead to the same qualitative conclusion that the social context variable is a significant predictor of the dependent variables. There are many issues that remain unresolved. We discuss these more or less in order of their potential threats to inference.

A major statistical issue for the analysis is the uncertainty (sampling error) in the elements of the P matrix. The parameter estimates in the first stage logistic regression are uncertain, as they are based on a sample of respondents. Past work has used bootstrapping methods to infer the standard errors of these parameters (Smith et al. 2014). We, however, use these estimates directly in solving for the elements of the P matrix, for the second stage. The spatial model thus (heroically) assumes that the elements of the P matrix are measured without error, although the consequences of our violation of this assumption are not obvious. We are not able to identify any mechanisms at this point by which the violation of this assumption will create a bias in the direction of our social context hypothesis, but it is possible that the standard error on the spatial term is underestimated.

Another problem worth exploring is the sensitivity of our logistic specification to the known absence of many other variables that constitute the dimensions of Blau space. Our basic logistic regression is quite simple, including terms for five demographic dimensions. It is likely, however, that other demographic dimensions are important and have not been included. As has been argued (McPherson and Ranger-Moore 1991; McPherson 2001), the number of Blau dimensions is a function of the complexity of the system. Since the United States is clearly a very complex system, one expects the dimensionality of Blau space to be very high. For example, our model does not include geographic space, which is a major source of variation in social contact. It is thus possible that our model is too simple and does a suboptimal job of assigning probabilities in the P matrix. We do not know how badly the elements in the P matrix are affected by the exclusion of important independent variables (and more generally a model that imperfectly predicts the probabilities). Once again, intuition suggests that this case may be conservative for our hypothesis, as a better model would yield more accurate imputations, but only careful analysis will resolve the question. Similarly, we opted for a very simple model of homophily, but future work could extend the model in a number of ways, including interactions between the demographic dimensions when predicting a tie.

More substantively, our approach does not account for other kinds of contextual effects, like living in the same neighborhood or town. This omission is more a question of data availability than anything else. With proper data, we could incorporate physical location as a Blau space dimension, capturing the idea that people who live close together are more likely to know each other. A researcher could also go further and include controls for the features of the neighborhood (town, city, etc.), such as local economic conditions or political climate. This is consistent with our own model, allowing a researcher to control more fully for the context when interpreting the effects of traditional demographic variables.

A more conceptually difficult issue is how well the relation we measure in the GSS represents the full range of social relations that should, ideally, be considered in the analysis of social context. The discuss important matters relation is an extremely strong tie, which might behave differently than weaker ties, such as work-related contacts, casual social contact, and so forth. For example, people may discuss different things with different people, depending on the strength of relationship (Cowan and Baldassari 2018). If individuals discuss politics in certain types of relationships and health in others, then it will be important to match the type of tie to the substantive outcome of interest. For example, our own analysis substantively focuses on politics and it would make sense to employ ego network data that captures political discussion directly.

Given these concerns, we have replicated the entire analysis, using the 2008 ANES ego network data as the basis for the initial homophily model. The data contain demographic information for ego and alter for the same characteristics as the GSS (race, religion, age, education and gender) but the relation is based on discussing politics; specifically people who the respondent talked with about government or elections. Each respondent was allowed to name up to 3 alters. We use this data to walk through steps 2–4 of the approach, estimating the initial homophily coefficients, estimating the probability of interaction between respondents, and estimating the regression while controlling for the imputed alters. The main data and variables of interest are the same as in the main analysis, based on the 2016 ANES; the only difference is that the input homophily coefficients are estimated from the 2008 ANES, rather than the GSS. The results are reported in the appendix, Table A2.

Overall, the results are almost identical to the results based on the GSS. The autocorrelation term is of a similar magnitude and the estimates for the demographic variables (race, gender, etc.) are very close. For example, looking at the Democrat Scale models, the coefficient for age in the main results is .389, while it is .391 in this supplementary analysis (using the 2008 ANES to estimate the initial homophily coefficients). This would suggest that individuals tend to discuss politics with people with similar characteristics as their own. The rate of homophily for discussing politics is similar (enough) to that found in the GSS data that the imputed alters end up being very similar and the results approximate each other. The choice of ego network data is thus not consequential, at least in this case.

This does not mean that the GSS ego network data will always be appropriate. A researcher studying another country, for example, would not be able to use the homophily coefficients estimated from the GSS. They would first have to find appropriate ego network data (step 1) for their population; they then would have to estimate the homophily coefficients (step 2), using the context-specific coefficients to impute the alters and estimate the spatial model (steps 3 and 4). The approach is thus general, but a researcher should seriously consider the proper data and inputs, and may not necessarily be able to skip steps 1–2.

We offer one final validity check. Here, we compare our results to a case where the alter attributes are known and can be used directly in the model. This offers a strong test, as we can ask if the imputed alter attributes mimic the effects of the true alter attributes. We again utilize the 2008 ANES. The 2008 ANES asked each respondent about their political discussion alters. Along with demographic characteristics (education, age, etc.), respondents were asked to report on the political ideology of each alter (ranging from 1-Strong Republican to 7-Strong Democrat). They were also asked an analogous question about themselves. This makes it possible to predict political ideology (of the respondent) as a function of the political ideology of their actual network alters. This serves as the true model. We then compare the true model to our imputed network model, where we assume no network information is available and must impute the network context. The results are reported in Table A3 in the appendix. Each model uses political ideology as the outcome of interest. Model 1 is the baseline model, with only demographic controls. Model 2 includes a variable for the true mean political ideology of the named alters. Model 3 is the same as Model 2 but uses the imputed alters, based on the approach outlined in this paper.

Overall, the results are consistent with the main findings reported above (see Table 2). If we compare Model 1 to Model 2, we can see that the coefficients for the demographic characteristics, like education and religion, are considerably reduced once we control for the true political environment surrounding the respondent, consistent with the general premise of the paper. The results are similar, but weaker, in Model 3, which uses the imputed alter attributes. For example, the female coefficient is reduced from −.508 to −.291 when we control for the true alter political ideology; the analogous coefficient is −.395 when we use the imputed values. Thus, controlling for the imputed network reduces the effect of gender on political ideology; the gender coefficient is not reduced as much, however, as in the true model. We see similar kinds of results for education, race and religion. This would suggest that the proposed model is doing exactly what we expect, approximating the respondent’s network in a reasonable, albeit imperfect, way. The effect is ultimately weaker than the true effect because of the measurement error in imputing the network attributes. The imputed model thus offers a conservative estimate on the effect of network context, and should be interpreted in that light.

Discussion

The approach presented here offers a unique take on the typical regression models in the social sciences. We develop a method for imputing ego network features where no network data are available. The method captures the exposure of sampled respondents to the attitudes, values, beliefs, etc. of their (imputed) confidants, with no recourse to the actual network data. In that way, any dataset could become a network one, making it possible to control for contagion effects in traditional regression models. We applied the approach to the 2016 ANES, predicting political attitudes as a function of demographic characteristics and imputed network features, which capture the likely attitudes of the respondents’ close confidants. We find that the imputed network features have important effects, reducing the coefficients on traditional variables, like age and education. Individuals who are likely to have conservative network alters (for example) are also likely to espouse conservative ideals; controlling for this tendency decreases the estimated coefficients of age, race, etc. in models of political ideology. In some cases, the coefficient becomes insignificant once we control for the imputed network features.

The model is based on a number of assumptions (discussed above); some we were able to formally consider, while other remain as outstanding questions. Assuming for the moment that our results are correct, there are two avenues for framing the implications of our method. First, one can argue that social context simply intervenes between our dependent variables and the institutional forces at the system level, such as education, occupation, age, and so forth. In this view, we have captured a more proximate mechanism in which the macrosocial forces at the societal level play out locally in Blau space. In essence, we are able to specify an intervening variable between the standard status attainment background characteristics and outcomes (Blau and Duncan 1967), even without network data available. A more radical interpretation is possible.

The alternative idea is that our very conception of exogenous variables is flawed; that variables like age or education should be recast in spatial terms (McPherson 2004). In this way, demographic characteristics are seen less as the properties of individuals, and more as social contexts, acting as loci for socially defined and transmitted information. We would thus move to a spatial, relational view of our core demographic variables (Smith 2017) — a view that is consistent with much sociological theory (e.g., Bourdieu’s (1972) version of habitus) but is at odds with how demographic variables are typically used in practice.

Different disciplines and sub-disciplines will react differently to the proposed model. The economist will see it as an attack on their (increasingly untenable) atomistic neoclassical model, the statistician will see it as an especially simple ERGM (exponential random graph model) model (Handcock et al 2008), the quantitative methodologist will see a model of socially fixed effects (Greene 2003) or a propensity score model (Rosenbaum and Rubin 1983), and the political scientist a new survey variable to control for in the pursuit of explaining voting patterns. The social network analyst will view it as a simple generalization of well-known properties of networks to the aggregate level of analysis. The fact that the model allows the construction of the social context variable for any survey that contains socio-demographic variables should make it a useful tool for scholars looking to reexamine core findings in survey analysis. It remains to be seen whether the model will stand up under the kind of scrutiny that we hope it gets from the disciplines.