Abstract
Urban Large-scale Public Spaces (ULPS) are important areas of urban culture and economic development, which are also places of the potential safety hazard. ULPS safety assessment has played a crucial role in the theory and practice of urban sustainable development. The primary objective of this study is to explore the interaction between ULPS safety risk and its influencing factors. In the first stage, an index sensitivity analysis method was applied to calculate and identify the safety risk assessment index system. Next, a Delphi method and information entropy method were also applied to collect and calculate the weight of risk assessment indicators. In the second stage, a Dempster-Shafer Theory (DST) method with evidence fusion technique was utilized to analyze the interaction between the ULPS safety risk level and the multiple-index variables, measured by four observed performance indicators, i.e., environmental factor, human factor, equipment factor, and management factor. Finally, an empirical study of DST approach for ULPS safety performance analysis was presented.
Keywords: traffic safety, risk assessment, Dempster-Shafer theory, normal cloud model, index system, large-scale public spaces
1. Introduction
Urban Large-scale Public Spaces (ULPS) are important carriers of urban culture and economic development, which are also an indispensable part of the cultural and economic life of the citizens. With the continuous increase of urban population and the higher frequency of social interaction, a variety of large-scale activities have promoted the construction of ULPS (e.g., theaters, stadiums, railway stations, subway stations, commercial streets, and supermarkets, etc.). According to the rough statistics in the ULPS all over the world from 2000 to 2018 shown in Table 1 [1], many kinds of risk incidents such as fire accidents and trampling incidents often occur. Therefore, the risk assessment issue in large-scale public spaces has become a hot topic at present [2].
Table 1.
Statistical results of casualty incidents in the Urban Large-scale Public Spaces (ULPS) across the world (2000–2018) [1].
| Time | Place | Type | Death | Injury | Reason |
|---|---|---|---|---|---|
| 9 March 2000 | Jiaozuo, China | Theatre | 74 | / | Fire |
| 25 March 2000 | Durban, South Africa | Ballroom | 13 | 150 | Fire |
| 9 May 2001 | Ghana | Stadium | 100 | / | Crowd |
| 3 September 2001 | Shaanxi, China | Yuquan Park | 16 | 6 | Crowd |
| 20 February 2002 | Egypt | Train | 350 | / | Fire |
| 19 February 2003 | South Korea | Train | 120 | 387 | Arson |
| 5 February 2004 | Beijing, China | Lantern Show | 37 | 15 | Crowd |
| 11 March 2004 | Spain | Station | 200 | 1800 | Terrorist Attack |
| 1 September 2004 | Russia | School | 300 | / | Terrorist Attack |
| 10 June 2005 | Shantou, China | Hotel | 31 | 15 | Fire |
| 7 July 2005 | London, UK | Metro | 52 | 700 | Terrorist Attack |
| 12 September 2006 | Yemen | / | 51 | 200 | Crowd |
| 18 July 2007 | Jinan, China | / | 25 | 170 | Rainstorm |
| 3 August 2008 | India | Temple | 162 | 47 | Crowd |
| 5 July 2009 | Urumqi, China | / | 184 | 939 | Terrorist Attack |
| 15 November 2010 | Shanghai, China | Apartment | 85 | 71 | Fire |
| 15 January 2011 | India | Temple | 102 | 100 | Crowd |
| 18 March 2012 | Egypt | Gathering | 3 | 137 | Crowd |
| 28 October 2013 | Beijing, China | Square | 5 | 40 | Terrorist Attack |
| 1 March 2014 | Kunming, China | Train Station | 29 | 143 | Terrorist Attack |
| 13 November 2015 | France | Stadium | 197 | / | Terrorist Attack |
| 21 May 2016 | Dalian, China | Market | 3 | / | Fire |
| 25 May 2017 | Henan, China | Senior Apartment | 39 | 6 | Fire |
| 14 May 2018 | Bengal | Ramadan Rally | 10 | 50 | Crowd |
| 25 August 2018 | Harbin, China | Hotel | 20 | 23 | Fire |
| 9 September 2018 | Luanda | Stadium | 5 | 7 | Crowd |
| 17 March 2019 | Northern Ireland. | Hotel | 3 | / | Human Crush |
| 26 June 2019 | Madagascar | Stadium | 16 | 101 | Human Crush |
Urban large-scale public spaces safety assessment has played a crucial role in the theory and practice of urban sustainable development. It is necessary to identify potential safety hazards in large-scale public spaces, so that relevant management departments would take measures to avoid risks promptly. It is of great significance to carry out research on safety risk assessment in ULPS, as follows: (1) to evaluate the current situation of ULPS and promote the construction of safety guarantee system; (2) to prevent the occurrence of various risk events and carry out active safety control; and (3) to promote the spread of risk knowledge in ULPS, and raise public awareness of risks. In addition, it also has important theoretical value and social significance for promoting the development of urban disaster prevention and mitigation.
Due to ULPS’s own architectural structure, spatial layout, personnel and wealth distribution, ULPS are vulnerable to various internal and external risks, such as fire, flood, explosion, and crowding. A large number of facts [1,2] have proved that, although the ULPS have a low probability of occurrence, it will inevitably cause irreparable casualties or property losses in the event of accidents. Hence, it is very helpful to identify and evaluate the possible risks in ULPS, which will not only help to assess the current situation of large-scale public places and promote the construction of safety guarantee system, but also prevent the occurrence of various risky incidents and carry out active safety regulation, and improve the level of information about risk knowledge of large-scale public spaces and enhance public awareness of risks.
Unfortunately, at present, although urban managers attach great importance to the safety risk assessment of ULPS, there are many shortcomings in the current research, such as risk assessment index system, advanced and feasible assessment methods. On the one hand, ULPS are important areas of urban culture and economic development, which are characterized by high-density gathering, high mobility, and high concentration, potential safety risks are associated with operations and production activities in large public spaces. On the other hand, the safety risk assessment of ULPS is a complex process involving multiple factors, multiple indicators, and uncertainties, many indicators are often difficult to accurately quantify and compare the risk analysis.
To fill this gap, we have divided the whole evacuation process for a ULPS into two periods. For the first period, we proposed a two-level risk assessment index system for the ULPS, which is calculated and identified by an index sensitivity analysis method; and next, a Delphi method and information entropy method were also applied to collect and calculate the weight of risk assessment indicators. For the second period, we have employed a Dempster-Shafer Theory (DST) method to integrate multi-source uncertainty information and apply this method to the security risk assessment of large-scale public spaces, which also helps calculate joint information from the sets of mass sources and conduct evidence fusion for all levels of risk indicators.
This research makes the following two contributions. Firstly, a scientific and practical risk assessment indicator system (RAIS) for ULPS was proposed, which includes four first-level indicators and 20 second-level indicators. Secondly, a Dempster-Shafer Theory (DST) with evidence fusion technique was employed to analyze the interaction between the RAIS and risk level in the ULPS. Conclusively, an empirical study of DST approach for ULPS safety performance analysis was verified and presented.
The remainder of this paper is organized as follows. Section 2 reviews the existing studies on risk analysis method and visualization of risk analysis. Section 3 introduces the Dempster-Shafer theory, identifies the risk assessment index system and determines the weight of risk assessment indicators. Section 4 describes a numerical example and presents the risk assessment results. Section 5 discusses the results obtained from the model. Section 6 draws the conclusions.
2. Related Studies
2.1. Risk and Risk Assessment Analysis
Risk analysis is related to the survival of humans and loss of property on ULPS, and during public place risk assessment, “risk” is associated with a number of factors or indicators [3], such as environmental factors, human factors, infrastructure factors, management factors and known as a public place safety outcome. In the field of urban large-scale public spaces safety, the “risk assessment” [4] is defined as identify and prevent any risk(s) associated with a decision and evaluating all possible outcomes and potential impacts of risk. In general, there are three steps for risk assessment analysis [5]. First, the risk influencing factors are analyzed; second, a reasonable and scientific risk assessment index system is established; third, a scientific risk assessment method is selected to form a comprehensive evaluation process based on the above two steps. It is the capacity to see problems as they arise, deal with them and try to prevent them from happening again.
There are a number of different risk analysis methods for researchers to choose from [6,7,8]. At present, they can be divided into three categories, i.e., qualitative risk assessment methods, semi-quantitative risk assessment methods, and quantitative risk assessment methods. For the qualitative risk assessment methods [9,10,11], which are easy to operate, the evaluation process and results are simple to express, such as (a) questionnaire survey method; (b) collective discussion method; (c) expert investigation method; (d) safety checklist method; and (e) risk assessment matrix (RAM). However, these methods rely more on the experience of the evaluators and lack depth in describing the risk of the system. The evaluation results of different types of evaluation objects are not comparable. Meanwhile, they have strict requirements on the professionalism of the personnel involved in the risk assessment.
For the semi-quantitative risk assessment methods, such as (a) fault tree analysis [12,13,14]; (b) event tree analysis [15]; (c) preliminary hazard analysis [16,17]; (d) failure mode and effect analysis [18,19]; and (e) index evaluation method [20,21], they are easy to implement and have stronger objectivity than qualitative analysis, but need a lot of preparatory work. For example, these methods can be used to evaluate the probability of accidents and risk analysis, but preparatory work such as (a) estimating the exposure time of people in a dangerous environment, (b) evaluating the severity of accidents, (c) determining the corresponding scores of different factors, and (d) drawing the evaluation conclusions, are needed to be prepared in advance.
As for the quantitative risk assessment methods, they can reflect the risk levels by mathematical calculation, such as (a) fuzzy comprehensive evaluation method [13]; (b) factor analysis [22,23]; (c) analytic hierarchy process [24]; (d) cluster analysis [25,26]; (e) regression analysis [27,28,29]; (f) Bayesian analysis [30,31,32]; (g) logit model [33,34,35]; (h) time series analysis method [36,37]; and (i) Dempster-Shafer theory [38,39]. These methods have an objective and direct evaluation through the observed parameters, so as to find out the dangerous and harmful factors in the evaluation system, and then put forward the corresponding solutions in technology and management to realize safety management.
2.2. DST and Applications
Dempster-Shafer theory (DST) is a general framework for reasoning with uncertainty by Dempster [38] in 1967, and the theory was later developed by Shafer [39] into a general framework for modelling epistemic uncertainty. Previously, risk assessment of ULPS has many characteristics such as multiple indicators and multiple knowledge areas, meanwhile, the risk assessment process has a lot of uncertainties and is difficult to strictly quantify. Fortunately, DST provides an opportunity to combine multiple evidence sources. This is because DST is an established technique that maintains a mechanism of multiple indicators inputs and integrated outputs for the evaluation of risk analysis.
DST is a technique that can handle all the available evidence from different sources and arrive at a degree of belief (represented by a mathematical object called belief function) [40,41,42,43]. Previously, DST is mainly used in artificial intelligence, pattern recognition, data fusion technology, expert system and decision analysis, and its application in risk assessment has gradually increased in recent years. For example, Sun et al. developed an alternative methodology for the risk analysis of information systems security under the DST of belief functions. Zeng et al. [44] proposed a technique for traffic incident detection, which combined multiple multi-class probability support vector machines using DST approach. Rassafi et al. [45] employed an DST approach for road safety assessment modelling as a complex multi attribute decision analysis problem to deal with unavoidable uncertainties such as ignorance and vagueness. Through the application of DST, we can analyse the multiple-index variables related to safety situations in urban large-scale public spaces. Analysis of risk level with reference to risk assessment indicators will be helpful in understanding safety performance of ULPSs.
2.3. Visualization of Risk Analysis Studies
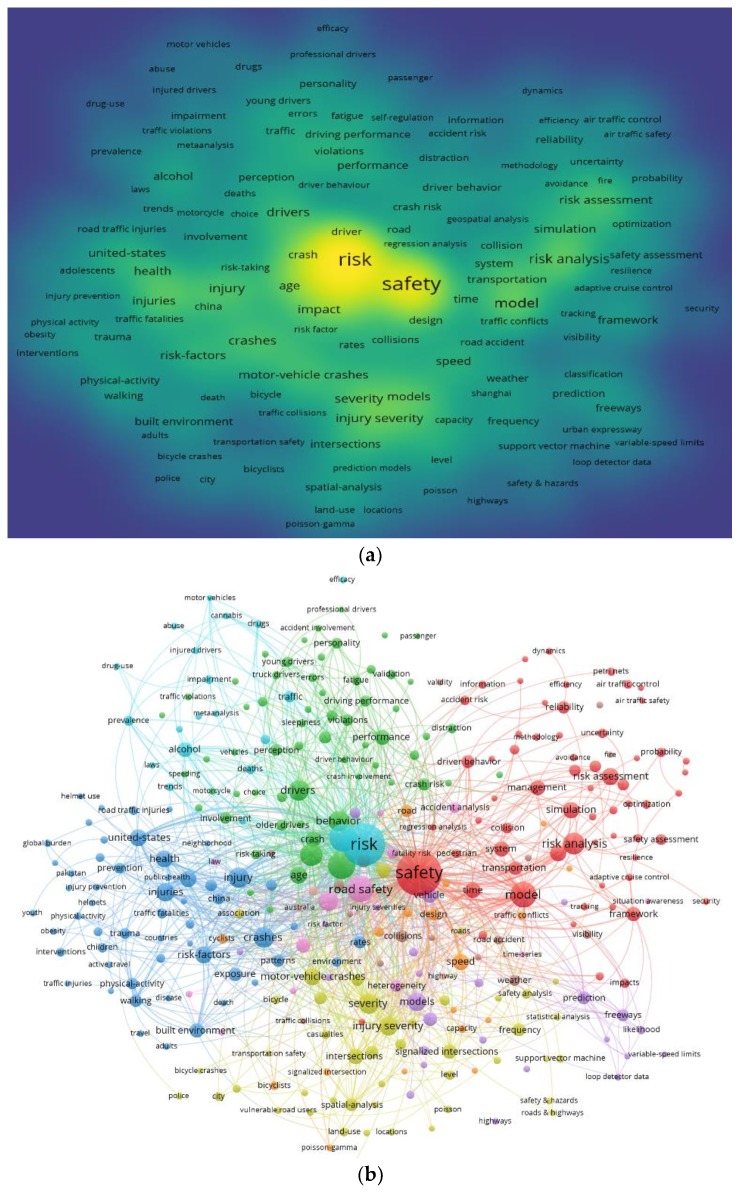
From the web of science database, 1997–2019, we have searched the main research countries, authors, and research institutions in risk analysis studies, our search topics are “traffic safety” and “risk analysis”, and we found that there were a total of 1400 + records, the number of authors was 4515, the number of research institutions was 1488, and the number of countries was 91. Next, the visualization of keywords in risk analysis studies, 1997–2019, were created by VOSviewer software [46], as shown in Figure 1.
Figure 1.
The keywords in risk assessment studies, 1997–2019. (a) The density of main research keywords; (b) the keywords co-occurrence network of risk analysis studies.
The keywords are an important part of a research paper, which carries important information about the fields of interests. A total of 5000+ keywords appeared in all the collected literature on traffic safety and risk analysis, see Figure 1. Figure 1a is the density of main research keywords and Figure 1b is the keywords co-occurrence network of risk analysis studies. It can be clearly seen that the research theme of risk assessment has roughly formed four clusters in Figure 1b, and there is a significant correlation between the keywords in each cluster.
The visualization of keywords in risk analysis studies indicates that previous studies [8,13,16,19,20,25,26] that focused on risk assessment in ULPS were undertaken at an aggregate level. Systematization is the key requirement in safety risk assessment. However, systematization firstly means the evaluation system is systematic, which reflects the performance of specific models; secondly, the evaluation system should comprehensively cover both qualitative and quantitative indicators. Most ULPS safety risk studies [8,13,16,19,20,25,26] rely on questionnaire survey data but do not provide much information about the index system of risk assessment. In addition, little is known about the underlying factors that affect the risk analysis of ULPS. Furthermore, there is a paucity of research discerning the interrelationships between the multiple-index system and risk assessment, and the contributory indicators and multiple-index weight at a disaggregated level using Delphi method and entropy method.
3. Method
3.1. Dempster-Shafer Theory (DST)
3.1.1. Framework of Discernment (FoD)
DST is a finite nonempty set of hypotheses as the frame of discernment (FoD) . Let be the universe: the set representing all possible states of a system under consideration. The power set is the set of all subsets of , including the empty set . For example, if , then .
The elements of the power set can be taken to represent propositions concerning the actual state of the system, by containing all and only the states in which the proposition is true.
3.1.2. Basic Belief Assignment (BBA)
The theory of evidence assigns a belief mass to each element of the power set. Formally, a function is called a basic belief assignment (BBA), which has two properties. First, the mass of the empty set is zero.
| (1) |
Second, the masses of the remaining members of the power set add up to a total of 1.
| (2) |
The mass m(A) of A, a given member of the power set, expresses the proportion of all relevant and available evidence that supports the claim that the actual state belongs to A but to no particular subset of A. The value of m(A) pertains only to the set A and makes no additional claims about any subsets of A, each of which have, by definition, their own mass.
From the mass assignments, the upper and lower bounds of a probability interval can be defined. This interval contains the precise probability of a set of interest (in the classical sense), and is bounded by two non-additive continuous measures called belief (or support) and plausibility.
The belief bel(A) for a set A is defined as the sum of all the masses of subsets of the set of interest.
| (3) |
The plausibility pl(A) is the sum of all the masses of the sets B that intersect the set of interest A.
| (4) |
The two measures are related to each other as follows.
| (5) |
And conversely, for finite A, given the belief measure bel(B) for all subsets B of A, we can find the masses m(A) with the following inverse function.
| (6) |
where |A−B| is the difference of the cardinalities of the two sets.
3.1.3. Dempster’s Combination Rule
Generally, the detailed combination rule is to calculate the distance between the two sets of masses mi and mj, and then modify the obtained mass function by the calibration coefficient. Finally, the combination rule is used for evidence fusion in the following manner.
Step1: The is a finite nonempty set of hypotheses as the FoD, the masses mi and mj are the base degrees of belief (or confidence, or trust) for the frame of discernment , the distance between the two sets of masses mi and mj is calculated by Equation (7).
| (7) |
where D is a matrix of 2N×2N, the element in the matrix is, D(Ai, Aj)=(|Ai ∩ Aj|)/(|Ai ∪ Aj|), i = 1, 2, … , 2N, and dij indicates the difference between the two sets of masses, dij∈[0,1].
The similarity between the sets of masses mi and mj is Sij, as shown in Equation (8).
| (8) |
The MASS function is compared in pairs, and the distance between the evidences is calculated to obtain the evidence similarity matrix Sim.
| (9) |
The degree to which evidence is supported by other evidence is described as Sup().
| (10) |
The credibility of the evidence is .
| (11) |
Due to the large number of professional fields covered by safety risk assessment in ULPS, experts in various fields have strong professional knowledge background and authority. In order to make the evaluation results more accurate, comprehensive consideration of each expert’s professional background and other factors, we give each expert the same weight [33,34] for the RAIS, the sum of weights is . From this, the credibility of expert i is .
| (12) |
Step 2: According to the credibility of the evidence and the credibility of the experts, the calibration coefficient of the evidence is obtained.
| (13) |
Supposing , it means that the credibility of evidence and the credibility of experts are of equal importance.
According to the calibration of coefficient , we adjust the MASS function of the indicator shown in Equations (14) and (15).
| (14) |
| (15) |
After modification by Equations (14) and (15), a new MASS function is obtained, then the Dempster’s rule of combination is used to merge the m experts’ comments on the second-level index , and the new MASS function is also obtained corresponding to each second-level index .
Step3: Dempster’s orthogonal rule of combination is determined by Equations (16) and (17).
| (16) |
| (17) |
where K is a measure of the amount of conflict between the two mass sets, if K = 0, it means that all evidence is completely contradictory, and the Dempster’s combination rule cannot be applied; Conversely, if K≠0, then the fusion of a set of evidence becomes the orthogonal sum, m is new evidence produced by the combination, and it also is a MASS function too. Note that , which represents the combination of , , and , carries the joint information from the sets of masses sources.
According to the principle of maximum membership degree, the MASS function of the second-level indicator and its weight are linearly weighted, and the risk level of the first-level indicator can be obtained, see Equation (18).
| (18) |
Similarly, the MASS function corresponding to each level indicator can be obtained, and the risk evaluation level of the large-scale public space is determined.
3.2. Risk Assessment Index System (RAIS)
3.2.1. Preliminary RAIS
The safety of the urban large-scale public spaces will be affected by various factors during the operation, especially when the high-density pedestrian flow is gathering. RAIS has played a crucial role in the risk assessment of ULPS’s development, while the scientific knowledge and comprehensiveness of index system will directly affect the accuracy of safety risk assessment in the ULPS. The principles [20,21] for selecting the preliminary RAIS in ULPS are as follows,
(1) Principle of scientific
All indicators in the RAIS can objectively reflect the risk factors faced by ULPS. The division of indicators has the basis of scientific theory for reference and can truly reflect the characteristics of security risks in ULPS.
(2) Principle of comprehensiveness
All indicators in the RAIS can comprehensively reflect the specific situation of security risks in ULPS. The selection of the preliminary risk indicators in ULPS not only includes the internal and external risk factors of the buildings, but also includes the surrounding environment, transportation facilities, system management, and other factors. Generally speaking, the selection of RAIS covers all factors affecting the security of ULPS.
(3) Principle of accuracy
All indicators in the RAIS are interrelated and independent, so as to ensure that the same type of evaluation indicators is not repeated, and indicators that have weak influence on security risks in ULPS should be eliminated to avoid statistical difficulties, calculation redundancy and credibility reduction.
(4) Principle of operability
All indicators in the RAIS need to be clear and easy to understand, and easy to conduct questionnaires or data collection. Principle of operability is to ensure the authenticity, effectiveness and operability of the risk assessment.
At the same time, based on the above principles and previous literatures [13,16,19,20,21,22,23,25,26,27,43,44,45], this study built a risk assessment index system including 4 first-level indicators, i.e., environmental factors, human factors, infrastructure factors and management factors, and 31 second-level indicators, as shown in Table 2.
Table 2.
Preliminary risk assessment index system.
| First-Level Indicators | Second-Level Indicators | Explanations |
|---|---|---|
| Environmental factors (A1) | Architectural layout (B11) | These indicators reflect the relationship between various environmental factors and safety risks in UPLS, and reflect the impact of random factors on safety risk assessment. |
| Weather (B12) | ||
| External traffic (B13) | ||
| Internal traffic (B14) | ||
| Public health (B15) | ||
| Social stability (B16) | ||
| Human factors (A2) | Crowd characteristics (B21) | These indicators reflect the relationship between human factors and risk level in UPLS, and reflect the impact of human factors on risk assessment level of UPLS. |
| Negligence behavior (B22) | ||
| Macroscopic fundamental diagram (B23) | ||
| Age and gender (B24) | ||
| Safety awareness (B25) | ||
| Physical fitness (B26) | ||
| Panic (B27) | ||
| Trip purpose (B28) | ||
| Infrastructure factors (A3) | Exit (B31) | These indicators reflect the relationship between infrastructure factors and risk level of UPLS, and reflect the impact of static factors on risk assessment level of UPLS. |
| Guide sign (B32) | ||
| Power system (B33) | ||
| Lighting system (B34) | ||
| Fume exhaust system (B35) | ||
| Drainage system (B36) | ||
| Alarm system (B37) | ||
| Firefighting system (B38) | ||
| Broadcasting and monitoring system (B39) | ||
| Management factors (A4) | Personnel training (B41) | These indicators reflect the relationship between the management mechanism of public places and risk level of public places, and reflect the impact of dynamic factors on risk assessment level of UPLS. |
| Public health management (B42) | ||
| Security risk management (B43) | ||
| Event organization and management (B44) | ||
| Fire safety management (B45) | ||
| Emergency evacuation management (B46) | ||
| Store management (B47) | ||
| Infrastructure management (B48) |
3.2.2. Sensitivity Analysis of Indicators
The risk assessment indicators established in the initial stage covered too much information, which not only caused the information redundancy but also increased the difficulty of risk assessment and reduced the accuracy of the evaluation results. Therefore, the indicators should be screened.
The Delphi method was used to analyze the sensitivity of evaluation indicators. In the process of sensitivity analysis, we take the factors that have a greater impact on the risk assessment as the sensitivity index, our purpose is to find the sensitive indicators and delete the non-sensitive indicators.
Let as the ith indicator of the degree of acceptance in the expert group , let as the ith indicator of the total average degree of acceptance in the expert group . The formula is as follows:
| (19) |
| (20) |
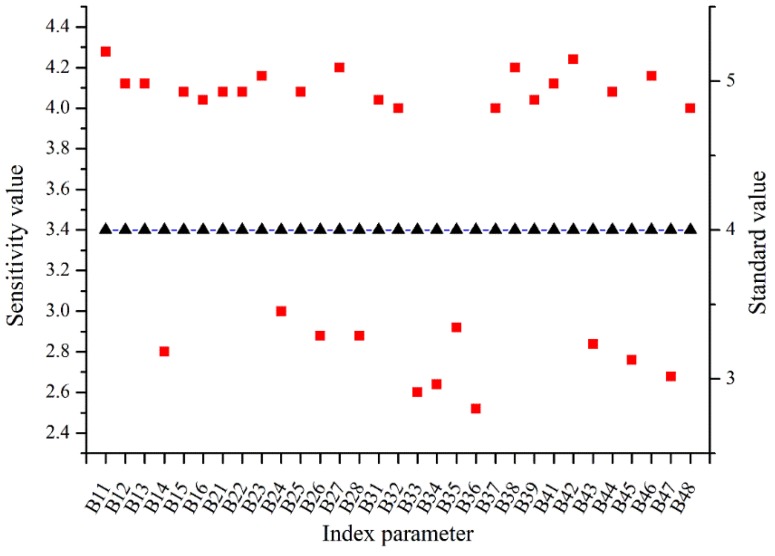
where is the number of experts who are considered to be -level in the expert group ; is the corresponding value of the -level importance of a certain indicator. The importance of indicators is divided into five levels: very unimportant (E1 = 1), unimportant (E2 = 2), generally important (E3 = 3), important (E4 = 4), very important (E5 = 5). Through the calculations of Equations (19) and (20), the total average acceptance of each indicator in all expert groups is calculated. The result of the sensitivity analysis is shown in Figure 2.
Figure 2.
Result of sensitivity analysis of indicators.
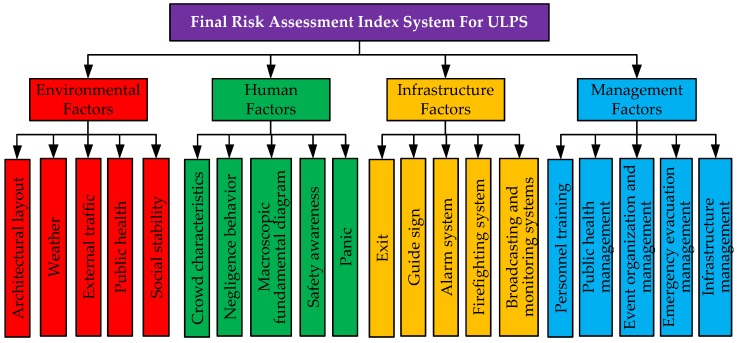
After removing the indicator with the value less than 4.0, the final 20 indicators are obtained, as shown in Figure 3.
Figure 3.
Result of the final risk assessment index system for Urban Large-scale Public Spaces (ULPS).
3.3. Determination of the Weight of Risk Assessment Indicators
In the process of risk assessment, the importance of various indicators in the evaluation system is different. Hence, it is necessary to establish the corresponding weights of indicators for ULPS. The entropy weight method is used to calculate the index weights, that is, firstly, the Delphi method [20,21] is used to collect the weight information by experts; secondly, the value of the ranking matrix of expert evaluation is calculated; thirdly, the entropy value is calculated by the entropy decision process, and final weights of indicators are obtained by the entropy weight method [20,21,22,30].
3.3.1. Collection of Expert Opinions for RAIS
The weight information is collected using Delphi method by experts. It is assumed that m experts are invited to participate in the weight information survey of the safety risk assessment indicators in LSPS, the survey requires that the experts hired to sort the evaluation index sets according to their rich knowledge, professionalism and practical experience. Five indicates that the index is "most important" and four indicates "important", and the importance decreases in turn until 1, allowing experts to have the same value for multiple indicators. The ranking matrix obtained by m experts is set to R.
| (21) |
where is the evaluation value of the mth expert for the nth indicator.
3.3.2. Calculation of Indicator Weight
To determine the entropy value, the ranking matrix is first transformed into the membership matrix [20,21]. The membership function of ranking transformation is defined as
| (22) |
where
| (23) |
We define as membership function, as shown in Equation (24),
| (24) |
Then,
| (25) |
where G is the ranking value given by the experts, N is the index value after standardization conversion, and n is the number of indicators.
The ranking number of each index is brought into the Equation (25), and the sorting matrix M can be converted into the membership degree matrix , and is called the membership degree of the ranking number G. Taking the column vectors in the membership matrix M as , and the average value of the membership in the vector is obtained, as shown in Equation (26).
| (26) |
Therefore, the mean square deviation of the membership in the vector can be obtained.
| (27) |
The comprehensive evaluation value of each index by m experts is recorded as , as shown in Equation (28).
| (28) |
Thereby, the risk evaluation vector of index can be obtained.
We normalize the weights of indicators, as shown in Equation (29).
| (29) |
Let be the weight vector of risk assessment index system , , and . Each value in W corresponds to the weight of each grade of indicators, and the larger the value, the stronger the impact of the index on the safety risk assessment of large-scale public spaces.
4. Case Study
Tian-yi Square, the largest commercial plaza in Ningbo City, was completed by the end of 2001, the total investment of the project was 1.25 billion RMB. It has 167,000 square meters of shops, 20,000 square meters of parking lots, 64,000 square meters of green space, 6,000 square meters of water areas and 1,000 square meters of performing stage. In the case study, we take the Tian-yi Square, one of the biggest large-scale public spaces in Ningbo, as an example, the DST method is proposed to evaluate the safety risk of ULPS, in order to verify the practicability and effectiveness of the risk assessment method.
4.1. Data Collection
We developed an expert questionnaire based on the RAIS given above. Experts from various research fields such as traffic engineering, traffic safety, municipal engineering and risk management were invited to evaluate the risk assessment indicators. According to the collected data, scores of RAIS by experts as shown in Table 3.
Table 3.
Scores of Risk Assessment Index System (RAIS) by experts.
| Indicators | The importance Value of RAIS a | The level Value of RAIS b, d | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| E1 c | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | |
| Environmental factor | 2 | 3 | 4 | 2 | 3 | / | / | / | / | / |
| Human factor | 2 | 2 | 2 | 3 | 1 | / | / | / | / | / |
| Equipment factors | 3 | 2 | 3 | 1 | 3 | / | / | / | / | / |
| Management factors | 1 | 1 | 1 | 1 | 2 | / | / | / | / | / |
| Architectural layout | 5 | 4 | 2 | 3 | 5 | 8 | 6 | 7 | 9 | 7 |
| Weather | 2 | 2 | 3 | 2 | 4 | 9 | 9 | 8 | 9 | 10 |
| External traffic | 3 | 3 | 4 | 4 | 3 | 7 | 8 | 9 | 8 | 9 |
| Public health environment | 1 | 1 | 1 | 3 | 2 | 9 | 10 | 8 | 8 | 9 |
| Social stability | 4 | 5 | 5 | 5 | 4 | 10 | 9 | 10 | 10 | 9 |
| Crowd characteristic | 3 | 3 | 2 | 3 | 1 | 7 | 9 | 8 | 8 | 10 |
| Negligence behavior | 4 | 1 | 4 | 3 | 4 | 9 | 8 | 9 | 8 | 8 |
| Macroscopic fundamental diagram | 1 | 2 | 2 | 4 | 2 | 9 | 8 | 9 | 8 | 9 |
| Safety awareness | 5 | 5 | 4 | 5 | 4 | 7 | 6 | 7 | 6 | 8 |
| Panic | 2 | 4 | 5 | 2 | 5 | 8 | 9 | 7 | 7 | 8 |
| Exit | 2 | 1 | 1 | 2 | 1 | 9 | 7 | 8 | 7 | 9 |
| Guide sign | 5 | 3 | 2 | 4 | 2 | 5 | 6 | 5 | 6 | 4 |
| Alarm system | 3 | 3 | 4 | 3 | 3 | 5 | 5 | 5 | 6 | 6 |
| Firefighting system | 4 | 4 | 4 | 5 | 4 | 6 | 6 | 7 | 7 | 6 |
| Broadcasting monitoring system | 1 | 2 | 2 | 1 | 2 | 10 | 10 | 9 | 9 | 10 |
| Personnel training | 1 | 2 | 2 | 1 | 2 | 6 | 5 | 7 | 6 | 8 |
| Public health management | 4 | 2 | 1 | 2 | 3 | 8 | 9 | 8 | 8 | 7 |
| Infrastructure management | 3 | 4 | 4 | 4 | 5 | 9 | 6 | 7 | 8 | 7 |
| Event organization and management | 2 | 3 | 3 | 3 | 4 | 8 | 7 | 7 | 6 | 8 |
| Emergency evacuation management | 2 | 1 | 2 | 1 | 1 | 8 | 6 | 6 | 8 | 7 |
Note: a denotes the importance value of risk assessment index system (RAIS), which is from 1–5. b denotes the level value of risk assessment index system (RAIS), which is from 1–10. c means the Expert 1. d a five-level risk assessment standard is proposed by the standard [47,48], the description of which is excellent, good, satisfactory, fair and poor. Next, the use of 10-scores scale that defines criterion for the hazard, is generally preferable to quantitative analysis, which are excellent (8 ~ 10], good (6 ~ 8], satisfactory (4 ~ 6], fair (2 ~ 4] and poor (0 ~ 2].
4.2. Calculation of Index Weight for RAIS
Experts’ decision-making is an important part of index weight calculation and risk assessment for the ULPS. In order to reduce the influence of different experts on the evaluation results, firstly, the assumption is that we fully believe and respect the scoring results of the experts, secondly, we employ as many experts from different fields as possible to score together and take the average, according to their rich knowledge, professionalism and practical experience. In addition, in the actual calculation process, we remove a maximum score, while removing a minimum score, and then calculate the average of the remaining index scores. According to the scores of expert survey results (see Table 2), the ranking matrix of expert opinions can be obtained.
The ranking membership matrix M of each grade of indicators can be obtained by Equations (21)–(24).
The mean square deviation of the membership matrix M can be obtained by Equations (25) and (26).
; ;
;
Then, the evaluation vector of each grade of indicators is obtained by Equation (27).
;
;
Finally, the weight vector of each grade indicator is obtained by Equation (28).
;
;
Results of the weights of primary indicators and secondary indicators are calculated by Equations (21)–(28), as shown in Table 4.
Table 4.
Results of the weights of indicators in Tian-yi Square.
| First-Level Indicators | Weights | Second-Level Indicators | Weights |
|---|---|---|---|
| Environmental factor | 0.200 | Architectural layout | 0.155 |
| Weather | 0.231 | ||
| External traffic | 0.208 | ||
| Public health environment | 0.271 | ||
| Social stability | 0.135 | ||
| Human factor | 0.259 | Crowd characteristic | 0.252 |
| Negligence behavior | 0.201 | ||
| Macroscopic fundamental diagram | 0.246 | ||
| Safety awareness | 0.139 | ||
| Panic | 0.161 | ||
| Equipment factors | 0.230 | Exit | 0.254 |
| Guide sign | 0.160 | ||
| Alarm system | 0.193 | ||
| Firefighting system | 0.144 | ||
| Broadcasting monitoring system | 0.249 | ||
| Management factors | 0.311 | Personnel training | 0.238 |
| Public health management | 0.193 | ||
| Infrastructure management | 0.140 | ||
| Event organization and management | 0.186 | ||
| Emergency evacuation management | 0.243 |
4.3. Evidence fusion Process of Security Risk Assessment
The membership matrix of security risk level can be obtained by forward generator in Normal Cloud (NC) Model [49,50] from Table 2 and Table 3. In this study, the NC model was used to evaluation the membership matrix of security risk level. The steps to construct a NC model were as follows.
Setp 1: NC model: Let be a quantitative domain and a qualitative concept on . If a certain value , then x is a random implementation of . The determinacy of x to is a random number with a stable tendency :→[0,1], ∀ , x→. Then, the distribution of x on the domain is called a cloud, and each x is called a cloud droplet. Three parameters are used to characterize the cloud model, which are the expectation Ex, the entropy En, and the super-entropy He.
Setp 2: NC generator: If the definition of x in the cloud satisfies x ~ N(Ex, En’) and En’ ~ N(En, He2), the determinacy of x to satisfies the following.
| (30) |
The NC model is widely used in solving probabilistic and ambiguous problems, which combines the normal distribution function with the bell-shaped membership function. All the cloud models used in this study referred to the NC model. By definition, the quantitative data obtained from cloud digital eigenvalues were forward NC generators, while those obtained from the quantitative data were backward NC generators. In this study, the forward NC generator was used to solve the problem of risk level.
Setp 3: Cloud synthesis: The synthesis of clouds was to combine the clouds of the same nature with a parent cloud. The parent cloud C (Ex, En, He) was synthesized using n child clouds Cn (Exn, Enn, Hen), expressed as follows.
| (31) |
| (32) |
where “◦” refers to the process of cloud synthesis and wi to the weight of the ith child cloud.
The process of the NC model followed three steps:
Step 1: Determining the digital features of the cloud
Let X = (x1, x2, …, , …, xn-1) be the threshold vector of an index in which denotes the threshold of the index at jth R degree. As the synthetic clouds were conducted in the same domain, the index needed to be standardized before calculating the digital features. Using the bigger-is-better and the smaller-is-better rules, the standardizations were as shown in Equations (33) and (34), respectively.
Bigger is better,
| (33) |
Smaller is better,
| (34) |
where is the standardized value of , and max {} and min {} are the maximum and minimum values for the threshold j, respectively.
The R degree j (j = 1, 2, … , n-1) is indicated by NCs in the semi-rising and semi-descending states, leading to the three digital features in Equation (35). Then, the other grades are indicated by NCs in full states (see Equation (36)), and their corresponding digital features are calculated as follows.
| (35) |
| (36) |
Step 2: Establishing the template cloud model
Synthesizing all the indexes of child clouds under the R degree criterion in n grade results in the parent cloud, which is called the template cloud or standardized cloud and uses a standard cloud map to assess the crowd state in the metro station. For example, a certain facility has three indexes, and each of their child cloud is denoted as Rj, Sj, and Tj. Thus, the parent cloud Uj was synthesized as Uj = Rj ◦ Sj ◦ Tj (j = 1, 2, …, n), and can be referred from Equation (32).
Step 3: Establishing the candidate cloud model
(a). Establish a forward cloud generator CGXj, according to the digital features of the R degree.
(b). Standardize the actual values x collected by the index and marked as x*. Let the standardization results of index in x ≤ min {} be 0 and index in x ≥ min {} be 1.
(c) Input the standardized values x* into the forward NC generators, please find detailed information from Refs. [49,50].
(d) Output of the cloud generator, (j = 1, 2, …, n), represents the degree of x belonging to Xj. The fuzziness and randomness nature of the NC model indicates that, instead of a determined number, is a random number with a stable tendency. The membership matrix of security risk level is consisted of these for each .
After normalizing all , Equation (37) shows the weights for each .
| (37) |
The MASS function of various indicators are obtained with these weights . Take the secondary indicator “Architectural layout (B2)” factor as an example, as follows, the others are listed in Appendix A.
Then, after normalization, the MASS function of various indicators are obtained by normalized processing technology.
When obtaining expert evidence comments, due to the large differences in the research fields and work experience of experts, there may be great conflicts between their evidence comments.
Therefore, in order to solve the above problems and make the results of the evidence fusion more accurate, we use the distance function as in Equation (7) to measure the degree of conflict between pieces of evidence, and the calibration coefficients are used to revise the evidence comments from experts.
Next, the evidence similarity matrix Sim is obtained by Equations (7)–Equation (9).
And, the credibility vector of each expert evidence is obtained by Equations (10)∓(11).
The credibility vector of experts are then obtained by expert weights
The calibration coefficient of the evidence is obtained by Equation (13), and the MASS function of the indicators is revised by Equation (14), the revised MASS function is obtained.
Finally, the experts’ MASS function is merged by the D-S evidence fusion theory given in Equations (10)–(14), and the result is .
The secondary indicator MASS function is obtained by Equations (7)–(14), as shown in Table 5.
Table 5.
Results of Mass function of secondary indicators.
| Secondary Indicators | R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|---|
| Architectural layout | 0.002 | 0.998 | 0.000 | 0.000 | 0.000 | 0.000 |
| Weather | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| External traffic | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Public health environment | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Social stability | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Crowd characteristic | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Negligence behavior | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Macroscopic fundamental diagram | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Safety awareness | 0.000 | 0.999 | 0.001 | 0.000 | 0.000 | 0.000 |
| Panic | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Exit | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Guide sign | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| Alarm system | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| Firefighting system | 0.000 | 0.995 | 0.005 | 0.000 | 0.000 | 0.000 |
| Broadcasting monitoring system | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Personnel training | 0.000 | 0.577 | 0.423 | 0.000 | 0.000 | 0.000 |
| Public health management | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Infrastructure management | 0.002 | 0.998 | 0.000 | 0.000 | 0.000 | 0.000 |
| Event organization and management | 0.002 | 0.998 | 0.000 | 0.000 | 0.000 | 0.000 |
| Emergency evacuation management | 0.000 | 0.886 | 0.114 | 0.000 | 0.000 | 0.000 |
According to the weight of secondary indicator and the MASS function, which are linearly weighted by the Equation (17). The result of risk level value is,
By Equations (7)–(14), the results of the MASS function of the primary indicators is obtained by D-S evidence fusion, as shown in Table 6.
Table 6.
Results of Mass function of primary indicators.
| First-Level Indicators | R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|---|
| Environmental factors | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Human Factors | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Infrastructure factors | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| Management factor | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
According to the weight of primary indicator and the MASS function, which are linearly weighted by the Equation (17). The result of risk level value of Tian-yi Square is,
4.4. Outcome of the Risk Assessment
(1) The security risk level for the primary indicators can be obtained by the principle of maximum membership, as shown in Table 7.
Table 7.
Results of Mass function of First-level indicators.
| Primary Indicators | Excellent a,b | Good | Satisfactory | Fair | Poor |
|---|---|---|---|---|---|
| Environmental factors | 0.845 | 0.155 | 0.000 | 0.000 | 0.000 |
| Human factors | 0.861 | 0.139 | 0.000 | 0.000 | 0.000 |
| Infrastructure factors | 0.503 | 0.143 | 0.354 | 0.000 | 0.000 |
| Management factors | 0.194 | 0.678 | 0.128 | 0.000 | 0.000 |
Note: a The criterion for judging risk level come from Production Safety Law of the People’s Republic of China [47], Detailed rule for the management and control system of electricity enterperise work safety risk classification [47], and DoD standard which is approved for use by all Military Departments and Defense Agencies within the Department of Defense (DoD) [48]. b Following the standard [47,48], in our study, a five-level risk assessment standard is proposed, the description of which is excellent, good, satisfactory, fair and poor. Next, the use of 10-scores scale that defines criterion for the hazard, is generally preferable to quantitative analysis, which are excellent (8~10], good (6~8], satisfactory (4~6], fair (2~4] and poor (0~2].
In Table 7, for the environmental factors, the value of the excellent level is 0.845, and the value of the good level is 0.155. Overall, the risk assessment level of environmental factors is excellent. For the human factors, the value of the excellent level is 0.861, and the value of the good level is 0.139. Overall, the risk assessment level of human factors is excellent. For the infrastructure factors, the value of the excellent level is 0.503, and the value of the good level is 0.143. Overall, the risk assessment level of infrastructure factors is also excellent. For the management factor, the value of the excellent level is 0.194, and the value of the good level is 0.678. Overall, the risk assessment level of management factors is good.
(2) The overall security risk level result of Tian-yi Square is obtained by the principle of maximum membership, that is, the value of the excellent level is 0.459, the value of the good level is 0.311, and the value of the satisfactory level is 0.230. Therefore, the risk assessment level of Tian-yi Square is safety. The reason is that, Ningbo city, one of the three economic centers in Zhejiang province, is located in the southeast coastal area and belongs to the subtropical monsoon climate, at the same time, Tian-yi Square is one of the famous public places in Ningbo city, the surrounding environment is comfortable, the transportation is convenient, and society is harmonious. Hence, the overall safety risk assessment is excellent.
However, due to the early completion of Tian-yi Square, many facilities and equipment cannot be updated in time, and there are some defects in large-scale event management, store management, and staff training, so the evaluation level of infrastructure factors and management factors is only good, not excellent.
5. Discussions
(1) Enhance the relevance of RAIS
The original of the risk assessment indicator system (RAIS) fully considers the factors affecting the environment, human, infrastructure and management. However, in order to improve the pertinence and applicability of the RAIS, considering the gaps in risk factors faced by different cities and different public places, the sensitivity analysis method is used to measure the entire primary RAIS in the process of index preparation. Finally, all the indicators involved in risk assessment are valuable and applicable.
The risk indicators covered in the established primary RAIS are diversified and multi-faceted, but in the end, the indicators used in the risk assessment questionnaire are screened and representative. Therefore, it is very important to improve the accuracy of risk assessment indicator system and reduce the impact of the low sensitivity of indicators to the overall risk analysis.
(2) Universality of risk assessment methods
The Dempster-Shafer Theory is used to analyze risk assessment in urban large-scale public spaces, which can effectively integrate multiple evidence. Regardless of how many secondary indicators are set in the entire risk assessment indicator system or how many experts are employed to participate in the risk assessment, the Dempster-Shafer theory can be used to combine the expert opinions and the final risk assessment results for urban large-scale public spaces is obtained. Hence, the Dempster-Shafer theory for the risk assessment has universality.
(3) Division of evaluation level
The Delphi method was used by the experts to evaluate the risk and divide the risk assessment criteria into five levels according to the principle of equidistance: excellent (8 ~ 10), good (6 ~ 8), satisfactory (4 ~ 6), fair (2 ~ 4), and poor (0 ~ 2). It is different from the two-level evaluation method that divides the evaluation level into only "good and bad", and which is also different from the percentage system and the thousand-point system of the unlimited-level evaluation level. That is, reasonably dividing the evaluation level into five levels, the real feedback expert’s risk assessment for the urban large-scale public space is also conducive to the fusion of D-S evidence.
6. Conclusions
The main purpose of this work is to identify potential safety hazards in large-scale public spaces as early as possible, so that relevant management departments can promptly take measures to avoid risks. Taking Tian-yi Square in Ningbo as an example, this paper analyzes the scientific and feasible safety risk assessment index system from four aspects: environmental factors, human factors, infrastructure factors, and management factors. The risk assessment method using Dempster–Shafer theory is not limited to a single risk event, but also a comprehensive assessment method of the multiple risk factors faced by urban large-scale public spaces. The main results are described as follows.
-
(1)
A robust risk indicator system for assessing the security risk of large-scale public spaces were selected by Delphi method and information entropy method, which included four first-level indicators and twenty second-level indicators. The first-level indicators were environmental factors, human factors, infrastructure factors, and management factors. There was five second-level indicators belonging to the environmental factors, which were architectural layout, weather, external traffic, public health, and social stability; and there was also five second-level indicators belonging to the human factors, which were crowd characteristics, negligence behavior, macroscopic fundamental diagram, safety awareness, and panic. Meanwhile, there was five second-level indicators belonging to the infrastructure factors, which were exit, guide sign, alarm system, firefighting system, broadcasting and monitoring system; and there was also five second-level indicators belonging to the management factors, which were personnel training, public health management, event organization and management, emergency evacuation management, and infrastructure management.
-
(2)
Data were collected in Ningbo, using an expert questionnaire survey approach based on the RAIS. The survey results showed that the risk indicator system for the ULPS assessment process is scientific and reasonable. In the risk index system, twelve variables were found to be statistically significant, which were ranked by weights: emergency evacuation management, personnel training, crowd characteristic, macroscopic fundamental diagram, public health management, exit, event organization and management, broadcasting monitoring system, public health environment, negligence behavior, weather, alarm system, infrastructure management, panic, external traffic, guide sign, safety awareness, firefighting system, architectural layout, and social stability. In addition, in the calculation process of weights, we fully considered the expert’s knowledge background and opinions, and reduce the uncertainty in the assessment, which was characterized by strong explanatory and high precision.
-
(3)
A Dempster-Shafer Theory with evidence fusion technique was employed to analyze the interaction between the RAIS and risk level in the ULPS. The results from the DST approach indicated that three variables were found to be excellent level, which were ranked by importance: environmental factors, human factors, infrastructure factors. Only one variable was found to be good level, which were management factors. The results from the value of the MASS function indicated that three indicators were found in higher risk level, which were guiding signs, alarm system, and personnel training. Simultaneously, eleven indicators were found in a higher safety level, which were weather, external traffic, public health environment, social stability, crowd characteristic, negligence behavior, macroscopic fundamental diagram, panic, exit, broadcasting monitoring system, public health management. The findings of this study provided insight into the factors associated with environmental factors, human factors, infrastructure factors, and management factors in the ULPS.
In the risk assessment of large-scale public spaces, we used the DST approach to conduct a multi-level risk assessment, and the risk grading of each evaluation index was also obtained. Taking Tian-yi Square as a case study, the results were consistent with the actual operation of large-scale public spaces, indicating that the DST approach has certain theoretical guiding significance and practical value.
However, there are some limitations in this study. Firstly, the survey was only conducted in Ningbo city, but studies based on multiple cities could help better understand and capture more risk factors affecting large-scale public spaces. Secondly, an update questionnaire survey and risk assessment index system could be conducted to capture more meaningful factor with risk assessment work. We have to accept that there are other indicators in the risk assessment of large-scale public spaces, such as building characteristic index (e.g. building density, height, fire resistance, ventilation, etc.) in Environmental Factors (A1), temporary shelter, emergency shelter, basement shelter, and flame retardant equipment in Infrastructure Factors (A3), and evacuation training, safety education in Management Factors (A4). Hence, it will be encouraged to build a risk assessment indicators database for large-scale public spaces in the future study. Thirdly, risk management was defined as a procedure to control the level of risk and to mitigate its effect. Hence, the generally steps of risk management in the ULPS could be captured and described, such as risk identification, risk analysis, risk response and etc.
Furthermore, the extension of this work should examine the different expert weights and experience scores for the RAIS, especially for unobserved heterogeneity across more experts or staff or passengers or tourists. To solve this problem, in the future study, we will establish a historical database to quantify risk assessment indicators to reduce the impact of expert subjective factors on the assessment results. Recent work only provided the framework of discernment DST model [38,39,40,41,42,43,44]. Under this framework, risk assessment effects on environmental factors, human factors, infrastructure factors, and management factors across various passengers (or tourists) in the large-scale public spaces can be estimated, we are expecting more research results to emerge by standing upon the shoulders of ours.
Abbreviations
The following list of symbols is used in this research.
| Symbol | Explain |
| Frame of discernment | |
| m(A) | Basic probability assignment function |
| bel(A) | Belief function, which is based on the basic probability assignment in the FoD |
| pl(A) | Plausibility function, which is based on the basic probability assignment in the FoD |
| Distance between two evidences, mi and mj | |
| D | A matrix of 2N×2N |
| Sim | Similarity matrix of evidence |
| Calibration coefficient, which is used to correct the original matrix | |
| K | Normalized constant |
| F | Linear weighting of the mass function and weight of each indicator |
| k | Number of experts in each group |
| n | Number of expert groups hired to participate in the review |
| k | Number of experts in each group |
| n | Number of expert groups hired to participate in the review |
| G | Ranking value given by the experts |
| N | Index value after standardization conversion |
| Membership degree | |
| n | Number of indicators |
| Index weight coefficient | |
| Ex | Expectation, that is the central value of the spatial distribution of cloud droplets in the universe |
| En | Entropy, that is a measure of the ambiguity of a qualitative concept, reflecting the range of cloud drip values that can be accepted by the concept space |
| He | Super-entropy, that is a measure of the uncertainty of entropy, reflecting the degree of dispersion of the cloud droplets and the thickness of the cloud. |
| ◦ | Process of cloud synthesis |
| Weight of the child cloud |
Appendix A
Table A1.
Results of original matrix and normalization
| Indicators | Original Matrix | Normalized Matrix | Indicators | Original Matrix | Normalized Matrix | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | IV | III | II | I | V | IV | III | II | I | V | IV | III | II | I | V | IV | III | II | I | ||
| Architectural layout | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.980 | 0.020 | 0.000 | 0.000 | 0.000 | Weather | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 0.017 | 0.100 | 0.000 | 0.000 | 0.000 | 0.145 | 0.855 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.980 | 0.020 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 0.017 | 0.100 | 0.000 | 0.000 | 0.000 | 0.145 | 0.855 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| External traffic | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | Public health | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 |
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| Social stability | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | Crowd characteristics | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 |
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| Negligence behavior | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | Macroscopic fundamental diagram | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 |
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| Safety awareness | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | Panic | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| Exit | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | Guide sign | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | ||
| 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.018 | 0.019 | 0.000 | 0.000 | 0.000 | 0.493 | 0.507 | 0.000 | ||
| Alarm system | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | Firefighting system | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 |
| 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| Broadcasting and monitoring system | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | Personnel training | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 |
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| Public health management | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | Event organization and management | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 |
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
| Emergency evacuation management | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | Infrastructure management | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | ||
| 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | ||
Table A2.
Results of similar matrix and modified matrix
| Indicators | Similar Matrix | Modified Matrix | Indicators | Similar Matrix | Modified Matrix | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | IV | III | II | I | V | IV | III | II | I | Θ | V | IV | III | II | I | V | IV | III | II | I | Θ | ||
| Architectural layout | 1.000 | 0.151 | 0.036 | 1.000 | 0.036 | 0.865 | 0.017 | 0.000 | 0.000 | 0.000 | 0.118 | Weather | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.151 | 1.000 | 0.530 | 0.151 | 0.530 | 0.000 | 0.483 | 0.442 | 0.000 | 0.000 | 0.075 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 0.530 | 1.000 | 0.036 | 1.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 0.036 | 1.000 | 0.036 | 0.865 | 0.017 | 0.000 | 0.000 | 0.000 | 0.118 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 0.530 | 1.000 | 0.036 | 1.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| External traffic | 1.000 | 0.036 | 0.036 | 0.036 | 0.036 | 0.009 | 0.515 | 0.000 | 0.000 | 0.000 | 0.477 | Public health | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Social stability | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | Crowd characteristics | 1.000 | 0.036 | 0.036 | 0.036 | 0.036 | 0.009 | 0.515 | 0.000 | 0.000 | 0.000 | 0.477 |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.036 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Negligence behavior | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | Macroscopic fundamental diagram | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Safety awareness | 1.000 | 0.530 | 1.000 | 0.530 | 0.036 | 0.016 | 0.958 | 0.000 | 0.000 | 0.000 | 0.026 | Panic | 1.000 | 1.000 | 0.036 | 0.036 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.530 | 1.000 | 0.530 | 1.000 | 0.151 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 0.036 | 0.036 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 0.530 | 1.000 | 0.530 | 0.036 | 0.016 | 0.958 | 0.000 | 0.000 | 0.000 | 0.026 | 0.036 | 0.036 | 1.000 | 1.000 | 0.036 | 0.013 | 0.755 | 0.000 | 0.000 | 0.000 | 0.233 | ||
| 0.530 | 1.000 | 0.530 | 1.000 | 0.151 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | 0.036 | 0.036 | 1.000 | 1.000 | 0.036 | 0.013 | 0.755 | 0.000 | 0.000 | 0.000 | 0.233 | ||
| 0.036 | 0.151 | 0.036 | 0.151 | 1.000 | 0.573 | 0.011 | 0.000 | 0.000 | 0.000 | 0.416 | 1.000 | 1.000 | 0.036 | 0.036 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Exit | 1.000 | 0.036 | 1.000 | 0.036 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | Guide sign | 1.000 | 0.478 | 1.000 | 0.478 | 0.493 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| 0.036 | 1.000 | 0.036 | 1.000 | 0.036 | 0.013 | 0.755 | 0.000 | 0.000 | 0.000 | 0.233 | 0.478 | 1.000 | 0.478 | 1.000 | 0.485 | 0.000 | 0.521 | 0.477 | 0.000 | 0.000 | 0.002 | ||
| 1.000 | 0.036 | 1.000 | 0.036 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.478 | 1.000 | 0.478 | 0.493 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 1.000 | 0.036 | 1.000 | 0.036 | 0.013 | 0.755 | 0.000 | 0.000 | 0.000 | 0.233 | 0.478 | 1.000 | 0.478 | 1.000 | 0.485 | 0.000 | 0.521 | 0.477 | 0.000 | 0.000 | 0.002 | ||
| 1.000 | 0.036 | 1.000 | 0.036 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.493 | 0.485 | 0.493 | 0.485 | 1.000 | 0.000 | 0.000 | 0.444 | 0.456 | 0.000 | 0.100 | ||
| Alarm system | 1.000 | 1.000 | 1.000 | 0.478 | 0.478 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | Firefighting system | 1.000 | 1.000 | 0.530 | 0.530 | 1.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 |
| 1.000 | 1.000 | 1.000 | 0.478 | 0.478 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 0.530 | 0.530 | 1.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 1.000 | 0.478 | 0.478 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.530 | 0.530 | 1.000 | 1.000 | 0.530 | 0.015 | 0.908 | 0.000 | 0.000 | 0.000 | 0.077 | ||
| 0.478 | 0.478 | 0.478 | 1.000 | 1.000 | 0.000 | 0.476 | 0.435 | 0.000 | 0.000 | 0.088 | 0.530 | 0.530 | 1.000 | 1.000 | 0.530 | 0.015 | 0.908 | 0.000 | 0.000 | 0.000 | 0.077 | ||
| 0.478 | 0.478 | 0.478 | 1.000 | 1.000 | 0.000 | 0.476 | 0.435 | 0.000 | 0.000 | 0.088 | 1.000 | 1.000 | 0.530 | 0.530 | 1.000 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | ||
| Broadcasting and monitoring system | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | Personnel training | 1.000 | 0.478 | 0.530 | 1.000 | 0.151 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.478 | 1.000 | 0.008 | 0.478 | 0.009 | 0.000 | 0.000 | 0.725 | 0.000 | 0.000 | 0.275 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.530 | 0.008 | 1.000 | 0.530 | 0.036 | 0.012 | 0.743 | 0.000 | 0.000 | 0.000 | 0.244 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.478 | 0.530 | 1.000 | 0.151 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.151 | 0.009 | 0.036 | 0.151 | 1.000 | 0.569 | 0.011 | 0.000 | 0.000 | 0.000 | 0.420 | ||
| Public health management | 1.000 | 1.000 | 1.000 | 1.000 | 0.036 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | Event organization and management | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.865 | 0.017 | 0.000 | 0.000 | 0.000 | 0.119 |
| 1.000 | 1.000 | 1.000 | 1.000 | 0.036 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.000 | 0.483 | 0.442 | 0.000 | 0.000 | 0.075 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 0.036 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.017 | 0.995 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 0.036 | 0.981 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.018 | 0.000 | 0.000 | 0.865 | 0.017 | 0.000 | 0.000 | 0.000 | 0.119 | ||
| 0.036 | 0.036 | 0.036 | 0.036 | 1.000 | 0.009 | 0.515 | 0.000 | 0.000 | 0.000 | 0.477 | 1.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Emergency evacuation management | 1.000 | 0.036 | 0.036 | 0.151 | 1.000 | 0.865 | 0.017 | 0.000 | 0.000 | 0.000 | 0.119 | Infrastructure management | 1.000 | 0.151 | 0.151 | 1.000 | 0.036 | 0.848 | 0.017 | 0.000 | 0.000 | 0.000 | 0.135 |
| 0.036 | 1.000 | 1.000 | 0.530 | 0.036 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 0.151 | 1.000 | 1.000 | 0.151 | 0.530 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | ||
| 0.036 | 1.000 | 1.000 | 0.530 | 0.036 | 0.016 | 0.984 | 0.000 | 0.000 | 0.000 | 0.000 | 0.151 | 1.000 | 1.000 | 0.151 | 0.530 | 0.000 | 0.522 | 0.478 | 0.000 | 0.000 | 0.000 | ||
| 0.151 | 0.530 | 0.530 | 1.000 | 0.151 | 0.000 | 0.483 | 0.442 | 0.000 | 0.000 | 0.075 | 1.000 | 0.151 | 0.151 | 1.000 | 0.036 | 0.848 | 0.017 | 0.000 | 0.000 | 0.000 | 0.135 | ||
| 1.000 | 0.036 | 0.036 | 0.151 | 1.000 | 0.865 | 0.017 | 0.000 | 0.000 | 0.000 | 0.119 | 0.036 | 0.530 | 0.530 | 0.036 | 1.000 | 0.013 | 0.796 | 0.000 | 0.000 | 0.000 | 0.191 | ||
Author Contributions
Conceptualization, J.Z.; Data curation, J.Z. and Y.W.; Methodology, J.Z. and Y.W.; Resources, S.D. and M.Z.; Supervision, X.M. and J.Z.; Writing-review & editing, J.Z. and Y.W.; Funding acquisition, J.Z and X.M.
Funding
This study was supported by the Natural Science Foundation of Zhejiang Province (No. LQ19E080003; LY17E080013), Philosophy and Social Science Foundation of Zhejiang Province (No. 18NDJC107YB), Educational Science Planning of Zhejiang Provincial Education Department (No. 2018SCG103), Natural Science Foundation of Ningbo Municipality (No. 2018A610127), Humanities and Social Science Research Program of Ministry of Education in China (No. 16XJCZH002) and the Fundamental Research Funds for the Central Universities (Grant Number 310823170657 and 300102238501).
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- 1.Wikipedia List of Human Stampedes: World Crowd Disaster Map. [(accessed on 3 July 2019)]; Available online: https://en.wikipedia.org/wiki/List_of_human_stampedes.
- 2.Generic Risk Assessment Model for Indoor and Outdoor Space Spraying of Insecticides. Department of Control of Neglected Tropical Diseases; World Health Organization; Geneva, Switzerland: 2018. [Google Scholar]
- 3.Cornett M.M., Saunders A. Financial Institutions Management: A Risk Management Approach (8th Edition) McGraw-Hill Education; New York, NY, USA: 2013. [Google Scholar]
- 4.Mohaghegh Z., Kazemi R., Mosleh A. Incorporating organizational factors into probabilistic risk assessment (PRA) of complex socio-technical systems: a hybrid technique formalization. Reliab. Eng. Syst. Safe. 2009;94:1000–1018. doi: 10.1016/j.ress.2008.11.006. [DOI] [Google Scholar]
- 5.Parry G.W. The characterization of uncertainty in probabilistic risk assessments of complex systems. Reliab. Eng. Syst. Safe. 1996;54:119–126. doi: 10.1016/S0951-8320(96)00069-5. [DOI] [Google Scholar]
- 6.Chen F., Song M., Ma X. Investigation on the injury severity of drivers in rear-end collisions between cars using a random parameters bivariate ordered probit model. Int. J. Environ. Res. Public Health. 2019 doi: 10.3390/ijerph16142632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ma C., Hao W., Xiang W., Yan W. The impact of aggressive driving behavior on driver-injury severity at highway-rail grade crossings accidents. J. Adv. Transport. 2018 doi: 10.1155/2018/9841498. [DOI] [Google Scholar]
- 8.Guo Y., Li Z., Liu P., Wu Y. Modeling correlation and heterogeneity in crash rates by collision types using full Bayesian random parameters multivariate Tobit model. Accid. Anal. Prev. 2019;128:164–174. doi: 10.1016/j.aap.2019.04.013. [DOI] [PubMed] [Google Scholar]
- 9.Brener N.D., Collins J.L., Kann L., Warren C.W., Williams B.I. Reliability of the youth risk behavior survey questionnaire. Am. J. Epidemiol. 1995;141:575–580. doi: 10.1093/oxfordjournals.aje.a117473. [DOI] [PubMed] [Google Scholar]
- 10.Zou P., Zhang G., Wang J. Understanding the key risks in construction projects in China. Int. J. Proj. Manag. 2007;25:601–614. doi: 10.1016/j.ijproman.2007.03.001. [DOI] [Google Scholar]
- 11.Guo Y., Zhou J., Wu Y., Li Z. Identifying the factors affecting bike-sharing usage and degree of satisfaction in Ningbo, China. PloS one. 2017 doi: 10.1371/journal.pone.0185100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shalev D.M., Tiran J. Condition-based fault tree analysis (CBFTA): A new method for improved fault tree analysis (FTA), reliability and safety calculations. Reliab. Eng. Syst. Safe. 2007;92:1231–1241. [Google Scholar]
- 13.Yazdi M., Zarei E. Uncertainty handling in the safety risk analysis: an integrated approach based on fuzzy fault tree analysis. J. Fail. Anal. Pre. 2018;18:392–404. doi: 10.1007/s11668-018-0421-9. [DOI] [Google Scholar]
- 14.Wu P., Meng X., Song L., Zuo W. Crash Risk Evaluation and crash severity pattern analysis for different types of urban junctions: fault tree analysis and association rules approaches. Transportation Research Record. 2019;2673:403–416. doi: 10.1177/0361198118822817. [DOI] [Google Scholar]
- 15.Mineo S., Pappalardo G., D’urso A., Calcaterra D. Event tree analysis for rockfall risk assessment along a strategic mountainous transportation route. Environmental earth sciences. 2017;76:620–630. doi: 10.1007/s12665-017-6958-1. [DOI] [Google Scholar]
- 16.Wu Y., Abdel-Aty M., Lee J. Crash risk analysis during fog conditions using real-time traffic data. Accid. Anal. Prev. 2018;114:4–11. doi: 10.1016/j.aap.2017.05.004. [DOI] [PubMed] [Google Scholar]
- 17.Cordeiro F., Bezerra B., Peixoto A., Ramos R. Methodological aspects for modeling the environmental risk of transporting hazardous materials by road. Transport. Res. D-Tr. E. 2016;44:105–121. doi: 10.1016/j.trd.2016.02.008. [DOI] [Google Scholar]
- 18.Liu H., You J., Duan C. An integrated approach for failure mode and effect analysis under interval-valued intuitionistic fuzzy environment. Int. J. Prod. Eco. 2019;207:163–172. doi: 10.1016/j.ijpe.2017.03.008. [DOI] [Google Scholar]
- 19.Faiella G., Parand A., Franklin B., Chana P., Cesarelli M., Stanton N.A., Sevdalis N. Expanding healthcare failure mode and effect analysis: A composite proactive risk analysis approach. Reliab. Eng. Syst. Safe. 2018;169:117–126. doi: 10.1016/j.ress.2017.08.003. [DOI] [Google Scholar]
- 20.Zhou J.B., Chen H., Yan B., Shi X., Li X.W. Risk assessment of operation safety in freeway tunnels: An evaluation approach using multiple safety indices. J. Transp. Saf. Secur. 2014;6:93–116. doi: 10.1080/19439962.2013.817494. [DOI] [Google Scholar]
- 21.Chen H., Zhou J., Wang J., Li X., GAN Z. Safety evaluation indexes and method for traffic environment of highway tunnels. J. Chang’an Univ., Nat. Sci. Ed. 2013;33:54–61. [Google Scholar]
- 22.Chen F., Wang J., Deng Y. Road safety risk evaluation by means of improved entropy TOPSIS–RSR. Saf. Sci. 2015;79:39–54. doi: 10.1016/j.ssci.2015.05.006. [DOI] [Google Scholar]
- 23.Tang J., Liang J., Han C., Li Z., Huang H. Crash injury severity analysis using a two-layer stacking framework. Accid. Anal. Prev. 2019;122:226–238. doi: 10.1016/j.aap.2018.10.016. [DOI] [PubMed] [Google Scholar]
- 24.Kokangül A., Polat U., Dağsuyu C. A new approximation for risk assessment using the AHP and Fine Kinney methodologies. Saf. Sci. 2017;91:24–32. doi: 10.1016/j.ssci.2016.07.015. [DOI] [Google Scholar]
- 25.Shen L., Lu J., Long M., Chen T. Identification of accident blackspots on rural roads using grid clustering and principal component clustering. Math. Probl. Eng. 2019;2019:1–12. doi: 10.1155/2019/2151284. [DOI] [Google Scholar]
- 26.Zou Y., Zhong X., Tang J., Ye X., Wu L., Ijaz M., Wang Y. A copula-based approach for accommodating the underreporting effect in wildlife-vehicle crash analysis. Sustainability. 2019 doi: 10.3390/su11020418. [DOI] [Google Scholar]
- 27.Rhee K.A., Kim J.K., Lee Y.I., Ulfarsson G.F. Spatial regression analysis of traffic crashes in Seoul. Accid. Anal. Prev. 2016;91:190–199. doi: 10.1016/j.aap.2016.02.023. [DOI] [PubMed] [Google Scholar]
- 28.Shi Q., Abdel-Aty M., Lee J. A Bayesian ridge regression analysis of congestion’s impact on urban expressway safety. Accid. Anal. Prev. 2016;88:124–137. doi: 10.1016/j.aap.2015.12.001. [DOI] [PubMed] [Google Scholar]
- 29.Ma C., Hao W., Wang A., Zhao H. Developing a coordinated signal control system for urban ring road under the vehicle-infrastructure connected environment. IEEE Access. 2018;6:52471–52478. doi: 10.1109/ACCESS.2018.2869890. [DOI] [Google Scholar]
- 30.Zong F., Chen X., Tang J., Yu P., Wu T. Analyzing traffic crash severity with combination of information entropy and Bayesian network. IEEE Access. 2019;7:63288–63302. doi: 10.1109/ACCESS.2019.2916691. [DOI] [Google Scholar]
- 31.Guo Y., Wu Y., Lu J., Zhou J. Modeling the unobserved heterogeneity in e-bike collision severity using full Bayesian random parameters multinomial logit regression. Sustainability. 2019 doi: 10.3390/su11072071. [DOI] [Google Scholar]
- 32.Guo Y., Essa M., Sayed T., Haque M.M., Washington S. A comparison between simulated and field-measured conflicts for safety assessment of signalized intersections in Australia. Transport. Res. C-Emer. 2019;101:96–110. doi: 10.1016/j.trc.2019.02.009. [DOI] [Google Scholar]
- 33.Chen F., Chen S., Ma X. Analysis of hourly crash likelihood using unbalanced panel data mixed logit model and real-time driving environmental big data. J. Safety. Res. 2018;65:153–159. doi: 10.1016/j.jsr.2018.02.010. [DOI] [PubMed] [Google Scholar]
- 34.Ma X., Chen S., Chen F. Multivariate space-time modeling of crash frequencies by injury severity levels. Anal. Methods. Accid. Res. 2017;15:29–40. doi: 10.1016/j.amar.2017.06.001. [DOI] [Google Scholar]
- 35.Chen F., Chen S. Injury severities of truck drivers in single-and multi-vehicle accidents on rural highways. Accid. Anal. Prev. 2011;43:1677–1688. doi: 10.1016/j.aap.2011.03.026. [DOI] [PubMed] [Google Scholar]
- 36.Yanmaz-Tuzel O., Ozbay K. A comparative Full Bayesian before-and-after analysis and application to urban road safety countermeasures in New Jersey. Accid. Anal. Prev. 2010;42:2099–2107. doi: 10.1016/j.aap.2010.06.023. [DOI] [PubMed] [Google Scholar]
- 37.Lord D., Mannering F. The statistical analysis of crash-frequency data: a review and assessment of methodological alternatives. Transport. Res. A-Pol. 2010;44:291–305. doi: 10.1016/j.tra.2010.02.001. [DOI] [Google Scholar]
- 38.Dempster A. Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer; Berlin, Germany: 2008. Upper and lower probabilities induced by a multivalued mapping; pp. 57–72. [Google Scholar]
- 39.Shafer G. A Mathematical Theory of Evidence. Princeton University Press; Princeton, NJ, USA: 1976. [Google Scholar]
- 40.Wikipedia Dempster-Shafer theory. [(accessed on 5 July 2019)]; Available online: https://en.wikipedia.org/wiki/Dempster%E2%80%93Shafer_theory.
- 41.Smets P. Advances in the Dempster-Shafer Theory of Evidence. John Wiley & Sons; New York, NY, USA: 1994. pp. 5–34. [Google Scholar]
- 42.Denoeux T. A neural network classifier based on Dempster-Shafer theory. IEEE Trans. Syst. Man. Cybern. A. Syst. Hum. 2000;30:131–150. doi: 10.1109/3468.833094. [DOI] [Google Scholar]
- 43.Sun L., Srivastava R., Mock T. An information systems security risk assessment model under the Dempster-Shafer theory of belief functions. J. Manage. Inform. Syst. 2006;22:109–142. doi: 10.2753/MIS0742-1222220405. [DOI] [Google Scholar]
- 44.Zeng D., Xu J., Xu G. Data fusion for traffic incident detection using DS evidence theory with probabilistic SVMs. J. Comput. 2008;3:36–43. doi: 10.4304/jcp.3.10.36-43. [DOI] [Google Scholar]
- 45.Rassafi A., Ganji S., Pourkhani H. Road safety assessment under uncertainty using a multi attribute decision analysis based on Dempster-Shafer theory. KSCE. J. Civil. Eng. 2018;22:3137–3152. doi: 10.1007/s12205-017-1854-5. [DOI] [Google Scholar]
- 46.Ma C., Yang D., Zhou J., Feng Z., Yuan Q. Risk riding behaviors of urban e-bikes: a literature review. Int. J. Env. Res. Pub. He. 2019 doi: 10.3390/ijerph16132308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Production Safety Law of the People’s Republic Of China, no. 13, Order of the President of the People’s Republic of China. Volume 13. Ministry of Emergency Management of the People’s Republic of China; Beijing, China: 2018. pp. 1–32. [Google Scholar]
- 48.Department of Defense Standard Practice System Safety (MIL-STD-882E) Department of Defense; Washington, WA, USA: 2012. pp. 9–20. [Google Scholar]
- 49.Li D., Liu C., Gan W. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009;24:357–375. doi: 10.1002/int.20340. [DOI] [Google Scholar]
- 50.Peng H., Wang J. A multicriteria group decision-making method based on the normal cloud model with zadeh’sz-numbers. IEEE. Trans. Fuzzy. Syst. 2018;26:3246–3260. doi: 10.1109/TFUZZ.2018.2816909. [DOI] [Google Scholar]