Mechanical Performance of Posterior Spinal Instrumentation and Growing Rod Implants: Experimental and Computational Study

Abstract

Study Design:

Experimental and computational study of posterior spinal instrumentation and growing rod constructs per ASTM F1717–15 vertebrectomy methodology for static compressive bending.

Objective:

Assess mechanical performance of standard instrumentation and growing rod constructs.

Summary of Background Data:

Growing rod instrumentation utilizes fewer anchors and spans longer distances, increasing shared implant loads relative to fusion. There is a need to evaluate growing rod’s mechanical performance. ASTM F1717–15 standard assesses performance of spinal instrumentation; however, effects of growing rods with side-by-side connectors have not been evaluated.

Methods:

Standard and growing rod constructs were tested per ASTM F1717–15 methodology; setup was modified for growing rod constructs to allow for connector offset. Three experimental groups (standard with active length 76mm, and growing rods with active lengths 76mm and 376mm; n=5/group) were tested; stiffness, yield load, and load at maximum displacement were calculated. Computational models were developed and used to locate stress concentrations.

Results:

For both constructs at 76mm active length, growing rod stiffness (49±0.8N/mm) was significantly greater than standard (43±0.4N/mm); both were greater than growing rods at 376mm (10±0.3N/mm). No significant difference in yield load was observed between growing rods (522±12N) and standard (457±19N) constructs of 76mm. Growing rod constructs significantly decreased from 76mm (522±12N) to 376mm active length (200±2N). Maximum load of growing rods at 76mm (1084±11N) was significantly greater than standard at 76mm (1007±7N) and growing rods at 376mm active length (392±5N). Simulations with active length of 76mm were within 10% of experimental mechanical characteristics; stress concentrations were at the apex and cranial to connector-rod interaction for standard and growing rod models, respectively.

Conclusions:

Growing rod constructs are stronger and stiffer than spinal instrumentation constructs; with an increased length accompanied a decrease in strength. Growing rod construct stress concentration locations observed during computational simulation are consistent with clinically observed failure locations.

INTRODUCTION

Posterior spinal instrumentation is commonly used. For patients with mature spines, the instrumentation is configured to obtain and maintain alignment while fusion occurs. For patients with immature spines, instrumentation is configured to correct the deformity and allow for continued spinal growth.^1,2 Fusion of the vertebral bodies minimizes the load distributed across the spinal instrumentation, while loads are continually shared with the growing rod configuration over the lifetime of the device; increasing the chance of failure in growing rod configurations.

Both configuration types (spinal instrumentation and growing rod) consist of anchors (pedicle screws or hooks), set screws, and rods with the addition of connectors (side-by-side or tandem) to allow for continued spinal growth with growing rod configurations. Anchor choice is based on patient characteristics, with pedicle screws being generally preferred.^2–9 Connector choice is also based on the patient’s characteristics and clinician preference; mechanically, the side-by-side connectors allow more mechanical play across the instrumentation, decreasing the chance for rod breakage.¹⁰ Even with the preferred type of anchor and connectors, growing rod configuration failure rates are approximately 20%.^10–15 Therefore, there is the need to understand the mechanical performance of growing rod configurations better – to optimize clinical performance of instrumentation.

Standard test methods for medical devices facilitate assessment of mechanical performance prior to clinical use, which aim to predict device failures during the lifetime of an implant.¹⁶ Spinal implants configurations are evaluated through standard test methods, such as ASTM F1717, which assesses the mechanical performance of a construct in an ex vivo environment.¹⁷ Currently, there is no adaptation to the ASTM F1717 standard to incorporate growing rod configurations.

Our purpose was to compare the mechanical performance of posterior spinal instrumentation constructs and growing rod constructs with side-by-side connectors through experimental testing per a modified ASTM F1717–15 standard. Furthermore, this study aimed to use computer simulations, validated by comparison with the mechanical characteristics (stiffness, yield load, and maximum load) obtained experimentally, to determine locations of stress concentrations.

MATERIALS and METHODS

Experimental Methods

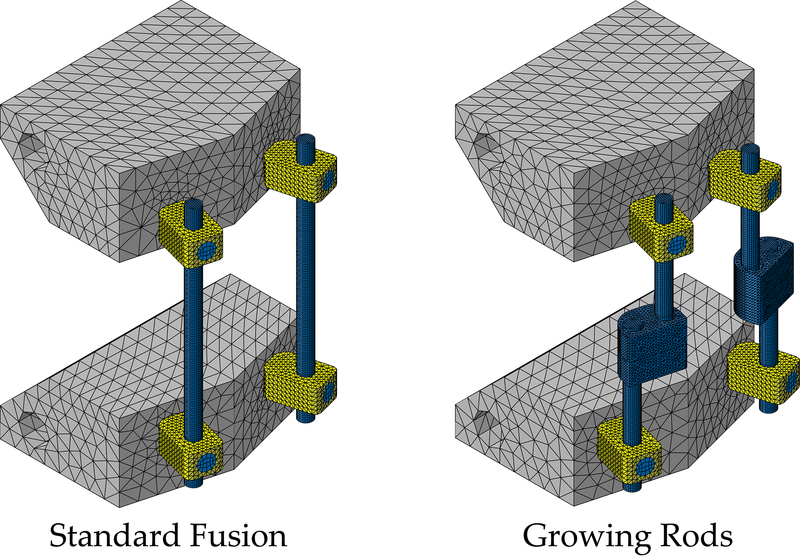
Experimental test setups and procedures were based on the ASTM F1717–15 standard for lumbar bilateral constructs.¹⁷ Per ASTM F1717–15, vertebrectomy construct for posterior spinal instrumentation (i.e., standard) consisted of 4 pedicle screws, 4 pedicle set screws, 2 rods, and 2 blocks (Figure 1). Growing rod constructs consisted of 4 pedicle screws, 4 pedicle set screws, 4 side-by-side connectors (two on each side), 8 connector set screws, 4 rods, and 2 modified blocks (Figure 1). Blocks used for the standard constructs were designed in accordance with ASTM F1717–15 specifications, with the distance between pilot holes set to 40mm. Blocks were modified for the growing rod constructs to incorporate offset pilot holes due to the inclusion of the connectors, where distance between pilot holes for pedicle screws were set to 29.7mm and 50.3mm for the cranial and caudal blocks, respectively (Figure 1). Blocks were composed of ultrahigh molecular weight polyethylene (UHMWPE); rods, set screws, connectors, and the pedicle screw shafts were composed of titanium alloy (Ti-6Al-4V), whereas the pedicle screw tulips were cobalt chrome (Co-28Cr-6Mo). Implants were part of Medtronic® CD Horizon® Spinal System, donated by Medtronic (Medtronic Sofamor Danek USA). Implant dimensions and specification were 6.5×40mm multi-axial pedicle screws with 5.5mm diameter rods and 5.5/6.0mm set screws for both constructs. Additionally, 5.5mm closed/closed domino (i.e., side-by-side) connectors were used with the growing rod constructs.

Figure 1 –

Left ASTM F1717–15 standard construct and Right growing rod construct modified for the inclusion of two side-by-side connectors, both are drawn to active length 76 mm

To ensure proper active lengths, a jig was utilized to place the cranial and caudal blocks. Pedicle screws were placed in pilot holes on the blocks and the tulip of the pedicle screw was flush to the block’s surface to minimize the movement of the tulip and shaft of the pedicle screw on the construct. Spinal rods were placed into the pedicle screw tulip, and pedicle set screws were used to lock the rods into place per surgical technique using the required tightening torque. For growing rod constructs, side-by-side connectors were placed at the active length midpoint with minimal overlap (17.4mm) between the cranial and caudal connectors (Figure 1); break-off set screws were used with the connectors to lock the cranial and caudal rod segments into place using the tightening torque as specified in the surgical technique. Once the constructs were assembled, each construct was mounted into specified ASTM F1717 specified uniaxial load frame supports, where the blocks were connected to side supports (Figure 2).

Figure 2 –

Experimental test setup showing 376 mm active length growing rod construct with hinge pin and side supports within a uniaxial MTS 858 Mini Bionix II testing machine

Three constructs were mechanically tested (n=5 per construct): (1) standard construct with a 76mm active length, (2) growing rod construct with a 76mm active length, and (3) growing rod construct with a 376mm active length. The 76mm active length was chosen based on ASTM F1717 standard, which is based off the work of Cunningham et al. that was determined from measurements of two spinal level constructs.^17,18 The 376mm active length chosen for the growing rod construct was based on the maximum length that may be clinically observed without anchors between the cranial and caudal endings of the instrumentation (i.e., a fully matured patient with growing rod instrumentation placed across T1 to S1.¹⁹

Mechanical testing was performed using a uniaxial servohydraulic test machine (MTS 858 Mini Bionix II, MTS Systems Corporation, Eden Prairie, MN, USA) configured with a 15kN tensile compressive load cell (Figure 2). Constructs were evaluated under static compressive load to failure at a displacement rate of 25mm/min, resulting as a bending of the construct. The test was stopped when contact between cranial and caudal blocks occurred (approximately 66mm for 76mm active length), or when the maximum actuator displacement occurred (approximately 135mm for 376mm active length). Force-displacement data were collected through an LVDT and recorded at 30Hz through an MTS interface cable to a high-speed analog to digital converter. Data were analyzed using a customized Matlab code (The Mathworks Inc., Natick, MA, USA). The following mechanical characteristics were calculated from the force-displacement data per ASTM F1717–15: stiffness, yield load and displacement from a 2% offset of the active length, and load at maximum displacement.

Finite Element Methods

Three-dimensional finite element (FE) models were designed and assembled per the modified ASTM F1717–15 static compressive bending test setup using ABAQUS/Standard (ABAQUS 2017 SIMULA; Providence, RI, USA). Pedicle screws in the experimental test setup were placed flush to the block’s surface; hence, the geometry of the pedicle screws, set screws, and connectors were constrained such that the rods could be placed in the same location and subjected to similar contact constraints as in the experimental testing. The interaction between two contacting surfaces was defined by tying the two surfaces to one another.

Standard eight-node three-dimensional continuum brick elements with incompatibility mode (C3D8I type elements) were used for the pedicle screw shaft, set screws, and rods; the pedicle screw tulip, blocks, and connectors were composed of four-node three-dimensional continuum linear tetrahedral elements (C3D4 type elements; Table 1, Figure 3). Mesh convergence analysis was completed for verification of the FE models; a mesh size of 0.65 was found to acceptable for our models.

Table 1 –

Number of elements in each computational model with respect to the whole model and the rod

	Whole Model	Rods
Standard at 76mm Active Length	58,646	23,560
Growing Rods at 76mm Active Length	117,316	27,664
Growing Rods at 376mm Active Length	187,604	97,888

Figure 3 –

Meshes of the standard (left) and growing rod (right) finite element models, both with active length 76mm. The colors represent different material property definitions assigned to the corresponding geometry: blue is the titanium alloy, yellow is the cobalt chrome, and gray is the UHMWPE material properties.

Each part within the models was considered to be isotropic and linear elastic-perfectly plastic. Material properties were extracted from current standards, literature, and online databases and shown in Table 2.^17,20–25

Table 2 –

Material properties used in the finite element models for instrumentation and blocks

	Young’s Modulus (GPa)	Poisson’s Ratio	Proportionality Limit (MPa)	Yield Stress (MPa)	Ultimate Stress (MPa)	Elongation (%)
Ti-6Al-4V	107.023	0.342	56822	76023	1,27223	3.224
Co-28Cr-6Mo20	210.0	0.290	—	590	1,192	14.0
UHMWPE17	0.8	0.460	—	—	—	—

Two reference points were introduced to simulate the experimental test boundary conditions between the hinge pin, construct, and load cell. They were kinematically coupled to the cylindrical surface of the block where the hinge pin was placed during experimental testing. The cranial reference point was limited to medial-lateral axis rotation and cranial-caudal translation. The caudal reference point only allowed for medial-lateral axis rotation.

An axial displacement of 66mm and 136mm for models with 76mm and 376mm active length, respectively, was applied to the cranial reference point. Each simulation calculated the reaction force of the cranial reference point with respect to the displacement and evaluated the von Mises stress throughout the model. The construct’s mechanical characteristics were calculated from force-displacement curve for each model. Maximum stress across the rods for each model was evaluated.

Statistical Analysis

Student’s unpaired pooled t-test with two-tailed distribution was used to analyze the experimental results for the difference between standard and growing rod constructs with the 76mm active length, and between growing rod constructs of active length 76mm and 376mm. Level of significance was set at 0.05 for all statistical analyses.

Each FE model was considered valid if the findings were within 10% of the respective experimental mechanical characteristics.

RESULTS

Two of the five experimental tests of the growing rod constructs with an active length of 76mm were excluded from analysis due to loosening of the cranial pedicle set screws during testing. These were the first two constructs experimentally tested and, these constructs were tightened to the manufacture’s recommended torque, the tightening torque for the remaining constructs was increased to minimize the observed pedicle set screw loosening.

Table 3 comprises the mechanical characteristics from experimental and FE simulations for standard and growing rod constructs. Growing rod constructs with the 76mm active length exhibited the greatest stiffness and loads, followed by standard constructs with the 76mm active length, then growing rods with the 376mm active length. Similar yield displacements were observed for both constructs with the 76mm active lengths, while the 376mm active length constructs demonstrated significantly greater displacements. FE models (standard and growing rod) with active lengths of 76mm were within 10% of the experimental mechanical characteristics. For the 376mm active length growing rod FE model, yield loads were within 10% of the experimental results; while stiffness, yield displacement, and maximum load were not with 10% of the experimental mechanical characteristics. Although the 376mm growing rod FE model was not within 10% of all the experimental mechanical characteristics, the stiffness was 3N/mm stiffer in the experimental test. Figures 4AB and 5 depict experimental and FE simulations force-displacement curves of each configuration. These curves show similarities between the experimental and FE simulated constructs.

Table 3 –

Mechanical characteristics from experimental results and FE analysis for standard and growing rod constructs (mean ± standard deviation, for experimental results; value and percent error between experimental and FE, for FE analysis). Statistical significance (p < 0.05) between the standard and growing rod constructs denoted by * and between growing rod constructs of varied lengths (76 and 376mm) denoted by **.

Configuration	Stiffness (N/mm)	Yield Load (N)	Yield Displacement (mm)	Maximum Load (N)	Maximum Displacement (mm)
Experimental, Standard
Active Length = 76mm	43 ± 0.4	457 ± 19	12 ± 0.5	1,007 ± 7	65 ± 1.2
Experimental, Growing Rod
Active Length = 76mm	49 ± 0.8*	522 ± 12*	12 ± 0.1	1,084 ± 11*	62 ± 0.9*
Active Length = 376mm	10 ± 0.3**	200 ± 2**	28 ± 0.7**	392 ± 5**	134 ± 2.4**
Finite Element, Standard
Active Length = 76mm	44.3 (‒2.0%)	484.0 (‒6.0%)	12.3 (‒3.8%)	935.9 (7.1%)	66.0 (1.4%)
Finite Element, Growing Rod
Active Length = 76mm	53.4 (‒7.9%)	503.4 (3.6%)	10.9 (9.8%)	1,068.3 (1.5%)	66.0 (‒5.9%)
Active Length = 376mm	7.6 (22.1%)	191.6 (4.0%)	32.3 (‒16.4%)	294.8 (24.8%)	136.0 (‒1.5%)

Figure 4 –

Force-displacement curves for experimental and computation simulations of the (A) standard and (B) growing rods models, both with active lengths of 76mm; with the solid line representing the experimental results and the dashed line representing the computational simulation during static compressive bending.

Figure 5 –

Force-displacement curves for experimental and computation simulations of the growing rods model with an active length of 376mm; with the solid line representing the experimental results and the dashed line representing the computational simulation during static compressive bending.

Figure 6 shows the von Mises stress observed across the standard and growing rod models with the 76mm active length at 66mm of displacement. Stress concentrations occur on the rods at the apex and cranial to the rod-connector interaction for the standard and growing rod models, respectively. Throughout the standard model’s simulation, the stress concentrations are on the anterior side of the rods, occurring closer to the cranial pedicle screws at the beginning of the simulation. For the growing rod model with an active length of 76mm, the stress concentrations throughout the simulation are cranial to the rod-connector interaction but occur on the anterior side of the rods at the beginning and posterior side of the rods at the end of the simulation. Figure 7 shows the von Mises stress across the growing rod model with active length of 376mm, with the stress concentration on the anterior side of the rods and cranial to the rod-connector interaction throughout the simulation.

Figure 6 –

Stress concentrations were 1,361MPa and 1,511MPa for the standard (left) and growing rod (right)) models found on the rod at the anterior side of the apex and on the rod at the posterior side and just cranial to the rod-connector interaction, respectively.

Figure 7 –

Stress concentration on the growing rods model with an active length of 376mm was on the anterior side of the rods just above the connector (1,174MPa)

DISCUSSION

The present study was the first to use the ASTM F1717–15 standard test method and modified for growing rod configurations with side-by-side connectors. There was an increase in stiffness and strength of a spinal implant construct with the inclusion of side-by-side connectors and a shorter active length. Previous studies on spinal instrumentation constructs^18,26–30 have investigated the mechanical characteristics with similar results to the present study but did not assess mechanical characteristics of growing rod constructs with side-by-side connectors. Kim et al. found that the growing rod constructs with tandem connectors were stiffer and stronger than standard constructs during static compression bending, the same pattern observed in the current study.²⁶ Our results are promising as they support accepted mechanical principles; increasing the amount of material within a configuration strengthens a construct. From a clinical perspective, it is advantageous to have a stronger construct for growing rod instrumentation as the construct is subjected to higher loads across the instrumentation with fewer anchors to share the load with the spine.

The growing rod construct with active length 76mm exhibited mechanical characteristics that were significantly different than those of growing rods with active lengths of 376mm. The shorter growing rods active length had greater stiffness and strength, while the longer growing rods active length had larger displacements. These results are consistent with known and accepted engineering principles; if the moment arm (i.e., active length) increases, then the amount of force required to displace the rod decreases.³¹ A longer construct would likely correspond to a greater load being placed across the construct; therefore, a longer construct would be unlikely to resist greater loads prior to yielding.

To properly interpret the FE model, the output needs to be compared against experimental results, therefore increasing the confidence in the interpretation of the FE models. An FE model was considered validated when the mechanical characteristics were within 10% of the experimental results and was determined separately for each construct. Both models with the 76mm active lengths had mechanical characteristics that were within 10% of experimental mechanical characteristics; hence, the models with active lengths of 76mm were validated. The 10% difference was arbitrarily chosen with the goal of constraining validation of the FE models to similar results as the experimental testing conditions. Although the 376mm growing rod FE model was not within 10% for the stiffness, and maximum load and displacement; the simulated stiffness was only 3N/mm less than the experimental test. Therefore, difference along with the percent error should be evaluated to determine the validity of a FE model, and caution should be taken when interpreting a FE models results.

Finite element analysis provides additional information on the mechanical performance that cannot be determined during experimental testing, such as stress observed across the construct and stress concentrations predicting potential failure mode. Location of stress concentrations are known to accelerate fatigue failures, occurring when the stresses exceed the strength of the material or construct.²² The primary mode of clinical failure in growing rod implants is bending fatigue near the rod-connector interface.¹⁰ Our growing rod simulation with 76mm active length had the largest stress concentration, which was observed just cranial to the rod-connector interface. When the length of the growing rod model was increased, the stress concentration decreased by more than 400MPa with a similar location – cranial to the rod-connector interface. Stress concentrations for both growing rod models are consistent with a common location of clinical failure of the spinal rods; therefore, computational simulations can assist with configuration and optimization of growing rod implants to minimize stress concentrations across the construct and improve the lifespan of the construct.¹⁰

There were also limitations to our study. The test setup used for both standard and growing rod constructs was designed for comparison of mechanical characteristics of different spinal implant assemblies, not to simulate in vivo conditions directly for spinal implant assemblies. The standard provides initial assessment of the device and design prior to clinical use; this should be supplemented with clinical assessment to minimize potential risks and failures within the patient. No fractures occurred while experimentally examining static compression bending load applied to the constructs but loosening of the set screws within the pedicle screw tulip was noted in two growing rod constructs with active length 76mm. Hence, these results were removed from the analysis, to decrease variability in the results to simulate the experimental test in situ. Lastly, there is uncertainty involved with the use of computational simulations. This uncertainty was addressed was by completing a mesh convergence analysis on the models and comparing mechanical characteristics of experimental and simulated results was completed. While the growing rod model with an active length 376mm had a greater percent difference than the allowable 10%, the absolute difference between experimental and simulated results was similar to the models with an active length 76mm. The materials of the implants were not properly characterized, since they were obtained via online databases and through the literature; which may have led to the discrepancies between the experimental and computational results. Additionally, all models were verified through a mesh convergence analysis.

In conclusion, modifications to ASTM F1717–15 standard test method can be used to assess growing rod configurations by increasing the active length (for a worst-case scenario) and incorporate connectors by an offset of the test block pilot holes, when needed. Furthermore, the computational simulations in our work gave insight into the regions of stress concentrations, indicating where there may be a greater risk for spinal rod failure. Therefore, computational simulations accompanied with ASTM F1717–15 standard may provide useful insight into modes of failure for configurations during the design and development stages of the device. Hence, we propose to modify the current ASTM F1717–15 standard to incorporate growing rod configurations and encourage the use of computational simulations to evaluate potential modes of failure.