MFPCA: Multiscale Functional Principal Component Analysis

Abstract

We consider the problem of performing dimension reduction on heteroscedastic functional data where the variance is in different scales over entire domain. The aim of this paper is to propose a novel multiscale functional principal component analysis (MFPCA) approach to address such heteroscedastic issue. The key ideas of MFPCA are to partition the whole domain into several subdomains according to the scale of variance, and then to conduct the usual functional principal component analysis (FPCA) on each individual subdomain. Both theoretically and numerically, we show that MFPCA can capture features on areas of low variance without estimating high-order principal components, leading to overall improvement of performance on dimension reduction for heteroscedastic functional data. In contrast, traditional FPCA prioritizes optimizing performance on the subdomain of larger data variance and requires a practically prohibitive number of components to characterize data in the region bearing relatively small variance.

1. Introduction

Functional principal component analysis (FPCA) is a key tool for performing dimension reduction on functional data that features infinite dimensionality and emerges in many machine learning applications (Ghebreab, Smeulders, and Adriaans 2008; Ramsay and Silverman 2005; Ferraty and Vieu 2006; Hsing and Eubank 2015). In classic FPCA referred to as single-scale FPCA in this paper, a single eigen-analysis is conducted for observed functions on the entire domain. Specifically, FPCA is built on eigen-analysis of the covariance function of functional data, analogous to the covariance matrix, from which we derive functional principal components. For the purpose of dimension reduction, only the principal components corresponding to the first few largest eigenvalues are retained. Related works include early development of FPCA (Rao 1958; Dauxois, Pousse, and Romain 1982; Besse and Ramsay 1986), and more recent advances such regularization techniques (Rice and Silverman 1991; Silverman 1996), estimation and theory (Yao, Müller, and Wang 2005; Hall, Müller, and Wang 2006; Li and Hsing 2010; Zhang and Wang 2016) for functional data that are sparsely observed, and interpretability (Chen and Lei 2015; Lin, Wang, and Cao 2016), to name a few. All of these works adopt the single-scale paradigm, which is briefly described in the next section.

Such one-size-fits-all scheme, as we show in Section 2, inevitably comes with a side effect that the leading principal components prioritize producing good approximation quality for functions on the subdomain that holds large data variance. However, for heteroscedastic functional data, where the variance of the data has substantially different scales over the domain, single-scale FPCA approach often needs a large number of principal components in order to characterize the behavior of the data on the subdomain with relatively small variance. However, it is notoriously difficult to accurately estimate high-order principal components. For example, for a fixed sample size, the estimation error for the kth principal components is approximately of the order k² (Mas and Ruymgaart 2015). This quadratic decay in estimation quality prohibits one from obtaining reliable estimates of principal components for a moderate sample size except for the first few leading ones. Consequently, for heteroscedastic functional data, single-scale FPCA may not be able to discover useful features in the area of low variance.

To address the issue of FPCA for heteroscedastic functional data, we consider a question, which states

“Could we modify standard FPCA to efficiently deal with heteroscedastic functional data?”

Our solution to the above question is the development of a novel multiscale FPCA framework. The key ideas of MFPCA are to partition the whole domain into several subdomains in the way that the variance of the data within a subdomain is approximately on the same scale, and then to conduct FPCA on each subdomain separately. Compared with the existing methods in the literature, three major methodological contributions in this paper are as follows:

• Our MFPCA approach is simple and yet powerful. Specifically, compared to single-scale FPCA, the multiscale approach alleviates the issue of estimating high-order principal components and leads to overall improvement of data representation, since fewer components are required for sufficient approximation of the data within each subdomain.

• Our MFPCA is able to discover useful patterns in the area of low variance, as demonstrated in the analysis of the brain microstructure in relation to multiple sclerosis using diffusion tensor imaging techniques; see Section 4 for details.

• Theoretically, we show that MFPCA has larger capacity of representation for functional data and yields higher estimation quality for principal components than singlescale FPCA. The theoretical analysis is complemented by numerical simulation in Section 4.

2. Classic Functional Principal Component Analysis

Without loss of generality, let X be a random process defined on an interval I such that $\mathbf{E}\Vert X{\Vert }_{{\mathcal{L}}_2}^2<\infty$ and EX = 0. FPCA is built on the concept of Karhunen-Loève expansion of X. Specifically, X (t) admits the following representation

$$X(t)=\sum _{k=1}^{\infty }{\xi }_k{\varphi }_k(t),$$ (1)

where ξ_k are centered uncorrelated random variables, ϕ_k(·) are normalized eigenfunctions of the covariance function $\mathcal{C}(s,t)=\text{Cov}\{X(s),X(t)\}$, and Var(ξ_k), often denoted by λ_k, is the eigenvalue of $\mathcal{C}$ corresponding to ϕ_k, i.e.,

$${\int }_I\mathcal{C}(\cdot ,t){\varphi }_k(t)\mathrm{d}t={\lambda }_k{\varphi }_k(\cdot ).$$ (2)

It is also conventionally assumed that λ₁ > λ₂ > · · · > 0. The eigenfunctions ϕ₁(·), ϕ₂(·),…, referred to as principal components in the context of FPCA, form an orthonormal basis of ${\mathcal{L}}^2(I)$.

The above FPCA is a single-scale approach in the sense that both (1) and (2) are defined on the entire interval I. It has the following global optimality of Karhunen-Loève expansion for approximation of X using the first few eigenfunctions. For any fixed K > 0, let B = {B₁,…, B_K} be a collection of K orthonormal real-valued functions in ${\mathcal{L}}^2(I)$, and define P_B the projection operator of the space spanned by B₁, …,B_K, i.e., $P_{\mathrm{B}}X={\sum }_{k=1}^K\langle B_k,X\rangle B_k$, where ⟨B_k, X⟩ = ∫_I B_k (t)X(t)dt. In principle, P_BX is the approximation of X using the basis functions B₁,…, B_K. The approximation error is often measured by $\epsilon (\mathbf{B})=\mathbf{E}(\Vert X-P_{B}X{\Vert }_{{\mathcal{L}}^2}^2)$. It can then be shown that ε(Φ) ≤ ε(B) for Φ = {ϕ₁,…, ϕ_K} and any B of K orthonormal functions in ${\mathcal{L}}^2(I)$.

Although such optimality of single-scale FPCA is attractive for approximating functional data, it has an undesired side-effect for functional data with different scales of variability on the interval I. To elaborate, we divide I into J equal subintervals I₁,…, I_J that form a partition of I, in the sense that ${\bigcup }_{j=1}^J$ I_j = I and I_j ∩ I_k = ∅ for 1 ≤ j ≠ k ≤ J. Denote X^(j)(t) as the restriction of X(t) to the subinterval I_j, i.e., X^(j)(t) = X(t) if t ∈ I_j and X^(j)(t) =0 if t ∉ I_j.

Then, we have

$$\begin{array}{cc}\hfill \epsilon (\mathbf{B})& =\mathbf{E}(\Vert X-P_{\mathbf{B}}X{\Vert }_{{\mathcal{L}}^2}^2)\hfill \\ \hfill & =\sum _{j=1}^J\mathbf{E}\left(\Vert X^{(j)}-(P_{\mathbf{B}}X{)}^{(j)}{\Vert }_{{\mathcal{L}}^2}^2\right)\hfill \\ \hfill & =\mathbf{E}(\Vert X{\Vert }_{{\mathcal{L}}^2}^2)\times \hfill \\ \hfill & \sum _{j=1}^J\frac{\mathbf{E}(\Vert X^{(j)}-(P_{\mathbf{B}}X{)}^{(j)}{\Vert }_{{\mathcal{L}}^2}^2)}{\mathbf{E}(\Vert X^{(j)}{\Vert }_{{\mathcal{L}}^2}^2)}\frac{\mathbf{E}(\Vert X^{(j)}{\Vert }_{{\mathcal{L}}^2}^2)}{\mathbf{E}(\Vert X{\Vert }_{{\mathcal{L}}^2}^2)},\hfill \end{array}$$

where (P_BX)^(j) denotes the restriction of P_BX to I_j. Let $w_j=\mathbf{E}(\Vert X^{(j)}{\Vert }_{{\mathcal{L}}^2}^2)∕\mathbf{E}(\Vert X{\Vert }_{{\mathcal{L}}^2}^2)$ for all j ≤ J, which are constants that are independent of B. We interpret the weights w_j as the variance density of X on I_j. Then, finding B to optimize ε(B), which the single-scale FPCA does, prioritizes minimizing the approximation error for the pieces with larger weights, i.e., with relatively larger variance density. Therefore, in order to capture features of pieces that have small weights, one needs a large number of principal components. As the principal components ϕ_k are unknown, one needs to estimate them from a finite sample. However, it is difficult to estimate the high-order principal components, in light of the fact that any estimate for ϕ_k based on n independently and identically distributed (i.i.d.) samples of X cannot have an estimation error less than ck² /n for some constant c > 0 (Mas and Ruymgaart 2015). Thus, if one applies single-scale FPCA to X(t) that exhibits multiscale variability over I, then the features in the area with low variance density might be concealed by those in the region of high variance density.

3. Multiscale Karhunen-Loève Expansion

To overcome the aforementioned shortcoming of singlescale FPCA, for heteroscedastic functional data, we adopt the following simple divide-and-conquer strategy to conduct FPCA: divide the interval I into several subintervals according to the scale of variance on I, and then perform FPCA on each subinterval. To be more precise, let I₁,…,I_J and X⁽⁽⁾,…,X^(J) be defined as in Section 2. Applying single-scale FPCA to each X^(j) on I_j, we can obtain the Karhunen-Loève approximation $X^{(j)}(t)\approx {\sum }_{k=1}^{K_j}{\xi }_k^{(j)}{\varphi }_k^{(j)}(t)$, where ${\varphi }_k^{(j)}$ is the kth leading eigenfunction of the multiscale covariance function ${\mathcal{C}}^{(j)}$ that is defined by ${\mathcal{C}}^{(j)}(s,t)=\text{Cov}\{X^{(j)}(s)X^{(j)}(t)\}$ on the square I_j × I_j. The approximation for X is then obtained by

$$X(t)\approx \sum _{j=1}^J\sum _{k=1}^{K_j}{\xi }_k^{(j)}{\varphi }_k^{(j)}(t).$$ (3)

Although there are ${\sum }_{j=1}^J$ K_j terms in (3), for each t ∈ I_j, only K_j of them are nonzero as ${\varphi }_k^{(j)}$ is zero outside I_j. The number of principal components, K_j required for a good approximation of X^(j) can vary among the subintervals, which allows for the adaptive approximation of X over different subintervals. For example, if sample paths of X are rough on I_j, then a relatively larger number of principal components can be used to obtain a good approximation, while for relatively smooth pieces, X^(k), a small number might be sufficient. In contrast, single-scale FPCA uses the same number of principal components for each t ∈ I and hence does not enjoy such extra adaptivity. Note that (3) automatically takes into account the fact that the sub-domains where the data have small variance contribute less than others to approximating the process X(t), by observing that the principal component scores ${\xi }_k^{(j)}$ have different scales of variance on different sub-domains. For those sub-domains with small variance, the scale of the corresponding principal component scores is also small. Nevertheless, the features of a small scale could be influential in supervised learning tasks, as demonstrated in Section 4.

As stated previously, single-scale FPCA has the global optimality property, which can be equivalently stated as $\mathbf{E}\Vert P_{\mathrm{\Phi }}X{\Vert }_{{\mathcal{L}}^2}^2\ge \mathbf{E}\Vert P_{\mathrm{B}}X{\Vert }_{{\mathcal{L}}^2}^2$, where Φ and B are defined in Section 2. The quantity $\mathbf{E}\Vert P_{\mathrm{\Phi }}X{\Vert }_{{\mathcal{L}}^2}^2$ is often interpreted as the amount of variance explained by the principal components in Φ. The optimality property essentially asserts that the first K eigenfunctions explain the variance of X more than any other K orthonormal functions for any K ≥ 1. However, by exploring local adaptivity, our MFPCA enjoys larger capacity of representation of functional data, i.e., it can explain larger variance than single-scale FPCA when the same number of principal components is used to approximate X (t) for each t ∈ I. The following proposition illustrates this point for K = 1.

Proposition 1. Let I1,…, I_j form a disjoint partition of I. Suppose that X is a random process satisfying $\mathbf{E}\Vert X{\Vert }_{{\mathcal{L}}^2}^2<\infty$ and (without loss of generality) EX = 0. Let ${\mathcal{S}}_j$ be the collection of function f such that $\Vert f{\Vert }_{{\mathcal{L}}^2}^2=1$ and support(f) ⊂ I_j. Then

$$\mathbf{E}\Vert P_{{\varphi }_1}X{\Vert }_{{\mathcal{L}}^2}^2=\mathbf{E}\langle X,{\varphi }_1{\rangle }^2\le \underset{{\psi }^{(j)}\in S_j}{\text{sup}}\sum _{j=1}^J\mathbf{E}\langle X,{\psi }^{(j)}{\rangle }^2.$$

The equality is possible only if $\mathbf{E}\langle X,{\varphi }_1^{(j)}\rangle =\mathbf{E}\langle X,{\varphi }_1^{(k)}\rangle$ for all 1 ≤ j, k ≤ J, where ${\varphi }_1^{(j)}$ denotes the restriction of the single-scale eigenfunction ϕ₁ onto I_j.

Proof. It is easy to see that the conclusion holds for J > 2 if it is true for J = 2. Suppose $\Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}>0$ and $\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}>0$; otherwise, the conclusion is trivial. Set ${\tilde{\varphi }}_1={\varphi }_1^{(1)}∕\Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}$ and ${\tilde{\varphi }}_2={\varphi }_1^{(2)}∕\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}$. Then

$$\begin{array}{cc}\hfill & \mathbf{E}\langle X,{\varphi }_1{\rangle }^2=\mathbf{E}\langle X,{\varphi }_1^{(1)}+{\varphi }_1^{(2)}{\rangle }^2\hfill \\ \hfill & =\mathbf{E}\langle X,{\varphi }_1^{(1)}{\rangle }^2+\mathbf{E}\langle X,{\varphi }_1^{(2)}{\rangle }^2+2\mathbf{E}(\langle X,{\varphi }_1^{(1)}\rangle \langle X,{\varphi }_1^{(2)}\rangle )\hfill \\ \hfill & =\Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}^2\mathbf{E}\langle X,{\tilde{\varphi }}_1{\rangle }^2+\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}^2\mathbf{E}\langle X,{\tilde{\varphi }}_2{\rangle }^2\hfill \\ \hfill & +2\Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}\mathbf{E}(\langle X,{\tilde{\varphi }}_1\rangle \langle X,{\tilde{\varphi }}_2\rangle )\hfill \\ \hfill & \le \Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}^2\mathbf{E}\langle X,{\tilde{\varphi }}_1{\rangle }^2+\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}^2\mathbf{E}\langle X,{\tilde{\varphi }}_2{\rangle }^2\hfill \\ \hfill & +\Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}^2\mathbf{E}\langle X,{\tilde{\varphi }}_2{\rangle }^2+\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}^2\mathbf{E}\langle X,{\tilde{\varphi }}_1{\rangle }^2\hfill \\ \hfill & =\mathbf{E}\langle X,{\tilde{\varphi }}_1{\rangle }^2+\mathbf{E}\langle X,{\tilde{\varphi }}_2{\rangle }^2,\hfill \end{array}$$

where the last equality is due to $\Vert {\varphi }_1^{(1)}{\Vert }_{{\mathcal{L}}^2}^2+\Vert {\varphi }_1^{(2)}{\Vert }_{{\mathcal{L}}^2}^2=1$. The equality holds if $\mathbf{E}\langle X,{\varphi }_1^{(1)}\rangle =\mathbf{E}\langle X,{\varphi }_1^{(2)}\rangle$. The fact that ${\tilde{\varphi }}_1\in {\mathcal{S}}_1$ and ${\tilde{\varphi }}_2\in {\mathcal{S}}_2$ concludes the proof. □

Principal components are unknown and need to be estimated from data in practice. Given n i.i.d. samples X₁, X₂,…, X_n, the single-scale covariance function $\mathcal{C}$ is estimated by its empirical version $\widehat{\mathcal{C}}(s,t)=n^{-1}{\sum }_{i=1}^n{X}_i(s)X_i(t)$. The kth single-scale principal component ϕ_k is then estimated by the kth principal component ${\widehat{\varphi }}_k$ of $\widehat{C}$. The quality of the estimator ${\widehat{\varphi }}_k$ is quantified by the error $\mathbf{E}\Vert P_{{\widehat{\varphi }}_k}-P_{{\varphi }_k}{\Vert }_{\infty }^2$, where ‖ · ‖_∞ denotes the operator norm on ${\mathcal{L}}^2(I)$. It is shown that $\mathbf{E}\Vert P_{{\widehat{\varphi }}_k}-P_{{\varphi }_k}{\Vert }_{\infty }^2\ge c{k}^2∕n$ for all k ≥ 1 and a universal constant c > 0 (Mas and Ruymgaart 2015). In Section 2, we point out that singlescale FPCA focuses on the region of high variance density. For heteroscedastic functional data, if one needs to learn features in the area of low variance density, then a potentially large number of principal components are required. However, due to the quadratic growth in estimation error, it is notoriously difficult to obtain reliable estimates for high-order principal components.

The difficulty of handling high-order principal components might be alleviated or even avoided if one takes a multiscale perspective. To give a more concrete example, we assume $X={\sum }_{j=1}^J{\sum }_{k=1}^j{\xi }_k^{(j)}{\varphi }_k^{(j)}+X_{\perp }$, where ${\varphi }_k^{(j)}$ are orthonormal, X_⊥ is orthogonal to all ${\varphi }_k^{(j)}$, and ${\xi }_k^{(j)}$ are uncorrelated and centered random variables with variance ${\mathrm{\lambda }}_k^{(j)}\equiv \mathbf{E}({\xi }_k^{(j)}{)}^2\asymp \{J(J+1)∕2-j(j-1)∕2+(k-j){\}}^{-\alpha }$ for some constant α > 1, i.e., ${\mathrm{\lambda }}_1^{(J)}>{\mathrm{\lambda }}_2^{(J)}>\cdots {\mathrm{\lambda }}_J^{(J)}>{\mathrm{\lambda }}_1^{(J-1)}>{\mathrm{\lambda }}_2^{(J-1)}>\cdots >{\mathrm{\lambda }}_1^{(1)}$. Also, if $\phi \in {\mathcal{L}}^2(I)$ and $\Vert \phi {\Vert }_{{\mathcal{L}}^2}=1$, then $\mathbf{E}\langle X_{\perp },\phi {\rangle }^2<\text{min}\{{\lambda }_k^{(j)}:j=1,\dots ,J,k=1,\dots ,j\}={\lambda }_1^{(1)}$. In other words, ${\varphi }_k^{(j)}$ are the first J (J + 1)/2 principal components of X. If one applies single-scale FPCA to obtain an estimate ${\widehat{\varphi }}_{k,S}^{(j)}$ for each principal component ${\varphi }_k^{(j)}$, then the estimation error for ${\varphi }_1^{(1)}$ is $\mathbf{E}\Vert P_{{\widehat{\varphi }}_{1,S}^{(1)}}-P_{{\varphi }_{1,S}^{(1)}}{\Vert }_{\infty }^2\ge c{J}^2(J+1{)}^2∕(4n)$. For multiscale FPCA, given the partition I₁, I₂,…, I_J, the multiscale estimator for ${\mathcal{C}}^{(j)}$ is given by its empirical version ${\widehat{\mathcal{C}}}^{(j)}(s,t)=\frac{1}{n}{\sum }_{i=1}^n{X}_i^{(j)}(s)X_i^{(j)}(t)$ and the principal component ${\varphi }_k^{(j)}$ is estimated by the kth leading principal components ${\widehat{\varphi }}_{k,M}^{(j)}$ of ${\widehat{\mathcal{C}}}^{(j)}$. In particular, ${\widehat{\varphi }}_{1,M}^{(1)}$ is the first leading principal component of ${\widehat{\mathcal{C}}}^{(1)}$. The estimation error of ${\varphi }_{1,M}^{(1)}$ is $\mathbf{E}\Vert P_{{\widehat{\varphi }}_{1,M}^{(1)}}-P_{{\varphi }_{1,M}^{(1)}}{\Vert }_{\infty }^2\le c{\log }^{2}n∕n$ (Mas and Ruymgaart 2015), which contrasts with the error cJ²(J + 1)²/(4n) for the single-scale estimate ${\widehat{\varphi }}_{1,S}^{(1)}$ when J ⪢ log n.

To conduct the dimension reduction in (3), X is approximated by its projection onto the principal components ${\varphi }_k^{(j)}$ for k = 1,2,…, K_j and j = 1,2,…, J simultaneously. This projection, denoted by P, is equivalent to the projection onto the linear space $span\{{\varphi }_k^{(j)}:k=1,2,\dots ,K_j,j=1,2,\dots ,J\}$. In practice, it is estimated by the projection ${\widehat{P}}_M$ onto the space $\text{span}\{{\widehat{\varphi }}_{k,M}^{(j)}:k=1,2,\dots ,K_j,j=1,2,\dots ,J\}$. The estimation error of ${\widehat{P}}_M$ is bounded in the following theorem.

Theorem 2. Let ${\mathrm{\lambda }}_1^{(j)}>{\mathrm{\lambda }}_2^{(j)}>\cdots$ be eigenvalues of ${\mathcal{C}}^{(j)}$, which satisfy $c_1{j}^{-1-\alpha }\le {\mathrm{\lambda }}_k^{(j)}\le c_2{j}^{-1-\alpha }$ for some constants c₁, c₂ > 0 and for all j and k. Then, we have

$$E\Vert {\widehat{P}}_M-P{\Vert }_{\infty }^2\le \frac{2c{\log }^{2}n}{n}\sum _{j=1}^J{K}_j^2,$$ (4)

where ${\widehat{P}}_M$ is the multiscale estimate of P based on n i.i.d. samples, and c > 0 is a universal constant.

Proof. Let P^(j) be the projection onto the linear space $\text{span}\{{\varphi }_k^{(j)}:k=1,2,\dots ,K_j\}$. Note that $\mathbf{E}\Vert {\widehat{P}}_M^{(j)}-P^{(j)}{\Vert }_{\infty }^2\le c{K}_j^2{\log }^{2}n∕n$ (Mas and Ruymgaart 2015), where ${\widehat{P}}_M^{(j)}$ is the multiscale estimate of P^(j). Then (4) follows from the fact $\mathbf{E}\Vert {\widehat{P}}_M-P{\Vert }_{\infty }^2\le 2{\sum }_{j=1}^J\mathbf{E}\Vert {\widehat{P}}_M^{(j)}-P^{(j)}{\Vert }_{\infty }^2$. □

Apply the theorem to the above example, we see that the estimation error of ${\widehat{P}}_M$ is bounded by $2c{n}^{-1}{\log }^{2}n{\sum }_{j=1}^J{K}_j^2\le 2c{J}^3{n}^{-1}{\log }^{2}n$. In particular, if we use P^(j) and $P_k^{(j)}$ to denote the projection operators for the linear spaces $\text{span}\{{\varphi }_k^{(j)}:k=1,2,\dots ,K_j\}$ and $\text{span}\{{\varphi }_k^{(j)}\}$, respectively, and denote their multiscale estimates by ${\widehat{P}}_M^{(j)}$ and ${\widehat{P}}_{k,M}^{(j)}$, respectively, then ${\text{sup}}_{Q\in \mathcal{P}}\mathbf{E}\Vert {\widehat{Q}}_M-Q{\Vert }_{\infty }^2\le 2c{J}^3{\log }^{2}n∕n$, where $\mathcal{P}=\{P\}\cup \{P^{(j)}:j=1,\dots ,J\}\cup \{P_k^{(j)}:k=1,2,\dots ,K_j,j=1,2,\dots ,J\}$, and ${\widehat{Q}}_M$ is the multiscale estimator for Q. However, for single-scale FPCA, one has ${\text{sup}}_{Q\in \mathcal{P}}\mathbf{E}\Vert {\widehat{Q}}_S-Q{\Vert }_{\infty }^2\ge \mathbf{E}\Vert {\widehat{P}}_{1,S}^{(1)}-P_1^{(1)}{\Vert }_{\infty }^2>c{J}^4∕(4n)$ which is larger than the multiscale one when J ⪢ log² n, where ${\widehat{Q}}_S$ is the single-scale estimator for Q. Note that the bounds in the above derivation are quite loose. The practical advantage of the multiscale approach could emerge for small J, as numerically illustrated by the simulation studies presented in the next section.

To apply multiscale FPCA, one needs to find a good partition of I. A simple and yet effective approach is to segment I according to the variance function V(t) = Var[X (t)] and in practice its empirical version $\widehat{V}(t)={(n-1)}^{\mathrm{-1}}{\sum }_{i=1}^n{\{X_i(t)\}}^2$. Practical functional data are often only recorded at some discrete points of I subject to potential measurement noise, rather than fully observed. There are two types of functional data, including dense data and sparse data. Dense functional data refer to the scenario that each X_i is recorded on a common, regular and dense grid t₁,…,t_m of I, where m denotes the number of observations for each subject X_i; while sparse functional data refer to the case that X_i are measured on an irregular and subject-specific sparse grid t_i1,…, t_imi, where m_i is the number of measurements for X_i. For dense data, the variance function at t_j can be estimated by $\widehat{V}(t_j)=\frac{1}{n-1}{\sum }_{i=1}^n\{X_i(t_j){\}}^2$. For sparse data, such a simple estimate does not work, and we adopt local linear smoothing (Zhang and Wang 2016) on the observations to obtain the estimate $\widehat{V}(t)={\widehat{b}}_{t0}$ with

$$\begin{array}{cc}\hfill ({\widehat{b}}_{t0},{\widehat{b}}_{t1})=& \underset{(b_{t0},b_{t1})\in {\mathbb{R}}^2}{\text{arg min}}\sum _{i=1}^n\frac{1}{m_i}\sum _{j=1}^{m_i}\mathcal{K}\left(\frac{t_{ij}-t}{h}\right)\hfill \\ \hfill & \times [\{X_i(t_{ij}){\}}^2-b_{t0}-b_{t1}(t_{ij}-t)\}{]}^2,\hfill \end{array}$$

where $\mathcal{K}$ is a kernel function supported on [−1,1], and h > 0 is the bandwidth to be chosen by cross-validation. Therefore, for both dense and sparse functional data, we can obtain the estimate of V(t) on a dense and regular grid t₁,…,t_m of I. To derive a partition on I for MFPCA, we apply a multiple change point detection method (Niu and Zhang 2012; Frick, Munk, and Sieling 2014) on $\widehat{V}(t_1),\dots ,\widehat{V}(t_m)$ to discover the change points of $\widehat{V}(t)$ and partition the interval I according to those points, or we may apply the propagation-separation method to partition I into disjoint regions (Polzehl and Spokoiny 2006; Spokoiny and Vial 2009; Zhu, Fan, and Kong 2014). These change point detection methods also provide data-driven approaches to select the number of change points, which determines the number J of subintervals of the partition. Alternatively, one can visualize the empirical variance function and then determine the number of change points manually, which is often sufficient and effective in practice. The number K_j of principal components can be selected by a threshold (e.g. 95%) on the fraction of variance explained (FVE) for the jth subinterval, j = 1,2,…,J. The complete algorithm is given below.

Algorithm 1 (MFPCA). Suppose that X₁,…,X_n are functional data on a common interval I, either given in the dense form or sparse form.

1. Obtain the estimate $\widehat{V}(t)$ on a dense and regular grid t₁ < … < t_m of I.

2. Apply a multiple change point detection method on $\widehat{V}(t_1),\dots ,\widehat{V}(t_m)$. Suppose there are J — 1 change points that are denoted by T₁ < … < T_J−1. Partition I into J subintervals according to T₁ < … < T_J−1. Denote the subintervals by I₁,…,I_J.

3. Apply single-scale FPCA on each I_j, with data $X_1^{(j)},\dots ,X_n^{(j)}$, recalling that $X_i^{(j)}$ denotes the restriction of X_i to I_j. Suppose ${\widehat{\mathrm{\lambda }}}_k^{(j)}$ for j = 1, 2,…,K_j and j = 1,2,…,J are the first $K={\sum }_{j=1}^J$ K_j empirical eigenvalues from all subintervals I_j and ${\widehat{\varphi }}_k^{(j)}$ are their corresponding eigenfunctions. Each function X_i is approximated by $X_i(t)\approx {\sum }_{j=1}^J{\sum }_{k=1}^{K_j}{\widehat{\xi }}_{i,k}^{(j)}{\widehat{\varphi }}_k^{(j)}(t)$, where the scores ${\widehat{\xi }}_{i,k}^{(j)}$ are computed by ${\int }_{I_j}{\widehat{\varphi }}_k^{(j)}(t)X_i^{(j)}(t)\mathrm{d}t$.

The number of overall principal components, K, can be determined by a fractional variance explained threshold, i.e., the smallest number of leading components required to account for at least 95% of the variance of the data. In practice, the multiscale features might be buried by the first singlescale principal component ϕ₁, i.e., the variance function of X does not exhibit multiscale features, but the variance function of X − P_ϕ1 X might. In this case, we can estimate the first single-scale principal component, denoted by ${\widehat{\varphi }}_{1,S}$, and then apply the above multiscale algorithm to the residuals $X_i-P_{{\widehat{\varphi }}_{1,S}}{X}_i$. Indeed, this procedure can be applied recursively to each partition to form hierarchical FPCA which is a multiscale system. In such a hierarchical structure, different layers represent FPCA that is performed at different scales, with the bottom layer corresponding to the finest.

4. Numerical Illustration

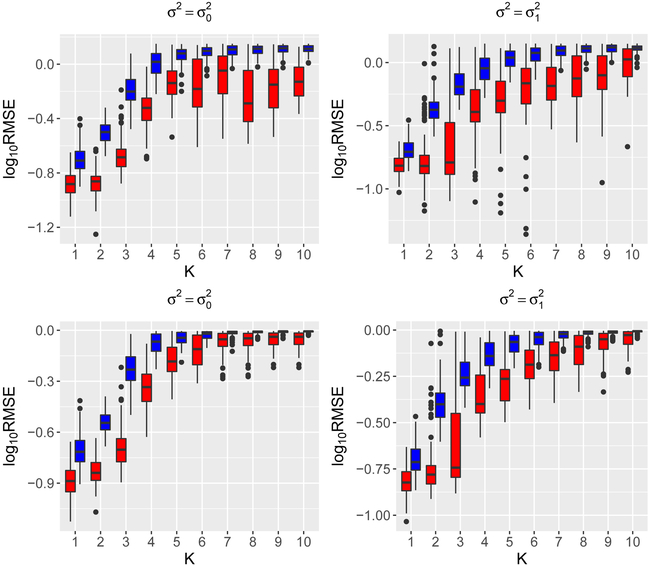
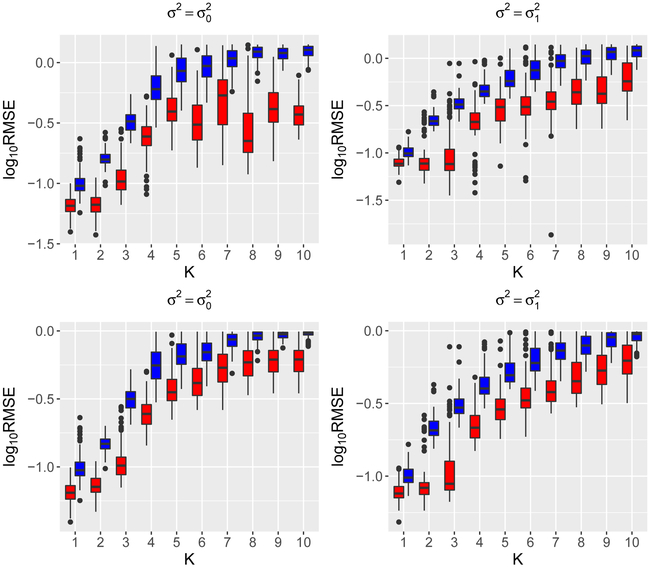
We illustrate the estimation of eigenfunctions ϕ and projection P_Φ via n = 50 and n = 200 simulated samples from a Gaussian process on the interval [0,1] with mean function μ(t) = e^{−(t−0.1)2/0.003} — 2e^{−(t+0.1)2/0.008} + e^{−(t−0.95)2/0.01} − 0.5e^{−(t−0.7)2/0.012}, variance function ${\sigma }_0^2(t)=e^{-(t-0.05{)}^2∕0.01}(t+0.05)+1.5e^{-(0.95-t{)}^2∕0.015}(1.05-t)$ and Matérn correlation function $\rho (s,t)=2^{1-\nu }(\sqrt{2\nu }\mid s-t\mid {)}^{\nu }{B}_{\nu }(\sqrt{2\nu }\mid s-t\mid )∕\Gamma (\nu )$, where B_ν is the modified Bessel function of the second kind of order ν, Γ is the gamma function, and we set ν = 0.1. The mean function and variance function are specifically designed to mimic the shape of the mean function and variance function in the data application that follows. For the purpose of comparison, we also include the case of variance function ${\sigma }_1^2(t)\equiv 1$, which might favor single-scale FPCA. We repeat each simulation setting N = 100 times independently. The estimation quality of an estimator $\widehat{\varphi }$ for an eigenfunction ϕ is quantified by the Monte Carlo root mean squared error (RMSE), defined by $(\widehat{\varphi })=\frac{1}{N}{\sum }_{r=1}^N\Vert {\widehat{\varphi }}_{(r)}-\varphi {\Vert }_{{\mathcal{L}}^2}$, while for an estimator $\widehat{P}$ of the projection P, the Monte Carlo RMSE is given by $(\widehat{P})=\frac{1}{N}{\sum }_{r=1}^N\Vert {\widehat{P}}_{(r)}-P{\Vert }_{\infty }$, where ${\widehat{\varphi }}_{(r)}$ and ${\widehat{P}}_{(r)}$ are the estimates produced in the rth simulation replication. The results, shown in Figure 1 and 2, suggest that the multiscale approach produces better estimation quality for eigenfunctions and projections, with more prominent advantage when data exhibit a multiscale feature, such as in the case of ${\sigma }^2(t)={\sigma }_0^2(t)$.

Figure 1:

log₁₀(RMSE) of the multiscale (red) and singlescale (blue) estimators for the first 10 eigenfunctions (top panels) and projection (bottom panels) onto the first k leading components for k = 1, 2,…,10 for n = 50.

Figure 2:

log₁₀(RMSE) of the multiscale (red) and singlescale (blue) estimators for the first 10 eigenfunctions (top panels) and projection (bottom panels) onto the first k leading components for k = 1, 2,…, 10 for n = 200.

We apply multiscale FPCA to analyze the brain microstructure in the corpus callosum of healthy subjects and patients with multiple sclerosis (MS). MS is a common demyelinating disease that is often caused by immune-mediated inflammation. More precisely, demyelination refers to damage to myelin, an insulating material that covers nerve cells, protects axons and helps nerve signal to travel faster. Patient with MS suffer from demyelination that occurs in the white matter of the brain and can lose mobility or even cognitive function (Jongen, Ter Horst, and Brands 2012). Myelin damage in the brain can be examined by diffusion tensor imaging (DTI), which produces highresolution images of white matter tissues by tracing water diffusion within the tissues. Fractional anisotropy of water diffusion can be determined from DTI and evaluated in relation to MS (Ibrahim et al. 2011).

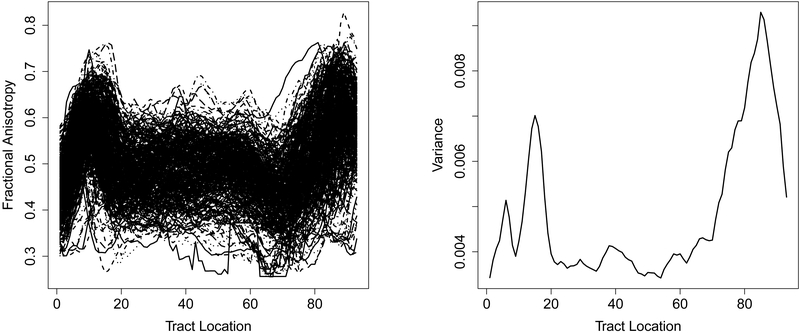
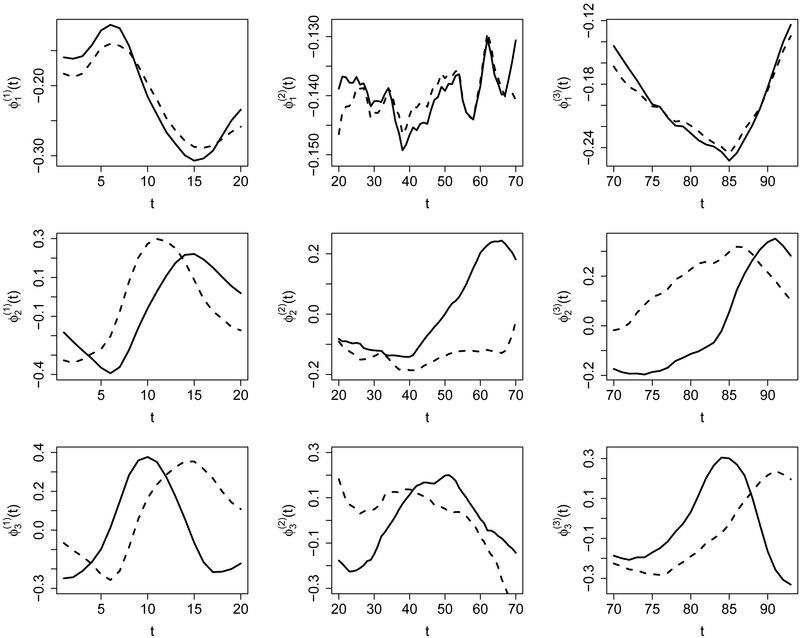
The DTI dataset we used in the following analysis was collected at Johns Hopkins University and the Kennedy-Krieger Institute. It consists of data from n₁ = 340 MS patients and n₂ = 42 healthy subjects. All fractional anisotropy profiles are recorded on a common grid of 93 points, as shown in the left panel of Figure 3. It seems that these profiles have larger variance at both ends relative to that in the middle. This is confirmed by the cross-sectional variance that is plotted in the right panel in Figure 3. We see that the variance function can be divided into three regions, including [0, 20], [20, 70] and [70,93], with relatively small variance density at [20,70]. This motivates us to apply the proposed multiscale FPCA on these regions separately. The first three estimated eigenfunctions of each region are shown in Figure 4, as well as the first three single-scale eigenfunctions. For comparison, the restriction of these single-scale eigenfunctions to each region is normalized to unit ${\mathcal{L}}^2$ norm. We observe that both the multiscale FPCA and single-scale FPCA yield similar results for the first principal component on each region, but differ substantially for the second and third components. For example, the first principal component on the region [20,70] is almost a straight line, which can be interpreted as a size component, i.e., subjects with a positive score have larger fractional anisotropy than an average subject on locations between 20 and 70. However, for the second component, the multiscale analysis is able to capture additional features of the data on the region [20,70], while the single-scale analysis still yields almost a straight line that is similar to the depiction of its first component within that region. This agrees with our analysis in Section 2: as fractional anisotropy has low variance density on [20,70], single-scale FPCA prioritizes other regions.

Figure 3:

Left panel: fractional anisotropy profile of 382 subjects. Right panel: empirical variance function of fractional anisotropy profile.

Figure 4:

The first 3 principal components of each partition by multiscale FPCA (solid) and single-scale (dashed) FPCA.

It is of interest to see whether the additional patterns uncovered by MFPCA are useful for subsequent analysis, such as predicting MS status based on fractional anisotropy. To answer this question, we study classification of MS patients and healthy subjects using a random forest classifier based on the scores derived from the first K principal components. To account for the imbalance of the data, we adopt a simple undersampling strategy to train the classifier as follows. We randomly sample 42 subjects among all 342 MS patients without replacement, and combine those data with the data from the 42 healthy subjects to form a new dataset, which we then randomly divide into two equal halves. The classifier is trained on one half, while the correct classification rate is computed on the other half. We repeat the above procedure 100 times independently for each K = 1,2,…, 12, where 12 is the number of components required to explain over 95% of the variance of the data. In reality, K could be determined by cross-validation or BIC criterion. We also compare the proposed method to wavelet transformation which is capable of localizing signals in time domain. Specifically, each fractional anisotropy profile is represented by a set of coefficients with respect to Daubechies’ least asymmetric wavelets (Daubechies 1992), and wavelet coefficients are fed into a random forest classifier. Different vanishing moments are considered, namely, from db1 to db6. Roughly speaking, wavelets of more vanishing moments can represent more complex function with a sparser set of wavelet coefficients.

The results, shown in Table 1, clearly suggest that MFPCA outperforms single-scale FPCA for all values of K except K = 3. We note that the first three multiscale components, ${\varphi }_1^{(2)}$, ${\varphi }_1^{(3)}$ and ${\varphi }_1^{(1)}$, are the first component from each region. As previously stated, the first multiscale principal component and the single-scale counterpart for each region are almost identical, which might explain why the performance of classification for both methods is quite close when K ≤ 3. A possible explanation for the observation that the multiscale method performs worse when K = 3 is that the third multiscale principal component might not be strongly related to MS status. In such case, including the component in the model does not reduce prediction bias, but increases prediction variability and thus reduces the correct classification rate.

Table 1:

Correct classification rates of the random forest classifier trained on wavelet basis coefficients, multiscale principal component scores and single-scale principal component scores, respectively.

K	1	2	3	4	5	6
Multiscale	66.2	71.0	69.9	70.5	72.9	73.4
Single-scale	64.7	69.8	70.5	69.8	70.7	70.9
K	7	8	9	10	11	12
Multiscale	74.5	73.5	73.9	72.5	72.8	72.6
Single-scale	71.1	70.9	71.1	69.5	69.7	69.9
	db1	db2	db3	db4	db5	db6
wavelet	69.5	70.8	68.6	70.1	69.5	69.1

As high-order components come into play, in particular when the fifth component ${\varphi }_2^{(3)}$, the sixth component ${\varphi }_2^{(2)}$ and the seventh component ${\varphi }_3^{(1)}$ are included, the advantage of MFPCA becomes more prominent. In contrast, for singlescale FPCA, the classification performance barely improves when more principal components are added. This demonstrates that MFPCA is able to discover useful features that might not be captured by single-scale FPCA in regions of low variance density. The MFPCA method also outperforms the wavelet method, likely due to the fact that principal components derived from MFPCA are innately data-driven, while wavelet bases are not. Such data-driven feature allows a parsimonious representation of functional data and is attractive in practice. For instance, in the above simulated functional data, on average 12 principal components are sufficient to account for 95% of variation of data, while over 50 wavelets are required to achieve a similar level of representation.

5. Concluding Remark

We have presented a multiscale FPCA method for functional data and demonstrated that it is numerically superior to its single-scale counterpart and the well known wavelet transformation, thanks to its data-driven nature and the ability to localize signals in time domain. It is worth of noting that while principal component scores from the same segment are uncorrelated, those from different segments could be correlated. Such correlation indeed accounts for the correlation structure among different segments. This is distinct from block-diagonal structures where functional data from different segments are uncorrelated or even independent for Gaussian processes. It is also of interest to apply the proposed MFPCA method to machine learning tasks other than classification, such as regression and clustering, which is one of our future research topics.