Abstract
The purpose of this study was to compare the power production characteristics of the jump squat (JS), hexagonal barbell jump (HEXJ), and jump shrug (JShrug) across a spectrum of relative loads. Fifteen resistance-trained men completed three testing sessions where they performed repetitions of either the JS, HEXJ, or JShrug at body mass (BM) or with 20, 40, 60, 80, or 100% of their BM. Relative peak power (PPRel), relative force at PP (FPP), and velocity at PP (VPP) were compared between exercises and loads. In addition, power-time curves at each load were compared between exercises. Load-averaged HEXJ and JShrug PPRel were statistically greater than the JS (both p < 0.01), while no difference existed between the HEXJ and the JShrug (p = 1.000). Load-averaged JShrug FPP was statistically greater than both the JS and the HEXJ (both p < 0.001), while no statistical difference existed between the JS and the HEXJ (p = 0.111). Load-averaged JS and HEXJ VPP were statistically greater than the JShrug (both p < 0.01). In addition, HEXJ VPP was statistically greater than the JS (p = 0.009). PPRel was maximized at 40, 40, and 20% BM for the JS, HEXJ, and JShrug, respectively. The JShrug possessed statistically different power-time characteristics compared to both the JS and the HEXJ during the countermovement and propulsion phases. The HEXJ and the JShrug appear to be superior exercises for PPRel compared to the JS. The HEXJ may be considered a more velocity-dominant exercise, while the JShrug may be a more force-dominant one.
Key words: jump squat, hexagonal barbell jump, jump shrug, force-velocity curve, power-time curve
Introduction
Lower extremity ballistic exercises (e.g. jumping exercises) are often used to develop power characteristics that may transfer to sport performance due to their ability to train the triple extension of the hip, knee, and ankle (plantar flexion) joints. In order to increase the intensity of the training stimulus, previous research has indicated that an external resistance can be added to the lifter (de Villarreal et al., 2009). Given that heavier loads can increase force production during jumping (Moir et al., 2012), weighted jumps have become popular resistance exercises for developing muscular power. The most common methods of applying resistance to jumps include using barbells, dumbbells, weighted vests, and elastic bands. Compared to traditional squat movements, loaded jumps may be more effective at enhancing jump performance due to their ballistic nature, movement specificity, and ability to avoid undesirable deceleration, which typically occurs during the concentric phase of most exercises (Newton et al., 1996; Suchomel et al., 2018b). While there are a number of variations to choose from, limited research has compared the differences between different types of loaded jumps (Swinton et al., 2012).
The jump squat (JS) may be the most commonly prescribed weighted jump (Loturco et al., 2015). Similar to a countermovement jump, the lifter stands with the barbell on their upper back, performs a rapid countermovement to a self-selected depth, and jumps as high as possible. Previous JS literature has investigated the load-power relationship (Bevan et al., 2010; Cormie et al., 2007; Stone et al., 2003), with the goal of identifying the load that maximizes power output. Some literature has indicated that the greatest power output occurred with loads ranging from 30 to 60% of an individual's one repetition maximum (1RM) back squat (Stone et al., 2003); however, additional research indicated that power was maximized at body mass (BM) or under an unloaded condition (Cormie et al., 2007; Dayne et al., 2011). Although a single load may maximize power output, a recent meta-analysis indicated that a range of loads should be prescribed to optimize power development (Soriano et al., 2015).
Another loaded jump variation includes the use of a hexagonal barbell (HEX). HEX exercises allow individuals to stand within the barbell frame and hold the resistance at arms’ length. Previous research indicated that HEX deadlifts (Swinton et al., 2011) and HEX jumps (HEXJ) (Swinton et al., 2012) produced greater force, velocity, and power compared to the same movements using a traditional barbell. Because the position of the external resistance is closer to the individuals' center of mass during HEX exercises, there appears to be a favorable change in the resistance moment arms at individual joints that results in an enhanced performance (Swinton et al., 2011). Previous research showed that the greatest power output during a HEXJ occurred between 2040% of a 1RM back squat (Swinton et al., 2012) and 10-20% of a 1RM box squat (Turner et al., 2015). From a loading standpoint, the HEXJ may have an advantage over other loaded jumps due to the orientation of the load, as described above. This may allow individuals to use heavier loads for power development, as the technique of the exercise may not be compromised compared to other exercises. Thus, due to its ability to produce high magnitudes of force and power, the HEXJ seems to be an effective alternative to the JS.
A third loaded jump exercise that has been investigated recently is the jump shrug (JShrug) (Kipp et al., 2018; Suchomel et al., 2013, 2014b, 2016b). The JShrug is a weightlifting pulling derivative that includes a unique countermovement (e.g. hip hinge and subsequent re-bending of the knee joints) compared to the JS and the HEXJ. Although different from the other exercises, an individual is still cued to jump as high as possible (Suchomel et al., 2014a). The JShrug has been shown to maximize power production at loads ranging from 30-45% of a 1RM hang power clean, although lighter loads have not been assessed (Kipp et al., 2018; Suchomel et al., 2013; 2014b; Suchomel and Sole, 2017b). While this exercise produced greater power output than other weightlifting derivatives across a loading spectrum (Suchomel et al., 2014b; Suchomel and Sole, 2017b), the authors noted that the technique of the JShrug may break down at heavier loads and may be most effectively programmed using lighter loads. Given that previous literature has indicated that weightlifting derivatives may produce greater relative power output compared to other resistance training exercises (Haff and Stone, 2015; Suchomel and Comfort, 2018), it is possible that the JShrug may produce similar or greater power output compared to the JS and HEXJ. However, no previous research has examined these differences.
Because previous literature has indicated that changing the position of the external load during multi-joint resistance exercises may alter power production characteristics, further research is needed to examine differences between the JS, HEXJ, and JShrug. The purpose of this study was therefore to compare the power production characteristics of the JS, HEXJ, and JShrug across a spectrum of relative loads. As lower body power output is often an emphasis while training in the weight room, sport scientists and practitioners may benefit from research that determines which exercise and load optimizes power output. It was hypothesized that the JShrug would produce the greatest power-time characteristics compared to the HEXJ and JS, and that the HEXJ would produce greater magnitudes compared to the JS. It was also hypothesized that power and velocity would decrease, while force would increase with heavier loads.
Methods
Design
A repeated measures design was used to examine the differences in power production characteristics between the JS, HEXJ, and JShrug exercises performed at BM and with 20, 40, 60, 80, and 100% of the participants’ BM (Lake et al., 2018; Mundy et al., 2017).
Participants
Fifteen resistance-trained men (age: 22.5 ± 3.3 y, body height: 163.0 ± 8.6 cm, BM: 73.0 ± 11.3 kg, relative back squat 1RM: 1.8 ± 0.3 kg·kg-1) who performed regular resistance training at least twice per week for the past two years volunteered to participate in this study. Each participant had previous experience with the JS and HEXJ exercises; although only 10 out of the 15 participants had previous experience with the JShrug. However, every participant had previous experience of training with the power clean and its variations. Each participant completed a 1RM back squat and familiarization session and three separate exercise testing sessions. Prior to the beginning of the study, each participant read and signed a written informed consent form in accordance with Carroll University’s institutional review board policies.
Procedures
Upon arrival for their 1RM back squat and familiarization session, the principal investigator collected information on the BM and estimated 1RM back squat of each participant. Afterwards, each participant performed a standardized warm-up consisting of brief light-moderate cycling followed by dynamic stretching (e.g. lunges, straight leg march, walking quadriceps stretch, etc.). Following the warm-up, each participant completed a 1RM back squat protocol as described previously (Suchomel et al., 2016a). A 1RM back squat was completed to provide further information about the training status of the participants. Briefly, participants performed warm-up back squat sets using submaximal loads of 30, 50, 70, and 90% of their estimated 1RM. The warm-up protocol included five repetitions at 30%, five repetitions at 50%, three repetitions at 70%, and one repetition at 90% of each participant’s estimated 1RM. The principal investigator and research assistants determined each maximal attempt load based on the final warm-up set and/or previous maximal attempts. A minimum 2.5 kg increase between maximal attempts was enforced. All warm-up and maximal attempts were performed with an Eleiko barbell and bumper plates (Eleiko USA, Chicago, IL, USA). Participants were given two minutes of rest following the first two warm-up sets, three minutes following the last two warm-up sets, and at least three minutes between 1RM attempts. Finally, in order to be considered a successful 1RM squat attempt, each participant was required to squat to a depth where the top of their thigh was parallel to the ground (visually monitored by an experienced strength and conditioning coach).
Following a self-selected rest period, each participant was familiarized with the JS, HEXJ, and JShrug exercises. Prior to practicing each exercise, the principal investigator demonstrated each exercise and included the jumping cues (3, 2, 1, Jump!) that would be used during the exercise testing sessions. Each participant then practiced each exercise using submaximal loads equating to 30 kg or less. Because several of the participants were unfamiliar with the JShrug, they were coached through the exercise using coaching cues provided in previous literature (Suchomel et al., 2014a). Each individual was considered to be competent with the JShrug exercise following this instructional period.
Participants returned to the laboratory on three occasions the week following the familiarization session for the JS, HEXJ, and JShrug exercise testing sessions. The first exercise testing session took place one week following the familiarization session and all of the exercise testing sessions were separated by 48-72 hours. In addition, the order of the testing sessions was randomized. Upon arrival for each testing session, the BM of each participant was recorded and used to calculate the loads during each jump, and to subsequently permit ratio scaling of the performance variables. Before performing their test repetitions, participants first completed the same standardized warm-up that was performed during the familiarization session and submaximal jumps of the exercise that was selected for that day. Specifically, participants completed two repetitions at 50 and 75% of their perceived maximal effort using 30 and 50% of their BM. Following the warm-up, each participant performed two maximal effort repetitions of either the JS, HEXJ, or JShrug at BM using a PVC pipe (< 1 kg) and with 20, 40, 60, 80, and 100% BM using various barbells (7.5, 15, and 20 kg) and bumper plates. Each load was rounded to the nearest 0.5 kg. For both the HEXJ and JShrug repetitions that were performed with 60% of BM or higher, participants wore lifting straps to prevent grip strength from being a limiting factor. The order of loads was randomized during the first testing session and was kept constant during the remaining testing sessions. This was done in an attempt to prevent a fatigue or potentiation order effect. One minute of rest was given between repetitions while two minutes were provided between different loads.
Each exercise started with the participant standing motionless with the external load for at least one second on a force platform (Model 609006, Bertec Corporation, Columbus, OH, USA). Each participant then received a countdown of “3, 2, 1, Jump!”. Upon hearing this command, each participant performed a maximal JS, HEXJ, or JShrug. The JS exercise was performed by holding the external load on the upper back, similar to a back squat. After hearing the jump command, the participants performed a rapid countermovement by flexing their hip, knee, and ankle joints (dorsiflexion) before rapidly extending the same joints in an effort to jump as high as possible. The HEXJ started with the participant standing within the HEX barbell or a custom-made HEX PVC apparatus and holding the external load at arm’s length. Following the countdown, participants performed a countermovement similar to the JS before maximally jumping as high as possible. Finally, the JShrug repetitions were performed based on previous recommendations (Suchomel et al., 2014a). Briefly, the participant started the movement in the mid-thigh (power) position (DeWeese et al., 2013). After hearing the countdown, the participant performed a countermovement by moving the barbell down their thighs to a position above the patellae by flexing forward at the hip and moving the hips posteriorly. Upon reaching this position, and without pausing, the participant transitioned back to the mid-thigh position. After reaching the mid-thigh position, the participant jumped as high as possible and shrugged their shoulders.
Measures
All JS, HEXJ, and JShrug repetitions were performed on a mounted, in-ground force platform sampling at 1000 Hz. The raw force-time data were collected directly from the force platform and were exported into a customized spreadsheet (Microsoft Inc., Redmond, WA, USA) for analysis. Prior to each jump repetition, participants stood motionless with the external load on the force platform to determine the system weight (BM + external load) (Owen et al., 2014). The onset threshold of each jump was determined by taking the standard deviation of the vertical ground reaction force across the first second and multiplying it by five. The onset of each jump was considered to have occurred 30 milliseconds prior to the instant where vertical force decreased below the calculated threshold (Owen et al., 2014). The force-time data were integrated to generate the velocity-time data. From here, the power-time curves of each trial were determined by multiplying the given force and velocity data at each time point. The velocity-time record was also used to determine the onset of the propulsive phase for each jump by identifying the instant at which velocity first exceeded 0.01 m·s-1 following the onset of the jump. The greatest power output that was produced during the propulsive phase of each movement was recorded as peak power (PP). The force and velocity magnitudes that occurred at PP were determined as the force at PP (FPP) and velocity at PP (VPP). Relative PP (PPRel) and FPP were calculated by dividing the power and force magnitudes by the participant’s BM. The power-time curves were time-normalized by equalizing the number of samples contained in each curve by adjusting the time delta between samples and then resampling the signal. Similar to previous research (Suchomel and Sole, 2017b), the power-time curves were then expressed as a percentage (0-100% of the jump) for comparison purposes.
Statistical Analyses
The normality of data distribution was assessed using the Shapiro-Wilk test. Relative and absolute reliability was assessed using two-way mixed methods intraclass correlation coefficients (ICC) and typical error (TE%) expressed as coefficients of variation percentages, respectively. Intraclass correlation coefficients (Koo and Li, 2016) and TE% (Cormack et al., 2008) were interpreted based on previous literature. A series of 3 (exercise) x 6 (load) repeated measures ANOVA with Bonferroni post hoc tests were used to examine power production differences between the JS, HEXJ, and JShrug exercises performed across a spectrum of loads (e.g. 0-100% of BM). If the assumption of sphericity was violated, Greenhouse-Geisser adjusted values were used. The effect of load within each exercise was determined using linear contrast analyses with Bonferroni post hoc tests. Hedge’s g effect sizes were calculated to determine the practical significance between each exercise performed at each load. Effect sizes were interpreted as trivial, small, moderate, large, very large, and nearly perfect if Hedge’s g values equaled 0.00-0.19, 0.200.59, 0.60-1.19, 1.20-1.99, 2.00-3.99, and ≥ 4.00, respectively (Hopkins, 2014). In addition, 95% confidence intervals (CI) were calculated for all pairwise comparisons. Power-time data were analyzed using 95% CI calculated at each time point within the time normalized curves for each exercise. All statistical analyses were performed within SPSS 25 (IBM, Armonk, NY, USA) and the criterion level for statistical significance was set at p ≤ 0.05.
Results
All variables were normally distributed and considered highly reliable (ICC ≥ 0.97) with acceptably low variability (TE% ≤ 3.6) (Table 1).
Table 1.
Relative peak power (PPRel), relative force at peak power (FPP), and velocity at peak power (VPP) reliability statistics for the jump squat (JS), hexagonal barbell jump (HEXJ), and jump shrug (JShrug) performed at different percentages of body mass (BM).
| (% Load BM) | Reliability Statistic | Exercise |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| JS |
HEXJ |
JShrug |
||||||||
| PPRel | FPP | VPP | PPRel | FPP | VPP | PPRel | FPP | VPP | ||
| BM | ICC | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 |
| TE% | 1.6 | 1.3 | 1.3 | 1.9 | 2.4 | 1.8 | 2.7 | 1.8 | 1.7 | |
| 20 | ICC | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.96 | 0.99 | 0.99 | 0.98 |
| TE% | 1.3 | 2.0 | 1.4 | 2.3 | 2.2 | 2.2 | 3.6 | 1.6 | 2.6 | |
| 40 | ICC | 0.99 | 0.99 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 |
| TE% | 2.4 | 2.1 | 1.8 | 1.7 | 2.3 | 1.7 | 2.1 | 2.7 | 1.7 | |
| 60 | ICC | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.99 | 0.98 | 0.99 |
| TE% | 2.2 | 1.7 | 1.4 | 1.9 | 1.9 | 2.1 | 2.3 | 2.9 | 1.6 | |
| 80 | ICC | 0.99 | 0.99 | 0.97 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 |
| TE% | 2.3 | 1.9 | 2.2 | 1.8 | 2.1 | 1.2 | 2.9 | 2.0 | 2.0 | |
| 100 | ICC | 0.98 | 0.99 | 0.97 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 |
| TE% | 3.6 | 1.9 | 2.2 | 2.1 | 1.3 | 1.6 | 3.6 | 2.6 | 2.1 | |
Exercise Main Effect
A statistically significant exercise main effect was present for PPRel, FPP, and VPP (all p < 0.001). Post hoc analysis revealed that the load-averaged HEXJ (p < 0.001, CI = 2.8-7.2) and JShrug (p = 0.002, CI = 2.1-9.6) PPRel was statistically greater than the JS with small (g = 0.52) and moderate (g = 0.60) effects being present, respectively. In contrast, there were no differences in PPRel between the HEXJ and JShrug (p = 1.000, g = 0.08, CI = -2.3-4.1). Load-averaged JShrug FPP was statistically greater than both the JS (p < 0.001, g = 1.17, CI = 4.5-8.4) and the HEXJ (p < 0.001, g = 0.91, CI = 3.6-7.2), while no statistical difference existed between the JS and the HEXJ (p = 0.111, g = 0.23, CI = -2.5-0.4). Load-averaged JS (p = 0.001, g = 0.45, CI = 0.06-0.25) and HEXJ (p < 0.001, g = 0.73, CI = 0.16-0.33) VPP was statistically greater than the JShrug. In addition, HEXJ VPP was statistically greater than the JS, although the difference was small (p = 0.009, g = 0.26, CI = 0.02-0.16).
Load Main Effect
Statistically significant load main effects existed for PPRel, FPP, and VPP (all p < 0.001). Figure 1 displays the post hoc analysis of exercise-averaged PPRel, FPP, and VPP. Exercise-averaged PPRel was maximized at 40% BM, which was statistically greater than the PPRel at 80 (p = 0.001, g = 0.31, CI = 1.2-4.9) and 100% BM (p < 0.001, g = 0.58, CI = 3.77.9). In addition, exercise-averaged PPRel at BM (p = 0.001, g = 0.43, CI = 1.6-6.9), 20% (p < 0.001, g = 0.52, CI = 2.5-8.2), 60% (p < 0.001, g = 0.51, CI = 3.3-6.9), and 80% (p < 0.001, g = 0.28, CI = 1.5-3.9) was statistically greater than the exercise-averaged PPRel at 100% BM. Finally, the exercise-averaged PPRel at 20% (p = 0.029, g = 0.25, CI = 0.2-5.1) was statistically greater than the exercise-averaged PPRel at 80% BM. As expected, exercise-averaged FPP was maximized at 100% BM, while VPP was maximized at BM. Statistically significant differences existed between each load for both FPP and VPP (all p < 0.001). Small to very large (g = 0.382.74) effects existed across loads for FPP and moderate to very large (g = 0.73-3.56) effects existed across loads for VPP.
Figure 1.
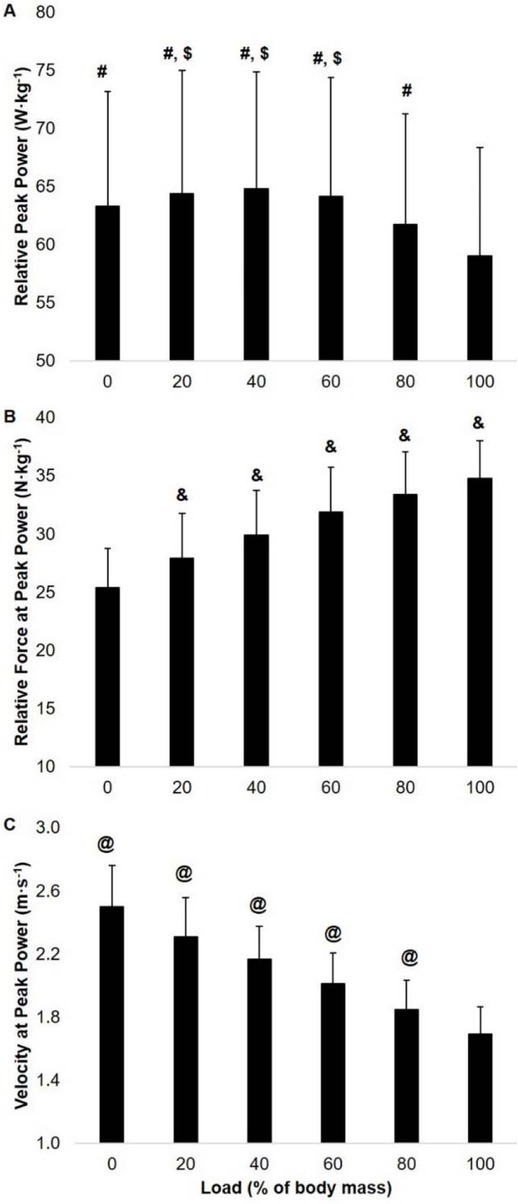
Load main effect post hoc analysis for exercise-averaged relative peak power (A), relative force at peak power (B), and velocity at peak power (C). # = significantly greater than relative peak power at 100% (p ≤ 0.001); $ = significantly greater than relative peak power at 80% (p ≤ 0.05); & = significantly greater than each of the preceding loads (p ≤ 0.001); @ = significantly greater than each of the subsequent loads (p ≤ 0.001).
Within-exercise Linear Contrast Analysis for Load
The within-exercise linear contrast analyses revealed statistically significant differences in PPRel across loads for the JS (p = 0.016), HEXJ (p = 0.021), and JShrug (p < 0.001). The contrast analyses also revealed statistically significant differences in FPP and VPP for the JS, HEXJ, and JShrug (all p < 0.001). The differences in magnitude for FPP displayed moderate-very large (g = 0.72-3.90), small-very large (g = 0.59-3.34), and trivial-very large (g = 0.06-2.70) effects across loads for the JS, HEXJ, and JShrug, respectively. The differences in magnitude for VPP displayed moderate-nearly perfect effects for the JS (g = 0.824.20) and HEXJ (g = 0.97-4.65) and moderate-very large effects for the JShrug (g = 0.73-3.44).
Exercise x Load Interaction Effect
Statistically significant exercise x load interaction effects existed for PPRel, FPP, and VPP (all p < 0.001). Table 2 displays the statistical and practical differences between exercises at each load, while Figures 2 and 3 show the loading effects and force-velocity profiles of each exercise, respectively.
Table 2.
Relative peak power (PPRel), relative force at peak power (FPP), and velocity at peak power (VPP) of the jump squat (JS), hexagonal barbell jump (HEXJ), and jump shrug (JShrug) performed at body mass (BM) and with 20, 40, 60, 80, and 100% of BM. Bold indicates the greatest magnitude produced for each variable. Hedge’s g effect sizes indicate the practical significance in relation to the greatest magnitude produced for each variable. * = significantly greater than BM (p ≤ 0.01); † = significantly greater than 80% (p ≤ 0.05); ‡ = significantly greater than 100% (p ≤ 0.05); & = significantly greater than each of the preceding loads (p ≤ 0.01); @ = significantly greater than each of the subsequent loads (p ≤ 0.01).
| Load | Exercise |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| JS |
HEXJ |
JShrug |
|||||||
| PPRel | FPP | VPP | PPRel | FPP | VPP | PPRel | FPP | VPP | |
| (W·kg-1) | (N·kg-1) | (m·s-1) | (W·kg-1) | (N·kg-1) | (m·s-1) | (W·kg-1) | (N·kg-1) | (m·s-1) | |
| BM | 59.2 ± | 23.5 ± | 2.5 ± | 63.8 ± | 24.3 ± | 2.6 ± | 66.3 ± | 28.4 ± | 2.3 ± |
| 9.1 | 2.3 | 0.2@ | 10.1 | 2.6 | 0.2@ | 10.0‡ | 3.0 | 0.3@ | |
| g | -0.65 | -1.78 | -0.33 | -0.24 | -1.42 | -1.16 | |||
| 20 | 60.0 ± | 25.4 ± | 2.4 ± | 65.2 ± | 26.8 ± | 2.4 ± | 67.9 ± | 31.5 ± | 2.1 ± |
| 9.2‡ | 2.5& | 0.2@ | 10.4‡ | 3.1& | 0.2@ | 11.2†‡ | 3.0& | 0.3@ | |
| g | -0.75 | -2.15 | -0.31 | -0.25 | -1.50 | -1.17 | |||
| 40 | 60.1 ± | 27.3 ± | 2.2 ± | 66.4 ± | 28.9 ± | 2.3 ± | 67.9 ± | 33.5 ± | 2.0 ± |
| 8.4†‡ | 2.3& | 0.2@ | 10.1*†‡ | 3.0& | 0.2@ | 10.3†‡ | 3.2& | 0.2@ | |
| g | -0.80 | -2.17 | -0.50 | -0.14 | -1.46 | -1.47 | |||
| 60 | 60.0 ± | 29.7 ± | 2.0 ± | 65.4 ± | 30.7 ± | 2.1 ± | 67.0 ± | 35.2 ± | 1.9 ± |
| 8.9‡ | 2.7& | 0.2@ | 10.3†‡ | 3.2& | 0.2@ | 10.7†‡ | 3.3& | 0.2@ | |
| g | -0.69 | -1.81 | -0.55 | -0.15 | -1.35 | -1.23 | |||
| 80 | 58.4 ± | 31.5 ± | 1.8 ± | 63.4 ± | 32.3 ± | 2.0 ± | 63.4 ± | 36.4 ± | 1.7 ± |
| 8.3 | 2.5& | 0.2@ | 9.8‡ | 3.2& | 0.2@ | 10.1‡ | 3.3& | 0.2@ | |
| g | -0.52 | -1.58 | -0.67 | 0.00 | -1.22 | -1.25 | |||
| 100 | 57.2 ± | 33.5 ± | 1.7 ± | 61.4 ± | 34.2 ± | 1.8 ± | 58.4 ± | 36.5 ± | 1.6 ± |
| 8.6 | 2.8& | 0.2 | 9.6 | 3.3& | 0.1 | 9.9 | 3.0& | 0.2 | |
| g | -0.13 | -1.02 | -0.58 | -0.71 | -0.31 | -1.27 | |||
Figure 2.
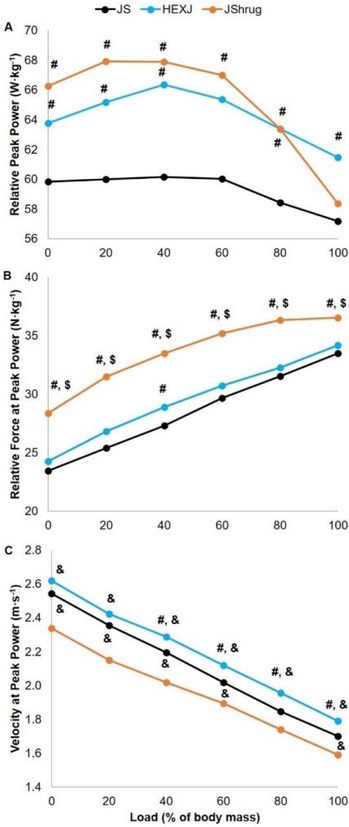
Load-power (A), -force (B), and -velocity (C) profiles of the jump squat (JS), hexagonal barbell jump (HEXJ), and jump shrug (JShrug) performed at body mass and with 20, 40, 60, 80, and 100% of body mass. # = significantly greater than the JS (p ≤ 0.05); $ = significantly greater than the HEXJ (p ≤ 0.001); & = significantly greater than the JShrug (p ≤ 0.05).
Figure 3.
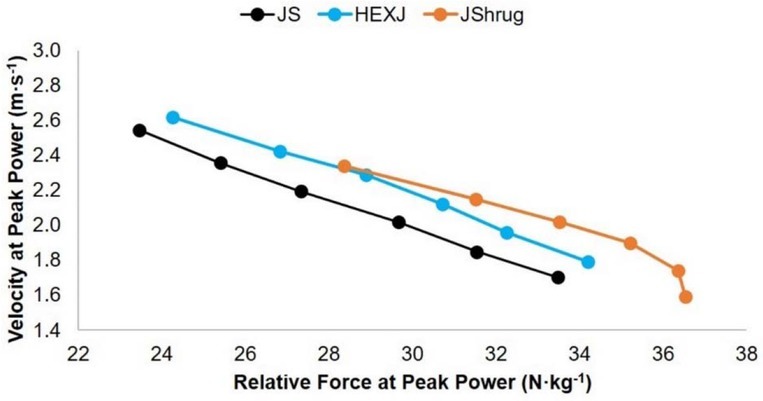
Force-velocity comparisons of the jump squat (JS), hexagonal barbell jump (HEXJ), and jump shrug (JShrug) performed at body mass and with 20, 40, 60, 80, and 100% of body mass.
Power-time Curve Comparison
Figure 4 displays the power-time curves of the JS, HEXJ, and JShrug performed at BM and 20, 40, 60, 80, and 100% BM. There were no statistically significant differences between the JS and HEXJ power-time curves at any load. In contrast, the JShrug possessed statistically different power-time characteristics compared to both the JS and HEXJ. Specifically, the JShrug power-time curves were different from 41-62% and 68-84% of the total jump at BM and 20% BM, 34-60% and 66-81% of the total jump at 40 and 60% BM, and 29-54% and 6679% of the total jump at 80 and 100% BM.
Figure 4.
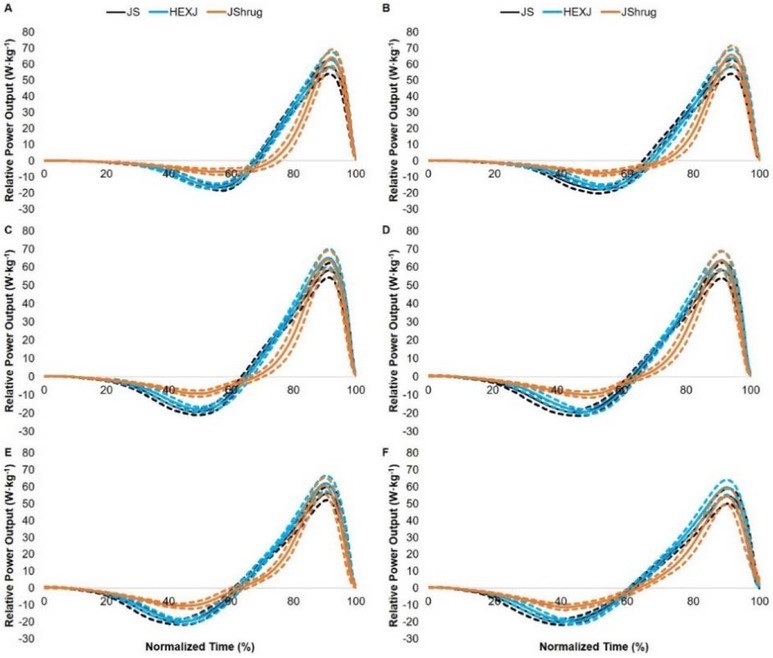
Jump squat (JS), hexagonal barbell jump (HEXJ), and jump shrug (JShrug) time-normalized relative power-time curves performed at body mass (A) and with 20 (B), 40 (C), 60 (D), 80 (E), and 100% (F) of body mass. Solid lines indicate the participant average relative power output at each time point, while the dashed lines represent the 95% upper and lower confidence limits.
Discussion
The aim of the current study was to compare the power production characteristics of the JS, HEXJ, and JShrug performed with the same relative loads. Greater PPRel was produced during the HEXJ and JShrug exercises compared to the JS across all loads, while no notable differences existed between the HEXJ and the JShrug. The JShrug produced greater FPP compared to both the JS and HEXJ exercises across the entire loading spectrum. In contrast, the HEXJ produced greater VPP compared to both the JS and JShrug. As hypothesized, there was a decrease in velocity and an increase in force as loads increased, across all exercises. Finally, the power-time characteristics of the JShrug were different than both the JS and HEXJ across all loads, while no differences existed between the JS and the HEXJ.
This is the first study to compare the power development characteristics of the JS, HEXJ, and JShrug performed across a spectrum of relative loads. The current findings support previous literature that indicated that the HEXJ produced greater jump heights, peak force, PP, and the rate of force development compared to the JS (Swinton et al., 2012). The current study also showed that greater PPRel was produced during the JShrug compared to the JS, although not statistically different to the HEXJ. The greatest PPRel at every load except 100% BM was produced during the JShrug. Small-moderate effects were present between the JShrug and the JS at loads from BM-80%, while trivial-small effects were present between the JShrug and the HEXJ at the same loads. PPRel at 100% BM was greatest during the HEXJ which resulted in small effects compared to both the JS and the JShrug. PPRel during the JS, HEXJ, and JShrug was maximized at loads of 40, 40, and 20% BM, respectively. Trivial-small effects existed across loads for PPRel during the JS and the HEXJ, while trivial-moderate effects existed for the JShrug. It is interesting to note that despite having the highest load-averaged PPRel, the JShrug also had the greatest decrease in PPRel across all loads (9.5 W·kg-1). In addition to previous studies (Kipp et al., 2018; Suchomel et al., 2013; 2014b; Suchomel and Sole, 2017b), the current study provides evidence that the JShrug may be best prescribed at lighter loads due to its unique movement characteristics (e.g. hip hinge) compared to the other movements; however, further research is needed to better examine these mechanical differences. In contrast, the JS and the HEXJ may be best prescribed at slightly heavier loads.
FPP and VPP were examined in the current study in an attempt to determine which exercises should be considered force- or velocity-dominant exercises. Large-very large effect sizes suggest that the JShrug appears to be a more force-dominant exercise compared to both the JS and the HEXJ. This trend continued until the heaviest load (i.e. 100% BM) was used. Although the JShrug still produced the greatest FPP compared to the other exercises, only moderate effects were present at 100% BM. As mentioned in previous research (Suchomel et al., 2013; 2014b), this may be due to a breakdown in technique at heavier loads. This is illustrated in the load-force (Figure 2B) and force-velocity profiles of each exercise (Figure 3). While a linear increase in FPP is displayed by the JS and the HEXJ, a noticeable change occurs at the heaviest load for the JShrug. Specifically, FPP is effectively maintained with a trivial increase from 80 to 100% BM. It is possible that this may be due to the horizontal displacement of the load that occurs during the hip hinge countermovement of the JShrug. While the countermovement of the JS and the HEXJ is essentially performed in the vertical plane, the JShrug requires an individual to displace the barbell down their thighs to the top of their patellae while flexing at the hip joint and shifting their hips posteriorly (Suchomel et al., 2014a). While this movement may result in the recruitment of the hamstring musculature that contributes to hip extension power production upon shortening (Kipp et al., 2018), it may also create a mechanical disadvantage if the load is displaced too far from the individual’s center of mass. Although beyond the current analysis, future research may consider analyzing the displacement and center of mass characteristics of the examined exercises.
In contrast to FPP, the greatest VPP was produced by the HEXJ at every load. While small to moderate effects existed between the HEXJ and JS exercises, the VPP magnitudes produced during the HEXJ resulted in moderate to large differences when compared to the JShrug. The findings comparing the JS and HEXJ are supported by previous literature that indicates that HEX exercises produce greater kinetic magnitudes (e.g. peak force, velocity, power, etc.) compared to traditional barbell exercises (Camara et al., 2016; Swinton et al., 2011; 2012). It should also be noted that the JS produced statistically greater VPP magnitudes compared to the JShrug (moderate effects). Based on the force-velocity profiles (Figure 3), it may be concluded that the JS and HEXJ exercises are velocity-dominant exercises. This is an interesting finding considering that the JShrug may be considered a velocity-dominant exercise when compared to other weightlifting derivatives (Suchomel et al., 2017a). However, if system velocity is the primary goal of an individual’s resistance training program, it appears that the JS and HEXJ may be preferable exercises.
The power-time analysis of each exercise displayed that there were unique power-time characteristics during the JShrug compared to both the JS and HEXJ exercises across all loads, while no differences existed between the JS and HEXJ. Specifically, the JShrug displayed a smaller reduction in relative power output from baseline during the countermovement phase of the movement. This is likely due to the length of the hip hinge countermovement rather than the traditional vertical countermovement of the JS and HEXJ. The other unique power-time characteristic of the JShrug occurred during the propulsion phase of the movement. The JShrug displayed a steeper rate of rise in power production (i.e. rate at which power is developed) compared to the JS and HEXJ. Following the downward displacement of the barbell during the hip hinge movement of the JShrug, the lifter transitions back to the mid-thigh position by re-bending their knees and shifting the hips forward before rapidly extending their hip, knee, and ankle joints (Suchomel et al., 2014a). This motion results in a “scooping” motion of the lower extremities and places the individual in the strongest position of weightlifting derivatives (Enoka, 1979), allowing for maximal force and power production to occur. While the current study focused on power development characteristics, future research should examine the force-time curve characteristics of each exercise to examine both the instantaneous and mechanistic variables that underpin performance.
Most exercises are prescribed based on a percentage of a 1RM or the performance of another lift. For example, the JS has been studied based on percentages of a 1RM back squat (Cormie et al., 2007; Dayne et al., 2011; Stone et al., 2003), while the HEXJ has been examined based on a 1RM back squat (Swinton et al., 2012) or box squat 1RM (Turner et al., 2015) and the JShrug has been examined based on percentages of a 1RM hang power clean (Suchomel et al., 2017b, 2018a; Suchomel and Sole, 2017a, 2017b). While this information is valuable, it is important to provide practitioners with different options for exercise prescription. During the current study, percentages of BM were used to compare the performance of the JS, HEXJ, and JShrug at the same relative loads. While this method of loading has its limitations (e.g. relative strength, body composition, etc.), the current findings may benefit practitioners that do not assess 1RM lifts or prescribe loads based on other exercises. It should also be noted that the percentages of BM may be converted into percentages of the 1RM back squat performed in this study. In that regard, participants in the current study maximized PPRel at 23-40% of their back squat 1RM during the JS and HEXJ and 15-26% of their back squat 1RM during the JShrug.
As mentioned above, the JShrug had the largest decrease in power output across the examined loading spectrum. This decrement in power output may be explained by the inclusion of a hip hinge movement, which may increase the displacement of an external load and system center of mass compared to the countermovement that occurs during the JS and HEXJ exercises. However, it should be noted that displacement differences were also displayed between the straight bar and HEX deadlift exercises (Camara et al., 2016; Swinton et al., 2011). While a greater displacement in the system center of mass may increase the potential to create a longer propulsion phase, and in turn a greater impulse and velocity (Sánchez-Sixto et al., 2018), the barbell position at the end of the JShrug countermovement (above the patellae) creates a large resistance moment arm. As loads increase, it may become more difficult to combat the moment arm created during the transition back to the mid-thigh position, which may prevent the lifter from effectively producing the necessary forces within these positions to create a large movement velocity. Although not a part of the current analysis, it should be emphasized that a wide range of relative strength levels was present (relative back squat = 1.51-2.58 kg·kg-1). It is possible that those with greater relative strength may display smaller decrements in performance across loads within each exercise; however, further research is needed to examine these differences.
This work has some limitations that should be considered when interpreting the results. First, the relative loading in this study was based on percentages of each participant’s BM (Lake et al., 2018; Mundy et al., 2017). While previous research has compared the power characteristics of different exercises using percentages of 1RM (e.g. 1RM back squat or box squat) (Swinton et al., 2012; Turner et al., 2015), the current study could not use the same procedures because no criteria exist for a 1RM JShrug. Second, the current study only included resistance-trained men. Although this information contributes to the existing literature on lower extremity power development, it is important to determine if the same trends in performance exist with resistance-trained women. Thus, it is recommended that future research examines the loading effects of the JS, HEXJ, and JShrug with female participants. Finally, no kinematic data were collected during the performances of each exercise. Based on previous research (Camara et al., 2016; Swinton et al., 2011; 2012), and noted within the discussion, the placement and magnitude of the load for each exercise may modify the lifter’s technique. In order to fully examine the differences between exercises, it is recommended that future research uses 3-dimensional motion analysis.
The HEXJ and JShrug appear to be superior exercises for PPRel compared to the JS; however, each provides unique power production characteristics across loads. The HEXJ may be considered a more velocity-dominant exercise, while the JShrug a more force-dominant one. The JS and HEXJ maximized PPRel at 40% BM, while the JShrug maximized PPRel at 20% BM. Due to their trends in PPRel, FPP, and VPP, it is recommended that the JS and JShrug are prescribed using light-moderate loads, while the HEXJ may be more effectively prescribed using moderate to heavier loads.
References
- Bevan HR, Bunce PJ, Owen NJ, Bennett MA, Cook CJ, Cunningham DJ, Newton RU, Kilduff LP. Optimal loading for the development of peak power output in professional rugby players. J Strength Cond Res. 2010;24:43–47. doi: 10.1519/JSC.0b013e3181c63c64. [DOI] [PubMed] [Google Scholar]
- Camara KD, Coburn JW, Dunnick DD, Brown LE, Galpin AJ, Costa PB. An examination of muscle activation and power characteristics while performing the deadlift exercise with straight and hexagonal barbells. J Strength Cond Res. 2016;30:1183–1188. doi: 10.1519/JSC.0000000000001352. [DOI] [PubMed] [Google Scholar]
- Cormack SJ, Newton RU, McGuigan MR, Doyle TLA. Reliability of measures obtained during single and repeated countermovement jumps. Int J Sports Physiol Perform. 2008;3:131–144. doi: 10.1123/ijspp.3.2.131. [DOI] [PubMed] [Google Scholar]
- Cormie P, McCaulley GO, Triplett NT, McBride JM. Optimal loading for maximal power output during lower-body resistance exercises. Med Sci Sports Exerc. 2007;39:340–349. doi: 10.1249/01.mss.0000246993.71599.bf. [DOI] [PubMed] [Google Scholar]
- Dayne AM, McBride JM, Nuzzo JL, Triplett NT, Skinner J, Burr A. Power output in the jump squat in adolescent male athletes. J Strength Cond Res. 2011;25:585–589. doi: 10.1519/JSC.0b013e3181c1fa83. [DOI] [PubMed] [Google Scholar]
- de Villarreal ESS, Kellis E, Kraemer WJ, Izquierdo M. Determining variables of plyometric training for improving vertical jump height performance: a meta-analysis. J Strength Cond Res. 2009;23:495–506. doi: 10.1519/JSC.0b013e318196b7c6. [DOI] [PubMed] [Google Scholar]
- DeWeese BH, Serrano AJ, Scruggs SK, Burton JD. The midthigh pull: Proper application and progressions of a weightlifting movement derivative. Strength Cond J. 2013;35:54–58. [Google Scholar]
- Enoka RM. The pull in Olympic weightlifting. Med Sci Sports. 1979;11:131–137. [PubMed] [Google Scholar]
- Haff GG, Stone MH. Methods of developing power with special reference to football players. Strength Cond J. 2015;37:2–16. [Google Scholar]
- Hopkins WG. A scale of magnitude for effect statistics. 2014. http://sportsci.org/resource/stats/effectmag.html Available at. accessed on 10.05.2019.
- Kipp K, Malloy PJ, Smith J, Giordanelli MD, Kiely MT, Geiser CF, Suchomel TJ. Mechanical demands of the hang power clean and jump shrug: A joint-level perspective. J Strength Cond Res. 2018;32:466–474. doi: 10.1519/JSC.0000000000001636. [DOI] [PubMed] [Google Scholar]
- Koo TK, Li MY. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med. 2016;15:155–163. doi: 10.1016/j.jcm.2016.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lake JP, Mundy PD, Comfort P, McMahon JJ, Suchomel TJ, Carden P. The effect of barbell load on vertical jump landing force-time characteristics. J Strength Cond Res. 2018 doi: 10.1519/JSC.0000000000002554. Epub ahead of print. [DOI] [PubMed] [Google Scholar]
- Loturco I, Nakamura FY, Tricoli V, Kobal R, Abad CCC, Kitamura K, Ugrinowitsch C, Gil S, Pereira LA, González-Badillo JJ. Determining the optimum power load in jump squat using the mean propulsive velocity. PLoS ONE. 2015;10:e0140102. doi: 10.1371/journal.pone.0140102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moir GL, Gollie JM, Davis SE, Guers JJ, Witmer CA. The effects of load on system and lower-body joint kinetics during jump squats. Sports Biomech. 2012;11:492–506. doi: 10.1080/14763141.2012.725426. [DOI] [PubMed] [Google Scholar]
- Mundy PD, Smith NA, Lauder MA, Lake JP. The effects of barbell load on countermovement vertical jump power and net impulse. J Sports Sci. 2017;35:1781–1787. doi: 10.1080/02640414.2016.1236208. [DOI] [PubMed] [Google Scholar]
- Newton RU, Kraemer WJ, Häkkinen K, Humphries B, Murphy AJ. Kinematics, kinetics, and muscle activation during explosive upper body movements. J Appl Biomech. 1996;12:31–43. doi: 10.1007/s004210050169. [DOI] [PubMed] [Google Scholar]
- Owen NJ, Watkins J, Kilduff LP, Bevan HR, Bennett MA. Development of a criterion method to determine peak mechanical power output in a countermovement jump. J Strength Cond Res. 2014;28:1552–1558. doi: 10.1519/JSC.0000000000000311. [DOI] [PubMed] [Google Scholar]
- Sánchez-Sixto A, Harrison A, Floría P. Larger countermovement increases the jump height of countermovement jump. Sports. 2018;6:131. doi: 10.3390/sports6040131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soriano MA, Jiménez-Reyes P, Rhea MR, Marín PJ. The optimal load for maximal power production during lower-body resistance exercises: a meta-analysis. Sports Med. 2015;45:1191–1205. doi: 10.1007/s40279-015-0341-8. [DOI] [PubMed] [Google Scholar]
- Stone MH, O'Bryant HS, McCoy L, Coglianese R, Lehmkuhl M, Schilling B. Power and maximum strength relationships during performance of dynamic and static weighted jumps. J Strength Cond Res. 2003;17:140–147. doi: 10.1519/1533-4287(2003)017<0140:pamsrd>2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Suchomel TJ, Beckham GK, Wright GA. Lower body kinetics during the jump shrug: impact of load. J Trainol. 2013;2:19–22. [Google Scholar]
- Suchomel TJ, Comfort P. Turner A, Comfort P. Advanced Strength and Conditioning - An Evidence-based Approach. New York, NY, USA: Routledge; 2018. Developing muscular strength and power; pp. 13–38. [Google Scholar]
- Suchomel TJ, Comfort P, Lake JP. Enhancing the force-velocity profile of athletes using weightlifting derivatives. Strength Cond J. 2017a;39:10–20. [Google Scholar]
- Suchomel TJ, DeWeese BH, Beckham GK, Serrano AJ, Sole CJ. The jump shrug: A progressive exercise into weightlifting derivatives. Strength Cond J. 2014a;36:43–47. [Google Scholar]
- Suchomel TJ, Giordanelli MD, Geiser CF, Kipp K. Comparison of joint work during load absorption between weightlifting derivatives. J Strength Cond Res. 2018a doi: 10.1519/JSC.0000000000002927. Epub ahead of print. [DOI] [PubMed] [Google Scholar]
- Suchomel TJ, Lake JP, Comfort P. Load absorption force-time characteristics following the second pull of weightlifting derivatives. J Strength Cond Res. 2017b;31:1644–1652. doi: 10.1519/JSC.0000000000001634. [DOI] [PubMed] [Google Scholar]
- Suchomel TJ, Sato K, DeWeese BH, Ebben WP, Stone MH. Potentiation following ballistic and non-ballistic complexes: The effect of strength level. J Strength Cond Res. 2016a;30:1825–1833. doi: 10.1519/JSC.0000000000001288. [DOI] [PubMed] [Google Scholar]
- Suchomel TJ, Sole CJ. Force-time curve comparison between weightlifting derivatives. Int J Sports Physiol Perform. 2017a;12:431–439. doi: 10.1123/ijspp.2016-0147. [DOI] [PubMed] [Google Scholar]
- Suchomel TJ, Sole CJ. Power-time curve comparison between weightlifting derivatives. J Sports Sci Med. 2017b;16:407–413. [PMC free article] [PubMed] [Google Scholar]
- Suchomel TJ, Taber CB, Sole CJ, Stone MH. Force-time differences between ballistic and non-ballistic half-squats. Sports. 2018b;6:79. doi: 10.3390/sports6030079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suchomel TJ, Taber CB, Wright GA. Jump shrug height and landing forces across various loads. Int J Sports Physiol Perform. 2016b;11:61–65. doi: 10.1123/ijspp.2015-0028. [DOI] [PubMed] [Google Scholar]
- Suchomel TJ, Wright GA, Kernozek TW, Kline DE. Kinetic comparison of the power development between power clean variations. J Strength Cond Res. 2014b;28:350–360. doi: 10.1519/JSC.0b013e31829a36a3. [DOI] [PubMed] [Google Scholar]
- Swinton PA, Stewart A, Agouris I, Keogh JW, Lloyd R. A biomechanical analysis of straight and hexagonal barbell deadlifts using submaximal loads. J Strength Cond Res. 2011;25:2000–2009. doi: 10.1519/JSC.0b013e3181e73f87. [DOI] [PubMed] [Google Scholar]
- Swinton PA, Stewart AD, Lloyd R, Agouris I, Keogh JW. Effect of load positioning on the kinematics and kinetics of weighted vertical jumps. J Strength Cond Res. 2012;26:906–913. doi: 10.1519/JSC.0b013e31822e589e. [DOI] [PubMed] [Google Scholar]
- Turner TS, Tobin DP, Delahunt E. Optimal loading range for the development of peak power output in the hexagonal barbell jump squat. J Strength Cond Res. 2015;29:1627–1632. doi: 10.1519/JSC.0000000000000802. [DOI] [PubMed] [Google Scholar]


