MRI-based treatment planning for liver stereotactic body radiotherapy: validation of a deep learning-based synthetic CT generation method

Abstract

Objective:

The purpose of this work is to develop and validate a learning-based method to derive electron density from routine anatomical MRI for potential MRI-based SBRT treatment planning.

Methods:

We proposed to integrate dense block into cycle generative adversarial network (GAN) to effectively capture the relationship between the CT and MRI for CT synthesis. A cohort of 21 patients with co-registered CT and MR pairs were used to evaluate our proposed method by the leave-one-out cross-validation. Mean absolute error, peak signal-to-noise ratio and normalized cross-correlation were used to quantify the imaging differences between the synthetic CT (sCT) and CT. The accuracy of Hounsfield unit (HU) values in sCT for dose calculation was evaluated by comparing the dose distribution in sCT-based and CT-based treatment planning. Clinically relevant dose–volume histogram metrics were then extracted from the sCT-based and CT-based plans for quantitative comparison.

Results:

The mean absolute error, peak signal-to-noise ratio and normalized cross-correlation of the sCT were 72.87 ± 18.16 HU, 22.65 ± 3.63 dB and 0.92 ± 0.04, respectively. No significant differences were observed in the majority of the planning target volume and organ at risk dose–volume histogram metrics ( p  >  0.05). The average pass rate of γ analysis was over 99% with 1%/1 mm acceptance criteria on the coronal plane that intersects with isocenter.

Conclusion:

The image similarity and dosimetric agreement between sCT and original CT warrant further development of an MRI-only workflow for liver stereotactic body radiation therapy.

Advances in knowledge:

This work is the first deep-learning-based approach to generating abdominal sCT through dense-cycle-GAN. This method can successfully generate the small bony structures such as the rib bones and is able to predict the HU values for dose calculation with comparable accuracy to reference CT images.

Introduction

CT is indispensable in the current practice of radiation therapy; it contains three-dimensional (3D) structural information required for treatment planning, and Hounsfield unit (HU) values that are necessary for dose calculation. Moreover, digitally reconstructed radiographs (DRRs) derived from planning CTs are standard for daily patient setup and localization. Despite these fundamental features, CT as the sole imaging modality leaves certain clinical needs unmet because of its inadequate soft-tissue contrast, which limits the clinician’s ability to precisely and robustly delineate target structures and organs at risk (OARs). It has been recognized that the variability in CT-based gross tumor volume (GTV) segmentation introduces more error than daily setup uncertainties.¹ In the era of highly conformal treatments, including intensity modulated radiotherapy (IMRT), stereotactic radiosurgery/body radiotherapy (SRS/SBRT), as well as proton/heavy ion therapy, accurate target delineation is of paramount importance.

MRI has been widely used in combination with CT because of its superior soft-tissue contrast, which can substantially improve soft tissue segmentation accuracy. Since CT and MR images are acquired separately, the images must be registered to allow the transfer of MR structural information to the CT. However, registration brings a level of complexity and uncertainty that can introduce a systematic error on the order of 2–5 mm depending on treatment sites.² Notably, this error persists throughout the treatment course, which can lead to a geometric miss and compromised tumor control.¹ To address this systematic error, recently attention has been given to MR-only treatment planning, in which MRI is the sole imaging modality, thus eliminating any potential registration errors.^3–7 Other benefits of MR-only treatment workflow include reduced cost, avoidance of CT radiation dose as well as a more efficient workflow.

One major challenge in any MR-only treatment workflow is the generation of synthetic CT (sCT) images for dose calculation. Unlike CT, electron densities are not uniquely related to the voxel-intensities in MRI. Therefore, electron density information must be derived from the MRI by generating a sCT. Until now, the main efforts to produce sCT broadly fall into the following three categories.¹ Segmentation-based methods, which assign single bulk densities to tissue classes delineated either from a CT or an MR image.⁸ MRI intensity to HUs conversion accuracy can be improved by using a second-order polynomial model to obtain subject-specific bone density.⁹ To overcome the limitation requiring manual delineation, fuzzy C-means algorithms^10,11 can be applied to automatically segment MR images into predetermined classes and then assign densities weighed by the probability of each tissue class at a given location. This approach is limited by the requirement to predetermine segmentation classes and bone segmentation errors from MR images.^{12 2} Atlas-based methods: the atlas can be a single template or a database of co-registered MR and CT pairs.¹³ First, the atlas MR images are deformably registered to the subject MR images; the same transformations are then applied to the corresponding atlas CT images. The HU information from the deformed atlas CT image can then be transformed to the subject MR images. If multiatlases are used, the atlas CT numbers can be fused to generate the final sCT. The deformable registration can be obtained by computing the voxelwise median, using a probabilistic Bayesian framework, arithmetic mean process or pattern recognition with Gaussian process or a local image similarity measure.¹² The drawbacks of this method are costly computation time and the lack of robustness in the case of large anatomical variations.^{5 3} Machine learning: the ability to automatically learn effective features from different datasets has made machine learning increasingly popular in generating sCTs. Sophisticated algorithms such as random forest and deep-learning have shown promising results in generating brain, head and neck, and pelvic sCT.^7,14 In general, a model is trained by a large number of databases of co-registered MR and CT pairs. Once the initial training has been implemented, the prediction of a new sCT can be done in a short amount of time when a testing MR is fed into the model. sCT images share the same structural information as MRIs, and the intensities are HU values that closely approximately the real CT. The drawback of current machine learning based methods is that they are often performed in two-dimensional (2D), and thus do not consider the 3D spatial relationships between organs.⁵ This can cause discontinuous prediction results across slices.

Although a number of publications have shown promising results of sCTs in sites such as brain and pelvis,^7,15,16 there has been limited work in abdominal sCT generation. The image quality of abdominal MRIs is commonly affected by intrinsic organ motion. Without motion management, the relatively long acquisition time of MRIs can lead to significant artifacts, which complicates registration between CT and MR images. In addition, differentiating air from bone regions on MR image is more challenging in the abdomen relative to brain or pelvis, because of the small size of ribs. To the best of our knowledge, we are the first to develop and evaluate a deep learning method for sCT generation in the abdomen.

In this work, we developed a deep learning-based algorithm to generate sCT in the context of liver stereotactic body radiation therapy. A novel dense-cycle-generative adversarial network (GAN) was introduced to capture multislices spatial information and to cope with local mismatches between MR and CT images. A novel compound loss function was also employed to better differentiate bone from air structures, as well as to retain sCT sharpness. sCT image and dosimetric accuracy were evaluated by comparing sCT with the real CT images.

methods and materials

Image acquisition

The study cohort was composed of 21 patients diagnosed with hepatocellular carcinoma and treated with liver SBRT. Image data were extracted retrospectively under an IRB-approved protocol. Routine abdominal CT and MR scans were acquired with either breath-hold or abdominal compression to minimize the respiratory motion. CT scans were acquired on a SIEMENS (Erlangen, Germany) Biograph40 with a voxel size of 1.523 × 1.523 mm×2 mm. Three MR scanners were used, including Siemens Skyra 3T, Siemens TrioTim 3T, and GE Signa HDxt 1.5T. T ₁ weighted 3D fat-suppressed fast field echo images were acquired at the Siemens Skyra (two patients) and Siemens TrioTim (two patients) using volumetric interpolated breath-hold examination (VIBE). The sequence applied for these two methods were echo time/repetition time (TE/TR) = 1.34/4.34 ms and TE/TR = 2.45, 2.46/5.27, 6.47 ms, respectively. Field of views (FOVs) were 440 × 275 mm and 440 × 288.75 mm respectively. The voxel sizes were both 1.375 × 1.375 mm×3 mm. T ₁ weighted 2D fat-suppressed fast spoiled gradient echo was applied at the GE Signa HDxt (17 patients). The sequence parameters were: TE ranging from 2.2 to 4.4 ms, TR ranging from 175 to 200 ms. FOV was 480 × 480 mm and the voxel size was 1.875 × 1.875 mm×3 mm. Anatomical structures were contoured by physicians for treatment planning.

Image pre-processing and registration

First, the intensity inhomogeneity of the MR images was corrected by the N4ITK MRI Bias correction filter, available at the open source 3D SLICER 4.8.1. The MR images were then rigidly registered and deformed to match with the corresponding CT images using Velocity AI 3.2.1 (Varian Medical Systems, Inc. Palo Alto, CA). Finally, the registered MR images and their CT pairs were uploaded into our machine-learning algorithm. For the cohort of 21 patients, we used leave-one-out cross-validation. For a given single test patient, the model was trained by the remaining 20 patients. The model was initialized and re-trained for each subsequent test patient by its corresponding group of 20 patients. The training data sets and testing data sets were separate and independent during each study.

sCT generation

The technique used in this study was based on deep learning methods that extract a hierarchy of features from raw input images through a multi layer model.¹⁷ Convolution neural network (CNN)¹⁴ was employed as it has been demonstrated highly accurate and efficient performance in medical image synthesis. However, these methods are valid only when the MR and CT images are perfectly registered, which are not feasible given the degree of organ motion between different image sets and the complexity of the required registrations. In the abdomen, local mismatch and misalignment exist at numerous locations, such as bone, bowel and body surface. In this study, a novel 3D cycle GAN that contains several dense blocks in the generator, so-called dense-cycle-GAN, was introduced to capture both the structural and textural information and to cope with local mismatches between MR and CT images. A novel compound loss function was also employed to effectively differentiate the structure boundaries with significant HU variations and to retain the sharpness of the sCT image. Figure 1 outlines the workflow schematic of the proposed model, which consists of training and synthesizing stages. The training stage consists of four generators and two discriminators. Each generator includes several dense-blocks. In the synthesizing stage, a new MR image is fed into the well-trained model to produce the sCT image. The section below describes the proposed algorithm.

Figure 1.

Schematic flow chart of the proposed algorithm for MRI-based sCT generation. The training stage of our proposed method, which is consisted of four generators and two discriminators, is shown on the left. Each generator includes several dense blocks. The synthesizing stage is shown on the right, in which a new MR image is fed into the well-trained model to produce the sCT. sCT, synthetic CT.

Local voxelwise misalignment of paired MR and CT images can lead to a reduction in the sCT image sharpness. To address this issue, GANs^18,19 were adopted in our architecture. GAN is a deep learning model that simultaneously trains two competing networks and incorporates an additional adversarial loss function to produce higher quality images. However, when applied to the generation of sCTs, it can result in erroneous predictions because the GAN only contains mapping from the MR to CT images. Compared to CT, MR images have more structural information and contrast in soft tissue regions and less at bone/air interfaces. Thus, the mapping is not one-to-one, but can be many-to-one or one-to-many functions. To cope with this issue, we introduced an inverse MRI-to-CT transformation model into the cycle GAN²⁰ to achieve one-to-one MR to CT mapping. 3D image patch (with patch size [64, 64, 5]) was adopted as the input of this model. The patches are extracted by sliding a patch size-based window from the training and prediction images, with overlap 56 × 56 × 2. After sCT image patches are predicted by the network, they are mean fused to produce a 3D image. In patches which overlap upon output, pixel values in the same position are averaged.

They contain more spatial information than the 2D image patches that have been used previously. As shown in Figure 1, in the training stage, the extracted patch from the training MRI was fed into the generator (MRI-to-CT) to produce equal-sized sCTs (synthetic CT). The sCT was then fed into another generator (CT-to-MRI) to generate (back) an equal-sized predicted MRI, termed cycle MRI. In order to maintain the forward–backward consistency, the extracted patch from the training CT was also fed into the two generators to obtain the synthetic MRI and cycle CT. The generator’s training objective is to produce synthetic images that are similar to the real images, while the discriminator’s training objective is to differentiate the synthetic images from the real images. Two discriminators are used in our networks. During training, all the networks are trained simultaneously. Back-propagation is applied in both networks to enhance the performance of both the generators and discriminators, which ultimately result in optimal sCT prediction.

To deal with the issue of transformation between the two different image modalities, dense blocks were employed in the proposed architecture. Residual blocks²¹ are capable of synthesizing images between similar modalities, such as image quality enhancement for low-dose CT and synthesizing CTs from cone beam CTs. In contrast, dense blocks combine low and high frequency information to effectively represent image patches between different imaging modalities. Specifically, the low frequency signal that contains the texture information is obtained from previous convolutional layers. The high frequency signal that contains the structural information is obtained from the current layer. In generator architecture, after two downsampling convolutional layers to reduce the feature map sizes, the feature map goes through nine dense blocks, and then two deconvolutional layers and a tanh layer to perform the end-to-end mapping. The end-to-end mapping denotes the mapping which has equal size input and output. The tanh layer works as a nonlinear activation function and makes it easy for the model to generalize or adapt to a variety of data and to differentiate between outputs, such as determining whether a voxel on a boundary is bony tissue or air. As shown in Figure 1, the dense block is implemented by six convolution layers. The first convolution layer is applied to the input to create $\mathrm{k}$ feature maps. The following four layers are applied to the concatenated information of all the previous feature maps and input to create more feature maps in sequence. The final output of these layers thus contains 5*k feature maps. Finally, the output goes through the last layer to shorten the feature maps to $\mathrm{k}$.²²

Generally, the ${\mathrm{l}}_2$ -norm or ${\mathrm{l}}_1$ -norm distance, i.e. the mean absolute distance or mean squared distance, have been used as generator loss function between the synthetic image and the original image. However, the use of an mean squared distance loss function in the network tends to produce images with blurry regions.²³ In this study, the generator loss function consisted of two losses: (1) the adversarial loss (${\mathrm{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}$) used for distinguishing real images from synthetic images; (2) the distance loss (${\mathrm{L}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}$) measured between real images and synthesis images²⁴ and the distance loss measured between real and cycle images. The accuracy of the generator directly depends on how suitable the loss function is designed. Suppose that the generator G obtains a synthetic image G(X) = Z from original image X to target image Y. A weighted summation of these two metrics forms the compound loss function for the proposed method:

$${\displaystyle \mathrm{G}=\mathrm{a}\mathrm{r}{\mathrm{g}}_{\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{{\lambda }_{\mathrm{a}\mathrm{d}\mathrm{v}}{\mathrm{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}\left(\mathrm{Z}\right)+{\lambda }_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}{\mathrm{L}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}\left(\mathrm{Z},\mathrm{Y}\right)\right\}}$$

Where ${\mathrm{\lambda }}_{\mathrm{a}\mathrm{d}\mathrm{v}}$ and ${\displaystyle {\lambda }_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}}$ are balancing parameter. The adversarial loss function is defined as

$${\mathrm{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}\left(\mathrm{Z}\right)=\mathrm{M}\mathrm{A}\mathrm{D}\left(\mathrm{D}\left(\mathrm{Z}\right),1\right)$$

in cycle GAN-based method.²⁵ For distance loss ${\mathrm{L}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}\left(\mathrm{Z},\mathrm{Y}\right)$ , we introduced a ${\mathrm{l}}_{\mathrm{p}}$ -norm ($\mathrm{p}=1.5$) distance, termed mean $\mathrm{p}$ distance (MPD). We also integrated an image gradient descent (GD) loss term into the loss function, with the aim of minimizing the difference of the magnitude of the gradient between the synthetic image and the original planning CT. In this way, the sCT will try to keep zones with strong gradients, such as edges, effectively compensating for the distance loss term. The generators are optimized as follows:

$$\begin{gathered} {\displaystyle \begin{array}{l}\left(G_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}},G_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}\right)\\ ={\arg }_{G_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}},\underset{G_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}}{min}\left\{\begin{array}{l}{\lambda }_{\mathrm{a}\mathrm{d}\mathrm{v}}\mathrm{M}\mathrm{A}\mathrm{D}\left({\mathrm{D}}_{\mathrm{M}\mathrm{R}}({\mathrm{G}}_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}({\mathrm{I}}_{\mathrm{C}\mathrm{T}}),1\right)\\ +{\lambda }_{\mathrm{M}\mathrm{P}\mathrm{D}}^{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}\Vert G_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}(G_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}(I_{\mathrm{C}\mathrm{T}})),I_{\mathrm{C}\mathrm{T}}{\Vert }_p^p\\ +{\lambda }_{\mathrm{G}\mathrm{D}\mathrm{L}}^{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}\mathrm{G}\mathrm{D}\mathrm{L}({\mathrm{G}}_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}({\mathrm{G}}_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}({\mathrm{I}}_{\mathrm{C}\mathrm{T}})),{\mathrm{I}}_{\mathrm{C}\mathrm{T}})\\ +{\lambda }_{\mathrm{M}\mathrm{P}\mathrm{D}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}\Vert G_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}(I_{\mathrm{C}\mathrm{T}}),I_{\mathrm{M}\mathrm{R}}){\Vert }_p^p\\ +{\lambda }_{\mathrm{G}\mathrm{D}\mathrm{L}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}\mathrm{G}\mathrm{D}\mathrm{L}({\mathrm{G}}_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}({\mathrm{I}}_{\mathrm{C}\mathrm{T}}),{\mathrm{I}}_{\mathrm{M}\mathrm{R}})\\ +{\lambda }_{\mathrm{a}\mathrm{d}\mathrm{v}}^{}\mathrm{M}\mathrm{A}\mathrm{D}({\mathrm{D}}_{\mathrm{C}\mathrm{T}}({\mathrm{G}}_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}({\mathrm{I}}_{\mathrm{M}\mathrm{R}})),1)\\ +{\lambda }_{\mathrm{M}\mathrm{P}\mathrm{D}}^{cycle}\Vert G_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}(G_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}(I_{\mathrm{M}\mathrm{R}})),I_{\mathrm{M}\mathrm{R}}{\Vert }_p^p\\ +{\lambda }_{\mathrm{G}\mathrm{D}\mathrm{L}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}\mathrm{G}\mathrm{D}\mathrm{L}\left({\mathrm{G}}_{\mathrm{C}\mathrm{T}-\mathrm{M}\mathrm{R}}\left({\mathrm{G}}_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}\left({\mathrm{I}}_{\mathrm{M}\mathrm{R}}\right)\right),{\mathrm{I}}_{\mathrm{M}\mathrm{R}}\right)\\ +{\lambda }_{\mathrm{M}\mathrm{P}\mathrm{D}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}\Vert G_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}(I_{\mathrm{M}\mathrm{R}}),I_{\mathrm{C}\mathrm{T}}{\Vert }_p^p\\ +{\lambda }_{\mathrm{G}\mathrm{D}\mathrm{L}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}\mathrm{G}\mathrm{D}\mathrm{L}({\mathrm{G}}_{\mathrm{M}\mathrm{R}-\mathrm{C}\mathrm{T}}({\mathrm{I}}_{\mathrm{M}\mathrm{R}}),{\mathrm{I}}_{\mathrm{C}\mathrm{T}})\end{array}\right\}\end{array} \\ } \end{gathered}$$

$$\begin{gathered} {\displaystyle GDL(z,y)=\sum _{i,j,k}\left\{\begin{array}{l}{\Vert \left|Z_{i,j,k}-Z_{i-1,j,k}\right|-\left|Y_{i,j,k}-Y_{i-1,j,k}\right|\Vert }_2^2\\ +{\Vert \left|Z_{i,j,k}-Z_{i,j-1,k}\right|-\left|Y_{i,j,k}-Y_{i,j-1,k}\right|\Vert }_2^2\\ +{\Vert \left|Z_{i,j,k}-Z_{i,j,k-1}\right|-\left|Y_{i,j,k}-Y_{i,j,k-1}\right|\Vert }_2^2\end{array}\right\} \\ } \end{gathered}$$

where ${\displaystyle {\Vert .\Vert }_p^p}$ denotes the ${\displaystyle l_p}$ norm, and GDL (.) denotes the gradient descentloss function²⁴ ${\displaystyle {\lambda }_{\mathrm{a}\mathrm{d}\mathrm{v}},{\lambda }_{\mathrm{M}\mathrm{P}\mathrm{D}}^{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}},{\lambda }_{\mathrm{G}\mathrm{D}\mathrm{L}}^{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}},{\lambda }_{\mathrm{M}\mathrm{P}\mathrm{D}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}}$ and ${\displaystyle {\lambda }_{\mathrm{G}\mathrm{D}\mathrm{L}}^{\mathrm{f}\mathrm{a}\mathrm{k}\mathrm{e}}}$are regularization parameters for different regularization. The discriminator loss is computed by mean absolute distance between the discriminator results of input synthetic and real images. To update all the hidden layers' kernels, the Adam gradient descent method was applied to minimize both generator loss and discriminator loss.

In the final synthesizing stage, patches of the new arrival image were fed into the MRI-to-CT generator to obtain the sCT patch end-to-end mapping. Then, the final sCT was obtained by patch fusion.

The learning rate for Adam optimizer was set to 2e-4, and the model was trained and tested on an NVIDIA TITAN XP GPU with 12 GB of memory with a batch size of 8. During training, 3.4 GB CPU memory and 10.2 GB GPU memory was used for each batch optimization. The training was stopped after 15,0000 iterations. Training the model took around 15 h, and sCT generation for one test patient took about 2 min.

Evaluation strategies

Image similarity

To quantify the prediction quality, three commonly used metrics were applied, including MAE, PSNR, and NCC. MAE represents the discrepancies between the predictions and the reference HU numbers. PSNR is the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. NCC is a measure of similarity between two series as a function of the displacement of one relative to the other. The three metrics are defined as:

$$MAE=\left|I_{CT}-I_{sCT}\right|/C$$

$$PSNR=10{log}_{10}\left(\frac{Q^2}{{\left|\left|I_{CT}-I_{sCT}\right|\right|}_2^2/C}\right)$$

$$NCC=\frac{1}{C}{\sum }_{x,y,z}\frac{\left(I_{CT}\left(x,y,z\right)-{\mu }_{CT}\right)\left(I_{sCT}\left(x,y,z\right)-{\mu }_{sCT}\right)}{{\sigma }_{CT}{\sigma }_{sCT}}$$

where $I_{CT}$ is the HU value of the ground truth CT image, $I_{sCT}$ is the HU value of corresponding sCT image, $Q$ is the maximal HU value between $I_{CT}$ and $I_{sCT}$ , and $C$ is the number of voxels in the image. ${\mu }_{CT}$ and ${\mu }_{sCT}$ are the mean of CT and PCT image, respectively. ${\sigma }_{CT}$ and ${\sigma }_{sCT}$ are the standard deviation of CT and PCT image, respectively. In general, a better prediction has lower MAE, and higher PSNR and NCC values.

Dosimetric agreement

Given the purpose of acquiring MR images in this patient cohort was to help target volume delineation in the liver, the derived sCT images only included the area directly adjacent to the liver. The sCT thus have fewer axial slices than broader CTs that are necessary for conventional treatment planning. To make the OAR comparison feasible, original CT slices were added to the sCT to create data set of equal size. Since only coplanar beams were used for treatment planning, the relevant dose always fell into the area that was fully covered by the generated sCT. The dosimetric impact from the shared information between the two evaluation sources was minimal.

The Anisotropic Analytical Algorithm (v. 13.7.16) in Eclipse treatment planning system (Varian Medical Systems, Inc. Palo Alto, CA) was used to calculate the treatment dose using the patient’s CT and sCT images. All plans were prescribed with a total dose of 45 Gy in three fractions and normalized to 95% of the planning target volume (PTV) receiving 100% of the prescription dose. According to the literature, normal hepatocytes are sensitive to radiotherapy and liver volume receiving 15 Gy (V15) >700 cm³ is associated with Grade III or higher Radiation Induced Liver Dysfunction.²⁶ Gastrointestinal bleeding is the most frequently encountered non-hepatic toxicity following SBRT. Stomach and bowel volumes receiving 20 Gy should be kept less than 20 cm³.²⁷ In this study, the differences between the sCT and CT for liver V₁₅, stomach and bowel V₂₀, and differences in PTV, OAR D_min, D₁₀, D₅₀, D₉₅ and D_max were evaluated.

To evaluate the plane dose difference of the CT and sCT, the plane dose DICOM files were exported from Eclipse to MyQA software (IBA Dosimetry, Germany), and γ analysis with 1%/1 mm criteria was carried out on the coronal plane that intersects with the treatment isocenter.

Comparison with existing methods

To demonstrate the advantages of the proposed method, we compared it to two state-of-art methods including a 3D fully convolutional neural network (FCN) proposed by Nie et al²⁸ and a GAN network proposed from the same group.²⁹ FCN generates the structured output that can preserve the spatial information in the predicted sCT images by extracting patch-based deep features. Nie et al then applied 3D FCN as a generator in a GAN framework where an additional adversarial loss is introduced with the purpose of producing more realistic sCT images. The MAE and dosimetric endpoints including D_min, D₁₀, D₅₀, D₉₅, D_mean and D_max were compared among our proposed dense-cycle-GAN, FCN and GAN based methods.

Results

In the results section, one representative patient is shown in the images for both HU and dose comparisons. For statistical comparisons, the cohort of 21 patients was evaluated.

sCT image evaluation

Table 1 summarizes the MAE, PSNR and NCC of this cohort. The MAE ranges from 43.74 to 126.54 HU, with mean and median of 72.48 and 65.37 HU, respectively. The PSNR ranges from 13.46 to 28.25 dB, with a mean and median value of 22.43 and 23.16 dB respectively. The NCC ranges from 0.81 to 0.97, with mean and median of 0.92 and 0.93 respectively.

Table 1.

Statistics for the MAE, PSNR and NCC values of the cohort

	Mean	SD	Median	Min	Max
MAE1 (HU)	72.87	18.16	66.46	43.74	126.53
PSNR2 (dB)	22.65	3.63	23.35	13.46	28.25
NCC3	0.92	0.04	0.93	0.81	0.97

MAE, mean absolute error; NCC, normalized cross-correlation; PSNR, peak signal-to-noise ratio; SD, standard deviation.

Figure 2 shows the HU comparison between the original CT and sCT of a representative patient (MAE 62.5). The absolute HU difference between CT and sCT is generally small except the discrepancy at spinous processes and body surface. In the coronal view, a relatively large discrepancy can be seen at the aorta site because of the contrast injection during CT acquisition. There is a slight underestimation of the sCT HU value as can been seen in the overall redness in the HU difference maps (which means the CT HU is higher than sCT HU number). However, the HU profile of the sCT image that includes muscle, rib, liver, kidney, vertebral body and spleen matches closely with the original CT profile (shown in the HU profile graph at the bottom), which means our deep-learning-based algorithm is capable of predicting accurate HU values with rapid structure change.

Figure 2.

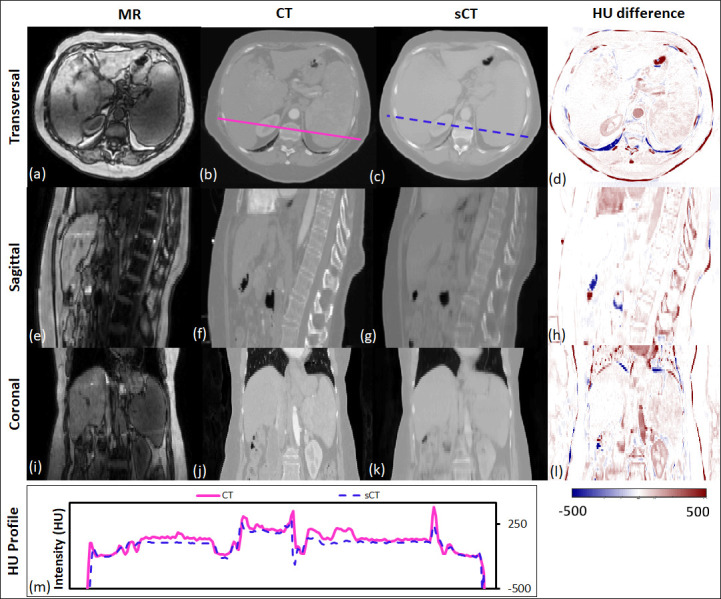
The transverse, sagittal, and coronal images of a representative patient. MR, CT and sCT images and the HU difference between CT and sCT are presented. The CT and sCT voxel-based HU profiles are shown at the bottom, to demonstrate the HU values highlighted in the solid and dash line in the transverse images. HU, Hounsfield unit; sCT, synthetic CT.

Dose evaluation

Plane dose distribution

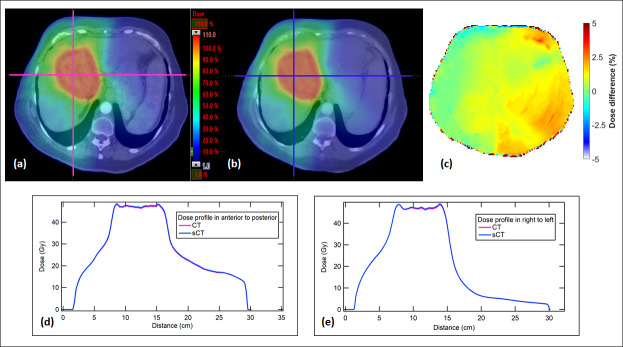
Figure 3 shows the dose distribution comparison in the axial plane from the representative patient. The dose color washes on CT and sCT are similar (Figure 3(a) , and (b)). The voxel dose differences were generally much less than 5% except at the body and air interface (Figure 3(c)). The dose profiles in anterior to posterior axis and right to left are shown in Figure 3(d) , and (e). The profiles from sCT and CT are in good agreement. The γ analyses (1%/1 mm) at the coronal plane all have a passing rate >99%.

Figure 3.

(a) Dose distribution calculated from the original CT. (b) Dose distribution calculated from the sCT. (c) Dose difference (%) distribution. (d) Dose profiles of CT and sCT in anterior to posterior direction. (e) Dose profiles of CT and sCT in right to left direction. sCT, synthetic CT.

Dose–volume statistics

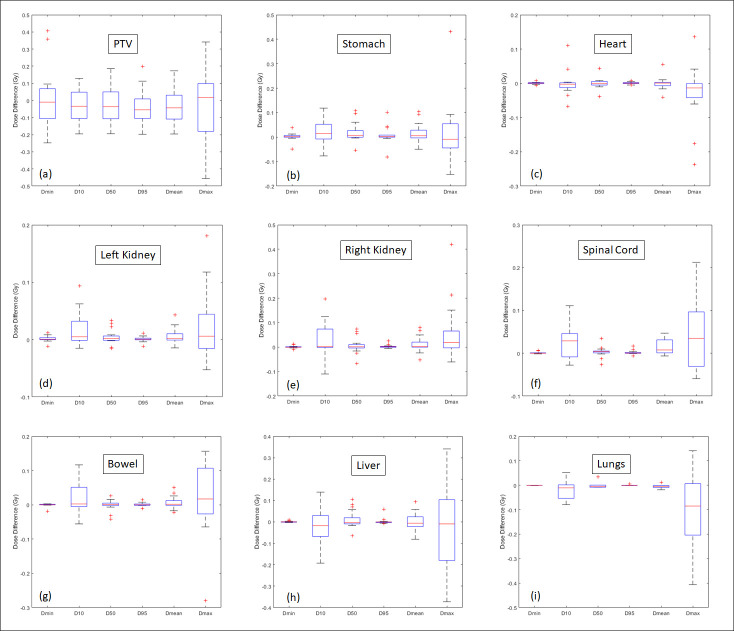
Figure 4 shows the dose–volume histograms (DVHs) of PTV, heart, liver, bowel and stomach from the representative patient. The curves from sCT are in good agreement with the original CT. Figure 5 shows the difference in absolute volume for three clinically relevant metrics: liver V₁₅, stomach V₂₀ and bowel V₂₀. Given a typical liver volume of greater than 1000 cm³, 5 cm³ is less than 0.5% difference. Table 2 summarizes the mean, and standard deviation (SD) for commonly used DVH metrics for the PTV and OARs. Figure 6 is the corresponding box plot. The overall dosimetric difference between the sCT and original CT are not significant. Though some DVH metrics p values are less than 0.05, indicating statistical significance, these cases would have a negligible clinical impact as the absolute dose differences are very small (less than 0.1 Gy).

Figure 4.

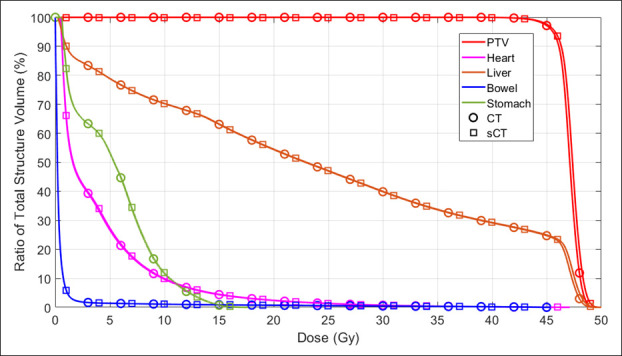
The DVHs of PTV, heart, liver, bowel and stomach of the exemplary patient. DVH, dose–volume histogram; PTV, planningtarget volume; sCT, synthetic CT.

Figure 5.

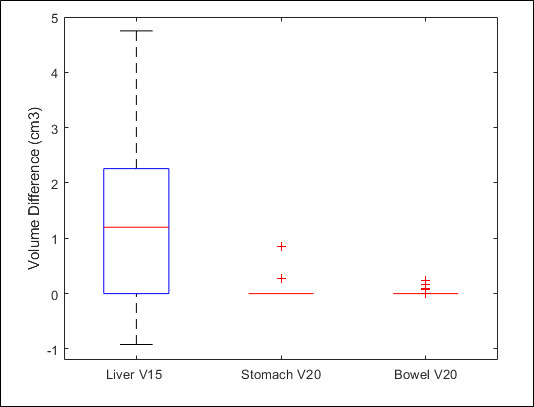
Box plot of liver V15, stomach V20 and bowel V20.

Table 2.

Statistics of the DVH metrics differences between the sCT and CT

		PTV	Liver	Left kidney	Right kidney	Stomach	Heart	Lungs	Bowel	Spinal cord
Dmin	Mean (Gy)	0.160	0.002	0.003	0.003	0.009	0.002	0.000	0.002	0.001
	SD (Gy)	0.227	0.002	0.004	0.004	0.014	0.002	0.000	0.005	0.002
	p-value	0.503	0.331	0.249	0.498	0.625	0.728	0.094	0.621	0.095
D10	Mean (Gy)	0.081	0.063	0.016	0.052	0.037	0.024	0.052	0.036	0.043
	SD (Gy)	0.049	0.051	0.025	0.053	0.033	0.034	0.032	0.040	0.034
	p-value	0.187	0.300	0.023	0.122	0.129	0.904	0.410	0.226	0.004
D50	Mean(Gy)	0.088	0.027	0.004	0.019	0.026	0.010	0.009	0.011	0.008
	SD (Gy)	0.058	0.031	0.010	0.026	0.036	0.015	0.012	0.013	0.009
	p-value	0.303	0.217	0.136	0.425	0.088	0.932	0.865	0.825	0.263
D95	Mean (Gy)	0.081	0.005	0.001	0.004	0.019	0.003	0.001	0.003	0.002
	SD (Gy)	0.059	0.013	0.004	0.006	0.031	0.002	0.002	0.005	0.004
	p-value	0.086	0.492	0.433	0.148	0.410	0.567	0.771	0.487	0.145
Dmean	Mean (Gy)	0.083	0.030	0.006	0.021	0.027	0.012	0.011	0.012	0.015
	SD (Gy)	0.055	0.025	0.011	0.024	0.033	0.018	0.006	0.016	0.016
	p-value	0.183	0.880	0.053	0.161	0.114	0.965	0.314	0.249	0.003
Dmax	Mean (Gy)	0.161	0.141	0.024	0.072	0.076	0.061	0.061	0.082	0.070
	SD (Gy)	0.123	0.106	0.048	0.102	0.103	0.078	0.141	0.076	0.054
	p-value	0.618	0.577	0.098	0.040	0.548	0.276	0.226	0.466	0.019

PTV, planning target volume; SD, standard deviation.

Mean and SD are based on the absolute difference. p-value is based on the comparison of the relative difference.

Figure 6.

Box plot of absolute difference between sCT and CT for Dmin, D10, D50, Dmean and Dmax for the PTV and OARs. The central red line indicates the median value, and the borders of the box represent the 25th and 75th percentiles. The outliers are plotted by the red “+” marker. OAR, organ at risk; PTV, planning target volume; sCT, synthetic CT.

Comparison with FCN and GAN

For the cohort of 21 patients, the mean MAE of our methods is 72.87 ± 18.16 HU compared to 94.34 ± 21.06 and 86.40 ± 13.95 for the FCN- and GAN-based methods. Figure 7 compares the MR, CT and sCT images in transverse views of a representative patient, and Table 3 lists the mean absolute differences in PTV and liver D_min, D₁₀, D₅₀, D₉₅, D_mean and D_max when dense-cycle-GAN-, FCN- and GAN-based are compared to the original CT-based dose calculation. As shown in Figure 7, the sCT images generated by our method have more definitive tissue boundaries and more accurate tissue HU prediction. The dense-cycle-GAN method can efficiently deal with the MR intensity inhomogeneity as can be observed at the anterior part. Generally, our method shows smaller mean absolute dose differences for most of the DVH endpoints. However, all of the dose differences are very small compared to the prescribed dose (45 Gy) and the p-value between our method and FCN and GAN are all larger than 0.05, which means there is no significant dose difference among these three methods. This suggests that volumetric modulated arc therapy (VMAT) plan employs multiple entry points that ultimately minimized the impact from local mismatch and HU inaccuracies. The sCT images generated by these three methods are all suitable for liver SBRT dose calculation.

Figure 7.

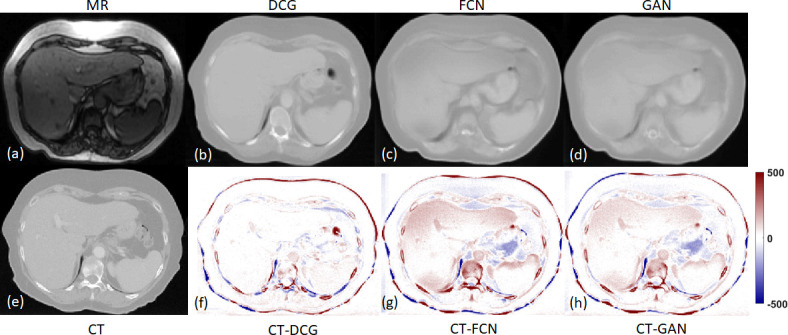
The transverse views of MR, CT, DCG-, FCN- and GAN-based sCTs. DCN, dense-cycle-GAN; FCN, fully convolutional neural network; GAN, generativeadversarial network.

Table 3.

Statistics of the DVH metrics differences between the DCG -, FCN- and GAN-based sCT and CT

		PTV
		Dmin	D10	D50	D95	Dmean	Dmax
DCG	Mean (Gy)	0.160	0.081	0.088	0.081	0.083	0.161
	SD (Gy)	0.227	0.049	0.058	0.059	0.055	0.123
FCN	Mean (Gy)	0.158	0.138	0.125	0.130	0.131	0.260
	SD (Gy)	0.171	0.121	0.134	0.102	0.124	0.247
GAN	Mean (Gy)	0.062	0.197	0.171	0.160	0.177	0.336
	SD (Gy)	0.055	0.239	0.258	0.146	0.231	0.211
p-value (DCG vs FCN)		0.020	0.358	0.491	0.272	0.422	0.170
p-value (DCG vs GAN)		0.083	0.878	0.977	0.693	0.933	0.334
p-value (FCN vs GAN)		0.745	0.588	0.555	0.686	0.587	0.793
		Liver
		D min	D 10	D 50	D 95	D mean	D max
DCG	Mean (Gy)	0.002	0.063	0.027	0.005	0.030	0.141
	SD (Gy)	0.002	0.051	0.031	0.013	0.025	0.106
FCN	Mean (Gy)	0.001	0.073	0.027	0.003	0.023	0.257
	SD (Gy)	0.001	0.060	0.035	0.005	0.028	0.248
GAN	Mean (Gy)	0.002	0.094	0.047	0.005	0.037	0.284
	SD (Gy)	0.002	0.144	0.075	0.008	0.068	0.230
p-value (DCG vs FCN)		0.771	0.376	0.815	0.720	0.686	0.102
p-value (DCG vs GAN)		0.915	0.976	0.506	0.552	0.683	0.378
p-value (FCN vs GAN)		0.415	0.218	0.331	0.355	0.206	0.439

DCG, dense-cycle-GAN; FCN, fully convolutional neural network; GAN, generative adversarial network; PTV, planning target volume; SD, standard deviation.

Mean,SD and p-value are based on the absolute difference.

Discussion

This work sought to establish a novel method on generating liver sCT from corresponding MRI data set by applying a dense-block cycle GAN model. To quantitatively evaluate the quality of the sCT, imaging end points (MAE, PSNR and NCC) and dosimetric end points (absolute mean difference of DVH metrics, p-value, and γ analysis) were performed. Side-by-side-imaging comparisons revealed good agreement. The overall average MAE, PSNR and NCC of the sCT were 72.87 ± 18.16 (HU), 22.65 ± 3.63 and 0.92 ± 0.04, respectively. These are competitive compared to counterpart values published from recent deep learning studies of sites such as brain and pelvis.^14,18,30 This small imaging uncertainty translated into minimal dosimetric differences in the PTV and OARs. The maximum absolute mean dose difference among all the DVH metrics of PTV was 0.16 Gy and was 0.14 Gy for the OARs. This is likely to be insignificant from a clinical perspective since the prescribed dose was 45 Gy. The side-by-side-γ analysis (1%/1 mm) of the coronal plane dose distribution all had a pass rate higher than 99%. Most of the p values were greater than 0.05, indicating no significant difference in dose metrics between the sCT and CT.

In this study, three different MR scanners were used. The MR sequences can be divided into 3 T 3D VIBE (four patients) and 1.5 T 2D fast spoiled gradient echo (17 patients). Only T ₁ weighted protocols were used. The mean MAE the four patients’ sCTs obtained based on 3 T 3D VIBE was 79.88 ± 12.76 HU (range: 63.75–94.67 HU), compared to 71.22 ± 19.15 HU (range: 59.49–126.53 HU) from the rest of the 17 patients’ sCTs obtained based on 1.5 T 2D fast spoiled gradient echo. Since the HU prediction accuracy relies much more on the degree of patient motion than the MR sequence, it is difficult to determine whether the trained model was biased towards the 1.5 T 2D fast spoiled gradient echo although a better mean MAE was observed with it. An enhanced prediction accuracy is anticipated with a uniform MR acquisition protocol.

One publication investigated abdominal MR to sCT based on fuzzy C-means method.¹⁰ A fast scanning sequence was applied to minimize the MRI motion artifact. The overlap of bone and air areas was aggravated by limiting MR sequences, which lead to degeneration of the tissue classification. This issue was addressed by adding prior learned shape information to preclude air from where it is not likely to reside. Both fuzz C-means method and our algorithm have shown high dosimetric accuracy for liver SBRT. However, our method better predicts small bony structures. This is because fuzzy C-means is a segmentation-based method that depends on the pre-determination of classes and ours is learning-based, which can effectively learn the features from the MR and CT pairs.

To demonstrate the advantage of our method over the state-of-art algorithm, we used FCN- and GAN-based method to predict the sCT images using the same patient cohort. Our DCG based method shows better imaging quality and lower mean MAE. However, the dosimetric differences were minimal, which means VMAT plans are generally no sensitive enough to the local mismatches and HU inaccuracies. Future work will include using proton plan to evaluate the capacity of the sCT images since proton is much more sensitive to the HU discrepancies in the beam line direction.

We identified several limitations of this study. Large HU and dose discrepancies mainly arose from areas containing body and air interface and at bone and tissue boundaries as shown in Figure 2. It may be caused by the registration errors between CT and MR images, or due to MRI artifacts that originate from patient-induced local variations in the magnetic field.³¹ In the HU difference map shown in Figure 3, discrepancies can be seen at the site of spinous process due to the relative small bone volume and the bone susceptibility artifact that can cause boundary perturbations. In addition, our current algorithm uses patch size of 64 × 64 × 5 instead of 64 × 64 × 64 due to the limitation of current GPU power. Future development will therefore focus on employing fully 3D patch to predict more accurate inter slice information. Another limitation arises from the truncated normal distribution, which is a common issue of deep-learning algorithm. Batch normalization is required for the deep-learning algorithm to maintain the stability of the architecture. In our network, we used 99.9% maximum HU value as the largest HU and 5% minimum HU value as the smallest HU value. This procedure will slightly shorten the range of sCT HU values, which causes HU inaccuracy. Future development will include the development of better mathematical model applied for batch normalization.

As liver SBRT depends on highly accurate image guidance, the impact of distortion inherent to MRI can be serious.^31,32 Although a standard procedure for comprehensive correction of MRI distortion has not been established, many manufacturers have supplied software to correct such distortion,^33–35 and a guideline charged by the American Association of Physicists in Medicine (AAPM) is currently under development (Task Group No. 117). With the continuous progress of distortion correction and standardized procedure, the accuracy of the sCT prediction can further improve in the future.

A substantial amount of discrepancies can be traced to image registration. It affects the model training process that results in erroneous prediction. Although we have divided the whole image into multiple overlapping small patches, the effect from inaccurate registration still exists. In this work, the image registration between MR and CT was particularly difficult due to variations introduced by respiratory motion and peristalsis during the simulation scan. The registered MR images after deformable alignment were more or less blurred and distorted, depending on the quality of the original MR images. This non-ideal MR image quality was translated into blurred and locally distorted sCT images. However, it did not appear to have a noticeable impact on dose calculation accuracy. This was mitigated, at least partly, by the overall consistency of the HU values as well as the use of VMAT. VMAT employs multiple entry points that ultimately minimized the impact from local blur or distortion. With the development of deformable image registration, the quality of the predicted sCT can be substantially improved.

More recently, commercially MRI simulators became available as part of radiation therapy platforms.³⁶ As opposed to diagnostic MRI systems, MR simulators have large bore size and flat tables that minimizes setup differences between CT and MR Novel imaging techniques³⁷ are also being developed to minimize MRI artifacts for treatment planning purposes. Multiparametric can provide functional information to aid treatment planning.³⁸ Rapid improvements in radiotherapy techniques demand high precision in target definition and treatment planning. In this regard, one logical avenue to follow is the MRI-only treatment process.

Conclusion

We proposed a novel learning-based approach to integrate dense-block into cycle GAN to synthesize an abdominal sCT image from a routine MR image for potential MRI-only liver SBRT. The proposed method demonstrated its capability to reliably generate sCT images for dose calculation, which supports further development of MRI-only treatment planning. Future directions include evaluating its dose prediction accuracy on liver SBRT proton therapy and exploring the possibility of generating elemental concentration maps instead of electron density maps that can be used for Monte Carlo simulation.