Long-range, through-lattice coupling improves predictions of microtubule catastrophe

Abstract

Microtubules are cylindrical polymers of αβ-tubulin that play critical roles in fundamental processes such as chromosome segregation and vesicular transport. Microtubules display dynamic instability, switching stochastically between growth and rapid shrinking as a consequence of GTPase activity in the lattice. The molecular mechanisms behind microtubule catastrophe, the switch from growth to rapid shrinking, remain poorly defined. Indeed, two-state stochastic models that seek to describe microtubule dynamics purely in terms of the biochemical properties of GTP- and GDP-bound αβ-tubulin predict the concentration dependence of microtubule catastrophe incorrectly. Recent studies provide evidence for three distinct conformations of αβ-tubulin in the lattice that likely correspond to GTP, GDP.P_i, and GDP. The incommensurate lattices observed for these different conformations raise the possibility that in a mixed nucleotide state lattice, neighboring tubulin dimers might modulate each other’s conformations and hence each other’s biochemistry. We explored whether incorporating a GDP.P_i state or the likely effects of conformational accommodation can improve predictions of catastrophe. Adding a GDP.P_i intermediate did not improve the model. In contrast, adding neighbor-dependent modulation of tubulin biochemistry improved predictions of catastrophe. Because this conformational accommodation should propagate beyond nearest-neighbor contacts, our modeling suggests that long-range, through-lattice effects are important determinants of microtubule catastrophe.

INTRODUCTION

Microtubules (MTs) are hollow cylindrical polymers of αβ-tubulin that have essential roles segregating chromosomes during cell division, organizing the cytoplasm, establishing cellular polarity, and more (Desai and Mitchison, 1997). These fundamental activities depend critically on dynamic instability, the stochastic switching of MTs between phases of growth and rapid shrinking (Mitchison and Kirschner, 1984). Dynamic instability is itself a consequence of αβ-tubulin GTPase activity and how it affects interactions between αβ-tubulin in the lattice and at the microtubule end. Although predictive molecular understanding of catastrophe remains elusive, the broad outlines of an understanding have been established (Mitchison and Kirschner, 1984; VanBuren et al., 2002; Gardner et al., 2011b; Bowne-Anderson et al., 2013; Brouhard, 2015; Brouhard and Rice, 2018; Duellberg et al., 2016). Unpolymerized, GTP-bound αβ-tubulin subunits readily associate at the growing tips of the MTs. Once they are incorporated into the lattice, αβ-tubulin GTPase activity is accelerated. The assembly dependence of GTPase activity results in a “stabilizing cap” of GTP- or GDP.P_i-bound αβ-tubulin near the ends of the growing microtubules. Loss of this stabilizing cap triggers catastrophe, the switch from growth to rapid shrinking, because it exposes the more labile GDP-bound microtubule lattice.

Two broad classes of computational models have been developed as part of longstanding efforts to understand in quantitative terms the connections between the properties of individual αβ-tubulins and the polymerization dynamics they collectively generate. “Biochemical” models attempt to recapitulate microtubule dynamics purely in terms of discrete elementary molecular reactions such as association, dissociation, and GTPase activity (Chen and Hill, 1983, 1985; Bayley et al., 1989, 1990; Martin et al., 1993; VanBuren et al., 2002; Gardner et al., 2011b; Margolin et al., 2012; Piedra et al., 2016). “Mechanochemical”’ models (Molodtsov et al., 2005; VanBuren et al., 2005; Coombes et al., 2013; Zakharov et al., 2015; McIntosh et al., 2018) use additional springlike energies to account for conformational strain inside individual αβ-tubulins and for the effect of the resulting mechanical stress on interactions with other αβ-tubulins in the lattice. A third class of “phenomenological” models (Flyvbjerg et al., 1994; Brun et al., 2009; Bowne-Anderson et al., 2013; Duellberg et al., 2016) use simplifying assumptions that obscure the relationship between tubulin biochemistry and observable MT behavior, so we do not consider them further here. Biochemical and mechanochemical models can each recapitulate microtubule growing and shrinking, and in both kinds of model, catastrophe emerges naturally as a consequence of GTPase activity.

Biochemical models are computationally inexpensive and relatively simple to interpret because they only contain a small number of adjustable parameters. In principle, all parameters could represent measurable quantities accessible to testing/perturbation using site-directed mutagenesis. A limitation of these models is that they fail to capture the correct concentration dependence and other aspects of catastrophe (e.g., VanBuren et al., 2002; Bowne-Anderson et al., 2013; Piedra et al., 2016). Mechanochemical models are computationally expensive and more complicated to interpret because they are more parameter-intensive. Some of the parameters describing the springlike properties of αβ-tubulin might also be hard to validate experimentally. However, the mechanochemical models better recapitulate the concentration dependence and other aspects of catastrophe where biochemical models fail (Coombes et al., 2013; Zakharov et al., 2015). Why mechanochemical models better capture the concentration dependence of MT catastrophe remains unclear.

In both biochemical and mechanochemical models, only two nucleotide states are used: GTP and GDP. However, recent structural studies (Alushin et al., 2014; Zhang et al., 2015; Manka and Moores, 2018) have revealed three mutually incommensurate conformations of αβ-tubulin in the body of MT: an “expanded” form that corresponds to an all-GTP lattice, a “compacted” form that correspond to an all-GDP lattice, and an intermediate “compact-twisted” form that correspond to an all-GDP.P_i lattice. Because each conformation prefers a different lattice geometry, they must presumably accommodate each other in mixed-nucleotide regions of the microtubule lattice. Reconstitution and structural studies of plus end–tracking EB proteins (Maurer et al., 2011, 2012, 2014; Zhang et al., 2015) support a role for these conformations in MT dynamics and regulation. Experiments with a slow-shrinking “conformation cycle” mutant of yeast αβ-tubulin (Geyer et al., 2015) that in the GDP state apparently does not relax all the way to the compacted conformation provided evidence that the αβ-tubulin conformation cycle contributes directly to microtubule shrinking rate and catastrophe frequency. It seemed plausible to us that not accounting for a GDP.P_i intermediate, or for the likely modulating influence of conformational accommodation in a mixed nucleotide state lattice (Brouhard and Rice, 2018), might explain why biochemical models fail to capture the concentration dependence of catastrophe.

In the present study, we asked whether incorporating various candidates for “missing state/biochemistry” into a computational model would improve predictions about the concentration dependence of microtubule catastrophe. We elaborated a Monte Carlo–based algorithm developed in the lab (Ayaz et al., 2014; Piedra et al., 2016; Mickolajczyk et al., 2018) to test whether incorporating a GDP.P_i state or long-range coupling (reflecting conformational accommodation) improved predictions of microtubule catastrophe. We incorporated the GDP.P_i state and conformational coupling separately for simplicity and to be able to assess the effect of each change in isolation. We did not explicitly incorporate mechanochemistry into the model because our goal was to identify minimal additions to biochemical models that improve their performance with respect to predicting catastrophe.

Our simulations revealed that incorporating a GDP.P_i intermediate state does very little to improve the predicted concentration dependence of catastrophe frequency. Long-range, through-­lattice conformational accommodation, acting to modulate GTPase rate or dissociation rates, did improve the prediction of catastrophe and its concentration dependence. Artificially restricting this modulation to short range abrogated the previously observed improvement. Thus, it seems that long-range, through-lattice interactions are important for recapitulating the concentration dependence of catastrophe in biochemical models. Because mechanochemical models effectively distribute strain throughout the lattice, the long-range coupling intrinsic to mechanochemical models may explain why they have been more successful at predicting catastrophe. By highlighting the importance of long-range, through-lattice effects, our computational experiments suggest that cooperative effects at the microtubule end are important determinants of microtubule catastrophe.

RESULTS

A two-state model for microtubule dynamics fails to capture the weak concentration dependence of catastrophe frequency

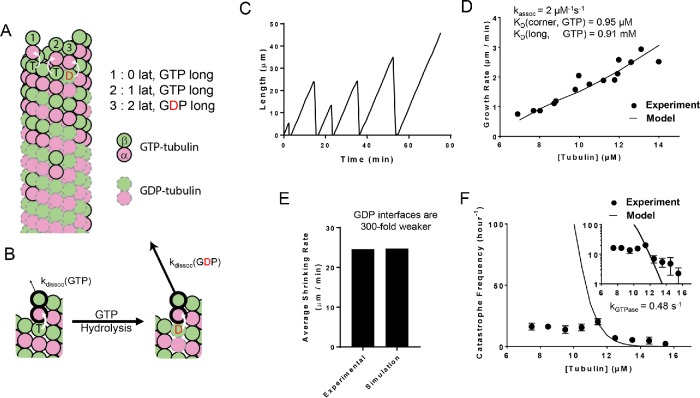
We refined our prior algorithm (Ayaz et al., 2014; Piedra et al., 2016; Mickolajczyk et al., 2018) that used a kinetic Monte Carlo algorithm (Gillespie, 1976; Gibson and Bruck, 2000) to simulate microtubule dynamics. The algorithm simulates one biochemical event (dimer association, dissociation, or GTP hydrolysis) at a time and therefore provides a “movie”’ of microtubule dynamics. As is commonly done (Chen and Hill, 1985; VanBuren et al., 2002; Molodtsov et al., 2005; Gardner et al., 2011a; Margolin et al., 2012; Zakharov et al., 2015), our model uses a two-dimensional representation of the microtubule lattice to track different kinds of binding environments or neighbor states (Figure 1A). To minimize the number of adjustable parameters in the model, we initially adopted a very simple parameterization that does not explicitly account for different conformations of αβ-tubulin (reviewed in Brouhard and Rice, 2014) and that also does not attempt to describe “mechanical” properties of αβ-tubulin and microtubules such as springlike conformational strain (reviewed in Brouhard and Rice, 2018; Figure 1A). The assumptions of this minimalist parameterization are that 1) there are only two nucleotide states (GTP and GDP); 2) nucleotide is trans-acting (Figure 1B), meaning that the strength of the longitudinal interface between dimers (and thus the dimer-binding affinity at the MT tip) is determined by the nucleotide located at the interface (Rice et al., 2008; Piedra et al., 2016); 3) the αβ-tubulin dissociation rate for a given subunit is determined by the total sum of free energies of all longitudinal and lateral interdimer interactions with other subunits; 4) the association rate for a given site does not depend on the local tip configuration; and 5) GTP hydrolysis occurs at the interdimer interface, meaning that GTP cannot be hydrolyzed on the most terminal subunit of any protofilament. In these kinds of models, catastrophe and rescue occur naturally (Figure 1C) in a way that depends on the specific parameters used. Our algorithm is constructed in a highly modular way that makes it easy to implement different biochemical assumptions (Piedra et al., 2016; Mickolajczyk et al., 2018). Later in the paper, we relax the minimalistic assumptions of the two-state model to test whether more complicated models that incorporate other states or kinds of biochemistry better predict the concentration dependence of catastrophe.

FIGURE 1:

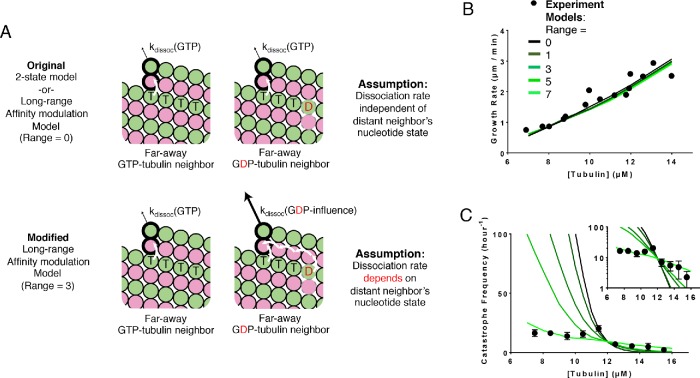
Simulations of a two-state biochemical model for microtubule dynamics. (A) Cartoon representation of a typical growing MT tip during a simulation. αβ-tubulin dimers are represented as pink and green circles; solid black and dashed gray outlines indicate GTP and GDP states, respectively. Dissociation rates depend on the number of lateral neighbors and the identity of the nucleotide at the longitudinal interface (vertical white arrows indicate trans-acting nucleotides; see B). (B) Illustration of trans-acting nucleotide. αβ-tubulins with GTP at the longitudinal interface dissociate more slowly than αβ-tubulins with GDP at the longitudinal interface. (C) Representative plot showing simulated MT length vs time at 12 µM αβ-tubulin. The simulation parameters are listed elsewhere (see D, E). Catastrophes occur naturally as a consequence of the biochemical rules. (D) Comparison between measured (black circles) and predicted (line) growth rates. Experimental data are taken from Walker et al. (1988). (E) Comparison between measured and predicted shrinking rates. (F) Comparison between measured (black circles) and predicted (line) catastrophe frequencies at different αβ-tubulin concentrations. The two-state model cannot recapitulate the measured concentration dependence of the catastrophe frequency. The y-axis is linear in the larger plot. The smaller inset graph displays the same data, but the y-axis is on log scale.

To obtain model parameters that could recapitulate MT elongation and shrinking rates and approximate the frequency of catastrophe, we followed the divide-and-conquer approach outlined previously (VanBuren et al., 2002; Piedra et al., 2016). We trained our model against a classic benchmark data set that is one of the only ones to report growth rates, shrinking rates, and catastrophe frequencies at multiple tubulin concentrations under consistent conditions (Walker et al., 1988). First, we used GTP-only simulations to search for parameters that recapitulated MT growth rates over a range of αβ-tubulin concentrations (Figure 1D). With those parameters fixed, we optimized the weakening effect of GDP on the longitudinal interface by tuning it to make all-GDP microtubules depolymerize at the observed average rate of postcatastrophe shrinking (Figure 1E). With that new parameter also fixed, we refined the GTPase rate to produce the correct frequency of catastrophe (Figure 1F). These parameters are not perfectly independent, so we applied this approach iteratively (this process resulted in a slightly higher affinity corner interaction than we had obtained in a prior study, Piedra et al., 2016; see Materials and Methods). For generality, we wanted to train our model against a second data set where the growth rates, shrinking rates, and catastrophe frequencies were somewhat different than in Walker et al. (1988) (Supplemental Figure 1). To our knowledge, however, besides Walker et al. (1988) there is not another study that reports microtubule growth rates, shrinking rates, and catastrophe frequencies at multiple tubulin concentrations under identical buffer conditions. Thus, we constructed a hybrid data set consisting of growth rates and catastrophe frequencies from Gardner et al. (2011b) and the shrinking rate from Lawrence et al. (2018). As observed in earlier studies, in fits to both data sets, the predicted catastrophe frequency varies much more strongly with tubulin concentration than has been observed in experiments (VanBuren et al., 2002; Bowne-Anderson et al., 2013; Piedra et al., 2016). For example, the model predicts a nearly 210-fold change in catastrophe frequency from 9.5 to 13.5 µM αβ-tubulin, while the Walker et al. (1988) data show only a 2.5-fold change in catastrophe frequency over the same range (Figure 1F). A similar discrepancy was observed in our fits to the alternative data set (Supplemental Figure 1A). Because the model could not recapitulate the concentration dependence of catastrophe, we chose 12 µM (the median concentration) for Walker et al. (1988) and 10 µM for Gardner et al. (2011b) and Lawrence et al. (2018) as the reference concentrations for determining GTPase rate. The parameters we obtain from training our models to the experimental data are listed in Supplemental Table 1 for Walker et al. (1988) and in Supplemental Table 2 for Gardner et al. (2011b) and Lawrence et al. (2018). The parameters are comparable between the two data sets and consistent with the differences between them: the differences in tubulin binding affinities are less than 1 k_BT, and the difference in GTPase rates is within an order of magnitude.

Incorporating a GDP-P_i intermediate state into the model does not improve prediction of the concentration dependence of catastrophe

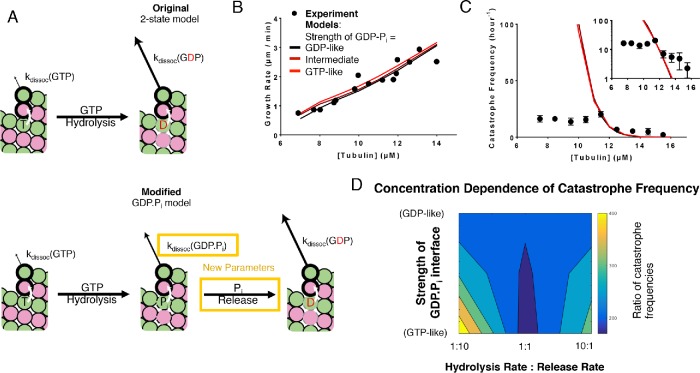
The overly steep concentration dependence of catastrophe predicted by the two-state model might occur because the model does not account for a state or kind of interaction that is important for catastrophe. We added a GDP.P_i intermediate between GTP and GDP to test whether a three-state model would better predict the concentration dependence of catastrophe than a two-state model. We made the following additional assumptions when implementing the GDP.P_i state (Figure 2A): 1) P_i (phosphate) release from the body of the lattice is a first-order process, like GTPase, and 2) the phosphate dissociates instantaneously when exposed at the tip. These new assumptions in the GDP.P_i model require two additional parameters: one that describes the strength of a longitudinal contact when GDP.P_i is at the interface, and the other that describes the rate of P_i release (Figure 2A).

FIGURE 2:

Three-state model that contains a GDP.P_i intermediate. (A) Cartoons illustrating the differences between models without (top) and with (bottom) a GDP.P_i intermediate. The GDP.P_i intermediate requires two additional parameters: a rate constant for P_i release and another for the strength of the longitudinal interaction when GDP.P_i is at the interface. Vertical white arrows indicate trans-acting nucleotides. (B) Comparison between measured (black circles) and predicted (lines; red, black correspond to GDP.P_i interfaces having the same strength as GTP and GDP interfaces, respectively; brown corresponds to GDP.P_i interfaces having intermediate strength) growth rates. All three scenarios can recapitulate observed growth rates. In this plot the ratio between the hydrolysis rate and the phosphate release rates has been set to 1:1. (C) Predicted catastrophe frequency as a function of concentration for different values for the strength of the GDP.P_i longitudinal interface. Varying the strength of the GDP-P_i interface has a limited effect on the concentration dependence of the catastrophe frequency. The ratio between the hydrolysis rate and the phosphate release rates has been set to 1:1. The y-axis is linear in the larger plot. The smaller inset graph displays the same data, but the y-axis is on log scale. (D) Contour plot of the predicted concentration dependence of catastrophe. The concentration dependence is defined as the ratio of catastrophe frequencies at 9.5 and 13.5 µM. The concentration dependence of the catastrophe frequency is lowest when the ratio between hydrolysis and release is 1:1 and the longitudinal interface with GDP-P_i is as strong as the interface with GTP.

We first examined how varying the strength of longitudinal contacts at the GDP.P_i interface affects the predicted frequency of catastrophe as a function of αβ-tubulin concentration. We varied the strength of the GDP.P_i interface from high (equivalent to the GTP interface) to intermediate (halfway between the GTP and GDP interfaces) to low (equivalent to the GDP interface), keeping the ratio of the GTPase rate and the P_i release rate constant. Note that setting the strength of the GDP.P_i interface to be identical to that of the GDP interface is effectively a control experiment because it yields a model that is functionally identical to the two-state model. Because increasing the strength of the GDP.P_i interface reduces the catastrophe frequency (by effectively reducing the rate of some subunit dissociations from the microtubule end), we retrained the GTPase rate to match the catastrophe frequency at the reference concentration (12 µM) for the high- and intermediate-strength GDP.P_i interface (Supplemental Table 1B). We kept the P_i release rate identical to the new GTPase rates, as stated above. Changing the GTPase rate or the strength of the GDP.Pi interface had little effect on the predicted growth rates (Figure 2B). Whereas in the two-state model the ratio of predicted catastrophe frequency between 9.5- and 13.5-µM concentrations was 210, for the model containing a GDP.P_i state the ratio was 170, still far from the experimentally observed ratio of 2.5 (Figure 2C). Thus, the predicted concentration dependence of catastrophe frequency did not improve substantially in response to these initial changes in the model.

We then used a grid search approach to explore how changing the ratio between the GTPase rate and the phosphate release rates affects the concentration dependence of catastrophe. We fixed the rate of phosphate release to be 10 times higher or lower than the rate of GTPase and varied the strength of the GDP.P_i interface (with retraining of the GTPase rate) as before. In both cases, these changes exacerbated the problems with the model: the predicted concentration dependence of catastrophe frequency actually increased (Figure 2D). We observed similar trends in fits to the other data set that we trained our model against (Gardner et al., 2011b; Lawrence et al., 2018; Supplemental Figure 3B). The predicted concentration dependence of catastrophe was lowest when the GTPase rate and the phosphate release rate were the same and the GDP.P_i interface was as strong as the interface with GTP. However, this best case scenario for incorporating a GDP.P_i state did not substantially improve prediction of the concentration dependence of catastrophe.

Nearest-neighbor conformational accommodation improves predictions of the concentration dependence of catastrophe when GTPase, but not αβ-tubulin dissociation, is modulated

The expanded conformation (seen in the all-GTP lattice) and the compacted conformation (seen in the all-GDP lattice) make lattices with different spacing of the lateral interfaces and other changes (Alushin et al., 2014; Zhang et al., 2015; Manka and Moores, 2018). How αβ-tubulins accommodate incommensurate GTP- and GDP-bound conformations in a mixed–nucleotide state lattice, as must occur near the tip of the growing MT, is not understood (reviewed in Brouhard and Rice, 2018). We speculated that this conformational mismatch might modulate the strength of lateral interactions between αβ-tubulins in different nucleotide states, or that it might modulate the rate of GTPase activity. We focused on lateral interactions because it seemed that those interfaces are where the mismatch between expanded and compacted conformations must be resolved. This would mean that a GTP- or GDP-tubulin would behave differently depending on the nucleotide state(s) of its neighbor(s), a kind of effect that is not captured in simple two-state models such as the one we described above. We implemented these two ideas (modulation of affinity or GTPase activity) into the model separately to test whether this kind of nearest-neighbor conformational accommodation could improve the predicted concentration dependence of catastrophe.

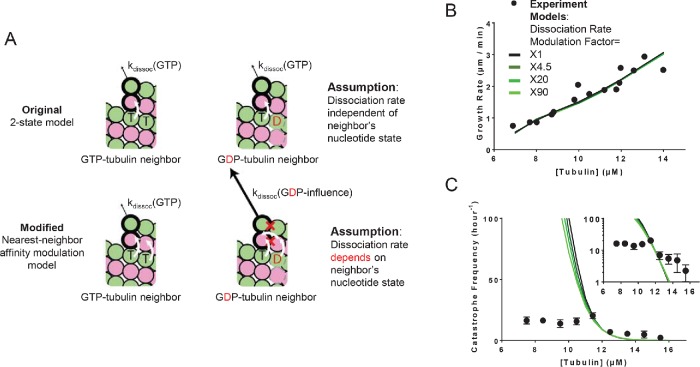
To implement neighbor-based modulation of lateral interactions, we assumed that the conformational mismatch/accommodation weakens the interaction (increases the dissociation rate). In other words, αβ-tubulin with a lateral neighbor that is in a different nucleotide state (conformation) dissociates more quickly than it would were the nucleotide states the same (Figure 3A). Owing to these changes, the “‘nearest-neighbor affinity modulation” model has only one additional parameter: the fold-faster dissociation rate for αβ-tubulin with a lateral nearest neighbor with differing nucleotide state. To examine how varying the new parameter affects the concentration dependence of catastrophe frequency in simulations, we set the αβ-tubulin with a lateral neighbor with a different nucleotide to dissociate faster by factors of 1, 4.5, 20, and 90 (these values correspond to free-energy changes of 0, 1.5, 3, and 4.5 k_BT, respectively, chosen so that the maximum parameter value of 90 remains less than the GDP weakening factor, which is 300 for this data set). We also tried a factor of 400 (6 k_BT), but we did not observe further improvement. Setting the fold increase in dissociation rate to 1 is effectively a control experiment because in that case the model behaves identically to the two-state model. We observed similar trends in fits to the other data set we trained our model against (Gardner et al., 2011b; Lawrence et al., 2018; Supplemental Figure 4A). The new parameter (the fold-faster dissociation rate) only modestly affected the predicted growth rates (Figure 3B), so we retained the affinities and GDP weakening factor from the two-state model. Keeping the other model parameters fixed, we adjusted the GTPase rate to obtain the correct catastrophe frequency at the reference concentration (see also Supplemental Table 1C). Compared with the two-state model, the range of predicted catastrophe frequency over the concentration range (9.5 and 13.5 µM) decreased from 210-fold to 150-fold (compared with a 2.5-fold change in the target data; Figure 3C). Thus, in contrast to incorporating a GDP.Pi intermediate, allowing interdimer interaction to be modulated by neighboring nucleotide state somewhat improved the predicted concentration dependence of catastrophe frequency.

FIGURE 3:

Model that incorporates nearest-neighbor modulation of the strength of lattice contacts. (A) Cartoons illustrating the differences between models without (top) and with (bottom) nearest-neighbor αβ-tubulin affinity modulation. Allowing αβ-tubulin affinity modulation requires one additional parameter: a fold increase in the αβ-tubulin dissociation rate due to the nearest-neighbor influence. Vertical white arrows indicate trans-acting nucleotides; the horizontal white arrow indicates the nearest-neighbor effect on affinity modulation. (B) Comparison between measured (black circles) and predicted (the blackest line corresponds to a onefold increase in dissociation rates and the greenest corresponds to a 90-fold increase) growth rates. All four scenarios can recapitulate observed growth rates. (C) Predicted catastrophe frequency as a function of concentration for different fold increases in αβ-tubulin dissociation rate. The y-axis is linear in the larger plot. The smaller inset graph displays the same data, but the y-axis is on log scale. Varying the magnitude of αβ-tubulin dissociation modulation has a limited effect on the concentration dependence of the catastrophe frequency.

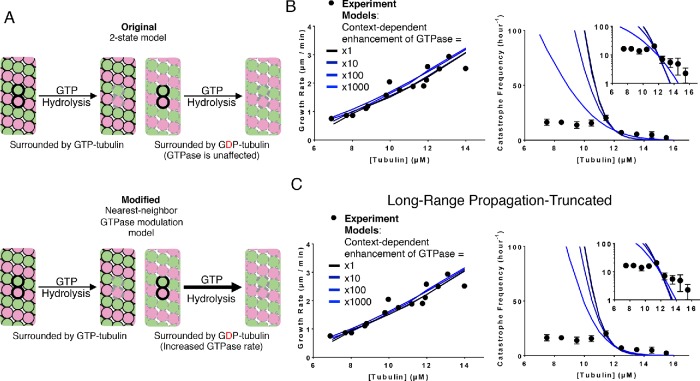
To implement neighbor-based modulation of GTPase activity, we assumed that αβ-tubulin with GTP next to αβ-tubulin bound to GDP hydrolyzes GTP more quickly (Figure 4A). In essence, this assumption is equivalent to saying that the GTPase rate is activated, and that αβ-tubulin adopting the accommodating intermediate conformation is the activating event. This nearest-neighbor GTPase stimulation model has one additional parameter: the fold increase in hydrolysis rate. We set this neighbor-dependent GTPase modulation to increase the rate by factors of 1, 10, 100, and 1000. Setting the fold increase in GTPase rate to 1 is effectively a control experiment, because that model is functionally identical to the two-state model. We adjusted the basal GTPase rate to maintain the correct catastrophe frequency at the reference concentration (Supplemental. Table 1D); other model parameters were kept fixed because the new parameter did not substantially affect predicted growth or shrinking rates (Figure 4B). Whereas in the two-state model the ratio of predicted catastrophe frequency at the low (9.5 µM) and high (13.5 µM) concentrations was 210, for this model with modulated GTPase the ratio was 21, substantially closer to the experimentally observed ratio of 2.5 (Figure 4B). We observed similar trends in fits to the other data set we trained our model against (Gardner et al., 2011b; Lawrence et al., 2018; Supplemental Figure 5, A and B).

FIGURE 4:

Model that incorporates nearest-neighbor modulation of GTPase activity. (A) Cartoons illustrating the differences between models without (top) and with (bottom) nearest-neighbor GTPase modulation. Allowing GTPase rate modulation requires one additional parameter: the fold increase in GTPase rate due to the nearest-neighbor influence. (B) Comparison between measured (black circles) and predicted (the blackest line corresponds to a onefold increase in GTPase rates and the bluest corresponds to a 1000-fold increase) growth rates. All four scenarios can recapitulate observed growth rates (left plot). Predicted catastrophe frequency as a function of concentration for different fold increases in GTPase rate (right plot). Varying the magnitude of GTPase rate modulation has a significant effect on the concentration dependence of the catastrophe frequency. The y-axis is linear in the larger plot. The smaller inset graph displays the same data, but the y-axis is on log scale. (C) Comparison between measured (black circles) and predicted (the blackest line corresponds to a onefold increase in GTPase rates and the bluest corresponds to a 1000-fold increase) growth rates in the propagation-limited GTPase model. All four scenarios can recapitulate observed growth rates (left plot). Predicted catastrophe frequency as a function of concentration for different fold increases in GTPase rate in the propagation-limited GTPase model (right plot). Artificially limiting the propagation of wavelike GTPase activity reverts the changes in predicted concentration dependence of catastrophe frequency observed in the original nearest-neighbor GTPase modulation model. The y-axis is linear in the larger plot. The smaller inset graph displays the same data, but the y-axis is on log-scale.

Why did this nearest-neighbor GTPase stimulation model improve predictions of the concentration dependence of catastrophe more substantially? Looking at the biochemical “movies” generated by the simulation, even though we implemented this as a nearest-neighbor effect, we observed that the GTP hydrolysis propagated through the lattice, like a wave (unpublished data). The wave of GTP hydrolysis starts from a random GTP hydrolysis in a locally all-GTP lattice, where hydrolysis is relatively slow, according to this model. Hydrolysis of one GTP to GDP effectively starts a local chain reaction because the nearest-neighbor αβ-tubulins gain increased GTPase activity. GTP hydrolysis at this second site then stimulates its neighbor to increased GTPase activity, and so on. Thus, although we constructed the model to have only nearest-neighbor effects, the resulting behavior showed longer-range propagation. The value of the high GTPase rate was restrained to ensure that the “wave” of GTPase was slower than the elongation rate—this avoids a scenario where a single GTPase event anywhere in the cap would be sufficient to cause catastrophe.

Was it the local change in GTPase rate or the longer-range propagation of GTP hydrolysis that was more important for improving the predicted concentration dependence of catastrophe? We examined this question by modifying the nearest-neighbor GTPase stimulation model so that the wave of GTP hydrolysis would be artificially prevented from propagating too far. To accomplish this, we disallowed across-seam interactions from stimulating GTPase activity. As before, we set the neighbor-dependent GTPase stimulation to increase by factors of 1, 10, 100, and 1000 and retrained the basal GTPase rate to match the catastrophe frequency at the reference concentration. Limiting the propagation of the nearest-neighbor stimulation of GTPase degraded the model’s ability to predict the concentration dependence of catastrophe (Figure 4C). Some of the predictive power gained in the untruncated version of the GTPase stimulation model was lost in the truncated version: where the untruncated model showed only a 21-fold change in catastrophe frequency over the measured concentration range, the truncated propagation version showed a 66-fold change, further from the 2.5-fold change observed experimentally. We observed similar trends in fits to the other data set we trained our model against (Supplemental Figure 5D).

In summary, nearest-neighbor modulation of the αβ-tubulin dissociation rate had a limited effect on the predicted concentration dependence of catastrophe. In contrast, nearest-neighbor stimulation of GTPase activity yielded a substantial improvement. The activation of GTPase propagated through the lattice, and this long-range propagation was required for improved predictions of catastrophe.

Incorporating long-range, through-lattice modulation of the strength of tubulin–tubulin interactions can also improve predictions of catastrophe

In the nearest-neighbor GTPase stimulation model, the wavelike propagation of GTP hydrolysis effectively allowed the nucleotide state at one site to indirectly affect the biochemistry of distant (beyond nearest-neighbor) αβ-tubulins. We wondered whether long-range, through-lattice modulation of αβ-tubulin:αβ-tubulin binding affinity could also improve the predicted concentration dependence of catastrophe.

Previously, in the nearest-neighbor affinity modulation model, we assumed for simplicity that the destabilizing interdimer interaction was limited to nearest neighbors. However, it stands to reason that if one subunit influences the conformation of its neighbor, then that neighbor should influence the conformation of its neighbor, and so on. In other words, the conformational accommodation should propagate beyond nearest-neighbor contacts. As a simple way to test whether beyond–nearest neighbor effects would be important, we implemented a model where the accommodation modulates the strength of lattice contacts over some specified distance (number of αβ-tubulin subunits). Basically, this entailed modifying the affinity model so that the nucleotide state of one tubulin affects the dissociation rate of other tubulins farther away. This time, we kept the modulated dissociation rate at 90, the highest value tried for the original nearest-neighbor affinity-modulation model. Then we varied the maximum range of modulation (Figure 5A). When the range is set to 0, the model is identical to the two-state model, while if the range is set to 1, the model is identical to the original nearest-neighbor affinity model. When the range is an integer greater than one, a given subunit affects that many of its neighbors to the left and to the right. To keep the model as simple as possible, we did not implement a distance-dependent fall-off in the strength of modulation, nor did we implement a counting scheme to account for the possible effects of mixed nucleotide state along the range of modulation. For each range of modulation, the GTPase rate was retrained to match the catastrophe frequency at the reference concentration. For increasing maximum ranges of through-lattice modulation of interdimer interaction, the predicted catastrophe frequency became substantially less sensitive to αβ-tubulin concentration (Figure 5C). Allowing long-range effects yielded a predicted catastrophe frequency that changed only 2.3-fold over the concentration range, nearly matching the experimentally observed a 2.5-fold change. We observed similar trends in fits to the other data set we trained our model against (Gardner et al., 2011b; Lawrence et al., 2018; Supplemental Figure 4D).

FIGURE 5:

Model that incorporates long-range modulation of the strength of lattice contacts. (A) Cartoons illustrating the differences between models without (top) and with (bottom) the long-range αβ-tubulin affinity modulation. Allowing the αβ-tubulin affinity modulation requires two additional parameters: the fold increase in αβ-tubulin dissociation rate due to the nearest-neighbor influence and the maximum range of modulation. Vertical white arrows indicate trans-acting nucleotides; the horizontal white arrow indicates the beyond–nearest neighbor effect on affinity modulation. (B) Comparison between measured (black circles) and predicted (the blackest line corresponds to the modulation range of 0 and the greenest corresponds to the modulation range of 7) growth rates. All five scenarios can recapitulate observed growth rates. In this plot the dissociation rate of the modulated αβ-tubulin is increased 90-fold. (C) Predicted catastrophe frequency as a function of concentration for different maximum ranges of modulation. Varying the maximum range of modulation has a significant effect on the concentration dependence of the predicted catastrophe frequency. The dissociation rate of the modulated αβ-tubulin is increased 90-fold. The y-axis is linear in the larger plot. The smaller inset graph displays the same data, but the y-axis is on log scale.

In summary, incorporating long-range, through-lattice modulation of tubulin–tubulin interactions improved predictions of the concentration dependence of catastrophe. Short-range (nearest-neighbor) modulation was much less effective. Incorporating a third state in the form of GDP.P_i also did not improve predictions of the concentration dependence of catastrophe. Thus, long-range, through-lattice effects, whether modulating GTPase or αβ-tubulin dissociation, may represent a missing ingredient required for biochemical models to recapitulate the concentration dependence of catastrophe.

An empirical decomposition of catastrophe frequency reveals differences in frequency of pausing and commitment to catastrophe between the models

To better understand why incorporating through-lattice, long-range modulation improved predictions of the concentration dependence of catastrophe, we took a closer look at the sequence of events that led to catastrophe in our different models. In all models, MT growth always paused (defined as a transient growth rate less than 25% of the average MT elongation rate) for a short time before undergoing a catastrophe (Figure 6A). Similar pausing/slowdown has been observed in experiments (Maurer et al., 2014). As we showed previously (Piedra et al., 2016), terminal GDP exposure can cause this slowing of elongation by transiently poisoning individual protofilaments. This transient pausing in turn accelerates erosion of the stabilizing cap, and the consequent complete loss of the cap leads to catastrophe. However, not all pausing episodes led to catastrophe in our simulations. If the GDP exposure can be overcome before the stabilizing cap erodes completely, the MT can resume growing at a normal rate (Figure 6B). We quantified the “growth-to-pause” frequency and the “pause-to-catastrophe” probability from simulation outputs of the two-state model (see Materials and Methods). The product of these two quantities faithfully reproduced the frequency of catastrophe (Figure 6C), indicating that catastrophe can be decomposed into two separate steps and that transient pausing is an obligate intermediate.

FIGURE 6:

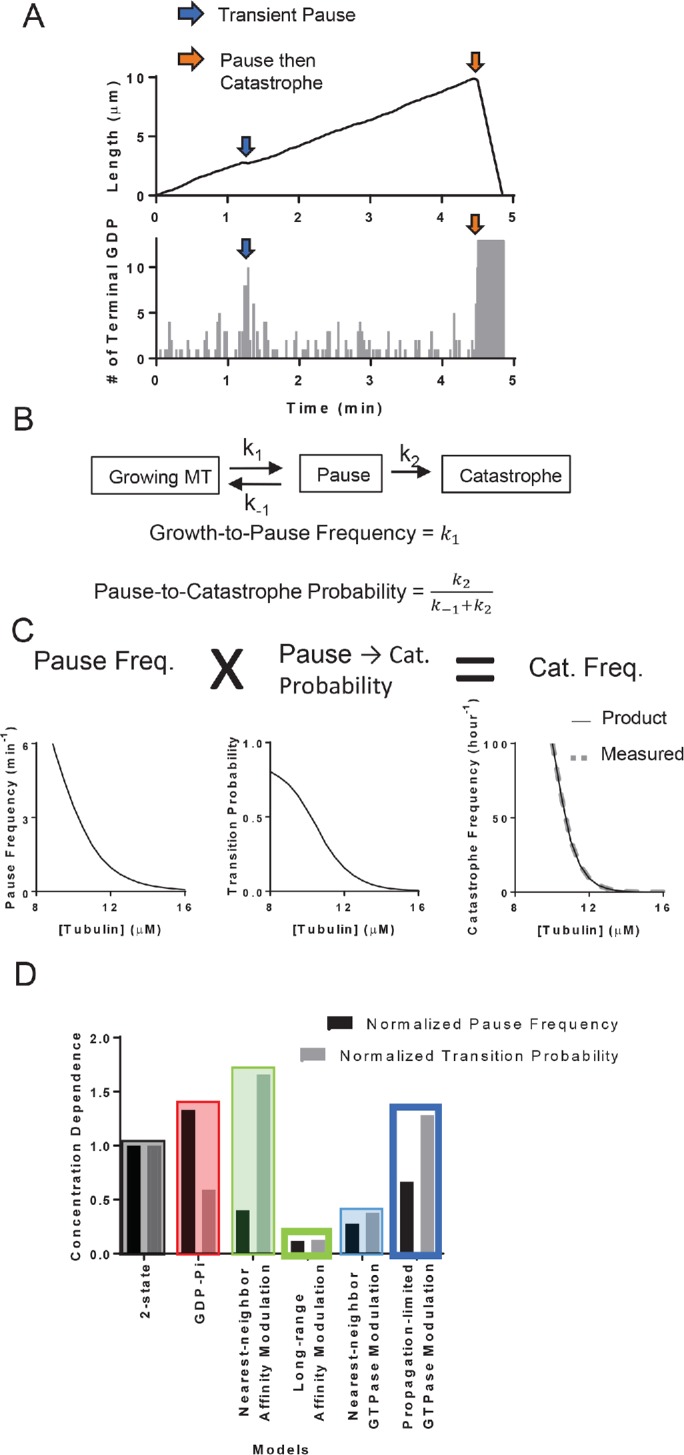
Microtubule catastrophe can be decomposed into two separate steps. (A) The plot of MT length vs. time (top panel) and the corresponding plot of terminal GDP-tubulin vs. time (bottom panel). The exposure of GDP-tubulins at the ends of some protofilaments (blue arrows) leads to transient pausing. The exposure at the end of all protofilaments can follow partial loss of the GTP stabilizing cap (orange arrows), leading to transient pausing followed by catastrophe. (B) Diagram of transient pausing and catastrophe as elementary processes (top). Growth-to-pause frequencies and pause-to-catastrophe probability defined in terms of the reaction rates to the elementary processes (bottom). (C) Plot of growth-to-pause frequencies (left), pause-to-catastrophe probabilities (middle), and the catastrophe frequencies (right) as functions of αβ-tubulin concentrations in two-state model. The multiplicative product (black line, bottom plot) of the growth-to-pause frequencies and the pause-to-catastrophe probabilities match the value of the predicted catastrophe frequency (gray dashed line, bottom plot). (D) The concentration dependencies of the growth-to-pause frequencies and the pause-to-catastrophe probabilities of different models normalized to the two-state model. Here, we defined the concentration dependence as the ratio of the growth-to-pause frequencies or the pause-to-catastrophe probabilities at 9.5 over 13.5 µM.

If the catastrophe frequency is the product of the growth-to-pause frequency and the pause-to-catastrophe probability, then the concentration dependence of the catastrophe frequency must also stem from the concentration dependence of these two components. To determine whether the concentration dependence can be attributed to the growth-to-pause frequency, the pause-to-­catastrophe probability, or both, we first characterized the growth-to-pause frequency and the pause-to-catastrophe probability as functions of tubulin concentration in the two-state model. Both the growth-to-pause frequency and the pause-to-catastrophe probability depended strongly on αβ-tubulin concentration (Figure 6C).

We then examined how different models affected the concentration dependencies of growth-to-pause frequencies and pause-to-catastrophe probabilities relative to the baseline provided by the two-state model (Figure 6D). Compared with the two-state model, all models showed substantial changes to the concentration dependence of growth-to-pause frequency and pause-to-catastrophe probability. In the models that did not allow long-range effects, the concentration dependence of the two components of catastrophe moved in opposite directions, effectively canceling each other, so that there was little improvement in the concentration dependence of the catastrophe. In contrast, in the models that allowed long-range effects, the concentration dependence of the two components of catastrophe moved in concert with each other, explaining why these long-range models better predicted catastrophe.

DISCUSSION

Simple two-state biochemical models fail to predict the weak concentration dependence of the catastrophe frequency. The studies described here were motivated by the hypothesis that this failure occurs because two-state models oversimplify the biochemistry, and sought to use modeling to get insight into what might be missing. The new kinds of biochemistry we tested were inspired by recent structural experiments (Alushin et al., 2014; Zhang et al., 2015; Manka and Moores, 2018) that revealed three distinct and apparently mutually incommensurate conformations of αβ-tubulin in the GTP, GDP.P_i, and GDP-bound microtubule lattices. These structural findings, along with results from reconstitution studies of EB proteins (Maurer et al., 2011, 2014), imply that models for microtubule dynamics might need to contain a third biochemical state (GDP.P_i), and/or that they might need to account for the likely effects of incommensurate conformations of αβ-tubulin that must modulate the properties of GTP- or GDP-tubulin in a context-dependent way (conformational coupling). We implemented different candidates for missing states or kinds of interactions in the simplest way possible, so that we would avoid a large increase in the number of model parameters. For the same reason, while a third state and conformational coupling might be required simultaneously, for simplicity in this work we chose to examine the two separately.

Adding a third state did little if anything to improve predictions of catastrophe, even though that model contained an extra adjustable parameter. In contrast, allowing conformational coupling to modulate either GTPase rate or lattice-binding affinity noticeably improved predictions of the concentration dependence of catastrophe, with modulation of affinity giving better performance. Because conformational coupling should propagate beyond nearest-neighbor interactions, our computational findings provide evidence that cooperative, through-lattice effects may be important determinants of microtubule catastrophe. The models we examined do not capture all aspects of catastrophe—some only partially improve the concentration dependence, and none recapitulates the “age-­dependence” that has been observed experimentally (Odde et al., 1995; Gardner et al., 2011b; Duellberg et al., 2016). This should not be surprising, because we intentionally chose the simplest (least parameter-intensive) ways to examine the possible consequences of candidate missing biochemistries, such as a GDP.P_i state or the coupling that arises from conformational accommodation.

Why does incorporating long-range effects improve predictions about the concentration dependence of catastrophe? In our model, catastrophes occur after the microtubule end becomes transiently “poisoned” by the exposure of multiple GDP-terminated protofilaments (Figures 6A and 7). This GDP exposure causes catastrophe because it stalls growth (induces a pause), leading to erosion of the stabilizing cap (Piedra et al., 2016). In the two-state model, exposure of GDP on the ends of multiple protofilaments is rare because the GTPase rate is constrained to be low in order to maintain a large enough stabilizing cap. Conversion from pause to catastrophe also shows substantial concentration dependence, because competing events such as association of new tubulins are themselves concentration-dependent. The essence of the two long-range models we explored is that they both amplify the impact of GTP hydrolysis near the microtubule end, allowing the first-order nature of GTPase to become more dominant in determining the overall concentration dependence of catastrophe: neighbor-based stimulation of GTPase makes it more likely to develop a patch of GDP-terminated protofilaments (Figure 7B), and neighbor-based change in binding affinity increases the impact of a single GDP-terminated protofilament (Figure 7C). Both changes make it harder to cover the GDP than in the two-state model.

FIGURE 7:

Cartoon illustrating some consequences of the different models. (A) In the two-state model, multiple protofilaments with exposed terminal GDP-tubulin tend to be required for MT pausing and catastrophe. Individual GDP-terminated protofilaments can be covered by subsequent associations of GTP-tubulins above and adjacent to the GDP-site (unpublished data), so the exposure of multiple GDP-terminated protofilaments typically requires multiple steps (black arrows) and is concentration-dependent. In these cartoons the size of the GTP-cap is represented by darker shading and becomes smaller in the paused state. (B) In the neighbor-stimulated GTPase model, the local amplification of GTPase makes developing a patch of GDP-terminated protofilaments more likely, and consequently it can occur in fewer concentration-dependent steps (fewer arrows than in A). (C) In the long-range affinity-modulation model, a single GDP-terminated protofilament is harder to cover (indicated by a white asterisk) because of the longer-range effect on sites adjacent to the capping site. This amplification of the impact of an individual GDP-terminated protofilament also reduces concentration dependence.

Mechanochemical models have outperformed biochemical models where catastrophe is concerned: mechanochemical models better recapitulate both the concentration and age dependence of microtubule catastrophe (Coombes et al., 2013; Zakharov et al., 2015). The mechanochemical models are more parameter-intensive because they also account for multiple features that the biochemical models do not: curved–straight conformational changes on the microtubule end, the partially curved conformations that occur at/near the microtubule end, different strengths for the same interface that result from allowing stretching of longitudinal and lateral bonds, and more. Consequently, precisely why these mechanochemical models predict the concentration dependence of catastrophe better than biochemical models has so far not been clear.

The work described here may begin to explain why mechanochemical models have been more successful at predicting catastrophe. Indeed, our simulations indicate that long-range, through-lattice coupling is required for improved predictions of catastrophe in biochemical models. Because of the way that they allow mechanical strain to be distributed through the lattice, this kind of long-range coupling is built into the mechanochemical models. In light of our results, it seems likely that incorporating long-range coupling into the lattice is one reason that mechanochemical models have been more successful in predicting microtubule catastrophe.

What we have described based on our modeling is a kind of cooperativity that operates within the microtubule. This resonates with a view of microtubule dynamics (Kueh and Mitchison, 2009; Brouhard and Rice, 2018) in which different conformations of αβ-tubulin can modulate or even override the nucleotide state in dictating biochemical interactions and rates in the lattice. Detecting such cooperativity experimentally and determining whether it operates on GTPase and/or the strength of lattice contacts are important challenges for future work. The recently introduced ability to work with tubulins from different species (Drummond et al., 2011; Widlund et al., 2012; Chaaban et al., 2018), to purify single isotypes and site-­directed mutants (Drummond et al., 2011; Johnson et al., 2011; Minoura et al., 2013; Geyer et al., 2015, 2018; Pamula et al., 2016; Ti et al., 2016; Vemu et al., 2016, 2017), and to measure αβ-tubulin:microtubule interactions at the single-molecule level (Mickolajczyk et al., 2018) has the potential to accomplish this, and promises to provide new kinds of data that will drive a deeper understanding of microtubule catastrophe.

In summary, our computational experiments indicate that beyond–nearest neighbor, through-lattice effects can make important contributions to microtubule catastrophe. The combination of this allosteric conformational coupling with the extended microtubule lattice has the potential to generate abrupt, switchlike changes (reviewed in Bray, 2013, for other systems) that could give rise to threshold-type behavior wherein the switch only happens upon reaching some critical percentage of GTP hydrolysis (or some other property). Interestingly, the onset of rapid shrinking has been observed to occur after a threshold loss of the stabilizing cap is exceeded (Maurer et al., 2014). A number of microtubule-associated proteins have recently been shown to alter the microtubule lattice upon binding (Zhang et al., 2015, 2017, 2018; Howes et al., 2017; von Loeffelholz et al., 2017; Peet et al., 2018; Shima et al., 2018), and these binding-induced conformational changes might also modulate properties of the lattice at greater distance. At least one study has proposed that EB proteins might influence the activity of XMAP215-family microtubule polymerases via long-range, through-lattice effects (Zanic et al., 2013), but the underlying mechanism was not specified. The apparent importance of long-range cooperative/allosteric effects suggests that material-like properties of the microtubule are important for catastrophe and may be targeted by regulatory factors.

MATERIALS AND METHODS

Computational simulation of the models

We created a computer program (coded in Fortran) to perform kinetic Monte Carlo simulations of MT plus ends. The model is similar to one we used previously (Ayaz et al., 2014; Piedra et al., 2016; Mickolajczyk et al., 2018), and was inspired by an earlier implementation by others (VanBuren et al., 2002). Briefly, the microtubule lattice is represented by a two-dimensional array with a periodic boundary condition to mimic the cylindrical wall of the microtubule. MT dynamics is simulated one biochemical reaction (αβ-tubulin subunit association or dissociation, and GTP hydrolysis) at a time. In a prior study we reported that the rate of GDP-to-GTP exchange at the microtubule end could modulate the frequency of catastrophe (Piedra et al., 2016). That reaction did not improve the predicted concentration dependence of catastrophe (Piedra et al., 2016), so for simplicity we did not include it in the models described here. For the two-state model, the association can happen at the tip of each protofilament, and the association rate is given by k_on × [αβ-tubulin], where k_on denotes the on rate constant. The terminal subunits can dissociate from the MT lattice at a rate given by k_on × K_D, where K_D is the affinity determined by the sum of all interdimer interactions and the entropy cost of binding to MT. The strengths of the longitudinal and lateral interactions are different, but they are isotropic otherwise. As described previously (Piedra et al., 2016), our parameterization assumes that the nucleotide (GTP or GDP) acts in-trans to affect the strength of longitudinal contacts such that GTP contacts are stronger than GDP ones. GTP hydrolysis is modeled for all nonterminal subunits with rate constant k_hyd.

Automated analysis of simulations

We created custom MATLAB routines to analyze the output from the simulations. These routines determine the instantaneous growth/shrinking rates by looking at the change in the total number of subunits over a 5-s time period. If the instantaneous growth rate falls below 25% of the average growth rate during the growth phase, the simulated MTs are considered to have paused for the duration of the slower growth. The pause episodes are left out of the growth/shrinking rate calculations and are used to determine how frequently the simulation pauses. The MATLAB routine automatically detects MT catastrophe using the following definition: the simulated MT must persistently be shrinking at a high rate (shrinking rate greater than 75% of the mode of shrinking rate distribution) for an extended period of time (at least 15 s). In the two-step decomposition of catastrophe, the frequency of pausing is tabulated to obtain the growth-to-pause frequency, and the likelihood of catastrophe following transient pausing gives the pause-to-catastrophe probability. We calculated these values for the simulation models trained to (Walker et al., 1988). We used the ratios between values at 9.5 and 13.5 µM as a measurement of the concentration dependencies of the growth-to-pause frequency and the pause-to-catastrophe probability. These ratios (the concentration dependencies) were normalized to the concentration decencies of the two-state models for model-to-model comparisons.

The parameterization of the two-state computational model

To parameterize the two-state model, we first assumed a value for k_on of 2 tubulin·s^-1·µM^-1 per protofilament for the data that we fit in the main text (Walker et al., 1988) and 1.5 tubulin·s^-1·µM^-1 per protofilament for the alternative data that we fit in the Supplemental Material (Gardner et al., 2011b; Lawrence et al., 2018). Then the strengths of the longitudinal (at the GTP-interface) and lateral interaction were determined by fitting the model predictions of growth rates (during the growth phase) to the experimental values. The strength of the longitudinal interaction at the GDP interface was determined by fitting the model predictions of shrinking rates (during the shrinking phase) to the experimental values. Then the GTPase rate was determined by fitting the model predictions on the catastrophe frequency at a single reference concentration (10 µM for the data [Gardner et al., 2011b; Lawrence et al., 2018] in the main text and 12 µM for the alternative set [Walker et al., 1988] in the Supplemental Material). Growth rates decrease in the presence of GTPase activity, and catastrophe frequency depends on growth rates. We therefore optimized the parameters iteratively. Owing in part to the use of this iterative approach, the model parameters for GTP–tubulin binding affinity (1 µM instead of 4 µM for corners) and GDP weakening factor (300 instead of 50) are different from what we previously reported (Piedra et al., 2016).

The GDP.P_i model

We incorporated a third intermediate state into our model, including GDP.P_i. This GDP.P_i model inherits the two-state model’s properties described above with some modifications. In this model, GTP is first hydrolyzed to GDP.P_i; then the P_i is released at a set rate to form GDP. We assumed that the P_i is released immediately when exposed at the tip of the MT, and that the strength of the longitudinal interface with GDP.P_i is different from that of those with GTP or GDP. This model has two additional parameters: the rate of P_i release and the strength of the longitudinal interface with GDP.P_i. We explored the parameter space of the additional adjustable parameters in a 3-by-3 grid pattern: setting the rate of P_i release to 0.1, 1, and 10-fold of the GTPase rate, and setting the strength of the longitudinal interface with GDP.P_i to high (GTP-like), intermediate, and low (GDP-like). Then, in order to maintain the correct frequency of catastrophe at the reference concentration, we retrained the GTPase rate. We kept the αβ-tubulin binding affinities the same as in the two-state model because we did not want to introduce confounding variation. Changes in growth and shrinking rates due to the modification were negligible.

The affinity modulation models

As before, the affinity modulation models inherit the two-state model’s properties described above, with some modifications. In the nearest-neighbor affinity modulation model, we assumed that the rate of αβ-tubulin dissociation is higher if the nucleotide state of the longitudinal interface of the nearest neighbor is different. This model has one new adjustable parameter: the energy cost of being next to a tubulin with different nucleotide. We explored the parameter space by setting the energy cost to different values and retraining the GTPase. As described above, we kept the αβ-tubulin binding affinities the same as in the two-state model. In the long-range affinity modulation model, the range of influence for the affinity modulation is an additional adjustable parameter. When the range is set to 0, the model behaves identically to the two-state model, and when the range is set to 1, the model behaves identically to the nearest-neighbor affinity modulation model; for values greater than 1, it gives beyond–nearest neighbor effects. For this model, we set the energy cost to the maximum value we used for the nearest-neighbor affinity modulation model and varied the range from 0 to 7.

The GTPase stimulation model

In the nearest-neighbor GTPase stimulation model, αβ-tubulin with GTP laterally next to αβ-tubulin bound to GDP hydrolyzes GTP faster. This model has one additional parameter: the context-dependent fold increase in GTPase rate. We set the fold increase to 1, 10, 100, and 1000 and retrained the basal GTPase rate, as before. This context-dependent increase in GTPase rate leads to a wavelike propagation of GTP hydrolysis. In all our simulations, the propagation speed of the wave of GTP hydrolysis was below the lowest growth rate experimental data. In the propagation-limited GTPase modulation model, we limited the wavelike propagation of the GTP hydrolysis by preventing GTPase modulation across the MT seam.

We created a similar model where the GTPase rate is stimulated by longitudinal neighbors, but these models predict catastrophe frequency more sensitive to the concentration than in the two-state model.

Code availability

Simulation codes will be shared upon request.

Abbreviations used:

EB

end binding

GDP

guanosine 5’-diphosphate

GTP

guanosine 5’-triphosphate

MT

microtubule