Integration Time in a Subset of Spinal Lamina I Neurons Is Lengthened by Sodium and Calcium Currents Acting Synergistically to Prolong Subthreshold Depolarization

Abstract

Lamina I of the spinal dorsal horn plays an important role in processing and relaying nociceptive information to the brain. It comprises physiologically distinct cell types that process information in fundamentally different ways: tonic neurons fire repetitively during stimulation and display prolonged EPSPs, suggesting operation as integrators, whereas single-spike neurons act like coincidence detectors. Using whole-cell recordings from a rat spinal slice preparation, we set out to determine the basis for prolonged EPSPs in tonic cells and the implications for signal processing. Kinetics of synaptic currents could not explain differences in EPSP kinetics. Instead, tonic neurons were found to express a persistent sodium current, I_Na,P, that amplified and prolonged depolarization in response to brief stimulation. Tonic neurons also expressed a persistent calcium current, I_Ca,P, that contributed to prolongation but not to amplification. Simulations using NEURON software demonstrated that I_Na,P was necessary and sufficient to explain amplification, whereas I_Na,P and I_Ca,P acted synergistically to prolong depolarization: initial activation of the slower current (I_Ca,P) depended on the faster current (I_Na,P) but maintained activation of the faster current likewise depended on the slower current. Additional investigation revealed that I_Na,P and I_Ca,P could dramatically increase integration time (>30×) and thereby encourage temporal summation but at the expense of spike time precision. Thus, by prolonging subthreshold depolarization, intrinsic inward currents allow tonic neurons in spinal lamina I to specialize as integrators that are optimally suited to encode stimulus intensity.

Introduction

Lamina I of the spinal dorsal horn is important for processing and relaying nociceptive information (Perl, 1984; Willis, 1985; Light, 1992; Craig, 1994, 2000). Until recently, little was known about intrinsic properties of lamina I neurons. We found that lamina I comprised four physiologically distinct cell types (Fig. 1) with clear morphological correlates (Prescott and De Koninck, 2002). Ruscheweyh and Sandkuhler (2002) found comparable cell types in lamina I, and other studies have described similar cell types in deeper spinal laminas (Thomson et al., 1989; Yoshimura and Jessell, 1989; Lopez-Garcia and King, 1994; Jo et al., 1998; Grudt and Perl, 2002; Schneider, 2003). The diversity of intrinsic cellular properties allows for a wealth of computational processes influencing transmission of sensory information through the dorsal horn (Morisset and Nagy, 1998; Russo and Hounsgaard, 1999; Derjean et al., 2003). However, processing that occurs in lamina I and its biophysical basis remain poorly understood.

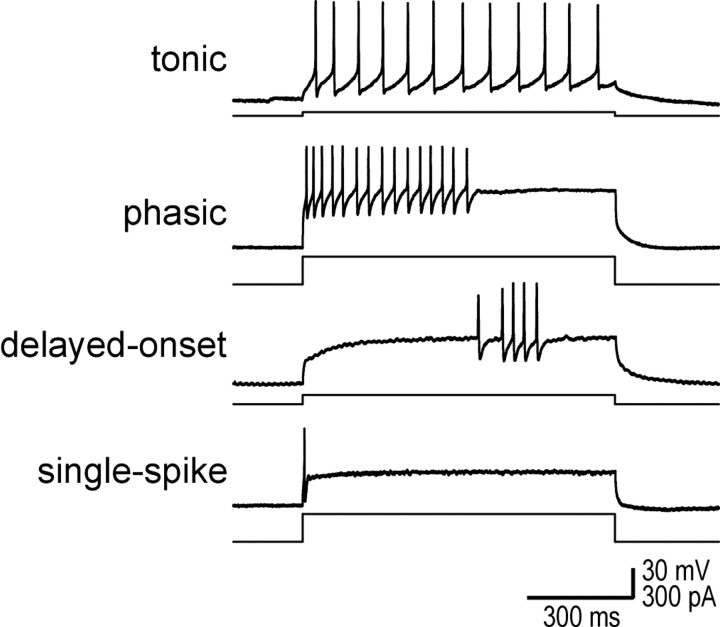
Figure 1.

Lamina I comprises four physiologically distinct cell types. Sample traces show representative responses to a 900 ms step depolarization. Tonic cells fire regularly throughout the stimulus. Phasic cells respond with a high-frequency burst of variable duration. Delayed-onset cells produce irregularly timed spikes, typically after a long delay from the onset of stimulation. Single-spike cells produce only one spike at the onset of stimulation.

The manner in which neurons process information is often described as integration or coincidence detection depending on whether integration time is long or short, respectively (Abeles, 1982; König et al., 1996; Rudolph and Destexhe, 2003). Within lamina I, tonic and delayed-onset neurons exhibit characteristics typical of integrators, whereas phasic and single-spike neurons behave as coincidence detectors (Prescott and De Koninck, 2002). Function of tonic neurons as integrators is facilitated by their EPSPs, which are significantly longer than in other cell types (Prescott and De Koninck, 2002) and therefore tend to summate. This study began with the goal of explaining why EPSPs are prolonged in tonic cells. Initial results revealed that prolonged EPSPs were not explained by differences in synaptic currents, suggesting that voltage-dependent currents were responsible.

The persistent sodium current can amplify synaptic depolarization (Crill, 1996, 1999; Lipowsky et al., 1996; Urban et al., 1998; Crill et al., 2002), but its capacity to prolong EPSPs is less well recognized (Deisz et al., 1991; Gonzalez-Burgos and Barrionuevo, 2001). A persistent sodium current has been described in lamina I neurons (Safronov et al., 1997; Safronov, 1999), but its differential distribution among cell types and its functional significance remain unknown. Calcium currents can also amplify synaptic depolarization (Gillessen and Alzheimer, 1997; Urban et al., 1998; Crill, 1999) and are involved in generating plateau potentials in deeper dorsal horn neurons (Morisset and Nagy, 1999). They are present in lamina I (Heinke et al., 2004), and the T-type current appears to be important for long-term potentiation (Ikeda et al., 2003). These currents can influence encoding by altering synaptic kinetics (Fricker and Miles, 2000; Axmacher and Miles, 2004) and also affect neuronal excitability and firing pattern (Llinás, 1988; Connors and Gutnick, 1990; Magee and Carruth, 1999; Geijo-Barrientos, 2000; Agrawal et al., 2001; Lee and Heckman, 2001). These issues remain relatively unexplored with regards to spinal lamina I. Therefore, using a combination of whole-cell recordings and computer simulations, we investigated the role of sodium and calcium currents in shaping EPSPs and the implications for signal processing by spinal lamina I neurons.

Materials and Methods

Slice preparation. All experiments were performed in accordance with regulations of the Canadian Council on Animal Care. Details of slicing have been described previously by Chéry et al. (2000). Briefly, adult male Sprague Dawley rats (>40 d of age) were anesthetized with an intraperitoneal injection of sodium pentobarbital (30 mg/kg) and perfused intracardially with ice-cold oxygenated (95% O₂ and 5% CO₂) sucrose-substituted artificial CSF (ACSF) containing the following (in mm): 252 sucrose, 2.5 KCl, 2 CaCl₂, 2 MgCl₂, 10 glucose, 26 NaHCO₃, 1.25 NaH₂PO₄, and 5 kynurenic acid, pH 7.35, 340-350 mOsm. Rats were decapitated, the spinal cord was removed by hydraulic extrusion, and 300- to 400-μm-thick parasagittal slices were cut from the lumbar and cervical enlargements. Slices were kept in normal oxygenated ACSF (126 mm NaCl instead of sucrose and without kynurenic acid; 300-310 mOsm) at room temperature until recording.

Recording and data acquisition. Patch pipettes were pulled from borosilicate glass capillaries (World Precision Instruments, Sarasota, FL), and the shank was coated in Sylgard to reduce capacitance. Pipettes were filled with an intracellular solution containing the following (in mm): 135 KMeSO₄, 5 KCl, 10 HEPES, 2 MgCl₂, 4 ATP (Sigma, St. Louis, MO), and 0.4 GTP (Sigma), pH was adjusted to 7.2 with KOH, and osmolarity ranged from 270 to 290 mOsm. Intracellular Ca²⁺ was not buffered to avoid possible effects on firing pattern (Schwindt et al., 1992; Staley et al., 1992; Zhang et al., 1994). Although morphology data are not described here, ∼0.1% Lucifer yellow (dipotassium salt; Sigma) was included in the recording solution to allow visualization of neuronal morphology after recording. To prevent potentially damaging effects of Lucifer yellow on neuronal function, labeled neurons were not fluoresced until after all physiological investigation was complete, and potassium rather than lithium salt was used. Based on these two important facts, criticism of our use of Lucifer yellow by Ruscheweyh et al. (2004) based on the study by Higure et al. (2003) is unjustified.

Slices were transferred to a recording chamber constantly perfused at ∼2 ml/min with oxygenated (95% O₂ and 5% CO₂) ACSF. All recordings were at room temperature (22-25°C). Slices were viewed with a modified Zeiss (Toronto, Ontario, Canada) Axioplan2 microscope equipped with infrared “gradient-contrast” optics (Dodt et al., 1998) and a 40× water-immersion objective (numerical aperture, 0.8; Achroplan; Zeiss). Visually identified neurons were patched on and recorded from in the whole-cell configuration using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA). Neurons were judged healthy on the basis of three criteria: resting membrane potential (V_m) less than -50 mV, spikes over-shooting 0 mV, and input resistance (R_in) >100 MΩ. Access resistance was monitored during recording, and testing was discontinued if it rose unrecoverably to >15 MΩ. Traces were stored on videotape using a digital data recorder (VR-10B; Instrutech, Port Washington, NY). Offline recordings were low-pass filtered at 10 kHz for current-clamp recordings or at 3-10 kHz for voltage-clamp recordings and sampled at 10-20 kHz on a computer using Strathclyde electrophysiology software (J. Dempster, Department of Physiology and Pharmacology, University of Strathclyde, Glasgow, UK). Data were analyzed using locally designed software (Y.D.K.).

Physiological experimentation and analysis. Resting V_m was determined shortly after breakthrough. Reported values of V_m were corrected for the liquid junction potential (Barry and Lynch, 1991) calculated to be 9 mV based on our recording solution. To standardize characterization of voltage-sensitive properties between neurons, prestimulus V_m was adjusted to -60 or -75 mV by injecting small amounts of current into the cell. Firing pattern was investigated with depolarizing pulses over a wide range of intensities, and cells were classified according to criteria described previously (Prescott and De Koninck, 2002). Membrane time constant (τ_membrane) and R_in were determined from responses to 900 ms hyperpolarizing steps, with the former based on the slowest time constant of exponential curve fits of the hyperpolarizing phase.

Spontaneous synaptic events were detected and analyzed as described previously (Chéry and De Koninck, 1999). In all cells included for synaptic analysis, both EPSPs and EPSCs were recorded (in current and voltage clamp, respectively) to allow direct correlation between kinetics within the same cell. EPSP decay time constants (τ_EPSP) and EPSC decay time constants (τ_EPSC) were determined from single exponential fits of the average EPSP and EPSC in each cell. Distributions of τ_EPSP and τ_EPSC were also investigated using fits of individual events.

In several experiments, neurons were stimulated with 20 ms current pulses applied as trains with an interval ≥200 ms. Stimulation by current injection allowed for reproducible stimuli with adjustable intensity, the polarity of which could be reversed to allow comparison between depolarization and hyperpolarization. Peak voltage change was determined as voltage deflection at the end of the stimulus. In some instances, the rate of repolarization was described by a decay time constant (τ_decay) determined by a single exponential curve fit. However, because decay kinetics were variable and not always well described by an exponential process, the rate of repolarization was quantified by measuring the area under the curve (time integral) based on the first 150 ms after the end of the stimulus. Because the area under the curve can be influenced by both amplification and changes in repolarization rate, effects of amplification were removed by rescaling the response to depolarizing stimulation so that peak depolarization equaled peak hyperpolarization before calculating area. Thus, changes in corrected area under the curve should reflect changes in the rate of repolarization without the confounding influence of amplification. Pulse intensity was increased in 20 pA increments. Focusing on the lowest intensity that elicited spikes in response to at least one pulse during the train, we analyzed those responses not associated with spikes, which we refer to as near threshold. Responses to hyperpolarizing pulses of equivalent amplitude were also measured, and both peak voltage change and the area under the curve were expressed as a ratio of depolarizing to hyperpolarizing responses. This facilitated comparison between cells and different prestimulus V_m in which the minimum stimulus intensity causing spikes varied.

The persistent sodium current (I_Na,P) was investigated in voltage-clamp mode by ramping the command voltage from -110 to -10 mV over 10 s (i.e., 10 mV/s). Ramping at this slow rate should cause complete inactivation of the fast sodium current (Fleidervish and Gutnick, 1996). The remaining I_Na,P component was isolated by subtracting the I-V curve after application of 1 μm TTX from the I-V curve before TTX. Calcium currents were investigated in the presence of TTX using various step protocols in voltage clamp and were isolated by taking the difference of the response in normal ACSF from that in either 1 mm Ni²⁺ or 0 Ca²⁺ ACSF (i.e., Ca²⁺ replaced with equimolar Mg²⁺). Potassium currents were left deliberately unblocked so that we could perform experiments in current-clamp mode both before and after application of TTX and/or Ni²⁺. Currents characterized in voltage clamp were correlated with effects of TTX and Ni²⁺ in current clamp.

All drugs were bath applied. AMPA receptors were selectively blocked by 50 μm 1-(4-aminophenyl)-3-methylcarbamyl-4-methyl-7,8-methylenedioxy-3,4-dihydro-5H-2,3-benzodiazepine (GYKI 53655) (Eli Lilly, Indianapolis, IN) (Paternain et al., 1995). The contribution of NMDA receptors was investigated using 40 μm d-2-amino-5-phosphonovaleric acid (d-AP-5; Tocris Cookson, Bristol, UK). Sodium channels were blocked by 1 μm TTX (Sigma). Voltage-dependent calcium channels were blocked by 0.5-1 mm Ni²⁺, which is a high-enough dose to produce a generalized blockade of all calcium channels (Lee et al., 1999).

Data are reported as mean ± SEM. Nonparametric statistical testing was performed using Systat 10 (Systat, Evanston, IL) and included the Kruskal-Wallis test, Mann-Whitney U test, and Wilcoxon signed-rank test as dictated by the comparison required.

Simulations. Simulations were performed in NEURON 4.3.1 (Hines and Carnevale, 1997) using a compartmental model with morphology based on a generic spinal lamina I fusiform neuron with dendrites branching up to fourth order, as used previously by Coull et al. (2003). An axon morphologically identical to that in the study by Mainen et al. (1995) was attached to the soma. Axial resistivity was 200 Ωcm, and membrane capacitance was 1 μF/cm², except in axon internodes where it was 0.04 μF/cm². Temperature for simulations was 23°C. Passive leak conductance, g_leak, was distributed throughout the cell at a density of 0.042 mS/cm² to give R_in of 330 MΩ, which matches the average value of R_in in real tonic neurons when tested with TTX present. Reversal potential was -65 mV. Fast voltage-dependent Na⁺ and K⁺ conductances (g_Na,F and g_K,DR, respectively) were inserted at different densities depending on the compartment (g_Na,F and g_K,DR in mS/cm²): soma and dendrites, 10, 6; initial segment, axon hillock and nodes, 100, 60; axon internodes, 0, 0. Kinetics was as described by Traub and Miles (1991). A slow variation of g_K,DR, which we refer to as g_K,S, was also included to generate the slow phase of the biphasic afterhyperpolarization (AHP) characteristic of tonic cells (Prescott and De Koninck, 2002). Data presented here suggest that I_K,S may be a Ca²⁺-activated K⁺ current, but this remains uncertain, and we therefore modeled it simply as a voltage-dependent current. Parameters were the same as for g_K,DR, but there was only one activation variable (i.e., n rather than n⁴), and τ_n was increased 10-fold to match AHP kinetics. Density was set to 0.3 mS/cm² throughout the soma and dendrites unless stated otherwise in the Results. A transient Ca²⁺ conductance, g_Ca,T, was also added to recreate TTX-insensitive rebound depolarization. Parameters were as described by Destexhe et al. (1994), with the exception that activation and inactivation curves (m_∞ and h_∞, respectively) were shifted 20 mV more hyperpolarized to reproduce the experimental data. Density was set to 0.03 mS/cm² throughout the soma and dendrites to recreate the amplitude of rebound depolarization observed in current-clamp experiments. We refer to the model neuron including only those conductances described above as the “basic model.”

We added to the basic model a persistent Na⁺ conductance, g_Na,P, and a persistent Ca²⁺ conductance, g_Ca,P, alone and in combination to investigate their roles in amplification and prolongation. In trying to simulate g_Na,P, we first attempted to modify g_Na,F to create a window current, but the m³h model could not reproduce the experimental I-V curve. As in the study by Herzog et al. (2001), we instead used an mh model based on modifications of g_Na,F described by the following equations:

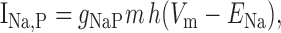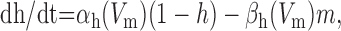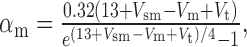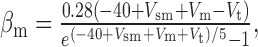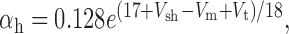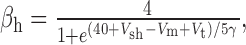where V_t = -55 mV, γ = 0.5, V_sm = -2 mV, and V_sh = -5 mV; V_sm and V_sh shift the functions describing m and h, respectively, to optimally fit the experimental data. This model accurately reproduced the empirical I-V curve, with peak steady-state activation at -42 mV. Density was set to 0.29 mS/cm² throughout the soma and dendrites.

The persistent Ca²⁺ conductance, g_Ca,P, was simulated by making minimal changes to the equations describing g_Ca,T. The inactivation variable h was removed so that activation was described as m² (the L-type current, for example, is typically described as m²) (Kay and Wong, 1987), the activation curve was shifted 5 mV more depolarized, and τ_m was increased by changing δ from 0 to 60 ms in the following equation:

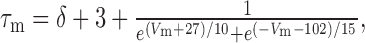thereby reproducing the slow activation/deactivation kinetics. Density was set to 0.02 mS/cm² throughout the soma and dendrites unless noted otherwise in the Results.

The model neuron was stimulated by injection of current (simulated as a point process) into the soma in a manner directly analogous to experiments. Tonically injected current was also used to maintain prestimulus V_m at -63 mV (which approximates the resting V_m in a typical tonic neuron) after addition of g_Na,P and/or g_Ca,P to the basic model. This method of maintaining V_m at a constant level was analogous to our experimental approach, and testing revealed that it gave results equivalent to changing the reversal potential of g_leak. Synaptic stimulation was modeled as a conductance change in a fourth-order dendrite described by the following:

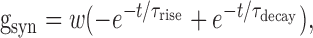where τ_rise = 0.1 ms, τ_decay = 5 ms, and synaptic strength w = 1 nS, thereby approximating EPSC amplitude and kinetics as reported in Figure 2. To demonstrate that the effects of intrinsic currents on integration time were independent of synaptic strength, w was decreased to 0.1 nS for one set of experiments. Synaptic reversal potential was 0 mV.

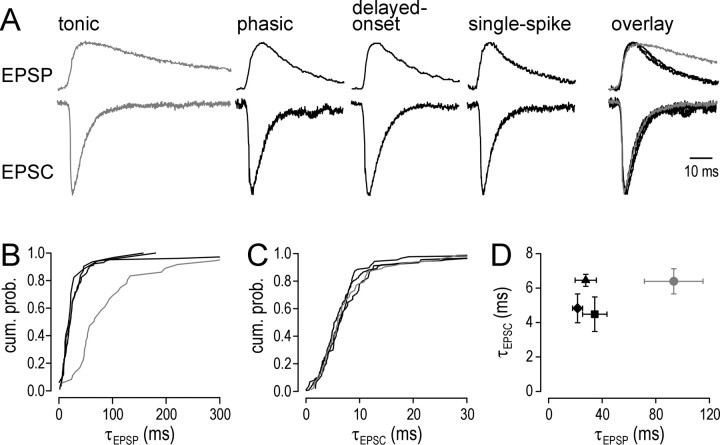
Figure 2.

EPSC kinetics do not explain prolonged EPSPs in tonic cells (gray). A, Traces show the average EPSP and EPSC based on spontaneous synaptic activity in a representative cell from each physiological class. Peak amplitude has been normalized across cells. Based on fits of the average EPSP, τ_EPSP was 72 ms for the tonic cell versus 19, 20, and 22 ms for the phasic, delayed-onset, and single-spike cells, respectively. Despite the much longer τ_EPSP in tonic cells, τ_EPSC in the same set of cells varied little between cell types: 6.4, 6.5, 6.8, and 5.7 ms for tonic, phasic, delayed-onset, and single-spike cells, respectively. Overlaying the responses demonstrates the prolonged EPSP in the tonic cell, whereas the EPSC was indistinguishable from EPSCs in other cell types. B, Cumulative probability distribution of τ_EPSP based on fits of all detected EPSPs in a representative cell from each physiological class. Distribution of τ_EPSP for the tonic cell is clearly shifted toward higher values compared with other cell types. C, Cumulative probability distribution of τ_EPSC based on fits of all detected EPSCs in the same cells shown in B. Unlike τ_EPSP, distributions of τ_EPSC for all cell types closely overlapped. D, Summary of τ_EPSP and τ_EPSC showing mean ± SEM. Membrane/holding potential was -60 mV in all cases. Tonic (circles), n = 4; phasic (squares), n = 5; delayed-onset (triangles), n = 2; single spike (diamonds), n = 5. τ_EPSP varied significantly between cell types (p < 0.05; Kruskal-Wallis test), whereas τ_EPSC did not. cum. prob., Cumulative probability.

Results

Prolonged EPSPs in tonic cells are not explained by EPSC kinetics

We previously reported that cell types that were physiologically distinct on the basis of spiking pattern also exhibited different synaptic kinetics (Prescott and De Koninck, 2002). Specifically, spontaneous EPSPs in tonic cells were significantly longer than EPSPs in other cells types, more than could be accounted for by differences in τ_membrane or by differences in EPSP rise times; this latter point rules out kinetic differences arising from differences in the site of EPSP origin (i.e., distance from soma) and, in turn, argues against any differential capacity to space-clamp EPSCs depending on cell type. Furthermore, previous investigation specifically tested space-clamp issues in lamina I neurons and revealed these cells to be electrotonically compact (Chéry and De Koninck, 1999). Thus, we began the current study by investigating the basis for the unexplained differences in EPSP kinetics.

If the difference in EPSP decay time constant (τ_EPSP) was attributable to a difference in transmitter and/or receptor properties, one would expect the decay time constant of underlying EPSCs (τ_EPSC) to be longer in tonic cells. We investigated this by measuring τ_EPSP and τ_EPSC of spontaneous synaptic events in the same cell by switching between current- and voltage-clamp mode over the course of the recording. Figure 2A shows the average EPSP (top traces) and corresponding average EPSC (bottom traces) from one representative cell of each physiological type. Overlaying the traces reveals that the average EPSP in the tonic cell was significantly longer than in other cell types, but the average EPSC was not prolonged (Fig. 2A, right). Cumulative distributions of τ_EPSP and τ_EPSC from single exponential fits of the individual synaptic events within a given cell confirmed the above findings: EPSPs were consistently longer in the tonic cell (Fig. 2B), but the equivalent was not true for EPSCs (Fig. 2C).

Figure 2D summarizes τ_EPSP and τ_EPSC based on fits from the average EPSP and EPSC in all cells for which synaptic activity was examined in both voltage and current clamp. Consistent with our previous study, τ_EPSP varied significantly between cell types (p < 0.05; Kruskal-Wallis test) and was significantly longer in tonic cells than in phasic or single-spike cells (p < 0.05; Mann-Whitney U tests). In contrast, τ_EPSC did not vary significantly between cell types (Kruskal-Wallis test).

This indicated that differences in EPSP kinetics were not attributable to differences in transmitter and/or receptor properties. Nonetheless, we confirmed that spontaneous synaptic events were uniquely AMPA receptor mediated by blocking all identifiable excitatory synaptic activity by 50 μm GYKI 53655 in cells from each physiological class (data not shown). GYKI 53655 is a noncompetitive antagonist of AMPA receptors with minimal effects on kainate receptors (Paternain et al., 1995). Moreover, addition of 40 μm AP-5 to tonic cells caused negligible changes to τ_EPSP (data not shown), arguing against any significant contribution by NMDA receptors to spontaneous EPSPs, consistent with the short EPSCs.

Intrinsic currents shape subthreshold responses

With passive membrane properties and EPSC kinetics excluded as explanations for the differences in EPSP kinetics, we investigated the role of intrinsic, voltage-dependent currents. Rather than analyze variably sized synaptic responses, we stimulated neurons with 20 ms current pulses. This gave reproducible responses and also allowed for comparison between depolarizing and hyperpolarizing stimulation. Figure 3A shows typical responses in a tonic neuron and in a single-spike neuron to depolarizing (black) and hyperpolarizing (gray) stimulation; the latter is reflected vertically to allow easy comparison with the former. As exemplified by the tonic neuron illustrated, repolarization after near-threshold stimulation was noticeably slower than repolarization after equivalent hyperpolarizing stimulation (Fig. 3A, top left); we henceforth refer to this as prolongation. Similarly, peak voltage change was greater in response to depolarizing stimulation than to hyperpolarizing stimulation; we henceforth refer to this as amplification. Both phenomena were substantially reduced with weaker stimulation (Fig. 3A, bottom left) and were absent when testing single-spike neurons (Fig. 3A, right). These features suggest involvement of voltage-dependent currents expressed selectively in tonic neurons.

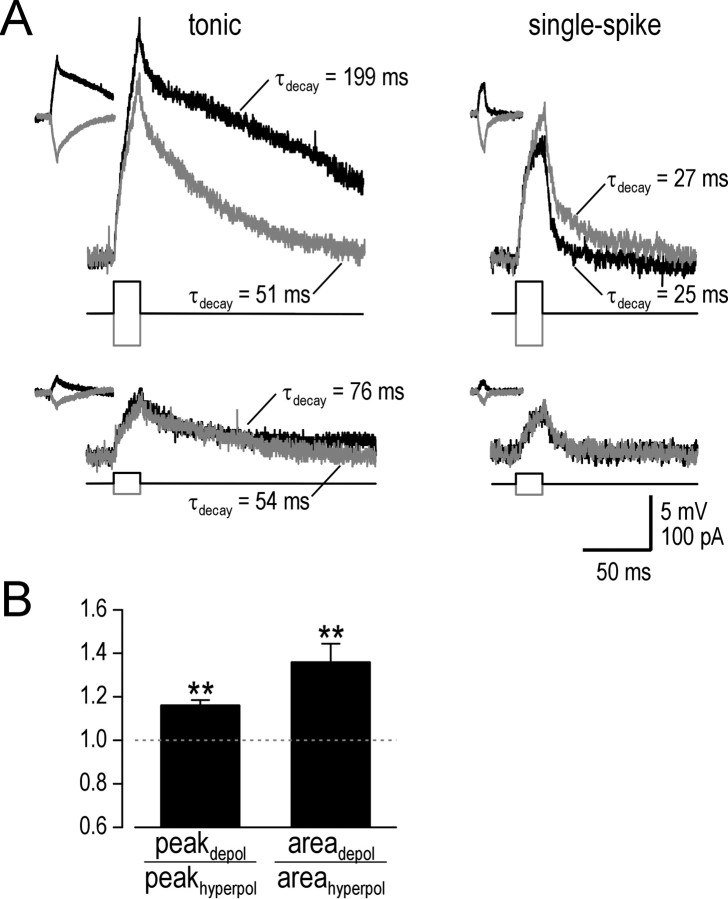
Figure 3.

Tonic cells respond to brief current pulses with prolonged depolarization. A, Traces show sample responses to 20 ms stimulation from prestimulus V_m adjusted to -75 mV. Responses to hyperpolarizing stimulation (gray) are reflected vertically to facilitate comparison with responses to depolarizing stimulation (black). Insets show original traces (i.e., before being reflected). Repolarization was fit with a single exponential decay. In the tonic cell, 60 pA depolarizing stimulation (top trace) led to slow repolarization (τ_decay = 199 ms), whereas equivalent hyperpolarizing stimulation was associated with faster repolarization (τ_decay = 51 ms), more consistent with τ_membrane = 49 ms. Repolarization after 20 pA depolarizing stimulation was faster than for 60 pA stimulation but still slower than for 20 pA hyperpolarizing stimulation (bottom trace). Unlike the tonic neuron, the single-spike neuron repolarized quickly regardless of stimulus intensity or direction (τ_decay = 25 and 27 ms for 60 pA depolarizing and hyperpolarizing stimulation, respectively), consistent with τ_membrane = 23 ms. Additionally, peak depolarization in the tonic cell was amplified in comparison with hyperpolarization (20.7 vs 17.1 mV for 60 pA stimulation), whereas the single-spike cell displayed the opposite rectification (10.6 vs 14.8 mV for 60 pA stimulation). B, Comparison of response to near-threshold depolarizing versus hyperpolarizing stimulation expressed as ratios of peak voltage change (peak_depol/peak_hyperpol) and area under the cuver (area_depol/area_hyperpol). Testing was performed from prestimulus V_m of -75 and -60 mV, but differences were insignificant, and data were therefore pooled with in each cell. The area under the curve was corrected for amplification (see Materials and Methods). The ratio of peak voltage change and area under the curve were both significantly >1 (n = 10; ^**p < 0.01; Wilcoxon signed-rank tests), thereby demonstrating amplification and prolongation, respectively.

We quantified amplification and prolongation by measuring peak voltage change and area under the curve, respectively, in response to near-threshold stimulation and to equivalent hyperpolarizing stimulation. Data are reported as ratios of depolarizing to hyperpolarizing responses. Based on 10 tonic cells tested, peak depolarization was 16 ± 2% larger than peak hyperpolarization (n = 10; p < 0.01; Wilcoxon signed-rank test) (Fig. 3B). After normalizing peak depolarization (see Materials and Methods), area under the curve for depolarization was 36 ± 9% larger than for hyperpolarization (p < 0.01; Wilcoxon signed-rank test), indicating significant prolongation (Fig. 3B). Amplification and prolongation were not limited to near-threshold stimulation but became less pronounced with weaker stimuli (data not shown). However, from a prestimulus V_m of -60 mV (which is close to the average resting V_m in tonic neurons), near-threshold stimulation was only 20 pA and caused depolarization similar in amplitude to a large spontaneous EPSP. Thus, amplification and prolongation occur under conditions that are physiologically relevant for tonic neurons.

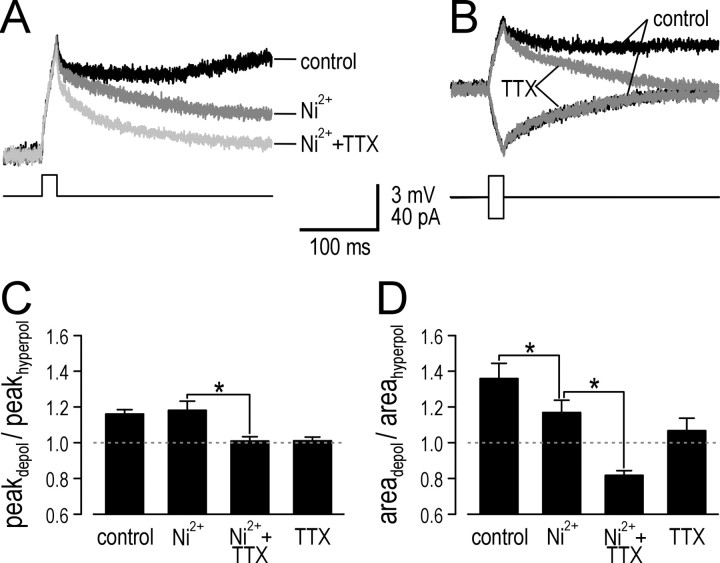
One interpretation of these data is that a voltage-dependent inward current present in tonic neurons amplifies and prolongs depolarization. This inward current could be through Na⁺ and/or Ca²⁺ channels. We blocked Na⁺ and Ca²⁺ currents using TTX and high-dose Ni²⁺, respectively, and thereby quantified the contribution of each current. Figure 4A shows the average response in a typical neuron tested under three conditions: control, after application of Ni²⁺, and after addition of TTX. After brief stimuli, there was a slow-depolarizing ramp under control conditions that was blocked by Ni²⁺, and subsequent application of TTX sped up repolarization even more. TTX applied on its own had a similar capacity to block slow depolarizing ramps and accelerate repolarization (Fig. 4B). Cumulative data showed that Ni²⁺ had no effect on peak voltage change, whereas TTX completely blocked amplification (n = 4; p < 0.05; Mann-Whitney U test) (Fig. 4C). With regard to prolongation (after normalizing peak depolarization), area under the curve, which was 36 ± 9% larger for depolarization compared with hyperpolarization under control conditions, was significantly reduced to 17 ± 7% by Ni²⁺ (n = 4; p < 0.05; Mann-Whitney U test) (Fig. 4D). The ratio was reduced further by TTX (n = 4; p < 0.05; Mann-Whitney U test), so that area under the curve for depolarization was in fact 18 ± 3% less than that for hyperpolarization.

Figure 4.

TTX reduces both amplification and prolongation, whereas Ni²⁺ selectively reduces prolongation. A, Average response in a typical tonic neuron to near-threshold stimulation under three conditions: control, with Ni²⁺, and with Ni²⁺ plus TTX. B, Average response in a different tonic neuron before and after application of TTX alone. As illustrated here, TTX did not noticeably affect the response to brief hyperpolarizing stimulation, which was similarly true for Ni²⁺ (data not shown). C, Cumulative data confirms that Ni²⁺ had no effect on ratio of peak voltage change (peak_depol/peak_hyperpol), whereas TTX significantly reduced it (n = 4; ^*p < 0.05; Mann-Whitney U test), implicating a Na⁺ current in amplification while ruling out Ca²⁺ currents. D, In contrast, the ratio of area under the curve (area_depol/area_hyperpol) was significantly reduced by Ni²⁺ (n = 4; ^*p < 0.05; Mann-Whitney U test), although subsequent application of TTX reduced it even further (n = 4; ^*p < 0.05; Mann-Whitney U test), indicating both Na⁺ and Ca²⁺ currents contribute to prolongation.

To summarize, these data indicated that a Na⁺ current was necessary for amplification, whereas prolongation required both Na⁺ and Ca²⁺ currents. Our approach for demonstrating sufficiency of those currents to produce amplification and prolongation was to characterize basic properties of the currents involved and to introduce those currents into a model neuron in an attempt to recreate the experimental data. Our next step was therefore to characterize the voltage-dependent currents implicated in amplification and prolongation.

Currents involved in amplification and prolongation

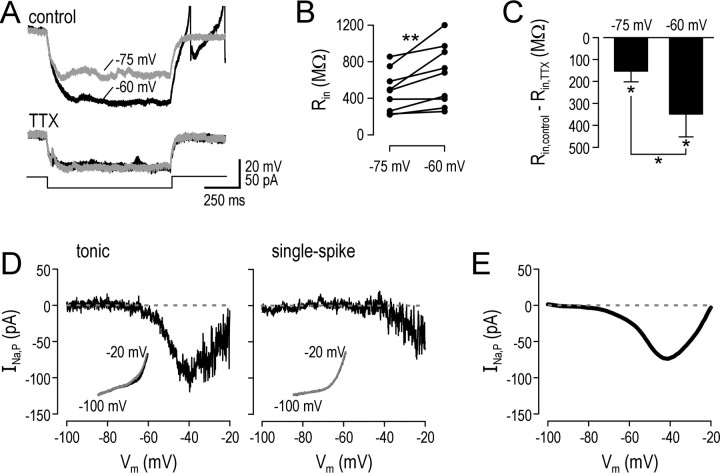
Effects of TTX indicated that tonic neurons express an Na⁺ current that amplifies and prolongs subthreshold depolarization. Other evidence was consistent with a TTX-sensitive inward current active at subthreshold potentials in tonic neurons. For instance, for a given stimulus intensity, hyperpolarization from a prestimulus V_m of -60 mV was consistently larger than hyperpolarization from a prestimulus V_m of -75 mV before TTX, but that was not the case after TTX. A typical example is illustrated in Figure 5A. This suggested that a persistent Na⁺ current, I_Na,P, was active at -60 mV and was deactivated by hyperpolarization, causing an exaggeration in the degree of hyperpolarization. At -75 mV, I_Na,P was already partially deactivated, and hyperpolarization therefore caused less deactivation, and the membrane behaved in a more linear manner. On average, R_in calculated from prestimulus V_m of -75 mV was 24 ± 5% less than R_in calculated from prestimulus V_m of -60 mV (n = 9; p < 0.01; Wilcoxon signed-rank test) (Fig. 5B). Application of TTX caused a reduction in R_in, more so at -60 mV than at -75 mV (n = 5; p < 0.05; Wilcoxon signed-rank test), which is consistent with the differential activation of I_Na,P at those two potentials, but the change in R_in caused by TTX was nevertheless significant for both prestimulus V_m (n = 5; p < 0.05; Wilcoxon signed-rank tests) (Fig. 5C).

Figure 5.

Tonic neurons express a persistent sodium current (I_Na,P). A, Responses from a typical tonic neuron illustrate that, under control conditions, R_in calculated from small hyperpolarizing steps from prestimulus V_m of -60 mV was 1190 MΩ, whereas from prestimulus V_m of -75 mV it was 780 MΩ. Voltage sensitivity of R_in was significantly less after TTX. TTX itself reduced R_in to 560 and 585 MΩ for V_m of -60 and -75 mV, respectively. This is consistent with a TTX-sensitive inward current that is persistently active at -60 mV and less so at -75 mV (a simple calculation suggests 23 and 7 pA, respectively) being deactivated by hyperpolarization. B, Cumulative data showing voltage sensitivity of R_in calculated from 20 pA hyperpolarizing steps under control conditions. R_in calculated from prestimulus V_m of -75 mV was 24 ± 5% less than R_in calculated from prestimulus V_m of -60 mV (n = 9; ^**p < 0.01; Wilcoxon signed-rank test). C, Effect of TTX on R_in expressed as difference in R_in before and after TTX for different prestimulus V_m. The effect at -60 mV was significantly greater than at -75 (n = 5; ^*p < 0.05; Wilcoxon signed-rank test), although both changes were significant relative to 0 (^*p < 0.05; Wilcoxon signed-rank tests). D, I-V curves were measured in voltage clamp by ramping command voltage at 10 mV/s between -110 and -10 mV. Insets show response before and after TTX (black and gray, respectively), and main graphs show the difference. The representative tonic cell clearly exhibited a TTX-sensitive inward current that peaked at approximately -40 mV but was still active at subthreshold potentials, consistent with amplitudes calculated in A. A representative single-spike cell showed no such inward current. E, I-V curve averaged across three tonic neurons tested and smoothed with a running average.

To better characterize I_Na,P, we ramped command voltage in voltage-clamp experiments slowly enough to allow inactivation of the fast Na⁺ current and subtracted the current after TTX from the current before TTX. Figure 5D shows the resultant I-V curves from a representative tonic and single-spike neuron. Whereas the single-spike neuron showed no persistent TTX-sensitive inward current active in the subthreshold voltage range, the tonic neuron clearly displayed such a current. Based on the average I-V curve from three tonic neurons tested with this voltage-clamp protocol (Fig. 5E), I_Na,P reached a peak of 75.2 ± 18.6 pA between -41 and -46 mV, dropped to 22.7 ± 12.1 pA at -60 mV, and dropped further to 5.1 ± 5.3 pA at -75 mV. This is consistent with current-clamp data; for example, data in Figure 5A correspond to a TTX-sensitive inward current of 23 and 7 pA at prestimulus V_m of -60 and -75 mV, respectively.

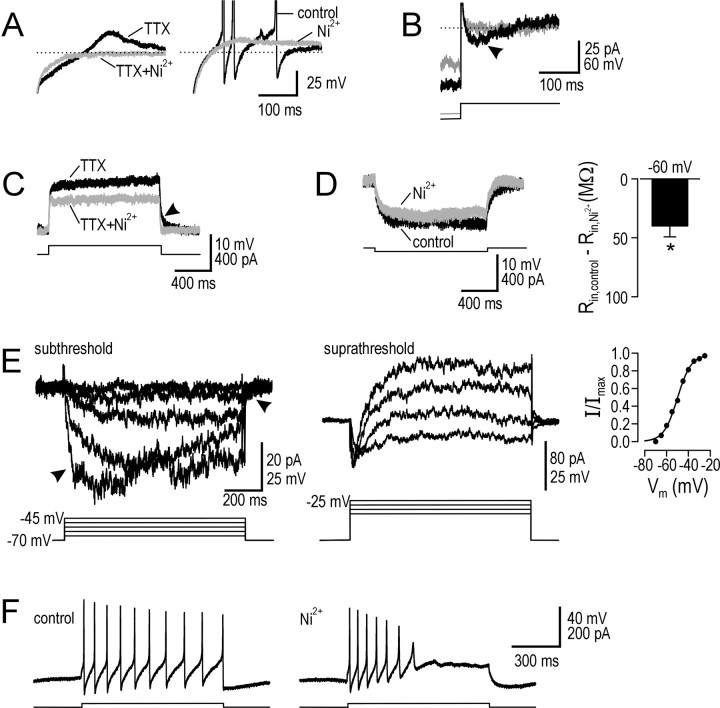
One of the defining features of tonic neurons is rebound depolarization and spiking after sufficiently strong hyperpolarization (Prescott and De Koninck, 2002), suggestive of a T-type Ca²⁺ current. In four neurons tested, all showed TTX-insensitive rebound depolarization that was blocked by subsequent application of high-dose Ni²⁺ (Fig. 6A, left). In four other neurons, application of Ni²⁺ before TTX consistently reduced rebound depolarization (Fig. 6A, right). However, significant rebound depolarization was seen only with hyperpolarization to less than -90 mV, consistent with voltage-clamp recordings in TTX (Fig. 6B). This requirement for strong prehyperpolarization to allow deinactivation makes I_Ca,T ill suited for contributing to prolongation of small depolarizations from resting V_m and, in addition, is inconsistent with prolongation being independent of prestimulus V_m (Fig. 3B). Moreover, step depolarization consistently produced regular firing (i.e., no initial burst) (Figs. 1, 6F), and step depolarization in TTX did not produce an initial hump (Fig. 6C). All of these features argue against any contribution from I_Ca,T to responses not preceded by strong hyperpolarization.

Figure 6.

Tonic neurons express multiple calcium currents. A, Sample responses from typical tonic neurons illustrate rebound depolarization after offset of hyperpolarizing step. TTX-insensitive rebound depolarization was blocked by application of Ni²⁺ (left). If Ni²⁺ was applied before TTX, rebound depolarization remained but was reduced in amplitude so that, in this example, rebound spikes did not occur (right). B, In voltage clamp with TTX present, stepping command voltage from -100 to -70 mV (black) activated a transient inward current (arrowhead), whereas stepping from -90 mV (gray) did not, consistent with lack of deinactivation at that potential. Properties of this transient calcium current (I_Ca,T) were consistent with rebound depolarization observed in current clamp. C, Sample response in TTX to step depolarization in a typical tonic neuron. There was no initial hump suggesting activation of I_Ca,T, consistent with inactivation of I_Ca,T at depolarized potentials. However, Ni²⁺ reduced depolarization and sped up repolarization (arrowhead), effects more consistent with a persistent calcium current. D, As with TTX, Ni²⁺ reduced R_in, suggesting a Ca²⁺ current was persistently active at -60 mV. Ni²⁺ reduced R_in by 39.8 ± 9.3 MΩ (n = 5; ^*p < 0.05; Wilcoxon signed-rank test). E, Responses in voltage clamp to steps in holding command from -70 mV in 5 mV increments under control conditions minus responses in 0 Ca²⁺ ACSF. Responses in the subthreshold regime (steps up to -45 mV) (left) showed an inward current with slow activation/deactivation kinetics (arrowheads) and little evidence of inactivation, consistent with current-clamp data. Responses in the suprathreshold regime (middle) showed eventual activation of an outward current (presumably a Ca²⁺-activated K⁺ current). Subtracting responses before and after 1 mN Ni²⁺ gave similar results. Cumulative data (n = 3) showed I_Ca,P to be half-maximally activated at approximately -50 mV (right). F, Typical responses to 20 pA step depolarization demonstrate that Ni²⁺ converted the tonic firing pattern into a phasic-like pattern.

However, sustained depolarization was reduced when high-dose Ni²⁺ was applied (Fig. 6C), suggesting contribution of a persistent, voltage-activated Ca²⁺ current, I_Ca,P. Like the effects of TTX illustrated in Figure 5C, Figure 6D shows that Ni²⁺ reduced R_in, presumably through inactivation of a persistently active Ca²⁺ current (n = 5; p < 0.05; Wilcoxon signed-rank test). Based on responses to command potential steps in voltage clamp, subtracting responses in 0 Ca²⁺ ACSF from responses in normal ACSF revealed I_Ca,P to have slow activation/deactivation kinetics active at subthreshold potentials (Fig. 6E). Stepping to suprathreshold potentials activated an outward current that presumably represents a Ca²⁺-activated K⁺ current and may correspond to I_K,S (see Materials and Methods); inactivation of I_Ca,P at suprathreshold potentials may also contribute to this response pattern. Similar responses in both the subthreshold and suprathreshold voltage regimes were seen when subtracting responses in 1 mm Ni²⁺ from responses before Ni²⁺, and data were therefore pooled (n = 3). I_Ca,P was half-maximally activated at approximately -50 mV where it was 23.3 ± 5.0 pA. Amplitude decreased to 8.5 ± 2.8 pA at -60 mV, consistent with current-clamp data in Figure 6D, which suggest a Ni²⁺-sensitive inward current of 7 pA at prestimulus V_m of -60. Thus, activation at subthreshold potentials together with its slow kinetics makes I_Ca,P ideally suited for contributing to prolongation.

One final observation is that, in all neurons tested (n = 4), Ni²⁺ converted the tonic firing pattern into a phasic-like pattern (Fig. 6F). Two explanations are possible: I_Ca,P may accelerate depolarization near spike threshold and thereby reduce Na⁺ channel inactivation, or hyperpolarization by a Ca²⁺-activated K⁺ current could encourage Na⁺ channel deinactivation. Removal of one or both mechanisms could contribute to the switch in spiking pattern caused by Ni²⁺ and would be consistent with the attenuation of spike amplitude illustrated in Figure 6F.

I_Na,P and I_Ca,P act synergistically to produce prolongation

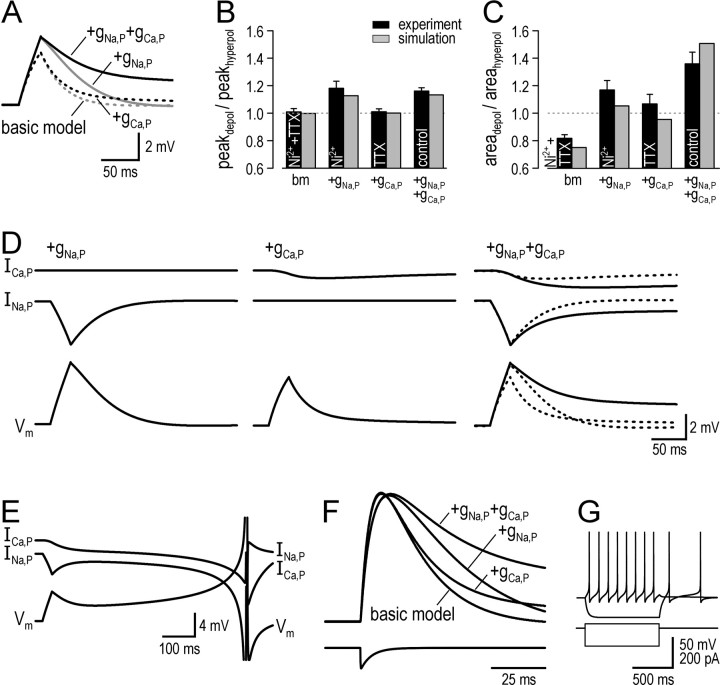
To investigate the roles of I_Na,P and I_Ca,P in producing amplification and prolongation, we built a compartmental model of a tonic neuron using the data described above to optimize parameters (see Materials and Methods). Using the same approach used for testing real neurons, we stimulated variants of the model neuron with 20 ms current pulses. Compared with the basic model, which contained only g_leak, g_Na,F, g_K,DR, g_K,S, and g_Ca,T, the model neuron with g_Na,P and g_Ca,P exhibited both amplification and prolongation (Fig. 7A). In fact, amplification could be fully accounted for by addition of g_Na,P alone and, contrariwise, addition of g_Ca,P alone caused no amplification. Thus, g_Na,P is necessary and sufficient to explain amplification, which was confirmed by comparing ratios of peak voltage change for simulation and experimental data (Fig. 7B). In terms of prolongation, adding g_Na,P or g_Ca,P individually to the basic model caused only moderate slowing of repolarization, whereas adding both together had a much more pronounced effect (Fig. 7A). Figure 7C compares ratios of area under the curve for simulation and experimental data. As with amplification, the model cell with different conductances reproduced the matching experimental data on prolongation quite well; in no case was simulation data significantly different from experimental data (Wilcoxon signed-rank tests).

Figure 7.

Amplification is explained by I_Na,P acting alone, whereas prolongation is explained through synergistic actions of I_Na,P and I_Ca,P. A, Responses of model neuron with inclusion of different conductances to 20 ms, 20 pA current pulses from resting V_m of -63 mV. Basic model (bm; dotted gray line) included only g_leak, g_Na,F, g_K,DR, g_K,S, and g_Ca,T. Adding g_Na,P alone (solid gray line) increased peak depolarization to the same amplitude seen in model neuron with both g_Na,P and g_Ca,P (solid black line) but produced only modest slowing of repolarization. Adding g_Ca,P alone (dotted black line) did not increase peak depolarization and produced only minor slowing of repolarization, suggesting g_Na,P and g_Ca,P act synergistically to produce the full degree of prolongation seen in the model with both g_Na,P and g_Ca,P. B, Ratio of peak depolarization to peak hyperpolarization (peak_depol/peak_hyperpol) in simulations (gray bars) for comparison with experimental data (black bars). Experimental data comes from Figure 4, and experimental conditions (i.e., TTX and/or Ni²⁺) are indicated in each bar. C, Ratio of area under the curve for depolarizing versus hyperpolarizing stimulation (area_depol/area_hyperpol). For both B and C, simulation data were not significantly different from experimental data for any condition (Wilcoxon signed-rank tests). D, Same voltage responses (bottom traces) as in A, along with I_Na,P (middle traces) and I_Ca,P (top traces). Kinetics of I_Na,P are fast (left); rapid activation of I_Na,P allows it to amplify peak depolarization but its equally rapid deactivation prevents it from producing more substantial prolongation. Kinetics of I_Ca,P are slow (middle); slow activation of I_Ca,P explains why it does not contribute to amplification and why initial activation relies on prolongation produced by I_Na,P (see Results). With I_Na,P and I_Ca,P together in the same model neuron (right), I_Na,P amplifies depolarization and causes some slowing of repolarization; the latter effect allows more robust activation of I_Ca,P, which, especially because of its slow kinetics, slows repolarization even further. Deactivation of I_Na,P is also slower with I_Ca,P present. Thus, fast activation of I_Na,P facilitates activation of I_Ca,P, and slow deactivation of I_Ca,P helps maintain activation of I_Na,P such that both currents prolong depolarization synergistically (i.e., more than the algebraic sum of their individual effects). E, Slow depolarizing ramps and spike generation at long latency after stimulation, as often seen in experimental data (see Figs. 4 A, 8), was observed when density of g_Ca,P was adjusted from 0.02 to 0.025 mS/cm². F, Responses of model neuron to synaptic conductance in distal dendrite. τ_EPSP was 86 ms in the model neuron with g_Na,P and g_Ca,P, which matches the experimental value for tonic cells (see Fig. 2 D). τ_EPSP decreased to 36 ms in the model with only g_Na,P and was reduced further to between 21 and 27 ms in other variations of the model; this range matches the experimental values for other cell types. G, Responses of the model with both g_Na,P and g_Ca,P to 20 pA depolarizing and 80 pA hyperpolarizing current steps for comparison with experimental data.

We also tested whether I_Ca,T could contribute to either amplification or prolongation. As predicted, it contributed to neither (data not shown) because of inactivation at depolarized potentials. If the activation and inactivation curves were shifted to be less negative (see Materials and Methods), I_Ca,T could prolong depolarization but its inactivation resulted in repolarization kinetics that did not resemble experimentally observed kinetics.

The above data therefore suggested that I_Na,P and I_Ca,P act synergistically to produce prolongation and are both necessary to fully replicate the experimental data. Figure 7D explains the mechanism through which this occurs. I_Na,P activates quickly and thereby amplifies peak depolarization, and although it also slows repolarization, its rapid deactivation prevents it from causing more substantial prolongation (Fig. 7D, left). Unlike I_Na,P, I_Ca,P activates slowly (Fig. 7D, middle), which explains why it does not contribute to amplification, but nor can it contribute to prolongation if it does not achieve substantial activation during a short stimulus. Activation of I_Ca,P is increased when I_Na,P is present in the model (Fig. 7D, right). In the model with I_Ca,P alone (Fig. 7D, middle), we find that if stimulus intensity is increased so that peak depolarization is equal to that achieved with I_Na,P present, activation of I_Ca,P is only slightly increased, whereas if it is stimulus duration that is increased to produce the same peak depolarization, greater activation of I_Ca,P is achieved (data not shown). In other words, duration of depolarization has greater impact on I_Ca,P activation than amplitude of depolarization, and, by extension, activation of I_Ca,P relies on initial prolongation produced by I_Na,P but is relatively insensitive to amplification produced by I_Na,P. Once activated, I_Ca,P is well suited for slowing repolarization because of its own slow kinetics. However, I_Ca,P also acts by delaying deactivation of I_Na,P (Fig. 7D, right), meaning I_Ca,P can slow repolarization more when combined with I_Na,P. Indeed, if stimulus parameters are adjusted to activate I_Ca,P equally in the model without I_Na,P as in the model with I_Na,P, prolongation is still less in the model without I_Na,P (data not shown). Thus, I_Na,P and I_Ca,P both act to prolong depolarization, and their effects are interdependent: initial activation of the slower current depends on the faster current, whereas maintained activation of the faster current depends on the slower current.

Extensive testing confirmed that the model neuron could reproduce the responses of real tonic neurons to short current pulses. In several cells (Figs. 4A, 8), a slow depolarizing ramp was observed that could lead to spike generation at significant delay after the initial stimulus. This could be recreated in a model neuron with g_Ca,P density of 0.025 mS/cm² (Fig. 7E). Given our initial goal of explaining the prolonged EPSPs observed in tonic cells, we also tested our model neuron with synaptic input. The EPSP in the model neuron with both I_Na,P and I_Ca,P was significantly prolonged (Fig. 7F), τ_EPSP = 86 ms, which compares well with the experimentally measured value of τ_EPSP for tonic neurons, 93 ± 22 ms (Fig. 2D). Removing I_Na,P and/or I_Ca,P from the model neuron gave values of τ_EPSP ranging from 21 to 36 ms, which compares well with the experimentally measured values of τ_EPSP for other cell types. In short, the voltage-dependent currents we characterized can account for the differences in EPSP kinetics between cell types.

Figure 8.

Subthreshold inward currents encourage temporal summation but at the expense of spike time precision. A, Traces show responses to a train of brief current pulses in a typical tonic neuron (top) and in the model neuron (bottom). Before TTX (black), repolarization was slow and allowed for temporal summation and spike generation. After TTX (gray), repolarization was much faster, thereby preventing temporal summation. Spikes in this and subsequent panels are truncated. B, In this sample recording, inward and outward currents were balanced so that the neuron acted as a nearly perfect integrator (i.e., very long integration time). Note the near-horizontal trajectory of V_m after each stimulus pulse, resulting in a stepwise depolarization toward each action potential. C, Sample responses to pairs of stimuli under control conditions (top) show that inward currents can produce slow depolarizing ramps that lead to spike generation at long and variable latencies after stimulation. The inset shows that latency to spike generation in response to spontaneous synaptic excitation was also highly variable, despite approximately the same initial depolarization and same prestimulus V_m. Blocking I_Ca,P with Ni²⁺ (bottom) prevented slow depolarizing ramps, and spike timing was more precisely associated with stimulation. D, Response of a typical single-spike neuron to trains of current pulses of three intensities. When spikes did occur, they were at consistently short latency after the stimulus onset. Decreasing stimulus intensity revealed the cell to be incapable of temporal summation.

Figure 7G demonstrates that, after addition of multiple currents, the model neuron displayed all of the hallmark properties of real tonic neurons, including relatively slow repetitive firing in response to step depolarization and rebound depolarization and spiking after hyperpolarization.

Significance for signal processing

Having explained the biophysical mechanisms underlying amplification and prolongation, we sought to explore the implications of those phenomena, particularly prolongation, for signal processing. Figure 8A (top) shows that with subthreshold inward currents intact, slow repolarization after each pulse allowed for temporal summation. In contrast, when I_Na,P was blocked, faster repolarization and lack of temporal summation meant that V_m did not approach voltage threshold. Reproducing these particular experimental data in simulations (Fig. 8A, bottom) was optimized using g_K,S density of 0.5 mS/cm² and g_Ca,P density of 0.025 mS/cm². In some cells, inward currents counterbalanced the outward currents so well that the neuron acted as a nearly perfect integrator, as evidenced by the near-horizontal trajectory of V_m after each current pulse (Fig. 8B). Significantly, this tells us that tonic cells sum inputs over a prolonged time interval or, in other words, use a long integration time.

Long integration time is usually synonymous with poor spike time precision (Fricker and Miles, 2000; Pouille and Scanziani, 2001; Axmacher and Miles, 2004). This was also true in our data. Figure 8C shows responses to multiple trials of pairs of current pulses. If the inward currents that produced prolongation were slightly stronger than the outward currents, a slow voltage ramp could develop that resulted in spikes at long and, importantly, highly variable latencies after the stimulus (Fig. 8C, top). Similar slow voltage ramps and variable spike latencies were seen in response to spontaneous synaptic events (Fig. 8C, inset). Spike timing was more consistent after the slow depolarizing ramp was blocked by application of Ni²⁺ (Fig. 8C, bottom). The temporal summation and poor spike time precision in tonic neurons were in stark contrast to the lack of summation and precisely timed spikes observed in single-spike neurons (Fig. 8D).

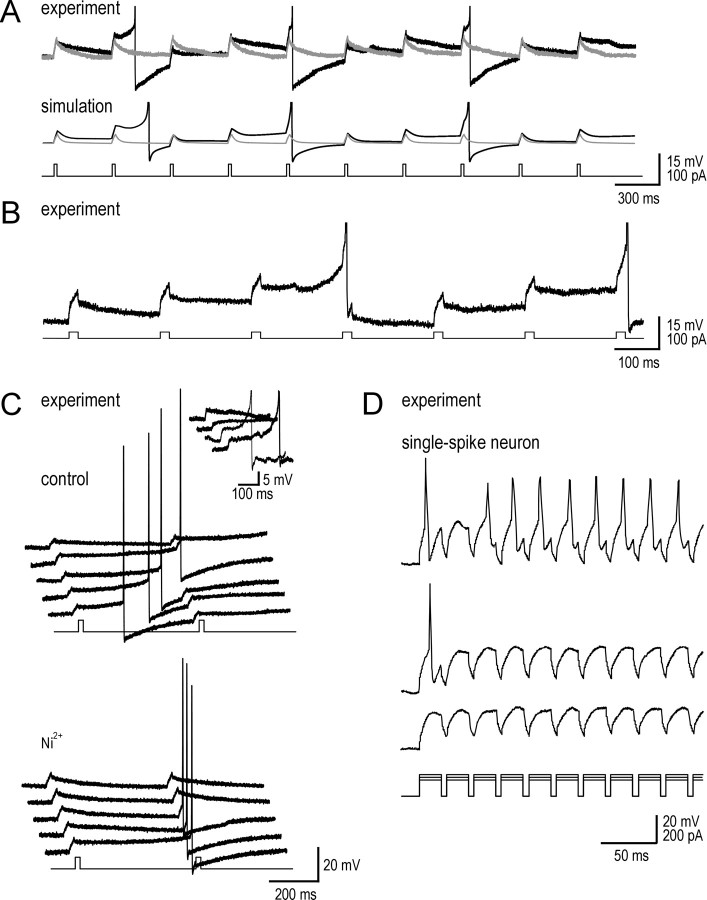
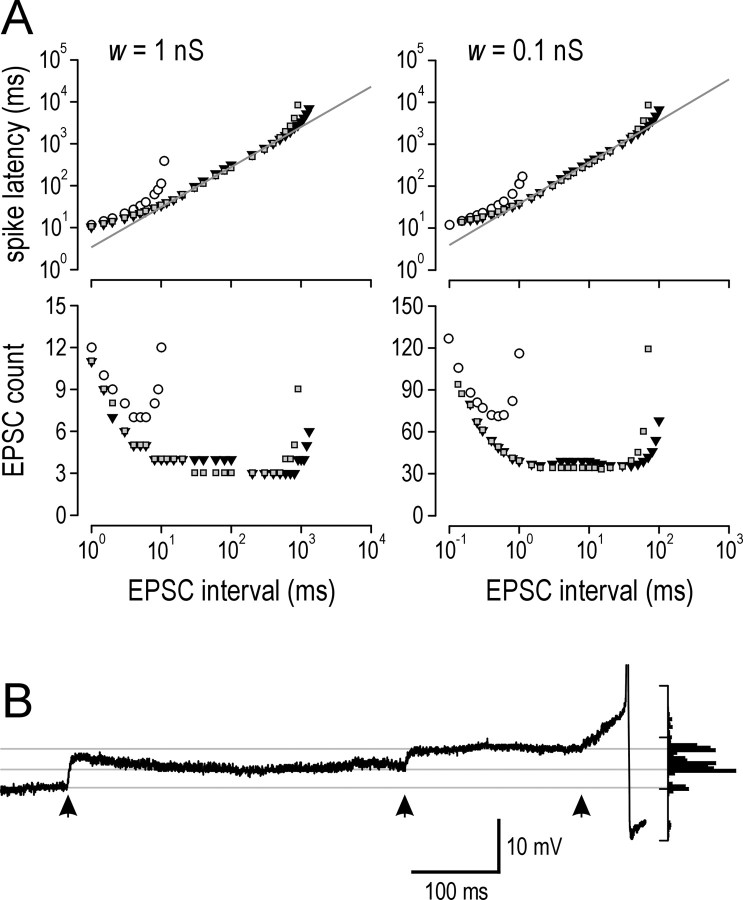
As outlined before, integration time represents the time interval over which a neuron can sum inputs and is the principal distinction between integration and coincidence detection. Train data in Figure 8 suggested that integration time is dramatically increased by the actions of subthreshold inward currents. We investigated this further using synaptic stimulation of the model neuron (Fig. 9A). Two strengths of synaptic input were tested; the stronger input (w = 1 nS) (Fig. 9A, left) is more representative of physiological input and is described below, whereas the weaker input (w = 0.1 nS) (Fig. 9A, right) simply confirms that results are independent of synaptic strength. Focusing on the stronger input (Fig. 9A, left), the bottom graph shows that model neurons with I_Na,P and I_Ca,P spiked after summation of as few as three to four EPSCs arriving over a broad range of intervals. In contrast, the model neuron without I_Na,P and I_Ca,P was less sensitive (i.e., required at least seven EPSCs) and required that those EPSCs arrived at comparatively short intervals. We measured latency to spike generation from the onset of synaptic input (Fig. 9A, top graph), because this represents the interval of time over which summation occurs. We defined integration time as the range of latencies in which the neuron operates at more than or equal to half-maximal sensitivity; for example, maximal sensitivity of the model neuron with inward currents was three EPSCs, so for that model, we measured latencies for responses to six EPSCs. Integration time was between 12 and 114 ms for the model neuron without inward currents, but the range increased dramatically to between 17 and 3665 ms in the model neuron with inward currents and increased even further to 6884 ms if g_Ca,P was increased from 0.02 to 0.025 mS/cm². Thus, prolongation caused by I_Na,P and I_Ca,P increased maximal integration time by >30×. Testing with weaker synaptic input gave virtually identical values after rescaling to account for the change in synaptic strength.

Figure 9.

Synaptic integration time is increased by subthreshold inward currents. A, Model neuron was stimulated with regularly timed EPSCs in a distal dendrite. Bottom graphs show the number of EPSCs necessary to elicit a spike. Top graphs show latency from stimulus onset to spike generation. Two variations of models with both I_Na,P and I_Ca,P were tested: model 1 (gray squares) had the same parameters as the complete model in Figure 7A; for model 2 (inverted black triangles), g_Ca,P was increased to 0.025 mS/cm², and g_K,S was increased to 0.5 mS/cm², like the model in Figure 8 A. Open circles represent basic model without g_K,S. For strong synaptic input (left), both models with I_Na,P and I_Ca,P spiked in response to three to four EPSCs arriving over a broad range of intervals, whereas the basic model was less sensitive and required at least seven EPSCs arriving at short intervals. For a 10-fold decrease in synaptic weight (right), 10× more EPSCs arriving at 10× shorter intervals were required to elicit a spike but, otherwise, the same trends as with stronger synaptic input were observed. Integration time was defined by latency to spike generation during operation at greater than or equal to half-maximal sensitivity (i.e., requiring equal or less than twice the number of EPSCs as the minima in bottom graphs). Integration time was between 12 and 114 ms for the basic model and increased to between 17 and 3665 ms for model 1 and between 17 and 6884 ms for model 2. In other words, the model neuron without intrinsic inward currents responded only to a relatively large number of EPSCs arriving in a short time, whereas the model neurons with intrinsic inward currents responded to a relatively small number of EPSCs arriving over a much broader time window. Gray lines represent linear regression of data used to calculated integration time for model 1. For w = 1 nS, latency = 3.4^*interval^0.956, and for w = 0.1 nS, latency = 38.3^*interval^0.987. B, Example in real lamina I tonic neuron of three spontaneous EPSPs (times indicated by arrows) summating over 650 ms interval. Probability distribution of V_m shown on right highlights stepwise depolarization toward spike generation, reminiscent of data in Figure 8. This demonstrates that the long integration times predicted by simulation data in A accurately describe the behavior of real tonic neurons.

We also observed that, over the range of latencies used to calculate integration time, latency was linearly related to EPSC interval when plotted on a log-log graph, suggesting a power law relationship. For w = 1 nS, latency = 3.4^*interval^0.956 where 3.4 represents the number of EPSCs required to generate a spike and the exponent, which is only slightly <1, implies a relationship that is nearly linear. In other words, firing rate should linearly encode EPSC rates between ∼1 and 100 Hz. Input rates in vivo likely fall within that range (Furue et al., 1999), suggesting that tonic neurons are well suited to encoding stimulus intensity in large part because of their long integration times made possible by the combined actions of I_Na,P and I_Ca,P.

These estimates of integration time seemed to be extremely long, although they were consistent with train data in Figure 8. Nonetheless, we reviewed our recordings to look for examples of synaptic summation over a time course consistent with data in Figure 9A. Several examples were found in multiple tonic cells. A typical one is shown in Figure 9B, in which three EPSPs summate and produce a spike 650 ms after the first EPSP; baseline V_m was stable, and, reminiscent of data in Figure 8, input caused step-like depolarization leading to the spike. No examples of temporal summation suggesting a comparably long integration time could be found in other cell types or in tonic cells after inward currents were blocked.

Discussion

Voltage-dependent inward currents shape subthreshold depolarization in tonic spinal lamina I neurons. Experiments and simulations demonstrated that I_Na,P was both necessary and sufficient to explain amplification. Prolongation, in contrast, required both I_Na,P and I_Ca,P working together in a synergistic manner. By establishing the biophysical mechanism through which EPSPs were shaped, we were able to reproduce that mechanism in a model neuron and explore the consequences for signal processing by tonic neurons. Both experiments and simulations demonstrated that prolonging depolarization facilitates temporal summation, increases integration time, and decreases spike time precision with the overall consequence of causing tonic neurons to act as integrators, as opposed to coincidence detectors.

Both sodium and calcium currents are known to influence EPSPs (Deisz et al., 1991; Stuart and Sakmann, 1995; Crill, 1996, 1999; Lipowsky et al., 1996; Gillessen and Alzheimer, 1997; Urban et al., 1998; Gonzalez-Burgos and Barrionuevo, 2001; Crill et al., 2002). The majority of previous studies focused on amplification of synaptic depolarization, which in turn relates to whether synaptic input to distal dendrites will manage to cause somatic depolarization (for review, see Magee, 2000). Some studies have reported an increase in the EPSP time integral with depolarization in hippocampal and neocortical pyramidal neurons (Deisz et al., 1991; Stuart and Sakmann, 1995; Fricker and Miles, 2000; Gonzalez-Burgos and Barrionuevo, 2001), which reflects amplification as well as slower repolarization. Gonzalez-Burgos and Barrionuevo (2001) investigated the biophysical basis for this in layer 5 pyramidal neurons and concluded that I_Na,P alone was responsible for shaping EPSPs, whereas calcium currents contributed only under nonphysiological conditions (i.e., when potassium channels were blocked).

In the present study, we isolated amplification and prolongation and determined the biophysical mechanism for each. The ability to completely block amplification by application of TTX and to fully recreate it by introducing I_Na,P into the model neuron demonstrates that I_Na,P is both necessary and sufficient to explain amplification. The mechanism for this is straightforward and simply involves fast activation of an inward current that contributes to depolarization. Prolongation, in contrast, involves a more complex mechanism. Application of TTX or Ni²⁺ reduced prolongation, but adding I_Na,P or I_Ca,P individually to the model neuron caused only modest prolongation, and the simple algebraic sum of their individual effects was insufficient to explain the degree of prolongation observed experimentally. Investigation of our biophysically accurate model neuron revealed the synergistic mechanism through which the two currents act to prolong depolarization: activation of the slower current (I_Ca,P) depends on the faster current (I_Na,P) to produce some degree of initial prolongation, but maintained activation of the faster current likewise depends on the slower current. Only working together can the two currents prolong depolarization to the degree observed experimentally. The model neuron was able to recreate slow repolarization extremely well and could also reproduce slow depolarizing ramps and late spikes seen in several tonic neurons. Furthermore, testing the model neuron with synaptic input indicates that prolongation produced by the combined actions of I_Na,P and I_Ca,P is sufficient to explain the prolonged EPSPs characteristic of tonic cells.

What are the consequences of amplification and prolongation for signal processing by individual tonic neurons? For one, temporal summation of synaptic input is clearly increased when EPSPs are slow. Because each synaptic input has a prolonged influence on V_m, spike generation results from inputs arriving over a comparatively long interval (i.e., the integration time is long). This is a defining feature of integrators (König et al., 1996). However, temporal resolution is inversely related to integration time (Pouille and Scanziani, 2001), meaning slow EPSPs result in poor spike time precision (Fricker and Miles, 2000). In the case of tonic lamina I neurons, we see that individual excitatory events (synaptic or short current pulses) result in long depolarizations that are typically associated with poor spike time precision and that allow for temporal summation. As illustrated in Figures 8 and 9, active inward currents can balance outward currents (predominantly I_leak) to the point that integration is nearly perfect, the implication being that integration time is extremely long. Consistent with this, simulations investigating summation of synaptic input showed that integration times could be in the order of seconds, whereas in the absence of intrinsic inward currents, maximum integration time was more than an order of magnitude less. Summation of spontaneous EPSPs in experimental data was consistent with the estimates of long integration times. Simulations also revealed that, because of their inward currents, tonic neurons are more sensitive to synaptic input and can sum inputs in a near-linear manner so that firing rate should accurately encode rate of synaptic input over a broad range of frequencies.

We therefore believe that tonic neurons act as good integrators and are well suited to encoding stimulus intensity because of their intrinsic membrane currents. Interestingly, we found that I_Ca,P not only contributed to prolongation but also allowed for repetitive spiking (Fig. 6F). The mechanism by which I_Ca,P encourages repetitive spiking may be either direct or indirect. I_Ca,P may accelerate depolarization near threshold and thereby decrease cumulative Na⁺ channel inactivation, and/or hyperpolarization by a Ca²⁺-sensitive K⁺ current may help deinactivate Na⁺ channels and similarly decrease cumulative Na⁺ channel inactivation. These mechanisms are not mutually exclusive and may well act in concert. Thus, the coexistence of features causing the neuron to act as a good integrator (i.e., repetitive firing and prolonged EPSPs) reflects a common mechanism (i.e., subthreshold intrinsic inward currents) rather than simply occurring by chance.

To summarize, we set out to determine the basis for prolonged EPSPs in tonic neurons in spinal lamina I and the implications for signal processing by those neurons. We found that EPSPs were shaped by the synergistic actions of two distinct subthreshold inward currents, I_Na,P and I_Ca,P. The mechanism we describe is novel and relies on the kinetic differences of the two currents involved. Additional experiments and simulations illustrated how those currents encourage temporal summation, increase integration time, and decrease spike time precision. By prolonging subthreshold depolarizations, intrinsic inward currents allow tonic neurons in spinal lamina I to specialize as integrators that are optimally suited to encoding stimulus intensity. The results thus demonstrate the importance of intrinsic currents in shaping synaptic responses and in determining the signal processing characteristics of individual neurons.