Functional Characterization and Neuronal Modeling of the Effects of Childhood Absence Epilepsy Variants of CACNA1H, a T-Type Calcium Channel

Abstract

Sequencing of the T-type Ca²⁺ channel gene CACNA1H revealed 12 nonsynonymous single nucleotide polymorphisms (SNPs) that were found only in childhood absence epilepsy (CAE) patients. One SNP, G773D, was found in two patients. The present study reports the finding of a third patient with this SNP, as well as analysis of their parents. Because of the role of T-channels in determining the intrinsic firing patterns of neurons involved in absence seizures, it was suggested that these SNPs might alter channel function. The goal of the present study was to test this hypothesis by introducing these polymorphisms into a human Ca_v3.2a cDNA and then study alterations in channel behavior using whole-cell patch-clamp recording. Eleven SNPs altered some aspect of channel gating. Computer simulations predict that seven of the SNPs would increase firing of neurons, with three of them inducing oscillations at similar frequencies, as observed during absence seizures. Three SNPs were predicted to decrease firing. Some CAE-specific SNPs (e.g., G773D) coexist with SNPs also found in controls (R788C); therefore, the effect of these polymorphisms were studied. The R788C SNP altered activity in a manner that would also lead to enhanced burst firing of neurons. The G773D-R788C combination displayed different behavior than either single SNP. Therefore, common polymorphisms can alter the effect of CAE-specific SNPs, highlighting the importance of sequence background. These results suggest that CACNA1H is a susceptibility gene that contributes to the development of polygenic disorders characterized by thalamocortical dysrhythmia, such as CAE.

Introduction

Absence epilepsies are characterized by short lasting (∼10 s) seizures that cause a sudden impairment of consciousness, interruption of ongoing activity, and an upward blank stare (Sander, 1996). During the seizure, there is a generalized synchronization of neuronal firing mediated by thalamic circuits, which produces a rhythmic 3 Hz spike and slow-wave discharge in the electroencephalogram (Gloor and Fariello, 1988; Crunelli and Leresche, 2002). Childhood absence epilepsy (CAE) is one of the more common forms of idiopathic generalized epilepsies, having a population frequency of ∼1 in 1000 (Sander, 1996). Some forms of idiopathic epilepsies follow an autosomal dominant, monogenic (or mendelian) pattern of inheritance, which facilitated the identification of the affected gene (Robinson and Gardiner, 2000). These mutations have been found in Cl^-, K⁺, and Na⁺ channels, adding to the list of channelopathies that affect excitable tissues (Meisler et al., 2001; Gargus, 2003). In contrast, CAE has a complex, polygenic (or non-mendelian) mechanism of inheritance, making the identification of affected genes more difficult (Robinson and Gardiner, 2000).

Physiological and pharmacological evidence suggests that overactive T-type Ca²⁺ channels might be a contributing factor in CAE. The first physiological role discovered for T-type Ca²⁺ channels was their ability to produce low threshold spikes (LTS) that could trigger Na⁺-dependent action potentials (Llinás and Jahnsen, 1982). Their ability to regulate neuronal firing is particularly important in thalamic neurons, in which they are expressed at high levels (for review, see Perez-Reyes, 2003). The ability of thalamic circuits to oscillate has been studied extensively both in vitro and in vivo (for review, see Steriade, 2001). Inappropriate oscillations of this circuit are thought to directly produce generalized seizures (Gloor and Fariello, 1988; Huguenard, 1999; McCormick and Contreras, 2001; Crunelli and Leresche, 2002), as well as other neurological disorders (Llinás et al., 1999). Studies in mouse models of absence epilepsy have found that mutations in high-voltage-activated (HVA) Ca²⁺ channels can lead to a compensatory rise in thalamic T-type currents (Zhang et al., 2002). Similarly, studies in a rat model of absence epilepsy have found increases in thalamic T-currents (Tsakiridou et al., 1995), as well as a corresponding increase in expression of Ca_v3.2 mRNA (Talley et al., 2000). The converse is also true: disruption of the Ca_v3.1 gene in mice leads to loss of thalamocortical T-currents and resistance to drug-induced absence seizures (Kim et al., 2001). Absence seizures in both human patients and animal models can be reduced by ethosuximide (Aizawa et al., 1997; Manning et al., 2004). Although other mechanisms of action have been proposed (Leresche et al., 1998), this drug is capable of blocking both native and recombinant T-channels at therapeutically relevant concentrations (Coulter et al., 1989; Gomora et al., 2001).

Therefore, T-channel genes may be an important susceptibility locus in human absence epilepsy, prompting us to sequence the genes encoding Ca_v3 channels in 118 CAE patients and 230 unrelated controls. Although no polymorphisms were discovered in the gene encoding Ca_v3.1, CACNA1G, many single nucleotide polymorphisms (SNPs) were discovered in the gene encoding Ca_v3.2, CACNA1H (Chen et al., 2003a,b). Twelve different nonsynonymous SNPs were found only in CAE patients, with one SNP, G773D, being found twice. We hypothesized that these SNPs might lead to a gain of channel function that would predispose thalamic circuits to oscillate and thereby play a major role in causing the absence seizure. Partial support for this hypothesis came from a study in which five of the CAE-specific SNPs were introduced into a rat channel (Khosravani et al., 2004). Both the sequence and biophysical properties of this rat Ca_v3.2 channel differ substantially from our human channel, making the interpretation of their results difficult. The goal of the present study was to introduce all 12 of the CAE-specific SNPs into the human Ca_v3.2 channel, study their biophysical properties, and then apply computer modeling to predict their affect on thalamic firing. Consistent with our hypothesis, we find that many of these SNPs alter gating in a manner that would increase the propensity of neurons to fire. We also report the finding of a third patient with G773D and the genetic status of their parents. In all three of the G773D cases, we also found a second SNP that changes the amino acid sequence at position 788 (R788C). Of note, R788C alone is capable of altering channel function and alters the impact of G773D on channel function. Therefore, our studies also suggest that absence epilepsy might be caused by combinations of polymorphisms in a T-channel gene. The frequency of R788C, 20.8% in our Chinese cohort and 13.7% in a Japanese cohort (Hirakawa et al., 2002), is consistent with the polygenic nature of absence epilepsy and extends the impact of our studies.

Materials and Methods

Genetic analysis. The rationale for selection of patients and methods used to sequence their CACNA1H gene were described previously (Chen et al., 2003b). The genes from parents of patients that contained the CAE-specific SNPs were sequenced. The status of each allele was deduced from the zygosity of the patient and their parents (trio).

Site-directed mutagenesis. A human Ca_v3.2a cDNA (GenBank accession number AF051946) contained in pUC-18 was mutated using oligo-nucleotide primers and the QuikChange site-directed mutagenesis kit (Stratagene, La Jolla, CA). The primers were obtained from Operon (Alameda, CA) and used without purification. The full-length cDNA (in pcDNA3; Invitrogen, Carlsbad, CA) was reassembled using a fragment of the mutated clone. The sequence corresponding to these fragments and flanking regions were verified by automated sequencing.

Transfections. Human embryonic kidney-293 (HEK-293) cells (CRL-1573; American Type Culture Collection, Manassas, VA) were grown in DMEM/F-12 (Invitrogen) supplemented with 10% fetal calf serum, penicillin G (100 U/ml), and streptomycin (0.1 mg/ml). Cells were transiently cotransfected with plasmid DNAs encoding each Ca_v3.2 variant and green fluorescent protein (GFP) (pGreen Lantern; Invitrogen), at a molar ratio of 12:1, using JET-PEI (Qbiogene, Montreal, Canada). After ∼24 h, GFP-positive cells were selected for electrophysiological recordings. The results were obtained from 43 transfections. Each construct was tested in at least two transfections, and control data were collected from 29 transfections.

Electrophysiology. Electrophysiological experiments were performed using the whole-cell configuration of the patch-clamp technique. Recordings were obtained using an Axopatch 200B amplifier, Digidata 1322A analog-to-digital converter, and pClamp 9.0 software (Molecular Devices, Union City, CA). Data were filtered at 2 kHz and digitized at 5 kHz, except for tail currents, which were filtered at 10 kHz and digitized at 50 kHz. Whole-cell Ca²⁺ currents were recorded using the following external solution (in mm): 5 CaCl₂, 166 tetraethyl ammonium (TEA) chloride, and 10 HEPES, pH adjusted to 7.4 with TEA-OH. The internal pipette solution contained the following (in mm): 125 CsCl, 10 EGTA, 2 CaCl₂, 1 MgCl₂, 4 Mg-ATP, 0.3 Na₃GTP, and 10 HEPES, pH adjusted to 7.2 with CsOH. Pipettes were made from TW-150-3 capillary tubing (World Precision Instruments, Sarasota, FL). Under these solution conditions, the pipette resistance was typically 2-3 MΩ. Access resistance and cell capacitance were measured using on-line exponential fits to a capacitance transient (Membrane Test, Clampex; Molecular Devices). Cell capacitance averaged 10 pF. Access resistance averaged 4.2 ± 0.1 MΩ. Data from cells in which the access resistance exceeded 5.5 MΩ were discarded. Series resistance was compensated between protocols to 70% (prediction and correction; 10 μs lag), resulting in maximal residual voltage error below 1.6 mV during measurement of the current-voltage (I-V) relationship. The data were corrected post hoc for a junction potential (-9.4 mV; calculated with the Junction Potential Calculator in Clampex) and surface charge screening (-4 mV; measured by comparing current-voltage relationships in 2 and 5 mm Ca²⁺).

Modeling. The NEURON model uses mathematical descriptors of ionic conductances to calculate whether a channel is open as a function of voltage and does this by applying Hodgkin-Huxley-type equations (Destexhe et al., 1996b, 1998). This requires a detailed characterization of the voltage dependence of activation, inactivation, as well as the voltage dependence of their kinetics. The voltage dependence of activation (m_∞; mid-point, V₅₀; slope, k) was determined by fitting the peak I-V data from each cell with the following form of the Goldman-Hodgkin-Katz equation:

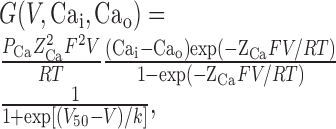where G is conductance, P_Ca is the permeability to calcium ions (in centimeters per second), Z is their valence (2), F is the Faraday constant, R is the gas constant, T is the temperature (kelvin), V is the test potential (volts), and Ca_i and Ca_o are the intracellular and extracellular concentrations of Ca²⁺ (molar), respectively. As observed with native T-channels (Bossu and Feltz, 1986; Herrington and Lingle, 1992), slow inactivation of recombinant Ca_v3.2 channels is a multiexponential process that can require >5 s to reach apparent steady state (Klöckner et al., 1999). Because the second goal of our studies was to use the biophysical properties of the channels to model neuronal firing, steady-state inactivation (h_∞) was approximated using the same 1-s-long prepulse used in the development of these models (Destexhe et al., 1996b). Normalized data using prepulses more depolarized than -100 mV were fit with a Boltzmann equation. The data from each cell were then averaged to calculate mean and SEM. The voltage dependence of the time constants of activation (τ_m) and inactivation (τ_h) were obtained using the following equation:

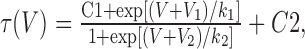where V is the test voltage, C1 and C2 are the voltage-independent rates at hyperpolarized or depolarized potentials, respectively, and V₁, V₂, k₁, and k₂ represent V₅₀ and slopes of the increasing and decreasing components of the curve, respectively. The equation was adapted from the NEURON model of Destexhe et al. (2001) of T-currents of cortical cells, which they modified from the thalamic cell model by adding C1. This improves the fit because the voltage-independent rate of recovery (C1) differs substantially from the voltage-independent rate of inactivation (C2). The kinetics of deactivation and activation approach a similar rate-limiting value at extreme test potentials, so in calculating τ_m, C1 equaled 0. In the voltage range in which channels open, τ_m and τ_h were calculated using data from standard I-V protocols, in which the traces were fit with two exponentials (Clampfit). The beginning of the fit range was set near the beginning of the inward current, thereby excluding an initial outward transient that may represent a gating current and any associated lag in activation (Kuo and Yang, 2001; Burgess et al., 2002). Values for τ_m at more hyperpolarized potentials were obtained from tail current protocols. The tail current protocol included a short 2 ms step to +45 mV to open channels, followed by repolarization to varying voltages. Because this evoked large currents (∼3 nA), precautions were taken to minimize series resistance errors, such as use of low-resistance pipettes and series-resistance compensation. Under these conditions, the rise time to the peak of tail current was <30 μs. The fit region began at the peak of the tail current and ended 50 ms later. As noted previously (Frazier et al., 2001; Gomora et al., 2002), this deactivation kinetic was best fit with two exponentials, so a weighted τ (τ_w) was calculated using the following equation:

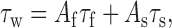where A_f and A_s are the normalized amplitude of the fast (τ_f) and slow components (τ_s). The data used to determine the voltage dependence of τ_h included the following: the rate of recovery from inactivation at -115 and -105 mV, the development of inactivation at -85 and -75 mV, and the rate of inactivation at more depolarized potentials from I-V data. Development of inactivation was measured by depolarizing the membrane for varying durations, and then channel availability was tested with a 20 ms pulse to -45 mV. These kinetics were also best fit with two exponentials, so a weighted τ_h was calculated as above. Channels were allowed to recover between sweeps by holding the membrane at -115 mV for 10 s.

The experimentally determined values of the recombinant human Ca_v3.2 channel were used to replace all parameters of the T-channel in the models of thalamic reticular (RE) or thalamocortical (TC) neurons (Destexhe et al., 1996b, 1998). In the simulations of the network behavior of these neurons, only the properties of the reticular neurons were altered (Destexhe et al., 1996a). For the modeling of the SNP-containing channels, only the set of parameters that were statistically significant (p < 0.05 determined using an unpaired Student's t test) from wild-type (WT) channels were changed. The current-clamp simulations used the three-compartment model with the current injected into the dendritic compartment and recorded from the virtual soma.

Results

Sequence

We reported previously the finding of 12 distinct nonsynonymous coding SNPs in the CACNA1H gene of CAE patients that were not found in controls (Chen et al., 2003b). The G773D SNP was found in two patients, and we now report the finding of a third patient with this SNP. We also reported finding seven other nonsynonymous SNPs that were present in both patients and controls (Chen et al., 2003b). Because the major goal of the present study was to predict the functional impact of these SNPs, we first determined whether the common and unique SNPs were on the same allele and, hence, contained in the same channel protein. To address this issue, we sequenced the CACNA1H gene of the parents of the CAE patients. Table 1 reports the occurrence of R788C in four families. Assuming mendelian inheritance of the whole gene, we could deduce the status of each allele. For example, in patient 1, the F161L and R788C SNPs exist on separate alleles because F161L was inherited from the father, whereas R788C came from the mother. In contrast, R788C was on the same allele for all three CAE patients with the G773D SNP. In the case of patient 2, all members of the trio were homozygous for R788C, indicating that the second allele also contained R788C. Therefore, we studied the effect of this common SNP alone and in combination with G773D. The sequence of a human Ca_v3.2a cDNA (Cribbs et al., 1998) was altered using PCR mutagenesis techniques.

Table 1.

Occurrence of the R788C SNP in trios

			SNPs on CAE patients
CAE patients	CAE SNP	R788 status	Allele 1	Allele 2
Patient 1	F161L (+/−)	R788C (+/−)	F161L	R788C
Father	F161L (+/−)	R788 (+/+)
Mother	F161 (+/+)	R788C (+/−)
Patient 2	G773D (+/−)	R788C (−/−)	G773D-R788C	R788C
Father	G773D (+/−)	R788C (−/−)
Mother	G773 (+/+)	R788C (−/−)
Patient 3	G773D (+/−)	R788C (+/−)	G773D-R788C
Father	G773 (+/+)	R788 (+/+)
Mother	G773D (+/−)	R788C (+/−)
Patient 4	G773D (+/−)	R788C (+/−)	G773D-R788C
Father	G773D (+/−)	R788C (−/−)
Mother	G773 (+/+)	R788 (+/+)

Zygosity is shown in parentheses, in which wild-type sequence is represented by a plus sign, and the SNP is represented by a minus sign.

Functional analysis

The next goal of this study was to determine whether these SNPs altered T-channel gating. Channel properties were studied in transiently transfected HEK-293 cells using the ruptured patch-clamp method. We used HEK-293 cells for the following reasons: under our growth conditions, they display little endogenous ionic currents (Berjukow et al., 1996), they can be transfected easily, they express recombinant T-channels at high density (Cribbs et al., 1998), and they are spherically compact, which minimizes space-clamp errors that can affect neuronal recordings. In contrast to the oocyte expression system (Lee et al., 1999), the biophysical properties of recombinant T-channels expressed in HEK-293 cells are nearly identical to recordings from isolated neurons (for review, see Perez-Reyes, 2003). The α2δ and β subunits of high-voltage-activated Ca²⁺ channels were not included because there is no evidence that they are subunits of low-voltage-activated channels and do not modulate the biophysical properties of Ca_v3.2 currents (Lambert et al., 1997; Dubel et al., 2004). Although these subunits can modestly (twofold) increase current density in some heterologous systems, this was not required because expression of the T-channel α1 subunit alone produced robust currents. The composition of the extracellular and intracellular solutions were chosen to minimize the contribution of contaminating currents and to minimize alterations in channel gating attributable to Ca²⁺ overload or ATP depletion (Zhang et al., 2000). The charge carrier was 5 mm Ca²⁺. Under these conditions, the typical transfected cell expressed a maximum of 1000 pA peak current (100 pA/pF when normalized to cell capacitance) of inward current during test pulses to -45 mV from a holding potential of -115 mV. For all cells, we first recorded currents elicited by such a pulse for 2-3 min to allow for dialysis of the cell, adjusted series resistance and compensation, and then recorded the currents elicited by varying voltages (I-V protocol). In one set of experiments, this was followed by measurements of steady-state inactivation and deactivation kinetics. Variants that displayed changes in inactivation kinetics were further studied in a second set of experiments designed to measure the development of inactivation at subthreshold voltages and recovery from inactivation. The time and voltage dependence of these properties will be presented in a similar order. We studied the effect on channel gating of all 12 SNPs found specifically associated with CAE patients, as well as the effect of an SNP (R788C) that was found in both control and in combination with a CAE SNP (G773D-R788C). Table 2 summarizes the voltage dependence of activation and inactivation, Table 3 summarizes the kinetics properties of the channels, and the figures illustrate data from channels that displayed statistically significant differences from wild type (WT).

Table 2.

Steady-state activation and inactivation properties of Ca_v3.2 variants

	m∞			h∞
	V50 (mV)	k	V50 (mV)	k
Wild-type	−54.8 ± 0.4	7.4 ± 0.1 (43)	−85.5 ± 0.8	−7.2 ± 0.2 (29)
F161L	−53.3 ± 1.0	7.2 ± 0.2 (11)	−82.3 ± 0.9*	−5.9 ± 0.1 (7)**
E282K	−53.4 ± 0.7	7.9 ± 0.2 (15)**	−83.9 ± 1.2	−6.3 ± 0.1 (7)*
C456S	−59.9 ± 0.9**	7.4 ± 0.1 (26)	−85.1 ± 1.0	−6.8 ± 0.1 (16)
G499S	−54.2 ± 0.6	7.4 ± 0.2 (13)	−85.5 ± 1.6	−7.2 ± 0.4 (8)
P648L	−53.9 ± 0.5	7.5 ± 0.2 (19)	−81.7 ± 1.7*	−6.7 ± 0.3 (8)
R744Q	−53.9 ± 0.6	7.4 ± 0.1 (15)	−84.2 ± 2.0	−6.6 ± 0.3 (7)
A748V	−56.2 ± 1.1	7.1 ± 0.2 (9)	−85.5 ± 1.4	−6.6 ± 0.2 (5)
G773D	−51.8 ± 1.0**	8.0 ± 0.2 (15)**	−82.2 ± 1.1*	−8.0 ± 0.4 (8)*
G784S	−54.0 ± 0.6	7.3 ± 0.2 (21)	−85.4 ± 1.6	−6.6 ± 0.3 (10)
R788C	−52.5 ± 0.9*	7.9 ± 0.2 (13)*	−83.2 ± 1.1	−8.5 ± 0.2 (7)**
G773D-R788C	−53.0 ± 0.9	7.4 ± 0.1 (7)	−84.8 ± 1.5	−8.5 ± 0.5 (7)**
V831M	−52.2 ± 0.8**	7.5 ± 0.1 (14)	−86.5 ± 1.3	−6.7 ± 0.2 (8)
G848S	−54.6 ± 0.8	7.1 ± 0.1 (16)	−83.3 ± 2.1	−6.6 ± 0.3 (7)
D1463N	−52.8 ± 0.8	7.4 ± 0.2 (8)	−85.8 ± 0.7	−6.3 ± 0.4 (4)

The values of V₅₀ and k were calculated for each cell and then averaged. Data shown are mean ± SEM from the number of cells shown in parentheses. Statistically significant differences (determined with Student's t test) are marked with a single asterisk if p < 0.05 and with a double asterisk if p < 0.01.

Table 3.

Kinetic properties of Ca_v3.2 variants

	Activation τ			Deactivation τ	Recovery	Inactivation τ					Persistent current
	−55 mV (ms)	−15 mV (ms)	−105 (ms)	−105 mV (ms)	−75 mV (ms)	−55 mV (ms)	−15 mV (ms)	−65 mV (% max)
Wild-type	6.2 ± 0.2	2.1 ± 0.1 (36)	2.8 ± 0.1 (16)	2648 ± 154 (33)	474 ± 68(12)	23.5 ± 0.9	15.1 ± 0.4 (36)	8.5 ± 0.3 (43)
F161L	6.8 ± 0.3	2.1 ± 0.1 (8)	3.2 ± 0.2 (4)	2092 ± 480 (3)	212 ± 48 (3)	26.4 ± 2.1	12.9 ± 0.51 (9)*	7.9 ± 0.6 (11)
E282K	6.3 ± 0.3	2.4 ± 0.2 (16)	3.4 ± 0.6 (3)			24.4 ± 1.3	15.5 ± 0.5 (16)	7.8 ± 0.6 (16)
C456S	5.1 ± 0.6*	1.6 ± 0.1 (17)**	2.7 ± 0.3 (6)	2838 ± 302 (4)	506 ± 101 (5)	20.2 ± 1.5	14.8 ± 0.6 (17)	6.7 ± 0.7 (17)**
G499S	6.6 ± 0.6	2.1 ± 0.1 (12)	3.1 ± 0.2 (5)	2612 ± 820 (3)	374 ± 114 (3)	24.7 ± 1.5	16.2 ± 0.7 (12)	10.0 ± 0.6 (13)*
P648L	6.6 ± 0.4	2.2 ± 0.1 (19)	3.0 ± 0.2 (5)	2052 ± 289 (7)	1686 ± 749 (5)*	27.7 ± 1.1**	16.1 ± 0.4 (19)	9.7 ± 0.3 (21)*
R744Q	6.8 ± 0.5	2.2 ± 0.2 (15)	3.2 ± 0.3 (6)			24.7 ± 1.3	15.3 ± 0.7 (15)	9.4 ± 0.6 (16)
A748V	5.4 ± 0.3*	1.9 ± 0.1 (9)	3.0 ± 0.3 (4)			21.6 ± 1.0	14.6 ± 0.5 (9)	8.7 ± 0.3 (9)
G773D	8.4 ± 0.6**	2.9 ± 0.2 (11)**	3.6 ± 0.2 (6)**	1875 ± 438 (5)	799 ± 267 (4)	31.0 ± 1.8**	19.2 ± 0.6 (11)**	10.9 ± 0.7 (15)**
G784S	7.1 ± 0.4*	2.1 ± 0.1 (21)	3.2 ± 0.2 (6)	2611 ± 217 (9)	248 ± 43 (7)*	24.9 ± 1.2	15.1 ± 0.5 (21)	8.6 ± 0.4 (21)
R788C	7.2 ± 0.9	2.6 ± 0.2 (8)*	3.3 ± 0.2 (6)*	2038 ± 126 (6)	424 ± 15 (3)	32.6 ± 2.1**	17.1 ± 0.7 (8)*	11.3 ± 0.4 (9)**
G773D-R788C	6.4 ± 0.6	2.3 ± 0.1 (7)	3.6 ± 0.1 (2)*			25.6 ± 3.1	15.3 ± 0.4 (7)	9.1 ± 0.3 (7)
V831M	7.2 ± 0.3**	2.2 ± 0.1 (13)	3.4 ± 0.1 (7)*	1845 ± 234 (7)*	595 ± 190 (4)	31.6 ± 3.0**	16.9 ± 0.6 (13)*	9.4 ± 0.6 (15)
G848S	6.7 ± 0.3	2.2 ± 0.1 (14)	3.5 ± 0.1 (6)**			25.1 ± 1.9	15.7 ± 0.8 (14)	9.1 ± 0.7 (16)
D1463N	6.5 ± 0.5	1.8 ± 0.1 (8)*	3.3 ± 0.1 (4)			24.6 ± 1.8	14.3 ± 0.8 (8)	7.8 ± 0.6 (8)

Data shown are mean ± SEM from the number of cells shown in parentheses. Data at −55 and −15 mV are from the same cells. Statistically significant differences are marked with a single asterisk if p < 0.05 and with a double asterisk if p < 0.01.

Voltage dependence of channel activation

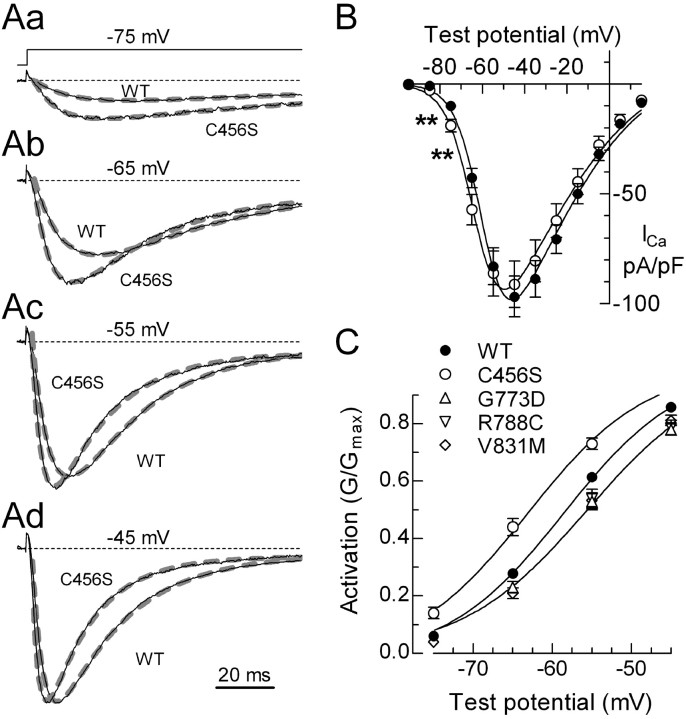
The voltage dependence of activation was measured using a standard I-V protocol with 150 ms steps to varying potentials delivered every 10 s. Representative traces that were normalized to the peak observed in that cell are shown (Fig. 1Aa-Ad). C456S channels displayed more current than WT during test pulses to voltages just beyond threshold (Fig. 1B). Because there was no increase at the peak of the I-V, this result indicates that C456S shifts activation to more hyperpolarized potentials. To quantitate this effect, peak currents for each cell were fit with a modified Goldman-Hodgkin-Katz equation (see Materials and Methods) to determine the potential of half-maximal activation (V₅₀) and the voltage dependence (k). An example of the fit obtained to the average I-V curve is shown in Figure 1B. On average, the C456S I-V was shifted -5 mV (Table 2). Normalized conductance as a function of test potential illustrates this shift (Fig. 1C). A similar shift in activation was observed when the I-V data were fit with a Boltzmann-Ohm function (Gomora et al. 2002) or when using tail currents evoked at the peak of the inward current (data not shown). C456S was the only SNP that shifted activation to more hyperpolarized potentials, whereas G773D and V831M shifted activation 2-3 mV to more depolarized potentials (Fig. 1C; Table 2). Two CAE SNPs (E282K and G773D) and the common R788C SNP reduced the voltage dependence of activation, as reflected in a larger slope factor (k) (Table 2).

Figure 1.

Effect of C456S on the current-voltage relationship of Ca_v3.2. Aa-Ad, Representative current traces recorded during depolarizing voltage steps. Schematic of the voltage protocol is shown in Aa. Holding potential was -115 mV. Zero current baseline is indicated with a dotted line. The currents were normalized to the peak current observed in that cell, which was typically observed at -45 mV. Also shown are the exponential fits (thick gray dashed lines) to the currents that were used to estimate activation and inactivation kinetics. Scale bar applies to all four sets of traces. B, Peak current-voltage relationships normalized to cell capacitance. Cells expressing C456S channels had significantly more current at negative test potentials (marked with ^**p < 0.01). Smooth curves represent fits to the average data using a modified form of the Goldman-Hodgkin-Katz equation (see Materials and Methods). C, To illustrate this shift in voltage dependence, activation is represented by the normalized conductance (G/G_max). G was calculated using a derivation of Ohm's law, G = I/(V_T-V_R), where I is the peak current, V_T is the test potential, and V_R is the reversal potential. Data represent mean ± SEM, in which the number of cells used to calculate the average is reported in Table 2. Only data that were significantly different from WT is plotted. Smooth curves represent fits to the average data using a Boltzmann equation.

Voltage dependence of channel inactivation

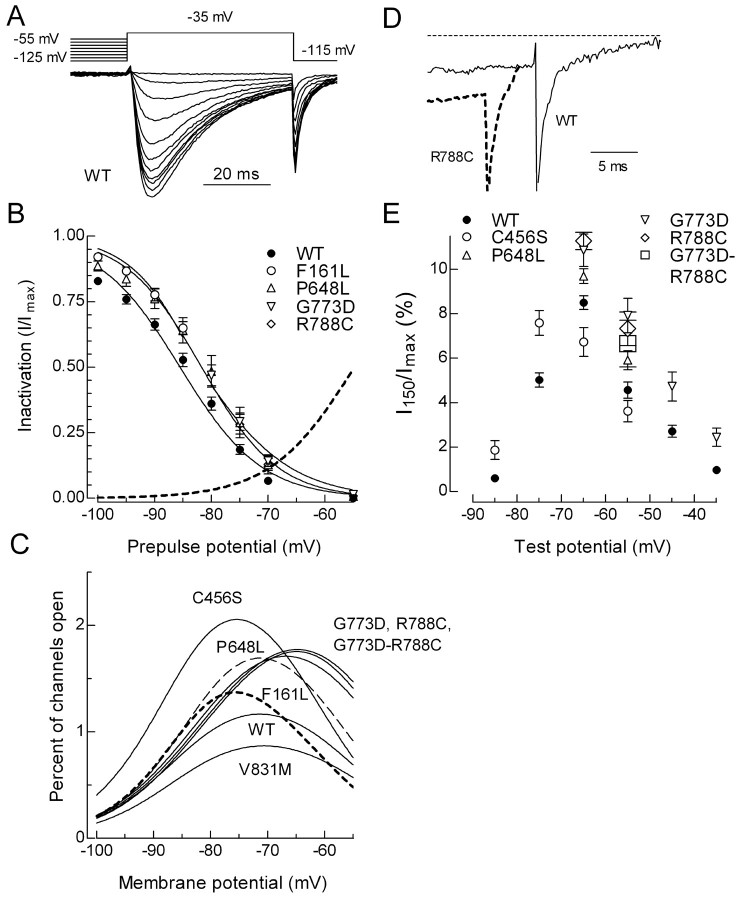
The voltage dependence of inactivation (h_∞) was measured using prepulses to varying potentials and a 50 ms test pulse to -35 mV to measure channel availability (Fig. 2A). Inactivation as a function of prepulse potential was calculated by dividing the peak current in the test pulse by that observed when the prepulse potential was -125 mV (Fig. 2B). Data from each cell were fit with a Boltzmann function and then averaged. The midpoint of the h_∞ curve was shifted 3-4 mV to more depolarized potentials in F161L, P648L, and G773D channels, whereas F161L and R788C channels displayed an altered slope factor (Fig. 2B; Table 2).

Figure 2.

Effect of SNPs on Ca_v3.2 steady-state inactivation and persistent currents. A, Representative current traces obtained during a test pulse to -35 mV after 1 s prepulses to varying potentials. Voltage protocol is shown above the traces. The cell was held at -115 mV for 10 s between sweeps. After the last depolarizing prepulse (-55 mV), the cell was tested again with a -125 mV prepulse. Typically, 95% of the original current was recovered, thereby excluding the effect of rundown. B, Inactivation (h_∞) was calculated as the fraction of current available after each prepulse (I) divided by the current recorded after the first prepulse to -125 mV (I_max). Data from each cell were fit with a Boltzmann equation, and the resulting values of V₅₀ and k were averaged (number of cells and values reported in Table 2). Smooth curves represent the average fits. Dotted line represents the activation curve for WT channels as described in Figure 1. The activation and inactivation curves overlap at approximately -70 mV. C, The percentage of channels in the overlap region was calculated as the product of the Boltzmann functions describing each process. D, Representative current traces obtained at the end of 150 ms depolarizing pulses to -55 mV. The downward spike represents the tail current triggered by repolarization. Dotted line represents the zero current baseline. E, The residual current at 150 ms (I₁₅₀) was divided by the maximal current observed in that cell (I_max), averaged, and then plotted as a function of test potential. Data represent mean ± SEM, in which the number of cells used to calculate the average is reported in Table 3. Only data that were significantly different from WT is plotted.

The overlap in the voltage dependence of activation and inactivation suggests that there are voltages at which T-channels are not fully inactivated but are available for opening, thereby generating a sustained window current. T-window currents play a key role in firing of thalamic neurons (for review, see Crunelli et al., 2005). In addition to inducing bistability of the membrane potential, these currents can increase intracellular Ca²⁺ (Bijlenga et al., 2000; Chemin et al., 2000). The percentage of channels that might participate in these window currents was estimated by multiplying the fraction of channels inactivated and activated at any given voltage. Four CAE SNPs and the common R788C SNP increased the percentage of channels in the overlap region: 176% of control for C456S; ∼150% for P648L, G773D, R788C, and the G773D-R788C combination; and 117% for F161L (Fig. 2C). One SNPs decreased the overlap region, V831M (∼74% of control). An experimental confirmation of window currents can be provided by the existence of persistent currents at the end of a depolarizing pulse that is at least four times longer than the inactivation τ (Wolfe et al., 2002). To provide an estimate of the fraction of channels contributing to these currents, we normalized the residual current (Fig. 2D) by the peak current observed in that cell. As predicted from the overlap of the h_∞ and m_∞ curves, the persistent current showed a bell-shaped distribution centered around -65 mV (Fig. 2E). Significantly increased residual currents were detected for the following channels: C456S (-85 and -75 mV); P648L (-65 and -55 mV); G773D (-55 to -35 mV), R788C (-65 and -55 mV), and G773D-R788C (-55 mV) (Fig. 2E; Table 3).

Channel kinetics

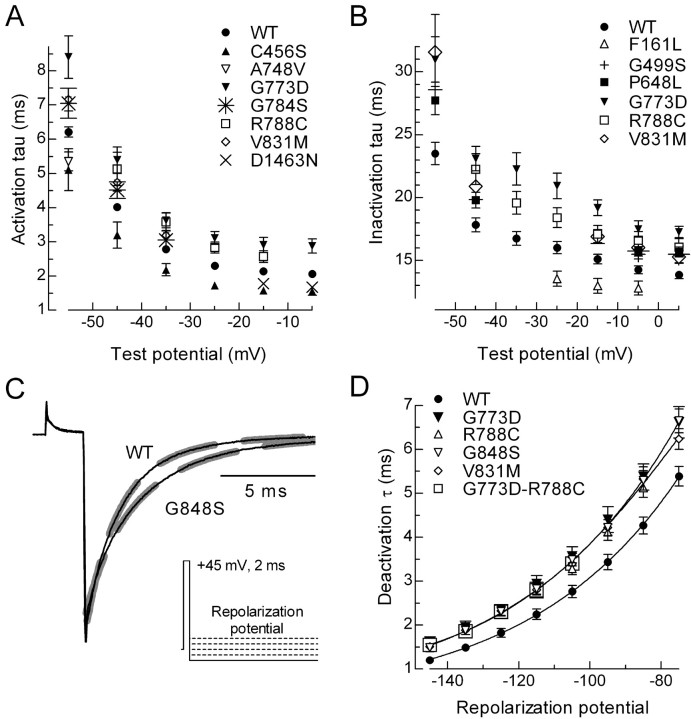
Because the time course of transitions between closed, open, and inactivated states of the T-channel can determine the size and shape of the LTS, we examined these kinetics in detail. Transitions from both closed-to-open and open-to-inactivated states can be estimated from the currents recorded with the I-V protocol (Fig. 1). In this case, the currents are simultaneously fit with two exponentials, in which one describes the kinetics of activation and the other inactivation. The current wave forms for all channels were fit very well, and representative data are shown in Figure 1. T-type Ca²⁺ channel kinetics are both time and voltage dependent. For example, small depolarizations from the holding potential cause a slowly activating and slowly inactivating current, whereas stronger depolarizations induce more rapidly activating and inactivating kinetics (Fig. 3A,B; Table 3). In general, SNPs had a greater effect on currents elicited just beyond threshold, which is closer to the resting membrane potential of most neurons. Activation kinetics were faster than wild type for three channels (C456S, A748V, and D1463N) and slower with four (G773D, G784S, R788C, and V831M) (Fig. 3A; Table 3). The effects of SNPs on inactivation kinetics were more uniform, with only one channel showing faster inactivation (F161L), whereas five inactivated more slowly than wild-type (G499S, P648L, G773D, R788C, and V831M) (Fig. 3B; Table 3).

Figure 3.

Effect on activation, inactivation, and deactivation kinetics. Average activation (A) and inactivation (B) kinetics for channels that significantly differed from WT. Kinetics were estimated using double-exponential fits to the currents generated during the I-V protocols (Fig. 1 A). Only data that were significantly different from WT is plotted. C, Representative tail current traces obtained after repolarization to -105 mV. The voltage protocol is shown in the inset. Thick dashed lines represent exponential fits to the tail current. D, Average deactivation kinetics for WT and variants. Data represent mean ± SEM, in which the number of cells used to calculate the average is reported in Table 3. Only data that were significantly different from WT is plotted.

The transition from open-to-closed channels can be estimated by exponential fits to the tail current. The voltage protocol begins with a strong depolarizing pulse to open channels, followed by repolarization to negative potentials below the threshold at which channels open (Fig. 3C, inset). As noted previously for Ca_v3.3 channels (Frazier et al., 2001; Gomora et al., 2002), Ca_v3.2 tail currents decayed in a biexponential manner. For the modeling studies, deactivation was reduced to a single τ by weighting the contribution of each τ based on the amplitude of the exponentials. Deactivation kinetics were slowed in five channels: G773D, V831M, G848S, R788C, and G773D-R788C (Fig. 3D; Table 3).

Similar to HVA channels, T-channels can also inactivate from intermediate closed states (Serrano et al., 1999). The voltage protocol used to measure this included a subthreshold depolarizing pulse to move channels into intermediate closed states, followed by a test pulse to measure the fraction of channels available to open (Fig. 4, inset). Channel availability was then measured after inactivating pulses of increasing durations, and the data (I) were normalized to the peak current observed in the absence of any inactivating pulse (I_max). Representative traces are shown in Figure 4A, and averaged time courses are shown in B. Closed-state inactivation was significantly affected in two channels, P648L showed a slower rate, and G784S showed a faster rate (Fig. 4B; Table 3).

Figure 4.

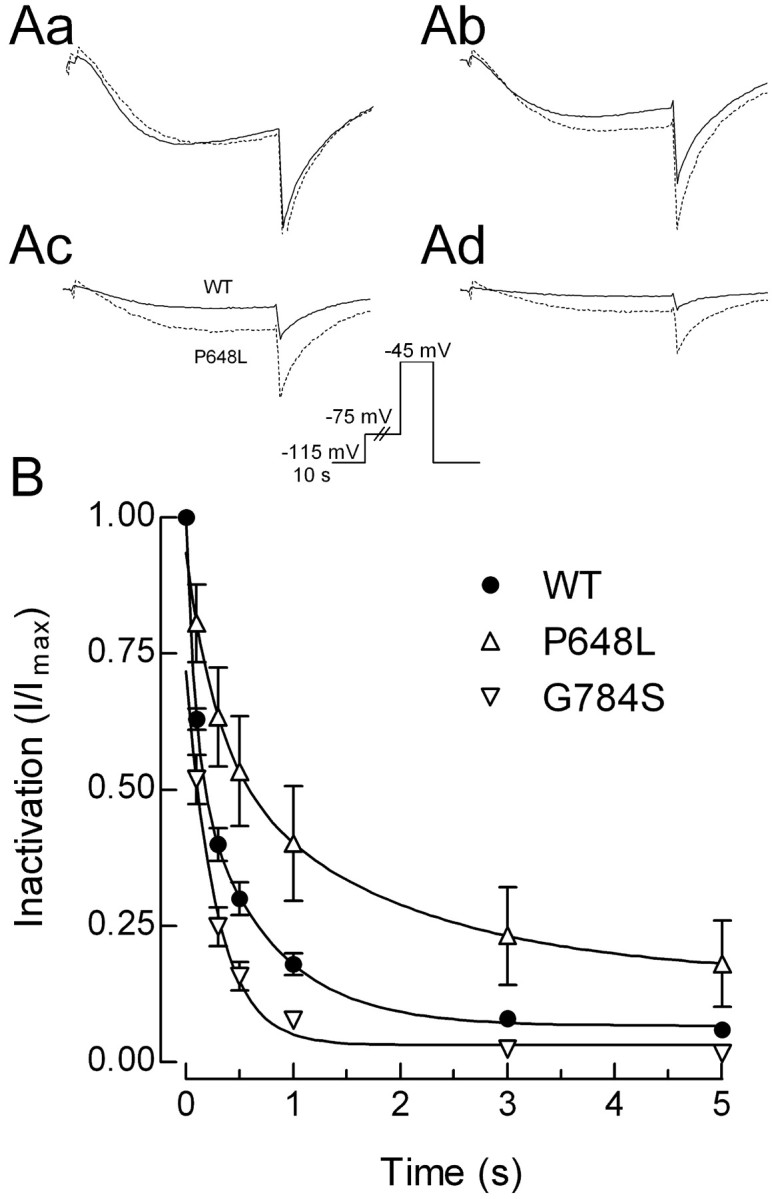
Development of inactivation at subthreshold voltages. Aa-Ad, Representative current traces recorded during test pulses to -45 mV. The duration of the inactivating pulse was 0 s (Aa), 1 s (Ab), 5 s (Ac), or 10 s (Ad). Solid line represents data obtained from a cell transfected with WT channels, and the dotted line represents P648L channels. B, Average time course of inactivation at -75 mV for WT, P648L, and G784S channels. Curves represent fits to the average data.

Recovery from inactivated states is also measured with a multistep protocol, but, in this case, channels are first inactivated, allowed to recover for varying lengths of time, and then tested for channel availability (Fig. 5, inset). Only one SNP was found to affect this rate of recovery, with V831M channels recovering faster than wild-type channels (Fig. 5; Table 3).

Figure 5.

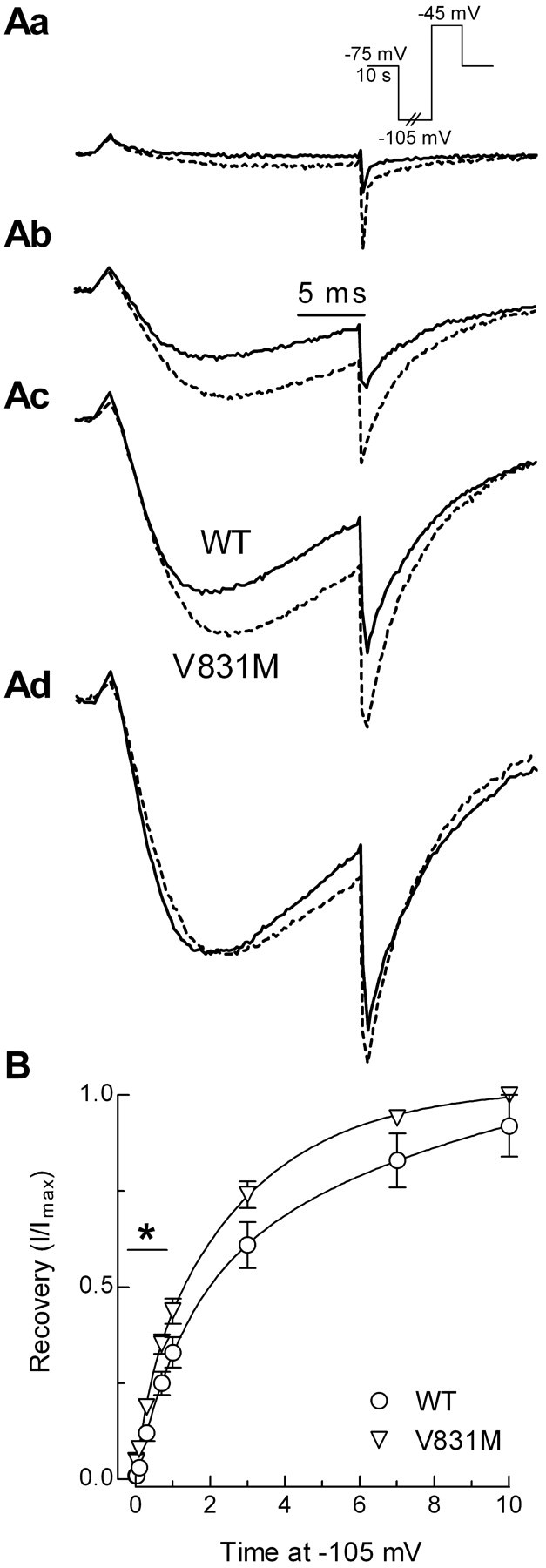
Time course of recovery from inactivation. Aa-Ad, Representative current traces recorded during test pulses to -45 mV. Channels were inactivated by holding the membrane at -75 mV for 10 s. Recovery at -105 mV was measured after pulses of 0.01 s (Aa), 0.7 s (Ab), 3 s (Ac), or 10 s (Ad). Solid line represents data obtained from a cell transfected with WT channels, and the dotted line represents V831M channels. B, Average time course of recovery for WT and V831M channels. Curves represent fits to the average data.

Modeling of neuronal firing

To determine the net effect of changes in channel gating, we used computer models of thalamic neurons and circuits. Models that include T-currents have been developed and validated by Destexhe and Sejnowski (2003) for use in the NEURON simulation program (Hines and Carnevale, 2001). These models use Hodgkin-Huxley-type equations to predict T-channel availability as a function of voltage and time. The values for the activation curve (m_∞) were obtained after fitting the I-V data with a Goldman-Hodgkin-Katz equation (see Materials and Methods and data in Table 2). The data for the inactivation curves (h_∞) were described above (Fig. 2; Table 2). The transition rates between closed and open channels (τ_m) at different voltages can be calculated with a single equation (see Materials and Methods) that is based on the data obtained from channel-opening kinetics measured during the I-V protocol, and channel-closing kinetics measured during the tail current protocol (Figs. 1, 3). Similarly, transitions into and out of inactivated states (τ_h) at different voltages can be calculated with the same equation to fit inactivation kinetics observed during the I-V, closed state inactivation (Fig. 4), and recovery kinetics (Fig. 5). Representative fits to the data are shown in Figure 6, A for (τ_m) and B for (τ_h).

Figure 6.

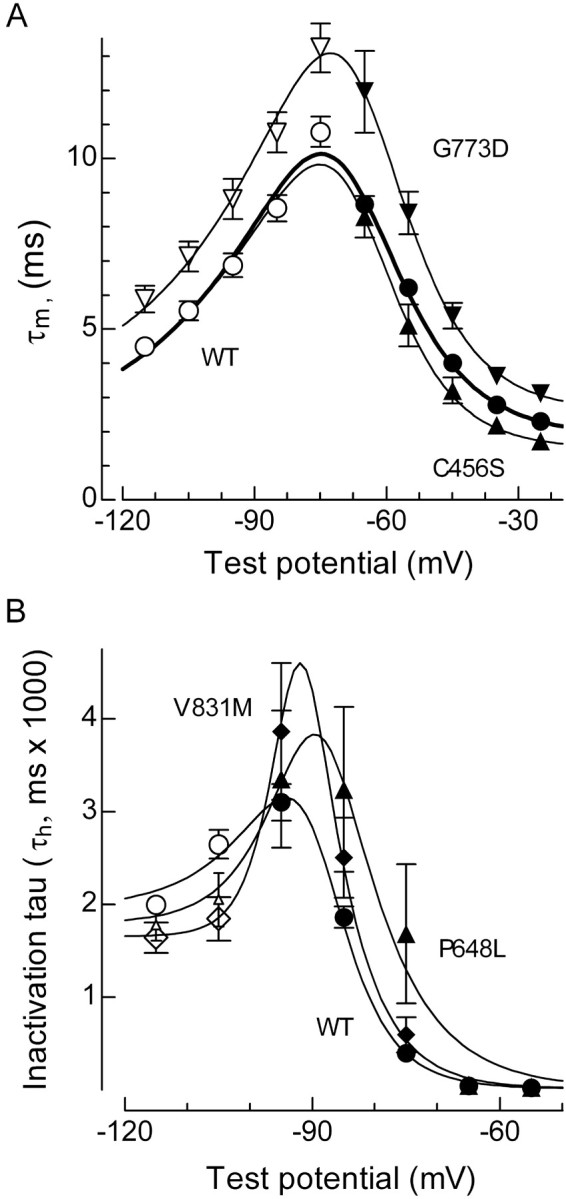
Voltage dependence of activation and inactivation kinetics. A, Activation (filled symbols) and deactivation kinetics of WT (circles), C456S (triangles), and G773D currents (inverted triangles) were fit with a single equation to calculate the voltage dependence of τ_m (smooth curves; see Materials and Methods). B, Voltage dependence of τ_h (smooth curves) for WT (circles), P648L (triangles), and V831M (diamonds). Open symbols represent recovery from inactivation. The data at -95, -85, and -75 mV represent development of inactivation at near subthreshold potentials as described in Figure 4. The data at -65 and -55 mV represent the inactivation τ measured during the I-V protocol.

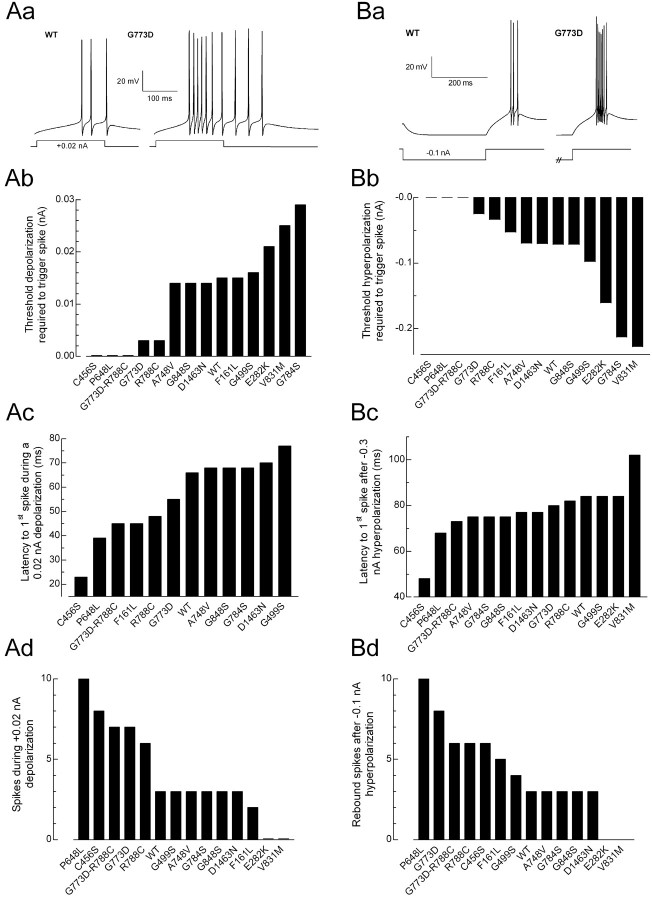
Simulations of thalamic neurons were performed using the values obtained for wild-type recombinant Ca_v3.2 channels and those containing SNPs when these values were statistically different from WT. Therefore, no modeling was performed of the R744Q channel. We modeled the responses that would occur after EPSPs by depolarizing the dendrite of the model neuron (100 ms; range, 0.01-0.05 nA) and IPSPs by hyperpolarizing the dendrite (300 ms; range, 0.05-1 nA). The size and duration of the T-channel-mediated LTS was measured using the latency and number of Na-dependent spikes that were triggered at the soma of the model neuron. Results obtained with WT channels were in good agreement with those obtained in native neurons and from previous modeling studies (Destexhe et al., 1996b, 1998), with burst firing occurring after both mock EPSPs and IPSPs (Fig. 7A,B, respectively).

Figure 7.

Simulations of RE neuron firing. Current-clamp responses to mock EPSPs (A) or IPSPs (B) using values obtained with WT and R788C channels. The EPSP pulse consisted of a +0.02 nA current injection for 100 ms. The IPSP pulse consisted of a -0.1 nA current injection for 300 ms. The minimum current injection required to trigger a Na-dependent spike during an EPSP (Ab) or after an IPSP (Bb) is shown for each channel. Latency to the first Na spike triggered by a +0.02 nA depolarization (Ac) or a -0.3 nA hyperpolarization (Bc) for each channel. The number of Na spikes triggered during a +0.02 nA depolarization of 100 ms (Ad) or after a -0.1 nA hyperpolarization of 300 ms (Bd). E282K and V831M require stronger depolarizations to trigger firing.

Substitution of the channel behavior altered by nine of the SNPs, and the double SNP G773D-R788C, resulted in enhanced firing compared with WT. All 10 displayed a lower threshold for spike initiation after a mock EPSP (C456S, P648L, G773D, R788C, G773D-R788C, A748V, G784S, G848S, and D1463N), nine of these channels also had a decreased latency to the first spike, and five produced more spikes per burst (Fig. 7Ab-Ad). Similar results were obtained after mock IPSPs: nine channels had a lower threshold for spike initiation (C456S, G499S, P648L, G773D, R788C, G773D-R788C, A748V, G784S, and D1463N), five showed a decreased latency to the first spike, and seven showed more spikes per burst. In contrast, two of the SNPs (E282K and V831M) are predicted to decrease neuronal firing, requiring stronger depolarizations or hyperpolarizations to elicit spikes, and increased latencies to firing.

Similar effects of the SNPs were obtained using a model of either RE or TC relay neurons (Destexhe et al., 1998). Interestingly, four of the SNPs (C456S, P648L, G773D, and R788C) and the double G773D-R788C could induce spontaneous oscillations in the TC model, whereas only two did so in the RE model (C456S and P648L). To uncover this activity, we used constant current injections close to the threshold of spike initiation. Using G773D as an example, some conditions produced a mixture of subthreshold and suprathreshold oscillations, whereas at others the rhythmic LTS triggered Na⁺ spikes on each oscillation (Fig. 8A,B, respectively). The frequency of these oscillations varied between 2 and 4 Hz (Fig. 8C). Notably, 3 Hz oscillations are observed in the EEG of CAE patients (Gloor and Fariello, 1988; Crunelli and Leresche, 2002). P648L and R788C also required depolarizing current injections, G773D-R788C did not require any current injection, and C456S required hyperpolarizing current injections to trigger these oscillations (Fig. 8C). Simulations with WT properties never displayed this type of activity.

Figure 8.

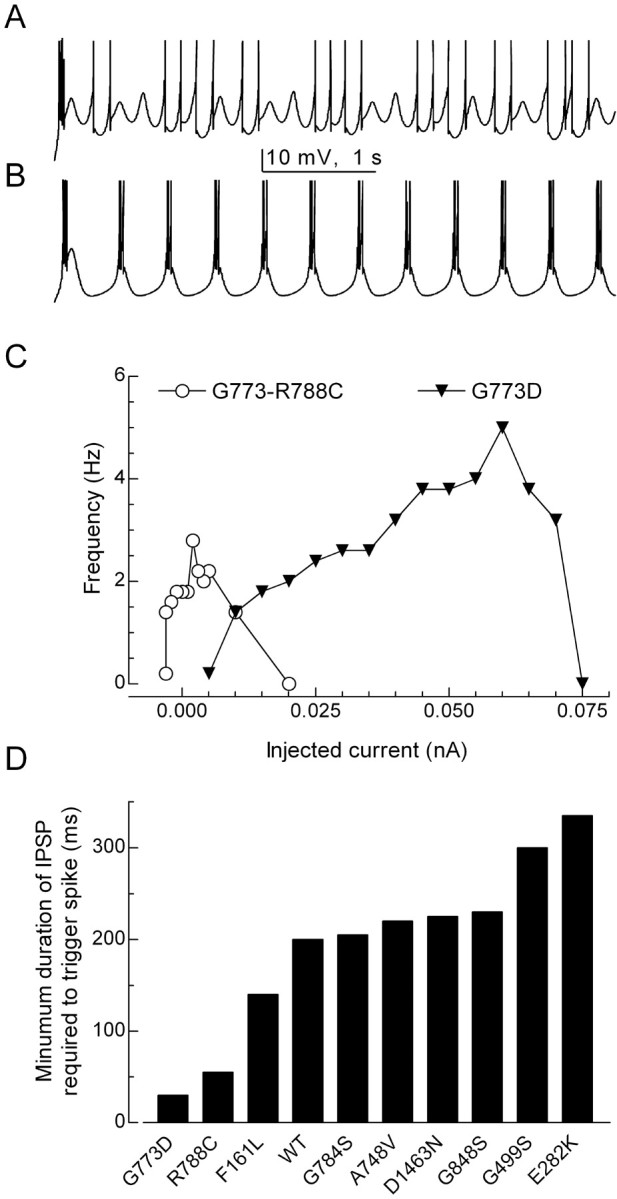
Spontaneous oscillations induced by G773D, G773D-R788C, and C456S in a model of TC neurons. Simulated neuron-containing G773D channels was depolarized from rest (-74 mV) by a constant current injection of either 0.065 nA (A) or 0.025 nA (B). C, The frequency of subthreshold and suprathreshold oscillations is plotted as a function of current injection. The membrane potential varied between -80 and -60 mV.

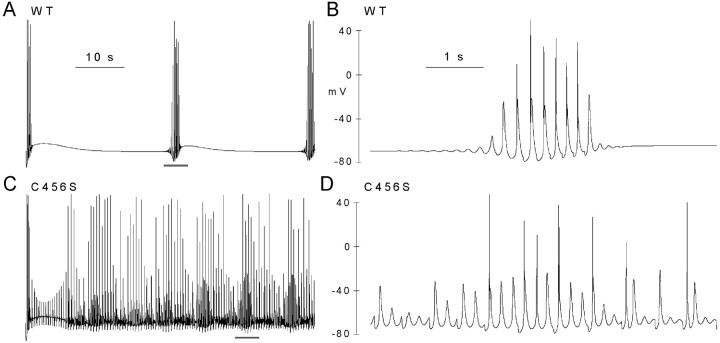
Computer models have also been developed to simulate spindle oscillations using a network of interconnected TC and RE neurons (Destexhe et al., 1996a). The ability of this model to mimic spindles was not affected by replacing the RE cell T-channel properties with those of recombinant WT channel (Fig. 9A,B) or with most of the SNPs. In contrast, substitution with C456S channel properties induced spontaneous oscillations that led to longer-lasting and more frequent spindles (Fig. 9C,D).

Figure 9.

Simulations of spindle oscillations in a network model of TC and RE neurons. The biophysical properties of WT (A, B) and C456S (C, D) channels were introduced into the RE neurons. WT channels triggered spindle oscillations that were quite similar to the original model (Destexhe et al., 1996a). Traces represent the responses recorded from the soma of TC (0). The region underlined in A and C is shown in an expanded time scale in B and D, respectively.

Discussion

Mutations in ion channel genes have been associated with various neurological and muscular diseases (Gargus, 2003). The link between genotype and phenotype is more easily defined in monogenic disorders with a clear pattern of mendelian inheritance. In contrast, childhood absence epilepsy is a polygenic disorder, making identification of candidate genes more difficult. Studies on animal models have suggested that increased T-type Ca²⁺ channel expression may directly lead to enhanced neuronal firing of the thalamocortical circuit and precipitate absence-type seizures (Tsakiridou et al., 1995; Zhang et al., 2002). Therefore, we hypothesized that gain-of-function polymorphisms in human T-channel genes may be a contributing factor in CAE. We reported previously the finding of 20 single nucleotide polymorphisms that change the coding sequence of the gene for Ca_v3.2 channels CACNA1H and that 12 of these SNPs were only found in CAE patients (Chen et al., 2003b). Most of these SNPs were only found in a single patient, indicating that they are rare (1 in 118 CAE patients). These SNPs were not found in a separate study of 192 patients (34 with CAE). Although four different CACNA1H SNPs were found, they were in patients with different types of idiopathic generalized epilepsy (Heron et al., 2004). A not-so-rare SNP in our patients was G773D, which we have now found in three distinct families (3 in 166). Interestingly, all three of these patients also have the common SNP R788C. The goal of the present study was to establish whether these SNPs altered channel gating and then use computer modeling to evaluate whether these alterations would enhance neuronal firing.

Results obtained using whole-cell recording showed that five of the CAE-specific SNPs altered the voltage dependence of activation. Three of these SNPs and three others also altered the voltage dependence of inactivation. Eleven SNPs affected the transitions between open, closed, and inactivated states. Only one SNP (V831M) altered the rate of recovery of channels from the inactivated state (deinactivation). R744Q channels were indistinguishable from wild type. We conclude that SNPs in Ca_v3.2 alter channel gating and therefore might contribute to the development of epilepsy.

A similar conclusion was made in a recent study in which five of the rare CAE-specific SNPs were introduced into a rat Ca_v3.2 cDNA (Khosravani et al., 2004). In this study, introduction of C456S and D1463N had no effect, F161L and E282K shifted activation -10 mV, and V831M shifted inactivation +9 mV. Our results using the human channel are similar in that D1463N had only modest effects but are quite different both qualitatively (C456S affects many channel parameters in the human channel) and quantitatively (our shifts in V₅₀ were in the 2-5 mV range). The effect of SNPs on channel activity may be sequence specific, and this might explain the apparent discrepancies. One region in which these channels differ is the III-IV linker, in which the human clone represents the “a” isoform, whereas the rat clone is a “b” isoform. These alternatively spliced variants were discovered in a study of Ca_v3.2 in testis (Jagannathan et al., 2002). This study also examined the expression of these isoforms using PCR and found that only the “a” isoform is in brain. The rat and human Ca_v3.2 channels also differ substantially in the sequence of their I-II linker, in which most of the SNPs are located (only 68% identity) and, as noted previously (McRory et al., 2001), show major differences in their gating properties. A possible species dependence of Ca_v3.2 SNPs will be of importance to future studies that may attempt to knock-in an SNP into the mouse genome as performed with the CACNA1A gene (van den Maagdenberg et al., 2004).

Of the 14 CAE patients with unique CACNA1H SNPs, 10 also contained SNPs that were found in the control population. Of particular interest is the SNP R788C, which we found in 20.6% of the CAE patients. This SNP (reference number rs3751664) is found in 13.7% of Japanese (Hirakawa et al., 2002) and in 5% of Caucasians (Celera database). Of note, the SNP R788C was found in all three patients with G773D. Our studies show that the gating of R788C channels was quite different than WT and is predicted to increase neuronal firing. Sequencing of the parent's DNA indicated that one allele encoding the Ca_v3.2 channel harbored the F161L transition, whereas the second allele harbored the R788C transition. This may provide an example of gene dosing: the overactivity induced by a single SNP can be compensated but not entirely when both alleles are affected.

In contrast, in patients 2-4 (Table 1), one allele contained both G773D and R788C transitions. Therefore, we also studied the effect of the R788C transition in combination with G773D. Although many properties of G773D-R788C resembled the activity of G773D, it was significantly different in terms of activation (p < 0.04) and inactivation (p < 0.01) kinetics. The close proximity of these amino acids in the secondary sequence suggests that both SNPs disrupt the same functional domain. Also located in this region is G784. In contrast to G773D and R788C that alter channel gating and result in the loss of a charged residue, the G784S SNP has a modest effect on channel properties and no effect on charge. All of these residues are quite close to the first-membrane-spanning domain of the second repeat (IIS1). Although the role of this segment in Ca²⁺ channel gating is unknown, it is interesting to speculate that charged residues in this region may play a role in coupling movements of repeat I to repeat II. The finding that all three patients with G773D also contained R788C on the same allele may provide an example of how a common SNP can combine with a second SNP to alter function.

The ability of T-type channels to open near the resting membrane potential allows them to create low-threshold spikes after an EPSP, depolarizing the neuron beyond the threshold for Na-dependent action potentials. In neurons whose resting membrane potential is relatively depolarized (e.g., TC cells in relay mode), T-channels are inactivated; however, their ability to recover from inactivation during small IPSPs allows them to open when the membrane potential returns to rest, thereby creating a low-threshold spike that is crowned by a burst of Na-dependent action potentials. The kinetics of T-channel activation and inactivation determines the duration of this LTS and hence the duration of the burst. For example, RE neurons contain a slowly inactivating T-current and fire in long-lasting bursts, whereas TC neurons contain a fast inactivating T-current and fire in shorter bursts (Huguenard and Prince, 1992). Therefore, SNPs could induce neuronal hyperexcitability by shifting inactivation to less hyperpolarized potentials (h_∞), shifting activation to more hyperpolarized potentials (m_∞), accelerating the rate channels open, slowing the rate channels inactivate, or accelerating the rate channels recover from inactivation. We found that CAE-specific SNPs could affect all of these properties, but, in many cases, the effects opposed each other. For example, the G773D SNP had effects that would either increase excitability (positive shift in h_∞; slowed inactivation kinetics) or decrease excitability (positive shift in m_∞; slowed activation kinetics). To determine the net effect of these SNPs, we used simulations of neuronal firing.

Destexhe et al. (1996a,b, 1998) have developed and tested a series of models of thalamic neurons that incorporate T-currents. Substitution of the biophysical properties of the recombinant Ca_v3.2 channel into these models also produced simulations that resembled native firing patterns, displaying burst firing after both mock EPSPs and IPSPs. The properties of Ca_v3.2 closely resemble Ca_v3.1 and native TC T-currents, whereas the slowly inactivating Ca_v3.3 more closely resembles RE T-currents (Chemin et al., 2002). Nevertheless, in situ hybridization studies indicate that RE neurons express mRNA for both Ca_v3.2 and Ca_v3.3, whereas TC neurons express Ca_v3.1 (Talley et al., 1999). We used models of thalamic neurons because the role of T-currents has been validated in these neurons and models; however, absence seizures may originate in the cerebral cortex (Meeren et al., 2002). Ca_v3.2 mRNA was also found in the cortex (Talley et al., 1999), so it may be expressed in the bursting neurons that contribute to intracortical spike-wave oscillations (Destexhe et al., 2001). In any case, we obtained similar results in RE and TC models. In either model, the largest effects on burst firing were found when using the properties of C456S, P648L, G773D, R788C, and G773D-R788C. With these channels, there was an increase in the number of spikes triggered per burst, a decrease in the latency to first spike, and membrane potentials in which spontaneous oscillations occurred. A common characteristic of these SNPs is that they all increase persistent currents, which would lead to a prolonged depolarization of the membrane. A similar gain-of-function phenotype has been observed in studies of voltage-gated sodium channel SNPs found associated with generalized epilepsy with febrile seizures (GEFS+) (Lossin et al., 2002). The presence of persistent T-currents was predicted by the overlap of the steady-state activation and inactivation curves and shown experimentally by an increase in the fraction of current remaining after a 150 ms pulse. T-channel window currents can induce stable changes in the resting membrane potential of many neurons and are thought to play a key role in thalamic oscillations (for review, see Crunelli et al., 2005). Ca_v3.2-mediated window currents can also induce changes in intracellular Ca²⁺ concentration (Chemin et al., 2000), leading to the activation of many second-messenger cascades, such as those involved in hormone secretion and myoblast fusion (Chen et al., 1999; Bijlenga et al., 2000).

The ability of Ca_v3.2 SNPs to alter channel activity in a manner that enhances burst firing confirms our initial hypothesis: enhanced burst firing of Ca_v3.2-containing neurons in thalamocortical circuits may directly trigger the generalized spike-wave discharge observed during absence seizures. The finding that some SNPs (E282K and V831M) decreased simulated firing seemingly contradicts this hypothesis. A similar discrepancy between channel phenotype and genotype was found in Ca_v1.1 SNPs associated with periodic paralysis (Lapie et al., 1996), Ca_v1.4 SNPs associated with night blindness (McRory et al., 2004), and Na_v1 channel SNPs associated with GEFS+ (Lossin et al., 2003). One possibility is that the T-channel SNPs alter activity in a manner that cannot be detected when Ca_v3.2 is expressed alone in heterologous expression systems. SNPs might alter interactions of the T-channel α1 subunit with other proteins, such as an unidentified subunit that modulates activity, one that controls their distribution within neurons, or with protein kinases (Wolfe et al., 2002). Another possibility is that Ca²⁺ flux through T-channels modulates expression of channels or pumps that regulate excitability. Notably, many mouse models of absence epilepsy have loss-of-function mutations in HVA Ca²⁺ channel subunits, leading to upregulation of T-channel expression at the plasma membrane (Zhang et al., 2002).

In conclusion, we describe the functional effects of CAE-specific sequence polymorphisms that occur in the gene encoding Ca_v3.2 T-type Ca²⁺ channels. We also show that common SNPs can also alter channel activity. This result is consistent with the polygenic, non-mendelian inheritance pattern observed in CAE (Robinson and Gardiner, 2000) and suggests that individual variations in the CACNA1H gene produces mild effects on channel activity that can be compensated by other gene products. We suggest that CACNA1H be considered a susceptibility gene, with the seizure phenotype also depending on SNPs in other genes or environmental factors. It may also be a susceptibility gene for a wider range of neurological disorders characterized by thalamocortical dysrhythmia (Llinás et al., 1999). Identifying other susceptibility genes and elucidating how they interact to produce dysrhythmia in networks will be the next important challenge.