Intrinsic Musculoskeletal Properties Stabilize Wiping Movements in the Spinalized Frog

Abstract

The mechanical stability properties of hindlimb-hindlimb wiping movements of the spinalized frog were examined. One hindlimb, the wiping limb, was implanted with 12 electromyographic (EMG) electrodes and attached to a robot that both recorded its trajectory and applied brief force perturbations. Cutaneous electrical stimulation was applied to the other hindlimb, the target limb, to evoke the hindlimb-hindlimb wiping reflex. Kinematic and EMG data from both unperturbed trials and trials in which a phasic perturbation was applied were collected from each spinalized frog. In the perturbed behaviors, we found that the initially large displacement attributable to the perturbation was compensated such that the final position was statistically indistinguishable from the unperturbed final position in all of the frogs, thus indicating the dynamic stability of these movements. This stability was robust to the range of perturbation amplitudes and nominal kinematic variation observed in this study. In addition, we investigated the extent to which intrinsic viscoelastic properties of the limb and proprioceptive feedback play a role in stabilizing the movements. No significant changes were seen in the EMGs after the perturbation. Furthermore, deafferentation of the wiping limb did not significantly affect the stability of the wiping reflex. Thus, we found that the intrinsic viscoelastic properties of the hindlimb conferred robust stability properties to the hindlimb-hindlimb wiping behavior. This stability mechanism may simplify the control required by the frog spinal motor systems to produce successful movements in an unpredictable and varying environment.

Introduction

The mechanical response of an animal's limb to external and internal perturbations is a critical aspect of motor behavior. The mechanics of limb movement, including inertial, viscous, and elastic components, are intimately related to the neural control of movement: limb mechanics influence the neural control strategies used to generate movement (McIntyre and Bizzi, 1993; Kawato, 1999), whereas neural control can alter limb mechanics (Hogan, 1985a,b; Burdet et al., 2001). Thus, an appreciation of limb mechanics is necessary for understanding the neural control of movement.

Although the inertial mechanics of limb movements are well characterized (Hollerbach and Flash, 1982), a similar understanding of the limb viscoelastic properties (i.e., viscosity and stiffness) has been more elusive. This likely reflects both the difficulty in estimating viscoelastic properties during movement (Burdet et al., 2000) and the modulation of these properties across tasks (Osu et al., 2003). Furthermore, the physiological mechanisms underlying viscoelasticity during movement have not been explored generally. Total limb viscoelasticity is derived from intrinsic musculoskeletal properties and effects of reflex action. The intrinsic musculoskeletal properties include the passive viscoelasticity of muscle and connective tissue, the length/velocity dependencies of active muscle force generation, and configuration-dependent muscle moment arms. These intrinsic musculoskeletal properties are generally both state dependent (e.g., the force-length property of muscles) and time dependent (e.g., the time-varying muscle activation pattern) and their combined mechanical action is referred to simply as the intrinsic viscoelasticity of the limb.

Although it has been suggested that intrinsic viscoelasticity might be significant during movement, there are few such demonstrations during routine behavior. Polit and Bizzi (1979) showed that, after deafferentation and without visual feedback, monkeys compensated for perturbations during reaching, suggesting a relatively high intrinsic limb stiffness. However, the monkeys in those experiments may have learned compensatory strategies using feedback from remaining dorsal roots (Lackner and DiZio, 1994). Other work has shown that intrinsic viscoelasticity can be significant during human arm movements but only when subjects enhance these properties via voluntary cocontraction of antagonistic muscles; in routine reaching behaviors, intrinsic stiffness is low (Popescu et al., 2003).

We therefore examine here the intrinsic viscoelasticity of goal-directed hindlimb wiping movements produced by the frog spinal motor system. Several studies of spinal frogs have suggested that these movements should exhibit significant viscoelasticity, although this property was assessed only isometrically (Giszter et al., 1993) or with tonic loads (Schotland and Rymer, 1993b). Here, we use phasic loads applied during movement to better explore the full dynamics of the behavior. Furthermore, the ability to systematically examine the mechanisms responsible for any such viscoelasticity combined with the similarity of movements produced in spinal and intact animals (Giszter et al., 1989), allows us to assess, for the first time in a multijoint movement, the potential contributions of intrinsic viscoelastic properties to routine behavior. We assessed the dynamic stability of wiping by applying perturbations to the hindlimb during movement. Assessing dynamic stability gives a model-independent, functional characterization of viscoelasticity, reflecting the ability of total viscoelastic limb forces to dominate inertial and applied external forces (Won and Hogan, 1995).

We find that hindlimb wiping movements are robustly capable of compensating for phasic perturbations. Importantly, we show that this compensation is accomplished primarily by intrinsic viscoelastic properties and not by reflex action. Thus, this work provides a clear demonstration of a goal-directed, multi-joint limb behavior with significant intrinsic viscoelasticity. An abstract of this work was previously presented (Richardson et al., 2002).

Materials and Methods

Surgical preparation. All of the procedures were approved by the Committee for Animal Care at Massachusetts Institute of Technology. Sixteen adult bullfrogs (Rana catesbeiana) were used in these experiments. Animals were anesthetized with a combination of tricaine (5% solution; 0.5-0.7 ml) and ice. The skin overlying the skull was opened, the muscle tissue and ligament between the first vertebra and the skull were removed, and the skull overlying the tectum and brainstem was removed. The dura was opened, and the exposed spinal cord was aspirated at the caudal margin of the fourth ventricle, completely separating the spinal cord from the brainstem. All of the neural tissue rostral to the brainstem was then removed by aspiration, and the remaining cranial cavity was packed with Gelfoam to minimize bleeding. Gelfoam was also placed over the exposed spinal cord and brainstem, and the wound was closed using staple sutures.

Animals were then implanted with bipolar electromyographic (EMG) electrodes. Electrodes were constructed from braided stainless-steel wires, insulated with Teflon (seven strands; 0.023 mm). Pairs of wires were knotted together at one end, and the knot was covered with modeling wax to insulate the two cut ends, forming a wax ball at the end of the electrode pair. The Teflon insulation covering each wire was then stripped for a length of ∼1 mm, separated from the wax ball by a distance of ∼1-2 mm. The wires were then inserted in the muscle, so that the stripped regions of the electrode pair were located inside the muscle belly with the pair secured by the wax ball. The orientation of the electrode pair was parallel to the orientation of the muscle fibers. The following muscles were implanted: semitendinosus (ST), sartorius, rectus internus (RI), adductor magnus, vastus internus, semimembranosus (SM), vastus externus (VE), biceps femoris (BF), iliopsoas (IP), rectus anterior, tibialis anterior, and gastrocnemius. EMG electrodes were tunneled subcutaneously to an exit point on the back and attached to a connector strip.

The dorsal tibiofibula just proximal to the ankle was then exposed. Two bone screws were placed in the tibiofibula, dental cement was poured around them, and a vertically oriented threaded socket was placed in the cement. The socket was used to couple the frog hindlimb to the robot during experiments (see below).

In one-half of the frogs (eight), we also performed a deafferentation. For this procedure, we exposed the seventh, eighth, and ninth dorsal roots by dorsal laminectomy, either at the level of the cauda equina or at the level of the dorsal root entry zones into the spinal cord. The dura was opened by bipolar electric cautery. In cases in which the cauda equina was exposed, spinal dorsal roots were identified by a lack of motor response observed after low-intensity electrical stimulation with silver hook electrodes placed around each nerve. In cases in which the dorsal root entry zone was exposed, dorsal roots were identified visually. After identifying the dorsal roots and bathing the exposed spinal cord in tricaine (5% solution), the dorsal roots were cut. We observed no motor response on cutting the roots, although animals were reflexive before bathing the exposed spinal cord in anesthetic, suggesting a lack of injury discharge after sectioning of dorsal roots. Gelfoam was placed on the exposed spinal cord, and the wound was closed in layers, as the muscles and then the skin were sutured together. Completeness of the deafferentation was confirmed the following day by the absence of all of the motor responses evoked from scratching sites on the deafferented hindlimb.

After these procedures, animals were refrigerated and allowed to recover overnight.

Experimental setup and data collection. The following day, the animals were placed on a stand and secured by a clamp placed around the pelvis. The hindlimb was attached to a Phantom 1.0 robot (SensAble Technologies, Woburn, MA) using the threaded socket cemented to the tibiofibula. Hindlimb movements were confined to the horizontal plane so that the coupled robot-frog system could be fully actuated by the motors of the robot. This was achieved by mechanically constraining the robot to move only in the horizontal plane and vertically adjusting the frog-robot attachment point such that the tibiofibula was parallel with this plane. This restriction also allowed the hindlimb configuration to be uniquely determined from the measured endpoint position. A schematic of the relative orientation of the robot and frog is shown in Figure 1 A. Although attaching the animal to the robot will clearly alter the dynamics of hindlimb movements by eliminating gravitational forces and adding a mass to the leg, for several reasons these alterations should not affect the issues examined here. First, the muscle activation patterns and kinematics observed here were very similar to those described in previous studies in freely moving animals (Fukson et al., 1980; Schotland and Rymer, 1993a; Kargo and Giszter, 2000b). We also observed a modulation of EMGs and hindlimb kinematics with initial limb position and with wiping limb deafferentation similar to that shown previously (Kargo and Giszter, 2000b), further suggesting that the attachment of the robot did not significantly alter basic characteristics of the observed motor behavior. Second, consideration of the dynamics of the robot suggests that the consequence of coupling the robot to the hindlimb was essentially to add a relatively small point mass to the ankle of the frog. In particular, the apparent endpoint mass of the Phantom robot was on the order of only 50 g (SensAble Technologies), although it varied with position. To better understand the inertial effects of the robot on the hindlimb, we calculated the position-dependent endpoint mobility tensor (inverse of the inertia tensor) for both the hindlimb, modeled as two rigid links, and the coupled hindlimb-robot system, modeled as four rigid links, using estimated mass parameters for both frog and robot [cf. Bhushan and Shadmehr (1999) for model equations used in this simulation]. The principal eigenvectors of the hindlimb and coupled hindlimb-robot endpoint mobility tensors differed by <10° for all of the positions except those at the very edge of the workspace. Thus, the acceleration-dependent forces of the coupled system were primarily in the same direction as those of the hindlimb alone. Velocity-dependent forces (i.e., centrifugal and Coriolis forces) will also be altered by coupling the robot to the frog hindlimb. However, these forces should be relatively small compared with the acceleration-dependent forces, particularly immediately after a phasic perturbation applied to the hindlimb, which was the critical event in our experimental protocol as described below, when the acceleration magnitude was much larger than the velocity magnitude. Finally, we also note that the primary motivation for these experiments was to examine the compensation of movements in response to phasic perturbations of the hindlimb, rather than to examine details of the nominal, unperturbed trajectories that might be altered by coupling the hindlimb to the robot.

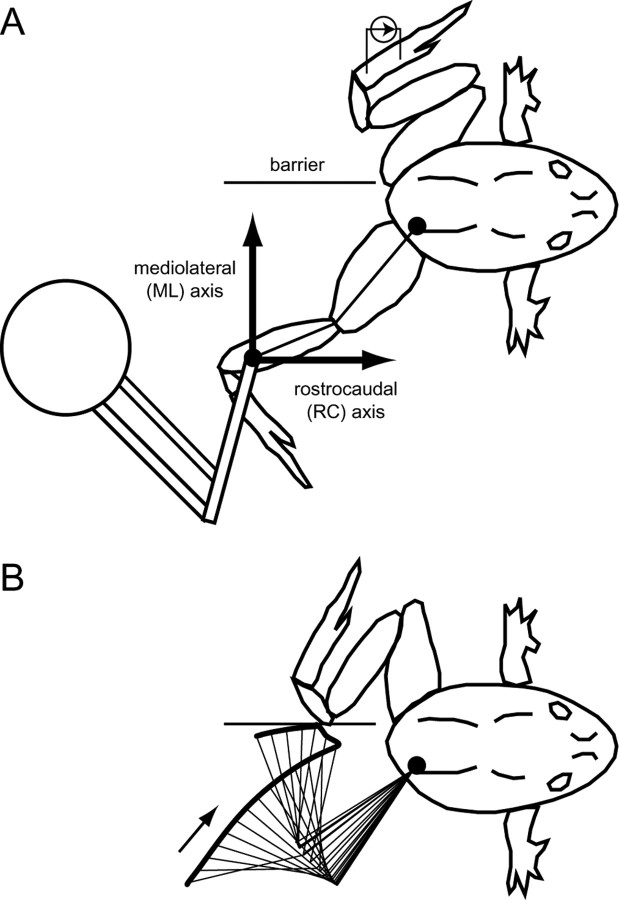
Figure 1.

Experimental setup. A, One frog hindlimb (the wiping limb) was attached to the endpoint of a robotic arm. The robot both measured the wiping hindlimb endpoint kinematics and applied force perturbations to the wiping limb. The endpoint kinematics were measured relative to the mediolateral (ML)-rostrocaudal (RC) coordinate system. To evoke the hindlimb wiping reflex, a cutaneous electrical stimulus was applied to the other hindlimb (the target limb). A barrier was placed near the animal's midline to prevent the target limb from affecting the measured wiping limb kinematics. Each trial began with the wiping limb in an extended, lateral configuration, as indicated. B, On stimulation of the target limb, both limbs moved toward the midline with the objective of wiping off the noxious stimulus. The trajectory of the recorded, wiping limb is shown for the same trial shown in Figure 2 B. The arrow indicates the direction of movement.

Hindlimb wiping behaviors were evoked by stimulation applied through a pair of electrodes placed on the skin of the foot contralateral to the limb attached to the robot. The cutaneous electrical stimulation evoked a movement of both the stimulated hindlimb and the hindlimb attached to the robot toward the midline (Kargo and Giszter, 2000a,b). To prevent the two hindlimbs from colliding and affecting the kinematics of the measured hindlimb, we placed a barrier near the animal's midline. This barrier guaranteed that, on repeated wipes, the trajectory of the measured hindlimb was not affected by the contralateral leg.

Activity on EMG electrode pairs was differentially amplified and filtered (1000 gain; 10-10,000 Hz passband; A-M Systems, Carlsborg, WA) and sampled at 1000 Hz using LabVIEW software (National Instruments, Austin, TX). The kinematics of the hindlimb attached to the robot were measured on a computer running custom software written in C++ using the Ghost class library (SensAble Technologies). Kinematic data were collected at 1000 Hz. The data acquisition systems on the computers collecting the kinematics and EMGs were synchronized by triggers sent between them. The synchronization between the computers was verified in separate experiments by an external clock signal sent to each computer. All of the data were saved for off-line analysis.

Experimental protocol. We examined the trajectories and EMG patterns produced in hindlimb wiping behaviors. The trajectory and EMG activity of only the unstimulated, “wiping” limb were measured. Both unperturbed behaviors and behaviors in which a phasic perturbation was applied were recorded for each frog.

For each trial, a behavior was evoked by electrical stimulation applied to the contralateral, “target” hindlimb. Electrical stimulation consisted of trains of biphasic stimulus pulses (train duration, 600-1700 ms; pulse frequency, 25-35 Hz; pulse duration, 1-2 ms; pulse amplitude, 1-1.8 mA). Regularly spaced intervals of 2-5 min (fixed for each animal) were allowed between repeated stimulation trains, so as to minimize habituation or potentiation of behaviors. Kinematic and EMG data were recorded for a period of 4 s after the onset of the electrical stimulation. Between trials, the robot moved the wiping hindlimb back to the same initial position. The initial wiping hindlimb position was chosen visually for each frog as an extended lateral position, as shown schematically in Figure 1 A. The initial position of the target hindlimb was not experimentally regulated; however, this limb consistently adopted a flexed, resting configuration between trials (Fig. 1 A).

In perturbed trials, the onset of the perturbation was triggered from the recorded EMG pattern. This EMG-based trigger was used rather than one based on a fixed time after stimulation onset to ensure that the perturbation was applied at a consistent time in the evoked motor behavior (for examples, see Fig. 4). Perturbations were applied early in the evoked motor pattern, usually within the first 100 ms of the EMG activity. The integrated EMG from the earliest activated muscle (ST, BF, or IP; determined for each frog individually) was measured on-line in 5 ms bins and accumulated until it crossed a threshold level. When this threshold was crossed, a perturbation was applied to the frog hindlimb. The threshold was chosen for each frog so that the perturbation was consistently triggered within the first 100 ms of observed EMG. Several observations suggest that the perturbation sensitivity of behaviors in the frog might be especially high during the early phases of movement production (Ottoson, 1976; Kargo and Giszter, 2000b), and therefore perturbations applied early should have the highest probability of evoking measurable compensations. Perturbations applied early during the movement also allow the limb trajectory enough time to recover from the perturbation before the end of the movement. Perturbations were applied in two different directions, defined with respect to the instantaneous velocity of the ankle. In most animals, clockwise (CW) perturbations were applied at an angle of +135°, whereas counterclockwise (CCW) perturbations were applied at an angle of -135°. In one animal, perturbations were applied at ±90°. CW perturbation trials, CCW perturbation trials, and unperturbed (U) trials make up the three groups of trials referred to in the data analysis. The perturbation command consisted of a square force pulse (amplitude, 0.35-1.50 N; duration, 25-75 ms). We confirmed that the specified peak amplitude and duration of the perturbation were actually applied by the robot in separate experiments using a force transducer attached to the robot. For each frog, care was taken to avoid applying perturbations that were so large as to drive the limb into the boundaries of the frog's workspace. Such cases could be observed by a clear and immediate return of the hindlimb toward the unperturbed trajectory after the perturbation, and any such trials were excluded from additional analysis.

Figure 4.

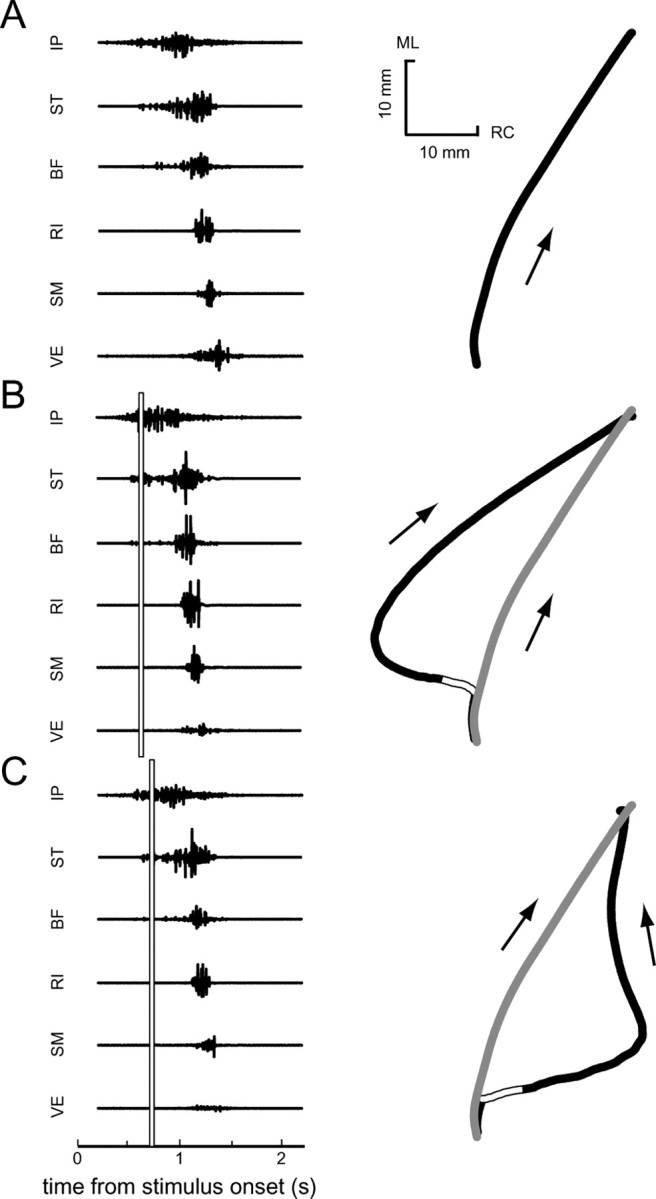
EMGs and initial-movement kinematics from an unperturbed trial (A), counterclockwise perturbed trial (B), and clockwise perturbed trial (C) from one frog are shown. The direction of movement is indicated by an arrow next to each path. The onset and duration of the perturbation are indicated by a white bar in B and C. The unperturbed path from A is shown as a gray line in B and C. ML, Mediolateral; RC, rostrocaudal.

Data analysis: kinematics. All of the analyses were performed using Matlab software (MathWorks, Natick, MA). The hindlimb wiping behaviors observed in this experiment were generally composed of several discrete movements, or phases, as found in previous studies of this behavior (Giszter et al., 1989; Schotland and Rymer, 1993a). For example, the wiping movement shown in Figure 1 B begins with a movement bringing the limb in the rostromedial direction, followed by phases that are directed mostly medial and then caudal. For the stability analysis described here, we were interested only in the initial movement. The initial movement was always directed to a particular hindlimb posture, followed by one or more ballistic movements for removal of the noxious stimulus (Fukson et al., 1980). Given that a particular final position may be regulated, it is reasonable to assume that stability is important for this initial phase of the behavior, as has been suggested in other experiments (Kargo and Giszter, 2000a). The end of this first portion of the behavior was determined for each trial by identifying the position at which the limb trajectory made a sharp change in direction corresponding to the end of the first peak in the velocity profile, as shown in Figure 2 (see Results) (Schotland and Rymer, 1993a). Note that the trial shown in Figure 2 B is the same trial used in Figure 1 B to provide perspective on the wiping limb trajectory relative to the frog's body. For the remainder of this paper, “final position” refers to the position of the recorded limb at the end of this initial, goal-directed movement.

Figure 2.

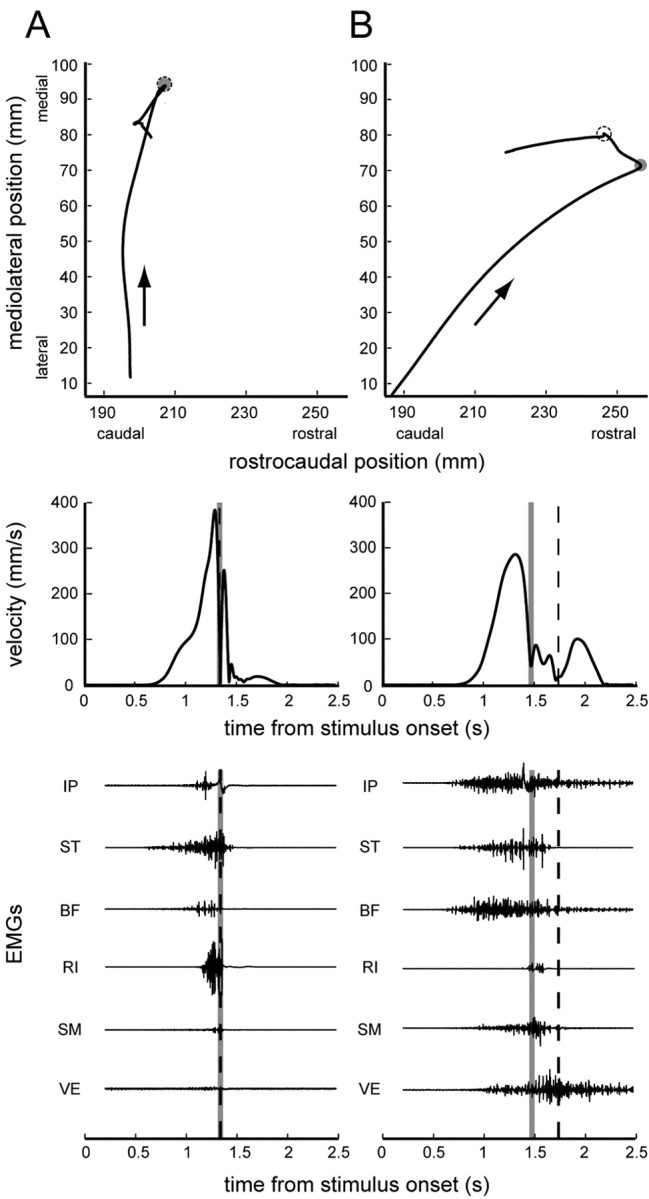
Examples of the nominal wiping reflex behavior from two frogs are shown. A, In the first frog, the initial movement, corresponding to the first velocity peak and moving in the direction of the arrow, is medial, because of fairly synchronous activity in both limb flexor muscles (IP, ST, BF) and hip extensor muscles (RI, SM). There is little activity of VE and correspondingly no final, caudally directed whisking movement. B, In the second frog, the initial movement is more rostral, because of staggered limb flexor and hip extensor muscle activity. Subsequently, there is a distinct whisking phase corresponding to the VE activity. The end of the initial movement is indicated by gray circles and lines. The midline contact point is indicated by dashed circles and lines.

The perturbed kinematics were analyzed to determine the mechanical stability of the hindlimb wiping behavior. For each perturbed trial, two displacements were computed, the initial displacement and the final displacement, both measured with respect to the mean unperturbed path. The mean unperturbed path was calculated by first spatially resampling the path of each unperturbed trajectory using spline interpolation, such that there was an equal distance between each point along the resampled path from initial to final position. The resampled paths were then averaged point by point to obtain the mean unperturbed path. The initial displacement attributable to the perturbation was defined as the maximum distance from the mean unperturbed path in a 100 ms window after perturbation offset, with the distance calculated along the direction perpendicular to the mean unperturbed path. This window after the perturbation included the time in which the hindlimb was still moving away from the unperturbed path after the initial acceleration caused by the perturbation, attributable to the inertial properties of the limb. The final displacement was defined as the distance between the final position of the perturbed trial and the final position of the mean unperturbed path. To evaluate the distributions of displacements for perturbed trials and to assess the degree of trial-to-trial variability in this behavior, we calculated similar values of initial and final displacements for unperturbed trials. For the distribution of unperturbed final displacements, we simply calculated the displacement between each individual unperturbed trial and the mean final unperturbed position. For the distribution of unperturbed initial displacements, we similarly calculated the distance between each trial and the mean unperturbed path, using the distance measured at the time at which the perturbation would have occurred based on the integrated EMG threshold crossing. To ensure that the perturbation affected the limb trajectory substantially, thereby allowing a good test of the stability properties of the limb, we included only those perturbation conditions for which the distribution of initial displacements after perturbations was significantly different from the distribution of initial displacements for unperturbed trajectories (as assessed by a Kruskal-Wallis ANOVA; p < 0.05). This criterion eliminated 3 of the 32 perturbation conditions recorded across animals.

Data analysis: EMGs. Magnitude, duration, and timing parameters were extracted from the recorded EMGs. First, the onset, peak, and offset times of muscle activity were determined for each muscle on each trial. These times were determined using an automatic detection routine, verified visually, and adjusted manually when necessary. The duration was defined as the time from onset to offset. The magnitude was defined as the area under the rectified and filtered EMG (acausal fifth-order low-pass Butterworth filter; 20 Hz nominal cutoff), between onset and offset. Many timing parameters were examined, with the most relevant for the wiping behavior being the latency between ST, BF, or IP onset and RI or SM peak activity (Kargo and Giszter, 2000b). For analysis of EMG alterations after the perturbation, mean EMGs were computed for each perturbation group (CW and CCW) of each frog after aligning the EMGs on perturbation onset. For the unperturbed group, trials were aligned on when the perturbation would have occurred, using the same EMG threshold criterion mentioned above. For a statistical analysis of EMG alterations after the perturbation, we looked at differences between perturbation conditions (U, CW, CCW) with respect to magnitude, duration, and timing of activity for each recorded muscle. Each test was performed using a nonparametric Kruskal-Wallis ANOVA.

Results

Nominal hindlimb wiping behaviors

The kinematics and motor patterns of nominal (i.e., unperturbed) wiping behaviors were analyzed for the 16 spinal frogs (8 afferented, 8 deafferented) examined in this study. Frog hindlimb-hindlimb wiping behaviors have been described thoroughly in previous studies (Giszter et al., 1989; Schotland and Rymer, 1993a), and we observed the same basic organization described in those studies. Representative trials from two different animals are shown in Figure 2. Hindlimb-hindlimb wiping consisted of a sequence of muscle activations, beginning with an initial activation of the predominantly flexor muscles ST, BF, and IP, followed by activation of the hip extensor muscles SM and RI, and concluding with activation of the knee extensor VE. In some cases, this last knee extension phase was deleted from the behavior entirely (see also Figs. 2A and 4) (Kargo and Giszter, 2000a).

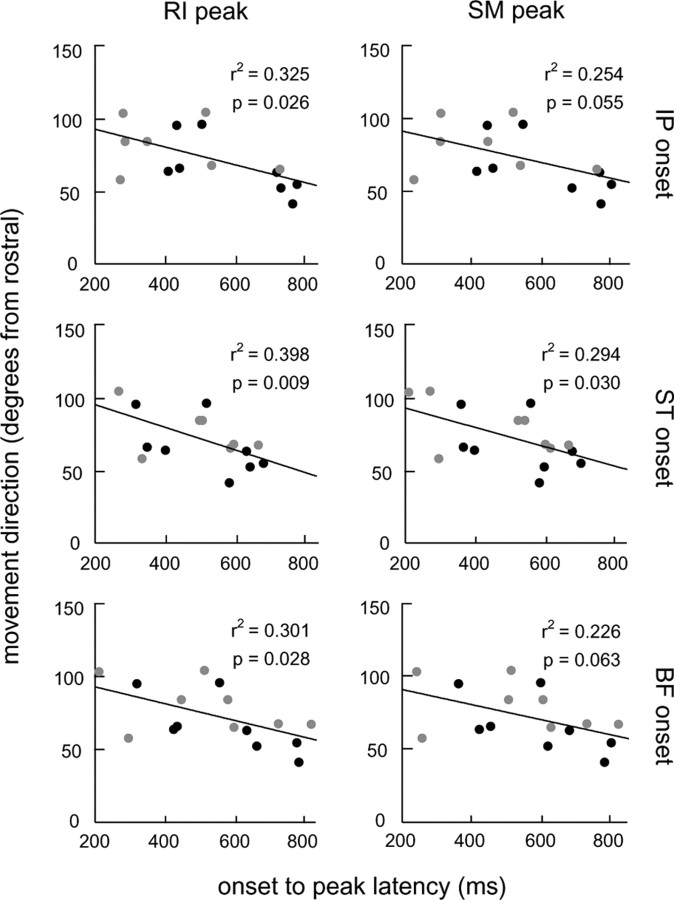
The delay between the activation of the initial phase of flexor muscles and the following phase of extensor muscles varied between different frogs, as noted previously by Kargo and Giszter (2000b). In the trial shown in Figure 2A, the two phases were nearly synchronous, separated by ∼100 ms. In the trial shown in Figure 2B, the two phases were much more staggered, separated by >600 ms. The difference in latency between these two phases resulted in a clear difference in hindlimb kinematics: in animals with short latencies, the path of the limb was directed more caudally than in animals with longer latencies. Figure 3 examines the relationship between EMG latency and movement direction (measured as the direction of the best fit line to the mean unperturbed path) for each of the six relevant comparisons between EMG timing parameters (i.e., onset of ST, BF, IP vs peak of SM, RI) (Kargo and Giszter, 2000b). In four of the six comparisons, this relationship was significant (p < 0.05), with a longer delay between flexor EMGs and extensor EMGs resulting in a more rostrally directed movement. The staggering of separate phases was also evident in the examination of the velocity traces of the hindlimb trajectories. As shown in Figure 2, in animals with substantial staggering between EMG phases, there was a clear second peak in the velocity profile of the limb before reaching the midline (B, midline contact indicated by the dashed line), whereas in animals with more synchronous phases only a single peak was evident before reaching the midline (A). In the analyses described in subsequent sections, we focused on the initial phase of these movements, which was defined to end at the first local minimum after the initial peak in the velocity profile (indicated by the gray circles and lines in Fig. 2). For more caudally directed movements, this final position corresponded to the midline contact point (Fig. 2A). For more rostrally directed movements, the final position was the end of the distinct flexion phase (Fig. 2B). Note that, in general, the endpoint velocity was not zero at this final position, because it was an intermediate point between phases of the behavior.

Figure 3.

Correlation of the average initial movement direction with the average latency between onset of limb flexion muscle activity (IP, ST, BF) and peak hip extension muscle activity (RI, SM). For each plot, the latency refers to the time between onset of the limb flexor muscle indicated to the right of the row and peak of the hip extensor muscle indicated at the top of the column. The linear least-squares fit to the data is indicated on each plot along with the r² statistic and p value for the regression. Data from afferent-intact frogs are indicated by black circles, whereas those of frogs with a deafferented wiping limb are indicated by gray circles.

Of the 16 frogs examined in this analysis, as well as in the perturbation analysis below, no single animal was assessed in both afferented and deafferented conditions. However, unperturbed trajectories were examined before and after deafferentation in two additional animals. In these animals, we observed that the nominal trajectories of the wiping limb after deafferentation were more caudally directed than those before deafferentation (mean of 100.5 and 66.5° from rostral, respectively; p < 0.05). These more caudally directed movements were accompanied by a reduced latency between flexor muscle and hip extensor muscle activations in 6 of 12 tests (p < 0.05). Such changes in the kinematics and motor patterns of nominal wiping behaviors after deafferentation are similar to those described previously (Kargo and Giszter, 2000b).

Hindlimb wiping behaviors compensate for phasic perturbations

We examined the effects of phasic perturbations on the limb trajectories observed during hindlimb-hindlimb wiping behaviors. In particular, we examined whether hindlimb movements compensated for these phasic perturbations by returning the limb to the path of the nominal movements described in the previous section. Figure 4 shows examples of kinematics and EMGs observed during three trials in one frog. As can be seen in Figure 4A, the unperturbed trajectory in this animal was directed toward a position located rostral and medial in the hindlimb workspace. Figure 4, B and C, shows example trials from this same animal in which perturbations were applied in either a counterclockwise (B) or clockwise (C) direction with respect to the hindlimb trajectory. The onset and duration of the perturbation are indicated in the EMG traces by the vertical bar and in the hindlimb kinematics by the white segment of the path. Although the perturbations caused large deviations from the unperturbed path in this animal, in both cases the hindlimb returned to the same region of the workspace as the unperturbed final position. Figure 5A shows data from all of the trials, both unperturbed and perturbed, which were collected from this frog. For both clockwise and counterclockwise perturbation trials, the hindlimb generally returned to a similar final position as in the unperturbed trials. Hindlimb movements observed in a different animal, one in which the initial deviations attributable to the perturbation were smaller and more representative of our data set, are shown in Figure 5B. As seen in the previous frog, the hindlimb movements exhibit compensation for the phasic perturbations. In particular, in both frogs the initial deviation from the unperturbed trajectory was compensated for by the end of the trajectory.

Figure 5.

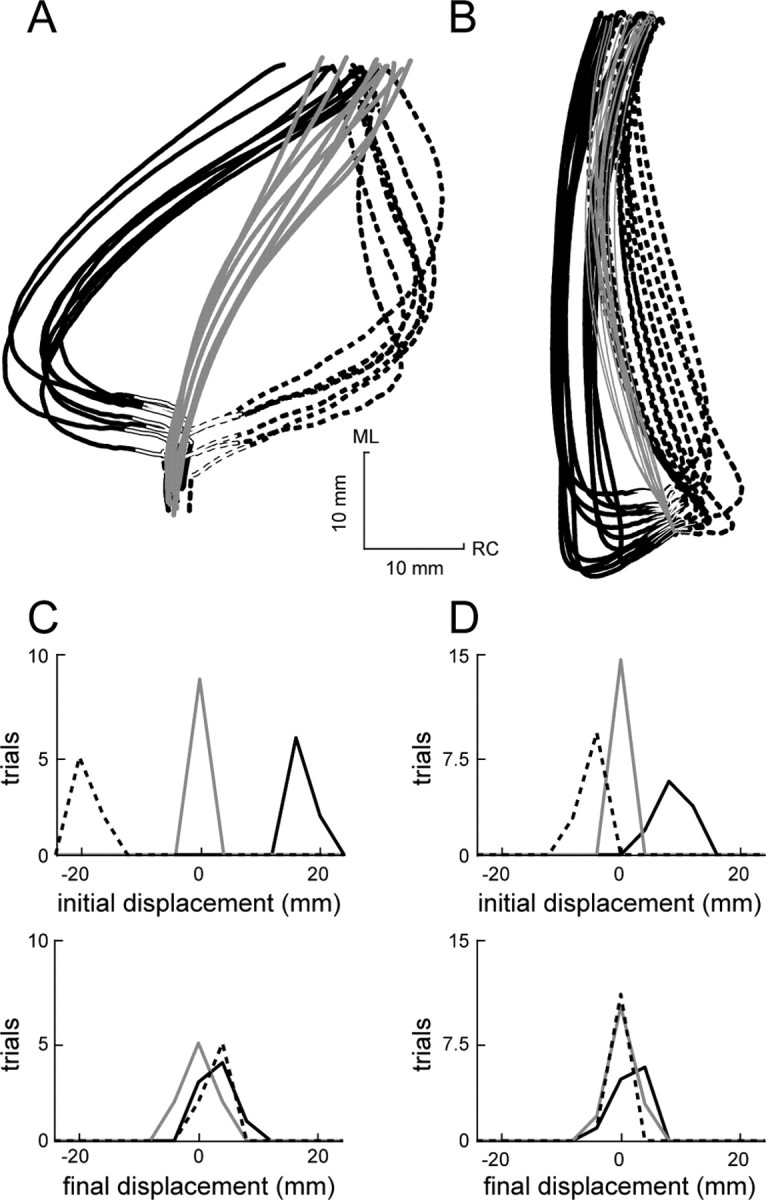
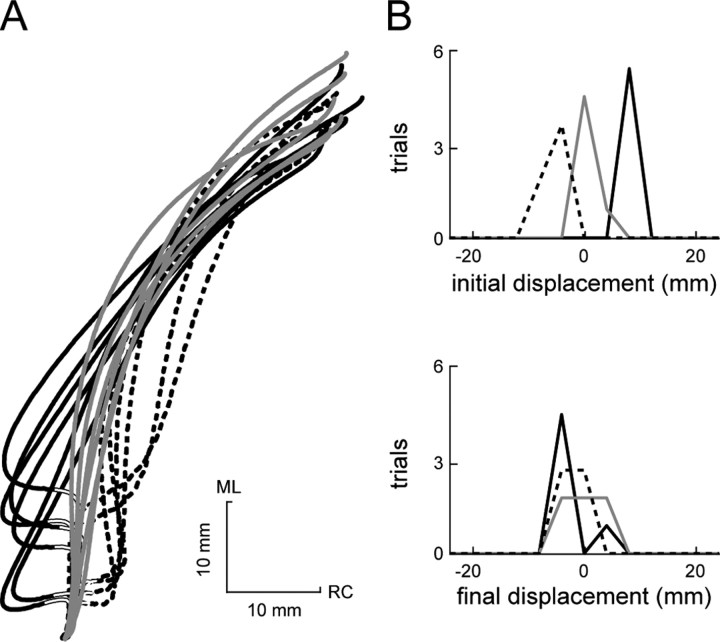
Stability summary for two afferent-intact frogs. All of the trials from a frog exposed to particularly large perturbations (A) and a frog exposed to more moderate perturbations (B) are shown. Counterclockwise perturbation paths are indicated by solid black lines, unperturbed paths are indicated by solid gray lines, and clockwise perturbation paths are indicated by dashed black lines. The portion of the path during which the force perturbation was applied is indicated by an overlaid white line. The distributions of initial and final displacements from the unperturbed mean path are shown in C and D, corresponding to the data in A and B, respectively. ML, Mediolateral; RC, rostrocaudal.

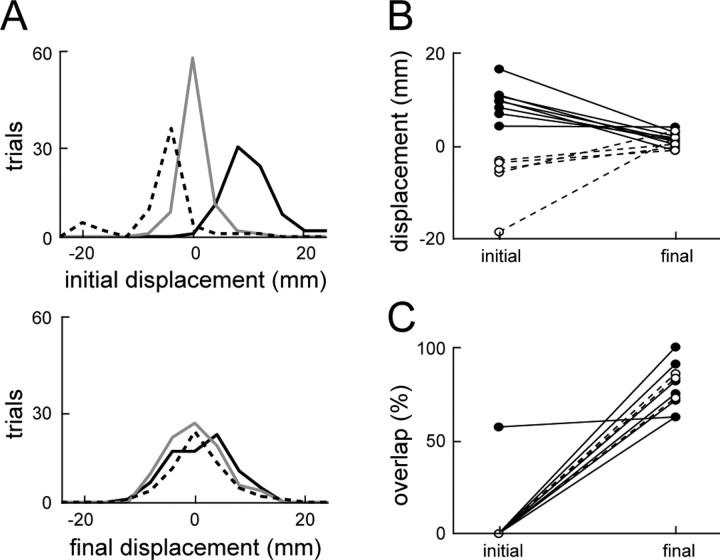
The compensatory behavior seen in Figure 5, A and B, is summarized in Figure 5, C and D, respectively. For the panels of this figure, we measured the displacement between individual trials and the mean of the unperturbed trials. This displacement was measured both for perturbed trials (CCW and CW), to examine the effects of the perturbation, and for unperturbed trials, to examine the trial-to-trial variability in the nominal behavior. Displacements were measured both at the final position of the trajectory (final displacements) and at the time of initial maximal deviation from the mean unperturbed trajectory caused by the perturbation (initial displacements). In Figure 5, C and D, the distributions of both initial (top) and final (bottom) displacements for the two animals are shown. As indicated by the initial displacement distributions, perturbations in both animals caused a substantial deviation of the trajectories away from the unperturbed trajectory. In the first animal (Fig. 5A, C), this deviation was 16.7 ± 2.0 and -18.5 ± 1.4 mm (mean ± SD) for counterclockwise and clockwise perturbation trials, respectively (displacements on the clockwise side of the unperturbed mean path were arbitrarily defined as negative). In the second animal (Fig. 5B, D), the initial displacements were 8.3 ± 2.1 mm (mean ± SD) for counterclockwise perturbations and -4.9 ± 1.9 mm (mean ± SD) for clockwise perturbations. The final displacement distributions shown in Figure 5, C and D, illustrate that, at the end of the trajectory, these initial displacements were mostly compensated for. In neither case was the difference between the mean of the U, CCW, and CW distributions for final displacement significant (p > 0.05). In fact, in no frog examined with afferents intact was there a significant difference in the final displacement distribution means (p > 0.05), although in each animal the perturbations were large enough to produce a significant difference between trajectories at the time of perturbation (p < 0.05). These effects are summarized for the entire set of eight animals studied with afferents intact in Figure 6A. In these plots, the distributions of initial (top) and final (bottom) displacements are compiled from all of the trials across all of the afferent-intact animals. As was observed in the individual animals shown in Figure 5, although the initial displacements caused by the perturbations were significantly different from one another (p < 0.001), these differences were no longer significant at the end of the trajectory (p > 0.05), even with the large number of trials used in this population analysis.

Figure 6.

Stability summary for all of the afferent-intact frogs. A, The summed initial (top) and final (bottom) displacement distributions of all eight afferent-intact frogs. The solid black line, solid gray line, and dashed black line indicate the displacement distribution for counterclockwise perturbation trials, unperturbed trials, and clockwise perturbation trials, respectively. B, The mean initial and final displacements for each afferent-intact frog. C, The percentage overlap of the middle 95% of the perturbed and unperturbed final displacement distributions for each afferent-intact frog. In B and C, mean displacements and percentage overlaps, respectively, are shown for counter clockwise perturbations (solid lines and black circles) and clockwise perturbations (dashed lines and white circles).

The amount of compensation observed in each individual frog is summarized in Figure 6B, in which for each frog the mean initial and final displacements for clockwise and counterclockwise perturbations are shown. It can be seen that, for each frog, the initial displacement attributable to either counterclockwise or clockwise perturbations was substantially reduced by the end of the movement, although there were different degrees of compensation observed in different animals. Furthermore, by the end of the trajectory, there was no significant difference between the mean final displacements of the CW and CCW perturbation groups when grouped across individual animals (mean ± SD, 0.93 ± 1.70 vs 1.63 ± 1.55 mm; p > 0.05). This result, taken with the results shown in Figure 6A, demonstrates that strong compensations to the perturbations were consistently observed in all of the afferent-intact animals.

However, additional analysis suggested that there remained a residual effect of the perturbations. In Figure 6C, we examined the amount of overlap between the middle 95% of perturbed and unperturbed final displacement distributions. If perturbations were entirely compensated for, one would expect that the perturbed and unperturbed final displacement distributions should overlap entirely. As seen in Figure 6C, the overlap between unperturbed and perturbed final displacement distributions was consistently high for all of the frogs, especially compared with the initial displacement distribution overlap, which was at or near zero in all but one case. That case of a high initial overlap in Figure 6C corresponds to the smallest mean counterclockwise initial displacement in Figure 6B, indicating that in this case the initial perturbation, although statistically significant, was not large enough to cause a substantial difference in the hindlimb trajectories. Although Figure 6C shows that there was a high degree of overlap between final displacements for perturbed and unperturbed trials, the overlap was not complete. The mean overlap of the CCW and CW final displacement distributions with the unperturbed distributions were 80.5 and 88.4%, respectively, compared with the 97.8% expected if the perturbed distributions were indistinguishable from the unperturbed distributions (bootstrap analysis on samples taken with replacement from the pooled unperturbed final displacements for all eight afferent-intact frogs). Together, the results of this section indicate that, in spinal frogs with hindlimb afferents intact, there was a high degree of compensation for the effects of phasic perturbations during wiping behaviors, although this compensation was not entirely complete.

Stability of wiping behaviors is primarily attributable to intrinsic musculoskeletal properties

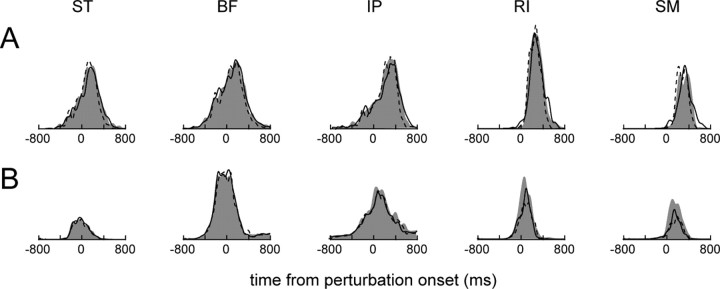
Next, we were interested in the relative contribution of intrinsic musculoskeletal viscoelasticity and afferent feedback to the mechanical stability observed in the hindlimb wiping behaviors. Using data from the eight afferent-intact frogs, we tested whether there was any significant modulation of the EMGs after the perturbation, which would indicate involvement of afferent feedback in the compensatory response. Figure 7 shows the mean rectified and filtered EMGs for two afferent-intact frogs recorded during perturbed CW and CCW trials, and for unperturbed trials, aligned to the perturbation onset. Generally, between the three perturbation conditions, the differences in magnitude, duration, and timing of the EMGs were quite small. In Figure 7A, only differences in SM duration were significant (p < 0.05). For the data shown in Figure 7B, no significant differences were found. Of the 16 EMG parameters tested (5 magnitude, 5 duration, and 6 timing parameters) for each of the eight afferent-intact frogs, only 5 of the 128 tests reached significance at the α = 0.05 level, which is no more than expected by chance. These observations suggest that the phasic perturbations in these experiments resulted in minimal alterations in muscle activation attributable to reflex pathways and, furthermore, suggest that most of the compensation described in the previous section was accomplished by intrinsic musculoskeletal properties.

Figure 7.

The rectified, filtered, and averaged EMGs for two afferent-intact frogs (A and B) are shown. The average unperturbed trial EMGs are the filled gray regions, whereas the average counterclockwise perturbed trial EMGs and clockwise perturbed trial EMGs are indicated by dashed and solid black lines, respectively. Averages were computed after aligning trials on the perturbation onset.

To further assess the stability brought about by intrinsic properties of the musculoskeletal system, the wiping hindlimb of eight spinal frogs was deafferented and exposed to the same force perturbations as that of the afferent-intact frogs. All of the perturbed and unperturbed hindlimb paths from one such deafferented frog are shown in Figure 8A. As with the afferent-intact animals, the perturbed hindlimb paths for this frog generally converged back to the unperturbed paths. The corresponding initial and final displacement distributions for this frog are shown in Figure 8B. The initial displacements in response to counterclockwise and clockwise perturbations were 7.8 ± 0.9 and -5.5 ± 1.2 (mean ± SD), respectively. Although the initial displacement means differed significantly (p < 0.001), at the final position the mean displacements for the three conditions (U, CW, CCW) were statistically indistinguishable (p > 0.05). In five of the eight deafferented frogs, there was no significant difference between the distributions of final displacement, similar to the results observed in animals with afferents intact, suggesting that a large component of the compensation to perturbations was accomplished by intrinsic muscle properties. However, in the remaining three deafferented animals, there was a significant difference between the distributions of final displacement (p < 0.05). Although these results indicate that the amount of compensation after perturbations was reduced after deafferentation, it should be noted that post hoc analyses (pairwise Kruskal-Wallis ANOVAs between the CCW, CW, and U final displacement distributions with Bonferroni adjustment for overall α = 0.05) revealed that, in two of these three animals, the clockwise perturbations were actually overcompensated such that mean final displacements of the CW and U groups were significantly different but that of the CW and CCW groups were not. Furthermore, compensation after phasic perturbations was observed in deafferented animals when trials from all of the frogs were considered to be a population. The initial and final displacement distributions for all of the trials from deafferented animals combined is shown in Figure 9A. As was observed for the individual animal in Figure 8, the CCW, CW, and U mean final displacements did not significantly differ for the population (p > 0.05).

Figure 8.

Stability summary for one deafferented frog. The initial paths for all of the trials are shown (A) along with the corresponding distributions of initial and final displacements from the unperturbed mean path (B). Counterclockwise perturbation trials are indicated by solid black lines, unperturbed trials are indicated by solid gray lines, and clockwise perturbation trials are indicated by dashed black lines. In A, the portion of the path during which the force perturbation was applied is indicated by an overlaid white line. ML, Mediolateral; RC, rostrocaudal.

Figure 9.

Stability summary for all of the deafferented frogs. A, The summed initial (top) and final (bottom) displacement distributions of all eight deafferented frogs. The solid black line, solid gray line, and dashed black line indicate the displacement distribution for counterclockwise perturbation trials, unperturbed trials, and clockwise perturbation trials, respectively. B, The mean initial and final displacements for each deafferented frog. C, The percentage overlap of the middle 95% of the perturbed and unperturbed final displacement distributions for each deafferented frog. In B and C, mean displacements and percentage overlaps, respectively, are shown for counterclockwise perturbations (solid lines and black circles) and clockwise perturbations (dashed lines and white circles).

Figure 9B shows the mean initial and final displacements for the CW and CCW perturbation groups in each individual deafferented animal. As can be seen in the figure, each animal showed substantial compensation, and, as observed for animals with afferents intact, there was no significant difference between the distributions of final displacement for CW and CCW perturbations when grouped across individual animals (mean ± SD, 1.45 ± 3.91 vs 0.98 ± 2.43 mm; p > 0.05). Figure 9C shows the amount of overlap between the central 95% of the distributions of final displacements for perturbed and unperturbed trials. The mean percentage overlap of the CW and CCW final displacement distributions with the unperturbed final displacement distributions were 59.6 and 71.7%, respectively. Although this represents a fairly large recovery from the perturbations, considering the initial overlap was near zero, both values are well below the 98.3% expected if the perturbed distributions were indistinguishable from the unperturbed distributions (bootstrap analysis on samples taken with replacement from the pooled unperturbed final displacements for all eight deafferented frogs). Thus, as was observed in animals with afferents intact, examination of the overlap between distributions at the end of the trajectory suggests the perturbations were not fully compensated for by the end of the trajectory.

Finally, we directly compared the amount of compensation observed in animals with afferents intact and deafferented animals. First, we compared the mean final displacements grouped across individual afferent-intact (Fig. 6B) and deafferented (Fig. 9B) animals. A two-way ANOVA (factors, afferented vs deafferented and CCW vs CW perturbation group) found no significance in the main effects or interaction indicating a comparable degree of compensation for each frog regardless of whether afferents were intact or not. Second, we compared the percentage overlap of the perturbed and unperturbed final displacement distributions in the afferented (Fig. 6C) and deafferented (Fig. 9C) conditions. Grouping the mean CW and CCW overlaps together, the percentage overlap in the deafferented condition was significantly less than in the afferent-intact condition (mean ± SD, 65.7 ± 20.4 vs 83.5 ± 14.0%; p < 0.05). This reduced overlap between final displacement distributions suggests that the lack of afferent feedback prevented these frogs from achieving the level of compensation seen in the afferent-intact frogs.

However, as noted previously, several deafferented frogs overcompensated for the perturbations. Such cases of overcompensation, although demonstrating a discrepancy between perturbed and unperturbed conditions, do not suggest that the limb had insufficient viscoelasticity to compensate for perturbations. On the contrary, such cases suggest that the viscoelasticity of the limb is in fact high, and cases of overcompensation could still be considered to be evidence for significant viscoelastic properties of the limb. We therefore performed a modification of the overlap analysis described above to take this issue into account. In this analysis, we examined only the fraction of undercompensated trials (i.e., for CW and CCW perturbations, those trials which remained perturbed in a CW and CCW direction, respectively, from the mean unperturbed path). This fraction was calculated for both deafferented animals and for afferented animals. Note that there were also cases of overcompensation, although not significant, in the afferented animals, as can be seen by inspection of Figure 6B. With this analysis, we found that the fraction of overlap between afferented and deafferented animals was not significantly different (mean ± SD, 84.6 ± 17.7 vs 88.9 ± 12.9%; p > 0.05). Note that for both afferented and deafferented conditions, these percentages reflect a less-than-perfect compensation, because they were both less than the percentages (98.8 and 99.2%) expected if the perturbed distributions were identical with the unperturbed trials. Nonetheless, the lack of difference in the overlap between distributions suggests that perturbation trials in afferented animals were not compensated for to a greater extent than in deafferented animals. The results of this modified analysis, although clearly ad hoc, are consistent with the previous results of this section, suggesting that a large portion of the compensation observed in afferented animals is mediated by intrinsic properties of the limb.

Stability is robust to changes in nominal behavior and perturbation parameters

In the results above, we addressed the compensatory response of the hindlimb wiping behavior to phasic perturbations, demonstrating that spinalized frogs are capable of mostly compensating for such perturbations and that a substantial portion of this compensation is produced by intrinsic properties of the limb. To conclude our analysis, we examined whether the previous results on the stability of the hindlimb wiping behavior changed as the nominal behavior or perturbation parameters varied. This analysis was motivated by the notion that, for mechanical stability to be a useful property of motor behaviors, it should be robust to variations in the desired trajectory or particular characteristics of the perturbations.

To assess this issue of robustness, we first examined whether the degree of compensation observed after a perturbation depended on characteristics of the nominal behavior. As described above, the mean nominal path taken by the wiping limb varied substantially between frogs, from 41 to 104° from rostral, depending on the synchrony between the activation of flexor muscles and hip extensor muscles (Fig. 3). We found that across frogs (both afferented and deafferented) the mean final displacement was not correlated with the mean unperturbed movement direction. Thus, changes in the nominal behavior did not affect the degree of compensation achieved in response to the perturbation. Second, we examined whether the compensation to perturbations depended on the parameters of the perturbations. Across frogs, the perturbations applied to the wiping limb varied from 0.35 to 1.50 N in amplitude and 25 to 75 ms in duration. This resulted in a wide range of initial displacements of the hindlimb, from 1.1 to 26.7 mm (absolute value). However, across frogs (both afferented and deafferented), there was no correlation between the mean initial displacement and the mean final displacement. Thus, the compensation to perturbations was robust across a range of force amplitudes and durations, producing a larger compensation in response to larger perturbations. Although these variations in desired trajectory and perturbation parameters by no means cover the entire range of possible variations in either behaviors or perturbations, the results of this section suggest a clear robustness in the stability properties of the frog hindlimb.

Discussion

This paper has presented a stability analysis of wiping movements in the spinal frog. We demonstrate that external perturbations applied to the hindlimb during the wiping behavior evoke a robust compensatory response. This compensation was primarily attributable to intrinsic musculoskeletal properties, because similar levels of compensation were observed after hindlimb deafferentation and no large changes in EMGs were observed after the perturbation.

Hindlimb-hindlimb wiping in the spinal frog

Hindlimb-hindlimb wiping in spinal frogs has been examined by several studies, characterizing basic features of these movements and their neural control (Berkinblit et al., 1986; Giszter et al., 1989; Ostry et al., 1991; Schotland and Rymer, 1993a,b; Kargo and Giszter, 2000a,b). Of relevance here, it has been suggested that the initial phase of this behavior has a high degree of positional control. In hindlimb wiping, as well as back and forelimb wiping, the wiping limb reaches a particular intermediate position before performing the final whisking movement (Fukson et al., 1980). This intermediate position effectively divides the wiping behavior into two stages: an initial stage, dependent on the initial position of the wiping limb, and a final stage, independent of initial conditions. Mechanical stability might therefore be expected to be a relevant property of the initial stage. The robust compensation to phasic perturbations described here demonstrates that such stability is in fact an important feature of the initial phase of wiping.

Although not the focus here, we also observed that between frogs the direction of the first phase of movement varied with the latency between activation of hindlimb flexor muscles and subsequent hip extensor activations. This extends a similar result described by Kargo and Giszter (2000b) after deafferentation, suggesting that the kinematic variability of hindlimb wipes, both between individual afferent-intact animals and between intact and deafferented animals, is primarily characterized by temporal shifts between activations of limb flexor and extensor muscle groups.

Stability of hindlimb wiping movements

Across all of the frogs used in this study, we observed an appropriate compensatory response to relatively large phasic perturbations. Several previous studies have perturbed wiping reflexes of the spinal frog to explore the underlying control strategy. Schotland and Rymer (1993b) found that attaching a weight to the wiping limb did not alter the final position of the initial hindlimb wiping movement, defined in a manner similar to our study. Similar robustness to tonic disturbances was seen in forelimb wiping reflexes by Fukson et al. (1980) showing that wipes were insensitive to increased gravitational work. Our results using large phasic, rather than tonic, perturbations are consistent with these previous observations.

A related set of experiments demonstrated the static stability of movements produced by spinalized frogs (Bizzi et al., 1991; Giszter et al., 1993). By measuring isometric forces evoked throughout the workspace, these experiments demonstrated that motor responses such as those from wiping and withdrawal or from intraspinal microstimulation were characterized by convergent force fields, such that the limb was driven toward a common position, regardless of its initial position. Although these results suggested significant static stability of the hindlimb, it was not clear whether these responses were also dynamically stable when the limb was allowed to move. By examining these same behaviors during movement, the present experiments suggest that these responses also possess strong dynamic stability properties.

Previous work has suggested that hindlimb-hindlimb wiping can be described as the combination of a small number of basic units of motor output, or “motor primitives” (Kargo and Giszter, 2000a), based on hypotheses from microstimulation experiments (Bizzi et al., 1991; Giszter et al., 1993). Theoretical work (Slotine and Lohmiller, 2001) has suggested that, if such motor primitives possessed a particular form of dynamic stability, then their combination would also possess this same stability. Such a scheme would potentially simplify movement production, first by reducing the degrees of freedom that need to be specified, and furthermore by ensuring that the resulting movement had at least a minimum of stability. The finding here that hindlimb-hindlimb wiping, thought to result from combinations of motor primitives, has dynamic stability properties is consistent with this theoretic work. However, the exact relationship between the stability demonstrated here and that characterized theoretically remains unclear, as does the question of whether or not individual primitives, rather than their supposed combinations, also possess dynamic stability properties.

Mechanisms stabilizing hindlimb wiping movements

In addition to demonstrating the robust stability of hindlimb wiping behaviors, we exploited the experimental advantages of our preparation to determine the mechanisms responsible for this stability. We found that the compensatory response was not significantly degraded after deafferentation nor was there significant modulation of EMGs after perturbations in afferent-intact animals. These observations suggest that intrinsic viscoelasticity confers significant dynamic stability to hindlimb wiping movements, independent of modulation of motor patterns through afferent feedback. Our results on the intrinsic stabilization of wiping movements are consistent with previous work in the spinal frog demonstrating significant static stability of motor behaviors evoked from intraspinal stimulation after transection of the dorsal roots (Loeb et al., 1993). In addition, several similar examples of the stabilization of motor behaviors through intrinsic musculoskeletal properties have been documented, including forearm movements in deafferented monkeys (Polit and Bizzi, 1979) and locomotion in cockroaches (Jindrich and Full, 2002). It should be noted that compensatory control strategies using feedback from remaining dorsal roots, as has been suggested (Lackner and DiZio, 1994), are unlikely in the acutely spinalized frogs used here, and such alterations were not observed in recorded EMGs. Together, these experiments suggest that intrinsic musculoskeletal properties can make significant contributions to the stabilization of movement.

In several recent studies, however, total viscoelasticity of arm movements in humans has been estimated to be quite low (Gomi and Kawato, 1996, 1997; Popescu and Rymer, 2000; Mah, 2001; Hinder and Milner, 2003; Popescu et al., 2003). These studies suggest that human arm movements do not possess stability properties similar to those demonstrated here. There are several potential reasons for this discrepancy including differences in the mechanical properties of the limbs studied, possibly attributable to differences in the operating range of the muscles used in each task, or basic differences in the control strategies being used in each behavioral situation. It is also important to note that, although our results demonstrate strong stability properties of hindlimb-hindlimb wiping in the frog, it is also apparent that this stability was imperfect. For example, although there were not significant differences in the mean final displacements of unperturbed and perturbed trials, there was an incomplete overlap between the unperturbed and perturbed final displacement distributions, suggesting incomplete compensation. This observation might suggest basic limitations in the degree of stability that intrinsic properties are capable of conferring in this experimental system. To obtain the more precise accuracy characteristic of many human behaviors, such as those studied by others (Popescu and Rymer, 2000; Hinder and Milner, 2003; Popescu et al., 2003), it might therefore be necessary to rely more on afferent feedback for the regulation of stability.

Although our results demonstrate the strong contribution of intrinsic properties to the stability of hindlimb-hindlimb wiping in the frog, it is clear that afferent feedback can also play an important role in limb stabilization (Soechting and Lacquaniti, 1988). Our conclusion regarding the absence of postperturbation EMG modulation is based on accepting the null hypothesis, and therefore an effect of afferents cannot be entirely excluded. It also remains possible that different perturbations or behaviors would result in a greater afferent response. An additional consideration is whether afferent feedback should be expected to compensate for the external perturbations here, considering that the functional role of proprioceptive reflexes in the multijoint limb may not simply be to regulate length or stiffness as in stretch reflexes of isolated muscles (Stein, 1982; Lacquaniti and Soechting, 1984). An alternative role for afferent feedback in stabilizing hindlimb wiping may be to compensate for internal disturbances arising from interaction torques, as demonstrated in spinal cats (Smith and Zernicke, 1987) and deafferented humans (Sainburg et al., 1995). In support of this hypothesis, Kargo and Giszter (2000b) found that deafferented frogs performing hindlimb wipes had increased hip velocity, knee velocity reversals, and increased endpoint path curvature compared with afferent-intact frogs, all of which suggest the knee experienced increased interaction torques after deafferentation. Such a role of afferents in controlling interaction torques would predict large changes in nominal trajectories after deafferentation, as described by Kargo and Giszter (2000b), but lesser changes in the compensation of movements to phasic perturbations, as described here.

In summary, the main contribution of the present study is to show, in a behaviorally relevant context, that intrinsic musculoskeletal properties can make a significant contribution to movement stability. These results have several potential implications for the control of movement. For instance, at a basic level, such intrinsically mediated stability might provide immediate compensation to unexpected perturbations, thereby simplifying the neural computations underlying the stable control of movement (Brown and Loeb, 2000). These results are also related to the equilibrium point hypothesis of motor control (Feldman, 1986; Bizzi et al., 1992), particularly in regard to the contribution of muscle properties to the specification of stable limb equilibria. The spinal motor systems of the frog might therefore exploit limb stability properties by adopting an equilibrium point control strategy (McIntyre and Bizzi, 1993), although this hypothesis was not directly evaluated here. Regardless of whether such control strategies are used, the present results reemphasize the significant contributions that intrinsic viscoelastic properties of the limb can make to the production of movement. How these properties are exploited by the nervous system will likely be specific to the particular behavior and particular skeletomotor system being studied.