Developmental Changes in Parvalbumin Regulate Presynaptic Ca²⁺ Signaling

Abstract

Certain interneurons contain large concentrations of specific Ca²⁺-binding proteins (CBPs), but consequences on presynaptic Ca²⁺ signaling are poorly understood. Here we show that expression of the slow CBP parvalbumin (PV) in cerebellar interneurons is cell specific and developmentally regulated, leading to characteristic changes in presynaptic Ca²⁺ dynamics (Ca_i). Using whole-cell recording and fluorescence imaging, we studied action potential-evoked Ca_i transients in axons of GABA-releasing interneurons from mouse cerebellum. At early developmental stages [postnatal days 10-12 (P10-P12)], decay kinetics were significantly faster for basket cells than for stellate cells, whereas at P19-P21 both interneurons displayed fast decay kinetics. Biochemical and immunocytochemical analysis showed parallel changes in the expression levels and cellular distribution of PV. By comparing wild-type and PV(-/-) mice, PV was shown to accelerate the initial decay of action potential-evoked Ca_i signals in single varicosities and to introduce an additional slow phase that summates during bursts of action potentials. The fast initial Ca_i decay accounts for a previous report that PV elimination favors synaptic facilitation. The slow decay component is responsible for a pronounced, PV-dependent, delayed transmitter release that we describe here at interneuron-interneuron synapses after presynaptic bursts of action potentials. Numerical simulations account for the effect of PV on Ca_i kinetics, allow estimates for the axonal PV concentration (∼150 μm), and predict the time course of volume-averaged Ca_i in the absence of exogenous buffer. Overall, PV arises as a major contributor to presynaptic Ca_i signals and synaptic integration in the cerebellar cortex.

Introduction

In small mammalian synaptic terminals, Ca²⁺ concentration gradients subside on a time scale of the order of 1 msec, after which the Ca²⁺ concentration may be considered homogeneous (for review, see Meinrenken et al., 2003), as predicted from previous work on squid axon (Simon and Llinás, 1985; Llinás et al., 1992). Therefore, volume-averaged Ca²⁺ measurements on single terminals give valuable recordings of the Ca²⁺ concentration intervening ≥1 msec after action potential (AP)-induced Ca²⁺ entry. This signal was called “[Ca²⁺]_volumeavg” by Meinrenken et al. (2003) and is designated as Ca_i hereafter for simplicity. It has attracted comparatively little attention, probably because it is not directly related to phasic neurotransmitter release. However, it carries much physiological significance. The elevated Ca_i that follows one or several APs contributes to setting the duration of the after spike hyperpolarization and hence the maximum firing frequency of the presynaptic terminal (for review, see Rudy et al., 1999). It is responsible for delayed transmitter release and facilitation (Goda and Stevens, 1994; Atluri and Regehr, 1998; Felmy et al., 2003; for review, see Van der Kloot and Molgo, 1993; Zucker and Regehr, 2002), and it may influence the kinetics of vesicle recycling (Smith et al., 1998; Burrone et al., 2002).

Measurements of Ca_i are affected by the presence of the Ca²⁺ probe, which acts as a buffer, as well as by the concentration and binding properties of endogenous buffers (for review, see Neher, 1998). Certain neurons are known to possess large concentrations of specific Ca²⁺-binding proteins (CBPs) such as calbindin D-28k (CB), calretinin (CR), or parvalbumin (PV), but the consequences of having one rather than the other on presynaptic Ca_i dynamics are unknown. The effects of CBPs on synaptic transmission are just starting to be considered (Edmonds et al., 2000; Blatow et al., 2003; for review, see Schwaller et al., 2002).

PV is a particularly interesting case. Because the two EF-hand domains of PV have a high affinity for Mg²⁺, it has a slow apparent binding rate with Ca²⁺ (Lee et al., 2000). Moreover, PV displays a rather slow dissociation rate with Ca²⁺. It can be predicted that PV should not affect much the fast Ca²⁺ signal responsible for phasic neurotransmitter release and that it may act specifically on the slower processes governed by Ca_i. It was shown that at basket cell-Purkinje cell synapses, which contain PV presynaptically (Celio, 1986; Meyer et al., 2002), elimination of PV converts a depressing synapse into a facilitating one, and it was suggested that PV reduces paired-pulse facilitation by altering presynaptic Ca_i kinetics (Caillard et al., 2000). We have tested this prediction in the present study by comparing the time course of AP-evoked Ca_i transients in single basket and stellate cell terminals under different conditions. We found characteristic bi-phasic decay kinetics associated with the presence of this CBP that explain not only the previously found effect of PV deletion on facilitation but also a newly uncovered effect of PV elimination on delayed transmitter release.

Materials and Methods

All procedures for animal use were in accordance with guidelines approved by the host institutions where experimental work was performed, namely the University Paris 5 (Paris, France) and the University of Fribourg (Fribourg, Switzerland).

Preparation and solutions. Sagittal cerebellar slices (180 μm thick) were prepared as described previously (Llano et al., 1991), following decapitation after cervical dislocation, in accordance with animal welfare protocols approved by our host institution, from wild-type (WT) (C57 Black 6 strain) and PV(-/-) mice, raised on the same C57 background. Two different age groups were studied: postnatal days 10-12 (P10-P12) and P19-P21. Experiments were done at 20-23°C in interneurons of the cerebellar molecular layer (MLIs). Recordings were obtained from two groups of cells: MLIs with somata located in the proximal third of the molecular layer, within 25 μm of the outer border of the Purkinje cell layer, which were considered as basket cells, and MLIs with somata in the distal two thirds of the molecular layer, which were considered as stellate cells. Slices were perfused (1.5 ml/min) with a saline containing (in mm) 125 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 26 NaHCO₃, 2 CaCl₂, 1 MgCl₂, and 10 glucose, equilibrated with a 95% O₂-5% CO₂ mixture, pH 7.3. Tight-seal whole-cell recordings (WCRs) were performed with borosilicate glass pipettes (5-8 MΩ) filled with a solution containing (in mm) 140 K-gluconate, 5.4 KCl, 4.1 MgCl₂, 9.9 HEPES-K, 0.36 Na-GTP, and 3.6 Na-ATP. The free Mg²⁺ concentration in this solution was 660 μm considering a K_D of 100 μm for the binding of ATP to Mg²⁺ (Baylor and Hollingworth, 1998). Oregon Green-BAPTA 1 (OG1; Molecular Probes Europe, Amsterdam, The Netherlands) was added at a concentration of either 20 or 100 μm. To determine the K_D of OG1 for Ca²⁺, we performed in vitro calibration using the same intracellular solution (with 20 μm OG1) adjusted to Ca²⁺ concentration values ranging from 0 to 1.35 μm with concentrated K₂-EGTA and Ca²⁺-EGTA stocks from the Ca²⁺ calibration buffer concentrate kit (C-3723; Molecular Probes Europe). The estimated K_D was 170 nm.

An EPC-9 amplifier (HEKA Elektronik, Lambrecht/Pfalz, Germany) was used for data acquisition and electrical control. Data collection times ranged from 8 to 35 min after initiation of the WCRs for all experimental groups studied.

Fluorometric Ca_i imaging. Fluorescence imaging was done in two different setups: (1) a digital imaging system from T.I.L.L. Photonics (Grafelfing, Germany) consisting of a scanning monochromator (wavelength for the present study was set at 488 nm) and a cooled CCD camera (IMAGO QE; 1376 × 1040 pixels; pixel size: 206 nm after 63× magnification and 2 × 2 binning); and (2) a homemade two-photon fast laser-scanning system based on the design of Tan et al. (1999), with some modifications. Briefly, two-photon excitation was performed with a MaiTai Ti-Sapphire laser (Spectra Physics, Mountain View, CA) set at an excitation wavelength of 820 nm; the average power at the specimen plane was kept below 10 mW. Axonal subregions were scanned by displacing the laser beam in the x-y direction with two galvanometers, using scanning and signal acquisition procedures as described previously (Tan et al., 1999). The effective pixel size was set at 250 nm. The emitted light was focused on the active surface of a photon-counting avalanche photodiode (SPCM-AQR-13; PerkinElmer Optoelectronics, Fremont, CA) and sampled at 10 μsec/point as detailed by Tan et al. (1999). The pseudocolor range for fluorescence images obtained through this detector are reported in Hertz, calculated from the number of photons acquired during the 10 μsec sampling interval. For most experiments, images were acquired with a dwell time of 50-100 msec per image in both the digital-imaging system and the two-photon system. Faster frame rates (10 msec per image) were used in a subset of experiments performed to determine the rise time of Ca_i transients. Both systems used upright Zeiss microscopes (Zeiss, Oberkochen, Germany) equipped with a63× water immersion lens (numerical aperture, 0.9).

To induce axonal Ca_i rises, trains of APs (two or four APs at 20 msec intervals) were produced by depolarizing the cell for 3 msec to 0 mV from a holding value of -70 mV (Tan and Llano, 1999). Analysis was performed by calculating the average fluorescence in regions of interest (ROI) as a function of time. The size of the ROI was chosen as to just enclose the entire bouton and ranged from 1.5 to 4.5 μm². Values are expressed as the percentage of change in fluorescence with respect to control, ΔF/Fo = 100 × (F-Fo)/(Fo-B), where F is the measured fluorescence signal at any given time, Fo is the average from the prestimulus period, and B is the average value, at each time point, of the background fluorescence from four regions of the imaged field that do not contain any part of the dye-filled cell.

Collection and statistical analysis of ROI kinetic data. In each experiment, an axonal zone containing several hot spots was examined. Data were collected typically from two to six ROI in each zone. The signal/noise ratio for individual ROI was often improved by averaging over two to four trials, spaced at 1 min intervals. The resulting average ΔF/Fo signal as a function of time was then fitted by single- and double-exponential functions. The fit was considered biexponential if both of the following criteria applied: (1) the ratio of the two time constants (fast time constant, τ_f; slow time constant, τ_s) was >3 and, (2) the amplitude coefficients for the slow time constant (As) and for the fast time constant (Af) were such that As/(As + Af) fell between 0.15 and 0.85. Peak ΔF/Fo amplitudes were calculated as the sum of the two amplitude coefficients for ROI described by a double-exponential decay. If one of the above criteria (or both of them) was not fulfilled, the kinetics were considered monoexponential, and the peak ΔF/Fo amplitude was the amplitude coefficient of the single-exponential fit. After fitting the Ca_i decay, amplitude and kinetic parameters were averaged over the various ROI belonging to one cell. Finally, results from different cells were pooled together to yield the mean values reported. Statistical variations in the text always refer to cell-to-cell variations; values of n refer to the number of cells, not the number of ROI. These values are given as mean ± SEM. To assess the statistical significance of decay time between different experimental conditions, an ANOVA test was performed to control for multiple comparisons. Student's t tests were used to identify significant differences among pairs; p values <0.05 were considered significant.

Formulation of the functional equation system. Each reaction depicted in Table 1 was described by two differential equations according to the law of mass action. In the present simulations, the Runge-Kutta of the fifth-order method was used to solve the differential equations. Numerical simulations were performed with routines written in the IGOR Pro programming environment (WaveMetrics, Lake Oswego, OR). To simulate a four-AP stimulation, four successive instantaneous Ca²⁺ increases were introduced in the model, at 20 msec intervals. The magnitude of the Ca²⁺ load was adjusted at 11 μm per AP to approach the experimentally measured peak ΔF/Fo of PV(-/-) data and then kept constant. Altering the Ca²⁺ load in the range 6-15 μm did not change appreciably the kinetics of the simulated decay (data not shown).

Table 1.

Parameters used for simulations

Definition	Symbol	Value	Source
0G1 with Ca2+	kon′ CaD	8.24 × 108 m−1 sec−1	Calculated
	koff, CaD	140 sec−1	Eberhard and Erne (1991)a
	kD, CaD	170 nm	Measuredb
PV with Ca2+	kon, PVCa	3.64 × 108 m−1 sec−1	Coutu et al. (2002)
	koff, PVCa	4.03 sec−1	Coutu et al. (2002)
	kD, PVCa	11 nm	Coutu et al. (2002)
PV with Mg2+	kon, PVMg	1.42 × 105 m−1 sec−1	Calculated
	koff, PVMg	2.2 sec−1	Westerblad and Lannergren (1991)
	kD, PVMg	15 μm	Haiech et al. (1979)c
ATP with Ca2+	kon, ATPCa	1.5 × 108 m−1 sec−1	Baylor and Hollingworth (1998)
	koff, ATPCa	3 × 104 sec−1	Baylor and Hollingworth (1998)
	kD, ATPCa	200 μm	Baylor and Hollingworth (1998)
ATP with Mg2+	kon, ATPMg	1.5 × 106 m−1 sec−1	Baylor and Hollingworth (1998)
	koff, ATPMg	150 sec−1	Baylor and Hollingworth (1998)
	kD, ATPMg	100 μm	Baylor and Hollingworth (1998)

^a Data are for Calcium Green-1.

^b Estimated from in vitro calibrations performed as detailed in Materials and Methods.

^c The value used is the one given in this manuscript for mammalian α - PV.

Exchange out and into the compartment under consideration. The single compartment under study (varicosity) exchanges Ca²⁺ with other cell compartments, as well as with the extracellular medium, using various processes operating on a time scale of tens of milliseconds to seconds. As a first approximation, extrusion processes can be represented collectively byaCa²⁺ flux that is proportional to the difference between the equilibrium Ca_i value (taken as 40 nm) and the current Ca_i value (Lee et al., 2000). This can be modeled by the following simple kinetic reaction:

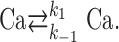Here, Ca on the left side of the reaction represents intracellular Ca²⁺, and Ca on the right side of the reaction represents extracellular Ca²⁺. This scheme translates into d[Ca]_i/dt = -k₁[Ca]_i + k_-1[Ca]_e, where [Ca]_i and [Ca]_e represent, respectively, the intracellular and extracellular Ca²⁺ concentrations, and k₁ and k_-1 represent the rate constants of Ca²⁺ extrusion and influx. [Ca]_e is constant at a value of 2 mm. Note that k₁ corresponds to the extrusion rate gamma described by Lee et al. (2000). In the simulations, k₁ was first determined on the basis of decay kinetics. k_-1 was then calculated as = k₁/50,000, such that the equilibrium value of Ca_i remained at 40 nm. Simulations are displayed in terms of ΔF/Fo for comparison with experimental results.

Diffusion equilibration. MLI axons display a succession of hot spots, where voltage-gated Ca²⁺ entry occurs, and passive regions. Hot spots correspond mainly to varicosities and are spaced ∼5 μm apart (Forti et al., 2000). The time course of equilibration between dendritic spines and dendritic shaft in CA1 pyramidal cells was measured as 140 msec (Majewska et al., 2000), close to the value of τ_f in the present study. Because dendritic spines have approximately the same size as varicosities, it seemed possible that the fast component of decay could be contaminated by diffusion equilibration. If this were the case, however, one would have expected to observe a fast component both in the WT and in the PV(-/-) strains, whereas in the latter case, the percentage of cells showing the fast component was significantly reduced. Thus, the fast component of biexponential decays is not primarily attributable to diffusion. Nevertheless, it appeared possible that diffusion out of the varicosities could have distorted the results, particularly in the younger age group, because it has been shown that the separation between varicosities and linking axon segments becomes more apparent with age (Forti et al., 2000) (see Fig. 1, compare A1-B2 with C1,C2). To address this issue, we compared the analysis of the decay kinetics of the signal performed on small ROI, as illustrated in Figure 1, and on one very large ROI encompassing the entire frame (and hence including several calcium hot spots and intervening “cold” axon). This analysis was performed on basket cell signals from P10-P12 WT mice. It was found that the decay required a biexponential fit independently of whether small or large ROI were used, confirming that exit from the hot spots is not the main reason for biexponential decay time courses. Furthermore, quantitative differences between the results of the two analyses were modest. The largest difference concerned τ_f, which was 25% larger with the large ROI than with the small ones (respective means, 0.23 ± 0.02 sec and 0.18 ± 0.01 sec); however, even this difference did not reach statistical significance at the p < 0.05 confidence level. These results indicate that errors linked to the diffusion out of the varicosities are small and justify our treatment with a one-compartment model.

Figure 1.

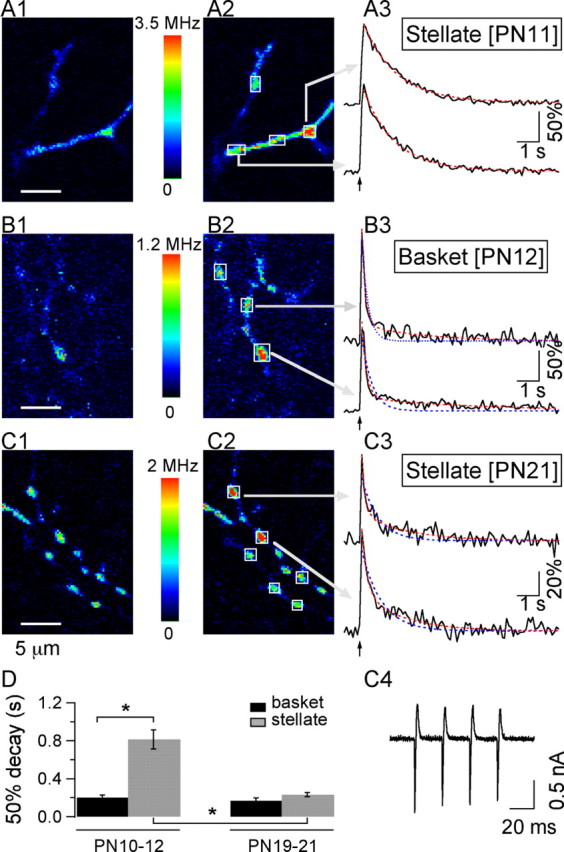
Age- and interneuron subtype-dependent changes in Ca_i signaling at presynaptic varicosities. A1, A2, Two-photon pseudocolor images of the OG1 Ca²⁺-dependent fluorescence from a P11 stellate cell axon at rest (A1) and at the peak of the response to a 50 Hz train of four APs(A2). A3, Time course of the relative changes in fluorescence (ΔF/Fo) in ROI identified by the arrows in A2. Superimposed on the data traces are the fits of the decay phase by single-exponential (blue dotted lines) and double-exponential (red dotted lines) functions, which in this case are equivalent, indicating that the decay kinetics are well described by a single exponential. Note that the data traces as well as the corresponding fits return to prestimulus levels. B1-B3, Similar analysis for the AP-evoked Ca_i rises in a P12 basket cell axon. For this type of interneuron, the decay time course is fast and follows a double-exponential function. C1-C3, At P21, stellate cell axonal Ca_i rises have evolved toward a fast and biphasic decay. C4 presents the AP-evoked current traces for this neuron. D, Comparison of the average decay time course, estimated as the time to decay to 50% of peak amplitude, for stellate and basket cells of the two age groups. The analysis contains data from six basket and seven stellate cells at P10-P12 and for five basket and six stellate cells at P19-P21. Basket cell somata were located in the lowest 25 μm of the ML for both age groups. The range of distances between the outer border of the Purkinje cell layer and the stellate cell somata was 50-75 μm at P10-P12 and 70-110 μm at P19-P21. The bars denote the SEM. The ANOVA test for this data yields F = 26.29 (p < 0.0001). The asterisks indicate groups that are statistically significant, using Student's t test.

Recording and analysis of IPSCs. MLIs were maintained under voltage clamp in the WCR configuration at a holding potential of -70 mV. The intracellular solution contained (in mm) 150 KCl, 2.4 MgCl₂, 10 HEPES-K, 1 mm EGTA-K, 0.4 Na-GTP, and 2.4 Na-ATP, pH 7.3. Series resistance values ranged from 15 to 25 MΩ and were compensated for by 60%. Currents were filtered at 1.3 kHz and sampled at a rate of 250 μsec/point. dl-2-Amino-5-phosphonopentanoic acid (Tocris, Bristol, UK) and 6,7-dinitroquinoxaline-2,3-dione (Tocris), antagonists of ionotropic glutamate receptors, were included in the bath solution at concentrations of 50 and 5 μm, respectively. Extracellular stimulation of presynaptic axons was performed by applying voltage pulses (100-200 μsec duration; 40-70 V amplitude) between a reference platinum electrode and a pipette filled with a solution containing (in mm) 145 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, and 10 HEPES-Na (input resistance, 2-3 MΩ). This pipette was displaced in the molecular layer until a stable synaptic response was evoked. The standard experimental protocol consisted of acquiring 1 sec of baseline currents, followed by the application of a 50 Hz train of 10 stimuli. This protocol was repeated 10-20 times at 10-20 sec intervals. Detection and analysis of IPSCs were performed off-line with routines written in the IGOR Pro programming environment (WaveMetrics). Results are reported in terms of the frequency of synaptic events as a function of time, relative to the prestimulus period.

Immunocytochemistry. Immunocytochemistry was performed on C57 Black 6 mice from P10 to P38. Animals were anesthetized by an intraperitoneal injection of 150 μl of pentobarbital (Sanofi, La Ballastiere, France) diluted five times in a 0.9% NaCl solution and perfused transcardialy with a cold (5-6°C) 0.9% NaCl solution, followed by a cold fixative solution consisting of 4% paraformaldehyde, 0.2% glutaraldehyde, and 0.2% picric acid in 0.15 m phosphate buffer at pH 7.4. After 20 min, the cerebellar vermis was removed and postfixed overnight in the same fixative solution, excluding glutaraldehyde. Sagittal cerebellar slices (50 μm thick) were cut after a 24 hr fixation in cold 0.15 m phosphate buffer with a Leica VT1000S vibratome (Leica, Weltzlar, Germany). All incubations were performed under continuous agitation at room temperature in 24-well culture plates. The sections were washed thoroughly in PBS (0.03 m phosphate buffer with 0.9% NaCl), then incubated for 2 hr in PBS containing 0.2% Triton (PBST) for permeabilization and 2% bovine serum albumin (BSA) (Sigma A2153; Sigma, St. Louis, MO). Sections were incubated overnight with one or two of the following pairs of antibodies prepared in PBST: (1) a polyclonal rabbit anti-PV (PV-28; dilution, 1:1000; Swant, Bellinzona, Switzerland) and a monoclonal mouse anti-CB (300; dilution, 1:1000; Swant); (2) a polyclonal rabbit anti-CB (CB-38; dilution, 1:1000; Swant) and a monoclonal mouse anti-GABA (3A12; dilution, 1:1000; Swant). After several washes with PBST, slices were incubated in the dark for 2 hr in one of the following pairs of secondary antibodies, both prepared in PBST: (1) fluorescein anti-rabbit IgG (FI-1000; dilution, 1:200; Vector Laboratories, Burlingame, CA) and Texas Red anti-mouse IgG (TI-2000; dilution, 1:200; Vector Laboratories); (2) Cy3 anti-rabbit IgG (111-165-144; dilution, 1:300; Jackson ImmunoResearch Europe, Cambridgeshire, UK) and Alexa 488 anti-mouse IgG (A-11001; dilution, 1:300; Molecular Probes Europe). After several washes with PBS, slices were mounted on glass slides in Prolong Antifade kit mounting medium (P 7481; Molecular Probes Europe).

The first control consisted in incubations without the primary antibodies and with the two secondary antibodies; no specific signal was detected. The second control was to omit one of the two primary antibodies from the incubation medium, maintaining the two secondary antibodies. The signal was positive for the primary antibody that remained and had the same pattern as that observed in double immunostaining.

Confocal images were acquired with an LSM 510 confocal microscope (Zeiss) equipped with two lasers, argon multiray (used at 488 nm) and helium (543 nm). Sections were analyzed using a 40× oil-immersion objective with a numerical aperture of 1.3. The pin hole aperture and the laser power were, respectively, 74 μm and 8% for the argon laser and 65 μm and 30% for the helium laser.

Biochemistry. Mice (P5-P25 and young adults; n = 3 for each age group) were deeply anesthetized by inhalation of CO₂ and briefly perfused transcardially by ice-cold PBS solution. Cerebella were dissected and homogenized in 10 mm Tris-HCl and 1 mm EDTA, pH 7.4 [containing one tablet of protease inhibitor mixture (Roche Diagnostics AG, Rotkreuz, Switzerland) per 10 ml of buffer, added just before use] using a Polytron homogenizer. Soluble protein fractions were prepared by centrifugation of homogenates at 30,000 × g for 30 min and by recovering the supernatant. Proteins (25 μg) were separated by one-dimensional PAGE (15%) and transferred on nitrocellulose membranes using a semidry transfer system (Bio-Rad, Glattbrugg, Switzerland). The membranes were controlled for even load and possible transfer artifacts by staining with Ponceau red solution. After blocking with a 10% solution of nonfat milk in TBS-T buffer (TBS with the addition of 0.05% Tween 20), membranes were incubated with primary antibodies against PV (PV-28; dilution, 1:1000; Swant) for 90 min. All antibodies used were dissolved in TBS-T solution containing 1% protease-free BSA. Incubation of membranes with primary antibodies was followed by extensive washing using TBS-T solution and subsequently by incubation of membranes with antirabbit secondary biotinylated antibodies (dilution, 1:10,000; Vector Laboratories). After extensive washing, membranes were incubated with avidinbiotin-conjugated peroxidase (Vector Laboratories) solution in TBS-T and washed again. The bands corresponding to PV were visualized and quantified by the Molecular Imager (Bio-Rad) using the ECL chemiluminescence method (Pierce, Perbio Science SA, Lausanne, Switzerland).

Results

Decay kinetics of axonal Ca_i signals are different in basket cells and stellate cells at early developmental stages

MLIs are traditionally classified as basket and stellate cells. The former neurons have cell bodies in the lower third of the molecular layer and make extensive synaptic contacts with Purkinje cell somata, whereas the latter ones have cell bodies in the upper two thirds of the molecular layer and innervate preferentially Purkinje cell dendrites (for review, see Palay and Chan-Palay, 1974). The two classes of neurons are closely related and are sometimes considered as a continuum (Sultan and Bower, 1998). No functional difference has been revealed so far between them, except for the fact that the current evoked in Purkinje cells is larger for presynaptic basket cells than for presynaptic stellate cells (Vincent and Marty, 1996). However, we found that at P10-P12, there was a striking difference between MLIs with somata located within 25 μm of the outer border of the Purkinje cell layer (here-after called basket cells) and MLIs with somata that were placed in the upper two thirds of the molecular layer (hereafter called stellate cells) concerning the time course of decay of Ca_i transients. Figure 1, A and B, illustrates the AP-evoked fluorescence changes reported by OG1 (100 μm) in axons of P10-P12 MLIs. Fluorescence signals were collected at small hot spots that represent putative release sites onto Purkinje cells and onto other MLIs (Llano et al., 1997; Tan and Llano, 1999; Forti et al., 2000). Analysis was performed in terms of the percentage of change in fluorescence over the baseline period (ΔF/Fo) in small ROI, the size of which was set to just encompass the entire bouton (see Materials and Methods). After a 50 Hz train of four APs, ΔF/Fo increases of 100-150% were measured, corresponding to >2-fold Ca_i rises. The fluorescence signals decayed back to baseline within a few seconds. The decay was much faster in basket cells than in stellate cells. This functional difference is exemplified in Figure 1, A and B, in which two-photon fluorescence images corresponding to scans of axonal regions at rest and at the peak of the response to the stimulus are displayed, along with the time course at selected ROI. On average, the time of decay to half of the peak amplitude (50% decay) was fourfold slower for stellate cells than for basket cells (0.813 ± 0.09 sec, n = 7 cells and 0.202 ± 0.02 sec, n = 6 cells, respectively), a highly significant difference (Student's t test; p < 0.0002) (pooled data in Fig. 1D). Furthermore, whereas a large fraction of the stellate cell signals could be well approximated by a single-exponential function (Fig. 1A3), data for basket cells (Fig. 1B3) were much better fitted by a double exponential (red traces) than by a single exponential (blue traces). Using the criteria explained in Materials and Methods, we found that decay kinetics were monoexponential in 49 ± 18% of the signals from of P10-P12 stellate cells (average τ, 1.45 ± 0.21 sec; n = 7 cells), whereas a double exponential was required to describe Ca_i transients in 89 ± 7% of P10-P12 basket cells [τ_f, 0.18 ± 0.01 sec; τ_s, 1.86 ± 0.48 sec; As/(Af + As): 0.29 ± 0.06; n = 5 cells]. Thus, the kinetic difference between stellate and basket cell signals involved not only a difference in overall speed but also in the very shape of the decay.

Age-dependent changes in the temporal dynamics of axonal Ca_i signals in cerebellar interneurons

We next explored whether Ca_i decay kinetics changed differentially for basket and stellate cells during development. To quantify the effects, two age groups were considered; they covered the ages P10-P12 and P19-P21. Basket cell Ca_i signals changed little between the two age groups that were examined [at P19-P21: 50% decay time, 0.168 ± 0.03 sec; biexponential fits required for 90 ± 10% of the transients; τ_f, 0.140 ± 0.02 sec; τ_s, 1.38 ± 0.46 sec; As/(Af + As): 0.33 ± 0.05; n = 5 cells). In contrast, the 50% decay time for stellate cells was approximately four times shorter at P19-P21 (0.234 ± 0.02; n = 6 cells) than at P10-P12, a highly significant change (Student's t test comparison of P10-P12 and P19-P21 stellate cells: p < 0.0002). As a result of this remarkable change with age, at P19-P21 there was no significant distinction between the decay time course of the two interneuron subtypes (see summary results for 50% decay in Fig. 1D). Furthermore, all the stellate cells in the P19-P21 group had a biexponential time course (τ_f, 0.176 ± 0.02 sec; τ_s, 1.83 ± 0.22 sec; As/(Af + As): 0.39 ± 0.03; n = 6 cells) (Fig. 1C) similar to that describing the decay of P10-P12 and P19-P21 basket cells.

The expression of PV in the developing cerebellum

Ca_i kinetics are shaped by a complex interaction between extrusion mechanisms, exchange with intracellular Ca²⁺ stores (for review, see Pozzan et al., 1994; Berridge, 1998), diffusion (Majewska et al., 2000), and endogenous Ca²⁺ buffers (Neher and Augustine, 1992). In several systems, the contribution of these processes to the decay of Ca_i transients has been inferred from the relative goodness of fit by either a monoexponential or a biexponential function. Monophasic decays were attributed to linear Ca²⁺ extrusion mechanisms and rapid kinetics of Ca²⁺ buffers (Lee et al., 2000). Biphasic decay kinetics have been interpreted in terms of different mechanisms including nonlinear Ca²⁺ extrusion (Fierro et al., 1998), saturation of high-affinity CBPs such as CB (Maeda et al., 1999; Blatow et al., 2003), or delayed buffering by PV (Lee et al., 2000). Because MLIs express neither CR nor CB but are known to be rich in PV (Kosaka et al., 1993), we next examined whether a correlation exists between PV expression levels and kinetics of presynaptic Ca_i transients.

In the cerebellar molecular layer, PV is present not only in MLIs but also in Purkinje cells. The extensive dendritic arborization of Purkinje cells hinders the visualization of the small MLI somata when slices are stained with antibodies for PV. We therefore performed double stainings with antibodies for PV and CB, as shown by the confocal images presented in Figure 2A. Because of the choice of secondary antibodies (see Materials and Methods), cells containing both CBPs (Purkinje cells) appear yellow-orange, and MLIs, which express only PV, appear green. At P10 (Fig. 2A1), the distribution of PV was clearly heterogeneous in the molecular layer, with a much lower staining in the outer part, corresponding to stellate cells, than in the inner part, corresponding to basket cells (see below). These data suggest that the difference between the decay kinetics of basket and stellate cells observed at this age is directly determined by the level of PV expression: the low PV-expressing stellate cells have a decay that is primarily determined by clearance of Ca²⁺ and that is therefore monoexponential according to the predictions of the simple “one-compartment model” (Neher, 1998), whereas for basket cells, Ca²⁺ binding to PV accelerates the initial part of the Ca_i decay, producing a biexponential time course.

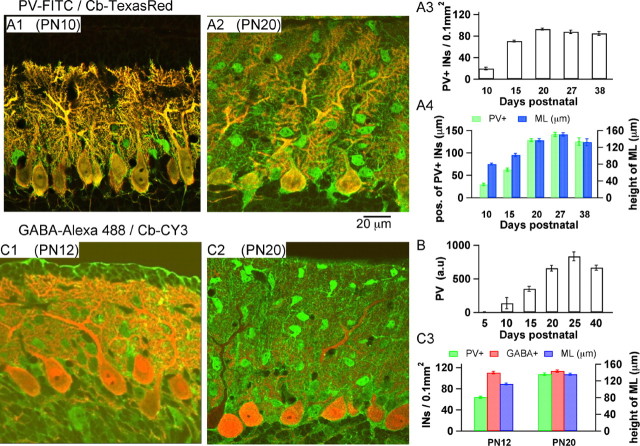
Figure 2.

Developmental profile of PV expression in cerebellar interneurons. A1, A2, Confocal images from slices of a P10 (A1) and a P20 (A2) mouse cerebellum. Double staining with PV and CB antibodies was performed as described in Materials and Methods. Because of the choice of secondary antibodies (see Materials and Methods), PV-containing cells show as green in these images, whereas cells expressing PV and CB appear yellow. Thus, the prominent yellow stain identifies Purkinje cells, well known to express both CBPs, and green identifies interneurons, which express PV but not CB. At P10, PV-containing interneurons are located primarily in close proximity to the Purkinje cell layer and can thus be identified as basket cells. At P20, in contrast, numerous PV-containing interneurons are visible in the middle and outer molecular layer, the location of stellate cells. A3, Evolution of the number of PV-positive interneurons per surface area of 0.1 mm² as a function of age. The bars represent the SEM. A4, Maximal excursion of PV-expressing interneurons in the molecular layer as a function of age. The blue bars correspond to the height of the molecular layer at each age. B, Age-dependent increase in the total quantity of PV in mouse cerebellum, as determined by quantitative Western blots, parallels the immunocytochemical observations. C1, C2, Confocal images from slices of a P12 (C1) and a P20 (C2) mouse cerebellum. Double staining with GABA and CB antibodies is shown. MLIs appear green and are seen to be present throughout the molecular layer since P12. C3, Quantitative comparisons for the evolution of PV and GABA expression between P12 and P20.

During development, there was a marked general increase in the level of PV expression, as determined by quantitative Western blots from cerebellar slices (Fig. 2B). PV was just detectable at P5. Between P10 and P20, the increase was approximately fivefold. The counts of the number of PV-positive interneurons from PV/CB stains of slices in the same age window were in agreement with this developmental trend (example of staining at P20 in Fig. 2A2; quantitative analysis at different ages in Fig. 2A3). Furthermore, the pattern of PV expression throughout the molecular layer evolved with age, such that at early ages most PV-positive MLIs were located close to the Purkinje cell layer and with increased age PV-positive MLIs started to appear farther into the molecular layer (Fig. 2A4). To quantify the density of MLIs in the two age groups studied, we performed double stainings with antibodies for GABA and CB. Examples of this type of stain are shown in Figure 2, C1 (at P12) and C2 (at P20). Here cells containing GABA and CB appear red-orange (prominent staining in Purkinje cells), whereas MLIs appear green (GABA positive, CB negative). The analysis of this type of staining showed that the density of GABA-positive MLIs was not significantly different between P12 and P20, whereas the density of PV-positive MLIs increases between the two developmental stages (Fig. 2C3).

Stellate and basket cells, along with Golgi cells, were demonstrated in lineage tracing studies to derive postnatally from precursors near the IVth ventricle that migrate through the white matter to the cerebellar cortex. Basket cells settle down first in the lower part of the molecular layer. As the depth of this layer increases, stellate cells gradually move in to fill more distal locations (Zhang and Goldman, 1996). Thus, at P10-P12, corresponding to the final phase of the buildup of the molecular layer, basket cells have been occupying their location for some time, whereas stellate cells are newcomers. The results of Figure 2 suggest that MLIs have little PV at first but that they acquire PV a few days after settling down in the molecular layer.

In addition, these results parallel the above finding that the decay time course of stellate cells changes much more dramatically than that of basket cells with age, and they account for the nature of the kinetic change, which converts a monophasic, low-PV decay to a biphasic, high-PV decay. Together, the results indicate a strong correlation between the level of PV expression and the degree of biphasicity of the Ca_i decay.

Ca_i signaling in axons from PV(-/-) mice

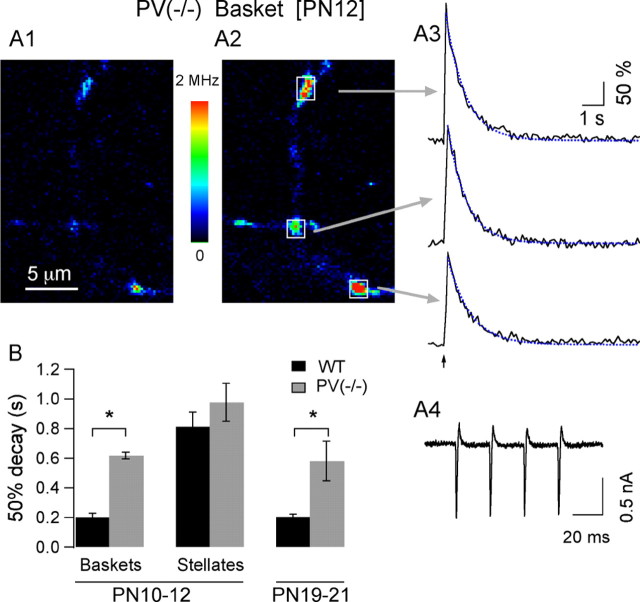
If the above reasoning and conclusions are correct, eliminating PV expression by genetic deletion of a functional PV gene should have little effect in stellate cells from P10-P12 mice, but it should convert the biphasic decay of P10-P12 basket cells and that of both types of interneurons at P19-P21 into a slower, monophasic decay similar to that measured in WT stellate cells at P10-P12. To test these predictions, decay kinetics were analyzed in a PV null-mutant, PV(-/-) mouse strain (Schwaller et al., 1999) and compared with age-matched controls. The two P10-P12 groups were differently affected by PV deficiency. There was no change in kinetics for stellate cells (50% decay: 0.977 ± 0.13 sec; Student's t test; p < 0.37; monophasic decay for 50 ± 28% of the signals; Student's t test; p < 0.97; n = 3 cells). For basket cells, in contrast, lack of PV led to a marked slowing of the decay (50% decay: 0.618 ± 0.02; Student's t test; p < 0.00002), which was described by a single exponential in 83 ± 16% of the signals (Student's t test; p < 0.002; n = 3 cells). A representative example of the AP-evoked Ca_i transients obtained in axonal varicosities of a PV(-/-) P12 basket cell is shown in Figure 3A. For P19-P21 PV(-/-) mice, the decay of Ca_i signals was much slower than that observed in MLIs from age-matched WT animals. Statistical comparisons were performed by pooling data from basket and stellate cells together, because at this age the two cell types display similar decay kinetics, both in the WT and in PV(-/-) strain. The average 50% decay values in P19-P21 PV(-/-) mice were 0.62 ± 0.12 sec (n = 10 cells), threefold higher than controls (pooled average from age-matched controls: 0.203 ± 0.019 sec; n = 11 cells; Student's t test; p < 0.003). The difference applies as well to the shape of the decay, which was well described by a single exponential for 66 ± 10% of the signals in PV(-/-) mice (average τ, 0.93 ± 0.18 sec; n = 10 cells), whereas in WT MLIs at this age, a double exponential was required to describe Ca_i decay kinetics for 95.5 ± 4.5% of the signals (n = 11 cells; Student's t test; p < 0.00002). These results, summarized in Figure 3B, show that the absence of PV essentially maintains P19-P21 interneurons at P10-P12 stellate cell kinetics, thus matching exactly the above predictions and strongly reinforcing our conclusion that PV is the major determinant in shaping the biphasic decay kinetics in MLI axons.

Figure 3.

Absence of PV cancels the age-dependent changes in presynaptic Ca_i signaling. A1, Resting fluorescence of an axonal region of a P12 basket interneuron from a PV(-/-) mouse. A2, Corresponding image at the peak response to a four-AP train. A3, In contrast to the WT phenotype at this age, the time course to the AP-evoked Ca_i signals acquired at the varicosities indicated by the arrows in A2 is slow and well described by a single exponential (blue dotted traces). Thus, PV removal converts the Ca_i decay kinetics in MLIs back to the slow monophasic decay that is observed at P10-P12 in the wild type. A4, AP currents were not different in PV(-/-) mice and in WT mice (compare with Fig. 1C4). B, Comparison of the average decay time course indicates significant differences between WT and PV(-/-) basket cells at P10-P12 but no difference for the stellate cells of this age group. At P19-P21, deletion of PV(-/-) also leads to a significant change in decay time course. The number of cells for the WT groups are 6, 7, and 11 for the P10-P12 basket cells, P10-P12 stellate cells, and P19-P21 interneurons, respectively. The PV(-/-) groups include three basket cells and three stellate cells at P10-P12 and 10 interneurons at P19-P21. The ANOVA test for this data yields F = 10.20 (p < 0.0001). The asterisks indicate groups that are statistically significant, using Student's t test.

Finally, peak amplitudes were compared in WT and in PV(-/-) mice. Because PV has slow binding kinetics with Ca²⁺, the presence of PV is expected to have little influence on the peak amplitude and rise time of Ca_i transients (Lee et al., 2000; Schmidt et al., 2003a). In accordance with this prediction, peak ΔF/Fo values in P19-P21 PV(-/-) mice (147 ± 11%; 10 cells) were not significantly different from those obtained in age-matched WT (109 ± 14%; 11 cells; Student's t test; p < 0.06). Furthermore, times from stimulus onset to peak for trains of four APs, analyzed in a subset of experiments performed with sampling rates of 10 msec per image, were similar in both groups (WT, 81.9 ± 1.9 msec; PV(-/-), 99.1 ± 21.9 msec; n = 3 cells per group; Student's t test; p < 0.48).

When comparing Ca_i signals at different ages and PV conditions, the question arises as to the possible differences on the washout of cytosolic components among the experimental groups. As mentioned in Materials and Methods, data were gathered at WCR times ranging from 8 to 35 min in all experimental groups. Neither peak amplitudes nor decay time course, including the degree of biphasicity and τ values of the Ca_i decay in MLIs from WT mice showed any correlation with WCR time. We therefore conclude that PV does not readily diffuse out of MLI axons within the time window of the present experiments.

Modeling AP-evoked presynaptic Ca_i transients

We simulated volume-averaged Ca_i for different experimental conditions (1) to estimate the endogenous PV concentration and (2) to predict the actual shape of Ca_i decay in the absence of exogenous buffer (i.e., Ca²⁺ indicator). These simulations were based on the “one-compartment approximation” as developed in chromaffin cells, which assumes a homogeneous Ca²⁺ concentration in the compartment (Neher and Augustine, 1992). The simulations obeyed a system of differential equations describing (1) the reactions of Ca²⁺ with its various binding partners (OG1, PV, and ATP), (2) the reaction of Mg²⁺ with PV and ATP, and (3) an exchange of the compartment with other cell compartments and with the extracellular medium, based on a simple reaction with Ca²⁺-independent rate constants (see Materials and Methods and Table 1 for reaction parameters). Additionally, an endogenous fast buffer was included, following the evidence presented below.

Evidence indicating the presence of an endogenous buffer distinct from PV

Besides PV, MLIs may contain some fast endogenous buffer that could be upregulated or downregulated during development and that could affect the kinetics of Ca_i decay. Dissecting individual buffer contributions in a cell containing PV plus one (or more) fast buffers is complicated and can easily lead to erroneous conclusions (for review, see Markram et al., 1998). PV(-/-) conditions are more advantageous, because the absence of a slow buffer greatly simplifies the system of equations describing Ca_i decay. In this situation, the strength of the endogenous buffer can be estimated by extrapolating the linear relationship between τ and probe concentration (Neher and Augustine, 1992; Lee et al., 2000) as follows:

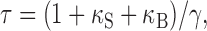1

where κ_S and κ_B, respectively, represent the buffering capacity of the endogenous fast buffer and of the dye, and γ is the rate constant representing extrusion from the compartment. We used the predictions of Eq. 1 to assess the presence of a fast buffer in MLIs. We reexamined PV(-/-) data both in P10-P12 and in P19-P21 animals, using a much lower concentration of OG1 (20 μm instead of 100 μm). Even with the low dye concentration, good quality signals could be collected, as illustrated in Figure 4A for a P19 PV(-/-) stellate cell. The AP-evoked Ca_i transients were well described by a single exponential in all cells tested (Fig. 4A3), with τ values of 1.02 ± 0.10 sec (four cells) at P10-P12 and 0.47 ± 0.15 sec (four cells) at P19-P21. Corresponding average peak ΔF/Fo were 146 ± 18% at P10-P12 and 204 ± 28% at P19-P21. Using Eq. 1, κ_S was calculated for the two age groups. Values were 1170 and 350 for P10-P12 and P19-P21 MLIs, respectively. Thus, the analysis of PV(-/-) data indicates that MLIs contain a substantial amount of a fast endogenous buffer, with a buffering capacity that declines with age.

Figure 4.

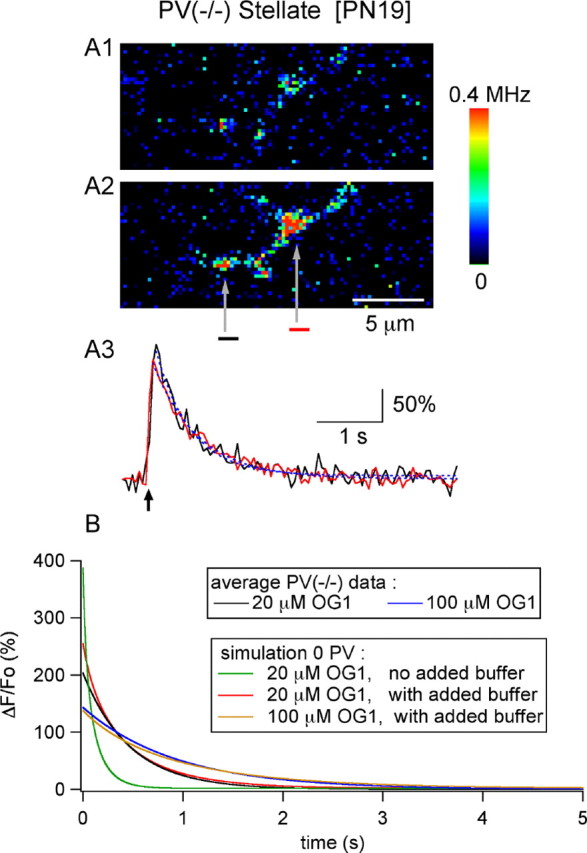
Measurements of AP-evoked Ca_i with 20 μm OG1 and estimation of fast endogenous buffer capacity. A1, A2, Resting and peak Ca_i images (after a 4-AP stimulus) from an axon dialyzed with 20 μm OG1 [P19 stellate cell, from a PV(-/-) mouse]. A3, Time course of decay for the two ROI depicted in A2 (black and red traces). Both decay time courses could be approximated with a single exponential (blue dotted lines; time constants, 0.58 and 0.69 sec). The average peak ΔF/Fo and 50% decay time from similar experiments (4 cells) were 204 ± 28% and 0.32 ± 0.10 sec, respectively. B, Average decay time course for PV(-/-) data from experiments performed with 20 μm OG1 (black trace) and 100 μm OG1 (blue trace) are compared with numerical simulations (red and yellow traces, for low and high dye concentration, respectively). The best approximations to the experimental data were obtained with a resting Ca_i of 40 nm, a Ca load of 11 μm per AP, extrusion/influx kinetic constants of k = 550 sec^-1 and k_-1 = 0.011 sec^-1, and an endogenous buffer capability equivalent to 60 μm OG1. The same simulation parameters fail to approximate the 20 μm OG1 experimental data if the endogenous buffer is not included (green trace).

We next proceeded to simulate the Ca_i transients for the PV(-/-) data, focusing on the P19-P21 group. Figure 4B shows the results of the first set of simulations, aimed at determining (1) the magnitude of the Ca²⁺ load and (2) the kinetic parameters for the extrusion from the compartment. Averaged experimental results from the PV(-/-) P19-P21 group for 20 μm OG1 (black trace) and 100 μm OG1 (blue trace) are displayed along with the best approximations to the data (red and yellow traces for 20 and 100 μm OG1, respectively). The simulations, which include an endogenous buffer with aκ_S of 350 (i. e., equivalent to 60 μm OG1), yield a Ca²⁺ load of 11 μm per AP and extrusion/influx kinetic constants k₁ and k_-1 of 550 sec^-1 and 0.011 sec^-1, respectively. In the absence of endogenous buffer, the predicted time course for 20 μm OG1 (green trace) is much faster than the experimental data (continuous black trace) in accordance with the presence of a substantial fast endogenous buffer.

Modeling the effects of PV on Ca_i decay

Using the parameters that best approximated PV(-/-) P19-P21 results, we set out to determine the concentration of PV in axons of WT MLIs. For this, we compared numerical simulations with the average experimental data obtained with 100 μm OG1. As shown by the family of curves in Figure 5A and in accordance with previous publications (Lee et al., 2000; Schmidt et al., 2003a,b; for review, see Schwaller et al., 2002), the decay kinetics in the presence of PV are described by a double exponential. Changes in PV concentration had little effect on the peak ΔF/Fo value but altered markedly the kinetics of the Ca_i decay. With increasing PV concentration, the fast time constant of the decay became faster, whereas the slow time constant of the decay slowed down (data not shown) (Lee et al., 2000). However, independently of the PV concentration, these simulations differed significantly from the experimental results, represented by the black trace in Figure 5A. An acceptable approximation to the WT P19-P21 data could only be achieved by increasing the extrusion rate constants twofold. This is shown in Figure 5B, in which a PV concentration of 150 μm yields the best approximation to the parameters extracted from WT P19-P21 MLIs subjected to four AP trains, including peak ΔF/Fo, τ_f, and τ_s, as well as the ratio of the corresponding amplitude coefficients [average values from 11 MLIs: peak ΔF/Fo, 109.5 ± 14.6%; τ_f, 0.16 ± 0.01 sec; τ_s, 1.63 ± 0.23 sec; As/(Af + As): 0.36 ± 0.03].

Figure 5.

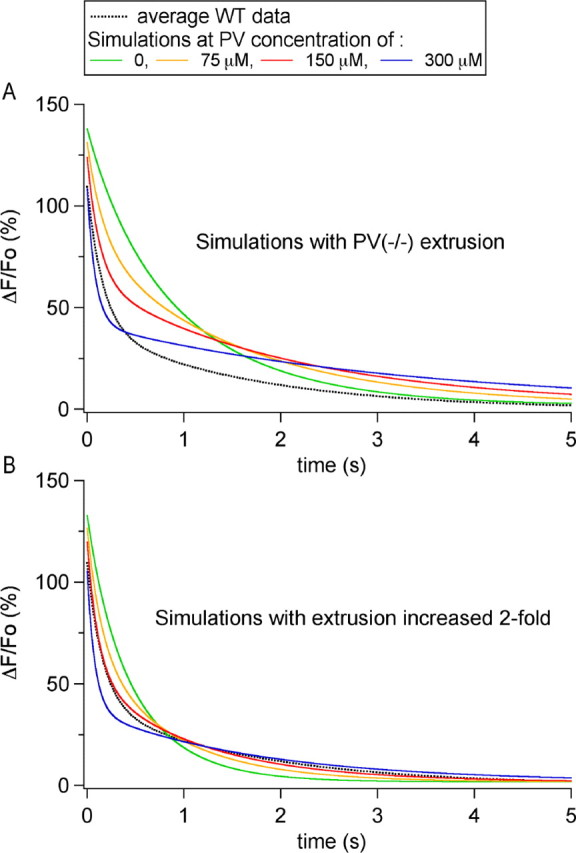
Determination of the endogenous PV concentration. A, Numerical simulations of the time course of decay of Ca_i signals for PV concentrations ranging from 0 to 300 μm, obtained using the simulation parameters that gave the best approximation to the PV(-/-) data, namely a resting Ca_i of 40 nm, a Ca²⁺ load of 11 μm per AP, extrusion/influx kinetic constants of k₁ = 550 sec^-1 and k_-1 = 0.011 sec^-1 and an endogenous buffer capability equivalent to 60 μm OG1. Note that, regardless of the PV concentration, there is a large discrepancy with the average decay obtained in WT P19-P21 MLIs (dotted black trace). B, Family of simulations performed with extrusion/influx kinetic constants increased by a factor of 2 (k₁ = 1100 sec^-1 and k_-1 = 0.022 sec^-1). A concentration of 150 μm closely approximates the average WT data (dotted black trace).

It is important to stress here that changing the extrusion rate from the PV(-/-) simulation was the only satisfactory solution to remove the discrepancy shown in Figure 5A. In particular, changing the value of κ_S (the buffering capacity of the fast endogenous buffer) between WT and PV(-/-) was unable to produce a satisfactory fit. Likewise, even if the affinity and binding rates of OG1 for Ca²⁺ were artificially modified, no single set of parameters could account for WT and PV(-/-) data without altering the exit rate between the two conditions (data not shown). A compensatory change in the extrusion rate was found previously after deletion of CB in Purkinje cells (Schmidt et al., 2003a).

All simulations so far assume a resting Ca_i level of 40 nm, both for WT and PV(-/-) conditions. Reported neuronal basal Ca_i values range from 20 nm (Fierro and Llano, 1996) to 70 nm (Jackson and Redman, 2003). Satisfactory sets of simulations could be obtained with different resting Ca_i values, provided that the model parameters were readjusted; thus, the best PV concentration was 175 μm for a resting Ca_i level of 20 nm and 120 μm for a resting Ca_i level of 70 nm. Note also that the 150 μm PV concentration estimate also depends on the value that is taken for the PV-Ca²⁺-binding rate (Coutu et al., 2002).

Does PV saturate during bursts of AP firing?

PV is a high-affinity buffer that is partially Ca²⁺ bound at resting Ca_i levels. In chromaffin cells that were infused with PV, repetitive stimulation was shown to increase the degree of saturation of PV, leading to supralinear Ca_i increases and to slower decay kinetics (Lee et al., 2000). In the present case, the calculated apparent dissociation constant (based on parameters listed on Table 1) of PV for Ca²⁺ was rather high (450 nm) because of the comparatively large concentration of Mg²⁺ that was included in the pipette solution. Accordingly, only 9% of PV were bound to Ca²⁺ under resting conditions. The amount of free PV dropped to 78% of the total PV after one AP (calculated 20 msec after the AP), to 60% after a three-AP train, and to 41% after a nine-AP train (simulations not shown). Thus, it is predicted that the kinetics of PV binding to Ca²⁺ will be mildly altered with AP number, at least for trains of a few APs.

This was tested experimentally. Results presented so far have been restricted to four-AP trains at 20 msec intervals. This protocol was chosen because Ca_i signals had a good signal/noise ratio and gave reliable kinetic data. However, results with shorter trains were also gathered in some experiments to explore the possible consequences of activity-driven PV saturation. Because τ_f is related to the PV concentration, as discussed above, we focused our attention on this parameter. In WT P19-P21 animals, the average τ_f values were 0.14 ± 0.03 sec and 0.16 ± 0.01 sec for Ca_i rises evoked by two and four APs, respectively (8 and 11 cells, respectively; 100 μm OG1). These results are in agreement with the above notion that PV is not saturated for short AP trains.

Simulation of the dye-free Ca_i transient

The preceding analysis gives an estimate of the PV concentration as well as the buffering capacity of the fast endogenous buffer but does not allow to estimate separately the concentration and the affinity of this buffer. However, within the time scale pertaining to this study, knowledge of the buffering capacity is all that is needed to simulate the Ca_i time course dictated by the endogenous buffers, without the perturbation of added calcium indicator. Fig. 6A shows the calculated decay of the Ca_i transient induced by the standard experimental protocol (i.e., a 50 Hz four-AP train) as well as by a stronger stimulus (10 APs; 50 Hz). For both stimulation protocols, comparison of the WT (Fig. 6A, black traces) with the PV(-/-) (Fig. 6A, gray traces) prediction illustrates the dramatic impact of PV on Ca_i decay. In the absence of PV, Ca_i has returned close to baseline levels 1 sec after reaching its peak. In contrast, when PV is present, a long-lasting tail characterizes the Ca_i decay. Actual PV effects could be even larger, for two reasons. First, the free Mg²⁺ concentration that was chosen for our intracellular solution (660 μm) is at the upper limit of likely physiological values (Li-Smerin et al., 2001); any lower Mg²⁺ con-centration would increase the apparent affinity for Ca²⁺ and thus increase the efficacy of PV to bind Ca²⁺, prolonging the slow decay. Second, it cannot be excluded that some washout of PV occurred during our experiments. For these two reasons, the biphasic pattern of WT Ca_i decay is, if anything, even more marked than is apparent in Figure 6A.

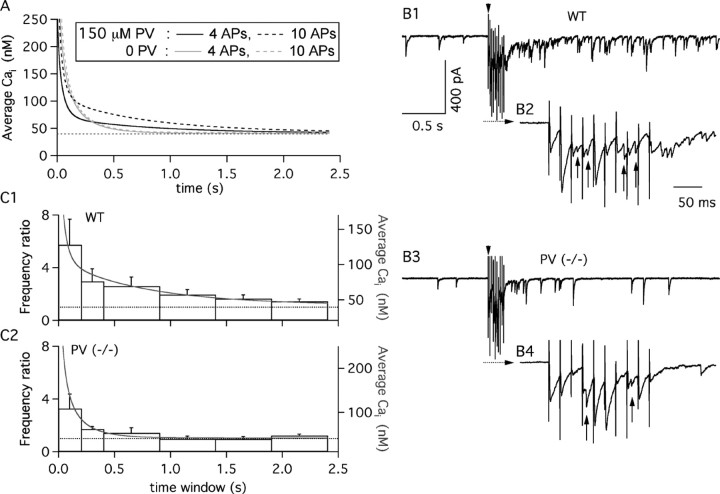
Figure 6.

The time course of Ca_i governs delayed transmitter release at MLI-MLI synapses. A, Predicted averaged Ca_i time course. The black solid trace presents the simulated Ca_i decay after a 50 Hz train of four APs, in the absence of the calcium indicator. The simulation parameters are a resting Ca_i of 40 nm, Caload of 11 μm/AP, 150 μm PV, 60 μm OG1-like buffer, and extrusion kinetic constants of k₁ = 1100 sec^-1 and k_-1 = 0.022 sec^-1. This Ca_i decay is characterized by a biexponential decay (τ_f, 39 msec; τ_s, 626 msec; corresponding amplitude coefficients, 144 and 29 nm). The black dashed trace presents the decay simulated with the same parameters after a 50 Hz train of 10 APs. The Ca_i decay for the PV-free conditions (gray solid trace, 4-AP train; dotted gray trace, 10-AP train) used the following simulation parameters: resting Ca_i of 40 nm, Ca²⁺ load of 11 μm per AP; 60 μm OG1-like buffer; extrusion rates of k₁ = 550 sec^-1 and k_-1 = 0.011 sec^-1. Traces have been truncated at 250 nm to highlight differences in the slow decay phase. B, Comparison of delayed transmitter release in WT and PV(-/-) mice. B1, Representative recording of currents obtained from a P20 WT MLI. The arrowhead indicates the onset of a 50 Hz train of 10 presynaptic stimulations. B2, Expanded view of the recording during the stimulation train, as denoted by the dashed line with the arrow in B1. B3, B4, Representative experiment from a P20 PV(-/-) interneuron. Glutamatergic activity has been blocked as detailed in Materials and Methods. C1, C2, Histograms of the temporal evolution of the mean frequency of synaptic events over the prestimulus frequency, pooled from nine WT and six PV(-/-) interneurons (P19-P21). The error bars represent the SEM. Time 0 corresponds to the end of the extracellular stimulation. The gray traces display the Ca_i time course calculated for a 50 Hz train of 10 APs in A. Values for the WT group were significantly different from one (p < 0.05) for all time bins. For the PV(-/-) group, only the first two time bins have a similar statistical significance.

PV enhances delayed transmitter release

When MLIs discharge in short bursts at 10-50 Hz, as they do under resting conditions in vivo (Eccles et al., 1966; Ekerot and Jörntell, 2001), little summation is expected for the fast component of Ca_i decay, because of a lack of synchronization. The amplitude of the slow decay component, however, increases with the number of spikes. Note the contrast in Figure 6A between the dashed black trace, reflecting the Ca_i decay after 10 APs, with the continuous black trace, simulating four-AP train data. By comparison, residual Ca_i decay in PV(-/-) conditions is short and almost independent of AP number (Fig. 6A, dashed and continuous gray traces). Because bursts of up to 10 APs have been observed in MLIs after parallel fiber stimulation in vivo (Eccles et al., 1966), the question arises as to whether the slow return of the presynaptic Ca_i elevation predicted by the model could induce a measurable increase in transmitter release.

To test these predictions, GABAergic synaptic currents were studied in response to trains of presynaptic stimulations (10 stimuli at 50 Hz) in WT and PV(-/-) mice. Experiments were performed on P19-P21 mice to ensure the presence of PV in all presynaptic fibers of the WT group. As observed previously at other GABAergic synapses (Lu and Trussell, 2000; Kirischuk and Grantyn, 2003), asynchronous release was apparent during the train, with a frequency that increased with stimulus number (Fig. 6B2,B4, vertical arrows point to asynchronous events). However, there was no significant difference between WT and PV(-/-) data concerning asynchronous release frequencies (WT: 10 ± 4 Hz after the 1st stimulus and 29 ± 5 Hz after the 10th stimulus; PV(-/-): 8 ± 2 Hz after the 1st stimulus and 25 ± 4 Hz after the 10th stimulus). Delayed transmitter release (Kirischuk and Grantyn, 2003) was apparent both in the WT (Fig. 6B1) and in the PV(-/-) (Fig. 6B3) groups. Here striking kinetic differences appeared between the two groups. In WT, delayed release extended up to 2400 msec after the train (Fig. 6C1), whereas in PV(-/-) mice, significant delayed release stopped 400 msec after the end of the train (Fig. 6C2). Furthermore, we found that both in the wild type and in PV(-/-), the Ca_i decay predicted from the model (Fig. 6C1,C2, gray curves) superimposed with WT and PV(-/-) data after appropriate scaling. The required scaling factors were in a ratio of 1.5, indicating that in PV(-/-), a given Ca_i signal was 1.5 times less efficient than in wild type in eliciting delayed release. This may be related to the fact that the synapse is depressing in wild type but facilitating in PV(-/-) (Caillard et al., 2000) [likewise in the present experiments, the amplitude ratio of the 10th IPSC over the first was, on average, 0.76 in wild type and 1.11 in PV(-/-)]. We conclude that delayed release is prominent in MLI-MLI synapses and that the presence of PV in the presynaptic terminals markedly prolongs its time course.

Discussion

The presence of PV is a main determinant of Ca_i decay kinetics

Ca²⁺ extrusion is generally mediated by axolemmal pumps and exchangers as well as by intracellular uptake via SERCA pumps and into mitochondria (for review, see Pozzan et al., 1994). All these systems work on similar time scales and together with endogenous Ca²⁺ buffers such as PV shape the decay of Ca_i signals. We found three situations in which the presence of PV profoundly affected the shape of the Ca_i decay in MLI axons, as follows. (1) At P10-P12, PV was present only in basket cells. At this age, basket cells had biphasic Ca_i decay, whereas a large fraction of stellate cells displayed a monoexponential decay. (2) PV was present in stellate cells at P19-P21 but not at P10-P12. We found that the Ca_i decay of P19-P21 stellate cells was best approximated by a biexponential function in a large majority of the recordings, in contrast to young stellate cells. (3) Finally, WT and PV(-/-) results were compared for P10-P12 basket cells and for P19-P21 MLIs. In both cases, removal of PV converted a biexponential decay into a monoexponential one. From these results, we conclude that the presence of PV in MLIs confers a specific kinetic signature for Ca_i decay, characterized by a biexponential time course. This change is accompanied by a marked acceleration of the first part of the decay.

Despite this, a fraction of the decays required a biexponential fit under conditions in which the PV concentration was small or null: in stellate cells from young WT animals, as well as in MLIs from mature PV(-/-) mice. As discussed previously (Koester and Sakmann, 2000), nonlinear clearance systems and/or deviations from the assumptions of the single-compartment model are likely explanations for these findings.

Ca_i decay and intrinsic calcium-buffering capacity in GABAergic versus glutamatergic terminals

Using the single-compartment approximation (Neher, 1998) and procedures developed in chromaffin cells (Neher and Augustine, 1992), estimates have been obtained for κ_S at various glutamatergic terminals. The results ranged from 19 (Jackson and Redman, 2003) to 140 (Koester and Sakmann, 2000), whereas the extrapolated dye-free decay time constant ranged from 30 msec [CA1-CA3 boutons (Sinha et al., 1997)] to 100 msec [calyx of Held (Helmchen et al., 1997)]. From the present study, it appears that the buffering capacity of P19-P21 terminals amounts to 670 (for PV) plus 350 (for the fast endogenous buffer), adding up to a total κ_S value of 1020. Therefore, MLI terminals have a buffering power comparable with that of Purkinje neurons (Fierro and Llano, 1996), one to two orders of magnitude higher than that reported for glutamatergic terminals. Because many GABAergic interneurons are known to contain high concentrations of CBPs, this may reflect a basic difference between the functioning of GABAergic and glutamatergic synapses. In cerebellar MLIs, the endogenous fast buffer and PV exert opposite effects on the speed of the initial decay phase, so that the estimated dye-free decay time constant (39 msec) ends up similar to those calculated for glutamatergic terminals. Thus, the presence of PV may have evolved as a mean to combine the large buffering power common to many GABAergic neurons with the need to obtain a sufficiently fast initial Ca_i decay. In addition, PV induces a prominent second component with a time constant of 0.6 sec. Below, some of the functional consequences of the specific shape of Ca_i decay of MLI terminals are envisaged. An additional, more practical consequence of the large buffering power of GABAergic terminals is that perturbations linked to dye loading are expected to be much less severe in measurements taken from GABAergic than from glutamatergic terminals, making the analysis of presynaptic Ca_i signals easier.

PV and development

Our results suggest that PV expression increases precisely at the time when MLIs stop migrating and start establishing functional synapses. The appearance of PV increases temporal separation between responses to consecutive Ca_i-raising stimuli by accelerating the initial slope of Ca_i decay. Furthermore, it may increase spatial separation between such stimuli, because buffering by PV may decrease the apparent diffusion constant of Ca²⁺. In contrast, the fast buffer that is strongly expressed at P10-P12 slows Ca_i signals and (if it is readily diffusible) may promote their spread along the axon. Our PV(-/-) data suggest that the strength of this buffer declines as PV concentration increases. Thus, the replacement of the fast initial buffer by PV likely contributes to the transition from widespread and slow Ca_i signals used for trophic effects (cell migration and neurite outgrowth) to local and fast Ca_i signals used for synaptic transmission.

Physiological implications

The implications of CBPs in cerebellar function has been assessed previously through the analysis of somato-dendritic Ca_i signaling and motor behavior in mice lacking the fast buffer CB (Airaksinen et al., 1997; Barski et al., 2003; Schmidt et al., 2003a,b). In the present study, we focused on the presynaptic role of the slower buffer PV. As pointed out before (Neher, 1998), the addition of Ca²⁺ buffers does not alter the integral of the Ca_i transient, but rather its kinetics. Therefore, physiological effects are expected mainly on nonlinear or nonintegrating calcium sensors. For instance, in hair cells, the presence of high concentrations of a fast endogenous buffer has long been proposed on experimental and theoretical grounds to regulate calcium-dependent K⁺ channels and hence to influence the cell responses to fast sensory inputs (Roberts, 1993, 1994; Ricci et al., 1998). This buffer has recently been identified as CR in frog saccular hair cells (Edmonds et al., 2000). In the present case, several possible effects of adding or suppressing the slow Ca²⁺ buffer PV may be envisaged.

First, for doublet stimulations, the presence of PV insures a quick decay to a small amplitude slow component, so that facilitation and asynchronous release are both minimal. We found previously that in WT animals, MLI-Purkinje cell synapses display no paired-pulse facilitation (interpulse intervals, 30-100 msec), whereas these synapses display substantial paired-pulse facilitation in PV(-/-) mice (Caillard et al., 2000). This study was performed in P7-P12 MLIs; in retrospect, it appears likely that most recordings were performed with basket cells, given the present finding of selective staining of these cells with a PV-directed antibody.

Second, the presence of PV slows down the late part of the Ca_i decay. We have shown that this effect leads to a prominent slow presynaptic residual Ca_i signal after a train of APs and is then responsible for a very pronounced delayed release that lasts for seconds. Delayed release can be very prominent in GABAergic synapses after trains of ≥10 APs (Lu and Trussell, 2000; Kirischuk and Grantyn, 2003). Our results suggest that this property does not require a special molecular machinery responsible for exocytosis but, more simply, that it is attributable to a prolongation of Ca_i decay because of the presence of powerful Ca²⁺ buffers. They also suggest that PV is particularly effective in this respect because of its slow binding properties. It is important to stress that because of delayed release, a bursting MLI generates a significant synaptic signal even during interburst intervals. Indeed, the integral of the delayed signal in the record illustrated in Figure 6B2 is larger than that of the signal generated during the trains, which is limited by synaptic depression and by receptor saturation (Auger and Marty, 1997). It is therefore interesting to reflect on this unconventional mode of synapse operation. During the interburst period, the MLI gives a random, almost steady synaptic output, with a mean intensity that is primarily determined by the number of APs in the preceding burst. Thus, during bursting, MLIs (and possibly, many other PV-containing interneurons) adopt alternately a phasic signaling mode during the bursts and an integrating signaling mode between bursts.

Third, the Ca²⁺ binding kinetics of PV together with its role on “buffered” diffusion, as discussed above, might affect intracellular Ca²⁺ release channels and could play an important role in shaping GABA release at the presynaptic terminals of MLIs. In Xenopus oocytes, it has been elegantly demonstrated that overexpression of PV can induce Ca²⁺ puffs, which were attributed to spontaneous Ca²⁺ release through inositol trisphosphate receptors (IP₃Rs) (John et al., 2001). More recently, in the same preparation, PV was shown to regulate the spatial distribution of IP₃R-mediated Ca²⁺ puffs (Dargan et al., 2004). No evidence is as yet available for the existence of functional IP₃Rs in MLIs. However, work from our laboratory has shown that ryanodine-sensitive Ca²⁺ stores are functional at their axonal terminals and that they produce highly localized spontaneous Ca_i transients that contribute to neurotransmitter release (Llano et al., 2000). The spatial and temporal dynamics of these events will certainly be shaped by the rather high PV concentration at MLIs terminals predicted from the present study.