Optimal Compensation for Changes in Task-Relevant Movement Variability

Abstract

Effective movement planning should take into account the consequences of possible errors in executing a planned movement. These errors can result from either sensory uncertainty or variability in movement planning and production. We examined the ability of humans to compensate for variability in sensory estimation and movement production under conditions in which variability is increased artificially by the experimenter. Subjects rapidly pointed at a target region that had an adjacent penalty region. Target and penalty hits yielded monetary rewards and losses. We manipulated the task-relevant variability by perturbing visual feedback of finger position during the movement. The feedback was shifted in a random direction with a random amplitude in each trial, causing an increase in the task-relevant variability. Subjects were unable to counteract this form of perturbation. Rewards and penalties were based on the perturbed, visually specified finger position. Subjects rapidly acquired an estimate of their new variability in <120 trials and adjusted their aim points accordingly. We compared subjects' performance to the performance of an optimal movement planner maximizing expected gain. Their performance was consistent with that expected from an optimal movement planner that perfectly compensated for externally imposed changes in task-relevant variability. When exposed to novel stimulus configurations, aim points shifted in the first trial without showing any detectable trend across trials. These results indicate that subjects are capable of changing their pointing strategy in the presence of externally imposed noise. Furthermore, they manage to update their estimate of task-relevant variability and to transfer this estimate to novel stimulus configurations.

Introduction

The outcome of any planned movement is governed by the movement plan itself, but it is also subject to sensory and motor variability. Thus, if you intend to reach across your desk to pick up a pencil quickly, you may spill your cup of coffee instead. The mover's own variability (sensory uncertainty, execution of the motor command) and deviations in the motor trajectory caused by extrinsic sources of noise (unreliability of feedback, externally imposed perturbations) contribute to movement outcome. Variability must be taken into account to maximize the probability of reaching targets while minimizing the probability of hitting other objects.

Experiments indicate that humans use an estimate of sensorimotor variability in selecting a movement plan. For example, as a target is made smaller, people sacrifice speed to increase pointing accuracy (Fitts and Petersen, 1964; Schmidt et al., 1979; Meyer et al., 1988; Plamondon and Alimi, 1997; Smyrnis et al., 2000; Murata and Iwase, 2001; Bohan et al., 2003). Models of motor control have also emphasized that planning needs to take movement variability into account. Specifically, a plan should be chosen that minimizes task-relevant variability while not constraining task-irrelevant variability (Sabes and Jordan, 1997; Harris and Wolpert, 1998; Hamilton and Wolpert, 2002; Todorov and Jordan, 2002).

There are various strategies that the motor system could use to reduce the variability of motor output. For example, the motor system can counteract external physical (force) perturbations by increasing arm stiffness (Burdet et al., 2001; Franklin et al., 2003). In addition, visual and proprioceptive information about the position of the target and the hand as well as previously acquired information can be combined (Körding and Wolpert, 2004; Saunders and Knill, 2004; Sober and Sabes, 2005).

Despite the central role of sensorimotor variability in planning effective movements, there is little experimental evidence that a subject's own variance is incorporated in a quantitatively correct manner. Baddeley et al. (2003) manipulated two types of variability in the relationship between hand position and visual feedback. They found that human pointing was consistent with optimal compensation for those sources of error, suggesting that changes in variability were indeed taken into account in motor planning. However, given their experimental design, they could not determine the specific way in which such changes were incorporated. Other studies have observed behavior consistent with incorporating an estimate of the variability (Körding and Wolpert, 2004) but have not measured independently the variability and change in motor plan.

Our experimental approach allowed us to manipulate task-relevant variability directly. The form of the added variability was impossible for the subjects to counteract. Furthermore, the experimental design allowed us to calculate the optimal adjustment in the aim point of the movement, given the introduced variability, and compare it with subjects' responses. The calculation of the optimal aim point had no free parameters. Thus, the data and analysis reported here are the first to test directly whether subjects optimally compensate for changes in motor variability.

Materials and Methods

Apparatus. Visual stimuli were displayed on a computer display suspended from above. Subjects viewed the stereoscopically displayed visual stimulus in a mirror using CrystalEyes liquid-crystal shutter glasses. A head-and-chin rest limited head movement. A lightly textured, fronto-parallel plane was presented in front of the subject, and the stimuli were presented on this plane. A PHANToM force-feedback device tracked the three-dimensional (3-d) position of the right index fingertip. A more detailed description of the apparatus can be found in Ernst and Banks (2002) (supplemental material, available at www.jneurosci.org). The hand itself was not visible, but the fingertip was represented visually by a small cursor (4 mm diameter). The apparatus was calibrated so the visual and haptic stimuli were superimposed in the workspace. In some conditions, the visual representation of the fingertip was displaced from its actual position thereby perturbing the visual feedback (supplemental material, available at www.jneurosci.org). When the finger reached the visually rendered frontal plane, haptic feedback was provided by the PHANToM: the finger “hit” the plane.

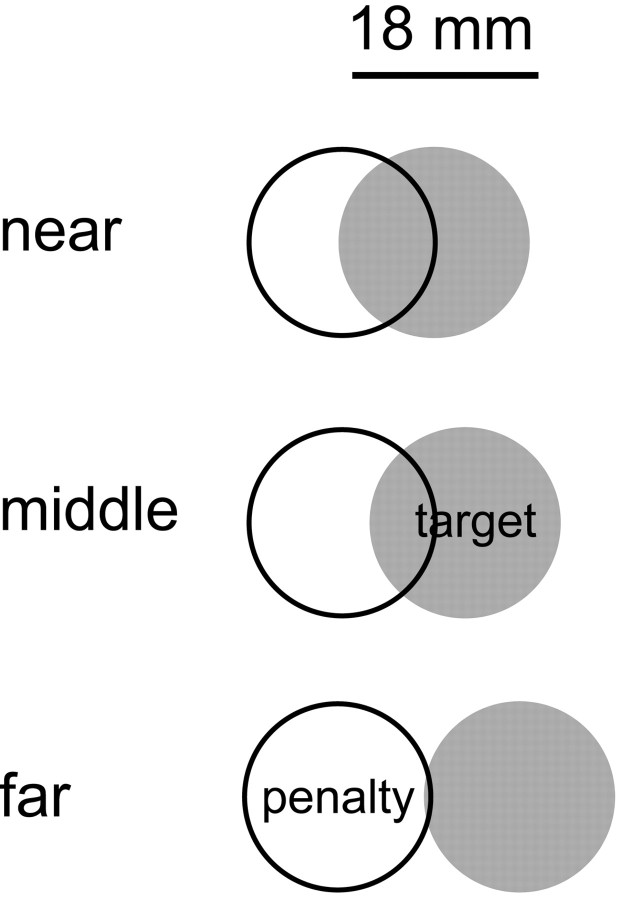
Stimuli. The stimuli consisted of one target region and one penalty region. The target region was a filled green circle, and the penalty region was an unfilled red circle. Overlap of the target and penalty was readily visible. The target and penalty regions had radii of 9 mm. The center of the penalty region was 9 (near), 13.5 (middle), or 18 mm (far) left or right of the center of the target region (Fig. 1).

Figure 1.

Stimulus configurations. The green target (indicated by a gray disk) and red penalty areas were circular, with diameters of 18 mm. The target was displaced leftward or rightward relative to the penalty region by one of three amounts:near, medium, and far (9, 13.5, and 18 mm, respectively).

The position of the penalty region was selected randomly on each trial to prevent subjects from using preplanned movements; the position was chosen from a uniform distribution with a range of ±44 mm relative to screen center. A central 200 × 100 mm frame indicated the area within which the target and penalty regions could appear.

Procedure. In the task, subjects earned money by rapidly hitting targets that carried a known reward (100 points) while avoiding hitting a nearby penalty region carrying a known loss (0, 200, or 500 points). Subjects were instructed to earn as many points as possible. They were required to complete the finger movement within 650 ms of the presentation of the stimulus; if they did not, they incurred a timeout penalty of 700 points. Three amounts of isotropic Gaussian perturbation of the visual feedback of the finger position were added: zero, medium, or large perturbation.

Subjects first underwent a training session with no perturbation to learn the speeded pointing task, including its time constraints. They were then presented with the three amounts of perturbation in different experimental sessions (ordered randomly). With each new amount, they performed training trials to learn the new task-relevant variability. Conditions in the training sessions (only penalties of 0 and 200 points, and middle and far condition) differed from those used in the actual experiment. After the training session, they were presented experimental trials with the three penalties (0, 200, and 500 points) and the three target-penalty configurations (near, middle, and far). The configurations were presented in random order, and the position of the configuration was selected randomly on each trial to prevent subjects from using preplanned movements.

The procedure in a single trial was similar to the one used by Trommershäuser et al. (2003a,b). The appearance of a fixation cross indicated the start of a new trial. The subject moved the right index finger to the starting position, represented by a 24 mm sphere. He or she was required to stay at the starting position until the stimulus appeared (otherwise, the trial was aborted). The frame was then displayed, followed 500 ms later by the target and penalty regions. Subjects were required to touch the stimulus plane within 650 ms or they would incur a timeout penalty of 700 points. The point in which the subject touched the plane is the end point of the movement, denoted (x, y). If the subject touched the plane at a point within the target or penalty region, the region “exploded” visually. The points awarded for that trial were then shown, followed by the total accumulated points for that session.

A target hit was always worth 100 points. A penalty hit cost 0, 200, or 500 points and was altered between blocks of trials. If the stimulus plane was touched in the region in which the target and penalty overlapped, the reward and penalty were both awarded. If a subject moved from the starting position before or within 100 ms after stimulus presentation, the trial was abandoned and repeated later during that block.

Subjects ran a total of 10 sessions. The first was a practice session during which the timing of the task was learned. In the practice session, subjects first ran 32 trials (eight repeats of each of the four spatial configurations far/left, far/right, middle/left, middle/right) in the zero-penalty condition with no time limit. This was followed by four blocks of 24 trials (i.e., six repeats) with a moderate time limit of 850 ms, followed by six blocks of 24 trials with a 650 ms time limit. Then, three consecutive sessions were run with each amount of perturbation. The first of the three sessions was a learning session in which the subject learned the new task-relevant variability. In the learning session, the subject first ran a warm-up block of 32 trials with zero penalty. Then, the cumulative score was reset to 0, and 10 additional blocks of 24 trials were run (five blocks with penalty zero and five with a penalty of 200; penalty level alternating between blocks, with six repeats of each middle and far target location in each block). The learning session was followed by two experimental sessions of 372 trials each. Experimental sessions consisted of 12 warm-up trials followed by 12 blocks of 30 trials (four blocks for each of the three penalty levels; five repetitions per target location per block) in random order. Sessions with different amounts of perturbation were run on different days to facilitate learning of the new task-relevant variability. The order of exposure to the different amounts of perturbation was counter-balanced across subjects. Each session lasted ∼45 min.

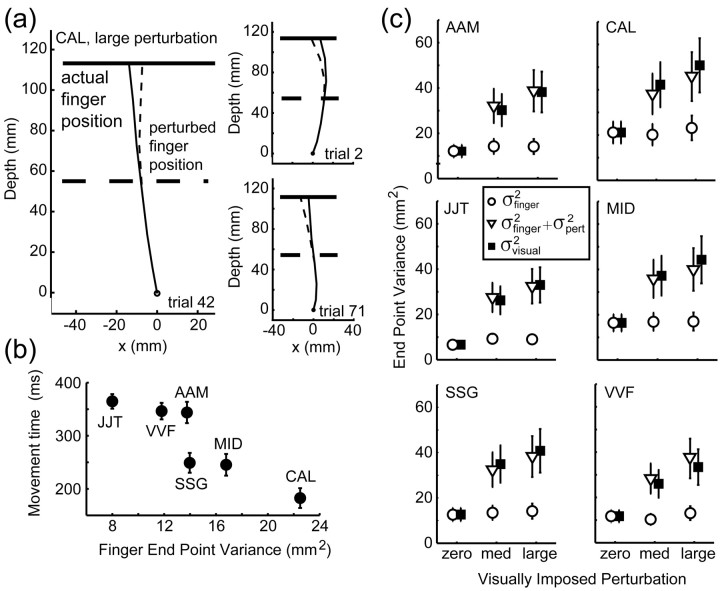
Visually imposed increase in task-relevant variability. At the beginning of each trial, the visually specified position of the fingertip (the cursor) was in the same 3-d location as the fingertip itself. The actual end point where the finger hit the stimulus plane was (x,y). On perturbation trials, the cursor was displaced smoothly relative to the true, but invisible, location of the fingertip during the second half of the movement (supplemental material, available at www.jneurosci.org). The displacement on each trial (Δx,Δy) was chosen from a bivariate Gaussian distribution with mean (0,0), and a spatially isotropic variance; displacements >12 mm were not presented to avoid subjects missing the target by amounts much larger than the target radius. The cursor hit the plane at the visually specified end point (x +Δx,y +Δy) (see Fig. 4a). Rewards and penalties were scored based on the perturbed (and more variable) visually specified finger position, forcing subjects to estimate their new task-relevant variability to optimize performance. Three different SDs of the Gaussian perturbation distribution were used (0, 4.5, and 6 mm). Given the truncation at 12 mm, this resulted in perturbation SDs σ_pert = 0 mm (zero perturbation), σ_pert = 4.4 mm (medium perturbation), and σ_pert = 5.3 mm (large perturbation).

Figure 4.

Effect of perturbation on finger position. a, Trajectories of actual (solid line) and perturbed (dashed line) finger position of subject CAL during individual trials (trials 2, 42, and 71 in the large perturbation condition). b, Correspondence between variance of the actual finger position and movement times (variance estimates averaged across all conditions per subject). c, Effect of varying the perturbation for each subject. Filled squares represent the measured variance 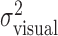of the perturbed cursor position, open circles represent the measured variance of the actual finger position 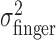, and open triangles represent the sum of the variance of the actual finger position and of the applied perturbation 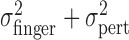. The sum of the two variances is similar to the values of 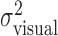, indicating that subjects did not compensate for the added perturbation. (Variance estimates are based on 720 data points per level of perturbation; data were pooled across x and y directions. Error bars indicate SEM for averaging variances across the 36 conditions.)

Subjects and instructions. Six subjects participated; four were unaware of the experimental purpose, and the other two were authors (JJT, SSG). The four naive subjects were paid for their participation; they also received bonus payments determined by their cumulative score (25 cents per 1000 points). The naive subjects were not informed of the visual feedback perturbation. Before each new perturbation condition, subjects received instructions that a “slight change” had been introduced that might interfere with their accuracy and would require them to practice the task again, before “they would be exposed to the more difficult conditions again” (i.e., those used during data recording). All subjects used their right index finger for the pointing movement. Subjects were informed of the payoffs and penalties before each block of trials. All subjects but one were righthanded, and all had normal or corrected-to-normal vision. Subjects gave informed consent before testing.

Model of optimal movement planning. In previous work, we developed a model of optimal movement planning based on statistical decision theory (Trommershäuser et al., 2003a,b). We assumed that the goal of movement planning was to select an optimal visuomotor movement strategy (i.e., a movement plan) that specifies a desired movement trajectory, a method for using visual feedback control, and so on. In this model, MEGaMove (Maximize Expected GAin for MOVEment planning), the optimal movement strategy is the one that maximizes expected gain. The model takes into account explicit gains associated with the possible outcomes of the movement, the mover's own task-relevant variability, biomechanical costs, and costs associated with the time limits imposed on the mover. Here, we summarize the key elements of the model as applied to our task.

For the conditions of our experiment, the scene is divided into three regions: a circular target region (R₁) with a positive gain, a circular penalty region (R₂) with no gain or a negative gain, and the background (no gain). An optimal visuomotor strategy, S, on any trial is one that maximizes the subject's expected gain, as follows:

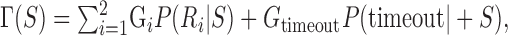(1)

where G_i is the gain the subject receives if region R_i is reached on time (G₁= 100 points for hitting R₁; G₂ = 0, -200, or -500 points for hitting R₂). P(R_i|S) is the probability, given a particular choice of strategy S, of reaching R_i before the time limit (t = timeout) has expired, as follows:

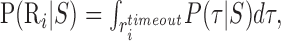(2)

where R^timeout_i is the set of trajectories τ, that pass through R_i at some time after the start of the execution of the visuomotor strategy and before the timeout. Because the task involves a penalty for not responding before the time limit (G_timeout = -700), Equation 1 contains a term for this timeout penalty. The probability that a visuomotor strategy S, leads to a timeout is P(timeout|S).

In our experiments, subjects win and lose points by touching the reward and penalty regions on a plane before the timeout. Penalties and rewards depend only on the position of the end point in this plane, so a strategy S can be identified with the mean end point on the plane (x,y), which results from adopting strategy S. We found that subjects' movement variance was the same in the vertical and horizontal directions (and stable throughout the experiment). Thus, we assume that the movement end points (x′,y′) are distributed according to a spatially isotropic Gaussian distribution with width σ, as follows:

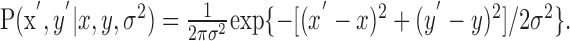(3)

The probability of hitting R_i is then:

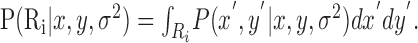(4)

In our experiments, the probability of a timeout is effectively constant over the limited range of relevant screen locations. Therefore, for a given end point variance σ², finding an optimal movement strategy corresponds to choosing a strategy with mean aim point (x,y) that maximizes:

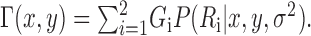(5)

This integral was solved by integrating Equation 4 numerically (Press et al., 1992) and using the results to maximize Equation 5.

In our experiments, the optimal strategy depends on the position and magnitude of the penalty and on the distribution of the subject's end points. When the penalty is zero, the optimal aim point (and hence the mean end point) is the center of the target region. When the penalty is nonzero and near the target, the optimal aim point shifts away from the penalty region and, therefore, away from the center of the target. This shift is larger for greater penalties, for penalty regions closer to the target, and for larger perturbations of visual feedback (Fig. 2).

Figure 2.

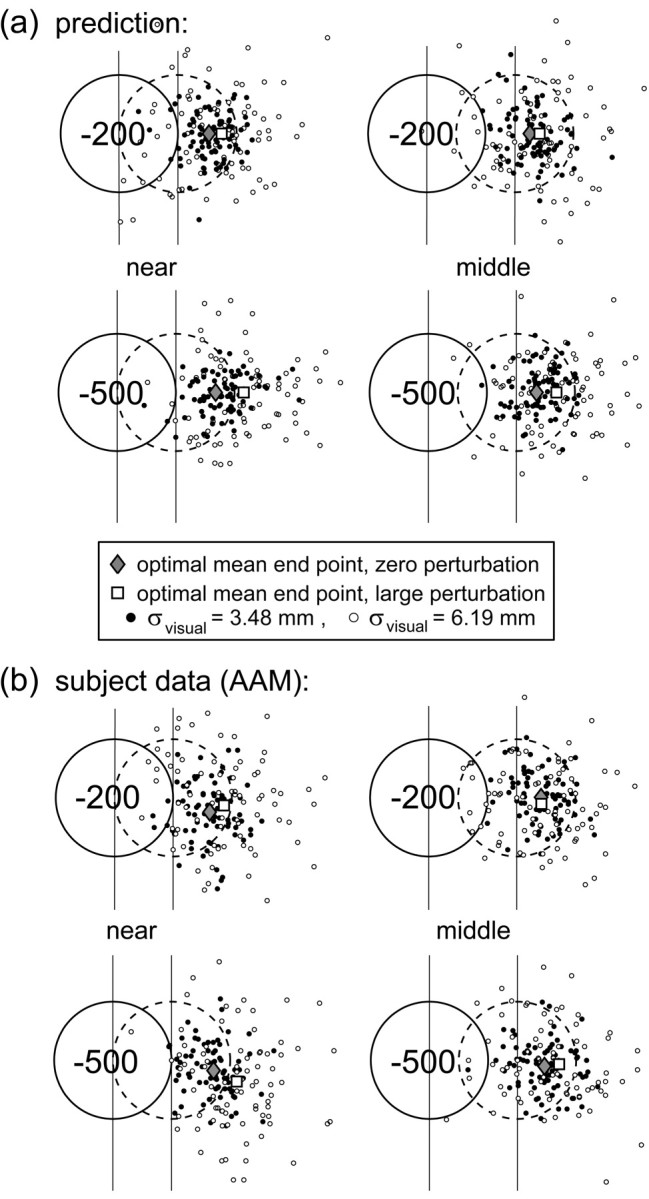
Predictions for an optimal movement planner and actual subject data. a, Simulations of an optimal movement planner. Eighty simulated responses are shown per condition for the zero and large perturbation conditions and four combinations of penalty value and target position. The circles represent the penalty (solid line) and target (dashed line) regions (centers indicated by the vertical lines). The two levels of task-relevant variability (filled circles, σ_visual = 3.48 mm; open circles, σ_visual = 6.19 mm) correspond to subject AAM's estimated task-relevant variability in the conditions with zero and large perturbation. The gray diamond indicates the optimal mean end point in the condition with zero perturbation, and the open square indicates the optimal mean end point in the condition with large perturbation. The optimal movement planner aims at the center of the target circle in no-penalty conditions (data not shown) but aims farther away from the penalty circle as penalty value and amount of perturbation increase and distance to the penalty circle decreases. b, Subject AAM's actual movement end points for the same four conditions and two levels of task-relevant variability as in a. Data are combined for spatially symmetric configurations (80 data points per condition).

For all conditions, we compared subjects' mean end points to those of an optimal movement planner that maximizes expected gain by taking into account its own task-relevant variability. Once we measured the task-relevant variability for each subject and for each level of perturbation, our model yielded parameter-free predictions of optimal behavior for all experimental conditions.

Data analysis. For each trial, we recorded reaction time (the interval from stimulus display until movement initiation), movement time (the interval from leaving the start position until the screen was touched), the movement end position of the actual finger position, the movement end position of the visual cursor, and the score. Trials in which the subject left the start position <100 ms after stimulus onset or hit the screen after the time limit were excluded from the analysis.

Data format. Each subject contributed ∼2160 data points (i.e., 80 repetitions per condition) (with data collapsed across left-right symmetric configurations). On each trial, the actual end-point positions (x_j, y_j), j = 1,... 80, were recorded relative to the center of the target circle. The corresponding visually specified end-point positions were (x_j +Δx_j, y_j + Δy_j).

Responses in symmetric configurations. The target was displaced leftward from the penalty region in one-half of the trials and rightward in the second half. We asked whether the distribution of movement end points differed with respect to symmetric configurations and found that there were no significant differences (sum of mean movement end points with respect to symmetry axis not significantly different from zero; p > 0.05 in all conditions). This means that the distributions of end points were not skewed differently for trials in which the penalty was to the left of the target as opposed to trials in which it was to the right of the target. The observation of symmetry justifies averaging data across the leftward and rightward target displacements for each condition, and we did so.

Tests of homogeneity and isotropy of variance of movement end points. From the end-point data, we estimated the subject's actual end-point variance 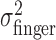for each level of perturbation. The subject's task-relevant variability 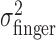was estimated similarly to 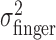, using (x_j +Δx_j, y_j + Δy_j) in place of (x_j, y_j). For each amount of perturbation and each subject, we tested whether actual end-point variances, 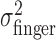, and task-relevant variances, 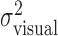, in the x and y directions were affected by manipulations of target location and penalty value. Levene tests (Howell, 2002) were performed to test for the homogeneity of the variances in the x and y directions across the 18 spatial and penalty conditions. We found no significant differences in either variance across stimulus configurations and penalty amounts. We then compared variances (pooled across spatial and penalty conditions) in the x and y directions and found that the distribution of end points was isotropic. We also found no evidence of correlation between the x and y directions.

These results justify computation of one estimate of task-relevant end-point variance per subject and perturbation condition by averaging over the x and y directions, all spatial configurations, and all penalty values. For each perturbation condition, we averaged the 36 variance estimates, resulting in pooled estimates of 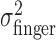and 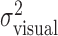. We checked whether the subject's actual end-point variance 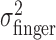was constant across perturbation conditions and found that it was. Subjects did not change movement strategy in different perturbation conditions, with changes in penalty amount, or penalty position in a way that affected the variability of the movement. Thus, changes in movement strategy could be well characterized by changes in mean end points.

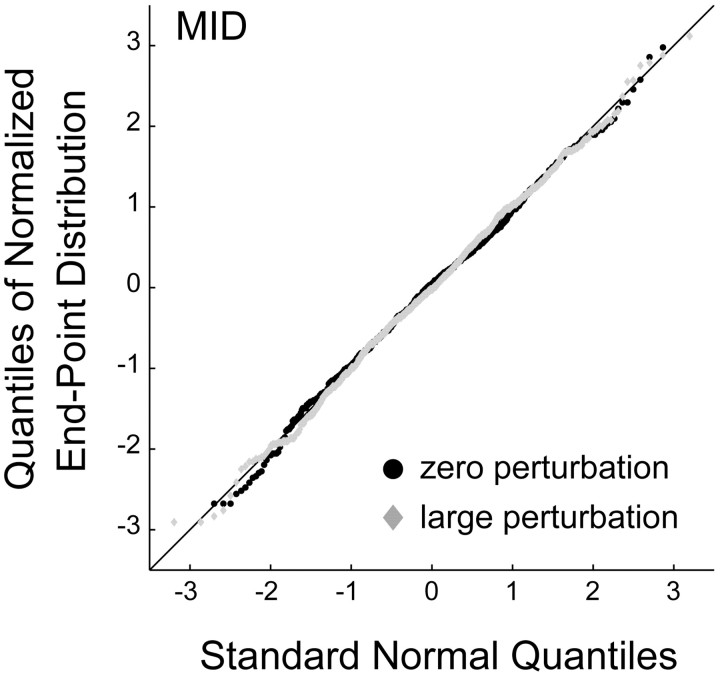
Fit of movement end points by a Gaussian distribution. In our analysis, subjects' performance is compared with the model of optimal movement planning individually for each subject, based on each subject's recorded estimate of task-relevant movement variability, 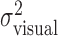. Our model assumes that movement end points are distributed according to a (spatially isotropic) Gaussian distribution. To test this assumption, we compared the distribution of task-relevant movement end points to a Gaussian distribution (Fig. 3). In constructing the figure, the x and y coordinates of each end point were treated identically, as if they were drawn from the same distribution. For each quantile of this combined set of x and y end points, the quantile-quantile plot in Figure 3 plots a point with ordinate value equal to the z-score of the corresponding end-point position and abscissa value equal to the quantile for a normal distribution with mean = 0 and SD = 1 (Gnanadesikan, 1997; Rencher, 2002). The close correspondence between the resulting data points and the solid diagonal line is strong evidence that the distribution is Gaussian. This was the case in all subjects, for all three amounts of perturbation including 0. In addition, the distribution of task-relevant movement end points in the large perturbation condition did not differ significantly in shape from a Gaussian distribution [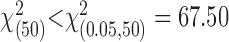, for all subjects; χ² values, subject AAM, 41.81; subject CAL, 45.53; subject JJT, 56.84; subject MID, 55.17; subject SSG, 59.83; subject VVF, 33.35].

Figure 3.

Distribution of task-relevant variability. Quantile-quantile plots (Gnanadesikan, 1997;Rencher, 2002) of subject MID's task-relevant movement end points. Black corresponds to end points with zero perturbation, and gray corresponds to end points with large perturbation (720 data points per condition; data pooled across x and y directions; data for subject MID with zero perturbation were collected in sessions 2-4, and data for large perturbation were collected in sessions 8-10).

As noted above, the Gaussian distribution of added perturbations was truncated at 12 mm. This implies that the Gaussian distribution of applied perturbations was cut off at the 0.4th and 99.6th percentile for σ_pert = 4.4 mm and the 2.28th and 97.7th percentile for σ_pert = 5.3 mm. However, as indicated by the above results, the distribution of the visual cursor position still did not deviate significantly from a Gaussian distribution.

Tests of compensation for perturbation of visual feedback. We tested whether observers compensated for the imposed perturbation in two ways. First, if the subject's actual end points were independent of the perturbation, then 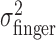should equal the sum 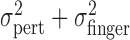. We found this to be the case (Fig. 4c). We then tested directly whether subjects managed to compensate for the perturbation in visual feedback during a single trial by asking how much of the actual finger position correlated with the trial-by-trial perturbation. For each trial, we computed the two-dimensional (2-d) deviation of the actual finger position from the mean of the corresponding condition and correlated it with the 2-d perturbation on that trial. Data in the large perturbation condition were pooled across penalties and spatial configurations and across x and y components to estimate an overall correlation coefficient. If subjects compensated for the perturbation during a trial, one would predict a significant negative correlation between actual finger position and perturbation. Correlations between actual finger position and perturbation were low (see Results). We also tested whether compensation occurred according to the perturbation in the previous trial. To estimate errors induced by the perturbation in the previous trial, we computed the correlation between the perturbation (Δx_j, Δy_j) and deviations in finger position from the mean in the respective condition of the finger position in the following trial (x_{j + 1} - x̄, y_{j + 1} - ȳ). Thus, a single correlation coefficient was computed per subject across all conditions; it indicated that the effect induced by perturbations of the previous trial was small (see Results).

Reaction times and movement times. We also looked for changes in reaction and movement times across conditions. We analyzed both measures for each subject in a three-factor, repeated-measures ANOVA. These factors were target position, penalty level, and amount of perturbation. We found no significant differences in reaction or movement time across these variables.

Effect of spatial and penalty conditions. To determine whether subjects shifted their movement end points in response to changes in perturbation amount (i.e., σ_pert, the task-relevant variability), we analyzed the end points for each subject in a three-factor, repeated-measures ANOVA. The factors were target position (averaged over symmetric configurations), penalty level, and amount of perturbation. The data are displayed in Figures 5 and 6.

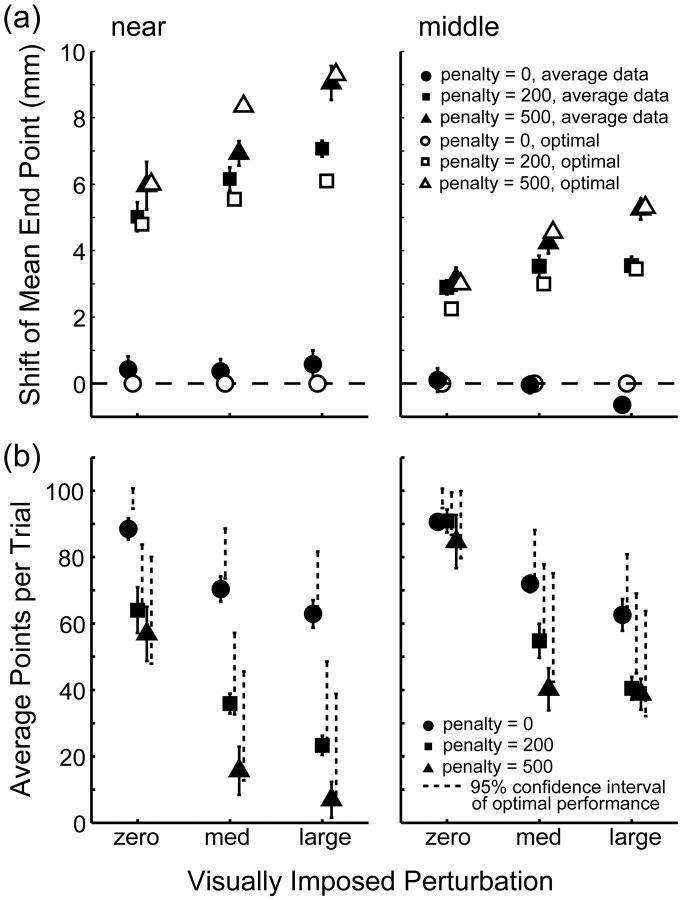
Figure 5.

Comparison of average subject data with the optimal performance model. a, Horizontal shift of actual end points from the center of the target away from the penalty averaged across subjects as a function of added perturbation for the near (left) and middle (right) conditions. The filled triangles, squares, and circles represent recorded shifts when the penalty value was 500, 200, and 0, respectively. Open symbols indicate shifts as predicted for an optimal movement planner (with averaged movement variability). The shift is larger with larger penalty, larger perturbation, and closer penalty region. b, Points scored averaged across subjects. Average points per trial are plotted as a function of added perturbation for the near (left) and middle (right) conditions. Dashed lines indicate the corresponding 95% confidence interval of optimal performance. Performance drops with larger penalty, larger perturbation, and closer penalty region. Error bars indicate SEM for averaging across the six subjects.

Figure 6.

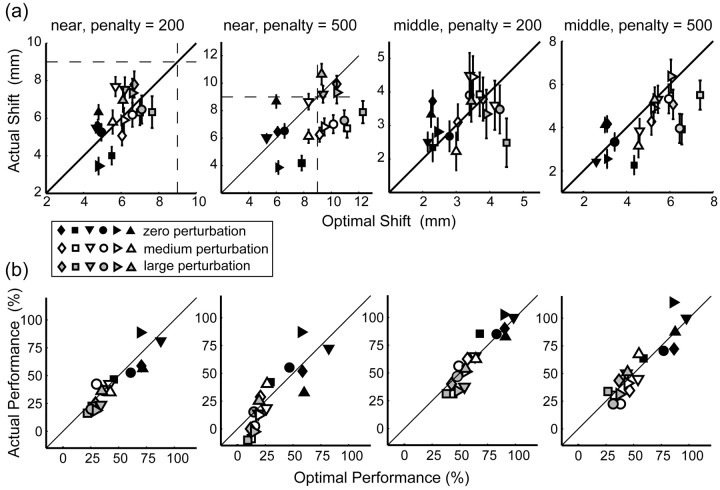
Comparisons of observed and optimal shifts and performance for individual subjects. Data are displayed for the near and middle conditions for penalty values of 200 and 500. a, Horizontal shift of mean end points from target center plotted against the optimal shift predicted by our model. Model predictions were computed based on each subject's variance. Diagonal lines represent perfect correspondence of observed and predicted optimal end points. Vertical and horizontal dashed lines indicate the position of the edge of the target circle. Symbol color represents different amounts of perturbation (black, zero perturbation; white, medium perturbation; gray, large perturbation). Different symbols represent data from different subjects (from left to right: AAM, CAL, JJT, MID, SSG, and VVF). Error bars indicate SEM. b, Average number of points earned per trial plotted against optimal number of points per trial as predicted by our model. Model predictions were computed based on each subject's variance.

Comparison to model predictions. Mean movement end points for each condition were compared with the end points predicted by our model of optimal movement planning. We calculated the optimal end points (x_opt, y_opt) based on each subject's estimated task-relevant variability 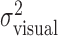, for each amount of perturbation. Note that y_opt = 0 for all conditions. The comparisons are displayed in Figures 5 and 6.

Distribution of optimal performance and computation of efficiency. The model predicts clear differences in mean movement end points when the penalty is large and not far from the target. Thus, when discussing the results, we focused on penalties of 200 and 500 and on the near and middle configurations. We computed the cumulative score across these conditions for each subject and for the model. Efficiency was then computed for each subject individually as the ratio of the subject's cumulative score and the optimal score (i.e., maximum expected gain) predicted by the model. The optimal scores were computed in a Monte Carlo simulation consisting of 100,000 runs of the optimal movement planner performing the experiment with each subject's variance (for the equivalent number of conditions and repetitions).

Testing optimality. We tested whether subjects' performance is optimal. Because optimality corresponds to a failure to reject the null hypothesis, it is important to determine the power of the hypothesis test (Mood et al., 1974). For example, if a subject's efficiency was in fact only 90%, the power of the test is the proportion of experiments for which the null hypothesis would be correctly rejected for this subject (1 - type II error rate). The summary power statistics that we reported in Table 1 are the efficiencies that would lead to correct rejection of the null hypothesis of optimality with probabilities 0.5 and 0.95.

Table 1.

Efficiency

	Efficiency
Subject	Zero perturbation	Medium perturbation	Large perturbation
AAM	92.2% (98.5%; 80.2%)	103.5% (95.6%; 62.7%)	102.5% (94.2%; 59.2%)
CAL	107.0% (96.7%; 67.3%)	92.8% (94.4%; 52.5%)	82.4% (93.7%; 50.6%)a
JJT	96.6% (99.6%; 84.2%)	92.2% (97.0%; 68.5%)	93.0% (95.8%; 63.0%)
MID	100.1% (98.1%; 77.8%)	93.2% (95.0%; 57.7%)	93.6% (93.9%; 54.4%)
SSG	114.7% (98.4%; 76.5%)	99.7% (95.5%; 61.5%)	88.8% (94.0%; 58.3%)
VVF	93.8% (81.2%; 65.1%)	109.4% (96.7%; 65.1%)	113.3% (94.9%; 61.2%)

Data are reported for the six subjects and three levels of task-relevant variability. Efficiency is the cumulative score in the penalty of 200 and 500 conditions in the near and middle configuration divided by the corresponding expected score of an optimal movement planner with the same task-relevant variability. The numbers in parentheses correspond to efficiencies for which the probability of correctly rejecting the hypothesis of optimality is 0.5/0.95 (corresponding to a type II error rate of 0.5/0.05).

^a Significant deviations from optimality (outside the 95% confidence interval).

Results

There are several aspects to the results, and here we first provide a brief overview. We report that subjects did not adjust their movements on a given trial to correct for the perturbation applied on that trial. This is important because it shows that our manipulation of task-relevant variability was effective. We then examine how well subjects managed to adjust for increases in task-relevant variability. We compare the observed shifts in movement end points with increasing task-relevant variability with the shifts of an optimal movement planner. Our results are consistent with the claim that subjects adjusted their end points optimally to compensate for increases in task-relevant variability. Next, we present data that indicate that subjects acquired a new estimate of their task-relevant variability and are able to use that estimate in novel conditions. Finally, we present evidence that subjects' behavior was stable before data recording began and remained so throughout the experiment.

No compensation for perturbation of visual feedback

We first tested whether subjects compensated for the experimentally imposed perturbation (Δx_j, Δy_j) by altering finger position during the movement. When asked about their experience during the experiment, the naive subjects reported that they had noticed a decrease in pointing accuracy and a drop in score (in the conditions in which we added a perturbation) but could not explain the cause of this effect. Consistent with these reports, four pieces of evidence show that subjects did not compensate for the added perturbation on a given trial during the movement on that trial.

First, we examined the variance of the actual finger position, 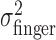, for the three different amounts of perturbation (Fig. 4c, open circles). Clearly, 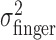did not change when a perturbation was applied (p > 0.05 for all subjects in all cases). (Also, 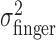did not vary with target-penalty configuration nor with the amount of the penalty; p > 0.05 for all subjects in all cases.)

Second, we looked for evidence of compensation for the applied perturbation during a single trial. For each subject, we computed the overall correlation between the trial-by-trial variation of the actual finger position and the trial-by-trial direction of the applied perturbation. This correlation coefficient differed significantly from 0 for only one of six subjects, and the r values were quite small, accounting for <1% of the variance (r values, subject AAM, -0.08^*; subject CAL, -0.01; subject JJT, -0.03; subject MID, 0.02; subject SSG, -0.02; subject VVF, -0.08, the asterisk indicates significance at p = 0.05; ∼1430 data points for all subjects), indicating that subjects failed to compensate on a given trial for the applied perturbation on that trial. We also tested whether compensation for the applied perturbation occurred in the next trial and found little correlation between the direction of the applied perturbation and finger position in the following trial, again accounting for <1% of the variance (r values, subject AAM, 0.09; subject CAL, -0.02; subject JJT, -0.04; subject MID, 0.05; subject SSG, -0.08^*; subject VVF, -0.10^*; the asterisk indicates significance at p = 0.05; ∼1430 data points for all subjects).

Third, we analyzed the dynamics of individual trajectories and found no evidence that subjects made an on-line correction to their movement in response to the applied perturbation. Trajectories showed no change in direction in response to the applied perturbation (Fig. 4a). Average movement times were stable for three conditions of perturbation, as well as across spatial and penalty conditions, and fell in the range of 191 ± 46 ms (subject CAL) to 367 ± 34 ms (JJT) (Fig. 4b). The perturbation was not applied until the second half of the movement (Fig. 4a) (see supplemental material, available at www.jneurosci.org), which is approximately the final 90-150 ms of the movement. The use of visual feedback has a latency of ∼200 ms (Saunders and Knill, 2004), so the visual perturbation almost certainly occurred too late to affect the movement.

Fourth, we noted above that the trial-by-trial measurements of finger position were uncorrelated with the added perturbations. This lack of compensation implies that the sum of motor variability and added perturbation (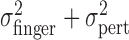) is equal to 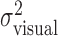, the variance of the visually specified end points. Figure 4c shows 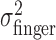(open circles) and the sum of the variances 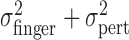(open triangles). The sum is indeed not significantly different from 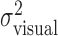(Fig. 4c, filled squares) (F test; all p > 0.05).

Optimal compensation for changes in task-relevant variability

We next quantified how well subjects managed to compensate for the manipulation of their task-relevant variability. The data of most interest here are the shifts in mean end points with changes in penalty value, target-penalty configuration, and, most importantly, task-relevant variability. We compared these observed shifts with the shifts of an optimal movement planner (Trommershäuser et al., 2003a,b).

The optimal planner exhibits larger horizontal shifts of the aim point (and therefore the mean end point) away from the penalty region with increasing penalty, closer spatial configurations, and larger perturbation (Fig. 2 shows an example of predictions based on subject AAM's variability and how the predictions compare with subject AAM's data as recorded during the experiment).

Figure 5a compares the observed shifts in mean end points (the actual positions of the finger at the end of the movements) away from the center of the target (averaged over trials and subjects) with the predicted shifts in mean end points (predictions based on an averaged estimate of movement variability). An optimal movement planner will not shift aim point when the penalty is zero. Subjects behaved similarly: mean end points did not shift in the zero-penalty condition. An optimal movement planner will shift aim point when the penalty is greater than zero, more so as the penalty becomes large, the penalty region becomes closer to the target region, and as the perturbation becomes larger (data are not displayed for y direction and far condition). Subjects exhibited quite similar behavior. They shifted when the penalty was different from zero. They shifted farther from the target center with higher penalties, closer target positions, and larger perturbations. In general, the observed shifts are similar to the shifts of the average optimal planner (Fig. 5a).

Figure 6a also compares observed shifts of mean end points with the shifts of an optimal movement planner but for each subject individually (model predictions based on each subject's individual task-relevant variability). All subjects shifted farther from the penalty region when a larger perturbation was applied (gray symbols), when penalty and target regions were closer (near vs middle), and when the penalty was greater. There was one condition in which subjects clearly deviated from the predictions for an optimal movement planner. In the near, high-penalty condition, an optimal movement planner aims several millimeters outside of the target region (the outer edge of which is represented by the vertical and horizontal dashed lines). Subjects shifted their end points away from the target center but not consistently outside the target region. We suspect that the reluctance to aim outside the target reflects the subject's long-standing experience that hitting a target requires aiming at it or at least near it (Körding and Wolpert, 2004).

Subjects were instructed to earn as many points as possible and not to aim at a certain point. Thus, it is important to compare the points that subjects scored with the score of the optimal movement planner with the same movement variability. The comparison is shown in Figure 5b, which displays the score per condition (averaged across subjects and conditions) and the 95% confidence intervals for an optimal movement planner (with averaged task-relevant variability). Subjects' scores were similar to those of the optimal planner; subjects' and model scores were lower with higher penalties, closer penalty regions, and larger perturbations. Figure 6b shows the individual data of the six subjects and how their scores compare with the scores of the corresponding optimal movement planner. The correspondence between observed and predicted optimal scores is excellent (Table 1) except for one subject in one condition (subject CAL; in the condition with largest perturbation) (Fig. 6b, gray squares). Scores were otherwise statistically indiscriminable from optimal.

Overall, performance did not differ significantly from optimal, indicating that subjects compensated for visually imposed changes in their task-relevant variability by appropriately adjusting their movement end points. We report summary power statistics for the hypothesis tests in Table 1. These serve as bounds on the possible deviations of subjects from optimal efficiency.

Transfer of variability to novel conditions

The shifts in movement end point with increasing perturbation (Figs. 5a, 6a) show that subjects took their task-relevant variability into account in planning their movements. It is therefore reasonable to assume that the motor system has access to a representation of this variability. We next analyzed the data to look for hints as to how the system generates such an estimate.

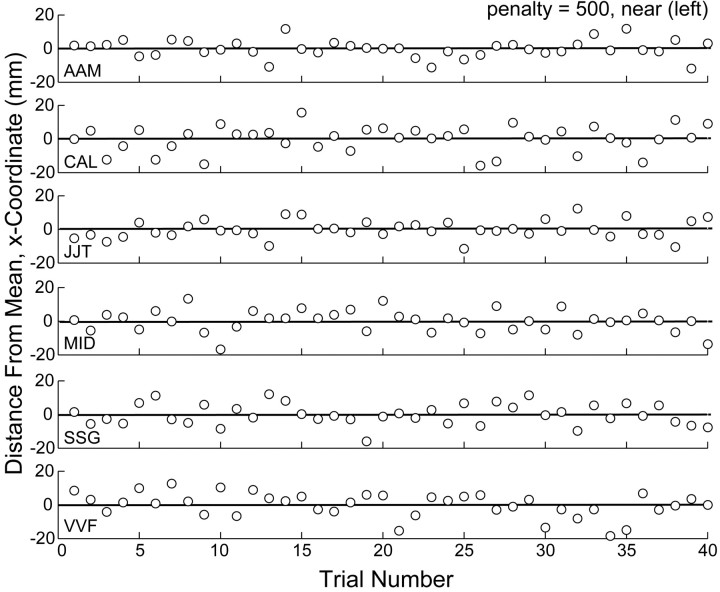
Before we started data collection for a given perturbation, subjects practiced with that perturbation for 272 trials with penalties of 0 and 200 and with the middle and far conditions. The variances of the actual end points 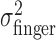reached stable values within the first five blocks (i.e., the first 120 trials) of the learning session (Fig. 7). Subjects were never exposed in this learning session to penalties of 500 or to the near-spatial condition. When data collection began, aim points in the near, penalty 500 condition shifted in the first trial without any detectable trend across trials. Furthermore, there was no systematic shift with increasing trial number (Fig. 8). These results show that subjects incorporated the change in task-relevant variability into their movement plan for a novel situation by the first trial. Thus, they were able to apply their estimate of variability optimally, or nearly so, without previous feedback in the novel situation.

Figure 7.

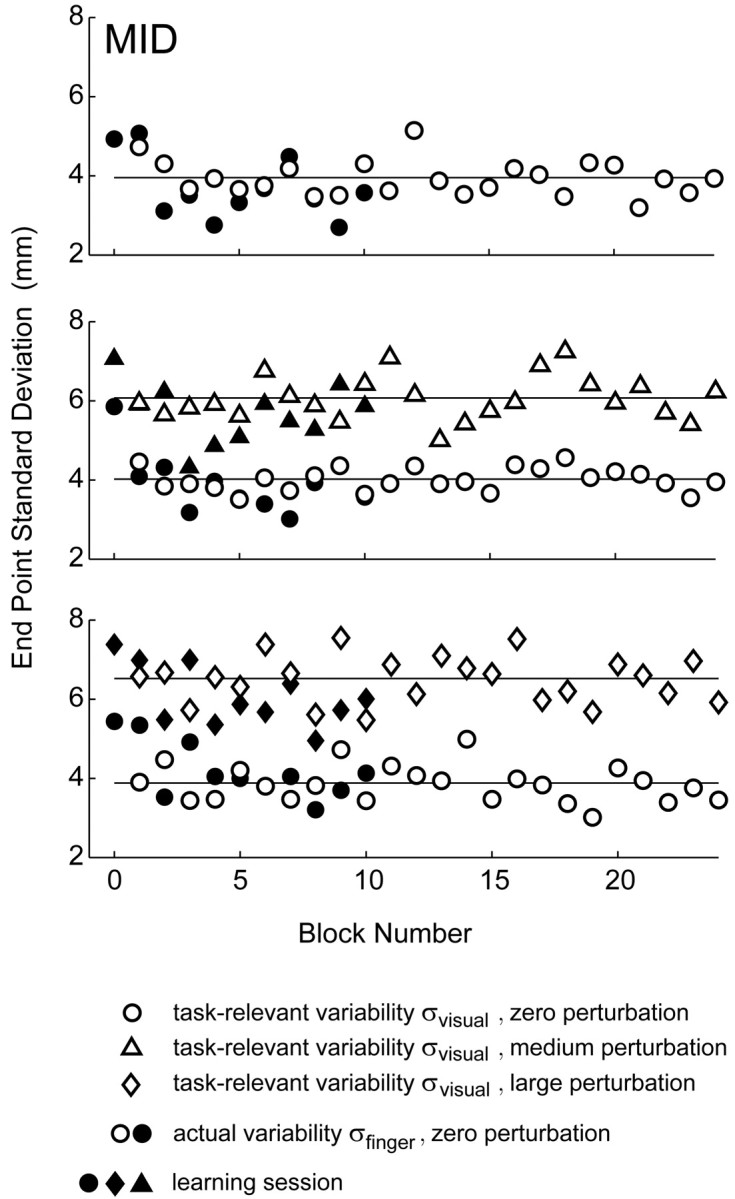
Stability and distribution of task-relevant variability. Task-relevant (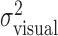) and actual (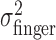) movement variability (expressed as SDs) as a function of block number. Filled symbols indicate data from blocks in the learning sessions; open symbols indicate data from subsequent blocks in the experimental sessions (block number 0 corresponds to the first 32 trials in the learning session). In the plots corresponding to conditions with added noise, the circles indicate σ_finger, and the triangles and diamonds indicate σ_visual.

Figure 8.

Trial-by-trial data. Deviations of movement end points (x coordinate) from the mean (solid line) as a function of trial number are shown. Data are shown for all six subjects in the penalty = 500, near condition (in the condition in which the target was to the left of the penalty region), starting from the first trial in which the subject was exposed to the configuration.

Homogeneity of movements after training

We finally report evidence that subjects' behavior was stable before data recording began and remained so during the course of the experiment. Reaction times and movement times were constant for the duration of the experiment and did not differ significantly across conditions (p > 0.05 for each subject in all cases). This indicates that the timing of movements was the same for all experimental conditions.

It is interesting to note that subjects with faster responses (e.g., subject CAL, movement times of 191 ± 46 ms) exhibited a larger movement variability than subjects with slower responses (e.g., JJT, movement times of 367 ± 34 ms) (Fig. 4b). These results fit observations that movement time and accuracy of a movement are inversely related (Fitts and Petersen, 1964).

Discussion

We asked how the human motor system deals with externally imposed perturbations that increase task-relevant variability. We manipulated variability by perturbing the visually specified position of the finger unpredictably during the movement and then scoring responses based on the finger's perturbed end-point position. Subjects did not compensate on a given trial for the visual perturbation of finger position on that trial, so the manipulation of the visual feedback caused a commensurate increase in their task-relevant variability.

In our task, subjects earned money by rapidly hitting targets carrying a known monetary reward while avoiding nearby penalty regions carrying known losses. When exposed to a change in variability, subjects rapidly acquired an estimate of their new variability within fewer than 120 trials and adjusted their aim points accordingly. We compared subjects' performance to the performance of an optimal movement planner that maximizes expected gain. We found that subjects' compensation for externally imposed changes in task-relevant variability was indistinguishable from optimal.

Our results provide the first direct experimental support for the assumption that movement planning takes task-relevant variability into account in a quantitatively correct manner. We found that the estimate of variability includes not only trial-by-trial variability caused by noise in sensory processing or execution of the motor command but also variability because of extrinsic perturbations that interfere with the task goals.

Our results extend the finding that humans estimate statistical regularities in motor tasks to improve their performance. For example, Baddeley et al. (2003) examined how movement planners accumulate information across trials to compensate for visual displacements of the hand. On a given trial, subjects were instructed to align a cursor with a target. The cursor's position was perturbed relative to the actual finger position by a random component (independent over trials) and a correlated component (random walk over trials). The results were well described by a model in which subjects modified their estimate of the perturbation on each trial as a weighted average of the previous estimate and the current error. Their task did not involve explicit payoffs and penalties and was not a speeded motor response. Efficiency was high, indicating that subjects did have some internal estimate of the form and amount of task-relevant variability. In a different approach, Körding and Wolpert (2004) added a fixed perturbation on each trial to the visual specification of finger position. They asked how much weight is given to the visual specification in directing the finger toward a target compared with the weight given to previously acquired knowledge of the average perturbation. They varied the uncertainty of the visual information as to the displacement of the target and found that subjects rely more on previous experience when the visual specification of finger position is less reliable. They could not determine whether task-relevant variability is incorporated quantitatively correctly, because they did not measure the changes in task-relevant variability that accompanied their experimental manipulation.

Our results are complementary to these findings. Optimal performance in our task requires an estimate of target and finger position but also requires an estimate of the variability. In other words, an optimal movement strategy has to take into account not only the consequences of the intended movement but also the consequences of unintended outcomes (i.e., errors). In our experiment, these errors are caused by noise in sensory processing, motor execution, and unpredictable experimenter-imposed external perturbations, which are not part of the motor system.

Our model also complements a recent model of motor coordination based on stochastic optimal feedback control. Todorov and Jordan (2002) introduced a “minimal intervention” principle that assumes that deviations from the average trajectory are corrected only when they interfere with task performance. The idea behind this model is that variance is not eliminated but rather allowed to accumulate in task-irrelevant dimensions. However, our results do not immediately fit with this picture. Within the constraints of our task (in which the penalty only appeared with a horizontal offset from target center), minimal intervention could have suggested a decrease of task-relevant variability in the x direction compared with the variability in the less task-relevant y direction. We did not observe this reshaping of variability. Yet, optimality in our task requires more than minimizing variability. Task relevance is defined explicitly for the subject by the payoffs and penalties associated with different outcomes. Subjects must reach the target within a specified timeout period; otherwise, they incur a large penalty. To meet the time constraint, they accept an increase in movement variability. In our task, minimal intervention means that movement variability should be reduced as much as possible by using all the time available. Our subjects learned to time their movements such that they hit the screen just before the end of the timeout. As a result, ∼75% of the arrival times (which comprise both the reaction time until the movement is initiated and the time for movement execution) fell between the 500 ms and 650 ms time limit in all subjects. Subjects hardly ever hit the screen later than 650 ms (<10 timeouts per subject in 2160 trials).

Under different task constraints, subjects will choose a different strategy. They may endure higher biomechanical costs to improve the stability of their movements (Burdet et al., 2001; Scheidt et al., 2001; Donchin et al., 2003; Franklin et al., 2003). In other words, every task comes with its own cost function based on the explicit gains and losses associated with the possible outcomes of the movement, perceptual and biomechanical demands and constraints, and the costs associated with the time limits imposed on the mover (Eq. 1). Behavior can only be classified as optimal or suboptimal with respect to this prespecified cost function. Finally, most approaches in which human behavior is compared with a standard of optimality make implicit assumptions about the cost function specific to the task. In our experiment, the cost function is completely constrained by the experimental design and explicitly communicated to the subject. This design allows a parameter-free comparison of human to optimal behavior.

Our results indicate that subjects are optimal in selecting the end point of their (arm) movement. This is not always the case. For example, when eye movements are directed at a visual target, search efficiencies are as low as ∼20%, depending on the saliency of the visual target (Eckstein et al., 2001; Najemnik and Geisler, 2005).

Subjects may deviate from optimality for a variety of reasons. In our experiment, subjects' performance was close to optimal with one statistically significant exception (subject CAL in the large-perturbation condition). It is interesting to note that all subjects demonstrated the same suboptimal behavior in this condition: when the optimal planner predicted an end point outside the target region, subjects' mean end points were closer to the penalty region than predicted, although only two subjects, CAL and SSG, exhibited efficiencies <90% (Table 1). Despite the consistent failures to aim outside the target region, subjects maintained their performance in these conditions, because the expected gain landscape is shallow in conditions with high-task-relevant variability. We conclude that it is unlikely that these small deviations from optimality indicate that subjects failed to update the estimate of their own task-relevant variability. Rather, the optimal strategy in this condition may have been in conflict with previous experience. It is hard to imagine naturally occurring situations in which the best way to reach for an object is to attempt to miss it.

In summary, our subjects compensated for visually imposed increases in variability, and their performance did not differ significantly from optimal. Our results suggest that humans take their task-relevant variability into account in planning movements and that they update their estimates of movement variability in response to external factors that increase task-relevant variability. When they take variability into account, they do so in a manner that is close to optimal.