Abstract
Previous studies have suggested that the motor system may simplify control by combining a small number of muscle synergies represented as activation profiles across a set of muscles. The role of sensory feedback in the activation and organization of synergies has remained an open question. Here, we assess to what extent the motor system relies on centrally organized synergies activated by spinal and/or supraspinal commands to generate motor outputs by analyzing electromyographic (EMG) signals collected from 13 hindlimb muscles of the bullfrog during swimming and jumping, before and after deafferentation. We first established that, for both behaviors, the intact and deafferented data sets possess low and similar dimensionalities. Subsequently, we used a novel reformulation of the non-negative matrix factorization algorithm to simultaneously search for synergies shared by, and synergies specific to, the intact and deafferented data sets. Most muscle synergies were identified as shared synergies, suggesting that EMGs of locomotor behaviors are generated primarily by centrally organized synergies. Both the amplitude and temporal patterns of the activation coefficients of most shared synergies, however, were altered by deafferentation, suggesting that sensory inflow modulates activation of those centrally organized synergies. For most synergies, effects of deafferentation on the activation coefficients were not consistent across frogs, indicating substantial interanimal variability of feedback actions. We speculate that sensory feedback might adapt recruitment of muscle synergies to behavioral constraints, and the few synergies specific to the intact or deafferented states might represent afferent-specific modules or feedback reorganization of spinal neuronal networks.
Keywords: deafferentation, locomotion, frog, feedback, afferent, non-negative matrix factorization, central pattern generators, jumping, swimming
Introduction
Motor coordination can be understood as the mechanism by which the CNS controls the many degrees of freedom in the redundant musculoskeletal system to achieve purposeful behaviors (Bernstein, 1967). Previous experiments have suggested that the CNS may simplify control by activating a small number of modules (Grillner, 1985; Bizzi et al., 1991; Stein and Smith, 1997; Tresch et al., 2002), formulated as muscle synergies, or activation profiles across a set of muscles, the linear combination of which can generate diverse motor patterns (Tresch et al., 2002; Hart and Giszter, 2004; Ting and Macpherson, 2005). Previous studies examining this hypothesis have relied on animals with intact afferents (Saltiel et al., 2001) or have characterized predominantly feedforward, ballistic movements, such as cutaneous reflexes (Tresch et al., 1999) and kicking (d'Avella et al., 2003). The role of sensory feedback in synergy organization and activation has thus remained an open question.
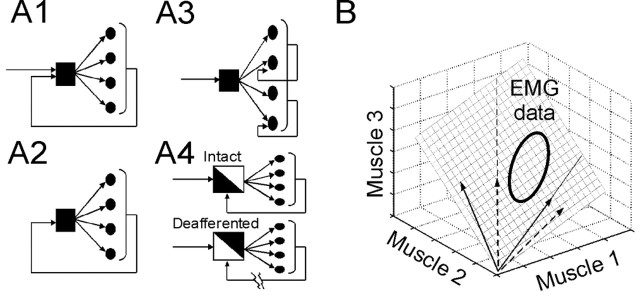
The simplest role of feedback in such a modular motor system would be to modulate activation of centrally organized synergies (see Fig. 1A1). Spinal and/or supraspinal neuronal networks would specify the particular muscle activation balance of each synergy, with sensory feedback playing no role in its specification. It is well established that complex electromyographic (EMG) patterns during many behaviors can be generated without afferents (Grillner, 1975; Delcomyn, 1980). Force field primitives of the spinalized frog before and after deafferentation were also very similar (Loeb et al., 1993), suggesting the presence of modules directly activated by central commands.
Figure 1.
Hypotheses and concepts invoked in this study. A, Different possible roles of sensory feedback in a modular motor system. Each black square represents a CNS neuronal network specifying the muscle activation balance with in a muscle synergy, and each circle represents the motoneuron pool for a muscle. A1, In this scheme, synergies are organized centrally and activated by spinal and/or supraspinal commands. Sensory feedback can modulate their activation but plays no role in specifying the activation balances within the synergies. A2, Centrally organized synergies specifically accessible by sensory inflow. These synergies may be responsible for the corrective responses seen during limb perturbations (Forssberg, 1979; Kargo and Giszter, 2000a). A3, Centrally organized synergies acting as templates for motor output generation. Each muscle within each synergy is independently regulated by afferent signals. A4, Feedback reorganization of CNS neuronal assemblies, resulting in altered synergy structures after deafferentation. It is possible that, when feedback is available, some interneurons capable of generating motor patterns under the deafferented condition are not activated, whereas some other interneurons requiring sensory signals for activation are recruited instead. This scheme is similar to the model put forth by Pearson (2004). B, The concept of synergy bases spanning a subspace. Shown in the diagram is a hypothetical case with EMG data collected from three muscles. The EMG data are described by two different sets of synergy bases, indicated by solid and dashed arrows, respectively. Despite having different structures, these two synergy sets span the same 2 d subspace within the 3 d EMG space and can describe the EMG data equally well.
In addition, there may be synergies organized within the CNS but specifically accessible only by feedback signals (see Fig. 1A2). This possibility is suggested by the corrective responses observed during limb perturbations in the cat (Forssberg, 1979) and frog (Kargo and Giszter, 2000a). Alternatively, sensory inflow may modify activations of individual muscles within a synergy (see Fig. 1A3) or contribute to specification of synergies by reorganizing interneuronal networks (Pearson, 2004) (see Fig. 1A4). Yet another possibility is that synergies arise as emergent properties of the entire neural network comprising both central circuits and feedback loops. Whether differences between afferented and deafferented EMGs (Grillner and Zangger, 1984; Kargo and Giszter, 2000b) reflect afferent modulation of centrally organized synergies, recruitment of afferent-specific synergies, feedback reorganization of existing synergies, or emergent properties of the motor circuitry has remained unclear.
In this study, we assess to what extent the CNS relies on centrally organized synergies accessible by central commands (see Fig. 1A1) to generate motor outputs for locomotor behaviors. We collected hindlimb EMGs from intact frogs during swimming and jumping, before and after ipsilateral deafferentation. Then, we exploited a non-negative factorization algorithm (Lee and Seung, 1999) to identify synergies shared by, and synergies specific to, the intact and deafferented data sets. Our analyses indicate that, to a large degree, both data sets can be explained by a set of shared synergies. We conclude that a small number of centrally organized synergies, activated by central commands but modulated by sensory feedback, plays a predominant role in generating complex motor patterns for locomotor behaviors.
Materials and Methods
Surgeries and experimental procedure. Four adult bullfrogs (Rana catesbeiana, 270-590 g) were studied. On each frog, three surgeries were performed on separate days. In all surgeries, the frog was anesthetized with ice and tricaine (ethyl 3-aminobenzoate methanesulfonate, 0.1 mg/g; Sigma, St. Louis, MO) injected into the left iliac lymph sac. In the first surgery, the dorsal nerve roots were exposed by rongeuring vertebrae 5-6 and cauterizing the dura mater. In the second surgery, bipolar EMG electrodes were implanted into 13 muscles in the right hindlimb, including the following (according to the nomenclature of Ecker, 1971): rectus internus major (RI), adductor magnus (AD), semimembranosus (SM), semitendinosus (ST), iliopsoas (IP), vastus internus (VI), rectus femoris anticus (RA), gastrocnemius (GA), tibialis anticus (TA), peroneus (PE), biceps (or iliofibularis) (BI), sartorius (SA), and vastus externus (VE). All wires were passed subcutaneously to a 37-pin d-subconnector, secured to the back skin with a custom-made plastic platform and Nexaband glue (Veterinary Products Laboratories, Phoenix, AZ). The crimp contacts were insulated by epoxy. The third surgery was a deafferentation procedure: dorsal roots 7-9 on the right side were severed at the level of the sixth vertebra. After some of the surgeries, antibiotic (enrofloxacin, 10-3 mg/g; Bayer, Shawnee Mission, KS) was also administered subcutaneously for prophylaxis.
Patterns of EMG during unrestrained swimming and jumping, performed in a specially designed tank and cage, respectively, were collected after electrode implantation and before deafferentation during one to two experimental sessions conducted over 1-3 d. After deafferentation, another one to two sessions of EMG data were collected over 1-3 d. Between surgeries and experimental sessions, the frog was allowed at least 18 h for recovery. Episodes of both in-phase and out-of-phase swimming (Nauwelaerts and Aerts, 2002) were either spontaneous or elicited by lightly touching the hindlimbs with a plastic rod. During all swimming trials, removable light-bodied Permlastic (Kerr USA, Romulus, MI) was also used to provide additional insulation of the EMG-electrode connector against water. For the jumping responses, a few of them were spontaneous, but most of them were elicited by lightly scratching the skin of either hindlimb with a pair of sharp forceps. All swimming and jumping experimental trials were also videotaped, and the EMG and video recordings were approximately synchronized by a digital counter. Correct placement of electrodes was confirmed in postmortem examinations after all experimental procedures. All procedures were approved by the Massachusetts Institute of Technology Committee on Animal Care before experimentation.
Data collection and preprocessing. Continuous EMG signals, both intact and deafferented, were amplified (gain of 10,000), bandpass filtered (10-1000 Hz) through differential alternating current amplifiers, and digitized (1000 Hz). Using custom software written in Matlab (Math-Works, Natick, MA), the EMG traces were manually parsed into segments, each containing a single jump or consecutive swimming cycles. The parsed data were then high-pass filtered [window-based finite impulse response (FIR); 50th order; cutoff of 50 Hz] to remove any motion artifacts. Subsequently, the data were rectified, low-pass filtered (FIR; 50th order; 20 Hz) to remove noise, and integrated over 10 ms intervals. The EMGs were not normalized before further analyses.
Analysis stage I: extracting muscle synergies separately. We modeled EMGs of each behavior as the linear combination of a set of muscle synergies, each represented as an activation profile across the 13 recorded muscles, and activated by a time-varying activation coefficient. We hypothesized that the synergies and their activations are non-negative and are identifiable by applying the non-negative matrix factorization (NMF) algorithm (Lee and Seung, 1999) to the EMG data. The NMF algorithm is a reasonable method for extracting synergies because, as a result of its non-negativity constraint imposed on both the synergies and their activations, the synergies extracted tend to be sparse rather than holistic and, thus, more physiologically interpretable (Lee and Seung, 1999). Also, unlike methods such as the independent component analysis (Bell and Sejnowski, 1995; Hyvärinen and Oja, 2000), NMF does not rely on the assumption that synergy activations are statistically independent; hence, NMF is more compatible with the previous finding that activations of multiple synergies might be correlated (Saltiel et al., 2001).
Our synergy analyses were divided into two stages. In stage I, our goals were to estimate the number of intact and deafferented synergies, the number of synergies shared by the two data sets, as well as the amount of variance representing systematic variation within each data set. We considered the intact and deafferented data sets separately and extracted synergies from each of them. Stated formally, our model in stage I has the following mathematical form:
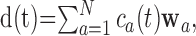 |
(1) |
where, for the 13 recorded muscles, d(t) represents the EMG data at time t, wa is a 13-dimensional vector denoting the ath synergy, ca(t) is the time-varying scalar activation coefficient for wa, and N is the total number of synergies extracted. Note that Equation 1 can also be stated in matrix notation as D = WC, where D, W, and C are the data, synergy, and coefficient matrices, respectively. In stage I, the above model was applied separately to each of the intact and deafferented data sets, for each of the swimming and jumping behaviors.
The intact and deafferented synergies and their activation coefficients were extracted by implementing the NMF multiplicative update rules (Lee and Seung, 2001) in Matlab. Under these update rules, at each iteration, new estimates of W and C were calculated by multiplying the current estimates by factors depending on D and current estimates of W and C. This iterative estimation procedure was stopped after convergence of the reconstruction error ∥D - WC∥, defined here as having 20 consecutive iterations with a change of EMG reconstruction error < 0.01%.
The NMF algorithm requires the number of synergies extracted to be specified before application of the algorithm. Because such information was not known a priori, for each behavior, we extracted 1-10 synergies from subsets of the intact and deafferented data sets, respectively. At each number of synergies, we performed cross-validation (Browne, 2000) as a step for estimating the correct number of synergies (see also next section, Estimating the numbers of intact and deafferented synergies for stage I). In our cross-validation procedure, the jumping or swimming EMG segments were first divided into four equal partitions. Three of the four partitions were pooled together, and synergies were extracted from this pooled data set. These synergies were then validated by fitting them to the remaining unused partition (using NMF with W held fixed and C updated across iterations), and the quality of fit was quantified as an R2 value. This cross-validation procedure was repeated 20 times at each number of synergy, each time with different random W and C (uniformly distributed between 0 and 1) initiating NMF, and with different randomly selected data partitions for cross-validation.
For each number of synergies, a baseline cross-validation R2 was also computed by repeating the extraction-validation procedure described above on the same training and testing EMG segments but with the samples of each muscle in each data set independently and randomly shuffled. An actual cross-validation R2 higher than this baseline cross-validation R2 suggests that systematic variation in the data set is captured by the synergies.
Estimating the numbers of intact and deafferented synergies for stage I. In cross-validation, when more synergies are extracted than necessary, some synergies may capture random fluctuations rather than systematic variation within the extraction data set. In such a case, the quality of fit of the synergies to the validation data is expected to be reduced. Thus, the correct number of intact or deafferented synergies (denoted by Nin* and Nde* for the intact and deafferented data sets, respectively) can be estimated by plotting the cross-validation R2 against the number of synergies extracted. A point beyond which additional increase in the number of synergies decreases the R2, or at which the slope of the R2 curve changes sharply, indicates that any additional synergies beyond that point capture only noise and/or a small additional fraction of data variation. This point should then, in principle, be the correct number of synergies.
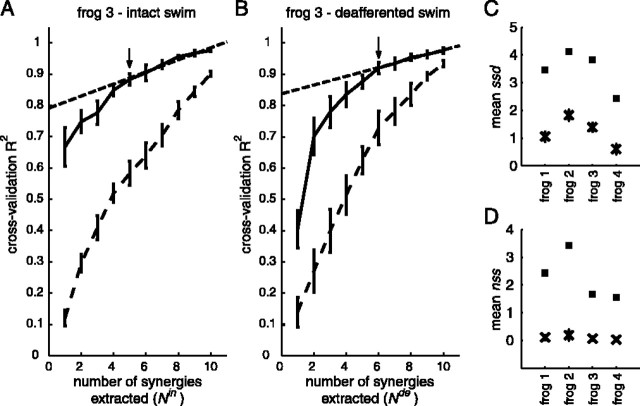
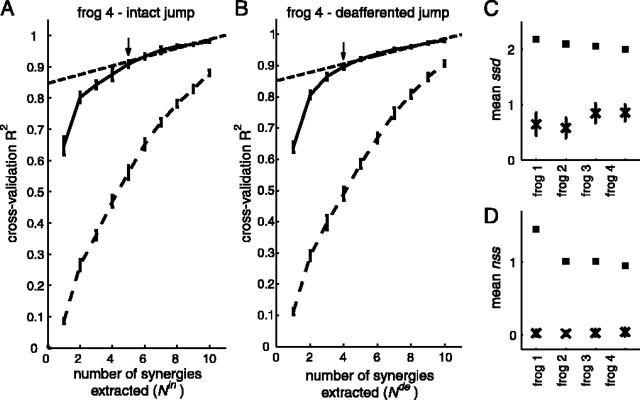
However, our previous experience with cross-validation R2 curves from frog EMGs during natural behaviors has shown that the slope of the curve usually decreases gradually as the number of synergies extracted increases, making it difficult to determine the number of synergies by visual inspection of the R2 curve. To estimate Nin* and Nde* objectively, we fit portions of the R2 curve to straight lines using standard least-squares technique, first including all data points on the curve in the fit, and then the 2nd to 10th points, and so on until only the 9th and 10th points were included. As the range of the fit moves toward the right side of the curve, the mean squared error (MSE) of the fit is expected to decrease because the R2 curve approaches a straight line as the number of synergies extracted increases. The correct number of synergies can then be estimated as the first point on the R2 curve at which the linear fit of all points from that point to the 10th point produces a small MSE. In other words, this chosen point represents the point at which the R2 curve plateaus to a straight line. In our analyses, the first point on the R2 curve for which the corresponding MSE falls below 10-5 was selected as the correct number of synergies for stage I (see Fig. 3 A, B, arrows). This criterion resulted in numbers of synergies corresponding to qualitative inspection of the R2 curves but performed this identification objectively.
Figure 3.
Stage I analysis of swimming EMGs before and after deafferentation. A, B, In analysis stage I, we extracted and cross-validated 1-10 synergies from the intact and deafferented data sets, respectively, and the quality of fit of the synergies to the validation data was quantified as R2 values. To assess the R2 expected by chance, we also repeated the extraction and validation procedures on the same training and testing data sets but with the samples of each muscle in both independently and randomly shuffled. We then estimated the correct number of intact and deafferented synergies by fitting decreasing portions of the actual R2 curve to straight lines, and the first point on the curve for which the portion approximates a straight line (as indicated by a small mean squared error in the linear fit) was selected as the correct number of synergies. A, Cross-validation R2 curves for the intact swimming data set of frog 3. Solid curve, R2 curve from original data (mean ± SD; n = 20). Dashed curve, R2 curve from shuffled data (mean ± SD; n = 20). The black arrow indicates the correct number of intact synergies estimated by our procedure, and the dashed straight line is its corresponding linear fit. B, Cross-validation R2 curves for the deafferented swimming data set of frog 3. Same key as A. C, D, Assessing similarity between the intact and deafferented synergies using two approaches. C, The degree of overlap between the subspaces spanned by the intact and deafferented synergy sets, respectively, is indicated by the average ssd values (▪; n = 20 × 20 = 400). The average ssd values expected by chance were computed by calculating principal angles between shuffled synergy sets (×; mean ± 5 × SD after 20 trials of shuffling). D, The number of stage I intact synergies for which the actual structures were preserved after deafferentation was indicated by the average nss values (▪; n = 20 × 20 = 400). The average nss values expected by chance were computed by calculating scalar products between shuffled synergy sets (×; mean ± 5 × SD after 20 trials of shuffling).
Two approaches of assessing synergy similarity for stage I. After estimating the correct numbers of synergies, we proceeded to assess similarity between the intact and deafferented synergy sets. The intact and deafferented synergy sets each define a lower-dimensional subspace within the 13-dimensional EMG space. The intact and deafferented synergies can be similar in the weaker sense that their subspaces overlap each other or in the stronger sense that the actual synergy bases of the two synergy sets are similar. Thus, it is possible that the intact and deafferented synergy sets are similar only in their subspaces but not in their actual synergies. For example, in Figure 1 B, the two sets of synergies, represented by solid and dashed arrows, respectively, are different in their structures (i.e., they point to different directions in the EMG space), but they nonetheless span the same two-dimensional subspace within the three-dimensional EMG space. Comparing the intact and deafferented subspaces as well as the structures of the synergies underlying them, we can then assess whether the NMF algorithm is capable of finding only the shared subspace or the actual synergy bases spanning the shared subspace as well.
For the first approach of similarity assessment, we evaluated the degree of overlap between the two subspaces spanned by the intact and deafferented synergies, respectively, by computing a set of principal angles using an algorithm described by Golub and Van Loan (1983, pp 428-430). If, for instance, the intact and deafferented subspaces share a three-dimensional common subspace, the cosines of the first three principal angles should be close to one. We refer to the number of principal angles with cosines ≥0.90 as the shared subspace dimensionality (ssd) between two synergy sets. If the intact and deafferented subspaces completely overlap each other, then ssd is the number of intact or deafferented synergies, whichever number is smaller.
The second, more stringent method of assessing similarity between the intact and deafferented synergies evaluates the degree of similarity between the actual synergy vectors using scalar products. We first computed the best-matching scalar products between the intact and deafferented synergy sets. The vector norm of each synergy was first normalized to one. Each synergy in the intact set was then matched to the synergy in the deafferented set giving the maximum scalar product between them. If two or more synergies from one set were matched to the same synergy in the other set, we isolated all multiply-matched and unmatched synergies, and the total scalar product of every possible matching combination between those two sets of remaining synergies was calculated; the combination giving the maximum total scalar product was then considered to be the best match. We refer to the number of best-matching scalar products ≥0.90 as the number of shared synergies (nss), representing the number of synergies that are similar between the intact and deafferented synergy sets.
Because extraction of synergies was repeated 20 times, there were 20 × 20 = 400 intact and deafferented synergy sets for comparison, and thus, 400 ssd and 400 nss values. The average ssd and nss values were calculated for each animal and each behavior.
Baseline synergy similarity for stage I. The procedures described above estimate the number of shared dimensions (ssd) and the number of shared synergies (nss) between intact and deafferented data sets. To assess the significance of these values, we computed baseline ssd and nss values using a randomization procedure. For each of the 400 pairs of intact-deafferented synergy sets, two sets of random synergies comprising Nin* and Nde* vectors were generated by random shuffling of the vector components in the original intact and deafferented synergy sets, respectively. The ssd and nss values between these two sets of random synergies were then determined. Calculation of baseline ssd or nss, between every intact-deafferented pair of synergy sets, was repeated 20 times, each time with the vector components shuffled anew. For each repetition, the average baseline ssd and nss across the 400 pairs of synergy sets were also calculated.
Analysis stage II: simultaneous extraction of shared and data set-specific synergies. In the stage I procedures described above, synergies were extracted separately from the intact and deafferented data sets. The subspaces spanned by these synergies were then compared with one another, and the similarity between the synergies themselves was assessed. However, there are a number of potential shortcomings with the stage I analysis.
First, although the stage I intact and deafferented subspaces may share a common subspace, the synergies extracted from either data set may not actually span this common subspace, because this common subspace does not necessarily coincide with the subspace defined by any subset of the extracted synergies. To see this, consider a three-dimensional space defined by three synergies, represented as vectors along the x-, y-, and z-axes, respectively. Suppose further that the common subspace is a two-dimensional tilted plane within this three-dimensional space. Obviously, this plane is not spanned by any two of the three synergies. In such a case, the compositions of the two synergies preserved after deafferentation remain unclear from the stage I extraction results.
Second, separate extraction of synergies performed in stage I might be expected to underestimate the number of intact or deafferented synergies (Nin* or Nde*). If the activation of two synergies tended to covary within one of the two data sets, NMF would tend to combine these synergies together into a single synergy. If in the other data set these two synergies were activated independently, NMF would identify them correctly for this data set. Thus, if, for instance, two of five intact synergies tended to covary in the deafferented data set, the stage I estimates of Nin* and Nde* would be 5 and 4, respectively, whereas the correct estimates should be 5 and 5. Therefore, the stage I estimates of data set dimensionalities are expected to underestimate the true number of intact and deafferented synergies.
Beyond this problem in identifying the correct numbers of synergies, such covariation of synergies might also result in an underestimation of the number of synergies preserved after deafferentation. Again, if, for instance, two synergies tended to covary in the deafferented but not in the intact data set, the combined deafferented synergy uncovered by NMF would be seen as dissimilar to its two corresponding intact synergies. Thus, if there were five synergies in fact shared between the two data sets, the nss value would indicate that only three synergies were shared.
To account for such possibilities, we therefore performed a second stage of analysis, using a novel reformulation of the NMF algorithm. Information from both data sets is used simultaneously in this reformulation, allowing both for synergies shared between the data sets and for synergies observed specifically within one data set or another. We let the NMF algorithm search, by itself, for synergies common to both data sets while at the same time allowing the algorithm to isolate synergies relevant only to each data set. Our model in stage II can be stated formally as follows:
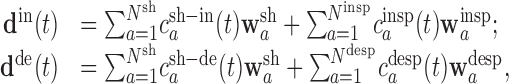 |
(2) |
where the superscripts “in” and “de” stand for intact and deafferented, respectively, and “sh,” “insp,” and “desp” stand for synergies shared by the two data sets, synergies specific to the intact data set, and synergies specific to the deafferented data set, respectively. Note that the coefficients, 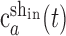 and
and 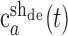 , although activating the same synergy
, although activating the same synergy 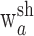 , in fact contribute to the intact and deafferented EMG data, respectively. The number of intact or deafferented synergies in the stage II model is then the sum of the number of shared synergies and the number of synergies specific to each data set (i.e., N for intact data set = Nsh + Ninsp; and N for deafferented data set = Nsh + Ndesp). Converting Equations 2 into their matrix forms, we have
, in fact contribute to the intact and deafferented EMG data, respectively. The number of intact or deafferented synergies in the stage II model is then the sum of the number of shared synergies and the number of synergies specific to each data set (i.e., N for intact data set = Nsh + Ninsp; and N for deafferented data set = Nsh + Ndesp). Converting Equations 2 into their matrix forms, we have
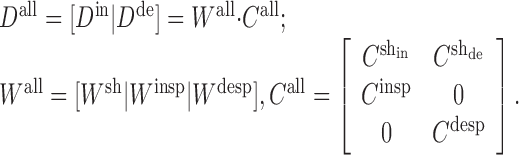 |
(3) |
In the above equations, for the columns in Call corresponding to the range of the deafferented data, the rows for the intact-specific synergies were set to zero, because by definition they do not contribute to the generation of the deafferented data. Similarly, in the Call columns used for reconstructing the intact data, the rows for the deafferented-specific synergies were set to zero.
We extracted shared and specific synergies simultaneously from equal numbers of intact and deafferented EMG segments using the NMF algorithm. As a result of its multiplicative update rules, if the initial condition of any matrix component is zero, the estimate of that matrix component after any number of iterations remains zero. Thus, the only manipulation necessary for stage II is to set the relevant matrix components of the initial Call to zero (as indicated in Eq. 3) while choosing random values (uniformly distributed between 0 and 1) for all the nonzero entries. These initial conditions ensure that the specific synergies in Wall will explain only one of the two data sets.
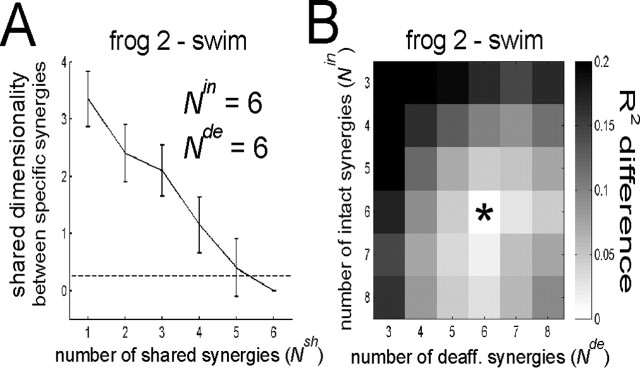
Estimating the numbers of intact and deafferented synergies for stage II. As in stage I, the stage II procedure we described requires the number of synergies to be specified before application of the algorithm. To estimate the number of shared synergies (Nsh*), stage II synergies were extracted with Nsh progressively increasing from 1 to the smaller of Nin or Nde.As Nsh increases, the degree of overlap between the subspaces defined by the intact-specific and deafferented-specific synergies is expected to decrease, because every time Nsh is increased by one, another feature shared between the intact and deafferented EMGs is taken up as a shared synergy. Thus, Nsh* is indicated by the Nsh at which there is minimal overlap between the subspaces spanned by the intact- and deafferented-specific synergies. The degree of this overlap between the specific synergies was quantified as a dimensionality value by finding the number of principal angles with cosines ≥0.90. The smallest Nsh with a mean shared dimensionality between the specific synergies (averaged across 20 extraction repetitions) below 0.25 was taken to be the correct number of shared synergies. This threshold of 0.25 ensures that, at the chosen Nsh*, sharing between the specific synergies is observed in less than five of the 20 extraction runs.
The above procedure estimates the correct number of shared synergies given particular total numbers of intact and deafferented synergies, comprising shared synergies and synergies specific to each data set. To estimate the correct total numbers of synergies, we used the results of the stage I analysis, choosing the total numbers of intact and deafferented synergies to be those numbers that gave an R2 in the stage II analysis closest to the R2 obtained in the stage I analysis (see Fig. 5B). This R2 criterion guarantees that the stage II solution explains the intact and deafferented data sets as well as the stage I solution, while directly identifying the synergies that are shared between intact and deafferented data sets.
Figure 5.
Determining the numbers of synergies in analysis stage II. In our stage II model, three numbers of synergies, Nin*, Nde*, and Nsh*, need to be specified. Our strategy for estimating the correct values of these three parameters was to extract synergies with Nin, Nde = 3... 8 (i.e., 6 × 6 = 36 combinations of Nin and Nde), and, at each of these combinations, estimate Nsh* for that particular combination of Nin and Nde. We then proceeded to estimate Nin* and Nde* by examining the difference between the stage II and stage I R2 values. A, Estimating the correct number of shared synergies in frog 2 swimming given Nin, Nde = 6. As Nsh was progressively increased, the dimensionality of the subspace shared between the specific synergies decreased. The correct number of shared synergies can be estimated by noting the point at which the specific synergies do not share a common subspace. Shown in A is the mean shared dimensionality between the specific synergies (mean ± SD; n = 20). The shared dimensionality at the maximum Nsh was defined to be zero, because at this point there are no specific synergies to be compared. The smallest Nsh with a shared dimensionality falling below 0.25 was selected to be Nsh*. B, Estimating the correct total numbers of intact and deafferented synergies (frog 2 swimming). For each of the intact and deafferented data sets, wecomputed an R2 value for the stage II solution at each combination ofNin and Nde and calculated the absolute difference between the stage I cross-validation R2 and the stage II R2. The intact and deafferented differences were then summed together. We reason that the correct stage II estimates of Nin* and Nde* are the combination for which the R2 values come closest to the stage I values. In B, this R2 difference across the 36 combinations of Nin and Nde is depicted as a grayscale map: the darker the color, the more R2 difference at a combination. The combination with the minimum R2 difference is marked with an asterisk.
Clustering synergies of different frogs. After selecting the stage II numbers of synergies, for each frog and behavior, the synergy solution for the extraction repetition giving the highest overall R2 was selected for additional analyses. For each behavior, the shared and data set-specific synergies from the four frogs were pooled together and grouped into classes by cluster analysis. The Matlab statistics-toolbox functions pdist (Minkowski option; p = 3), linkage (ward option), and cluster were applied sequentially to the pooled synergy matrix. The number of clusters was determined by selecting the minimum number of clusters partitioning the synergies such that no two synergies within each cluster were from the same frog.
Analyzing the coefficients of the stage II shared synergies. For each frog and each behavior, the activation coefficients of the stage II shared synergies before and after deafferentation were analyzed. The coefficients of each shared synergy were multiplied by the magnitude of that synergy vector, so that the coefficients represent activation of unit vectors. A Matlab graphical user interface was then built for manual parsing of the coefficient time traces into extension and flexion phases, so that the extension phase of each cycle would correspond to a burst of activation of the extension synergies. The peak coefficient amplitudes of each phase and of each shared synergy, before and after deafferentation, were compared (t test, α = 0.05).
Effects of deafferentation on the duration of synergy activation were characterized by first fitting the coefficient time trace of each phase to a Gaussian function using standard nonlinear least-squares method (Bates and Watts, 1988, pp 32-42). The time points corresponding to mean ± 2 × SD of the Gaussian function were defined to be the offset and onset of the activation burst, respectively. For the extension phases, if the burst offset as defined above lay within the flexion phase after that extension phase, the burst offset was redefined to be the last time point of that extension phase. Likewise, for the flexion phases, if the burst onset as defined above lay within the adjoining extension phase, the onset was redefined to be the first time point of that flexion phase. The coefficient burst duration of each phase and of each shared synergy, before and after deafferentation, were then compared (t test, α = 0.05). Only the phases in which the Gaussian fit explained the original coefficient time trace with R2 ≥ 60% were included in our statistics of burst duration.
Patterns of correlation between synergies. To investigate whether the activation of two or more synergies are coordinated by central mechanisms or sensory feedback, we computed the Pearson's correlation coefficient (r) between the peak coefficient amplitudes of every pair of shared synergies for each of the two phases, for each of the intact and deafferented conditions, and for each behavior. Statistical significance of the difference between the intact r and the deafferented r was determined by Fisher's r-to-Z transformation method [α = 0.01 (Hays, 1994, pp 647-651)].
Results
From four frogs, we collected and analyzed EMG signals from 13 hindlimb muscles during intact swimming (91, 315, 311, and 200 cycles from frogs 1-4, respectively), deafferented swimming (56, 205, 169, and 140), intact jumping (97, 47, 76, and 50 jumps), and deafferented jumping (172, 60, 22, and 56).
Synergies underlying intact and deafferented behaviors: visual inspection of EMG data
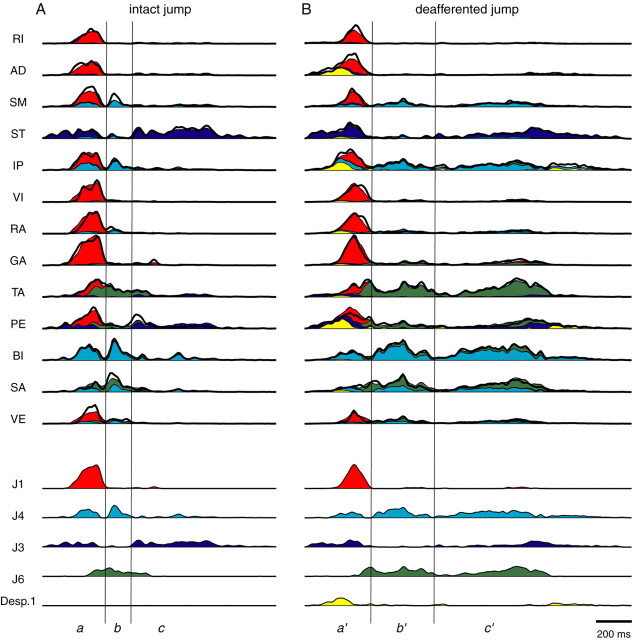
Figure 2 shows representative examples of EMG segments, all collected from frog 1, during intact and deafferented swimming and jumping. In Figure 2A, there are five consecutive swimming cycles. Notice that, in this episode, the muscles SM, GA, and VE tend to be coactivated as a group and that their peak cycle amplitudes stay relatively constant across these five cycles. The muscles RI, AD, and IP tend to be coactive with the SM-GA-VE group, but their peak cycle amplitudes from the first to last cycles decrease gradually. More importantly, the same two muscle groups seem to underlie the deafferented swimming EMG patterns in Figure 2B as well. Both the SM-GA-VE and RI-AD-IP groups are present in the two episodes of Figure 2B, but the amplitude of the latter group appears to be significantly smaller in the second episode than in the first episode. Thus, visual inspection of EMG data suggests that some of the swimming muscle synergies may be preserved after deafferentation and that their activation across time may be differentially modulated.
Figure 2.
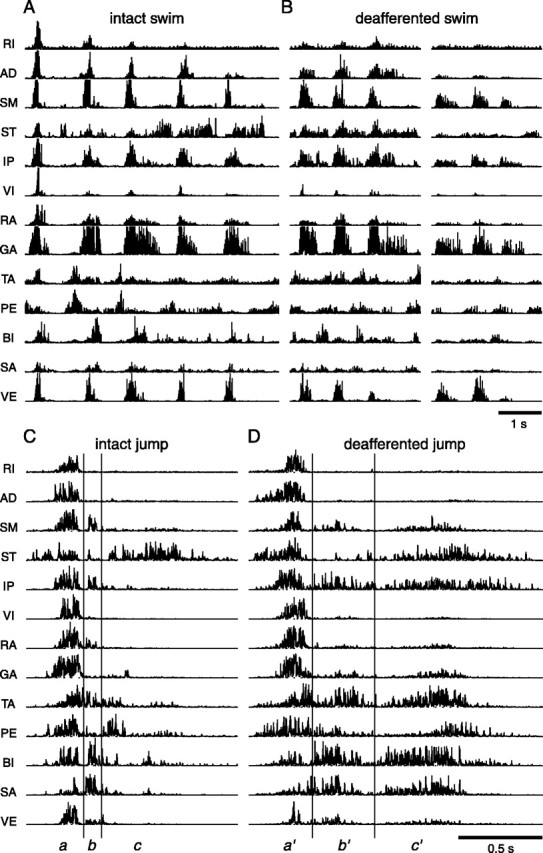
Examples of EMG data collected from intact and deafferented locomotor behaviors. Shown are EMG data collected from 13 hindlimb muscles of frog 1, high-pass filtered (50th-order FIR; cutoff of 50 Hz) to remove motion artifacts, and subsequently rectified. A, EMGs of five consecutive swimming cycles before dorsal root transection. B, Two different swimming episodes after deafferentation, each of which comprises three consecutive cycles. C, EMGs of a representative jump before deafferentation. D, EMGs of a deafferented jump. C and D are divided into three phases for ease of visual inspection. Notice that the deafferented EMGs appear to involve the same muscle groups embedded within the intact EMGs. Comparison of the onset times of AD, ST, IP, and PE in phase a of C with those in phase a′ of D suggests that there may be synergies specific to the intact or deafferented state. For more detailed descriptions, see Results.
Shown in Figure 2C is an EMG segment collected during an intact jump. It is divided into three phases, labeled a, b, and c, for ease of visual inspection. Phase a is characterized by activation of all 13 muscles. In phase b, we notice EMG bursts in SM, IP, BI, and SA. Phase c, however, features a prominent ST with some activity in TA and PE. A similar tripartite structure is also seen in deafferented jumping EMGs, exemplified by Figure 2D. The three phases in Figure 2D, labeled a′, b′, and c′, are analogous to phases a, b, and c of Figure 2C, respectively. Despite the fact that b′ has a longer duration than b, the SM-IP-BI-SA group active in phase b is also noticeable in the deafferented episode but in both b′ and c′. Note also that the TA and PE bursts in c′ have larger peak amplitudes and longer durations than those in phase c. It appears therefore that, in jumping, at least some of the synergy structures remain invariant after deafferentation, although the amplitudes and time courses of their activation may be affected.
A more detailed comparison between phase a (Fig. 2C) and phase a′ (Fig. 2D) shows that the relative onset times of some muscles were altered after dorsal root transection. In phase a, ST activity precedes that of all other muscles; in phase a′, however, the onset times of ST, AD, IP, and PE seem to be the same. Thus, it is possible that the structures of some muscle synergies are changed after deafferentation.
The above observations motivated us to hypothesize that swimming and jumping EMGs can be generated by linear combination of muscle synergies represented as time-invariant activation profiles across the 13 muscles and to expect that most of these synergies are preserved after feedback deprivation. We further hypothesized that the structures of the muscle synergies, as well as their corresponding time-varying activation coefficients, can be identified by applying the NMF algorithm (Lee and Seung, 1999; Tresch et al., 1999) to the EMG data. As explained in Materials and Methods, for each of the swimming and jumping behaviors, we systematically assessed the number of synergies preserved after deafferentation and identified the structures of the preserved synergies in two stages of analyses. In stage I, we extracted synergies from the intact and deafferented data sets separately and assessed similarity between the two synergy sets. Our comparison in stage I led us to realize some limitations of extracting synergies from individual data sets separately, prompting us to analyze our data in a second analytical stage in which we extracted synergies from pooled intact and deafferented data. We will first illustrate our two-stage method using the swimming EMGs as an example. The swimming synergies will then be presented, followed by the analytical results of the jumping EMGs.
Muscle synergies underlying swimming before and after deafferentation
Analysis stage I: intact and deafferented swimming EMGs have low and similar dimensionalities
We first estimated the number of synergies in the intact and deafferented data sets by extracting 1-10 synergies from each of them. Extraction results at each number of synergies were cross-validated (see Materials and Methods). The quality of fit in the validation step was quantified as an R2 value.
Figure 3, A and B, shows plots of R2 against the number of swimming synergies extracted for both the intact and deafferented data sets of frog 3 (solid curve; mean ± SD; n = 20), along with the R2 levels expected if the data sets were not generated by muscle synergies (shuffled data, dashed curve; mean ± SD; n = 20). It is clear that, in both the intact and deafferented conditions, ∼90% of variance in the original swimming EMGs is explained by five to six synergies (i.e., R2 ≈ 90%), whereas by chance, the same amount of variance is explained only when 10 synergies are used. This result indicates that both the intact and deafferented swimming data sets possess low and similar dimensionalities. Similar results were obtained from the other three frogs.
To systematically compare synergies of intact swimming with those of deafferented swimming, the numbers of synergies present in the intact and deafferented data sets (denoted by Nin* and Nde*, respectively) need to be determined. Ideally, the point on the R2 curve at which the slope changes sharply indicates such a number. As exemplified by the R2 curve of Figure 3A, however, the slopes of most of our R2 curves decrease gradually as the number of synergies extracted increases, making estimation of Nin* and Nde* by visual inspection of the R2 curves difficult.
Nonetheless, all of our R2 curves do seem to approach a straight line as the number of synergies extracted increases (Fig. 3A,B). This observation prompted us to estimate the correct number of synergies by fitting decreasing portions of each R2 curve to straight lines and choosing the first point at which a straight line fits the portion of the R2 curve well (for more details, see Materials and Methods). In Figure 3, A and B, the point of the best estimate of the number of synergies on the R2 curve is indicated by an arrow; its corresponding linear fit is shown as a dashed straight line. For frog 3 swimming (Fig. 3 A, B), then Nin* and Nde* are 5 and 6, respectively, confirming that the intact and deafferented dimensionalities are similar for the swimming EMGs.
Table 1 summarizes our estimates of the numbers of synergies in frogs 1-4. With the exception of frog 1 (the frog with the least amount of swimming data collected), in all frogs, Nin* and Nde* are either the same or differ only by one, further suggesting that the number of synergies underlying intact swimming is similar to that underlying deafferented swimming. Note also in Table 1 that, in all frogs, a high percentage of data variance (∼90%) is explained by the chosen numbers of synergies, indicating that our estimates of Nin* and Nde* provide a good description of the observed data.
Table 1.
Estimating the number of synergies shared between the intact and deafferented synergy sets in two stages of analyses
|
|
Stage I |
Stage II |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CV R2 (%) |
R2 (%) |
|||||||||||||||||||||||
| Frog/behavior |
Nin*
|
Nde*
|
ssd |
nss |
Intact |
Deaff |
Nin*
|
Nde*
|
Nsh*
|
Ninsp*
|
Ndesp*
|
Intact |
Deaff |
|||||||||||
| Frog 1, swim | 6 | 4 | 3.46 | 2.43 | 89.0 | 91.3 | 6 | 4 | 4 | 2 | 0 | 88.4 | 91.5 | |||||||||||
| Frog 2, swim | 6 | 6 | 4.13 | 3.44 | 91.2 | 89.7 | 6 | 6 | 6 | 0 | 0 | 91.1 | 90.2 | |||||||||||
| Frog 3, swim | 5 | 6 | 3.83 | 1.66 | 88.3 | 92.0 | 5 | 6 | 5 | 0 | 1 | 87.4 | 91.5 | |||||||||||
| Frog 4, swim | 4 | 4 | 2.43 | 1.56 | 86.3 | 91.7 | 5 | 4 | 4 | 1 | 0 | 87.0 | 92.4 | |||||||||||
| Frog 1, jump | 4 | 4 | 2.18 | 1.45 | 91.3 | 90.4 | 4 | 5 | 4 | 0 | 1 | 90.6 | 90.0 | |||||||||||
| Frog 2, jump | 4 | 4 | 2.10 | 1.01 | 90.3 | 90.6 | 4 | 5 | 4 | 0 | 1 | 89.6 | 89.9 | |||||||||||
| Frog 3, jump | 4 | 5 | 2.06 | 1.01 | 90.1 | 91.1 | 4 | 5 | 3 | 1 | 2 | 89.2 | 90.9 | |||||||||||
| Frog 4, jump |
5 |
4 |
2.00 |
_0.95 |
90.9 |
89.7 |
6 |
4 |
4 |
2 |
0 |
91.1 |
88.8 |
|||||||||||
In analysis stage I, we compared the intact and deafferented (Deaff) synergies using two approaches: by assessing the degree of overlap between the subspaces spanned by the intact and deafferented synergies (ssd), respectively, and by calculating scalar products to estimate the nss before and after deafferentation. In analysis stage II, the number of synergies preserved after deafferentation is reflected by the Nsh* value at our estimates of the correct total numbers of intact and deafferented synergies (Nin* and Nde*). The R2 values listed refer to the percentage of data variance explained by the listed numbers of synergies (averaged across 20 extraction repetitions). CV, Cross-validation.
Analysis stage I: assessing similarity between the intact and deafferented swimming synergies
To assess whether the intact and deafferented swimming synergies are similar, we first assessed the degree of overlap between the subspaces spanned by the sets of Nin* intact synergies and the Nde* deafferented synergies (ssd), respectively, by computing principal angles (Golub and Van Loan, 1983).
Figure 3C shows the mean ssd between the intact and deafferented swimming synergies of each frog (▪; n = 20 × 20 = 400) and the corresponding mean baseline ssd between random synergies (×; mean ± 5 × SD after 20 trials of shuffling). It is clear that, in all four frogs, the actual ssd lies well above the baseline ssd (p < 0.01), suggesting that there is a nontrivial degree of intersection between the intact and deafferented synergy subspaces. Rounding the mean ssd values, we see that, on average, three of six, four of six, four of five, and two of four dimensions of the intact synergy subspaces of frogs 1 through 4, respectively, are shared with their corresponding deafferented synergy subspaces. Our analyses thus far indicate that NMF succeeded in identifying swimming synergies before and after deafferentation sharing a common subspace, although the two subspaces do not completely overlap each other.
We then directly compared intact and deafferented synergies by calculating scalar products between the intact and deafferented synergy sets, estimating the nss between the intact and deafferented synergy sets.
Figure 3D shows the mean nss values of frogs 1-4 (▪; n = 20 × 20 = 400) together with their baseline nss values computed by matching randomly shuffled synergies (×; mean ± 5 × SD after 20 trials of shuffling). In all frogs, the nss value is clearly above its baseline (p < 0.01), indicating that the sharing of synergies is well above that expected by chance. Rounding the mean nss of each frog, we see that, on average, two of six, three of six, two of five, and two of four synergies extracted from the intact data sets of frogs 1-4, respectively, are similar to those extracted from deafferented data sets. Note that, in all frogs except frog 4, the mean nss is smaller than the mean ssd. Therefore, extracting intact and deafferented swimming synergies separately, NMF found synergies sharing a common subspace, but the shared synergies themselves do not span the entire shared subspace, as illustrated in the following example.
The shared stage I synergies do not span the entire shared subspace: illustrative examples
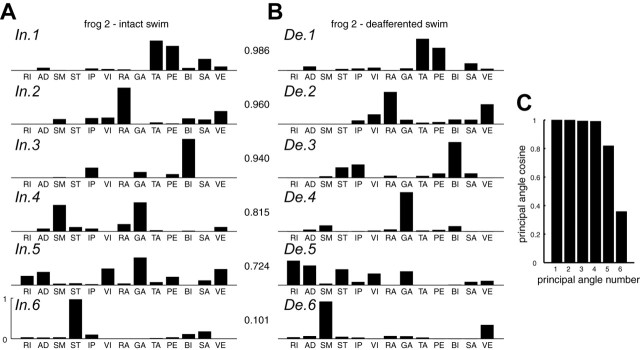
Shown in Figure 4, A and B, is an example of intact and deafferented synergy sets identified for frog 2 swimming. The topmost synergy pair, In.1/De.1, is the pair with the highest scalar product (value shown between panels), and the bottommost pair, In.6/De.6, is the pair with the smallest. As can be seen, synergies In.1 and In.2 are almost identical in structure to De.1 and De.2, respectively. Synergy In.6, with its prominent ST component, is not found in the deafferented synergy set, although both De.3 and De.5 have more ST activation than In.3 and In.5, respectively. Similarly, although synergy De.6 (SM and VE) is not found in the intact synergy set, In.4 has more prominent SM and VE than its corresponding De.4. These observations already suggest that, although only three of the six scalar products are >0.90, the degree of similarity between the two sets of synergies shown in Figure 4, A and B, may well be more than three. Examination of the cosines of the six principal angles between the two synergy sets of Figure 4, A and B, is consistent with such a possibility. As illustrated in Figure 4C, the cosines of the first four angles are close to one, suggesting that the intact and deafferented synergy subspaces defined by the synergies in Figure 4, A and B, share a four-dimensional common subspace. In other words, although In.1-In.3 (or De.1-De.3) are three of the synergies spanning this common subspace, there is at least one more common synergy embedded within the subspace defined by In.4-In.6, or that defined by De.4-De.6.
Figure 4.
Examples of swimming synergies from analysis stage I. A, B, A pair of intact and deafferented swimming synergy sets of frog 2.Each of the six intact synergies was matched to the deafferented synergy giving the best-matching scalar product, its actual value shown between the two panels. C, The cosines of the six principal angles between the intact and deafferented subspaces defined by the synergies shown in A and B. Notice that, whereas only three of six best-matching scalar products are >0.90 in A and B, the cosines of four of six principal angles are >0.90. This indicates that, although only three synergies are apparently similar to one another, the two subspaces actually share a four-dimensional common subspace. Therefore, the nss by itself potentially underestimates the degree of similarity between the intact and deafferented synergies. For additional discussion, see Results.
Together, the results in Figure 3, C and D, and the examples in Figure 4 suggest strongly that (1) there are shared synergies underlying both the intact and deafferented swimming data sets and (2) at this analytical stage, NMF un-covers synergies sharing a common subspace but is unable to find an explicit set of non-negative synergies spanning this shared space. Moreover, as described in Materials and Methods, combinations of synergies within one data set would be expected to result in stage I underestimating the number of intact or deafferented synergies, as well as the number of synergies preserved across deafferentation. This underestimation is a consequence of the fact that stage I identifies muscle synergies by extracting them separately for each data set. In the stage II analysis described below, we attempted to overcome these limitations to better assess the number of shared synergies underlying both the intact and deafferented EMG data sets.
Analysis stage II: extracting shared and data set-specific swimming synergies
In the second stage of our analyses, we used a different synergy extraction method to obtain an explicit set of synergies spanning the subspace shared by intact and deafferented EMGs. In stage II, we pooled these two data sets together and exploited the NMF update rules to search for synergies common to both data sets while simultaneously allowing the algorithm to isolate any synergies specific to either data set.
In stage II, three parameters, the number of intact, deafferented, and shared synergies, have to be specified before application of the NMF algorithm. Figure 5A is an example from frog 2 swimming, illustrating our method of estimating the correct number of shared synergies (Nsh*) given particular numbers of intact and deafferented synergies (both of which were set to be six in this example). As the number of shared synergies (Nsh) was progressively increased, the dimensionality of the subspace shared between the specific synergies also decreased as expected. As can be seen, the shared dimensionality fell below our predefined threshold of 0.25 only when six shared synergies were extracted. Thus, in this example, if there were six intact and six deafferented swimming synergies, all six intact synergies were preserved after deafferentation.
On the other hand, the correct total numbers of intact (Nin*) and deafferented (Nde*) synergies for stage II, each of which comprises both shared and specific synergies, were estimated by comparing the stage II R2 values at different combinations of total numbers of intact and deafferented synergies with the R2 values obtained in stage I (see Materials and Methods and legend to Fig. 5). Figure 5B illustrates the difference between the stage I and stage II R2 values as the total numbers of intact and deafferented synergies were, respectively, varied from three to eight. At each of these 36 (= 6 × 6) combinations, the number of shared synergies was estimated using the method illustrated in Figure 5A. For frog 2 swimming (Fig. 5B), the stage II R2 values came closest to the stage I R2 values when six intact synergies and six deafferented synergies were extracted. Together, results of Figure 5, A and B, thus suggest that, for frog 2 swimming, the stage II estimates of Nin*, Nde*, and Nsh* are 6, 6, and 6, respectively; that is, there are six synergies underlying both the intact and deafferented swimming data sets, all six of which are preserved after feedback deprivation.
We applied the above methods to all frogs to determine the number of total and shared synergies, and our results are shown in the right column of Table 1. In all frogs, the degree of sharing between the intact and deafferented synergy sets suggested by stage II (as indicated by Nsh*) is greater than that suggested by stage I (as indicated by ssd) by one to two synergies. More importantly, if we compare the total numbers of intact and deafferented synergies (Nin* and Nde*) determined in stage I with those estimated in stage II (Table 1), we see that the stage I numbers are the same as the stage II numbers in all but one instance (Nin* of frog 4 swimming). Therefore, the increased sharing discovered in stage II is not a consequence of explaining the data sets with more synergies. This observation further supports that the shared synergies identified in stage II represent underlying structures shared by the intact and deafferented data sets rather than being just the result of the algorithm averaging out structures specific to each data set.
Most swimming synergies are preserved after deafferentation
Figure 6 shows all the shared and data set-specific synergies from the extraction repetition with the highest overall R2 in each frog. As can be seen, for frogs 1-4, respectively, four of six, six of six, five of six, and four of five synergies appear as shared synergies, suggesting that most synergies underlying intact swimming are preserved after deafferentation. Therefore, the swimming EMGs are predominantly generated by centrally encoded synergies accessible by spinal and/or supraspinal commands.
Figure 6.
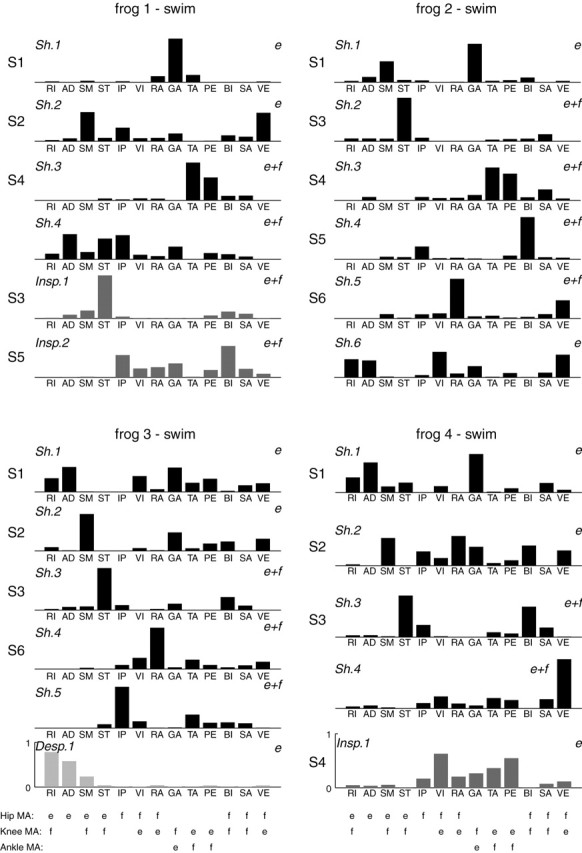
Swimming synergies of all frogs (analysis stage II). Shown in this figure are the stage II synergies of the extraction repetition with the highest R2 of the four frogs. The synergies shared between the intact and deafferented data sets are labeled Sh, synergies specific to the intact data set are labeled Insp, and synergies specific to the deafferented data set are labeled Desp. Synergies active only during the extension phase of the swimming cycle are marked with e on their right sides, and those active in both the extension and flexion phases are marked e+f. All synergies shown in this figure were clustered into six classes (S1-S6), and the class of each synergy is marked on its left side. The sign of the moment arms (MA) around the hip, knee, and ankle joints of the 13 muscles included in this study are listed below the synergies of frog 3 and frog 4 (e, extensor action; f, flexor action). Moment arm signs are based on results of Kargo and Rome (2002) and González (2003).
Inspection of synergies in Figure 6 further suggests that many of the swimming synergies are similar across frogs. For instance, in both frog 1 and frog 2, a shared synergy with TA and PE activation can be seen, and all frogs possess a shared synergy with a prominent ST component. Some synergies appear to be frog specific, however. For instance, synergy Sh.4 of frog 4, with its prominent VE component, does not resemble any synergy from the other three frogs.
In light of the similarity of the swimming synergies across frogs, we proceeded to group them into classes by cluster analysis. We progressively increased the number of clusters until no two synergies in each cluster were from the same frog. Six clusters of shared swimming synergies (denoted by S1-S6) were identified; four of them (S1-S4) were found in at least three of the four frogs. The principal muscles involved in these six groups of synergies are summarized below. Refer to Figure 6 for a summary of the functions of each muscle listed (as reflected by the signs of the moment arms).
Synergy S1 is an extension synergy comprising the ankle extensor GA (all frogs) and the hip extensors RI and AD (frogs 3 and 4). Synergy S2 is another extension synergy comprising SM, VE, and GA, extensors of the hip, knee, and ankle, respectively (frogs 1, 3, and 4). Synergy S3 includes the hip extensor/knee flexor, ST (all frogs) and the hip-knee flexor BI (frogs 3 and 4). Synergy S4 includes two knee extensors/ankle flexors, TA and PE (frogs 1, 2, and 4), as well as the hip-knee flexor SA (frog 2). Synergy S5 features the hip flexor IP and the hip-knee flexor BI (frogs 1 and 2). Synergy S6 features two hip flexors/knee extensors, RA and VE (frogs 2 and 3).
Both S1 and S2 were active only during the extension phase of the swimming cycle. All the rest of the synergies, except the S4 of frog 4, were active in both the extension and flexion phases of the swimming cycle.
To summarize our analyses of the swimming EMGs, in our stage I analysis, we established that both the intact and deafferented swimming data sets possess similar and low dimensionalities (Fig. 3A,B; Table 1). The intact and deafferented synergy sets identified in stage I share a common subspace (Figs. 3C, 4C), indicating that at least some synergies are preserved after deafferentation. To tackle some potential limitations of stage I (see Materials and Methods), we proceeded to our stage II analysis (Fig. 5). The degree of sharing was found to be higher in stage II (Table 1), suggesting that our stage II analysis can better assess the degree of sharing through combining information from different data sets. Most of the stage II synergies were identified as synergies shared between the intact and deafferented data sets (Fig. 6), suggesting that most synergies underlying the swimming behavior are centrally encoded modules activated by spinal and/or supraspinal commands. Six classes of swimming synergies were identified (Fig. 6), two of which (S1 and S2) were activated during the extension phase only.
Muscle synergies underlying jumping before and after deafferentation
We applied the same two-stage method illustrated above for swimming EMGs to the data collected during jumping to assess whether the same conclusions hold for the jumping behavior.
Stage I analysis of jumping EMGs: the intact and deafferented data sets possess similar low dimensionalities
Our stage I analyses of the jumping EMGs show that, like the swimming data sets, the intact and deafferented jumping data sets possess low and similar dimensionalities. Shown in Figure 7, A and B, are the stage I cross-validation R2 curves for frog 4 jumping analogous to those shown in Figure 3, A and B, for frog 3 swimming. We see that, in both the intact and deafferented data sets, four to five synergies are sufficient to explain ∼90% of data variance. The R2 curves resulting from extracting synergies from the unshuffled data sets (solid curve; mean ± SD; n = 20) also lie well above those expected by chance (shuffled data, dashed curve; mean ± SD; n = 20), confirming that actual data structures within the data sets are captured by our synergies. By fitting the R2 curves to straight lines, Nin* and Nde* for frog 4 jumping were determined to be 5 and 4, respectively (Fig. 7A,B, arrows). Similar results were obtained from the other three frogs (Table 1).
Figure 7.
Stage I analysis of jumping EMGs before and after deafferentation. A, B, We applied the same stage I procedure as applied to the swimming EMGs (described in the legend for Fig. 3 A, B) to our jumping EMGs. A, Cross-validation R2 curves for the intact jumping data set of frog 4. Solid curve, R2 curve from original data (mean ± SD; n = 20). Dashed curve, R2 curve from shuffled data (mean ± SD; n = 20). The black arrow indicates the correct number of intact synergies estimated by our procedure, and the dashed straight line is its corresponding linear fit. B, Cross-validation R2 curves for the deafferented jumping data set of frog 4. Same key as A. C, D, Assessing similarity between the intact and deafferented synergies using two approaches. C, The degree of overlap between the subspaces spanned by the intact and deafferented synergy sets, respectively, is indicated by the average ssd values (▪; n = 20 × 20 = 400). The average ssd values expected by chance were computed by calculating principal angles between shuffled synergy sets (×; mean ± 5 × SD after 20 trials of shuffling). In all frogs, the actual mean ssd is well above its corresponding baseline value (p < 0.01). D, The number of stage I intact synergies with actual structures that were preserved after deafferentation was indicated by the average nss values (▪; n = 20 × 20 = 400). The average nss values expected by chance were computed by calculating scalar products between shuffled synergy sets (×; mean ± 5 × SD after 20 trials of shuffling). In all frogs, the actual mean nss is higher than its corresponding baseline value (p < 0.01).
We also compared the similarity between the subspaces defined by each synergy set (ssd), and between the actual synergies in each set (nss). Although the nss values indicate that, for all four frogs, on average only one intact jumping synergy also appears as a deafferented synergy (Fig. 7D), our subspace analysis suggests that the intact and deafferented synergy subspaces share a two-dimensional subspace (Fig. 7C). As in swimming, the difference between the ssd and nss values implies that, in stage I, NMF finds only a common subspace shared between the intact and deafferented jumping synergies but not all of the synergies spanning this shared subspace.
Stage II analysis of jumping EMGs: most jumping synergies are preserved after deafferentation
We then proceeded to stage II and determined Nin*, Nde*, and Nsh* for each frog by pooling the intact and deafferented jumping data sets together. As summarized in Table 1, our stage II analyses suggest that four of four, four of four, three of four, and four of six intact jumping synergies for frogs 1-4, respectively, are preserved after deafferentation, and reconstruction of the original EMGs using these numbers of synergies yields R2 values of ∼90%. Therefore, the hypothesis that most synergies underlying the intact EMGs are preserved after feedback deprivation holds not only for swimming but for jumping as well. All of the shared and data set-specific jumping synergies of each frog from the extraction repetition with the highest overall R2 are summarized in Figure 8.
Figure 8.
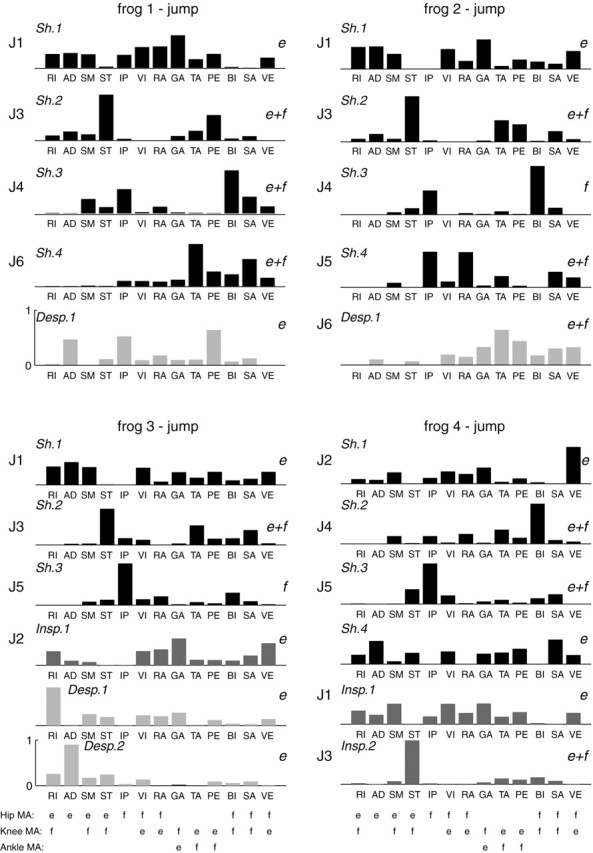
Jumping synergies of all frogs (analysis stage II). Shown in this figure are the stage II synergies of the extraction repetition with the highest R2 of the four frogs. The synergies shared between the intact and deafferented data sets are labeled Sh, synergies specific to the intact data set are labeled Insp, and synergies specific to the deafferented data set are labeled Desp. Synergies active only during the extension phase of jumping are marked with e on their right sides; those active only during the flexion phase are marked with f, and those active in both phases are marked e+f. All synergies shown in this figure were clustered into six classes (J1-J6), and the class of each synergy is marked on its left side. The sign of the moment arms (MA) around the hip, knee, and ankle joints of the 13 muscles included in this study are listed below the synergies of frog 3 and frog 4 (e, extensor action; f, flexor action). Moment arm signs are based on results of Kargo and Rome (2002) and González (2003).
For frog 3, if we compare its intact-specific synergy (Insp.1) with one of its deafferented-specific synergies (Desp.1), we see that both contain activation of similar muscles (RI, SM, VI, RA, GA, and VE) but in different balances between these muscles. The intact-specific synergy (Insp.1) has relatively more GA and VE than its deafferented counterpart (Desp.1) but less RI and SM. One interpretation of this observation is that sensory feedback may fine-tune the activation of individual muscles within a synergy, thereby altering the muscle activation balance profile of the synergy (Fig. 1A3). A similar interpretation may account for the similarity and difference between frog 4's Sh.1 and Insp.1 (Fig. 8).
As in our analysis of the swimming synergies, we grouped our jumping synergies into classes by cluster analysis. We found six classes of shared jumping synergies (denoted by J1-J6), four of which (J1-J4) were found in at least three of the four frogs. Their principal muscles are summarized below. Refer to Figure 8 for a summary of the functions of each muscle listed (as reflected by the signs of the moment arms).
Synergy J1 is an extension synergy found in all frogs comprising all major extensors of the hindlimb, RI, AD, and SM (hip extensors), VI, RA, VE, TA, and PE (knee extensors), as well as GA (ankle extensor). Synergy J2 is an extension synergy found only in frogs 3 and 4. It includes RI (frog 3), SM (frog 4), and the extensors VI, RA, GA, and VE. Synergy J3 includes the hip extensor/knee flexor ST (all frogs), the knee extensors/ankle flexors TA and PE (frogs 1, 2, and 3), and the hip flexor/knee flexor SA (frogs 2 and 3). Synergy J4 includes the hip flexor IP and the hip-knee flexor BI, with more BI than IP (frogs 1, 2, and 4), the hip extensor/knee flexor SM is found in frogs 1 and 4, and the hip-knee flexor, SA, is found in frogs 1 and 2. Synergy J5 features mostly the hip flexor IP (frogs 2, 3, and 4), and also RA (frogs 2 and 3), SA (frogs 2 and 4), and ST (frog 4). Synergy J6 contains activation in the two knee extensors/ankle flexors TA and PE, as well as SA, BI, and VE (frogs 1 and 2).
In all frogs, synergies J1 and J2 were active only during the extension phase of jumping. Most of the rest of the synergies were active in both the extension and flexion phases of jumping.
Although a detailed analysis of the similarities and differences between the swimming and jumping synergies is beyond the scope of this study (but see d'Avella and Bizzi, 2005), it is evident from our results (Figs. 6, 8) that some synergies are shared between the two behaviors (e.g., compare frog 2's S5, J4 and frog 3's S1, J1), whereas some other synergies appear to be specific to swimming (e.g., S2) or jumping (e.g., frog 2's J5). Our results thus support the idea that there are pattern-generating circuitries shared between behaviors so that control is simplified (Grillner, 1985; Soffe, 1993; Stein, 2005), as well as behavior-specific modules adapted to the specific demands of each task (Pratt et al., 1996; Jing et al., 2004).
To summarize our analyses of the jumping EMGs, in stage I, we found that both the intact and deafferented jumping data sets possess low and similar dimensionalities (Fig. 7A,B). In stage II, most of the synergies were extracted as synergies shared between the intact and deafferented data sets (Fig. 8), allowing us to conclude that most synergies underlying the jumping behavior are centrally organized modules activated by spinal and/or supraspinal commands. Six classes of jumping synergies were identified (Fig. 8), two of which (J1 and J2) were activated during the extension phase only. We note also that many jumping synergies appear to be similar to our swimming synergies (Figs. 6, 8).
Effects of deafferentation on the activation of synergies
Reconstructing EMG data with synergies and their coefficients
The results of the previous two sections show, that for both swimming and jumping, there is a large degree of sharing between synergies before and after deafferentation. However, as can be seen in Figure 2, there were also substantial changes in the EMGs observed after deafferentation. We therefore investigated how such EMG alterations were produced by examining patterns of synergy activation coefficients used to reconstruct the observed EMGs before and after deafferentation. In Figure 9, the jumping EMG examples shown in Figure 2 are reconstructed from the jumping synergies of frog 1 (Fig. 8). We see that activation of SM, IP, BI, and SA in phase c′, as noted previously, is explained by prolonged activation of synergy J4 (light blue) in the deafferented example. The increased amplitude and duration of TA and PE after deafferentation, however, are explained by a prolonged and increased activation of synergy J6 (green) in phase c′ compared with phase c. Also, the altered relative onset times of AD, ST, IP, and PE in phase a′ is accounted for by the deafferented-specific synergy (yellow). The examples in Figure 9 therefore suggest that the altered EMG patterns after deafferentation can be characterized by changes in the amplitude and temporal patterns of the shared synergy coefficients and, to a lesser extent, by the data set-specific synergies.
Figure 9.
Reconstructing the original EMGs with synergies and their coefficients. The intact and deafferented EMG examples shown in Figure 2, C and D, are reconstructed using the stage II synergies extracted from the jumping EMGs of frog 1 (Fig. 8). The original EMG data, filtered and integrated (for filtering and integration parameters, see Materials and Methods), is indicated by thick black lines, and the time-varying coefficients of the synergies are shown below the EMGs. The reconstruction of the motor pattern is superimposed onto the original EMGs. The colors composing the reconstruction match the colors of the coefficients such that the colors reflect the respective contribution of each synergy to the reconstruction at each time point. Note that synergy Desp1 (yellow) is deafferented specific; thus, by definition, it contributes to the reconstruction of only the deafferented EMG episode. For more discussion, see Results.
Deafferentation alters both the amplitude and temporal patterns of synergy activation
We proceeded to systematically analyze effects of deafferentation on both the amplitude and temporal patterns of the synergy coefficients.
The percentage changes of the extension and flexion peak amplitudes of the different classes of synergies after deafferentation are summarized in the left half of Table 2. For the extension synergies (S1, S2, J1, and J2), deafferentation had a much more pronounced effect on the jumping synergies (J1, J2) than on the swimming synergies (S1, S2). As summarized in Table 2, for three of the four frogs, there was a 25-44% decrease in the extension peak amplitude of J1 after deafferentation. In contrast, the extension peak amplitude of S1 for frogs 1 and 2, as well as that of S2 for frogs 1, 3, and 4, was not altered by deafferentation. One explanation for this difference is that sensory feedback plays a much more important role in reinforcing the activation of jumping extension synergies than that of the swimming extension synergies. Although other interpretations (such as muscle fatigue) are possible, we think that the above interpretation is likely because it makes biomechanical sense (see Discussion). We speculate that the exceptional increase in S1 extension amplitude for frog 4 (Table 2) might be attributable to a more-than-usual denervation supersensitivity to inputs in the spinal interneurons or motoneurons induced by our surgical procedure.
Table 2.
Effects of deafferentation on the amplitude and temporal patterns of synergy coefficients
|
Synergy |
Frog |
Ext. peak amp. (% change) |
Flex. peak amp. (% change) |
Ext. burst duration (% change) |
Flex. burst duration (% change) |
|---|---|---|---|---|---|
| S1 | Frog 1 | NC | NA | NC | NA |
| Frog 2 | NC | NA | −14.9 | NA | |
| Frog 3 | −42.4 | NA | +38.3 | NA | |
| Frog 4 | +266.7 | NA | NC | NA | |
| S2 | Frog 1 | NC | NA | +29.0 | NA |
| Frog 3 | NC | NA | NC | NA | |
| Frog 4 | NC | NA | −27.6 | NA | |
| S3 | Frog 1 | Insp | Insp | Insp | Insp |
| Frog 2 | −42.3 | −65.2 | NC | NC | |
| Frog 3 | +79.4 | NC | +15.8 | −19.4 | |
| Frog 4 | +68.9 | NC | −61.4 | −50.1 | |
| S4 | Frog 1 | NC | +115.1 | NC | NC |
| Frog 2 | −28.6 | NC | −17.7 | NC | |
| Frog 4 | Insp | NA | Insp | NA | |
| S5 | Frog 1 | Insp | Insp | Insp | Insp |
| Frog 2 | −24.1 | −29.6 | NC | NC | |
| S6 | Frog 2 | −26.3 | −25.9 | −16.3 | +57.2 |
| Frog 3 | +90.6 | +128.0 | +65.2 | NC | |
| J1 | Frog 1 | −25.1 | NA | −23.8 | NA |
| Frog 2 | −39.7 | NA | −19.1 | NA | |
| Frog 3 | −43.7 | NA | +25.1 | NA | |
| Frog 4 | Insp | NA | Insp | NA | |
| J2 | Frog 3 | Insp | NA | Insp | NA |
| Frog 4 | +50.2 | NA | −20.2 | NA | |
| J3 | Frog 1 | −33.6 | −51.4 | −14.5 | +24.6 |
| Frog 2 | −57.9 | −59.4 | −34.6 | −60.4 | |
| Frog 3 | NC | NC | NC | NC | |
| Frog 4 | Insp | Insp | Insp | Insp | |
| J4 | Frog 1 | −33.8 | −26.3 | NC | +276.9 |
| Frog 2 | NA | −37.1 | NA | −50.3 | |
| Frog 4 | +32.2 | +44.0 | −25.8 | NC | |
| J5 | Frog 2 | −37.4 | −58.5 | −27.5 | −64.5 |
| Frog 3 | NA | +35.7 | NA | −57.9 | |
| Frog 4 | NC | NC | NC | NC | |
| J6 | Frog 1 | −22.3 | +22.2 | NC | +69.6 |
|
|
Frog 2 |
Desp |
Desp |
Desp |
Desp |
Changes in coefficient peak amplitude (amp.) and coefficient burst duration after deafferentation for both the extension (Ext.) and flexion (Flex.) phases were quantified as percentage changes. Instances for which the null hypothesis that the intact and deafferented means are the same cannot be rejected (t test; p > 0.05) are marked with NC, standing for no change. The abbreviation NA, standing for not available, means that the synergy was not activated during that particular phase. Insp and Desp stand for intact- and deafferented-specific synergies, respectively. For an explanation of how burst duration was determined, see Materials and Methods.
For the non-extension synergies (S3-S6, J3-J6), except S5 and J3, the effects of deafferentation on the peak coefficient amplitude were much less consistent across animals. For instance, whereas in frog 2 there was a 59% decrease in flexion peak amplitude of J5, in frog 3, this synergy increased by 36%, and in frog 4, the difference between the intact and deafferented means of the same synergy are not statistically significant (p > 0.05).
The right half of Table 2 summarizes the percentage change of coefficient burst duration for both the extension and flexion phases. Again, results across animals tend not to be very consistent. For example, we have seen in Figure 9 that, in frog 1, activation of J4 (SM, IP, BI, SA) during the flexion phase was prolonged after deafferentation. Consistent with this observation, our burst duration analysis indicates that, on average, there was a 2.8-fold increase in the flexion burst duration for synergy J4 in frog 1. However, for frog 2, a 58% decrease in flexion burst duration was noted for the same synergy, and, for frog 4, no change in flexion burst duration was indicated instead. We thus conclude that deafferentation alters the temporal patterns of the synergy coefficients, but, for each synergy, individual frogs might rely on sensory feedback differently to sculpt the temporal profile of synergy activation.
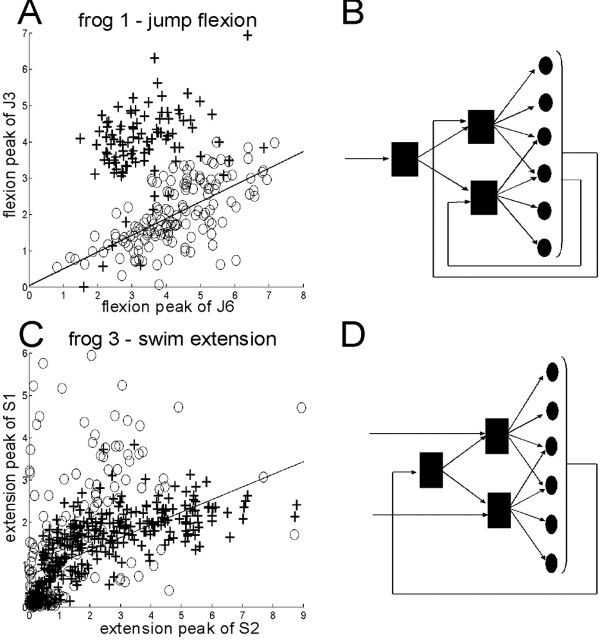
Sensory feedback can uncouple or couple the activation of synergies
To investigate the possible roles of feedback in correlating or decorrelating the activations of two synergies, we calculated the Pearson's correlation coefficient (r) between the peak coefficient amplitudes of every pair of shared synergies, for each frog, each behavior, each of the extension and flexion phases, and each of the intact and deafferented data sets. We then compared the intact and deafferented r values to assess whether deafferentation causes an increased or decreased correlation between the peak amplitudes of the synergies. An increase in correlation after deafferentation between two synergies would indicate that, although activation of each synergy may be modulated by sensory feedback, activation of both may be correlated and coordinated by central mechanisms. Conversely, a decrease in correlation after deafferentation would indicate that feedback signals play a role in correlating their activation.
Among all pairs of swimming or jumping synergies, we identified 10 pairs with extension or flexion peak coefficient amplitudes that are well correlated under either the intact or deafferented condition (r ≥ 0.6; p < 0.01) and with an intact r that is smaller than the deafferented r (p < 0.01). One such pair, J3 and J6 of frog 1 (flexion peak), is shown in Figure 10A as an example. We see that, although the intact flexion peak coefficient amplitudes (+) between the two synergies are not well correlated (r = 0.3156; p < 0.01), the deafferented peak amplitudes (○) are strongly correlated (r = 0.6736; p < 0.01). The difference between the intact and deafferented r values in this case is also statistically significant (p < 0.01). Thus, sensory feedback may function to uncouple two centrally coupled synergies by modulating activation of each synergy independently (Fig. 10B). Note that, in Figure 10A, there are 15 intact jumps (+) for which the J3 and J6 activation patterns overlap with those of the deafferented jumps and appear to be correlated much like the deafferented samples. It is possible that, in those jumps, feedback signals were gated (Burke, 1999) or were less effective, thereby causing those jump flexion phases to be similar to the deafferented cases.
Figure 10.
Sensory feedback can uncouple or couple the activation of synergies. We calculated the Pearson's correlation coefficient (r) peak coefficient amplitudes of every pair of shared synergies, for each behavior, each of the extension and flexion phases, and each of the intact and deafferented conditions. A, The flexion-phase peak coefficient amplitudes of synergies J3 and J6 (frog 1). The intact samples are shown as crosses (+), and the deafferented samples are shown as circles (○). This is an example of a pair of synergies showing an increase in correlation after deafferentation (intact r = 0.3156; deafferented r = 0.6736). The straight line represents the least-squares fit to the deafferented samples. B, Interpretation of the results shown in A. Each black square represents a central neuronal network coding for a muscle synergy or a network coordinating the activation of multiple synergies; each black circle represents the motoneuronal pool of a particular muscle. The finding that the deafferented samples are highly correlated suggests that J3 and J6 (frog 1) are coordinated by central mechanisms upstream of the synergies. However, the smaller correlation with afferents intact suggests that one or both synergies might be modulated by sensory feedback. For more discussion, see Results. C, The extension-phase peak coefficient amplitudes of synergies S1 and S2 (frog 3). Again, the intact samples are shown as crosses (+), and the deafferented samples are shown as circles (○). This is an example of a pair of synergies showing a decrease in correlation after deafferentation (intact r = 0.7065; deafferented r = 0.5011). The straight line represents the least-squares fit to the intact samples. D, Interpretation of the results shown in C. That the deafferented r is relatively small suggests that S1 and S2 are controlled as two relatively independent modules by feedforward commands, but the high correlation observed under the intact state implies that sensory afferents might help to couple the activation of these two synergies during swimming extension.
The other pairs of shared synergies showing a similar increase in correlation coefficient after deafferentation are as follows: S1/S4 (frog 1, extension); S2/S4 (frog 1, extension); S1/Sh.4 (frog 1, extension); J1/J3 (frog 1, extension); J3/J4 (frog 1; flexion); S1/Sh.6 (frog 2, extension); S1/S3 (frog 3, extension); S3/Sh.4 (frog 4, extension); and S2/S3 (frog 4, extension). It is noteworthy that, among these 10 pairs of synergies showing an increase in correlation after feedback deprivation, six of them involve J3 or S3, both of which possess a prominent ST component (Figs. 6, 8). It therefore appears that the two ST synergies are more likely to be uncoupled from other synergies by sensory inflow.
In addition, we found another four pairs of shared synergies for which the extension peak coefficient amplitudes are correlated under either the intact or deafferented condition (r ≥ 0.6; p < 0.01) and for which the intact r is greater than the deafferented r (p < 0.01). Frog 3's S1 and S2 (extension peak) belong to one of these pairs (Fig. 10C). In this example, the intact and deafferented r values are 0.7065 (p < 0.01) and 0.5011 (p < 0.01), respectively, and the null hypothesis that the two r values are the same can be rejected (p < 0.01). That the deafferented r is relatively small suggests that S1 and S2 are controlled as two relatively independent modules by feedforward commands (Fig. 10D), but the high correlation observed under the intact state implies that sensory afferents might help to couple the activation of these two synergies during swimming extension (Fig. 10D). Hence, sensory feedback might function to couple two independently organized synergies.
The other three pairs of shared synergies showing a similar decrease in correlation coefficient after deafferentation are as follows: S1/S6 (frog 2, extension); J3/J5 (frog 2, extension); and J2/J4 (frog 4, extension).
Finally, we did not observe consistent coupling and uncoupling actions of feedback between the same pairs of synergies across frogs, once again suggesting that the roles of sensory feedback in modifying synergy activation patterns show substantial interanimal variability.
In summary, the results of this section suggest that the differences between the intact and deafferented EMG patterns can be characterized as changes in the amplitude and temporal patterns of the synergy coefficients (Fig. 9). Our coefficient analyses further suggest that sensory feedback plays an important role in reinforcing the jumping extension synergy but not the swimming extension synergies (Table 2). For the amplitudes of the non-extension synergies and for the burst duration of the coefficients, effects of deafferentation were not consistent across animals, however (Table 2). Finally, our correlation analysis reveals that feedback can either uncouple or couple two centrally organized modules (Fig. 10).
Discussion
In this study, we assess to what extent locomotor EMGs are generated by centrally organized muscle synergies. For both swimming and jumping, we established that EMGs before and after deafferentation possess similar low dimensionalities (stage I) and that most synergies were preserved after feedback deprivation (stage II). Deafferentation also altered the amplitude and temporal patterns of activation of the shared synergies.
Muscle synergies as centrally organized modules
The main finding of this study is that both intact and deafferented behaviors are primarily generated by the same set of synergies. Therefore, most, but not all, of the muscle synergies underlying frog locomotor behaviors are centrally organized modules activated by spinal and/or supraspinal commands. Such a result is similar to previous observations of invariant structures after deafferentation in the newt (Székely et al., 1969), frog (Loeb et al., 1993; Kargo and Giszter, 2000b), and cat (Grillner and Zangger, 1984; Giuliani and Smith, 1987; Koshland and Smith, 1989).
The present study extends these previous results. By recording EMGs from intact, freely moving animals, we have obtained results that might reflect strategies used by the CNS to produce natural behaviors, not just features of the isolated spinal cord or of constrained tasks. By systematic and quantitative analyses of EMGs from a large number of muscles, we have established the sufficiency of a small number of synergies to describe both the intact and deafferented data sets well. Thus, our results support the hypothesis that the CNS simplifies the daunting task of deriving appropriate muscle patterns for many behaviors by flexible combination of a small number of synergies (Tresch et al., 1999; Hart and Giszter, 2004; Ting and Macpherson, 2005). Our findings also validate our means of identifying the synergies: the NMF algorithm would have failed to uncover any shared synergies if there had been a gross mismatch between the assumptions of the algorithm (such as linearity) and our conceptual model of synergy combination.
The observation of invariant synergies also suggests that our synergies may reflect what are commonly referred to as central pattern generators (CPGs), circuitries capable of generating motor patterns without sensory input (Grillner, 1981; Rossignol, 1996; Marder and Bucher, 2001). The finding that combination of synergies can explain our data well and the observation of synergies shared between behaviors (see Results) further suggest that our synergies may correspond to building blocks of the CPGs, sometimes formulated as a mosaic of “unit burst generators” (Grillner, 1985). Our linear combination model of synergies provides not only an explicit formulation of how these building blocks can be combined but also a means of identifying them. Our model can then be seen as a more general formulation of the unit burst generator hypothesis, in which each “unit” can consist of muscles acting across different joints, and the interconnected units need not be activated in strict alternation with one another. Such a formulation can include experimentally observed synergies such as the mixed knee extensor-ankle flexor synergy of cat paw shaking (Smith et al., 1985).
We further speculate that each synergy subserves some basic biomechanical functions (Raasch and Zajac, 1999; Ting et al., 1999; Ting and Macpherson, 2005), such as powering jump extension (Olson and Marsh, 1998) or compensating for interaction torque (Zernicke and Smith, 1996; Gribble and Ostry, 1999). An understanding of the principles guiding the composition of locomotor synergies will require additional experimental and modeling studies.
Afferent roles in synergy activation and organization
Although we found that most synergies were preserved after deafferentation, the EMGs themselves were changed (Fig. 2), similar to some previous findings that the intact and deafferented muscle patterns could be quite different (Grillner and Zangger, 1984; Hiebert and Pearson, 1999). Our coefficient analyses indicate that such changes could be characterized primarily as alterations in the amplitude and temporal patterns of activation of shared synergies (Fig. 9; Table 2). Therefore, one important role of feedback might be to shape behaviors by modulating recruitment of centrally organized synergies (Fig. 1A1), consistent with the long-standing hypothesis that motor outputs depend on interactions between the coordinative structures within CPGs, supraspinal commands, and sensory inflow (Grillner, 1981; Clarac, 1991; Prochazka, 1996; Rossignol, 1996; McCrea, 2001).
More specifically, sensory inflow during a behavior might adapt recruitment of synergies to the constraints imposed by the task. For instance, we found that, during extension, feedback plays a prominent role in enhancing the activation amplitude of the jumping but not the swimming synergies (Table 2). This difference in the importance of feedback might be attributable to the different biomechanical demands of the two behaviors. During jump extension, the frog needs to generate more power to accelerate the body against gravity within the shortest possible time. Power generation might be enhanced by an increased activation of the Golgi tendon organs and Ib interneurons [attributable to increased extensor tension caused by the frog's weight being borne solely by the hindlimbs (Roberts and Marsh, 2003, their Fig. 5)], assisting in maximal activation of the extensor synergies through a positive feedback loop after Ib input onto the extensor motoneurons is reversed from inhibitory to excitatory (Pearson and Collins, 1993). A similar reflex reversal mechanism is believed to contribute to stance-phase reinforcement of the extensors in the walking cat (Whelan, 1996).
Our analysis of coefficient amplitudes also reveals that feedback uncouples multiple synergies that are centrally organized (Fig. 10); therefore, afferents might allow for more individuated control of each synergy. The synergies uncoupled by feedback may have distinct and/or opposing functions. For example, in Figure 10A, whereas J3 includes the knee flexor ST, J6 comprises TA and PE, the knee extensor action (González, 2003) of which may oppose the knee flexor action of J3. Conversely, the synergies coupled by feedback may subserve similar biomechanical functions. Both synergies in Figure 10C, for instance, are synergies of extensors.
Among the 10 identified pairs of shared synergies that sensory inflow uncoupled (listed in Results), six of them involve J3 or S3, two synergies dominated by ST. In the frog, ST is both a knee flexor and a hip extensor (Mai and Lieber, 1990; Kargo and Rome, 2002). That the ST synergies seem more likely to be uncoupled from other synergies by feedback is consistent with the proposal that bifunctional muscles like ST are more susceptible to feedback modulation (Perret and Cabelguen, 1980; Pratt et al., 1996; Ting et al., 2000).
Synergies specific to intact or deafferented behaviors
Besides shared synergies, our algorithm also identified synergies specific to the intact or deafferented data sets. The intact-specific synergies may represent CNS modules accessible only by feedback (Fig. 1A2), functioning to compensate for perturbations (Forssberg, 1979; Kargo and Giszter, 2000a). Alternatively, the data set-specific synergies may indicate feedback reorganization of the CNS neuronal assemblies (Pearson, 2004), i.e., the specific synergies reflect the difference between the networks activated under the intact and deafferented conditions (Fig. 1A4). For frogs 3 and 4, the observation that some of the specific and shared synergies involve the same set of muscles, but in different balances (see Results and Fig. 8), suggests that some centrally activated synergies may serve only as templates for motor output generation; activities of individual muscles within those synergies might then be fine-tuned by feedback (Fig. 1A3) (Pearson, 2000). Finally, the possibility of the nonshared synergies being consequences of neuronal plasticity (Goldberger, 1988) cannot be excluded.
Interanimal variability of feedback actions
We have seen that the roles of sensory feedback in modulating the amplitude and temporal patterns of each synergy may vary between animals (Table 2), suggesting that how feedback sculpts the activation pattern of each synergy may depend on the previous experiences of each animal. Such a possibility is supported by the proposal that the reflex gain of the rat withdrawal reflex system may be fine-tuned in an experience-dependent manner (Schouenborg, 2002). Also, the architectural heterogeneity of the musculature across animals may necessitate individually tailored recruitment of certain muscles (Loeb, 1993).
A novel method of identifying common and specific structures
Another contribution of this study is our method of exploiting the NMF algorithm to search for shared and specific structures from multiple data sets, introduced in our stage II analysis. Although our stage I method of applying the algorithm to each data set separately is an obvious way to search for shared and specific synergies (d'Avella et al., 2003; Hart and Giszter, 2004), it has several limitations (see Materials and Methods). Our stage II method overcomes these limitations by taking information from all data sets into consideration. We have focused on using this method to find commonalities and differences between the intact and deafferented data sets, but the same methodology can be extended to extract synergies shared between behaviors (d'Avella and Bizzi, 2005), preparations, or animals.
Almost a century ago, Brown (1911) proposed that “intrinsic factors” within the spinal cord are responsible for generating motor outputs for locomotion. In light of Bernstein's (1967) problem, we propose that a small number of centrally organized muscle synergies, activated by central commands but regulated by sensory inflow, plays a predominant role in the generation of complex, high-dimensional motor patterns for natural behaviors.
Footnotes
This work was supported by the Chyn Doug Shiah Memorial Fellowship and the Schoemaker Foundation Fellowship (V.C.K.C) and by National Institutes of Health/National Institute of Neurological Disorders and Stroke Grants NS09343 and NS39865 (E.B.). We give special thanks to Emery N. Brown for his encouragement and constant support of this work. We also thank Steve G. Massaquoi and Philippe Saltiel for many helpful discussions, Simon Overduin for comments on this manuscript, Margo Cantor for technical support, and Charlotte Potak for administrative assistance.
Correspondence should be addressed to Andrea d'Avella, Department of Neuromotor Physiology, Istituto di Ricovero e Cura a Carattere Scientifico, Fondazione Santa Lucia, Via Ardeatina 306, 00179 Rome, Italy. E-mail: a.davella@hsantalucia.it.
Copyright © 2005 Society for Neuroscience 0270-6474/05/256419-16$15.00/0
References
- Bates DM, Watts DG (1988) Nonlinear regression analysis and its applications. New York: Wiley.
- Bell AJ, Sejnowski TJ (1995) An information-maximisation approach to blind source separation and blind deconvolution. Neural Comput 7: 1129-1159. [DOI] [PubMed] [Google Scholar]
- Bernstein N (1967) The co-ordination and regulation of movements. Oxford: Pergamon.
- Bizzi E, Mussa-Ivaldi FA, Giszter S (1991) Computations underlying the execution of movement: a biological perspective. Science 253: 287-291. [DOI] [PubMed] [Google Scholar]
- Brown TG (1911) The intrinsic factors in the act of progression in the mammal. Proc R Soc Lond B Biol Sci 84: 308-319. [Google Scholar]
- Browne MW (2000) Cross-validation methods. J Math Psychol 44: 108-132. [DOI] [PubMed] [Google Scholar]
- Burke RE (1999) The use of state-dependent modulation of spinal reflexes as a tool to investigate the organization of spinal interneurons. Exp Brain Res 128: 263-277. [DOI] [PubMed] [Google Scholar]
- Clarac F (1991) How do sensory and motor signals interact during locomotion? In: Motor control: concepts and issues (Humphrey DR, Freund H-J, eds), pp 199-221. New York: Wiley.
- d'Avella A, Bizzi E (2005) Shared and specific muscle synergies in natural motor behaviors. Proc Natl Acad Sci USA 102: 3076-3081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- d'Avella A, Saltiel P, Bizzi E (2003) Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci 6: 300-308. [DOI] [PubMed] [Google Scholar]
- Delcomyn F (1980) Neural basis of rhythmic behavior in animals. Science 210: 492-498. [DOI] [PubMed] [Google Scholar]
- Ecker A (1971) The anatomy of the frog (Haslam G, translator). Amsterdam: Asher.
- Forssberg H (1979) Stumbling corrective reaction: a phase-dependent compensatory reaction during locomotion. J Neurophysiol 42: 936-953. [DOI] [PubMed] [Google Scholar]
- Giuliani CA, Smith JL (1987) Stepping behaviors in chronic spinal cats with one hindlimb deafferented. J Neurosci 7: 2537-2546. [PMC free article] [PubMed] [Google Scholar]
- Goldberger ME (1988) Partial and complete deafferentation of cat hindlimb: the contribution of behavioral substitution to recovery of motor function. Exp Brain Res 73: 343-353. [DOI] [PubMed] [Google Scholar]
- Golub GH, Van Loan CF (1983) Matrix computations. Baltimore: Johns Hopkins UP.
- González IC (2003) Linear control model of the spinal processing of descending neural signals. Masters degree thesis, Massachusetts Institute of Technology.
- Gribble PL, Ostry DJ (1999) Compensation for interaction torques during single- and multijoint limb movement. J Neurophysiol 82: 2310-2326. [DOI] [PubMed] [Google Scholar]
- Grillner S (1975) Locomotion in vertebrates: central mechanisms and reflex interaction. Physiol Rev 55: 247-304. [DOI] [PubMed] [Google Scholar]
- Grillner S (1981) Control of locomotion in bipeds, tetrapods, and fish. In: Handbook of physiology, Sec 1 (Brooks VB, ed), pp 1179-1236. Bethesda, MD: American Physiological Society.
- Grillner S (1985) Neurobiological bases of rhythmic motor acts in vertebrates. Science 228: 143-149. [DOI] [PubMed] [Google Scholar]
- Grillner S, Zangger P (1984) The effect of dorsal root transection on the efferent motor pattern in the cat's hindlimb during locomotion. Acta Physiol Scand 120: 393-405. [DOI] [PubMed] [Google Scholar]
- Hart CB, Giszter SF (2004) Modular premotor drives and unit bursts as primitives for frog motor behaviors. J Neurosci 24: 5269-5282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hays WL (1994) Statistics. Belmont, CA: Wardsworth.
- Hiebert GW, Pearson KG (1999) Contributions of sensory feedback to the generation of extensor activity during walking in the decerebrate cat. J Neurophysiol 81: 758-770. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A, Oja E (2000) Independent component analysis: algorithms and applications. Neural Netw 13: 411-430. [DOI] [PubMed] [Google Scholar]
- Jing J, Cropper EC, Hurwitz I, Weiss KR (2004) The construction of movement with behavior-specific and behavior-independent modules. J Neurosci 24: 6315-6325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kargo WJ, Giszter SF (2000a) Rapid correction of aimed movements by summation of force-field primitive. J Neurosci 20: 409-426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kargo WJ, Giszter SF (2000b) Afferent roles in hindlimb wipe-reflex trajectories: free-limb kinematics and motor patterns. J Neurophysiol 83: 1480-1501. [DOI] [PubMed] [Google Scholar]
- Kargo WJ, Rome LC (2002) Functional morphology of proximal hindlimb muscles in the frog Rana pipiens J Exp Biol 205: 1987-2004. [DOI] [PubMed] [Google Scholar]
- Koshland GF, Smith JL (1989) Mutable and immutable features of paw-shake responses after hindlimb deafferentation in the cat. J Neurophysiol 62: 162-173. [DOI] [PubMed] [Google Scholar]
- Lee DD, Seung HS (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401: 788-791. [DOI] [PubMed] [Google Scholar]
- Lee DD, Seung HS (2001) Algorithms for non-negative matrix factorization. In: Advances in neural information processing systems, Vol 13 (Leen TK, Dietterich TG, Tresp V, ed), pp 556-562. Cambridge, MA: MIT. [Google Scholar]
- Loeb GE (1993) The distal hindlimb musculature of the cat: interanimal variability of locomotor activity and cutaneous reflexes. Exp Brain Res 96: 125-140. [DOI] [PubMed] [Google Scholar]
- Loeb EP, Giszter SF, Borghesani P, Bizzi E (1993) Effects of dorsal root cut on the forces evoked by spinal microstimulation in the spinalized frog. Somatosens Mot Res 10: 81-95. [DOI] [PubMed] [Google Scholar]
- Mai MT, Lieber RL (1990) A model of semitendinosus muscle sarcomere length, knee and hip joint interaction in the frog hindlimb. J Biomech 23: 271-279. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D (2001) Central pattern generators and the control of rhythmic movements. Curr Biol 11: R986-R996. [DOI] [PubMed] [Google Scholar]
- McCrea DA (2001) Spinal circuitry of sensorimotor control of locomotion. J Physiol (Lond) 533.1: 41-50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nauwelaerts S, Aerts P (2002) Two distinct gait types in swimming frogs. J Zool 258: 183-188. [Google Scholar]
- Olson JM, Marsh RL (1998) Activation patterns and length changes in hindlimb muscles of the bullfrog Rana catesbeiana during jumping. J Exp Biol 201: 2763-2777. [DOI] [PubMed] [Google Scholar]
- Pearson KG (2000) Neural adaptation in the generation of rhythmic behavior. Annu Rev Physiol 62: 723-753. [DOI] [PubMed] [Google Scholar]
- Pearson KG (2004) Generating the walking gait: role of sensory feedback. Prog Brain Res 143: 123-129. [DOI] [PubMed] [Google Scholar]
- Pearson KG, Collins DF (1993) Reversal of the influence of group Ib afferents from plantaris on activity in medial gastrocnemius muscle during locomotor activity. J Neurophysiol 70: 1009-1017. [DOI] [PubMed] [Google Scholar]
- Perret C, Cabelguen J-M (1980) Main characteristics of the hindlimb locomotor cycle in the decorticate cat with special reference to bifunctional muscles. Brain Res 187: 333-352. [DOI] [PubMed] [Google Scholar]
- Pratt CA, Buford JA, Smith JL (1996) Adaptive control for backward quadrupedal walking. V. Mutable activation of bifunctional thigh muscles. J Neurophysiol 75: 832-842. [DOI] [PubMed] [Google Scholar]
- Prochazka A (1996) Proprioceptive feedback and movement regulation. In: Handbook of physiology, Sec 12 (Rowell LB, Shepherd JT, eds), pp 89-127. New York: Oxford UP.
- Raasch CC, Zajac FE (1999) Locomotor strategy for pedaling: muscle groups and biomechanical functions. J Neurophysiol 82: 515-525. [DOI] [PubMed] [Google Scholar]
- Roberts TJ, Marsh RL (2003) Probing the limits to muscle-powered accelerations: lessons from jumping bullfrogs. J Exp Biol 206: 2567-2580. [DOI] [PubMed] [Google Scholar]
- Rossignol S (1996) Neural control of stereotypic limb movements. In: Handbook of physiology, Sec 12 (Rowell LB, Shepherd JT, eds), pp 173-216. New York: Oxford UP.
- Saltiel P, Wyler-Duda K, d'Avella A, Tresch MC, Bizzi E (2001) Muscle synergies encoded within the spinal cord: evidence from focal intraspinal NMDA iontophoresis in the frog. J Neurophysiol 85: 605-619. [DOI] [PubMed] [Google Scholar]
- Schouenborg J (2002) Modular organisation and spinal somatosensory imprinting. Brain Res Brain Res Rev 40: 80-91. [DOI] [PubMed] [Google Scholar]
- Smith JL, Hoy MG, Koshland GF, Phillips DM, Zernicke RF (1985) Intralimb coordination of the paw-shake response: a novel mixed synergy. J Neurophysiol 54: 1271-1281. [DOI] [PubMed] [Google Scholar]
- Soffe SR (1993) Two distinct rhythmic motor patterns are driven by common premotor and motor neurons in a simple vertebrate spinal cord. J Neurosci 13: 4456-4469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein PSG (2005) Neuronal control of turtle hindlimb motor rhythms. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 191: 213-229. [DOI] [PubMed] [Google Scholar]
- Stein PSG, Smith JL (1997) Neural and biomechanical control strategies for different forms of vertebrate hindlimb motor tasks. In: Neurons, networks, and motor behavior (Stein PSG, Grillner S, Selverston AI, Stuart DG, eds), pp 61-73. Cambridge, MA: MIT.
- Székely G, Czéh G, Vörös G (1969) The activity pattern of limb muscles in freely moving normal and deafferented newts. Exp Brain Res 9: 53-62. [DOI] [PubMed] [Google Scholar]
- Ting LH, Macpherson JM (2005) A limited set of muscle synergies for force control during a postural task. J Neurophysiol 93: 609-613. [DOI] [PubMed] [Google Scholar]
- Ting LH, Kautz SA, Brown DA, Zajac FE (1999) Phase reversal of biomechanical functions and muscle activity in backward pedaling. J Neurophysiol 81: 544-551. [DOI] [PubMed] [Google Scholar]
- Ting LH, Kautz SA, Brown DA, Zajac FE (2000) Contralateral movement and extensor force generation alter flexion phase muscle coordination in pedaling. J Neurophysiol 83: 3351-3365. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Saltiel P, Bizzi E (1999) The construction of movement by the spinal cord. Nat Neurosci 2: 162-167. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Saltiel P, d'Avella A, Bizzi E (2002) Coordination and localization in spinal motor system. Brain Res Brain Res Rev 40: 66-79. [DOI] [PubMed] [Google Scholar]
- Whelan PJ (1996) Control of locomotion in the decerebrate cat. Prog Neurobiol 49: 481-515. [DOI] [PubMed] [Google Scholar]
- Zernicke RF, Smith JL (1996) Biomechanical insights into neural control of movement. In: Handbook of physiology, Sec 12 (Rowell LB, Shepherd JT, eds), pp 293-330. New York: Oxford UP.