On the Computations Analyzing Natural Optic Flow: Quantitative Model Analysis of the Blowfly Motion Vision Pathway

Abstract

For many animals, including humans, the optic flow generated on the eyes during locomotion is an important source of information about self-motion and the structure of the environment. The blowfly has been used frequently as a model system for experimental analysis of optic flow processing at the microcircuit level. Here, we describe a model of the computational mechanisms implemented by these circuits in the blowfly motion vision pathway. Although this model was originally proposed based on simple experimenter-designed stimuli, we show that it is also capable to quantitatively predict the responses to the complex dynamic stimuli a blowfly encounters in free flight. In particular, the model visual system exploits the active saccadic gaze and flight strategy of blowflies in a similar way, as does its neuronal counterpart. The model circuit extracts information about translation velocity in the intersaccadic intervals and thus, indirectly, about the three-dimensional layout of the environment. By stepwise dissection of the model circuit, we determine which of its components are essential for these remarkable features. When accounting for the responses to complex natural stimuli, the model is much more robust against parameter changes than when explaining the neuronal responses to simple experimenter-defined stimuli. In contrast to conclusions drawn from experiments with simple stimuli, optimization of the parameter set for different segments of natural optic flow stimuli do not indicate pronounced adaptational changes of these parameters during long-lasting stimulation.

Introduction

Locomotion generates complex patterns of retinal image movements, the so-called optic flow (Gibson, 1979; Lappe, 2000; Eckert and Zeil, 2001). In blowflies, the neuronal computations underlying optic flow processing have been analyzed in great detail: the outputs of local motion-sensitive elements are spatially pooled by large-field neurons, the so-called tangential cells (TCs) responding best to different optic flow patterns (for review, see Hausen, 1984; Egelhaaf and Warzecha, 1999; Krapp et al., 2001; Borst and Haag, 2002; Egelhaaf et al., 2002). One particular TC, the horizontal system equatorial (HSE) cell, is commonly assumed to encode yaw rotations of the animal and to be involved in controlling visually guided behavior (Hausen, 1982a,b; Haag et al., 1997; Horstmann et al., 2000; Krapp et al., 2001).

In free flight, blowflies execute series of saccadic turns with angular velocities of up to several thousand degrees per second; between saccades, the gaze is kept stable (i.e., rotational velocities are one to two orders of magnitude smaller than during saccades) (Schilstra and van Hateren, 1998, 1999; van Hateren and Schilstra, 1999). As a consequence of this saccadic gaze strategy, the rotational optic flow component is essentially squeezed into the saccades and can be separated from the translational component.

Only if the velocities and velocity changes are relatively small can the angular velocity be reconstructed faithfully from the TC responses (Egelhaaf and Reichardt, 1987; Bialek et al., 1991; Haag and Borst, 1997). Using behaviorally generated optic flow as a stimulus, recent electrophysiological experiments showed that during saccades the system operates far beyond its linear range (Kern et al., 2005). Instead of encoding saccadic rotations, the HSE was concluded to provide rich information about translational optic flow, which dominates at low frequencies between saccades, and thus, indirectly, about the spatial layout of the animal's surroundings (Kern et al., 2005). These results stress that the functional significance of neuronal mechanisms can only be assessed when the system is analyzed under natural operating conditions.

The mechanisms underlying visual motion computation have been accounted for by an algorithmic model. Local correlation-type motion detectors are spatially pooled by integrating elements representing motion-sensitive TCs, such as HSE cells (for review, see Borst and Egelhaaf, 1989, 1993; Egelhaaf and Borst, 1993). Although various elaborations of the model can explain the neuronal responses to conventional experimenter-defined stimuli (Borst et al., 1995; Harris and O'Carroll, 2002; Reisenman et al., 2003), it is not obvious whether these models are also sufficient to explain the neuronal responses to complex naturalistic optic flow. The properties of blowfly TCs were shown to change as a result of stimulus history (Maddess and Laughlin, 1985; Harris et al., 1999a,b; Borst et al., 2003; Reisenman et al., 2003), which further complicates the analysis of responses to naturalistic optic flow.

Here, we challenge the model of blowfly motion vision with naturalistic optic flow to investigate whether it still can be regarded as a viable basis for explaining visual motion computation.

Materials and Methods

Spatial eye model

The input images of the visual motion pathway are sampled by Gaussian-shaped spatial low-pass filters (σ = 2°). The output of these filters forms the input to the photoreceptors that are equally spaced at 2° along the elevation and azimuth of the eye. The array of photoreceptors forms a rectangular grid in the cylindrical projection with 51 rows and 86 columns. The model visual field covers -50° ≤ φ ≤ 120° in azimuth and -50° ≤ θ ≤ 50° in elevation for the right HSE. For the left HSE, the mirrored input field covers -120° ≤ φ ≤ 50° in the azimuth. Zero degrees corresponds to the frontal equatorial direction. Receptive fields of HSEs include contralateral input conveyed by spiking TCs (Hausen, 1984). This geometry of the receptor array represents only a rough approximation to the retinal mosaic found in flies (Petrowitz et al., 2000).

Model of the spatiotemporal processing

The model of the spatio-temporal processing done by the blowfly motion vision pathway can be subdivided into three functional modules (Fig. 1). The first module preprocesses luminance changes at the input by elements corresponding to the photoreceptors and their postsynaptic elements. The second module is built by local elementary motion detectors that are fed by the preprocessed luminance signals. In the third module, the motion detector outputs are spatially pooled by elements corresponding to the dendrites of TCs. For each of these modules, several different model elaborations were proposed in the literature or will be proposed here.

Figure 1.

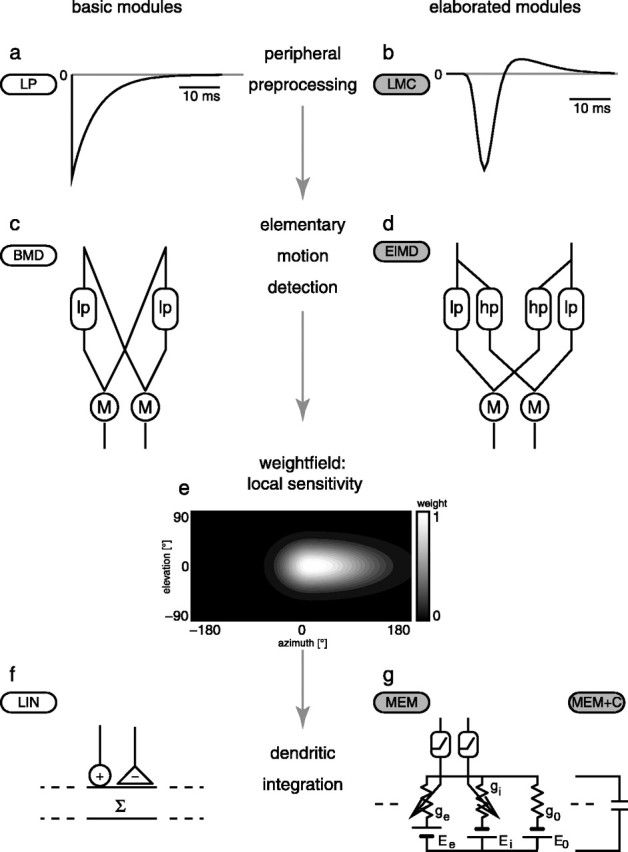
Schematic of the model of the visual motion pathway of the blowfly and the various modules from which it is composed. The basic modules are labeled by white capsules; their elaborated counterparts are labeled by gray capsules. a, Impulse response of the low-pass filter approximating the dynamical properties of the photoreceptors. b, Impulse response of the LMC/photoreceptor linear filter. c, Basic correlation-type motion detector. d, High-pass filter elaboration of the motion detector. e, The weight field of the local sensitivity distribution of the right model HSE (contour plot in cylindrical projection; brighter areas indicate greater sensitivities) is the same for all model variations; the frontal equatorial viewing direction is at 0° azimuth and elevation, and the left HSE is mirror symmetric. f, Linear dendritic summation of positive and negative detector output. g, Circuit representation of the passive membrane model. g₀, Leak conductance of the pooling neuron; g_e and g_i, excitatory and inhibitory synaptic conductances driven by the output of the multiplication after rectification; E₀, E_e, and E_i, corresponding reversal potentials. The model referred to here as the “basic model” is composed of the components a, c, e, and f. The most elaborated version, composed from b, d, e, and g, can be parameterized to fit the neuronal data best. lp, First-order linear low-pass filter; M, algebraic multiplication; hp, first-order high-pass filter.

Peripheral preprocessing

The temporal properties of the peripheral elements, the photoreceptors, and the second-order neurons, the so-called large monopolar cells (LMCs), are modeled in two different ways (Fig. 1a,b).

(1) In the basic model, the entire peripheral preprocessing is jointly modeled as a single first-order linear low-pass filter with a fixed time constant of τ_p = 8 ms, approximating the corner frequency measured for the response of blowfly photoreceptors to white-noise luminance fluctuations (Juusola et al., 1995; van Hateren and Snippe, 2001). The output of this low-pass filter is inverted to account for the sign inversion of the synapse between the photoreceptor and LMC (Laughlin, 1994). Figure 1a shows the impulse response of this filter:

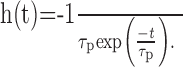(1)

This peripheral module will be called “LP” here.

(2) As an elaboration of the peripheral temporal filtering, a linear filter kernel derived from an experimental analysis of the LMCs of the fly to white-noise light intensity fluctuations was applied to the two-dimensional, time-dependent retinal image (LMC). The filter kernel shown in Figure 1b was defined by James (1992) as follows:

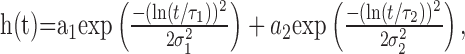(2)

where a₁ = -1.06, τ₁ = 12 ms, σ₁ = 0.197, a₂ = 0.167, τ₂ = 21 ms, and σ₂ = 0.345. For these values, the function qualitatively fits the linear component of the blowfly LMC response (Juusola et al., 1995) at approximately the brightness conditions of our electrophysiological analysis (Kern et al., 2005).

Elementary motion detectors

The basic elementary motion detector model is a simple correlation-type motion detector composed of a first-order linear low-pass filter and an arithmetic multiplication of the low-pass-filtered signal originating from one photoreceptor and the unfiltered signal originating from a neighboring horizontally displaced photoreceptor. The motion detector consists of two mirror symmetrical subunits [basic motion detector (BMD)] (Fig. 1c). The time constant of the temporal low-pass filter in the BMD was set initially to τ_lp = 35 ms to get a steady-state velocity tuning of the simulated TC with an optimum at 5 Hz temporal frequency (the quotient of angular velocity and spatial wavelength of the stimulus pattern), matching the previously described steady-state properties of HSE (Hausen, 1982b).

An elaborated version of the motion detector circuit [elaborated motion detector (ElMD)] incorporates into the second input branch of the multiplier a first-order linear high-pass filter (impulse response

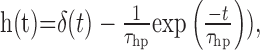(3)

where δ(t) is a Dirac pulse at t = 0 (Fig. 1d) (but see O'Carroll et al., 1997). This elaboration was previously shown to account for a better fit of transient responses to a motion step (Borst et al., 2003). It also allows for an elegant mechanism of adaptation by dynamically adjusting the high-pass time constant (Borst et al., 2003).

Local sensitivities

The weights of the different movement detectors that subserve the visual field are set according to the spatial sensitivity distribution of the HSE cell. The weight field for the spatial integration is determined by a two-dimensional Gaussian function (Eq. 4) (Fig. 1e, shown for the right HSE only) fitted to the local sensitivity distribution of the HSE (Krapp et al., 2001). For the retinal positions given by the eye model, the sensitivity weights are computed as follows:

where φ denotes the azimuth and θ denotes the elevation angle. The receptive field center is on the equator of the eye (θ = 0°) at φ_c = 15° for the right HSE and at φ_c = -15° for the left HSE. The angular width of the receptive field is defined for the elevation by σ_θ = 33° and for the azimuth by σ_φ+ = 102°, and σ_φ- = 45° is defined for the right HSE. For the left cell, the values are interchanged (σ_φ+ = 45°, σ_φ- = 102°). Note that the contralateral input is conveyed to the HSE via spiking TCs from the contralateral eye (Hausen, 1984). Calculating the contralateral input in the way described here is a simplification of this circuit, ignoring the nonlinearities introduced by the spike generation. Because the contralateral input of the HSE is much weaker than the ipsilateral one, even if the responses are recorded close to the output terminal of the cell (Hausen, 1982b; Krapp et al., 2001), we regard this simplification appropriate for our current purposes.

Spatial pooling

In the basic model, the spatial pooling corresponding to the dendritic tree of the HSE neuron is modeled as a linear weighted summation of the elementary motion detector outputs [linear integration (LIN)] (Fig. 1f). The outputs of the mirror symmetrical subunits of the movement detectors are subtracted from each other.

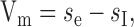(5)

where

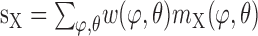(6)

are the weighted sums of the outputs m_e and m_i of the motion detector subunits.

As an elaboration, the summation of the outputs of the two types of motion detector subunits are interpreted as the conductances of excitatory and inhibitory synapses on the integrating cell (Borst et al., 1995). The electrical equivalent circuit of a one-compartment passive membrane patch (MEM) (Fig. 1g) calculates the resulting membrane potential of the integrating element.

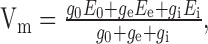(7)

where E₀ denotes the resting potential of the cell, E_e and E_i denote the reversal potentials of the excitatory and inhibitory synapses, respectively, g₀ indicates the leak conductance of the membrane, and g_e and g_i indicate the conductances of the excitatory and inhibitory synapses, respectively (Fig. 1g).

For further simplification of Equation 7, we set the resting potential of the model neuron to E₀ = 0 mV. g_e and g_i are given by the summated outputs of the two types of motion detector subunits after weighting them according to the spatial sensitivity distribution of the HSE (see above). The leak conductance g₀ and the ratio of the synaptic reversal potentials E_i/E_e are free parameters of the model. These two parameters were determined by an optimization procedure (see below).

An additional type of nonlinearity is introduced to the model by the transfer characteristics of the synapses between the movement detector output and integrating element. The postsynaptic conductances are calculated as follows:

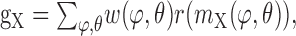(8)

where r(x) is the synaptic transfer function. For the present analysis, we assume that the synapses have rectifying characteristics: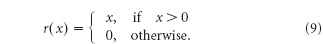

The multiplication stage of the detector subunits of the ElMD can have both positive and negative outputs, because the high-pass filter removes the constant positive offset of the input signals resulting from the mean luminance of the stimulus. Thus, both positive and negative values are present at the output of the multiplier. Because of the rectification nonlinearity (Eq. 9), these negative values cannot lead to negative postsynaptic conductances g_e and g_i in the postsynaptic neuron, too. Negative values would cause numerical problems if the denominator of Equation 7 gets close to zero.

The integrating neuron also has temporal filter properties (MEM+C). The membrane capacitance C_m of the neuron and the input resistance

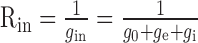(10)

form a low-pass filter. g_in represents the overall input conductance of the integrating model cell, g₀ represents the leak conductance, and g_e and g_i represent the conductances controlled by the excitatory and the inhibitory detector subunits, respectively. With the synaptic conductances varying in time, the input conductance and thus also the corner frequency

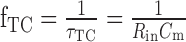(11)

depend on the presynaptic input. Because the model performance improves only slightly by introducing a variable corner frequency (for details, see Appendix), the properties of this filter are, for convenience, approximated by applying to the integrated signal a first-order low-pass filter with a constant corner frequency.

Parameter settings

For all model versions, several parameters were optimized by stepwise variation to fit the model HSE response to the natural (i.e., behaviorally generated) stimuli. The time constants of the temporal filters in the motion detector (τ_lp, τ_hp) were optimized first. For the optimal parameterization of the motion detectors, the leak conductance (g₀) and the ratio of the synaptic reversal potentials (E_i/E_e) of the nonlinear spatial integration model, as well as the time constant of the low-pass filter of the integrating element (τ_TC), were then optimized. Because the typical conductance changes of the input synapses are not known, we parameterized the leak conductance only with arbitrary units. The values given below depend on the scaling of the input conductances and the number of modeled input channels we chose. However, the input resistance of the HSE typically measured in electrophysiological experiments lies in the range of R_in ≈ 5 MΩ (Borst and Haag, 1996).

The optimal parameter settings for the elaborated model were τ_lp = 10 ms, τ_hp = 60 ms, g₀ = 1295, E_i = -0.95 × E_e, and τ_TC = 8 ms. We regard a parameter set as optimal if it minimizes the difference measure defined below. We also counterchecked that the optimal setting for the time constants does not depend on the parameterization of the integrating neuron.

Stimuli

Free-flight data recorded by Schilstra and van Hateren (1999) and van Hateren and Schilstra (1999) were used to generate the optic flow stimuli used in this analysis. The data were recorded using miniature coils attached to the head of a blowfly flying in a cubic flight arena. Based on these data, on the spatial layout of the flight arena, and on the textures covering the arena walls, the retinal image sequences were reconstructed by computer graphics at a temporal resolution of 1000 Hz for the model simulations and 370 Hz for the electrophysiological experiments [for details on stimulus generation, see Lindemann et al. (2003)].

Electrophysiological data

The reconstructed optic flow was replayed to flies using a high-speed panoramic display device [FliMax; for details, see Lindemann et al. (2003)], and the resulting neuronal responses of HSE neurons were recorded intracellularly. Three different flight trajectories were used. The input of the mirror symmetrical contralateral HSE cell was simulated by presentation of mirrored versions of the stimuli. For the resulting six stimuli, between 12 and 35 sweeps of data were recorded.

The HSE neuron responds to image motion with graded membrane potential changes superimposed by action potentials (Hausen, 1982a,b; Haag et al., 1997). The graded potentials are thought to represent the postsynaptic signals in the HSE cell as corresponding to the pooled outputs of the local motion detectors in our model. Therefore, we attenuated the action potentials in the electrophysiological data, which are not generated by the model, by applying a Gaussian convolution mask (σ = 2 ms) to the individually recorded signals. From the resulting low-pass-filtered responses, an average over sweeps was calculated for each stimulus (see example in Fig. 2c). The model in its current version does not include neuronal noise. Therefore, the model responses will be compared with the averaged neuronal responses, because these reflect best the stimulus-induced response component by averaging out signal components that are not related to the stimulus.

Figure 2.

Example flight path (the segment shown lasts 2 s) and three-dimensional model of the experimental setup of a behavioral recording, from which the optic flow was reconstructed. The downward view of a flight trajectory (dotted line), with the head position and head yaw orientation shown every 90 ms, is shown.

Steady-state stimuli

To evaluate the model responses to classical stimuli, constant velocity stimuli were generated by virtually rotating the model for 1 s at a constant velocity in a cylindrical setup covered with a sinusoidal pattern (spatial wavelength, 10°)_. Like the HSE cell, the model responds to such a stimulus with a transient response, followed by a mostly constant reaction. The level of this so-called steady state was computed as the mean over the last 500 ms of this period.

Difference measure

To quantify the difference between neuronal and model responses, we used the root-mean-squared (rms) difference of the signals.

The model does not contain all latencies present in the neuronal system but mostly the phase shifts introduced by the various temporal filters. Only the filter kernel used for the simulation of the temporal properties of the photoreceptor and LMC introduces a true latency. Therefore, a temporal shift of the model response was introduced to correct for the latency. The size of this shift was determined for each model variant by cross-correlation of the neuronal and model signal.

Because the model response is not automatically scaled to the physiological range of membrane potentials, it was scaled by a factor f that minimizes the mean-squared difference between the temporally shifted model responses m(t) and the electrophysiological signals e(t).

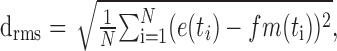(12)

where

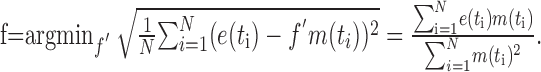(13)

For a given combination of model parameters, f typically varies by ∼10% of its value across the responses to different stimuli.

To assess the intertrial variability of the cellular responses, we calculated the square root of the squared difference between the individual response traces (with spikes removed as described above) and the average electrophysiological response. This intertrial difference is, on average, d_rms = 2.6 ± 0.8 mV (mean ± SD).

Saccade-triggered average responses

An interesting qualitative feature of the behavioral data are the occurrence of sharp saccadic changes in gaze approximately every 100 ms (Schilstra and van Hateren, 1999; van Hateren and Schilstra, 1999). Therefore, we calculated prototypic responses of both the electrophysiological and the model data to the saccadic yaw velocity. To detect saccades, local maxima and minima above a threshold of 400°s^-1 in the yaw velocity trace were localized. Segments lasting from 50 ms before and 100 ms after the maximum were aligned with respect to the maximum and averaged across trials. These prototypic saccade-triggered average responses serve as a qualitative benchmark for the model performance.

Coherence analysis

The coherence between two signals is a frequency-dependent measure of the linearity of the relationship between these signals. A coherence of 1 means that one signal can be constructed perfectly from the other signal with a linear filter. Lower values indicate noise or a nonlinear relationship between the signals. As in our experimental analysis (Kern et al., 2005), we calculated the coherence for the model and the neuronal data for the intersaccadic segments of the responses.

Masking out saccades. Masks selecting saccadic segments in the stimulus and response were obtained by gating a region surrounding saccades. Like the segments used for the saccade-triggered averages, the masks were centered on the peaks in the total angular velocity of the head during a saccade. The region was large enough to include all parts of both the saccadic stimulus and corresponding response. Saccades that were close together were merged to reduce boundary effects. Edges of the masks were tapered with a 12.5 ms cos²-taper to reduce spectral leakage biasing the coherence estimate at high frequencies. The intersaccadic mask, used for suppressing the saccadic stimulus and response, equals one minus the saccadic mask. Masked data consisted of gated data intermitted with blocks of zeroes. Although the mask shapes the power- and cross-spectra of the masked data, this shaping occurs in a similar way for all spectra in the numerator and denominator of the definition of coherence. Consequently, the mask by itself does not generate coherence for uncorrelated data, as was checked in control computations with uncorrelated noise. The coherence of the masked data include the zero blocks and therefore should be regarded as belonging to the entire masked signal, not just to its intersaccadic part (gated signal).

Calculation of the coherence functions. Coherence between a stimulus parameter (e.g., yaw velocity) and model response was calculated according to our previous experimental study (Kern et al., 2005), as follows:

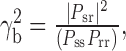(14)

where P_sr is the cross-spectral density of the stimulus and response, P_ss is the power-spectral density of the stimulus, and P_rr is that of the response. Spectra were calculated by a periodogram averaging of 50% overlapping data segments, with each periodogram the discrete Fourier transform of a cos²-tapered zero-mean data segment of 256 ms, extended by zero-padding to 512 ms. Results were not strongly dependent on segment length. Segments from all flights used as a stimulus for a particular cell were included in the periodogram averaging. Bias in the coherence estimate was corrected (van Hateren et al., 2002) by

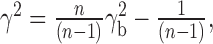(15)

where n is the total number of segments.

For calculation of the model coherence, we assume additive noise with a power density of 0.03 mV²/Hz, similar to the densities we measured in HSE (see also Warzecha et al., 1998).

Results

Performance of the model of the blowfly visual motion pathway

The velocity profile of yaw rotations reflects the blowfly's saccadic flight style: when making a curve, the fly does not change its gaze and body orientation smoothly but executes a series of saccadic turns in which the head shows peaks in yaw velocity approaching several thousand degrees per second (Fig. 3a,b, top traces). Between saccades, the gaze is kept basically stable, and the resulting optic flow is much smaller than during saccades. For most of the time during the flight, the HSE is depolarized relative to the resting potential of the cell. This depolarization is interrupted by brief hyperpolarizations during saccades evoking null-direction motion (null-direction saccades) (Fig. 3a, downward pointing saccades). In contrast to expectations from responses to conventional stimuli (Hausen, 1982a,b; Haag et al., 1997; Horstmann et al., 2000; Krapp et al., 2001), the HSE does not consistently depolarize during preferred-direction saccades relative to the overall depolarization level (Kern et al., 2005).

Figure 3.

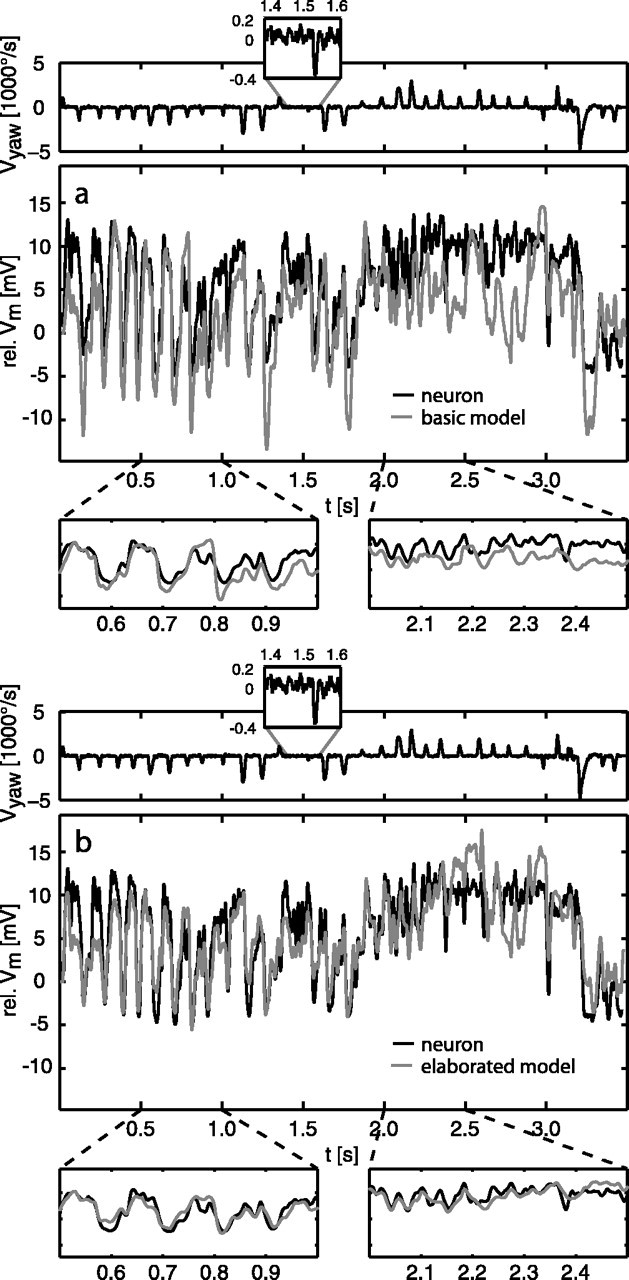
Examples of a model response (gray lines) of the basic (a) and elaborated (b) models compared with the neuronal response (black lines). Zoomed from the response traces are segments dominated by saccades inducing preferred-direction (right boxes) and null-direction (left boxes) motion, respectively. The yaw velocity of the fly's head is shown in the traces above the response; the insets show, at higher resolution, a section of the angular velocity trace with a small-amplitude saccade and a typical example of the yaw velocities between saccades (note the different scaling of y-axes). The model response was shifted in time by 22.5 ms to correct for neuronal delays not present in the model. rel., Relative.

The responses to behaviorally generated optic flow of the basic model (modules LP-BMD-LIN) fit qualitatively the time course of the experimentally determined neuronal signals (Fig. 3a). For segments dominated by saccadic turns inducing null-direction motion (Fig. 3a, left zoom box), the neuronal response is matched quite well by the model. The deviations of the model from the neuronal response are more pronounced in segments characterized by a more constant activation of the HSE cell, as observed during sequences of preferred-direction saccades (Fig. 3a, right zoom box). This characteristic can be found consistently for all analyzed motion sequences. The overall difference between model and neuronal responses is d_rms = 5.6 ± 0.8 mV, on average. For the example segment governed by null-direction saccades, the difference drops to d_rms = 4.3 mV; for the example segment governed by preferred-direction saccades, the difference between model and neuronal responses goes up to d_rms = 5.6 mV.

For the most elaborated model (modules LMC-ElMD-MEM+C) with an optimized parameter set for natural, behaviorally generated stimuli, the model performance is considerably better compared with the performance of the basic model (Fig. 3b). The time course of the neuronal responses is matched more closely, and the overall difference between the model and neuronal response drops to d_rms = 2.9 ± 0.3 mV. The most prominent improvement can be observed for segments dominated by preferred-direction saccades. The difference for the example segment shown in Figure 3b (right zoom box) drops to d_rms = 2.3 mV. For segments characterized by null-direction saccades, the improvement in performance is less. For the example segment shown in Figure 3b (left zoom box), the difference is reduced to d_rms = 2.4 mV. In other response segments, the fit might be slightly worse.

In conclusion, the model of the fly visual motion pathway can account quite well for the complex time course of the neuronal responses to behaviorally generated optic flow, although fidelity depends on the model version. For the elaborated model, the rms difference between model and neuronal responses is in the order of the intertrial difference between experimentally determined neuronal responses, which amounts to d_rms = 2.6 ± 0.8 mV.

The model we present here was tuned to the responses of HSE neurons. Because of their very similar response mode and presumably common input elements, it is likely that other motion-sensitive neurons of the blowfly, such as the other HS cells (Hausen, 1982a,b) and the vertical system cells (Hengstenberg, 1982; Krapp et al., 2001), could be modeled in a similar way.

Steady-state tuning of the model

Conventionally, the steady-state velocity tuning is regarded as an important characteristic of the fly motion detection system. If the fly motion detection system is stimulated with a sinusoidal pattern moving at constant velocity, the output gets almost constant after an initial transient response (Hausen, 1982a,b; Egelhaaf and Borst, 1989). The steady-state response amplitude was found to depend on the temporal frequency of the input (the ratio of the angular velocity and spatial wavelength of the stimulus pattern). It increases with increasing temporal frequency, reaches an optimum of ∼5 Hz, and decreases again (Hausen, 1982b).

Because most of the elaborations of the model of the visual motion pathway discussed below affect the steady-state velocity tuning, we discuss these effects here in some detail before looking at the results obtained for natural stimulation.

Although the bell shape of the tuning curve is an inherent feature of the mechanism of motion detection, the location of the optimum of the curve along the temporal frequency axis is determined by the systems parameters. For the basic detector, the tuning can be computed analytically (Borst et al., 2003). Without an additional filter in the input channels, a time constant of 35 ms has to be chosen to get an optimum at 5 Hz (Fig. 4a, black line). Additional filters in the input channels shift the optimum. A low-pass filter used for prefiltering the retinal input shifts the optimum toward lower frequencies; a bandpass filter, such as an LMC, has the opposite effect (Fig. 4a). To recalibrate the response to a peak at 5 Hz with the LMC as a peripheral element, the time constant of the low-pass filter in the movement detector has to be larger than without the LMC (∼55 ms vs 35 ms). The additional high-pass filter in the elaborated detector (ElMD) does not affect the temporal frequency optimum, if the time constants of the high-pass and the low-pass filters are equal (Borst et al., 2003). If the time constant of the high-pass filter is larger than that of the low-pass filter, the tuning gets broader and becomes double-peaked for very large time constant differences (i.e., τ_hp ≫ 6τ_lp). The experimentally determined steady-state tuning of TCs is also broader than the tuning of the BMD (Hausen, 1982b). In contrast, the optimal time constants found for natural optic flow in all variants of the model cause a steady-state tuning with a peak at much higher frequencies (Fig. 4b). This finding indicates either that the system properties change with the stimulus dynamics or that some system component shaping the steady-state tuning is not covered in the present model. It should be noted, however, that the difference between model and neuronal responses to behaviorally generated optic flow increases by only ∼10-15% when we change the movement detector time constants from the optimal values to values that also fit the experimentally determined steady-state velocity tuning (see below) (Figs. 4c, 5). Hence, the responses to constant velocity motion and to behaviorally generated dynamical stimuli may well be explained by a single set of movement detector time constants.

Figure 4.

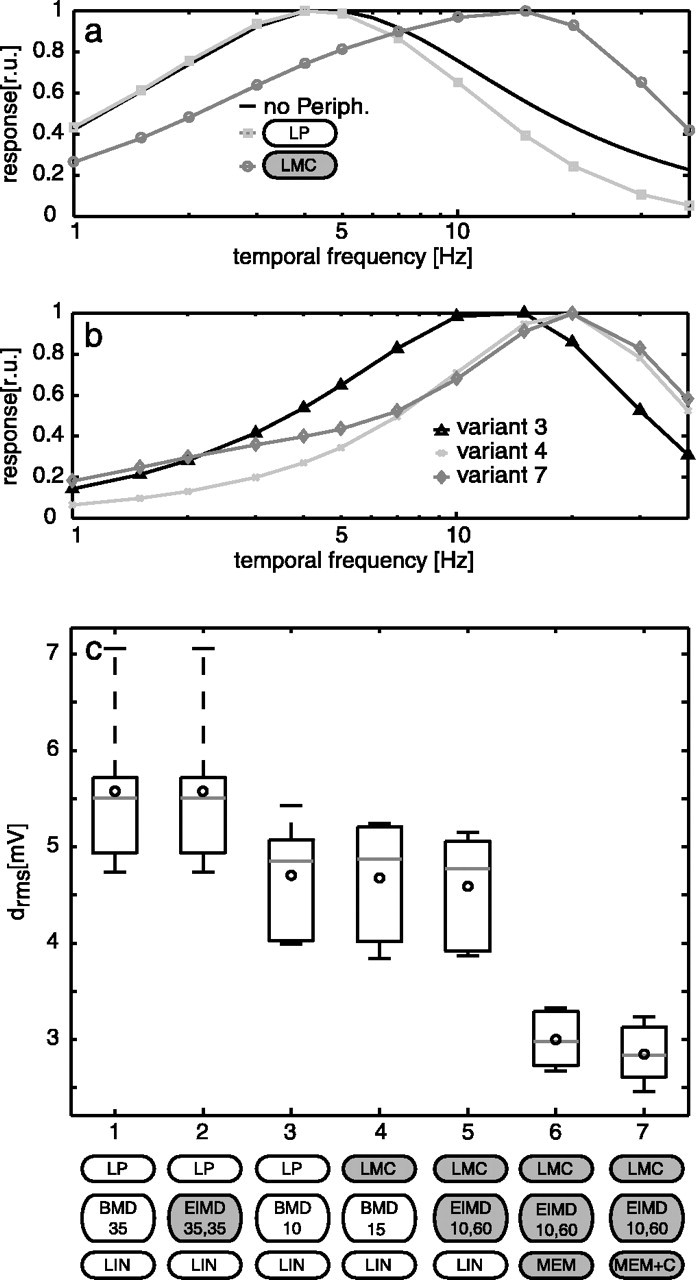
Responses of the model of the blowfly visual motion pathway to constant velocity motion and to behaviorally generated optic flow. a, The theoretical steady-state tuning for constant velocity motion of the BMD without peripheral (Periph.) elements (black line), with a peripheral low-pass filter in the input line of the movement detector (LP; dark gray squares) and the LMC kernel (light gray circles). b, The steady-state tuning of optimal parameterized model variant 3 (black triangles), variant 4 (dark gray crosses), and variant 7 (light gray diamonds). c, Box-and-whisker plots of average differences between the neuronal and the model responses for the various variants of the model. The variants [using the labels from Fig. 1, extended by the parameter(s) for the motion detector time constant(s)] shown are as follows: (1) LP-BMD-LIN; (2) LP-ElMD-LIN, parameters match the steady-state tuning of the cell, same time constant for the motion detector low-pass and high-pass filters (τ_lp = 35 ms, τ_hp = 35 ms); (3) LP-BMD-LIN (τ_lp = 10 ms); (4) LMC-BMD-LIN (τ_lp = 15 ms); (5) LMC-ElMD-LIN, different time constants of motion detector low-pass and high-pass filter (τ_lp = 10 ms, τ_hp = 60 ms); (6) LMC-ElMD-MEM; (7)LMC-ElMD-MEM+C. For each variant, the circle indicates the mean, the gray horizontal lines within the boxes show the median, the box includes the upper and lower quartiles, and whiskers denote maximum and minimum d_rms of the responses to six stimuli. r.u., Relative units.

Figure 5.

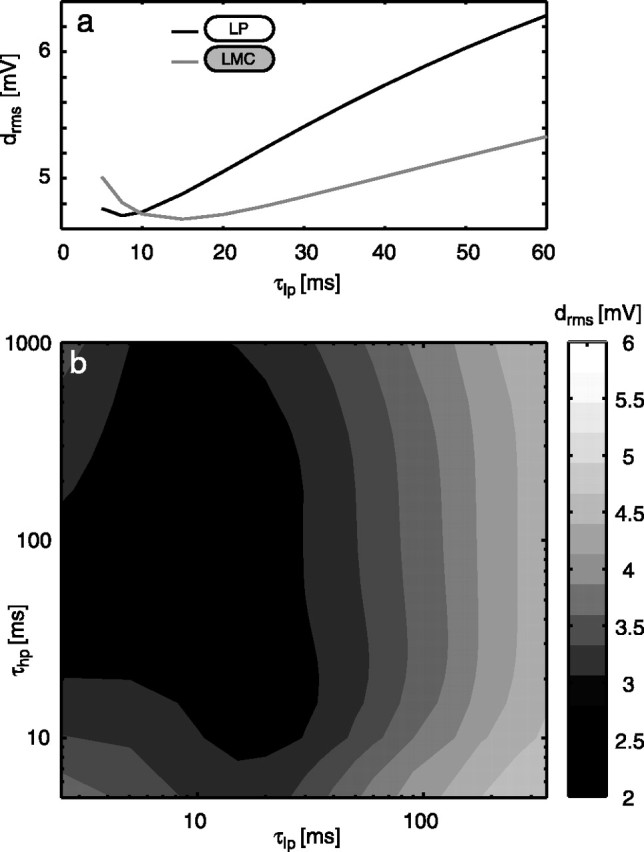
Systematic variation of the time constants in the motion detector. a, Dependency of the rms difference between model and neuronal responses on the time constant of the basic model with a low-pass filter in the input lines to the motion detectors (black line; variant 1 in Fig. 4c) and an LMC kernel (gray line; variant 4 in Fig. 4c) as a peripheral element. Note the ordinate scale indicating that within a realistic range, the d_rms error does not depend on the time constants much. b, Dependency of the rms difference between model and neuronal responses on the two time constants of the ElMD (variants 5-7 in Fig. 4c). Average d_rms for all six stimuli is plotted as a contour plot.

Significance of the model components

To assess which of the model elaborations are the main determinants of the model performance in response to behaviorally generated optic flow, the basic model was elaborated in various steps, eventually resulting in the most elaborated LMC-ElMD-MEM+C model. The consequences of the different model elaborations on the model performance are cumulated in Figure 4c.

Motion detector variants

Elaborating the motion detector with a high-pass filter does not change the model performance (ElMD) compared with the basic model, if the same filter time constants (here τ_lp = τ_hp = 35 ms) are used for both filters, as has been proposed previously (Borst et al., 2003) (Fig. 4c, variants 1 and 2).

Basic motion detector time constant

Optimizing the low-pass filter time constant of the BMD to fit the responses to natural optic flow leads to a time constant value smaller than expected from the steady-state responses (see above) [Fig. 4c, compare variants 3 (τ_lp = 10 ms) and 1 (τ_lp = 35 ms)]. Note that this time constant value may not strictly be the optimal one, because no clear minimum in the rms difference of the signals is found within the variation range (Fig. 5a). Shorter values, however, would lead to numerical problems by getting too close to the sampling interval of the simulation.

An optimal time constant shorter than the expected one for the steady-state tuning is also obtained if the retinal input is preprocessed by the LMC filter (Fig. 4c, variant 4). Then, however, the optimal time constant of the low-pass filter in the elementary movement detector shifts to 15 ms, consistent with the effect of the LMC bandpass characteristics observed in the steady-state case. With the optimized time constants of the movement detector low-pass filter, the performance of the model improves compared with the initial parameterization (Fig. 4c, compare variants 3, 4 with variants 1, 2).

Peripheral elements

Interestingly, the nature of peripheral preprocessing (i.e., simple low-pass filter or LMC) does not affect the model performance much for natural optic flow, as long as the movement detector low-pass filter is optimized for the respective type of preprocessing. However, even deviations from the respective optimal time constants by more than a factor of 2 affect the performance of either model only slightly (Fig. 5a).

Elaborated motion detector parameters

Figure 5b shows the dependence of the rms difference between the simulated and the experimentally determined responses on both the low- and high-pass filter time constants of the ElMD (average rms difference for all behaviorally generated stimulus sequences). The smallest difference is located at τ_lp ≈ 10 ms and τ_hp ≈ 100 ms. However, this parameter setting would lead to double-peaked, steady-state velocity tuning curves of the detector. Because double-peaked, steady-state velocity tuning curves have never been described for the HSE neuron of the blowfly, although the velocity optimum is relatively broad and the temporal frequency tuning is almost flat between 1 and 10 Hz (Hausen, 1982b), we used τ_lp = 10 ms and τ_hp = 60 ms for the simulations plotted in Figure 3b. These settings lead to only an insignificantly larger difference value compared with the combination of optimal time constants (Fig. 5b).

Spatial integration

All improvements gained from elaborations in the peripheral elements and the detector time constants are small compared with the performance increments achieved by introducing into the model the nonlinear spatial pooling of TCs (Fig. 4c, variant 6). Introduction of this nonlinearity reduces the difference between model and neuronal response to ∼[2-3] (Fig. 4c, compare variants 5, 6).

The optimal parameterization of the nonlinear spatial pooling was determined by systematic variation of the parameters g₀, the leak conductance of the cell, and the ratio of the reversal potentials of the negative and positive inputs of the cell E_i/E_e (Fig. 6a). Whereas the model performance does not depend much on the leak conductance g₀, the ratio of the reversal potentials E_e and E_i has a prominent effect. The optimal ratio is E_i = -0.95E_e, mainly regardless of the leak conductance g₀. For any value of g₀ < 10⁴, the performance does not change much but has a weak minimum at g₀ ≈ 1.3 × 10³ (Fig. 6b). For this value also, the dependency of the steady-state response of the model on pattern size fits corresponding experimental results (Hausen, 1982b; Egelhaaf, 1985; Haag et al., 1992) reasonably well (Fig. 6c), ensuring that the responses are relatively invariant against changes in pattern size and density. It should be noted that this gain control relies critically on the increase in the input conductance of the neuron with the increasing number of activated input channels and thus on the relationship of the leak conductance and the synaptically controlled conductances of the cells. This feature requires that the movement detector output is essentially independent of the background luminance, because otherwise the background luminance dominates the synaptic conductances regardless of whether the stimulus pattern is stationary or moving. Elimination of the effects of background luminance is accomplished in the model by a bandpass filter in the peripheral visual system (Fig. 1, LMC) and/or a high-pass filter in one branch of the movement detector (Fig. 1, ElMD). Hence, although these two elaborations of the model of the visual motion pathway do not directly affect the model performance under natural stimulus conditions, they are necessary for the non-LIN at the level of the model output cell to become operative.

Figure 6.

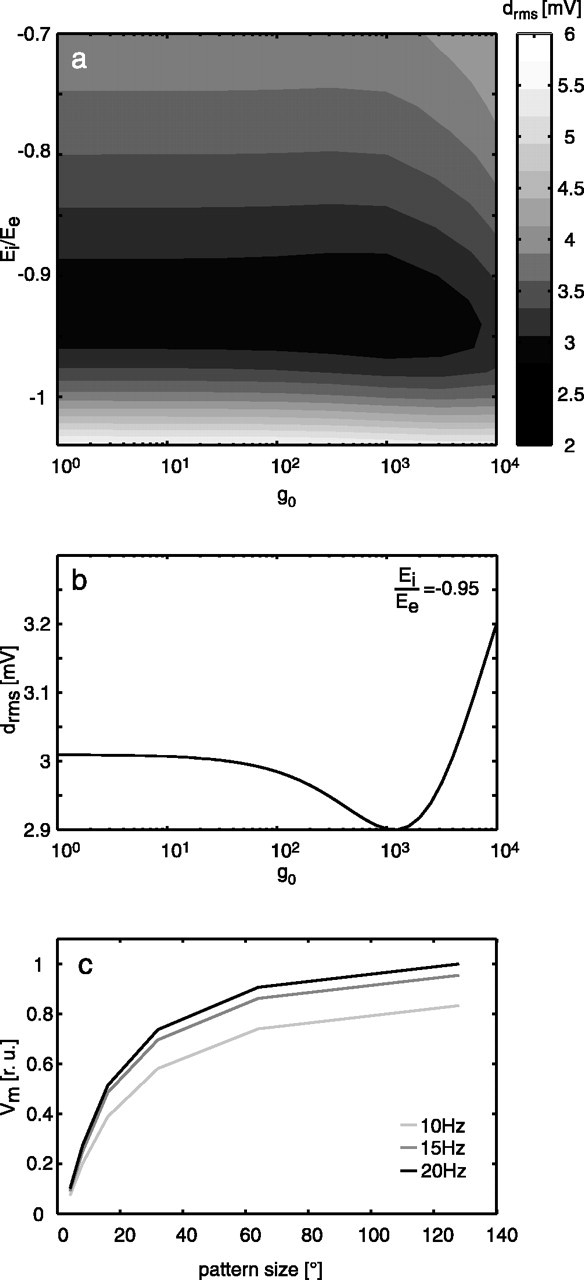
Consequences of systematic parameter variation of the membrane model of the pooling neuron. a, Contour plot of the rms difference between model and neuronal responses depending on g₀, E_i/E_e. The average d_rms of six stimuli is coded in gray levels. b,The rms difference between model and neuronal responses as a function of g₀ only, E_i/E_e = -0.95. c, Steady-state response of the elaborated model (variant 7 in Fig. 4c) as a function of pattern size hinting at the gain control properties of the model neuron (see Results; sinusoidally modulated pattern; 10, 15, and 20 Hz temporal frequency; constant velocity motion; g₀ = 1295).

Although we can account for the major features of the responses of the HSE on the basis of a one-compartment model of the spatial integration stage, it is possible that a more realistic model of the dendritic tree of the HSE (Borst and Haag, 1996; Haag et al., 1999) would also improve the fit between model and neuronal response.

Temporal properties of the TCs

Postprocessing of the model response by a low-pass filter improves the model performance only slightly (Fig. 4c, compare variants 6, 7). For the coherence analysis, this model component was even disadvantageous (see below).

Robustness of the parameter optimum

The optimal parameter set was calculated from the average difference for all stimuli. However, all optima calculated from the individual stimuli lead to a similar average difference. The individual optima for the detector time constants and for the parameters of the integrating neuron lay within the contour corresponding to the lowest range of differences between neuronal and model responses, as shown in Figures 5b and 6a. Thus, the average difference for each of these parameterizations at least halves the difference calculated for the basic model, which indicates that the elaborations improve the model performance also for stimuli that were not taken into account for the parameter optimization.

Adaptation of the visual motion pathway during stimulation with natural optic flow?

The blowfly visual motion pathway has been concluded in previous studies to adapt to the prevailing stimulus conditions (see Introduction). This conclusion is based on experiments demonstrating that the responses to particular test stimuli, such as an instantaneous retinal image displacement, are affected by stimulus history (see Discussion). Part of the adaptational changes described for the neuronal responses could be explained by assuming activity-dependent changes of several model parameters (Borst et al., 2003). If motion adaptation takes place within some hundreds of milliseconds, the optimal parameter set of the model HSE cell should change during ongoing motion stimulation. Adaptive changes during stimulation with behaviorally generated optic flow would lead to a different optimal parameter set for the beginning and the end of neuronal responses to a stimulus trace. To check this potential consequence of motion adaptation, we optimized separately the parameter set of the model to match the initial and a later segment of the neuronal responses.

The optimal sets of filter time constants for the initial 0.5 s and the last 1.5 s of the 3.5 s response trace did not reveal any consistent difference across stimuli. Figure 7a shows the average difference for all stimuli between model and neuronal response in dependence of the low- and high-pass time constants for the initial response segment. Figure 7b displays this difference for the late response segment. Direct comparison of the optimal parameters found for segments of the individual responses to the six stimulus sequences did not reveal a consistent tendency either (Fig. 7c). Optimal parameter combinations for two short stimulus segments lie outside of the plausible range of values (Fig. 7c, symbols on the axes). The plots in Figure 7a-c only suggest a weak tendency for the low-pass filter time constant toward shorter values in the late segment. However, the change in rms difference is very low between the optimal sets for early and late segments.

Figure 7.

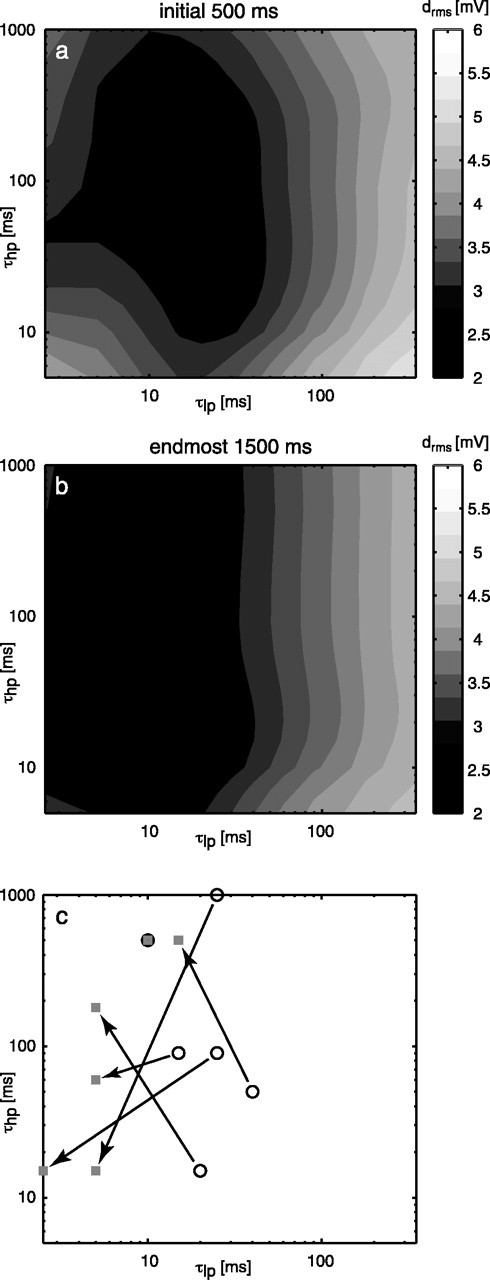
Consequences of variations of τ_lp and τ_hp for the elaborated model (variant 7 in Fig. 4c) for an early and a late segment of the stimulus trace. The average rms difference between the model and the neuronal responses to six stimuli is coded in gray levels for the initial 0.5 s (a) and the endmost 1.5 s (b) of each stimulus. c, Optima for the time constants obtained when the model is parameterized separately for the different stimulus sequences. Circles show the optima for the initial 0.5 s, and squares show the optima for the endmost 1.5 s of the stimulus duration. The optima for a common stimulus are connected by arrows.

Another adaptational effect found in TCs is a change in the response gain during ongoing stimulation (Harris et al., 2000). This effect is reflected in the model responses by an increase in the optimal scaling factor f between the initial and the late response segment. For an optimal fit, this factor has to be, on average, 20% lower for the later stimulus segment than for the first 500 ms of the presentation. However, the fit quality for the initial segment is slightly worse than for the later segment for all stimuli, even with this lower scaling factor. Regardless of this qualification, the model simulations of the neuronal responses to behaviorally generated stimuli indicate that there is some adaptation in the overall gain of the system, whereas there are no consistent changes in other systems parameters obvious.

Coding properties of the model HSE neuron

The quantitative difference measure that was used to relate the model and the experimentally determined neuronal responses facilitates the comparison of the different model variants. A difference between the model response and the average neuronal response almost as small as the intertrial difference of individual neuronal responses indicates a good fit of the model to the electrophysiological responses. However, even such small residual deviations between model and original responses do not necessarily mean that the model covers the important coding properties of the neuronal response. In particular, it is not clear whether the remaining deviations are relevant with respect to what is encoded by the neuron about the animal's self-motion or the spatial relationship between the fly and objects in the outside world. Therefore, we selected two particularly relevant coding properties of the HSE cells that were recently inferred from electrophysiological responses to behaviorally generated optic flow (Kern et al., 2005) and try to reproduce these characteristics from the model responses.

Responses to saccades

The first characteristic pertains to the responses of the HSE cells to the optic flow evoked by saccades (i.e., the abrupt changes in gaze) (Fig. 2). Figure 8a shows the average responses of the HSE neuron to saccadic turns into the preferred and null directions that occurred during free flight. The HSE responds with a transient hyperpolarization to saccades inducing null-direction motion on the retina as would be expected from a neuron encoding yaw rotations of the animal. In contrast to expectations, it does not respond with a strong depolarization to saccades inducing preferred-direction motion but with a small drop in membrane potential after a small transient depolarization relative to the overall depolarization level of the cell (Kern et al., 2005). This behavior is also found in the responses of the elaborated model (Fig. 8b). The responses of the model to saccades inducing null-direction and preferred-direction motion are remarkably similar to the corresponding neuronal response. Interestingly, already the responses of the basic model to saccades (Fig. 8c) lead to the same conclusions as the neuronal responses, although the similarity of the model to the neuronal response is slightly smaller than for the elaborated model. This finding suggests that the main reason for HSE cells not encoding faithfully the time course of yaw rotations during saccades is the nonlinear velocity encoding of the local movement detectors, rather than of the nonlinear spatial pooling at the level of the TCs. Note that the model responds differently to saccades in the two directions, although it is almost mirror symmetrical. This is because between saccades, the motion detection system is stimulated mainly by preferred-direction motion, and the (integrating) cell is depolarized for most of the time as a consequence of the translational flow. As a consequence of nonlinearities inherent in the movement detectors, the responses to the translational flow and to preferred-direction saccades are similar in size despite angular velocities that differ by more than one order of magnitude.

Figure 8.

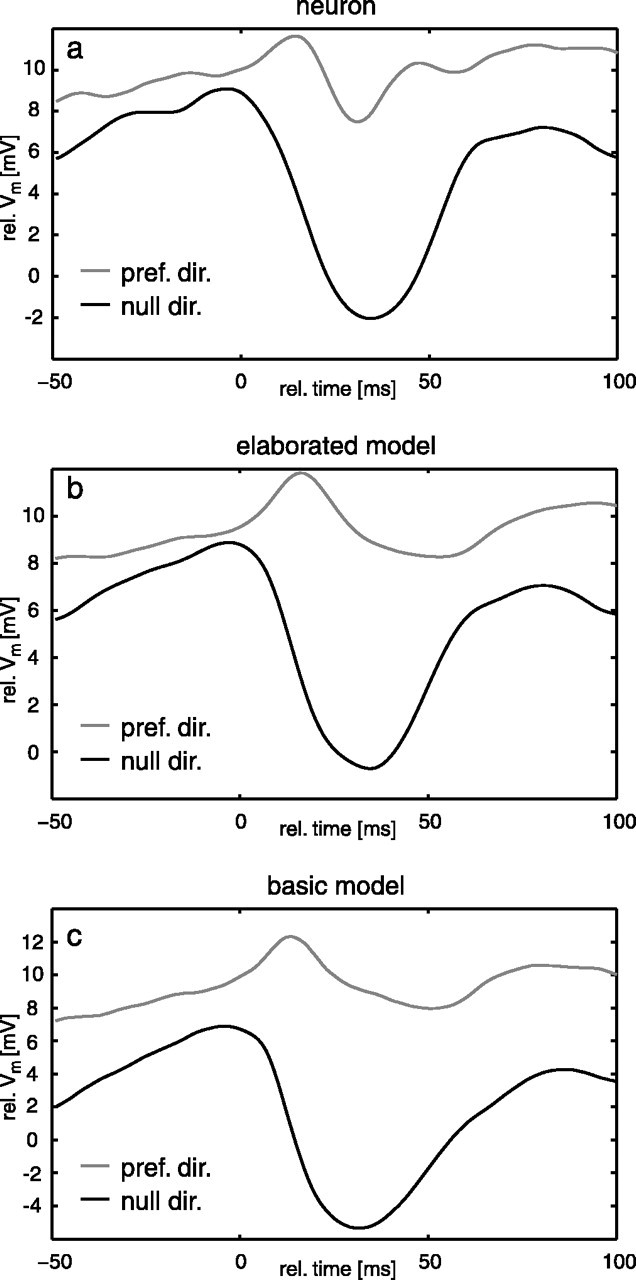
Saccade-triggered averages of the neuronal data (a) compared with responses of the elaborated model (b) and the basic model (c). Responses to saccades inducing preferred- and null-direction motion are plotted in gray and black, respectively. Experimental data are taken from Kern et al. (2005). pref. dir., Preferred direction; null dir., null direction; rel., relative.

Coherence of the model response with self-motion parameters

The HSE neuron may show pronounced depolarizations between saccades, although then the optic flow on the eyes is much smaller than during saccades (Kern et al., 2005) (Figs. 2, 3). Therefore, the HSE has been concluded to encode behaviorally relevant information especially between saccades (Kern et al., 2005). Between saccades, blowflies keep their gaze stable apart from small-amplitude, broadband yaw rotations and may thus gather useful information about the outside world from the translational optic flow components that dominate at low frequencies in the intersaccadic intervals. Indeed, this could be shown for the sideward translation by determining the optimal linear filter to estimate the time-dependent sideward velocity from the neuronal responses. How well the real sideward velocity of the blowfly corresponds to the estimated one and thus is reflected in the neuronal responses is quantified by the coherence that varies between 0 (i.e., both signals are unrelated) and 1 (i.e., perfect reconstruction). There is considerable coherence between sideward velocity and the neuronal intersaccadic responses at low frequencies up to ∼20 Hz. This coherence is even enhanced when the difference signal between HSE neurons in the right and left halves of the brain is taken into account (Fig. 9a). As long as the fly flies sufficiently close to environmental objects, the coherence between the intersaccadic yaw velocity and the neuronal response is significant only at frequencies between ∼20 and 60 Hz (for details, see Kern et al., 2005). Applying the same analysis to the responses of the elaborated model (LMC-ElMD-MEM) leads to similar results (Fig. 9b). Because the coherence of individual neuronal responses and the different self-motion parameters was calculated in the experimental study (Kern et al., 2005), we approximated the noise in their membrane potential fluctuations by adding to the model response individual noise traces with the variance of the noise corresponding to the experimentally determined values (see Materials and Methods). At low frequencies, the coherence between the sideward velocity and the difference response of the right and left model HSE neuron is similar to the coherence found for the neuronal response. The coherence between yaw velocity and model response is also significant in a frequency range >20 Hz, although it is somewhat smaller than the coherence found in the neuronal data. Hence, the elaborated model can account well for one of the most decisive coding features of real HSE cells.

Figure 9.

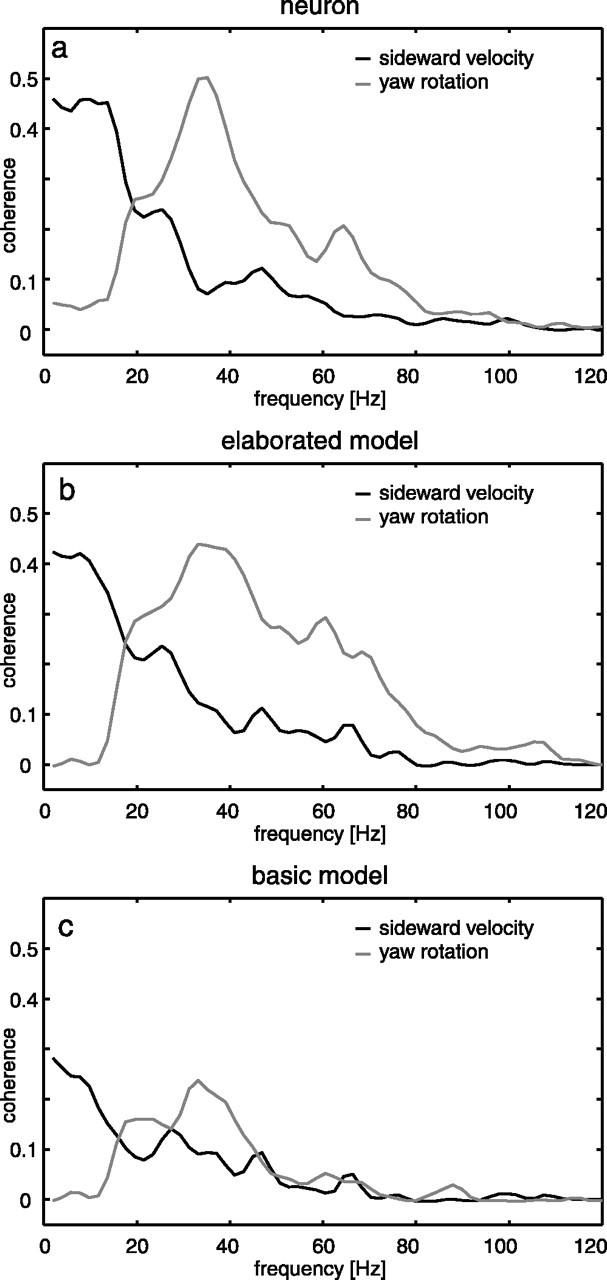
Coherence between the intersaccadic segments of the neuronal responses (a), the responses of the elaborated model without the TC low-pass filter (b), and the responses of the basic model (c) to the yaw velocity (gray) and the sideward velocity (black). For the computation of the coherence, noise was added to the model responses (see Materials and Methods for details). Experimental data are taken from Kern et al. (2005).

The basic model generally shows significantly smaller coherences (Fig. 9c) than the elaborated model (Fig. 9b). Nonetheless, the coherences have similar frequency dependence for both model versions. Hence, the model of the fly visual motion pathway reveals, in a similar way as the experimentally determined responses, that the pair of HSE cells represents between-saccades information on both sideward and yaw velocity at the same time in adjacent frequency bands. This characteristic is rendered possible because the intersaccadic yaw velocities are smaller by an order of magnitude than the yaw velocity during saccades. Hence, both the experimental results and the model simulations suggest that saccades should be viewed primarily as a specialization in steering behavior that enables the fly to extract translatory optic flow amid rotatory optic flow. If only smooth yaw rotations, instead of saccadic turns, were used for steering, the latter would dominate the stimulus and response all the time. Because the translational optic flow component depends on the distance to objects in the environment, the HSE neurons and their model counterpart thus provide indirectly information about the three-dimensional layout of the environment. It should be noted that distance is signaled only relative to the fly's own velocity, because retinal velocities evoked during translation are inversely proportional to distance and proportional to translation velocity. This implies that in walking flies, the visual surroundings should affect the responses of the HSE cell only when the fly is very close to environmental structures, just as has been found previously (Kern et al., 2001a,b). This implicit scaling of distance information by the actual speed of the animal may be a parsimonious and advantageous way to extract, from the optic flow, behaviorally relevant information about the outlay of the environment. For instance, evasive actions evoked by obstacles in the path of locomotion need to be evoked only at a smaller distance when the animal moves slower.

Texture-independent responses

The motion sequences that were used for our electrophysiological experiments (Kern et al., 2005) and the model simulations shown so far are characterized by the dynamical features as are characteristic of retinal image displacements in free flight. Moreover, they were obtained in a flight arena covered with the images of natural scenes. To test how relevant the textural properties of the environment are for shaping the responses to motion sequences with natural dynamics, we changed the textural properties of the flight arena, when reconstructing the image sequences, while leaving the dynamics of optic flow unaltered. We exchanged the textures on the arena walls by random dot patterns (composed of black and white squares of 1.6 × 1.6 cm) and vertical sinusoidal gratings (3.64 cm per period). This analysis was motivated by the pronounced texture dependence of the steady-state responses of blowfly TCs (Eckert, 1980).

The average difference between the responses of the elaborated model and the HSE cell obtained with the natural texture and those obtained with the random texture are very similar (for numerical values, see Table 1). Moreover, the difference between the different model responses obtained with either wall texture is also in the same range. Only for sinusoidal gratings the differences are slightly larger. A noticeable qualitative difference between the response to the sinusoidal grating and to the original texture is a double-peaked response to null-direction saccades, similar to what was previously described for sinusoidal variation of high-velocity simple stimuli (Egelhaaf and Reichardt, 1987).

Table 1.

Comparison of the HSE and model counterpart

	Model, natural texture	Model, random dot texture	Model, sinewave texture
Neuron, natural texture	2.9 ± 0.3 mV	2.9 ± 0.4 mV	4.5 ± 1.9 mV
Model, natural texture		2.6 ± 0.3 mV	3.8 ± 1.1 mV

Data are d_rms values for different wall textures.

The robustness of the HSE response to variations of the environmental texture was also corroborated in an electrophysiological control experiment in which the natural texture covering the flight arena was exchanged between the different walls (R. Kern, unpublished results). However, the predictions of the model indicate that this robustness might extend to much more pronounced changes in the textural patterns.

Discussion

The optic flow perceived by blowflies in free flight is characterized by peculiar dynamical properties. These are the consequence of the saccadic flight and gaze strategy (Schilstra and van Hateren, 1999; van Hateren and Schilstra, 1999). This active vision strategy separates the main rotational from the translational components of the optic flow. The translational optic flow encoded by wide-field, motion-sensitive neurons contains information about the three-dimensional layout of the environment and can be exploited in behavioral tasks like obstacle avoidance (Tammero and Dickinson, 2002). Recently, the motion-sensitive, wide-field HSE neuron of the blowfly could be shown to extract information about the sideward translational optic flow during the intersaccadic intervals (Kern et al., 2005). This finding was surprising, because based on experiments with conventional experimenter-designed stimuli, the HSE had been implied to be mainly responding to yaw rotations of the animal (Hausen, 1982a,b; Haag et al., 1997; Horstmann et al., 2000; Krapp et al., 2001). Here, we show by model simulations that the relevant features of the responses of the HSE neuron to natural optic flow can be reproduced by relatively simple computations. In particular, the model does not encode the time course of the yaw velocity during saccades in a linear way. Moreover, in the intersaccadic intervals, the model provides, in a similar way as the HSE cell, information about sideward motion. Although the specific input organization of the HSE and, in particular, its input from contralateral motion-sensitive neurons has been interpreted as a specific means to enhance its sensitivity to yaw rotations (Hausen, 1982a,b; Krapp et al., 2001), this input organization is also consistent with the finding that the HSE encodes sideward translation seen in the frontal visual field between saccades. Hence, the saccadic gaze strategy may facilitate the encoding of behaviorally relevant information about the spatial structure of the surrounding.

Our model of the blowfly's visual motion pathway is similar to model versions proposed previously based on systems analyses with conventional experimenter-designed stimuli (Egelhaaf and Borst, 1989; Egelhaaf et al., 1989; Borst et al., 1995, 2003; Haag et al., 1999; Kern et al., 2000, 2001b) and with optic flow experienced by walking flies (Kern et al., 2001b). It is composed of many retinotopically arranged motion detectors extracting local motion information and the subsequent spatial pooling of their outputs. The spatial pooling stage corresponds to the dendrite of the HSE neuron. Starting from a basic model, we introduced various model elaborations and documented the consequences of these elaborations on the response to behaviorally generated stimuli.

Already a very basic version of the model that linearly summates the outputs of simple correlation-type movement detectors reproduces essential features of the neuronal responses to naturalistic optic flow. Elaborations of the basic model improve the performance. Only small improvements are gained by introducing temporal filters in each input channel of the model to approximate the properties of the peripheral visual system. Even the introduction of an additional temporal filter into the motion detector that changes the model dynamics in response to conventional stimuli considerably (Borst et al., 2003) leads to only a small improvement of the response to behaviorally generated motion. However, implementing the nonlinear spatial integrating properties of the HSE neuron improves tremendously the fit of the model response to its experimental counterpart. The nonlinearities of spatial pooling, together with the opponent organization of the local motion detectors, were previously concluded to represent a gain control mechanism, which makes the responses of the HSE and other blowfly motion-sensitive TCs relatively invariant against changes in texture size (Borst et al., 1995) and texture density (Kern et al., 2001b), while still allowing them to encode changes in pattern velocity. This gain control mechanism requires that the movement detector output is essentially independent of the background luminance, as is accomplished in the model by either a bandpass filter in the peripheral visual system and/or a high-pass filter in one branch of the movement detector. Hence, although these two temporal filters do not directly affect the model performance under the naturalistic stimulus conditions tested here, they are necessary for the gain control mechanism to become operative.

In contrast to the expectation that the HSE cell mainly responds to self-rotation, the HSE cell and its model counterpart do not represent the yaw velocity during saccades in a linear way, and not even in a monotonic way. Saccades leading to preferred-direction motion do not depolarize the cell relative to its mainly depolarized intersaccadic response. This characteristic feature was obtained already with the basic model and thus can be concluded to be a consequence of the nonlinear encoding of velocity by the local motion detectors when velocity and accelerations get large (Egelhaaf and Reichardt, 1987; Haag and Borst, 1997). Rather than interpreting this feature as a limitation of the motion detection system, it can be interpreted as advantageous in the context of encoding of naturalistic optic flow. Because during saccades the motion vision system operates beyond its linear range, it can resolve the much smaller translational optic flow component between saccades and thus provide information about the spatial layout of the environment. If the motion vision system would encode the entire angular velocity range in a linear way, the translational responses would be negligible and could hardly be resolved given the limited operating range of neurons and the noisiness of neuronal signals (for review, see Warzecha and Egelhaaf, 2001).

Surprisingly, the performance of the model is much less sensitive to parameter changes when confronted with complex behaviorally generated optic flow than when much simpler experimenter-designed stimuli are used. This leads us to the somewhat paradoxical conclusion that simple experimenter-defined stimuli may facilitate the precise estimation of system parameters, whereas the precision of these parameters apparently does not matter much to account for the responses to behaviorally relevant stimulus features. This general conclusion appears to pertain to two additional aspects that are important from a functional point of view:

(1) Although the encoding properties of the model rely mostly on the specific dynamical features of behaviorally generated optic flow, they are relatively invariant to changes in the environmental texture. This finding may be surprising, given the fact that for simple constant-velocity stimuli, the responses of blowfly TCs are known to depend strongly on the textural properties (Eckert, 1980). Nonetheless, even for constant velocity motion, the texture dependence is reduced for stimuli with natural scene statistics (Dror et al., 2001). From a functional point of view, it appears to be appropriate that the neuronal encoding of self-motion and of the spatial relationship of the animal to its environment is as independent as possible from the accidental textural properties of the environment.

(2) Several features of TC responses depend on a stimulus history that may be regarded as adaptive. However, neither the underlying mechanisms nor the functional significance of most of these phenomena have yet been clarified. Adaptive processes have been studied by very different stimulus paradigms ranging from brief displacements of the stimulus pattern or constant velocity stimulation (Maddess and Laughlin, 1985; Borst and Egelhaaf, 1987; Ruyter van Steveninck and Bialek, 1988; Harris et al., 1999a,b, 2000; Kurtz et al., 2000) to time-varying velocity fluctuations (Brenner et al., 2000; Fairhall et al., 2001). We find that the optimal motion detector time constants for the fit of neuronal responses to naturalistic optic flow are smaller than those estimated from the steady-state velocity tuning. However, the optimal time constants were almost identical for the initial and later segments of the responses to naturalistic optic flow. This would either imply a very quick adaptation to the dynamical stimulation (Fairhall et al., 2001) or could hint at additional filters in the neuronal system missing in our current model. It should be noted, however, that the model performance in response to naturalistic optic flow changes only little by shifting the movement detector time constants from the optimum to values that also fit the experimentally determined steady-state velocity tuning (see below) (Figs. 4c, 5). In contrast to the time constants in the visual motion pathway, the gain of the system decreases slightly during prolonged stimulation with behaviorally generated optic flow. This finding is in accordance with experimental evidence for changes in contrast sensitivity of the visual motion pathway (Harris et al., 2000).

The information about distances to environmental objects is not represented explicitly in the responses of the HSE cell and its model counterpart. Can this information be used in a simple way for controlling visually guided behavior? Because, for methodological reasons, it is hard to answer this question experimentally, we plan to incorporate the model of the visual motion pathway into a closed-loop system and to assess different strategies of decoding the HSE responses. By testing the resulting “virtual fly” in various behavioral tasks, such as in obstacle avoidance in complex environments, we can challenge our interpretation that the HSE cell extracts behaviorally relevant information about the layout of the environment under closed-loop conditions. Furthermore, we may contribute to the development of robots that are able to avoid obstacles solely based on optic flow information.

Appendix

The temporal properties of the integrating neuron can be approximated by a first-order linear low-pass filter (Koch, 1999). The corner frequency of this low-pass filter depends on the input resistance and the membrane capacitance of the cell

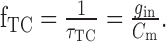The input resistance is the sum of the leak conductance of the cell and the synaptic conductances

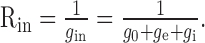Without synaptic input, the corner frequency is minimal, and the input resistance drops for any synaptic input. The lower bound for the corner frequency is

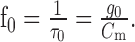Thus, the corner frequency of the neuron with a given synaptic input is given by

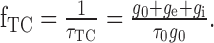Optimization of both parameters with respect to the difference d_rms by systematic variation leads to τ₀ = 30 ms and g₀ = 1100 (dimensionless for reasons discussed previously). The average difference between model and experimental data is d_rms = 2.83 mV. During stimulation with behaviorally generated optic flow, the corner frequency is much lower but varies only little as a function of the input resistance (τ_TC = 12.1 ± 5.9 ms; mean ± SD). The value of the corner frequency during motion stimulation is still within the same order of magnitude as the time constant of 1.82 ms measured for the HSE neuron by Borst and Haag (1996). Note, however, that we model the cell as a one-compartment neuron, although the cell may have different passive properties in the dendritic and the axonal regions.