Ensemble Coding of Vocal Control in Birdsong

Abstract

Zebra finch song is represented in the high-level motor control nucleus high vocal center (HVC) (Reiner et al., 2004) as a sparse sequence of spike bursts. In contrast, the vocal organ is driven continuously by smoothly varying muscle control signals. To investigate how the sparse HVC code is transformed into continuous vocal patterns, we recorded in the singing zebra finch from populations of neurons in the robust nucleus of arcopallium (RA), a premotor area intermediate between HVC and the motor neurons. We found that highly similar song elements are typically produced by different RA ensembles. Furthermore, although the song is modulated on a wide range of time scales (10-100 ms), patterns of neural activity in RA change only on a short time scale (5-10 ms). We suggest that song is driven by a dynamic circuit that operates on a single underlying clock, and that the large convergence of RA neurons to vocal control muscles results in a many-to-one mapping of RA activity to song structure. This permits rapidly changing RA ensembles to drive both fast and slow acoustic modulations, thereby transforming the sparse HVC code into a continuous vocal pattern.

Introduction

Birdsong is a complex learned behavior consisting of sequential vocal gestures over a wide range of time scales, from milliseconds to several seconds (Immelmann, 1969; Fee et al., 1998). Juvenile songbirds use auditory feedback to accurately reproduce a memorized tutor song by the time they reach adulthood (Konishi, 1965). Adult zebra finch song is composed of a 0.5-1.0 s sound pattern called a motif, which is repeated a variable number of times during a song bout. The motif itself is composed of song syllables, individual bursts of sound ∼100 ms in length that occur in a precise order. Syllables, in turn, are composed of stereotyped and often complex spectral structure, referred to as subsyllables, that can change rapidly (<10 ms time scale) or slowly (∼100 ms time scale).

Birdsong is generated by a set of brain nuclei known collectively as the song control system (see Fig. 1A) (Nottebohm et al., 1976, 1982). The premotor nucleus high vocal center (HVC) (Reiner, et al., 2004), near the top of this control system, encodes the temporal sequence in which sounds are generated (Yu and Margolias, 1996; Hahnloser et al., 2002). HVC neurons that project to the robust nucleus of the arcopallium (RA) (Reiner et al., 2004) generate single bursts of spikes (∼6 ms duration) at precisely reproduced times within the song motif (Hahnloser et al., 2002). RA, in turn, projects to the hypoglossal motor nucleus with a weak myotopic organization (Vicario, 1991) and to brainstem respiratory areas (Wild, 1993). RA projection neurons also make local connections within RA (Canady et al., 1988). In contrast to the extremely sparse neuronal firing patterns in HVC, syringeal and respiratory muscles are driven by continuous control signals that contain a wide range of time scales reflecting the motif, syllable, and subsyllable acoustic structure (Goller and Suthers, 1996; Wild et al., 1998). How is the sparse representation of the song observed in HVC transformed into the continuous activity of the vocal muscles?

Figure 1.

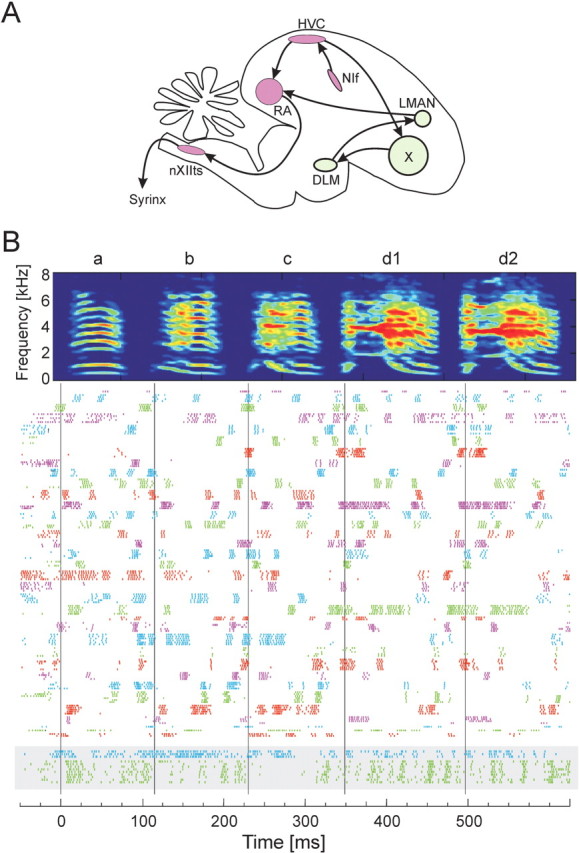
Recording of the activity of a large population of RA neurons in the singing zebra finch. A, Simplified schematic view of the oscine song control system. The premotor pathway from HVC to RA to nXIIts (hypoglossal nucleus) to the vocalorgan (syrinx) is highlighted in red. DLM, Medial nucleus of the dorsolateral thalamus; LMAN, lateral magnocellular nucleus of the anterior nidopallium (Reiner et al., 2004); NIf, nucleus interface of the nidopallium. B, Raster plot of song-aligned spike activity of all 34 RA projection neurons recorded during singing in bird 9. Each row shows the spikes produced during one song motif. Different colored spike trains represent the activities of different RA neurons, which have all been aligned to a common time axis using the song motif. Each RA neuron produced a pattern of bursts that was generally different from all other RA neurons. Two putative RA interneurons recorded in the same bird are shown at the bottom (gray box). The time-frequency spectrogram at the top of the figure shows a representative song motif for this bird.

As an intermediary between HVC and the brainstem motor nuclei, RA is likely to play an important role in this transformation. Stimulating RA while the bird is singing causes a brief perturbation in the bird's vocalization (Vu et al., 1994; Fee et al., 2004), which quickly returns to an unperturbed state, implying that RA encodes the song on a short time scale (10-20 ms). Previous single-neuron recordings in singing birds have shown that individual RA neurons generate several high-frequency bursts per motif (Yu and Margoliash, 1996). The burst onset times and the pattern of spikes within these bursts are highly stereotyped and are reproduced with millisecond timing precision relative to acoustic structure within the bird's song (Chi and Margoliash, 2001). The burst patterns in RA are thought to be driven by RA-projecting HVC neurons (HVC_(RA)) (Hahnloser et al., 2002), although RA also contains a long-range inhibitory network that may shape RA firing patterns during singing (Spiro et al., 1999). In addition to receiving input from HVC, RA is the only target of a basal ganglia circuit essential for vocal learning, implicating RA as a crucial locus for learning in the premotor pathway (Bottjer et al., 1984; Scharff and Nottebohm, 1991; Mooney, 1992; Stark and Perkel, 1999; Brainard and Doupe, 2000).

We investigated the role RA plays in the motor control of song by quantifying the structure of the RA population activity during singing and its relationship to the spectral and temporal structure in the bird's song. We present a model for how sparse patterns in HVC are transformed into continuous muscle-control signals. Finally, we will argue that many of the characteristics of the RA activity patterns could emerge as a result of learning and are a consequence of the structure of the premotor circuit.

Materials and Methods

Birds were housed in custom-designed Plexiglas cages and had ad libitum access to food and water. All four birds used in the experiment were adult male zebra finches, with crystallized songs, implanted with a small testosterone pellet to increase singing rate. Female zebra finches were housed in separate Plexiglas cages and were presented to the males after isolation of one or more RA neurons to elicit directed song.

Electrophysiology

Birds were anesthetized with 1-2% isoflurane, and the microdrive was implanted onto the skull in a 3 h surgical procedure (Fee and Leonardo, 2001). The microdrive weighs ∼1.5 g and contains three motorized positioners, allowing cells to be isolated remotely. Three independently controlled electrodes (Microprobe WE3003H3), bundled with 200 μm spacing, were advanced slowly throughout the dorsal-to-ventral extent of RA. A small lateral positioner allowed us to displace the bundle of electrodes by several tens of micrometers to make a fresh penetration. Our population of recorded neurons was thus sampled throughout RA. We were unable to ascertain the precise location of recording sites within the rough RA myotopy. High-quality single-neuron signals of 1-10 mV in amplitude were isolated on individual electrodes, comparable with that seen in a head-fixed anesthetized animal. Single-unit signals were verified by a spike refractory period in the interspike interval histogram. Neural and acoustic data were collected by custom-designed software written in Labview (National Instruments, Austin, TX). The placement of the electrodes within RA was verified histologically at the conclusion of the experiments.

Data analysis

Instantaneous firing rate. Throughout much of the analysis, we represented neural activities as instantaneous firing rates, R(t), defined at each time point as the inverse of the enclosed inter-spike interval as follows:

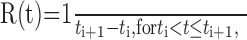where t_i is the time of the i th spike. A burst was defined as the interval over which the instantaneous firing rate exceeded a threshold of 125 Hz.

Song alignment. The lengths of zebra finch song syllables vary by 2-5% from song to song. This adds considerable noise to the structure of the RA spike trains if they are aligned only to the onset of each song motif. To compensate for this syllable-to-syllable time warping, we used each syllable onset in the motif as an alignment point. Spike times between each alignment point were linearly stretched or compressed to match the corresponding intervals in a representative template motif. This piecewiselinear time warping is based only on the song and is completely independent of the spike trains.

The song alignment algorithm proceeded as follows. Song syllables were initially segregated automatically using a threshold crossing of the acoustic power and were labeled manually (a, b, c, etc.). For each syllable n in motif i, we calculated the time derivative of the song spectrogram, defined as follows:

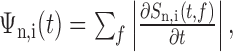where S_n,i(t,f) is the time-frequency spectrogram of the syllable. The time derivative typically exhibits a pronounced peak at the syllable onset. For the motif chosen as the template, the times of these peaks for the set of syllables within the template define a set of alignment times (T_n), with the time origin chosen such that T₁ = 0. The optimal alignment time (t_n,i) of each template syllable onset to the corresponding syllable in the dataset was found using cross-correlation of the time derivatives. The quality of the automatic alignments of the song syllables was checked manually. Each spike time was then linearly projected onto the time base of the template motif, using the following relationship:

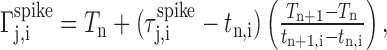where 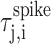is the time of the j th spike that occurs between t_n,i and t_n+1,i in motif i, and 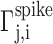is the time-warped spike time. From the resulting alignment of spike times across different motif renditions, we infer that the acoustic alignment was typically better than 1 ms, consistent with previous measurements of the alignment of acoustic features with RA spike trains (Chi and Margoliash, 2001).

Analysis of correlations between pairs of RA neurons. The correlation of instantaneous firing rates 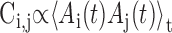was calculated for all pairs of neurons recorded in each bird (including simultaneously and sequentially recorded pairs). The distributions of correlations for all birds were combined into a single distribution that describes the paired correlations across the entire dataset. To determine whether the recorded neurons were significantly correlated, we estimated the distribution of correlations in a simulated data set that lacked any correlation between neurons. The distributions of burst width and interval durations were measured for the population of RA neurons in each bird, and simulated data were constructed with burst width and burst intervals chosen randomly from the measured distributions. The distribution of cell-cell correlations was calculated for 500 simulated data sets, and the mean and SD was determined for the resulting distribution combined over all birds. A Kolmogorov-Smirnov (KS) test was used to test the null hypothesis that the empirical correlations were drawn from the same distribution as the random correlations.

Neural ensemble correlation matrix. For each neuron in the recorded population, we found its mean instantaneous firing rate over all recorded motifs. We defined the representative instantaneous firing rate trace as the one that had the minimum squared error relative to the mean. The representative instantaneous firing rate of neuron i was the ith element of the time-dependent activity vector A_i(t). Based on this vector, the correlation between the two patterns of neural activity occurring at times t and t′ was calculated as follows:

Note that the instantaneous firing rate vector was mean-subtracted before calculating C_N; this improved the fine structure resolvable in the correlation matrix. The mean subtraction also resulted in a slight negative offset in the distribution of neural correlations (as seen in the conditional distributions) (see Fig. 6 D, G). Results equivalent to those discussed in this study are obtained even if the mean subtraction is not used. Times at which no neurons in the data set were bursting were excluded from the analysis, because they contained no data. The fraction of time in which there was no population activity (i.e., no bursts from any RA neuron) depended on the number of neurons recorded in each bird. For each bird, the number of neurons and the fraction of the motif containing no bursts (off) was as follows: bird 9, 34 neurons (1% off); bird 12, 26 neurons (8% off); bird 10, 10 neurons (30% off); bird 7, 6 neurons (45% off). In addition to the dot product correlation metric described here, we also used the Hamming distance to measure the neural ensemble correlations without change in results. The neural ensemble activity was estimated in a 0.5 ms window in 0.5 ms steps.

Figure 6.

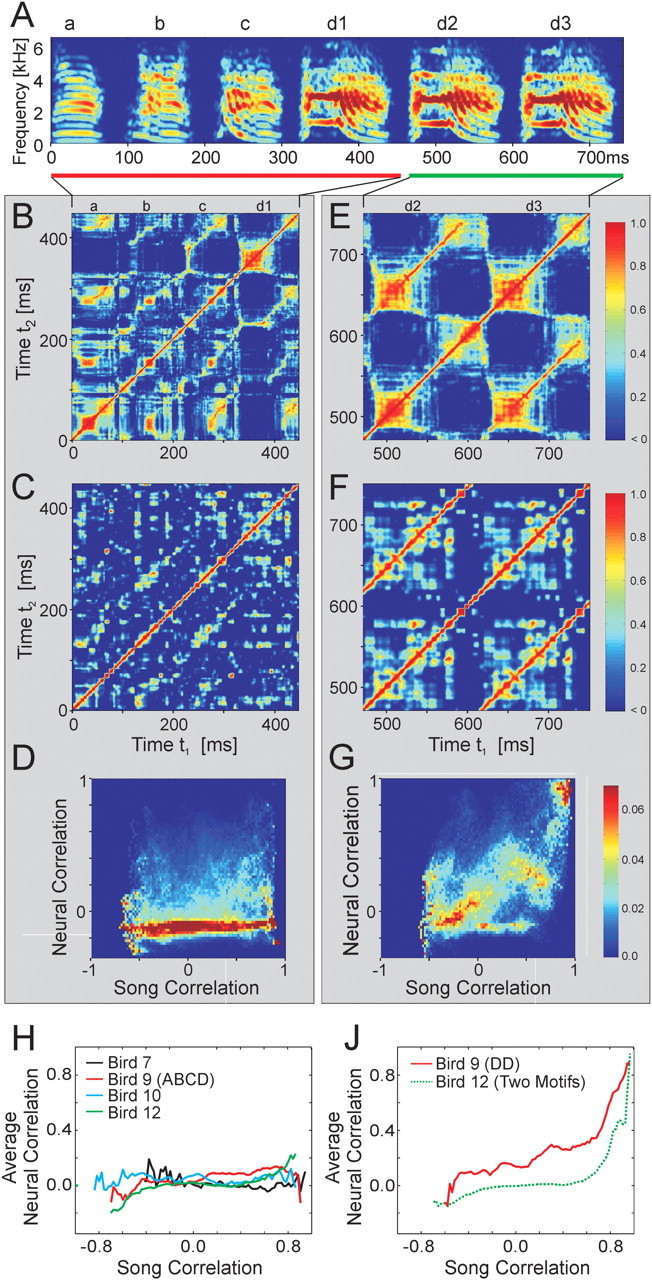
Analysis of correlation between patterns of activity in RA and acoustic structure in the song. A, Spectrogram of a song that contains repeated acoustic structure (bird 9). This bird stuttered syllable d a variable number of times (d1, d2, d3...). The song is divided into two sections, one with only repeated syllables (d2, d3; green bar) and another with different syllables that contain regions of similar subsyllables (a, b, c, d1; red bar). B, C, Song correlation matrix and neural correlation matrix for syllables a, b, c, and d1. D, Conditional probability distribution of neural correlations at different levels of song correlation. Each column represents the distribution of neural ensemble correlations associated with the level of song correlation indicated on the x-axis. E-G, Song correlation matrix, neural correlation matrix, and conditional probability distribution of neural correlations for syllables d2 and d3. During repeated syllables, the highly correlated sounds are associated with highly correlated neural ensembles. In contrast, during the production of different syllables with similar subsyllables, the highly correlated sounds are associated with uncorrelated neural ensembles. H, Average neural correlation as a function of song correlation for each bird for the portion of the song motif containing repeated subsyllables but not repeated syllables. J, Average neural correlation as a function of song correlation for repeated syllables d2 and d3 in bird 9 and for repeated song motifs in bird 12.

Song correlation matrix. A multitaper estimate (Thompson, 1982) of the log power spectrum S_i(t) of each song was calculated with a sliding 8 ms window, using a step size of 0.5 ms, and a time-bandwidth product of NW = 2, where i is the frequency bin and t is the time in the song. The song spectrogram was normalized by average song spectrum and average acoustic power to emphasize fine acoustic structure within syllables rather than simply spectral changes associated with syllables versus silent internals.

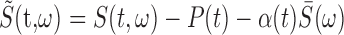, where 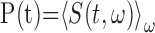, , 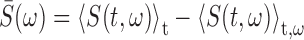and .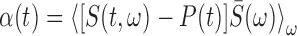

The song correlation matrix at times t and t′ was then calculated as follows:

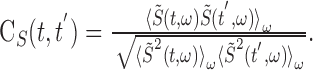In addition, we repeated the entire analysis using a set of univariate acoustic features. These features were designed to correspond, as much as possible, to the muscle control signals used to drive the vocal organ (Tchernichovski et al., 2000). All of the results and statistical analyses based on the song correlation matrix were reproduced using the univariate song features in place of the song spectrogram.

Latency correction. It was important to estimate the latency between neural activity in RA and the sound it generated to properly compare related time points in the song and neural correlation matrices. For each bird, we chose a latency correction, τ_L, that maximized the overlap of the structure in the neural and song correlation matrices (over a range of 0 ms < τ_L < 40 ms). For birds 9 and 12, we found 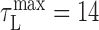ms; for bird 10, we found 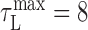. Because there was insufficient data to estimate the latency for bird 7, a value of 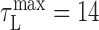was used. These values are consistent with a direct measurement of latency using brief electrical stimulation in RA during singing (τ = 15 ± 5 ms) (Fee et al., 2004). None of our results were sensitive to the value of latency used (tested over a range of 0-50 ms in 5 ms steps). The latency correction was applied to each song correlation matrix, such that in all subsequent analyses, the time t refers to a pattern of RA neural activity and the sound it generated.

Correlation width analysis. The correlation width of the song and neural signals was calculated from the width of the diagonal of each correlation matrix. For the time t, this was defined as the radius of the largest circle that could be drawn around the point (t, t) in the matrix without containing a correlation value less than the threshold C_T = 0.5. This procedure yielded a contour line around the diagonal of both the song and neural correlation matrices that corresponds to the instantaneous full-width half-height of the autocorrelation function. The correlation width effectively divides the song correlation matrix into two regions: correlations within the local acoustic structure of a syllable (points lying between the width contour line and the matrix diagonal) and nonlocal correlations between different syllables or subsyllables (points that occurred outside the width contour, far from the matrix diagonal). The scatter plot relating neural and song correlation widths quantifies the relationship between neural activity and acoustic structure within syllables. The results reported here do not depend on the choice of correlation threshold over a wide range of values (C_T = 0.2-0.9).

Conditional distributions. The conditional distribution analysis was used to quantify the relationship between neural activity and acoustic structure that occurred in separate syllables, that is, in regions of the correlation matrices that lie above the correlation-width contour. A two-dimensional histogram, H(C_N, C_s), of pairs of correlation values [C_N(t, t′), C_S(t, t′)] was accumulated over all time pairs (t, t′) greater than the width contour described above.

The conditional probability distribution, P_N, of neural correlations associated with a given value of song correlation (see Fig. 3d) was determined by normalizing the histogram at each value of song correlation as follows:

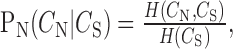Figure 3.

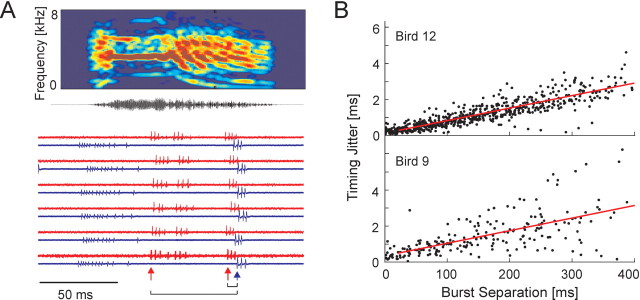
Spike timing precision with in RA. A, Simultaneous recording of three RA neurons shown for six renditions of one song syllable (syllable d, bird 9; see Fig. 1 B). One neuron was recorded on one electrode (top trace of each pair; red); two additional neurons were recorded on another electrode (bottom trace; blue). After the neural signals were aligned to the onset of syllable d, individual bursts were identified, and the time between the onset of each pair of bursts was measured. B, The timing jitter between burst onsets in pairs of neurons as a function of burst separation is shown for all pairs of bursts (n = 1299 burst pairs) in all pairs of simultaneously recorded neurons (n = 13 neuron pairs).

where

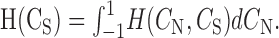The expected (mean) value of C_N in the conditional distribution was calculated at each value of song correlation as follows:

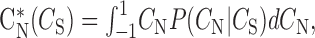as shown in Figure 6, D and G. To ensure that the neural and acoustic data had the same temporal resolution, the instantaneous firing rates used to calculate the neural correlation matrix were smoothed with the same window function used to calculate the time-frequency spectrum of the motif (8 ms width).

Temporal uncertainty calculation. To estimate the temporal uncertainty for a population of N neurons, the following procedure was used (for each bird). Firing rates were sampled at 10 ms intervals and were set to 0 or 1 using a threshold of 125 Hz. The neural correlation matrix C_N was then calculated using randomly selected subsamples of N neurons from our data set. Entries in the correlation matrix where C_N = 1 indicate pairs of times during which identical sets of neurons were active (independent of firing rate). The thresholded matrix was then searched to find the number of unique neural ensembles and the number of occurrences of each ensemble, from which the entropy of the RA code was calculated as follows:

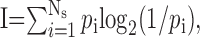where N_S is the number of unique neural ensembles exhibited by the population of RA neurons, and p_i is the probability of occurrence of ensemble i. 2^I represents the number of time steps that, on average, could be encoded by a population of neurons with entropy I. By dividing the length of the song (in milliseconds) by 2^I, we obtain the temporal uncertainty for the neural population of size N. This number represents the average temporal error (in milliseconds) that one would have in predicting the location in the song from a randomly chosen pattern of neural activity. By randomly resampling the original neural data set 500 times, we obtained a monte-carlo estimate of the mean and confidence intervals for the N neuron temporal uncertainty in motif time. This procedure was repeated for 1-34 neurons.

Results

Firing statistics of single RA neurons

A motorized microdrive (Fee and Leonardo, 2001) was used to record single-unit extracellular signals from neurons in nucleus RA in four freely behaving adult male zebra finches (Taeniopygia guttata; n = 78 total neurons). During singing, the majority of RA neurons we recorded generated well-defined bursts of action potentials (Figs. 1B, 2A, 4A), as observed previously (Yu and Margoliash, 1996). Based on their highly periodic spontaneous firing patterns (∼20-30 Hz) and large spike widths (202 ± 63 μs), these neurons were identified as putative projection neurons (n = 76) (Spiro et al., 1999), which project to downstream targets and also make local collaterals.

Figure 2.

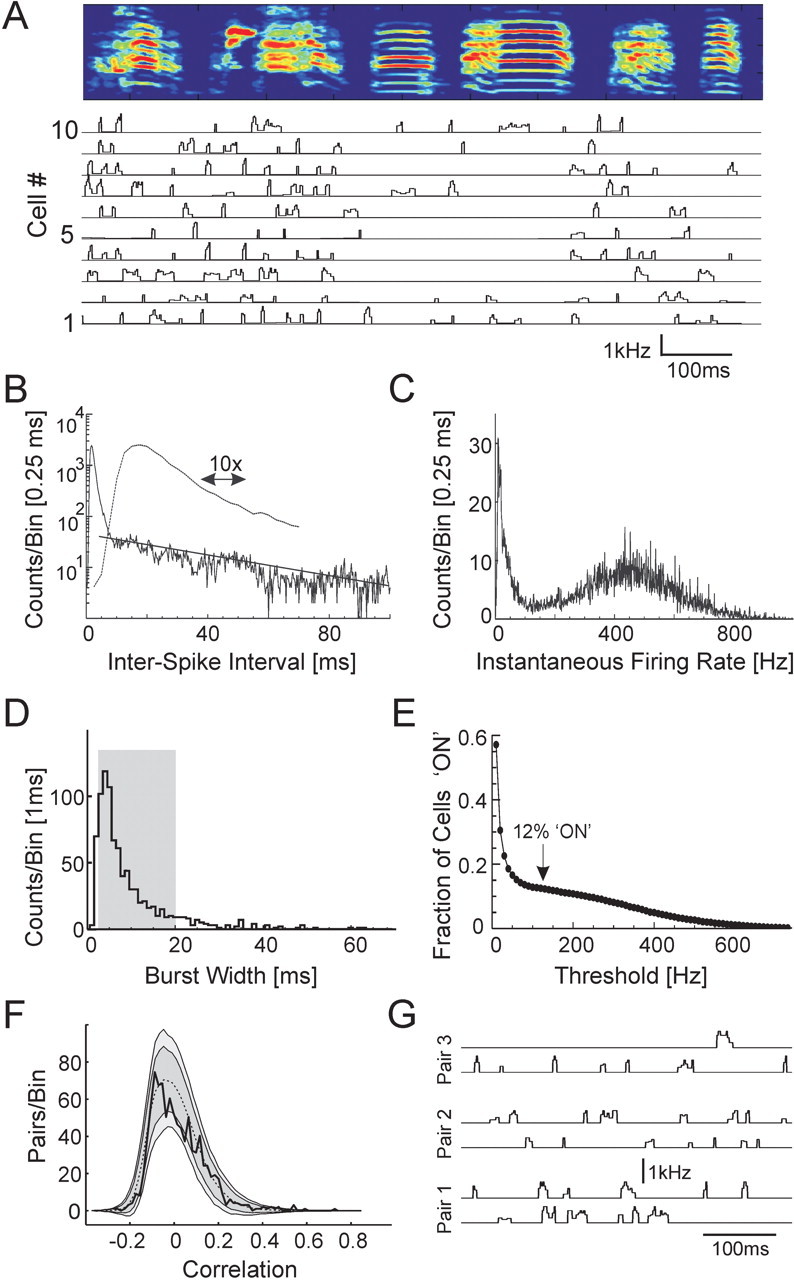
Statistics of RA firing patterns. A, Instantaneous firing rates of 10 RA neurons from bird 10 over the course of the song motif. RA neurons exhibit pronounced bursts with rapid onset and offset. At the top is the spectrogram of the bird's song. Note the reduction in RA burst density during the production of simple harmonic syllables versus complex nonharmonic syllables. B, Interspike interval histogram for all song-related RA spike trains (all birds; dashed line is a 10× zoom of the solid line). C, Distribution of instantaneous firing rates (all birds). D, Histogram of burst durations (threshold of 125 Hz; all birds). The mean burst length is 8.67 ms; the gray box marks the 10-90% interval. E, Average fraction of RA bursts with firing rates above threshold, as a function of threshold (all birds). Note the plateau at ∼125 Hz, with a fraction “on” of 12%. F, Distribution of correlations between all pairs of RA neurons recorded in each bird, accumulated across all birds (solid black line, 0.02 bin size; n = 946 pairs). The distribution for simulated data with randomly placed bursts is also shown (mean, dashed black line; ±2 SD, dark gray region; ±3 SD, light gray region). G, Instantaneous firing rate traces for three pairs of neighboring RA neurons in bird 9. Each pair was recorded simultaneously on the same microelectrode.

Figure 4.

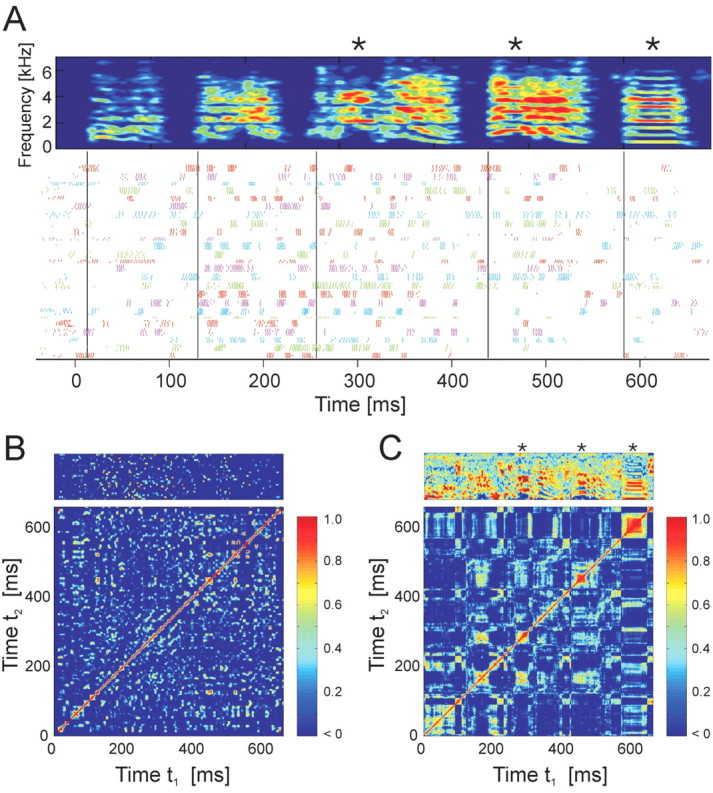
Correlation matrices of the RA population activity and song acoustic structure. A, Raster plot of song-aligned spike activity of 25 RA neurons recorded during singing in bird 12; cycled colors indicate different RA neurons as in Figure 1 B. The asterisks mark three syllables that are tracked in C and in Figure 5. B, Neural correlation matrix for the spike data shown in A. Each point (t₁, t₂) in the matrix represents the correlation of the pattern of neural activity at time t₁ with that at time t₂. The vector of neuronal firing rates is shown at the top. C, Song correlation matrix for the spectrogram shown in A. Each point in the matrix represents the correlation of the pattern of sound frequencies shown in the song spectrogram at time t₁ with that at time t₂. The normalized song spectrogram used in computing the song correlations is shown at the top.

A second class of neurons was found that had narrower peak-to-trough spike widths (75 ± 12 us) than the projection neurons and were not spontaneously active in the nonsinging bird (n = 2 in bird 9; see Materials and Methods). Narrow spike widths and a lack of spontaneous activity are both characteristics of RA interneurons observed in brain slice recordings, in contrast to RA projection neurons, which are spontaneously active and exhibit larger spike widths (Spiro et al., 1999). The two putative interneurons (Fig. 1B, bottom) became active during the song introductory notes and had firing rates of 107 ± 13 Hz (±SD) and 183 ± 8Hz(±SD) over the duration of the song. These neurons exhibited spike patterns that were qualitatively less bursting and less stereotyped than the majority type. The variability of the firing pattern of each neuron was quantified by computing the average correlation between all of the spike trains recorded for that neuron during singing. The average correlation between the spike trains of each interneuron was 0.62 ± 0.1. In contrast, the average correlation of the projection neuron spike trains from motif to motif was 0.90 ± 0.1 (averaged across 34 neurons; bird 9). The motif-to-motif correlations in interneuron spike patterns were significantly lower than those of the projection neurons (t test; p = 0.002). The putative interneurons were not included in the analysis or results described in the remainder of this study.

The interspike interval histogram of putative projection neurons during singing was sharply peaked at 2 ms and had a long exponentially decaying tail for intervals >8 ms (Fig. 2B). The distribution of instantaneous firing rates (the inverse of the interspike intervals) was strongly bimodal (Fig. 2C), with one mode reflecting the firing rates within RA bursts and the other mode reflecting the lower firing rate between bursts. Burst firing rates were peaked at 455 Hz with a width (at half maximum) of ±188 Hz. Burst onsets and offsets were defined using a threshold instantaneous firing rate of 125 Hz (see Materials and Methods). RA bursts had a mean width of 8.7 ms and ranged from 3 to 20 ms duration (10-90% of distribution; median, 6.0 ± 0.4 ms) (Fig. 2D). Intervals between RA bursts had a mean duration of 53.90 ± 50.1 ms SD. On average, each RA neuron generated 12 bursts per song motif (average burst rate, 16 ± 3.7 bursts/s) and was “on” for ∼12 ± 2% of the motif (relatively independent of the choice of threshold over a range of ±25 Hz) (Fig. 2E). Simultaneous recordings were made from 13 pairs of RA neurons (n = 6 in bird 9; n = 7 in bird 12) (Fig. 3A). Simultaneous bursts across neuron pairs exhibited spike-timing precision of 0.28 ± 0.3 ms rms jitter (Fig. 3B). At burst separations >20 ms, the jitter increased linearly at a rate of 0.7 ms per 100 ms separation.

Firing pattern correlations between pairs of RA neurons

Using the stereotyped acoustic features of the song, we were able to align the firing patterns of all of the RA neurons recorded in the same bird, thus reconstructing the patterns of neural activity that occurred across the entire population of putative projection neurons (n = 6, 34, 10, and 26 neurons in birds 7, 9, 10, and 12, respectively) (see Materials and Methods). A striking aspect of the RA burst patterns apparent from the aligned spike trains (Figs. 1B, 2A) was that most neurons generated a unique time-varying pattern of bursts. The mean correlation between firing patterns of different RA neurons was 0.015 ± 0.12 SD. Of the 946 pairwise correlations in the four birds, only 0.5% exhibited firing rate correlations >0.5 (three neuron pairs in bird 9, and one pair each in birds 10 and 12). Furthermore, the distribution of pairwise correlations was not significantly different from the distribution of correlations found for simulated data sets with randomly placed bursts (KS test; p = 0.07) (Fig. 2F) (see Materials and Methods).

Occasionally, two putative projection neurons were recorded on a single electrode in RA. In several cases (three neuron pairs for bird 9; one neuron pair for bird 12), the waveforms had a significantly different amplitude, such that the two neurons were easily distinguished. The close spatial proximity of these neuron pairs suggests they were in the same myotopic region of RA (Vicario, 1991). Neighboring RA neurons exhibited very different spiking patterns (Fig. 2G). The firing rate correlations between these simultaneously recorded pairs on the same electrode were small (0.00 ± 0.11).

RA population activity during simple and complex syllables

We first examined the relationship between bursting probability and song structure at a coarse level. The fraction of bursting neurons (firing rates above 125 Hz threshold) during nonharmonic notes was significantly higher than the fraction of bursting neurons during simple harmonic stack notes (0.155 ± 0.005 SE compared with 0.084 ± 0.007; KS test; p < 10^-6; n = 76 neurons; four birds) (Fig. 2A). In contrast, there was no significant difference between the fraction of neurons bursting during syllables and the fraction bursting during the silent intervals between syllables (0.128 ± 0.005 SE compared with 0.129 ± 0.007; KS test; p < 0.57; latency correction of 15 ms) (see Materials and Methods) (Fig. 4A).

Correlations between RA ensembles

An inspection of the song-aligned RA spike trains showed that different sets of RA neurons turned on and off in a highly predictable manner over the course of the bird's song (Figs. 1B, 2A, 4A). We refer to the collection of RA cells that were active at a given moment in time as a neural ensemble. Note that in our terminology, the ensemble is the active subset of a fixed population of RA neurons (each moment in the song may be associated with a different ensemble). To quantify this ensemble activity more precisely, we used a time-dependent activity vector A_i(t) to represent the instantaneous firing rate of the ith neuron at time t in the song motif of each bird (see Materials and Methods). The similarity of the RA neural ensembles active at different time points in the song was then determined from a neural correlation matrix C_N(t, t′), such that each element (t, t′) in the matrix was defined as the correlation of the pattern of RA neural activity at time t with the pattern of RA neural activity at time t′ (Fig. 4B) (see Materials and Methods). C_N(t, t′) is a symmetric matrix for which values can range from 1 (identical patterns of neural activity) to -1 (anticorrelated patterns of neural activity).

By projecting the neural correlation matrix along its diagonal, we calculated the lag autocorrelation, the function that describes the average length of time a pattern of neural activity remains correlated with itself (Fig. 5A). (Note that the autocorrelation of the time-dependent activity vector, A_i(t), is different from the average autocorrelation of the firing rates from individual cells.) For all four birds, the autocorrelation shows a strong peak at zero time with a width of 7.9 ± 1.4 ms (full-width at half-height) and is essentially uncorrelated at time lags >20 ms (C̄_N = 0.03 for|t - t′| > 20 ms). The width of the autocorrelation is consistent with the 8.7 ms mean burst width of the RA neurons. In summary, at each time in the song motif, an ensemble of ∼10% of RA neurons lasted for ∼10 ms, after which the activity evolved to a different, uncorrelated ensemble of RA neurons.

Figure 5.

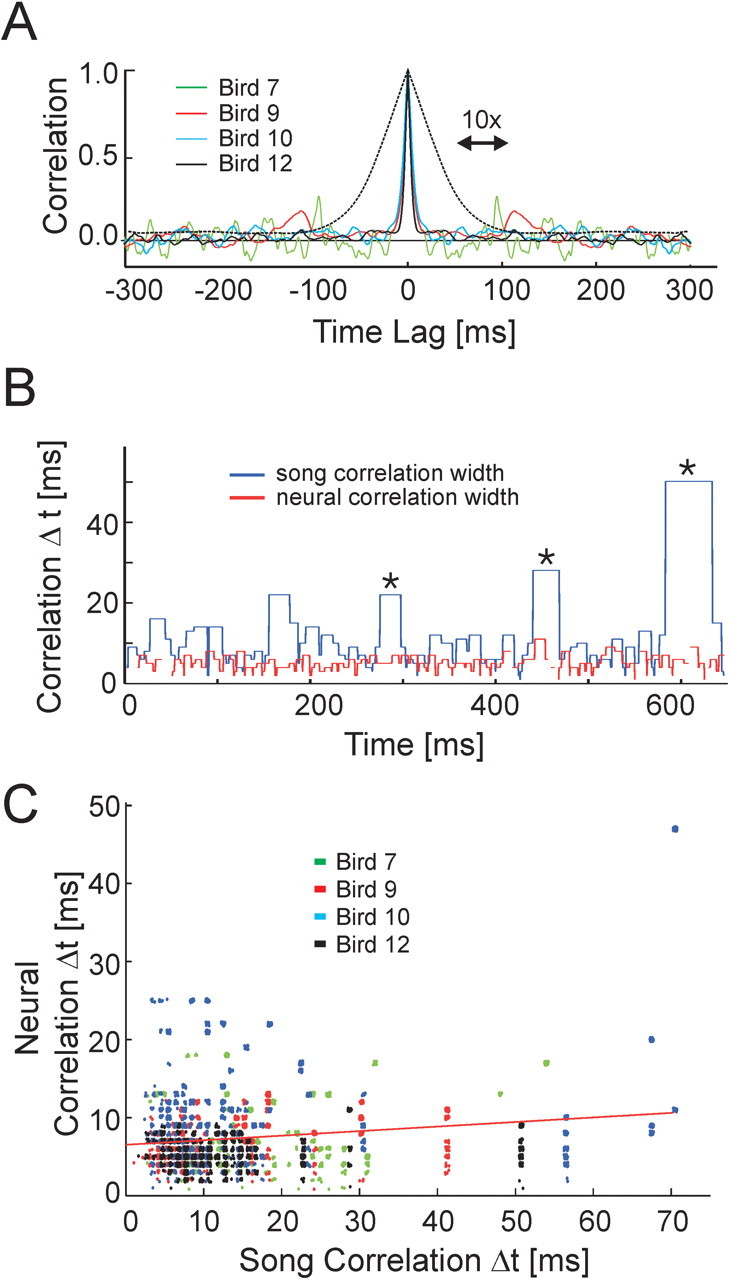
Temporal evolution of RA activity patterns and song acoustic structure. A, Autocorrelation of population firing patterns. The neural correlation matrix in Figure 4 B is averaged along its diagonals to estimate typical duration of a neural ensemble. The full-width at half maximum is 7.9 ms; the dashed line shows a 10× zoom of bird 12. B, The time varying width (Δt) of the song and neural correlation matrix diagonals (Fig. 4 B, C) shows that many slowly changing sounds were generated by rapidly changing patterns of RA neural activity. C, Cluster plot of song and neural correlation widths (Δt) pooled across all four birds.

Time scale of changes in acoustic structure and RA ensembles

The acoustic structure in zebra finch song contains a wide variety of time scales that must ultimately be represented by the spike patterns of neurons in the song control system. As discussed earlier, HVC_(RA) neurons encode the song with sparse bursts of activity, whereas the vocal muscle control signals are continuous with a wide range of temporal structure. Where are RA firing patterns located along this continuum of time scales? To address this question, we constructed a song correlation matrix C_S(t, t′) from the song spectrogram (Fig. 4C) in a manner analogous to the neural correlation matrix (see Materials and Methods). Each element in C_S represents the correlation between the acoustic spectra occurring at two different time points. The song and neural correlation matrices were corrected for the latency shift between the onset of RA activity and the generation of sound (see Materials and Methods), such that corresponding times (t, t′) in each matrix refer to two RA ensembles and the sounds they generated. Equivalent results were obtained in the subsequent analyses using a set univariate acoustic features that may more directly correspond to patterns of muscle activation (Tchernichovski et al., 2000) (see Materials and Methods) (supplementary Fig. 1, available at www.jneurosci.org as supplemental material).

We used the song and neural correlation matrices to quantify the relationship between the time scale of changes in song structure and the time scale of changes in RA activity (see Materials and Methods). The song correlation width (Fig. 5B) was found to vary from very short lengths (10 ms) for complex sounds to much longer lengths (up to 70 ms) for slowly changing sounds such as harmonic stacks. In contrast, the same analysis for the neural correlation matrix revealed a consistently small neural correlation width (∼5-10 ms) throughout the motif. A linear regression confirmed that there was little correlation between widths of the song and neural correlation matrices (slope = 0.06; r² = 0.04; p < 10^-3). A scatter plot of these data illustrates that both slowly and rapidly changing acoustic structure in the bird's song are associated with sequences of rapidly changing RA ensembles (Fig. 5C, seen as vertical clusters of points). In short, whereas acoustic structure in the song spanned a wide range of time scales, the neural ensembles changed continuously on a short time scale, independent of the acoustic structure being generated.

Relationship between RA ensembles and song spectral structure

One fundamental question about RA is its relation to spectral structure in the bird's song. In a premotor system, one might typically examine the correlation between the firing patterns of individual neurons and motor activity. However, individual RA neurons burst only a few times per song motif, providing only a small sample of data in which to detect these correlations. Furthermore, because both the song and the neural firing patterns are so highly stereotyped, multiple song motifs give little more information than a single motif.

A more fruitful approach is to relate the firing patterns of a large population of RA neurons to song spectral structure. We use the presence of repeated vocal patterns in song to examine how similar vocal outputs at different times in the song are represented in RA. Not only does the bird repeat the song motif multiple times within a bout of singing, but some birds repeat individual syllables within a song motif. Associated with each pair of time points in the song (t, t′) is the correlation between the vocal signals C_S(t, t′) and the neural signals C_N(t, t′). To quantify the relationship between correlations in song structure and correlations in the associated RA ensembles, all pairs of sounds in the song (at times t and t′) were sorted by correlation strength (i.e., 100% correlated sounds, 99% correlated sounds, 98% correlated sounds, etc., in 1% bins). The distribution of neural correlations was then calculated within each specified level of acoustic correlation and displayed as the columns of a matrix (Fig. 6D,G) (see Materials and Methods).

Based on this analysis, we found that when the bird repeated an entire syllable at different times in the song [e.g., a syllable stuttered within a motif (Helekar et al., 2001) or the repetition of syllables across motifs], the RA ensembles were precisely repeated (Fig. 6E,F) and therefore were highly correlated (C̄_N = 0.63 ± 0.19 for C_S > 0.8) (Fig. 6G,J). This is consistent with previous studies showing that RA activity is precisely repeated from motif to motif (Yu and Margoliash, 1996) and serves as a useful confirmation that the analysis method indeed properly associates correlated patterns of acoustic and neural activity. The correlation between repeated song syllables and repeated patterns of RA activity is strong enough that it is easily seen in the spike raster patterns themselves (Fig. 1B).

In addition to repeating entire syllables (∼100 ms), zebra finches can also repeat shorter subsyllabic acoustic patterns (subsyllables) that can be as long as 30-50 ms (e.g., bird 9) (Fig. 6A). Are these sounds associated with similar RA ensembles (Fig. 6B,C)? We found that similar subsyllables were generally not associated with repeated patterns of RA activity. In fact, in the nonstuttered portion of the song motif, larger acoustic correlations were not associated with larger neural correlations (C̄_N = 0.071 ± 0.085 for C_S > 0.8) (Fig. 6D,H). Thus, repeated syllables (long sequences of sound >100 ms) were generated by repeated RA ensembles, whereas repeated or similar subsyllables (short sequences of sound <50 ms) were typically generated by different RA ensembles. These results were consistent across all four birds.

Predictability of temporal position in the song from RA ensemble identity

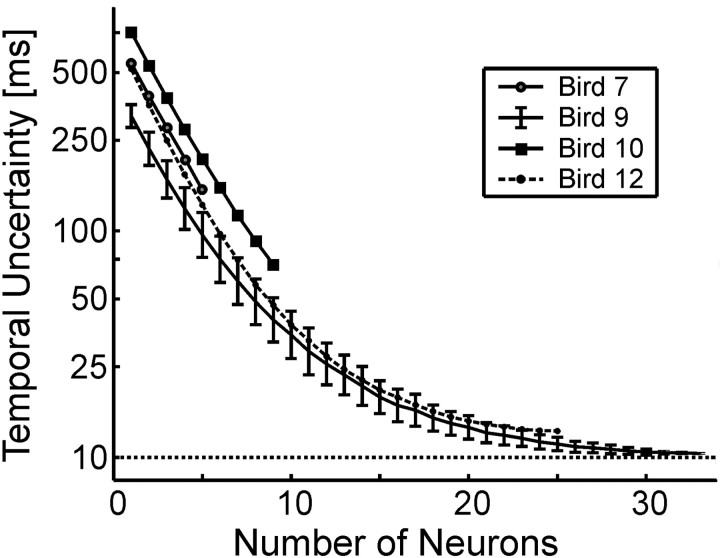
The lack of correlation between RA firing patterns at different times within the song motif suggests that there may be a one-to-one correspondence between RA ensembles and time, such that one could predict the exact temporal position in the song motif from the current neural ensemble. How many neurons would be required to do this? If we consider each RA neuron as having two states, on and off, a single observation that a particular RA neuron is on would constrain our uncertainty in the temporal position of the song to one of the ∼10 times that this neuron is known to be active during the motif. An observation of the state of two RA neurons would further constrain our uncertainty. By randomly sampling subsets of N neurons from the RA data, we estimated the average temporal uncertainty in song position as a function of neural population size (Fig. 7) (see Materials and Methods). For populations of ∼30 neurons or larger, the RA ensembles were sufficiently uncorrelated from one another that an observation of the state of these neurons could be used to predict the location in the song motif with 10 ms uncertainty, the time duration over which a typical RA ensemble was active (this does not apply for the stuttered syllables; in this case, the RA firing pattern predicts the location within the syllable but not the motif). On average, each 10 ms slice of the song was associated with a unique pattern of RA neural activity.

Figure 7.

Temporal uncertainty in song position as a function of RA sample size. Each pattern of RA activity specifies a temporal position in the song with a resolution that varies with the number of RA neurons in the sample. With ∼30 neurons, one can predict the temporal position in the song with a resolution comparable with the average RA burst width (∼10 ms).

Thus, one of the remarkable aspects of the activity of RA neurons is the paradoxical observation that RA firing patterns are precisely reproduced with each rendition of the song motif, and yet repetitions of highly similar sounds within a motif are often accompanied by very different firing patterns.

Discussion

By recording large numbers of RA neurons in individual birds, we have observed several striking properties of the RA circuit activity that provide insight into the mechanisms of song control: (1) there is a unique RA ensemble at each moment in the song; (2) RA ensembles change rapidly on a 5-10 ms time scale regardless of the temporal structure of the song; (3) similar subsyllables are associated with uncorrelated RA ensembles; and (4) there is no difference in RA firing patterns during syllables and silent intervals between syllables. Both appear to be active vocal gestures that are under explicit neural control. These findings form the basis of our interpretation that zebra finch song is generated by a dynamic circuit that operates on a single underlying clock which evolves continuously in time steps of 5-10 ms.

The lack of correlation between RA ensembles during repeated sounds is not merely a consequence of the features we used to characterize the song; similar results were obtained with other feature sets (supplementary Fig. 1, available at www.jneurosci.org as supplemental material). Is it possible that some other set of acoustic features would reveal strong correlations between RA spike patterns and vocal output? Only 0.5% of pairs of RA neurons exhibited correlations in their firing rate >0.5, implying that among the ∼8000 RA projection neurons, there are nearly this many uncorrelated patterns of activity. Even neighboring neuron pairs, presumed to be within the same myotopic regions in RA, showed no correlations in their activity patterns. In contrast, analyses of birdsong acoustic structure (Tchernichovski et al., 2000) suggest that the song can be represented by a small number of vocal parameters. If a small number of vocal parameters were encoded by a large number of RA neurons (each of which is correlated with a feature), then we would expect to see strong correlations between pairs of neurons. The weak correlations between neuron pairs suggest that RA neurons are not correlated with specific acoustic features. Note that even if individual RA neurons are causally linked to activity in particular syringeal muscles, the sparseness of burst patterns makes it likely that correlations between single-neuron RA activity and the continuous muscle activity will be small.

RA ensembles are thought to be driven on a short time scale by RA-projecting neurons in HVC (Hahnloser et al., 2002). Just as there is an RA ensemble for each time in the song, we infer that there is a corresponding HVC_(RA) ensemble for each time in the song. Furthermore, because HVC_(RA) neurons burst extremely sparsely, each RA ensemble must be driven by a unique HVC_(RA) ensemble. Figure 8 synthesizes these ideas into a simple model for the generation of RA burst sequences during song production. Interneurons and projection neuron collaterals may eventually be shown to play an important role in shaping RA activity; however, at this point, we adopt a simpler model that does not include these connections.

Figure 8.

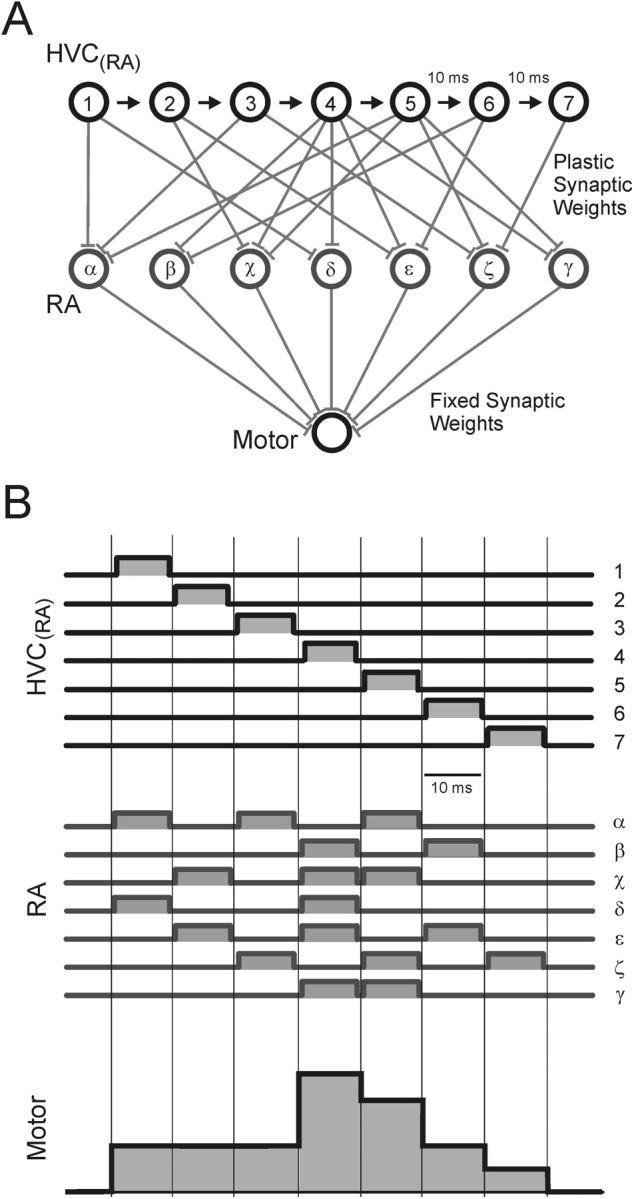
Model of song motor control. A, Working hypothesis for the generation of vocal control signals. Each HVC_(RA) neuron (1-7) bursts at a single time in the song motif. Each of these HVC neurons drives a different subpopulation of RA neurons (α-γ). Activity in RA is then integrated into continuous muscle control signals by the motor unit. Although only one motor output is shown, the model is easily extended to an arbitrary number of outputs. B, Activity patterns in the song motor control model. Discrete and sparse activity in HVC is converted to discrete and dense activity in RA. At each 10 ms time step in the song, a different population of RA neurons is active. Note that constant vocal outputs can be generated by rapidly evolving patterns of RA activity because of convergence and integration from RA to muscles (time steps 1-3). The end-to-end alignment of burst onsets and offsets is for graphical clarity only; it is not known whether burst patterns in populations of RA or HVC_(RA) neurons are organized in this manner.

It is known that repeated song motifs (the entire sequence of syllables) are produced by reactivating the same sequence of HVC and RA ensembles (Yu and Margoliash, 1996; Hahnloser et al., 2002). However, individual syllables can also be repeated at different times within a single motif. Yu and Margoliash (1996) have shown that syllable-length repetitions of vocal patterns may be associated with repeated RA firing patterns. This is similar to the repetition of RA activity we observe during the stuttered syllable of bird 9 (Figs. 1B, d1, d2, d3, 6). Although HVC_(RA) neurons were found to burst only once during a song motif, these recordings were not done in birds that repeated or stuttered song syllables (Hahnloser et al., 2002). The precise reproduction of RA ensembles during stuttered syllables suggests that HVC_(RA) sequences are also reactivated during repeated syllables, a prediction that could be tested by recording from both RA and HVC_(RA) neurons in birds that repeat syllables within the song motif.

With this picture in mind, we return to the fundamental question raised earlier: although the neural dynamics in HVC and RA evolve rapidly on a 5-10 ms time scale, the song itself evolves over a wide range of time scales, sometimes modulating rapidly on a ∼5-10 ms time scale and other times remaining approximately constant for ∼100 ms, as during a harmonic stack. How are the rapidly evolving RA ensembles transformed into continuous vocal patterns? We frame a simple hypothesis in terms of the convergence of RA neurons onto downstream motor circuits.

There are ∼8000 RA neurons that project to the brainstem (Gurney, 1981) and contribute to the activity of approximately seven syringeal muscles (Greenewalt, 1968), a ∼1000:1 convergence. Although the relationship between syringeal muscle forces and vocal output can be complex (Fee et al., 1998), recent dynamical models (Gardner et al., 2001; Mindlin et al., 2003) suggest that in many bird species, song generation is dominated by a small number of muscle control signals that have a fairly direct correspondence to acoustic parameters. Although the precise connectivity between RA neurons and brainstem motor units is not established, it is known that individual RA neurons project to subregions of the hypoglossal motor nucleus (Vicario, 1991), which in turn project to particular vocal muscles. Based on these findings, we consider a simplified view in which vocal parameters such as pitch are effectively generated by the convergent and weighted contributions of RA neuron activity onto the syringeal muscles (Fig. 8). Similar models have been proposed for cortical control of arm movements in primates (Fetz and Cheney, 1980; Todorov, 2000).

The striking relationship we observe between RA activity and song acoustic structure arises naturally from this model. RA outputs are linearly summed to produce vocal control parameters, allowing any pattern of RA activity that sums to the same value to generate the same vocal output. Because of the convergence, there are a large number of uncorrelated RA ensembles that can produce the same sum and, hence, identical sounds; there is a degenerate mapping between RA activity patterns and vocal output. (We use the term degenerate in the same sense that the genetic code is degenerate: different DNA sequences can encode a single amino acid.) A linear summation of RA outputs is not required; any mechanism that transforms the high-dimensional space of RA activity onto the low-dimensional space of muscle activity will produce a degenerate mapping. If 10 uncorrelated RA ensembles that produce the same syringeal configuration are generated in a sequence, the song will have constant acoustic structure for 100 ms (Fig. 8B, time steps 1-3). In this manner, slowly changing vocal control signals can be produced by rapidly changing patterns of RA activity (Fig. 5B,C). Likewise, if two degenerate RA ensembles occurred at different times in the motif, similar sounds could be produced at these different times (Fig. 6, left panel).

Our data suggest that there are two mechanisms by which the bird can repeat the same sound within the song motif: (1) by reactivating the same ensemble of HVC_(RA) neurons and driving the same RA sequence; and (2) by producing the same vocal output two times in a nonrepeating HVC_(RA) sequence that drives degenerate RA sequences. The reason these two mechanisms are used is not clear; however, if the bird must learn to reproduce the same sound within a nonrepeating HVC_(RA) sequence, the degeneracy between RA and the vocal organ makes it highly likely that the RA ensemble learned for each sound will be different. Thus, even during constant vocal outputs, the sequence of learned RA ensembles will evolve continuously on the short time scale, set approximately by the width of the HVC_(RA) bursts.

Degeneracy in the mapping from RA activity to vocal muscle activity can account for our observation that similar subsyllables are associated with different RA ensembles. However, convergence between RA and the vocal muscles is not the only possible source of degeneracy: The same sound could, in principle, be produced by different patterns of muscle activation or different configurations of the vocal organ (Suthers, 1996) in the same way that a given reach trajectory can result from different levels of activation of antagonistic muscles of the arm (Gribble et al., 2003). Convergence anywhere in the pathway from premotor neurons to vocal output would result in an effective many-to-one mapping between neural activity and vocal output.

Our analysis reveals a degenerate mapping between RA firing patterns and acoustic output. However, to definitively demonstrate a degenerate mapping between RA and muscle configuration, one would need to record RA neurons and syringeal EMG signals simultaneously. There may also be time dependencies in the motor pathway downstream from RA, such that the RA sequences required to produce a particular sound may depend on the recent history of the vocal configuration. Although previous results suggest that RA has a short time scale effect on vocal output (∼15 ms) (Fee et al., 2004), the repeated sequences we observe are also fairly short (30-50 ms). Thus, although we cannot completely rule out the importance of these effects, we favor the interpretation that the massive convergence from RA to syringeal muscles results in a many-to-one mapping of RA ensembles to muscle configuration.

We began by asking how the sparse activity in HVC could be transformed into continuous activity in the vocal muscles. One might have expected the time scale of the RA firing patterns to correspond directly to the time scale of song acoustic structure, with slow acoustic modulations produced by slowly changing RA ensembles. However, our data suggest a different solution: motor degeneracy can explain how the same sound can be produced at many different times in the motif by precisely reproduced but uncorrelated patterns of RA activity. The convergent mapping of many different neural ensembles to the same output state allows the dynamics of HVC and RA to operate on a single fast clock yet still generate acoustic modulation over a wide range of time scales. This degeneracy permits many different patterns of HVC to RA connectivity to solve the problem of learning a vocal output and may thereby result in faster or more efficient learning (Fiete et al., 2004).