Visual Control of Burst Priming in the Anesthetized Lateral Geniculate Nucleus

Abstract

Thalamic relay cells fire bursts of action potentials. Once a long hyperpolarization “primes” (deinactivates) the T-type calcium channel, a depolarizing input will “trigger” a calcium spike with a burst of action potentials. During sleep, bursts are frequent, rhythmic, and nonvisual. Bursts have been observed in alert animals, and burst timing is known to carry visual information under light anesthesia. We extend this finding by showing that bursts without visual triggers are rare. Nevertheless, if the channel were primed at random with respect to the stimulus, then bursts would have the same visual significance as single spikes. We find, however, that visual signals influence when the channel is primed. First, natural time-varying stimuli evoke more bursts than white noise. Second, specific visual stimuli reproducibly elicit bursts, whereas others reliably elicit single spikes. Therefore, visual information is encoded by the selective tagging of some responses as bursts. The visual information attributable to visual priming (as distinct from the information attributable to visual triggering of the bursts) was two bits per burst on average. Although bursts are reportedly rare in alert animals, this must be investigated as a function of visual stimulus. Moreover, we propose methods to measure the extent of both visual triggering and visual priming of bursts. Whether or not bursts are rare, our methods could help determine whether bursts in alert animals carry a distinct visual signal.

Introduction

Distinctive bursts of action potentials were noted in the earliest recordings in the lateral geniculate nucleus (LGN) (Hubel and Wiesel, 1961). LGN relay cells fire isolated action potentials during wakefulness or rapid eye-movement sleep and burst rhythmically during slow-wave sleep (Livingstone and Hubel, 1981; Hirsch et al., 1983; McCarley et al., 1983). Slow-wave sleep was also characterized by suppression of visual responses in cortex (Livingstone and Hubel, 1981) and hyperpolarization of LGN relay cells (Hirsch et al., 1983). Hyperpolarization deinactivates (“primes”) the calcium channel that underlies bursts in these cells (Jahnsen and Llinas, 1984). Several studies reported that bursts are rare in alert animals, comprising between 1 and 5% of spikes in the LGN (Guido and Weyand, 1995; Ramcharan et al., 2000; Weyand et al., 2001). These results suggest that bursts are not relevant to the transmission of visual information (Steriade, 2001).

Much of the evidence for a visual function of bursts has come from anesthetized animals. The state of the LGN under anesthesia differs from either sleep or wakefulness. The LGN cells fire bursts, but, unlike sleep, these bursts are arrhythmic and intermingled with single spikes (Guido et al., 1992, 1995; Guido and Weyand, 1995; Mukherjee and Kaplan, 1995; Reinagel et al., 1999). These arrhythmic bursts do not occur at random times; they are “triggered” by visual stimuli. The receptive field properties of bursts and single spikes are similar but distinct, both temporally and spatially (Guido et al., 1992; Reinagel et al., 1999; Kepecs and Lisman, 2003; Rivadulla et al., 2003; Lesica and Stanley, 2004; Alitto et al., 2005). Bursts provide better signal detection, whereas single spikes provide better signal discrimination (Guido et al., 1995). Bursts also transmit visual information with higher coding efficiency than single spikes, although at higher metabolic cost (Reinagel et al., 1999). Therefore, bursts may be important when signal-to-noise is low or may emphasize stimuli that are surprising in a given context (Sherman, 2001a). These results suggest a visual function of bursts in alert animals, even if bursts are infrequent (see Discussion).

LGN bursts are caused by calcium spikes via the T-type calcium channel. The channel is primed by prolonged hyperpolarization, but the calcium spike occurs only when triggered by a depolarizing input (for review, see Perez-Reyes, 2003). Both priming and triggering may depend on both visual and nonvisual inputs: only 10% of the synapses on an LGN relay cell come from retinal ganglion cells, the remainder coming from interneurons, cortical feedback, and nonvisual subcortical areas (Erisir et al., 1997). Previous studies have established that bursts can be visually triggered and suggest that bursts can also be visually primed. Here we explicitly separate the question of visual priming from that of visual triggering.

We find that natural stimuli evoke more bursts than other stimuli, suggesting that visual inputs can influence priming. This paper examines the extent, specificity, and reliability of the visual control of priming. Using information theory, we estimate the visual information specifically attributable to the visual control of priming. Our results support a visual function for bursts and suggest how this hypothesis could be better tested in alert animals.

Parts of this work have been published previously in abstract form (Denning et al., 2003).

Materials and Methods

Surgical preparation. Cats were initially anesthetized with ketamine HCl (20 mg/kg, i.m.), followed by sodium pentothal (2-4 mg · kg^-1 · h^-1, i.v., supplemented as needed). The animals were then ventilated through an endotracheal tube. Electrocardiogram, electroencephalogram, temperature, and expired CO₂ were monitored continuously. Animals were paralyzed with Norcuron (0.3 mg · kg^-1 · h^-1, i.v.). Eyes were refracted, fitted with appropriate contact lenses, and focused on a tangent screen. Electrodes were introduced through a 0.5 cm diameter craniotomy over the LGN. All surgical and experimental procedures were in accordance with National Institutes of Health and United States Department of Agriculture guidelines and were approved by the Harvard Medical Area Standing Committee on Animals.

Electrical recording. Single LGN neurons in the A laminas of the LGN were recorded with either Parylene-coated tungsten electrodes (AM Systems, Everett, WA) or Quartz-coated platinum/tungsten electrodes (System Eckhorn; Thomas Recording, Marburg, Germany). Recorded voltage signals were amplified, filtered, and passed to a personal computer running DataWave Technologies (Longmont, CO) Discovery software, and spike times were determined to 0.1 ms resolution. Preliminary spike discrimination was done during the experiment, but analysis is based on off-line spike sorting after the experiment using custom software. Only well isolated single units were analyzed. All cells used in this analysis were classified as X cells. All additional analysis was performed with custom programs written in the Matlab programming environment (Mathworks, Natick, MA).

Visual stimulation. Both natural and white-noise stimuli were spatially uniform (full-field) visual stimuli, modulated in time. Natural luminance time series were obtained from van Hateren (1997). White-noise stimuli were obtained by drawing independent random samples from the distribution of luminance values in the natural stimulus, thereby eliminating the temporal correlations of the natural stimulus but preserving the distribution of the stimulus intensities. Stimuli were 8-32 s long and were repeated 128 times. Stimuli were presented on either a cathode ray tube (CRT) monitor (128 frames per second; eight-bit grayscale; n = 9 cells) or a custom-made light-emitting diode (LED) display (1200 frames per second; 15-bit grayscale; n = 6 cells). All results reported here were the same for both CRT and LED data, so both are shown and both are included in all averages we report. In particular, stimulus presentation method was not correlated with burst frequency in these experiments.

Burst classification. We define a “burst” as a group of two or more action potentials separated by ≤4 ms, preceded by a period of >100 ms without spiking activity. This criterion was shown previously to reliably identify bursts that are attributable to low-threshold (T-type) calcium spikes in LGN relay cells of the cat (Lu et al., 1992). Subsequent studies (Lu et al., 1993; Ramcharan et al., 2000) have found these classification criteria to be conservative. We repeated our analysis with a less stringent burst criteria (preceding interval, <50 ms; internal interval, <6 ms); this increased our estimated burst frequency only slightly and did not qualitatively change any of the results reported here.

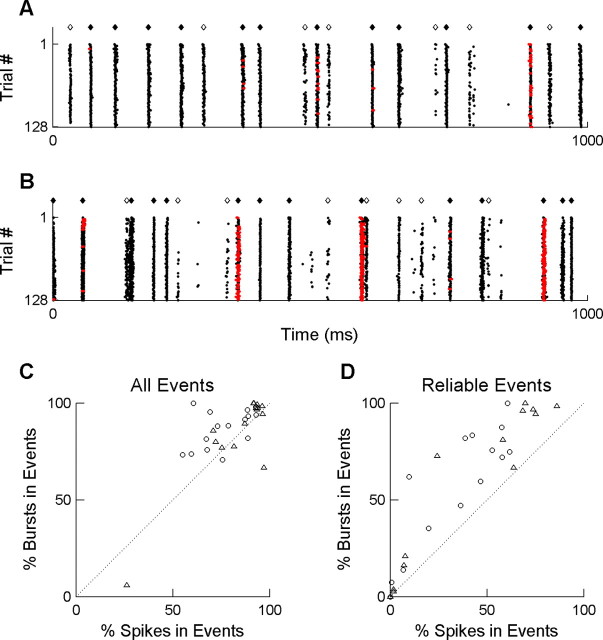
Event classification. We presented the same dynamic stimulus repeatedly for 128 trials and accumulated a peristimulus time histogram (PSTH), which represents the probability of firing as a function of time. We divided this PSTH into discrete firing events by the method of Berry et al. (1997). Briefly, the PSTH was smoothed by a Gaussian filter with σ = 10 ms, which smoothed the PSTH within events but preserved separation between events. In this smoothed PSTH, minima that were deep compared with adjacent maxima were taken as boundaries between distinct events. Specifically, our algorithm required that the minimum was less than or equal to two-thirds of the square root of the product of the adjacent maxima. These boundaries were then used to divide to the original, unsmoothed PSTH into discrete intervals, such that all spikes were assigned to one and only one interval. We excluded from additional analysis any interval that contained spikes in fewer than 10% of the trials. We fit a Gaussian curve to each peak individually and defined the time window of the event as the mean time ± 2σ of this best-fit Gaussian. Spikes that did not fall within any event so defined were classified as nonvisual responses. In the analysis of Figure 2 D only, we separately identified “reliable” firing events using the same method but including only events that contained spikes in at least 80% of trials.

Figure 2.

Visually triggered bursts. A, Raster plot of responses of an LGN neuron to 128 repeats of the same full-field white-noise stimulus. Each row represents a trial; each point represents the time of an action potential in that trial. Red points indicate the action potentials that were classified as being part of a burst (see Materials and Methods). Are presentative 1 s from the middle of an 8 s trial is shown. Diamonds indicate the times at which we classified the response as a visually evoked firing event (cell responded in >10% of trials; see Materials and Methods). Filled diamonds indicate the subset of firing events that were highly reliable (cell responded during the event in >80% of trials). B, Responses of the same neuron to 128 repeats of a full-field stimulus with a time course recorded in nature; all symbols as in A. C, Percentage of isolated spikes (x-axis) versus percentage of bursts (y-axis) that occurred during a visually evoked firing event (⋄ and ♦ in A and B). Each symbol represents results of a response for a single cell to either the natural stimulus (○) or the white-noise stimulus (▵). The dotted line indicates x = y. D, Percentage of isolated spikes (x-axis) versus bursts (y-axis) that occurred in a highly reliable visual event (♦ in A and B). Symbols as in C.

Burst probability and priming probability. We define the burst probability within a visual firing event as the percentage of trials containing a burst within the event time window. Conceptually, we define the probability of priming within a firing event as the fraction of trials in which the T-type calcium channel was deinactivated at the time of the event. Operationally, we estimated this from the fraction of all responding trials that contained a burst.

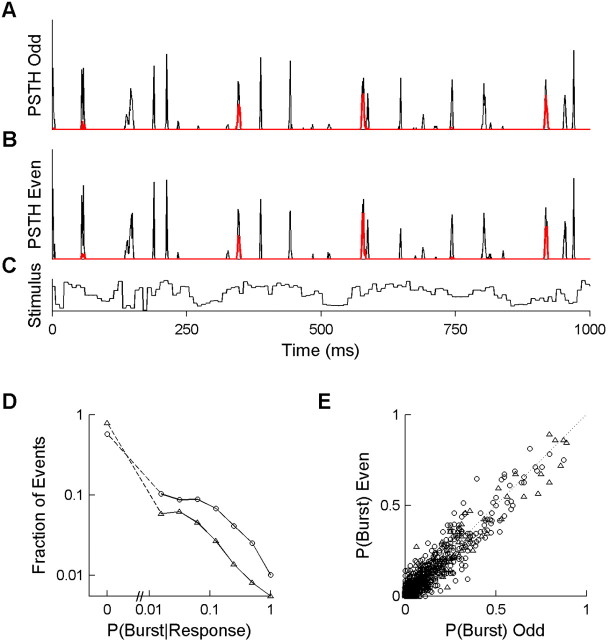
To determine reproducibility of burst probability, we divided the data from each cell and stimulus into two non-overlapping sets: the 64 odd-numbered trials and the 64 even-numbered trials. For each visual firing event as defined above, we determined the burst probability for each half of the data. These two independent estimates are compared in Figure 4 E. We also computed the probability of priming separately in the two data sets; the estimates were similarly well correlated (data not shown).

Figure 4.

Discrete firing events have reproducible, intermediate burst probabilities. A, PSTH of all spikes (thin black curve) and of the subset of spikes that were classified as bursts (thick red curve), derived from the 64 odd-numbered trials of the raster shown in Figure 2 B. B, PSTH as in A but from the 64 even-numbered trials. Events have a similar probability of bursting in both independent estimates. C, Luminance time course of the visual stimulus corresponding to the responses shown in A and B. The stimulus was drawn from the natural ensemble, and the cell was an ON cell with a 29 ms latency to peak response. D, Distribution of priming probabilities of firing events, pooled over all cells (n = 15). For each visual firing event (PSTH peak), the priming probability was defined as the probability of a burst given that any response was observed, P (Burst Response) (see Materials and Methods). Results are shown for both the natural stimulus (○; n = 3444 events) and the white-noise stimulus (Δ; n = 2342 events). The broken axis and dashed lines are used to show the fraction of events with P (Burst Response) = 0, which cannot be shown on the log scale. E, The absolute probability of bursting for each firing event, P(Burst), is defined as the probability across trials of observing a burst within the time of the event. Independent estimates from the odd trials (x-axis) and even trials (y-axis) are compared to assess reproducibility of our estimates. If burst probability was perfectly reproducible, points would lie on the identity line (dotted line). The majority of firing events had no bursts in 128 trials and therefore are plotted at the origin (n = 2575 events for natural; n = 2087 events for white noise).

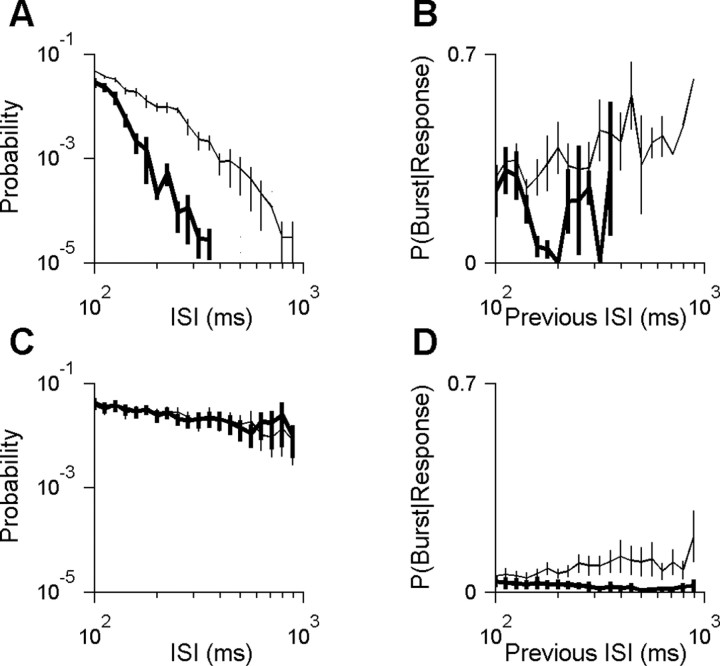
In Figure 5, B and D, the priming probability was determined as a function of the preceding interspike interval, without reference to identified firing events. In this case, priming probability is defined as the percentage of all of the responses with a given preceding interspike interval that were bursts.

Figure 5.

Stimulus-dependent burst rate is explained by two causes. A, The interspike interval (ISI) distribution for all cells with high burst rates (n = 4 cells with burst rates between 0.75 and 1.08 bursts per second in response to natural stimuli). Probability is defined as the absolute probability of a given interval length among all intervals, excluding within-burst intervals. Distributions were averaged across cells for either natural stimuli (thin curve) or white noise stimuli (thick curve). Only long intervals (>100 ms) are shown. Short intervals (≤100 ms) constituted 79 and 92% of intervals during the natural and white-noise stimuli, respectively. Responses to natural scenes had many more of the long intervals required to prime the channel. B, The probability of priming as a function of the previous interspike interval for the cells shown in A (see Materials and Methods). C, Interspike interval distribution as in A but for the group of all cells with intermediate burst rates (n = 7 cells with burst rates between 0.095 and 0.75 bursts per second). Short interspike intervals (≤100 ms; data not shown) constituted 54 and 53% of intervals during natural and white-noise stimuli, respectively. There is no difference in interspike interval distribution to explain why the natural stimuli evoked more bursts. D, The probability of priming as a function of the previous interspike interval as in B but for the cells shown in C. These cells were more likely to prime the T-type calcium channel after a given period of inactivity if the stimulus had natural temporal structure as opposed to white noise.

Information calculations. Our recorded neural data were represented as time-binned spike trains; in this study, a fixed bin size of δτ = 2 ms was used. The value in a time bin was set to zero if no spikes occurred during that time interval, one if a single spike occurred during that time interval, or two if the first spike of a burst occurred during that time interval. Only the first spike of each burst was represented. Because of the refractory period of the cells, the occurrence of two spikes in the same time bin was so rare as to be negligible.

We calculated the visual information in spike trains by the direct method (Strong et al., 1998), implemented exactly as by Reinagel and Reid (2000). Briefly, we analyzed the information contained in words (short strings of bins) and varied the number of bins in the words, L. For each word length, we measured two forms of word entropy: the average noise entropy, <H_noise>, which reflects the trial-to-trial variability of words when the stimulus was fixed, and the average total entropy, <H_total>, which reflects the variability of words across all stimuli in the ensemble. H_noise(t) was calculated from the distribution of words at a fixed time t relative to stimulus onset, in 128 repeats of the same sample of the stimulus. We performed a separate calculation of H_noise(t) for many different values of t (separated by one bin) within the 8 or 32 s stimuli. We then averaged over t to get the average noise entropy <H_noise>. We performed equally many separate calculations of H_total(i), but the set of words was instead selected using a different time t from each trial. We used 256 words for each single estimate of H_total(i) to compensate for the approximately twofold difference in entropy. We averaged over i get the average total entropy <H_total>. Finally, the mutual information between the visual stimulus and the spike train is defined as I = <H_total>-<H_noise>. We computed information as a function of word length. We extrapolated to infinite word length from the linear part of the curve H versus 1/L as described by Strong et al. (1998).

Extrapolation to infinite word length should, in principle, provide the best estimate of the total information, but the linear part of the curve was difficult to identify in some of our data. Therefore, we show results using a fixed word length of L = 8. We obtained similar results for infinite word lengths using L = [6,8,12] as the basis for extrapolation.

Data adequacy for entropy calculations. For all entropy estimates that we computed, we determined how our estimate of H converged as we used increasing fractions of the data and then corrected for finite data size according to the method of Strong et al. (1998). The correction is obtained by fitting a second-order polynomial to 1/(fraction of data) versus estimate. We are confident of our estimates when the total correction for finite data size was <10% and the second-order term of this correction was negligible, <1%. Results that passed these criteria are shown with filled symbols in Figure 6. For completeness, we also show our results from cells that did not pass the criteria (Fig. 6, open symbols).

Figure 6.

Visual information encoded by the state of the cell. A, The state information I_state is that visual information that can only be decoded by identifying which of the visually triggered responses were bursts (see Materials and Methods). Each symbol shows I_state in units of bits per second for the responses of one cell to the white-noise stimulus (x-axis) versus the natural stimulus (y-axis). The symbol size is proportional to the burst rate of the cell, averaged across the two stimulus conditions. Dotted lines indicate x = 0, y = 0, and x = y. Information rate estimates were empirically corrected for finite data size (see Materials and Methods). Filled symbols indicate cells for which this correction was small and linear under both stimulus conditions. Open symbols indicate cells that did not pass this criterion. Results shown are for spike trains binned at 2 ms resolution and words of length 8 bins; extrapolating to infinite word length gave qualitatively similar results. B, The state information expressed in bits per burst (I_state in bits per second divided by burst rate in bursts per second) compared with the trigger information expressed in bits per response (I_trigger in bits per second divided by response rate in responses per second, in which a response is either a single spike or an entire burst). Each symbol represents the response of a single cell to either the natural stimulus (○) or the white-noise stimulus (Δ). The symbol size is proportional to the burst rate of the cell for that stimulus. Filled and open symbols defined as in A. Calculation parameters as in A.

Results

We recorded from 15 neurons in the LGN of barbiturate-anesthetized cats during presentation of two different full-field visual stimuli: one that varied according to a naturally recorded time sequence (natural) and one that flickered randomly (white noise).

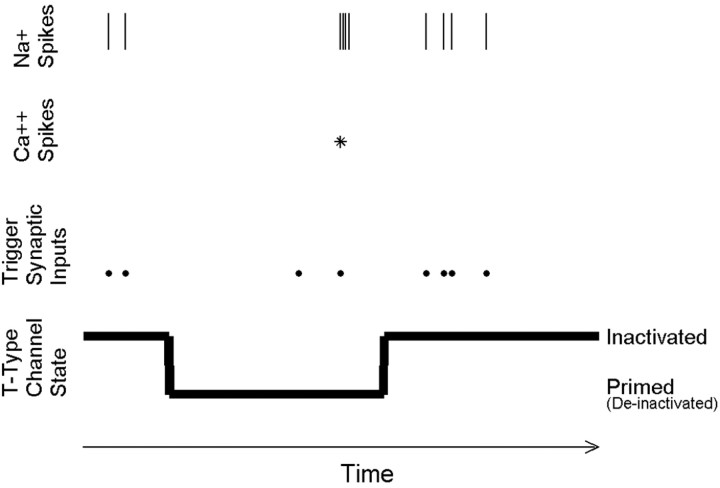
Throughout our analysis, we will refer to a simplified model in which the T-type calcium channels of a given LGN relay cell are either fully inactivated or fully primed. Each relay neuron can therefore be described as having a binary “state” that is defined at each moment in time. In the unprimed state, if a depolarizing input (trigger) causes the neuron to cross threshold, the LGN cell will fire a single action potential. In the primed state, the same depolarization would trigger instead a calcium spike via the T-type calcium channel and thus a burst of action potentials (Fig. 1). Although this is an oversimplification, it allows us to clearly separate the question of the visual control of priming from the visual control of triggering.

Figure 1.

A simplified conceptual model of LGN firing modes. Each LGN neuron at any given time is assumed to be in one of two binary states, depending on whether the T-type calcium channels are primed or inactivated. When we observe an isolated action potential in an extracellular recording, we infer that a retinal synaptic input most likely triggered the response and that the T-type calcium channels in the LGN cell were inactivated at the time. When we observe a burst of appropriate structure, we infer that a retinal input triggered a calcium spike, and therefore, the T-type calcium channels must have been primed. We note that we are ignorant of both retinal inputs and the state of the T-type calcium channels at other times.

Bursts occur and are visually triggered

Other studies have shown that bursts can be visually triggered. In LGN responses to white-noise flicker, the average stimulus preceding a burst (the burst-triggered average) reveals that bursts occur in response to luminance transients. Bursts and single spikes are triggered by similar features, with some significant differences (Reinagel et al., 1999; Kepecs and Lisman, 2003; Rivadulla et al., 2003; Lesica and Stanley, 2004; Alitto et al., 2005). Although reverse correlation can establish that many bursts are visually triggered, in general, this method cannot exclude the presence of additional, nonvisual bursts. To determine what fraction of bursts are visually triggered, it is necessary to determine for each individual burst whether it was visually evoked or random.

To answer this question, we made use of the fact that we repeated the identical visual stimulus 128 times. We defined a visual firing event as a discrete time interval relative to the stimulus during which spikes occurred in at least 10% of trials (Fig. 2A,B, open and filled diamonds) (see Materials and Methods). We identified putative T-type calcium bursts in our recordings by conventional interspike interval criteria (see Materials and Methods). In this paper, we will use the term “response” to refer to either a single spike or an entire burst. In accordance with other studies in anesthetized animals, we found stereotyped bursts intermingled among single action potentials (Fig. 2A,B).

Averaging over both stimuli, 86 ± 18% (mean ± SD) of bursts occurred during a visual firing event as defined by our criterion (Fig. 2C). Similarly, 80 ± 16% of single spikes occurred during a visual firing event. Given that visual firing events comprised only 22 ± 14% of the time in the trial, we would expect only ∼22% of bursts to fall in visual firing events by chance.

In the data shown in Figure 2, A and B, all of the bursts occurred during particularly reliable firing events. To test the generality of this finding, we determined what fraction of bursts and single spikes were restricted to the most reliable visual firing events [stimulus-locked activity that occurred in >80% of trials (filled diamonds)]. For every cell in our sample, regardless of the visual stimulus, we consistently found that bursts were more likely than single spikes to occur during a high-reliability firing event (Fig. 2D).

Burst frequency depends on visual stimulus

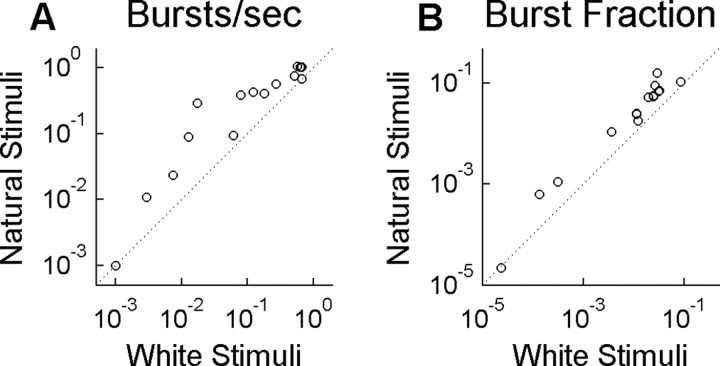
LGN cells fired more bursts per second during the natural visual stimulus than during the white noise-stimulus (Fig. 3A). A similar result was found by others comparing spatiotemporal natural movies with spatiotemporal white noise (Lesica and Stanley, 2004). The increase in bursts during our natural stimulus was not attributable to a general increase in firing rate: a higher fraction of all responses were bursts when the natural stimulus was shown (Fig. 3B). The fact that some types of stimuli elicit more bursts than others is strong evidence that visual inputs can influence the priming of the channel and thus the state of the cell, at least on average.

Figure 3.

Burst rate is higher for naturalistic stimulus. Fifteen LGN neurons were presented two different stimulus ensembles: one having a natural temporal modulation (Natural Stimuli) and the other having a random modulation (White Stimuli). Both stimuli were spatially uniform across the visual field. Each symbol represents results for a single cell under the two stimulus conditions. A, Burst rate, in bursts per second. B, The fraction of all responses that were bursts, in which a response is defined as either a single spike or an entire burst.

The burst state is primed at reproducible times

If the probability of priming is determined only by average stimulus properties, it should be approximately constant over time within a stimulus. Alternatively, if priming is determined by specific temporal features in the visual stimulus, we would expect that burst probability would vary across firing events. In our data, we found that bursts occurred in a specific subset of firing events (Fig. 4A, red curve) (see also Fig. 2A,B, red points).

Most firing events had a zero probability of a primed burst state at the time of the visual trigger. For example, the cell shown in Figure 4, A and B, responded with 163 stimulus-locked firing events over 8 s. Of these events, 104 excluded bursts (no bursts in 128 trials). In other firing events, the same cell had as high as 83% chance of being in the primed state when the visual trigger occurred (106 of 128 trials had a burst within the time window of a single firing event). Other visually triggered events had an intermediate, but reproducible, probability of the primed state (Fig. 4, compare A, B). Our findings are in agreement with other studies using different visual stimuli (Lesica and Stanley, 2004; Alitto et al., 2005). This result shows that the recent stimulus can reproducibly set the probability that the cell will be primed at the time of each visual trigger.

To summarize the result for all cells in our population, we estimated the probability of the primed state during a given firing event by the proportion of the responses that were bursts (the number of trials that burst during the event divided by the number of all trials with any spikes during the event). Across all cells, most firing events had 0% probability of the primed state, but this probability was as high as 94% for some individual firing events (Fig. 4D). As expected, more firing events contained bursts in the naturalstimulus experiment (Fig. 4D, compare the two curves). The absolute probability of firing a burst within a firing event ranged from 0 to 89% (Fig. 4E). Two independent subsets of the data gave highly correlated estimates of the burst probability (Fig. 4E, symbols lie near the line x = y). The probability of the primed state (Fig. 4D) was also reproducible in independent samples (data not shown).

Relationship of burst rate to the frequency of long silences

Biophysically, priming of the T-type channel requires a prolonged hyperpolarization (50-100 ms without any action potentials). Operationally, our definition of a burst requires >100 ms with no spikes before the burst. The simplest explanation for the increase of bursting during natural stimuli would be that the required long silences occurred more often. Alternatively, one could imagine that long interspike intervals were equally likely under both stimulus conditions but that the probability of priming during that interval is higher during natural stimuli, for example, because the cell was hyperpolarized more deeply and/or more continuously. A mixture of both causes is also possible. To test each of these possibilities, we examined the probability of long intervals as well as the conditional probability of priming given that a long interval has occurred.

Our population of cells could be divided into three groups according to their burst frequency. The first group of cells had the highest burst frequencies in our population (0.75 < x < 1.08 bursts per second; n = 4 cells). This group of cells was also distinguished by the fact that responses to natural stimuli had significantly more long interspike intervals than responses to white noise (average shown in Fig. 5A). For these cells, the higher frequency of long intervals could explain the higher burst frequency observed with natural stimuli.

The second group of cells had intermediate burst frequencies (0.095 < x < 0.75 bursts per second; n = 7 cells). In every cell in this group, the probability of long interspike intervals was similar under both stimulus conditions (average shown in Fig. 5C). Therefore, the frequency of long intervals could not explain the higher burst frequency of responses to natural stimuli. Instead, we found that, under natural stimulation, these cells had a greater probability of bursting after a long silence (Fig. 5D). We observed a similar trend in the first (high-bursting) group, but the result was statistically significant only for a few interval lengths (Fig. 5B). Shorter intervals are not expected to show an effect (compare with Fig. 5D), whereas longer intervals were too rare in white-noise responses (Fig. 5A) to allow an accurate estimate.

Finally, the third group consisted of the four cells with the lowest burst frequencies in our population (<0.095 bursts per second for our natural stimulus). This group was heterogeneous with respect to the relative likelihood of long interspike intervals in the two stimulus conditions (data not shown). The conditional probability of bursting after a long interval could not be determined because of the rarity of the bursts.

Visual information encoded by priming

The results presented above show that visual stimuli influence the probability of priming of the T-type channel in the LGN. It follows that some extra visual information is transmitted by the LGN as a result of having two states (primed and unprimed) with distinguishable outputs (bursts and single spikes). To estimate how much visual information is specifically attributable to priming, we asked how much information is present in the LGN spike train when bursts and single spikes are distinguished versus when they are not.

First, we identified the bursts in our recorded spike trains. We created a surrogate spike train in which each single spike was denoted by one symbol at the time of the spike, and each identified burst was denoted by a different symbol at the time of the first spike in the burst (see Materials and Methods). This “identified response train” retains information about the time of the triggers, as well as information about the state of the neuron at the time of the trigger (i.e., which responses were bursts), but it contains no additional information about the structure of the burst (number of spikes or interspike intervals within the burst). For purposes of this analysis, we will neglect any additional information that might be contained in burst structure. We will consider the information in the identified response train to be the total information in the LGN spike train, I_total.

We created a second “control response train” by randomizing which of the responses were labeled with the burst symbol. The control response train is matched for the frequencies of the two symbols and thus has the same overall burst rate. The control response train lacks any temporal information about the state of the cell (primed or unprimed) but retains all information about when responses occurred, i.e., when the triggering inputs occurred. Therefore, we interpret the information rate in this control response train as the information attributable to triggering alone, which we denote I_trigger.

We define the “state information” as the amount of visual information that was lost when the distinction between single spikes and bursts was removed: I_state = I_total - I_trigger. This is the information potentially transmitted to cortex solely by virtue of the ability of bursts to reveal the subthreshold state of an LGN neuron, information that could not have been transmitted if bursts did not occur.

We found that the state information I_state depended on the overall burst rate: cells with more bursts transmitted more information through the state variable (Fig. 6A, larger symbols are farther from the origin). The state information, I_state, was as high as 3.7 bits per second in experiments using the more natural stimuli. We emphasize that this is the visual information bursts transmitted by reporting the state of the LGN cell (primed vs unprimed), independent of and in addition to the information that bursts carried about triggering stimulus (response vs no response).

For most cells, I_state was greater for natural stimuli than white-noise stimuli (most symbols are above the diagonal; p < 0.05 by Wilcoxon's signed-rank test). The fraction of the total information carried by state (I_state/I_total) was also greater for the natural stimuli (p < 0.001). We find that the state information I_state measured in bits per burst was comparable to the trigger information I_trigger measured in bits per response (Fig. 6B).

Discussion

It has long been suggested that thalamic bursts may have a role in gating the flow of visual information to cortex (Singer, 1977; Crick, 1984; Sherman and Koch, 1986; McCormick and Feeser, 1990; Guido and Lu, 1995). It has remained controversial whether bursts occur or function during visual awareness (Sherman, 2001b; Steriade, 2001). In this study, we analyzed the visual properties of bursts that occur intermingled with single spikes under conditions of light anesthesia.

Almost all bursts are visually triggered

Previous studies have shown that the average spike and the average burst are visually triggered as opposed to being triggered by nonvisual inputs or noise (Reinagel et al., 1999; Kepecs and Lisman, 2003; Rivadulla et al., 2003; Lesica and Stanley, 2004; Alitto et al., 2005). Using binary white-noise visual stimuli, reverse correlation analysis revealed that almost every burst is preceded by a specific stimulus value at the peak spatial location and temporal delay, implying that few if any bursts are triggered by nonvisual inputs (Alitto et al., 2005). In our study, we used low-contrast grayscale stimuli, and the average stimulus preceding a spike or burst was always an intermediate luminance at all latencies. In this case, the spike-triggered average does not reveal the fraction of bursts that were visually triggered. Instead, we defined a response as visually triggered if it occurred during a brief time window that contained a reliable stimulus-locked firing events (Fig. 2). For both natural temporal flicker and white noise, most bursts were visually triggered by this criterion. Indeed, bursts were even more likely than single spikes to occur within a visual firing event. This result further demonstrates that these bursts are not driven by anesthesia-induced rhythms.

Visual stimuli influence the average probability of priming

Even if every burst were triggered by a visual stimulus, bursts could be merely interchangeable with single spikes. However, if the priming of the T-type calcium channel is visually controlled, a decoder could extract visual information by selectively responding to bursts. Thus, bursting could allow LGN neurons to multiplex two different streams of visual information in a single spike train.

Consistent with the second possibility, other studies found average burst frequencies to depend on parameters of simple stimuli, such as sinusoidal gratings (Grubb and Thompson, 2005) or flashing squares (Weyand et al., 2001). We report that LGN neurons are more likely to burst when visual stimuli contain temporal structure of natural scenes (Fig. 3) compared with white-noise stimuli, in agreement with other studies (Lesica and Stanley, 2004). Although we only tested one example of a natural stimulus, its spectrum was typical of natural stimuli in that power was inversely proportional to frequency (van Hateren, 1997). Random stimuli with a 1/f power spectrum caused intermediate burst frequencies (data not shown), showing that the phase alignment found in natural stimuli is important for the efficiency of priming. Our interpretation is that temporal stimulus features that prime the burst state (i.e., deinactivate the T-type calcium channel) are more prevalent in at least some natural scenes. The fact that some stimuli evoke more bursts than others is strong evidence that priming is visually controlled.

Visual control of the timing of state transitions

For both stimuli tested, we found that bursts occurred during specific firing events and not others (Fig. 4). We conclude that specific temporal sequences in the visual stimuli determine the probability of the primed state. Thus, downstream cortical neurons could detect the internal state of presynaptic LGN neurons by detecting the stereotyped interspike intervals of bursts, just as we have done in our analysis.

An integrate-and-(fire or burst) model predicts time-varying firing rates in the LGN significantly better than a model that lacks bursts (Lesica and Stanley, 2004). Nevertheless, we still cannot accurately predict the probability of priming at each firing event. This will probably require taking into account additional nonlinear dependencies on the visual stimulus.

Our experiment does not address the spatial information encoded by bursting (but see Rivadulla et al., 2003; Alitto et al., 2005). We also have not determined the specific temporal stimulus features that predict the probability of priming. Others have shown that the average stimulus preceding a burst has a longer and stronger inhibitory phase preceding the excitatory trigger, consistent with the idea that inhibitory visual stimuli prime the T-type calcium channel (Lesica and Stanley, 2004; Alitto et al., 2005). Our approach is complementary to reverse correlation analysis, which cannot separate whether bursts are visually primed or whether the cell in the primed state has different triggering requirements.

The length of the preceding interval is not sufficient to predict priming

Prolonged hyperpolarization is required to prime the burst state. All cells in our study burst more during natural stimuli than white-noise stimuli. We wondered whether this could be accounted for by a higher likelihood of long periods without spikes during the more slowly modulated natural stimuli.

For all cells with high burst rates, natural stimuli evoked responses with more long silences (periods without spikes) (Fig. 5A,B). In cells with low burst rates, however, long silences were equally likely for both stimuli; instead, the conditional probability of a burst given a long silence was higher if the stimulus had a natural time course (Fig. 5C,D). We conclude that the length of the preceding interval is not always sufficient to predict when bursts occur. We speculate that the natural stimulus either hyper-polarized the cells more deeply on average during the silent interval or hyperpolarized them more continuously. A direct test of this hypothesis will require in vivo intracellular recording of the LGN during visual stimulation.

Several cells essentially never fired bursts, regardless of the duration of the preceding interval. We cannot exclude the possibility that these units are inhibitory interneurons, although we have no specific reason to think so. Relay cells vary in their intrinsic tendency to burst (Weyand et al., 2001), perhaps because of different expression levels of the T-type calcium channel.

Information carried by state

Given that some visual stimulus sequences reliably prime the channel and others reliably prevent priming, the state of the cell necessarily encodes visual information. We found that up to 3.7 bits per second of visual information was carried by state as such, as distinct from and in addition to the information carried by the times of triggered spikes and bursts (Fig. 6). This information is accessible for decoding because cortical neurons can differentially respond to bursts (Usrey et al., 2000; Swadlow and Gusev, 2001).

Not surprisingly, cells with higher burst frequencies carried more state information. Responses to natural scenes had more bursts, and a greater fraction of the total visual information was carried in the state information compared with the responses to white noise.

Our analysis made the simplifying approximation that the state of the neuron is binary (Fig. 1). Intermediate priming states could be revealed by variability in burst structure (Kepecs and Lisman, 2003), potentially encoding even more information. Our cells, however, had relatively little variability in burst structure.

The state presumably encodes information about the visual history preceding the triggering stimulus feature, as others have suggested. Some information about visual history is encoded in the length of the preceding interspike interval. Still, it may be easier for downstream cortical cells to detect bursts than to keep track of long silences. Moreover, the preceding interval is not sufficient to determine whether an LGN cell will fire a burst (Fig. 5). Therefore, the state can encode additional information about the visual stimulus that could not be determined from the duration of the previous interval.

Are bursts important for vision?

Our results do not settle whether bursts are used for visual processing. At least some bursts occur in the LGN of alert animals (Guido and Weyand, 1995; Ramcharan et al., 2000; Ramcharan et al., 2001; Weyand et al., 2001; Martinez-Conde et al., 2002). Bursts have also been observed in thalamic relays of other sensory pathways in alert animals (Fanselow et al., 2001; Massaux et al., 2004). Although bursts are less frequent in alert than anesthetized animals, our results show that natural stimuli may be especially likely to elicit bursts. Therefore, it will be important to measure burst frequency in alert animals during natural visual stimulation. Even if bursts are rare, they could be important signals when they occur.

We addressed only the visual information encoded by state. State could also encode behaviorally relevant nonvisual information. Burst frequency correlates with global levels of arousal (Livingstone and Hubel, 1981; Hirsch et al., 1983; McCarley et al., 1983; Guido and Weyand, 1995; Weyand et al., 2001), and burst timing also correlates with specific behavioral states or events (Ramcharan et al., 2001; Martinez-Conde et al., 2002).

The fact that bursts are visually triggered only establishes that the T-type calcium channel does not interfere with visual transmission. To claim that bursts serve a distinctive function, it must also be shown that bursts and single spikes represent distinct visual inputs or behavioral conditions. Our data show that visual stimuli can control the priming of T-type calcium channels in LGN relay cells of anesthetized animals. If the same proves true in alert animals, bursts could serve a visual function by relaying information to cortex about subthreshold states in the thalamus.