Robustness of Burst Firing in Dissociated Purkinje Neurons with Acute or Long-Term Reductions in Sodium Conductance

Abstract

Cerebellar Purkinje neurons often generate all-or-none burst firing in response to depolarizing stimuli. Voltage-clamp experiments using action potential waveforms show that burst firing depends on small net inward currents that flow after spikes and reflect the net balance between multiple large currents. Given this, burst firing is surprisingly robust in the face of changes in the magnitude of the underlying currents from cell to cell. We explored the basis of this robustness by examining the effects of reducing the sodium current, the major contributor to the postspike inward current. Burst firing persisted in concentrations of tetrodotoxin that produced half-block of sodium current. This robustness of bursting reflects an acute feedback mechanism whereby waveform changes from the reduced sodium current (reduced spike height and a hyperpolarizing shift in postspike voltage) cause compensatory decreases in postspike potassium currents. In particular, reduced spike height reduces calcium entry and subsequent calcium-activated potassium current, and the hyperpolarizing shift in postspike voltage speeds deactivation of Kv3-like potassium channels. Other experiments examined bursting in Na_v1.6^-/- mice, in which sodium current density is reduced in the long term. Under these circumstances, there was upregulation of both T-type and P-type calcium current and a change in the balance of calcium current and calcium-activated potassium current such that their net influence shifted from being inhibitory during bursts in wild-type neurons to excitatory during bursts from Na_v1.6^-/- mutant neurons. Thus, Purkinje neurons have both acute and long-term feedback mechanisms that serve to maintain burst firing when voltage-dependent sodium conductance is reduced.

Introduction

Neurons express many types of ion channels carrying currents that combine to determine the firing pattern of each particular neuron. An important question is how tightly regulated the expression of each channel type must be to maintain the characteristic input-output properties of a neuron. In the crab stomatogastric ganglion, individual neurons with very similar firing properties can have densities of individual currents that vary over severalfold (Liu et al., 1998; Golowasch et al., 1999, 2002), even for currents that are clearly important for the output characteristics. On the other hand, the firing patterns of individual neurons can be affected dramatically by relatively small changes in a particular conductance (Burdakov and Ashcroft, 2002). These properties are not contradictory because, in principle, a large change in one conductance may produce little change in firing properties if accompanied by suitable changes in other conductances (Goldman et al., 2001; MacLean et al., 2003).

We investigated how firing patterns of cerebellar Purkinje neurons depend on the density of particular ionic currents. Purkinje neurons offer a well defined and easily quantified behavior, all-or-none burst firing, which occurs not only in response to climbing fiber stimulation (Eccles et al., 1966) but also in response to depolarizing current injections or anode break (Callaway and Ross, 1997; Cavelier et al., 2002) and even spontaneously (Cingolani et al., 2002; Womack and Khodakhah, 2002). Burst firing apparently reflects intrinsic membrane properties of Purkinje neurons, because it is present even in acutely dissociated Purkinje neurons (Raman and Bean, 1997; Raman et al., 1997). Using this preparation, which allows the underlying ionic currents to be studied under voltage clamp, we found that after the first spike of a burst, multiple large inward and outward components sum to give a small net inward current (Swensen and Bean, 2003) that drives the depolarization leading to a subsequent spike. These results suggest a fine balance of postspike currents in which a small change in the size of any individual current, through slow inactivation, modulation, or other perturbation, could have dramatic effects on bursting.

Relating channel density to firing properties is inherently difficult because of the complicated interactions between multiple voltage-dependent currents. Mathematical modeling is one approach, but it requires knowledge of the kinetics and voltage dependence of all channels in the cell. If cells can be voltage clamped on the time scale of the action potential, an experimental approach is possible, using the action potential clamp technique to quantify the ionic currents flowing during natural firing. We took this approach using dissociated cerebellar Purkinje neurons to explore the consequences for burst firing of both acute and long-term reductions in the sodium current. The results demonstrate acute feedback mechanisms acting to preserve burst firing in the face of the reduced sodium current, as well as different long-term mechanisms based on changes in the expression of the calcium current and its coupling to the calcium-activated potassium current. The existence of both acute and long-term mechanisms tending to preserve burst firing suggest its importance for the proper physiological function of Purkinje neurons.

Materials and Methods

Cell preparation. Experiments were performed on mouse cerebellar Purkinje neurons enzymatically isolated with dissociation techniques similar to those described previously (Raman et al., 1997; Swensen and Bean, 2003). Mice (postnatal days 13-17) were anesthetized with isoflurane (Abbott Laboratories, North Chicago, IL) and decapitated, and cerebella were dissected out and minced in ice-cold dissociation solution containing the following (in mm): 82 Na₂SO₄, 30 K₂SO₄, 5 MgCl₂, 10 HEPES, 10 glucose, and 0.001% phenol red, buffered to pH 7.4 with NaOH. The tissue was then transferred to 10 ml of room-temperature dissociation solution containing 2.5 mg/ml protease XXIII (pH 7.4 with NaOH) and subsequently incubated at 33°C for 7-9 min. After incubation, the tissue was washed in ice-cold dissociation solution containing 1 mg/ml bovine serum albumin and 1 mg/ml trypsin inhibitor and maintained on ice in either dissociation solution or a sucrose-based solution containing the following (in mm): 30 Na₂SO₄, 2 K₂SO₄, 0.3 CaCl₂, 5 MgCl₂, 10 HEPES, 10 glucose, and 185 sucrose, pH 7.4 with NaOH. Tissue was withdrawn as needed and triturated with a fire-polished Pasteur pipette to liberate individual neurons. Purkinje cells were identified by their large diameter and characteristic pear shape attributable to the stump of the dendritic tree.

Electrophysiology. Recordings were made using an Axopatch 200A amplifier (Axon Instruments, Foster City, CA). Electrodes were pulled from borosilicate glass micropipettes (VWR Scientific, West Chester, PA) and had resistances from 1.5 to 3 MΩ when filled with the internal solution, which consisted of the following (in mm): 122 K-gluconate (Kgluc), 9 NaCl, 1.8 MgCl₂, 0.9 EGTA, 9 HEPES, 14 Tris-creatine PO₄, 4 MgATP, and 0.3 Tris-GTP, pH 7.4 with KOH. Electrode shanks were wrapped with Parafilm (American National Can, Greenwich, CT) to within several hundreds of micrometers of the tip to reduce capacitance. Reported membrane potentials are corrected for a -10 mV liquid junction potential between the internal solution and the Tyrode's solution in which the current was zeroed before sealing onto the cell, measured using a flowing 3 m KCl bridge as described by Neher (1992).

K gluc was used as the primary internal anion because it seemed especially favorable for formation of high-resistance seals. In some preparations, intracellular K gluc has been reported to inhibit some ion channels, including calcium-activated potassium channels (Velumian et al., 1997). However, in a previous series of experiments, we saw no difference in the magnitude of calcium-activated potassium current when potassium methanesulfonate was used instead of K gluc in recordings from isolated Purkinje neurons (Swensen and Bean, 2003).

After establishing the whole-cell recording, cells were lifted and placed in front of a row of flow pipes. The control physiological Tyrode's solution consisted of the following (in mm): 155 NaCl, 4 KCl, 2 CaCl₂, 2 MgCl₂, and 10 HEPES, pH 7.4 with ∼5 NaOH. With the amplifier in fast current-clamp mode, steady holding current was applied to hyperpolarize the cells enough to stop spontaneous firing (typically to near -90 mV), and action potentials were elicited by a series of 1 ms current injections of incrementing amplitude, which elicited all-or-none firing of a burst. The amplifier was then switched to voltage-clamp mode, and the recorded burst was used as a command voltage. In voltage-clamp mode, cell capacitance was nulled electronically using the circuitry in the amplifier, and series resistance, which ranged from 2 to 6 MΩ, was compensated by 70-85%. Experiments were done at 22-24°C.

To quantify individual ionic currents flowing during the burst, cells were moved between a series of flow pipes containing different solutions, and the command waveform was repeated in each solution. The sodium current was obtained as the current sensitive to 500 nm or 1 μm TTX and was studied with reduced NaCl (25 or 50 mm) in the external solution to minimize series resistance errors, with tetraethylammonium chloride (TEACl; 130 or 105 mm) replacing the sodium omitted. The calcium current was obtained by subtracting currents before and after replacement of 2 mm Ca²⁺ by 2 mm Mg²⁺, with both solutions containing 105 or 130 mm TEA to block potassium currents. Pharmacological dissection of the interspike calcium current was performed using 300 nm ω-Aga-IVA to block the P-type calcium current (Mintz et al., 1992a,b), followed by 10 μm mibefradil to block the T-type current. Mibefradil was always applied after ω-Aga-IVA had blocked the P-type calcium current so as to minimize errors from the effect of mibefradil on P-type channels (McDonough and Bean, 1998). In both Na_v1.6^+/+ and Na_v1.6^-/- neurons, the calcium current remaining after application of ω-Aga-IVA appeared to be purely T-type, with fast and complete inactivation for steps positive to -50 mV and slow kinetics of deactivation at -80 mV, and when applied, mibefradil always blocked all of the remaining inward current in the presence of ω-Aga-IVA. The statistics for deactivation kinetics of the T-type current included some measurements on the current recorded in the presence of 300 nm ω-Aga-IVA, even if mibefradil subtraction was not performed successfully. All other reported data for magnitude or kinetics of the T-type current were from cells in which both ω-Aga-IVA and mibefradil were applied sequentially. Mibefradil subtraction worked well for currents elicited by depolarizations <0 mV. Above 0 mV, there were often residual voltage-activated potassium currents not blocked by external TEA that were clearly affected by mibefradil (apparent time-dependent block), so we confined analysis of T-type currents to voltages of ≤0 mV.

Total potassium current (I_Ktotal) was determined as current blocked by replacing 105-155 mm sodium chloride by the same amount of TEACl (both solutions containing 500 nm or 1 μm TTX). Purely voltage-dependent potassium current (I_Kv) was obtained by the same subtraction but in a background of zero calcium (replaced by equimolar magnesium) to eliminate calcium-activated potassium currents. Calcium-activated potassium currents (I_KCa) were then calculated by subtracting I_Kv from I_Ktotal. To quantify interspike currents between the first and second spikes of the bursts, currents were averaged over a 1.3 ms time window starting 1.5 ms after the peak of the first action potential. As shown in Figure 1, this window was near the middle of the interspike interval for bursts with relatively short interspike intervals. Although sodium currents were measured with reduced sodium, when expressing sodium current density, we scaled the currents to those expected with physiological sodium (155 mm) using the Goldman-Hodgkin-Katz current equation (Hille, 2001).

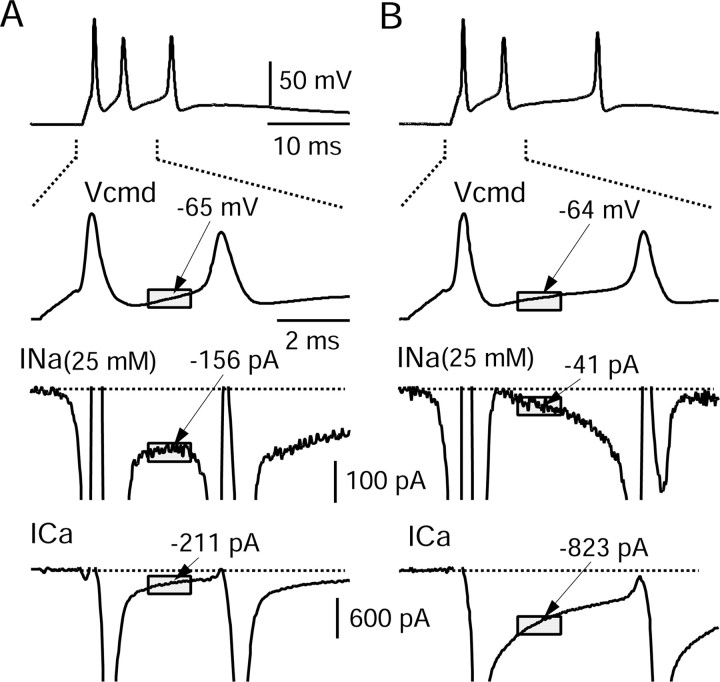
Figure 1.

Inward currents underlying bursts in two dissociated Purkinje neurons. A, Top, All-or-none burst elicited by short (1 ms) injection of depolarizing current from a steady holding voltage near -90 mV (established by steady hyperpolarizing current to stop spontaneous firing). The second panel shows the first interspike interval on an expanded time scale and illustrates the period over which interspike voltage and current was measured (shaded box). The two bottom panels show sodium current elicited by this waveform (in the same cell in which the waveform was recorded), obtained by subtracting the current measured before and after 500 nm TTX (using reduced external sodium to improve voltage control), and calcium current elicited by the waveform (bottom), obtained by subtracting currents before and after replacement of 2 mm Ca²⁺ by 2 mm Mg²⁺, both solutions containing 130 mm TEA to block potassium currents. B, The same as A but for a different neuron. In A and B, the sodium current axis has been expanded 6.18-fold relative to the calcium current axis based on the expected scaling factor from the Goldman-Hodgkin-Katz current equation when scaling the sodium current measured in 25 mm sodium to that expected in physiological (155 mm) sodium. Currents were averaged over a 1.3 ms time window starting 1.5 ms after the peak of the first action potential (gray boxes). Although the burst waveforms are very similar in the two cells, for the cell in A the interspike sodium current was much bigger than the calcium current (when adjusted for sodium concentration), whereas the opposite was true in B. Vcmd, Command waveform.

All chemicals and drugs were obtained from Sigma (St. Louis, MO), except for ω-Aga-IVA (Peptides International, Louisville, KY) and mibefradil (a kind gift from Dr. Eric Ertel, F. Hoffmann-La Roche, Basel, Switzerland).

Data acquisition and analysis. Currents and voltages were low-pass filtered at 10 kHz, digitized at 50 kHz, and controlled using a Digidata 1200 interface, controlled by pClamp 8 software (Axon Instruments). Analysis was done with Igor Pro (version π; Wavemetrics, Lake Oswego, OR) using DataAccess (Bruxton, Seattle, WA) to import pClamp files. In some cases, the traces shown were additionally digitally filtered with an effective corner frequency of 4 kHz. Cell capacitance was measured by integrating the average of 10-15 current responses to a step from -85 to -95 mV (with capacitance nulling turned off), filtering at 10 kHz, and acquiring at 50 kHz. Data are presented as mean ± SD, and comparisons were done using Student's t test, unless noted otherwise.

Na_v1.6-null mice. Heterozygous Scn8a^med mice were obtained from The Jackson Laboratory (Bar Harbor, ME). To compare only homozygous null animals with wild-type littermates, we genotyped mice before use and used homozygous med (Na_v1.6^-/-) or wild-type (Na_v1.6^+/+) littermates. Genotyping used DNA extracted from mouse tails (DNeasy tissue kit; Qiagen, Valencia, CA). PCR amplification used the following primers (5′ to 3′): for the wild-type allele, GGAGCAAGGTTCTAGGCAGCTTTAAGTGTG and GTCAAAGCCCCGGACGTGCACACTCATTCC (Kohrman et al., 1996); for the mutant allele, TCCAATGCTATACCAAAAGTCCC and GGACGTGCACACTCATTCCC (The Jackson Laboratory). The reaction consisted of 20 s at 94°C, 30 s at 66°C, and 35 s at 72°C (12 repetitions), followed by 20 s at 94°C, 30 s at 60°C, and 35 s at 72°C (25 repetitions) and 5 min at 72°C. PCR products were separated on a 2% agarose gel, allowing resolution of a 230 bp product for the wild-type allele and a 194 bp product for the mutant allele.

Results

Variability of ionic currents in Purkinje neurons with similar firing patterns

Previous work has shown that during burst firing in isolated Purkinje neurons, the primary inward currents flowing after the first spike to generate the depolarization leading to the second spike are TTX-sensitive sodium current and voltage-dependent calcium current, with a minor role played by I_h (Swensen and Bean, 2003). Typically, both TTX-sensitive sodium current and voltage-dependent calcium current flowing after a spike are each much larger than the net inward current that drives the after-spike depolarizations; they are opposed by substantial currents through both calcium-activated and purely voltage-activated potassium channels flowing at the same time.

Examining currents during the interval between the first two spikes in a burst, each individual type of interspike current showed considerable variability from cell to cell, even among cells with very similar firing behavior. Figures 1 and 2 illustrate this pattern for interspike sodium and calcium currents compared with the firing pattern and the net inward current. Figure 1 shows sodium and calcium currents flowing in between the first two spikes of two cells that displayed very similar firing patterns of a three-spike burst in response to a short (1 ms) depolarizing current injection from a holding potential near -90 mV. The interspike currents were determined by using the action potential pattern from each cell as a voltage command and then determining the sodium current as the current blocked by 500 nm TTX (using a reduced sodium concentration of 25 mm for better voltage control) and the calcium current as the current obtained by subtraction when calcium was replaced by equimolar magnesium (with a background of 130 mm TEA to block calcium-activated potassium currents). Despite the similarity in firing patterns, in one cell (Fig. 1A) the sodium current (when scaled from the measured current in 25 mm sodium to the current expected with physiological sodium) was far larger than the calcium current (left panels), whereas in the other cell (Fig. 1B), the reverse was true (right panels). Figure 2 shows the interspike sodium and calcium currents determined by action potential clamp in each of three cells that fired very similar three-spike bursts (Fig. 2A) and three cells that fired two-spike bursts (Fig. 2B). For both patterns, individual cells could have either the sodium or calcium current as by far the dominant inward current or have similar contributions from the two. Clearly, these individual currents, and their relative contributions, can be highly variable among cells showing almost identical firing characteristics.

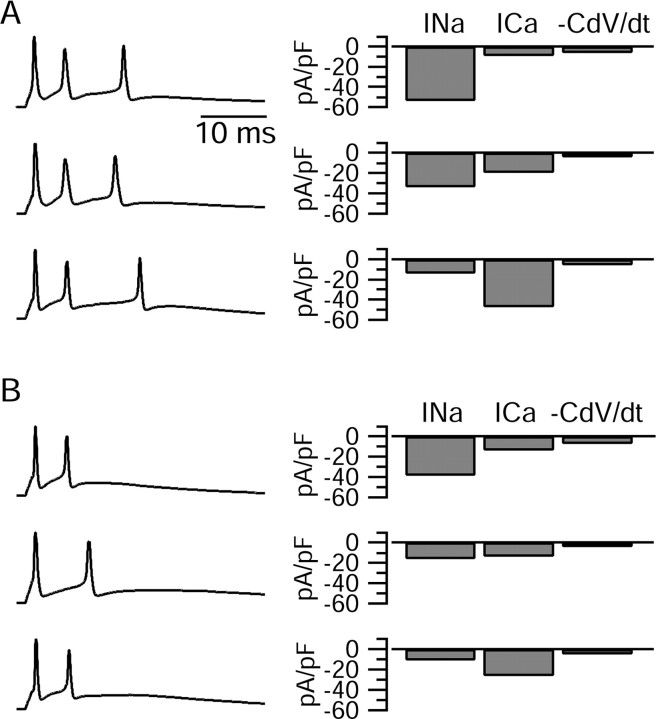
Figure 2.

Inward current profiles during the first interspike interval of bursts in six different Purkinje cells are shown. The bursts from different Purkinje cells are displayed (left) along with bars showing the magnitude of the sodium, calcium, and net ionic current (calculated from -C × dV/dt) during the first interspike interval of each cell (right). A, Three cells that fired similar bursts consisting of three spikes. B, Three cells that fired two-spike bursts. Across both populations, some cells had a dominant sodium current, some had a dominant calcium current, and some had comparable sodium and calcium currents. In all cases, the dominant current was many-fold larger than the net inward ionic current driving depolarization toward the second spike. Sodium currents were recorded in either 25 or 50 mm sodium and have been scaled up to those expected with 155 mm sodium based on the Goldman-Hodgkin-Katz current equation.

Robustness of bursting with acute reduction in sodium current

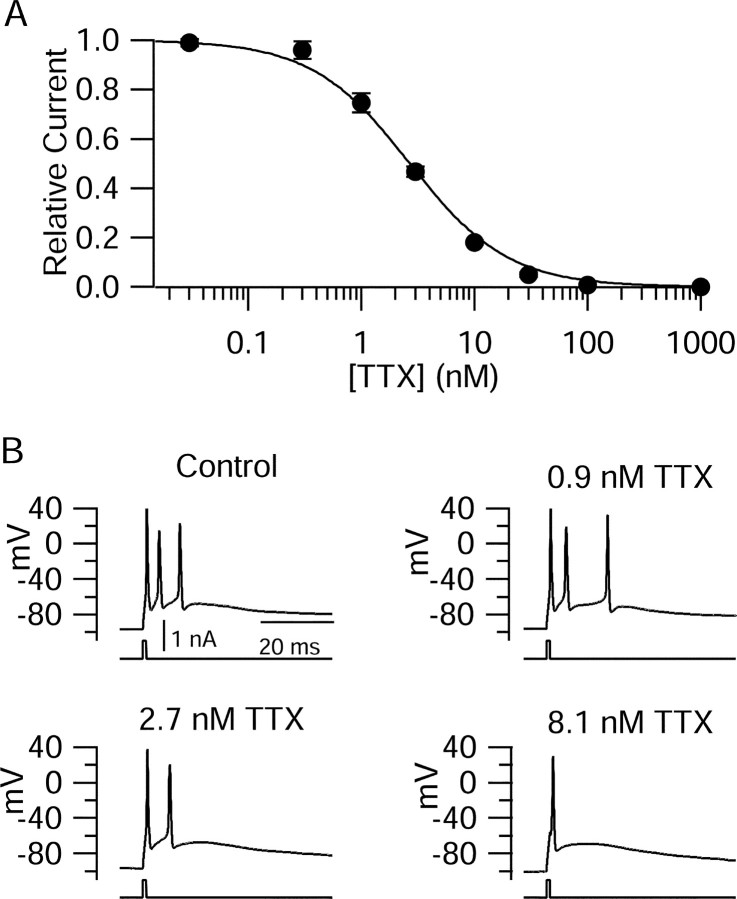
The high degree of variability in the individual currents in cells with similar firing behavior does not necessarily imply that the ability to burst is insensitive to current sizes and ratios. The net ionic current flowing during the interspike interval, calculated from -C × dV/dt, is small compared with the size of the individual current components (Fig. 2), and it is this net ionic current that will determine whether a cell depolarizes after a first spike enough to reach threshold for a second spike. Thus, in principle, a change in any one of the individual currents, even changes much smaller than the differences observed between cells, could have dramatic effects on bursting. To explore this issue, the effect of an acute reduction in the sodium current on bursting was examined. Of all the interspike currents, the sodium current is especially suitable to this analysis because it can be reduced in a well defined manner by a very specific blocker, TTX. We first established the dose-response curve for TTX block of sodium currents in the neurons (Fig. 3A) to calibrate its reduction in the sodium current. The dose-response curve could be fit very well assuming 1:1 binding, with a half-blocking concentration of 2.7 nm. We then examined the effect on bursting of TTX concentrations chosen to produce 25, 50, and 75% block of the sodium current. Figure 3B shows a typical example for a cell that initially fired an all-or-none three-spike burst. Bursting seemed surprisingly robust in the face of sodium current reduction. With 0.9 nm TTX (expected to produce ∼25% reduction in sodium current), all cells (7 of 7) continued to burst, and with 2.7 nm TTX (expected 50% reduction) most cells (7 of 10) continued to burst. It required 8.1 nm TTX (expected 75% reduction) to eliminate bursting in all cells (zero of seven).

Figure 3.

Effect of calibrated reduction in sodium conductance on bursting in Purkinje neurons. A, Dose-response relationship for TTX inhibition of sodium current in Purkinje neurons. Sodium current was measured as the peak current elicited using a voltage step from -75 to -10 mV. Each point in A shows current relative to control averaged over five cells, except for 100 nm TTX (complete block in 2 cells). The solid line is drawn according to 1/(1 + [TTX]/2.7 nm). The external solution consisted of the following (in mm): 50 NaCl, 105 TEACl, 4 KCl, 2 CaCl₂, 2 MgCl₂, and 10 HEPES, pH 7.4 with ∼5 NaOH. B, Effects of increasing degrees of sodium current block on all-or-none burst firing in a Purkinje cell. Concentrations of TTX were selected to produce 25, 50, and 75% block of sodium current. The external solution consisted of the following (in mm): 155 NaCl, 4 KCl, 2 CaCl₂, 2 MgCl₂, and 10 HEPES, pH 7.4 with ∼5 NaOH.

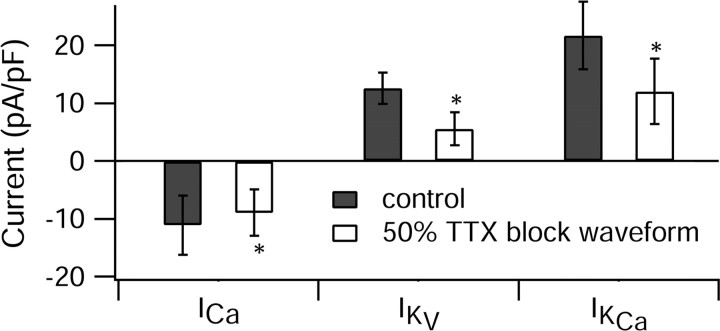
To explore how other currents in the cells might be changing during bursts to help compensate for the reduced sodium current drive, we used the action potential clamp to directly compare interspike currents during normal bursts and bursts with reduced sodium conductance. For each cell, we recorded (in current clamp) first a control burst and then the burst with 2.7 nm TTX (the half-blocking concentration) and then switched to voltage clamp and played both waveforms back as the voltage commands. Figure 4 summarizes the results. A priori, given the maintenance of bursting with reduced sodium conductance, one might expect that a compensatory mechanism could involve increased calcium current, given that this is the other major depolarizing current during the interspike interval. In fact, however, the interspike calcium current was actually smaller in the bursts with reduced sodium conductance. Instead, the compensatory changes came from substantial reductions in interspike potassium currents. There was a reduction in both the calcium-dependent potassium current and purely voltage-activated potassium current flowing between spikes. On average, the interspike calcium current was 19% smaller during the reduced sodium conductance bursts, whereas the calcium-dependent potassium current was 45% smaller and the purely voltage-activated potassium current was 56% smaller. Evidently, it is reduction in interspike potassium currents that plays the major role in partially compensating for the loss of sodium current to maintain a net inward balance of interspike currents and thus preserve bursting.

Figure 4.

Interspike currents between the first and second spikes of all-or-none bursts elicited by control burst waveforms (solid bars) and waveforms recorded (in the same cells) in the presence of 2.7 nm TTX to block sodium current by 50% are shown. The calcium current was measured over the first interspike interval as in Figure 1. Potassium currents were measured over the same interval. The total potassium current was determined by subtracting currents before and after replacing the external sodium (155 mm) by equimolar TEA, with a background of normal (2 mm) calcium. The purely voltage-dependent potassium current (I_Kv) was determined by the same manipulation but with a background of zero calcium (replaced by magnesium). The calcium-activated potassium current (I_KCa) was calculated by subtracting I_Kv from the total potassium current. Bars and error bars represent mean ± SD for measurements in six cells for calcium current and four cells for potassium currents. ^*p < 0.05; paired t test.

What is the mechanism underlying this decrease in the potassium current? TTX was applied acutely, and the ability to burst was assayed within seconds, so it is highly unlikely that this mechanism requires second-messenger systems or other relatively slow adaptive changes. The most obvious possibility is that the changes in other currents are mediated acutely through changes in the action potential waveform caused by the decreased sodium current. A comparison of the burst waveforms with full and reduced sodium conductance showed a reduction in the height of the action potential (+44 ± 2 mV in control vs +38 ± 2 mV in 2.7 nm TTX; p = 0.002; paired t test; n = 6). In addition, bursts with reduced sodium conductance had a more hyperpolarized interspike voltage (-67 ± 3 mV in control vs -72 ± 1 mV in 2.7 nm TTX; p = 0.02; paired t test; n = 6).

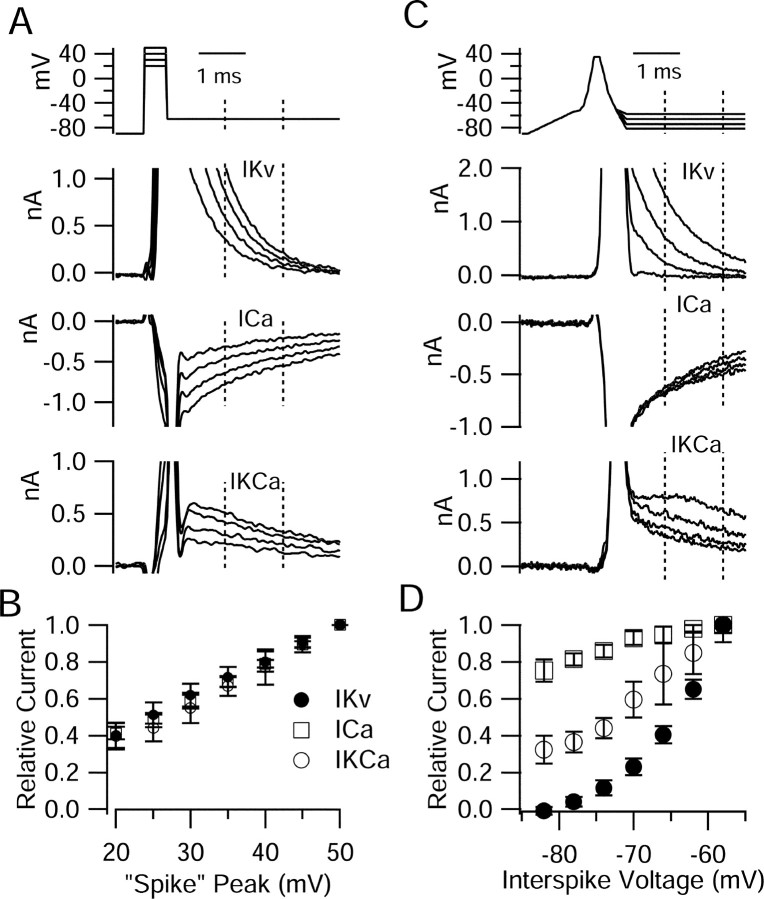
We examined how each of these changes in waveform influences potassium and calcium currents after the first spike. The ionic currents carried by depolarization-activated channels during the interspike interval are essentially “tail” currents, reflecting deactivation after being activated during the spike. We approximated the effect of changing spike height by using a 0.5 ms depolarization from -90 mV to various voltages (between +50 and +20 mV) as a surrogate for the spike (Fig. 5A). (We considered using a more spike-like waveform, as in Fig. 5C, but the interpretation for such a waveform seemed complicated, because any change in peak height would be accompanied by changes in the trajectory to and from the peak.) Both the purely voltage-dependent potassium current and calcium current were largest after depolarizations to more positive voltages, as expected if neither reaches full activation during these relatively brief depolarizations. For both the purely voltage-dependent potassium current and calcium current, the decrease in the postspike current predicted by a change in the “spike” peak from +44 to +38 mV (the change seen with the half-block by TTX) was modest, ∼15% (Fig. 5B). The calcium-activated potassium current changed by a similar amount, presumably reflecting partly the decreased calcium entry and partly the voltage-dependent properties of large-conductance calcium-activated potassium (BK) channels.

Figure 5.

Evaluation of effect of changing spike height or postspike voltage on postspike ionic currents. A, Changes in spike height were approximated by changing the height of a 0.5 ms step to voltages between +50 and +20 mV (in 5 mV increments, from -90 mV), followed by repolarization to -66 mV. Currents after the short depolarization are shown for “spike” heights of +50, +40, +30, and +20 mV. Solution changes as in Figure 4 were used to determine currents carried by purely voltage-dependent potassium channels, by calcium channels, and by calcium-activated potassium channels. B, A current during repolarization to -66 mV as a function of preceding spike voltage. Currents integrated over the period shown were normalized to the largest current (which followed a step to +50 mV in all cases) in each cell. The mean ± SD is shown for experiments in seven cells. C, Ionic currents after spike repolarization to different voltages. In this case, a more realistic artificial spike was used (constructed by piecewise approximation), followed by repolarization to various fixed voltages. Currents are shown for repolarizations to -58, -66, -74, and -82 mV (currents were determined at 4 mV intervals, but not all are shown). D, Current as a function of repolarization voltage, integrated over the period shown. Currents were normalized to the current during repolarization to -58 mV. Bars and error bars represent mean ± SD for experiments in nine cells.

The effects on potassium currents of changes in the postspike voltage were much larger. To test the effect of changing the voltage after the spike, we constructed a series of waveforms consisting of a constant spike-like shape (with a shape modeled on a representative recorded spike), followed by a steady voltage that was varied from -58 to -82 mV in different sweeps (Fig. 5C). Both the purely voltage-dependent potassium current and calcium-activated potassium current after the spike were powerfully affected by changing postspike voltage in this range. The strongest effect was on the purely voltage-dependent potassium current, which was reduced by ∼50% for a change in postspike voltage from -67 to -72 mV (the change seen when bursts were elicited with reduced sodium conductance). The calcium-activated potassium current was reduced somewhat less, by ∼35%. The calcium current was far less sensitive to changes in postspike voltage, changing by ∼25% over the full range from -58 to -82 mV and by only ∼5% from -67 to -72 mV.

The changes of the various currents with postspike voltage can be rationalized in terms of the properties of the various currents. The main component of the potassium current elicited by spikes in Purkinje neurons is highly TEA sensitive and appears to come from Kv3 family channels (Raman and Bean, 1999; Southan and Robertson, 2000; Martina et al., 2003; McKay and Turner, 2004). These potassium channels require relatively large depolarizations for activation and activate and deactivate very rapidly (Rudy and McBain, 2001). At voltages near -70 mV, the kinetics of potassium channel tail currents in Purkinje neurons are rapid (time constant, ∼1 ms), and the speed of deactivation is voltage dependent, becoming faster with increasing hyperpolarization (Martina et al., 2003). From the data in Figure 5C, it appears to be the voltage sensitivity of deactivation kinetics that is most important for the reduction in the potassium current with increasing postspike hyperpolarization, together with the effect of decreased driving force as voltages get closer to the potassium equilibrium potential. The postspike calcium current is dominated by contributions from the T-type current (Swensen and Bean, 2003); from Figure 5C, it appears that the rate of deactivation of these channels is only mildly voltage dependent over the relevant voltage range. Interestingly, the interspike calcium-activated potassium current decreases much more than the interspike calcium current with increasing postspike hyperpolarization. This may be partly because the calcium-activated potassium current appears to be triggered preferentially by the P-type calcium current (Womack et al., 2004), which is large immediately after a spike but deactivates quickly and contributes less than the T-type current in the middle of the interspike interval (Swensen and Bean, 2003). It is possible that calcium entry through P-type channels (during and immediately after a spike) is more sensitive than the interspike T-type current to changes in postspike voltage. The decrease in the calcium-activated potassium current with increasing postspike hyperpolarization probably also reflects more rapid deactivation of BK calcium-activated potassium channels, which carry most of the calcium-activated potassium current during the interspike interval (Swensen and Bean, 2003) and are likely to have strongly voltage-sensitive deactivation kinetics. The reduced driving force for potassium with increasing hyperpolarization must also contribute to the reduction in calcium-activated potassium current.

The combined effect of changes in spike height and interspike voltage predicted from the results in Figure 5 for each current type fit well with the changes seen with the reduced sodium conductance burst waveforms. For the purely voltage-dependent potassium current, the data in Figure 5 predict reduction by a factor of 0.85 × 0.50, effect of spike height × effect of postspike voltage, predicting an overall reduction by 58%, similar to the reduction of 56% actually seen (Fig. 4). The calculation for the calcium-activated potassium current (0.85 × 0.65) predicts a reduction of 45%, exactly what was seen. The calculation for calcium current (0.85 × 0.95) predicts a reduction of 19%, also exactly the average observed with the reduced sodium conductance bursts. Although the nearly exact correspondence of the numbers predicted from the waveform changes in Figure 5 and those measured in Figure 4 is clearly somewhat coincidental, given the substantial SD of each set of measurements (performed using different populations of cells), the agreement supports the idea that the essential compensatory element is reduced potassium current as a consequence of the reduced spike height and hyperpolarizing shift in postspike voltage. The reduction in purely voltage-dependent potassium current is mainly attributable to the hyperpolarizing shift in interspike voltage, resulting from the voltage sensitivity of deactivation of Kv3-type potassium channels in this voltage range. The reduction in the calcium-activated potassium current is likely a result of both the reduction in calcium entry and the shift in postspike voltage, which promotes deactivation of BK channels and also reduces the potassium driving force.

Like both potassium channels and calcium channels, the postspike gating of sodium channels will be affected by the reduction in spike height and the hyperpolarizing shift in the interspike interval. However, the expected changes in gating are more complicated for sodium channels. Sodium channel activation is much faster than for calcium channels and potassium channels and is probably maximal during the spike regardless of peak height (at least in the range of +20 to +50 mV). The sodium current flowing during the interspike interval is in large part resurgent sodium current (Raman and Bean, 1997, 2001), which shows very little change in amplitude over the range of -60 to -80 mV when activated after a short, large depolarizing pulse similar to a spike (Raman et al., 1997). Thus, the hyperpolarizing shift in the interspike interval might be expected to have relatively little effect on the degree of activation of sodium channels during this part of the burst. In fact, when we directly measured the decrease in the interspike sodium current caused by the altered waveform (comparing the current carried by 50 mm sodium in response to either a control waveform or reduced sodium conductance waveform in the same cell), there was a 14 ± 8% decrease (n = 4; data not shown). Thus, although the hyperpolarization of the interspike interval with the half-block of sodium channels does reduce the activation of the remaining channels during the interspike interval, this is a relatively small effect, similar to the reduction in calcium current and much less than the reduction in potassium current.

Robustness of bursting with chronic reduction in sodium current: Na_v1.6^-/- cells

Possible adaptive feedback mechanisms operating on a longer time scale were examined using mice null for the sodium channel Na_v1.6. This is one of several sodium channels expressed in Purkinje neurons, and Purkinje neurons from Na_v1.6^-/- mice were found previously to have transient sodium current reduced by ∼40% (Raman et al., 1997; Khaliq et al., 2003; Do and Bean, 2004), with more dramatic reductions in both steady-state persistent sodium current and resurgent sodium current. Spontaneous firing was found to be significantly slower in Purkinje neurons from Na_v1.6^-/- mice (Khaliq et al., 2003). All-or-none burst firing elicited from hyperpolarized voltages was found to be reduced in frequency of occurrence and in average number of spikes per burst but not eliminated (Raman et al., 1997).

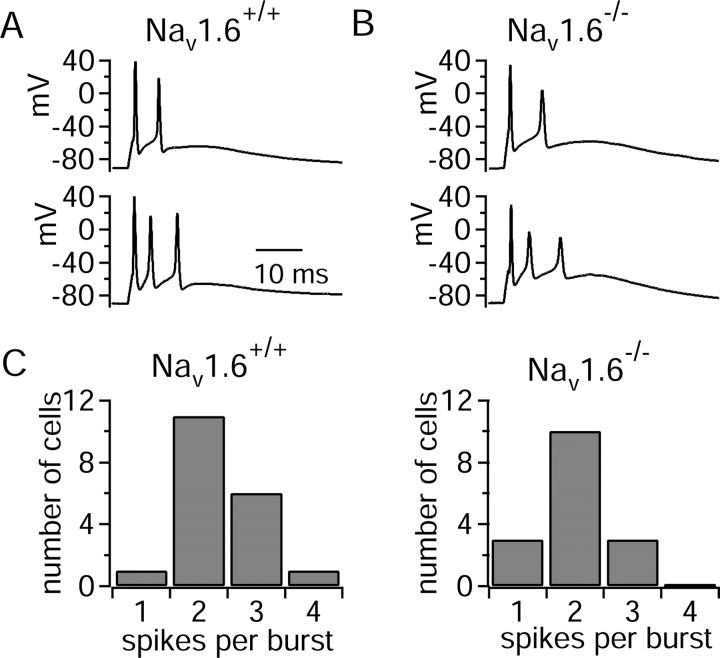
We compared burst firing in Purkinje neurons from homozygous Na_v1.6^-/- mice to that in neurons from homozygous wild-type littermates (Fig. 6). Most (13 of 16) Purkinje neurons from Na_v1.6^-/- mice fired all-or-none bursts, not dramatically different from the wild-type littermates (18 of 19). The average number of spikes per burst was also only moderately lower for mutant animals (2.0 ± 0.6; n = 16) than for wild-type animals (2.4 ± 0.7; n = 19). This is a less dramatic change than seen in previous experiments, in which the number of spikes per burst changed from 6.6 ± 1.0 to 2.9 ± 0.6 (Raman et al., 1997). A likely explanation for the difference is that the previous experiments were done with an internal solution with higher calcium buffering (9 mm EGTA vs 0.9 mm EGTA), which would favor longer bursts by reducing the current carried by small-conductance calcium-activated channels (Swensen and Bean, 2003). Another difference that may be relevant is that the previous experiments were done with a different mouse line (med^Tg) in which a transgene-induced null allele of Na_v1.6 is maintained in a mouse strain (C57BL/6J), different from the med line used here, in which the null allele of Na_v1.6 was caused by insertion of an L1 element and is maintained in a CH3 background (Sprunger et al., 1999). In any case, the results are qualitatively consistent in that in both cases bursting was reduced but not eliminated in the Na_v1.6^-/- mice.

Figure 6.

All-or-none bursting in Purkinje neurons from Na_v1.6^-/- mice compared with neurons from wild-type mice (homozygous normal littermates). A, Two-spike (top) and three-spike (bottom) bursts from Na_v1.6^+/+ mice. B, Two-spike (top) and three-spike (bottom) bursts from Na_v1.6^-/- mice. C, Distribution of the number of spikes per burst for cells from Na_v1.6^+/+ and Na_v1.6^-/- mice.

Interspike currents in Na_v1.6^-/- cells: increase in calcium current

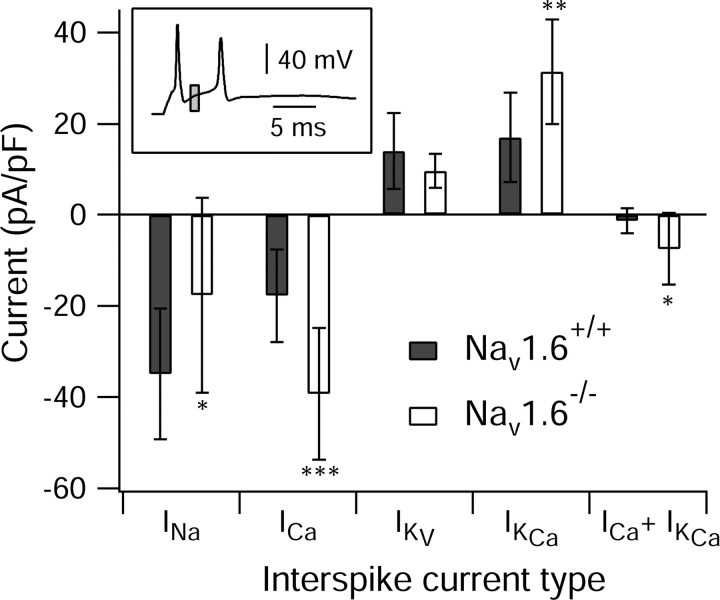
Figure 7 shows the results of action potential clamp experiments comparing the interspike currents underlying bursting in wild-type and Na_v1.6^-/- cells. As might be expected, the sodium current between the first two spikes of bursts was reduced in cells from the Na_v1.6^-/- mice, by ∼50%. Of the other ionic currents during the interspike interval, the largest change was in calcium current, which increased by 122%. The purely voltage-dependent potassium current was decreased by 31%, and the calcium-activated potassium current was increased by 85%. There was no difference in the interspike hyperpolarization-activated current, I_h (p = 0.81; t test; data not shown), which was always very small compared with other currents (Swensen and Bean 2003). These results suggest that the main factor tending to preserve bursting in the face of substantial loss of sodium current in cells from Na_v1.6^-/- mice is an increase in the calcium current flowing in the interspike interval, along with a quantitatively less important reduction in voltage-activated potassium current.

Figure 7.

Interspike currents between the first and second spikes of all-or-none bursts in action potential clamp experiments in cells from Na_v1.6^+/+ animals (filled bars) versus Na_v1.6^-/- animals (open bars) are shown. Inset, Example of a command waveform showing the window over which currents were averaged (gray box). Contributions of individual currents determined by ionic and pharmacological subtraction as in Figures 1 and 4. Sodium current was measured in reduced sodium (50 mm) to reduce clamp errors and scaled up to expected values for 155 mm sodium. Bars and error bars show mean ± SD. I_Na, n = 14 for wild type and n = 11 for mutants; I_Ca, n = 14 wild type and n = 14 mutants; I_Kv, n = 13 wild type and n = 11 mutants; I_KCa, n = 13 wild type and n = 9 mutants; I_Ca + I_KCa, n = 13 wild type and n = 9 mutants. ^*p < 0.05; ^**p < 0.01; ^***p < 0.001.

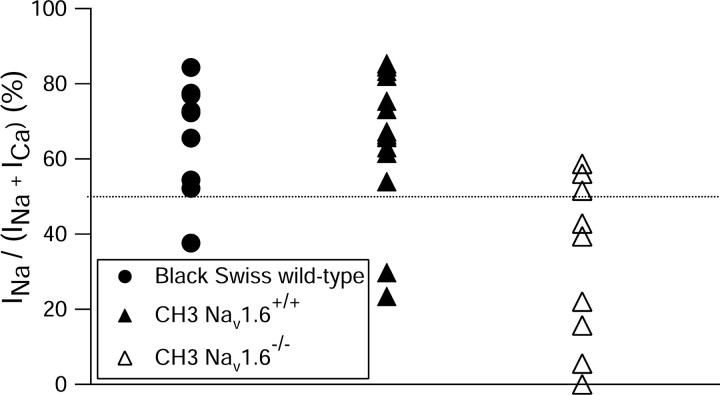
The large increase in calcium current accompanying the reduction in sodium current during bursts in Na_v1.6^-/- mutants suggests a shift in the mechanism of bursting from being dependent on the sodium current in wild-type neurons to being dependent on the calcium current in the mutants. However, as discussed already, even in wild-type animals there were individual Purkinje neurons in which the calcium current was larger than the sodium current between spikes (Fig. 1). Conversely, we found that although the interspike calcium current was larger than the sodium current in most cells from Na_v1.6^-/- mutants, there were individual cells in which the sodium current was larger. Figure 8 shows a scatter plot illustrating the relative sizes of interspike sodium and calcium currents for individual cells from wild-type and Na_v1.6^-/- mutant mice. Two strains of wild-type mice were studied and gave similar results. In wild-type Black Swiss mice, eight of nine cells had an interspike sodium current greater than the interspike calcium current. Similarly, for wild-type CH3 mice (the homozygous Na_v1.6^+/+ littermates of the Na_v1.6^-/- mice), the sodium current dominated over the calcium current in 12 of 14 cells. In contrast, for cells from Na_v1.6^-/- mice, the calcium current was greater than the sodium current in six of nine cells.

Figure 8.

Relative magnitude of inward current from sodium channels and calcium channels between the first two spikes in bursts in individual cells from Na_v1.6^+/+ animals and Na_v1.6^-/- animals. The y-axis plots the fraction of total inward current in the interspike interval carried by sodium channels. The sodium current and calcium current during the first interspike interval were determined in each cell in action potential clamp experiments using the action potential of each cell as in Figure 1. Filled circles, Cells from series of experiments using Black Swiss mice; closed triangles, cells from wild-type littermates of Na_v1.6^-/- mice (CH3 strain background); open triangles, cells from Na_v1.6^-/- animals.

Changes in current density in Na_v1.6^-/- mutant cells

The changes in ionic currents during the interspike interval in Na_v1.6^-/- mutants may not be linearly related to the underlying changes in the expression of the various channels, because the exact waveform of the first spike and the interspike interval are somewhat variable from cell to cell and may change systematically in the mutants. Indeed, although the bursts in neurons from Na_v1.6^-/- mice look generally similar to those from wild-type animals, there were significant population differences in various characteristics of the waveforms (Table 1). Most notably, the peak of the first action potential was significantly less positive in bursts from mutant animals, and the voltage during the interspike interval was more depolarized in the mutant bursts. The changes in both spike height and interspike voltage would be expected to affect the degree of activation (or inactivation) of the currents during the interspike interval, as already seen in the context of acute reductions in sodium conductance.

Table 1.

Comparison of burst parameters in wild-type and Na_v1.6^−/− mutant bursts

	Nav1.6+/+ (n = 19)	Nav1.6−/− (n = 16)	t test results
Action potential peak	+41 ± 3 mV	+32 ± 7 mV	p < 0.001**
Interspike voltage	−68 ± 4 mV	−64 ± 4 mV	p = 0.01*
Interspike interval	6.4 ± 3.2 ms	8.4 ± 2.8 ms	p = 0.07
Action potential threshold	−53 ± 3 mV	−43 ± 3 mV	p < 0.002**
Action potential width (at 0 mV)	0.41 ± 0.07 ms	0.43 ± 0.06 ms	p = 0.589
Afterhyperpolarization	−74 ± 2 mV	−70 ± 4 mV	p = 0.003*
Afterdepolarization	−68 ± 3 mV	−62 ± 5 mV	p < 0.001**

The action potential peak was measured for the first spike of the burst. The interspike voltage was averaged over a 1.3 ms time window starting 1.5 ms after the peak of the first action potential. The interspike interval was measured between the peaks of the first and second spikes. The action potential threshold was defined as the voltage at which dV/dt exceeded 20 mV/ms (measured for the first action potential), and action potential width was defined as the width at 0 mV. The afterhyperpolarization was the most negative voltage reached after the first spike, and the afterdepolarization was the most positive voltage reached after the last spike. ^*p ≤ 0.01; ^**p < 0.002.

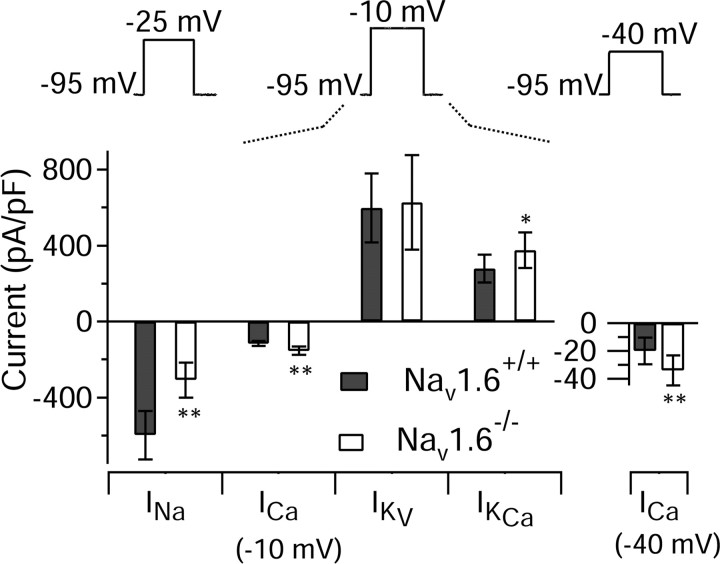
To better determine how the density of various types of ionic currents were altered in Purkinje neurons from Na_v1.6^-/- animals independent of the changes in burst waveform, we used standard step voltage-clamp commands (Fig. 9). As expected, the sodium current (elicited by steps from -95 to -25 mV) was reduced, from -599 ± 128 pA/pF (n = 16) in Na_v1.6^+/+ mice to -308 ± 94 pA/pF (n = 17) in Na_v1.6^-/- mice, a reduction of 49%. These results are similar to previous results reporting reductions of ∼ 40% in Purkinje neurons from Na_v1.6^-/- animals (Raman et al., 1997; Do and Bean, 2004). There was no significant change in the magnitude of the purely voltage-dependent potassium current activated by steps from -95 to -10 mV. The calcium current elicited by steps to -10 mV was significantly larger in cells from Na_v1.6^-/- mice: -117 ± 13 pA/pF (n = 14) in cells from wild-type littermates and -154 ± 21 pA/pF (n = 15) in cells from Na_v1.6^-/- animals. The increase in calcium current elicited by steps to -10 mV was accompanied by an increase in the calcium-activated potassium current (determined with the same voltage protocol), from 278 ± 73 pA/pF (n = 12) in cells from wild-type littermates to 376 ± 95 pA/pF (n = 12) in cells from Na_v1.6^-/- animals.

Figure 9.

Densities of various ionic currents determined by voltage steps in Purkinje neurons from Na_v1.6^+/+ (filled bars) and Na_v1.6^-/- (open bars) animals are shown. Currents were activated with voltage steps from a steady holding potential of -95 mV. Sodium currents were measured with steps to -25 mV in reduced sodium (25 or 50 mm) and scaled using the Goldman-Hodgkin-Katz equation to the current expected in 155 mm sodium. Calcium and potassium currents were measured with steps to -10 mV; calcium currents were also measured using steps to -40 mV to obtain currents with a higher fractional contribution from T-type channels. All currents were recorded using normal physiological solutions using the same subtraction procedures as for action potential clamp experiments to isolate individual currents. Bars and error bars show mean ± SD. I_Na, n = 16 for wild type and n = 17 for mutants; I_Ca, n = 14 wild type and n = 15 mutants; I_Kv, n = 13 wild type and n = 13 mutants; I_KCa, n = 12 wild type and n = 12 mutants. ^*p < 0.01; ^**p < 0.001.

There was no significant change in the magnitude of I_h (elicited by steps from -50 to -130 mV; data not shown), which was -5 ± 4 pA/pF (n = 10) in wild-type mice and -6 ± 5 pA/pF (n = 5) in mutant mice. The lack of change in I_h is consistent with the results from the action potential clamp and also with previous experiments on Na_v1.6^-/- Purkinje neurons (Khaliq et al., 2003).

It was notable that the increase in calcium current seen with steps to -10 mV (32%) was substantially less than the increase seen during the interspike interval (122%). An important consideration for this comparison is that most of the calcium current elicited by steps to -10 mV is from P-type channels, whereas the majority of the interspike current is from T-type channels (Swensen and Bean, 2003). Therefore, we also examined calcium current density using steps from -95 to -40 mV, for which T-type channels carry a larger fraction of current. The increase in calcium current elicited by steps to -40 mV [from -20 ± 10 pA/pF in wild type (n = 14) to -34 ± 11 pA/pF in mutants (n = 15)] was larger than the increase observed with steps to -10 mV (an increase of 70% vs 32%). This suggests that the T-type current, which makes a more substantial contribution to the calcium current at -40 mV, is upregulated to a larger degree.

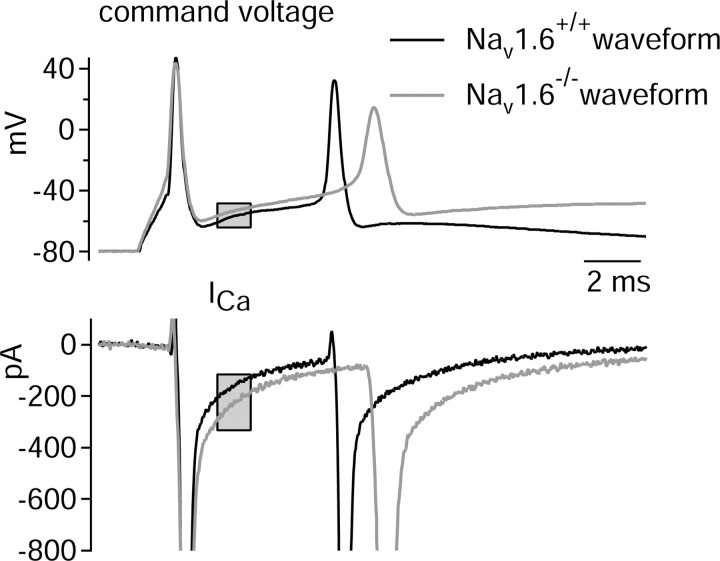
The 70% increase in calcium current elicited by steps to -40 mV in cells from the mutant animals is less than the increase seen during the interspike interval (122%). A logical possibility is that the difference results from the differences in voltage waveforms seen in mutant cells compared with control animals. We examined this directly by comparing activation of calcium current in the same (wild-type) cell by two different burst waveforms typical of cells from wild-type and mutant animals. Figure 10 shows an example. The waveform from the Na_v1.6^-/- animal resulted in a substantially larger interspike calcium current (∼40% larger) when the two currents were measured in the same cell. In collected results, the average calcium current was 45% larger during the burst from the Na_v1.6^-/- animal (-180 ± 49 pA/pF vs -124 ± 23 pA/pF; n = 9). Thus, in addition to an upregulation of the density of both T-type and P-type channels, the available calcium channels are activated more fully in the interspike intervals of bursts from Na_v1.6^-/- cells.

Figure 10.

Comparison of calcium current elicited in a single cell (from Na_v1.6^+/+ animal) by burst waveforms characteristic of Purkinje neurons from Na_v1.6^+/+ (black traces) and Na_v1.6^-/- (gray traces) animals is shown. The gray box indicates the time over which interspike current was measured.

The particular waveforms (Fig. 10) used for these experiments were selected because they had parameters (especially the peak of first action potential and interspike voltage) typical of bursts from Na_v1.6^+/+ and Na_v1.6^-/- cells. To examine whether more efficient activation of available calcium current during bursts was true in general for burst waveforms from Na_v1.6^-/- animals, an “efficiency” index was derived. This parameter was calculated as the ratio of the calcium conductance elicited by the burst waveform (measured in the interspike interval) to the calcium conductance elicited by a step to -40 mV and thus gives a measurement of how effectively the calcium channels that are present are activated between spikes. Calcium conductance was calculated from the calcium current using a reversal potential for a calcium current of +50 mV. The efficiency index was 0.70 ± 0.16 (n = 13) for wild-type bursts and 0.94 ± 0.29 (n = 12) for null mutant bursts (p = 0.02). This supports the idea that burst waveforms from Na_v1.6^-/- animals are different in such a way as to produce greater activation of calcium channels during the interspike interval. [The reasons for this are not obvious. By itself, a reduction in peak height of the first spike would reduce the postspike calcium current (Fig. 5A,B). The depolarizing change in interspike voltage would have an enhancing effect on the postspike calcium current, but the results in Fig. 5C suggest that the 4 mV depolarizing shift that was seen would have relatively little effect. However, a factor not addressed in the experiment of Fig. 5 is the modest broadening and slowed upstroke and downstroke of the action potential that accompanies the decrease in height in the mutant animals.] The combined effect of the 1.7-fold increase in calcium current density measured for steps to -40 mV and the 1.3-fold increase in efficiency of activation during the interspike interval predicts an overall 2.2-fold increase in calcium current during the interspike interval, exactly what was measured for the interspike current. Thus, the increased interspike calcium current during bursts in Na_v1.6^-/- cells can be accounted for as a combination of increased calcium current density and increased activation attributable to changes in the burst waveform.

Pharmacology of calcium currents

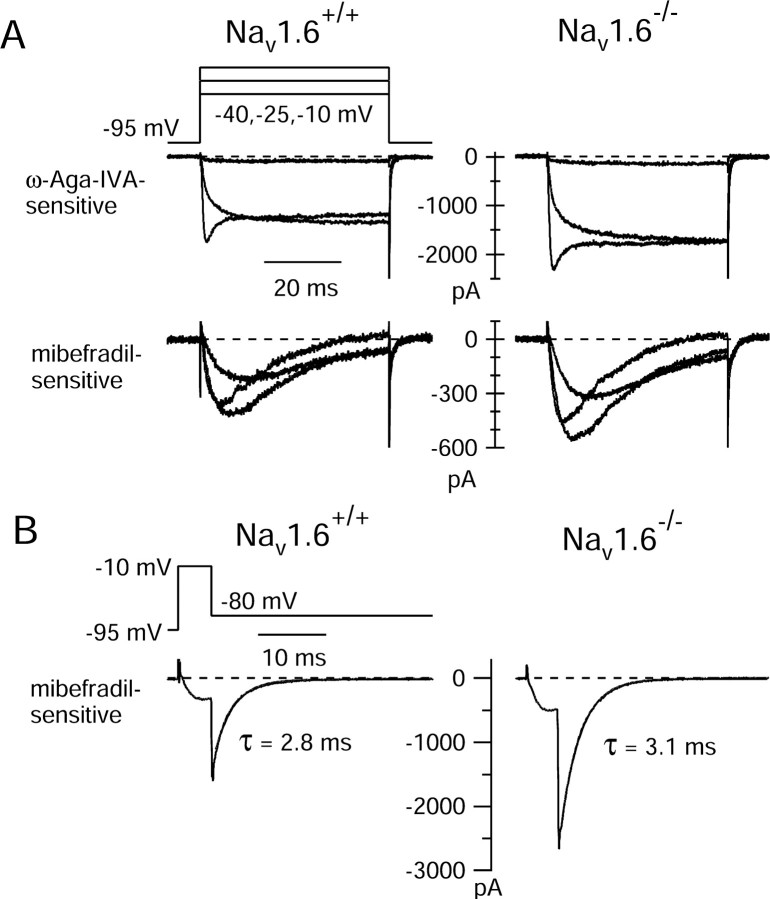
To explore more directly which calcium channel types underlie the increased interspike calcium current in cells from Na_v1.6^-/- mice, we used blockers of P-type and T-type calcium channels, which underlie the great majority of calcium current in wild-type neurons. Using the blockers ω-Aga-IVA (300 nm) and mibefradil (10 μm; applied after block of P-type channels with ω-Aga-IVA) to define components of P-type and T-type calcium current, we found that T-type channels carry most of the interspike calcium current in both Na_v1.6^+/+ (70 ± 6%; n = 8) and Na_v1.6^-/- (74 ± 25%; n = 9). Both P-type and T-type calcium current flowing during the interspike interval were increased in mutants compared with wild-type animals. Defined by the successive addition of ω-Aga-IVA and mibefradil, the interspike P-type current was -5 ± 2 pA/pF (n = 8) in cells from wild-type animals and -10 ± 10 pA/pF (n = 9) in cells from Na_v1.6^-/- animals, and the interspike T-type current was -12 ± 5 pA/pF (n = 6) in cells from wild-type animals and -20 ± 9 pA/pF (n = 5) in cells from Na_v1.6^-/- animals. The combination of 300 nm ω-Aga-IVA and 10 μm mibefradil blocked all of the interspike calcium current (101 ± 2%; n = 5) in the Na_v1.6^-/- mutant bursts, just as for wild-type neurons (99 ± 4%; n = 6).

Experiments using step voltage protocols also showed increases in both the P-type and T-type calcium current. P-type current density (measured as the ω-Aga-IVA-sensitive current at -10 mV) increased 37%, from -95 ± 11 pA/pF (n = 9) in cells from Na_v1.6^+/+ wild-type animals to -130 ± 25 pA/pF (n = 10) in cells from Na_v1.6^-/- animals, and T-type current density (measured as the mibefradil-sensitive current at -40 mV) increased 50% from -12 ± 4 pA/pF (n = 7) in cells from Na_v1.6^+/+ animals to -18 ± 5 pA/pF (n = 5) in cells from Na_v1.6^-/- animals. Thus, current density from both types of channels is upregulated in the mutants, but the increase is somewhat larger for T-type current than P-type current.

There was no evident difference in the voltage dependence or kinetics of either the P-type or T-type current in cells from Na_v1.6^-/- animals compared with Na_v1.6^+/+ animals. Figure 11A shows examples of the components of the calcium current blocked by ω-Aga-IVA and mibefradil in wild-type (left column) and Na_v1.6-null (right column) Purkinje neurons. For both components of current, the voltage sensitivity and kinetics were essentially identical in cells from wild-type and mutant animals. For both wild-type and mutant neurons, the mibefradil-sensitive current showed the activation by small depolarizations and the rapid inactivation typical of T-type current, with kinetics indistinguishable between wild-type and mutant animals. Figure 11B compares the deactivation kinetics of T-type current in wild-type and mutant cells, using a brief step to -10 mV to activate channels, followed by a repolarization to -80 mV. The kinetics of T-type current were essentially identical in the wild-type and mutant cells, both showing the slow deactivation typical of T-type channels. In both cases, the tail current could be fit well by a single exponential with a time constant near 3 ms.

Figure 11.

Kinetics and voltage dependence of the components of calcium current in Purkinje neurons from Na_v1.6^+/+ animals and Na_v1.6^-/- animals. A, Comparison of ω-Aga- IVA-sensitive and mibefradil-sensitive components of calcium current in a wild-type cell (left column) and in an Na_v1.6-null cell (right column). Note the identical voltage sensitivity and kinetics for each component of current in mutant versus wild-type cells. B, Comparison of mibefradil-sensitive calcium current elicited by a pulse protocol designed to highlight channel deactivation kinetics. Tail currents are fitted by smooth single-exponential curves with the indicated time constants.

The lack of change in calcium channel voltage dependence or kinetics suggested by the cells compared in Figure 11 was supported by population results. There was no significant difference in the midpoint of activation (V_mid) or in the slope factor (k) for the P-type current [V_mid = -27 ± 1 mV, k = 4.8 ± 0.4, n = 8, for Na_v1.6^+/+; V_mid = -26 ± 2, k = 4.9 ± 0.7, n = 6, for Na_v1.6^-/-; p = 0.51 for midpoint; p = 0.57 for slope factor]. Activation kinetics for the P-type current (measured for a step from -95 to -10 mV and fit with a single time constant) were similar in Na_v1.6^+/+ (0.52 ± 0.07 ms; n = 8) and Na_v1.6^-/- (0.53 ± 0.09 ms; n = 8) animals (p = 0.68), and there was also no difference in deactivation kinetics of the P-type current, which were rapid [at -95 mV, fit by two exponentials, with time constants of 0.05 ± 0.02 and 0.49 ± 0.05 ms in Na_v1.6^+/+ cells (n = 6) and 0.05 ± 0.01 and 0.50 ± 0.02 ms in Na_v1.6^-/- cells (n = 8); p values of 0.62 and 0.52, respectively]. Similarly, the voltage dependence of activation of the T-type calcium current was not changed [V_mid = -42 ± 2 mV, k = 7.5 ± 0.9, n = 6, for Na_v1.6^+/+; V_mid = -42 ± 5, k = 6.9 ± 0.2, n = 5, for Na_v1.6^-/-; p = 0.72 for midpoint; p = 0.15 for slope factor], and there was no difference in the kinetics of inactivation of the T-type current [time constant at -25 mV of 19.3 ± 2.5 ms in Na_v1.6^+/+ animals (n = 6) and 19.2 ± 3.2 ms in Na_v1.6^-/- animals (n = 4); p = 0.94]. Consistent with the cells shown in Figure 11B, there was also no clear difference in the kinetics of deactivation of T-type current [time constant at -80 mV of 3.0 ± 0.2 ms in Na_v1.6^+/+ animals (n = 4) and 3.1 ± 0.2 ms in Na_v1.6^-/- animals (n = 3); p = 0.48].

The lack of change of either voltage dependence or kinetics of the mibefradil-sensitive current, and the fact that mibefradil always blocked all the current remaining in ω-Aga-IVA, argues against the possibility that there is significant upregulation of L-type, N-type, or R-type calcium channels in addition to upregulation of P-type and T-type currents. At 10 μm, mibefradil would certainly have blocking activity against other channel types (Bezprozvanny and Tsien, 1995), but if these contributed a significant fraction of current in the mutant cells, the kinetics or voltage dependence of the current in ω-Aga-IVA would have been altered, which was not seen. In both wild-type and mutant animals, the voltage dependence and kinetics of the current remaining in ω-Aga-IVA were consistent with being essentially pure T-type current.

Shift in balance between calcium current and calcium-activated potassium current

In our previous study of Black Swiss wild-type mice, we found that although there is substantial interspike calcium current, blocking calcium currents enhanced rather than suppressed burst firing, as if the role of the inward calcium current in promoting bursts is outweighed by the role of calcium-activated potassium currents in terminating bursts (Swensen and Bean, 2003). If the same were true for cells from Na_v1.6^-/- animals, then the enhancement of calcium currents seen in the mutants would actually truncate bursts rather than promote them.

The increase in the interspike calcium current in cells from Na_v1.6^-/- animals was accompanied by an increase in calcium-activated potassium current (Fig. 7). To explore possible changes in the balance between the calcium current and calcium-activated potassium current, we calculated the sum of these two currents, averaged over the standard 1.3 ms interspike interval. In cells from Na_v1.6^+/+ animals, the sum of I_Ca + I_KCa averaged over this period was very near zero (-1.3 ± 2.8 pA/pF; n = 13). However, in cells from Na_v1.6^-/- animals, the sum of I_Ca + I_KCa was net inward (-7.5 ± 7.8 pA/pF; n = 9; p = 0.02).

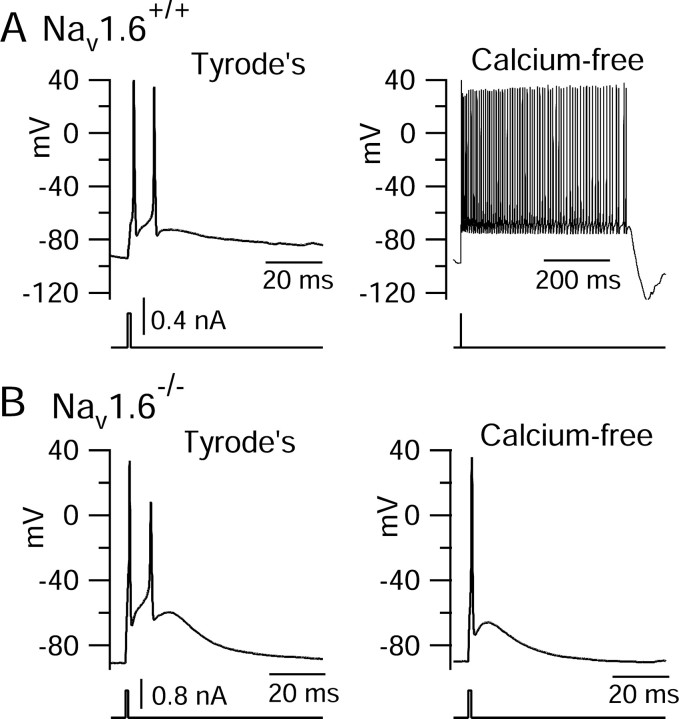
This result suggested that there might be a qualitative difference in response to blocking calcium entry in mutant animals under current-clamp conditions. This turned out to be the case. As shown in Figure 12, blocking the calcium current by replacing calcium with magnesium promoted bursting in cells from wild-type littermates (Fig. 12A), just as seen previously in Black Swiss mice. However, in cells from Na_v1.6^-/- animals, removal of calcium had the opposite effect, reducing bursting (Fig. 12B). These results were typical. In wild-type Na_v1.6^+/+ neurons, removal of calcium enhanced bursting in six of seven cells (and had no effect on bursting in one cell), whereas in neurons from Na_v1.6^+/+ animals, removal of calcium inhibited bursting in four of seven cells and had no effect on the number of spikes per burst in three cells.

Figure 12.

Effects of calcium removal on bursting in cells from wild-type and Na_v1.6^-/- animals. A, All-or-none bursts in a Purkinje neuron from an Na_v1.6^+/+ animal recorded in control Tyrode's solution containing 2 mm calcium and 2 mm magnesium (left) and after moving the cell to a solution in which calcium was replaced by equimolar magnesium (right). B, Same for a Purkinje neuron from an Na_v1.6^-/- animal.

Discussion

Our results show that during burst firing of Purkinje neurons, the voltage dependence and kinetics of the major ionic currents result in a feedback mechanism whereby acute reductions in sodium conductance are counteracted by reductions in both purely voltage-dependent potassium current and calcium-activated potassium current flowing after the first spike. The feedback is mediated by reduced spike height and by a hyperpolarizing shift of the postspike voltage, probably mainly attributable to reduction in resurgent sodium current flowing after the spike (Raman and Bean, 1997). A major element of the feedback mechanism is a powerful sensitivity of voltage-dependent potassium current to the postspike voltage in the range of -65 to -75 mV. This reflects the properties of Kv3-family potassium channels that play the dominant role in repolarizing Purkinje cell spikes, in particular the rapid, voltage-sensitive deactivation kinetics of these channels in this voltage range. Thus, the functional significance of Kv3-family channels in Purkinje cells is not only in promoting burst firing to begin with (by deactivating quickly after the first spike) but also in buffering burst firing against decreases in the postspike sodium current. The feedback mechanism also involves a substantial (45%) reduction in postspike calcium-activated potassium current, reflecting reduction in calcium entry (in turn mainly because of decreased spike height) and probably also enhanced deactivation of BK channels. The decreased potassium driving force probably also contributes significantly to reduction in both voltage-dependent and calcium-activated potassium current by the hyperpolarizing shift of postspike voltage.

The analysis of the mechanism of the “feedback” changes occurring in potassium currents in these experiments does not depend on the exact amount of block produced by TTX. The concentration we used to perturb firing (2.7 nm TTX) was chosen to produce 50% block of sodium channels, but the dose-response curve for TTX was measured using somewhat different conditions (i.e., external sodium reduced to 50 mm for optimal voltage control, replaced by TEA) from those used for current clamp (155 mm sodium), and we cannot be sure that the exact amount of block is not affected by this. However, the key element of the mechanism, that the hyperpolarizing shift of interspike voltage produces a dramatic reduction in interspike potassium current, does not depend on the exact degree of sodium channel block necessary to produce this shift.

Previous work has shown that when the density of available TTX-sensitive sodium channels is reduced by 50%, the upstroke velocity of single action potentials changes by much less, only ∼10% (Cohen et al., 1984; Madeja, 2000). This is because for membranes with a fairly high density of sodium channels, only a small fraction of available sodium channels is activated before the maximum upstroke is reached; with fewer channels available initially, the fraction activated at maximal upstroke increases, so sodium current flowing at maximum upstroke (reached now a few millivolts more positive) is little affected (Cohen et al., 1984). Sodium current flowing between spikes in Purkinje neuron bursts behaves very differently, decreasing slightly more than the density of available channels (“extra” reduction of 14%). Thus, although the ability to fire bursts, like the shape of single action potentials, is “buffered” against reductions in sodium conductance, the mechanisms involved are very different, with the preservation of burst firing depending on changes in currents from potassium channels rather than the intrinsic kinetics of sodium channels.

The mechanism underlying preservation of bursting when sodium current is reduced chronically by loss of Na_v1.6 channels is completely different from the acute feedback mechanism. With chronic reduction in sodium current, the interspike voltage shifts in the depolarizing direction, opposite to that produced with acute reduction. If the density of the various conductances were unaltered, the change in waveform alone would likely reduce rather than enhance bursting. It is clearly the change in density of other currents that is most important for maintaining bursting in Purkinje neurons from Na_v1.6^-/- animals. In particular, an increase in density of both T-type and P-type calcium currents seems most significant for the maintenance of bursting in Na_v1.6^-/- neurons. Our results also suggest that cells from Na_v1.6^-/- animals have a reduced coupling between calcium entry and activation of calcium-activated potassium channels, and this augments the effect of increased calcium current in promoting bursting. The apparent plasticity of this coupling, for which calcium entry through P-type channels seems preferentially important (Womack et al., 2004), emphasizes its importance in determining whether calcium entry promotes or reduces the overall excitability of neurons.

In addition to these changes, previous work with Na_v1.6^-/- Purkinje neurons has shown an increase in resting resistance and a depolarizing shift in the voltage dependence of a subset of potassium channels (Khaliq et al., 2003), both of which would tend to enhance bursting. Perhaps surprisingly, I_h, which contributes to bursting in other types of neurons, is not upregulated (Khaliq et al., 2003; present results) and plays no significant role in the bursting of isolated Purkinje neurons from either Na_v1.6^+/+ or Na_v1.6^-/- animals.

The reduction in sodium current by loss of Na_v1.6 channels differs qualitatively from that produced by TTX block. TTX produces (at least approximately) an equal block of transient and resurgent components of current (T. K. Aman and I. M. Raman, personal communication) and probably of persistent current as well (cf. Kay et al., 1998; Taddese and Bean, 2002), whereas loss of Na_v1.6 channels reduces resurgent and persistent sodium currents much more than transient sodium current (Raman et al., 1997). If current from Na_v1.6 channels were completely removed acutely, the ability to fire bursts would probably be compromised far more than by the half-block of all sodium channels by TTX, because the sodium current flowing during the interspike interval is a combination of resurgent current (immediately after the spike) and persistent current (later in the interspike interval). If acute loss of Na_v1.6 channels reduced resurgent current by >80% and persistent current by 60% (as does chronic loss), interspike sodium current would be reduced much more than 50%. This would likely cause failure of bursting. Thus, upregulation of calcium currents (and reduction in coupling to calcium-activated potassium channels) accompanying chronic loss is probably a necessity for maintenance of bursting in the Na_v1.6^-/- animals.

Our experiments demonstrate robustness of bursting in isolated Purkinje neurons from Na_v1.6^-/- animals. There could well be additional plasticity in intact neurons arising from conductances in dendrites, including I_h (cf. Magee, 1998) and Cav2.3 (α1E) channels (Yokoyama et al., 1995; Pouille et al., 2000), both of which could contribute to bursting in intact neurons. Electrical coupling between dendrites and soma, which has been proposed to be controlled in part by BK channels (Cavelier et al., 2002), also might change.

We studied a somewhat artificial form of bursting elicited by short depolarizations from negative voltages. Our protocol might exaggerate the influence of T-type current because of unphysiologically negative holding potentials. However, in a previous study we found that spontaneously occurring bursts had very similar relative average contributions of T-type current and sodium current as elicited bursts (Swensen and Bean, 2003). Thus, it seems likely that the upregulation of T-type channels is also relevant under more physiological conditions. Single-spike pacemaking activity (the most typical spontaneous behavior) seems more disrupted than burst firing in Na_v1.6^-/- animals (Raman et al., 1997; Khaliq et al., 2003), possibly reflecting a lesser contribution of T-type channels. When present in Na_v1.6^-/- animals, pacemaking can sometimes be disrupted by blocking calcium current, unlike in wild-type animals (Raman et al., 1997), consistent with upregulation of calcium channels partially compensating for the loss of resurgent and persistent sodium current.

The results show that the mechanism of bursting, in terms of the primary postspike inward current, can vary considerably, from being almost completely dependent on sodium current in some wild-type neurons to almost completely dependent on calcium current in some Na_v1.6^-/- neurons (Fig. 8). The contribution of calcium current is dominant even in a few individual wild-type neurons. These results offer a clear illustration in a mammalian neuron of a principle proposed previously for invertebrate neurons and from modeling studies, namely that there can be multiple “solutions” to the combinations of current densities necessary to yield a particular firing pattern (Liu et al., 1998; Goldman et al., 2001). Our results leave open the question of whether the adjustment of current densities in Na_v1.6^-/- Purkinje neurons is attributable to activity-dependent regulation of current densities (Desai et al., 1999) or other mechanisms not dependent on activity (MacLean et al., 2003). It is easy to imagine the existence of activity-dependent mechanisms for controlling the ability to fire in bursts, because bursts would be expected to give distinctive patterns of calcium influx, a ubiquitous signal controlling gene expression. The existence of both acute and long-term feedback mechanisms acting to preserve burst firing suggest that this mode of operation is important for the proper physiological function of Purkinje neurons. Flexibility in achieving burst firing by multiple combinations of channel densities may be especially important in allowing cells to retain this capability in the face of variable expression of channels during processes such as cell growth and development.