Modeling Spontaneous Activity in the Developing Spinal Cord Using Activity-Dependent Variations of Intracellular Chloride

Abstract

We investigated how spontaneous activity is generated in developing, hyperexcitable networks. We focused our study on the embryonic chick spinal cord, a preparation that exhibits rhythmic discharge on multiple timescales: slow episodes (lasting minutes) and faster intraepisode cycling (∼1 Hz frequency). For this purpose, we developed a mean field model of a recurrent network with slow chloride dynamics and a fast depression variable. We showed that the model, in addition to providing a biophysical mechanism for the slow dynamics, was able to account for the experimentally observed activity. The model made predictions on how interval and duration of episodes are affected when changing chloride-mediated synaptic transmission or chloride flux across cell membrane. These predictions guided experiments, and the model results were compared with experimental data obtained with electrophysiological recordings. We found agreement when transmission was affected through changes in synaptic conductance and good qualitative agreement when chloride flux was varied through changes in external chloride concentration or in the rate of the Na⁺-K⁺-2Cl^- cotransporter. Furthermore, the model made predictions about the time course of intracellular chloride concentration and chloride reversal potential and how these are affected by changes in synaptic conductance. Based on the comparison between modeling and experimental results, we propose that chloride dynamics could be an important mechanism in rhythm generation in the developing chick spinal cord.

Introduction

Spontaneous activity is an important property of the developing nervous system (Katz and Shatz, 1996; O'Donovan, 1999). It usually involves episodes of rhythmic discharge, during which many neurons are activated synchronously, separated by longer quiescent periods. Although the phenomenon is not fully understood, it may influence several aspects of neuronal or synaptic development (Gu and Spitzer, 1995; Katz and Shatz, 1996; Li et al., 1996; Zhang and Poo, 2001; Borodinsky et al., 2004).

It has been proposed that spontaneous activity is generated in hyperexcitable networks that are subject to some form of activity-dependent depression (Feller et al., 1999; O'Donovan, 1999; Opitz et al., 2002). During development, the classical inhibitory neurotransmitters GABA and glycine can be functionally excitatory because the chloride equilibrium potential is above rest as a result of an elevated intracellular chloride concentration (Chub and O'Donovan, 2001) (for review, see Ben Ari, 2002). This leads to a predominance of excitatory synapses that renders developing networks hyperexcitable. We proposed that, in the chick embryo spinal cord, a fast form of depression, operating on a timescale <1 s, regulates cycle generation within the episodes, whereas a much slower form of depression (timescale of minutes) regulates the expression of episodes (Fedirchuk et al., 1999; Tabak et al., 2000). This prolonged time course of the slow depression (from a few minutes to more than 30 min) is highly unusual and cannot be explained by traditional forms of synaptic depression (e.g., transmitter depletion) or channel inactivation, which are much faster (Varela et al., 1997).

Recently, it was found that intracellular chloride concentration undergoes significant changes during spontaneous activity in the chick cord (Chub and O'Donovan, 2001). After an episode, the chloride equilibrium potential falls by ∼10 mV, corresponding to a decline of intracellular chloride of ∼15 mm. The intracellular chloride concentration is restored during the interepisode interval, presumably attributable to inward chloride pumping via the developmentally regulated cationic-chloride cotransporter NKCC1 (for review, see Delpire, 2000). The effect of chloride extrusion during an episode is to reduce the driving force for chloride-mediated synaptic potentials and hence network excitability. During the subsequent interepisode interval, intracellular chloride recovers, leading to a progressive increase in network excitability. Moreover, the observation that network activity is essentially unchanged in the presence of glutamatergic and cholinergic transmitter antagonists suggests the importance of chloride-mediated transmission (Chub and O'Donovan, 1998).

Collectively, these observations have led to the proposal that the slow depression controlling the interepisode interval might be a manifestation of the reduction of intracellular chloride that accompanies the episode (Chub and O'Donovan, 2001). In this paper, we investigated whether activity-dependent changes of intracellular chloride can indeed result in the expression of spontaneous episodes. We developed a model network with recurrent excitatory connections that was subject to activity-dependent changes of intracellular Cl^- concentration. We show that the behavior of the model reproduces the observed pattern of episodic activity, and we make several predictions, which we test experimentally.

Parts of this work have been published previously in abstract form (Marchetti et al., 2003).

Materials and Methods

Theoretical. We develop and use a mean field three-variable model for a population of “functionally excitatory” cells. The primary activity variable is mean membrane potential, V(t), considered to be temporally averaged over the timescale of a few spikes (Pinto et al., 1996). This V determines the instantaneous firing rate f(V), represented by the sigmoid function and scaled by the maximal firing rate as follows:

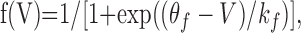where k_f defines the steepness of the sigmoid, and θ_f corresponds to V at which half-maximal firing occurs. This threshold is an approximate measure of firing threshold (chosen to be -43 mV from Chub and O'Donovan, 2001). The other two dynamic variables are as follows: d, synaptic depression (the fraction of synapses not affected by fast synaptic depression), and Cl_i, the intracellular Cl^- concentration that affects firing and coupling through its influence on the GABAergic synaptic reversal potential E_Cl. The following equations describe the network dynamics; the variables represent averages over the population and describe the state of the “typical cell”:

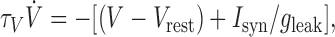(1)

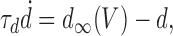(2)

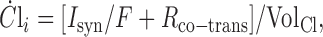(3)

where Ẋ denotes time derivative dX/dt.

The first equation corresponds to the current-balance condition in a cell. In this idealization, spikes have been averaged out because, most of the time, a cell is sitting near rest or driven by strong synaptic inputs to depolarized levels. Therefore, only an effective leakage term remains from the intrinsic spike-generating mechanisms. The time constant τ_V is not merely the membrane time constant. It incorporates the average effect of recruitment in the network (see a few paragraphs below), the membrane time constant, axonal conduction velocity, and synaptic/dendritic delays.

The synaptic current is defined by:

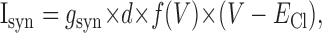(4)

where the effective synaptic conductance is proportional to the maximal level, g_syn (if no synapses are depressed and all cells are firing at the maximal rate), times the fraction of nondepressed synapses d and the firing rate f(V). The synaptic reversal potential E_Cl satisfies the Nernst equation:

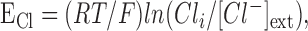(5)

where RT/F is a constant (RT/F ≃ 25 at room temperature). In control conditions, external Cl^- concentration ([Cl^-]_ext) was set to 150 mm.

Equations 2 and 3 describe the dynamics of the variables that reduce synaptic throughput within the network on two different timescales. Synaptic depression on a fast timescale is represented by d; its interaction with V gives rise to intraepisode cycling (Tabak et al., 2000), with cycle periods of hundreds of milliseconds. Because d decreases with activity, d_∞(V) is a decreasing function, which we take to be sigmoidal:

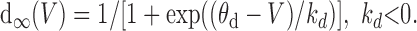Because we averaged over spikes, d_∞(V) incorporates the dependence of the firing rate on V.

On the slower timescale, the chloride dynamics are responsible for episode generation that occurs with intervals of minutes. The slowly changing intracellular chloride concentration, Cl_i, underlies slow depression through its effect on the synaptic driving potential, without a direct effect on synaptic conductance. In accordance with previous experimental data (Chub and O'Donovan, 2001), intracellular chloride is on average extruded during an episode (through chloride-selective ligand-gated synaptic channels) and recovers to pre-episode levels during the interepisode interval, through an active mechanism that transports chloride inward, i.e., the NKCC cotransporter. Equation 3, the Cl^--balance equation, embodies these two mechanisms. It states that the rate at which Cl_i changes depends on two flux terms. The electrical current I_syn when divided by Faraday's constant (F = 9.6485 × 10⁴ C/mol) is converted to molecular flux (moles per second). Because V < E_Cl, this term is negative, corresponding to efflux. The NKCC cotransporter pumps Cl^- inward with the rate R_co-trans (moles per second). These fluxes, when divided by the effective intracellular volume for Cl^-, equal their contributions to the change (per second) in chloride concentration (molar units). We note that, because this cotransporter is non-electrogenic, it produces no net electrical current, and, therefore, the current-balance Equation 1 has no term for it.

In our model, g_leak represents the mean resting conductance for ions other than Cl^-. This is why there is no explicit term for Cl^- leakage current in Equation 3. However, because f(V_rest) is non-zero, there is some Cl^- current at rest. This could be thought to include a leakage component as well as spontaneous GABA-mediated current and spontaneously firing cells (Chub and O'Donovan, 2001); our idealized model does not distinguish these factors.

Currently, we have estimates for only a few cellular parameter values. The resting potential (V_rest = -60 mV) and the leak conductance (g_leak = 3 nS) were estimated from perforated-patch recordings (Chub and O'Donovan, 2001). Effective Cl^--handling volume (Vol_Cl = 0.6 × 10^-9 cm³) was chosen with typical anatomical length scales in mind; in the case of a sphere, it corresponds to a diameter of ∼10 μm. We first estimated R_co-trans by noting that a 10 min interepisode interval increases intracellular chloride by 15 mm (Chub and O'Donovan, 2001). This gave us a value of 15 × 10^-6 pmol/s. This value was increased because I_syn is small but non-zero during the interepisode interval (Chub and O'Donovan, 2001), thereby creating an outward flux of Cl^-. Because we used younger embryos than Chub and O'Donovan (2001), they exhibited shorter interepisodes intervals (∼5 min). For these reasons, we chose R_co-trans = 12 × 10^-5 pmol/s, which resulted in interepisode intervals of ∼3 min (for g_syn = 30 pS) in the model.

We use absolute values for quantities such as g_syn and R_co-trans. Had we used per unit area densities instead, the associated flux terms might have different functional areas. Our model does not distinguish these possibilities.

In Equation 4, g_syn, the maximal total synaptic conductance of a cell, was chosen to be in the range of 18-36 nS and was varied in some figures. This range is consistent with estimates of GABAergic conductance of ∼15 nS (Chub and O'Donovan, 2001); our range for the model is higher to account for the glycinergic component of the Cl^--based synaptic current. The values of τ, θ, and k that we used in the simulations are given in Table 1. For finite values of V, f(V) is never zero, i.e., there is always a minimal level of background activity or fraction of spontaneously active neurons in the network.

Table 1.

Parameter values used in simulations

	τ(s)	k(mV)	θ(mV)
V	τv = 0.1 to 0.2
d∞(V)	τd = 0.6	kd = 2	θd = −45
f(V)		kf = −3	θf = −43

How do we choose values for the parameters τ_V and τ_d? Because we do not have a mathematical derivation of our V formulation of the mean field model, we rely on a rough estimate for what we think is the major contributor to the effective network time constant τ_V. It sets the timescale for recruitment of cells throughout the network, i.e., the time it takes the cells in the distributed network to respond to changes of an exogenous or endogenous input. We estimated the recruitment time empirically as the time it takes for the ventral root (VR) slow potential to rise from baseline to the first peak of an episode (Fig. 1C, NRT). In our experimental conditions (i.e., in the presence of glutamatergic and cholinergic blockers), the average “network recruitment time” NRT was 570 ± 80 ms (n = 11). Therefore, because this value is a few multiples of τ_V, we chose a value for τ_V on the order of 100-200 ms. In some other neural systems, the timescale of synaptic depression τ_d has been estimated to be on the scale of hundreds of milliseconds (Chance et al., 1998). These estimates provide the opportunity for cycle periods in the desired range. In our model, the values for τ_d and τ_V are further constrained by the fact that the output must show fast cycling at a frequency comparable with observed values. In Results, we will see that the behavior of the model in this regard is quite sensitive to the ratio τ_d/τ_v.

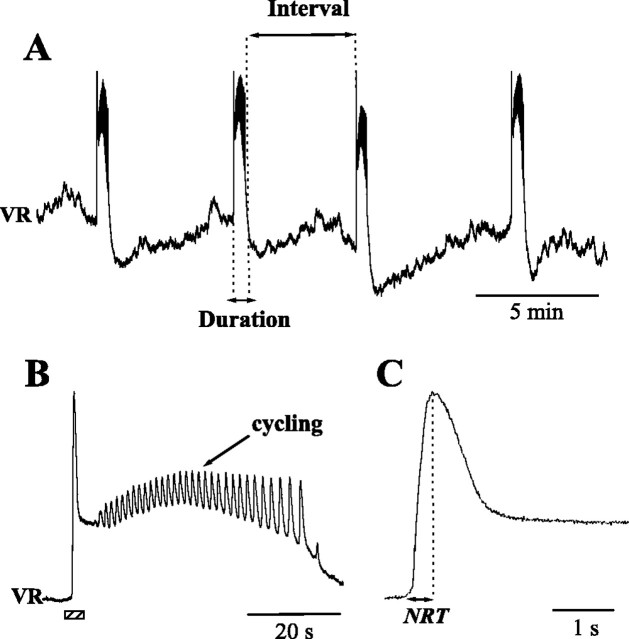
Figure 1.

A, Example of spontaneous rhythmic activity in an E10 chick embryo spinal cord, recorded from a VR. B, Expansion of a single episode (third one from the trace in A), showing the presence of intraepisode cycling. C, Expansion of the first peak (from B, indicated by the bottom bar). Network recruitment time was measured as the time between the onset and the peak of ventral root activity.

The model equations were implemented within XPPAUT (freely available software by G. B. Ermentrout, http://www.pitt.edu/~phase/), an interactive package for numerically solving and analyzing differential equations, which also includes a tool (AUTO) for computing bifurcation diagrams. Simulations were performed using the Gear or the Runge-Kutta method, with a time step of 0.001 s: we confirmed that this gave good accuracy by verifying that results were insensitive to an additional decrease in the time step.

Experimental. Experiments were performed on the isolated spinal cord of embryonic day 9 (E9) to E11 chick embryos. The spinal cord was dissected out in cold (15°C), oxygenated (95% O₂, 5% CO₂) Tyrode's solution containing the following (in mm): 139 NaCl, 3KCl, 17 NaHCO₃, 12 glucose, 3 CaCl₂, and 1 MgCl₂. The solution was then allowed to reach room temperature, and, at that point, the preparation was transferred to a recording chamber. Recordings were started at least 2 h after heating the bath solution at 28°C. The superfusing Tyrode's solution was then kept at 28°C for the duration of experiments. The majority of experiments were performed in the presence of glutamatergic and cholinergic blockers (Chub and O'Donovan, 1998) because we were focusing on the Cl^- (E_Cl) mechanism for episode termination and recovery. For this reason, [K⁺]_o was raised to 5 mm, minimizing the slowing of spontaneous episodes that occurs when these blockers are used, without altering the characteristics of the activity (Chub and O'Donovan, 1998). Glutamatergic and cholinergic blockers were used at the following concentrations: 50 μm AP-5, 5-20 μm 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), 5 μm atropine, 50 μm mecamylamine, and 50 μm dihydro-β-erythroidine (DHβE).

Neuronal activity was recorded with tight-fitting suction electrodes from VRs or muscle nerves. Signals were amplified with high-gain direct current amplifiers [model 3000 (A-M Systems, Carlsborg, WA) or DAM 50 (World Precision Instruments, Sarasota, FL)]. A typical extracellular recording is shown in Figure 1 A: the voltage recorded from one VR sharply rises when an episode begins and decays on a slower timescale. Intraepisode cycling is visible in Figure 1 B, in which one episode is shown at an expanded time base. We measured episode duration and the interepisode interval that is defined as the time between the end of an episode and the beginning of the following one (Fig. 1 A).

Electrical stimulation (0.5 ms pulses at 5-10 μA) was delivered to the cord through the ventrolateral funiculus (VLF) and was used to monitor the effect of drugs that decrease GABAergic activity. Because these experiments were performed in the presence of glutamatergic and cholinergic blockers, we assumed that the responses we were recording were predominantly mediated by GABA and glycine (Chub and O'Donovan, 1998). We measured the early part of the evoked potential, i.e., within 5 ms of the onset, to minimize contributions from polysynaptic pathways. We compared the averages from at least 10 responses obtained under control conditions and 10 min after bicuculline application.

Whole-cell voltage-clamp recordings (“blind patch”) were made with an Axopatch 200B amplifier (Axon Instruments, Union City, CA) from ventral horn neurons located in spinal segments LS1-LS3. Micropipettes were pulled from thin-walled glass capillaries (TW 100-3; World Precision Instruments) with a Flaming/Brown puller (P-80/PC; Sutter Instruments, Novato, CA). Tip resistances in the extracellular solution were 4-6 MΩ. GABAergic currents were recorded in modified Tyrode's solution containing the following (in mm): 129 NaCl, 5 KCl, 17 NaHCO₃, 1 MgCl₂, 0.5 MnCl₂, 12 glucose, 10 tetraethylammonium (TEA)-acetate, 5 CsCl, and 0.001 TTX. To separate indirect effects of the bumetanide on GABAergic conductance, which arise from changing the intracellular Cl^- concentration after blockade of the Na⁺-K⁺-2Cl^- cotransport (NKCC1), we used intracellular solution with high Cl^- concentration containing the following (in mm): 140 CsCl, 10 HEPES, 1.1 EGTA, 1 MgCl₂, 0.1 CaCl₂, 4 Na₂ATP, 0.5 Na-GTP, 1 phosphocreatine, and 10 TEA-acetate. This solution, in contrast to recent perforated-patch recordings (Sung et al., 2000), clamps the intracellular Cl^- concentration and therefore allows measurement of the effects of the NKCC blocker bumetanide on GABA currents, unaccompanied by changes in the intracellular Cl^- concentration.

All signals were digitized through a Digidata 1322A, stored, and analyzed with pClamp 8 software (Axon Instruments). Voltage-ramp protocols, for measurements and analysis of GABA currents, were similar to that published recently (Chub and O'Donovan, 2001).

To maintain constant osmolarity in solutions in which the [Cl^-]_ext was changed (+15 or -15 mm), we raised osmolarity by 30 mOsm in all experiments of this type. In control Tyrode's solution ([Cl^-]_ext = 152 mm), 30 mm sucrose was added. In the case of [Cl^-]_ext = 137 mm, 15 mm NaCl in the Tyrode's solution was replaced with an equal amount of Na-propionate, and 30 mm sucrose was also added. Finally, for [Cl^-]_ext = 167 mm, only 15 mm cholene-Cl was added. For these experiments, glutamatergic blockers (50 μm AP-5 and 20 μm CNQX) were also added to all bath solutions. Receptor antagonists and bumetanide were bath applied. In whole-cell experiments, GABA was locally applied from micropipettes as described previously (Chub and O'Donovan, 2001) by using custom made picospritzer. CNQX, d-amino-phosphonovalerate (AP-5), DHβE, mecamylamine, atropine, bicuculline, dehydroepiandrosterone sulfate (DHEAS), bumetanide, and other chemicals were purchased from Sigma (St. Louis, MO). Significance of data were tested with ANOVA or t tests with an accepted level of significance of 0.05.

Results

In this study, we developed an idealized network model with recurrent functionally excitatory, synaptic connections and used it to show that slow, activity-dependent variations in the chloride reversal potential, E_Cl, produce episodes of activity. The firing rate-like framework of our model provides a plausible approximation to the actual network behavior because spontaneous activity generated by the spinal cord does not depend on the details of network architecture (Ho and O'Donovan, 1993; Chub and O'Donovan, 1998). Furthermore, the model does not require details of the connectivity or biophysical properties of individual spinal neurons (Tabak et al., 2000, 2001).

Our previous ad hoc model exhibited spontaneous switching between two steady states (a low-activity stable one and a high-activity oscillatory one), qualitatively reproducing the experimentally observed rhythmicity, through the interaction of three dynamic variables: an activity variable (a), which represented the average firing rate [f(V) in the present model]; a fast depression variable (d) that acted to limit activity within an episode; and a slow depression variable (s) responsible for terminating an episode and recovering on the timescale of the interepisode interval (Tabak et al., 2000, 2001). Depression variables appeared in the model as activity-dependent multiplicative factors that modulated synaptic input to a cell but were not related to biophysical observable quantities.

In the present work, we propose that intracellular chloride concentration, Cl_i, is the physiological realization of the slow depression variable and that Cl^- (hence, E_Cl) dynamics are, at least in part, the biophysical mechanism that accounts for synaptic depression in the cord. This formulation is less ad hoc, incorporating semiquantitative estimates for some biophysical parameters. The activity-like variable is V, mean membrane potential, temporally averaged over the timescale of a few spikes; synaptic depression, d, on the fast timescale of cycling is like that in our previous model (Tabak et al., 2000, 2001). The mathematical formulation for this three-variable model is given in Materials and Methods (Eqs. 1-5). We show that our model is able to account for the generation of spontaneous episodic activity with intraepisode cycling, as observed in the chick spinal cord. In addition, we used the model to make several predictions and test them by manipulating experimentally accessible parameters, such as GABAergic conductances and [Cl^-]_ext. By comparing model predictions and experimental results, we conclude that Cl^- dynamics is a plausible mechanism contributing to episode generation in the developing spinal cord.

Episodic behavior in the model

Figure 2 demonstrates the behavior of our model and its ability to generate multicycle episodes, in a manner similar to our previous model. Between episodes, most cells are silent and most synapses are inactive, and there is a slow increase in mean membrane potential V (Fig. 2A) as E_Cl is being restored by Cl^- influx (transported by NKCC1) (Fig. 2B). The transport rate R_co-trans determines the timescale of the interepisode interval. When a certain threshold for Cl_i is reached, an episode is initiated and Cl^- flux reverses (Fig. 2B). During an episode, membrane potential is depolarized (Fig. 2A) and Cl^- efflux is very strong (through synaptic channels), as indicated by negative values of Cl^- flux in Figure 2B. As a consequence, Cl_i decreases (also shown in Fig. 2B), and eventually the driving force for synaptic current, V-E_Cl, is not sufficiently excitatory to maintain activity, thereby ending an active phase. When V-E_Cl reaches its minimum, Cl^- flux reverses, becoming positive, and slowly restores higher levels of Cl_i. In this model, the instantaneous firing rate f(V) can be small for low V but never zero (and similarly for the synaptic current). Therefore, a certain fraction of cells is always spontaneously active, and this feature provides the opportunity for recurrent connections to build and propagate activity and generate a new episode.

Figure 2.

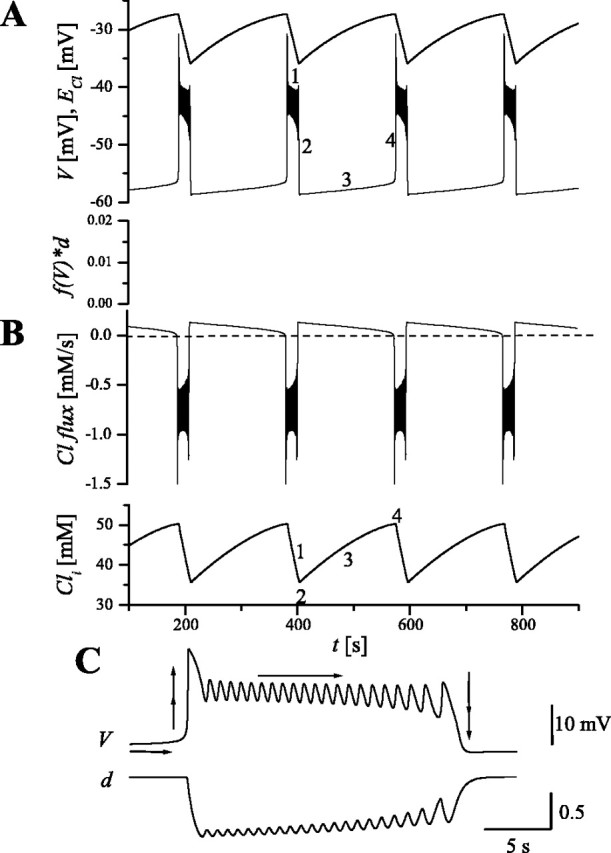
Episodic activity generated by the model. A, Time courses of V and E_Cl (top traces). E_Cl decreases during an episode and recovers during the interepisode interval. Note that V is always lower than E_Cl. Bottom trace is time course of fraction of Cl^- conductance, showing slow rise during interepisode phase (clipped during episode for better visualization). B, Time course of Cl^- flux and Cl_i. Cl^- flux is positive during silent phases (influx attributable to active cotransporter), thus increasing Cl_i, and negative during episodes when chloride flux is dominated by the synaptic current. C, Time course of V and d during an episode, revealing fast cycling; d represents the fraction of nondepressed synapses.τ_d/τ_v = 4, g_syn = 33 nS. Numbers and arrows on time courses refer to features of the episodic rhythm (see Results, Episodic behavior in the model and Fig. 3).

Variations of E_Cl follow changes in the intracellular Cl^- concentration (according to the Nernst relationship; Eq. 5), rising slowly during silent phases and decreasing faster during episodes. E_Cl spans a depolarized range (between -35 and -27 mV for this particular case; values for the parameters of the model are given in the figure legend), in good agreement with values deduced from experiments (Chub and O'Donovan, 2001). The model predicts that, during the time course of an episode and silent phase, the short-time averaged membrane potential V is below E_Cl (and above V_rest). Examining the time courses within an episode (Fig. 2C), we see the cycling activity of V, also in agreement with experimental traces (compare with Fig. 1B). The fast depression variable d oscillates ∼90° out of phase with V, peaking during the down stroke of V during each cycle (Fig. 2C, bottom).

Insight into how the activity switches, between a low-voltage resting state and a high-voltage cycling one, emerges from examining the current-voltage (I-V) relationship (Fig. 3). For this, we rely on the fact that the variable Cl_i varies at a much slower rate than V and d. Therefore, at a given instant of time, we can think of Cl_i having a fixed value, and, to a first approximation, regard it as a parameter of the model rather than as a dynamic variable. We can then find the steady states of the system (that satisfy V̇ = 0 with d simultaneously satisfying ḋ = 0) over a certain range of Cl_i. Figure 3 shows a plot of the two current terms that contribute to voltage dynamics. The term I_leak = g_leak (V - V_leak) is linear in V. Conversely, synaptic current I_syn is non-zero only between V_rest and E_Cl and has negative values because it is an inward current (carrying negatively charged Cl^- ions outward). Here, we assume that the fast depression is equilibrated, i.e., we set d = d_∞(V), and note that the slow variable E_Cl is fixed. The total current I_tot = I_leak + I_syn gives rise to a curve whose shape depends on the E_Cl value (Fig. 3B). This value in turn affects the intersections that the curve has with the abscissa (I = 0). The voltage values for these zero-current crossings define the steady states of the system. In the case of low E_Cl (E_Cl = -42 mV in the figure), there is only one intersection at low V (at approximately -60 mV). Here, the network is not very active because of its low functional connectivity [as implied by the sigmoidal shape of f(V)]. Conversely, if E_Cl is high enough (E_Cl = -23 mV in the figure), there is only one intersection at high V (at approximately -40 mV), corresponding to a state of steady high firing. Finally, for intermediate values of E_Cl, the I-V curve has three zero-current crossings. The low-voltage steady state is stable, the middle state is unstable, and the stability of the high state depends on the relative timescales of V and d, i.e., on the ratio τ_d/τ_v (see below, Changing τ_d/τ_v and the emergence of oscillatory behavior).

Figure 3.

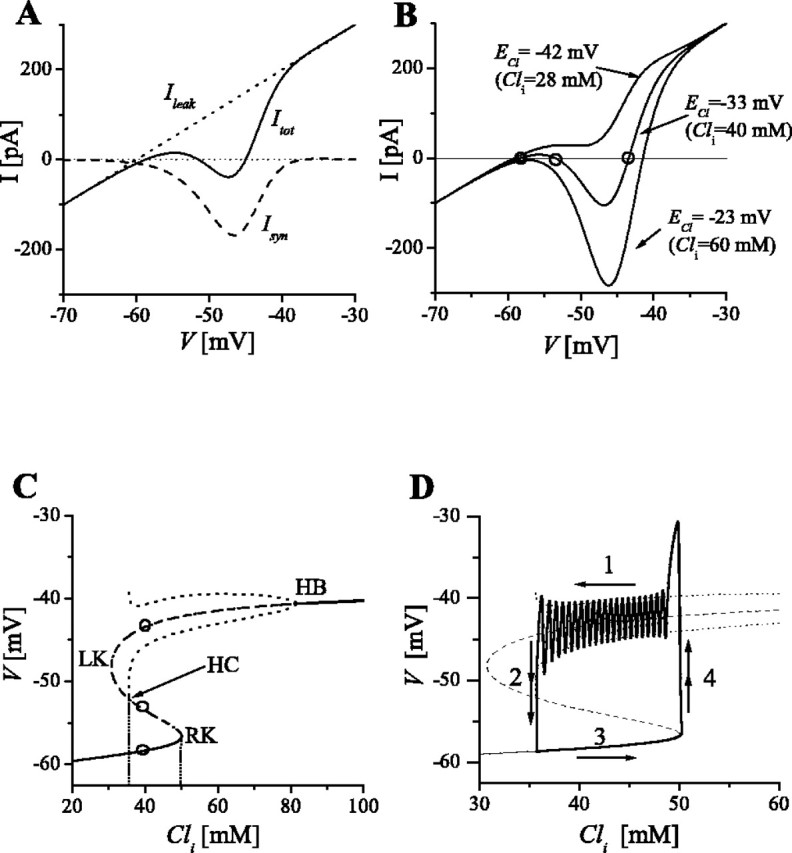
Emergence of bistability. A, Curves showing the variations with V of I_leak (dotted; outward for V > V_rest), steady-state I_syn (dashed; inward, E_Cl = -37 mV), and I_tot = I_leak + I_syn (solid; N-shaped). B, Current-voltage relationship I_tot(V) for different E_Cl values. Steady states are defined by I_tot(V) = 0 and thus graphically correspond to the intersections of the I_tot(V) curve and the horizontal axis. When E_Cl is low (top curve), there is only one intersection, corresponding to a stable steady state of low voltage (V close to V_rest). When E_Cl is high (bottom curve), there is only one intersection, at high V. For intermediate values of E_Cl, there are three intersections with the abscissa (open circles), corresponding to three steady states of different stability (see Results). C, Plot of the steady-state values of V for a range of Cl_i values. The resulting curve is S-shaped, with a lower branch, an upper branch, and a middle branch delimited by the left and right knees (LK and RK). The three steady states shown in B for E_Cl = -37 mV are shown as open circles. Solid portions of the S-shaped curve (lower branch and part of the upper branch) indicate stable states; dashed portions (middle branch and part of the upper branch) indicate unstable states. At the transition from stable to unstable state on the upper branch (HB point), the V-d system with Cl_i treated as a parameter becomes oscillatory, with minimum and maximum values of the voltage indicated by the dotted line. Cycling amplitude increases with decreasing Cl_i until the minimum of the oscillation intersects the middle branch (HC point). The V-d subsystem is bistable for the Cl_i range defined by values associated with HC and RK. D, When Cl_i varies slowly according to Equation 3, it sweeps back and forth over the range of bistability, with the V-d subsystem showing slow evolution (of cycling) during an episode with Cl_i decreasing and then increasing during the interepisode phase; rapid switching between the low activity state and the upper state of cycling occurs at the transition points HC and RK (see Results and Fig. 4 B). The V and Cl_i variables corresponding to the rhythmic time course in Figure 2 are projected here as a trajectory that falls precisely on the path that is predicted. The numbers and arrows here correspond to those from Figure 2 and they represent the following: 1, episode; 2, termination of episode and rapid switch to silent phase; 3, the interepisode phase of low activity; 4, the rapid transition to start of next episode. τ_d/τ_v = 4; g_syn = 33 nS.

The dependence of the steady states of the system on Cl_i, when it is treated as a parameter, are compactly described with a plot in the V-Cl_i plane (Fig. 3C). The S-shaped curve represents the voltage values at steady state over a range of Cl_i values. The lower branch of this S-curve corresponds to the low-V zero-current crossing in Figure 3B. The upper branch of the S-curve corresponds to the high-V zero-current crossing. In the Cl_i range between the left and right knees (LK and RK), there are three steady states of the V-d fast subsystem, with the middle branch of the S-curve corresponding to the middle zero-crossing in Figure 3B. A steady state is unstable at points on the S-curve that are dashed; solid denotes stable. Note that, over much of the Cl_i range shown here, the high-V state is unstable. Hence, stability is not necessarily guaranteed, although the slope of the steady-state relationship, I_tot versus V, is positive. The dynamic interaction between V and d affect the stability of the steady state. However, over much of the Cl_i range shown, here the high-V steady state is “surrounded” by a stable high-V oscillatory state, indicated by the dotted “fork” whose two branches correspond to the maximum and minimum V values of the oscillation. These oscillations correspond to the cycling observed during an episode in the chick spinal cord. The high-V oscillations begin at the point labeled HB (Hopf bifurcation), at which the steady state loses stability. As Cl_i decreases, the oscillation amplitude (peak to trough) grows. The oscillation disappears at the point labeled HC (homoclinic) when its trough decreases to just meet the middle-V value, when the minimum activity in a cycle drops to/below a threshold value.

A significant feature in this model is that, over the Cl_i range between HC and RK, the V-d subsystem is bistable. There is a stable state of high-V oscillations (for cycling within an episode) and a coexistent stable low-V steady state (that corresponds to the silent phase between episodes). One can imagine that, if Cl_i (treated as a control parameter here) were varied slowly back- and-forth throughout this range (and just a bit beyond the two knees), that V would exhibit the time course of an episodic rhythm, switching alternately between a silent phase and an active phase of cycling. This is the essence of what happens in the full three-variable model when Cl_i, coupled mutually through E_Cl to the V-d dynamics, follows its dynamical prescription. To illustrate this point, we take the time course of V and Cl_i (from Fig. 2) and project it as a trajectory (Fig. 3D) onto the (S with fork) diagram from Figure 3C. The numbers and arrows here correspond to those in Figure 2. During an episode (Fig. 3D, 1), the system is in the high-V state of cycling; chloride channels are open, Cl^- efflux dominates, and Cl_i slowly decreases. The system point is drifting leftward along the trajectory. When Cl_i decreases to a critical level (at HC) and activity V during a cycle falls below a threshold level, the episode terminates (Fig. 3D, 2) and V drops down abruptly (Fig. 2D, double arrow) to a low value. During a silent phase (Fig. 3D, 3), when I_syn is very small and the influx of the chloride cotransporter dominates, Cl_i slowly increases and, on the phase plane, the system drifts rightward along the lower branch of the S-curve. At a critical value of Cl_i (at RK on the S-shaped curve), the low-V steady state meets the slowly falling threshold (middle branch) and disappears; V increases abruptly (Fig. 3D, 4), and a new episode begins.

Such bistability in the fast subsystem is a qualitative feature, also seen in our previous models for episodic rhythmogenesis (Tabak et al., 2000, 2001). Based on this bistability, we predicted and confirmed (experimentally and computationally) that, by using a brief stimulus, one could reset the rhythm, e.g., kick the system during the silent phase and abruptly into an episode. Moreover, we confirmed the additional prediction that the duration of the ensuing episode would be shorter if the kick occurred earlier in the silent phase (Tabak et al., 2001).

Note that, during the silent phase, while tracking the lower branch, the system approximately satisfies dV/dt = 0. The net ionic current is zero, and the voltage is essentially satisfying the equilibrium condition (Goldman-Hodgkin-Katz): V ≈ (g_leak V_rest + g_syn,eff E_Cl)/(g_leak + g_syn,eff), where g_syn,eff = g_syn-d f(V). However, the system is slowly depolarizing. This is because E_Cl is slowly increasing as Cl_i increases. The slow depolarization is seen experimentally in many intracellular recordings.

As technical points, we note that response diagrams such as in Figure 3C are called bifurcation diagrams; they indicate how features of solutions vary with parameters and critical parameter values in which solutions emerge or bifurcate. The high-V oscillatory state emerges at point HB, via a Hopf bifurcation (Strogatz, 1994) (see also Rinzel and Ermentrout, 1998), in which the high-V steady state undergoes an exchange of stability, changing from a damped to a growing oscillation as Cl_i decreases. The high-V oscillatory state terminates at HC when the minimum V just reaches the middle-V steady state, forming a homoclinic orbit connection (Strogatz, 1994) (see also Rinzel and Ermentrout, 1998); at this point, the oscillation has zero frequency or infinite period. In our models for episodic rhythms, the cycle frequency drops precipitously at the end of an episode, as apparent in many experimental recordings.

Changing τ_d/τ_v and the emergence of oscillatory behavior

As mentioned in Materials and Methods, the relative values of the time constants τ_d and τ_V significantly affect certain features of the model, especially whether or not bistability and cycling-like oscillations occur in the fast subsystem. Figure 4 illustrates how variations of the ratio τ_d/τ_v lead to different behaviors in the full three-variable model and how these are understood from corresponding effects in the V-d subsystem. The left panels show the time courses of V as obtained from simulations of the full system. The right panels, analogous to Figure 3C, show the response diagrams on the V-Cl_i plane, i.e., the S-shaped curve. The trajectory of the full system is superimposed on the V-Cl_i plane, and, as we expect, it tracks along the stable states, circulating counterclockwise. Notice that, because different values of τ_d/τ_v do not effect the values of steady states in the V-d subsystem, the shape of the S-shaped curve does not change with τ_d/τ_v, although the stability along the curve is strongly affected by the ratio τ_d/τ_v.

Figure 4.

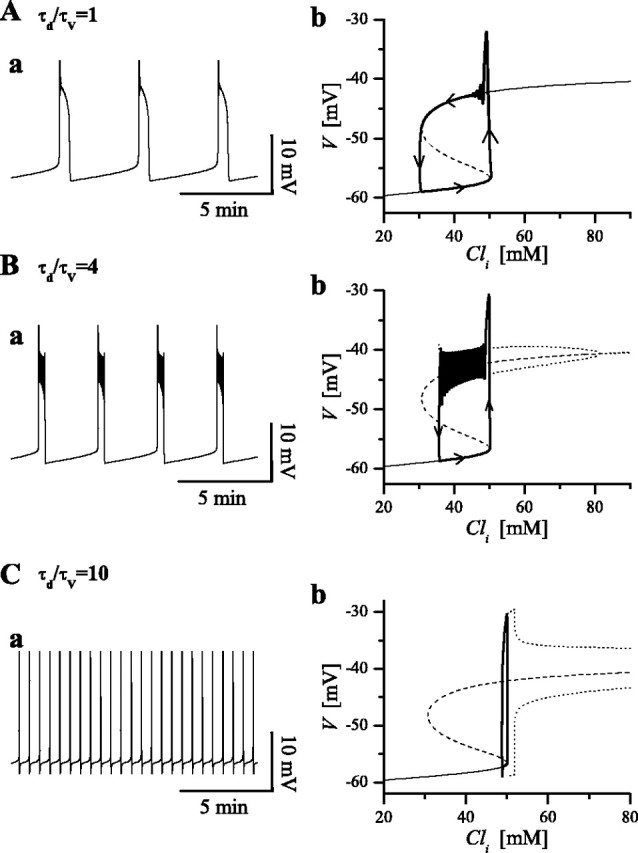
Dependence of bistable behavior on τ_d/τ_v value. A, For low τ_d/τ_v values (τ_d/τ_v = 1), the system is bistable but shows no oscillations in the upper state, as can be seen in the V trajectory (a) and in the response diagram (b). b also shows the trajectory on the V-Cl_i plane, and arrows indicate the direction along which the system moves. B, For τ_d/τ_v = 4, the system is bistable, with a quiescent low-voltage state and an upper oscillatory state, as seen in the V trajectory (a) and in the response diagram (b). During the silent phase, Cl_i slowly increases, and the system moves along the lower branch until it hits a threshold value (corresponding to the RK) and abruptly goes to the upper state. In the active phase, Cl_i decreases along the upper branch, in which it undergoes oscillations because of the presence of the fast depression variable d. When Cl_i reaches the low critical value (at the HC), the voltage drops, and the system goes to the low quiescent state. C, For high τ_d/τ_v values (τ_d/τ_v = 10), the system loses bistability and goes into continuous “spiking” [V trajectory (a) and the response diagram (b)].

For low values of τ_d/τ_v the negative feedback from depression is relatively fast. If it is too fast, cycling oscillations during the active phase are precluded, as seen in time course of V (Fig. 4Aa, for the case of τ_d/τ_v = 1). The corresponding fast subsystem response diagram (Fig. 4Ab) shows that the low-V and high-V steady states are each stable. Therefore, the system shows bistability over the full Cl_i range between LK and RK (Fig. 3C).

As τ_d/τ_v is increased (Fig. 4B), the negative feedback caused by depression is delayed, and this leads to oscillations around the high-V steady state (Fig. 4Bb, dotted curves). The range of Cl_i for which the low-voltage steady state and the high-voltage oscillatory state coexist has changed with respect to the previous case. Now bistability in the fast subsystem occurs over a narrower Cl_i range, between the HC and RK (Fig. 3C).

As τ_d/τ_v is further increased, the range of bistability is further decreased and disappears (Fig. 4Cb), as HC moves to coincide with RK. In this case, the system goes into a regimen of continuous cycling (Fig. 4Ca); such oscillations might be viewed as single-cycle episodes.

In studying the model, we focused our attention on the range of τ_d/τ_v values (∼1-5) in which bistability in the V-d subsystem is expressed over a wide range of g_syn values. With larger values of this ratio, the homoclinic point moves closer to the right knee as g_syn is decreased, thereby reducing the range for bistability. The consequences of this are considered more fully in Discussion.

Effects of g_syn in the model

Within this restricted range of τ_d/τ_v values, we explored the dependence of the model on other parameters that can be related to experimentally accessible variables, thereby allowing for comparison between theory and experiments. First, we investigated how the model was affected by changing the synaptic conductance g_syn, anticipating experiments in which chloride synaptic conductance was decreased, i.e., experiments in which GABAergic conductances were partially blocked (see below, Effects of GABA antagonists in experiments).

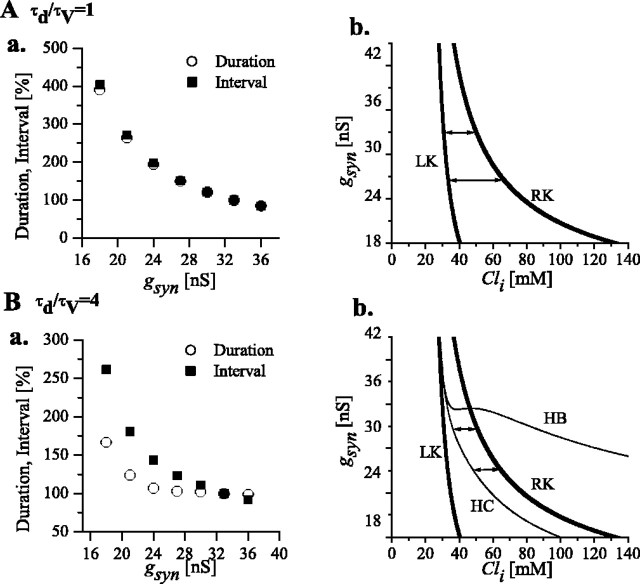
Our simulations show that the episode duration and interepisode interval are affected by g_syn in ways that differ with the τ_d/τ_v ratio, shown in Figure 5 (left) for two values of τ_d/τ_v. Figure 5 (right) presents response diagrams for the V-d subsystem, which show how critical features of the S-shaped curve, including the Cl_i range for bistability of Figure 3C, shift when g_syn is changed.

Figure 5.

Dependence of interval and duration of episodes on g_syn and τ_d/τ_v. A, τ_d/τ_v = 1. a, Duration (open circles) and interval (filled squares) of episodes obtained from simulations for different g_syn values. Data for duration (interval) is normalized to the duration (interval) value at g_syn = 33 pS (control value, also used in Fig. 6). b, Two-parameter response diagrams show how the right knee and the left knee shift with g_syn. The bistability range (range of values covered by Cl_i during episodic behavior) increases with decreasing g_syn; consequently, both interval and duration increase with decreasing g_syn. Double arrows indicate the Cl_i range covered during episodic activity, for two values of g_syn (33 and 27 nS). B, τ_d/τ_v = 4. a, Duration and interval for different g_syn values. b, Two-parameter response diagrams show how the RK and LK (thick lines) and the HC and HB (thin lines) shift with g_syn. Contrary to the previous case, Cl_i covers the range between HC and RK during episodic activity (double arrows; shown for g_syn = 33 and 27 nS). With decreasing g_syn, this range does not increase as much as in A, so interval and durations are less affected.

In the case of τ_d/τ_v = 1 (Fig. 5Aa), we found that both interval (filled squares) and duration (open circles) increased as g_syn decreased. The two-parameter response diagram of Figure 5Ab defines the range of g_syn and Cl_i values over which the bistable regimen occurs, i.e., the area between the right knee and the left knee curves obtained as the two parameters vary. When, during a silent phase, the system follows the low-V branch of the S-shaped curve of Figure 4Ab, Cl_i increases. This corresponds, in Figure 5Ab, to moving from the LK curve toward the RK curve, at a fixed value of g_syn. Analogously, during an episode, the system moves leftward from the RK curve to the LK curve, covering the same Cl_i interval as it did during a silent phase but in the opposite direction.

If g_syn is decreased, the system moves along another parallel line, lower than the preceding one (still between the two curves), and Cl_i is shifted toward higher values. This upward shift in the Cl_i range leads to an increase in both duration and interval when we decrease g_syn.

When τ_d/τ_v is increased to 4 (Fig. 5B), interval and duration of episodes are affected differently than in the previous case. This is because now the Cl_i range spanned is determined by the interval between the right knee RK and the homoclinic point HC (Fig. 5Bb) rather than the left knee as in the previous case. Simulations show that decreasing g_syn over a certain range (18-36 nS) leads to essentially no change in duration, whereas interval decreases significantly (Fig. 5Ba, open circles and filled squares, respectively). The difference with the previous case (τ_d/τ_v = 1, no oscillations) is attributable to the fact that the oscillatory states are affected by a change in g_syn in a different way than the steady states.

Effects of GABA antagonists in experiments

To reproduce experimental conditions comparable with the theoretical ones, we performed experiments in the presence of cholinergic blockers (50 μm mecamylamine, 50 μm DHβE, and 5 μm atropine) and glutamatergic blockers (5 μm CNQX and 50 μm AP-5) to isolate the GABA/glycinergic network. This was regarded as our control condition. Our goal was then to reduce chloride conductance, a manipulation that corresponded to lowering g_syn in the model. To do so, we bath applied low doses of GABAergic receptor antagonists: either the competitive GABA_A antagonist bicuculline (1-2 μm) or the neurosteroid DHEAS (5 μm), an allosteric GABA_A receptor modulator (Majewska et al., 1990; Shen et al., 1999) that reduces open-channel frequency (Mienville and Vicini, 1989). By using two different antagonists, we ensured that the effect was not dependent on the specific blocker.

We first tried to establish how much GABAergic transmission was reduced by the concentrations of bicuculline that we used. This was done by comparing the amplitude of ventral root potentials evoked by stimulation of the VLF before and after drug application. Because these experiments were performed in the presence of glutamatergic and cholinergic blockers, we assumed that the responses we were recording were predominantly GABA/glycinergic. Also, because synaptic responses are depressed after an episode (Fedirchuk et al., 1999), we waited several minutes after an episode before applying the antagonist, thus ensuring that the evoked response had recovered. We then compared the averaged response taken after the antagonist application with the one right before the application, by measuring the amplitude within 5 ms of the onset, to include only the monosynaptic component (see Materials and Methods). We found that, on average, the response was decreased by 26 ± 9% (n = 4; p < 0.05) by bicuculline (a similar decrease was obtained with DHEAS in two other experiments). This decrease can therefore be taken as an indication of the amount of reduction in chloride synaptic transmission in the network and can be used to make comparisons with g_syn manipulations made in the model.

Having established the amount by which synaptic transmission was depressed by low doses of bicuculline (1-2 μm) or DHEAS (5 μm), we investigated the effects of such reduction in GABA transmission on the duration of active and silent phases. Application of the blocker usually stopped episodes for some time, prolonging the silent phase from tens of minutes to up to 1-2 h. After this adjustment period, activity resumed at a slower rate.

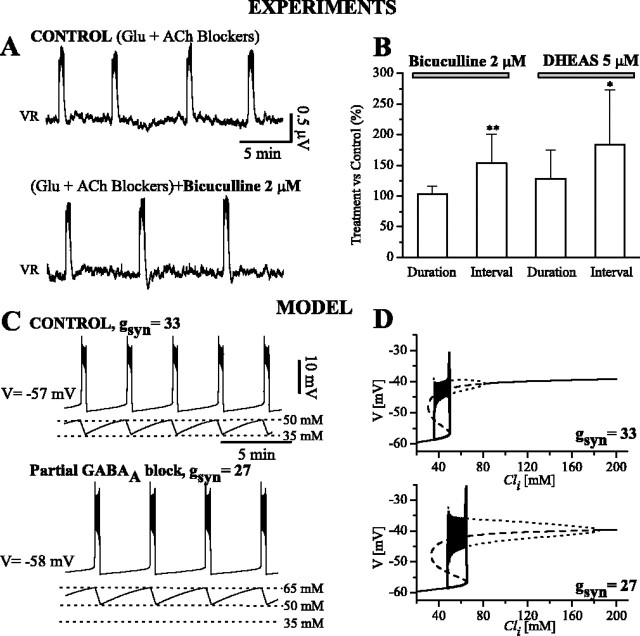
Figure 6A illustrates the slowing of spontaneous episodes by a low dose of bicuculline, and Figure 6B summarizes results for interval and duration with the two treatments. We found that episode duration was not significantly affected in either case, whereas the interepisode interval significantly increased. In the presence of bicuculline, the interepisode interval lengthened to 166 ± 50% (n = 11; p < 0.005) of control, whereas for DHEAS the increase was 180 ± 80% (n = 8; p < 0.05). Episode duration was similar to control in the presence of either drug (bicuculline, 104 ± 12%, n = 11, p > 0.05; DHEAS, 129 ± 44%, n = 8, p > 0.05).

Figure 6.

Effects of decreased synaptic transmission on episodic activity. A, Ventral root recordings from an E10 embryo cord. Control condition is in the presence of glutamate (Glu) and acetylcholine (ACh) receptor blockers. When bicuculline (2 μm) is added, the interepisode interval increases (in this case, by 22%), whereas duration shows no significant change. B, Interval and duration of episodes for pooled data, in the case of bicuculline (n = 11) or DHEAS (n = 8). Data are normalized with respect to control. All experiments were performed in the presence of glutamatergic and cholinergic blockers. Only interval is significantly different from control (^*p < 0.05; ^**p < 0.005). C, Time course of V and Cl_i from simulations (τ_d/τ_v = 4) for g_syn = 33 nS (corresponding to control) and g_syn = 27 nS (corresponding to bicuculline treatment). Interval in this case increases by 19%, and Cl_i range is shifted upward. D, Response diagram and trajectory on the V-Cl_i plane for g_syn = 33 and 27 nS; the Cl_i range over which bistability occurs is higher for lower g_syn.

Constraining model parameters with experiments on synaptic blockade

We found experimentally that inhibiting chloride currents leads to a lengthening of the silent phase, although the active phase duration is not significantly affected. Our model best predicted this behavior in the case of τ_d/τ_v = 4 (Fig. 5Ba). In fact, for a change of g_syn from 33 to 27 nS, there is good agreement between theory and experiments, in which an increase in interval and no significant change in episode duration are obtained (Fig. 6C).

In the model, the correct change in interval is given by a conductance change of ∼20%. This is in accordance with the amount of depression of the synaptic potential that we obtained experimentally from the evoked responses (26 ± 9% in the case of bicuculline).

The prediction for the effects on system behavior when g_syn is decreased can also be visualized, for the model, on the V-Cl_i response diagram (Fig. 6D) (fixed ratio, τ_d/τ_v = 4). In this case, the V values for the lower and upper states are hardly changed, whereas the S-curves and cycling regimen (between HC and HB points) shift rightward by different amounts. This leads to a higher operating range of Cl_i, as well as to a change in amplitude of the oscillations. In particular, for lower g_syn, the Cl_i range spanned is at higher values (Fig. 6C,D). Simulations show that, for this value of τ_d/τ_v, the duration of episodes is not significantly affected, whereas the interepisode interval is lengthened, as shown in the simulation of Figure 6C.

Effects of changing Cl^- flux dynamics

Additional comparison between model and experiments comes from analyzing the response of the system to changes in parameters related to the Cl^- flux, such as the exchange rate of the cotransporter and [Cl^-]_ext.

Experiments to influence these two sources of Cl^- flux are presented in Figure 7. First, we tested the effects of applying bumetanide, a blocker of the cotransporter. If the Cl^- dynamics regulate activity as we suggest, pharmacological blockade of the cotransporter with bumetanide (under glutamatergic blockade) should abolish activity. We found that even low doses (10 μm) of the blocker completely and reversibly abolished spontaneous activity (Fig. 7A, top). We found (Fig. 7A, bottom) that, in our experimental condition, bumetanide only slightly reduces the GABAa conductance from 2.9 ± 0.5 to 2.6 ± 0.4 nS, although the change was not statistically significant (n = 4; t test).

Figure 7.

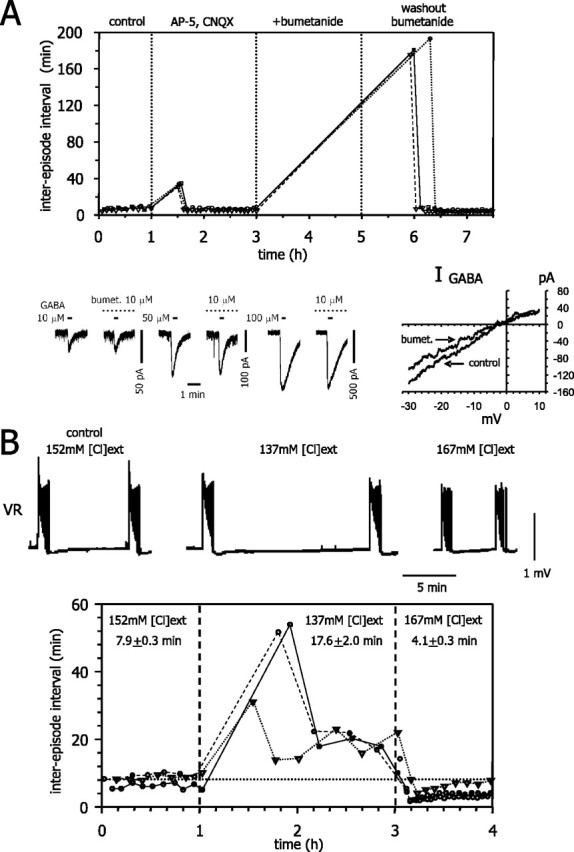
Experimental manipulations of Cl^- flux. A, Blockade of the Cl^- cotransporter with bumetanide. Top, Interepisode intervals before, during (50 μm AP-5 plus 20 μm CNQX) plus 10 μm bumetanide, and during washout of bumetanide. Bumetanide (bumet) completely suppressed activity, which recovered after an initial blockade (3 experiments, in the presence of AP-5 and CNQX, E10-E11 embryos). Bottom, Left, Whole-cell current response of spinal neuron to short (20 s) pressure applications of different GABA concentrations (10, 50, and 100 μm; marked by short lines) in the absence or presence of bath-applied bumetanide (10 μm; marked by dotted lines). Bumetanide does not block the GABAergic current. Currents were recorded from the same cell at a holding potential of -40 mV. Current-voltage relationship for 50 μm GABA application, under control conditions, and in the presence of 10 μm bumetanide (shown on right). Bumetanide has no effect on the reversal potential for GABA but has a slight effect on the conductance. GABA and bumetanide were applied as in the left panel experiments, but a voltage-ramp protocol was used for measurement of the current-voltage relationship. B, Manipulations of [Cl^-]_ext. Top, Ventral root recordings for three different values of [Cl^-]_ext. Decreasing the [Cl^-]_ext has minimal effect on episode duration but strongly increases interepisode interval. Bottom, Plot of the interepisode intervals under three different [Cl^-]_ext (as in the top panel in B; 3 experiments). Numbers on graph are mean ± SE, which at p = 0.05 were significantly different (ANOVA test). The changes in extracellular chloride were made in the presence of glutamatergic antagonists (for additional details, see Materials and Methods).

Another way to affect Cl^- flux, and therefore Cl_i dynamics (in both experiments and simulations), is to manipulate [Cl^-]_ext. We anticipated that such manipulations would affect not only the chloride equilibrium potential but also the rate of inward chloride pumping (R_co-trans). Changing [Cl^-]_ext modifies the NKCC1 rate (Russell, 2000), although the precise quantitative relationship between the two variables is unknown for chick spinal neurons. Experimentally, we found that decreasing [Cl^-]_ext led to a significant increase in the interepisode interval, with little effect on episode duration (Fig. 7B).

To dissociate the effects of changes in E_Cl and R_co-trans on episode behavior, we performed model simulations in which changes in extracellular chloride produced either a change in E_Cl or alternatively altered both E_Cl and R_co-trans. We first ran simulations in which changes of [Cl^-]_ext only affected E_Cl. When [Cl^-]_ext was decreased, the duration of both the episode and the interepisode interval decreased. Conversely, when [Cl^-]_ext was increased, both phases lengthened (Fig. 8A). To understand this, consider a sudden reduction of extracellular chloride during the interepisode interval. This will elevate E_Cl and the driving force for GABA/glycinergic synaptic potentials which, in turn, will produce a premature episode. Because the interepisode interval is shortened, intracellular chloride will not recover to its usual pre-episode level. In addition, this premature episode will be slightly longer than normal, resulting in a greater efflux of chloride. As a consequence, the system will now operate at a lower intracellular chloride concentration, and E_Cl will be to close to its value before the external chloride was changed. A similar argument applies to increases of [Cl^-]_ext.

Figure 8.

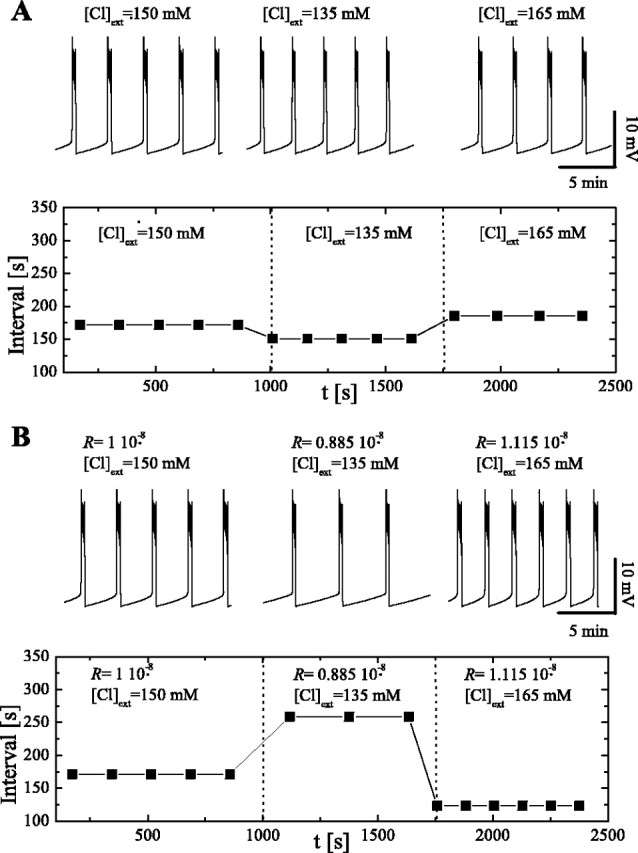
Model behavior under different external Cl^- concentrations. A, Variations of [Cl^-]_ext. Top, Time course of average membrane potential under diferent conditions. [Cl^-]_ext minimally affects episode duration and interepisode interval. Bottom, Plot of the interval under the same conditions as in the top panel. Compare with Figure 7B. B, Variations of [Cl^-]_ext and R_co-trans (rate of Cl^- cotransport). R_co-trans is changed in parallel with [Cl^-]_ext. Top, Time course of average membrane potential under different conditions. Decreasing R_co-trans increases interepisode interval. Bottom, Plot of the interval under the same conditions as in the top panel. Results are similar to experimental results shown in Figure 7B.

These results differ from those observed experimentally. To investigate this further, we performed simulations in which both E_Cl and R_co-trans changed in response to external chloride (Fig. 8B). We allowed R_co-trans to change by ±11% for a correspondent increase or decrease of 15 mm in external chloride. When external chloride was reduced, the interepisode interval lengthened (Fig. 8B), consistent with the experimental data. Accordingly, when it was increased, the interepisode interval shortened. Although there were small changes in episode duration, the dominant effects were on the interepisode interval. These results suggest that the effects of changing extracellular chloride on episodic behavior are primarily attributable to its effects on inward chloride pumping (i.e., on R_co-trans).

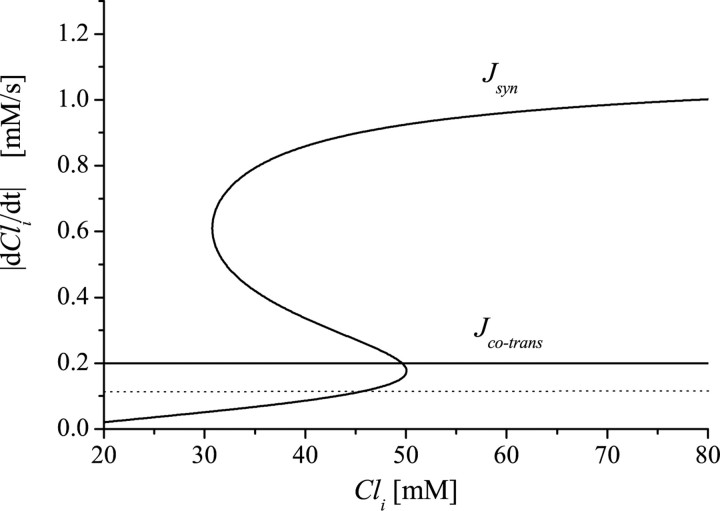
Why do changes in R_co-trans have such powerful effects? This parameter directly affects the net Cl^- flux. These effects can be more easily understood using another graphical representation of the model. We use a response diagram analogous to that of Figure 3C, but now, instead of V, we plot as a measure of response the Cl^- flux (per unit volume) through synaptic channels versus Cl_i. We let J_syn = -I_syn/(F·Vol_Cl) (flux per volume) and plot its value given the steady-state values of V and d (i.e., that correspond to V̇ = 0, ḋ = 0) versus Cl_i to get an S-shaped curve (Fig. 9). We also plot the Cl^- flux per volume through the cotransporter, J_co-trans = R_co-trans/Vol_Cl (horizontal line). Now to analyze the dependence on R_co-trans, we refer back to the Cl^- balance equation, Equation 3 in Materials and Methods, which can be rewritten as dCl_i/dt = J_co-trans - J_syn. If J_co-trans > J_syn, Cl_i is increasing, whereas it is decreasing if the inequality is opposite. When we compare the curve for J_syn and the horizontal line corresponding to the constant J_co-trans, we see graphically that Cl_i increases during the silent phase and decreases during the active phase. Moreover, we see now that, if R_co-trans is decreased (the horizontal line drops down), the velocity of Cl_i is decreased in the silent phase and increased in the active phase, i.e., the interepisode interval increases as we expect intuitively. This treatment predicts that, as R_co-trans is decreased, the percentage of active phase decreases and also that the Cl_i range during the episodic pattern is independent of R_co-trans. In addition, if R_co-trans is decreased such that the horizontal line representing J_co-trans intersects the lower branch of the S-shaped J_syn curve (Fig. 9, dotted horizontal line), activity stops because there is no net Cl^- flux to switch the network to the active phase. It will be worthwhile to test these theoretical predictions when a selective blocker of the Cl^- cotransporter that allows for titrating its rate becomes available.

Figure 9.

Response diagram for J_syn = -I_syn/ (F·Vol_Cl). This diagram shows the steady-state Cl^- flux per volume attributable to synaptic current (J_syn; solid S-shaped curve) and the opposite of the Cl^- flux per volume attributable to the Cl^- cotransporter (J_co-trans; horizontal line). It is similar to the V response diagram but allows graphical determination of the net Cl^- flux. The derivative of Cl_i is equal to (J_co-trans - J_syn) and therefore is represented on the diagram by the vertical distance between the horizontal line and the S-shaped curve. During the interepisode interval, the system is tracking the lower branch, so the derivative is small but positive (Cl^- slowly flows inside). During an episode, the system tracks the upper branch, and the derivative is large and negative (large outward Cl^- flux). If the cotransporter rate is decreased, the horizontal line moves down, closer to the lower branch. This decreases the inward Cl^- flux during the intervals and (slightly) increases the outward Cl^- flux during the episodes. If J_co-trans is too small (dotted horizontal line), the horizontal line moves under the right knee, its intersection with the lower branch of the S-shaped curve defines a stable steady state, and episodic activity is lost.

Discussion

We formulated and implemented a new firing rate model (i.e., mean V) to help explain the emergence of spontaneous rhythmic activity in the developing chick spinal cord. Our model shows how a biophysical mechanism based on chloride dynamics (i.e., slow variations in Cl^- concentration) can underlie the episodic rhythmic activity. It involves three essential mechanistic ingredients: bistability in the recurrent (functionally) excitatory network, constraints on the timescales τ_d and τ_v (to achieve cycling during episodes), and slow dynamics of Cl^- handling. Admittedly, our mean field description is highly idealized compared with a biophysically detailed cell-based network model. Nevertheless, our model incorporates plausible chloride dynamics. Values for the chloride conductance, the leak conductance, and the rate of inward chloride pumping are in fact derived from measurements on embryonic chick spinal neurons (Chub and O'Donovan, 2001). However, for the emergence of bistability, it is the ratio of conductances (total synaptic to leakage) that is more critical than the absolute value of these parameters. Episodic activity in the model occurred only when the ratio was large enough but within a fairly broad range of values (∼6-12).

Time constants of the model

There are two distinct timescales in the model: a slow one, determined by Cl^- dynamics (giving rise to episodes), and a fast one, determined by τ_d and τ_v (underlying the cycling and its frequency). The parameter τ_v, appearing in the voltage equation, is not simply a membrane time constant but also reflects the timing of the network input to the neuron. Therefore, it can be related to a “network recruitment time constant” that accounts for buildup of activity within the population of neurons. We estimated this value based on the time-to-peak of the ventral root potential recorded at episode onset. Setting τ_v in this manner resulted in intraepisode cycle frequencies that are in good agreement with those observed experimentally (∼1 Hz at the beginning of the episode).

A critical parameter in the model is the ratio τ_d/τ_v. We found that this ratio had to be within a certain range for the model to display fast cycling. If it was too small, i.e., fast depression was speeded or network recruitment was slowed, cycling was lost (although bistability and cycle-less episodes were retained). If, conversely, τ_d/τ_v was too big, i.e., depression is slow compared with network recruitment, then bistability was lost and the model did not exhibit episodes of activity. The sensitivity of our model to the ratio of these time constants is analogous to that of conductance-based models of bursting for neurons or pancreatic β-cells. In such models, the timescale in the fast subsystem of negative feedback and that of the autocatalytic process should be comparable (Rinzel, 1985; Sherman et al., 1988).

As the ratio τ_d/τ_v increased, on the two parameter response diagrams (Fig. 5B) the homoclinic point moved toward the right knee, thereby limiting the range of bistability. Under these conditions, decreasing g_syn led to an increase in interepisode interval and no significant change in the duration of the episode, as observed experimentally. Additional (but not too much) increase of the ratio led to a decreasing trend of both episode duration and interepisode interval (with decreasing g_syn), which was not observed experimentally. Increasing τ_d/τ_v even more eliminated typical episodic behavior and led to single-cycle rhythmicity, a prediction for possible future experiments.

Comparison of model predictions and experiment

We found that a 20% decrease in g_syn replicated an ∼25% decrease in the amplitude of GABAa/glycinergic ventral root potentials, for a reasonable range of τ_d/τ_v, as mentioned above. We also found that the effects of changing extracellular chloride on interepisode interval could be explained if we assumed that R_co-trans covaried with the extracellular chloride concentration (Russell, 2000). We found, however, that the experimentally observed increase in interepisode interval in the presence of reduced extracellular chloride (Fig. 7B) differed from the model results (Fig. 8B) in two respects. First, the model did not exhibit the partial recovery shown by the experiment. Experimentally, we found that the interepisode interval initially increased by ∼3-5× when the external Cl^- concentration was reduced and then recovered to a stable lower (2×) level. The most likely explanation for this difference is that experimental changes in external chloride will affect other systems not represented in the model. In our previous model (Tabak et al., 2000, 2001), we note that spontaneous activity naturally compensates for externally imposed perturbations, and this may be another example of this homeostatic effect. The second difference between theory and experiment was that the experimental increase in the interepisode intervals was greater (∼3-5×) than in the simulations (∼1.5). The smaller changes in the interepisode intervals of the model probably occurred because the decrease in R_co-trans was limited to ∼11%. If it was lower than this, episodic activity ceased.

Our model gave several important results regarding Cl^- dynamics that could be tested in future experiments using chloride-sensitive electrodes or imaging. First, in the model, the mean membrane potential V is always lower than E_Cl throughout the episode, implying that GABA is depolarizing throughout the episode. Second, the model predicts an upward shift of the Cl_i range as g_syn decreases. This mechanism acts to compensate the decrease in g_syn (within certain limits) and allows episodes to recover without the involvement of any additional mechanisms. This prediction is analogous to the one that emerged in the previous s model, in which a loss of glutamatergic synapses was compensated by an increase in the amplitude of GABA/glycinergic synaptic potentials (Tabak et al., 2001).

Limitations of the model

Our model is necessarily incomplete because developing spinal networks include glutamatergic and cholinergic synaptic connections. During development, the relative balance of the various neurotransmitters systems changes. For example, in the early development of the chick cord, spontaneous activity appears to be most dependent on cholinergic transmission (Milner and Landmesser, 1999). With additional development, GABAergic systems dominate (Chub and O'Donovan, 1998), but, as the chloride equilibrium potential falls, glutamatergic connectivity becomes more important. At the ages we examined in the present work, GABA/glycinergic systems dominate. Indeed, by performing manipulations of extracellular chloride, we were able to demonstrate that the effects on episode duration and interepisode interval could be explained by changes in the inward rate of chloride pumping.

A second shortcoming of the model is that it takes no account of the location of GABA/glycinergic synapses on the neuronal surface. Closely related to this point is the fact that we assumed that the effects of the chloride conductance are exclusively excitatory, but the balance of excitatory and inhibitory effects of GABA depends on the synaptic location (Sernagor et al., 1995; Gulledge and Stuart, 2003). In fact, it has been shown previously that the conductance can sometimes be functionally inhibitory, presumably because of shunting (O'Donovan, 1989; Sernagor et al., 1995; Marchetti et al., 2002).

Finally, we emphasize that this model provides no explanation of the “fast” form of synaptic depression that regulates cycling within the episode. Although we believe that short-term transmitter depletion is the most likely mechanism responsible for this depression, we have no direct evidence to support this idea for neurons participating in rhythmogenesis. It has been shown that primary afferent synapses of the chick cord do exhibit a short-term synaptic depression (Lee and O'Donovan, 1991) that has been identified with transmitter depletion in the neonatal rat spinal cords (Lev-Tov and Pinco, 1992; Seebach and Mendell, 1996; Li and Burke, 2002). In future experiments, it will be important to investigate the dynamics of synaptic transmission to establish whether this type of depression exists in neurons participating in rhythmogenesis.

Significance of the model

Our model is consistent with the idea that chloride dynamics play an important role in the genesis of spontaneous activity in the in vitro chick spinal cord between E9 and E11. In addition, it may also explain some of the developmental changes in the nature of spontaneous activity in the developing spinal cord. Early in development, episodes of activity comprise one to two bursts separated by interepisode intervals of 1-2 min. As age increases, both the episode duration and the interepisode interval lengthen (Tabak et al., 2000). A possible explanation from the model could be that, because the surface to volume ratio decreases as cell size increases with development, chloride dynamics slow during both the episode and the interepisode interval. This slowing increases both episode duration and the interepisode interval.

Chloride dynamics may also be important in the spontaneous episodic activity of adult networks. Cohen et al. (2002, 2003) suggested that focal epilepsy of the mesial temporal lobe, characterized by synchronized bursts originating in the subiculum, resulted from a resurgence of developmental features after trauma. In particular, they showed that, in epileptic tissue, some pyramidal cells were depolarized by GABA and that these depolarizing GABA responses contributed to the epileptic activity. Given the similar temporal structure between interepisode epileptic activity of adult network and spontaneous episodic activity in developing networks, it may be that both types of activity are regulated through similar mechanisms, with Cl^- homeostasis playing a critical role in both.