Modeling Cooperative Volume Signaling in a Plexus of Nitric Oxide Synthase-Expressing Neurons

Abstract

In vertebrate and invertebrate brains, nitric oxide (NO) synthase (NOS) is frequently expressed in extensive meshworks (plexuses) of exceedingly fine fibers. In this paper, we investigate the functional implications of this morphology by modeling NO diffusion in fiber systems of varying fineness and dispersal. Because size severely limits the signaling ability of an NO-producing fiber, the predominance of fine fibers seems paradoxical. Our modeling reveals, however, that cooperation between many fibers of low individual efficacy can generate an extensive and strong volume signal. Importantly, the signal produced by such a system of cooperating dispersed fibers is significantly more homogeneous in both space and time than that produced by fewer larger sources. Signals generated by plexuses of fine fibers are also better centered on the active region and less dependent on their particular branching morphology. We conclude that an ultrafine plexus is configured to target a volume of the brain with a homogeneous volume signal. Moreover, by translating only persistent regional activity into an effective NO volume signal, dispersed sources integrate neural activity over both space and time. In the mammalian cerebral cortex, for example, the NOS plexus would preferentially translate persistent regional increases in neural activity into a signal that targets blood vessels residing in the same region of the cortex, resulting in an increased regional blood flow. We propose that the fineness-dependent properties of volume signals may in part account for the presence of similar NOS plexus morphologies in distantly related animals.

Introduction

The gas nitric oxide (NO) is a signaling molecule in the CNS of both vertebrate and invertebrate animals (for review, see Garthwaite and Boulton, 1995; Davies, 2000; Jacklet, 2001). The small size and nonpolarity of NO mean that it can pass through lipid membranes and rapidly diffuse away from the source neuron with limited impediment from intervening cellular structures (Lancaster, 1997; Liu et al., 1998, 2002). Because NO synthase (NOS) is not necessarily confined to presynaptic or postsynaptic specializations, NO can potentially be released from extensive extrasynaptic regions of nitrergic neurons (for counter-examples, see Cao and Eldred, 2001; Burette et al., 2002; and Discussion). These features suggest that NO participates in non-synaptic volume signaling in which a relatively extensive region containing many potential targets may be affected (Gally et al., 1990; Montague et al., 1991; Edelman and Gally, 1992; O'Shea et al., 1997; Ott et al., 2001). Physiological evidence for such extensive NO signals that function without synapse specificity over distances exceeding 150 μm has been obtained in rat cerebellum (Hartell, 1996, 2001; Jacoby et al., 2001).

A number of studies have shown that source morphology influences the spatial and temporal properties of the NO signal (Gally et al., 1990; Montague et al., 1991; Lancaster, 1997; O'Shea et al., 1997; Philippides et al., 2000). Considering this, it is noteworthy that NOS-expressing neurons frequently adopt similar plexus morphologies in widely differing organisms. In the mammalian cerebral cortex, for example, a sparse scattered population of NOS-expressing neurons invade the entire neuropil with an extensive network of exceedingly fine fibers (Vincent and Kimura, 1992; DeFelipe, 1993). The fiber diameters approach the practical lower limits imposed by the need to accommodate essential organelles. In other words, it appears that, if these nitrergic fibers could be finer, they would be. We document in this study that a strikingly similar picture emerges from an analysis of nitrergic neurons in invertebrates. Such a widespread occurrence of a fine plexus morphology suggests that it confers some functional advantage over a system comprising fewer coarser fibers. In previous work, however, we showed that the smaller the NO source, the less effective it is in generating an NO signal in its vicinity (Philippides et al., 2000). This suggests that an effective volume signal cannot be generated by very slender fibers unless many in the same region cooperate in a manner proposed by Gally et al. (1990) and Montague et al. (1991).

Although these were important early models of volume signaling, they were not intended as analyses of the signals or of the spatial scale over which cooperation might occur (Montague et al., 1991). Using a model that is explicit about the spatial and temporal scales of NO diffusion, we show that effective cooperation between fine fibers will indeed occur over the spatial scales encountered in real plexus morphologies over a wide range of parameter values. Moreover, the ensuing spatiotemporal properties of the volume signal provide one possible functional explanation for the widespread occurrence of ultrafine plexus morphologies adopted by nitrergic neurons.

Materials and Methods

NOS histochemistry. NADPH diaphorase (NADPHd) histochemistry was used to reveal the detailed arborization morphology of NOS-expressing neurons (Dawson et al., 1991; Hope et al., 1991). Frozen sections of formaldehyde-fixed rat brain were prepared and stained following the protocol of Vincent and Kimura (1992). For detection of NOS-related NADPHd expression in locust, brains including the optic lobes and ocelli were fixed in methanol/Formalin and treated with acetate buffer, pH 4. The protocol is described and discussed in detail by Ott and Elphick (2002). To optimize anatomical resolution further, a polyester wax preembedding technique was used in place of frozen sections. The protocol was given in detail previously (Kurylas et al., 2005). In brief, intact brains were stained en bloc and dehydrated following the whole-mount NADPHd protocol of Ott and Elphick (2003), infiltrated with polyester wax (BDH, Poole, UK) at 40°C (15 min each in 20, 40, 60, and 80% polyester wax in methanol and two times for 1 h pure polyester wax), and cut at 5-10 μm. Sections were dewaxed in methanol and mounted in aqueous medium (Immu-Mount; Shandon, Pittsburgh, PA).

General NO diffusion model. Diffusion of NO was modeled using the structure-based model of Philippides et al. (2000, 2003). A complete explanation of the methods used is given by Philippides (2001). Briefly, in this approach, the dynamics of diffusion are governed by the modified diffusion equation with first-order decay:

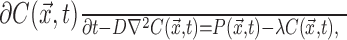(1)

where 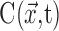is the concentration at point 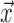and time t and

(2)

The following values were used for parameters pertaining to the properties of NO except when stated otherwise. The production rate Qρ = 1.32 × 10^-4 mol · μm^-3 · s^-1, which gives a good match to experimental data (Philippides et al., 2000), although its value is likely to vary not only with the degree of activation of a particular nitrergic neuron but also between different types of NOS-expressing neurons. Note, however, that after integrating Equations 1 and 2 to produce solutions, the production rate is a constant that multiplies the resulting concentrations as in Equation 3 below. Thus, the results are qualitatively independent of Qρ, and the effect of a different value can be seen simply by rescaling the concentrations. The diffusion coefficient D = 3300 μm² · s^-1 as measured in an aqueous salt solution (Malinski et al., 1993). Because NO is dilute, D is assumed to be independent of NO concentration and thus constant (Vaughn et al., 1998b). This value has been used widely (Lancaster, 1994; Wood and Garthwaite, 1994; Vaughn et al., 1998a). The decay rate is λ = 0.1386 s^-1, giving a half-life (t_1/2) of 5 s, which is that recorded for dissolved NO perfused over living tissues in oxygenated saline (Moncada et al., 1989). The effects of varying D and λ are explored in detail in Results.

Single fiber sources. For straight NO-producing fibers with a circular cross-sectional area, Equations 1 and 2 can be solved analytically to give the following:

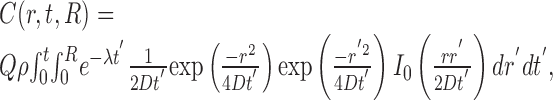(3)

where C(r, t, R) is the NO concentration at a distance r from the center of a fiber of radius R that has emitted NO continuously for the previous t seconds (Carslaw and Jaeger, 1959; Philippides et al., 2003). Note that the solution is radially symmetric and has no dependence on the length of the source because the fiber is infinitely long (see below). Equation 3 was integrated numerically using an extended trapezoidal rule (Press et al., 1992) for the outer integration (over time) and an adaptive recursive Newton Cotes 8 panel rule (Davis and Rabinowitz, 1984) for the inner integration (over radial distance). This integral is improper at t = 0, and so it should be noted that, at t = 0, the instantaneous solution (i.e., the value of the inner integral at t = 0) is as follows:

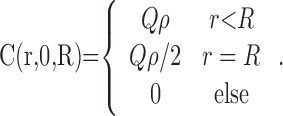(4)

Routines were written in the programming language Matlab (MathWorks, Natick, MA) using a custom program for the outer integration and the “quad8” function for the inner, with solutions evaluated to a relative accuracy of 0.5%.

Numerical solution for multiple and branched sources. For multiple or branched fiber sources, Equations 1 and 2 were solved numerically using alternating direction implicit (ADI) finite difference methods in two and three space dimensions (Ames, 1992). In these schemes, space is first discretized into a square or cubic grid, and then each time step is split into two or three substeps, one for each spatial dimension. For each substep, only one spatial derivative is evaluated at the advanced time step, which ensures that the resultant subsystem is tridiagonal and therefore tractable (Press et al., 1992). For the two-dimensional version we have the following:

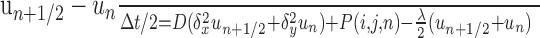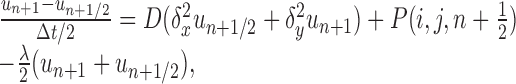(5)

where Δx, Δy, and Δt are the spatial and temporal step-sizes, respectively, and

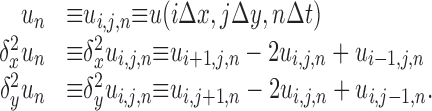(6)

Note that concentrations at the advanced time step u_n+1 are derived using the solution at the intermediate time step u_n+1/2, which is not itself a valid concentration but rather an approximation to the solution at the time n+1. For the three-dimensional version, two subsequent approximations, u^*_n+1 and u^**_n+1, to the solution at the advanced time step are generated in the course of deriving the actual solution, u_n+1, as follows:

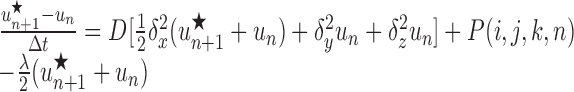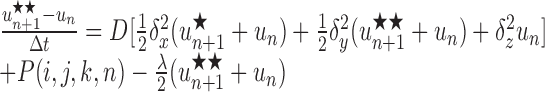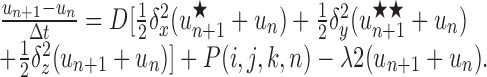(7)

Here the notation has been extended from two to three dimensions in the obvious way so that, for instance, Δx, Δy, and Δz are the spatial step sizes and

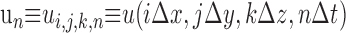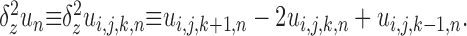(8)

Fibers in the difference equation models have square cross-sectional areas, and the length of one side of the square is referred to as the “diameter” of the source. Because solutions are generated on a grid of finite size, the concentration gradient at the edge of the grid must be specified as a boundary condition. For the data presented here, we assumed that the gradient is flat at the edge of the grid. To ensure that this assumption and the size of the grid had negligible effect on the solutions (<0.5% relative error), we reran the models with a constant gradient at grid edges. Spatial and temporal scales were also checked by rerunning with smaller values and were found to have negligible effect. The program to solve the equations was written in C; for full details of the implementation and a broader introduction to the methods used, see Philippides (2001).

Arrays of parallel fibers. To model the diffusion of NO from parallel arrays of straight, unbranched fibers, we used the two-dimensional variant of the ADI finite difference equation technique with a 1000 × 1000 μm² or 3000 × 3000 μm² grid, a spatial scale (step size) of 1 μm, and a time step of 1 ms. Ordered arrays were constructed by spreading fibers evenly within a central square region of the grid referred to as the “synthesizing region” so that each fiber is the same distance, S, from its immediate neighbors. This distance is the “separation” of the fibers and is measured from the center of one fiber to the center of its neighbor.

Both the single fiber model (analytical solution) and the two-dimensional ADI model (parallel fiber arrays) assume fibers of infinite length. Because the fibers are straight and the arrays parallel, the solution is symmetric along the z-axis. Thus, we give results only for cross-sectional slices in a single plane perpendicular to the direction of the fibers. For finite fibers, the results are for obvious reasons dependent on fiber length, with shorter fibers yielding lower lateral NO concentrations. However, in the present context, we are concerned solely with the signaling implications of different fiber diameters and configurations, and infinite fiber length was assumed throughout. Moreover, for finite fibers of the dimensions seen in the locust optic lobe (2 μm diameter, >250 μm long), the signal around the center of the fiber is negligibly different from the infinite case (Philippides, 2001).

Plexus of fibers. To model NO diffusion from plexuses of fibers, we used the three-dimensional version of the ADI difference equation technique with a 300 × 300 × 300 μm³ cubic grid, a spatial step size of 1 μm, a time step of 4 ms, and the same flat boundary condition as for arrays. Plexuses with a density of 0.01 were generated in the central 100 × 100 × 100 μm³ subvolume of the main volume (referred to as the “synthesizing volume”) using the following growing algorithm. (1) Randomly select a face of the inner cube that is the synthesizing volume. (2) Randomly select a starting point on the face. (3) Randomly select fiber length (in the range [5, 50]) and orientation (ensuring fiber grows forward with respect to parent fiber). (4) Randomly decide (with a probability of 0.25) whether the fiber branches at its endpoint or not. (5) If fiber branches, repeat from step 3 for each branch, ensuring that each fiber grows into a different hemisphere; if not, repeat from step 3. The process continues until a density of source of 0.01 is reached inside this volume. If a fiber exits the synthesizing volume, that fiber is terminated at the exit point. If at any point there are no fibers remaining for further growth, one restarts the process from step 1, keeping the fibers already produced. Several different parameter values for the maximum and minimum fiber length and probability of branching were tried, with negligible effects on the results (Philippides, 2001). The algorithm is not meant to mimic any particular instance of a neuronal growth strategy but simply to be a random growth process. Note also that, in our case, the growth process is not itself shaped by NO but serves only to create a plexus in which to study the effect of morphology on the NO signal generated by it. This is complementary to the model of Montague et al. (1991), who studied the effect of a diffusible signal on activity-dependent connectivity and branching morphology.

Results

The fine NOS plexus in mammalian and invertebrate brains

The NADPH diaphorase reaction is a sensitive histochemical marker for NOS (Bredt et al., 1991; Dawson et al., 1991; Hope et al., 1991) that delineates NOS-expressing neurons in sharp, Golgi-like anatomical definition. An analysis of NOS expression in the brains of both vertebrate and invertebrate animals reveals the widespread occurrence of extensive, disordered, and seemingly random meshworks, composed predominantly of exceedingly slender fibers (Fig. 1). In the mammalian cerebral cortex, NADPH diaphorase staining shows a sparse and scattered population of NOS-expressing neurons (Bredt et al., 1991; Vincent and Kimura, 1992). As illustrated in Figure 1, A and B, the perikarya of these relatively few neurons give rise to an extensive plexus of remarkably fine nerve fibers that invade the entire volume of the cortex. Similar plexus architectures, consisting of very fine NOS-positive fibers, have also been observed in the two major invertebrate Phyla, namely mollusks [e.g., in the brain of the cuttlefish, Sepia officinalis (Di Cosmo et al., 2000)] and arthropods [e.g., in the CNS of the locust, Schistocerca gregaria (Elphick et al., 1996; Ott and Burrows, 1998)]. A particularly striking example of a fine NOS-positive plexus can be seen in the medulla neuropil of the optic lobe associated with the compound eye of the locust (Fig. 1C,D).

Figure 1.

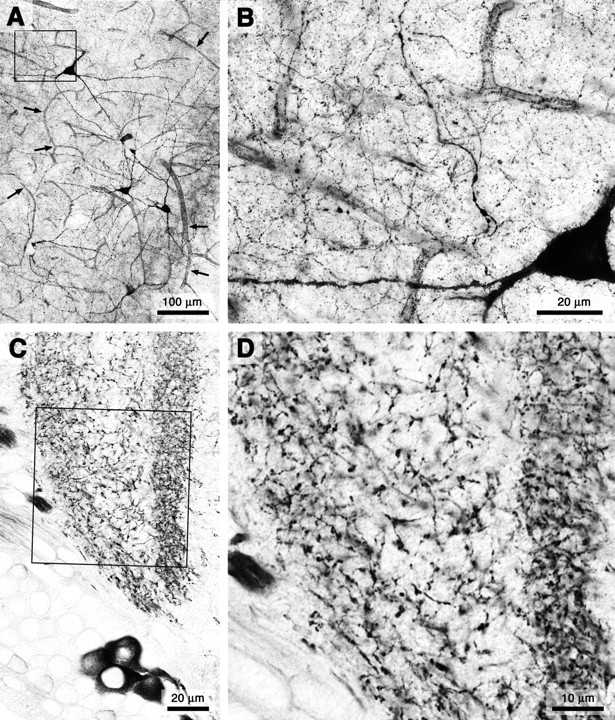
Plexus morphology of NOS-expressing fibers in the brain of a vertebrate (rat; A, B) and an insect (locust; C, D). Both groups of animals have convergently adopted an NO source architecture in which extensive meshworks of exceedingly fine fibers arise from comparatively few neurons. A, The plexus of NOS-expressing fibers in the rat cerebral cortex arises from a scattered population of neurons. Targets include both an extensive volume of (synaptic) gray matter and the blood vessels within it (small arrows in A). B, High-power image of the region indicated by the black frame in A reveals the ubiquity of exceedingly fine fibers that constitute the plexus. C, The plexus of NOS-expressing fibers in the medulla of the locust optic lobe is similarly derived from few neurons and pervades an extensive volume of synaptic neuropil. D, High-power view of the region indicated by the black frame in C.

In all cases, the great majority of the plexus fibers is far less than 1 μm in diameter, and such fibers therefore are likely to have only very limited capacity for NO signaling (Philippides et al., 2000, and below). Nonetheless, it is reasonable to assume that NO generation by an ultrafine plexus does serve a signaling role and, moreover, that an effective signal within a region may result from the summation of NO derived from many small dispersed sources. This however does not explain why ultrafine fibers appear to have been favored by evolution, because the same targets could be affected by scattering fewer but larger sources within the same region (e.g., by a coarse plexus). Because this clearly does not correspond to the typical NOS plexus architecture, there may be signaling advantages to be gained by dispersing many small NO sources rather than adopting a morphologically simpler arrangement using fewer larger ones.

In the following sections, we investigate the properties of plexus-mediated NO signaling. We first analyze the relationship between source diameter and the spread of NO from single fibers. We then examine the spatial and temporal dynamics of NO signals generated by multiple cooperating fibers. In interpreting the data, it is important to note that there is continuing uncertainty in the literature about the half-maximally effective concentration (EC₅₀) of NO on its primary receptor, soluble guanylyl cyclase (sGC). The range reported is from ∼1 μm (Artz et al., 2001) to ∼1 nm (Mo et al., 2004). The reported sensitivity of another NO target, the respiratory enzyme cytochrome c oxidase, whose inhibition by NO causes synaptic depression, falls in the middle of this range (IC₅₀ values of ≈120 nm at 20-30 μm O₂) (Bon and Garthwaite 2001, 2002; Bellamy et al., 2002). At times, it is nevertheless helpful to assume a nominal threshold concentration that must be reached within a region for NO to be effective. This allows us to refer to an “affected region” as the volume of the brain containing NO above the nominal threshold concentration and then to quantify and compare the extent of the volume signals that arise from different source configurations. It is important to bear in mind, however, that no sharp threshold exists for a graded signal such as NO.

NO signaling by single nerve fibers: effect of fiber diameter

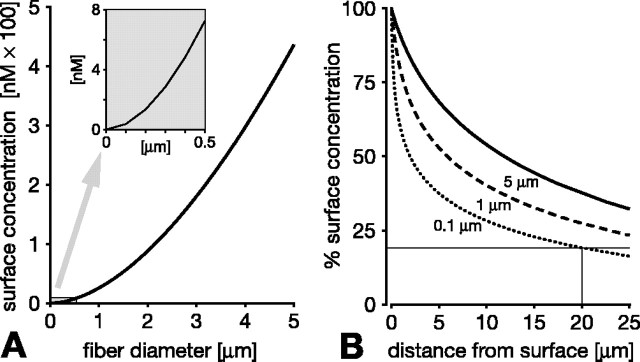
For spherical NO sources, size is a major factor limiting the range of an effective NO signal (Philippides et al., 2000). To assess the signaling efficacy of nitrergic nerve fibers rather than spheres, we modeled the diffusion of NO from long cylinders of varying caliber (Fig. 2). Again, source size, in this case fiber diameter, is a decisive factor in limiting signaling range. The most obvious manifestation of this is that the concentration of NO at the fiber surface is lower the more slender the fiber (Fig. 2A, showing surface concentrations after 1 s of synthesis). On the surface, a signal of 10 nm cannot be achieved by fibers less than ∼0.6 μmin diameter, and, for a 100 nm surface signal, fiber diameter must be at least 2.5 μm. The surface concentration is of course the maximum that is reached anywhere external to the fiber because, as NO diffuses away from the source, its concentration decreases with distance. Importantly, this decline is considerably steeper around thinner fibers, further diminishing their distance-signaling capability. Thus, the distance over which NO declines to 50% of the surface concentration is 12 μm for a 5 μm diameter fiber, 6 μmfora1 μm fiber, and just 2 μm for a 0.1 μm fiber (Fig. 2B). In summary, thinner fibers generate less NO on their surface, and this initially weak signal declines more steeply over distance. Consequently, the region around a fiber that experiences NO above a given concentration shrinks rapidly as the fiber diameter decreases.

Figure 2.

The signaling efficacy of a single NO-producing fiber critically depends on its diameter. A, The NO concentration at the fiber surface declines dramatically for thinner fibers. Surface concentrations after 1 s of continuous synthesis are 440, 25.5, and 0.37 nm for fiber diameters of 5, 1, and 0.1 μm, respectively (diameters chosen with reference to B). The inset in A shows the graph at a larger scale for diameters below 0.5 μm. B, The problem of the lower surface concentration of thinner fibers is exacerbated by a steeper decline of the NO concentration as one moves away from the fiber surface. NO concentration is plotted over distance from the fiber surface as percentage of the surface concentration for fiber diameters of 5 μm (solid line in B), 1 μm (dashed line in B), and 0.1 μm (dotted line in B). Note, however, that even very thin (0.1 μm) fibers reach ∼20% of the surface concentration 20 μm away from the surface after 1 s of synthesis (hairlines in B). This extensive spread is the basis of cooperative volume signaling (compare with Fig. 4).

This limitation cannot be overcome by extending the duration of NO synthesis because, for fine fibers, the NO concentration quickly approaches a steady state at which the amount of NO being produced equals that diffusing away. The smaller the fiber, the sooner a steady-state concentration is approached, and hence the lower this steady-state concentration is. For fiber diameters under 1 μm, effective steady state (defined as above 80% of maximum NO concentration) is reached around the fibers within 100 ms. Further extending the duration of NO synthesis does not therefore appreciably increase the local NO concentrations or extend its radius of action.

Although a small NO-generating fiber is a relatively ineffective source, it would be a mistake to think that a wide region around it does not contain NO. On the contrary, a steep initial concentration gradient drives NO rapidly away from the source into the initially empty surround. Thus, the small amount of NO generated by a small source spreads quickly to occupy an extensive volume around the source, albeit at a very low concentration. Even a 0.1 μm fiber covers a region stretching beyond 20 μm from itself in a very light “fog” of NO at >20% of the surface concentration (Fig. 2B, hairlines). Appreciating this point is the key to understanding how very slender and individually ineffectual sources can cooperate in the generation of an effective regional signal, as we show below. However, before doing so, it is necessary to establish the degree to which this effect depends on the choice of parameter values in the model.

Robustness of predicted spread to altering the parameter values

How sensitive are our model predictions to altering the values of NO inactivation (half-life), diffusion coefficient (D), and production rate (Qρ)? It is clearly important to test the robustness of our predictions because there is uncertainty and disagreement in the literature about the values of parameters that would seem intuitively to affect both the concentration of NO at the fiber surface and the spread of NO away from the source.

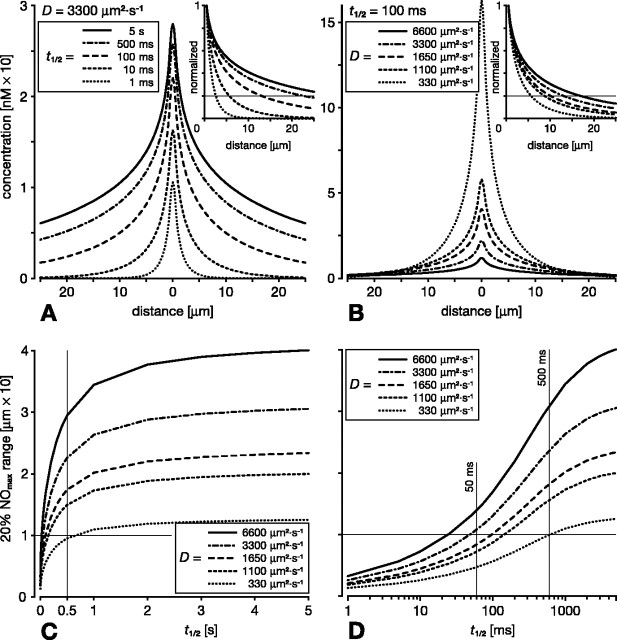
Concerning inactivation, there is uncertainty about the half-life of NO in vivo because it is curtailed by the availability of reaction partners in the tissue. Lancaster (1997) gives the reported range of half-lives as 5-15 s. The cellular sink mechanism reported by Griffiths and Garthwaite (2001) would result in an effective half-life of ∼100 ms, which tallies with an early in vivo measurement by Kelm and Schrader (1990). In vertebrates, the half-life will be affected by the proximity of blood vessels, because hemoglobin acts as a strong NO sink. Thomas et al. (2001) estimated the extravascular half-life to be between 90 ms and >2 s, depending on the propinquity of vessels. In consideration of these findings, we have varied half-life between 5 s and 1 ms and examined the consequences for the spread of NO from a single fiber source of 1 μm diameter after 1 s of synthesis (Fig. 3A). Note that there is little effect on the surface concentration or on the spread of NO for half-lives between 5 s and 500 ms, and, furthermore, a half-life of 100 ms still preserves the general relationship between concentration and spread. Only with significantly shorter half-lives of 10 ms or less does the spread of NO drop enough to significantly affect the potential of the NO source to cooperate with other nearby sources. This can be judged by reference to the range over which the NO signal falls to say 20% of its concentration at the surface of the source (the 20% NO_max range) (Fig. 3A, hairline in inset). For half-lives of 10 ms or less, the 20% NO_max range is <6 μm. This is because shortening the half-life diminishes the relative signal strength more at greater distances from the source. Thus, whereas shortening the half-life 5000-fold from 5 s to 1 ms reduces the surface concentration to 30% of its original value, at 10 μm from the fiber surface, the NO concentration is reduced to <0.25%. In summary, only extremely short half-lives will severely hamper cooperation, based as it is on significant concentrations spreading significant distances. Such very short half-lives are expected within the lumen of blood vessels, but, in the extravascular space, half-lives are >90 ms (Thomas et al., 2001). Therefore, the spread and, by implication, the ability of sources to cooperate is affected little over the expected physiological range of half-lives in the brain (50 ms to 5 s).

Figure 3.

Influence of half-life (t_1/2) and diffusion coefficient (D) on the spread of NO from a single fiber of 1 μm diameter after 1 s of continuous NO synthesis. Main plots in A and B show the absolute NO concentrations plotted against distance from the center of the fiber. In the insets, these concentrations are normalized to the concentration at the fiber surface. The distance over which the concentration drops to 20% of the surface concentration (the 20% NO_max range; hairline in insets) serves as a measure of the relative spread. A, Varying t_1/2 5000-fold between 5 s and 1 ms while keeping D constant at 3300 μm² · s^-1 has little effect on the NO concentration at the source (∼30 and ∼10 nm, respectively). Although concentrations are affected more at distant points (as is evident from the diverging lines in the inset), the spread is curtailed significantly only when t_1/2 is substantially shorter than 100 ms. For example, 10 μm away from the source, the concentration is only halved by reducing t_1/2 from 5 s to 100 ms. Likewise, the 20% NO_max range drops below 10 μm only when t_1/2 is significantly shorter than 100 ms (hairline in inset). B, Varying D between 2× and 0.1× its standard value while keeping t_1/2 constant at 100 ms impacts on the absolute concentration at the source but has much less effect at more distant points. The relative spread is likewise little affected (inset in B). A significant drop of the 20% NO_max range below 10 μm is predicted only with D = 330 μm² · s^-1, 1/10 of its standard value. C, D, The 20% NO_max range shown as a function of t_1/2 for different D values. C, Varying t_1/2 between 5 and ∼0.5 s has no significant effect on the spread, and the 20% NO_max range is 10 μm or more even for D = 330 μm² · s^-1 (crossed hairlines). D, Over the range of t_1/2 = 50-500 ms, spread changes more steeply. Importantly, however, with physiologically realistic values of D > 1000 μm² · s^-1, the 20% NO_max range is of the order of 10 μm or more (crossed hairlines).

Next we investigated how a change in the diffusion coefficient D affects the spread of NO and our model predictions. Some studies indicate that NO does not diffuse in vivo nearly as freely as predicted from its behavior in aqueous salt solutions or lipids. In addition, in the retina, membrane-associated diffusion barriers have been invoked to explain the apparent retention of NO within individual cells and processes (Blute et al., 2000; Eldred, 2001). We did not model the effect of such local NO retention, but, at first approximation, its effect and the effects of distributed retention may be inferred from a marked reduction of the diffusion coefficient D. We have therefore varied D from 1/10 to twice the standard value measured in aqueous salt solution (3300 μm² · s^-1) (Malinski et al., 1993). In our initial examination of the effect of D on NO spread from a single 1 μm fiber after 1 s of synthesis, we selected a short half-life of 100 ms to investigate the limits on cooperation (Fig. 3B). The lower the value of D, the slower NO spreads away from the source and the greater the NO concentration is in the immediate vicinity of the source. Farther away from the source, however, for instance at 10 μm, the value of D has a minimal effect on the absolute NO concentration. If we now consider the effect of D on relative NO concentration, we see that doubling the standard value of D or reducing it to one-third has relatively little effect (Fig. 3B, inset). Thus, at the standard value of D, the 20% NO_max concentration is reached at ∼13 μm, doubling D increases this to 17 μm, and reducing D to one-third decreases the range to 8 μm (Fig. 3B, hairline in inset).

Our analysis has shown that, for a diffusing messenger, both its half-life and D do affect spread. However, within a wide range of parameter values, cooperative signaling is permitted and has the same qualitative character. The interplay between half-life and D in governing the spread of NO is illustrated in Figure 3, C and D. This figure shows the 20% NO_max range of a single 1 μm fiber as a function of half-life for different values of D. Lowering D decreases spread. However, even for the lowest value of D (330 μm² · s^-1; probably an unrealistically low value for NO diffusion in vivo), a 1 μm fiber still achieves the 20% NO_max concentration at just over 10 μm distance for any half-life longer than 0.5 s (Fig. 3C, crossed hairlines). In fact, for any value of D, the spread is mostly independent of the half-life, provided half-life is longer than 0.5 s (Fig. 3C). For shorter half-lives, between 50 ms and 0.5 s, spread increases more steeply with increased half-life. Importantly, however, for physiologically realistic half-lives (>50 ms) and values of D (>1000 μm² · s^-1), the spread of NO from a 1 μm source is clearly sufficient for cooperation over distances likely to be of significance in neural systems (tens of micrometers) (Fig. 3D, crossed hairlines).

Finally, we consider the impact of the NO production rate Qρ = 1.32 × 10^-4 mol · μm^-3 · s^-1 on our predictions. The value will vary depending on both the degree of activation of a particular NOS-expressing neuron and the type of neuron in question. In this context, it should be noted that very different NO concentrations have been reported in vivo. In rat cerebellar slices, electrical stimulation elevated NO by ∼6-60 nm (Shibuki, 1990; Maffei et al., 2003). In contrast, Rivot et al. (1997) estimated a basal extracellular NO concentration of ∼0.5 μm in rat dorsal horn, and concentrations exceeding 3 μm were reported after electrical stimulation of sensory neurons (Schulte and Millar, 2003). These discrepancies may reflect different production rates and/or different methods used to measure NO. The value of Qρ is therefore the least precisely known parameter value in the model. Importantly, however, it is also the value that least affects the conclusions of this paper because Qρ acts only as a scaling factor of concentration (Eq. 3). We emphasize this particularly for the two properties that are key to cooperative signaling, namely, the relative drop of NO concentration over distance from the fiber surface and the dependency of this drop on the source fiber diameter. For this reason, Qρ does not impact on the spatial and temporal dynamics and scales over which cooperative signaling is expected to occur.

In summary, our analysis has shown that a diffusing signal will spread tens of micrometers away from a fiber source at a significant fraction of the maximal (surface) concentration over a wide range of model parameter values. Our predictions concerning cooperative volume signaling between separated fiber sources are therefore robust. This is not to say, however, that extreme parameter values might not preclude significant spread external to a source. Indeed, in the retina, it seems that some NOS-expressing cells retain NO because of the presence of a strong, but not well understood, NO-binding property of the cell membrane (Blute et al., 2000; Eldred, 2001). In this case, if NO has an intercellular signaling function, it must be confined to the immediate vicinity of the source, and cooperative signaling, if it occurs at all, must be between very close neighbors only.

Cooperative NO synthesis in parallel arrays of fibers

To analyze the spatial and temporal interaction of signals in systems of multiple sources that release NO simultaneously, we first modeled the geometrically simple case of ordered parallel arrays of fibers. That NO can summate within such a system was indicated by the model of Lancaster (1997). A real-world example of this arrangement is found in the retinotopic projections of NOS-expressing small-field visual interneurons in the insect optic lobe (Elphick et al., 1996). Here near-neighbors are activated by the same visual stimuli and hence generate NO at the same time; the angle subtended by the visual stimulus will determine the number of parallel units that are coactivated. The anatomical arrangement found in the insect's optic lobe was modeled with arrays of 2-μm-diameter parallel fibers with a near-neighbor separation of 10 μm.

Figure 4A shows the spatial distribution of the NO signal after 1 s of simultaneous synthesis by 1, 4, 9, 16, 25, and 36 parallel NO-generating fibers. As expected, a single 2 μm fiber is ineffectual (Fig. 4A, 1 fiber), producing a peak NO concentration of 120 nm and a sharp decline in the very close vicinity of the fiber. In contrast, simultaneous activation of many such fibers yields substantial concentrations over large regions. For instance, 36 fibers generate a peak of 1300 nm and the region above 100 nm extends significantly beyond that occupied by the array itself (Fig. 4A, 36 fibers). The volume that experiences an NO signal above a given concentration (e.g., 100 nm) thus increases with the number of active sources (Fig. 4B). Recall that a single fiber fails to generate a significant volume signal principally because the speed of diffusion means that NO spreads rapidly away from the source, becoming diluted within a large nearby volume. It is this that enables well-separated fibers to cooperate in raising the concentration of NO throughout a region.

Figure 4.

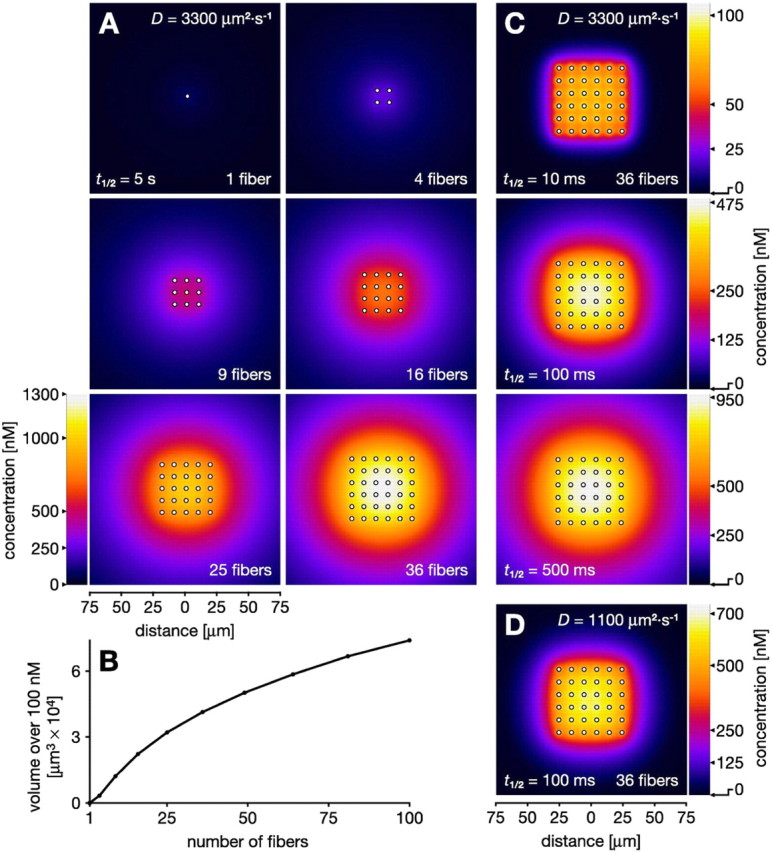
Cooperative volume signals produced by ordered arrays of parallel NO-synthesizing fibers after 1 s of synthesis. Fiber diameters (2 μm) and spacing (10 μm) approximate that in the locust optic lobe (Elphick et al., 1996). A, Concentration distribution of NO in 300 × 300 μm² slices across increasing numbers of active fibers (indicated by white dots). A single fiber is a relatively ineffectual NO source (1 fiber in A). Increasing numbers of fibers separated by 10 μm result in a cumulative buildup of NO to substantial concentrations (4-36 fibers in A). B, As the number of fibers increases, so does the volume that is affected by an NO signal over a particular concentration, here 100 nm. C, Cooperative generation of a volume signal is robust to variation in half-life (t_1/2) within the limits reported in the literature. When t_1/2 is reduced to 100 ms (Griffiths and Garthwaite, 2001), 1/50 of the value in A, the concentrations in the target volume fall to only approximately one-third (250-475 vs 700-1300 nm). Further reduction of t_1/2 to 10 ms yields a more spiky concentration distribution with 100 nm peaks at the fibers. However, at least 50% or more of this peak concentration is still reached everywhere throughout the target volume. D, Strong cooperation is still observed when t_1/2 is relatively short (100 ms) and D is reduced to 1100 μm² · s^-1, one-third of its standard value. Compared with the result with standard D (middle part of C), the volume signal shows less encroachment into areas outside the array.

We have already seen in Figure 3 that the spread of NO from a single fiber is reduced a little by a half-life of 100 ms and further curtailed by a half-life of 10 ms. This is reflected in Figure 4C in which we see how cooperation between fibers occurs for half-lives of 10, 100, and 500 ms. As expected from Figure 3, reducing the half-life from 5 s to 500 ms has very little effect on the cooperative volume signal generated after 1 s of synthesis (Fig. 4, compare bottom of C with 36 fibers in A). Further reducing the half-life to 100 and 10 ms still leads to the production of a cooperative volume signal. In fact, without changing the fiber separation, for a half-life of only 10 ms, the entire volume occupied by the array experiences an NO signal at >50% of the peak concentration (Fig. 4C, top). In an additional test of the robustness of the volume signal predictions, we combine a shortened half-life (100 ms) with a diffusion coefficient D reduced to one-third of the standard value. As predicted from results obtained for single fibers, this combination still allows significant interaction to occur and for the consequent generation of a cooperative volume signal (Fig. 4D).

Spatial and temporal effects of source separation

Although the above results show that separated fibers can indeed cooperate in the generation of a volume signal, it is clear that the same volume could be affected by a variety of source configurations of equivalent NO-generating power, for example, by placing fewer but larger sources in the same volume or by a single large source at its center. However, the predominance of fine and diffuse NOS plexus morphologies in real brains suggests that a highly dispersed arrangement confers particular signaling advantages.

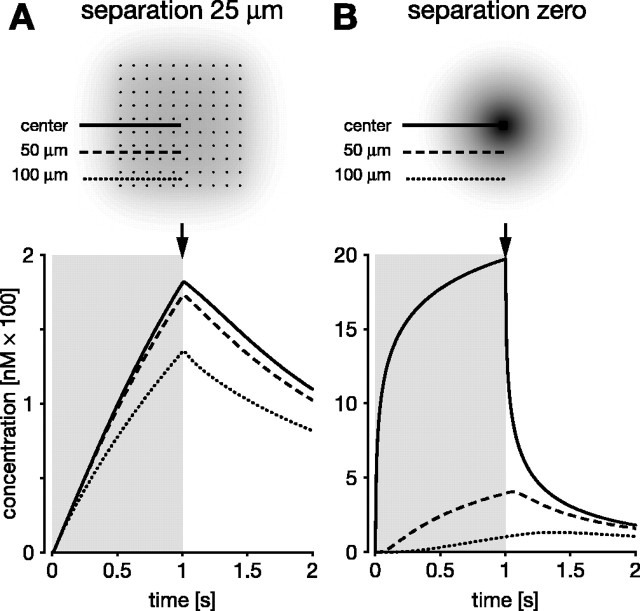
The effect of source dispersal on the spatiotemporal characteristics of the NO signal was investigated by varying fiber separation in ordered arrays of fibers (Figs. 5, 6, 7). In Figure 5, we compare the spatial distribution of NO at the end of a 1 s burst of NO synthesis by 100 identical 1-μm-diameter fibers arranged contiguously, in effect a single source (Fig. 5A), or separated by 25 μm (Fig. 5B) or 35 μm (Fig. 5C). The most obvious effect of fiber separation is uniformity of the NO signal in space. Whereas a contiguous arrangement (zero separation) results in a sharp local peak reaching 2000 nm (Fig. 5A), a separation of 25 μm gives a much broader spatial distribution with a peak concentration of less than 1/10 of this value (Fig. 5B). Moreover, the volume that experiences low concentrations is considerably larger when the sources are separated. Therefore, as long as separated fibers are capable of cooperating enough to produce an effective signal (of say at least 100 nm), separation extends the affected volume (Fig. 5, compare A, B, heavy black outlines in bottom panels). Indeed, depending on the concentration required to activate targets within a region, separation can be increased to affect a volume many times the size affected by a single large source producing the same amount of NO. For instance, assuming threshold concentrations of 100, 10, and 1 nm, 100 evenly separated fibers can affect regions 1.8×, 8×, and 24× greater than that affected by the same fibers acting as a single source at the center. Clearly, however, if the separation is too great, NO from neighboring fibers may fail to reach the effective concentration. This is illustrated in Figure 5C in which the separation is 35 μm and the nominal effective concentration is set to 100 nm. Notice, however, that the greater separation has also resulted in an even more uniform distribution of NO and that, at the end of the synthesis burst, most of the region covered by the array experiences the same concentration.

Figure 5.

Separation of the source fibers critically determines the spatial distribution of NO. Concentrations after 1 s of synthesis are shown for an ordered array of 10 × 10 parallel fibers of 1 μm diameter. Bottom row, The resultant NO cloud (shaded) in a 400 × 400 μm² slice across the fibers (black dots indicate fiber profiles). Top row, Concentration profile along the dashed line through the center of the array. A, Contiguous arrangement of the fibers leads to a sharp local NO peak of nearly 2 μm, because they act as a single 10 × 10 μm source. B, Separation of the fibers by 25 μm results in a much broader and more homogeneous distribution. The peak concentration is ∼10 times lower than in A, but the region that experiences concentrations over 100 nm (heavy black outlines in bottom row) is substantially larger in B. C, Further increase in separation to 35 μm yields an even more homogeneous concentration profile, but the region over 100 nm is dramatically reduced and discontinuous. Note that, in A-C, the same amount of NO was produced over the same time.

Figure 6.

Separation of the source fibers promotes synchrony and uniformity of the NO volume signal. Local NO concentrations generated during and after 1 s of synthesis by an ordered array of 10 × 10 fibers (fiber diameter of 1 μm), measured at three points: at the center of the array (solid lines) and 50 μm (dashed lines) and 100 μm (dotted lines) away from the center. The duration of synthesis indicated by gray rectangles in bottom row. Top row, Points of measurement and fiber profiles (black dots) superimposed on a snapshot of the spatial NO distribution (shaded) at the end of synthesis (arrows). A, Fibers separated by 25 μm. The entire region synchronously experiences a very similar time course of NO that is characterized by a relatively slow and approximately linear rise and fall. B, Fibers arranged contiguously so they act as a single 10 × 10 μm source. The center instantaneously experiences concentrations far in excess of 100 nm; rise and fall are highly nonlinear. Points away from the center encounter a much slower rise and fall with different temporal characteristics depending on their distance from the center. In particular, the farther from the center, the longer NO continues to rise after the end of synthesis.

Figure 7.

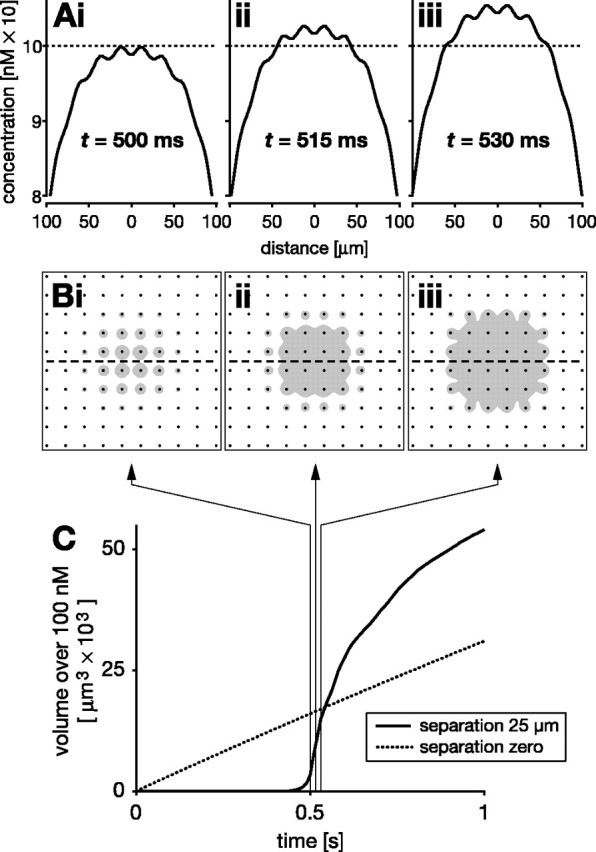
Delayed volume signaling by separated NO sources (10 × 10 array of 1-μm-diameter NO-synthesizing fibers separated by 25 μm). A, B, Spatial concentration distributions at three time points after the onset of synthesis: 500 ms (i), 515 ms (ii), and 530 ms (iii). A, NO concentration profiles across the center of the array, along the dashed line in B. For illustrative purposes, a nominal threshold concentration of 100 nm is assumed (dotted line in A). B shows the region over 100 nm (gray) in cross sections through the array (fibers are indicated by black dots). There is a substantial delay between the onset of synthesis and NO reaching 100 nm anywhere within the volume of the array. After 500 ms of continuous synthesis (i in A, B), NO reaches 100 nm in the vicinity of central fibers. Additional synthesis pushes a large part of the target volume near simultaneously over 100 nm (ii, iii in A, B). C, Plotting the volume that experiences >100 nm NO over time shows a sharp, nonlinear rise after an initial delay of ∼500 ms (solid line). Three hairlines with arrows indicate the time points shown in A and B. Also shown for comparison is the near-linear rise (dotted line in C) that is observed for the volume over 100 nm when the same 10 × 10 fibers are arranged contiguously as a single source.

The greater spatial uniformity of the signal also results in greater temporal uniformity across the target volume. This effect of separation on the temporal dynamics is illustrated in Figure 6. Within the dispersed array (separation of 25 μm), the NO concentration at the center and at 50 and 100 μm from the center develops very similarly over time during synthesis (Fig. 6A). In contrast, when the same amount of NO is generated by the same fibers acting as a single source, the signal rises very rapidly at the center, but the rate of increase at distances 50 and 100 μm from the center is markedly slower (Fig. 6B). Another, but less obvious, consequence of reducing separation is that the NO concentration at points distant from the sources will continue to rise for a significant period of time after the end of synthesis. This effect can be seen in Figure 6B for the 100 μm distance, in which the NO concentration continues to rise for 0.5 s after the end of the synthesis pulse. The postsynthesis rise is attributable to the NO that accumulated at the center during synthesis flowing out into more distant regions after the end of synthesis.

Source separation has one additional and important consequence. There is a substantial delay before the cooperation between separated sources becomes significant, i.e., reaches a nominal threshold of say 100 nm (Fig. 7). During synthesis, concentration rises steadily throughout the region containing the sources until it is just below 100 nm in a large fraction of that region (Fig. 7A,B, i). Any additional synthesis now pushes the entire volume, more or less simultaneously, over the nominal threshold (Fig. 7A,B, ii, iii). By examining the size of the region over 100 nm (Fig. 7B, gray areas), one therefore sees a delay of ∼0.5 s before this concentration is reached anywhere, but, over the next few tens of milliseconds of synthesis, the volume over 100 nm rises rapidly (Fig. 7C, solid line). In contrast, the same fibers with no separation generate a concentration above 100 nm almost immediately, and the region above that concentration rises linearly during synthesis (Fig. 7C, dotted line). Although counterintuitive in view of the high speed of NO diffusion, the delay is attributable to the time taken for NO from separate fibers to build up to a significant concentration at any point within the array. The length of delay will of course depend on what concentration is effective and the fiber separation. Although these factors will vary, whenever an effect requires NO from multiple sources to summate, there will be a delay. The delay can be regarded as a low-pass filter because there must be persistent NO synthesis before separated fibers can generate an effective signal.

Cooperative NO synthesis in a random plexus

By modeling ordered arrays, we have seen how cooperating small fibers can produce an evenly spread NO volume signal. Here we present results obtained for randomly branched fibers that better approximate the plexus morphology found in real brains. Because the aim is to gain insight into the consequences of plexus fineness, we compared signals generated by plexuses composed of either 1 or 5 μm diameter fibers. The plexuses were “grown” randomly within a defined bounding volume (the synthesizing volume), and the sum total of source fiber volume, and hence the total rate of synthesis within the volume, was the same for the fine (1 μm) and coarse (5 μm) plexuses.

In comparing the consequences of NO synthesis by the two plexus types, measurements were taken among a population of 30 plexuses for each fiber diameter This is because no two of the random artificial plexuses of the same fineness and dispersal are exactly alike. The same is true for naturally occurring plexuses that occur as repeated modules, such as are found in the simple eye (ocellar) neuropil of the locust, for instance (Fig. 8A) (cf. Kurylas et al., 2005). It is immediately evident that the precise branching morphology within each module is not fixed (i.e., not developmentally specified in detail), and we can safely assume that each instance of a plexus will generate different volume signals. Importantly, however, the finer the constituent fibers, the more consistent the NO signal will be. Fineness, and the signal homogeneity that accompanies it, therefore decrease the dependency of the signal on a particular branching morphology and hence increase the consistency of the volume signals across the population. This can be shown by measuring the NO concentration at the center of each plexus in a population of either fine or coarse plexuses (Fig. 8B,C). The mean concentration (430 vs 470 nm) is approximately the same whether generated by 1 or 5 μm fibers (Fig. 8Bii,Cii, arrowheads and dotted lines). The range of concentrations, however, is much higher across the population of coarse plexuses (Fig. 8Bii,Cii).

Figure 8.

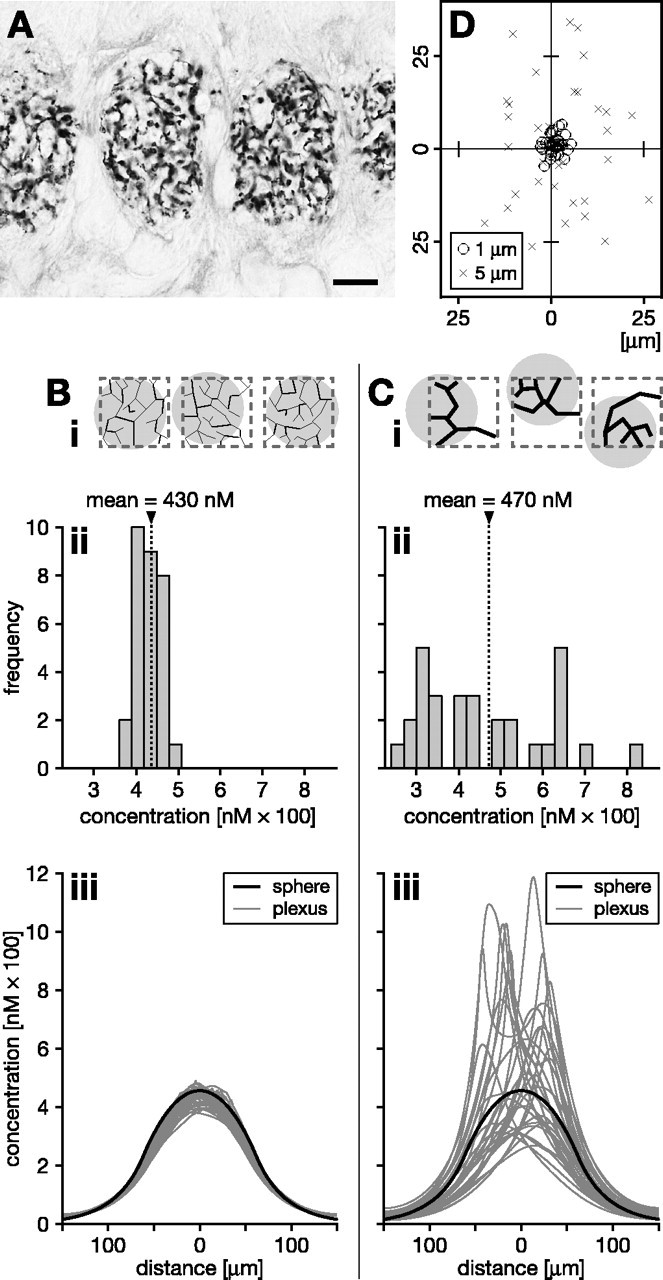
Signaling properties of coarse versus fine nitrergic plexus morphologies with random fiber distributions. A, An example of multiple nitrergic plexuses is found in the ocellar neuropil of the locust. Fine fibers arborize in a pseudorandom manner. Scale bar, 10 μm. B, C, NO signals generated by a finer plexus are less dependent on the details of the random plexus morphology, more homogeneous, and more centered relative to the synthesizing volume. Populations of model plexuses (n = 30) composed of 1- μm-diameter fibers (B) or 5- μm-diameter fibers (C) were grown by a random branching algorithm, yielding the same overall source density within a synthesizing region of 100 × 100 × 100 μm³. Three instances of each population are shown schematically in Bi, Ci (synthesizing region indicated by dashed gray outlines). Bii, Cii, After 1 s of NO synthesis, the frequency distribution of the NO concentrations encountered in the center is much narrower across the population of fine plexuses. This indicates greater independence from the morphological details of the plexus and greater homogeneity of the concentration distribution across the synthesizing volume. Biii, Ciii, Compare the concentration profiles across the center of random plexuses (fine gray lines; n = 30) with that across a homogeneous spherical source (heavy black line). The spherical source has the same overall source strength as each plexus and occupies the same volume as the synthesizing region within which the plexuses were grown. The signals from fine plexuses (Biii) approximate much more closely that of a homogeneous source than those generated by coarse plexuses (Ciii). Moreover, with finer plexus morphologies, the NO cloud is better centered over the synthesizing region. This is shown schematically in Bi and Ci by gray circles, indicating the clouds, and quantitatively in D by plotting the center-of-mass positions of the clouds across populations of fine (circles) and coarse (crosses) plexuses on a slice through the center of the synthesizing region.

Plexus fineness also ensures that the NO signal is more centered on the region occupied by active fibers (indicated schematically by gray circles in Fig. 8 Bi,Ci). This effect can be quantified by examining, across populations of either coarse or fine plexuses, the position of the center-of-mass of the NO cloud in a two-dimensional slice through the center of the synthesizing volume (Fig. 8 D). To understand the reason for this consequence of plexus fineness, remember that, to have the same rate of NO synthesis in a region, a fine plexus must have many more fibers than a coarse one. Because the fibers are located randomly, the same volume containing the fine plexus will necessarily have a more uniform distribution of NO sources within it. A fine plexus is therefore much more likely to generate an NO cloud that is centered on the bounding volume than a coarse plexus. So when generated by a fine plexus, not only does the NO cloud cover the region more evenly, it is also better targeted to the active region.

Our comparison of fine and coarse plexuses above suggests that, if smoothness and repeatability of the signal are desiderata, the ideal NO source distribution would be uniform. That is, fibrous NO sources would ideally be evenly smeared throughout the synthesizing volume into a single continuous source of the same overall production rate. We therefore have investigated how the fine and coarse plexuses perform compared with a continuous spherical source centered on the synthesizing volume, with the same overall size and the same NO generating strength as a single plexus (Fig. 8Biii,Ciii). In this analysis, we examined the spatial distribution of NO generated by 30 instances of the fine and coarse plexuses. The continuous source serves as a reference for how closely populations of our hypothetical fine and coarse plexuses (Fig. 8Biii,Ciii, fine gray lines) come to generating the “ideal signal” of the continuous model (Fig. 8Biii,Ciii, bold black lines). Note that the signal from the continuous source is smooth throughout the source and, obviously because the source structure is perfectly uniform, the same signal would be generated on each repetition of a 1 s bout of NO synthesis. The same cannot be said of the plexuses. However, our fine 1 μm plexuses (Fig. 8Biii) come much closer to the ideal than the 5 μm plexuses (Fig. 8Ciii). Clearly, the 1 μm plexuses generate highly invariant NO concentration profiles that cluster close to the profile of the homogeneous source (Fig. 8Biii). Because biological NOS plexuses are generally finer, they are therefore expected to generate a signal that approaches very closely that of a continuous source of the same strength spread throughout the volume occupied by the plexus. The NOS plexus in the cortex, for example, is characterized by a highly uniform spread of submicrometer arborizations, possibly arising from an intrinsic growth strategy similar to that shown by retinal ganglion cells (Montague and Friedlander, 1989, 1991).

Fineness affects the temporal properties of the NO signal in much the same way as dispersal acts as a low-pass filter in the parallel arrays (Figs. 6, 7). The finer the fibers of the plexus are, the longer the delay to accumulate an effective NO signal. For example, in a plexus of 5 μm fibers, a concentration of 100 nm can be achieved almost immediately (within 1 ms of activation), but, for such a brief synthesis duration, this concentration will only be reached in scattered small regions. In contrast, in a plexus of 1 μm fibers, the same concentration is first reached after 35 ± 7 ms of NO synthesis (which compares with 77 ms for the ideal source). For the fine plexus, however, this concentration is then achieved near simultaneously throughout a large volume. This means that a fine plexus will selectively translate only persistent increases in local neural activity into an effective NO signal in that region. As with parallel arrays of separated fibers, a fine plexus therefore acts as a low-pass filter that reduces the likelihood that short-term random fluctuations in NOS activity (noise) result in an effective signal.

Our model assumes a uniform distribution of NOS along neuronal fibers of constant diameter, which is clearly not the case for real neurons. However, the same effects of source dispersal on the resulting NO signal apply when NOS is distributed unevenly, for instance, in beads along the fiber length. This is because the distribution of coactivated NOS within a particular volume determines the characteristics of the volume signal. Thus, both the size and number of active sites (fibers or beads), and whether they are evenly spread out or clumped together, will influence the distribution and thus the properties of the NO signal. The reader is referred to the equivalent scenario of “clumping” fibers in an array (Fig. 5). We also assumed that multiple plexus fibers in the same region will be activated concomitantly and release NO at the same time. This will ultimately depend on intracellular calcium dynamics in response to the pattern of inputs to the plexus (cf. Montague et al., 1991) but does not imply that activated fibers belong to the same neuron nor that they represent all of the NOS in a given region or indeed all the NOS within a particular neuronal arbor. Furthermore, the predictions are robust to asynchronous synthesis over time windows that are on the order of the NO half-life or synthesis duration (whichever is shorter; data not shown). Hence, our model predicts that cooperation between multiple sources will occur independently of the precise timing and regardless of whether the active NOS resides in all or some of the fibers, beads, or spines of one or many neurons within a volume.

Discussion

We set out to analyze the effect of the widespread NOS plexus architecture on the properties of the resultant diffuse NO signal. The ability of a diffuse NO signal to integrate regional neural activity over space and time has been investigated previously (Gally et al., 1990; Montague et al., 1991). In these models, differing temporal patterns of presynaptic firing are integrated into a diffuse spatial signal that can guide development, leading to the formation of neural structures such as columns. This important work showed how temporal correlation in presynaptic activity could result in spatially segregated synapses through the action of a diffuse signal and by implication that different NO source distributions lead to different NO signals. These previous models correctly postulated the importance of spatiotemporal interaction between separate sources of diffusing messengers. They do not, nor do they claim to, represent a computational exploration of the diffusion of particular substances because the spatial and temporal scales were either unspecified (Montague et al., 1991) or large [compartment size of 100 × 100 × 100 μm³ and time step of 0.46 s (Gally et al., 1990)]. In contrast, we do not model the synaptic activity generating NO or the downstream effects of NO. Rather, we focus at high resolution on the influence of source morphology on the temporal and spatial dynamics of the NO signal. The strength of our model is that it is explicit about spatial scale. This has allowed us to gauge the extent to which sources of a particular morphology will interact over distance, something that cannot be intuited from the general principles of diffusion. Our results suggest strongly that, with sources approximating neurons in size and shape, cooperative interaction will occur over distances of tens of micrometers.

By modeling the spread of NO from multiple fibers, we have demonstrated that their diameter and dispersal significantly shape the spatial and temporal dynamics of the signal. We conclude that there are distinct functional advantages to using very small and dispersed sources over an arguably simpler system using fewer larger ones. A plexus of very fine fibers favors four interrelated aspects of the ensuing NO signal, namely, (1) cooperative dispersal over an extensive region, (2) homogeneity within the region, (3) regional targeting, and (4) selective responsiveness to persistent regional activity. Ultrafine plexus morphologies thus appear to be configured to generate a homogeneous cooperative volume signal that complements conventional synaptic neurotransmission. The question of neuronal fineness has also been discussed in the context of point-to-point synaptic transmission. Neurons are thought to be selected for fine and highly branched processes, first, because it allows a cell to cover a volume without occupying a significant proportion of that volume, and second, because it allows many neurons to cover a particular volume (Montague and Friedlander, 1991). Our analysis suggests an additional potential evolutionary pressure toward fineness that applies specifically to neurons that use diffusible signals.

Central to our functional interpretation is that the size of an NO source will limit its radius of action. It is clear from results presented here and previously (Philippides et al., 2000, 2003) that this is the case regardless of what constitutes an effective NO concentration [a subject of ongoing debate (Artz et al., 2001; Mo et al., 2004)]. The limiting effect of source size has been confirmed experimentally in clusters of macrophages comprising variable numbers of cells (Porterfield et al., 2001). Moreover, experimental data from neuronal systems suggest that, unless there is some retention factor, this range is on the order of 10 μm for neuronal fibers of ∼5 μm diameter (Blute et al., 2000), increasing to ∼100 μm for larger sources (Park et al., 1998). The principal reason why very small fibers fail to achieve significant concentrations in their vicinity is the high speed of diffusion, resulting in the rapid spread of NO, which achieves a very low concentration in an extensive volume around the small source. Thus, the same feature of NO diffusion that prevents small sources from acting alone allows cooperation between them. Of course, if there is exceptionally rapid destruction of NO, or strong NO retention as suggested in some retinal neurons (Blute et al., 2000; Eldred, 2001), cooperation will be significantly limited. Indeed the uncertainty about the spread and half-life of NO in vivo requires predictions based on models of NO diffusion to be relatively insensitive to reasonable variations in the values of these key parameters. We have shown that cooperative volume signaling is likely to occur over a wide range of parameter values that govern the spread of NO. We do not want to imply, however, that the spatial and temporal characteristics of volume signaling we describe are exclusive to NO. On the contrary, we would expect to come to a similar conclusion about other transmitters that are released by neuronal plexuses so long as their spread is isotropic and rapid. Our predictions may not therefore describe accurately the spread of larger polar transmitters such as dopamine, which nonetheless is known to mediate volume signaling (Cragg et al., 2001).

In some neurons, for instance, in the retina, NOS is expressed specifically at synaptic sites (Cao and Eldred, 2001). Also, in a subset of CA1 dendritic spines in the mammalian hippocampus, NOS is concentrated at postsynaptic densities (Burette et al., 2002). Moreover, ∼50% of these NOS-positive spines are in direct apposition to presynaptic endings that contain the NO receptor sGC. Together, these observations suggest that, in some circumstances, NO acts as a local synapse-specific transmitter. Whether NO can perform this function without cooperation between synapses will depend on the sensitivity of its receptors. Although our model does not rule out synapse-specific signaling, it does indicate that the NO concentration at a single active synapse is limited by the size of individual synaptic sources. In the mammalian cerebral cortical plexus, NOS is clearly not confined to the synapse. The same applies to some hippocampal neurons (Burette et al., 2002) and to plexus neurons in invertebrate brains (Elphick et al., 1996; Ott and Burrows, 1998; Ott and Elphick, 2002; Kurylas et al., 2005). In all of these situations, even in neurons in which NOS is highly localized to the synapse, as NO will spread, significant cooperation between synapses is possible. Direct evidence for a physiologically relevant spread of NO over distances exceeding 150 μm has been obtained in heterosynaptic long-term depression and potentiation in the rat cerebellum (Hartell, 1996; Jacoby et al., 2001). These data predict that cerebellar long-term depression and potentiation will not be input specific at the single cell level under conditions that give rise to NO/cGMP production (Hartell, 2001).

A key feature of the signal generated by suitably dispersed sources is uniformity in space and time throughout the volume. Thus, cooperating systems of fine fibers avoid the generation of “hot spots” of potentially toxic NO concentrations. Moreover, the spatial uniformity of the signal suggests that, rather than individual NO sources affecting individual targets, the plexus affects targets within the volume of the brain in which the plexus and targets coexist. This idea may help to account for the ability of NOS plexus neurons in the mammalian cerebral cortex to translate increased regional neuronal activity into a regionally targeted increase in cerebral blood supply (for review, see Estrada and DeFelipe, 1998). Although some individual fibers of the plexus do come into close apposition to arterioles (DeFelipe, 1993; Estrada and DeFelipe, 1998; Lovick et al., 1999), our analysis suggests that such direct targeting could contribute only weakly to NO-mediated vasodilation. According to our model, however, the fact that a majority of cortical plexus fibers do not contact arterioles does not matter because the whole plexus is suited morphologically to generate a regional signal. Such a signal would integrate the energy demand in a volume of cortex and relate it to its vascular supply, as hypothesized by Gally et al. (1990). In this interpretation, the low-pass filtering predicted for plexus-mediated signaling acquires functional significance because it would ensure only a persistent and regional increase in neural activity causes vasodilation.

Whether NO is targeting blood vessels or other targets in the brain, the same spatial and temporal properties of plexus-derived NO volume signals will apply. It is these functional properties that strongly suggest a role for plexuses in the integration of brain activity in space and time. We propose that the properties predicted by our model may in part explain the presence of ultrafine plexus morphologies in distantly related animals and in a variety of functional contexts. That is, the plexus morphology may represent a general structural adaptation for cooperative volume signaling by NO and by other diffusing messenger molecules.