Axonal Propagation of Simple and Complex Spikes in Cerebellar Purkinje Neurons

Abstract

In cerebellar Purkinje neurons, the reliability of propagation of high-frequency simple spikes and spikelets of complex spikes is likely to regulate inhibition of Purkinje target neurons. To test the extent to which a one-to-one correspondence exists between somatic and axonal spikes, we made dual somatic and axonal recordings from Purkinje neurons in mouse cerebellar slices. Somatic action potentials were recorded with a whole-cell pipette, and the corresponding axonal signals were recorded extracellularly with a loose-patch pipette. Propagation of spontaneous and evoked simple spikes was highly reliable. At somatic firing rates of ∼200 spikes/sec, <10% of spikes failed to propagate, with failures becoming more frequent only at maximal somatic firing rates (∼260 spikes/sec). Complex spikes were elicited by climbing fiber stimulation, and their somatic waveforms were modulated by tonic current injection, as well as by paired stimulation to depress the underlying EPSCs. Across conditions, the mean number of propagating action potentials remained just above two spikes per climbing fiber stimulation, but the instantaneous frequency of the propagating spikes changed, from ∼375 Hz during somatic hyperpolarizations that silenced spontaneous firing to ∼150 Hz during spontaneous activity. The probability of propagation of individual spikelets could be described quantitatively as a saturating function of spikelet amplitude, rate of rise, or preceding interspike interval. The results suggest that ion channels of Purkinje axons are adapted to produce extremely short refractory periods and that brief bursts of forward-propagating action potentials generated by complex spikes may contribute transiently to inhibition of postsynaptic neurons.

Introduction

In cerebellar Purkinje neurons, as in other neurons, initiation of action potentials occurs in the axon (Stuart and Häusser, 1994; Stuart and Sakmann, 1994; Colbert and Johnston, 1996), producing two types of somatic spikes. Simple spikes, which occur spontaneously, exceed 100 spikes/sec in response to excitation from parallel fibers (Thach, 1968; Gilbert and Thach, 1977; Kitazawa et al., 1998). Complex spikes, which are elicited by climbing fiber excitation, consist of a large-amplitude action potential followed by a series of spikelets having a frequency that approaches 500 Hz (Llinás and Sugimori, 1980; Schmolesky et al., 2002). Although action potentials forward-propagate reliably at low firing rates in several cell types (Mackenzie et al., 1996; Cox et al., 2000; Forti et al., 2000; Koester and Sakmann, 2000; Raastad and Shepherd, 2003) (but see Debanne et al., 1997), high firing rates can promote propagation failures (Debanne, 2004). Moreover, in the specific case of Purkinje neurons, it is unknown whether axonal ion channels produce refractory periods as brief as those in somata (Raman and Bean, 1999), a requirement for a one-to-one correspondence between somatic and axonal spikes. These issues raise the question of the reliability with which high-frequency action potentials of Purkinje cells propagate and contribute to inhibition of target cells in the cerebellar and vestibular nuclei.

Consistent with simple spike propagation that is, for the most part, effective, acceleration of simple spiking in Purkinje neurons increases synaptic inhibition of cerebellar nuclear neurons in vivo (McDevitt et al., 1987a). Similarly, climbing fiber stimulation evokes one to five spikes in Purkinje axons in anesthetized cats (Ito and Simpson, 1971; Campbell and Hesslow, 1986b) and elicits bursts of IPSPs in cerebellar nuclear cells in vitro (Llinás and Mühlethaler, 1988), confirming that complex spikes indeed yield multiple axonal spikes. These results, however, leave open the cellular question of what proportion of somatic spikes propagate to the terminal and evoke transmitter release. Specifically, across Purkinje cells, the height, width, and number of somatic spikelets of complex spikes vary widely (Campbell and Hesslow, 1986a), suggesting that certain spikelets may be more likely to propagate than others.

Also, within a given cell, the complex spike waveform changes with holding potential (Llinás and Sugimori, 1980), with repeated climbing fiber stimulation (Campbell and Hesslow, 1986a), and with short- or long-term depression of the underlying EPSCs (Dittman and Regehr, 1998; Silver et al., 1998; Hansel and Linden, 2000; Foster et al., 2002). These observations raise the additional question of whether the forward-propagating signals of complex spikes are also susceptible to modulation, thereby influencing the pattern of corticonuclear inhibition (Schmolesky et al., 2002; Foster and Regehr, 2004).

To address these questions, we have made dual somatic and axonal recordings from Purkinje cells in mouse cerebellar slices. The results indicate that simple spikes propagate reliably up to maximal somatic firing rates. On average, complex spikes produce two to three axonal spikes, the frequency of which depends on the previous activity of the Purkinje neuron, and, across a range of conditions, the attributes of the spikelet waveform can predict the probability with which each spikelet propagates.

Materials and Methods

Preparation. Cerebellar slices were prepared from 17- to 21-d-old C57BL/6 mice. In accordance with institutional guidelines, animals were anesthetized with halothane and transcardially perfused with ice-cold, artificial CSF (ACSF) containing (in mm): 123.75 NaCl, 3.5 KCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, 10 glucose, bubbled with 95/5% O₂/CO₂. After decapitation, the cerebellum was removed, and parasagittal slices (200 μm) were cut on a Vibratome (Leica VT100S). Slices were incubated in warm (32°C), oxygenated ACSF for ∼1 hr. Recordings were made within 6 hr of incubation. Except as noted, chemicals were from Sigma-Aldrich (St. Louis, MO).

Electrophysiology. Slices were bathed in oxygenated ACSF with 10 μm SR95531 to block GABA_A receptors. Purkinje cells were visualized with a Zeiss Axioskop FS2 with a 63× objective. Cells were selected for recordings only if their axons were visible for >50 μm under infrared differential interference contrast optics. Somatic, whole-cell recordings were made with borosilicate patch pipettes (3-4 MΩ) filled with an internal solution containing (in mm): 120 KCH₃SO₃, 10 NaCl, 10 HEPES, 2 MgCl₂, 1 EGTA, 0.066 Alexa 594 (Molecular Probes, Eugene, OR), and 0.3% biocytin, buffered to a pH of 7.35 with KOH. Somatic action potentials were recorded in current clamp with an Axoclamp 2B amplifier and pCLAMP 8.2 software (Axon Instruments, Union City, CA). Data were acquired at 20 or 50 kHz and filtered at 10 kHz. Recordings were made at 33 ± 2°C.

After a somatic recording was established, cells were allowed to fill for 15-25 min. Fluorescence was used sparingly to track or confirm the identity of the axon as it passed through the granule cell layer and entered the corticonuclear tract. For most experiments, the area of fluorescent illumination was constrained to a 50 × 50 μm square, and a 150 msec light pulse (590 nm) flashing at ∼3 Hz was used for excitation. After the most distal part of the main axon was identified, a loose-patch seal was made onto the myelinated axon, near or proximal to the cut end of the axon. Loose-patch pipettes (5-7 MΩ) were filled with a solution containing (in mm): 145 NaCl and 10 HEPES, buffered to a pH of 7.35 with NaOH. Axonal signals were recorded using a second amplifier (Axopatch 200B) in current-clamp (bridge) mode, so that no current was injected through this electrode, and data were acquired at 20 or 50 kHz and filtered at 5 kHz. Because axonal spikes could be measured extracellularly as action potentials jumped across the internode (Zhou and Chiu, 2001), recording through the myelin minimized the possibility that the loose-patch pipette would interfere with the propagation or regeneration of action potentials, at least up to the recording point. The distance of the axonal electrode from the soma was estimated with a reticule on the microscope, and an image was stored to document the location of the axonal recording site. Confocal imaging was later used for more precise estimates of recording distances (below). All axonal recordings were made >70 μm from the soma.

To evoke complex spikes, a theta glass pipette filled with 145 mm NaCl and 10 mm HEPES, pH 7.35, and containing the stimulating and ground electrodes was positioned in the granule cell layer, and climbing fibers were activated with 100 μsec voltage pulses via a stimulus isolation unit (IsoFlex; A.M.P.I., Jerusalem, Israel). Minimal stimulation intensities were used, so that records in which the stimulus failed to evoke a response could be used for subtraction of stimulus artifacts. For experiments in subsaturating tetrodotoxin (TTX) (Alomone, Jerusalem, Israel), somatic and axonal complex spikes were first measured in control solutions, with the axonal electrode positioned >125 μm from the soma. Next, a puffer pipette was used to apply 5 nm TTX to a ∼25 μm stretch of the axon between 100 and 125 μm from the soma, and recordings of somatic and axonal complex spikes were repeated. This concentration of TTX blocks just over 50% of voltage-gated Na channels in Purkinje cells (Raman and Bean, 1999). Axonal perfusion of TTX left the somatic complex spike relatively unchanged, but control experiments in which the whole slice was bathed in 5 nm TTX verified that this concentration reduces the number of spikes per burst, and/or spike rate of rise (dV/dt).

Analysis. All data were analyzed with Igor Pro 4 (Wavemetics, Lake Oswego, OR). To obtain a measure of success or failure of axonal propagation, the peak axonal response corresponding to a somatic spike was measured and compared with the noise level by the following method. Somatic spikes were first identified with a threshold detection protocol (usually 0 mV for simple spikes and -20 mV for complex spikes evoked from hyperpolarized potentials). For each somatic spike, the time of peak (t_{pk_soma}) was recorded, and the maximum value from the corresponding axonal trace (V_{max_axon}) was measured in a 1.2 msec time window centered on t_{pk_soma}. The minimum value in the axonal trace (V_{min_axon}) was then measured in a 0.8 msec window after V_{max_axon}, and the difference was recorded as the peak-to-peak axonal signal (V_{max_axon} - V_{min_axon}). Next, the peak-to-peak axonal noise was measured in 0.5 msec intervals during which no somatic action potentials occurred. Intervals within 0.5 msec of somatic spikes were excluded. The axonal noise values (∼300 per recording) were averaged to find the mean and SD of the axonal noise. Axonal signals corresponding to somatic spikes were classified as successfully propagating action potentials if their amplitudes exceeded 3 SDs from the mean noise. In each cell, 18-34 complex spikes were recorded, and the failures and successes were averaged to obtain a probability of propagation for each spikelet.

Although spikelets of complex spikes evoked from negative holding potentials (to silence spontaneous activity, i.e., “quiet” recordings) could be unambiguously detected (see Results), the spikelets of complex spikes evoked during spontaneous activity (“activity” recordings) were often less distinct. Because the amplitude of the second spikelet was often very small and the third and fourth spikelet occasionally merged, the analysis protocol was modified for complex spikes evoked during activity. In four of eight neurons, the third and fourth spikelets merged into a broad, bimodal spike, which was counted as a single spike. In the other cells, the complex spike recorded in quiet served as a template to identify the time of occurrence of each of the first three spikes, and the axonal signal corresponding to these spike times was measured. The remaining spikelets of the activity trace were analyzed with the standard protocol.

When no significant pause followed a complex spike evoked during activity (see Fig. 3B), the complex spike was distinguished from subsequent simple spikes by the persistence of a depolarization during the interspike interval (ISI). Peak-to-peak amplitudes of somatic action potentials were defined as the difference between the trough preceding the spike and the maximal amplitude of the spike (see Figs. 5, 6). Data are reported as mean ± SE. Statistical significance was assessed with t tests, which were paired except as noted.

Figure 3.

Axonal action potentials triggered by complex spikes at different holding currents and interstimulus intervals. A, B, Somatic and axonal recordings of complex spikes evoked by a pair of climbing fiber stimulations with a 40 msec interval. A, Tonic hyperpolarizing current held the cell near -70 mV. B, no holding current. The axonal electrode was 406 μm from soma (same cell as Fig. 1). Plot of axonal signal and noise as in Figure 1. C, D, Summary of the number of somatic (solid symbols) and axonal (open symbols) spikes per climbing fiber stimulation, plotted versus interstimulus interval, with (C) (n = 7) and without (D) (n = 5) holding current. The response to the first stimulus is as labeled (rightmost symbol). E, F, Propagation efficiency for the first and second stimulations (stim), given as the ratio of the number of axonal to somatic spikes (“axon/soma ratio”) with (E) (n = 7) and without (F) (n = 5) holding current.

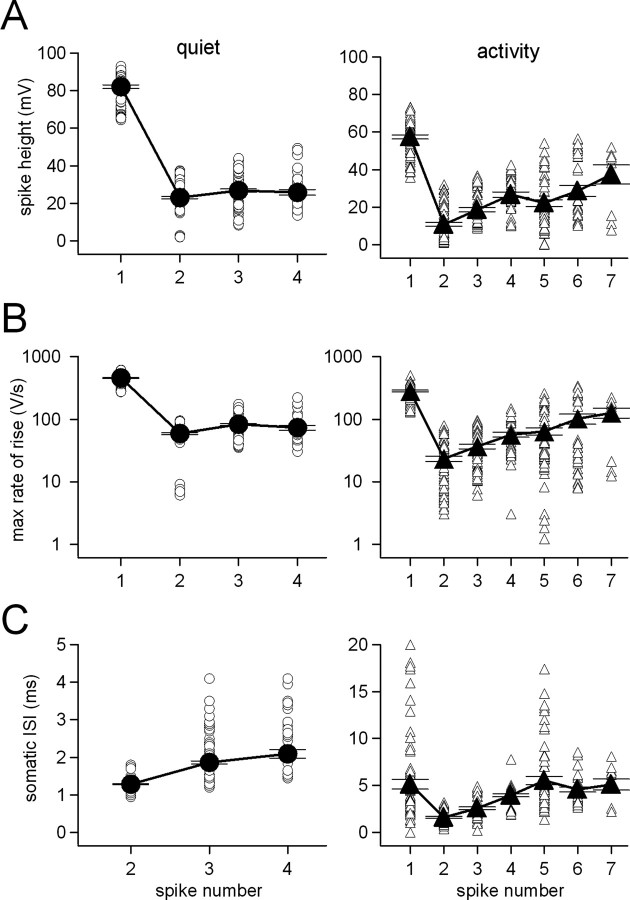
Figure 5.

Attributes of individual spikelet waveforms of complex spikes. Data from somatic complex spikes recorded in quiet (left) and during activity (right) for individual spikelets (open symbols), with mean values superimposed (closed connected symbols). A, Spike heights versus spikelet number. B, Maximal rate of rise versus spikelet number. C, Interspike interval preceding the spikelet versus spikelet number. Note no data for spike 1 for recordings in quiet; for recordings during activity, the ISI for spike 1 indicates the time since the previous simple spike. Note y-scale difference.

Figure 6.

Probability of propagation for spikelets of complex spikes as a function of spikelet attributes. Binned propagation probability for all 501 spikelets in quiet (closed symbols) and all 380 spikelets in activity (open symbols). In all panels, horizontal placement of symbol indicates mean x-value per bin. A, Propagation probability versus somatic spikelet height. Solid line is a fit to the combined quiet and activity data with a sigmoid function of the form y = 1/(1 + exp(-(x - V_half)/k), which gives a spikelet height with probability of 0.5 (V_half) of 26.9 mV and slope factor (k) of 7.9 mV. B, Propagation probability versus rate of rise of somatic spikelet. Solid line is a fit to the combined quiet and activity data with a Hill function of the form y = 1/(1 + ((dV/dt_half)/x)ⁿ), which gives a spikelet rate of rise with probability of 0.5 (dV/dt_half) of 58.5 V/sec and steepness coefficient (n) of 1.5. C, Propagation probability versus interspike interval preceding each spikelet. Data from quiet and activity were fit separately with sigmoid functions (solid lines) of the form y = 1/(1 + exp(-(x - ISI_half)/k), which give ISIs with probability of 0.5 (ISI_half) of 1.7 msec (quiet) and 3.8 msec (activity) slope factors (k) of 0.3 msec (quiet) and 1.6 msec (activity).

Histology. After experiments, slices were fixed in 4% paraformaldehyde for >24 hr. Biocytin-filled cells were visualized with standard procedures. Slices were incubated in a solution containing 1% H₂O₂ in 10% methanol/90% PBS for 30 min and rinsed. Cells were permeabilized with 2% Triton X-100 and treated with ABC Vectastain Kit (Elite Pk-6100 Standard; Vector Laboratories, Burlingame, CA) for 2 hr and rinsed. Sigma-Fast DAB kit was then used to visualize the stain (Sigma). Cells were viewed on a Leica DM IRE2 confocal microscope, and axonal recording distances were measured with ImageJ software (NIH).

Results

To measure the reliability of action potential propagation in cerebellar Purkinje cells, we made simultaneous somatic and axonal recordings. A whole-cell, current-clamp recording was established at the soma, with a pipette containing a physiological intracellular solution that included 66 μm Alexa 594. The fluorescence allowed visualization of the axon and facilitated the positioning of an extracellular, loose-patch pipette, over the myelin, at the most distant part of the axon that could be resolved. Figure 1A illustrates a labeled Purkinje cell, with arrows indicating the recording sites at the soma and 406 μm from the base of the soma. Although branch points were occasionally visible as axons exited the Purkinje cell layer (Fig. 1A, inset, arrow), all axonal recordings were made from the main axon.

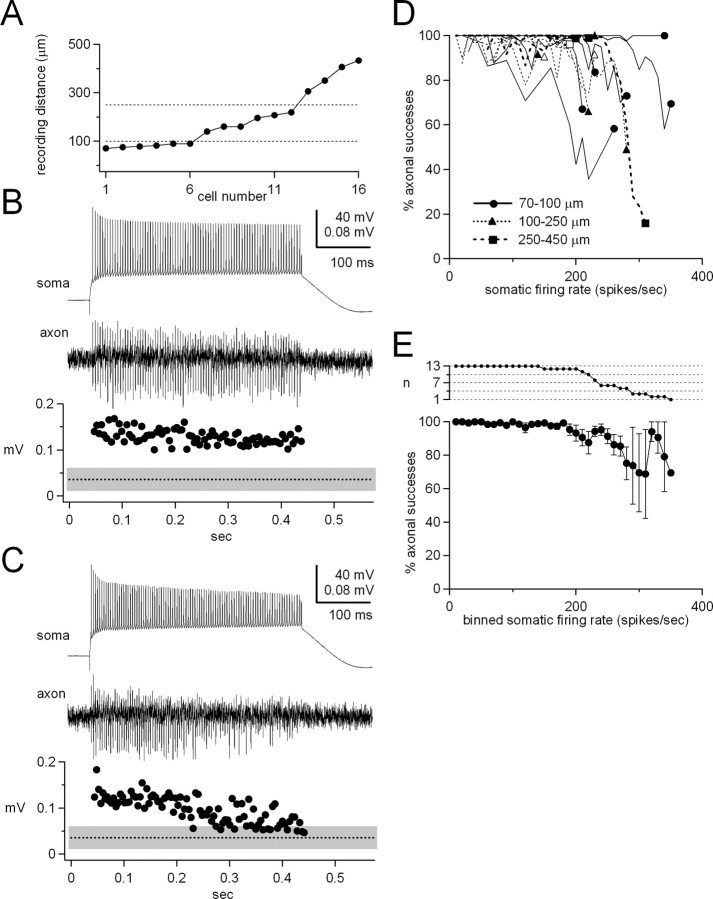
Figure 1.

Dual somatic and axonal recordings from Purkinje neurons. A, Purkinje cell stained with DAB. Arrows indicate sites of somatic recording and axonal recording 406 μm from soma. Inset, Main axon at higher gain, with arrow indicating an axon collateral. B, Spontaneous somatic (top) and axonal (middle) action potentials from the cell in A. A single axonal action potential is shown on an expanded time base at right. Bottom, Peak-to-peak amplitude of the axonal signal in a time window corresponding to each somatic action potential (circles) plotted with the mean (dotted line) ± 3 SDs (gray shading) of the axonal noise signal recorded in intervals lacking somatic spikes (see Materials and Methods).

With no current injection and with GABA_A receptors blocked, Purkinje cells fired regular, spontaneous action potentials (Häusser and Clark, 1997; Smith and Otis, 2003) that were recorded through the somatic electrode (Fig. 1B, top panel). Simultaneous signals were recorded in current-clamp mode through the axonal electrode (Fig. 1B, middle panel). For each somatic action potential, a voltage transient occurred in the axon. The initial deflection was positive, consistent with the predicted voltage signal from action potentials recorded through the myelin at internodes (Huxley and Stämpfli, 1949; Zhou and Chiu, 2001). Axonal signals were accepted as representative of propagating action potentials if withdrawal of the axonal recording pipette by a few micrometers resulted in a loss of spike-like deflections, and if the putative axonal spikes had a relatively constant latency with respect to each somatic action potential. The latter criterion provided the basis for identifying successful propagation at higher frequencies (see Materials and Methods). Briefly, if the peak-to-peak axonal signal in a 1.2 msec window corresponding to a somatic spike (Fig. 1B, bottom panel, circles) exceeded 3 SDs from the mean axonal noise, measured in intervals lacking somatic spikes (Fig. 1B, bottom panel, dotted line and shading), it was counted as a successfully propagating spike.

The dataset included 16 cells with axonal recording distances that were classified as close (70-100 μm; n = 6), mid-range (100-250 μm; n = 6), and distant (250-450 μm; n = 4) (Fig. 2A). To test the reliability of simple spike propagation, a constant hyperpolarizing current was injected to silence the cells by holding the soma near -70 mV, and 400 msec depolarizing current steps of increasing amplitude were applied to evoke simple spikes. In the example of Figure 2B, in which the axonal recording site was 90 μm from the soma, a 1.62 nA injection evoked 91 spikes (207 spikes/sec), of which 100% corresponded to axonal signals that were well above the noise. With a larger current injection (2.07 nA), the somatic firing rate increased to 231 spikes/sec, but the axonal successes dropped to 87% (Fig. 2C). In Figure 2D, the percentage of axonal successes is plotted for each cell against the somatic firing rate evoked with current steps of increasing amplitude (n = 16). In the seven cells that were systematically examined for branch points after the recordings, four had one branch off the main axon between the soma and the axonal recording pipette; the other three axons had no branches. At all recording distances, however, even in axons lacking branches proximal to the axonal recording site, propagation failures occurred at high firing rates.

Figure 2.

Reliability of simple spike propagation. A, Summary of axonal recording distances for each cell. Dotted lines indicate boundaries between close, mid-range, and distant recordings. B, C, Somatic and axonal recordings of simple spikes, with plots of axonal signal and noise amplitudes as in Figure 1. The axonal electrode was 90 μm from soma. Tonic hyperpolarizing current held the cell near -70 mV. Spikes were evoked by 400 msec current injections, and firing rates were 207 spikes/sec (B) and 231 spikes/sec (C). Percentage propagation was 100% (B) and 87% (C). D, Percentage axonal successes versus somatic firing rate for 16 cells. Recording distances are as labeled. Filled symbols indicate data from cells driven to their maximal somatic firing rate (n = 13); open symbols indicate cells not driven to their maximal firing rates (n = 3). E, Data from the 13 cells driven to maximal rates in D, binned and averaged; bin width = 10 spikes/sec. Inset graph, Number of cells that fired at each rate.

These results provide evidence that the axonal recording sites were distal to the spike initiation zone, which has been estimated to be 30-60 μm from the soma in unmyelinated axons (Colbert and Johnston, 1996) but may be farther out in myelinated axons (Colbert and Pan, 2002). We reasoned that if our axonal recording sites had been upstream from the spike initiation zone, every somatic spike would have corresponded to an axonal success as the action potential back-propagated toward the soma. Because propagation failures were evident, however, the axonal recording electrode was more likely to have been beyond the spike initiation zone. As an additional test, we examined the axonal noise measurements for instances of spike-like events occurring in the absence of somatic action potentials, because axonal successes with somatic failures have been documented for axonal recordings between the soma and the spike initiation zone (Colbert and Johnston, 1996; Williams and Stuart, 1999). In our recordings, however, no axonal spikes were ever observed in the absence of a somatic action potential. Together, these data are consistent with the idea that close, mid-range, and distant recordings all represented forward-propagating action potentials.

The range of recording distances predicts maximal latencies between the somatic and axonal spikes of 70-450 μsec for conduction velocities of 1 m/sec or 7-45 μsec for velocities of 10 m/sec. These values will be further reduced, or even negative, if the action potential is initiated between the somatic and axonal recording site. Although the temporal resolution of latency measurements in these experiments was limited by our sampling rate of 50 μsec per point, we calculated the average lag between the peak somatic and axonal spikes for spontaneously occurring action potentials in each cell. These latencies ranged from -40 to +210 μsec, generally consistent with average conduction velocities between 1 and 10 m/sec.

To estimate the percentage of successful propagation as a function of somatic firing rate, the data from Figure 2D were binned and averaged. In the 13 cells driven to their peak firing rates (Fig. 2D, solid symbols), the maximal somatic rate was 262 ± 16 spikes/sec. At 200 spikes/sec, failures were relatively rare, with 93 ± 5% of somatic spikes leading to axonal successes (n = 12) (Fig. 2E) (Monsivais and Häusser, 2003). At 270 spikes/sec, the axonal successes fell to 81 ± 7%; however, only six cells could maintain somatic firing at this rate (Fig. 2E, inset). That propagation failures became apparent near the maximal somatic firing rate indicates that simple spike propagation along the main axon is highly reliable.

Nevertheless, the propagation failures generate some predictions about the propagation of complex spikes. Most failures occurred late in the 400 msec current step, as the trough-to-peak amplitude of somatic spikes decreased. For instance, in Figure 2C, the percentage of propagation was 100% for the first 45 spikes, but only 73% for the last 46 spikes. Concurrent with the gradual decrement in somatic spike height, the amplitude of the axonal signal decreased (8 of 16 cells). This decrement raised the possibility that late, small spikelets of complex spikes may also propagate with relatively low probability or that they may not always maintain a stereotyped waveform.

To measure propagation of individual spikelets of complex spikes directly, we stimulated climbing fibers while recording simultaneously from the soma and axon (n = 9). In seven of these neurons, we also generated a range of complex spike waveforms by evoking pairs of complex spikes, at four different stimulus intervals and at two different holding potentials. The first series of complex spikes was evoked during constant hyperpolarizing current injections to hold cells near -70 mV (in quiet). Figure 3A (top panel) illustrates a pair of complex spikes elicited in quiet, with a 40 msec interval. In all cells, the first complex spike consisted of one large spike followed by two shorter spikelets (“spikelets 2 and 3”), with an additional spikelet (“spikelet 4”) that appeared at full amplitude on some trials but not others in five cells. Excluding the all-or-none variation of spikelet 4, the complex spike in each neuron tended to maintain the same somatic waveform across trials. The axonal recordings indicated that only a subset of the spikelets propagated (Fig. 3A, middle and bottom panels). On average, complex spikes evoked in quiet had 3.4 ± 0.1 somatic spikelets and 2.0 ± 0.2 axonal spikes, which occurred with a mean interspike interval of 2.67 ± 0.16 msec (n = 9). Despite the replicability of the somatic waveform, some spikelets propagated successfully on some trials and failed on others (quantified below).

Previous research has indicated that climbing fiber EPSCs are subject to shortterm depression (Dittman and Regehr, 1998; Silver et al., 1998), which may result in changes in the complex spike waveform (Foster and Regehr, 2004). To test whether such short-term modulation might affect the number of propagating action potentials, we compared the responses with the first and second climbing fiber stimulation (n = 7). As illustrated in Figure 3A, the second complex spike of the pair often had fewer spikelets than the first, consistent with synaptic depression of the second climbing fiber EPSC (∼50-70% for the intervals tested) (Dittman and Regehr, 1998; Silver et al., 1998) and possibly incomplete recovery of voltage-gated channels that inactivated during the first complex spike. A reduction in the number of somatic spikelets often corresponded to fewer axonal spikes (Fig. 3A). To quantify and compare the number of somatic with axonal spikes at each interval, recordings of complex spike pairs were repeated (with a 2 sec intertrial interval), and the mean number of somatic and axonal spikes was calculated. As shown in Figure 3C, the first climbing fiber stimulation (rightmost symbols) elicited 3.2 ± 0.2 somatic spikelets (n = 7), which resulted in 2.0 ± 0.2 axonal action potentials. With the second climbing fiber stimulation, the number of somatic spikes dropped slightly, but significantly, at all intervals (p < 0.05). Despite changes in the somatic waveform, the mean number of axonal spikes dropped only slightly at the 20 msec interval (to 1.5 ± 0.2; p = 0.1) and remained near 2 for all other intervals (p > 0.5). The propagation efficiency, calculated as the ratio of the numbers of axonal to somatic action potentials for each complex spike, was 63.5 ± 9% for the first stimulus, and although it increased slightly, remained statistically unchanged at all intervals (p > 0.5) (Fig. 3E).

In the intact organism, Purkinje neurons generally are not quiet in the absence of synaptic stimulation but maintain basal firing rates of several tens of Hertz. The level of activity of the cell is likely to modify its availability of intrinsic channels and may thereby modulate the waveform of the complex spike. To test how such changes may influence propagation, we repeated the experiments in the same neurons with no holding current, so that the cells could fire spontaneously (at 77 ± 13 spikes/sec; n = 9; “during activity”). Under these conditions, each spikelet of the complex spike was generally of lower amplitude and longer duration than those recorded in quiet, but more spikelets were superimposed on the underlying depolarization. Pauses after complex spikes were brief (18.5 ± 0.5 msec; n = 9) but could become longer when complex spikes were elicited after depolarizing current steps that increased the rate of simple spikes (data not shown). In the example of Figure 3B (top panel), the first climbing fiber stimulation evoked seven somatic spikelets, including the initial spike. The first action potential of the complex spike propagated, as did the simple spikes preceding and after synaptic stimulation, but two of the spikelets lacked a corresponding axonal action potential (Fig. 3B, middle and bottom panels). Across cells, the first stimulation resulted in 5.4 ± 0.3 somatic spikelets, of which 2.3 ± 0.3 propagated (n = 8; the 9th cell was excluded because climbing fiber stimulation elicited an antidromic action potential that obscured the first spike). Thus, although each complex spike had significantly more somatic spikelets in activity than during quiet (p < 0.01; unpaired), the number of propagating spikes remained fairly constant (p = 0.5; unpaired). The mean interspike interval of propagating axonal spikes, however, decreased to 6.6 ± 1.0 msec, a value more than twice that in quiet.

To test the effects of short-term depression of climbing fiber EPSCs, paired climbing fiber stimuli were also applied during activity in five cells. The waveform of the second complex spike of the pair generally differed from that of the first (Fig. 3D), although only with a 20 msec interval did the mean number of somatic spikelets significantly decrease (from 4.8 ± 0.4 spikelets to 3.7 ± 0.8; n = 5; p < 0.05) (Fig. 3F). In the axon, however, the numbers of spikelets that propagated after each stimulation were indistinguishable (p > 0.1; all intervals). The propagation efficiency, which was 60 ± 8% for the first complex spike, rose to 73 ± 9% for the complex spike evoked after 20 msec (p < 0.05) but fell back to ∼65% for the longer intervals (p > 0.5; all intervals) (Fig. 3F). Thus, manipulations that evoked a relatively wide range of somatic spikelets had only a moderate effect on the mean number of forward-propagating action potentials.

Nevertheless, on a trial to trial basis, it was clear that different complex spike waveforms corresponded to different numbers of propagating spikes (Fig. 3A,D) and that certain spikelets appeared more likely to propagate than others. To compare the probability of propagation of each depolarization, we analyzed the individual spikelets composing the complex spikes (elicited either by the first stimulus in a paired-pulse protocol or by an unpaired stimulus; n = 9). For each somatic spikelet, the ratio of successful propagations to number of trials was calculated. The complex spike waveforms evoked in quiet are illustrated in Figure 4A for all cells included in the analysis, and individual as well as mean values for the probability of propagation of each spikelet are plotted in Figure 4B. Not surprisingly, the first spike propagated with 100% reliability. For spikelet 2, however, the mean probability of propagation dropped to 28%, before increasing to 62 and 52% for spikelets 3 and 4 (n = 9). For spikelets 2, 3, and 4, however, the responses of individual cells covered the full range of probabilities. In the eight cells examined during activity, the mean reliability of propagation was lower for each spikelet (Fig. 4C,D). The mean propagation probability was 81% for the initial spike, fell to 9% for the second spikelet, and tended to increase for subsequent spikelets. Except for spikelet 2, the other late spikelets had a wide range of propagation probabilities across cells.

Figure 4.

Propagation probabilities for individual spikelets composing complex spikes. A, Complex spikes elicited in quiet by climbing fiber stimulation for nine neurons. Tonic hyperpolarizing current held each cell near -70 mV. Color coding identifies individual cells in all panels. In the black trace, an antidromic action potential preceded the first spike. B, Probability of axonal propagation for each spikelet, calculated from multiple trials. Small symbols are offset for clarity. Large symbols represent mean data. C, D, Traces and plots as in A and B but with no holding current. In some cells, simple spikes after the complex spike are also shown. Gray cell from A and B is excluded because of antidromic action potentials that obscured the first spike. Spikelets 3 and 4 merged in the turquoise, brown, blue, and red cells, and the propagation probability is plotted as a single point at spike 3 in D.

Inspection of the individual records suggested that, like the high-frequency simple spikes occurring late in trains, several spikelets that had relatively low amplitudes also propagated with low probability (Fig. 4, brown and gray traces and symbols). Such a correlation is not surprising, because small somatic spike heights may reflect a low availability of Na channels, which in turn is likely to correlate with refractoriness of the axonal spike initiation site. To quantify the dependence of propagation probabilities on spikelet waveform, we began by measuring the trough-to-peak spike height for each spikelet in each complex spike evoked in each Purkinje cell. Plotting the somatic spike height for each spikelet confirmed that spike height and mean propagation probability had a similar dependence on spikelet number, both in quiet (Fig. 5A, left) (n = 146 complex spikes in 9 cells) and during activity (Fig. 5A, right) (n = 78 complex spikes in 8 cells). Specifically, the amplitude of the first spike was high, dropped substantially for the second spikelet, and increased gradually for subsequent spikelets.

Next, because spike height is likely to depend in part on the amplitude of the underlying depolarizing currents, we measured and plotted the maximal rate of rise (dV/dt), which should be proportional to inward current, against spikelet number for each complex spike (Fig. 5B). These data also followed the same trend as the propagation probability. Last, plotting the interspike interval preceding each spikelet against spikelet number indicated that the intervals became longer between successive pairs of spikelets. Although the intervals were generally briefer in quiet than during activity (Fig. 5C), the data paralleled the dependence of propagation probability on spikelet number in each condition. The observation that, to a first approximation, all plots follow the same trend as the plots of propagation probability is consistent with the basic principle that longer interspike intervals permit more recovery from inactivation of depolarizing (Na and possibly Ca) currents, thereby accelerating the rate of rise and increasing the amplitude of spikelets.

To test the possibility that the propagation probability of any spikelet, regardless of its position in the complex spike, might have a simple dependence on the extent of recovered and therefore available somatic inward current, we reexamined each spikelet of each complex spike, tagged either as a propagation success (1) or failure (0). The data were binned according to spike height, rate of rise, and interspike interval, and the probability of propagation in each bin was calculated (n = 501 spikelets in quiet; n = 380 spikelets in activity). Figure 6A illustrates that, independent of the background activity or spikelet number, propagation probability could generally be well described by a smooth function of somatic spikelet height. Fitting the data estimated that a spike height of 26.9 mV predicted a 50% probability of propagation. The probability also varied directly with the rate of rise of each spikelet. In quiet as well as during activity, a dV/dt of 58.5 V/sec predicted a 50% likelihood of propagation (Fig. 6B). The dependence of propagation probability on interspike interval, however, depended on background activity (Fig. 6C). In quiet, propagation probability was a steep function of interspike interval, with 100% propagation occurring with a 4 msec interval. In contrast, during activity, a 4 msec interval predicted only a ∼50% probability of propagation, with intervals as long as 8 msec necessary for a probability of 80%. Thus, the probability with which each spikelet of a complex spike propagates can be defined by a saturating function of spike height or rate of rise, the values of which increase with preceding interval and with previous hyperpolarization.

These results are consistent with a faster recovery of voltagegated inward currents at the more negative interspike intervals achieved with tonic hyperpolarizing current injections in quiet. As a simple test of this idea, we recorded somatic and axonal complex spikes in two more cells. Cells were held quiet at -70 mV, and recordings were made first in control conditions and then while perfusing a ∼25 μm segment of the axons, between the somatic and axonal recording pipettes, with a concentration of TTX that is predicted to block voltage-gated Na channels by ∼50% (5 nm) (Raman and Bean, 1999) (see Materials and Methods). In control solutions, the spikelets had a mean interspike interval of 1.48 ± 0.02 msec (n = 389 spikelets; 2 cells), which propagated with a probability of 39% (data not shown). These data are consistent with the fitted curve in Figure 6C, which predicts a 40% propagation probability with this interspike interval. When subsaturating TTX was applied to the axons (see Materials and Methods), the mean interspike interval of the somatic complex spikelets was 1.61 ± 0.03 msec (n = 189 spikelets; same 2 cells), but the propagation probability dropped to 17%, just less than half the value in control solutions (data not shown). These results are consistent with the simple interpretation that successful propagation depends to a great extent on the availability of voltage-gated Na channels in Purkinje axons.

Discussion

These results indicate, first, that simple spike propagation along Purkinje axons is highly reliable, even up to maximal somatic firing rates (200-250 spikes/sec). Second, for complex spikes, 60-70% of the somatic spikelets (including the initial spike) correspond to propagating action potentials, independent of background activity or depression of the underlying climbing fiber EPSC. Third, although the number of axonal spikes per climbing fiber stimulation remains near two to three per stimulus, the instantaneous frequency of the axonal spikes varies widely, depending on ongoing Purkinje cell activity. Finally, on a trial to trial basis, independent of simple spike activity, the trough-to-peak amplitude of any spikelet may be used to predict the probability of its propagation.

Evidence for specializations of axonal channels

To date, propagation in axons has been measured primarily with low-frequency trains or with high-frequency trains of ≤10 stimuli (Cox et al., 2000; Koester and Sakmann, 2000; Soleng et al., 2003). The present data indicate that, in Purkinje axons, reliable propagation at 200 spikes/sec can persist for ≥100 action potentials. This result provides information about the properties of axonal ion channels, for which little kinetic data are available. Specifically, to transmit action potentials successfully at such high rates for relatively sustained periods, the refractory periods produced by axonal channels, like those of somatic channels, must be extremely brief (<5 msec). In Purkinje somata, several specialized voltage-gated channels interact to minimize the refractory period (Raman and Bean, 1999). For example, somatic voltage-gated Na channels have “resurgent” kinetic properties that promote rapid recovery from inactivation even at potentials that are only moderately hyperpolarized (Raman and Bean, 2001). This rapid recovery appears to be facilitated primarily by Na_V1.6 α subunits associated with a putative protein that limits inactivation (Raman and Bean, 1997; Grieco et al., 2002; Khaliq et al., 2003; Grieco and Raman, 2004). Although Na_V1.6 is the primary Na channel α subunit in nodes in most parts of the nervous system (Caldwell et al., 2000; Krzemien et al., 2000), it is unknown whether the nodal Purkinje Na channels share the distinctive kinetics of the somatic channels. Our data suggest that Purkinje axonal Na channels are likely to either have another, axon-specific mechanism for rapid recovery of Na channels (Smith et al., 1998) or a regulatory mechanism similar to that in the soma.

The K channels of Purkinje somata include voltage-gated K_V3 channels as well as Ca-gated BK channels, which are also well adapted for high-frequency firing. Currents through these channels activate and deactivate rapidly, thereby limiting Na channel inactivation, facilitating Na channel recovery, and permitting depolarization soon after a spike (Gähwiler and Llano, 1989; Raman and Bean, 1999; Southan and Robertson, 2000; Womack and Khodakhah, 2002; Edgerton and Reinhart, 2003; Khaliq et al., 2003). The present results are suggestive of axonal K channels with similarly rapid gating kinetics. Consistent with this idea, K_V3 channels have been detected by immunolabeling in Purkinje axons of Apteronotus electric fish (Rashid et al., 2001).

Complex spikes and propagation of action potential “bursts”

Action potential propagation has been studied in layer 5 pyramidal neurons of the rat neocortex that produce bursts of two to six somatic spikes at ∼300 Hz; in these cells, axonal recordings up to 40 μm from the soma, as well as paired presynaptic and postsynaptic recordings, indicate that forward-propagation of action potentials is secure (Williams and Stuart, 1999). Similarly, cartwheel cells of the mouse dorsal cochlear nucleus produce spontaneous somatic spike bursts, which correlate with bursts of PSPs in their targets (Golding and Oertel, 1997), suggestive of reliable propagation all the way to the terminal. In both cell types, however, the late spikes of the somatic bursts often have clearly defined spike-like waveforms, unlike the smaller, slower depolarizations that typify the middle spikelets of Purkinje complex spikes. In fact, paired recordings indicate that, on the occasions when cartwheel cells produce bursts with late depolarizations that resemble the short, shallow-sloped spikelets of Purkinje cell complex spikes, only the high-amplitude, steeply rising action potentials reliably evoke PSPs in postsynaptic cells (Tzounopoulos et al., 2004).

Our data are consistent with these results, in that the probability of propagation of each Purkinje spikelet varied predictably with the simplest attributes of the spikelet waveforms, i.e., spike height and rate of rise. A remaining question, however, is how many of these propagating spikelets actually reach Purkinje terminals. Our quantitative estimates of the probability of propagation as a function of these variables (50% propagation with a 27 mV height or 60 V/sec slope) may be generalizable only to recordings made under ionic conditions and temperatures similar to those in our experiments. Also, although most of our recordings were made >100 μm from the soma, most axons extend for ≥1 mm, projecting through the corticonuclear tract and into the cerebellar nuclei. Moreover, before terminating in the cerebellar nuclei, Purkinje axons branch extensively (Chan-Palay, 1977), a feature that increases propagation failures in some preparations (Debanne, 2004).

Our estimates, therefore, may provide only an upper limit on the number of spikes that trigger transmitter release. Nevertheless, they offer a basis for evaluating the complex spikes: first, as forward-propagating signals, and second, as signals that may be subject to modulation. Specifically, the results provide evidence that the propagating action potentials resulting from simple and complex spikes are apparently indistinguishable in the axon. For both simple and complex spikes, however, the amplitude of the axonal signals decreases after extremely brief interspike intervals, suggesting that propagating action potentials may not always be all or none. An interesting possibility is that the lower-amplitude axonal signals may be indicative of spike broadening, which correlates with enhanced transmitter release in other preparations (Geiger and Jonas, 2000).

Regarding modulation, the most significant change that we observed in the forward-propagating signals of complex spikes was a doubling in the instantaneous frequency of the axonal spikes in quiet relative to activity. Generalizing this result predicts that the interspike interval between forward-propagating action potentials elicited by complex spikes will increase with the level of somatic depolarization. The number of propagating action potentials per complex spike, however, was less subject to modulation. This result arose, in part, because only 60-65% of the somatic spikelets propagated, thereby blunting the axonal consequence of changing the number of somatic spikelets. For example, to increase the number of axonal spikes from two to three, the number of somatic spikes per stimulus would have had to increase from three to nearly five, a change that rarely occurred in response to our manipulations. Our data predict, however, that manipulations that increase the height or steepness of somatic spikelets are likely to increase the number of propagating spikes, even if the total number of somatic spikelets were to remain constant. In vivo recordings demonstrate a range in the number of spikes per stimulus even in a single Purkinje axon (Ito and Simpson, 1971; Campbell and Hesslow, 1986b), consistent with the possibility that the somatic waveform of individual spikelets in the intact animal may vary widely.

Signaling by complex spikes

The informational role of the complex spike has been extensively studied, debated, and reviewed (Simpson et al., 1996; Schmolesky et al., 2002). In general, the signals that have been ascribed to complex spikes can be categorized as either long term or real time. The long-term signals are mediated by the large dendritic influx of Ca, which has several effects, including depression of the strength of parallel fiber EPSCs (Linden and Connor, 1993; Ito, 2001). The real-time signal, which is likely to be intensified by synchronized activity of multiple Purkinje cells, consists of any forward-propagating action potentials of the complex spike itself, as well as the pause and the subsequent resumption of firing after the complex spike (Llinás and Sasaki, 1989; Simpson et al., 1996; Lang et al., 1999; Lang, 2003).

Although bursts of action potentials indeed propagate after climbing fiber stimulation (Ito and Simpson, 1971; Campbell and Hesslow, 1986b; present results), it remains possible that the contribution of forward-propagating action potentials of complex spikes may be less informationally significant than the pause and consequent disinhibition of postsynaptic cells. Specifically, the most salient feature of poststimulus time histograms triggered to complex spikes in Purkinje neurons is an increase in cerebellar nuclear cell firing (McDevitt et al., 1987b), which makes a strong inhibitory role for the complex spike acting alone seem questionable. Cellular-level studies, however, provide evidence that cerebellar nuclear cell firing is highly sensitive to the frequency and amplitude of inhibitory inputs (Gauck and Jaeger, 2000; Telgkamp and Raman, 2002). Moreover, high-frequency synaptic inhibition can strengthen rebound firing of Purkinje cell targets (Aizenman and Linden, 1999; Sekirnjak and du Lac, 2002), which may trigger plasticity in both the cerebellar and vestibular nuclei (Aizenman et al., 1998; Nelson et al., 2003). In the context of these data, it seems plausible that high-frequency, forward-propagating spikelets evoked by climbing fiber stimulation, acting in conjunction with ongoing simple spikes, may contribute to a transient enhancement of inhibition, thereby promoting an increase in postsynaptic rebound firing during the pauses that often follow complex spikes.