Determinants of Action Potential Propagation in Cerebellar Purkinje Cell Axons

Abstract

Axons have traditionally been viewed as highly faithful transmitters of action potentials. Recently, however, experimental evidence has accumulated to support the idea that under some circumstances axonal propagation may fail. Cerebellar Purkinje neurons fire highfrequency simple spikes, as well as bursts of spikes in response to climbing fiber activation (the “complex spike”). Here we have visualized the axon of individual Purkinje cells to directly investigate the relationship between somatic spikes and axonal spikes using simultaneous somatic whole-cell and cell-attached axonal patch-clamp recordings at 200-800 μm from the soma. We demonstrate that sodium action potentials propagate at frequencies up to ∼260 Hz, higher than simple spike rates normally observed in vivo. Complex spikes, however, did not propagate reliably, with usually only the first and last spikes in the complex spike waveform being propagated. On average, only 1.7 ± 0.2 spikes in the complex spike were propagated during resting firing, with propagation limited to interspike intervals above ∼4 msec. Hyperpolarization improved propagation efficacy without affecting total axonal spike number, whereas strong depolarization could abolish propagation of the complex spike. These findings indicate that the complex spike waveform is not faithfully transmitted to downstream synapses and that propagation of the climbing fiber response may be modulated by background activity.

Introduction

The axon of mammalian central neurons is traditionally thought to be a highly reliable information transmission line, providing a tight link between somatic action potentials and activation of axonal boutons. This view has been supported by stimulation experiments (Hessler et al., 1993; Allen and Stevens, 1994), paired recording studies of synaptic transmission (Miles and Wong, 1986; Williams and Stuart, 1999), and more recently by calcium imaging (Mackenzie and Murphy, 1998; Cox et al., 2000); however, modeling studies have indicated that some axonal geometries, particularly at branch points, may be unfavorable for reliable propagation along the axon, depending on the density and availability of voltage-gated Na and K channels (Goldstein and Rall, 1974; Luscher and Shiner, 1990; Kopysova and Debanne, 1998). Furthermore, considerable experimental evidence has accumulated from both invertebrate and mammalian axons suggesting that under some conditions axonal propagation may indeed fail, particularly at high rates of activity (for review, see Debanne, 2004). Investigation of axonal propagation has been hampered by the fact that most evidence for propagation failure has been relatively indirect. Although electrophysiological recordings from visualized individual axons have become possible recently (Raastad and Shepherd, 2003; Meeks and Mennerick, 2004), thus far it has been difficult to investigate directly the relationship between individual somatic and axonal spikes during physiological patterns of stimulation.

Propagation of spikes in the axons of cerebellar Purkinje cells is particularly important because these axons form the sole output of the cerebellar cortex. All computations of the cerebellar cortical circuitry are therefore condensed into the spike trains of Purkinje cell axons, which must transmit this information to the deep cerebellar nuclei, several millimeters distant. Purkinje cells in vivo exhibit continuous firing of “simple spikes” at rates that can transiently exceed 200 Hz when driven by sensory input (Armstrong and Rawson, 1979; Bower and Woolston, 1983; Marple-Horvat et al., 1998; Kahlon and Lisberger, 2000). Each Purkinje cell is also innervated by a single climbing fiber (CF), with activation of the CF producing a characteristic burst of spikes at the Purkinje cell soma known as the “complex spike” (CS) (Eccles et al., 1967). The individual “spikelets” within the CS can attain extremely high rates (>500 Hz) (Eccles et al., 1967). The CF input to the Purkinje cell has been proposed to act as a precise timing signal related to coordination of movement (Welsh and Llinas, 1997). It is therefore essential to determine how effectively individual spikelets in the CS are propagated down the axon to assess whether the CF conveys information to downstream synapses not only by its timing, but also by the pattern of spikes. Recordings from putative Purkinje cell axons in vivo have suggested that propagation is variable both from cell to cell and within a given cell, with from one to five axonal spikes being detected after CF activation (Ito and Simpson, 1971; Campbell and Hesslow, 1986). The origin of this variability and the factors that determine propagation of individual spikelets in the somatic CS remain unknown. Here we have visualized the axon of cerebellar Purkinje cells in cerebellar slices to allow direct measurement of axonal propagation using simultaneous somatic and axonal patch-clamp recordings.

Materials and Methods

Slice preparation. Parasagittal slices (150-250 μm thick) of cerebellar vermis were prepared from postnatal day 18-26 Sprague Dawley rats using previously described methods (Häusser and Clark, 1997) in accordance with national and institutional guidelines. Briefly, rats were decapitated, and the brain was quickly removed and immersed in ice-cold oxygenated (95% O₂, 5% CO₂) artificial CSF (ACSF) solution containing (in mm): 125 NaCl, 25 NaOH, 25 glucose, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, pH 7.4. Slices were incubated at 34°C for at least 45 min before being transferred to a 2 ml recording chamber and superfused continuously with oxygenated ACSF at a rate of 4-5 ml/min. All recordings were made at 34 ± 1°C.

Electrophysiology. Patch pipettes were made from borosilicate glass and pulled to a resistance of 3-5 MΩ. For whole-cell recording, pipettes were filled with an intracellular solution that contained (in mm): 133 methanesulfonic acid (Fluka, Ronkonkoma, NY), 7.4 KCl, 0.3 MgCl₂, 3 Na₂ATP, 0.3 Na₂GTP, pH 7.2 with KOH (285 mOsm). For visualization of Purkinje cell axons, 45 μm Alexa 488 (Molecular Probes, Eugene, OR) and biocytin (0.145%) were also included in the solution. For extracellular axonal and somatic recordings, pipettes were filled with ACSF. Slices were viewed with an upright microscope (Olympus BX51; Olympus Optical, Southall, UK) using oblique illumination or fluorescence optics, using either a high-resolution cooled CCD camera (Imago QE; T.I.L.L. Photonics, Martinsried, Germany) or a standard CCD camera (VX-55; T.I.L.L. Photonics) to identify the axon in the contrast-enhanced infrared image. Fluorescence excitation was minimized by using brief exposures (80 msec, 2-5 Hz) timed with a monochromator (Polychrome IV; T.I.L.L. Photonics). Whole-cell current-clamp and cell-attached voltage-clamp recordings were made using a Multiclamp 700A amplifier (Axon Instruments, Union City, CA). The estimated propagation efficacy was similar when axonal recordings were made in current-clamp mode. During somatic whole-cell recordings, access resistance was monitored continuously, and bridge balance and capacitance compensation were adjusted as required; recordings were terminated if access resistance exceeded 25 MΩ. Axonal recordings were made by pressing the pipette tip against a visually identified primary axon and applying negative pressure to form a seal (30-500 MΩ). In some cases recordings were made from the cut end of the primary axon, which appeared as a rounded, bulb-like stump. There was no difference in the failure probabilities of axons recorded in either configuration. In other experiments, recordings were made from unlabeled Purkinje cell axons, which were identified on the basis of their characteristic spontaneous firing and the rapid enhancement of firing rate after high K⁺ solution was puffed onto the Purkinje cell layer directly above the recording electrode. CF inputs were stimulated (1-9 V, 0.1 msec, 1 Hz) with an ACSF-filled patch pipette placed in the granule cell layer beneath the Purkinje cell body.

Data acquisition and analysis. Data were sampled at 66-100 kHz using an ITC-18 board (Instrutech, Port Washington, NY), acquired with Axograph software (Axon Instruments), and analyzed using Axograph, Igor Pro (Wavemetrics, Oswego, OR) and Mathematica (Wolfram Research, Champaign, IL). Somatic and axonal spike waveform analysis were performed in Mathematica. Both the original and a low-pass filtered (Gaussian kernel, σ = two sampling intervals) version of the somatic voltage waveform were used. The filtered waveform was used to detect the peaks of somatic spikelets (defined by a local maximum in voltage and a second time derivative more negative than -50 mV·msec^-2), and the original waveform was then used to measure the voltages at the time of peak and in the trough preceding the somatic spikelet. Spikelet amplitude was defined as peak voltage minus trough voltage. Maximum peak amplitude and rate of rise (dV/dt) were searched for and measured in the time interval between the trough and the peak. Failures of propagation were determined semiautomatically (with threshold set at ∼50% of maximal amplitude) and confirmed by visual inspection of each individual spike. Instantaneous spike frequency was calculated as the reciprocal of the preceding spike interval. Unless indicated otherwise, data are reported as mean ± SEM, and statistical significance was determined using Student's paired t test.

Results

Simultaneous somatic and axonal recordings in cerebellar Purkinje cells

Purkinje cell axons were visualized by filling them via somatic whole-cell recordings with a fluorescent dye (Alexa 488). After 5-10 min of whole-cell recording, fluorescent Purkinje cell axons could be visualized within the white matter using a cooled CCD camera. Cell-attached patch-clamp recordings were made from visually identified axons at distances of 200-800 μm from the soma (mean = 398 ± 39 μm; n = 19). Simultaneous whole-cell recordings were made from soma of the same neuron to directly establish the relationship between somatic and axonal spikes. Figure 1A illustrates the typical recording configuration. In each experiment, we confirmed that the activity of only one axon was being recorded by manipulating the activity of the neuron via somatic current injection. Figure 1B demonstrates the correspondence between somatic and axonal spikes during such a recording. An overlay of all somatic and axonal spikes (Fig. 1C) shows that each axonal spike was associated with a spike recorded at the soma, confirming that the axonal recording is exclusively reporting spikes from a single neuron.

Figure 1.

Simultaneous somatic and axonal recording from a Purkinje cell. A, Fluorescent image of a Purkinje cell filled with Alexa 488. The locations of somatic whole-cell and axonal cell-attached recordings are indicated schematically. B, Trace from the simultaneous somatic whole-cell and axonal cell-attached recording (425 μm from the soma) shown in A. Depolarizing and hyperpolarizing somatic current pulses (+0.5 and -0.2 nA, respectively) activated and inhibited spiking in both recordings. C, Overlay of all axonal spikes from B shows that each has a corresponding somatic spike, confirming that the axonal recording is exclusively from that neuron.

High-frequency simple spikes and calcium spikes fail to propagate

Spontaneous somatic action potentials were propagated down the axon with 100% fidelity (Fig. 2A) (n = 19; mean firing rate 38.4 ± 1.5 Hz); however, when firing rate was elevated to high rates by somatic current injection, failures of axonal propagation were observed. Figure 2A shows somatic and axonal spikes recorded in response to application of a strong depolarizing current step. A sufficiently strong step led to high-frequency firing of fast sodium spikes, interspersed with calcium spikes (Llinas and Sugimori, 1980). Because simple spike frequency increased to ∼300 Hz, “dropouts” were observed in the axonal recording, where the amplitude of the axonal signal became indistinguishable from the noise; these were categorized as propagation failures (Fig. 2B, open circles). Failure of axonal propagation was followed rapidly by complete inactivation of simple spikes at the soma and initiation of broad calcium spikes. Calcium spikes failed to propagate down the axon (Fig. 2A, arrowheads) (n = 3).

Figure 2.

High-frequency simple spikes and calcium spikes fail to propagate. A, Simultaneous somatic and axonal (200 μm) recording from a Purkinje cell. Injection of a strong (1.3 nA) depolarizing current pulse triggers rapid simple spike firing and calcium spikes. Note failure of axonal propagation of high-frequency simple spikes and calcium spikes (arrowheads). B, Plot of instantaneous spike frequency of somatic spikes from the same trace as in A (same timescale), illustrating which spikes propagate successfully down the axon (•) and which fail to propagate (○).

To investigate more quantitatively the relationship between somatic simple spike firing frequency and axonal propagation failure, we depolarized the soma with a current ramp, which allowed finely graded control of spike frequency (Williams et al., 2002). Toward the end of a ramp (Fig. 3A, boxed region), propagation failures were observed when the somatic firing rate approached ∼300 Hz (Fig. 3B, asterisks). To quantify the frequency at which propagation failure occurs, we plotted the amplitude of the axonal spike signal as a function of the instantaneous somatic firing frequency. Because firing frequency increased, the somatic action potential amplitude gradually decreased. In contrast, the axonal action potential amplitude exhibited a sharp drop-off above a critical frequency of somatic spike firing (Fig. 3C). Because both successes and failures occurred at this frequency, we converted the analog axonal signal into binary data and plotted propagation probability against somatic firing frequency (Fig. 3D). This relationship revealed an abrupt collapse in propagation above 300 Hz, which was well fit by a sigmoidal function. Across cells, the critical frequency for propagation failure, defined as the somatic spike frequency associated with 50% propagation efficacy, was 257 ± 17 Hz (n = 8). The frequency limit for axonal spike firing was reached just before spike failure was observed at the soma, which occurred at a somatic frequency of 288 ± 18 Hz (n = 13; p > 0.05). This indicates that failure of spike initiation and axonal propagation failure are tightly linked. The maximal instantaneous axonal spike frequency measured using this protocol was 236 ± 15 Hz (n = 9), corresponding to a minimal interspike interval (ISI) of 4.4 ± 0.25 msec.

Figure 3.

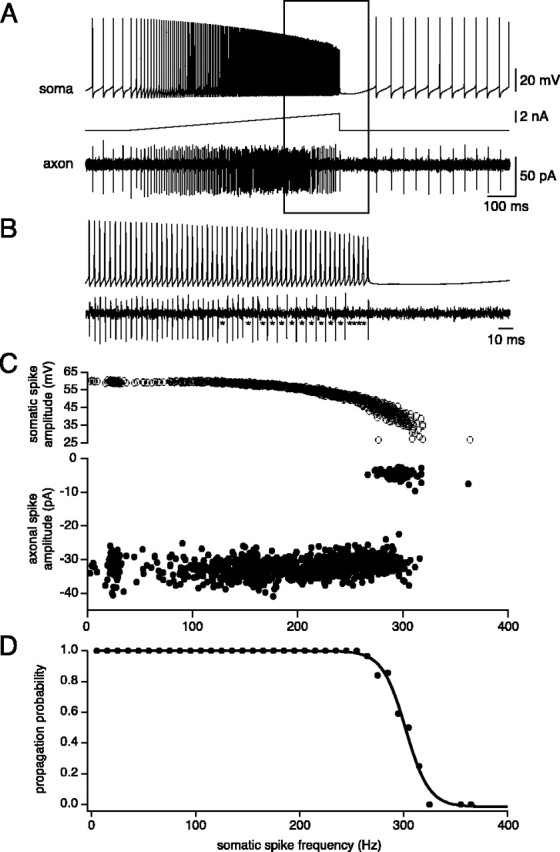
Frequency limit for axonal propagation during a ramp current injection. A, Simultaneous somatic and axonal (475 μm) recording from a Purkinje cell during injection of a depolarizing current ramp via the somatic recording. B, Inset from the sweep in A (box). Note failed axonal propagation of somatic spikes (asterisks). C, Relationship between amplitude of somatic spikes (top), axonal spikes (bottom), and instantaneous somatic spike frequency. Note that failure of axonal propagation is associated with somatic spike amplitudes of ∼40 mV (although there is considerable scatter). D, Relationship between axonal propagation probability of individual spikes and instantaneous somatic spike frequency (binned at 10 Hz). A sigmoidal fit to the data is shown, indicating a 50% reduction of propagation probability at 302 Hz.

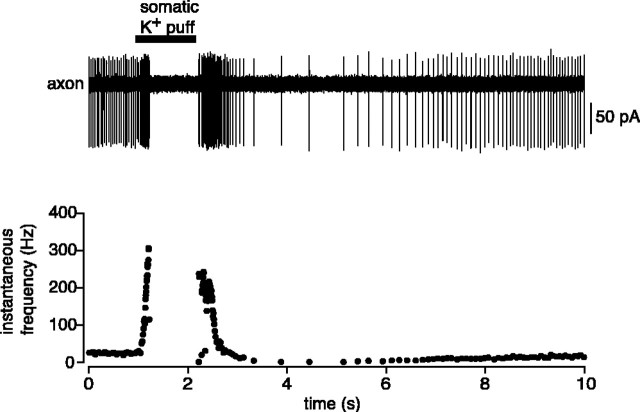
We confirmed the frequency limit for propagation using an entirely noninvasive approach. An extracellular recording was made from an unlabeled Purkinje cell axon in the white matter, and the frequency of spontaneous firing was enhanced using a brief puff of high K⁺ Ringer's solution at the soma. This produced a ramp-like increase in axonal spiking that eventually led to cessation of spiking (Fig. 4). The minimal axonal ISI observed using this approach was 4.4 ± 0.27 msec (n = 4), indistinguishable from that observed during the ramp protocol in whole-cell recording (p > 0.05). This approach was also used to noninvasively record from the axons of Purkinje cells filled previously with fluorescent dye via a somatic whole-cell recording. Similar spontaneous firing rates (control: 37.1 ± 2.2 Hz, n = 13; Alexa: 43.8 ± 14.3 Hz, n = 4; p > 0.2) and minimal axonal ISIs (control: 4.4 ± 0.27 msec, n = 4; Alexa: 4.5 ± 0.44 msec, n = 4; p > 0.5) were observed in these recordings, indicating that dye filling and visualization did not affect Purkinje cell excitability or axonal propagation.

Figure 4.

Noninvasive determination of the frequency limit for propagation. Shown is extracellular recording from the axon of a Purkinje cell, 350 μm from the soma. Brief application of high-K⁺ (150 mm) extracellular solution to the soma of the same neuron rapidly increased spontaneous firing rate, leading to failure of propagation above ∼300 Hz.

The frequency limit for propagation depends on the history of activity

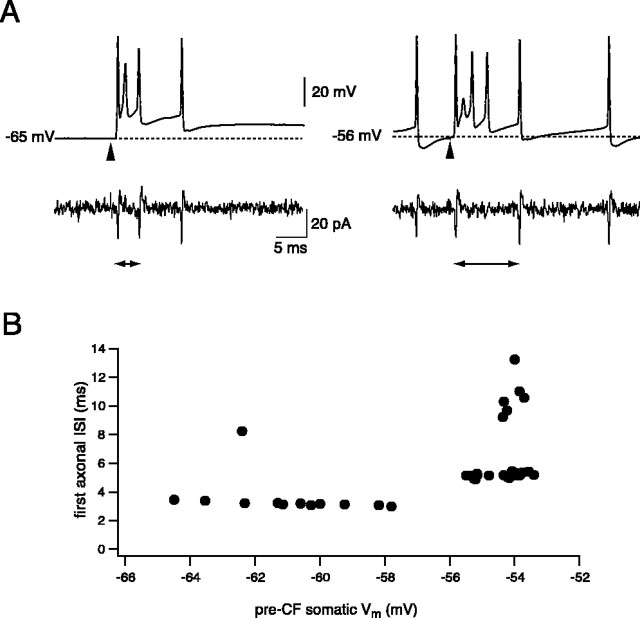
To determine whether the frequency limit for axonal propagation is a function of the history of activity, we used a paired-pulse current injection protocol at the soma to directly control the timing of individual somatic spikes. Purkinje cells were held at just subthreshold membrane potentials, and pairs of somatic spikes were evoked using brief (0.5 msec) current pulses separated by variable intervals (Fig. 5A). These experiments showed that using brief current injections, it was possible to reach much higher somatic and axonal firing frequencies than observed using long pulses. The minimal axonal ISI obtained was 2.4 ± 0.2 msec, corresponding to a maximal instantaneous axonal action potential frequency of 438 ± 37 Hz (n = 7), whereas the minimal somatic ISI was 2.2 ± 0.1 msec, corresponding to a maximal somatic spike frequency of 462 ± 29 Hz (p > 0.05). The higher maximal frequency of action potential propagation observed using this method indicates that the cumulative effect of high-frequency firing and/or the depolarized membrane potentials during prolonged current injection lower the critical frequency for axonal propagation failure. The importance of membrane potential for propagation efficacy is shown in Figure 5B, demonstrating that somatic depolarization can cause propagation failures for pairs of somatic spikes that propagated successfully at more hyperpolarized potentials.

Figure 5.

Frequency limit for axonal propagation using a double-pulse protocol. A, Simultaneous recording from the soma and axon (425 μm) of the same Purkinje cell. Two brief current pulses (0.5 msec duration) at a range of intervals were used to evoke pairs of somatic spikes at different frequencies. Even at the shortest interval (2 msec), the somatic spike successfully propagated down the axon. B, In a different neuron (axon recorded at 800 μm from the soma), propagation of the second somatic spike (2 msec interval) was abolished by depolarization to -43 mV.

Propagation of the complex spike

The failure of axonal propagation of somatic spikes at high frequencies suggests that the high-frequency burst of somatic spikes associated with CF activation may not reliably propagate down the axon. We therefore activated CF input and evaluated the correspondence between individual spikelets in the somatic complex spike burst and axonal spikes (Fig. 6A,B). On average, the number of somatic spikes in the CF response was 4.1 ± 0.5 (n = 10; measured during resting firing). In contrast, the number of propagated axonal spikes was substantially lower, averaging 1.7 ± 0.2 spikes (p < 0.001) and corresponding to an average propagation efficacy of 42 ± 5%. In each case, the number of axonal spikes was less than the corresponding number of somatic spikes, with the number of axonal spikes being related only relatively loosely to the number of somatic spikes across cells (Fig. 6C).

Figure 6.

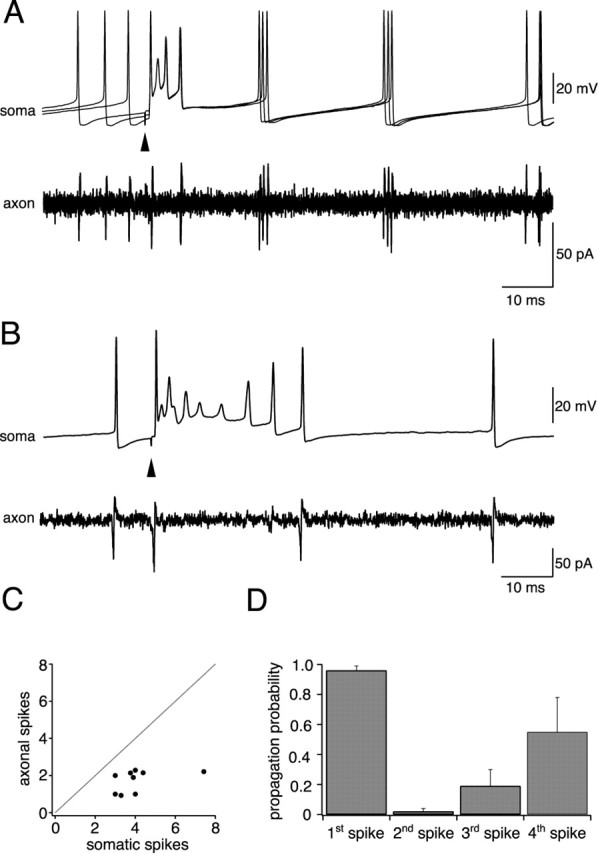
Axonal propagation of complex spikes. A, Simultaneous somatic and axonal recording (233 μm from soma) showing axonal propagation of the complex spike (3 sweeps are overlaid). From four somatic spikes, only two are successfully propagated down the axon. B, Simultaneous somatic and axonal recording (200 μm from the soma) from another Purkinje cell exhibiting a more elaborate somatic complex spike; from nine somatic spikes in this sweep, only two are propagated. C, Correlation between the average number of somatic spikes within the complex spike versus the number of propagated axonal spikes for 10 different Purkinje cells (correlation coefficient, r = 0.49). D, Probability of axonal propagation of successive spikes in the somatic complex spike (n = 5 cells).

The probability of propagation of individual spikes in the complex spike was dependent on their relative position within the complex spike waveform (Fig. 6D). The first spike in the complex spike exhibited the most reliable propagation (probability of 0.96 ± 0.03 at resting firing rates; n = 10). In 30% of Purkinje cells, only this single spike was propagated down the axon. The second, third, and fourth spikes in the complex spike waveform exhibited much lower probabilities of propagation (0.02 ± 0.02, 0.19 ± 0.11, and 0.55 ± 0.23, respectively), such that the second and third somatic spikes were usually “skipped” in the axonal response. As a consequence, the spike frequencies achieved in the axon during the complex spike were always substantially lower than at the soma. Within the somatic complex spike, a minimal ISI of 1.3 ± 0.1 msec was observed (corresponding to a maximal frequency of 805 ± 63 Hz; n = 10), whereas the minimal ISI observed in the axon was 4.1 ± 0.5 msec (corresponding to a maximal frequency of 267 ± 38 Hz).

Membrane potential influences complex spike propagation

To test whether the propagation of complex spikes can be modulated by somatic membrane potential, we activated CF input and used somatic current injection to either hyperpolarize the neuron to below the threshold for spontaneous firing or depolarize it to increase spike firing. Figure 7A shows a representative experiment during which the cell was silenced by hyperpolarizing with steady current. Silencing the neuron (by hyperpolarizing to -66 ± 1.7 mV; n = 9) typically improved the propagation efficiency of individual spikes within the complex spike, with the overall propagation probability of axonal spikelets being increased to 54 ± 6% (p < 0.05). This was not associated with a significant increase in the number of axonal spikes in the CS response (1.7 ± 0.3; p > 0.05), however, because the number of somatic spikes in the CS was also reduced (to 3.1 ± 0.2 spikes; p < 0.05). The increase in overall propagation efficacy was associated with improvements in propagation of the third spike in particular (axon/soma ratio increased to 0.59 ± 0.17; p < 0.05), with propagation efficacy of the first and second spikes being similar to that at rest (1.00 and 0, respectively; p > 0.05). Hyperpolarization also changed the timing of spikes in the axonal response (Fig. 7B), shortening the interval between the first two axonal spikes to 4.0 ± 0.5 msec from 5.4 ± 0.6 msec (n = 5; p < 0.05) at rest.

Figure 7.

Hyperpolarization modulates complex spike propagation. A, Simultaneous recording of CF spikes from the soma and axon (217 μm) of a Purkinje cell hyperpolarized to -65 mV (left panel) or firing spontaneously (right panel). Note the decrease in the first interspike interval (arrowheads) in the axonal CF response on hyperpolarization. B, The first interspike interval of propagating CF spikes is dependent on the membrane potential. First interspike intervals plotted against the membrane potential averaged over 10 msec before the CF stimulus for the cell shown in A. The step-like transitions in the ISI on depolarization correspond to successful propagation of the second axonal spike shifting between individual spikelets within the somatic complex spike.

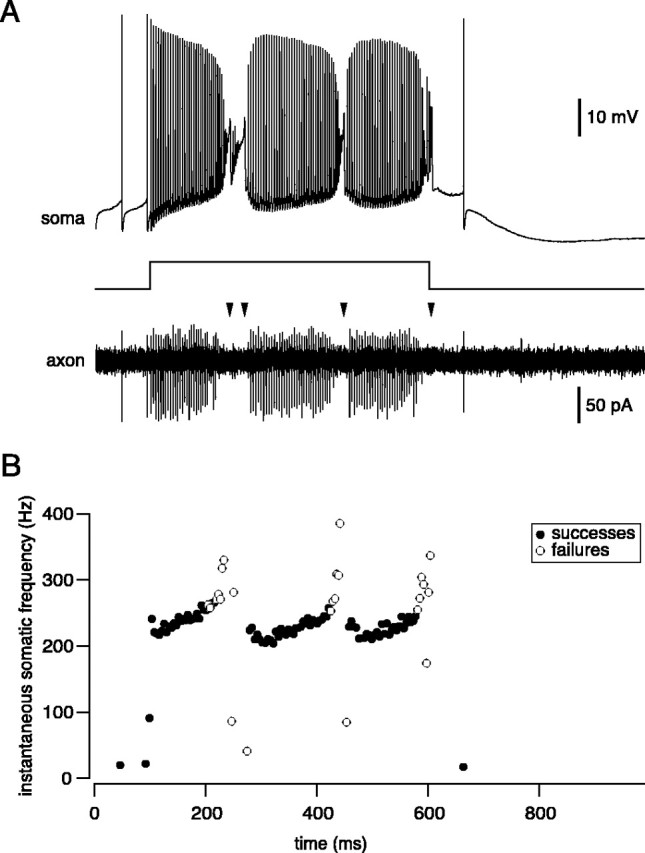
Whereas hyperpolarization improved propagation efficacy of the complex spike, depolarization had the opposite effect. As shown in Figure 8A, injection of strong depolarizing current (sufficient to inactivate simple spike firing) could completely abolish all axonal spikes associated with the complex spike. When more modest levels of depolarizing current were delivered, increasing simple spike firing rates to 89 ± 5Hz(n = 8), the overall propagation probability of spikes in the CS was decreased to 33 ± 7% (p < 0.01 compared with rest). This reduction in propagation efficacy was reflected in a decrease in the number of propagated axonal spikes to 1.2 ± 0.3 (p < 0.01) in the face of a similar number of somatic spikes (3.5 ± 0.2; p > 0.05). The reduction in overall propagation efficacy primarily reflected reduced propagation of the first spike in the response, decreasing to 0.72 ± 0.11 (p < 0.05 compared with rest), whereas the propagation probability of subsequent spikes was not altered significantly (0.03 ± 0.01 and 0.17 ± 0.1 for second and third spikes, respectively; p > 0.05).

Figure 8.

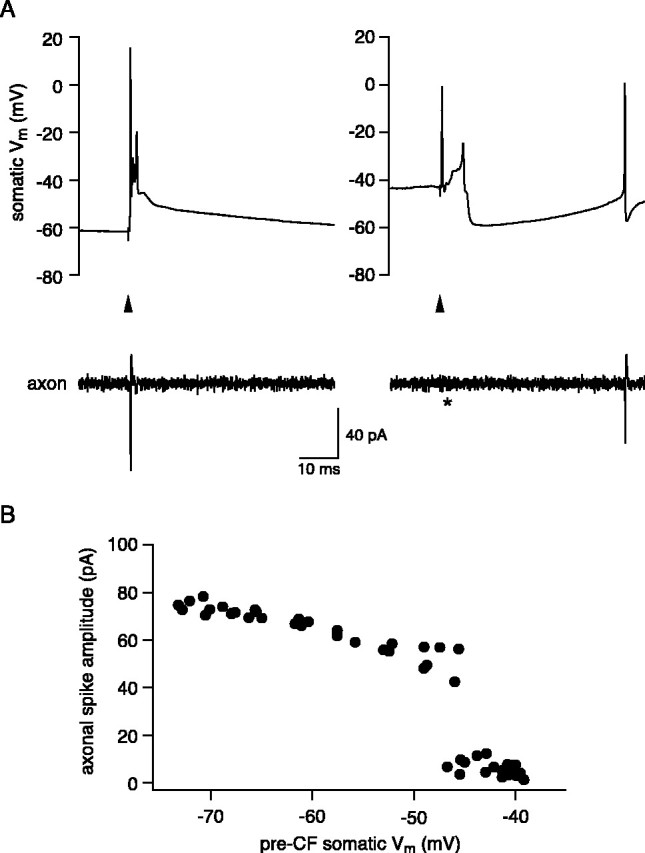
Depolarization can block complex spike propagation. A, Evoked CF response in a cell in which just one spike was propagated (axon recording, 220 μm). Strong depolarization with somatic current injection abolished axonal propagation of the CF spike; the ensuing calcium spike was also not propagated. B, Plot of amplitude of the axonal spikelet against the membrane potential averaged over 10 msec before the CF stimulus for the cell shown in A. Note the sharp transition to failed propagation at approximately -45 mV.

Factors governing propagation of complex spikelets

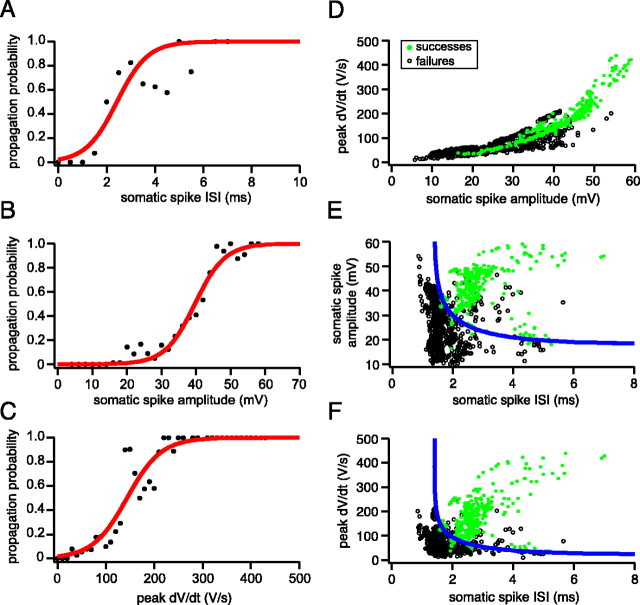
To understand the factors that determine the propagation of spikelets, we measured features of individual spike waveforms and correlated them with propagation probability. The ISI of the somatic spike provided an effective predictor of propagation, with a 50% failure probability for propagation of spikelets occurring at intervals of 2.4 ± 0.1 msec (SD; n = 7) (Fig. 9A). The dV/dt of somatic spikes were also good predictors of propagation (Fig. 9B,C), with 50% probability of propagation occurring at a somatic spike amplitude of 39.7 ± 0.5 mV (SD) (Fig. 9B) and a peak dV/dt of 144 ± 5 V·sec^-1 (SD) (Fig. 9C). Because dV/dt and amplitude were strongly correlated (Fig. 9D), their combination did not improve discrimination of successfully propagating spikes from those that failed; however, by combining either the amplitude or dV/dt with the somatic ISI, a highly reliable prediction of propagation efficacy could be achieved (Fig. 9E,F). This is because propagating spikes were characterized by both a large amplitude and a large ISI, whereas nonpropagating spikes either had a small amplitude or were preceded by another spike in the previous few milliseconds. In an attempt to separate the nonpropagating from propagating somatic spikelets, a curve was fitted to data based on the assumption that propagation depends on a factor that recovers exponentially with ISI duration, and a second factor activated sigmoidally with spike amplitude, as would be expected for Na channels. This curve is described by the following equation:

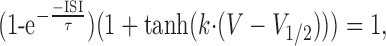1

Figure 9.

Somatic spike parameters predict axonal propagation of the complex spike. A, Probability of axonal propagation plotted against the preceding somatic ISI (pooled data from 7 cells). B, Probability of axonal propagation plotted against the amplitude of the corresponding somatic spikelets (pooled data from 7 cells). C, Probability of axonal propagation plotted against the peak dV/dt of each somatic spikelet (pooled data from 7 cells). The data points in A-C have been fit with a sigmoidal function. D, Plot of peak dV/dt against somatic spike amplitude. The data points are color-coded to indicate propagating (green filled circles) and nonpropagating (black open circles) axonal spikes. E, Plot of somatic spike amplitude against ISI. The blue line represents the best-fit separatrix defined by Equation 1, with τ = 2.0 msec, k = 0.056 mV^-1, and V_1/2 = 18.1 mV. F, Plot of peak dV/dt against ISI. The values for the best-fit separatrix (blue line) are τ = 2.04 msec, k = 0.0097 sec·V^-1, and V_1/2 = 22.4 V·sec^-1.

where τ represents the time constant of the recovery process described by the first factor, V_1/2 represents the half-maximal activation voltage, and k represents the steepness of the transition described by the second factor. As shown in Figure 9, E and F, the curve was able to classify axonal propagation successes and failures with high accuracy for both the amplitude-ISI relationship (85% accuracy) and the dV/dt-ISI relationship (88% accuracy). This approach therefore allows us to predict propagation of spikelets within the complex spike from somatic recordings alone.

Discussion

We have investigated axonal propagation of action potentials in Purkinje cells using direct patch-clamp recordings from visualized axons. Simultaneous somatic and axonal recordings were used to determine the propagation efficacy of individual somatic spikes, revealing that simple spikes propagate faithfully at physiological frequencies, whereas calcium spikes do not. Individual spikelets within the complex spike do not propagate faithfully, with only approximately half of somatic spikelets resulting in propagating axonal action potentials. The ability for propagation efficacy of spikelets to be modulated by membrane potential may allow the axonal complex spike pattern to encode levels of Purkinje cell activity at downstream synapses.

Frequency-dependent propagation of simple spikes

Simple spikes propagated down the axon with complete fidelity during spontaneous firing of Purkinje cells. This is consistent with recent imaging experiments (Mackenzie and Murphy, 1998; Cox et al., 2000) and direct electrophysiological recordings (Raastad and Shepherd, 2003; Meeks and Mennerick, 2004) from pyramidal cell axons activated repetitively at ≤50 Hz. We demonstrate, however, that at higher firing rates driven by injected current, propagation failed at a critical frequency that depended on the nature of the stimulus. Prolonged high-frequency firing driven by long current pulses or ramps resulted in maximal axonal firing frequencies of <250 Hz. In contrast, when pairs of individual spikes were evoked with brief current pulses, much higher instantaneous axonal firing frequencies could be achieved. The axonal refractory period of ∼2.5 msec observed with paired-pulse stimulation is similar to the minimal refractory period for extracellular stimulation measured in CA1 pyramidal cell axons (Anderson, 1960; Raastad and Shepherd, 2003). The stimulus dependence of the refractory period that we have observed in Purkinje cells indicates that the frequency limit for axonal propagation depends on both the immediate and long-term history of membrane potential, presumably reflecting both short-term and long-term components of Na and K channel inactivation (Colbert et al., 1997; Jung et al., 1997; Mickus et al., 1999; Raman and Bean, 1999, 2001).

Interestingly, we observed that calcium spikes (Llinas and Sugimori, 1980) were not converted directly into axonal spikes. This may be related to the fact that calcium spikes were triggered only at strongly depolarized potentials when simple spikes were inactivated. This finding also suggests that the density and/or properties of calcium channels in Purkinje cell axons (Callewaert et al., 1996) cannot sustain active propagation of axonal calcium spikes in the absence of Na spikes.

Determinants of complex spike propagation

Our results demonstrate that individual spikelets in the complex spike waveform are not propagated reliably down the axon. On average, only one or two spikes are propagated down the axon in response to CF activation. These findings confirm and extend observations made from recordings of putative Purkinje cell axons in vivo (Ito and Simpson, 1971; Campbell and Hesslow, 1986). In particular, dual somatic and axonal recording has allowed us to directly examine the propagation of individual spikelets and identify whether a low number of axonal spikes is attributable to a correspondingly low number of somatic complex spikelets or to failure of propagation. We have shown that, on average, propagation efficacy of individual spikelets is low, averaging ∼50% under resting conditions across all spikelets. The probability of propagation for an individual spikelet depends critically on its position within the complex spike, with the first spike propagating highly reliably in almost every case and intermediate spikes propagating poorly.

Examination of the relationships between individual somatic spike parameters and propagation efficacy revealed that the combination of interspike interval and either spike amplitude or rate of rise provides an excellent predictor of propagation efficacy. The separatrix function demonstrates that no spikes will propagate below a critical interspike interval defining the absolute refractory period, but above this interspike interval the spike amplitude is the major determinant. What are the biophysical mechanisms underlying these phenomenological features of propagation failure? The effect of hyperpolarization argues against a major role of A-type K channels in propagation failure (Debanne et al., 1997; Kopysova and Debanne, 1998). Rather, both spike amplitude and dV/dt, which we have identified as critical determinants of propagation efficacy, are closely related to available Na current (Hodgkin and Katz, 1949; Colbert et al., 1997). It has been shown that even relatively small reductions in Na current can increase the refractory period, reduce maximal firing frequency (Madeja, 2000), and inhibit propagation of action potentials in axons (Cooley and Dodge, 1966; Goldstein and Rall, 1974; Kopysova and Debanne, 1998). A direct relationship between propagation failure and reductions in spike amplitude, dV/dt, and Na channel current has been demonstrated in CA1 pyramidal cell dendrites, in which trains of action potentials cause inactivation of Na channels, leading to failure of active propagation (Colbert et al., 1997; Mickus et al., 1999). The similarity between the time constant of recovery identified in our separatrix function (∼2 msec) and the fast phase of recovery of Na current from brief depolarizations [2.0 msec at physiological temperatures in pyramidal cells (Mickus et al., 1999); 3.8 msec at room temperature in Purkinje cells (Raman and Bean, 2001)], together with the effects of membrane potential, strongly suggest that Na channel inactivation is a key determinant of propagation failure.

Functional implications

The frequency limit for propagation during tonic firing that we have identified is unlikely to affect the propagation of simple spikes down the axon, because their frequency only rarely exceeds 200 Hz in vivo (Armstrong and Rawson, 1979; Bower and Woolston, 1983; Marple-Horvat et al., 1998; Kahlon and Lisberger, 2000), indicating that simple spikes are faithfully relayed to the downstream synapses onto deep cerebellar nucleus neurons. This is functionally important because it permits the continuous inhibition of deep nuclear neurons to be finely modulated over a wide range of frequencies on the millisecond-to-millisecond timescale.

The frequency limit, however, has serious consequences for propagation of individual spikes in the complex spike, in which instantaneous frequencies >500 Hz are typical. In most cases, only a doublet of spikes is propagated down the axon in response to CF activation, even when a prolonged burst of somatic spikes is elicited. Further propagation failures may occur at branch points of the Purkinje cell axon in the deep cerebellar nuclei. This situation is in contrast to pyramidal cells in hippocampus (Miles and Wong, 1986) and cortex (Williams and Stuart, 1999), which appear to faithfully transmit somatic bursts to postsynaptic neurons (possibly because of lower spike rates during the burst). It resembles, however, the situation in cartwheel neurons in the dorsal cochlear nucleus, during which only the first two spikes within high-frequency bursts are reliably relayed to postsynaptic targets (Tzounopoulos et al., 2004).

What is the purpose of the elaborate somatic complex spike if it is not faithfully propagated down the axon? Aside from regulating synaptic plasticity at parallel fiber (PF) synapses (Daniel et al., 1998), the complex spike may also regulate Purkinje cell excitability independently of any direct consequences for downstream neurons. Individual simple spikes are relatively ineffective at shunting ongoing synaptic potentials in Purkinje cells (Häusser et al., 2001), and thus the large synaptic and intrinsic conductances underlying the complex spike can provide a much more effective reset of synaptic integration. The wide range of spikelet numbers and frequencies possible at the soma, and their sensitivity to background excitation, may provide a more graded signal to fine-tune homeostatic mechanisms in the dendrites and proximal region of the axon (Cerminara and Rawson, 2004). Furthermore, because spikes are energetically expensive (Attwell and Laughlin, 2001), particularly when propagating over long distances, the limit on axonal firing may represent a protective mechanism to reduce the overall energetic costs of complex spike firing.

Ultimately, however, the role of the complex spike must also be understood in the context of its effect on downstream neurons. Intracellular recordings from cerebellar nuclear neurons have indicated that CF activation of Purkinje cells exerts a powerful effect on these neurons (Llinas and Muhlethaler, 1988). The axonal doublet evoked by the complex spike in most neurons, associated with an interspike interval far shorter than is present in typical simple spike trains, in itself may represent a sufficiently distinct signal to be “recognized” by the downstream synapses as arising from CF and not PF activation. The modulation of this interval by membrane potential, by synaptic input (Campbell and Hesslow, 1986), or by plasticity of the CF synapse (Hansel and Linden, 2000) may represent a way of encoding at downstream synapses the recent history of activity in the cerebellar cortex [with detection of subtle differences amplified by CF synchrony (Welsh and Llinas, 1997)]; however, for the subset of Purkinje cells in which the complex spike is translated into a single axonal spike, the complex spike will be indistinguishable from neighboring simple spikes, and no interval coding is possible. In this case, the effectiveness of CF activation on the deep nuclear neurons must rely on a population code, with synchrony of CF activation (Welsh and Llinas, 1997) required to generate a significant postsynaptic response despite the impact of CF-driven activity in single Purkinje cell axons being indistinguishable from background PF-driven activity. Alternatively, the substantial pause in axonal spiking produced by the failure of propagation of successive somatic spikelets may itself be particularly relevant in the context of high background firing rates in Purkinje cells (which alone would tend to further enhance complex spike failure). Because the Purkinje cell connection with the deep nuclear neurons is tonically depressed during continuous firing (Telgkamp and Raman, 2002; Pedroarena and Schwarz, 2003), the 5-15 msec period of silence in axonal firing triggered by CF activation may allow both rebound firing of the deep nuclear neurons and recovery of the inhibitory synapses from depression.