The Temporal Impulse Response Underlying Saccadic Decisions

Abstract

Models of perceptual decision making often assume that sensory evidence is accumulated over time in favor of the various possible decisions, until the evidence in favor of one of them outweighs the evidence for the others. Saccadic eye movements are among the most frequent perceptual decisions that the human brain performs. We used stochastic visual stimuli to identify the temporal impulse response underlying saccadic eye movement decisions. Observers performed a contrast search task, with temporal variability in the visual signals. In experiment 1, we derived the temporal filter observers used to integrate the visual information. The integration window was restricted to the first ∼100 ms after display onset. In experiment 2, we showed that observers cannot perform the task if there is no useful information to distinguish the target from the distractor within this time epoch. We conclude that (1) observers did not integrate sensory evidence up to a criterion level, (2) observers did not integrate visual information up to the start of the saccadic dead time, and (3) variability in saccade latency does not correspond to variability in the visual integration period. Instead, our results support a temporal filter model of saccadic decision making. The temporal impulse response identified by our methods corresponds well with estimates of integration times of V1 output neurons.

Introduction

Current models of perceptual decision making assume that observers accumulate sensory information over time to gauge which of several response alternatives to choose (Gold and Shadlen, 2001). For instance, when there are two items between which to choose, the optimal strategy would be to integrate the likelihood ratio of the first hypothesis versus the second, given the available sensory evidence (Green and Swets, 1966; Gold and Shadlen, 2001). In terms of underlying neurophysiology, it has been proposed that a decision unit within the brain “reads out” sensory signals from lower-level sensory areas, transforms these signals into an approximately optimal decision variable, and integrates this quantity until it reaches some criterion level (Gold and Shadlen, 2003; Mazurek et al., 2003). Importantly, the sampling from lower-level sensory areas is assumed to continue until a decision criterion is reached.

Saccadic eye movement decisions are among the fastest and most frequent perceptual decisions the human brain has to make. Humans make approximately three to four saccades every second. The present study investigates whether these more general principles of perceptual decision making are the basis of saccade generation. In this study, like many others in the oculomotor literature, observers generated saccades with latencies on the order of 250-300 ms. This latency period consists of at least two components: a visual integration period, followed by the saccadic “dead time” (see Fig. S1, available at www.jneurosci.org as supplemental material). This dead time corresponds to the final period within the fixation duration, during which new visual information can no longer alter the upcoming movement, and its duration is generally thought to be ∼80 ms (Becker, 1991; Hooge et al., 1999). The common assumption is that variability in saccade latency corresponds to variability within the visual integration period, with observers integrating the visual information until the start of the dead time (Beutter et al., 2003). This study addresses the following questions: (1) are the decision-making processes underlying saccade generation characterized by integration of visual signals up to a threshold? (2) Are visual signals integrated up to the dead time? To address these questions, we sought to identify the temporal impulse response underlying saccadic eye-movement decisions.

Observers were presented with two patches that fluctuated in luminance over time (Caspi et al., 2004). One patch, the saccade target, was on average brighter than the other, distracting patch. However, at any one point, the target could actually be dimmer than the distractor. Integrating the visual signals over time is clearly a sensible and optimal strategy in this situation, because it allows for a more reliable distinction between the target and distractor. In experiment 1, we develop a method of relating the stimulus at different points in time to the observers' saccadic decisions. This method identifies the temporal impulse response of the decision mechanism. In experiment 2, we test predictions derived from this temporal impulse response.

Materials and Methods

Observers

Six observers (age range, 23-38 years) were tested in the two experiments. The first author was the only observer to take part in both experiments (observer 3). The remaining observers were naive about the purpose of the study. Four observers were tested in experiment 1; three were tested in experiment 2. All were experienced psychophysical observers with normal or corrected-to-normal vision and were familiar with eye-tracking studies. Data for experiment 1 were collected in multiple sessions distributed over a number of weeks. Experiment 2 consisted of two sessions, performed on different days. The study was approved by the local ethics committee.

Equipment

Stimuli were generated with custom-written software for a VSG2/3 graphics card (Cambridge Research Systems, Kent, UK). They were presented on a 21 inch monochrome monitor (FlexScan T965; Eizo, Tokyo, Japan), which was linearized and running at 80 Hz. The monitor resolution was 1024 × 770 pixels. It was viewed from a distance of 57 cm, with the head stabilized by a chin rest.

An example display sequence is illustrated in Figure 1. A trial started with the presentation of a black central fixation cross. After a variable delay of 200-700 ms, the stimuli were presented for 1000 ms in experiment 1 and for 500 ms in experiment 2. [In experiment 1, only 3-4% (range across observers) of the saccades had a latency over 500 ms. This allowed us to restrict the viewing time in experiment 2.] The fixation point remained visible throughout the trial. Stimuli were two-dimensional Gaussian patches with an SD of 0.5°. Observers were presented with two patches at 8° eccentricity. The target patch could occur in one of four locations, at either end of the major oblique meridians. The distractor patch was located at an angle of either -90 or +90° away from the target. All different combinations of target and distractor locations were presented equally often, in a randomized order within a block of 96 trials.

Figure 1.

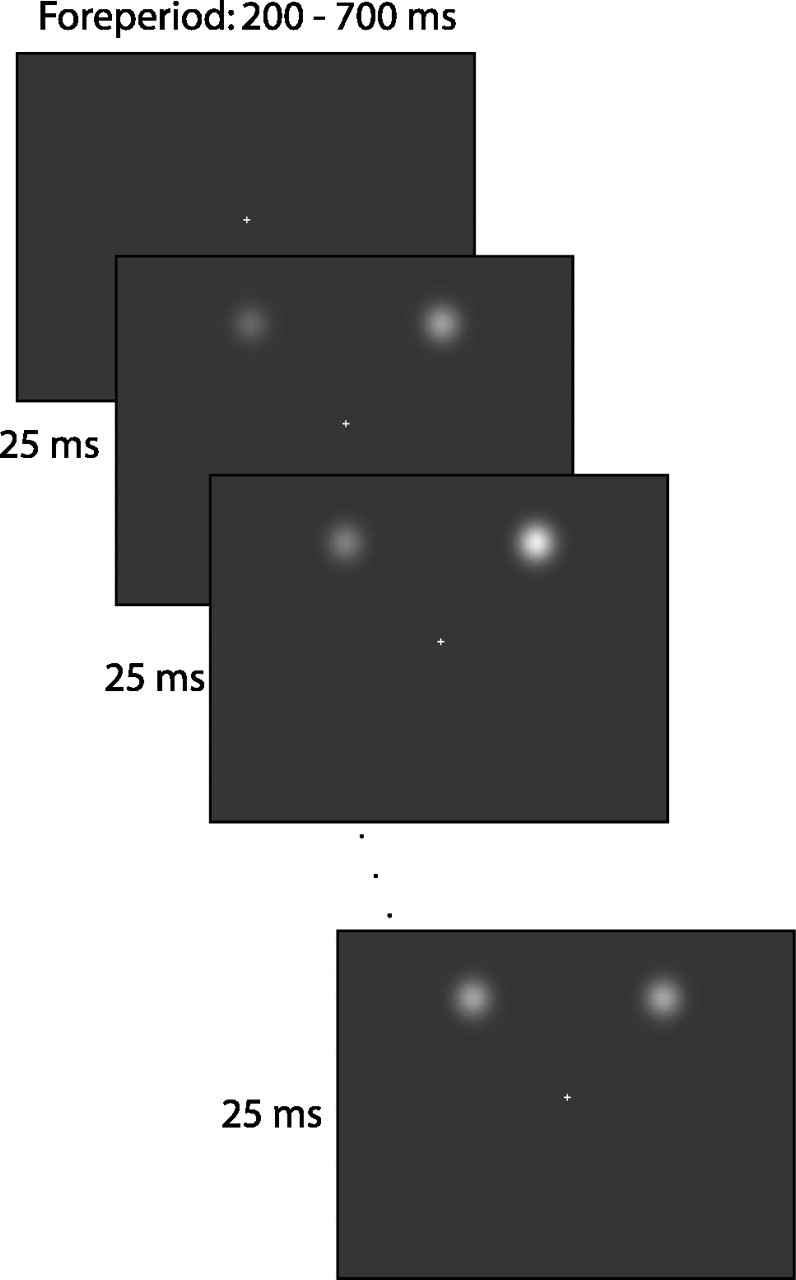
Display sequence on a given trial in experiment 1. The contrast of the stimuli is enhanced for illustrative purposes. A trial started with a fixation display presented for some random period between 200 and 700 ms, after which the two Gaussian patches were presented. The luminance of the target (right patch in this example) and distractor was resampled every 25 ms. The items were visible for 1 s.

The luminance of the background was set at 25.3 cd/m² (corresponding to a gray level of 0.25) throughout the experiment. The target and distractor gray level values were resampled independently at 40 Hz from Gaussian distributions with identical SDs of 0.1 (gray level units). In experiment 1, the mean target and distractor gray levels were 0.75 and 0.60, respectively (corresponding to δ contrasts of 2 and 1.4). On resampling the luminance of the two patches, the gray level values were constrained to lie within two SDs from the mean of the distribution from which they were drawn.

In experiment 2, there were two additional conditions. In the “same-different” condition, the distractor luminance was drawn from the same distribution (μ = 0.75) as the target during the first 100 ms but from a different distribution (μ = 0.60) for the remainder of the trial. In the “different-same” condition, the pattern was reversed: the distractor luminance was drawn from a different distribution (μ = 0.60) for the first 100 ms but from the same distribution (μ = 0.75) as the target afterward. The three trial types in this experiment were randomly intermixed within a block of trials. Feedback was not provided in either experiment.

Eye movements were recorded with the EyeLink II (SR Research, Osgoode, Ontario, Canada). This infrared system tracks the center of the pupil with an accuracy of ∼0.3° and a sampling rate of 500 Hz. Saccades were detected using velocity and acceleration criteria of 30°/s and 8000°/s², respectively. The eye tracker was calibrated at the start of each block. A session generally consisted of a run of four to six blocks.

Data analysis

Only the first saccade after display onset was analyzed. Trials were rejected if the observer fixated >1° away from the display center at the time of display onset, if the saccade latency was shorter than 80 ms, if the saccade amplitude was outside the range of 6-10°, or if the observer fixated an empty quadrant.

The temporal impulse response. The purpose of experiment 1 was to identify the temporal impulse response by relating the visual noise to the saccadic decisions. One way to achieve this is through reverse correlation (Caspi et al., 2004). This procedure is analogous to aligning neural spike activity on movement onset and then averaging over many trials to obtain a representation of the activity profile preceding a certain type of movement. Instead of spike trains, the luminance samples at the location of the saccade end point are averaged to obtain a representation of the average stimulus that triggered a saccade of a particular type. The temporal integration window is the period during which the representations for different types of movements (e.g., target vs distractor-directed saccade) differ. As such, reverse correlation is more appropriately regarded as a reverse model (from response to stimulus) rather than a forward model of decision making (from stimulus to response). To derive such a forward model, we used a different analysis technique.

In our study, there were only two possible responses (with an implicit Bernoulli distribution). In this situation, a linear model optimized using least squares (implicitly assuming normally distributed responses) is inappropriate as a forward model. Instead, decision making in this context can be modeled using logistic regression. As a decision variable, we chose the luminance difference between the clockwise and anticlockwise patch in the display at each instance of time (in 25 ms steps, from display onset onwards). A positive luminance difference constitutes evidence in favor of the clockwise patch; conversely, a negative difference constitutes evidence in favor of the anticlockwise patch. Taking the luminance difference between the two items implies that saccadic decisions may be guided not only by the signals from the location of the saccade end point but also by signals from other regions in the visual field. This variable is monotonically related to the optimal (Bayesian) decision variable that was discussed in the Introduction (Green and Swets, 1966; Gold and Shadlen, 2001). The predictor variables entered into the analysis corresponded to the value of the decision variable at each 25 ms time sample (i.e., 40 predictor variables for a 1 s trial).

The dependent variable was the probability of making a saccade to the clockwise patch. Logistic regression then involves finding the maximum likelihood solution for the following equation: P(clockwise|D_{1... k}) = f(b₀ + b₁D₁ +... + b_kD_k), where D_k refers to the value of the decision variable at sample k (integers from 1 to 40), and f(x) = 1/(1 + exp(-x)) is the logistic link function for a Bernoulli variable (McCullagh and Nelder, 1989). The regression weights b₁... b_k are plotted in Figure 2. Note that this model contains, as a special case, the Bayesian ideal observer for this task that would weigh all samples equally (Bishop, 1995).

Figure 2.

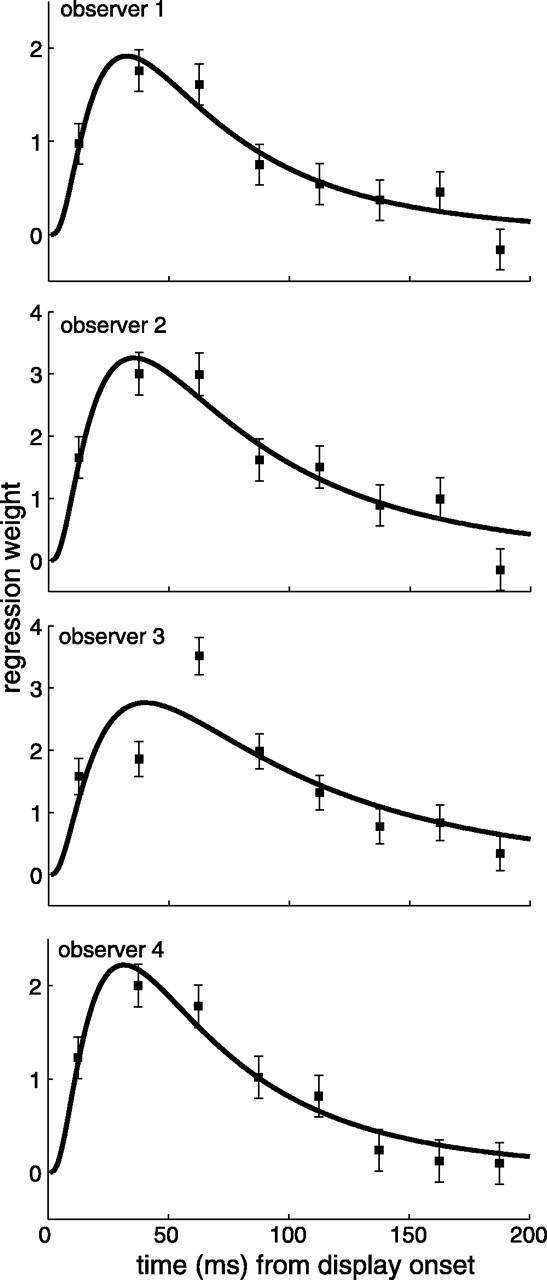
Logistic regression weights as a function of time after display onset. Error bars are SE. The solid lines are best-fitting log-Gaussian functions.

Saccade latency analysis. In our analyses of saccade latency in experiment 2, we deal with normalized latencies to remove the effects of display configuration (i.e., the particular combination of target and distractor location). For instance, it is well known that downward saccades generally have longer latencies than upward saccades (Honda and Findlay, 1992). The normalization involves aligning saccade latency distributions from each individual display configuration so that they all share the same (grand) mean. This procedure is analogous to that used to remove between-subject effects in a repeated-measures ANOVA. As a result of the normalization, each display configuration contributes approximately equally to a particular latency band. This is important when it comes to comparing the accuracy in different saccade latency bands. The normalization ensures that the longest latency band does not solely consist of, for example, downward saccades.

Results

Experiment 1

The analyses were based on 5755, 4242, 6059, and 6168 trials for observers 1-4, respectively. Their respective error rates were 29, 14, 14, and 24%. Median saccade latencies were 298, 261, 320, and 298 ms for observers 1-4, respectively.

Figure 2 illustrates the regression weights and their associated SEs as a function of time from display onset. The profiles for all observers were remarkably similar: the second and third samples (25-75 ms) after display onset were the ones driving the decisions most strongly, followed by a gradual decay in the contribution of subsequent samples.

The solid lines are fits of a log-Gaussian function of the following form: a exp(-0.5(ln(t/b)/c)²), where t is time in milliseconds, a determines the peak of the function, and b and c correspond to the location and scale of the function, respectively. The location and scale parameter estimates and associated goodness-of-fit statistics are listed in Table 1. The functions generally provided an excellent description of the weights, except perhaps for the weights of observer 3. However, this observer's weights still follow a pattern similar to that of the other observers: the largest weight is assigned to the third sample (50-75 ms after display onset), followed by the gradual drop-off.

Table 1.

Parameter estimates of the log-Gaussian fits to the logistic regression weights

Observer	Location	Scale	r2
1	32.47	0.80	0.91
2	35.47	0.80	0.91
3	40.04	0.91	0.66
4	31.52	0.81	0.95
Fredericksen and Hess (1998)	36.77	0.68

Based on this analysis, we conclude that the saccadic decisions were largely driven by the visual signals presented in the first 100 ms after display onset. The visual system tends to be less sensitive to subtle variations in luminance at or around the time of large transient onsets. This is the result of adaptive contrast gain control. If, in the current experiment, the stimulus onset had saturated the contrast response of the underlying mechanisms, the ability to signal the subsequent luminance variations would be impaired for some period after the onset and would only gradually recover over time (Pokorny et al., 2003). One would then expect this to hinder the target-distractor discrimination. As such, although contrast gain control is likely to occur in our paradigm, it does not prevent our observers from attributing the largest weight to the evidence presented immediately after stimulus onset.

Numerical simulations (Fig. S2, available at www.jneurosci.org as supplemental material) revealed that an integration-to-threshold model of the type sketched in the Introduction can account for the temporal weighting functions, provided that the threshold is generally reached within the first 100 ms after display onset. However, given decision latencies of ∼100 ms and saccade latencies of ∼300 ms, it appears that the data are not consistent with the idea that visual signals are integrated up to the start of the dead time. Through simulations, we verified that the average dead time would have to be close to 200 ms to begin to approach the temporal weighting profiles illustrated in Figure 2. This dead time estimate is two to three times the commonly accepted estimates of 60-80 ms.

If integration to threshold was indeed the underlying mechanism driving saccadic decision making, it is unclear why saccade initiation was delayed for so long after the threshold had been reached. Apart from the efferent delays between selecting the saccade target and the beginning of the actual movement, there is nothing to stop the observer from moving as soon as the decision has been made. An alternative model of saccadic decisions in this paradigm is suggested by the shape of the temporal weighting functions in Figure 2. These functions closely resemble the psychophysically derived impulse response function of early temporal filters in the visual system (Johnston and Clifford, 1995; Fredericksen and Hess, 1998). Fredericksen and Hess (1998) modeled such filters with log-Gaussian functions, and their average parameter estimates are also listed in Table 1. These values are remarkably similar to our estimates, particularly taking into account the large differences in experimental paradigms (contrast detection in noise vs saccadic decision making between suprathreshold luminance patches). A simple temporal filter model holds that saccadic decisions were driven by the output of early temporal filters that respond to the onset of the display. These filters integrate over a relatively fixed period of time, which is independent from the difficulty of the perceptual discrimination on a given trial. This latter assumption provided the basis for experiment 2.

Experiment 2

The aim of experiment 2 was to distinguish between the integration to threshold and the temporal filter accounts of the results of experiment 1. To this end, we manipulated the availability of useful visual information in different time epochs during a trial. In the same-different condition, the target and distractor luminance values were drawn from the same distribution for the first 100 ms but from different distributions thereafter. In the different-same condition, the target and distractor luminance values were sampled from different distributions in the first 100 ms but were sampled from the same distribution for the remainder of the trial. Thus, in the former condition, the critical visual information was only presented after 100 ms had elapsed, whereas, in the latter, the critical visual information was only available during the first 100 ms of the trial. We compared the accuracy of performance with the standard condition of experiment 1 (“different-different”). These analyses were based on 828, 832, and 838 trials for observers 1-3, respectively.

The integration to threshold and temporal filter models can be distinguished in their predictions for the same-different condition. If observers integrate to a threshold, integration should continue until enough information to distinguish the target has been acquired. This would result in prolonged saccade latencies, and the resulting accuracy should be above chance. In contrast, the temporal filter model predicts that accuracy in this condition should be at, or close to, chance because no useful signals were included in the integration period of the filter. In addition, it predicts that the saccade latencies should be comparable with that of the remaining two conditions.

Figure 3A illustrates the proportion of correct saccades for each of the three observers. For each individual observer, performance in the same-different condition was significantly worse than performance in the different-different condition (χ² test; all p < 0.01). The binomial SEs include the 0.5 level for all three observers, indicating that performance in this condition was not reliably above chance. In addition, performance in the different-same condition was not different from the different-different condition (all p > 0.35).

Figure 3.

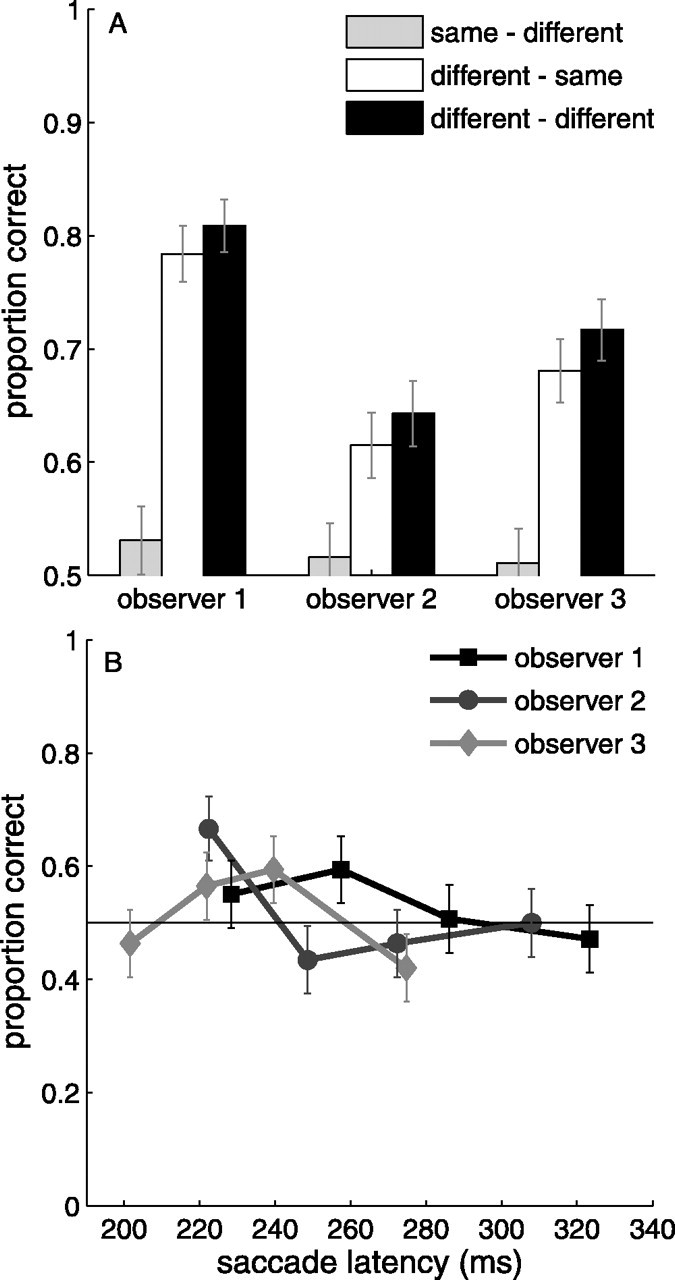
Proportion of correctly directed saccades in experiment 2. A, Proportion correct for the three conditions. B, Proportion correct as a function of saccade latency in the same-different condition. Error bars are binomial SEs. Chance level is 0.5.

There was no difference in saccade latency between any pairing of saccade latency distributions in this experiment (Mann-Whitney test; all p > 0.40). Figure 3B shows the accuracy as a function of saccade latency for all three observers in the same-different condition. The integration-to-threshold model links variability in saccade latency with variability in the integration window. As such, this model (along with an integration-to-dead time model) predicts an increase in the accuracy as a function of saccade latency. Clearly this is not what we found. All three functions are essentially flat, and, even for the longest latencies, accuracy was still at chance.

Discussion

Models of perceptual decision making generally assume that observers integrate sensory information until the evidence in favor of one alternative is sufficiently large. Saccadic decisions are among the most frequent and important perceptual decisions that humans make. Using stochastic visual stimuli, we identified the temporal impulse response underlying saccadic eye-movement decisions. This method enables an assessment of whether saccade generation, as typically studied in behavioral and neurophysiological oculomotor experiments, is driven by an integration to threshold mechanism. In addition, we examined the common assumption that visual integration continues up to the start of the relatively fixed saccadic dead time and the associated assumption that saccade latency variability maps onto variability in the visual integration period. More broadly, this study addressed the generality of integration to threshold as a mechanism for dealing with noise in sensory encoding and the origin of saccade latency variability.

Our findings are summarized as follows: (1) saccadic decisions were driven by the sensory information presented in the first 100 ms (in particular, the 25-75 ms epoch) after display onset. (2) Observers did not use all the time that is available to them. That is, visual integration did not proceed up to the start of the saccadic dead time. (3) Variability in saccade latency did not correspond to variability in the visual integration window.

Together, these findings argue against a view that saccade generation is driven by integration of sensory information up to a threshold. Instead, they support a temporal filter model, in which saccadic choices are driven by the response of early temporal filters to the onset of the display. These filters integrate over a relatively fixed time period that is independent of the difficulty of discrimination on a particular trial. It appears that this integration period is ∼100 ms. However, the temporal filter model evokes the same question that we asked in the context of the integration to threshold model: why was saccade initiation delayed for so long after the temporal filters responses?

One possibility is that the filter outputs are transmitted to a higher stage of processing that consists of an oculomotor decision unit. Within this unit, a saccade is triggered when activity associated with a particular movement program reaches a threshold (Carpenter and Williams, 1995). In addition, with multiple saccade programs (two filter responses in this paradigm), some conflict resolution is required to make sure that only one saccade target is selected (Leach and Carpenter, 2001; Ludwig et al., 2005). A simple lateral inhibition mechanism at this stage would result in the patch that triggered the stronger filter response suppressing the other, weaker item. We suggest that saccade latency variability predominantly stems from this decision process, which can take the form of trial-by-trial fluctuations in drift rate and baseline or threshold levels (Carpenter, 2004). Although this model does assume an accumulation of activity to a critical threshold level, it is critical that the rise to threshold is driven by the “single-shot” output of early filters that integrate over a fixed period. This contrasts with the integration-to-threshold model, which assumes a continuous read out of sensory information from lower-level areas until the evidence is strong enough.

We hypothesize that the early temporal filters that provide the relevant input into the oculomotor system are located at the level of striate cortex. V1 output neurons have integration periods estimated to range from 50 to 100 ms (Hawken et al., 1996). One of the targets of these V1 output neurons is the midbrain superior colliculus (Schiller, 1996), which plays an important role in saccade control (Munoz and Wurtz, 1995a,b; Wurtz, 1996). In addition, these neurons will project to parietal areas, which, in turn, are well connected with the frontal eye fields. These eye-movement structures may be regarded as a functional oculomotor decision unit (Hanes and Schall, 1996; Ratcliff et al., 2003).

In conclusion, we suggest that decision making, at least in this paradigm, was driven by the single-shot output of early visual filters. Observers did not use the visual information for as long as possible (i.e., up to the dead time); instead, their decision was based on the filter responses to the onset of the display. The sensitivity of the oculomotor system to rapid onsets may be a sensible adaptation to more natural viewing situations in which observers are interested in the physical properties of objects. Plain luminance may be an unreliable signal of object properties because it is confounded by effects of illumination. However, rapid changes in luminance (as associated with the appearance or motion of an object) are a better signal of behaviorally relevant events in the visual world.