Rapid Reshaping of Human Motor Generalization

Abstract

People routinely learn how to manipulate new tools or make new movements. This learning requires the transformation of sensed movement error into updates of predictive neural control. Here, we demonstrate that the richness of motor training determines not only what we learn but how we learn. Human subjects made reaching movements while holding a robotic arm whose perturbing forces changed directions at the same rate, twice as fast, or four times as fast as the direction of movement, therefore exposing subjects to environments of increasing complexity across movement space. Subjects learned all three environments and learned the low- and medium-complexity environments equally well. We found that subjects lessened their movement-by-movement adaptation and narrowed the spatial extent of generalization to match the environmental complexity. This result demonstrated that people can rapidly reshape the transformation of sense into motor prediction to best learn a new movement task. We then modeled this adaptation using a neural network and found that, to mimic human behavior, the modeled neuronal tuning of movement space needed to narrow and reduce gain with increased environmental complexity. Prominent theories of neural computation have hypothesized that neuronal tuning of space, which determines generalization, should remained fixed during learning so that a combination of neuronal outputs can underlie adaptation simply and flexibly. Here, we challenge those theories with evidence that the neuronal tuning of movement space changed within minutes of training.

Introduction

The ease with which people move belies the complex computations that underlie human behavior. One such computation transforms desired movement into appropriate muscle forces and joint torques. People carry out this inverse dynamic transformation when moving their unencumbered arms (Wolpert and Ghahramani, 2000). Foundational psychophysical studies demonstrated that humans could also adapt their motor behavior to move skillfully in novel dynamic environments (Lackner and Dizio, 1994; Shadmehr and Mussa-Ivaldi, 1994). After extended training in one environment, people generalized motor memory to affect behavior in other tasks (Conditt et al., 1997), directions of movement (Gandolfo et al., 1996), hand positions (Shadmehr and Moussavi, 2000), speeds (Goodbody and Wolpert, 1998), or in novel visuomotor (Krakauer et al., 2005) or dynamic environments (Shadmehr and Brashers-Krug, 1997). These studies identified computational properties of motor memory resulting from hundreds of sensed movements and dependent on both nervous system processing and the investigator-designed training paradigm.

Movement-by-movement transients of motor adaptation more directly identify the computational properties of incrementally learning an inverse dynamic model. Recent studies (Thoroughman and Shadmehr, 2000; Scheidt et al., 2001) used system identification to show that error in a single movement induces adaptation in the immediately subsequent movement. This incremental adaptation generalized across a broad subset of movement directions (Thoroughman and Shadmehr, 2000). A neural network model mimicked this generalization if the force estimate relied on neural units broadly tuned to movement direction and speed. This model exemplified a broader theory of neural computation, that the weighted linear combination of broadly tuned neurons allows for generalization and that learning may occur solely in the changing of the weights (Poggio, 1990; Poggio and Bizzi, 2004). Additional studies have indicated that this broadly tuned neural network model mimicked motor learning in several viscous environments (Donchin et al., 2003), as well as position-dependent environments (Hwang et al., 2003). The constancy of this broad movement-by-movement generalization supports the theory that fixed neuronal tuning simplifies learning and, in motor adaptation, provides a simple, consistent expectation of environmental complexity (Pouget and Snyder, 2000).

Although broad generalization has been hypothesized to be immutable as human subjects learn novel environments (Shadmehr, 2004), to date, these environments mimicked natural environments in their low spatial complexity across movement space. Here, we trained human subjects in dynamics with low, medium, and high complexity, and found that people could learn all three environments. Most surprisingly, subjects quickly changed their movement-by-movement adaptation to match the complexity of their environment. This reshaping of motor adaptation suggests that people can rapidly change the internal mapping of movement space that informs transformations of sense into action.

Materials and Methods

Twelve right-handed subjects (three women and nine men), aged 21–29, with no known neurological disorders, performed a reaching task while holding the handle of a five-link, two-bar robotic manipulandum (IMT, Cambridge, MA). Encoders recorded the subjects' hand positions and velocities; two DC motors could generate torque about the manipulandum joints. The Washington University Hilltop Human Studies Committee approved the experimental protocol; all subjects gave informed consent.

A computer monitor displayed a cursor representing the position of the robotic handle. Before the onset of a trial, subjects held the handle at the workspace center. A target appeared in 1 of 16 directions (0–337.5° with 22.5° separation) in the periphery of the monitor, cueing a 10 cm movement. We pseudorandomly distributed target directions across trials. Subjects needed to reach the target within 0.45–0.55 s for a successful movement, turning the target color green. The robot then returned the subject's arm to the start position.

Subjects performed the task for four consecutive days. On day 1, the robot generated no forces, a condition termed the null field. On each of days 2–4, the robot generated a single environment, termed a force field, determined by the following equation:

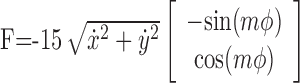(1)

where ẋ, ẏ, and ϕ are the Cartesian components and direction of hand velocity. Increasing m increased the spatial complexity of the function mapping velocity direction into force direction (see Fig. 1 A–C). On different days, the force direction changed as fast (m = 1; field 1), twice as fast (m = 2; field 2), or four times as fast (m = 4; field 4) as the velocity direction. Across subjects, we altered the order of force-field presentation to counterbalance for across-day adaptation.

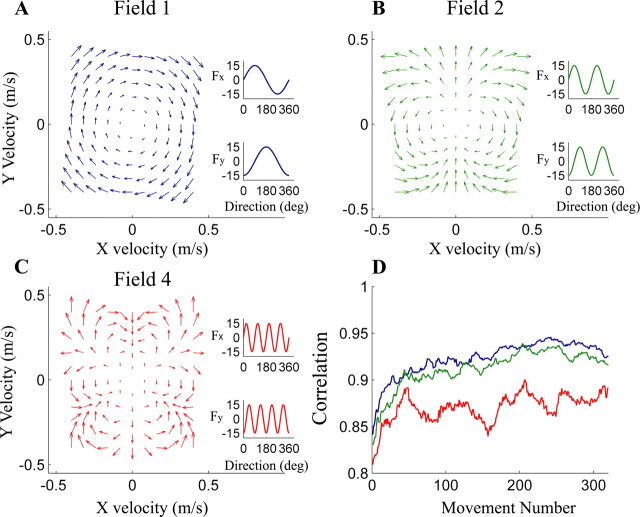
Figure 1.

Mean subject performance (D) in fields 1 (A; blue), 2 (B; green), and 4 (C; red). The numbers of the fields identify their spatial frequency (Eq. 1). The magnitude and direction of the applied force (arrows) depend on the x- and y-components of hand velocity, represented on the x- and y-axes, respectively. Insets show the dependence of x- and y-components of force on velocity direction. D, Correlation coefficients plotted against movement number as subjects train in fields 1 (blue), 2 (green), and 4 (red). Correlation coefficients were smoothed using a 20-movement moving average.

Each training day had four sets of 160 movements each. Subjects had a 5 min break between sets; total training each day lasted 45–60 min. In the first two sets of days 2–4, the force field was always present. In the last two sets, the forces were removed pseudorandomly on 20% of the trials, termed “catch trials.”

Data analysis. We quantified adaptation in the force field by correlating (Shadmehr and Brashers-Krug, 1997) the velocity time series of each movement to the last movement made in the same direction on day 1 (null field). We smoothed correlation coefficients using a 20-movement rectangular window, and then fit an exponential function to the smoothed data. Improvement and asymptotes of behavior equaled the rise and plateau of the exponential function. We quantified significance by bootstrapping (Fisher, 1993) as follows: we resampled our subject pool with replacement 1000 times, found the mean statistics of each resampling, and then sorted the results to determine p values.

We quantified aftereffects generated in catch trials by comparing, within subjects, the hand displacement at peak speed in catch trials and in the last movement made in the same direction on day 1. We tested for significance using a t test.

To determine the trial-by-trial generalization of error into adaptation, we fit subject behavior with a state-space model as follows:

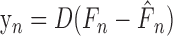(2)

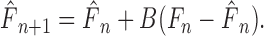The input (F) was a two-dimensional unit vector pointing in the direction of the applied force, but it equaled zero in catch trials. The output (y) was the measured error (difference from null-field movements) in hand position at peak velocity. The modeled-force estimate (F̂) was updated by the force error (F – F̂) scaled by the sensitivity parameter (B). The error of a particular movement depended on the force estimate for only that movement direction (as parameterized by D); that error, however, then updated force estimates in all 16 directions. We used the Gauss–Jordan method to find parameters that minimized the squared difference between subject and state-space model performance.

We analyzed the dependence of the sensitivity parameter B on the angular difference between the movement direction in which error occurred and the direction to which that error updated force prediction. We determined the changes in this dependence as subjects learned the three force fields; the significance of these changes was determined by bootstrapping.

Simulation. The small incremental adaptations after each movement made possible a linear neural network (Pouget and Snyder, 2000) of the inverse dynamic model as follows:

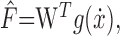(3)

where F̂ is the force estimate and W is the weight matrix. The neuronal tunings (g) encoded velocity only, because perturbing forces were viscous. In response to force error experienced in a movement, indexed 1, the adaptation rule that minimizes squared force error is as follows:

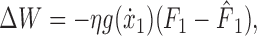(4)

where η is the learning rate. In the subsequent movement, indexed 2, the change in predicted force equals the following:

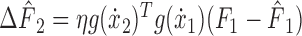(5)

(see Fig. 4 B). Comparing the neural network (Eq. 5) to the state-space model (Eq. 2) reveals the equivalency of the sensitivity parameter and generalization of neuronal tuning functions across movement space:

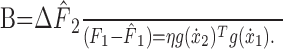(6)

The state-space estimation of generalization, therefore, is proportional to the projection (or dot product) of neuronal network activity across two movements. We used this relationship to find model neuronal tuning that best fit our subjects' generalization.

Figure 4.

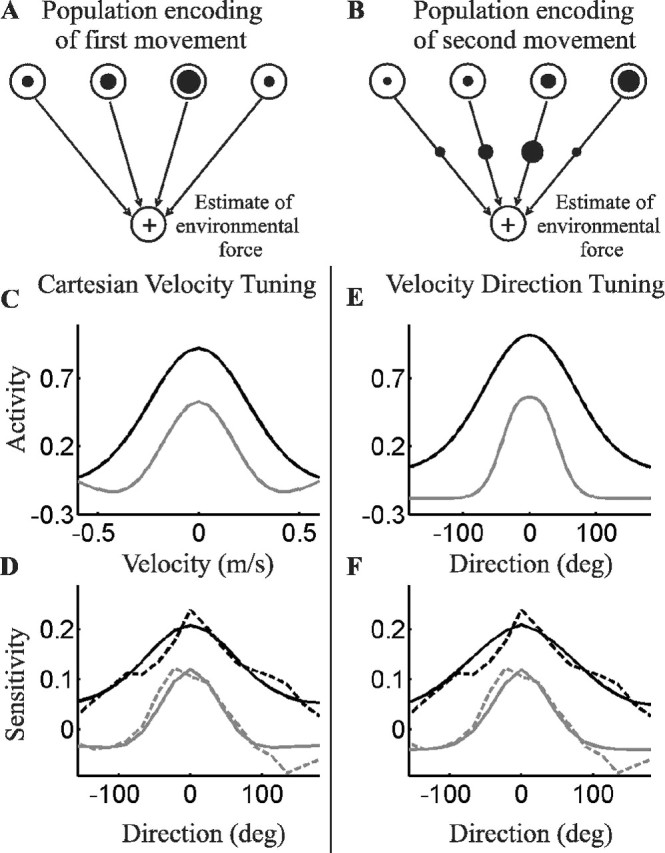
Neural network model (A, B) and model neuron tuning (C, E) that mimicked (D, F) movement-by-movement generalization in fields 1 and 2. A, Upper-level neurons, encoding desired movement space, projected to lower-level neurons, encoding predicted force (Eq. 3). The radii of the circles within the upper-level neurons represent activity in one movement. B, After this movement, the error-induced weight change (Eq. 4) is represented by the circles on the interlayer connections. A second movement then activated different portions of the upper neuronal tuning curves, as represented by new circles. C, Individual neuronal tuning functions, encoding Cartesian velocity, that best fit subject movement-by-movement sensitivity in fields 1 (black) and 2 (gray). The tuning was symmetrically dependent on the x- and y-components of hand velocity (only one dimension is shown). D, Simulations of sensitivity functions, as determined by the neuronal tunings in C and calculated using Equation 6. The dashed lines replot the human sensitivities from Figure 3. E, F, Best-fitting individual tuning functions (E) and simulated sensitivity functions (F) with neurons that encode velocity direction and scale activity with movement speed.

To generate an estimate of the underlying neuronal tuning, we needed to calculate the change in force estimates between two movements (Eq. 6). Therefore, we simulated two-movement sequences: sensed movement in one direction and then adapted control in another direction. This sequence was repeated for all possible movement direction combinations.

We implemented this simulation using two tuning assumptions. In the Cartesian velocity model, each unit was modeled as a difference-in-Gaussian tuning curve:

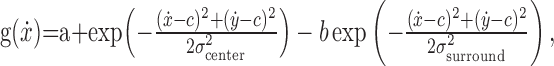(7)

where a is baseline activity, ẋ and ẏ are the desired velocity components, c is the preferred velocity of the cell, b is the relative scaling of center and surround tuning, and σ_center and σ_surround are the widths of center and surround tuning, respectively. The neural network consisted of a 25 × 25 grid of neurons; the collection of preferred velocities, c, were fixed and homogeneously tiled the x- and y-velocity space from –60 to +60 cm/s at 5 cm intervals.

In the directional tuning model, 120 neurons were individually tuned to velocity direction using a difference-in-Gaussian model; activity linearly scaled with movement speed. Tuning centers were equally spaced 3° apart.

The tuning parameters (Eq. 7) were determined, using the Gauss–Jordan method, to minimize the squared difference between the human sensitivity function and the dot products of neural network activity between two movements (Eq. 6). We did not optimize the learning rate because it affected only the scale, not the shape, of generalization.

We performed simulations and analyses using Matlab (Mathworks, Natick, MA).

Results

Subjects learned dynamics of low, medium, and high spatial complexity

All subjects, on days 2–4, experienced all three environments (Fig. 1A–C). To quantify adaptation, we correlated the velocity time series of each movement to that subject's last movement in the same direction in null-field training on day 1 (Fig. 1D).

In adaptation to fields 1 and 2, the improvement (p > 0.9) (see Materials and Methods) in performance was very similar. The smaller improvement (p < 0.04) and lower asymptote (p < 0.001) of performance in field 4 are significantly different from the other two fields, indicating that subjects did not learn the forces of the highest complexity as well as the other two fields.

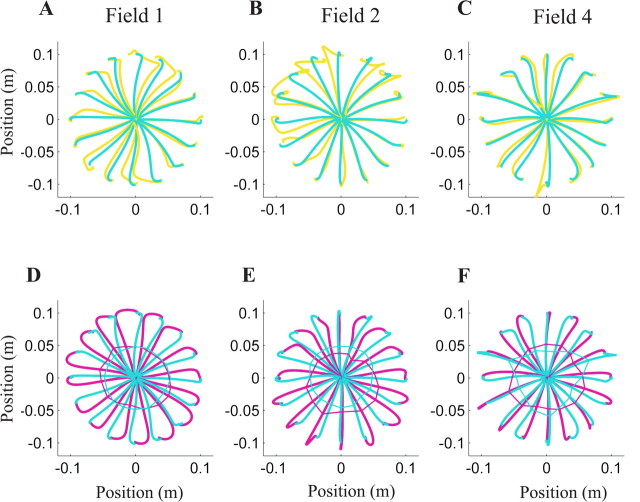
Aftereffects generated during catch trials demonstrated that improved performance was not attributable to cocontraction stiffening the arm but instead to specific learning of the force fields, even in field 4. In the second half of each training day, subjects experienced occasional catch trials, in which forces were unexpectedly removed. Subjects generated aftereffects in these catch trials in which the displacement opposed the direction of the perturbing force (Fig. 2D–F). We quantified these aftereffects by subtracting each subject's catch-trial trajectories from their last null-field trajectory. At peak speed, the hand displacement was significantly opposed to the force direction (fields 1 and 2, p < 0.0001; field 4, p < 0.005). The dynamics of field 1 were similar to naturally occurring dynamics in that forces changed direction at the same rate as movement direction, but the spatial complexity of fields 2 and 4 would rarely occur naturally. Subjects acquired specific information about not only field 1 but also novel environmental forces that varied at twice and four times the complexity of natural dynamics.

Figure 2.

Mean subject hand trajectories during fielded movements (A–C) and catch trials (D–F) in fields 1 (A, D), 2 (B, E), and 4 (C, F). Axes represent x and y hand positions. A–C, The gold lines represent the first movement in the force field, and the blue lines represent a movement immediately before a catch trial. D–F, Catch-trial trajectories are plotted in magenta with the replotted, blue precatch-trial trajectories. The vertices of the polygons connect positions at peak velocity. Magenta vertices outside blue vertices indicate that subjects anticipated a resistive force; blue outside magenta indicates anticipation of an assistive force.

Subjects quickly reshaped trial-by-trial generalization of error into adaptation

How could people learn complex dynamics, given the broad generalization across movement directions demonstrated previously? Did subjects alter their transformation of error into incremental adaptation? We used a set of state-space equations to identify this trial-by-trial adaptation (Eq. 2). The model maintained force estimates for all 16 directions of movement. A particular movement was controlled using the force estimate for that movement direction; the resultant error, however, was used to update force estimates in all 16 directions. The dependence of the update on the angular difference (θ) between input and output movement directions formed a sensitivity function, termed B, and identified the overall magnitude and spatial extent of movement-by-movement generalization (Fig. 3).

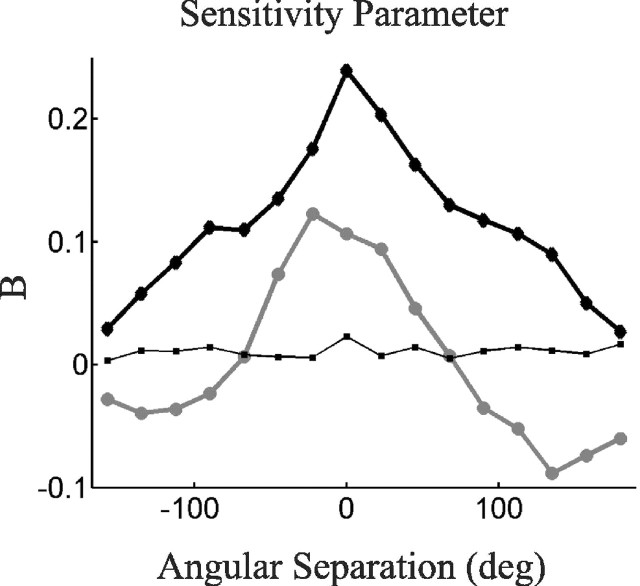
Figure 3.

The sensitivity function (B in Eq. 2) plotted against the angular difference (θ) between sensed and adapted movement directions. The sensitivity function is estimated in fields 1 (thick black diamonds), 2 (thick gray circles), and 4 (thin black squares), based on movements averaged across the subjects.

The overall magnitude of generalization decreased with environmental complexity. The function B at θ = 0, for example, decreased from 0.24 in field 1 to 0.10 in field 2 (significant difference, p < 0.005). This particular component of B quantified transfer of error into adaptation within the same movement direction; hence, the magnitude of this within-direction sensitivity dropped by more than one-half.

The sensitivity function for field 4, however, was very small. The function B at θ = 0 was significantly greater than 0 (p < 0.005) but on average equaled only 0.023. This indicated that even within movement directions, only 2% of sensed error was transformed into updated predictions. Sensitivity across directions was even smaller. The smallness of the field 4 sensitivity led us to exclude this sensitivity function from additional analysis and modeling.

The sensitivity functions in fields 1 and 2 differed not only in size but also in shape. The sensitivity function of field 1 was broad and always positive, such that an error sensed in one direction generated the same sign (positive or negative) of adaptation in all subsequent movement directions. For example, an unexpected rightward force experienced reaching away from the body would generalize to a prediction of a rightward force, even while reaching toward the right or toward the body. Field 2 sensitivity was narrower above the x-axis and featured negative components in directions far away from sensed error. Here, a rightward force experienced reaching away from the body would not generalize to movements toward the right (as B ≈ 0 for θ = 90°) and would generalize to an expectation of a leftward force for movements toward the body (as B < 0 for θ = 180°).

All state-space fits correlated well with the average subject behavior (field 1, r = 0.821; field 2, r = 0.839; field 4, r = 0.908). To test the predictive power of the state-space model, we fit the model to the third set of movements (field 1, r = 0.906; field 2, r = 0.882) and found that these parameters explained behavior in the fourth set (field 1, r = 0.863; field 2, r = 0.872) almost as well as parameters fit solely with the fourth set data (field 1, r = 0.902; field 2, r = 0.890).

The width of positive components of the sensitivity function, as measured by the half-width at half-maximum, were significantly larger for field 1 than for field 2 (p < 0.002). Negative components of the sensitivity function were significantly present for field 2 (p < 0.001) and significantly absent for field 1 (p < 0.05). Furthermore, we fit sensitivity functions with Gaussians; the field 2 sensitivity was narrower (p < 0.02) and had a lower baseline (p < 0.03) than the field 1 sensitivity. This second fit confirmed that the overall sensitivity function for field 2 was not simply shifted downward but also narrowed.

Neural networks mimicked reshaping of generalization when neurons reshaped their tuning of movement space

What does this change in sensitivity between fields 1 and 2 imply about the underlying neuronal representation of movement? The inverse dynamic model transforms a desired trajectory into appropriate joint torques or muscle forces. This transformation may be modeled by a predictive control network, in which an upper layer of neurons encoding desired movement are functionally connected to a lower layer that predicts the appropriate force (Fig. 4A). In this construction, the sensitivity function (B) equaled the product of activities in the upper layer neurons between one (erroneous) movement and the next (adapted) movement (Fig. 4B, Eqs. 3–6) (also see Materials and Methods).

This mathematical equivalency enabled us to infer certain properties of the neuronal representation of movement space and therefore eliminate incompatible neuronal tunings from possible contribution to motor adaptation. To illustrate this power, we simulated a layer of neurons that collectively tiled hand-velocity space and were individually tuned to a specific velocity. Each neuron used a difference-in-Gaussian function similar to center-surround tuning (Eq. 7). With this network, we could replicate the sensitivity functions for fields 1 and 2 (Fig. 4D), but the parameters of the tuning function depended on the field (Fig. 4C). The broad, always-positive tuning fit the field 1 generalization well [root mean square error (rmse) = 0.020] but fit the field 2 generalization poorly (rmse = 0.114). Conversely, the narrower “Mexican-hat” tuning fit field 2 generalization well (rmse = 0.018) but field 1 generalization poorly (rmse = 0.120). We also mimicked human sensitivity in both fields (Fig. 4F) using neurons whose activity was proportional to hand speed and was tuned to velocity direction (Fig. 4E); note the necessary narrowing of tuning for field 2. Different models of population and individual neuronal tuning will produce different best-fitting tuning functions, but all will require a dramatic change in that tuning to mimic the subjects' narrowing of generalization from field 1 to field 2.

Discussion

Population coding theory has hypothesized that individual neuronal tuning functions generate the spatial resolution of the encoded representation (Poggio, 1990; Poggio and Bizzi, 2004). Fixed tuning simplifies learning by enabling a population of neurons to provide a consistent expectation of environmental complexity (Pouget and Snyder, 2000) and to adapt rapidly by altering connections flowing from those neurons (Poggio and Bizzi, 2004). These models therefore hypothesized that motor adaptation can occur solely through adapted connectivity. Our results directly challenge this hypothesis and instead suggest that the expectation of environmental complexity, as encoded by neuronal tuning, changed as a function of experience.

We identified how mere minutes of training can inform not only what we learn but also how we learn; movement-by-movement generalization reduces and narrows in response to increased complexity of environmental dynamics. Broad tuning is advantageous to learn environments in which the dynamical conditions slowly change across movement space, but if dynamics change rapidly, the broad generalization will be destructive (Thoroughman and Shadmehr, 2000). Reducing the gain of sensitivity and narrowing tuning in response to a more complex environment will limit this destructive interference.

The dramatic changes in the gain of sensitivity across the three environments could arise from activity reduction in neurons representing movement space, via gain modulation (Salinas and Sejnowski 2001; Salinas 2004), or from a reduction in the cortical connectivity adaptation rate, represented by η in our simulation. At first, this result does not seem to be consistent with the learning of fields 2 and 4, quantified by correlation coefficients (Fig. 1D) and aftereffects in catch trials (Fig. 2F). In the first half of each training day (Fig. 1D), subjects constantly experienced force fields. We introduced catch trials only in the second half; catch trials generated the across-trial variance that made sensitivity function calculation possible. We hypothesize that, in all fields, subjects adapted to acquire specific environmental knowledge in the first few dozen movements, and then subsequently reduced the gain in field 2 and shut down adaptation in field 4 when performance failed to further improve. We therefore propose that the reshaping of neuronal tuning in the motor system could underlie narrower spatial generalization and smaller gains of motor adaptation.

Could the brain accomplish this neuronal tuning change within minutes of training? There is evidence of experience-induced plasticity in the motor system in the form of changes in somatotopy, preferred direction, and tuning widths during motor training (Gandolfo et al., 2000; Paz and Vaadia, 2004), as well as plasticity induced by brain–computer interfaces (Taylor et al., 2002). In addition, there is neurophysiological evidence for sharpening neuronal tuning in attention (Spitzer et al., 1988; Lee et al., 1999), perceptual learning and adaptation (Schoups et al., 2001; Teich and Qian, 2003), and sound localization (Fitzpatrick et al., 1997) experiments. The observed activity changes, however, occurred over repeated days of training, rather than within minutes. Alternatively, subpopulations of neurons could have different tuning functions, but only select neurons, appropriate for the current environment, would participate in movements and adaptation. A candidate for contributing to selection among cortical neurons is the cerebellum, because it is necessary for visuomotor adaptation (Baizer and Glickstein, 1974; Martin et al., 1996) and has a unique structure (Marr, 1969) suitable for rapid adaptation of an internal model (Schweighofer et al., 1998a,b). This circuitry provides a likely mechanism for rapid fine-tuning of cortical networks by selectively gating those neurons that beneficially contribute to compensate for specific environments.

Here, we found that people change their trial-by-trial generalization during motor adaptation in response to environmental complexity. A linear relationship (Eq. 2) fit the human transformation of sensed error into incremental adaptation; a linear neural network (Eqs. 3–5, Fig. 4) then mimicked human generalization. Why does this linear approach work, considering that motor transformations and brain interconnectivity are highly nonlinear? We identified how sense from a single movement induced incremental adaptation of predictive control. People generated a conservative response to each error; the maximum of the sensitivity function B (Fig. 3) indicated that people incorporated at most 25% of the sensed error into trial-by-trial adaptation. This conservatism enabled a reasonable linear approximation of the adaptive process. The actual neural systems underlying adaptation, however, made small enough changes that a Taylor series expansion of connectivity would leave primarily the linear term. The trial-by-trial approach therefore induces neural circuitry, with its complexities and nonlinearities, to respond in a locally linear manner. The linear adaptation term, similar to Equation 4, depends on the neural encoding of movement space that projects to neurons adaptively predicting the environment. We propose that this trial-by-trial approach has broad applicability to identify the neural basis of sensory and motor adaptation, because incremental learning generates a novel window into the neuronal encoding of sensory and motor space.