Organization of the Human Trichromatic Cone Mosaic

Abstract

Using high-resolution adaptive-optics imaging combined with retinal densitometry, we characterized the arrangement of short- (S), middle- (M), and long- (L) wavelength-sensitive cones in eight human foveal mosaics. As suggested by previous studies, we found males with normal color vision that varied in the ratio of L to M cones (from 1.1:1 to 16.5:1). We also found a protan carrier with an even more extreme L:M ratio (0.37:1). All subjects had nearly identical S-cone densities, indicating independence of the developmental mechanism that governs the relative numerosity of L/M and S cones. L:M cone ratio estimates were correlated highly with those obtained in the same eyes using the flicker photometric electroretinogram (ERG), although the comparison indicates that the signal from each M cone makes a larger contribution to the ERG than each L cone. Although all subjects had highly disordered arrangements of L and M cones, three subjects showed evidence for departures from a strictly random rule for assigning the L and M cone photopigments. In two retinas, these departures corresponded to local clumping of cones of like type. In a third retina, the L:M cone ratio differed significantly at two retinal locations on opposite sides of the fovea. These results suggest that the assignment of L and M pigment, although highly irregular, is not a completely random process. Surprisingly, in the protan carrier, in which X-chromosome inactivation would favor L- or M-cone clumping, there was no evidence of clumping, perhaps as a result of cone migration during foveal development.

Introduction

The precise topography of the trichromatic cone mosaic constrains the postreceptoral circuits that subserve spatial and color vision. Whereas the short-wavelength-sensitive- (S) cone submosaic has been relatively well characterized (Williams et al., 1981; de Monasterio et al., 1985; Ahnelt et al., 1987; Curcio et al., 1991), the organization of long-wavelength-sensitive (L) and middle-wavelength-sensitive (M) cones in the human retina has proven more elusive, because they exhibit no known morphological or histochemical differences and their pigments are 96% identical (Nathans et al., 1986). Several studies using indirect measurements have suggested that there are on average more L cones than M cones, with large intersubject variability (DeVries, 1946; Rushton and Baker, 1964; Cicerone and Nerger, 1989; Pokorny et al., 1991; Yamaguchi et al., 1997; Hagstrom et al., 1998; Brainard et al., 1999; Deeb et al., 2000; Kremers et al., 2000; Otake and Cicerone, 2000; Carroll et al., 2002). A limitation of these estimates is that they often involve the untested assumption that each M cone and each L cone contribute equally to the molecular, physiological, or psychophysical mechanisms being monitored to derive L:M ratio estimates. Microspectrophotometry is not subject to this concern (Dartnall et al., 1983; Bowmaker et al., 2003), although it is restricted to use on postmortem tissue. Roorda and Williams (1999) developed an in vivo method combining high-resolution retinal imaging with retinal densitometry, allowing the first direct measurements of L- and M-cone arrangement and relative numbers in the living human eye. We have improved this method, expanding the number of eyes studied to more thoroughly characterize the foveal cone mosaic.

Although interobserver variability in L:M cone ratio is now well established, questions remain about how these cone classes are arranged within the mosaic. Using microspectrophotometry, Mollon and Bowmaker (1992) observed a random arrangement of L and M cones in patches of talapoin monkey retina, and Bowmaker et al. (2003) reported a random arrangement of L and M cones in patches of human retina, consistent with a random assignment of these pigments to cones (Nathans, 1999). Roorda et al. (2001) also reported a random arrangement of human foveal L/M cones for two subjects. However, there is accumulating evidence for nonrandom arrangement of L and M cones. Hagstrom et al. (1998) and Bowmaker et al. (2003) both found that L:M cone ratio increases greatly in the far periphery in human retina. Deeb et al. (2000) showed a nasal-temporal asymmetry in L/M cone ratio in the macaque. Packer et al. (1996), using photopigment transmittance imaging of excised patches of peripheral primate retina, reported a tendency for L and M cones to clump more than would be expected from random packing. Departures from the random assignment of L and M photopigment in the cones would have important implications for models of the formation of the cone mosaic. We used the method by Roorda and Williams (1999) to directly investigate L-, M-, and S-cone topography in the retinas of eight living humans, providing a more sensitive indicator of departures from randomness that might provide clues to the mechanisms that guide mosaic formation.

Materials and Methods

Subjects. All research followed the tenets of the Declaration of Helsinki, and study protocols were approved by the institutional review boards at the University of Rochester and the Medical College of Wisconsin. Informed consent was obtained from each participant after explanation of the nature and possible consequences of the study. The color-vision phenotype of each of the eight subjects (seven males and one female, known to be a carrier of protan color vision deficiency) was assessed using the Rayleigh match, pseudoisochromatic plates (AO-HRR, Dvorine, and Ishihara), and the Farnsworth-Munsell 100 hue test. The performance of each subject on all tests fell within the accepted criteria for normal color vision. The color vision genotype of each subject was determined using previously described assays (Kainz et al., 1998; Neitz and Neitz, 2001). Genetic analysis of the female subject confirmed her status as a protan carrier (Kainz et al., 1998). The male subjects had L/M gene arrays indicative of normal color vision (Drummond-Borg et al., 1989; Neitz and Neitz, 1995, 2001), with one L gene and one to three M genes. Color-vision phenotype and genotype data for subjects RS, BS, and JC were reported previously [Carroll et al. (2002), subjects 43, 15, and 03, respectively]. For each subject, the estimated numbers of L and M genes are as follows: RS, JP, JC, and MD each had one L with two M; BS and AP each had one L with one M; YY had one L with three M; HS had one array with only M genes and a second array with an L gene followed by an undetermined number of M genes, confirming her status as a carrier of a protan color vision deficiency (Kainz et al., 1998).

High-resolution retinal imaging. Imaging was done using the Rochester second generation adaptive optics ophthalmoscope (University of Rochester) (for system details, see Hofer et al., 2001; Pallikaris et al., 2003), which provides better and faster optical correction and increased quantum efficiency than the previous system (Liang et al., 1997; Roorda and Williams, 1999). For each subject, the head was stabilized using a dental impression on a bite bar, the right eye was dilated with tropicamide (1%), and monochromatic aberrations were measured over a 6.8 mm pupil with a Shack-Hartmann wavefront sensor at 15 or 30 Hz. Corrections were made in a continuous loop with a 97 channel deformable mirror (Xinetics, Devin, MA) until the root mean square (rms) wavefront error fell below a minimum value (0.06-0.10 μm, depending on the subject) or 12 iterations, whichever happened first (Liang et al., 1997; Hofer et al., 2001). Once a wavefront correction was obtained, a retinal image was acquired by illuminating the retina with a 1° diameter, 4 ms flash [550 nm, 25 nm bandwidth (full width at half maximum)] from a krypton arc flash lamp. The short duration of the flash minimizes the effects of motion blur on the retinal image. Imaging was performed over a 6 mm pupil to avoid edge artifacts from the deformable mirror. To control the retinal location imaged, subjects were instructed to fixate on particular intersections of black radial lines and concentric circles on a white background. Between seven and 30 images were collected for each condition described below, registered with subpixel accuracy (Putnam et al., 2005), and added together. To minimize the deleterious effects of fluctuations in cone reflectivity over time (Pallikaris et al., 2003), the different imaging conditions were interleaved over a period of 1-3 d.

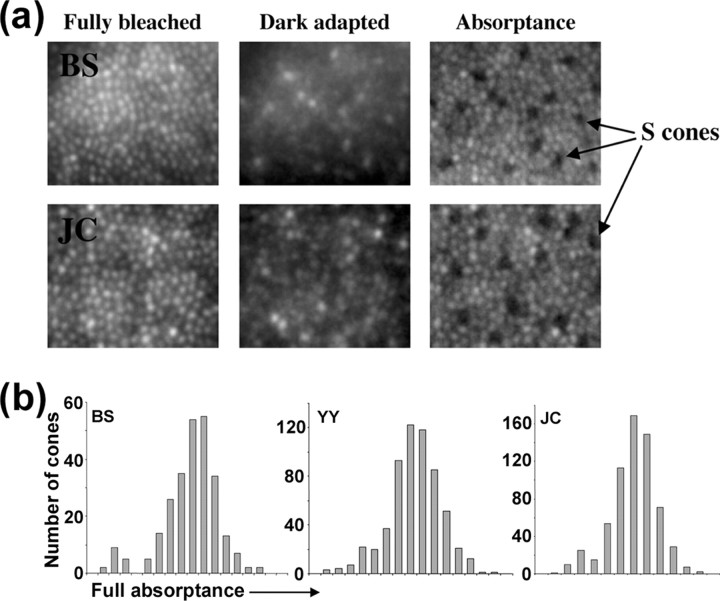
Using methods similar to those described in detail by Roorda and Williams (1999) and Roorda et al. (2001), we classified individual cones by comparing images taken when all of the photopigment was bleached with those taken when it was fully regenerated or when one class of photopigment was bleached selectively with either a 470 or 650 nm light. S cones absorb negligibly at our imaging wavelength of 550 nm (whereas the L and M cones absorb strongly), so they appear as dark cones in the absorptance image (which is defined as 1 minus the ratio of the dark adapted image to the corresponding fully bleached image) (Fig. 1 a). Figure 1 b shows the distribution of these absorptance values for cones in the mosaics of three subjects; S cones appear as the small peak on the lower end of the absorptance distribution. These distributions were fit with the sum of two Gaussian functions representing S and L/M cones, which allowed us to estimate the absorptance below which it is more likely that a cone is an S cone than either an L or M cone. In many subjects, it was not possible to use this single criterion to identify all S cones across the image, because of, for example, systematic variations in absolute pigment absorption across the field caused by changes in cone outer-segment length or more local variations in apparent cone pigment density caused by variability in the reflectivity of individual cones (Wade and Fitzke, 1998; Pallikaris et al., 2003; Rha et al., 2005). In these subjects, an absorptance criterion was used as a guideline, but local information, if a cone exhibited significantly lower absorptance than its neighbors, was also considered in the final determination.

Figure 1.

Identification of S cones in the cone mosaic. a, Averaged retinal images after a full bleach of L- and M-cone pigment, after dark adaptation, and calculated absorptance images. S cones are identified as a sparse array of dim cones in the absorptance image. b, Histogram of individual cone full absorptance values. S cones are identifiable as a low-absorptance peak.

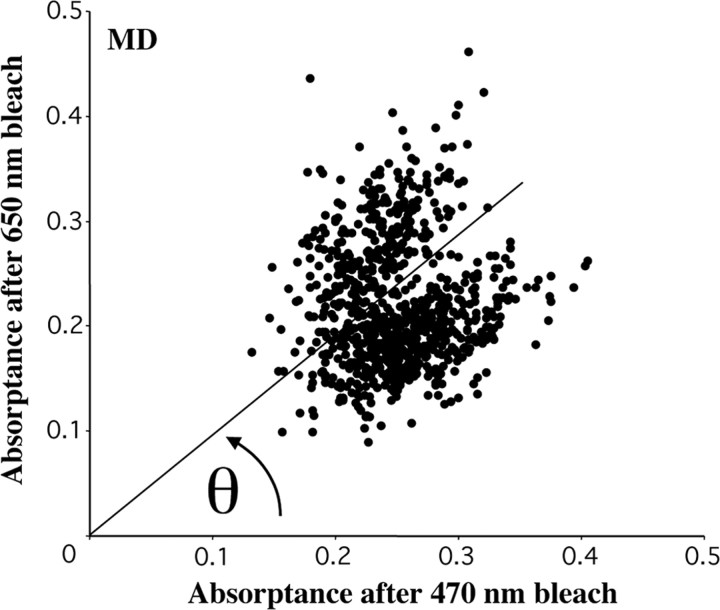
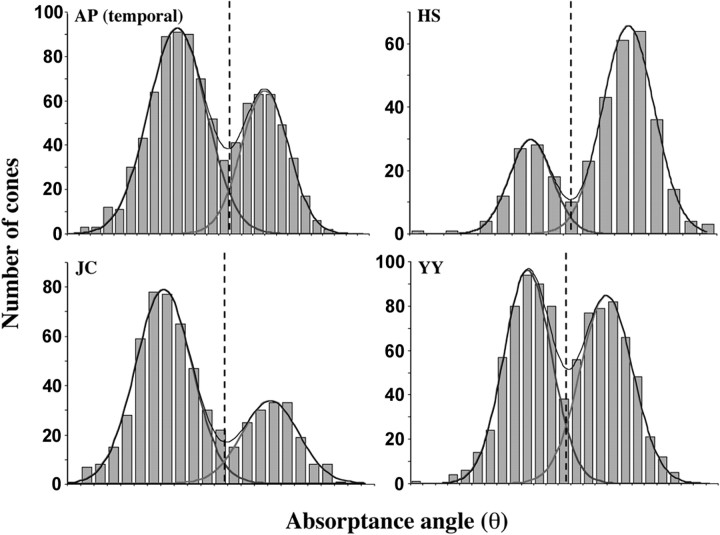
S cones thus identified were removed from subsequent analysis, and the remaining cones were classified as M or L cones by comparing their absorptance after the 650 nm bleach with that after the 470 nm bleach (absorptance is defined here as 1 minus the ratio of the selectively bleached image to the corresponding fully bleached image) (Fig. 2). Bleaching levels were set to maximize the difference in photopigment concentration between the L- and M-cone classes. (Bleaching levels were ∼25 × 10 ⁶ Troland-seconds for the 550 nm full bleach, ∼7.7 × 10 ⁶ Troland-seconds for the 650 nm bleach, and ∼5.2 × 10 ⁶ Troland-seconds for the 470 nm bleach. The difference in photopigment concentration after the 650 and 470 nm bleaches is ∼0.70 and 0.21, respectively.) To distinguish L from M cones, the polar angle (θ) of each data point in the scatter plot was calculated. Because the radial spread of the data in the scatter plot is mainly related to the optical density of a cone and not its spectral identity (L or M) (Packer et al., 1996; Roorda and Williams, 1999; Roorda et al., 2001), we can restrict our attention to the θ of each data point in the scatter plot. The absorptance angle distribution was fit as a sum of two Gaussian functions representing L and M cones, and the absorptance angle at which they intersected was taken as the criterion for deciding whether an individual cone was likely to be L or M (for representative examples from our subjects, see Fig. 3). The percentage of cones expected to be misidentified was calculated from the overlap of the Gaussian functions. The ratio of the heights of the L- and M-cone Gaussians to the sum of the two functions at any particular absorptance angle provided an estimate of the probability that an individual cone with that absorptance angle value was L or M. The ratio of the areas under the Gaussian curves provided an estimate of the L:M ratio of the population of cones represented by the particular subset analyzed. The accuracy of L- and M-cone assignments estimated in this way is good, with ∼95% or more of L/M assignments correct for each subject (Table 1).

Figure 2.

Scatter plot of cone absorptance after 650 nm bleach versus after 470 nm bleach. L and M cones comprise two distinct distributions. L cones are represented by the lower distribution, because they absorb relatively less after the 650 nm bleach and relatively more after the 470 nm bleach than M cones. S cones have been excluded from this plot.

Figure 3.

Examples of absorptance angle histograms used to identify L and M cones. The best-fitting L- and M-cone Gaussians and their sum are superimposed on each histogram. The vertical dashed line marks the intersection of the L and M curves; cones falling to the left of this line are identified as L, and cones falling to the right are identified as M.

Table 1.

Relative numbers of L, M, and S cones in eight subjects with normal color vision

Subject	Location	Percentage S	Percentage L (100 × L/(L + M))	Percentage of L-M misassignments	Percentage of S-L/M misassignments	Number of cones analyzed
HS	1° nasal	6.4	27.2 ± 3.6	1.8		375
YY	1° nasal-superior	6.4 ± 1.3	52.7 ± 3.2	5.3	1.5	1000
AP	1.25° nasal	5.6	55.4 ± 2.0	4.8		1003
AP	1° temporal	6.6	63.9 ± 3.2	4.6		1000
MD	1.25° nasal	5.8	65.3 ± 3.7	3.5		897
JP	1° temporal	4.7	69.9 ± 4.0	1.1		812
JC	1.25° temporal	5.5 ± 1.5	70.2 ± 4.2	2.7	0.87	645
RS	1.25° nasal	4.6	71.1 ± 2.8	5.05		897
BS	1.25° nasal	5.5 ± 2.9	94.3 ± 2.6	0.71	0.82	734
AP	Both locations	6.1	59.7 ± 1.9	4.7		2003

Flicker photometric electroretinogram. The flicker photometric electroretinogram (ERG) has been described in detail previously (Neitz and Jacobs, 1984; Jacobs et al., 1996; Carroll et al., 2000). Only a short summary of the technique is given here. The subject's pupil was dilated with a mydriatic (tropicamide; 0.5%). The electrode configuration used to record the ERG signal was as follows: a reference electrode placed on the skin below the right eye, a ground electrode above the right eye, and an electrode made with fiber from the Dawson-Trick-Litzkow plus electrode was used as the active corneal electrode. The stimulus was presented in Maxwellian view, illuminating a circular portion of the retina subtending ∼70°. Spectral sensitivity was determined by adjusting the intensity of a monochromatic test light until the ERG signal it produced exactly matched that produced by a fixed-intensity reference light. The test and reference lights were alternately presented at 31.25 Hz. These “null points” were obtained at 10 nm increments over a range of 480-680 nm, and this was done twice for each subject. An electronically tunable filter (Varispec; Cambridge Research & Instrumentation, Boston, MA) was used to control the wavelength of the test light. Final spectral sensitivity values were corrected for lens absorption with an age-dependent lens correction (Pokorny et al., 1987). To obtain an estimate of L:M cone ratio, a subjects' spectral sensitivity data are best fit to a weighted sum of an L- and an M-photopigment template (Jacobs and Neitz, 1993; Carroll et al., 2000). Individual differences in the spectral sensitivity of the L photopigment have been shown to greatly influence estimates of L:M cone ratio derived from flicker photometry (Bieber et al., 1998; Carroll et al., 2000). We remove variability in L-cone spectral sensitivity as a source of error by sequencing each subject's L gene and using an individualized L-photopigment template to estimate their L:M ratio (Carroll et al., 2002).

Results

Retinal mosaics of color-normal subjects

Summarized in Table 1 are the data for the relative numbers of L, M, and S cones identified in patches of retina near 1° eccentricity for eight human subjects who were demonstrated to have normal color vision (see Materials and Methods). Subjects BS and HS were chosen for this study as representing the upper and lower limits of normal L:M cone ratios, respectively. Subject HS is a genetically confirmed carrier of a protan color vision defect and thus was expected to have a low L:M cone ratio (Miyahara et al., 1998). Previous results from the flicker photometric ERG indicate that subject BS had an L:M cone ratio near the high end of the normal distribution (Carroll et al., 2002) (see Fig. 7). Figure 4 shows pseudo-color images of the cone mosaics in nine patches of the eight subjects' retinas.

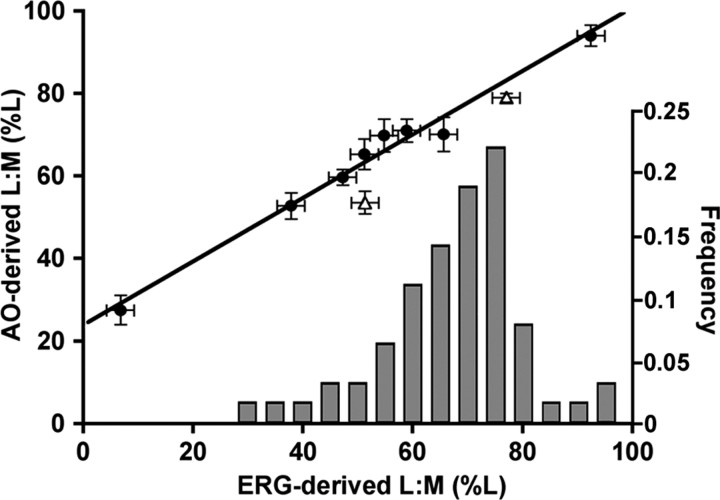
Figure 7.

Comparison of adaptive optics- and ERG-derived estimates of L:M cone ratio. Eight subjects were from this study (filled circles), and two subjects were from the study by Roorda and Williams (1999) (open triangles). ERG data for these two subjects were published previously (Brainard et al., 2000). Shown on the abscissa is a histogram of ERG-derived L:M ratios for 62 color-normal males (Carroll et al., 2002) (including JC, BS, and RS from the current study). The solid line is the best-fitting linear regression for the eight subjects in the current study (r ² = 0.98). Inclusion of the Brainard et al. (2000) data only slightly diminishes the correlation (r ² = 0.95). Error bars represent SD.

Figure 4.

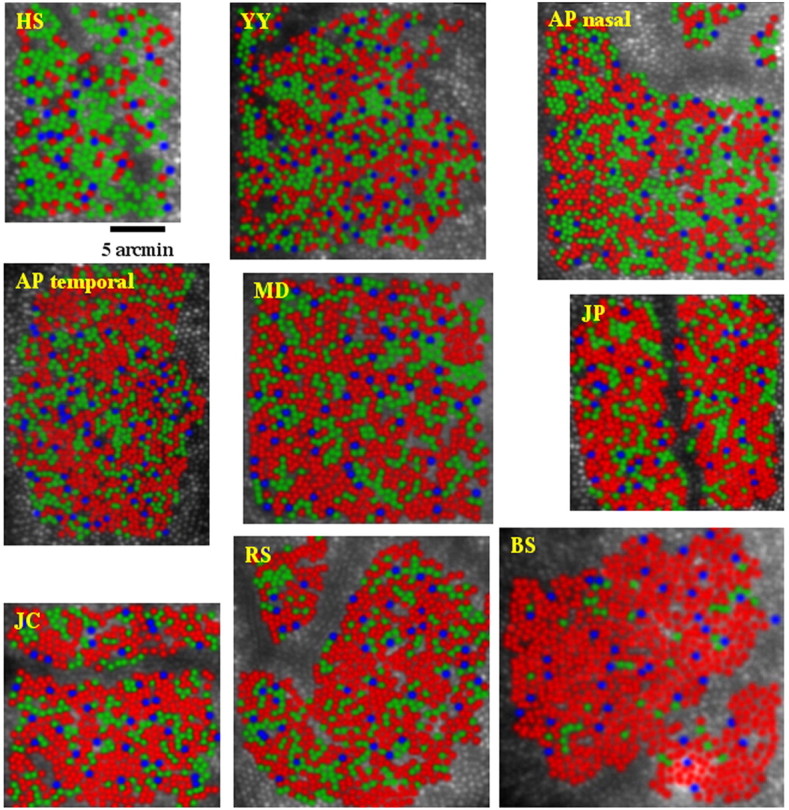
False color images showing the arrangement of L (red), M (green), and S (blue) cones in the retinas of different human subjects. All images are shown to the same scale.

Arrangement of S cones in the human retina

Recently, Roorda et al. (2001) evaluated two human eyes at 1° eccentricity using retinal densitometry combined with adaptiveoptics (AO) imaging to determine whether S cones were randomly distributed, whether they tended to be at discontinuities in the triangular cone mosaic, and whether they showed a tendency to neighbor either L or M cones. Here, we conducted the same analysis on a larger group of subjects, including two subjects with highly skewed L:M cone ratios. Results for the eight subjects examined here are shown in Figure 6 and Tables 1 and 2. It is not always possible to quantify the uncertainty of the S-cone identifications with the spatially localized retinal densitometry technique. In subjects for whom this was the case, no uncertainty for percentage S is listed in Table 1.

Figure 6.

Cumulative histogram comparison plots for the S-cone submosaic. The solid line is the fraction of inter-S-cone separations within a particular distance value for the actual mosaic versus that for the average of 100 random simulations. The dashed lines represent the maximum and minimum bounds of the random simulations. If the solid line lies entirely between the two dashed lines, then the arrangement of the S-cone submosaic is indistinguishable from random.

Table 2.

Fraction of L cones surrounding S cones and the expected fraction if S-cone placement is random

Subject	Fraction of L cones surrounding S cones (%L)	Expected %L and SD
BS	93.98	94.23 ± 1.59
JP	72.04	69.99 ± 3.16
JC	71.58	71.29 ± 3.34
AP nasal	52.90	55.29 ± 2.99
AP temporal	61.59	64.20 ± 2.76
YY	54.55	54.19 ± 2.74
MD	63.74	65.05 ± 2.89
RSa	64.15	71.34 ± 3.11
HS	30.69	26.57 ± 4.4

^a %L is significantly lower than the random expectation (p < 0.05).

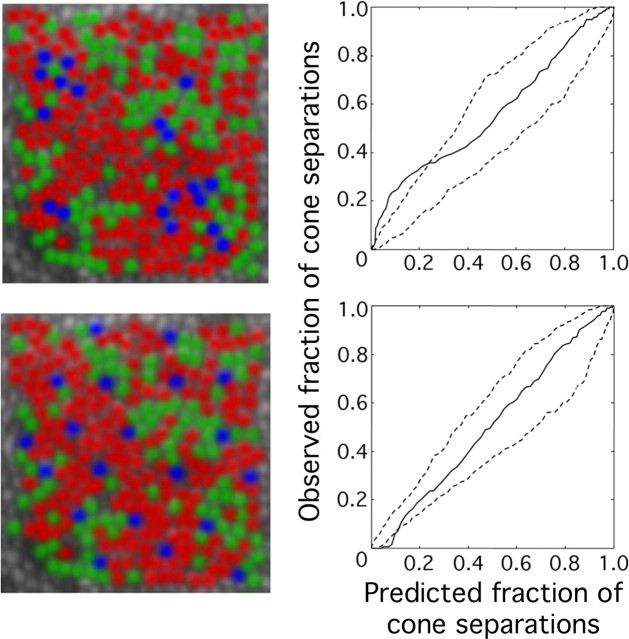
A test described by Diggle (1983) was used to assess whether the arrangement of S cones in our eight subjects is random, clumped, or regular. This test uses information about the mosaic on all spatial scales and is therefore superior to similar tests of randomness that concern themselves only with the distribution of nearest neighbor cone separations. In this test, an array of intercone distances between each S cone and every other S cone is computed. A cumulative histogram is calculated from this array, giving for each distance the fractions of inter-S cone distances that fall above and below this value. This cumulative histogram is then compared with that expected if S cones were arranged randomly. Monte Carlo simulations were used to compute the expected distribution of inter-S cone distances in a randomly arranged S-cone submosaic. One hundred random S-cone submosaics were generated by taking the actual locations of all the subject's cones and randomly assigning a constant fraction of them, the observed fraction of S cones for that subject, to be S cones. Cumulative histograms for each of these 100 mosaics were calculated and compared with the actual cumulative histogram for that subject.

Figure 5 shows cumulative histogram comparisons for two theoretical S-cone submosaics, one with S-cone clumping and one in which S cones are distributed in a regular array. If the cumulative histogram for the actual mosaic shows fewer short (or more large) inter-S cone distances compared with the random simulations, then the actual mosaic is more regularly distributed than a random array. Conversely, if it shows more short (or fewer large) inter-S cone distances, the real mosaic is more clumped than a random array. Figure 6 shows cumulative histogram comparisons for our subjects. Mosaics were deemed indistinguishable from random if the rms deviation of the cumulative histogram of the actual mosaic from the averaged cumulative histogram of the simulated mosaics was within the 95th percentile of the same statistic calculated for each of the 100 random simulations (p < 0.05) and if the values of the actual cumulative histogram lay within the extremes predicted from the simulations for all distance values (p < 0.01). For only one subject (AP temporal retina), the rank of the rms statistic was above the 95th percentile. In addition, for four of the eight subjects (AP temporal, AP nasal, JC, MD, and YY), the results from the actual mosaic fell outside the bounds established by the simulations in at least one place, in the direction of a more regular S-cone distribution.

Figure 5.

Examples of cumulative histogram comparison plots for hypothetical clumped (top) and regularly distributed (bottom) S-cone submosaics. The solid line is the fraction of inter-S-cone separations within a particular distance value for each mosaic versus that for the average of 100 simulated mosaics with random S-cone placement. The dashed lines represent the maximum and minimum bounds of the random simulations. If the solid line were to lie entirely between the two dashed lines, then the arrangement of the S cones in the hypothetical mosaics would be indistinguishable from random. The clumped mosaic shows significantly more short inter-S-cone separations than expected for a random mosaic, whereas the regularly distributed mosaic exhibits significantly fewer short inter-S-cone separations than the random expectation.

The S cones as a submosaic

As a result of tight packing, the foveal cone mosaic appears crystalline with triangular ordering (Hirsch and Hylton, 1984; Williams, 1988; Hirsch and Curcio, 1989). Thus, in a perfectly ordered mosaic, all foveal cones would have six neighbors. However, in reality, large patches of sixneighbored cones are separated by cones with greater or fewer neighbors (Curcio and Sloan, 1992). Pum et al. (1990) found that S cones were preferentially involved in these mosaic discontinuities. For three of our subjects (YY, JC, AP temporal), the SD of the number of cones surrounding S cones was significantly larger than for L or M cones, as expected if S cones occurred at points of discontinuity in the triangular cone mosaic (data not shown). This would be expected based on differences in the morphology of S cones compared with the L and M cones (Ahnelt et al., 1987; Curcio et al., 1991). In addition, given the topographic variation in S-cone density, it would be interesting to more carefully examine packing geometry as a function of eccentricity.

Table 2 shows the ratio of L to M cones surrounding S cones compared with the expectation based on random S-cone placement. For seven subjects, the ratio of L to M cones surrounding S cones is not significantly different from the overall L:M cone ratio in the mosaic, indicating that S cones show no affinity toward either L or M cones. For one subject (RS), there was a tendency for S cones to preferentially neighbor M cones (p < 0.05). However, this same subject showed L/M cone clumping that could be attributed to the effects of optical blur (see below), thus the association between S and M cones could be a consequence of a small uncertainty in identifying L versus M cones in this individual.

Relative numbers of S cones have been reported previously (Ahnelt et al., 1987; Curcio et al., 1991; Bumsted and Hendrickson, 1999; Roorda et al., 2001). However, the large number of individuals examined with our technique allows an estimate of the interobserver variability in the relative number of S cones at a given retinal location. The average percentage of S cones in this sample (all at ∼1° eccentricity) was 5.72 (Table 1). The SD is very small (±0.69), in striking contrast to the large variability reported for relative proportions L to M cones (see below). Together, the above contrasts between the S and L/M submosaics support the idea that they are formed by separate, and probably independent, processes (Curcio et al., 1991).

Ratio of L to M cones in the human retina

As shown in Figure 4 and Table 1, we found huge variability in L:M cone ratio. For the color-normal males, L:M ratio ranged from 1.1:1 to 16.5:1 (52.7-94.3% L). Remarkably, despite this variation, the subjects were normal on all color vision tests used, highlighting either the insensitivity of the human visual system to variability in L:M cone ratio or the inadequacy of standard color vision tests. Surprisingly, for one subject (AP), the L:M cone ratio was found to be different between two retinal locations. This difference is significantly larger than expected by chance given a binomial probability distribution [1.24:1 and 1.77:1 (55.4 and 63.9% L) in nasal retina and temporal retina, respectively; p < 0.0025]. This demonstrates the existence of large-scale nonrandomness in the L/M submosaic (see below). In addition, we obtained the first direct estimate of L:M ratio in a carrier of a protan color-vision defect. We observed a very low L:M cone ratio (0.37:1; 27% L), which was expected based on her phenotype and genotype (Miyahara et al., 1998). [In females, X inactivation produces, on average, expression of pigment genes from each chromosome in one-half of the cones. Therefore, it is possible to predict the L:M ratio of carriers; assuming an L:M ratio of 2:1 produced by the normal X chromosome, a typical protan carrier would have an L:M ratio of 0.5:1 (33% L).]

Comparison with ERG-derived estimates of L:M ratio

Over the past 60 years, a number of indirect techniques have suggested that there are more L than M cones with intersubject variability in the exact ratio (DeVries, 1946; Rushton and Baker, 1964; Dartnall et al., 1983; Pokorny et al., 1991; Jacobs and Neitz, 1993; Yamaguchi et al., 1997; Hagstrom et al., 1998; Brainard et al., 1999; Kremers et al., 2000; Carroll et al., 2002). However, it has only been with the advent of AO retinal imaging that these techniques have begun to be validated directly in vivo [although Deeb et al. (2000), using postmortem monkey retina, showed that mRNA-derived L:M cone ratios correlate with those inferred from electrophysiological recordings of cone signal gain in H1 horizontal cells]. For example, the relative contributions of the L- and M-cone derived signals to the flicker photometric ERG have been used as an index of the variability in cone ratio among males with normal color vision (Jacobs and Neitz, 1993; Carroll et al., 2002). Recently, Brainard et al. (2000) used the flicker photometric ERG to estimate L:M cone ratio in the two subjects from the original Roorda and Williams (1999) study. They found the ERG-derived estimates agreed with those obtained from direct imaging with AO (Brainard et al., 2000). Their finding supports the hypothesis that individual variability in L:M cone ratio underlies individual variability in photopic luminous efficiency (Brainard et al., 2000). Here, by examining a larger number of subjects with more diverse L:M cone ratios, we were able to more rigorously test this hypothesis.

We obtained L:M cone ratio estimates from the ERG on all eight subjects. We found a very high correlation (r² = 0.98) between L:M ratio determined with AO and that estimated with the ERG (Fig. 7). The ERG estimates of L:M ratio reflect the cone ratio from an ∼70° field, whereas the AO estimates are derived from relatively small (∼0.5°) patches of retina. The close agreement between the two techniques corroborates previous reports that the local ratio of L to M cones varies little within the central ∼70° (Hagstrom et al., 1998; Deeb et al., 2000; Knau et al., 2001) (but see Albrecht et al., 2002). The histogram in Figure 7 shows that the range in L:M cone ratio for our seven male subjects reflects the overall range in the normal male population, based on the previously published ERG results (Carroll et al., 2002).

Despite the high correlation between the two measurements, the slope of the regression line is not 1. The discrepancy can be accounted for by a small systematic error in the L/M-driven neural signals measured with the ERG for which a correction factor can be derived using our AO/ERG comparison. Given the concordance reported for L:M cone ratio estimates from flicker photometric ERG and psychophysical flicker photometry (Kremers et al., 2000), it is likely that this same error exists in psychophysical estimates of L:M ratio. Although we do not know the physiological mechanism of this discrepancy, it is consistent with an ∼1.5-fold larger contribution of the signal from each M cone relative to the signal from each L cone. One possibility is that the L and M cone gains are separately modified by adaptation to the spectral properties of the measuring lights used (Eisner and MacLeod, 1981; Kremers et al., 2003). An immediate implication of this finding is that the average L:M cone ratio across normal humans is slightly higher than proposed previously from indirect methods (2:1 or 66% L), probably more like 2.5:1 (∼71% L). Moreover, the ERG/AO comparison suggests that by enabling a direct count of L and M cones, adaptive optics combined with retinal densitometry provides the first accurate measurements of L:M cone ratio in living humans.

Arrangement of L and M cones in the human retina

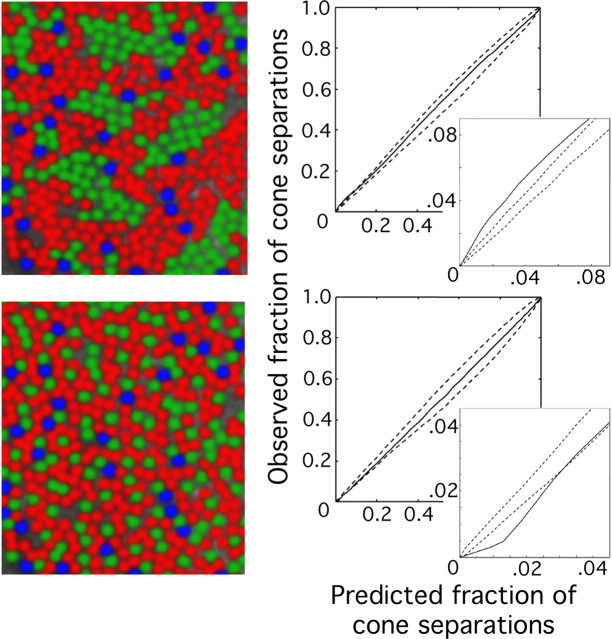
The larger number of cone mosaics, each with a large number of cones, analyzed in the present study compared with previous studies allowed a more rigorous test of the hypothesis that the L- and M-cone submosaics are randomly interleaved. For each of the nine mosaics reported here, cumulative histograms of all inter-M-cone separations (inter-L-cone separations for HS) were compared with those expected if arrangement were random. Figure 8 shows examples of the results of this test for two hypothetical mosaics with clumped and regularly distributed M cones. As with the S cones, mosaics were deemed nonrandom if the rms deviation of the cumulative histogram of intercone distances for the actual mosaic from the average of all simulations ranked above the 95th percentile compared with the same statistic measured for all simulations (p = 0.05) or if the cumulative histogram for the actual mosaic exceeded the bounds set by the 100 random simulations at any point (p = 0.01). Figure 9 shows the result of this test for the L-cone mosaic of HS and the M-cone mosaics of the other subjects. In only one subject (RS) was the rms statistic above the 95th percentile of the same statistic calculated for all random-simulation mosaics. In this subject, the L/M cones are more clumped than random. In three additional subjects (JC, BS, and MD), the cumulative histogram of all inter-M cone distances falls outside the bounds established by the 100 simulated random mosaics in at least one place (p < 0.01), in the direction of a clumped arrangement. The arrangement of L and M cones for the other four subjects is not statistically different from random.

Figure 8.

Examples of cumulative histogram comparison plots for hypothetical mosaics with clumped (top) and regularly distributed (bottom) L and M cones. The solid line is the fraction of inter-M-cone separations within a particular distance value for each mosaic versus that for the average of 100 simulated mosaics with random cone placement. The dashed lines represent the maximum and minimum bounds of the random simulations. If the solid line were to lie entirely between the two dashed lines, then the arrangement of the M cones in the hypothetical mosaics would be indistinguishable from random. The clumped mosaic shows significantly more short inter-M-cone separations than expected for a random mosaic, whereas the regularly distributed mosaic exhibits significantly fewer short inter-M-cone separations than the random expectation.

Figure 9.

Cumulative histogram comparison plots for the M-cone submosaic (L-cone submosaic for HS). The solid line is the fraction of intercone separations within a particular distance value for the actual mosaic versus that for the average of 100 random simulations. The dashed lines represent the maximum and minimum bounds of the random simulations. If the solid line lies entirely between the two dashed, lines then L- and M-cone arrangement is indistinguishable from random.

Optical blur can introduce errors in the identification of the L and M cones, because a fraction of the reflected light from an individual cone will appear to emanate from each of its neighbors. Each cone will therefore appear more like the average of its neighbors; an M cone surrounded by all L cones is more likely to be erroneously classified as an L cone and vice versa. Assignment errors caused by optical blur may result in a mistakenly clumped mosaic (Roorda et al., 2001). To see whether optical blur could account for the observed clumping in our four subjects, the amount of optical blur affecting each subject's images was estimated by computing the average local contrast of cones in retinal images acquired after a full bleach of photopigment. According to this metric, the four subjects whose mosaics appeared clumped ranked within the bottom five mosaics in terms of optical quality (Table 3). This suggests that optical blur could be contributing to the clumpy appearance of the mosaic in these subjects. Indeed, after considering the effects of optical blur (see supplemental material, available at www.jneurosci.org), only two subjects (BS and MD) showed evidence of L/M-cone clumping. In summary, the L- and M-cone arrangement in the human fovea is generally random but can occasionally bias toward clumping.

Table 3.

Average local cone contrast in the retinal region where L, M, and S cones were classified

Subject	Local cone contrast
JCa	0.09
MDa	0.15
AP nasal	0.19
BSa	0.20
RSa	0.21
HS	0.22
AP temporal	0.27
YY	0.31
JP	0.34

^a Subjects whose mosaics exhibited clumping of like-type cones.

Interobserver differences in L:M cone ratio

Interestingly, there appears to be uniformity of color experience across individuals with different L:M ratios. Unique yellow, the wavelength that appears neither reddish nor greenish and represents the neutral point of the red-green color mechanism, is thought to be driven mainly by differences in L and M cone excitation. Several investigators have noted that whereas estimates of L:M cone ratio vary widely, the wavelength that subjects judge uniquely yellow is nearly constant, varying with a SD of only 2-5 nm (Pokorny et al., 1991; Jordan and Mollon, 1997; Miyahara et al., 1998; Brainard et al., 2000; Neitz et al., 2002). In agreement with these studies, measures of unique yellow did not correlate with direct measurements of L:M cone ratio in six of our subjects (HS, YY, MD, JP, JC, and BS; data not shown). Recent evidence suggests that this decoupling between cone ratio and color perception is a consequence of a plastic mechanism that normalizes color experience based on the chromaticity of the environment (Neitz et al., 2002).

In cases of extreme L:M cone ratio, as occurs with nearly all female carriers of color-vision defects and even many males with normal color vision, visual consequences can be more readily observed. For example, there are reports that individuals with extreme L:M cone ratios have compromised color contrast sensitivity (Gunther and Dobkins, 2002) and have greater matching ranges on the anomaloscope than normal (Jordan and Mollon, 1993). As a result of the irregular assignment of L and M cones, these subjects would also tend to have larger patches of effectively color-blind retina (where only one cone class is present) than those with more balanced numbers of L and M cones. Using adaptive optics to present tiny, monochromatic (550 nm) flashes to the retina, Hofer et al. (2005) examined the fraction of spots subjects called white using subjects HS, YY, AP, MD, and BS. Consistent with the hypothesis in which larger patches of color-blind retina would lead to an increased fraction of white responses, they found that as the L:M cone ratio became more skewed, the fraction of white responses indeed increased.

Discussion

Implications of L/M cone arrangement for vision

The random arrangement of L and M cones typically observed may be the compromise of the visual system between the needs of spatial and color vision. As shown in Figure 4, a random cone arrangement gives rise to relatively large patches of retina in which only the L or M cone class is present. Although this patchiness can be disadvantageous for foveal color vision, it is likely beneficial for peripheral color vision and for high-acuity spatial vision, because neurons responsive to high spatial frequencies are more likely to draw their input from cones of the same spectral type, thus avoiding the confounding of spectral and spatial information. There will also be retinal locations for which the resolution of the M- or L-cone submosaic ought to be as high as for the full mosaic. This is likely to be the reason why acuity measured with stimuli that are visible to only L or M cones is not worse than acuity based on the entire mosaic (Green, 1968; Cavonius and Estévez, 1975; Williams, 1990; Carroll et al., 2004). A patchy cone arrangement may have the additional advantage in helping to ameliorate the spectral blurring that occurs as a result of electrical coupling between neighboring cones (Hsu et al., 2000; DeVries et al., 2002; Hornstein et al., 2004).

In the peripheral retina, there is convergence so that several neighboring cones drive the center of a midget ganglion cell (Dacey, 1999). This will result in a weakening of chromatic opponency if more than one cone type contributes to the ganglion cell center, and thus red-green color vision would be expected to deteriorate in the periphery. The patchiness in the mosaic that results from random L- and M-cone arrangement would lessen the negative effects of this neural convergence, because it makes it more likely that some peripheral midget cone centers will be driven by cones of the same spectral type. This could explain why color discrimination in the periphery is as good as in the fovea if large enough stimuli are used (Gordon and Abramov, 1977; Noorlander et al., 1983; van Esch et al., 1984; Abramov et al., 1991), although peripheral color vision is significantly disadvantaged for smaller fields (Noorlander et al., 1983; Mullen, 1991).

Despite this apparent advantage for peripheral color discrimination, these patches can be detrimental for color vision, because the retina is effectively color blind within them. The irregularity of L- and M-cone arrangement exacerbates the confounding of spatial and chromatic information on small scales, leading to errors in color appearance for fine spatial patterns (Williams et al., 1991). One example is the Brewster's colors phenomenon, in which irregular splotches of pastel colors are seen when viewing fine periodic black and white patterns (Brewster, 1832). Similarly, fine isoluminant chromatic patterns can appear as luminance and chromatic spatial noise (Sekiguchi et al., 1993). Another example is that subjects routinely misjudge the color appearance of tiny flashes of monochromatic light (Holmgren, 1884; Hartridge, 1954; Krauskopf, 1964, 1978; Cicerone and Nerger, 1989; Hofer et al., 2005).

Mechanisms that determine the relative numbers and arrangement of L/M cones

Although the departures from randomness may not have a large practical impact on color vision, the existence of nonrandomness can help us understand the process that forms the mosaic. Our data reveal that at least in some eyes, a developmental mechanism exists that creates departures from randomness. Previously, it was suggested that the L/M cone mosaic may depart from randomness on a large spatial scale by the increase in the L:M ratio in the far periphery of the human eye (Hagstrom et al., 1997, 1998; Bowmaker et al., 2003). We also observed a departure from random assignment of photopigment on a large spatial scale in subject AP whose L:M ratio was 1.24 (55.4% L) in nasal retina and 1.77:1 (63.9% L) in temporal retina. Deeb et al. (2000) reported a similar nasal-temporal asymmetry in L:M cone ratio in the monkey retina. Conversely, Roorda and Williams (1999) found very similar L:M cone ratios at two foveal locations in one subject (subject JW). Because there are only two human subjects for whom the ratio of L and M cones has been measured directly in more than one retinal location, we do not know how typical the variation observed in AP is. However, mRNA (Hagstrom et al., 1998; Deeb et al., 2000) and heterochromatic flicker photometry (Knau et al., 2001) estimates of L:M ratio at different locations in the same eyes would suggest that it is relatively constant within the central retina of most eyes. In two subjects, we observed departures from randomness on a small spatial scale in the direction of L/M cone clumping.

The appearance of the adult mosaic is likely a result of the interplay between at least two processes during development: the mechanism of cone cell-type differentiation, which must include a nonrandom element and a tendency toward clumping, and cell migration, which works to disrupt these clumps.

The role of cell migration

The developmental processes that determine whether a cone will be M or L in a normal eye remain primarily unknown. However, the protan carrier examined here represents a special case in which the production of L versus M cones is determined, in part, by a well characterized mechanism, inactivation of the X chromosome containing the normal opsin gene array. On average, in these carriers, one-half of the nascent L/M cones can express only M pigment from the protan gene array. X inactivation ensures that developing cells of a female, each of which have two X chromosomes, do not express twice the required amount of gene product. To be effective, this process must be initiated very early in development; in humans, this is at the 5- to 10-cell stage (Ray et al., 1997). As the eye grows, the daughter cells always inactivate the same X chromosome as their progenitors. If the cells maintain their relative positions through development, this would lead to patches containing only M cones and patches of normal mixtures of L and M cones in the protan carrier (Lyon, 1961; Wald et al., 1974; Born et al., 1976; Cohn et al., 1989). Although such patchiness has been observed in genetically engineered mice with three cone types (Smallwood et al., 2003), it was not seen here, consistent with the results of Bowmaker et al. (2003) on the marmoset, those of Mollon et al. (1984) on the squirrel monkey, and those of Lee et al. (2000) on the capuchin monkey. Our human protan carrier contained a skewed ratio of L:M cones as predicted from her genotype, but the L and M cones were intermixed and indistinguishable from a random arrangement. In this protan carrier's retina, in which the developmental choice of a cone to be L versus M is known to involve a process (X inactivation) that often leads to clumping, it is curious that no evidence of clumping is detectable in her foveal cone mosaic.

Perhaps the random arrangement of cones in the protan carrier eye is the result of intermixing of the inactivation patches during development, completely obscuring the fact that differentiation of L versus M cones in that eye involved a process that might otherwise lead to clumping. In the primate, one mechanism that could break up clumps from X inactivation is the migration of cones involved in the formation of the fovea (Hendrickson and Yuodelis, 1984; Yuodelis and Hendrickson, 1986; Diaz-Araya and Provis, 1992). This mechanism would predict that departures from randomness would be more obvious in the peripheral retina, which is less effected by foveal migration. Indeed, Packer et al. (1996) found significant clumping in the L and M cones of a nonhuman primate in peripheral retina, consistent with this hypothesis. Additional, circumstantial evidence that foveal cone migration disrupts nonrandom packing comes from Curcio's analysis of S-cone topography. She showed that peripheral S cones space themselves regularly in the peripheral mosaic, whereas near the fovea the arrangement tends toward randomness (Curcio et al., 1991). Whatever the mechanism is that establishes the regularity of the S-cone mosaic, such as perhaps tangential dispersion (Reese et al., 1999), it apparently cannot withstand the disruptive effects of cell migration during foveal development.

Nonrandomness in L versus M gene choice

Nathans (1999) suggested that, in the normal retina, L- versus M-gene expression is mediated by a random process. He proposed that in each cell, the L/M gene array locus control region forms a complex with the promoter of either an L or an M gene, thereby committing that cell to exclusively expressing one opsin gene. In males with only a single X-linked L/M gene array, this predicts an entirely random arrangement of these two cone classes. Contrary to expectation, the three departures from randomness reported in the present study all happened to occur in males. X inactivation cannot account for these departures from randomness, because males only have a single X chromosome. The clumping observed must therefore involve some other nonrandom process. This process is probably active in all normal human eyes, but the residual clumping may depend on several factors including the final ratio of L versus M cones, the relative timing of L/M gene expression relative to the formation of the fovea, or the amount of photoreceptor migration (Springer and Hendrickson, 2005).