Position, Direction of Movement, and Speed Tuning of Cerebellar Purkinje Cells during Circular Manual Tracking in Monkey

Abstract

The cerebellum plays an essential role in pursuit tracking with the eye and with the hand. During smooth pursuit eye movements, both tracking position and velocity are signaled by Purkinje cells. Purkinje cell simple spike discharge is also modulated by direction and speed during linear manual tracking. This study evaluated how all three parameters, position, movement direction, and speed, are signaled in the simple spike discharge of Purkinje cells during circular manual tracking.

Three rhesus monkeys intercepted and then tracked a target moving in a circle in both counterclockwise and clockwise directions across a range of constant target speeds. Two sets of analyses of the simple spike firing of 97 Purkinje cells examined the effects of position, movement direction, and speed. The first approach was the incremental improvement of regression models, initially modeling a pure position dependence, then incorporating movement direction, and finally incorporating speed dependence. The second was a model-independent approach, without any explicit assumptions about the character of the directional tuning or speed effects. Both analyses revealed the same three results: (1) Purkinje cell discharge is spatially tuned, to both the position and direction of movement, and (2) this spatial tuning is not altered by the speed, except (3) the speed scales the average firing and/or depth of modulation.

The results suggest that the population of Purkinje cells forms a representation of the entire position-direction space of arm movements, and that the speed modulates the scale of that representation. This speed scaling provides insights into the cerebellar processing of movement-related timing.

Introduction

Our ability to accurately track a small moving target with our eyes requires the cerebellum (Lisberger and Morris, 1987; Keller and Heinen, 1991). Electrophysiological, lesion, and imaging findings also implicate the cerebellum in manual tracking (Marple-Horvat and Stein, 1987; Miall et al., 1987, 2000, 2001; Vercher and Gauthier, 1988; van Donkelaar and Lee, 1994; Coltz et al., 1999). Psychophysical studies suggest that manual and oculomotor tracking use similar control signals and may share common neural resources (Viviani and Campadelli, 1987; Engel et al., 1999; Scarchilli and Vercher, 1999; Engel and Soechting, 2000). However, much less is known about the role of the cerebellum in pursuit tracking with the hand, particularly about the underlying neural mechanisms.

Early studies of single joint tracking movements found that Purkinje cell simple spike and cerebellar nuclei discharge had some directional modulation but no clear relationship to speed or position (Mink and Thach, 1991). During multijoint tracking, however, both direction and speed were shown to be signaled by the simple spike discharge (Marple-Horvat and Stein, 1987; Coltz et al., 1999). The contributions of position, movement direction, and speed and their interaction to the discharge of cerebellar neurons during reaching or tracking limb movements has not been determined (Fortier et al., 1989; Fu et al., 1997; Coltz et al., 1999). Most cerebellar studies have used a “center-out” task, in which the position and velocity vectors are aligned, making dissociation between them impossible. Furthermore, in our previous reaching movements studies, amplitude and speed were highly correlated (Fu et al., 1997). Our first goal was then to examine the encoding of position and the movement direction by having monkeys track a circularly moving target in both counter-clockwise (CCW) and clockwise (CW) directions (Leung et al., 2000). Purkinje cells encoding only position will have their maximal discharge at the same place on the circle for both CCW and CW tracking direction. Cells encoding only movement direction, however, will have their maximal discharge at positions 180° apart between CCW and CW tracking. Finally, for cells tuned to both position and movement direction, the shift in the position of maximal firing will be between 0 and 180°.

Another critical parameter of movement is the speed. The cerebellum has been implicated in controlling the speed of limb movements based on electrophysiological (Marple-Horvat and Stein, 1987; Coltz et al., 1999), behavioral (Beppu et al., 1984; Miall et al., 1987; Hore et al., 1991), and imaging (Turner et al., 1998; Lewis et al., 2003) findings. Speed is also of interest because of its inherent relation to movement timing in which the cerebellum has been hypothesized to play an important role (Braitenberg, 1967; Ivry and Keele, 1989; Thier et al., 2000). Movements at higher speeds require going through the same trajectory on a shorter time scale. Understanding how speed is represented in the cerebellum may provide insights into the role of the cerebellum in controlling timing. Therefore, the second goal was to determine how varying tracking speed affects positional and/or directional tuning of Purkinje cells.

Materials and Methods

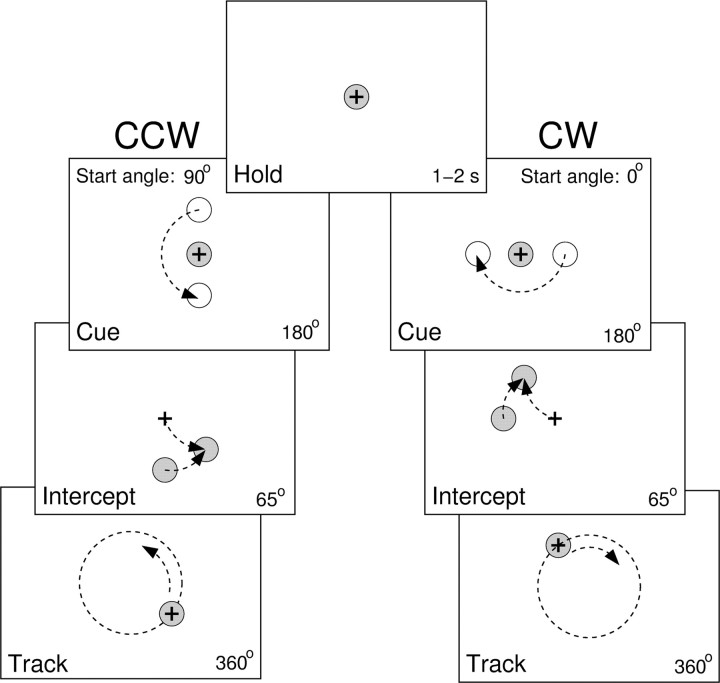
Behavioral task. Experimentation was conducted in accordance with the Policy on the Use of Animals in Neuroscience Research as endorsed by the Society for Neuroscience and was approved by the Institutional Animal Care and Use Committee of the University of Minnesota. Three female monkeys (H, M, and P, Macaca mulatta, 5-6 kg) were trained to use a two-jointed manipulandum to make visually guided arm movements in the horizontal plane (Fu et al., 1997; Coltz et al., 1999). Because the task has been described previously (Roitman et al., 2004), only a brief description is provided. The task included interception of a circularly moving target from a centrally located “hold” target and subsequent visually guided pursuit of the target for one rotation (Fig. 1). The trial sequence was initiated when the monkey held the cursor (1 cm black crosshair) on the hold target (1.8-cm-diameter red circle) for a random time between 1 and 2 s (hold period). A cue target (2.5-cm-diameter yellow circle) then appeared at a radius of 5 cm and moved around a circle (CCW or CW direction) centered on the hold target as the monkey maintained the cursor in the hold target (cue period). After 180° of circular travel, the cue target changed color (from yellow to red), signaling the onset of interception. The monkey had 65° of target travel to intercept the circularly moving target (intercept period). After intercepting the target, the monkey continued to track the target for another 360° (track period). Target speed, start angle, and direction were independently varied in a randomized, blocked manner. In monkey H, the target speeds ranged from 3.1 to 8.3 cm/s, with increments of either 1.7 or 1.3 cm/s. In monkeys M and P, the target speeds ranged from 4.3-9.6 cm/s in 1.3 cm/s increments. The difference in target speed reflected the performance limitations of monkey H at higher speeds. Start angle of the cue period varied from 0° to 270° in 90° increments. For each trial type, 10 repetitions were obtained for a total of 400 trials per experiment (2 directions × 4 start angles × 5 speeds × 10 repetitions). At any point in the trial sequence, deviation of the cursor from the hold or moving target aborted the trial. The monkeys could see their hand and the manipulandum, but the task requirements demanded that they view the vertically positioned monitor.

Figure 1.

Schematic of the circular manual tracking task. Hold period, Animal maintains the crosshair cursor inside a hold target for a random time between 1 and 2 s. Cue period, Animal maintains the cursor inside the hold target through 180° of the cue target travel. Intercept period, Animal has 65° of the target travel to intercept the target. Track period, Animal has to track the target through 360° of target travel. Tracking direction, start angle, and speed were independently and systematically varied between trials. Left, Example CCW tracking with a start angle of 90°. Right, Example CW tracking with a start angle of 0°.

Data acquisition and initial processing. Position data were acquired at 200 samples/s with precision potentiometers and were used to drive the cursor position on the monitor (Fu et al., 1997; Coltz et al., 1999). Velocity was calculated by numerical differentiation of the position and was filtered using a low-pass filter (12 Hz cutoff, 12th-order Butterworth) applied successively in forward and reverse directions to preserve the phase of the signal. This cutoff frequency was chosen to retain the physiological frequencies of the primate arm movements (Roitman et al., 2004). Speed and direction of movements were computed from the filtered velocity record.

Eye movements were recorded during some experiments using a high-frequency CCD video camera (200 frames/s) and a digital frame-grabber acquisition card (Thomas Recording, Giessen, Germany). Eye movements were then filtered using a 12 Hz low-pass filter, and the saccades were manually removed from the track period before averaging to yield the smooth pursuit component.

Intramuscular EMG recordings were obtained from 11 different shoulder, elbow, and wrist muscles during several experimental sessions in which neurons were not recorded. The recordings were made using metal electrodes from the following muscles: latissimus dorsi, pectoralis, cleidodeltoid, spinodeltoid, biceps, triceps, extensor carpi radialis and ulnaris, flexor carpi radialis and ulnaris, and brachioradialis. EMG signals were bandpass filtered on-line (100 Hz to 3 kHz) and amplified and then digitized at 6000 samples/s. The EMG data were digitally full-wave rectified and averaged over trials. For each recording session, the EMG activity from each muscle was normalized by the maximal activity of that muscle during the session.

The recording chamber was placed over the parietal cortex ipsilateral to the tracking arm, using antiseptic conditions and full surgical anesthesia (Coltz et al., 1999). The chamber was stereotaxically positioned to target the electrode recordings in the intermediate and lateral zones of lobules V-VI in which arm-related Purkinje cells have been described previously (Thach, 1968; Ojakangas and Ebner, 1992; Fu et al., 1997). Electrode targeting was subsequently verified by computerized axial tomography scanning. After full recovery, Purkinje cells were recorded extracellularly using paralyene-coated tungsten microelectrodes and identified by the presence of complex spikes (Thach, 1968; Ojakangas and Ebner, 1992; Fu et al., 1997). In monkey P, independent microdrives were used to position two electrodes simultaneously. Because of the large number of trials and their long duration (between 8 and 20 s), it was necessary to focus on optimizing the discrimination of the simple spikes, the primary interest of this study. Conventional techniques were used to amplify the spike waveforms before the discrimination of simple spikes. The discrimination was performed on-line using the Multiple Spike Detector system (Alpha-Omega Engineering, Alpharetta, GA), and the resulting spike trains were digitized and stored at 1 kHz. Both kinematic and spike train data were collapsed to 20 ms bins and averaged over 10 repetitions of the same parameters (i.e., trials with identical speed, direction, and start angle).

The experimental design included four start angles. The first step in the analysis averaged the 360° of the track period data across trials for each start angle. Next the firing was fitted to the position model described below (Eq. 1), and the dependence of the amplitude and the direction of the b_p vector (|b_p| and φ_p) on the start angle was evaluated. As described in Results, there were no significant differences in either |b_p| or φ_p across the four start angles. Therefore, the track period data were averaged over the four start angles across trials with the same speed and direction. The procedure was performed after aligning the track period data based on the angular position of the hand. The first 90° of the track period were discarded from this averaging to ensure that any intercept-related discharge transients had settled. Thus, each of the four start angles contributed three-quarters of circular tracking to the average, effectively yielding an average of 30 complete rotations of the track period (10 repetitions × 4 start angles × ¾ circle). The averaged track period data were further collapsed into 36 bins (10° each), resulting in a uniform number of data points for trials with different speeds. The duration of each bin was therefore dependent on speed and ranged from 91 ms (9.6 cm/s) to 282 ms (3.1 cm/s).

The cue period data were also averaged over the four start angles, similar to the track period. The entire 180° of the cue period was included, yielding an average of 20 complete rotations (10 repetitions × 4 start angles × ½ circle). The data from intercept period were not averaged over the start angles because the hand movements did not overlap.

Qualitative testing for passive arm movements was performed at the end of some neural recording sessions. The Purkinje cell activity was examined for modulation in response to brisk movements of the shoulder, elbow, and wrist joints of the monkey's arm performed by the researcher.

Analysis of simple spike firing during the track period. Several regression models of simple spike discharge as a function of task parameters were evaluated to sort out the contributions of position, movement direction, and speed. The goal was to obtain a model that reasonably fitted the data without an excessive number of parameters. Two of the models (Eqs. 2, 5) were aimed at dissociating position and movement direction as discussed in Introduction.

In the first model, the averaged simple spike firing (36 bins) from the track period for each direction and speed was fitted to a position model based on cosine tuning (Georgopoulos et al., 1982). We modified this model using a unit position vector because the radius of tracking was held constant throughout the study:

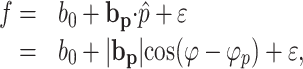(1)

where f is the simple spike discharge rate, p̂ = P/|P| is the unit position vector of the target, and b_p is the positional sensitivity vector of the cell. Note that, in this and following equations, the variables are functions of the 10° bins. Similar regression models based on time-varying neural activity as a dependent variable have been applied to motor cortical and cerebellar neural data (Ashe and Georgopoulos, 1994; Ebner and Fu, 1997). In this model, φ_p represents the point on the circle at which the cell discharge is maximal, and 180° from φ_p is where the cell firing is minimal. In this and the following regression models, target kinematics were used as the predictor for two reasons. First, the average hand kinematics were essentially identical to those of the target during track period because of the nature of the task (Roitman et al., 2004). Second, test regressions performed on the hand kinematics revealed virtually no difference from those performed on the target kinematics. Therefore, the target kinematics were used for simplicity.

The position model (Eq. 1) worked well for fitting the simple spike firing from a single type of trial (one direction at one speed) for most Purkinje cells. However, this model was not adequate for fitting the firing during tracking in both CCW and CW directions with a single set of parameters b₀ and b_p (see Results), implying that the simple spike discharge was also modulated by the direction of movement. Therefore, another model was examined that appended a similar unit velocity term to the position model. This model is similar to that previously used for two-dimensional smooth pursuit eye movements (Leung et al., 2000) and is described by the following equation:

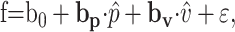(2)

where v̂ = V/|V| is the unit vector of target velocity, and b_v is the velocity sensitivity vector for a given cell. Note that unit velocity is equivalent to the movement direction, and these terms will be used interchangeably. The directions of b_p and b_v determine the preferred angular position (PAP) and preferred movement direction (PMD), respectively:

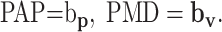(3)

The magnitudes of b_p and b_v were used to determine the relative dependence of the firing on position versus movement direction by computing an index of position-velocity contribution:

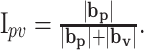(4)

By definition, the value of I_pv is always between 0 (pure movement direction tuning) and 1 (pure positional tuning). The fit of the firing to this model was performed both at each tracking speed and across speeds. Equation 2 is referred to as the unit position-velocity (UPV) model. Also tested was a variant of the UPV model using only the following unit velocity term: f = b₀ + b_v · v̂ + ϵ. This allowed us to test how critical the position term was by comparing the results of fitting this direction-only model with those of the full UPV model.

The examination of speed dependence of the parameters of the UPV model fitted separately at every target speed revealed that the b₀, |b_p|, and |b_v| were modulated by the speed, whereas PAP and PMD were not. Therefore, a final model was proposed to describe the behavior of Purkinje cell discharge across the entire set of experimental conditions. This model is referred to as the UPVS model and is described as follows:

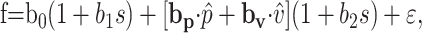(5)

where s denotes the target speed. The UPVS model accounts for speed modulation of both the overall average firing rate (via b₁) and the modulation depth (via b₂) of the speed-invariant UPV profile.

Using standard regression techniques, the significance of the fits for the models (Eqs. 1, 2, 5) was assessed for the overall fit and for the individual terms (F statistic, α = 0.05). Total and partial R² values were also determined. Comparisons between the models were based on adjusted R² values to accommodate the difference in the degrees of freedom (5 for UPV model, 7 for UPVS model). The adjusted R² values were computed as follows:

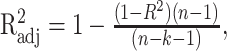(6)

where n is the number of data points used in the fit, and k is the number of degrees of freedom of the model.

Because the comparative analysis favored the UPVS model, this model was used for the rest of the study. The position and velocity sensitivity vectors, b_p and b_v, were obtained from the resultant fits of Equation 5. The PAP, PMD, and I_pv were determined using Equations 3 and 4, respectively.

The firing during the cue period was also fitted using the UPVS model (Eq. 5). Similar to the track period, the significance was determined for the overall fit as well as for the individual terms (F statistic, α = 0.05). Again, total and partial R² values were obtained and adjusted for the degrees of freedom. This analysis allowed an initial assessment of the degree to which target motion contributed to the simple spike modulation. To then examine whether the modulation during the cue period could account for the modulation during the track period, an additional analysis was performed. Based on the parameters obtained from the UPVS model for the cue period, the predicted firing during the track period, f_pred, was computed using position, movement direction, and speed of the target during the track period. Then the residual firing, f_res (the difference between the actual and predicted firing, f_res = f - f_pred), was fitted to the UPVS model. The resulting fits performed on the residuals were analyzed to determine the amount of variance during the track period accounted for by the target motion.

A model-independent analysis of the firing from the track period was also performed to confirm the basic tuning properties independent of the above models. As described in Results, some Purkinje cells exhibited nonlinearities in their simple spike firing patterns that were not fully captured by any of the models. The model-independent approach was undertaken to minimize the assumption of linear responses and to ensure that the findings were not dependent on the models studied. This additional analysis evaluated three properties of the tuning as functions of tracking direction and speed. First, to determine whether the positions of the maximum and minimum discharge were functions of speed, pairwise cross-correlations were computed for each pair of firing profiles at different speeds, separately for CCW and CW tracking. The cross-correlation method can capture the angular shift of any tuning pattern, not just harmonic or unimodal patterns. The maximum correlation corresponds to the best match between two discharge patterns, and the associated lead/lag was used as a measure of the angular shift between the pair of firing profiles. Second, to determine whether the positions of the maximum and minimum discharge were functions of the direction of movement, the cross-correlations were computed between the CCW and CW discharge profiles at each tracking speed. The lag corresponding to maximum correlation was determined and provided a direct measure of the angular shift between firing profiles for the two directions of movement. Finally, the average firing and modulation depth were determined for each experimental condition. The modulation depth was computed as the difference between minimum and maximum firing rate. The minimum and maximum firing rates were calculated as the lowest and the highest values, respectively, of a three-bin sliding average of the discharge data.

Predicting simple spike firing during the intercept period. The simple spike discharge of the intercept period could not be fitted with the regression models because the intercept period did not span a substantial portion of the position-velocity space. Instead, the parameters obtained from the model fitted on the track period data for each cell were used to predict the firing during the intercept period. There were two goals for this analysis. The first goal was to test whether the discharge tuning inferred from manual tracking holds true for the interception as well. It must be noted that the time course of speed profile is very different between intercept and track periods, making this a nontrivial test. The second goal was to determine the timing relationship (lead or lag) between the firing and the kinematics. Circular tracking cannot provide this information because any time lead or lag can be equivalently explained by corresponding rotation of the sensitivity vectors b_p and b_v.

The fitted parameters of the UPVS model (b₀, b_p, b_v, b₁, and b₂) were used in conjunction with the actual hand kinematics (p̂, v̂, and s) during intercept to produce predicted firing. The similarity between the predicted and the actual firing data were measured by computing their correlation coefficient.

The correlation between the predicted and the actual discharge improved when a delay between the firing and the kinematic parameters was introduced as follows:

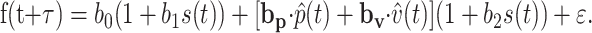(7)

Initially a wide range of delays were evaluated (-500 to 500 ms). However, for delays greater than ±200 ms, the delays at which the maximum correlation occurred tended toward the extreme values. The physiological relevance of such delays is questionable. Therefore, the delay values studied were restricted to the range of -200 to 200 ms in 20 ms increments. For each delay τ, a regression was performed based on the track period data to yield a set of parameters. Then the reconstruction of firing for both the intercept and track periods was performed using Equation 7. Finally, the correlation was computed between the reconstructed and the actual firing, and the optimal τ was selected as the one resulting in the maximum correlation. The distribution of the optimal delays across the population of Purkinje cells was analyzed.

Note that the reconstruction was performed and compared with the actual discharge for each start angle and not on the data averaged over four start angles. This is because the hand positions and directions during the intercept periods were completely different across start angles.

Histology. After the completion of all neural, muscle, and eye movement recordings, electrolytic lesions were made at selected chamber coordinates. The following procedures were performed on two monkeys (H and M). The third monkey (P) had identical recording targets and is still being studied. The animals were initially anesthetized with ketamine/xylazine, followed by an intraperitoneal injection of pentobarbital sodium (150 mg/kg) to produce a deep anesthesia. The animals were then perfused with saline containing heparin, followed by Zamboni's fixative (Coltz et al., 1999). After removal, the cerebellum was postfixed in Zamboni's fixative. The cerebellum was then sectioned (50 μm) and stained with thionin to recover lesions and electrode tracks.

Results

Task-related kinematics

All three animals successfully intercepted and tracked the target with the hand in this error-constrained task. Figure 2 shows averaged hand movement trajectories (A), hand speed profiles (B), and eye movement traces (C) for five target speeds (monkey H). The hand position trajectories closely followed the target except for small undershoots or overshoots during the interception. Hand speed consisted of an initial bell-shaped profile during the intercept period, followed by subsequent smaller-amplitude fluctuations around the required target speed during the track period. The task design ensured that the position and velocity of the target were linearly independent, because these two parameters differed in phase by 90°. This is also true for the actual hand kinematics, because the averaged hand movement data were essentially identical to the target movement (see Materials and Methods).

Figure 2.

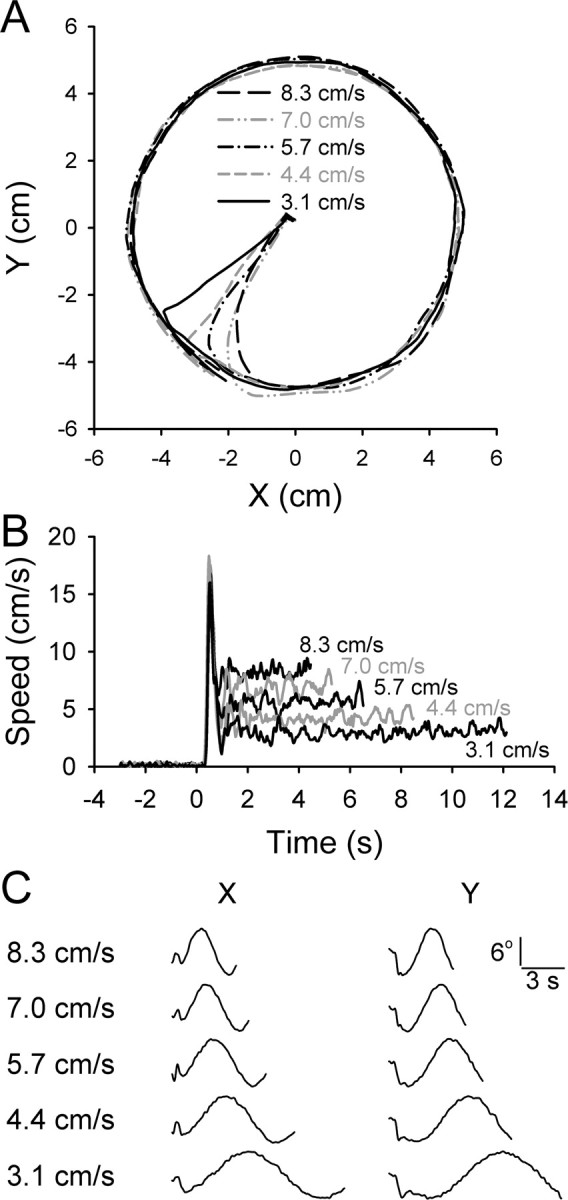
Movement kinematics during the task. A, Example trajectories including intercept and track periods at each of the five speeds as indicated. Each trajectory is the average of 10 trials, with the target moving in a CCW direction with the start angle of 0°. B, The average speed profiles from the same trials shown in A. Initial peak in speed is during the intercept period, followed by the track period speed. C, The horizontal (x) and vertical (y) components of eye movements averaged over four to five trials. The initial component is the eye movement during the intercept period followed by the smooth pursuit.

Both x and y components of the eye movements closely followed the cursor during the track period, indicative of smooth pursuit behavior. During the intercept period, the eyes used both saccades and smooth pursuit movements to follow the cursor.

The delay in the initial speed increase relative to the target speed reflects the reaction time (Fig. 2B). Using a speed threshold of 3 cm/s, the average reaction times were 370 ± 71 ms for monkey H, 263 ± 148 ms for monkey P, and 184 ± 127 ms for monkey M. Throughout the paper, linear variables are reported as mean ± SD and circular variables as circular mean ± angular dispersion (Batschelet, 1981). Monkey M attempted to predict the onset of the interception by beginning to move during the cue period (yet staying within the hold target) to a considerably larger extent than did other animals. Therefore, a considerable fraction of the reaction times of monkey M were lower than those of H and P.

Neuronal database and basic response properties

The simple spike discharge recordings of 134 Purkinje cells were obtained from the three animals (42 from monkey H, 18 from M, and 74 from P). Of these, 97 Purkinje cells (72%) were modulated during the track period based on a criterion of R² ≥ 0.2, using Equation 1 for each speed-direction condition. The remainder of Results focuses on the analysis of the discharge of these 97 cells. Passive arm movement testing was performed for 27 of these cells. Twenty-four cells were categorized as modulated in response to passive movements about at least one joint of the animal's arm. In three cells, passive movements about any joint did not evoke obvious changes in firing.

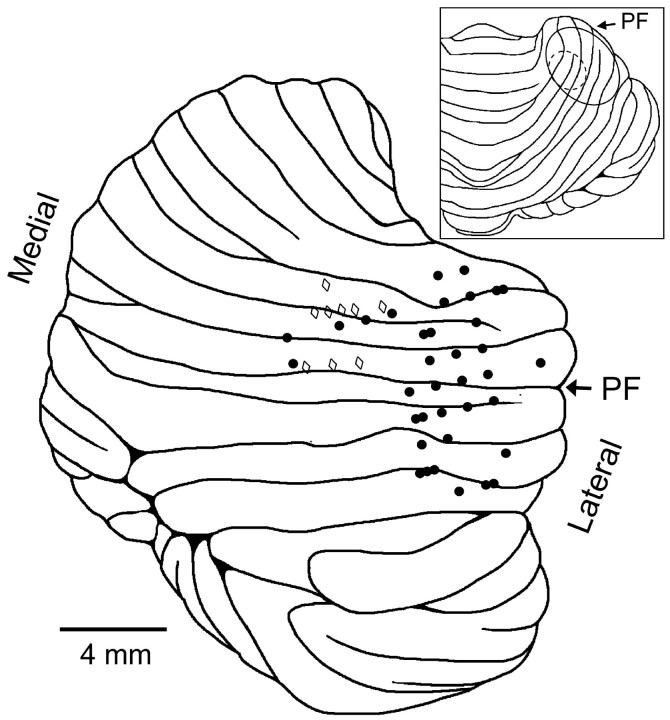
The histological results show that, for monkeys H and M, the analyzed cell recordings were centered on the primary fissure. The majority of the recordings in animal M were in the intermediate zone of lobules IV and V (Fig. 3). The recordings in monkey H were more lateral in lobules IV-VI. The location of the recordings are consistent with previous studies that observed motor- or visuomotor-related Purkinje cell discharge in tasks involving visually guided arm movements (Marple-Horvat and Stein, 1987; Fu et al., 1997; Coltz et al., 1999; Liu et al., 2003).

Figure 3.

Recording sites in two animals, H and M. Shown is the lateral view of the cerebellum with the locations of electrode penetrations for monkey H (filled circles, right side of the cerebellum) and those for monkey M (open diamonds) mapped from the actual side (left) to the right side of the cerebellum. The primary fissure is marked with the arrow labeled PF. Only recording sites for the 46 cells used in the analysis from H and M are displayed (some recording sites correspond to several cells). Inset shows dorsal view of the cerebellum, with the ovals denoting the penetration regions for animals H (solid line) and M (dashed line).

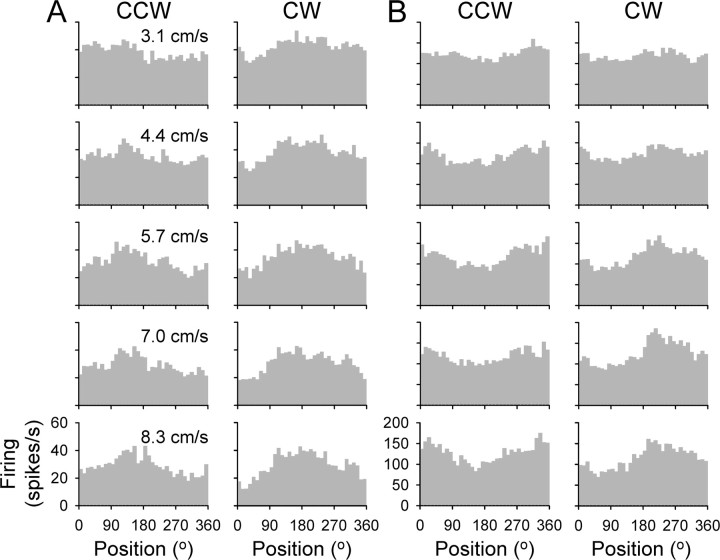
The discharge histograms for two example Purkinje cells are plotted against angular hand position in Figure 4, A and B. Plotted are the track period data across all experimental conditions, showing both directions and all speeds of tracking. Examination of these histograms reveals three properties: (1) the positions of the maximum and minimum discharge differ between CCW and CW tracking; (2) these positions are not affected by tracking speed; and (3) speed affects the average and/or the modulation depth of the discharge rate. For example, the simple spike discharge for the Purkinje cell in A is maximal at 133 ± 27° for CCW tracking and at 174 ± 26° for CW tracking. The firing for the Purkinje cell in B is maximal at 334 ± 13° for CCW tracking and at 218 ± 20° for CW tracking. These shifts in the position of maximal firing demonstrate that the simple spike discharge of these two cells signal a combination of hand position and movement direction.

Figure 4.

Histograms of the simple spike discharge from two example Purkinje cells. A, Track period firing for CCW (left column) and CW (right column) tracking across all target speeds (3.1, 4.4, 5.7, 7.0, and 8.3 cm/s, top to bottom row) for one example Purkinje cell. B, Same for another example Purkinje cell. Histograms represent the average firing rate in 10° bins and are the average of 30 trials.

Speed did not affect the position of the maximal modulation. However, the depth of modulation for both cells increased with speed, from 15 ± 4 to 24 ± 5 spikes/s for the cell in A and from 35 ± 10 to 78 ± 4 spikes/s for the cell in B. Also for the Purkinje cell in A, the average firing decreased with increasing speed (from 40 ± 3 to 29 ± 1 spikes/s), whereas for the cell in B, the average firing changed little with speed (from 120 ± 3 to 121 ± 8 spikes/s). Below we quantitatively examine these properties across the population of recorded cells.

Contributions of position, movement direction, and speed to the discharge

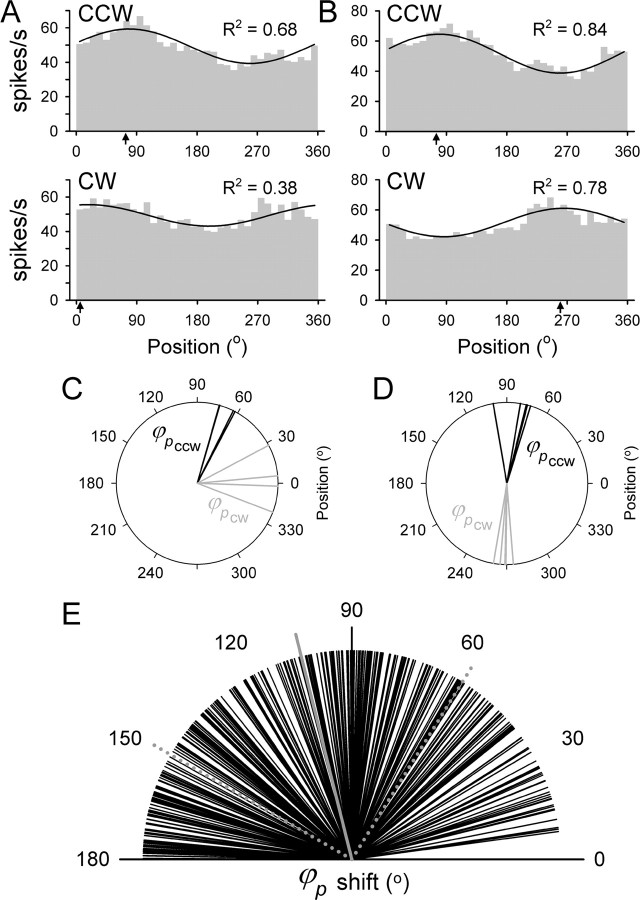
Simple spike firing during the track period was initially fitted to the position model (Eq. 1) at each start angle. Neither the φ_p (Watson-Williams test, p > 0.05) nor the amplitude of the position tuning (ANOVA, p > 0.05) depended on the start angle of tracking. Therefore, additional analyses were performed on the data averaged over four start angles, as described in Materials and Methods, unless stated otherwise. Next the model was fitted separately for different directions of tracking (CCW and CW) at each target speed. If the simple spike firing was solely position dependent, then changing the direction of tracking would not alter the modulation. However, this possibility was quickly rejected. As demonstrated for the two Purkinje cells shown in Figure 5, the simple spike discharge was highly dependent on the direction of tracking, shifting the position of their maximal discharge (φ_p in terms of Eq. 1) between CCW and CW tracking. For the first cell, the φ_p shifted from 73.9° for CCW tracking to 5.2° for CW tracking (Fig. 5A). For the second cell, the φ_p shifted from 75.2° for CCW tracking to 260.5° for CW tracking (Fig. 5B). This shift in the φ_p obtained from the position model was observed and similar across the different speeds (Fig. 5C,D). Therefore, movement direction contributed to the simple spike discharge of both cells.

Figure 5.

Illustration of the pure position model. A, B, Plotted are the histograms and fits for the two Purkinje cells shown in Figure 4 for CCW and CW tracking for the speeds of 6.5 cm/s (A) and 7.0 cm/s (B). The arrows on the abscissa denote the φ_p based on the model. C, D, The φ_p for the CCW (black) and CW (gray) tracking are determined separately for each direction at each speed, for the Purkinje cells in A and B, respectively. E, Shift in the φ_p between CCW and CW tracking for all target speeds across the population of cells. The solid gray line is the mean difference, and the dotted gray lines are the angular dispersion.

Both the change in the φ_p as a function of tracking direction and consistency of φ_p across speeds for a given direction were observed for the population of 97 cells. The average φ_p difference between CCW and CW tracking (absolute value modulo 180°) was 104 ± 46° (Fig. 5E), demonstrating that most cells signal a contribution of position and movement direction. Using circular statistics (Batschelet, 1981; Fisher, 1993), there were no significant differences found in the φ_p across different target speeds for 71% of cell-direction combinations (Watson-Williams test, p > 0.05). A post hoc analysis of the remaining 29% of combinations was performed using subgroup comparisons. This analysis revealed that the significance was triggered by only one speed condition being different from the others for most of these combinations. The speed at which the difference occurred was not consistent across tested combinations, and the differences themselves were weak and inconsistent. The percentage of cell-direction combinations in which more than one speed condition resulted in a different φ_p was only 6%. Therefore, speed had no significant effect on the φ_p for either CCW or CW tracking for the vast majority of the population. The φ_p for each tracking direction was uniformly distributed across the population of cells (Rayleigh test, p > 0.05), as was the difference in φ_p between CCW and CW directions. A model based on purely positional tuning with a single set of parameters cannot explain the simple spike firing during both CCW and CW tracking directions.

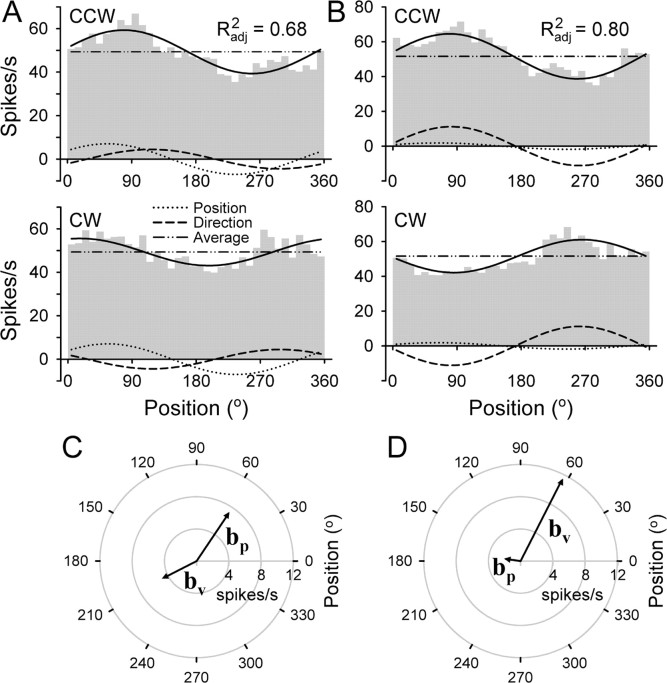
The failure of the position model to capture the difference in firing between CCW and CW tracking reflects that movement direction was a significant determinant of the simple spike discharge. Therefore, the model was refined to incorporate both unit position and unit velocity terms (Eq. 2), similar to the model proposed previously for smooth pursuit (Leung et al., 2000). The UPV model was fitted simultaneously for both directions of tracking at each target speed. The results for the same two Purkinje cells shown in Figure 5 are illustrated in Figure 6. At the speed shown (medium speed; 5.7 cm/s), the UPV model fit was significant (R²_adj = 0.68 and R²_adj = 0.80, for cells A and B, respectively). By incorporating the unit velocity term, the shift in the position of maximal firing was now accounted for in both cells. The shift was explained by each cell having both a PAP (56.0 and 63.1°, respectively) (Fig. 6C) and a PMD (207.1 and 172.0°, respectively) (Fig. 6D). Note that, according to Equation 2, the contributions of the unit velocity term were maximal at diametrically opposite locations between CCW and CW tracking (Fig. 6A,B, dashed lines). The I_pv values for the two cells were 0.61 and 0.14, respectively. Therefore, the modulation of the simple spike discharge was affected by both position and direction of movement, with one cell having a greater position contribution (Fig. 6A,C) and the other cell having a greater movement direction contribution (Fig. 6B,D).

Figure 6.

Illustration of the UPV model. A, B, Plotted are the histograms and fits for the two Purkinje cells shown in Figure 5. The overall fit is shown by the solid black line with the total adjusted R² as indicated. The fit involves both directions of tracking. The contribution of individual model components of position, direction of movement, and average firing are also shown. C, D, Diagrams displaying the preferred vectors, b_p and b_v.

The average adjusted R² across the population of Purkinje cells for the UPV model was 0.35 ± 0.19. However, for the direction-only variant of the UPV model, the adjusted R² was 0.17 ± 0.18. This confirms that both position and direction of movement were necessary to capture the Purkinje cells discharge modulation. Neither a pure position nor a pure direction model adequately described the track period modulation. Our previous studies based on center-out reaching or linear tracking (Fu et al., 1997; Coltz et al., 1999) were not able to dissociate these two parameters.

An argument can be made that a temporal lead or lag between the firing and the kinematics can make “pure” position or movement direction tuning appear as the combination of these two variables. However, the lags necessary to explain the observed differences between CCW and CW tracking were on the order of seconds in this task, which is prohibitively long. For a shift of 90°, the lags were 0.4 s for the fastest speed and 1.3 s for the slowest speed. During other limb movement tasks, simple spike activity generally leads or lags kinematics by ∼100 ms (Fortier et al., 1993; Coltz et al., 2000). Similar temporal relationships have been described for motor cortical cells (Moran and Schwartz, 1999b). Therefore, the timing between the firing and the kinematics cannot explain the shifts in the position of maximal firing.

The UPV model fits were performed separately at each target speed. However, fitting the simple spike firing to the same model across all target speeds resulted in an adjusted R² of 0.25 ± 0.15, suggesting that speed altered the modulation. Examination of the firing patterns across different target speeds revealed that speed modulated the overall simple spike discharge without changing the position of maximal and minimal firing (Fig. 4). To obtain a quantitative estimate of the invariance of the position and movement direction tuning across target speeds, the fitted parameters of the UPV model were examined as functions of target speeds. The results were essentially identical to the previous analysis of φ_p obtained from the position model. There were no significant differences in either PAP or PMD across different target speeds for 73% of Purkinje cells (Watson-Williams test, p > 0.05). For the remaining 27% of cells, a post hoc analysis revealed that the significance was triggered by one speed condition being different from the others for most of cells, suggesting that the shift was not consistent. The percentage of cells for which more than one speed condition resulted in a different PAP or PMD was only 1 and 8%, respectively. Therefore, speed had no significant effect on PAP or PMD for the vast majority of the Purkinje cells. In contrast, the amplitude of the sensitivity vectors, |b_p| and |b_v|, as well as the average firing, b₀, all significantly depended on speed across the population of cells (ANOVA with repeated measures, p < 0.05).

Therefore, speed modulated both the average firing as well as the depth of modulation without altering either PAP or PMD. Because the overall firing patterns (as found by the above analysis of the φ_p of CCW and CW tracking across speeds) were also not affected by speed, the speed must equally scale both the unit position and unit velocity terms. Otherwise, the basic pattern of simple spike modulation would change across speeds, and this is ruled out by the above results. To quantify the observed speed dependence of the discharge, the UPVS model was proposed (Eq. 5) that retains the unit position and unit velocity terms (as in Eq. 2) but incorporates speed as an amplitude modulating factor, for both the average firing and the modulation depth.

The UPVS model provided an improved fit across all target speeds. For the Purkinje cell in Figure 7A (same cell as in Fig. 4A), the depth of modulation increased (larger differences in firing in outer circles compared with the inner ones) and the average firing decreased (overall cooling from inside out) with increasing target speed, yielding an adjusted R² of 0.73. The UPV model by definition cannot capture this speed dependence, yielding only an adjusted R² of 0.42 for this cell. For the cell in Figure 7B (same cell as in Fig. 4B), the depth of modulation increased with increasing speed. Again, this is captured by the UPVS (R²_adj = 0.70) but not the UPV (R²_adj = 0.63) model. The average adjusted R² was 0.39 ± 0.15 for the 97 cells compared with 0.25 ± 0.15 for the UPV model. Therefore, the UPVS model provides the first demonstration that speed contributes significantly to Purkinje cell simple spike activity, independent of position and movement direction.

Figure 7.

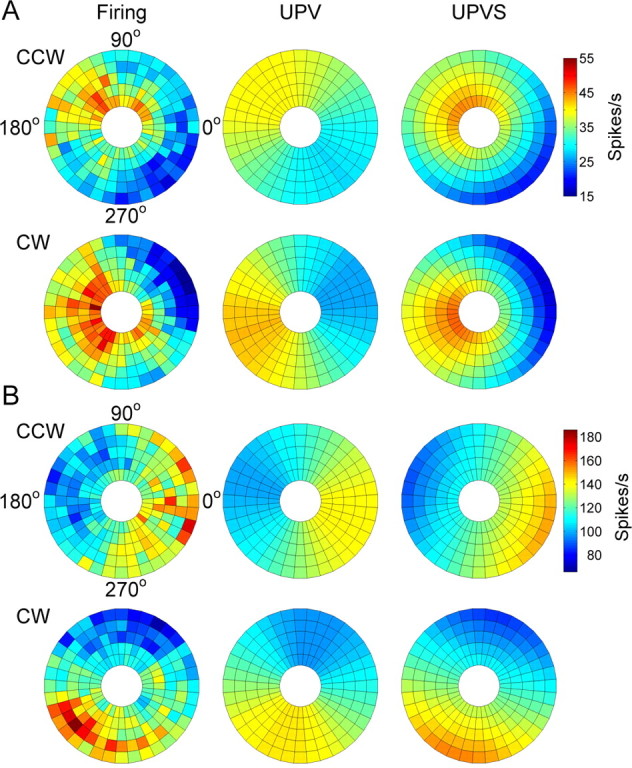
Comparison of actual firing with UPV and UPVS model fits. A, B, The actual firing and firing predicted by the model are shown as pseudocolor polar plots for the two example Purkinje cells shown in Figure 4. The angular coordinate represents angular position of the hand during tracking. The radial coordinate represents the target speed (3.1, 4.4, 5.7, 7.0, and 8.3 cm/s, from inside out).

Additional analysis of track period firing using the UPVS model revealed that the unit position term was significant for all but 10 Purkinje cells (n = 87, 90%), and the unit velocity term (i.e., movement direction) was significant for all but 10 cells (n = 87, 90%). For all but one cell (n = 96, 99%), either unit position or unit velocity term was significant. The partial R² values for unit position and unit velocity, for the cells with the significant appropriate term, were 0.12 ± 0.10 and 0.17 ± 0.13, respectively. The position-velocity contribution index, I_pv, was distributed widely across the population (Fig. 8B). The distributions of the PAP and PMD across the population of cells were uniform (Rayleigh test, p > 0.05). Also, the difference between PAP and PMD was uniformly distributed across the cells (Rayleigh test, p > 0.05), ruling out a coupling between PAP and PMD. This difference (absolute value modulo 180°) is shown in Figure 8C and had an average of 96 ± 48°.

Figure 8.

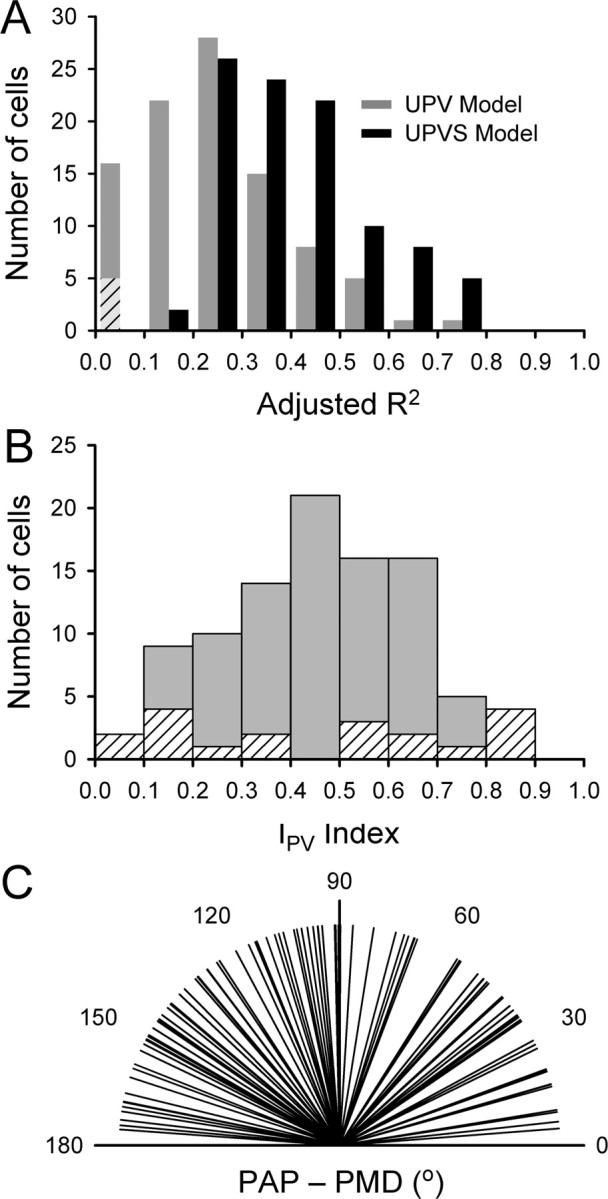
Population results for the UPVS model. A, Comparison of adjusted R² values for UPV (gray bars) and UPVS (black bars) models. The bars represent the number of cells with an appropriate value of adjusted R². Diagonal stripes denote cells for which the UPV model fit was not significant. B, Histogram of the position-velocity contribution index I_pv. Diagonal stripes represent cells for which either unit position or unit velocity term was not significant, so that the I_pv is not reliable. C, Distribution of the differences between PAP and PMD.

The speed modulation of the average firing was significant for all but 16 cells (n = 81, 84%), whereas the speed modulation of the position-direction tuning pattern was significant for 30 cells (31%). Overall, for 87 cells (90%), speed significantly affected the firing by scaling the average and/or the modulation depth. The partial R² corresponding to the speed dependence was 0.15 ± 0.13 for the cells with significant speed modulation. The relative change in average firing attributable to speed was 53.5 ± 189.9%, and the relative change in modulation depth was 41.3 ± 65.1% across the speed range of 3.1-8.3 cm/s. Both increases and decreases in the average firing and in the modulation depth were observed with speed. However, increases with speed were much more common than decreases in both the average firing (increases, n = 58, 72%; decreases, n = 23, 28%) and in the depth of modulation (increases, n = 24, 80%; decreases, n = 6, 20%).

The fractions of the variance captured by the position, movement direction, and speed terms (i.e., the partial R²s contribution toward the total R²) were tested for differences across the monkeys. There were no significant differences (ANOVA, p > 0.05) in variance captured by either the position or movement direction terms. Although there was a difference detected by ANOVA in the partial R² for the speed terms, the post hoc analysis with a Bonferroni's correction did not find significant differences between any of the tested animals. Therefore, on average, the tuning to position, movement direction, and speed was similar across monkeys.

Intercept period

To determine the generalizability of the results obtained from the track period and estimate the lead/lag between the simple spike discharge and the kinematics, the discharge during the intercept period was reconstructed as described in Materials and Methods.

As shown for the example Purkinje cell in Figure 9A, the simple spike firing during the intercept period was successfully reconstructed by the UPVS model. Most notable are the sharp declines in firing during the intercept period that occurred for some start angles (90 and 180° for CCW and 90, 180, and 270° for CW tracking). The model correctly predicted these decreases attributable to the negative sensitivity in the additive speed term (b₁ < 0 in Eq. 7). This term resulted in the decreased firing as the hand speed increased during the intercept period. For other start angles (i.e., 0 and 270° for CCW and 0° for CW tracking), the hand speed profiles were similar, as was the effect of the additive speed term. However, the actual simple spike firing did not decrease, nor did the reconstructed firing. For these start angles, the values of angular position and movement direction of the hand during the intercept period were close to the PAP and PMD, so that the contribution of the position-direction tuning (Eq. 7, term in the brackets) was maximal. Moreover, the modulation depth of the position-direction tuning was further increased by the positive sensitivity in the multiplicative speed term (b₂ > 0 in Eq. 7). Effectively, for these start angles, the contributions of the two speed terms cancelled each other, thereby minimizing the effect of speed increase on the discharge during the intercept period.

Figure 9.

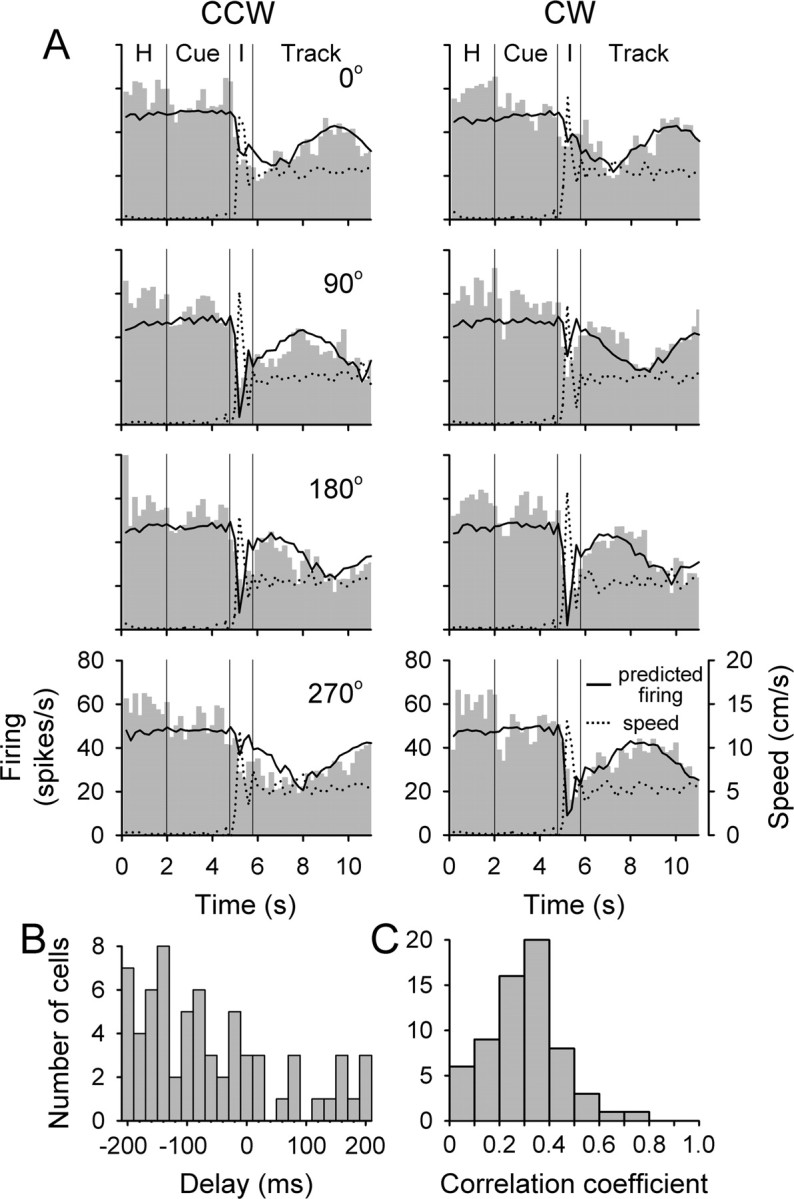
Reconstruction of the discharge based on the UPVS model. A, Reconstruction for the cell from Figure 4 A. Plotted are the histograms of average simple spike firing (gray bars), the predicted discharge (solid line), and the speed of the hand (dotted line). Data shown is for medium target speed (5.7 cm/s), for both CCW (left column) and CW (right column) tracking directions and all start angles (0, 90, 180, and 270°, top to bottom row). Included are the hold (H), cue, intercept (I), and track periods. B, Distribution of temporal lags yielding the best prediction across the population of Purkinje cells. C, Distribution of correlation coefficients between actual and predicted discharge rate across the population of Purkinje cells.

Of 97 Purkinje cells, there were significant correlations between reconstructed and actual firing in 96 cells (t test, p < 0.05). For 66% of those (64 cells), the correlation coefficient had a maximum within the range of delays evaluated (-200 to 200 ms), allowing determination of the optimal delay. The optimal delay τ for the cell in Figure 9A was 0 ms. The distribution of optimal delay values for these cells is shown in Figure 9B. The majority of the cells had a negative delay, with an average of -60 ± 120 ms, corresponding to firing leading the kinematics. The distribution of the correlation coefficients based on the optimal delay is shown in Figure 9C. These results demonstrate that position, movement direction, and speed signals during tracking can successfully predict complex features of the simple spike discharge modulation during the interception phase. Although previous studies of the fronto-parietal networks have investigated the cerebral cortical signals related to interception of a moving target (Lee et al., 2001; Port et al., 2001; Merchant et al., 2004), the present results are the first to compare interception and tracking for Purkinje cells.

Cue period

Examination of the histograms revealed modest modulation during the cue period. The modulation consisted of a brief change in firing with the appearance of the cue target (Fig. 9A, CW tracking for 90-270° start angles) and/or sinusoidal modulation throughout the cue period. Neither would be predicted by the methods used above for the intercept period, because there was no hand movement in the cue period.

Modeling the neural discharge in the cue period with the UPVS model revealed that 79 cells (81%) had a significant fit with the mean adjusted R² of 0.14 ± 0.10. The unit position term was significant for 49 cells (51%), with the partial R² of 0.06 ± 0.06. The unit velocity term was significant for 50 cells (52%), with the partial R² of 0.06 ± 0.05. Of the 79 cells with significant model fit, for 73 (92%), either unit position or unit velocity term was significant. The speed modulation of the average firing was significant for 64 cells (66%), whereas the speed modulation of the position-direction tuning pattern was significant for 14 cells (14%). Overall, for 66 cells (68%), speed significantly affected the firing by scaling the average and/or the modulation depth, with the partial R² of 0.10 ± 0.09.

An additional analysis examined whether the modulation during the cue period, possibly attributable to target motion, could account for the firing in the track period. Using the parameters obtained from the UPVS model for the cue period, the track period firing was predicted and the residuals from that prediction were fit to the UPVS model. This yielded an adjusted R² of 0.38 ± 0.17, the same quality of fit as obtained with the original firing (0.39 ± 0.15). No differences were detected (ANOVA, p > 0.05) in the distribution of R² values across cells between the fits performed on the residuals and on the actual firing. This suggests that the motion of the target contributed little, if any, to the simple spike modulation during the track period.

Therefore, based on the number of cells with significant modulation and the size of the effects, the simple spike firing during the cue period was considerably less modulated than that observed during the intercept and track periods. Furthermore, modulation during the cue period cannot account for the modulation during the track period. Both findings suggest that arm movement is the predominant determinant of the simple spike firing for Purkinje cells recorded in this location (Coltz et al., 1999; Liu et al., 2003). However, the modest cue period modulation suggests that Purkinje cells may be participating in preparatory or predictive activity (Marple-Horvat and Stein, 1990; Liu et al., 2003).

The subtraction of modulation attributable to eye movements in a similar manner could not be performed, because the hand and eye movements were highly correlated. On average, the correlation coefficient between the hand and eye movements was 0.93 for the track period and 0.77 for the intercept period, for both x and y components. Experiments designed to specifically dissociate hand and eye movements will be required to address this question, for example, by altering the visuomotor feedback. However, the locations of the recordings and responses to passive arm movement provide evidence that the modulation was attributable to arm and not eye movements (see Discussion).

Nonharmonic discharge modulation

On average, the UPVS model explained 39% of the variance of the simple spike discharge, comparable with other linear models of Purkinje cell simple spike discharge (Fu et al., 1997; Coltz et al., 1999). This prompted the following question: what aspects of the modulation were not well captured by this model? For some Purkinje cells, the simple spike modulation was not purely harmonic with the periodicity of the circle but instead exhibited nonlinearities. An example is shown in Figure 10A, in which the fit to the UPVS model yielded a PAP of 141.2° and a PMD of 232.5° (R²_adj = 0.51). However, the model did not capture the sharp decrease in firing at ∼300° during CCW tracking. Also, for CW tracking, there is a narrow peak in firing at ∼240°, superimposed on an approximately harmonic modulation.

Figure 10.

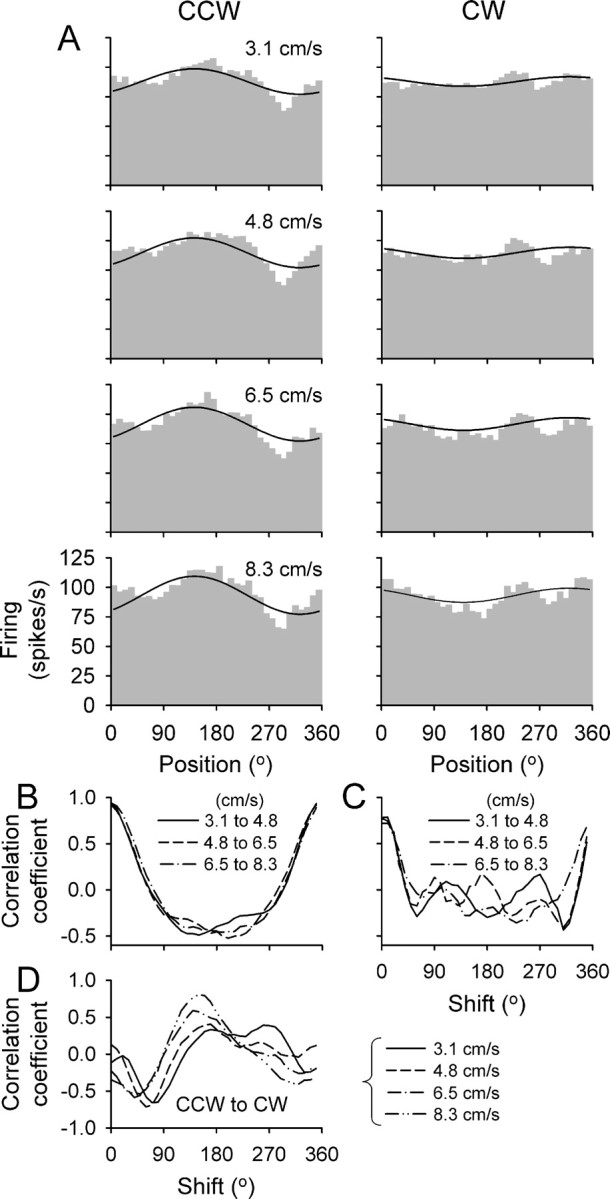
Example of nonharmonic discharge modulation. A, Simple spike histograms are shown for four speeds for CCW (left column) and CW (right column) tracking. The solid black line is the fit of the UPVS model. B, C, Cross-correlograms between discharge rates for the three pairs of speed conditions shown in A for CCW and CW tracking, respectively. D, Cross-correlograms between discharge rates of CCW and CW tracking for each of four target speeds. Plotted in B-D are the cross-correlation coefficients as functions of the angular shift between the two firing profiles.

Even with the deviations from perfect unimodal harmonic behavior, the overall firing pattern was consistent across speeds for each tracking direction as the average firing and the depth of modulation increased. Approximating the nonlinear discharge behavior would require more sophisticated linear and/or nonlinear models incorporating skewed, flat, or sharp harmonic functions, or nonharmonic multimodal distributions (Coltz et al., 1999; Amirikian and Georgopoulos, 2000). Increasing the complexity of the model would increase the quality of the fit but at a cost of introducing more parameters. This type of modeling was not performed, because the focus was on keeping the model as parsimonious as possible and still explaining a large fraction of the discharge modulation for the majority of the cells. To provide an estimate of the number of Purkinje cells with nonlinear simple spike modulation, we visually examined the firing histograms for bimodal (or multimodal) firing or particularly obvious nonsinusoidal discharge patterns. Using these qualitative criteria, 26 of the 97 Purkinje cells (26.8%) exhibited nonlinear modulation.

The model-independent analysis described in Materials and Methods was used to test whether the discharge modulation exhibited the three basic properties observed with the position, UPV, and UPVS models: (1) directional tuning of the simple spike firing differed between CCW and CW tracking, (2) this tuning pattern was not shifted by tracking speed, and (3) speed affected the average and/or the modulation depth of the firing.

The results confirmed that the simple spike discharge exhibited these three firing characteristics. For the example Purkinje cell (Fig. 10), the cross-correlograms based on the firing between CCW and CW tracking at each speed peaked at 180 ± 55°, reflecting the shift in directional tuning for the two tracking directions. In contrast, the cross-correlograms computed between the pairs of different speed conditions for either CCW or CW tracking peaked at 3 ± 5°, demonstrating that the directional tuning was not affected by tracking speed (Fig. 10B,C). The average firing increased from 88 ± 1 to 94 ± 2 spikes/s (relative change of 6.8 ± 2.3%), and the modulation depth increased from 26 ± 19 to 38 ± 12 spikes/s (relative change of 46.2 ± 85%) across the speed range of 3.1-8.3 cm/s.

For the population of Purkinje cells, the average shift of the peak in the cross-correlations attributable to speed was 0.8 ± 1.0° per 1 cm/s, equivalent to a total shift of only 4.2 ± 5.2° across the range of speeds studied. The average shift in directional tuning between CCW and CW tracking was 107.5 ± 47.3°, nearly identical to the average φ_p shift obtained using the position model (104 ± 46°). For 59 cells (61%), the average firing significantly changed with speed (p < 0.05). For these cells, the change of average firing attributable to speed was 1.9 ± 1.5 spikes/s per 1 cm/s, for a total of 10.0 ± 7.9 spikes/s (relative change of 44.4 ± 68.6%) across the speed range. Both increases and decreases in the average firing were observed, but increases (n = 42, 71%) were much more common than decreases (n = 17, 29%). For 29 cells (30%), the modulation depth significantly changed with speed (p < 0.05). For these cells, the change of the modulation depth attributable to speed was 6.2 ± 4.2 spikes/s per 1 cm/s, for a total of 32.5 ± 22.1 spikes/s (relative change of 144.6 ± 182.9%) across the speed range. Both increases and decreases in the depth of modulation were observed, but increases (n = 23, 79%) were more common than decreases (n = 6, 21%).

Therefore, regardless of the analyses used, the results are the same: the simple spike discharge signaled both position and the direction of movement independent of tracking speed. In contrast, speed scaled either the average discharge and/or the depth of modulation.

Task-related muscle activity

Task-related EMG activity was observed in 10 of the 11 recorded muscles (all except biceps). The average EMG activity of the cleidodeltoid, triceps, and extensor carpi ulnaris muscles as a function of angular position is shown in Figure 11A. As expected, the muscles showed positional tuning that was a function of tracking direction (Buchanan et al., 1986; Flanders and Soechting, 1990).

Figure 11.

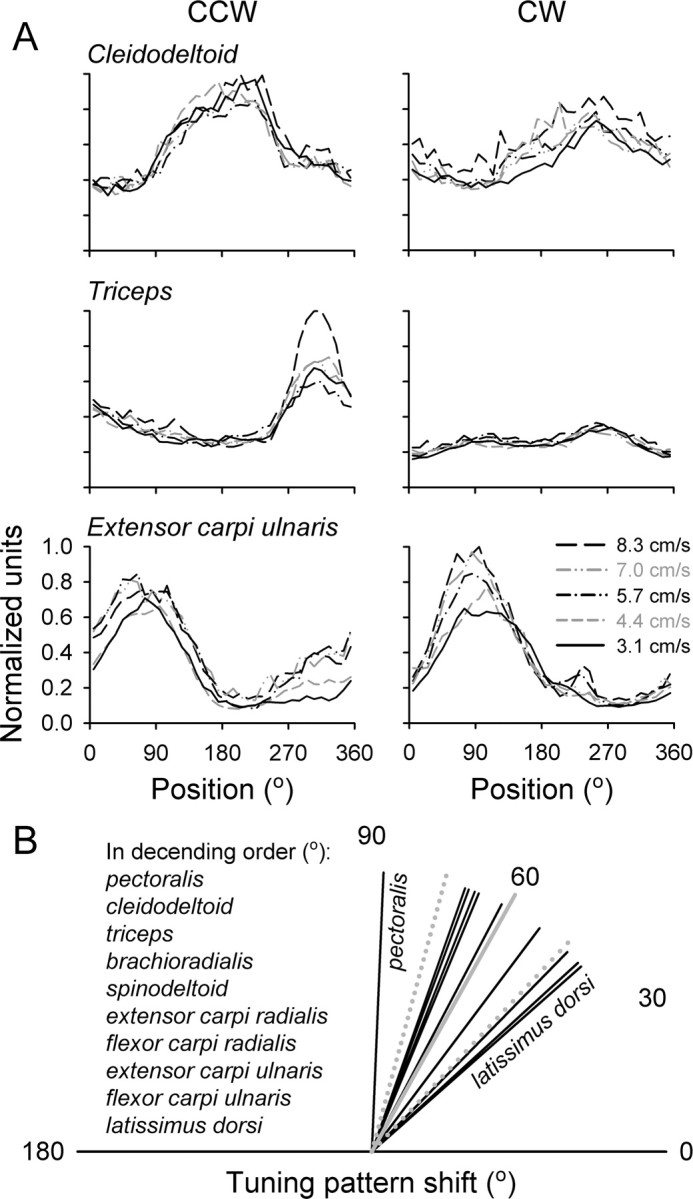
EMG activity during tracking. A, Plotted is the activity of the triceps, cleidodeltoid, and extensor carpi ulnaris for the CCW (left column) and CW (right column) tracking. Each line represents the average activity over at least 10 trials at the indicated target speed. B, Tuning pattern shift between CCW and CW tracking across muscles. Each line is the average shift across five tracking speeds and two to three recording sessions. The solid gray line is the mean shift, and the dotted gray lines are the angular dispersion.

The properties of the muscle tuning patterns were analyzed using the model-independent methodology described above. The average EMG, the modulation depth, and the tuning pattern shift were determined as functions of tracking speed (Table 1). The average EMG activity changed significantly with speed for eight muscles (all increases; p < 0.05), with a mean relative value of 5.7 ± 3.1% per 1 cm/s, for a total of 29.5 ± 16.3% across the speed range. The modulation depth changed significantly with speed for seven muscles (five increases, two decreases; p < 0.05), with a mean relative value of 3.9 ± 2.9% per 1 cm/s, for a total of 20.3 ± 15.1% across the speed range. The tuning pattern shift attributable to speed was significant but small for six muscles, with the average absolute value of 0.4 ± 1.9° per 1 cm/s, for a total of 2.1 ± 9.9° across the speed range. The tuning pattern shift between CCW and CW tracking was not uniformly distributed around the circle (Rayleigh test, p < 0.05), clustering around 60.9 ± 14.1°, in contrast with the Purkinje cell data. This shift in the tuning pattern was similar for the 10 modulated muscles (Fig. 11B) and did not differ significantly between the muscle groups (Watson-Williams test, p > 0.05).

Table 1.

Speed effect on the simple spike Purkinje cell firing and EMG activity

	n significant/total	n increases/significant	Relative change (%)
Average activity
Purkinje cells
UPVS model	81/97	58/81	53.5
Model independent	59/97	42/59	44.4
EMG	8/10	8/8	29.5
Depth of modulation
Purkinje cells
UPVS model	30/97	24/30	41.3
Model independent	29/97	23/29	144.6
EMG	7/10	5/7	20.3

Among the muscle groups, the EMG activity of the wrist muscles was the most dependent on speed (40.3 ± 7.17% for average activity and 28.9 ± 13.2% for depth of modulation across the speed range across all wrist muscles). In contrast, the EMG activity of the shoulder and elbow muscles changed little across speeds (11.5 ± 6.9% for average activity and 13.9 ± 14.5% for depth of modulation across all elbow and shoulder muscles). Therefore, the largest speed-related change was observed in scaling of the wrist EMG activity. For all muscles, the tuning pattern shift attributable to the speed increase was negligible.

Discussion

This study made three analysis-independent observations on Purkinje cell simple spike discharge during circular manual tracking. First, the position of maximal firing on the circle differs between CCW and CW tracking, reflecting that each cell is tuned to both position and the direction of movement. Second, the overall firing pattern as a function of position and direction of movement is not altered by the speed of tracking. Finally, the effect of speed on the simple spike discharge is characterized by scaling its average amplitude and/or depth of modulation. These results elucidate the fundamental properties of simple spike tuning with respect to position, movement direction, and speed, parameters used to control manual tracking (Engel and Soechting, 2000; Roitman et al., 2004).

Spatial tuning of the simple spike discharge

The first two properties reveal a basic simple spike firing pattern tuned to the geometry of the movement. Neither a positionnor direction-based model adequately describes the firing, failing to account for the shifts in the position of maximal discharge between CCW and CW tracking. Only a combined position-direction model explains the shift and establishes that both position and movement direction are significant predictors. Both parameters contribute independently to the discharge modulation. Even for Purkinje cells exhibiting firing nonlinearities, both position and movement direction are necessary to explain the tuning pattern shifts. Although similar signals are carried by flocculus and paraflocculus Purkinje cells during oculomotor tracking (Leung et al., 2000), this is the first study of how position and movement direction contribute to limb movements, during both tracking and interception.

Tracking speed does not alter the basic tuning pattern. The UPVS model results imply that the spatial tuning depends specifically on position and direction of movement, and not on other similar variables. For example, the model proposed for twodimensional smooth pursuit used position and velocity vectors (Leung et al., 2000). If true for manual tracking, the tuning patterns would have shifted systematically because the velocity contribution would increase as target speed increases, whereas the position contribution would not. Instead, the tuning to the position and direction of movement scaled equally with speed. Therefore, the simple spike firing has a fundamental tuning pattern that depends on the position of the hand in space and where the hand is headed. The spatial tuning is defined by movement geometry and is not altered by tracking speed or other time-related parameters.

Speed dependence of the discharge

Tracking speed, however, scaled the average firing and/or the modulation depth. This scaling was similar for both tracking directions. Extending previous findings that simple spike discharge encodes tracking speed (Marple-Horvat and Stein, 1987; Coltz et al., 1999, 2000), the new results clarify the specific contributions of position, direction, and speed. Speed dependence is best characterized as globally increasing/decreasing and sharpening the basic position-direction tuning. Similar results were observed in the motor cortex (Moran and Schwartz, 1999a).

Tracking at higher speeds requires generating the same trajectory on shorter time scales. Sharper tuning at greater speeds is potentially useful, both for feedback and feedforward control. If Purkinje cells carried feedback signals, the sharpened pattern may facilitate increasing the gain of the feedback. If Purkinje cells carried feedforward signals, the sharpened pattern may reflect the need to scale the motor command to generate faster movement.

Speed is the only time-related parameter controlled in the study. The cerebellum has been hypothesized to control timing, from the timing of movements (Braitenberg, 1967; Hallett et al., 1991; Hore et al., 1991; Timmann et al., 1999) to more global time-keeping functions (Ivry and Keele, 1989; Ivry and Spencer, 2004). How movement timing is represented in cerebellar neuronal discharge remains elusive. Although this experiment was not designed to study temporal processing, insights about timing can be obtained. The speed scaling results mirror findings reporting decreased duration and increased amplitude activity of Purkinje cells during saccades of shorter duration (Thier et al., 2000). Both results suggest that time-related processing in the cerebellum is based on the temporal requirements of the movement rather than an absolute “clock.” An increase in speed (or shorter timing) may be encoded by scaling the amplitude of the control signals.

Modulation during the intercept period

The simple spike discharge dependence on position, movement direction, and speed during tracking was capable of predicting the discharge during the intercept period. The UPVS model accounted for the large variations in firing attributable to start angle. The similarity in the Purkinje cell signals during tracking and reaching generalizes the validity of the findings and provides support for psychophysical findings that common neural mechanisms are used to control interception and tracking (Port et al., 1997; Engel and Soechting, 2000; Roitman et al., 2004).

The simple spike modulation could be attributable to feedforward and/or feedback signals. The lead/lag analysis of the intercept period firing revealed that the discharge for a large number of cells led the kinematics, consistent with a feedforward contribution (Thach, 1968; Fortier et al., 1989; Fu et al., 1997; Coltz et al., 1999). Conversely, the wide distribution of leads and lags is consistent with a significant feedback contribution to the firing (Bauswein et al., 1984; Chapman et al., 1986). Given the bidirectional connections between the cerebellum and motor cortices and the numerous afferent inputs to the cerebellum (Ito, 1984), it is not unexpected that both feedforward and feedback signals are present.

Nonlinearities and comparison with linear tracking

The Purkinje cell discharge exhibited nonlinearities not captured by the UPVS model. The limitations of linear models to completely account for the simple spike firing has been noted previously (Fu et al., 1997; Coltz et al., 1999). For example, a more complex regression model with quadratic predictors was needed to explain ∼60% of the firing variability during linear tracking without dissociating between the position and the direction of movement (Coltz et al., 1999).

The present results agree with our linear tracking findings in that direction and speed are predictors of simple spike discharge (Coltz et al., 1999). However, the new findings do not argue for a preferred velocity signal. The differences are most likely attributable to major differences in the tasks and analyses. First, the present experiments almost doubled the range of tracking speeds. The larger range provides a better test of speed dependence and reduces the likelihood of overemphasizing local extrema. Second, the task dissociated angular position, direction of movement, and speed. As shown for the intercept period, the interplay among these three parameters has major effects on the discharge. Finally, the linear tracking study used a model with quadratic terms accommodating both maxima for speed tuning and bimodality for directional tuning. The present study refrained from this type of models to capture only fundamental discharge properties and verified the model results with model-independent analysis that captured nonlinear tuning patterns. Therefore, the present findings extend our previous results based on linear tracking, clarifying the specific contributions of position, movement direction, and speed to the simple spike modulation and how these parameters interact.

EMG activity, eye movements, and control space

The discharge of cerebellar neurons has been argued to reflect motor commands in muscle-based coordinates (Miller and Houk, 1995). Theories proposing that the cerebellum is the site of inverse dynamic models predict that the neuronal discharge is highly related to forces and muscle activity (Shidara et al., 1993; Schweighofer et al., 1998). The EMG activity of most muscles had spatial tuning patterns similar to the cells, with shifts in the tuning pattern between CCW and CW tracking. However, these shifts clustered around 61°, in contrast with the uniform distribution for the Purkinje cells. The EMG activity exhibited limited and weak modulation with speed (Table 1), as found for linear tracking (Coltz et al., 1999). Moreover, viscous and elastic forces have little effect on Purkinje cell modulation in this task (Pasalar et al., 2005). These findings suggest a dissociation between muscle activity and the cell firing and reinforce the conclusion that Purkinje cell firing does not simply specify patterns of muscle activation.

The residual analysis demonstrated that visual target motion contributed little to the track period simple spike firing. Ruling out the possibility or estimating the contribution of eye movements to the simple spike modulation is difficult because of the strong coupling with the arm movements. However, the regions of the cerebellar cortex studied have little eye movement-related activity (Marple-Horvat and Stein, 1987; Mano et al., 1991; Liu et al., 2003), and stimulation does not result in eye movements (Ron and Robinson, 1973). Moreover, the majority of the Purkinje cells were modulated by passive arm movements. Therefore, eye movements do not dominate the simple spike modulation.

This study only considered the relationship between Purkinje cell firing and endpoint parameters, i.e., hand position, movement direction, and speed. Likely, similar results would be obtained in joint angle space, for either individual or combinations of joints, and the results are consistent with either endpoint or joint control. Because the movements are highly stereotypic, it is difficult to dissociate endpoint from joint control without experiments explicitly designed to do so (Reina et al., 2001). However, the results are not diminished by this uncertainty. The tuning is purely spatial, i.e., the Purkinje cell activity depends on the position and movement direction of the controlled plant. The tracking speed of movement scales but does not alter the spatial tuning. This separation of spatial and temporal information is independent of the control space.