NMDA/AMPA Ratio Impacts State Transitions and Entrainment to Oscillations in a Computational Model of the Nucleus Accumbens Medium Spiny Projection Neuron

Abstract

We describe a computational model of the principal cell in the nucleus accumbens (NAcb), the medium spiny projection (MSP) neuron. The model neuron, constructed in NEURON, includes all of the known ionic currents in these cells and receives synaptic input from simulated spike trains via NMDA, AMPA, and GABA_A receptors. After tuning the model by adjusting maximal current conductances in each compartment, the model cell closely matched whole-cell recordings from an adult rat NAcb slice preparation. Synaptic inputs in the range of 1000-1300 Hz are required to maintain an “up” state in the model. Cell firing in the model required concurrent depolarization of several dendritic branches, which responded independently to afferent input. Depolarization from action potentials traveled to the tips of the dendritic branches and increased Ca²⁺ influx through voltage-gated Ca²⁺ channels. As NMDA/AMPA current ratios were increased, the membrane showed an increase in hysteresis of “up” and “down” state dwell times, but intrinsic bistability was not observed. The number of oscillatory inputs required to entrain the model cell was determined to be ∼20% of the “up” state inputs. Altering the NMDA/AMPA ratio had a profound effect on processing of afferent input, including the ability to entrain to oscillations in afferent input in the theta range (4-12 Hz). These results suggest that afferent information integration by the NAcb MSP cell may be compromised by pathology in which the NMDA current is altered or modulated, as has been proposed in both schizophrenia and addiction.

Introduction

The nucleus accumbens (NAcb), part of the ventral striatum in the basal ganglia, occupies a privileged position in the vertebrate brain. The NAcb receives afferent input from the prefrontal cortex (PFC), hippocampus (HC), and amygdala, as well as the thalamus, and projects to the ventral pallidum, ventral tegmental area, and the lateral hypothalamus (Groenewegen, 1991; Heimer et al., 1991; O'Donnell and Grace, 1995; Finch, 1996; Zahm, 2000). NAcb is therefore uniquely positioned to influence the integration of cognitive and limbic pathways for motivated behavior (Pennartz et al., 1994).

The predominant cell in the NAcb is the medium spiny projection (MSP) neuron, a GABAergic cell that comprises 95% of the NAcb cell population (O'Donnell and Grace, 1993). The remainder of the population is comprised of cholinergic and GABAergic interneurons (Wilson, 1993). Each MSP cell receives ∼7500-15,000 inputs based on spine density counts (Wilson et al., 1983; Wilson, 1998). The MSP cell has a rich assortment of K⁺ currents that dominate the spontaneous and evoked behavior of the cell (Nisenbaum and Wilson, 1995). Two hallmarks of MSP behavior are a large ramp before the first action potential (AP) during current injection and bimodal behavior of the membrane potential during spontaneous activity (Wilson and Groves, 1981; O'Donnell and Grace, 1995). The bimodality refers to the tendency of the membrane to be in one of two states: a hyperpolarized (“down”) state dominated by an inwardly rectifying potassium current (K_IR), and a more depolarized (“up”) state dominated by A-type potassium currents (K_Af/K_As) during which action potentials occur (Wilson and Kawaguchi, 1996; Stern et al., 1997). This bimodality has been suggested as a mechanism for gating afferent inputs to the NAcb, and abnormal gating has been proposed to mediate the pathophysiology of schizophrenia (O'Donnell and Grace, 1995; Grace, 2000). Disruption or pathological modulation of this pathway has also been proposed as the primary neurological basis of addiction (Kelley, 2004).

Presented here is a multicompartment model of the MSP neuron with biophysical parameters constrained by in vitro intracellular whole-cell recordings from NAcb MSP cells in an adult rat slice preparation. All of the known intrinsic and synaptic ionic currents were included in the model, and appropriate kinetics were taken from the ventral striatum when available. After matching the model behavior to the in vitro MSP recordings via tuning of compartmental conductances, the number of inputs required to modulate the membrane potential between states was investigated. The effects of various synaptic currents and conductance ratios on dendritic and cellular integration of afferent input were determined. We found that changes in the NMDA/AMPA ratio dramatically increased the hysteretic properties of the cell. By partially synchronizing the afferent input, we were able to determine the minimum number of afferents required to entrain the model cell to oscillations in the theta range, as has been reported for in vivo ventral striatal cells (Berke et al., 2004). We found that changes in the NMDA/AMPA ratio have a profound impact on the ability of the cell to entrain to these oscillations.

Materials and Methods

In vitro recordings

Whole-cell current-clamp recordings were performed from MSP neurons within the core region of the NAcb in rat brain slices maintained in vitro. All experimental procedures were performed according to the United States Public Health Service Guide for Care and Use of Laboratory Animals and were approved by the Albany Medical College Institutional Animal Care and Use Committee. Adult (48-59 d old) male Sprague Dawley rats (Charles River Laboratories, Wilmington, MA) were maintained on a 12 h light/dark cycle with food and water available ad libitum until the time of experiment. Rats were deeply anesthetized with chloral hydrate (400 mg/kg, i.p.) before decapitation. Brains were removed into ice-cold artificial CSF (ACSF) containing the following (in mm): 125 NaCl, 25 NaHCO₃, 10 glucose, 3.5 KCl, 1.25 NaH₂PO₄, 0.5 CaCl₂, and 3 MgCl₂, pH 7.45 (osmolarity, 295 mOsm). Sagittal slices (300 μm) containing the NAcb, the striatum, and the prefrontal cortex were cut on a vibratome in ice-cold ACSF. Slices were transferred and incubated in a warm (35°C) ACSF solution constantly oxygenated with 95% O₂-5% CO₂ for at least 1 h before recording. Slices were transferred to a submersion-type recording chamber maintained at 33-35°C and superfused with oxygenated recording ACSF at a flow rate of 2 ml/min. In the recording ACSF, CaCl₂ was 2 mm and MgCl₂ was 1 mm. Patch pipettes (5-10 MΩ) were filled with the following (in mm): 115 K-gluconate, 10 HEPES, 2 MgCl₂, 20 KCl, 2 Mg-ATP, 2 Na2-ATP, and 0.3 GTP, pH 7.3 (280 mOsm). Neurobiotin (0.125%) was added to the internal solution for labeling the recorded cell.

NAcb MSP neurons were identified under visual guidance using infrared differential interference contrast video microscopy. The image was detected with an infrared-sensitive CCD camera and displayed on a monitor. Whole-cell current-clamp recordings were performed with an Axoclamp-2A amplifier (Axon Instruments, Union City, CA) and acquired with Axoscope 8.1 (Axon Instruments) at a sampling rate of 10 kHz. Electrode potentials were adjusted to zero before recording but without correcting for the liquid junction potential. This potential was then calculated using the Junction Potential Calculator routine in Clampex (Axon Instruments), determined to be -10.4 mV, and subtracted from all in vitro data. In each experiment, the I-V curve was obtained by injection of 500 ms current pulses (-250 to +250 pA) every 10 s. Suprathreshold depolarizing current pulses were applied and adjusted to evoke up to five action potentials. The number of spikes at each current injection amplitude was counted for each cell, and a line was fit to the data using linear regression. The model was adjusted to match the slope of this line for a representative cell. At the end of the electrophysiology experiment, the slices were placed in 4% paraformaldehyde, and a subsequent avidinbiotin reaction was used to label Neurobiotin-injected cells.

MSP model Passive properties.

The 189-compartment NAcb MSP cell was developed using the NEURON simulation environment (Hines and Carnevale, 1997). Simulations were performed on an Apple Computers (Cupertino, CA) dual 2.5 GHz Power Macintosh G5 or in parallel on a 12-node cluster with dual 2.8 GHz processors per node (Penguin Computing, San Francisco, CA). The model presented here extends previous MSP models in several ways (Wilson, 1995; Mahon et al., 2000; Kitano et al., 2002; Gruber et al., 2003; Wood et al., 2004). Notably, this is the first MSP model to individually include all reported species of calcium and calcium-dependent potassium currents as well as recently updated parameters for several potassium currents. Whenever feasible, channels were taken directly from published reports in accumbens or striatum and used in the model with minimal adjustments (detailed below). The cell was tuned to match in vitro accumbens recordings solely by balancing the conductance of these intrinsic currents. Also of note, individual synaptic inputs to morphologically detailed dendrites of the MSP cell are simulated, which enables in-depth analysis of dendritic processing. The resulting model represents the most detailed model of the NAcb MSP cell and its afferent input to date.

A multicompartment stylized morphology of the cell was developed based on anatomical data in accumbens (O'Donnell and Grace, 1993). We include four primary dendritic branches (O'Donnell and Grace, 1993) compared with the six branches reported in dorsal striatal cells (Wilson, 1992). Each primary branch bifurcates twice, resulting in 16 tertiary dendrites. A stylized model of the cell was chosen to avoid the computational overhead of explicitly modeling spines or thousands of membrane compartments. To ensure sufficient spatial accuracy of numerical solutions, a spatial grid for each compartment of the cell was specified using a d-lambda value of 0.15 (Hines and Carnevale, 2001). This resulted in 11 nodes per tertiary dendrite and one node each in soma, primary, and secondary dendrites, giving a total of 189 compartments in the model.

Published values of dendritic length and diameter in NAcb (O'Donnell and Grace, 1993) match those in dorsal striatum (Wilson, 1992). These values were adjusted to compensate for additional membrane area attributable to spines using these equations:

(Segev and Burke, 1998).

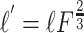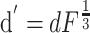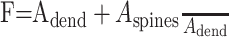Here, l and d are in vitro length and diameter, whereas l′ and d′ are the adjusted length and diameter used in the model (Table 1). The surface area parameters A_dend and A_spines were based on published values of spine density in striatal MSP cells (Wilson, 1992). Leak conductance and the inwardly rectifying potassium current conductance were tuned to the apparent input resistance of 79.7 MΩ of our in vitro cells. Membrane capacitance was set to 1 μF/cm² and axial resistance to 100 Ω/cm, standard values for neurons (Gentet et al., 2000). Leak conductance was modeled using the passive channel included in the standard NEURON library with g_bar = 11.5e^-6 S/cm² and E_rev = -70 mV.

Table 1.

Anatomical dimensions of the model

	N	l (μm)	l′ (μm)	d (μm)	d′ (μm)	F
Soma	1	16		16
Proximal dendrites	4	20	20	2.25	2.25	0
Middle dendrites	8	20	24.23	1	1.1	1.33
Distal dendrites	16	190	395.2	0.5	0.72	3

Intrinsic currents. A full list of parameters used for active properties in the model is included as Table 2. We detail the sources and parameter selection for each channel in Appendix and concentrate here on a discussion of the novel aspects of the present MSP model. Briefly, the prevailing strategy was to include published parameters for accumbens, supplementing these with dorsal striatal parameters, and finally using measurements from other neurons when necessary. Voltage-dependent kinetics were used when available (tabulated values, available at www.jneurosci.org as supplemental material). Activation and inactivation steady-state Boltzmann curves were taken directly from published reports. Activation and inactivation time constants were temperature corrected to 35°C to match electrophysiology recordings. When current localization was unknown, it was assumed that currents were situated at uniform conductance per membrane area throughout the cell, except when detailed below. The cell was tuned solely by balancing the maximum conductance levels of intrinsic currents against each other to match the present in vitro adult rat accumbens current injection data. The same cell tuning was used for all experiments.

Table 2.

Parameters used for active properties in the model

	gbar (S/cm2)	HHform		V1/2 (mV)	k(mV)	τ(ms)
NaF	1.5, soma	m3 × h	m	−23.9	−11.8	Tabulated
	0.0195, dendrites		h	−62.9	10.7	Tabulated
NaP	4e-5, soma	m × h	m	−52.6	−4.6	Eq.A11
	1.38e-7, dendrites		h	−48.8	10	Tabulated
KAf	0.225, soma and proximal	m2 × h	m	−10.0	−17.7	Tabulated
	0.021, middle and distal		h	−75.6	10	4.67
KAs	0.0104, soma and proximal	m2 × (a × h + (1 − a))	m	−27.0	−16	Eq. A12
	9.51e-4, middle and distal	a = 0.996	h	−33.5	21.5	Eq. A13
KIr	1.4e-4	m	m	−82	13	Tabulated
KRp	0.001	m × (a × h + (1 − a))	m	−13.5	−11.8	Tabulated
		a = 0.7	h	−54.7	18.6	Tabulated
BK KCa	0.001
SK KCa	0.145

	Pbar (cm/s)	HHform		V1/2 (mV)	k (mV)	τ (ms)
CaL 1.2	6.7e-6	m2 × (a × h + (1 − a))	m	−8.9	−6.7	Eq.A14
		a = 0.17	h	−13.4	11.9	14.77
CaL 1.3	4.25e-7	m2 × h	m	−33.0	−6.7	Eq.A14
			h	−13.4	11.9	14.77
CaN	1.0e-5	m2 × (a × h + (1 − a))	m	−8.7	−7.4	Eq.A15
		a = 0.21	h	−74.8	6.5	23.33
CaQ	6.0e-6	m2	m	−9.0	−6.6	0.377
CaR	2.6e-5	m3 × h	m	−10.3	−6.6	1.7
			h	−33.3	17	Tabulated
CaT	4e-7	m3 × h	m	−51.73	−6.53	Tabulated
			h	−80	6.7	Tabulated

We included two sodium currents, fast (NaF) and persistent (NaP), and six different potassium currents: inwardly rectifying (K_IR), slow A-type (K_As), fast A-type (K_Af), 4-AP resistant persistent (K_RP), small-conductance calcium dependent (SK), and large-conductance calcium dependent (BK). We also incorporated six calcium currents: N-, Q-, R-, T-, Ca_v1.2 [high-voltage activated (HVA)] L- and Ca_v1.3 [low-voltage activated (LVA)] types (for review, see Catterall, 2000). Most channels used standard Hodgkin-Huxley equations, detailed in Appendix. However, a number of the currents (K_As, K_RP, CaN, CaL1.2) are described as partially inactivating, and, in these cases, we used a modified version of the Hodgkin-Huxley formulation:

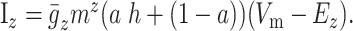(1)

The variable a can be adjusted between 0 (no inactivation) and 1 (fully inactivating) to increase or decrease the amount of inactivation. We used a reversal potential of E_Na = 50 mV for sodium and E_K = -90 mV for potassium.

Sodium currents. Based on observations of blockade of dendritic calcium influx after TTX application (Kerr and Plenz, 2002), we distributed both sodium channels (fast and persistent) throughout the model. Placing sodium in the dendrites assisted backpropagation, but it was not essential. The total conductance of sodium in the soma was set to be 10 times the total conductance of sodium in the dendrites, a level that ensured reliable spiking without inducing doublets.

Potassium currents. The behavior of MSP cells at hyperpolarized potentials is dominated by the presence of K_IR (Uchimura et al., 1989). The non-inactivating K_IR current used in the model is primarily associated with subunits of the KIR2 family and substance P-expressing MSP cells in the NAcb (Mermelstein et al., 1998; Pruss et al., 2003). The steady-state activation curve was fitted to a mouse K_IR channel composed of KIR2.1 subunits expressed in human embryonic kidney cells (Kubo and Murata, 2001). The K_IR current is sensitive to extracellular potassium concentration, and the steady-state curve was therefore shifted to match our [K⁺]_o and potassium reversal potential (for review, see Lu, 2004). The kinetics of this current have not been characterized in the rat, requiring us to use data from Aplysia (Hayashi and Fishman, 1988). However, the time constant of activation was adjusted to match the kinetics evident during hyperpolarizing current injection (see Results). In agreement with experimental data (Pruss et al., 2003) as well as previous modeling efforts (Wilson, 1992, 1995), this channel is distributed throughout the model. The maximum conductance of the K_IR channel was adjusted to match the in vitro response to hyperpolarizing current injection of the present NAcb recordings.

Two types of A-type potassium currents have been observed in striatal MSP cells, K_As and K_Af. The classic K_As current (Nisenbaum et al., 1994) has been recently attributed to Kv1.2 channels (Shen et al., 2004). For the K_Af current, we used a Kv4.2 channel, because this channel has been shown to be a major contributor to A-type potassium current in striatal neurons (Tkatch et al., 2000) and has kinetics similar to the classic K_Af current (Surmeier et al., 1989). Both currents are active during action potential repolarization as well as during the subthreshold ramp response to depolarizing current injection and were tuned to provide appropriate cell behavior during both. Based on reports of their existence in the dendrites of other neurons (Sheng et al., 1992; Hoffman and Johnston, 1998), as well as previous speculation that K_A exists in the dendrites of MSP cells (Wilson, 1995), we placed both K_As and K_Af throughout the cell. This assumption is validated in that doublets begin to appear when the conductance of these channels is reduced by 50%. For both channels, we had to set the total conductance of the soma and primary dendrites equal to the total conductance of the secondary and tertiary dendrites (G_soma + G_pri = G_sec + G_ter) to achieve realistic behavior.

K_RP (Nisenbaum et al., 1996) was placed only in the soma because there is no current evidence indicating its existence in MSP dendrites. The maximum conductance of the K_RP channel was set to provide appropriate interspike intervals (ISIs) without eliminating the ramp-to-first spike during current injection.

The existence of calcium-dependent potassium channels in both dorsal and ventral striatum is well documented (Pineda et al., 1992; Bargas et al., 1999; Martin et al., 2004). We accounted for two types of K_Ca channels: the SK (small-conductance, I_ahp, mI_ahp, or g_Kca) and the BK (large-conductance, I_c, or I_fast) channels (for review, see Sah and Davies, 2000). Both channels were taken from previous modeling studies (Moczydlowski and Latorre, 1983; Shao et al., 1999). The total conductance of the BK current was adjusted to shape spike width, and the SK channel was necessary to shape the spike afterhyperpolarization (AHP).

Calcium currents. Calcium currents were modeled using the Goldman-Hodgkin-Katz equation, which accounts for current rectification at elevated membrane potentials (see Appendix) (De Schutter and Smolen, 1998). The parameters for each current are listed in Table 2. Our model includes six calcium currents: N-, Q-, R-, T-, Ca_v1.2 (HVA) L- and Ca_v1.3 (LVA) types. Because of the tremendous importance of dopaminergic modulation to striatal function and because many of the effects of dopamine are believed to involve calcium currents (Hernández-López et al., 1997; Olson et al., 2005), an important contribution of our model is the explicit inclusion of each of these currents, the resulting calcium dynamics, and their effect on calcium-dependent potassium channels.

Most of our data were derived from adult rat accumbal cells (Churchill and Macvicar, 1998). This is the most complete study on NAcb MSP calcium channels to date; however, it was performed on acutely isolated cells rather than whole cells. This required us to correct the whole-cell calcium currents upwards to account for loss of current attributable to removal of the dendrites in the preparation (see Appendix). This correction resulted in a peak whole-cell HVA calcium current of 3.64 nA, ∼10 times the value in the dissociated cell (0.305 nA), with peak low-threshold inactivating (LTI) current set to 7.2% of this value (Churchill and Macvicar, 1998). HVA calcium current was divided among the N-, Q-, R-, and Ca_v1.2 L-type channels according to observed ratios established using various toxins (Churchill and Macvicar, 1998). Channel kinetics and steady-state parameters were taken primarily from this report but supplemented with other studies when required (for details, see Appendix). As mentioned previously, partially inactivating channels (Ca_v1.2 and CaN) were described using Equation 1 above. HVA currents actually decreased the spike frequency of the model through their relation with K_Ca channels.

An LTI calcium current was also observed in NAcb MSP cells. This current was initially attributed to T-type channels (Churchill and Macvicar, 1998). However, the authors note that this current is partially sensitive to nimodopine [indicating Ca_v1.3 presence (Catterall, 2000)], and, based on recent evidence that adult rats exhibit both striatal 1.3 L-type (J. Surmeier, personal communication) and T-type (McRory et al., 2001) calcium channels, we included both currents. Using a uniform distribution of both currents throughout the cell, we adjusted each to carry approximately half of the total LTI conductance to match reports in NAcb (Churchill and Macvicar, 1998). These currents increased the spiking frequency of the cell in response to current injection and helped to round out the AHP. This stands in contrast to increases in N-, Q-, and R-type currents, which actually slowed spiking and deepened the AHPs through their interactions with K_Ca channels.

Calcium dynamics

The internal calcium concentration in a thin shell just inside the cell membrane was tracked for each compartment using standard modeling methods (Destexhe et al., 1993). Calcium influx was balanced against diffusion and pumping activity to provide appropriate calcium sensitivity for both SK and BK K_Ca channels.

Experimental data has indicated that striatal calcium-dependent potassium channels are activated by calcium influx through N- and Q-type calcium channels but not L-types (Vilchis et al., 2000). Accordingly, we specify a calcium pool for 1.2 and 1.3 L-type currents and a separate calcium pool for N-, Q-, and R-type calcium currents with which the calcium-dependent potassium channels are associated. Based on our observations, we did not associate the T-type current with the K_Ca channels and instead placed it into the L-type pool.

Synaptic currents. NMDA, AMPA, and GABA currents were modeled using a modified two-state synapse (based on the Exp2Syn synapse in NEURON), providing both summation and saturation. These currents obeyed the equation

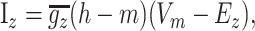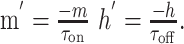The NMDA current was modified to account for voltage-dependent magnesium blockade (Jahr and Stevens, 1990).

The summation and saturation of each synapse was adjusted to match published reports (Mainen et al., 1999). Rise and decay time constants for AMPA and NMDA channels were taken from the NAcb (Gotz et al., 1997; Chapman et al., 2003), and we used neocortical pyramidal cell data for GABA time constants (Galarreta and Hestrin, 1997). NMDA decay time constants are significantly greater in ventromedial striatum compared with dorsolateral striatum (320 vs 231 ms at 22°C), which may represent an important difference between dorsal and ventral striatum (Chapman et al., 2003). Because the rate limiting step in synaptic transmission is diffusion of transmitter across the synaptic cleft, we divided by a factor of 2 to adjust time constants from 22°C to 35°C (Gutfreund, 1995). NMDA synaptic strength was set to match published values of single-channel conductance (Dalby and Mody, 2003) multiplied by 5, an accepted value for number of NMDA channels per synapse (Dalby and Mody, 2003). AMPA synaptic strength was set to match the reported ratio of NMDA/AMPA conductance (0.5:1 in magnesium-free solution) (Myme et al., 2003). GABA synaptic strength was set to reported single-synapse conductance levels (Nusser et al., 1998). AMPA and NMDA reversal potentials were set to accepted values of 0 mV (Jahn et al., 1998; Dalby and Mody, 2003), whereas the E_Cl for GABA was set to -60 mV to match published reports (Czubayko and Plenz, 2002; Tepper et al., 2004). Parameters for synaptic currents are listed in Table 3. Ten percent of NMDA current and 0.5% of AMPA current contributed to calcium influx to match published reports (Carter and Sabatini, 2004).

Table 3.

Parameters for synaptic currents

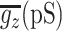
Synaptic currents		Ez (mV)	τon (ms)	τoff (ms)
AMPA	593	0	1.1	5.75
GABA	435	−60	0.25	3.75
NMDA	300	0	2.82	160

Synapses were distributed throughout the cell based on available literature. Glutamatergic synapses in MSP cells are generally located in spines, which are primarily located in the mid-to-distal dendrites (Wilson, 1992). Accordingly, we distributed our glutamatergic synapses in the dendrites only, with one synapse per primary dendrite, two synapses per secondary dendrite, and four per tertiary dendrite. AMPA and NMDA channels were colocalized one-to-one at each synapse and received the same inputs. Previous studies have indicated that GABA synapses are located throughout MSP cells in the striatum but with higher concentration near the soma (Fujiyama et al., 2000). We therefore placed 16 GABA synapses in the soma, three synapses in each primary and secondary dendrite, and two in each tertiary dendrite.

Simulations. Synaptic inputs were modeled using a modified version of the NetStim object provided in the NEURON package. Each synapse (AMPA, NMDA, or GABA) received an independent spike train generated using Matlab (MathWorks, Natick, MA). Each spike train was generated using the following algorithm: first, a constant ISI train was generated at the desired frequency. Each spike was then pulled anew from a Gaussian distribution centered at the original spike time. The resulting train was then randomly shifted, and this process was repeated for each of the 168 total synapses. Non-oscillatory input was generated by using a large shift (one ISI) and a large SD (one-fourth of the ISI). State transitions were generated using this method solely by changing the mean frequency of inputs to the cell between 3 Hz/synapse and 7.5 Hz/synapse. The ratio of glutamatergic inputs to GABA inputs was held constant at ∼1:1 for all simulations (Blackwell et al., 2003).

Oscillatory inputs were generated in a similar manner. First, a background set of non-oscillatory input was created using the algorithm above with mean frequency of 5.5 Hz/synapse and used for all entrainment experiments. Next, glutamatergic inputs from this set were randomly chosen and replaced with input at the desired frequency (4, 8, or 12 Hz). These trains were not shifted relative to each other, and, by using a smaller SD for the Gaussian distribution (15% of the ISI), we were able to examine the response of the cell to periodic input. We were able to analyze the number of oscillating inputs required to entrain the cell by replacing between 2 and 20 background inputs with oscillatory inputs. The results were quantified by calculating the SD of the spike time of the cell with respect to the peak in the sine wave input for each period. The relative ability of the cell to entrain to oscillatory input at different NMDA/AMPA ratios was compared using a two-tailed F test to determine whether the SD under each condition was significantly different. Eleven oscillatory synapses gave reliable entrainment without unrealistic fluctuations in baseline voltage, so this value was used for the remainder of the experiments. The phase response of the cell was quantified using a peristimulus time histogram (PSTH) created by binning spikes into 30 bins equally spaced throughout each sine wave period. The PSTH was plotted over 720° and centered at 0° to more clearly illustrate the response of the cell.

The instantaneous input frequency plot in Figure 3 was created using a sliding-window analysis of the inputs to the cell. At each time step, the number of inputs in the last 50 ms was counted and the corresponding frequency was calculated. Dendritic correlations were calculated using the corrcoef function in Matlab, which calculates the 0th-lag correlation coefficient between points indicated.

Figure 3.

Response of the model to changes in synaptic input and influence of different synaptic currents. GABAergic and glutamatergic synaptic input to the model were simulated as independent spike trains distributed throughout the cell (see Materials and Methods.) State transitions in the model V_m (A; black trace) were generated by changing the mean frequency of synaptic input from 504 Hz (3 Hz/synapse) to 1260 Hz (7.5 Hz/synapse) (C; red line). Blockade of NMDA currents prevents the model from fully reaching the up state (A; red trace). Synaptic input patterns are the same for both control and no-NMDA cases. B, Whole-cell synaptic currents underlying the activity of the model: AMPA dominates the transition into the up state. NMDA lags the AMPA current and is highly prominent in the transition to the down state. There is relatively little GABA current because V_m is close to the Cl^- reversal potential. As the membrane potential increases during action potentials, the sudden increase in driving force can lead to a temporary increase in Cl^- current through open channels. C, Mean instantaneous frequency per synapse is plotted over the simulation time (red). A sliding-window filter (50 ms wide) of the instantaneous frequency at all synapses combined is plotted in black. Note that the somatic membrane potential matches this in many respects, with a slight delay for dendritic processing of the inputs. D, The influence of GABA on cell output is subtle. Blockade of GABA (orange trace) and fivefold increase of GABA conductance (black trace) affect spike output and timing only slightly (compare with control trace in top panel). There is a loss of one spike in the gGABA^*5 condition compared with control, whereas a complete block of GABA results in no extra action potential generation. Synaptic inputs for both cases are the same as in A.

Input ramps for hysteresis experiments (see Fig. 5) were generated using the NEURON Netstim generator. The mean frequency was held at low (3 Hz/synapse) frequency for 300 ms, ramped smoothly from low to high (7.5 Hz/synapse) over 50 ms, held at high for 600 ms, and then ramped back down at the same rate. Up-state extension during this protocol was calculated by running 48 trials of the same input to the cell at several different NMDA/AMPA ratios from 0.5 to 4 and comparing the time of last spike for each ratio to that of control. To examine hysteresis in the cell, we reflected the averaged cell voltage on the down slope of the ramp and plotted it against the averaged cell voltage on the up slope of the ramp for three NMDA/AMPA ratios: 0.5, 1.5, and 2.5. Intrinsic hysteresis of the cell (as opposed to synaptically mediated) was examined by injecting a current ramp and performing the above analyses. The contribution of realistic levels of NMDA current influx to negative slope conductance was examined by voltage clamping the cell during synaptic input at 1042 and 2084 Hz. The 1042 Hz input level was chosen because it leads to 10 Hz spike output during a prolonged up state. AMPA and GABA currents were disabled during this experiment to test the effect of the NMDA current alone on negative slope conductance. The cell was stepped from -87.75 mV (rest) to potentials from -120 to -20 mV, and the resulting current was measured 600 ms after each step.

Figure 5.

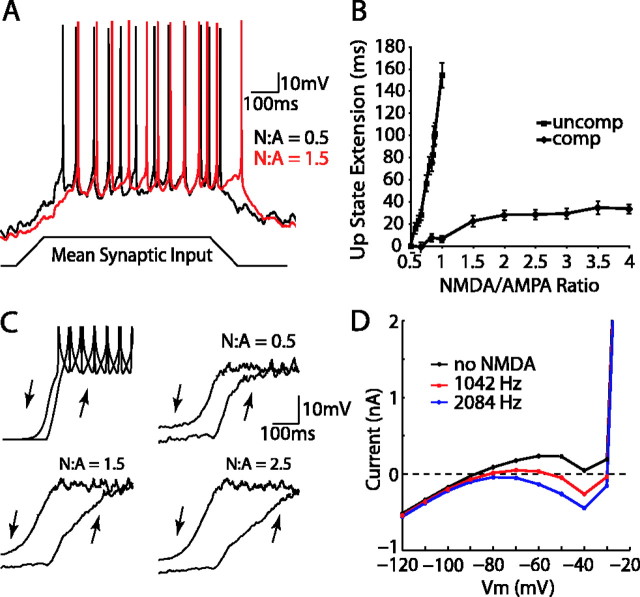
Increasing the NMDA/AMPA (N:A) ratio contributes to hysteresis in the MSP model membrane potential during synaptic input ramps. A, An NMDA/AMPA ratio of 1.5 (red trace) results in a delayed and extended up state compared with a 0.5 NMDA/AMPA ratio (black trace) in a synaptic input ramp experiment. The same input stimulus consisting of a ramp up, plateau, and ramp down was used for both traces and is indicated at bottom. B, The average extension of the up state for both uncompensated (squares) and compensated (diamonds) NMDA/AMPA ratios. Each point represents the mean extension of the up state past control (defined by time of last spike) for 48 simulations (error bars indicate SD). C, The model cell V_m takes different paths between states depending on transition direction and NMDA/AMPA ratio. Top left, The path of the V_m from down to up state is only slightly different under current injection. As NMDA/AMPA ratio increases from 0.5 to 1.5 to 2.5, the transitions become increasingly more distinct from one another in time. Each subplot is the average V_m of 48 trials reflected at the midpoint of the symmetrical ramp input. D, Steady-state current after steps to a range of voltages during somatic voltage clamp (see Materials and Methods). NMDA activation via synaptic stimulation at 1042 Hz (red trace) and 2084 Hz (blue trace) enhances the negative slope conductance and causes a double crossing of the zero-current axis at an input frequency of 1042 Hz.

NMDA/AMPA ratios were set by changing the total conductance of each synapse. For Figures 1, 2, 3, 4, the NMDA/AMPA ratio was set to 0.5 (Myme et al., 2003). However, because published values of NMDA/AMPA vary widely (0.5 to 4) (Myme et al., 2003) and may change after dopaminergic modulation (Flores-Hernandez et al., 2002) or cocaine addiction (Thomas et al., 2001), this represented a baseline condition for upwards modulation and should be regarded as a conservative estimate of the normal ratio. The ratio was changed by multiplying the baseline synaptic conductance of each synapse by a constant weight. We used three classes of ratios: uncompensated, compensated, and spike output compensated (SOC). Uncompensated ratios, representing an initial increase in NMDA receptor, kept the AMPA conductance at baseline levels but increased the NMDA conductance. This resulted in an extremely high level of spiking, which would likely cause the cell to downregulate both AMPA and NMDA receptor expression in response. Accordingly we investigated a “compensated” condition with the same total synaptic conductance as the initial unmodulated condition but at the new NMDA/AMPA ratio. However, this level resulted in lower spike output compared with baseline, so we propose that the long-term modulated state would be “spike output compensated,” in which the cell spikes at baseline levels by maintaining a slightly higher total conductance compared with baseline conditions. We set SOC levels by matching the average number of spikes at each condition to baseline for the synaptic input ramp experiments. The SOC condition was used for all modulation experiments except when indicated.

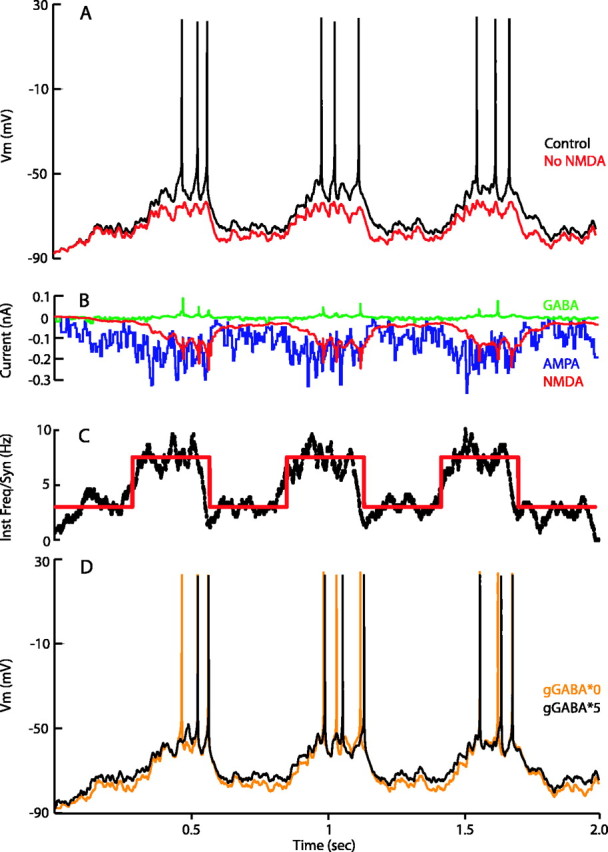
Figure 1.

Comparison of nucleus accumbens MSP cell and model. A, An example of an MSP cell filled with Neurobiotin from which whole-cell recordings were performed. Scale bar, 50 μm. B, Morphology of the MSP cell model. Dendritic length and diameter have been increased to compensate for spine membrane area. Scale bar, 50 μm. C, Response of an NAcb MSP cell to current injections of -0.227, 0.225, and 0.271 nA. D, Response of the model to current injections of -0.227, 0.248, and 0.271 nA. The model reproduces the inward rectification during negative current injections attributable to the activation of K_IR current (arrows). The model is tuned to match the slope of the mean spike output per current injection level for all in vitro cells. E, Comparison of the current-voltage relationships of the model and the mean of seven NAcb MSP cells; voltages were recorded 450 ms into a 500 ms current pulse. The response of the model (squares) is within the SD of the responses of the cell (circles; error bars indicate SD). The model cell was matched to the mean resting membrane potential of -87.75 mV. Inset, Frequency-current relationship of the model (solid black line), the representative cell to which the model was tuned in C (solid gray line), and six other NAcb MSP cells (dashed black lines). F, In vitro (left) and model (right) response to five current injections resulting in spike frequencies of 2-10 Hz. The cell is the same as in C.

Figure 2.

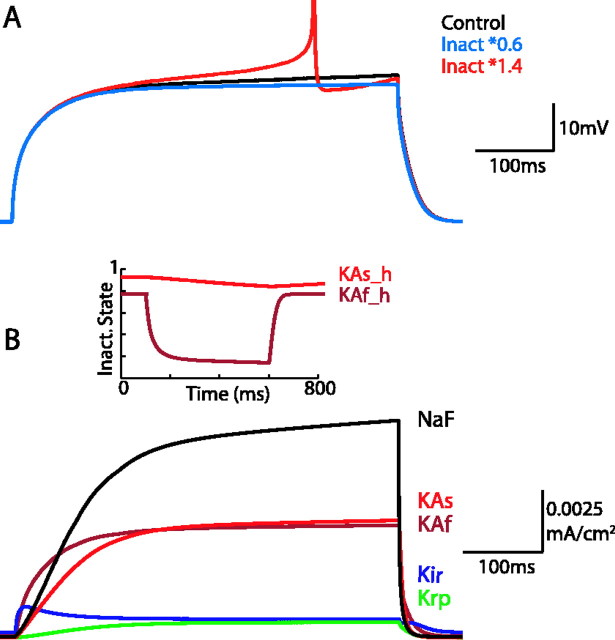
Somatic currents during response of model to current injection. A, A 40% increase (red trace) or decrease (blue trace) in the inactivation parameter (a in Eq. 1) of the K_As current has a significant effect on the response of the model to the same current injection level (0.232 nA). When inactivation is increased, AP threshold is reached. When inactivation is decreased, the slope of the ramp decreases. B, Major somatic currents involved in the depolarizing ramp before spiking during current injection. After the initial response to injection, K_As current continues to increase throughout the duration of the ramp because inward NaF current depolarizes the cell membrane. The relatively slow inactivation kinetics of K_As in relation to its activation and K_Af inactivation cause the current to increase during the ramp but become progressively less available with time (inset).

Figure 4.

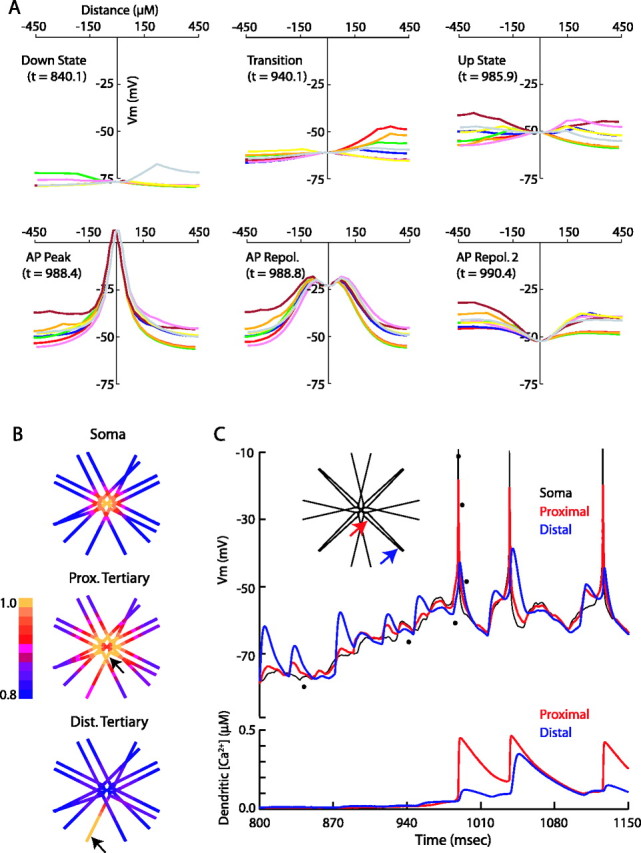
Dendritic activity of MSP model during synaptic input. A, Membrane potential of the soma and dendrites during state transitions. Each colored line represents voltages along a distinct path from one distal dendritic tip through the soma to a different distal dendritic tip. The soma is at x = 0. The time points indicated for each snapshot correspond to the voltage trace in C and are represented by the dots at those time points. Note that the dendrites act independently of each other except during state transitions or action potentials. State transitions occur after the depolarization of at least ∼25% of the dendrites, with the dendrites leading the soma into the up state. Action potentials are initiated at the soma and voltage propagates to the distal tips of the dendrites. B, Correlations of membrane potential with all other compartments of the cell during a 2 s simulation. The soma is well correlated with the proximal and secondary dendrites (top). The proximal node of the tertiary dendrites correlates well with other proximal segments and correlates somewhat with the distal portion of its own dendrite (middle). The distal node of the tertiary dendrite correlates well with itself only, with a slight increase in correlation with the distal dendrite attached to the same secondary branch relative to other distal dendrites (bottom). C, Top, The membrane potential of the soma and one tertiary dendrite recorded during the times indicated (APs chopped at -10 mV). Voltage was recorded at the soma (black) and at the proximal (red) and distal (blue) ends of the same tertiary dendritic compartment (indicated by arrows, inset). Bottom, The intracellular calcium concentration at the dendritic locations indicated in the inset. Action potentials initiated in the soma are able to invade even the distal ends of the dendrites and may result in calcium influx, particularly if synaptic activity has already depolarized the dendritic compartment. Note that the distal calcium response is nonlinear, because a relatively small increase in depolarization (∼4 mV in the second spike) can lead to a threefold difference in resulting calcium concentration.

Results

Response to current injection

A stylized model of the NAcb MSP cell with all known intrinsic currents was constructed that captured the main features of the morphological structure of the cell (see Materials and Methods) (Fig. 1A,B). To calibrate model parameters, the electrophysiological properties of NAcb MSP cells were examined under current clamp using whole-cell patch recordings in vitro on NAcb MSP cells in slices of the young adult rat. Conductance parameters were tuned so that the response of the model cell matched that of in vitro MSP cells to both subthreshold and suprathreshold current injections.

As current injection levels were increased above threshold, cells in the in vitro preparation produced a linear increase in spike frequency within the reported range of physiological firing (<10 Hz) (Pennartz et al., 1994). The mean slope of the output spike frequency in relation to increasing current injection of the in vitro cells was 6.43 ± 0.22 (AP/0.1 nA) (Fig. 1E, inset). Of seven cells examined, two showed a small amount of spike frequency adaptation, which could be matched in the model by increasing the level of the Ca²⁺-dependant K⁺ currents (data not shown). Adjustment of the K_RP and Ca²⁺-dependent K⁺ maximal conductances enabled a reasonable match between the in vitro cell and the ISI for a given current input. A slope of 6.25 (AP/0.1 nA) was chosen for the model cell to match the response of the cell represented in Figure 1, C and D, and this parameter set was used for the remainder of the experiments. We were unable to match the U-shaped AHP well with the model (Fig. 1D,F), possibly because of an inaccurate kinetic characterization of the Ca²⁺-dependent K⁺ currents or the fast Na⁺ current. The impact of the K_IR current on V_m in response to negative current injection can be seen in the bottom-most traces of the current (arrows). The response to subthreshold current injection was obtained in vitro from 12 MSP cells by measuring the voltage at 450 ms into a 500 ms pulse (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). The relationship between current injection and voltage response of the 12 cells was nonlinear, with a small amount of inward rectification during negative current injections (Fig. 1E). The current responsible for the nonlinearity below the resting potential is a K⁺ inward rectifier, which opens at hyperpolarized membrane potentials (V_m) and closes as the cell moves closer to AP threshold (Uchimura et al., 1989) (Wilson, 1992; Mermelstein et al., 1998). This inward rectification was not as prominent as has been reported for the dorsal striatum but is consistent with previous results in the ventral striatum (O'Donnell and Grace, 1993; Wilson, 1993). The model cell matched this current-voltage relationship well. The mean resting V_m was -87.75 mV in the in vitro experiments, which was matched in the model by adjusting the leak and K_IR currents. Although the frequency-current slope was not perfectly matched to the example cell by the model, minor adjustments in the intermediate current injection values revealed similar behavior of the in vitro cell and the model (Fig. 1F).

A hallmark of the striatal MSP cell is the long depolarizing ramp before the first AP in response to threshold depolarizing pulses (Surmeier et al., 1989; Nisenbaum et al., 1994). The model allows examination of the underlying kinetic processes and current contributions to this ramp, seen in the control trace in Figure 2A (for currents during synaptically driven states, see supplemental Fig. 2, available at www.jneurosci.org as supplemental material). Inward sodium current (NaF) and inactivation of the K_As current are the major constituents of this subthreshold ramp, with lesser contributions from K_IR and K_Af (Fig. 2B). A delicate balance between inward and outward currents creates this ramp. The K_IR current is open at resting V_m and increases immediately during injection of depolarizing current. As V_m depolarizes, K_IR deactivates slightly within 50 ms because the activation curve decreases significantly as V_m moves closer to spike threshold. The K_Af channel activates simultaneously with the increase in K_IR current. K_As has a longer time constant of activation (8.5 ms at -50 mV at 35°C compared with ∼1 ms for K_Af), and therefore the K_As current increases more slowly in response to the current pulse. At ∼250 ms, there is temporary equilibrium of all four voltage-dependent outward currents in the soma. In concert with these outward currents, the fast Na⁺ current depolarizes the membrane, which creates an interplay between the inactivation of K_As and the activation of the inward Na⁺ current that leads to the ramp before an AP. A-type currents have been demonstrated previously to play a role in these aspects of membrane behavior as well as contributing to the nonlinearity of the membrane (Nisenbaum et al., 1994; Nisenbaum and Wilson, 1995).

The importance of the K_As inactivation in shaping the ramp and the time to first action potential can be seen by scaling the level of its inactivation (see Materials and Methods). A 40% increase in the inactivation parameter led to an action potential, whereas a 40% decrease led to a reduction of the ramp (Fig. 2A). These results suggest that the inactivation parameter of this current would be a good target for dopaminergic modulation of the time to first spike as well as the number of spikes produced from a given current injection (data not shown).

Response to synaptic input

The NAcb MSP cells express a mixture of NMDA and AMPA receptors at afferent glutamatergic synapses, and GABAergic inputs originate from both interneurons and lateral connections (Chang and Kitai, 1986; Pennartz et al., 1991; Plenz, 2003; Taverna et al., 2004; Tepper et al., 2004). We examined the combined effect of these currents on the membrane response of the cell by simulating the afferent inputs these cells might receive. To understand the response of the cell to changes in input, we varied the mean frequency of Gaussian-distributed input the cell received at all types of receptors (see Materials and Methods). Previous studies have demonstrated that the ratio of GABAergic and glutamatergic input remains constant with shifts between the up and down state (Blackwell et al., 2003). The ratio of GABAergic and glutamatergic inputs was therefore held constant in the model during the variation of the mean input frequency.

An increase in the synaptic input from the baseline level of 504 inputs/s to 1260 inputs/s led to a clear shift in the membrane potential from -75 mV to approximately -55 mV (Fig. 3A, black trace). The cell makes fast transitions into the up state, although the first AP may be delayed for some time after the transition. The model fired approximately one AP per up state at a mean input frequency of 1075 Hz, and three APs per up state at a mean frequency of 1260 Hz. APs were only generated during up states, in agreement with in vivo and in vitro observations (Wilson and Groves, 1981; O'Donnell and Grace, 1993, 1995; Kerr and Plenz, 2002; Vergara et al., 2003). Blackwell et al. (2003) have estimated the number of inputs during the up and down states in an MSP cell in an organotypic rat slice preparation. Our results agree with their findings that the number of inputs per second in the up state is ∼800 Hz.

During the periods of greater synaptic input, there are no transitions back to the down state until the input is reduced. Despite significant variation in the instantaneous input frequency (see Materials and Methods), the response of the cell appears to closely follow a time-averaged window of afferent activity of ∼50 ms (Fig. 3A,C). This suggests that transitions to the up state are robust phenomena that accurately reflect the underlying structure of consistent increases in afferent input over a limited time period.

At the beginning of the up transition, the total amount of AMPA current is greater than total NMDA current attributable to the Mg²⁺ block that is removed from the NMDA channels as the transition continues (Fig. 3B). When the input is decreased to baseline levels, the cell hyperpolarizes toward the down state with an exponential time course (Fig. 3A). During the transition to the down state, AMPA current decreases faster than the NMDA current attributable to its shorter time constant of deactivation (5.75 vs 160 ms at 35°C). The time constant of an exponential fit to this transition (104 ms) is more compatible with the NMDA deactivation τ than that of AMPA. With NMDA blocked and AMPA conductance increased to compensate for the loss of inward current, the time constant of this transition is reduced to 25 ms, suggesting a large contribution of the NMDA current deactivation to the time course of this state change (data not shown). Total GABAergic synaptic current appears to remain relatively constant despite these transitions attributable to the proximity of the membrane potential to the reversal potential of GABA (-60 mV).

For the model, the NMDA/AMPA conductance ratio was set at a conservative value of 0.5 based on published data (Myme et al., 2003; Watt et al., 2004), although estimates range up to >5 in the literature. Even at this low ratio, the NMDA current becomes critical, contributing to maintaining the up state in a V_m range in which APs are generated (Sandstrom and Rebec, 2003; Vergara et al., 2003). When NMDA currents were blocked in the model, the mean V_m reached during the up state was less depolarized and the cell did not fire APs (Fig. 3A, red trace). This effect has been demonstrated previously during spontaneous oscillations in slice experiments in the dorsal striatum (Vergara et al., 2003).

Feedforward and lateral GABAergic inputs have been proposed to play an important role in shaping both AP timing and response to glutamatergic input (Plenz, 2003; Tepper et al., 2004). In the up state, V_m is close to the reversal potential of Cl^- (-60 mV), which is above the resting membrane potential in the NAcb and below the spiking threshold (O'Donnell and Grace, 1993; Czubayko and Plenz, 2002; Plenz, 2003). We therefore predicted that the GABA current would clamp the membrane subthreshold and prevent firing but stabilize up states. We tested the effects of increased GABAergic input by increasing the conductance of the GABA receptors by a factor of 5. This resulted in the down states moving closer to the reversal potential of GABA and a loss of one AP in the up states (Fig. 3D compared with control in A). Surprisingly, the membrane potential trace did not differ significantly from control results when GABA was removed completely (Fig. 3D) or when E_Cl was changed to either -50 or -70 mV (data not shown). This suggests that GABAergic input is perhaps involved in fine control of spike timing and that blocking GABA in the NAcb in vivo would not result in paroxysmal activity.

Dendritic processing

It has been proposed recently that the backpropagation of APs into the dendrites of the MSP cell may be responsible for an increase in calcium in the dendrites, possibly leading to spike-timing-dependent plasticity in striatal cells (Kerr and Plenz, 2002, 2004). It has also been shown that the firing of APs in the up state leads to calcium influx into dendritic spines via glutamatergic receptors and voltage-gated calcium channels (Carter and Sabatini, 2004). However, because of the small diameter of the dendrites, dendritic membrane potential behavior has been difficult to assess directly during synaptic input and was therefore examined in the model.

During synaptic input in the down state, there were variations in V_m between different dendrites of up to 20 mV (Fig. 4A). When ∼25% of the distal dendrites are depolarized above -60 mV, a transition to the up state occurred that favored the transition of the remaining dendrites to the up state. Once in the up state, dendritic membrane potentials again changed independently with variations of up to 20 mV until the AP threshold was reached at the soma (supplemental movie, available at www.jneurosci.org as supplemental material). To quantify the correlation of V_m between different parts of the cell, correlations were calculated between five different points on the cell and the V_m of the rest of the cell over a 2 s simulation run (see Materials and Methods). The values of the correlation ranged from 0.74 to 1, with the lowest correlations between the tips of the distal dendrites and the tips of other distal dendrites or the soma, because these are most electrotonically distant from one another (Fig. 4B, Dist. Tertiary). The correlation between the distal tip and the proximal portion of other distal dendrites attached to the same secondary branch was slightly higher (0.87). The soma was well correlated with the primary and secondary dendrites and the most proximal portion of the tertiary dendrite (0.93). The proximal portion of the tertiary dendrites were most correlated to each other and least correlated to the tips of other dendrites (Fig. 4B, Prox. Tertiary). These results suggest that each distal tertiary dendrite processes input independently but that the proximal portions begin to integrate information from each other and their respective distal portion.

During an action potential, the depolarization was backpropagated along the entire dendritic tree (Fig. 4C). With a 10:1 ratio of somatic to dendritic Na⁺ conductance in the dendrites (see Materials and Methods), there was an ∼30 mV depolarization at the proximal end of the distal dendrite after an action potential, with an ∼15 mV depolarization transmitted to the most distal segment of the dendrites. At this level of potential change in the distal dendrites, there is a substantial change in intracellular calcium in these dendrites attributable to influx through voltage-gated Ca²⁺ channels. Calcium influx in the dendrites does not occur until the cell has reached the up state. Depolarization of the dendrites attributable to synaptic input before the backpropagation of the AP appears to accentuate the amount of calcium influx to these dendrites during the AP. These results support previous studies suggesting that backpropagation of APs may induce voltage changes sufficient to lead to Ca²⁺ influx in the dendrites (Kerr and Plenz, 2002, 2004; Carter and Sabatini, 2004). Kerr and Plenz (2004) have reported a greater influx of Ca²⁺ through the NMDA receptor after action potentials in the up state, suggesting one mechanism whereby plasticity can be induced because of AP timing.

Effect of NMDA/AMPA ratio on nonlinearity

The NMDA/AMPA ratio has been reported to increase in the NAcb of cocaine-addicted rats and is potentially altered in schizophrenia (Thomas et al., 2001; Coyle et al., 2003). We tested the effect of varying this ratio on the behavior of the NAcb cells in response to patterned depolarizing input. Multiple runs of a synaptic input ramp with a small plateau were used to examine hysteretic properties of the membrane at various NMDA/AMPA ratios (Fig. 5A). These simulations revealed that an increase in NMDA current was capable of extending the depolarization of the cell past the end of the input plateau by 73 ms at a 0.8 NMDA/AMPA ratio. There was a linear increase of this extension to 154 ms at an NMDA/AMPA ratio of 1 (Fig. 5B). At NMDA/AMPA ratios higher than 1, without a reduction in the overall synaptic weight, the cell began to spike before the input ramp (data not shown).

We wanted to explore the possibility that cells may compensate for aberrant NMDA/AMPA ratios by adjusting other properties that affect the input/output relationship. Therefore, simulations were also performed using ratios from 0.5 to 4, during which the total output of the cell was compensated by reducing synaptic input weights such that the total number of spikes was equal to that of the control condition (NMDA/AMPA of 0.5). At an NMDA/AMPA ratio of 1, the up state was only mildly extended (6 ms) instead of increasing to the 154 ms extension of the uncompensated condition. The time of extension of the last spike in the up state increased to 21 ms at the 1.5 ratio and, as the ratio was further increased, leveled off at ∼30 ms.

These results suggest that the NMDA current is responsible for a hysteretic component of the membrane potential during the transition to down states. To reveal this hysteresis graphically, we symmetrically reflected the V_m trace at the midpoint of the input, thus superimposing the transitions to the up and down states (Fig. 5C). There is little hysteresis in response to current injection, indicating a small role for intrinsic properties. When performed with synaptic input, hysteresis is evident in the control condition and accentuated by the increase in the NMDA/AMPA ratio from the control (0.5) to medium (1.5) and high (2.5) levels.

NMDA has been demonstrated to induce a region of negative slope conductance in striatal cells (Vergara et al., 2003), which may lead to bistable behavior (Schiller and Schiller, 2001). We examined this feature by voltage clamping the model at several potentials between -120 and -20 mV and recording the steady-state currents 600 ms after each voltage step. By stimulating the NMDA synapses of the model at different frequencies (0, 1042, and 2084 Hz), we were able to analyze the effects of realistic levels of NMDA on the negative slope conductance of the model. Moderate amounts of NMDA (1042 Hz stimulation), such as may be experienced during an up state, enhanced the negative slope conductance of the cell and led to a double crossing of the zero current axis (Fig. 5D). Increasing the amount of NMDA to 2084 Hz further enhanced negative slope conductance and led to “self-triggering” behavior (Schiller and Schiller, 2001). These results are in agreement with previous experimental data from the dorsal striatum demonstrating an increase in the negative slope conductance and double crossing of the zero current axis during NMDA bath application (Vergara et al., 2003). The model demonstrates that an increase in negative slope conductance via NMDA current at realistic synaptic input levels can achieve this result but without the apparent induction of bistability (Fig. 5C).

Oscillatory entrainment

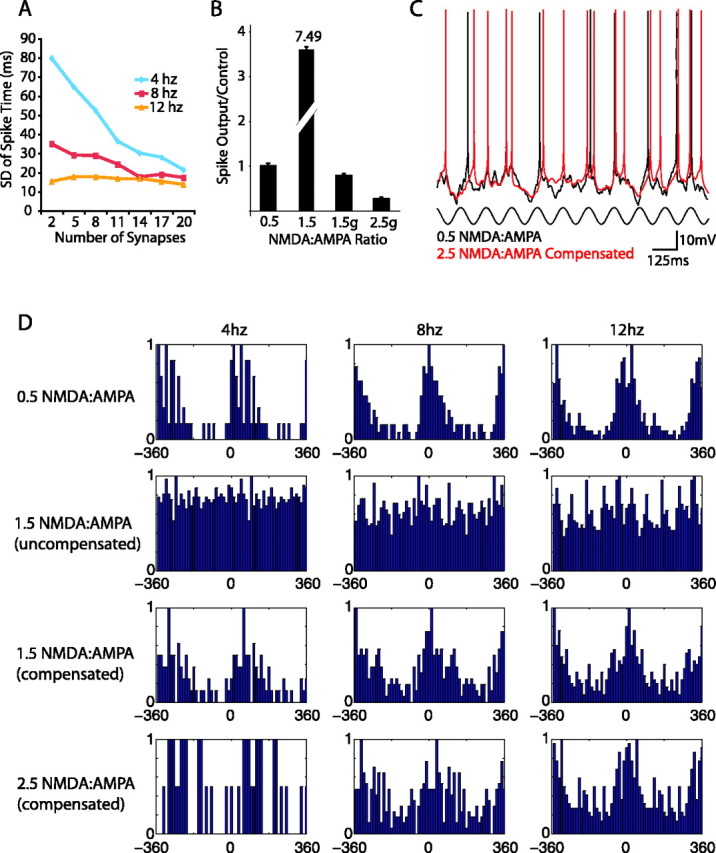
Previous reports have demonstrated strong oscillatory entrainment between HC and NAcb in the anesthetized rat (Goto and O'Donnell, 2001). Cells in the striatum and the PFC have been demonstrated to entrain to theta rhythms (4-12 Hz) arising from the HC, and there is evidence that ensembles of these entrained cells may be involved in consolidation of memory (Berke et al., 2004; Pennartz et al., 2004; Siapas et al., 2005). We investigated whether afferent input in the theta frequency range could entrain the model cell and determined the number of afferent cells required to entrain the model cell. Variation of the number of afferent cells participating in the oscillation was modeled by partially synchronizing the input trains (see Materials and Methods). The degree of entrainment was dependent on the frequency at which the afferent cells were oscillating. At 4 Hz, the entrainment improved as the number of synapses activated by oscillatory input increased (Fig. 6A). This behavior was evident at 8 Hz as well, but, at this frequency, the best entrainment was reached with a smaller number of afferents. At 12 Hz, the afferent input was capable of entraining the model cell well at all of the synapse numbers tested. The minimum number of afferent cells that induced entrainment to theta at all frequencies (11 of 84 glutamatergic synapses) was used for the remainder of the experiments. Based on the number of inputs required to keep the model cell in the up state and firing (∼1300/s), the number of afferent cells synchronized at a frequency of 8 Hz could be as low as 20.

Figure 6.

Increasing the NMDA/AMPA (N:A) ratio degrades the ability of the cell to entrain to oscillatory input. A, The number of synapses receiving oscillatory input is plotted against the SD of the spike time in relation to the oscillation peak. The 4 Hz oscillation requires 20 synapses receiving the oscillation to achieve the same entrainment as the 8 and 12 Hz oscillations at 11-14 synapses. Eleven synapses equates to ∼20% of the afferent input during an up state. B, The number of spikes in the MSP model per sine wave are plotted relative to control. Without any compensation, there is a large increase in total output of the cell. Conductance compensation (by reducing overall synaptic weight to match total synaptic conductance at 0.5 NMDA/AMPA ratio) leads to a loss of APs during oscillations at the 1.5g and 2.5g NMDA/AMPA ratios. C, At lower values of NMDA/AMPA (0.5), the cell spikes regularly in response to 8 Hz oscillatory input (black trace). At a higher NMDA/AMPA ratio (2.5), with weights increased to give approximately one spike per period, the cell does not entrain as regularly to the input. D, PSTHs of MSP spikes relative to peak of sine wave input are plotted. For clarity, the PSTH is centered at 0° and plotted in both directions. At 0.5 NMDA/AMPA ratios, a clear peak is evident at 4, 8, and 12 Hz oscillatory input, indicating that the cell is entraining well to the input. Increased values of NMDA/AMPA that are not compensated for spike output lead to loss of entrainment (uncompensated condition). With overall synaptic weight increased to give approximately one spike per cycle, as the NMDA/AMPA ratio is increased, the response of the cell to the oscillatory input becomes more variable (1.5 and 2.5 compensated conditions). This is evidenced by the loss of a clear peak and spurious spikes throughout the phase cycle.

We investigated whether the hysteretic properties of the membrane mediated by NMDA/AMPA ratio (above) have an effect on the ability of the model cell to entrain to this oscillatory input. Increasing the NMDA/AMPA ratio to 1.5 from 0.5 led to a more than sevenfold increase in the number of spikes per oscillation (Fig. 6B). Neurons are known to actively adjust to changes in the NMDA/AMPA ratio, so we tested different strategies that the cell might use to compensate for the increase in total output (Watt et al., 2004). The first strategy (conductance compensation) was to uniformly decrease the total synaptic input weights while maintaining the increased ratios of inputs, such that the total synaptic conductance remained the same (see Materials and Methods). This strategy resulted in a loss of total output from the cell at the 1.5 and 2.5 NMDA/AMPA ratios (Fig. 6 B). The second strategy consisted of adjusting the synaptic weights such that the ratio remained the same but also that the output per cycle for each frequency was equal to 1 (see Materials and Methods). This strategy was used for the remainder of the “compensated” experiments.

An example of the model cell entraining to input at 8 Hz at 0.5 and 2.5 NMDA/AMPA ratios is presented in Figure 6C. The cell is entrained well by the oscillatory input at lower NMDA/AMPA ratios, but there are clearly aberrant spikes with the increased NMDA levels, even after compensating for total output per cycle. To quantify this effect, peristimulus time histograms were created at each frequency while varying the NMDA/AMPA ratio. At lower NMDA/AMPA ratios, the cell is entrained well at 4, 8, and 12 Hz, as evidenced by the peaks around the zero phase of the oscillation (SD of spike time in relation to peak of the oscillation was 43.1, 23.3, and 15.4 ms, respectively) (Fig. 6D, top row). As the NMDA/AMPA ratio was increased without compensation, the variance of the response of the cell in relation to the input went up significantly (Fig. 6D, second row) [SD of spike times of 71.3, 54.2, and 48.9 ms for 4, 8, and 12 Hz respectively, significance measured via F test (see Materials and Methods)]. When the total spike output was compensated, the cell entrained reasonably well to the input at an NMDA/AMPA ratio of 1.5, although significantly less well than at 0.5 (Fig. 6D, third row) (SD of 57.1, 28.7, and 19.4 ms, significant via F test compared with 0.5 levels). At the highest levels of NMDA/AMPA tested with this paradigm (2.5), the cell appeared to not entrain at all at 4 Hz, and the 8 and 12 Hz oscillations were significantly degraded compared with the 0.5 level but not significantly different from the 1.5 ratio (Fig. 6D, bottom row) (SD of 75.7, 30.9, and 20.5 ms). These results suggest an optimal NMDA/AMPA ratio between 0.5 and 1.5 for entrainment to oscillatory input in the theta range.

Discussion

MSP models and intrinsic properties

We developed a model of the NAcb MSP cell that reproduces many of the known responses of these cells to current injection and synaptic input. The model is a modification and extension of Wilson's dorsal striatal MSP cell model (Wilson, 1992, 1995). This new model contains all ionic channels reported in these cells and allows investigation of how the interaction of morphology, intrinsic properties, and synaptic input generates specific membrane behaviors. The model incorporates recent data describing the K_Af and K_As currents, as well as a full description and implementation of all known calcium currents in the NAcb. This model also contains detailed synaptic ionotropic currents that allow investigation of the response of an MSP to synaptic input and changes in the ratio of synaptic currents. The model was tuned to the in vitro properties of an adult rat NAcb MSP cell and was then used to determine the type of inputs necessary to reproduce the behavior of the cell in slice culture and in vivo (O'Donnell and Grace, 1995).

The interplay of intrinsic properties has been investigated in previous models of MSP cells in the dorsal striatum. The effect of inward and outward rectifying potassium currents on both the synaptic input and the electrotonic properties of MSP dendrites with spines have been extensively studied (Wilson, 1992, 1995). Our results are in agreement with previous experimental and modeling results on the role of K_IR and K_A currents in determining up and down states (Wilson and Kawaguchi, 1996; Gruber et al., 2003) and the importance of the inactivation of K_As in the ramp to first spike (Nisenbaum et al., 1994; Mahon et al., 2000).

The relatively sharp transitions between up and down states has prompted discussion of MSP cells as “bistable” (Nicola et al., 2000; Gruber et al., 2003). A true bistable cell is one that has intrinsic or synaptic properties that allow it to maintain each of two states and to avoid the voltage range between these states. In our model, there is clearly a down state stabilized by the inwardly rectifying conductance, yet it is less clear that there is a stable up state, or that there is a voltage space between these states in which the cell cannot remain. The up state must be maintained with synaptic input, and, with realistic levels of NMDA, the up state can be maintained for up to 150 ms past the decrease in synaptic inputs during input ramp experiments. However, we found no evidence of a true plateau potential from the present intrinsic properties, and therefore we propose that the MSP cell is not intrinsically bistable but becomes mildly hysteretic when enough NMDA current is available. These conclusions hold true only for the unmodulated behavior, however, and the addition of dopamine modulation or pharmacological manipulations may lead to an increase in the nonlinearity of the membrane such that the cell becomes even more hysteretic or possibly bistable at higher levels of modulation (Hernández-López et al., 1997; Gruber et al., 2003). L-type calcium currents, particularly the low-voltage activated 1.3 variety demonstrated most prominently in the dorsal striatum, when targeted by modulation or drugs may have a larger impact on the hysteretic properties than that found here (Vergara et al., 2003).

Synaptic input processing

One of the unexpected results of these simulations was the lack of changes in membrane potential and spike output when GABA was either eliminated or increased by a factor of five. The slight changes in spike output from the increased GABA conductance suggest that to suppress spike output, input arriving from afferent pathways along both lateral and feedforward GABAergic pathways must have a different temporal structure than the glutamatergic input. We also found it striking that the membrane potential of the cell was so accurately represented by a 50 ms sliding-window filter of the instantaneous frequency of the glutamatergic input. It appears from these results that the cell is integrating all inputs in a linear manner when viewed from the somatic V_m. This is surprising given our results that the dendrites are effectively independent.

NMDA/AMPA ratio and oscillatory entrainment

NMDA appears to be necessary to maintain the up states of these cells at control NMDA/AMPA ratios. This confirms previous work in the dorsal striatum demonstrating that blocking the NMDA current has a profound effect on oscillations in the slice (Vergara et al., 2003). The close match between transitions to the down state in the model and in vivo also suggest an abrupt decline in afferent input to the in vivo NAcb under anesthesia, as shown previously in the cortex (Contreras et al., 1997).

By structuring a portion of the afferent input to simulate oscillations in the theta range (4-12 Hz), we were able to entrain the output of the model MSP cell to this oscillatory input. There is a large functional projection from the hippocampus to the ventral striatum, and the entrainment of cells in the ventral striatum and the PFC to hippocampal theta has been demonstrated recently in awake rats (Berke et al., 2004; Siapas et al., 2005). Modification of the NMDA/AMPA ratio appears to have a number of effects on the cell, many of which appear to be deleterious to the ability of the cell to process input or entrain to afferent oscillations. Increasing the NMDA/AMPA ratio increases the hysteretic properties of the membrane, which in turn drastically changes the output of the cell in response to oscillatory input. Local infusion of NMDA agonists and antagonists to the NAcb under behaving conditions requiring HC theta could be examined to test how these modulations might affect on-line processing.

Afferent ensembles

Our results combined with previous reports of the number of inputs required for an up state make predictions about the afferent input to each NAcb MSP cell. The mean requirement for input to keep the cell in the up state appears to be ∼1000 inputs per second. If we assume an average maximal firing rate of 10 Hz during active behavioral tasks for afferent cells and a 1:1 convergence between afferents and MSPs, then each cell is only sampling from ∼100 cells in a given second. If for simplicity we use a value of 10,000 spines per MSP cell, then ∼1% of the synapses are active in a given second. This suggests that each MSP cell can sample from a minimum of 100 sets of different ensembles of afferent cells. A relatively small cohort of cells in each afferent structure may drive a single NAcb MSP cell, a prediction that is also supported by our finding that ∼20 afferent cells locked to an oscillation are capable of entraining the cell to theta.

The accumbens is therefore well positioned to detect multiple patterns of highly selected inputs, perhaps as few as 20 inputs from each afferent structure. Although these 20 inputs could be from widely separated cells in an afferent structure (i.e., PFC), it is possible that the active cells constitute a functionally coherent neuronal group (Edelman and Finkel, 1984; Gerstein et al., 1989; Miller and Zucker, 1999). This lends support to the idea that the striatum is an area in which dimensionality reduction may take place (Bar-Gad et al., 2003) but further suggests that the NAcb may be examining and integrating local features of these assemblies. In combination with our finding that the MSP integrates input over a relatively large time window (∼50 ms), this suggests that the NAcb detects the co-occurrence of signature patterns of input relating context, emotion, and working memory.

Implications for pathology

Given the fine balance of intrinsic and synaptic mechanisms underlying MSP function, the accumbens appears exceptionally susceptible to the effects of drugs and disease. Dopamine, which is implicated in both schizophrenia and addiction, has been demonstrated to modulate many of the parameters in the model presented here, most notably K_As (Hopf et al., 2003), K_IR (Nicola et al., 2000), Na⁺ and L-type Ca²⁺ channels (Foehring and Surmeier, 1993; Surmeier et al., 1995; Hernández-López et al., 1997), and NMDA and AMPA receptors (Cepeda and Levine, 1998; Hernandez-Echeagaray et al., 2004). NMDA hypofunction has been proposed to play a role in schizophrenia (Coyle et al., 2003; Farber, 2003; Moghaddam, 2003). A decrease in the NMDA/AMPA ratio may lead to a reduction in the number or specificity of afferent ensembles that can be represented by each cell, because more inputs per cell would be required to reach the up state. This reduction may be associated with the loss of active parallel pathways through the striatum and may correlate with the reduction of potential serial memory tasks in schizophrenia (Fraser et al., 2004). During addiction, the increase in the NMDA/AMPA ratio may play a role in the effect of dominance of a single behavioral pathway over others, leading to such findings as cocaine-sensitive cells in the NAcb (Carelli, 2002; Kelley, 2004; Peoples et al., 2004).

Although this is one of many possible models that could capture the physiological properties of NAcb MSP cells, its strength lies in the characterization of the consequences of altering the NMDA/AMPA ratio. The NMDA/AMPA ratio appears to play a significant role in determining how the MSP cell responds to input during state transitions and to entraining oscillatory input. Alteration of these ratios via dopamine modulation or pathology could have profound effects on both the encoding of afferent information in the NAcb network and the cellular output that leads to motivated behavior.

Appendix

Intrinsic currents

The general equation for sodium and potassium currents is given by Equation A1:

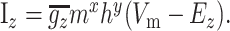(A1)

The parameters m and h are calculated according to the Hodgkin-Huxley formulation,

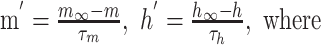(A2)

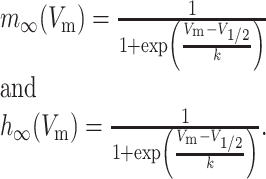(A3)

Here, m and h represent the activation and inactivation state of the channel, respectively, and m_∞, h_∞, τ_m, and τ_h are the steady-state activation curves and time constants for m and h at membrane voltage V_m. V_1/2 and k represent the half-activation voltages and slope of the steady-state Boltzmann fit to m_∞ and h_∞. E_Z is the reversal potential for each ion species; these values are E_Na = 50 mV for sodium and E_K = -90 mV for potassium. Parameters for all currents are listed in Table 2.

A number of the currents (K_As, K_RP, CaN, and CaL1.2) are described as partially inactivating. In these cases, Equation A1 is modified to be

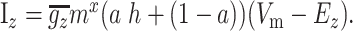(A4)

The variable a can be adjusted between 0 (no inactivation) and 1 (fully inactivating) to increase or decrease the amount of inactivation and was set to match published data.

Sodium currents

For the fast sodium current, we used a sodium channel isolated from rat hippocampal CA1 pyramidal neurons (Martina and Jonas, 1997). For the persistent sodium current, steady-state parameters and voltage-dependent kinetics for inactivation were taken from entorhinal cortical stellate cells (Magistretti and Alonso, 1999). Voltage-dependent kinetics for the time constant of activation were taken from a computational model of a rat layer 2/3 pyramidal neuron (Traub et al., 2003). Because a uniform density of sodium resulted in unrealistic cell behavior, the total conductance of sodium in the soma was set to be 10 times the total conductance of sodium in the dendrites; that is, G_soma = 10 × G_dend.

Calcium currents

Calcium channels were modeled using the Goldman-Hodgkin-Katz equation, which accounts for current rectification at elevated membrane potentials:

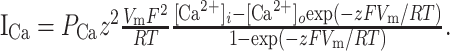(A5)

Here, z = 2, F = 96,489 C/mol, r = 8.31 J/mol-K, T = 35°C is temperature, V_m is membrane potential, and [Ca²⁺]_o = 5 mm and [Ca²⁺]_i = 0.001 mm are extracellular and intracellular calcium concentration, respectively. P_Ca, channel permeability to calcium ions, can be approximated using a Hodgkin-Huxley-like formalism:

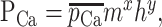(A6)

with m and h calculated as in Equations A2 and A3 above (De Schutter and Smolen, 1998). The parameters for each current are listed in Table 2.

Data for calcium currents was taken from the most complete information regarding these currents in NAcb MSP cells (Churchill and Macvicar, 1998). This study was performed on acutely isolated cells rather than whole cells, requiring us to correct whole-cell currents upwards for loss of membrane area attributable to removal of the dendrites in the preparation. We assumed that the current density in the acutely isolated cells was constant for the entire cell and applied this density to our whole-cell model. This gave a peak whole-cell HVA calcium current of 3.64 nA, ∼10 times the value in the dissociated cell (0.305 nA). We then separated this current among the four HVA channels according to the ratios detailed by Churchill and Macvicar (1998): 1.2 L-type = 18%, N-type = 25%, Q-type = 17%, and R-type = 32%. LTI current in this study was ∼7% of peak HVA current, or 0.262 nA. LTI current was distributed evenly between 1.3 L-type and T-type channels.

Both the activation kinetics (Kasai and Neher, 1992) and the activation steady-state parameters (Churchill and Macvicar, 1998) for the 1.2 L-type channels have been characterized. As Churchill and Macvicar report, 1.2 L-type calcium currents are mostly non-inactivating but do exhibit a decay of 11% over a 120 ms voltage pulse (Churchill and Macvicar, 1998). We matched this decay by including an inactivation variable as described in Equation A4. Inactivation parameters for 1.2 L-type calcium channels are not available, so we used parameters for 1.3 L-type channels, including a time constant of inactivation of 14.77 ms (Bell et al., 2001).

The 1.3 L-type channel is only partially characterized, so the same activation kinetics as for the 1.2 L-type were used (Kasai and Neher, 1992). Churchill and Macvicar (1998) provide a k value for activation of the LTI current but not a V_1/2; we calculated V_1/2 by matching experimental data for the I-V response of rat 1.3α₁ subunits expressed in Xenopus oocytes (Xu and Lipscombe, 2001). Inactivation steady-state parameters and kinetics have been published previously (Bell et al., 2001).

The activation kinetics (Kasai and Neher, 1992) and the steady-state activation parameters for the N-type channel have been characterized (Churchill and Macvicar, 1998). According to published reports, N-type calcium currents decay 17% over a 120 ms voltage pulse (Churchill and Macvicar, 1998). This decay rate was matched using Equation A4. Inactivation parameters for N-type calcium channels have been documented (McNaughton and Randall, 1997), although voltage-dependent kinetics are not available; we used a constant value of 23.33 ms (McNaughton and Randall, 1997).

Based on toxin sensitivity, it was reported that accumbal cells possess primarily Q-type channels and few, if any, P-type channels. Activation curves for this current have been reported (Churchill and Macvicar, 1998). A single τ value of 1.13 ms was used based on reports from other brain areas (Randall and Tsien, 1995). No inactivation was modeled, because the current is described as either having a long time constant for inactivation (∼2 s at 22°C) (Mermelstein et al., 1999) or no inactivation at all (Churchill and Macvicar, 1998). R-type currents are generally defined by their resistance to toxins that block other calcium channels. These channels are relatively poorly characterized yet comprise a large portion of HVA calcium current in accumbal cells. R-type channels were modeled using steady-state activation curves from Churchill and MacVicar (1998). Inactivation steady-state curves were taken from dorsal striatum (Foehring et al., 2000). Voltage dependence is available for the inactivation time constant (Brevi et al., 2001) but not activation time constant, for which we used a constant value of 1.7 ms (Foehring et al., 2000).

Calcium dynamics

The calcium concentration [Ca²⁺]_i in a thin shell just inside the cell membrane was tracked for each compartment by calculating calcium influx attributable to calcium-channel currents, calcium efflux attributable to active pumps in the membrane, and intracellular diffusion:

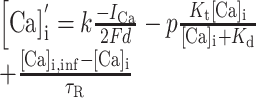(A7)

(Destexhe et al., 1993).

For the current influx term, I_Ca is incoming calcium current, F = 96,489 C/mol, and d = 0.1 μm is shell depth. The pump term is represented using the Michaelis-Menten formulation with K_t = 10^-4 mm/ms and K_d = 10^-4 mm. The diffusive term uses τ_R = 43 ms (Jackson and Redman, 2003) and [Ca²⁺]_i,inf = 10^-5 mm. The parameters k = 10000 and p = 0.02 were set to balance calcium influx and efflux and give reasonable calcium sensitivity for both SK and BK K_Ca channels.

Synaptic currents

NMDA, AMPA, and GABA currents were modeled using a modified two-state synapse (based on the Exp2Syn synapse in NEURON), providing both summation and saturation. These currents obeyed the equation

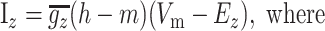(A8)

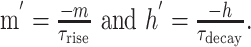(A9)

The NMDA current was modified to account for voltage-dependent magnesium blockade by multiplying Equation A2 by a factor B(V_m), where

(A10)

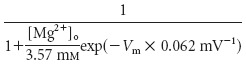(Jahr and Stevens, 1990).

Time constant equations

NaPτ_m

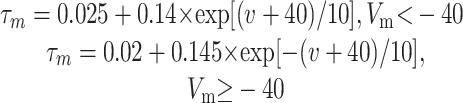(A11)

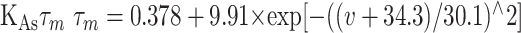(A12)

K_Asτ_h

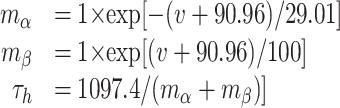(A13)

CaLτ_m

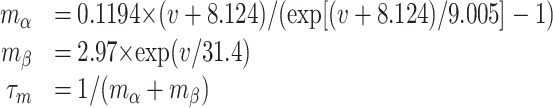(A14)

CaNτ_m

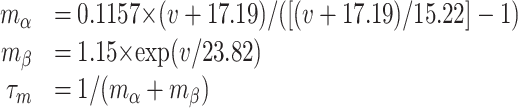(A15)