Abstract
In nature, sounds from multiple sources sum at the eardrums, generating complex cues for sound localization and identification. In this clutter, the auditory system must determine “what is where.” We examined this process in the auditory space map of the barn owl's (Tyto alba) inferior colliculus using two spatially separated sources simultaneously emitting uncorrelated noise bursts, which were uniquely identified by different frequencies of sinusoidal amplitude modulation. Spatial response profiles of isolated neurons were constructed by testing the source-pair centered at various locations in virtual auditory space. The neurons responded whenever a source was placed within the receptive field, generating two clearly segregated foci of activity at appropriate loci. The spike trains were locked strongly to the amplitude modulation of the source within the receptive field, whereas the other source had minimal influence. Two sources amplitude modulated at the same rate were resolved successfully, suggesting that source separation is based on differences of fine structure. The spike rate and synchrony were stronger for whichever source had the stronger average binaural level. A computational model showed that neuronal activity was primarily proportional to the degree of matching between the momentary binaural cues and the preferred values of the neuron. The model showed that individual neurons respond to and synchronize with sources in their receptive field if there are frequencies having an average binaural-level advantage over a second source. Frequencies with interaural phase differences that are shared by both sources may also evoke activity, which may be synchronized with the amplitude modulations from either source.
Keywords: auditory scene analysis, binaural, inferior colliculus, masking, sound localization, stream segregation
Introduction
We are able to listen selectively to a single sound source in acoustical environments cluttered with multiple sounds and their echoes. This feat is more than localizing the individual sources. The listener must also identify the sound (e.g., comprehend speech) emanating from each source. In other words, the auditory system must determine “what is where.”
In the barn owl (Tyto alba), a predator specialized for spatial hearing, the external nucleus of the inferior colliculus (ICx) contains a topographic representation of space built of auditory neurons with discrete spatial receptive fields (RFs) (Knudsen and Konishi, 1978). The RFs of these space-specific neurons are based on neuronal sensitivity to interaural differences in the timing (ITD) and level (ILD) of sounds, the major cues for sound localization in owls and humans (Rayleigh, 1907; Moiseff and Konishi, 1983; Peña and Konishi, 2001). Lesions of this auditory space map lead to scotoma-like defects in sound localization, and microstimulation of the optic tectum, which receives a direct, topographic projection from the ICx, evokes a rapid head turn to that area of space represented at the point of stimulation (duLac and Knudsen, 1990; Wagner, 1993).
The space map underlies the bird's ability to determine the location and identity of sounds. In an anechoic environment with only a single source, neurons appropriately signal the location of the source and synchronize their spiking to the envelope of the sound (Knudsen and Konishi, 1978; Keller et al., 1998). With multiple sources, the sound waves from each source will add in the ears, and if the sounds have overlapping spectra, the binaural cues will fluctuate over time in a complex manner (Bauer, 1961; Takahashi and Keller, 1994; Blauert, 1997; Roman et al., 2003). Such dynamic cues may make it difficult for the space map to image the sources accurately and may also compromise the abilities of the cells to signal the temporal characteristics intrinsic to each source.
Nevertheless, spatial hearing is remarkably resistant to noise. For instance, adding a second source of equal or lesser intensity only slightly degrades the localizability and speech intelligibility of the first source (Good and Gilkey, 1996; Blauert, 1997; Best et al., 2004). Although reverberation in echoic environments may contribute to the quality of a sound, the sound coming directly from an active source often dominates localization (for review, see Litovsky et al., 1999). In owls and humans, two sources are individually localizable only if they differ in frequency or are uncorrelated in overlapping frequency bands (Perrott, 1984a,b; Takahashi and Keller, 1994; Keller and Takahashi, 1996; Best et al., 2002, 2004). The underlying mechanisms of such processes are of great interest, and numerous models of auditory neural function have been proposed to explain these psychoacoustic phenomena (Jeffress, 1948; Durlach, 1972; Colburn, 1977; Blauert and Cobben, 1978; Lindemann, 1986; Stern et al., 1988; Gaik, 1993; Hartung and Sterbing, 2001; Best et al., 2002; Braasch, 2002; Roman et al., 2003; Faller and Merimaa, 2004; Fischer and Anderson, 2004). Only rarely, however, have the responses of the models been compared with those of central auditory neurons involved in auditory localization (Hartung and Sterbing, 2001).
In the present study, we asked whether space-specific neurons could resolve two sound sources emitting uncorrelated noise bursts, each of which was sinusoidally amplitude modulated at a different rate, and assessed the fidelity with which the temporal spiking pattern represented the amplitude modulations inherent to the sound from each source. We then used a simple model to determine the extent to which the activity of a space-specific neuron was proportional to the match between the momentary frequency-specific binaural cues and those to which the neuron was tuned. We use the model to predict the pattern of activity across the space map in response to the two sound sources.
Materials and Methods
All procedures were performed under a protocol approved by the Institutional Animal Care and Use Committee of the University of Oregon.
Surgical procedures. Recordings were obtained from 13 captive-bred adult barn owls (T. alba) anesthetized by intramuscular injection of ketamine (KetaVed, Vedco; 0.1 ml at 100 mg/ml) and valium (diazepam; 0.08 ml at 5 mg/ml; Abbott Laboratories, Abbott Park, IL) as needed (approximately every 3 h). Each bird was fit with a headplate for stabilization within a stereotaxic device and also with bilateral recording wells through which electrodes were inserted (Euston and Takahashi, 2002; Spezio and Takahashi, 2003).
Stimulus generation and experimental procedure. Stimulus construction, data analysis, and model development were performed in Matlab (version 6.5.1; Mathworks, Natick, MA).
The main experiment consisted of presenting sounds simultaneously from two sources in virtual auditory space (VAS) separated by 30 or 40° horizontally, vertically, or diagonally. Sounds were filtered through individualized head-related impulse responses (HRIRs) that were recorded and processed as described by Keller et al. (1998) (5° resolution, double polar coordinates). Stimuli consisted of broadband noises either 100 ms or 1 s in duration (flat amplitude spectrum between 2 and 11 kHz, random phase spectrum, 5 ms rise/fall times). In most cases, the noises were further amplitude modulated to 50° depth with a sinusoidal envelope of either 55 or 75 Hz. Modulations of the envelope are crucial in such auditory tasks as the detection of prey and the recognition of conspecific vocalizations (Brenowitz, 1983; Schnitzler, 1987; Drullman, 1995; Shannon et al., 1995; Bodnar and Bass, 1997, 1999; Wright et al., 1997; Tobias et al., 1998) and thus constituted our operational definition of sound-source identity. These stimuli were convolved in real time with location-specific HRIRs [Tucker Davis Technologies (TDT; Alachua, FL) PD1], convolved again with inverse filters for the earphones, attenuated to 20-30 dB above threshold (TDT PA4), and impedance matched (TDT HB1) to a pair of in-ear earphones (ER-1; Etymotic Research, Elk Grove Village, IL).
Extracellular single-unit recordings were obtained from the ICx using tungsten microelectrodes (Frederick Haer, Brunswick, ME). Spike times were recorded to computer disk. After isolation, cellular responses were first characterized by varying ILD, ITD, and level by frequency-independent adjustments of the signals to each ear. For more precise testing, we used location-specific HRIRs to present stimuli from a checkerboard pattern of locations across the frontal hemisphere in VAS. Such a test was called “fully cued” because all sound localization cues varied in a natural manner. By convention, negative azimuths correspond to locations left of the midline, and negative elevations correspond to locations below eye level.
The majority of cells in our sample had RF centers near to the center of gaze (median eccentricity, 19.2°; interquartile range, 16.0°) in double-polar coordinates (n = 102). The RFs of nearly all cells were highly spatially restricted. We used an index of spatialization (SI) to characterize the spatial tuning of each cell to fully cued stimuli: SI = 1 - ∑space(firing rate × distance from RF center) × ∑space(distance from RF center).
SI values near 0 indicate activity that was uniformly distributed across the space map, whereas values near 1 indicate RFs that were highly spatially restricted. The distribution of SI values increased exponentially toward high values and obtained a median value of 0.94 (interquartile range, 0.08). A regression of the SI values on the eccentricities of the RF center for all cells showed no significant trend in SI values across the space map (slope of the regression not significantly different from zero; p < 0.90).
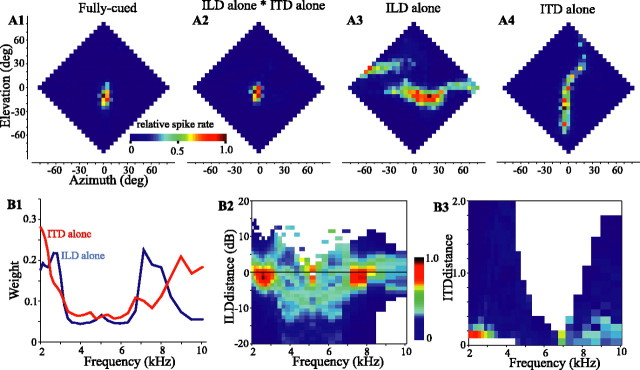
Our analysis requires the assessment of the sensitivity of a cell to ITD and ILD within each frequency band. We estimated this frequency-specific tuning from “ITD-alone” and “ILD-alone” RFs, as described below. As opposed to the fully cued case, in an ITD-alone test, broadband noise was filtered with the ITD spectrum for each location in frontal space and presented to the cell, whereas the ILD spectrum was fixed at values corresponding to the best location of the cell. Conversely, in the ILD-alone test, the noise stimulus was filtered with the ILD spectrum of each location, whereas the ITD was fixed at the optimal value of the cell (for details, see Euston and Takahashi, 2002). Results from one cell are shown in Figure 1 A1-A4. The ILD-alone RF (Fig. 1 A3) is elongated horizontally. The ITD-alone RF (Fig. 1 A4), in contrast, is elongated vertically with a curve to the right above the horizon, a common feature of these plots, which matches a similar curve in ITD plots of the head-related transfer functions (HRTFs) (Keller et al., 1998). The intersection of these single-cued RFs, obtained by a point-by-point multiplication of the ITD-alone and ILD-alone responses, approximates the fully cued RF measured directly (Fig. 1, compare A1, A2). All of these observations are in agreement with previous descriptions (Euston and Takahashi, 2002; Spezio and Takahashi, 2003).
Figure 1.
Responses of an ICx neuron to fully cued (A1), ILD-alone (A3), and ITD-alone (A4) stimuli. Each plot presents the firing rate of the cell, color-coded and normalized over each plot, as a function of azimuth and elevation of the stimulus. Data have been interpolated from a checkerboard pattern obtained at a 10° resolution. In A2, the point-by-point multiplication of A3 by A4 is shown for comparison with A1. B1, Frequency weights for this cell estimated from the response of the cell to frequency-specific differences (dILD, dITD) between the binaural cues for each stimulus location and the optimal of the cell for each cue. The activity of the cell (normalized and color-coded) as a function of frequency and dILD (B2) or dITD (B3) is shown. Cell 939FG is shown. deg, Degree.
The shapes of the ILD-alone RFs have been shown to reflect the sum of spatial plots of ILD obtained from HRTFs for a given frequency, weighted by the ILD tuning of the cell at that frequency (Spezio and Takahashi, 2003). Similarly, although to a lesser degree, ITD tuning varies with frequency. ITD-alone RFs are also well described as the weighted sum of frequency-specific spatial plots of the ITD obtained from the HRTFs. The ILD-alone and ITD-alone RFs could therefore be decomposed into plots of neural activity as a function of frequency and ILD or ITD by the following procedure. We first passed each HRIR through a bank of 29 gammatone filters (2000-10,079 Hz) (Slaney, 1993) with  -octave separation, which were each constructed to approximate the owl's auditory nerve tuning curves (Köppl, 1997). We then obtained the ITD and ILD for each frequency band and at each location in space. The ILD was calculated as the decibel difference in intensity (right minus left), and the optimal ILD (ILDopt) of a cell was defined as the ILD spectrum at the best location of the cell in the ILD-alone RF. The difference between the ILD spectrum at each location and the ILDopt of the cell was termed the “ILD distance” (dILD = ILD - ILDopt). The ITD was calculated as a spectrum of cross covariances between the left and right ear signals for each location in space. Each cross covariance was normalized internally. At the best location of the cell, the peak height of the binaural cross covariance (BCopt) and its delay were extracted for each frequency band. The dITD for each location and frequency was calculated as the absolute difference in peak height (dITD = |BCopt - BC|) at the delay identified from the best location (Albeck and Konishi, 1995; Saberi et al., 1998). These parameters, dILD and dITD, quantified the difference between the cue values at each location and optimum of the cell. In Figure 1, B2 and B3, the spike activity of the exemplar cell for each location is color-coded and plotted against frequency (horizontal axis) and either dILD or dITD. Figure 1B2 shows strong peaks in activity for small values of dILD at ∼2.5 and 7.5 kHz and a broader distribution of weak activity at other frequencies. The ITD-alone plot reveals the involvement of similar, although not identical, frequency bands (Fig. 1B3).
-octave separation, which were each constructed to approximate the owl's auditory nerve tuning curves (Köppl, 1997). We then obtained the ITD and ILD for each frequency band and at each location in space. The ILD was calculated as the decibel difference in intensity (right minus left), and the optimal ILD (ILDopt) of a cell was defined as the ILD spectrum at the best location of the cell in the ILD-alone RF. The difference between the ILD spectrum at each location and the ILDopt of the cell was termed the “ILD distance” (dILD = ILD - ILDopt). The ITD was calculated as a spectrum of cross covariances between the left and right ear signals for each location in space. Each cross covariance was normalized internally. At the best location of the cell, the peak height of the binaural cross covariance (BCopt) and its delay were extracted for each frequency band. The dITD for each location and frequency was calculated as the absolute difference in peak height (dITD = |BCopt - BC|) at the delay identified from the best location (Albeck and Konishi, 1995; Saberi et al., 1998). These parameters, dILD and dITD, quantified the difference between the cue values at each location and optimum of the cell. In Figure 1, B2 and B3, the spike activity of the exemplar cell for each location is color-coded and plotted against frequency (horizontal axis) and either dILD or dITD. Figure 1B2 shows strong peaks in activity for small values of dILD at ∼2.5 and 7.5 kHz and a broader distribution of weak activity at other frequencies. The ITD-alone plot reveals the involvement of similar, although not identical, frequency bands (Fig. 1B3).
A principal components regression, which closely resembles a goodness-of-fit analysis between activity and dILD (or dITD), was used to identify the frequency weights (Fig. 1 B1) (for details, see Spezio and Takahashi, 2003.) If a spectral component had a strong influence on the activity of the cell, the correlation between spike rate and distances was strong, and the dITD and dILD tuning curves for that spectral band were assigned a high weight reflecting the level of correlation. If a spectral band had only a weak influence on the activity of the cell, there was only a weak correlation, and that band was assigned a proportionally lower weight.
The procedure summarized above yields ITD and ILD tuning curves for every frequency, weighted by the influence of each spectral band. Such tuning could have been estimated by obtaining ITD and ILD curves using a series of narrowband stimuli such as tone bursts (Euston and Takahashi, 2002), but that takes far more time. Furthermore, space-specific neurons respond only poorly to narrowband stimuli, and the predictive ability of the tuning curves thus obtained is weaker than that of the tuning obtained with the method described above (Euston and Takahashi, 2002; Spezio and Takahashi, 2003).
Data analysis. We used several measures to compare the responses of a neuron given specific stimulus conditions. An index of maximum spike rates, Imaxrate, was used to compare the responses of a cell to one and two sources: Imaxrate = (maxrate 2sources - maxrate 1source)/(maxrate 2sources + maxrate 1source).
Another index, Ibalance, compared the “balance” of responses between the two response areas in a two source presentation: Ibalance = (maxrate sourceA - maxrate sourceB)/(maxrate sourceA + maxrate sourceB).
To assess the locking of a neuron to the amplitude modulation of the stimulus, vector strengths were calculated for modulation frequencies from 1 to 120 Hz (Goldberg and Brown, 1969; Kuwada and Yin, 1983). For each modulation frequency, the spike times gathered from one stimulus-pair location were converted modulo the period, and the magnitude of a mean vector was calculated. For some stimulus-pair locations that elicited only a small number of spikes, anomalously high vector strengths could be obtained. To mitigate this problem, all vector strengths obtained from a given stimulus-pair location were converted to z-scores relative to the vector strengths obtained over the 1-120 Hz range of modulations for that location. Thus, any location having a large variation in vector strengths across frequencies (e.g., because of a low number of spikes) would receive a low z-score.
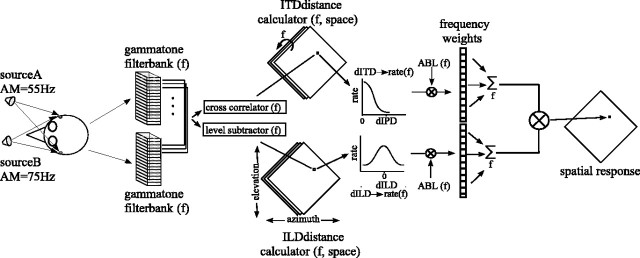
Modeling. Our model computes the time-varying, frequency-specific binaural cues obtained in a given two-stimulus configuration and estimates the response of a neuron to these acoustical parameters given its frequency-specific tuning for binaural cues. A snapshot in time of the model is shown schematically in Figure 2.
Figure 2.
Model to estimate neuronal response to two sound sources. One snapshot in time is shown, and succeeding time epochs were assumed to be independent. Each stimulus was convolved with the left- and right-ear HRIRs corresponding to the stimulus locations in head-centered space. The signals for each ear were then added together and passed through paired gammatone filterbanks. The outputs of each filter pair were cross-correlated to give the ITD, and their levels were subtracted (right minus left, in decibels) to give the ILD for that frequency band. For a given cell, these location- and frequency-dependent cues were then converted into dILD and dITD values by subtracting the ILDopt and ITDopt of the cell, respectively, and used as indices into the rate-distance functions of the cell. These functions supplied frequency-specific estimates of the firing rate response of the cell to each cue, which were then multiplied by the frequency-specific ABL of the stimulus and the frequency weights of the cell. The responses were then summed across frequency and multiplied together (ITD response × ILD response) to give a final estimate of the firing of the cell. The process was then independently repeated for each location in space and each succeeding time epoch. AM, Amplitude modulation; f, frequency.
First, binaural cues arising from a given stimulus configuration within a 5 ms time window were estimated (Wagner, 1992). To this end, stimuli were first convolved with the left- and right-ear HRIRs for the appropriate location(s), and the waveforms from each source received at one ear were added to derive the input signal for that ear. These signals were then passed through a gammatone filterbank, as described above, and ILD and ITD spectra were calculated. The frequency-specific average binaural level (ABL) spectrum was calculated as the mean of the time averaged rms-decibel magnitude of the left- and right-ear signals for each frequency band.
Next, for a given cell, these location- and frequency-dependent cues were then converted into dILDs and dITDs from the optimal values of the cell. The expected responses of the cell to these cues were estimated for each frequency band from the dILD- and dITD-rate functions estimated with the single-source ILD-alone and ITD-alone tests described above. Each of these frequency-specific rate functions is equivalent to a vertical cross section in Figure 1, B2 or B3. These estimates were then multiplied by the ABL and frequency weights and summed across frequencies. Finally, the responses to the ILD and ITD were multiplied to give an estimated response (Peña and Konishi, 2001). The process was then repeated for each location in space and each succeeding time epoch. In general, we parameterized the model with the frequency weights and dILD- and dITD-rate functions of the cell. In some instances, however, to test the necessity of using the values of the individual cell or to generalize the results, we substituted more “generic” values. These consisted of unitary frequency weights and Gaussian dILD- and dITD-rate functions (frequency-specific tuning widths estimated from the HRTFs of a “typical” owl).
Results
We mapped the responses of individual ICx neurons (n = 102) to a simple auditory scene in which two separate virtual sources simultaneously emitted uncorrelated broadband noises. Each noise was sinusoidally amplitude modulated at either 55 or 75 Hz, which are well within the temporal modulation transfer functions of the neurons (Keller and Takahashi, 2000). For a given trial, the sources were maintained in a particular spatial orientation, separated by 30 or 40° vertically, horizontally, or diagonally. Just as traditional single-source RFs are mapped, the responses of a cell were displayed as a function of the midway point between the two sources as they were presented simultaneously from different locations in space (Fig. 3). For example, in Figure 3A, source B is in the RF of the cell, and source A is above and to the left. The response of the neuron in this configuration was plotted at the location indicated by the black plus sign in Figure 3A and indicated by the arrow to Figure 3C. Most cells responded strongly when one (Fig. 3A) or the other (Fig. 3B; replotted RF from Fig. 3A) sound source was placed within the single-source RF of the cell and responded at most only weakly when neither source was within the RF (Fig. 3D,E; replotted RF from Fig. 3A). The result is a spatial response profile with two peaks of activity (Fig. 3C), one diagonally to either side of the single-source RF. The orientation and separation in space of these peaks is predicted (black contours) by the source offsets that were used to produce a given auditory scene, in this case 30° in azimuth and 30° in elevation. A simple model, described below, assumes that all ICx cells respond similarly to this and other cells, the responses of which are described herein. The model suggested that, under certain conditions, the activity across the space map is capable of simultaneously imaging two separate sound sources even when their spectra overlap.
Figure 3.
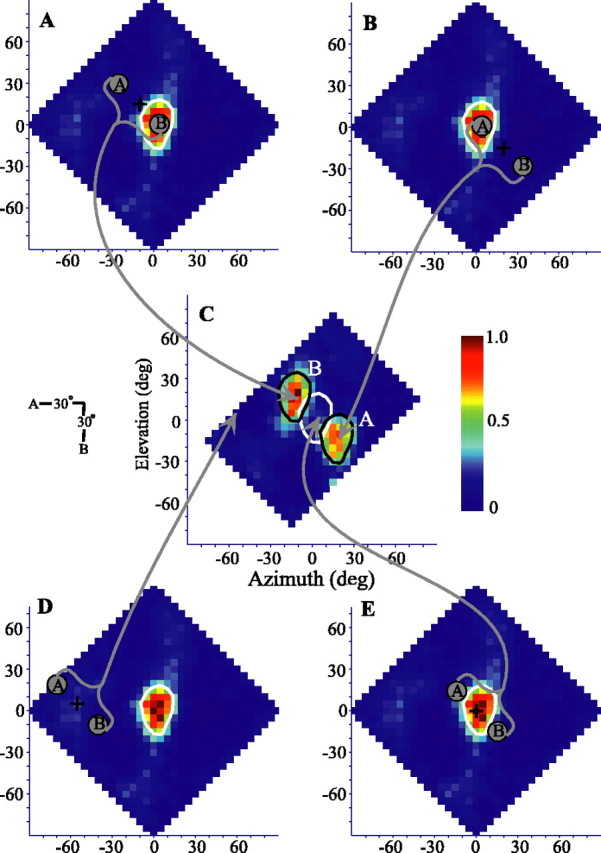
Construction of two-source spatial response profiles for a neuron recorded in the ICx. A, Normalized spike-rate responses to a single source are plotted as a function of azimuth and elevation. The 75° of maximum iso-rate contour is drawn in white. The same plot is repeated in B, D, and E. C, Responses for a two-source test with the sources separated by 30° in azimuth and 30° in elevation (inset). The one-source contour is replotted in white and again in black, shifted by the source offsets to show the expected areas of responses to two sources. Note that these areas, denoted by a white A and B, are in the reverse orientation from the sound sources A and B. To illustrate this, the two-source “array” is shown schematically for a particular array center location (marked by a plus symbol) in A, B, D, and E. In A, for example, with source B placed with in the RF and source A to the top left, the cell responded strongly. In the two-source spatial response profile (C), this response is mapped to a location corresponding to the array center, above and to the left of the one-source RF of the cell as indicated by the arrow. Data are interpolated from a 10° resolution checkerboard pattern. Cell 913EA is shown (see also Figs. 8 and 9). deg, Degree.
Localization of two sources
The spatial response profile of one neuron to a single sound source is shown in Figure 4A. As is typical for ICx neurons, the response was highly spatially restricted and, for this cell, centered near to +5° azimuth, -5° elevation. The spatial response profiles for this same cell to two sources presented in four different orientations are shown in Figure 4B-D. For each orientation, the responses were clearly separated and occurred when one or the other source was placed within the RF of the neuron. The response was approximately equal for each source when presented on one diagonal (Fig. 4B) but asymmetrical when presented on the other diagonal, horizontally or vertically.
Figure 4.
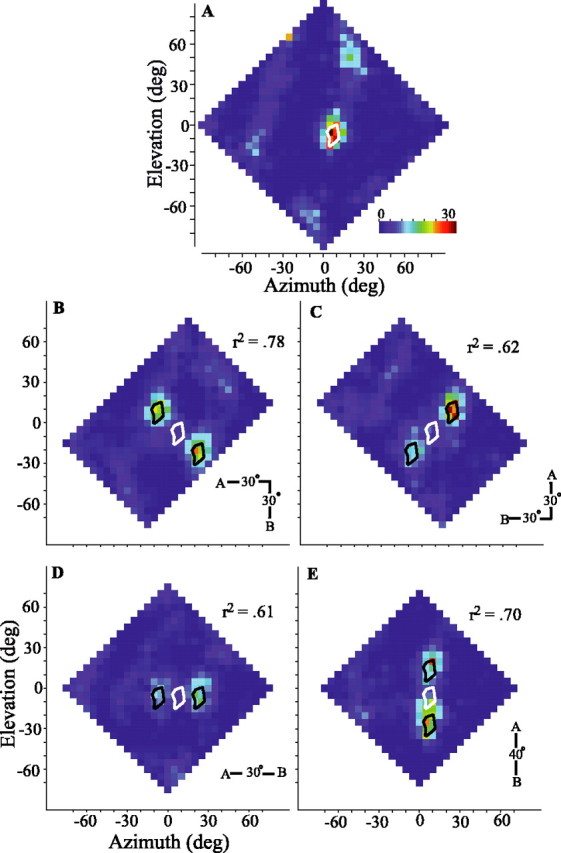
One- and two-source spatial response profiles of an ICx neuron. Two-source tests conducted for four spatial orientations (insets). A, Spike-rate responses to a single source plotted as a function of stimulus azimuth and elevation. The 75° of maximum iso-rate contour is shown in white. B-D, Responses to two sound sources offset by 30° in both azimuth and elevation (B, C), 30° in azimuth (D), or 40° in elevation (E). Data are as in Figure 3C, except that the actual spike rate (spikes per second) is presented with the same color scale for all plots. Values of r2 for each two-source plot indicate the maximum cross-correlation between the response of the cell and the response expected by appropriately shifting and averaging two copies of the single-source spatial response profile. Cell 913EF is shown. deg, Degree.
How well can the overall spatial pattern of responses to two sources be predicted from the single-source response? For each orientation, we compared by cross-correlation the two-source response of the cell with the average of two appropriately placed copies of the single-source spatial response profile. Although each comparison resulted in a strong correlation, the diagonal orientation showing greater symmetry (Fig. 4B) was most strongly predicted by the one-source response (r2 = 0.78). The r2 values for each orientation are given in Figure 4B-E. Histograms of the r2 values for all cells are shown in Figure 5A. For each source orientation and for almost all cells, the similarities were quite strong, with a mean r2 for all tests of 0.68 (±0.17 SD). More specific measures are discussed below.
Figure 5.
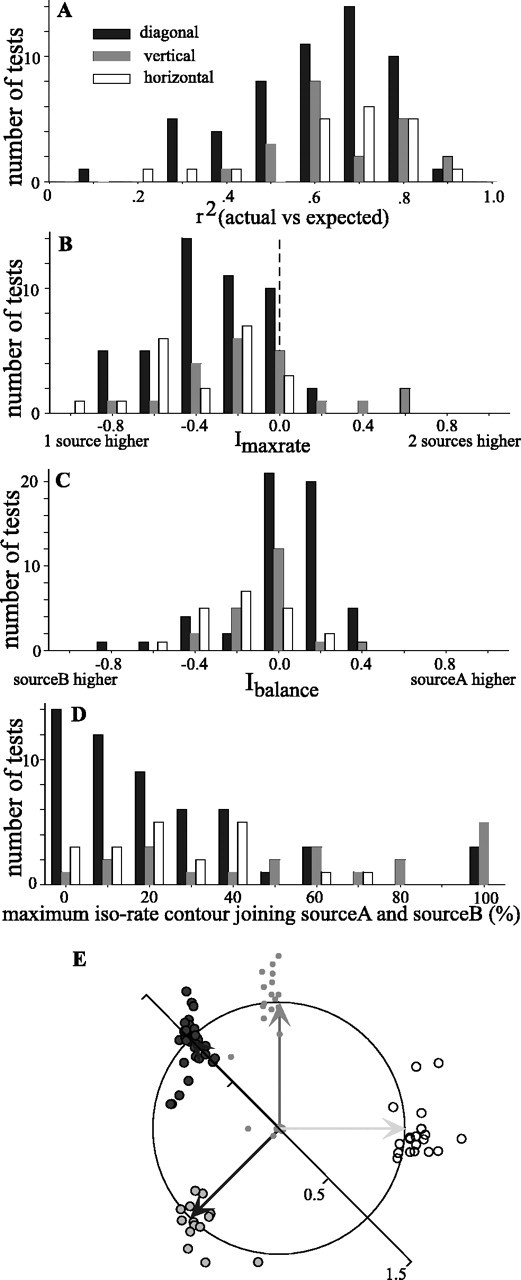
Summary of responses to two sound sources that were presented diagonally (filled), vertically (gray), or horizontally (open). A, Histograms of the r2 value obtained by cross-correlation of the two-source spatial response profile of the cell with one obtained by appropriately shifting and averaging two copies of the single-source spatial response profile. B, Histograms showing the distributions of Imaxrate, which compares the maximum firing rate in response to either of two sources versus that obtained in response to a single source. ndiag = 47 tests (43 cells); nhoriz = 21 (18 cells); nvert = 21 (21 cells). C, Distributions of Ibalance, which compares the maximum spike rates elicited by sources A and B. ndiag = 54 tests (46 cells); nhoriz = 21 (18 cells); nvert = 21 (21 cells). D, Distributions of the maximum normalized iso-rate contour at which the responses to sources A and B join. ndiag = 54 tests (46 cells); nhoriz = 21 (18 cells); nvert = 21 (21 cells) For all histograms, the abscissa shows the bin centers. E, Orientation and separation of responses to two sources. Each test is represented as the tip of an imaginary vector pointing from the origin of the unit circle. The direction of the vector indicates the angle made by the two response areas, and its magnitude indicates the distance between the two response areas normalized by the expected distance. The expected vectors for each of the four test orientations are shown as solid arrows projecting from the origin to the edge of the circle (horizontal, light gray vector, open circles; vertical, medium gray vector, gray circles; diagonal, dark gray vectors, filled circles).
For most cells, the maximum spike rate elicited with two sources was less than for one source. Figure 5B displays the values of an index comparing these spike rates (Imaxrate; see Materials and Methods). Negative values indicate that the maximal rate for the two-source condition was less than that for a single-source condition. The diminished response to two sources might be the result of lateral inhibition (Knudsen and Konishi, 1978; Mazer, 1989) acting between populations of cells responsive to each of the two sources. However, because the owl uses a binaural cross-correlation-like mechanism to compute the azimuth of a sound, the diminished response may simply reflect the lower level of binaural correlation in the two-source condition. Binaural decorrelation results from the jittering of ITD in time differentially in each frequency band, which in turn is caused by the interaction of the two uncorrelated sounds (discussed below in relation to Fig. 11). Given the present stimulus configurations, the broadband binaural correlation was typically lowered by 30-50°. Albeck and Konishi (1995) explicitly tested the responses of space-specific neurons to differing levels of binaural correlation at the best delay of each cell. Using their data, we calculated expected Imaxrate values of approximately -0.2 to -0.3, which agree with the data in Figure 5B.
Figure 11.
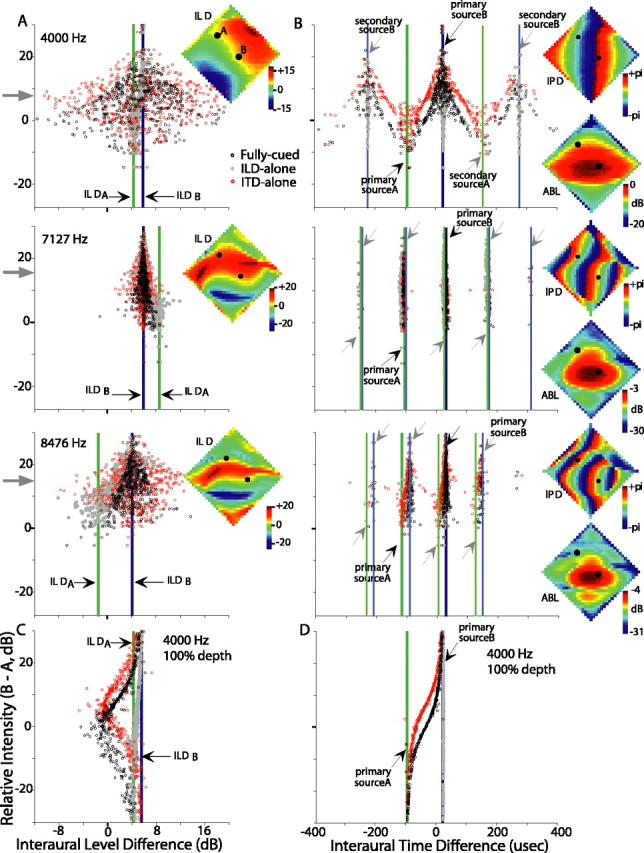
Binaural cues available from two diagonally arranged sources separated by 40° of azimuth and elevation. Momentary ILD (A, C) and ITD (B, D) cues are plotted against the momentary relative level of the two sources (source B minus source A, decibels). Each circle or dot represents the cue computed within successive 1 ms (nonoverlapping) time windows. The black circles represent fully cued conditions, gray dots represent the ILD-alone condition, and red circles represent the ITD-alone condition. Single-source ILDs and ITDs (primary peaks of the binaural correlogram) are depicted for each source by thick vertical lines (green, source A; blue, source B) and black arrows. Additionally, secondary ITD peaks are indicated by gray arrows and thinner lines in B. In A and B, cues for three frequency bands are shown (top, 4000 Hz; middle, 7127 Hz; bottom, 8476 Hz) when each source is modulated to 50° depth. The 4000 Hz band is shown in C and D for 100° modulation depth. For reference, the spatial distributions of single-source ILD, IPD, and ABL are shown in insets for each frequency band in A and B. ILD and ABL plots are scaled individually; IPD plots use a common scale. Source A is placed at +35° elevation, -25° azimuth and amplitude modulated at 55 Hz. Source B is placed at -5° elevation, +15° azimuth and amplitude modulated at 75 Hz. Black dots within the insets represent these source locations.
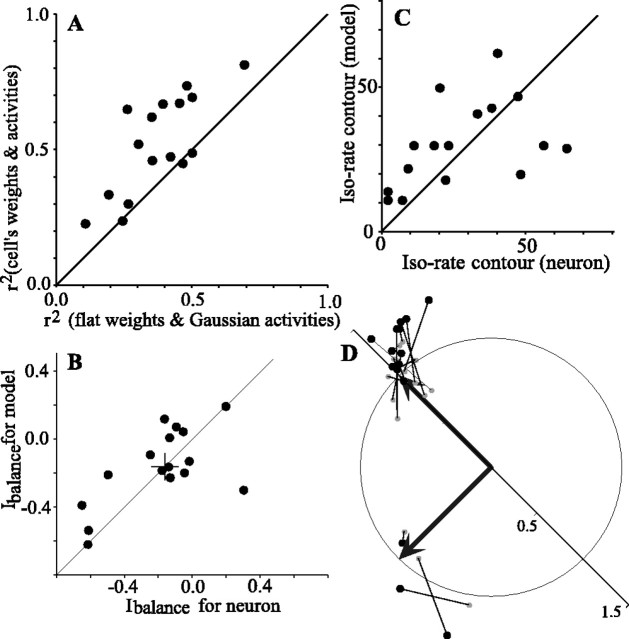
Figure 5 also provides several measures to examine the correspondence between the spatial response profile representation and the auditory scene that was presented. Figure 5C shows an index comparing the maximum spike rate at each of the two response peaks (Ibalance; see Materials and Methods). In general, this index is near zero, suggesting that the two peaks are of nearly equal strength. As seen in Figure 4C-E, however, some cells, under certain source orientations, showed strong biases to one source or the other even when the sources were presented with equal intensity. In fact, these biases appear to be systematically related to the balance of intensities at the eardrum of the two sources. This effect can be understood by considering the “binaural acoustical axis,” defined as the direction giving rise to the greatest ABL as determined from the HRTFs, either in the narrowband or the broadband sense. For cells with RFs distant from the binaural acoustical axis, it is possible to place one source in the RF (the “RF source”) and the other, “non-RF,” source at or near to the axis. In this configuration, the non-RF source will appear more intense, and the binaural cues will favor it over the cues for the RF source. The response of the cell would be weak. Placing the other source in the RF would now make the new non-RF source far distant from the axis, and the binaural cues will be strongly biased toward those of the RF source, eliciting a much stronger neuronal response. The resulting spatial response profile would therefore be asymmetrical. For most cells in our sample, however, the RFs were relatively close to the binaural acoustical axis (data not shown), and placing either source in the RF leaves the non-RF source about the same distance away from the axis. As a result, the binaural cues with either source in the RF are equally affected by the non-RF source, causing the cell to respond with equal strength to each source as it was placed in the RF.
For most cells, the two response peaks were clearly separable by an area of little or no activity. To quantify the separation of peaks, we determined the iso-rate contour (as a percentage of the maximum response) at which the two peaks joined (Fig. 5D). For diagonal and horizontal orientations, the large majority of neurons responded to each of the two sources completely separately, or nearly so. In 72° of the diagonal tests and 65° of the horizontal tests, the two-source response areas join at or below the 30° of maximum firing contour. Vertical separation was less complete, likely reflecting the fact that single-source RFs are taller than they are wide.
The expected orientation and separation of the two peaks of activity is summarized as a polar plot in Figure 5E. The origin of the plot represents the location of one of the two foci of activity in a spatial response profile, and the unit circle represents the expected distance to the other source. The arrows indicate the vertical, horizontal, and two diagonal configurations. Each dot represents the location of the other response peak for a given test. If the two foci of activity are separated in the same direction and by the same magnitude as the two VAS sources, the dot would fall on the unit circle, at the head of the arrow. For the 94 tests shown, the actual and expected values were quite similar.
Identification of amplitude-modulated sources
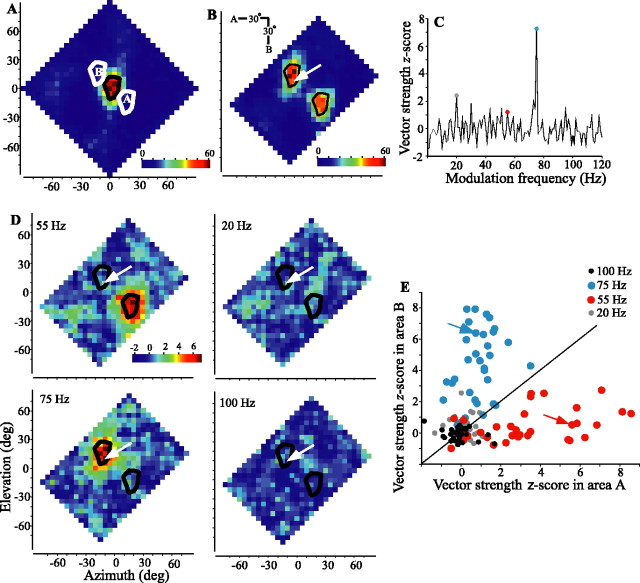
The spike rate plots of Figures 3 and 4 show that two foci of activity are resolvable on the spatial response profile but say nothing about the identity of the sound at each location in space. To assess the ability of the neuron to identify the two sources, each source was “tagged” by amplitude modulation, and spike synchrony to different modulation frequencies across the spatial response profile was measured. Figure 6 illustrates the process for one neuron tested diagonally with amplitude modulations of 55 and 75 Hz for sources A and B, respectively. The single-source response profile and 75° of maximum iso-rate contour of the cell are plotted in Figure 6A. Shifted contours are also plotted to show the expected locations for responses to each of the two sources, and the two-source spike rate response profile (Fig. 6B) is quite similar to this expectation. As shown in Figure 6C for one location (Fig. 6B, arrow), vector strengths of the evoked spike train were calculated for modulation frequencies between 1 and 120 Hz and then converted to z-scores. The selected location was within the area where a response to source B, modulated at 75 Hz, was expected, and the 75 Hz modulation rate (blue dot) attained a z-score that was clearly higher than that of any other frequency, including 55 Hz (red dot). Repeating this process at each location allowed construction of spatial response profiles of z-scores for modulation frequencies of interest (Fig. 6D). The strongest synchrony to 55 Hz coincided with test locations placing source A in the RF of the cell, whereas locking to 75 Hz occurred only when source B was in the RF. Locking to the amplitude modulation of the source outside the RF and to other frequencies, here exemplified by 20 and 100 Hz, was considerably weaker. Figure 6E plots mean vector-strength z-scores, for a population of cells, within the expected areas for sources A and B to modulation frequencies of 20, 55, 75, and 100 Hz. In nearly all cells, when source A was in the RF, synchrony was considerably stronger to 55 Hz than to any other modulation rate tested, and when source B was in the RF, synchrony was strongest to 75 Hz. Most ICx cells tested showed a clear spatial separation of locking to 55 or 75 Hz and little locking to other frequencies. Figure 7 shows similar data for the same cell shown in Figure 6 and for the population of cells tested with horizontally (A, C) or vertically (B, D) oriented sources. This cell clearly separated source identities to the expected response profile locations in each orientation tested. Additionally, the vertically oriented test (Fig. 7B) shows a clear separation by spike locking (center and right plots) that is not apparent in the spike rate plot (left).
Figure 6.
Spatial response and z-score vector strength profiles of an ICx neuron in response to one sound source or to two uncorrelated sound sources presented oriented diagonally. A, Spike rate in response to a single unmodulated source. The 75° of maximum iso-rate contour is shown in black and replotted in white to show the expected response areas for the two-source trial. Note that the orientation of response areas A and B is inverted from the orientation of sources A and B (B, inset), as explained in Figure 3. B, Responses to two diagonally oriented uncorrelated sound sources. Source A (source at top left) was amplitude modulated at 55 Hz, and source B (bottom right) was amplitude modulated at 75 Hz. C, Spike-locking to the stimulus envelope is quantified with z-score vector strengths shown for spikes recorded with the two-source array centered at the location indicated by the tip of the white arrow in B. D, Spatial distribution of z-scores, such as those shown in C, for four modulation frequencies. The response area for source A shows strong locking to 55 Hz but no other frequency, whereas response area B shows strong locking only to 75 Hz. Plotting conventions are as in Figure 3C. Cell 913EA is shown (see also Figs. 3 and 7). E, For each of the 33 cells and for each of the four frequencies shown in D for one cell, the average z-scores from response area A are compared with those for area B (gray, 20 Hz; red, 55 Hz; blue, 75 Hz; black, 100 Hz). The diagonal line indicates expected values when responses to a given frequency in both areas are equal. The arrows indicate values for the cell shown in A-D.deg, Degree.
Figure 7.
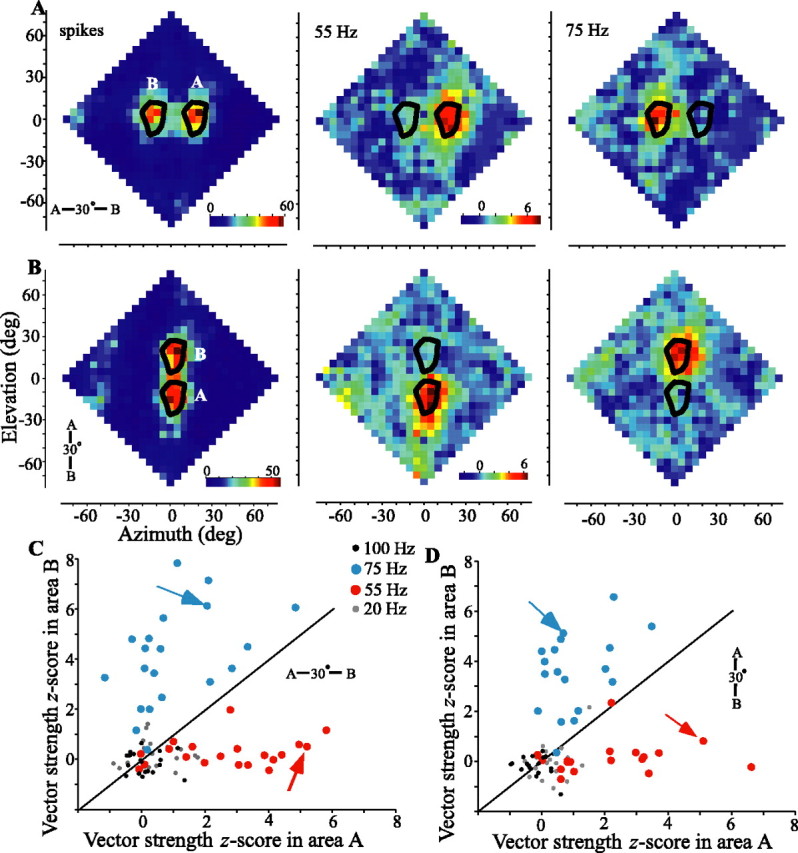
Spatial response and z-score vector strength profiles for two sounds presented oriented horizontally (A, C) or vertically (B, D). The plotting conventions are the same as in Figure 6 A-D (cell 913EA, also shown in Figs. 3 and 6). The leftmost plot in A and B shows spike responses, and the middle and rightmost plots show z-score vector strengths for 55 and 75 Hz, respectively. For each of 20 cells (C) or 18 cells (D), the average z-score vector strengths are compared between the areas where responses to source A or source B are expected (gray, 20 Hz; red, 55 Hz; blue, 75 Hz; black, 100 Hz). The arrows indicate values for the cell shown in A and B. deg, Degree.
Separation/grouping of sources
We demonstrated above that space-specific neurons can resolve two concomitant amplitude-modulated noise bursts and synchronize their spiking to the envelope of each source as it is placed within the RF. Is the segregation of the two sources contingent on their being amplitude modulated at different rates? If so, spatial response profiles obtained with two sources amplitude modulated at the same rate should contain only a single focus modulated at that rate. Such an observation would suggest that envelope modulations are used to group objects at the level of the midbrain and would predict that comodulated objects might lead to errors in parsing the auditory scene.
Results suggest, however, that the time-averaged responses to two sources do not depend on their having different modulation rates and that the space map does not show evidence of grouping based on envelope commonalities. Figure 8 shows the responses of one cell to stimulation with two diagonal sources when both were amplitude modulated at 55 Hz (AM55,55) (Fig. 8C) and when one was modulated at 55 Hz and the other at 75 Hz (AM55,75) (Fig. 8B). The spike rate plots (left column) show little difference between the two cases. In the AM55,55 presentation, the z-score profiles show two separate foci each locked to 55 Hz (Fig. 8C2). For the AM55,75 case, the two different modulation frequencies are mapped appropriately.
Figure 8.
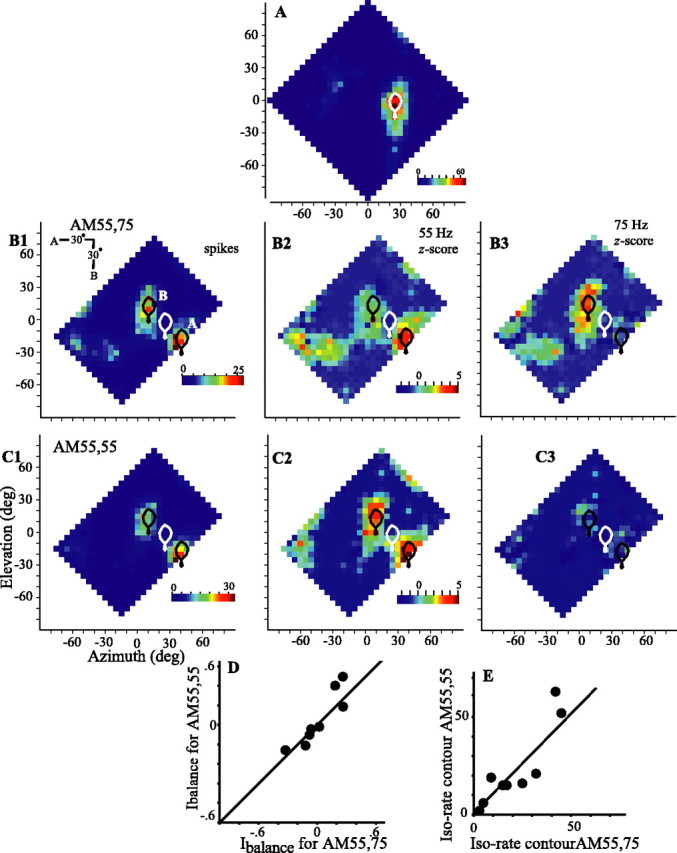
The representation of two separate sources is not contingent on differential amplitude modulation. A, The single-source response with 75° of maximum iso-rate contour is plotted in white for one cell. B, C, Two-source spike responses (left) and 55 Hz (center) and 75 Hz (right) z-score vector strengths for two sounds oriented diagonally and amplitude modulated at 55 and 75 Hz (B) or 55 and 55 Hz (C) (cell 886DH). The responses of nine cells to tests using different (AM55,75) or identical (AM55,55) rates of amplitude modulation are compared for the Ibalance (D), which compares the maximum spike rates for each source, and for the depth of the saddle between response areas A and B (E), measured as the maximum iso-rate contour joining the response areas. Data are presented as in Figure 3C. deg, Degree.
For nine cells tested in this manner, the mean coefficient of correlation between response profiles for AM55,55 and AM55,75 was 0.91 (SD, 0.06). Also, the relative symmetry of responses as estimated by Ibalance (Fig. 8D) and the iso-rate contour at which the two sources were separated (Fig. 8E) were similar for the AM55,55 and AM55,75 cases.
Comparison of model and cellular responses
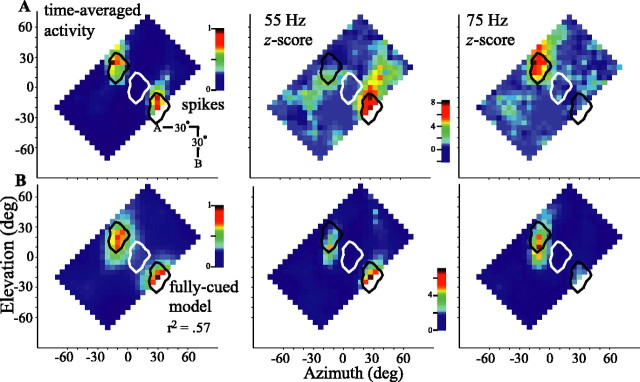
We developed a simple model to determine the extent to which the response of a cell can be explained by the degree to which the momentary binaural cues in each band match the frequency-specific tuning for binaural cues (see Materials and Methods) (Fig. 2). The model was endowed with the tuning characteristics of a given cell to frequency-specific binaural cues (Fig. 1) (see Materials and Methods), and, as was done for the cellular responses (Fig. 3), a spatial response profile for the model was generated. Thus, one test of the model is to compare, for each cell individually, the responses of the model with those of the cell on which it was based. As an example, the left plot in Figure 9A shows the time-averaged response of one cell to two sources that are presented diagonally. The spatial response profile of the cell shows two distinct foci of activity that straddle the RF of the cell centered at -5° elevation, +15° azimuth (white outline, repeated at expected offsets in black). When source A was placed in the RF, the cell fired strongly and in synchrony with the 55 Hz amplitude modulation of source A (middle column). Placing source B in the RF elicited activity locked to its 75 Hz amplitude modulation. In neither case did the non-RF source elicit significant locking of activity. The time-averaged response of the model is presented in the left column of Figure 9B and closely resembles the neuronal response (r2 = 0.57). The distributions of vector strengths for the model (Fig. 9B, middle and right columns) also closely follow those of the neuronal responses.
Figure 9.
Spatial response (left) and vector strength profiles (middle, 55 Hz; right, 75 Hz) of an ICx neuron and the associated model for stimulation by two sources presented in diagonal orientation (inset). A, Neuronal spatial response and vector strength profiles. B, Profiles of the fully cued model based on the single-source tuning of this cell to frequency-specific binaural cues. Data are presented as in Figure 3C. Cell 908BA is shown. deg, Degree.
Figure 10 compares several aspects of the output of the model with the responses of each cell to two sources positioned diagonally (n = 16 cells). For each cell, we first asked how well the overall pattern of predicted response correlated with the actual response of the cell and how this correlation was affected by the choice of frequency weights and the shape of the dILD- and dITD-activity curves. Figure 10A plots r2 values from cross-correlation of the time-averaged outputs of the model with the responses of the neuron. The figure compares the r2 value obtained using the weights and activity curves of each cell with the r2 value obtained using unitary weights for all frequency bands and Gaussian dILD- and dITD-activity curves. In 13 of 16 cases, the parameters of each cell out-performed the more generic values. Using the parameters of each cell, the r2 values range from 0.24 to 0.79 (mean, 0.52).
Figure 10.
Summary of the output of the model for 16 cells tested with two sources placed diagonally. A, r2 values for the peak of the two-dimensional cross-correlation when using the weights and activities of each cell are plotted against r2 values when using unitary weights and Gaussian activity curves. B, Comparison of the Ibalance, which measures the relative strength of responses to the two sources, for the model and the spike response of the cell. C, The maximum iso-rate contour at which the response areas for the two sources join is compared for the model and the spike responses. D, Orientation and separation of the responses of the model to the two sources. As in Figure 5E, each test is represented as the head of an imaginary vector (large filled circles) pointing from the origin in a direction equivalent to the angle made by the two response areas and with a magnitude equal to the distance between the two response areas normalized by the expected distance. Each modeled response is connected by a line with a small gray dot that shows the equivalent measures for the spike response of the cell. The two thick black arrows represent the expected vectors for the two different diagonal orientations.
Other, more specific measures comparing the output and neuronal responses of the model also show strong similarities. As with the neuronal responses, in the model the source configuration placing the non-RF source most peripherally was more effective. This is reflected in the relative strength of the representations of each source as summarized by Ibalance, which is shown to be quite similar for each neuron and its associated model (Fig. 10B). As with the cellular responses (Fig. 5D), the model typically showed a clear saddle of low activity between the response areas for each source. The magnitude of the normalized iso-rate contours at which the two peaks of activity join are plotted for the model and for the cells in Figure 10C. There may be a weak trend toward better separation (smaller values) by the cell than by the model. The spatial separation and orientation of the two response areas are depicted in Figure 10D. The angular position along the unit circle indicates the relative orientation of the responses and the radial position indicates their distance of separation. As in Figure 5E, each test gave an expected orientation and source separation that is depicted by one of the two thick vectors from the origin. The orientation and source separation for each model-versus-cell comparison is represented as a vector with its tip (large black dot) at the location of the response of the model and an origin (small gray dot) at the response of the cell. The model and cellular responses are in general agreement, although the responses of the model tend more often to fall outside the unit circle, suggesting a possible weak trend to greater separation by the model.
The close agreement between modeled and cellular responses suggest that the tuning parameters used in the model are the primary determinants of the cellular response. Given this agreement, we looked further into the responses of the model and extended the model to predict the pattern of firing for neurons across the auditory space map.
Analysis of the model
The starting point for the model is to use the sounds presented during unit recordings and the bird's HRTFs to estimate the frequency-specific ILD, ITD, and ABL within a given time window. When multiple sources are present, each spectral component from each source adds vectorially in each ear, giving rise to the binaural cues. These cues vary over time and frequency in a complex way as discussed below. In a simple case, when two sources emitting identical sounds differ only by their interaural phase difference (IPD), within each frequency band, the resultant binaural cues are the average of those of the individual sources. If the overall amplitude of one source is altered, without changing the spectral profile, the IPD is biased toward the more-intense source (Snow, 1954; Bauer, 1961; Blauert, 1997). If, on the other hand, one source is phase-advanced or phase-delayed relative to the other source, the ILD is biased toward the lagging source (Snow, 1954; Bauer, 1961; Blauert, 1997). When the relative phase and amplitude of the source both differ, these differences between the sources are each reflected in changes in both the ILD and IPD (Bauer, 1961). When the sounds of the two sources are statistically uncorrelated broadband noises, as were those used in the present study, the resultant frequency-specific binaural cues fluctuate over time in a manner dictated by the moment-to-moment relative amplitudes and phases of each source within the frequency band. Below we address the questions of how the envelope modulation of each source is conveyed and spatially separated within the model, and whether there are general principles for mixing of spatially separate sound sources that aid or disrupt the localization and characterization of the sound sources.
Temporal integration window
The extent to which binaural cues vary in time depends in part on the length of the time window over which the cues are computed. Within our model, time windows of ≥10 ms give relatively stable binaural cues that fluctuate between two small ranges of values reflecting those of each source presented by itself. Time windows of 5 ms (as used in Figs. 9 and 10) or shorter yield much more widely varying binaural cues. Whereas this implies that each source can be localized accurately if the integration time is long, a long integration window would conflict with the owl's ability to respond to the time-varying amplitude of each source. The owl is behaviorally able to discriminate amplitude modulations with a high-frequency cut-off of ∼100 Hz (Dent et al., 2002), and neurons of the ICx can follow amplitude modulations up to ∼200 Hz (Keller and Takahashi, 2000). The neurons up to and including the ICx must therefore have integration times <5 ms (Wagner, 1992). We therefore analyzed the binaural cues in 1 ms time windows to understand how the neurons might accurately localize both sources and encode their amplitude modulations.
Binaural cues
For any combination of source locations, each spectral band is characterized with its own combination of ITDs, ILDs, and ABLs, and thus the temporal pattern of resultant binaural cues will differ between bands. As an example, Figure 11, A and B, shows, respectively, the ILD and ITD cues calculated for three frequency bands [4000 Hz (top), 7127 Hz (middle), and 8476 Hz (bottom)] when the model is presented with two sources that were oriented diagonally (black dots in insets) and amplitude modulated to a depth of 50°. Source A is placed at +35° elevation, -25° azimuth and modulated at 55 Hz. Source B is placed at -5° elevation, +15° azimuth and modulated at 75 Hz. Fully cued ILDs (Fig. 11A) and ITDs (Fig. 11B) calculated in 500 successive 1 ms time windows are plotted with black circles along the horizontal axis. Momentary ILD and ITD values depend foremost on the momentary relative amplitude of the two sources, and this is plotted along the vertical axis (ABLB - ABLA) (Roman et al., 2003). The time-averaged relative amplitude is indicated by gray arrows pointing to the vertical axis. For reference, the single-source ILDs or ITDs (primary and secondary; see below) are plotted as vertical lines for each source [source A (green), source B (blue)]. In addition, the insets plot the two source locations as black dots overlain on spatial plots of the single-source ILD (Fig. 11A), IPD (Fig. 11B), or ABL (Fig. 11B) for each of the three frequency bands.
Because IPD is a cyclical variable, computed by a cross-correlation-like process, ITDs that differ by one or more periods of the center frequency give rise to the same IPD (Moiseff and Konishi, 1983; Sullivan and Konishi, 1984; Carr and Konishi, 1990). We refer to “primary” ITDs as those associated with a given source location (Fig. 11B, darker green or blue vertical lines) and “secondary” ITDs (light green and light blue lines) as those having the same IPD as the primary ITD. The pattern of IPDs repeating across space is clearly seen in the Figure 11B (top insets).
When source B is much more intense (positive relative amplitude), we expect the momentary ILDs and ITDs to cluster at the top of the graph and near to the ILD and ITDs of source B (blue lines). Conversely, when source A predominates (negative relative level), the momentary values should cluster near the bottom of the graph and around the ILD and ITDs associated with source A (green lines). When the two sources are of nearly equal level (0 dB on ordinate), the momentary values might be expected to smoothly transition between those for source A and source B, but this transition and the overall pattern are modulated in various ways that are explained below.
Binaural cues: ILD
At some frequencies, the ILDs do transition relatively smoothly between ILDA and ILDB (e.g., 7127 Hz and, to a lesser degree, 8476 Hz) and cluster around these values. In other words, at these frequencies, the ILD tends to assume the value of one source or the other. In contrast, at other frequencies (e.g., 4000 Hz), ILDs can attain values well outside of these bounds. ILDs are generally most extreme when the two sources are of nearly equal intensity. An understanding of the shapes of these plots reveals the quality of localizational information contributed by each frequency band. For the 4000 Hz frequency band, which shows a broad, spindle-shaped distribution of ILD values, the inset shows that the two source locations lie atop quite different values of IPD but share similar ILDs. Conversely, both the 7127 and 8476 Hz frequency bands, which show relatively little spread in their ILD plots, have approximately similar IPD values for each source. The primary ITD of one source lies near to the secondary ITD of the other source. Thus, when the IPDs within a frequency band of two sources are similar, the IPDs have little effect on the resultant ILDs, and the ILD varies simply with the weighted relative level of each source and would presumably provide reliable information for the localization of the two sources. When the IPDs of the two sources differ within a band, the ILDs vary more and can attain values well beyond the ILD of either source, an effect that is strongest when the two sources are of nearly equal intensity (near 0 dB on ordinate). Because an “optimal” frequency, in this sense, is one in which primary and secondary ITDs have the same phase difference as the primary ITDs of the two sources, the identity of optimal frequencies depends on source separation in azimuth.
The strong influence of differences in the ITD between sources is also supported by two additional experiments. First, we recomputed the resultant ILDs after having forced the ITDs for each source to those of source B. These recomputed ILDs are represented by the gray dots in Figure 11, A and C, and show considerably less scatter in all frequency bands. This explains why the ILD cues are most useful for segregating two fully cued sources separated only in elevation, when the ITDs of each source are nearly identical. Conversely, we held the ILDs for each source to values obtained for source B while allowing the ITDs to vary in the normal location-specific manner. This is equivalent to an ITD-alone test, but with two sources, and it isolates the contribution of the time-varying ITDs on the ILD. In this case, and despite holding the ILDs of the originating sources equal, the resultant ILDs (Fig. 11A,C, red circles) vary as much or more than in the fully-cued case (black circles).
Finally, the depth of modulation also strongly affects the momentary cues and thus the form of the plots. Figure 11C shows the ILDs computed within the 4000 Hz band when each source is modulated with a depth of 100° instead of the 50° depth used in most of the experiments. The spindle-shaped distribution seen in Figure 11A is replaced with a highly asymmetric displacement of ILD from source B values, but the general trends persist. With the increased modulation depth, moments strongly favoring one or the other source arise more frequently, allowing the ILDs to cluster around the value associated with that source alone. When the two sources are of nearly equal intensity, the resultant ILDs deviate most from the single-source values. It should also be noted that the breadth of the variation in the ILD increased if the bandwidth simulating the peripheral filters was narrowed or the time window shortened.
Binaural cues: ITD
Similar to the ILD, the momentary ITDs vary (Fig. 11B,D, black circles) from that obtained with source A alone to that of source B alone when the relative level of the two sources favor source A or source B, respectively. Secondary peaks of the ITD for each source (gray arrows) are seen in the Figure as alternative “attractors” when the respective source is more intense.
For the 4000 Hz band, when source B has slightly greater amplitude (+10 dB on the vertical axis), the black circles cluster around the ITD of source B, but with a scatter on the order of 100 μs, equivalent to >40° of azimuth in the owl. This scatter represents a significant degree of positional uncertainty and is several times the width at half-height of the ITD tuning curve of an ICx neuron. Removing the variation in source ILD from the computations (Fig. 11, red circles) has only a small effect, whereas setting the ITDs of source A identical to those of source B (gray dots) significantly lessens the horizontal spread of the resultant ITDs.
In contrast to the 4000 Hz band, the points for the 7127 Hz band have considerably less horizontal scatter (Fig. 11B). In this higher-frequency band, source A is within the secondary ITD of source B, and source B is within the secondary ITD of source A; thus, the two sources share the same IPD. At a still higher-frequency band (8476 Hz), the period is decreased further and the secondary regions are no longer coincident with the two sources, which in turn increases the scatter once again. As is most easily seen when the envelopes of the sources are more deeply modulated (Fig. 11D), the rate of transition from the ITD of one source to the other depends on the difference in ITDs. When the IPDs of the two sources are similar, the resultant ITDs fall at values intermediate between those of the two sources only for a small range of relative level differences (and thus for only short periods of time). Conversely, when the source ITDs are more different, the transition from the ITD of one source to the ITD of the other spans a wide range of level differences. Thus, in this latter case, ITDs dwell for shorter periods of times at “correct” values and vary over a wider variety of “incorrect” values for longer.
ABL
In each plot of Figure 11, A and B, there is a bias of points toward the top part of the plot. This bias reflects the ABL component of the HRTFs. In the present configuration, source B is positioned much closer to the (narrowband) binaural acoustical axis for each frequency shown. Given that sources A and B are presented at equal intensities, the HRTF makes source B appear more intense than source A. This ABL bias is frequency dependent. It can be quite large and, for this source configuration, ranges from ∼2 dB at 2 kHz to a peak of ∼16 dB at 7-8 kHz (Fig. 12D, compare solid black and solid red lines). At frequencies with a large ABL bias (e.g., 8476 and 7127 Hz in Fig. 11A,B), the points are shifted strongly upward, and the binaural cues tend to cluster about those of the more-intense source (source B). In contrast, at other frequencies (e.g., 4000 Hz) (Fig. 11A,B), ILDs can attain values well outside of these bounds. ILDs are generally most extreme when the two sources are of nearly equal intensity. The ABL bias is time independent and thus manifests as an overall shift of the binaural cues toward the more-intense source. The fine structure and envelope of the sounds themselves, however, give rise to time-varying differences in the relative level that cause the graph to spread out along the vertical axis. The most important of these sound-specific effects is the amplitude modulation imposed at 55 and 75 Hz. If the amplitude modulation were strong enough to completely overcome the bias imposed by the acoustical axis effect, as in Figure 11, C and D, separate clusters of points would appear at the ILDs and ITDs corresponding to each source as it became momentarily the strongest source. This is not the case with the 50° modulation depth (Fig. 11A,B), and the net ILD and ITD more or less cluster near to the values associated with source B as described above.
Figure 12.
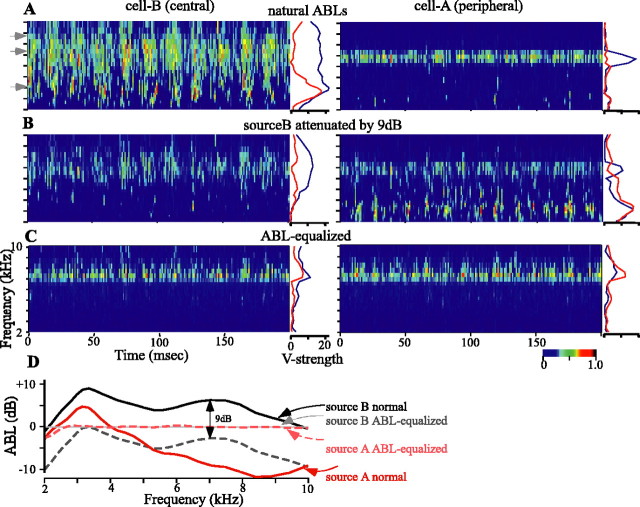
Modeled activity for two cells with RFs that are centered at the locations of source A (right column) and source B (left column), respectively, as shown in Figure 11. Each plot depicts the activity of the model cell over time and across frequency bands by the color scale at the bottom right. Source A is amplitude modulated at 55 Hz, source B is amplitude modulated at 75 Hz, and the locking within each frequency band to these modulations is shown as the vector strength plotted to the right of each activity plot (red, 55 Hz; blue, 75 Hz). A, Each source presented at the natural ABLs associated with their respective source location. Gray arrowheads indicate frequency bands plotted in Figure 11. B, Source B attenuated by 9 dB. C, Each source presented with nearly equivalent and nearly flat ABLs across frequencies as measured at the eardrum. D, Frequency-specific ABLs for each source in the three conditions (A-C). The 0 dB level is arbitrary.
Combining what and where
How would the firing patterns of two cells, the RFs of which coincided with source A (+35° elevation, -25° azimuth) and source B (-5° elevation, +15° azimuth), respectively, reflect this set of binaural cues? To answer this question, we assumed that hypothetical cells with RFs centered at locations A (cell A) and B (cell B) would be tuned to the frequency-specific ITDs and ILDs at their RF centers. The cells were assumed to be equally sensitive to all frequencies and to have Gaussian ILD and ITD tuning curves centered on the location-specific values. The activities of the hypothetical cells in any time window and frequency band were thus determined by the frequency-specific dILDs and dITDs resulting from the comparison of the tuning of each cell with the cues generated by the superposition of waveforms from sources A and B. The activity of the hypothetical cells in each frequency band are shown, respectively, in the right and left columns of Figure 12A-C. The vector strengths at 55 Hz (red, source A) and 75 Hz (blue, source B) modulation for each frequency band are shown to the right of each activity plot.
The single most important factor affecting the response of each cell is the ongoing difference in the frequency-specific ABL between the two sources, shown in Figure 12D (solid black line vs solid red line). In Figure 12A, the intensity of each sound at its source is equivalent. Source B, however, which is located close to the binaural acoustical axis, is more intense at the eardrum and therefore “pulls” the binaural cues toward it. Thus, overall, cell B is more active than cell A (Fig. 12A, left vs right). At frequencies above ∼4 kHz, at which source B retains a large ABL advantage over source A, the firing of cell B is strongly in synchrony with only source B. Between ∼3 and 4 kHz, at which the ABL of each source is more similar, cell B fires in synchrony with the amplitude modulations of both sources. The binaural cues favoring cell B fluctuate in synchrony with the ABL of source B (at 75 Hz) but are also pulled away by source A (at 55 Hz). At lower frequencies, the overall ABL of each source is too low to drive the cell very well. Under these same conditions, the more peripheral cell A, in which the RF source A lies, is driven only at frequencies in which the IPDs of the two sources are similar, as described above. At these frequencies, the ABL strongly favors source B, and thus cell A fires in synchrony with only source B. Note that at the lower frequencies, the binaural cues are pulled away from source B at the modulation rate of source A but are not pulled all the way to the values necessary to drive cell A.
The importance of the frequency-dependent nature of ABL bias is shown more clearly in Figure 12B, in which we attenuated source B by 9 dB. In this case, the ABLs obtained for frequencies below ∼5 kHz favor source A, whereas those >5 kHz favor source B, but less so than in Figure 12A (Fig. 12D, compare dashed black and solid red lines). The overall firing of cell B is now diminished but still strongest and most in synchrony with source B between ∼7 and 9 kHz, where the ABL bias most strongly favors source B. The firing of cell A is strongest in two bands: at higher frequencies at which the IPDs of the two sources are similar (and at the preferred values of cells A and B) and at lower frequencies at which the ABL bias favors source A. Activity elicited by the higher carrier frequencies is locked to the modulation of source B, whereas at the lower frequencies the modulation rates of both sources are represented. It should be noted that the activity of cell A is increased without having changed the level of source A itself.
Can both sources be represented when there is no intersource difference in the ABL at the eardrum for any frequency? In Figure 12C, we have equalized the ABL of each source for each frequency band (Fig. 12D, compare the light gray and dashed light red lines). Under these conditions, both cells are active only in the frequency bands in which the IPDs of each source are similar. The firing of each cell is locked to the modulation frequencies of both sources, but more strongly to the modulation frequency of the source lying within the respective RF of each cell.
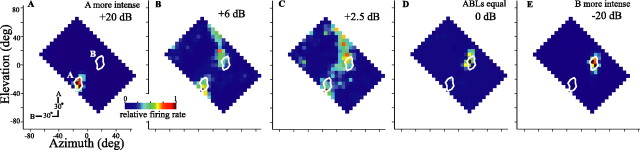
If we revisit actual cellular responses briefly, we see that the relative strength of firing to each source could be modified by adjusting the relative level at which each source was presented. One cell, the responses of which are shown in Figure 13, showed an asymmetrically strong response to source B when the two sources were presented with equal intensity (Fig. 13D). When source A was presented 2.5 dB more intensely than source B (Fig. 13C), the two response areas were about equally strong. At relatively higher source A levels (Fig. 13A,B), the response to source A predominated. Relatively weaker sources were often slightly mislocalized as is most evident in Figure 13, B and C, for responses to source B plotted to the top right.
Figure 13.
Adjusting the relative level of each source changes the strength and balance of the two-source representation within the spatial response profile of a neuron. A-E, All plots are from one cell recorded in the ICx while adjusting the relative level of the two sources (source A minus source B, decibels) and keeping the average level constant between sources. The color scale is the same for all plots. Conventions are as in Figure 3C. Cell 939FG is shown (see also Fig. 1). deg, Degree.
The activity patterns described above suggest that individual cells of the space map can respond to and synchronize with sources located within their RF if there are frequencies that have an ABL advantage over a second source. Even without an ABL advantage, frequencies with IPDs that are shared by both sources may evoke activity at the appropriate location on the space map, but that activity may be synchronized with the amplitude modulations from the “inappropriate” source.
The auditory image of the space map
We extended the ideas behind Figure 12 to ask how the auditory image for these two sources might be represented across the entire frontal space. Instead of testing the model as a spatial response profile (Fig. 9), we retained the sources at +35° elevation, -25° azimuth (source A) and -5° elevation, +15° azimuth (source B) and modeled the responses of cells with RFs centered at 5° intervals across the entire frontal hemisphere. Each cell was given a best-ILD and best-ITD based on the HRTFs for the RF center coupled with Gaussian dILD and dITD tuning and unitary frequency weights. Of course, because the model assumes that all areas of space are represented equally on the space map and that RF sizes are uniform, the modeled responses only approximate the representation of the auditory scene of the space map. Figure 14A shows the modeled responses when the two sources are presented at the same source intensity and thus with their natural ABLs, determined by their locations in space. The fully cued response (larger plot) shows a strong representation of the more centrally located (hence more intense) source B and, at most, a weak and mislocalized response to source A. The fully cued response is derived from a point-by-point multiplication of the single-cue plots (top, smaller plots), and thus inspection of these latter plots may provide insight into the nature of the fully cued response. The ILD-alone plot (top left) shows two broad, nearly equal peaks of activity, one centered near to source B and the other biased centrally from the location of source A. In contrast, the ITD-alone plot shows a strong response to source B and almost none to source A and thus has the strongest effect on the shape of the fully cued image. The distributions of vector strengths (right, smaller plots) show that the strong activity at the location of source B is locked strongly to the 75 Hz amplitude modulation of source B but also is somewhat contaminated by the 55 Hz amplitude modulation of source A. As suggested by Figures 11 and 12, this is primarily attributable to the frequency bands in which the primary and secondary IPDs of the two sources overlap.
Figure 14.
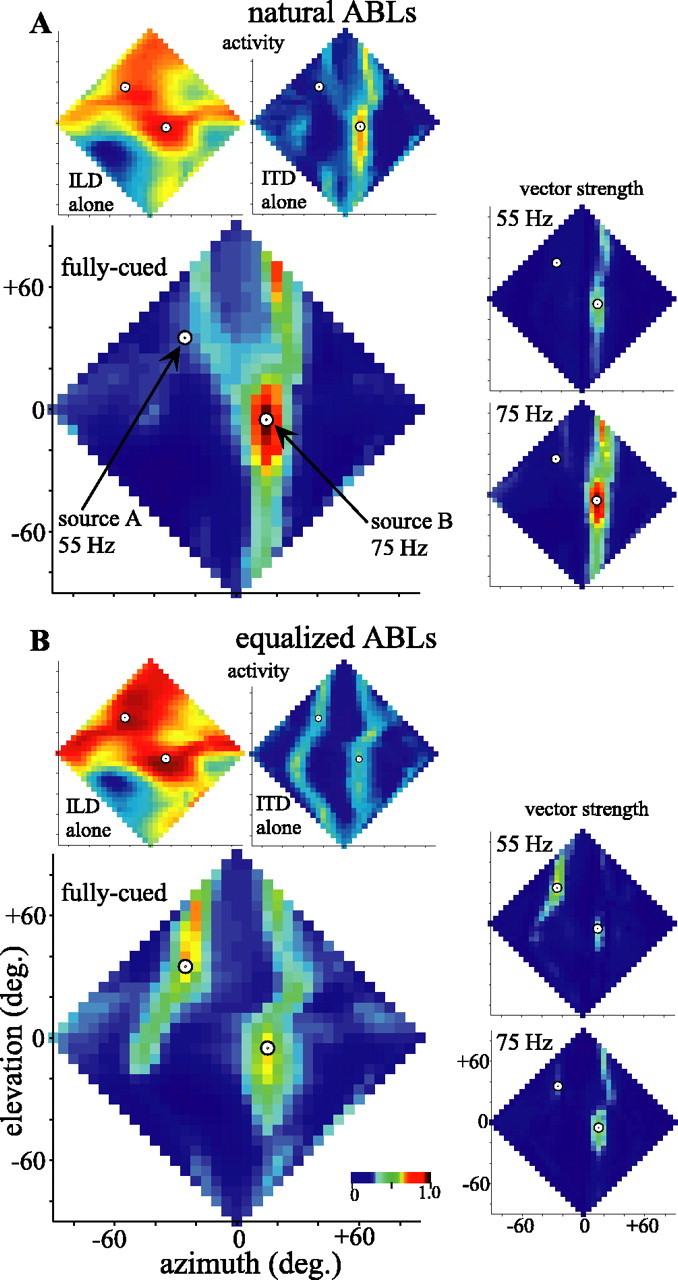
Activity representing the frontal hemisphere of auditory space inferred from the model in response to two amplitude-modulated uncorrelated noises played from the locations indicated by circles in each plot (as in Figs. 11 and 12). The leftmost plots represent the normalized activity predicted across a combined bilateral-space map with homogenous RFs and spatial representation. Top, Smaller plots show ILD-alone (left) and ITD-alone (right) activity. Larger plots show the fully cued activity. All neurons are assumed to have identical Gaussian tuning curves centered on their best ITD and ILD values obtained from the HRTFs for their location in space. All frequencies (2-10 kHz) are weighted equally. Smaller plots at the right give the spatial distributions of vector strengths, indicating locking to the amplitude modulation of the stimulus at 55 Hz (top plots) or 75 Hz (bottom plots). The color scales are normalized to the range of values across all single-cued or all fully cued activity, or all vector strength plots, respectively. A, Activity and locking inferred when each source was presented with its natural, frequency-dependent ABL determined from its location in space. B, Activity and locking inferred when the two sources were presented with nearly identical ABLs at the eardrum (see Fig. 12 D).
The modeled responses depicted in Figure 14B show how strongly the relative intensity of each source affects the image of the space map. In this case, the two sources were presented with ABLs that were equalized at the eardrum as in Figure 12C. The ILD-alone plot again shows nearly equal representations of each source, now perhaps more accurately localizing source A. In contrast to Figure 14A, the ITD-alone activity falls in two approximately equivalent vertical bands corresponding to the azimuths of each source. The resulting fully cued representation shows two foci of activity at approximately the locations of the two sources and synchronized primarily to the appropriate source. Note, however, that the overall activity and the degree of spike locking are less when the two sources are approximately equally represented than when the more central source predominates (Fig. 14 A).
These estimates for the cellular representation of two sources are something of a worst-case scenario. The cellular data provided above suggest that neuronal tuning to frequency and binaural cues may allow “better use” of the binaural cues than the generic weights and tuning curves used here (Euston and Takahashi, 2002; Spezio and Takahashi, 2003). Lateral inhibition, attention, and other processes may also shape the auditory image of the space map.
Discussion
In the auditory space map of the owl's inferior colliculus, the what and where of sounds determine, respectively, the temporal pattern and location of neuronal activity. When the environment contains multiple sound sources with overlapping spectra, the mixing of the sound waves at the eardrums dynamically alters the binaural cues and may therefore degrade both the temporal and place codes. We presented two sounds having complete spectral overlap, making the separation of sources most difficult even within individual frequency bands. Nonetheless, individual space-specific neurons were capable of resolving two sources separated in space horizontally, vertically, or diagonally and of faithfully signaling the amplitude modulation inherent to the source in its RF. Responses to sources having identical amplitude modulations were still spatially segregated, therefore there was no evidence for amplitude modulation based grouping of sounds at this level.
The performance of a neuron in this two-source environment is explained by the frequency-specific momentary binaural cues and by the sensitivity of the neuron to the ITD and ILD in each spectral band. Computation of these cues and estimates of the response of a neuron show that spatial separability follows directly from the dynamic relative level of sources within frequency bands. When a given source is stronger in a particular band, the binaural cues remain close to the cues for that source, and an appropriately tuned neuron fires in synchrony with the modulation of the stronger source. If the amplitude of the less-intense source is increased, the binaural cues are drawn away from the originally more-intense source, and our model predicts that the neuron would fire in synchrony with the amplitude modulations of both sources. The proximal cause of the temporal firing pattern of a cell in this two-source case is therefore the change of the binaural cues, but it is the inherent amplitude modulations of each source that affect the binaural cues in a multisource environment. Cues for source characterization and localization are thus directly linked. When the two sources are at similar levels within a band, the cues may differ widely from those of either source, and the neuron is only rarely driven by either source. In this case, the neuronal activity generated by these bands spreads widely across the space map over time. The ability to determine what is where is maximally compromised.
In our study, the two sources were separated by 30-40°, which, in the horizontal and diagonal configurations, made the IPDs of the sources at ∼7 kHz nearly equivalent (Fig. 11A). The momentary IPDs in this band change little, and the momentary ILDs fluctuate back and forth between values for each individual source. Time-averaged activity is focused at loci appropriate to each source, making this frequency useful for localization. However, the time-varying activity evoked at both loci is synchronized to the more-intense source, making this band less useful for identification of the less-intense source. Therefore, such a frequency band is useful for localization but not necessarily for identification. Humans and other mammals may not be sensitive to the IPD of the high frequencies to which the owls are sensitive, but because the IPD affects ILD, this point is relevant to human performance as well.
Comparisons with previous models
Our model has antecedents in previous models of human binaural localization (Gaik, 1993; Hartung and Sterbing, 2001; Best et al., 2002; Braasch, 2002; Roman et al., 2003; Faller and Merimaa, 2004). Each of these models incorporate HRTFs, peripheral filters, and processes, such as cross-correlation, for the computation of binaural cues in each frequency band. The models of Roman et al. (2003) and Faller and Merimaa (2004) are particularly relevant because they explicitly considered concurrent sources with overlapping amplitude spectra. Their models computed the time-varying, frequency-specific binaural cues and “selected” moments in time during which the resulting cues correspond to those of the target source. Their methods of selecting the moments in which to accept the cues differ in detail but are ultimately related. Roman et al. (2003) applied a learning algorithm to generate spectrotemporal masks that passed ITD and ILD information only when one source was stronger than the other, somewhat like the strategy of “glimpsing” whereby subjects comprehend masked speech by listening during intervals when the masker is relatively less intense (Miller and Licklider, 1950). The model of Faller and Merrimaa (2004) selected the ITDs and ILDs when the interaural correlation coefficient was above some threshold level. Because interaural correlation would be high at moments when one source or the other predominates, this strategy is closely related to that of Roman et al. (2003). Both binaural models accurately localized concurrent sounds (e.g., uncorrelated speech samples) and, in the study of Roman et al. (2003), preserved speech intelligibility. The model of Faller and Merrimaa (2004) could also be generalized to account for other psychoacoustical phenomena such as the precedence effect.
In our model, the selection of binaural cues was left up to the space-map neurons, which respond selectively for a subset of frequency-specific binaural cues generated by sounds in their RF (Moiseff and Konishi, 1983; Brainard et al., 1992; Euston and Takahashi, 2002; Spezio and Takahashi, 2003). As our results show, the effective combination of binaural cues for a neuron are generated when one source, the source in its RF, predominates, and therefore neuronal cue selection is based on the same principles as those of the human binaural models described above. Furthermore, binaural cues achieve favorable values for a neuron with a source in its RF at rates corresponding to the amplitude modulations of that source, thus also preserving the envelope of the sound in the RF. The space-map neurons of the owl's IC are thus biological instantiations of the cue-integration process predicted theoretically (Roman et al., 2004; Faller and Merrimaa, 2004).
To visualize the response across the space map, we made the simplifying assumption that all neurons are tuned broadly in frequency and have Gaussian-tuning curves for the frequency-specific ITDs and ILDs of a given location in space. Figures 11 and 12 make it clear, however, that not all frequencies or ITDs and ILDs are equally useful. The frequency, ITD, and ILD tuning of individual cells in the space map may be optimized for the localization and identification of arbitrary multisource configurations. This optimization may occur during the process of visually guided calibration in an acoustically cluttered environment (for review, see Knudsen, 2002). It also follows that frequencies providing the least contaminated cues for a given two-source configuration could be determined from the HRTFs and removed to hinder masked discrimination of amplitude modulations.
Involvement of monaural cues
Barn owls rely overwhelmingly on binaural cues for localization (Egnor, 2000), and therefore the present study focused on them. Monaural cues, however, may have a role in source identification. In humans, the monaural acoustical axes are directed strongly to the side (∼80-90° below 8 kHz to ∼60° above 12 kHz) (Algazi et al., 2001). When target and masker are separated horizontally, the target may be aligned near to the acoustical axis of one ear, and the masker may be aligned near the axis of the other ear. To comprehend masked speech or to detect a target, the subject need only to attend to the ear with the higher signal-to-noise ratio for the target. Indeed, Bronkhorst and Plomp (1988) showed that this strategy of using the “best ear” contributed somewhat more to speech intelligibility than did the difference in ITDs of the target and masker. In the frog, Lin and Feng (2001) compared the ability of auditory nerve fibers and midbrain neurons to signal the presence of species-specific vocalizations in the presence of a masker. In the auditory nerve, the improvement in detection obtained by separating target and masker could be explained, to a large extent, by the head-shadow effect favoring the ear closest to the target. At the midbrain, however, spatial segregation improved detection beyond that afforded by listening to the best ear, suggesting the involvement of other processes (Lin and Feng, 2001).
Is a best-ear strategy applicable in owls? In contrast to humans, the monaural acoustical axes of the owl lie near to the midline (Keller et al., 1998) and, above ∼6 kHz, are separated in elevation and azimuth by only 10-20°. Thus, for a masker and target separated spatially, neither ear may have a better signal-to-noise ratio. We evaluated the monaural and binaural cues by presenting the model with a “target” source near to the acoustical axis of one ear while placing the “masker” source 30° away horizontally, vertically, or diagonally. In these conditions, both the binaural cues for the location of the target and the monaural cues for the best ear were modulated strongly at the rate of amplitude modulation of the target and showed little evidence of contamination from the masker. At the location of the masker, activity is appropriately modulated by the masker, but both the binaural cues and monaural signal are heavily contaminated by the amplitude modulation of the target. In the extreme case, when the target is placed in the acoustical axis of one ear and the masker is placed in the acoustical axis of the other ear, the monaural cues for each location lock much more strongly to the appropriate modulation than do the binaural cues. Thus, it is possible, but not experimentally confirmed, that both monaural and binaural cues might aid source identification in the owl.
The acoustical basis for activity across the owl's space map, described above, provides the substrate on which additional neuronal processing might act to enhance spatial separability of concurrent sources. These ideas should also apply to mammalian and, in particular, human pre-attentive listening as modified by the particulars of the HRTFs of each species.
Footnotes
This work was supported by National Institute of Deafness and Communication Disorders Grant DC03925 and National Science Foundation Learning and Intelligent Systems Initiative Grant CMS9720334. We thank Hanna B. Smedstad, Dr. Michael Spezio, and Elizabeth A. Whitchurch for technical assistance. The comments of two anonymous reviewers are much appreciated.
Correspondence should be addressed to Dr. Clifford H. Keller, Institute of Neuroscience, University of Oregon, Eugene, OR 97403. E-mail: keller@uoneuro.uoregon.edu.
Copyright © 2005 Society for Neuroscience 0270-6474/05/2510446-16$15.00/0
References
- Albeck Y, Konishi M (1995) Responses of neurons in the auditory pathway of the barn owl to partially correlated binaural signals. J Neurophysiol 74: 1689-1700. [DOI] [PubMed] [Google Scholar]
- Algazi VR, Duda RO, Thompson DM, Avendano C (2001) The CIPIC HRTF database. In: IEEE Workshop on Applications of Signal Processing to Audio and Acoustics 2001, pp W2001-2001-W2001-2004. New Paltz, NY: IEEE.
- Bauer BB (1961) Phasor analysis of some stereophonic phenomena. J Acoust Soc Am 33: 1536-1539. [Google Scholar]
- Best V, Carlile S, van Schaik A (2002) The perception of multiple broadband noise sources presented concurrently in virtual auditory space. In: 112th Convention, Audio Engineering Society, paper number 5549. Munich: Audio Engineering Society.
- Best V, van Schaik A, Carlile S (2004) Separation of concurrent broadband sound sources by human listeners. J Acoust Soc Am 115: 324-336. [DOI] [PubMed] [Google Scholar]
- Blauert J (1997) Spatial hearing. The psychophysics of human sound localization. Cambridge, MA: MIT.
- Blauert J, Cobben W (1978) Some consideration of binaural cross-correlation analysis. Acustica 39: 96-104. [Google Scholar]
- Bodnar DA, Bass AH (1997) Temporal coding of concurrent acoustic signals in auditory midbrain. J Neurosci 17: 7553-7564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodnar DA, Bass AH (1999) Midbrain combinatorial code for temporal and spectral information in concurrent acoustic signals. J Neurophysiol 81: 552-563. [DOI] [PubMed] [Google Scholar]
- Braasch J (2002) Localization in the presence of a distractor and reverberation in the frontal horizontal plane: II. Model algorithms. Acust Acta Acust 88: 956-969. [Google Scholar]
- Brainard MS, Knudsen EI, Esterly SD (1992) Neural derivation of sound source location: resolution of spatial ambiguities in binaural cues. J Acoust Soc Am 91: 1015-1027. [DOI] [PubMed] [Google Scholar]
- Brenowitz EA (1983) The contribution of temporal song cues to species recognition in the red-winged blackbird. Anim Behav 31: 1116-1127. [Google Scholar]
- Bronkhorst AW, Plomp R (1988) The effect of head-induced interaural time and level differences on speech intelligibility in noise. J Acoust Soc Am 83: 1508-1516. [DOI] [PubMed] [Google Scholar]
- Carr CE, Konishi M (1990) A circuit for detection of interaural time differences in the brain stem of the barn owl. J Neurosci 10: 3227-3246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colburn HS (1977) Theory of binaural interaction based on auditory-nerve data. II. Detection of tones in noise. J Acoust Soc Am 61: 525-533. [DOI] [PubMed] [Google Scholar]
- Dent ML, Klump GM, Schwenzfeier C (2002) Temporal modulation transfer functions in the barn owl (Tyto alba). J Comp Physiol A Neuroethol Sens Neural Behav Physiol 187: 937-943. [DOI] [PubMed] [Google Scholar]
- Drullman R (1995) Temporal envelope and fine structure cues for speech intelligibility. J Acoust Soc Am 97: 585-592. [DOI] [PubMed] [Google Scholar]
- duLac S, Knudsen EI (1990) Neural maps of head movement vector and speed in the optic tectum of the barn owl. J Neurophysiol 63: 131-146. [DOI] [PubMed] [Google Scholar]
- Durlach NI (1972) Binaural signal detection: equalization and cancellation theory. In: Foundations of modern auditory theory, Vol 2 (Tobias JV, ed), pp 369-462. New York: Academic. [Google Scholar]
- Egnor R (2000) The role of spectral cues in sound localization by the barn owl. PhD thesis, California Institute of Technology.
- Euston DR, Takahashi TT (2002) From spectrum to space: the contribution of level difference cues to spatial receptive fields in the barn owl inferior colliculus. J Neurosci 22: 264-293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faller C, Merimaa J (2004) Source localization in complex listening situations: selection of binaural cues based on interaural coherence. J Acoust Soc Am 116: 3075-3089. [DOI] [PubMed] [Google Scholar]
- Fischer BJ, Anderson CH (2004) A computational model of sound localization in the barn owl. Neurocomputing 58-60: 1007-1012. [Google Scholar]
- Gaik W (1993) Combined evaluation of interaural time and intensity differences: psychoacoustic results and computer modeling. J Acoust Soc Am 94: 98-110. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB (1969) Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol 32: 613-636. [DOI] [PubMed] [Google Scholar]
- Good MD, Gilkey RH (1996) Sound localization in noise: the effect of signal-to-noise ratio. J Acoust Soc Am 99: 1108-1117. [DOI] [PubMed] [Google Scholar]
- Hartung K, Sterbing SJ (2001) A computational model of sound localization based on neurophysiological data. In: Computational models of auditory function (Greenberg S, Slaney M, eds), pp 113-126. Amsterdam: IOS.
- Jeffress L (1948) A place theory of sound localization. J Comp Physiol Psychol 41: 35-39. [DOI] [PubMed] [Google Scholar]
- Keller CH, Takahashi TT (1996) Binaural cross-correlation predicts the responses of neurons in the owl's auditory space map under conditions simulating summing localization. J Neurosci 16: 4300-4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller CH, Takahashi TT (2000) Representation of the temporal features of complex sounds by the firing patterns of neurons in the owl's inferior colliculus. J Neurophysiol 84: 2638-2650. [DOI] [PubMed] [Google Scholar]
- Keller CH, Hartung K, Takahashi TT (1998) Head-related transfer functions of the barn owl: measurement and neural responses. Hear Res 118: 13-34. [DOI] [PubMed] [Google Scholar]
- Knudsen EI (2002) Instructed learning in the auditory localization pathway of the barn owl. Nature 417: 322-328. [DOI] [PubMed] [Google Scholar]
- Knudsen EI, Konishi M (1978) Space and frequency are represented separately in auditory midbrain of the owl. J Neurophysiol 41: 870-884. [DOI] [PubMed] [Google Scholar]
- Köppl C (1997) Frequency tuning and spontaneous activity in the auditory nerve and cochlear nucleus magnocellularis of the barn owl Tyto alba J Neurophysiol 77: 364-377. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Yin TC (1983) Binaural interaction in low-frequency neurons in inferior colliculus of the cat. I. Effects of long interaural delays, intensity, and repetition rate on interaural delay function. J Neurophysiol 50: 981-999. [DOI] [PubMed] [Google Scholar]
- Lin WY, Feng AS (2001) Free-field unmasking response characteristics of frog auditory nerve fibers: comparison with the responses of midbrain auditory neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 187: 699-712. [DOI] [PubMed] [Google Scholar]
- Lindemann W (1986) Extension of a binaural cross-correlation model by contralateral inhibition. I. Simulation of lateralization for stationary signals. J Acoust Soc Am 80: 1608-1622. [DOI] [PubMed] [Google Scholar]
- Litovsky RY, Colburn HS, Yost WA, Guzman SJ (1999) The precedence effect. J Acoust Soc Am 106: 1633-1654. [DOI] [PubMed] [Google Scholar]
- Miller GA, Licklider JCR (1950) The intelligibility of interrupted speech. J Acoust Soc Am 22: 167-173. [Google Scholar]
- Moiseff A, Konishi M (1983) Binaural characteristics of units in the owl's brainstem auditory pathway: precursors of restricted spatial receptive fields. J Neurosci 3: 2553-2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peña JL, Konishi M (2001) Auditory spatial receptive fields created by multiplication. Science 292: 249-252. [DOI] [PubMed] [Google Scholar]
- Perrott DR (1984a) Concurrent minimum audible angle: a re-examination of the concept of auditory spatial acuity. J Acoust Soc Am 75: 1201-1206. [DOI] [PubMed] [Google Scholar]
- Perrott DR (1984b) Discrimination of the spatial distribution of concurrently active sound sources: some experiments with stereophonic arrays. J Acoust Soc Am 76: 1704-1712. [DOI] [PubMed] [Google Scholar]
- Rayleigh L (1907) On our perception of sound direction. Phil Mag 13: 214-232. [Google Scholar]
- Roman N, Wang D, Brown GJ (2003) Speech segregation based on sound localization. J Acoust Soc Am 114: 2236-2252. [DOI] [PubMed] [Google Scholar]
- Saberi K, Takahashi Y, Konishi M, Albeck Y, Arthur BJ, Farahbod H (1998) Effects of interaural decorrelation on neural and behavioral detection of spatial cues. Neuron 21: 789-798. [DOI] [PubMed] [Google Scholar]
- Schnitzler HU (1987) Echoes of fluttering insects: information for echolocating bats. In: Recent advances in the study of bats (Fenton MB, Racey P, Rayner JMV, eds), pp 226-243. Cambridge, UK: Cambridge UP.
- Shannon RV, Zeng FG, Kamath V, Wygonski J, Ekelid M (1995) Speech recognition with primarily temporal cues. Science 270: 303-304. [DOI] [PubMed] [Google Scholar]
- Slaney M (1993) An efficient implementation of the Patterson-Holdsworth auditory filter bank. In: Apple Computer technical report 35. Cupertino, CA: Apple Computer.
- Snow W (1954) The effects of arrival time on stereophonic localization. J Acoust Soc Am 26: 1071-1074. [Google Scholar]
- Spezio ML, Takahashi TT (2003) Frequency-specific interaural level difference tuning predicts spatial response patterns of space-specific neurons in the barn owl inferior colliculus. J Neurosci 23: 4677-4688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern RM, Zeiberg AS, Trahiotis C (1988) Lateralization of complex binaural stimuli: a weighted-image model. J Acoust Soc Am [Erratum (1991) 90: 2202] 84:156-165. [DOI] [PubMed] [Google Scholar]
- Sullivan WE, Konishi M (1984) Segregation of stimulus phase and intensity coding in the cochlear nucleus of the barn owl. J Neurosci 4: 1787-1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi TT, Keller CH (1994) Representation of multiple sound sources in the owl's auditory space map. J Neurosci 14: 4780-4793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobias ML, Viswanathan SS, Kelley DB (1998) Rapping, a female receptive call, initiates male-female duets in the South African clawed frog. Proc Natl Acad Sci USA 95: 1870-1875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner H (1992) On the ability of neurons in the barn owl's inferior colliculus to sense brief appearances of interaural time difference. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 170: 3-11. [DOI] [PubMed] [Google Scholar]
- Wagner H (1993) Sound-localization deficits induced by lesions in the barn owl's auditory space map. J Neurosci 13: 371-386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright BA, Lombardino LJ, King WM, Puranik CS, Leonard CM, Merzenich MM (1997) Deficits in auditory temporal and spectral resolution in language-impaired children. Nature 387: 176-178. [DOI] [PubMed] [Google Scholar]