Neural Activity in Macaque Parietal Cortex Reflects Temporal Integration of Visual Motion Signals during Perceptual Decision Making

Abstract

Decision-making often requires the accumulation and maintenance of evidence over time. Although the neural signals underlying sensory processing have been studied extensively, little is known about how the brain accrues and holds these sensory signals to guide later actions. Previous work has suggested that neural activity in the lateral intraparietal area (LIP) of the monkey brain reflects the formation of perceptual decisions in a random dot direction-discrimination task in which monkeys communicate their decisions with eye-movement responses. We tested the hypothesis that decision-related neural activity in LIP represents the time integral of the momentary motion “evidence.” By briefly perturbing the strength of the visual motion stimulus during the formation of perceptual decisions, we tested whether this LIP activity reflected a persistent, integrated “memory” of these brief sensory events. We found that the responses of LIP neurons reflected substantial temporal integration. Brief pulses had persistent effects on both the monkeys' choices and the responses of neurons in LIP, lasting up to 800 ms after appearance. These results demonstrate that LIP is involved in neural time integration underlying the accumulation of evidence in this task. Additional analyses suggest that decision-related LIP responses, as well as behavioral choices and reaction times, can be explained by near-perfect time integration that stops when a criterion amount of evidence has been accumulated. Temporal integration may be a fundamental computation underlying higher cognitive functions that are dissociated from immediate sensory inputs or motor outputs.

Introduction

Decisions often require the accumulation of evidence over time, and subsequent actions are often executed long after the relevant evidence has arrived at the senses. The physiological study of decision-making has begun to identify the neural mechanisms underlying the interpretation of sensory evidence, the maintenance of evidence in working memory, and the subsequent planning of appropriate motor actions (Schall, 2001, 2005; Platt, 2002; Glimcher, 2003; Romo and Salinas, 2003). To perform these operations that bridge sensory inputs with motor outputs, the brain needs to be able to integrate evidence over time, converting fleeting sensory events into persistent evidence that can be held and evaluated over longer timescales. The experiments described in this paper attempt to test whether neurons in the lateral intraparietal area (LIP) of the rhesus monkey brain reflect this temporal integration.

The hypothesis that LIP is involved in temporal integration comes from experiments in which monkeys perform a two-alternative direction-discrimination task (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002). In this task, monkeys decide the net direction of motion of a dynamic random dot stimulus and indicate their decision by making an eye movement to a corresponding choice target. Previous work has shown that the responses of middle temporal (MT) neurons reflect the direction and strength of the motion signal (Britten et al., 1993; Britten and Newsome, 1998). As the monkeys view and decide the direction of random dot motion, LIP responses increase or decrease gradually over time, depending on whether the monkey chooses a choice target within or outside of the response field (RF) of the LIP neuron under study. LIP activity thus appears to reflect the evolution of the monkey's decision in favor of one alternative over another. These gradual increases and decreases in spike rate are consistent with the proposition that LIP activity reflects the temporal integration (or accumulation over time) of the direction-selective sensory evidence represented in area MT (Mazurek et al., 2003).

To test the hypothesis that LIP activity reflects temporal integration of sensory signals in this task, we introduced brief directional “motion pulses” into the visual motion display. We reasoned that, if LIP activity truly reflects the time integral of visual motion signals, the effects of these brief sensory events should exert persistent changes in the spike rates of LIP neurons. Conversely, if LIP activity does not reflect substantial time integration, brief sensory events should exert only fleeting effects in the spike rates of LIP neurons. Consistent with the temporal integration hypothesis, we observed that 100-ms-long motion pulses affected decision-related activity in LIP for several hundreds of milliseconds, corresponding to the timescale used by the monkeys to form decisions in the task. We also observed a similar degree of temporal integration in the psychophysical choices. Our analyses suggest that LIP activity and psychophysical behavior may reflect near-perfect temporal integration of motion signals until a criterion amount of evidence in favor of one decision has been accumulated.

Materials and Methods

Methods for recording spikes and for monitoring eye position were described previously by Roitman and Shadlen (2002). Briefly, two male rhesus monkeys (Macaca mulatta; monkey I, ∼9.2 kg; monkey S, ∼8.5 kg) were implanted with a head-holding device, a recording cylinder (Crist Instruments, Damascus, MD) for transdural introduction of glass-coated tungsten electrodes (∼1 MΩ at 1 kHz; Alpha Omega, Nazareth Elite, Israel), and a scleral eye coil for monitoring eye position (C-N-C Engineering, Seattle, WA). All surgical and animal care methods conformed to the National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the University of Washington Animal Care Committee.

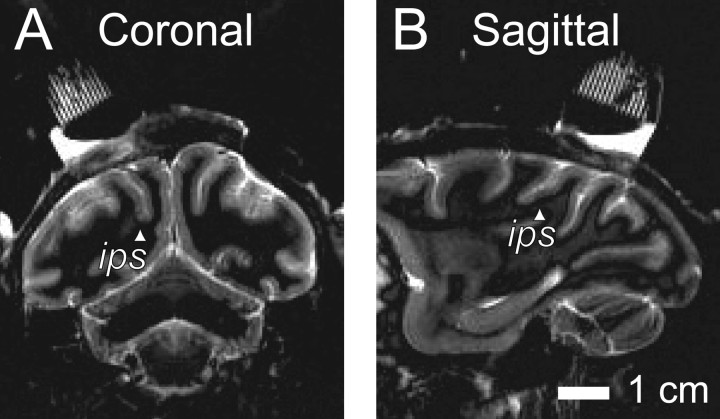
Identification and selection of neurons. We recorded from 54 well isolated LIP neurons in two monkeys (35 from monkey I, and 19 from monkey S). Neurons were selected according to anatomical and physiological criteria. Comparison of a postoperative magnetic resonance imaging (Fig. 1) to a standard atlas confirmed the location of the recording cylinder over the lateral bank of the intraparietal sulcus, using CARET software (Van Essen et al., 2001). Most neurons we recorded from were encountered 3-7 mm below the pia mater along a trajectory that ran approximately parallel to the intraparietal sulcus and most likely corresponded to the posterior two-thirds of ventral LIP (Lewis and Van Essen, 2000); a smaller number of neurons were encountered at shallower depths and most likely corresponded to dorsal LIP, although they had indistinguishable physiological properties based on our on-line assessments.

Figure 1.

Location of recording sites. Representative magnetic resonance images from one monkey show the recording cylinder positioned above the intraparietal sulcus (ips, arrowheads). Recordings were made from the lateral bank of the intraparietal sulcus in a region corresponding to ventral LIP by Lewis and Van Essen (2000). A, Coronal slice. B, Sagittal slice. Images were obtained using short T1 inversion recovery acquisition at 1.5 T using carotid radio-frequency coils placed adjacent to the head. Imaging voxel size was 0.47 × 0.47 mm square in plane, 3 mm thick.

We used a memory-guided saccade task to select neurons that showed spatially selective, persistent changes in spike rate while waiting to execute an eye movement (Hikosaka and Wurtz, 1983; Gnadt and Andersen, 1988). The monkey fixated a central point while a target appeared briefly (100 ms) in the periphery. To receive a reward, the monkey had to maintain gaze at the fixation point until its extinction (500-1500 ms) and then make a saccade to within 2-5° of the location of the remembered target (the size of the acceptable “window” was adjusted online to correspond to the eccentricity of the target). By varying the location of the target from trial to trial, we identified the location of the visual field that caused a sustained elevation in firing rate during the delay period, termed the RF. This hand-mapped location determined the position of the “preferred choice” target in the direction-discrimination task. This screening procedure identified 59 neurons for additional study.

Based on previous studies, we expected that neurons with spatially selective persistent activity would also discharge selectively when random dot motion instructed the monkey to make an eye movement to the preferred choice target (Shadlen and Newsome, 1996, 2001; Roitman and Shadlen, 2002). Before conducting the full battery of experiments, we confirmed this selectivity by having the monkey perform 10-20 trials of a simple version of the discrimination task using a relatively strong (easy) motion stimulus (51.2% coherence, described below) shown for 500 ms. We required the neuron to discharge selectively for preferred-target choices, during both motion viewing (500 ms) and a delay period between extinction of the random dot motion and the extinction of the fixation point, which signaled the monkey to make an eye-movement response. Five neurons failed to exhibit selectivity on this test and were excluded from additional testing. We recorded from the remaining 54 neurons in the main experiment for as long as the monkey would perform the reaction-time direction-discrimination task or for as long as we could maintain single-unit isolation.

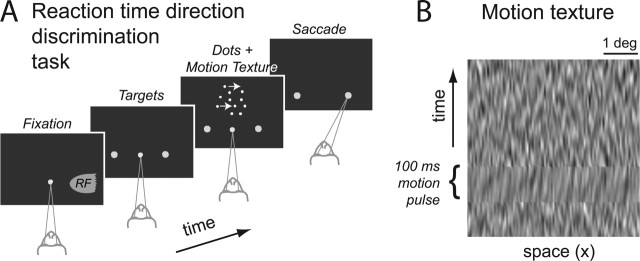
Reaction-time direction-discrimination task. Monkeys performed a single-interval, two-alternative, forced-choice direction-discrimination task (Fig. 2 A) using a stochastic random dot display (Newsome and Paré, 1988; Roitman and Shadlen, 2002). Each trial began when the monkey fixated a central fixation point. Then, two choice targets appeared, typically 180° degrees opposite one another, at the same eccentricity. After a random wait period (truncated exponential distribution: t_min = 150 ms; t_max = 3200 ms; mean = t_min + 550 ms), the random dot motion stimulus then appeared in a disk aperture (2.5° radius), centered 5° eccentric from the fixation point. The monkey's task was to discriminate the net direction of motion in this random dot motion stimulus.

Figure 2.

Direction-discrimination task. A, Monkeys performed a two-alternative RT direction-discrimination task. After fixation, two choice targets appeared in the periphery. One of the targets was within the RF of the neuron, indicated by the shading. After a random delay, dynamic random dots motion appeared in a 5° diameter aperture. Both the strength of motion (percentage coherence) and direction were randomized from trial to trial. The monkey indicated a direction choice by making a saccadic eye movement to one of the choice targets. The motion stimulus was extinguished as soon as the gaze moved from the fixation point. The RT is the time from motion onset until saccade initiation. On all trials, the random dots were superimposed on a dim dynamic pixel noise texture background. On two-thirds of trials, the texture included a 100-ms-long motion pulse in either the same or the opposite direction of the random dot motion. The pulse occurred at one of five possible times after dots onset. B, Space-time (x-t) profile of the dynamic background texture. This is the time course of luminance across one row of pixels in the display. Note the orientation in x-t during the pulse (indicated by the bracket). The vertical (y) dimension of the texture is not shown. In any one video frame, the luminance values at each pixel in a vertical column are independent, random values drawn from a Gaussian distribution. The range of luminance actually used in the display was the lowest 10% of the overall range of the display. The random dots that were superimposed on the background were shown at 100% intensity. For additional details, see Materials and Methods. Example movies can be downloaded from http://www.shadlen.org/~mike/movies/pulse/.

In this reaction time (RT) task, the monkeys controlled the motion viewing duration. Whenever they were ready to indicate their choice during dot viewing, they could complete the trial by making a saccadic eye movement from the fixation point to one or the other choice target. The dot display was extinguished when the monkey's saccadic response was detected. We measured both the accuracy and the reaction time of the decision on each trial. Choices were graded as correct if they corresponded to the direction of random dot motion. Reaction time is defined by the latency from onset of random dot motion to the initiation of the saccadic eye-movement response. The monkey was rewarded with water or juice for all correct choices and on half the trials at 0% coherent motion. On most trials, the fluid reward was delivered 100 ms after the saccade. We also imposed a minimum time from the onset of the dot display to the administration of fluid reward to discourage fast RTs. This minimum time to reward was 1000 ms for monkey I and 800-900 ms for monkey S. Incorrect responses elicited no fluid reward and an additional “time-out” delay before the beginning of the next trial. This error time out was an exponential function of the error RT, selected to especially discourage fast guessing (time = 20e^{(-4 RT)} s, up to a 4 s maximum). These reward and time-out contingencies helped to stabilize the monkeys' performance by providing an incentive to view the dots for long enough to ensure a reasonable level of accuracy. In similar experiments, human observers are often given instructions to establish a desired tradeoff between speed and accuracy (Reddi and Carpenter, 2000; Palmer et al., 2005).

During each experimental session, one of the choice targets was placed within the RF of the LIP neuron under study and is referred to as the preferred choice target. The other choice target was placed well outside the RF, typically in the opposite hemifield, and is referred to as the “null choice” target. Across trials, the correct direction of dot motion was randomized to two opposite directions, corresponding to correct choices of one or the other choice target. The strength of the random dot motion was chosen pseudorandomly from a list of six “motion coherence” values that spanned psychophysical threshold (0, ±3.2, ±6.4, ±12.8, ±25.6, and ±51.2% coherence). Motion coherence refers to the probability that a random dot seen at time t will be displaced according to the correct direction of motion when it is replotted 40 ms (three video frames) later. If a dot is not displaced in motion, it reappears at a random location in the display aperture. We refer to the two directions of dot and texture motion as positive and negative to reflect the fact that they supported eye movements to either the preferred or null choice target, respectively.

A dim, dynamic random-pixel texture was present within a 5° diameter patch. The center of the patch was 5° from the point of fixation, 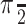radians counterclockwise along the circle through the choice targets. For example, if the preferred target was in the lower right quadrant, the dots would were centered in the upper right quadrant. The white dots (40 cd/m²) were superimposed on this texture and were distinct from the mean luminance of the texture (2 cd/m²). We used this dim background texture to perturb the motion energy in the display without making any changes to the random dot motion. On one-third of trials (“no-pulse”), the background texture modulated randomly, like dark television snow. On the other two-thirds of trials, the texture also contained a 100-ms-long motion pulse that could move in either direction (one-third of trials had “positive-direction pulses” and one-third of trials had “negative-direction pulses”). On each trial, the background pulse was presented at one of five possible times with equal probability (100, 150, 211, 287, and 392 ms after the onset of the dots). Importantly, the transitions from random modulation to a motion pulse (and back to random modulation) were seamless: the change in motion was not associated with a change in mean luminance or average contrast. Thus, pulse and nonpulse trials were not obviously different in appearance, and these perturbations were controlled independently of the random dot motion display. Outside the dot/texture aperture, the blank background of the display was equated with the mean luminance of the texture.

The motion-pulse textures were created starting with two dynamic textures, one that carried positive-direction motion signals and one that carried negative-direction motion signals. Their sum produced an undulating dark background with no net motion. We produced motion pulses by briefly perturbing the relative weight of the two textures while maintaining a fixed contrast. To create a moving texture, we filtered Gaussian white noise texture with a linear motion filter (Adelson and Bergen, 1985; Watson and Ahumada, 1985; Freeman et al., 1991; Carney and Shadlen, 1993; Schrater et al., 2000). Let W(x,y,t) represent a truncated Gaussian white-noise function, such that each pixel in each video frame is an independent draw from a Gaussian distribution with mean 0 and unit SD but resampled so that no values exceeds ±2 s. We convolved W with an impulse response of a broadband linear motion filter. A texture was created from the sum of two textures, D(x,y,t) and S(x,y,t), which were calculated as follows:

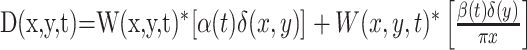(1A)

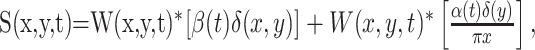(1B)

where x is the spatial dimension along the axis of motion, y is the orthogonal spatial dimension, and t is time. The ^* indicates convolution, δ(x)is the Dirac δ function, and α(t) and β(t) are the Adelson and Bergen (1985) temporal impulse response functions:

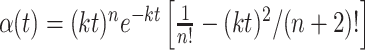(2A)

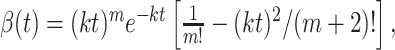(2B)

where n = 3, m = 5, and k = 40 s^-1. The patterns were spatially filtered to retain their broadband spatial characteristics but to incorporate displacements consistent with motion. One copy of the noise pattern was therefore convolved with a δ function (which effectively implements no spatial filtering), and the other was convolved with a hyperbolic (oddsymmetric) weighting function that effectively shifted the phase of all frequency components by 90° (the Hilbert transform of the Dirac δ function, here with sign inverted). The discrete implementation on pixels was achieved by defining the center pixel along x as 0. δ(x) equals the inverse of the pixel spacing, Δx^-1, at x = 0 and zero elsewhere. The desired normalization of the hyperbola was achieved by replacing with its sampled facsimile:

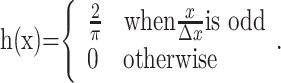(3)

In words, both textures D and S were made from the same white-noise pattern, W. To make D, we (1) began with two copies of a dynamic white-noise pattern W, (2) spatially filtered one of these copies to shift all spatial frequency components by 90° along the axis of motion, (3) passed the two copies of W (spatially filtered and unfiltered) through the temporal impulse responses, α(t) and β(t), and then (4) added them together. The result contains motion energy in one direction [Carney and Shadlen (1993), their Appendix].

For each trial, we created a base pair of these textures (positive and negative directions), moving in opposite directions. To create a dynamic texture with no net motion, the two textures were summed with equal weights (no-pulse trials). To create a pulse moving in one direction, the weight of one texture was temporarily increased as the other was decreased (positive-direction and negative-direction pulse trials). We then adjusted the mean luminance of the texture to 2 cd/m², the same as the screen background. The texture contrast was adjusted so that all luminance values spanned 0-4 cd/m², the bottom 10% of the intensity range of the display. The result was a subtle, dim texture that is not easily distinguished from a dark gray background. A space-time (x-t) slice of a background texture is shown in Figure 2 B. The orientation that is evident in a horizontal band of the image corresponds to a transient pulse of rightward motion. Demonstrations of the motion pulse stimulus are available on the internet at http://www.shadlen.org/~mike/movies/pulse/.

We used only the two cardinal axes (right-left or up-down motions) for the possible directions of dot and texture motions. For each experimental session, we chose the direction-of-motion axis that was closest to the axis defined by the choice targets, as determined by the location of the RF of the LIP neuron. Variations in task geometry (e.g., differences between dot motion direction and saccade target locations) had negligible effects on RT and accuracy.

Several factors led us to introduce the brief motion perturbations using background textures instead of simply “pulsing” the coherence of the moving dot display itself. One advantage of the background textures is that they provided more consistent motion perturbation across trials. The density of random dots (16.7 dots per squared degree per second) and their discrete nature limits the range of perturbations because of quantization and binomial variability. In comparison, we were able to manipulate the strength, direction, and timing of the fine texture motions more reliably because all pixels in the texture could carry motion information.

Most importantly, this strategy allowed us to maintain an unambiguous and simple reward scheme for the monkeys, who were trained to respond according to the direction of random dot motion. By perturbing the background texture and not the random dots, we could still reward for the correct discrimination of random dot motion. This logic follows the reward scheme applied in previous experiments during which motion viewing was perturbed not with motion pulses but with electrical microstimulation of area MT (Salzman et al., 1992; Ditterich et al., 2003). The optimal strategy given this reward scheme is to ignore the direction of the motion pulses entirely (just as it was optimal to ignore the microstimulation in previous studies).

Video display. Visual stimuli were presented on a 22 inch NEC/Mit-subishi FP1370 monitor (75 Hz refresh rate). The full display subtended 34° × 25° visual angle at a viewing distance of 65 cm (1 pixel = 0.04°²). The monitor was controlled by a 10-bit intensity resolution video card (ATI Radeon, Markham, Ontario, Canada) to better represent the intensities present in the dim background motion texture. This 10-bit display was programmed in Matlab 5.2.1 (MathWorks, Natick, MA) (for Macintosh) using functions in the Psychophysics Toolbox (Brainard, 1997).

Analysis of behavioral data. On each trial in which the monkey viewed the dots and successfully made a saccade to one of the choice targets, we recorded the accuracy (correct or incorrect) and reaction time (time from onset of random dots to initiation of saccade). Trials with exceptionally short (<100 ms) or long (>1650 ms) reaction times were removed from additional analysis but were very rare (1%). We excluded the rare short-RT trial because the responses were likely not based on viewing of the motion stimulus (“fast guesses”) and excluded the occasional long-RT trial because of technical limitations in presenting the background textures for extended durations. To assess the effects of motion pulses, we also excluded the trials on which the response was made before or during the motion pulse on that trial. These trials amount to an additional ∼3% of the data. Our results do not change appreciably if both types of excluded trials are included in our analyses, including our estimates of the temporal persistence of pulse effects.

For each motion coherence, we calculated the proportion of preferred-target choices and the mean RT. We fit a diffusion model to the dependencies of both choices and mean RTs on motion coherence (Wald, 1947; Stone, 1960; Link, 1975, 1992; Ratcliff, 1978; Smith, 1995; Ratcliff and Rouder, 1998) (for a similar application, see Palmer et al., 2005). The principle behind the diffusion model is to liken the decision process to the diffusion of a charged particle in an electric field from a starting position to a pair of absorbing boundaries. The motion strength biases the diffusion of a state variable (effectively the accumulated evidence for one direction and against the other) toward one absorbing boundary. The decision terminates when the state variable reaches one of the absorbing boundaries at ±A. The model makes the assumption that, in a time increment, dt, the state variable changes by a random increment drawn from a Gaussian distribution with mean μdt and variance dt. When there is no net motion, there is no bias to this diffusion, so the process, like Brownian motion, has an equal probability of stopping at the +A or -A bound. The chief advantage of the diffusion model is its capacity to jointly explain both choice and decision time as a function of drift bias μ and bound height A. Accordingly, the probability of making a preferred-target choice (i.e., stopping at the positive bound) is

(4)

and the mean time required to reach either bound is

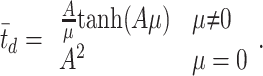(5)

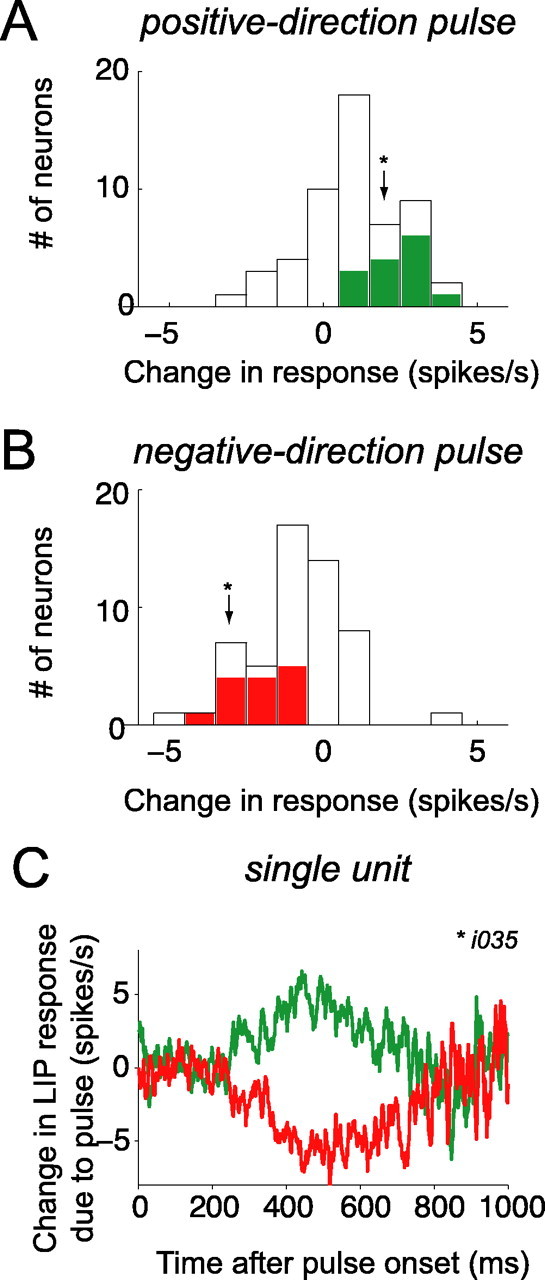
To fit the diffusion model to choice and RT data (see Fig. 3), we make the following three simplifying assumptions. (1) The mean RT is t̄_d plus the mean of an independent nondecision time t̄_nd that is not affected by motion strength or direction. (2) The drift bias, μ, is proportional to the signed motion coherence, C (the sign of C indicates the direction of motion). (3) Finally, we represent the effect of the background motion pulse as equivalent change in motion strength. This is not strictly correct because the pulse is only present for 100 ms, but the approximation simplifies the fitting equations and leads to a useful statistical comparison of the effect of the pulses on choice and RT. The quality of the fits in Figure 3 suggest that this is a fair approximation for analysis of the proportion of choices and mean RTs.

Figure 3.

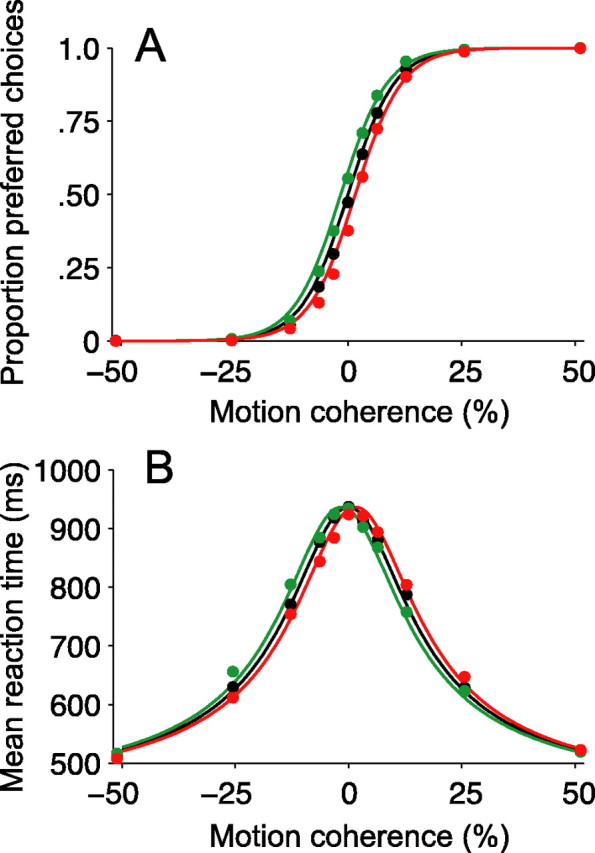
Motion pulses affect decisions and reaction times. A, Psychometric functions. The proportion of preferred-target choices is plotted as a function of motion strength. Positive and negative motion strengths (values along the x-axis) indicate motion for and against preferred-target choices, respectively. The black points show the proportion of preferred choices when no motion pulse was present. The green (or red) points show the proportion of preferred choices on trials when a positive- (or negative-) direction motion pulse accompanied the random dot motion. Positive- (negative-) direction pulses increased (decreased) the probability of preferred-direction choices. The smooth curves are described by logistic functions (Eq. 6). The horizontal displacement of the colored curves equates the pulses with the addition or subtraction of 1.6% coherent motion to the random dots stimulus. B, Chronometric functions. Mean reaction time is plotted as a function of motion strength. Same format as in A. Positive-direction pulses sped up RTs for preferred-target choices and slowed down RTs for null-target choices (green points below black points for positive motion coherences; green points above black points for negative motion coherences; green curve shifted leftward). Negative-direction pulses exerted corresponding effects (red points and curves). The smooth curves are described by Equation 7. Positive-direction (or negative-direction) pulses shifted the chronometric function by an amount equivalent to adding (or subtracting) 1.6% coherent motion to the random dot display. Mean RTs shown reflect both correct and error trials; a similar pattern is evident for just correct responses. All curves in both panels are described by a single fit of Equations 6 and 7 to all points in both panels.

Incorporating these assumptions into Equations 4 and 5 yields expressions for the psychometric function (probability of a positive direction choice) and chronometric function (mean RT) as a function of motion strength, C, and background motion pulse, π:

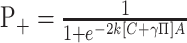(6)

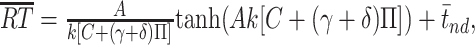(7)

where π represents the presence and sign of the background motion pulse (0 if absent, ±1 if present), and k, γ, δ, t̄_nd, and A are fitted parameters. Notice that the expressions k[C +...] substitute for μ to implement the assumptions above. The functions in Equations 6 and 7 are fit simultaneously to the choice and RT data on the idea that a single mechanism explains both the psychometric and chronometric function (Palmer et al., 2005). These functions share the same bound height and the same scaling between motion strength and drift bias. γ estimates the effect of the motion pulse on choices in units of C. We consider the possibility that the motion pulse might affect RTs by a different equivalent motion, γ + δ. Our fitting procedure simultaneously maximized the likelihood of both choices and RTs under the assumption that choice observations are distributed as binomial and mean RTs are distributed as normal with measured SE. This maximum-likelihood fitting procedure also furnished SEs of estimated parameters. These SEs were used to compute confidence intervals (CIs) and t statistics.

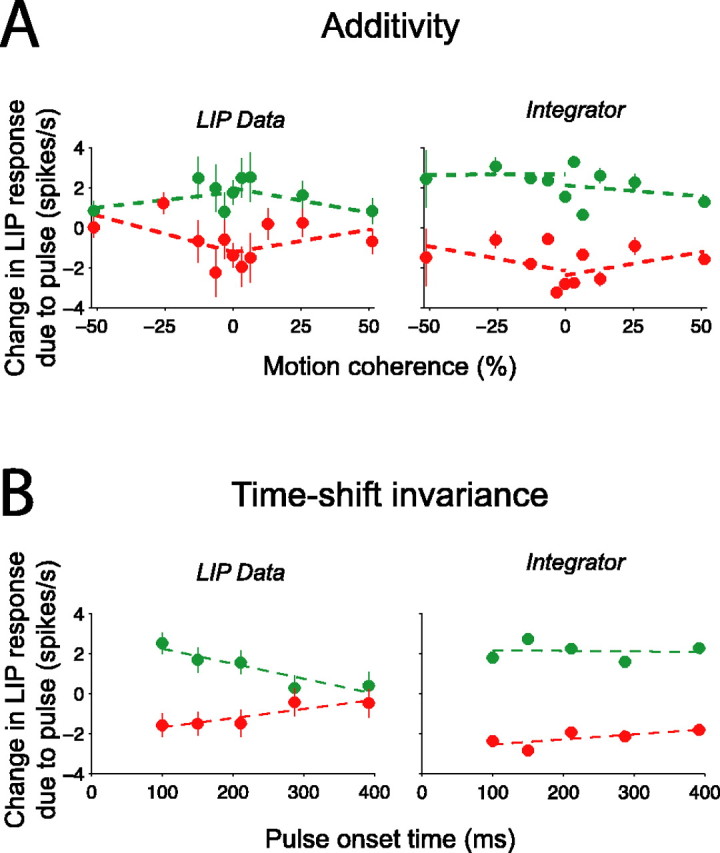
To assess the time course of the pulse effects on choices (see Fig. 4), we binned the data according to the time of the saccade (RT) relative to the pulse onset. We grouped trials into consecutive 75-ms-wide “relative-RT” bins and then quantified the effect of the pulse for each bin of trials by fitting the psychometric function and estimating the effective horizontal shift exerted by a pulse in either direction. To be able to apply the same RT criteria to no-pulse trials as for positive- and negative-direction pulse trials, we assigned virtual “onset times” to no-pulse trials, matching the distribution of actual pulse onset times for positive- and negative-direction pulse trials. We then fit each relative-RT bin of choice data with a logistic psychometric function:

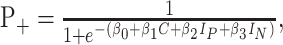(8)

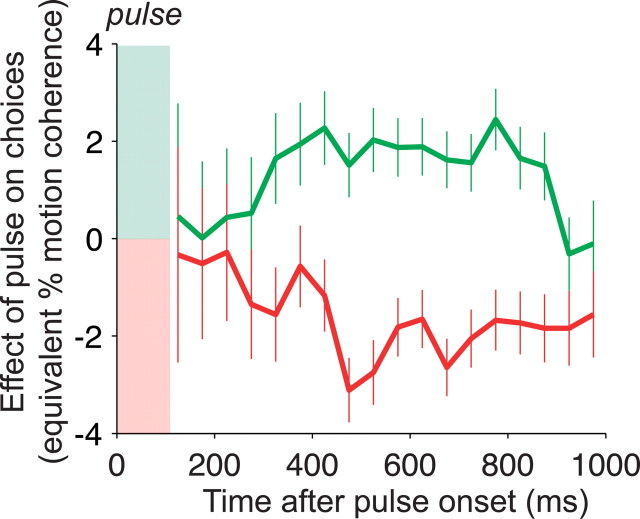
Figure 4.

Persistent effect of motion pulses on decisions. The effect of positive and negative motion pulses on the monkeys' choices is shown as a function of the time interval from the motion pulse to the choice. Pulse effectiveness is quantified by the shift it induces in the psychometric function along the motion coherence axis. Positive values on the y-axis correspond to left shifts of the psychometric function (like the green curve in Fig. 3), equivalent to the addition of y% coherent motion to the random dot stimulus (negative values correspond to right shifts; red curve in Fig. 3). Trials were grouped in 75 ms bins according to their latency from onset of the background motion pulse to initiation of the eye movement response: RT minus pulse onset time. A psychometric function was fit to these data (effect of motion strength on choice; Eq. 8) and compared with a comparison group of no-pulse trials with matching range of RT. The effects of positive-direction and negative-direction pulses are given by β₂/β₁ and β₃/β₁, respectively (see Eq. 8). Error bars are SEs of the estimates of β₂ and β₃, also expressed in units of equivalent motion strength. Choices made up to 900 ms after a pulse were affected in a direction-selective manner.

where C is motion coherence, I_P and I_N are indicator variables for the presence of a positive-direction and negative-direction pulse, respectively, and the β coefficients are fitted parameters.

To plot the data in Figure 4, we took the fitted pulse coefficients β₂ and β₃ and converted them to units of equivalent motion coherence by dividing them by the motion coherence coefficient, β₁. We converted the SEs of the pulse coefficients (returned from a maximum-likelihood fitting procedure) to motion coherence units similarly, using the average value of β₁ across all relative-RT bins.

Analysis of neural data. All physiological data reported in this paper were acquired from trials in which the monkeys completed the direction-discrimination task by choosing one of the two choice targets. Spike times were recorded to 1 ms precision and aligned to events in the trial. Trials were selected according to the same RT criteria for the analysis of psychophysical data, but our results do not change appreciably if all trials are included. To create the mean responses shown in Figure 5, we computed a standard peristimulus time histogram using 1 ms bins and smoothed the resulting responses with a 50 ms running mean.

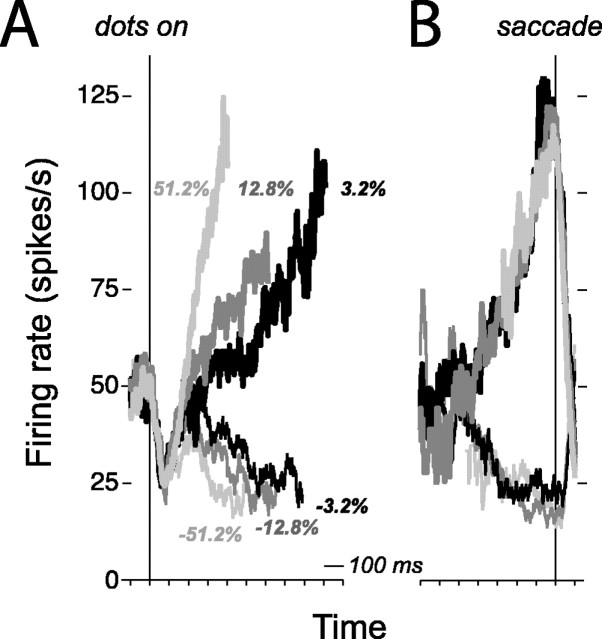
Figure 5.

LIP responses during performance of direction discrimination on stimuli with constant motion strength. Responses are averaged spike rates from a single, representative LIP neuron (i035). The traces are grouped by motion strength and the monkey's choice. Positive and negative motion strengths represent motion toward and away from the choice target in the response field of the neuron (thick and thin curves, respectively). Only correct choices are shown. A, Response averages are aligned to onset of random dot motion (left vertical line). Each trial contributes the early portion of its activity to the average: either up to 100 ms before the saccade or up to the median RT for the motion group, whichever occurs first. B, Response averages are aligned to initiation of the saccadic eye movement response (right vertical line). Each trial contributes the late portion of its activity to the average: either from 250 ms after onset of motion or the remaining amount of time corresponding to the median RT for that condition, whichever occurs last. The firing rate depends on motion strength during motion viewing and reaches a common level of activity preceding the eye movement response.

To analyze the effects of motion pulses (see Figs. 6, 7, 10), we first converted the spike times from each trial to a spike rate function (a “response trace”) by convolving the time series of spikes (δ functions) with an α function (rise time, 1 ms; decay time, 25 ms; kernel cropped at 100 ms). To focus on the changes in spike rate after the onset of a pulse, we subtracted the mean spike rate in the epoch 100-200 ms after pulse onset. This is the epoch that just precedes a detectable effect of the pulse on neural activity. This served to vertically align the response traces from individual trials at this common starting point.

Figure 6.

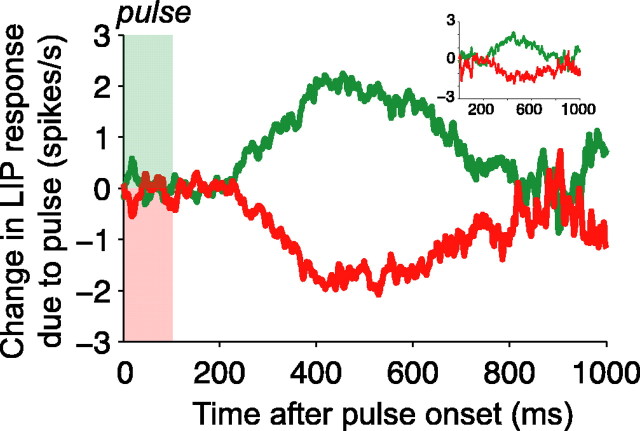
Temporal persistence of pulse effects on LIP responses. Graphs are averages of the pulse-induced change in firing rate as a function of time from pulse onset. The change in firing rate is estimated using the deviation of each trial from a template firing rate function. Template responses are averaged spike rates obtained from all trials sharing the same strength and direction of random dot motion and the same eye movement response (to the preferred- or null-choice target). Spike rates from single trials were calculated by convolution of the spike train with an α function (τ_rise = 1 ms, τ_decay = 25 ms; see Materials and Methods). These spike rates were used to compute both the templates and pulse-induced deviations. The deviations were aligned in time to the onset of the motion pulse and then averaged to produce the graph shown. The green and red curves show the deviation caused by positive- and negative-direction pulses, respectively, averaged over all motion strengths and directions. Pulse effects were evident from 225-800 ms after onset (n = 54 neurons from 2 monkeys, 55,014 trials total). The inset (top right) shows the pulse effect only for trials with RTs that occurred at least 750 ms after the onset of the pulse. Note that the latency and time course of the pulse effects are similar that shown in the main graph.

Figure 7.

Population summary of motion pulse effects on LIP activity. For each neuron, the pulse-induced change in firing rate was averaged over the 225-800 ms epoch after pulse onset. A, Frequency histogram of pulse-induced change in firing rate after positive-direction pulses. Positive-direction pulses increase LIP activity. Neurons with individually significant pulse effects are shaded (positive-direction pulse > negative-direction pulse; t test, p < 0.05). Arrowhead indicates the change in firing rate from the sample neuron (i034) shown in C. B, Frequency histogram of pulse-induced change in firing rate after negative-direction pulses. Negative-direction pulses decrease LIP activity. Same format as A (n = 54 neurons). C, Temporal persistence of pulse effects on responses of a single LIP neuron. Pulse effects seen in this neuron (i034) were similar to that observed in the population (same format as Fig. 6; note that the time course of the population average pulse effect shown in Fig. 6 was not affected by removal of this unit from the population).

Figure 10.

Analysis of additivity and time-shift invariance of LIP responses. A, Brief background pulses add or subtract a nearly constant offset to the LIP firing rate, regardless of the strength of random dot motion. The pulse-induced change in firing rate was measured in the epoch from 250 to 350 ms, using only the earliest pulse onset time (100 ms). The change in LIP firing rate is plotted as a function of the strength of random dot motion to which it was added (left). The same analysis was applied to simulated LIP responses (right), and a similar relationship between pulse effect and motion coherence was observed. Green points and lines, Positive-direction pulses; red points and lines, negative-direction pulses. Displayed regression lines were fit independently to each pulse and dot direction (4 total); statistics were computed on the results of a combined fit (Eq. 9). B, Background pulses add or subtract less when they occur later during motion viewing. The pulse-induced change in firing rate was measured in the epoch from 250 to 350 ms, separated by the onset time of the pulse. The change in LIP firing rate is plotted as a function of pulse onset time (left). Later pulses exerted weaker effects than earlier pulses. The same analysis was applied to simulated LIP responses (right). The decline of pulse effects with onset time in this model integrator is less steep than in the LIP data. Displayed regression lines were fit independently to each pulse direction; statistics were computed on the results of a combined fit (Eq. 10). Green points and regression lines, Positive-direction pulses; red points and lines, negative-direction pulses.

To isolate the deviations in spike rate attributable to pulses, we computed a set of reference responses against which we could gauge the effect of the motion impulse. Each of these “response templates” was the mean spike rate as a function of time for each neuron, for a given motion stimulus (motion coherence and direction) and a given choice made by the monkey (to the preferred target or to the null target). Each response template included no-pulse, positive-pulse, and negative-pulse conditions. To estimate the deviations in spike rate attributable to pulses, we subtracted response traces from trials with pulses from the appropriate response template. This strategy allows us to isolate the effect of a pulse, expressed in terms of a deviation in spike rate from the level that occurs as a function of motion, choice, and time. To produce the graph in Figure 6, we computed the average deviation in spike rate as a function of time, aligned to the time of the pulse onset. We calculated the response templates for each neuron individually but found that computing the response template using the average over all neurons yielded similar results. This technique isolates the effect of the pulse from the other factors that affect the neural response. In effect, this analysis reveals the change in spike rate as a function of time that can be attributed to the pulse.

We used a similar strategy to quantify the effectiveness of motion pulses in individual neurons (see Fig. 7). For each trial, we measured the deviation in spike rate attributed to the pulse (as described above). We then calculated the average change in spike rate in the epoch beginning 225 ms after pulse onset and ending either 800 ms after pulse onset or 100 ms before the saccade, whichever came first. We chose this time epoch to match the duration of pulse effects in the aggregate data (see Fig. 6). We were thus able to test whether the pulse effects in individual neurons were significant over the time frame exhibited in the population data. We performed two-sample t tests comparing the distributions of positive-pulse and negative-pulse effects (H₀: positive pulse = negative pulse). Averaging these deviations over trials also provided a single number for each neuron in our sample for each pulse direction. To test whether these average deviations in spike rate attributable to pulses were significant across our population of LIP neurons, we performed a one-way ANOVA (H₀: positive pulse = negative pulse = no pulse). To examine the effect of motion strength on the effectiveness of motion pulses (see Fig. 10 A), we measured the average deviation in spike rate (described above); we then calculated the average of this deviation in spike rate over the 250-350 ms after the pulse and analyzed these effects for each motion coherence separately. We considered neural responses within this time range because we wanted to estimate the instantaneous effect of a pulse across different motion coherences, without considering the longer-lasting effects of the pulse. To examine the effect of pulse onset time on the effectiveness of motion pulses (see Fig. 10 B), we measured the average deviation in spike rate over the 250-350 ms after each pulse, thus quantifying the instantaneous pulse effect for each pulse onset time separately.

For the additivity and time-shift invariance analyses (see Fig. 10), we fit lines to ascertain the effect of motion strength or time of pulse on the neural response after the motion pulse. To enhance the power of the analyses, we combined data from both directions of random dot motion and both directions of background pulses to estimate a single effect of motion strength,

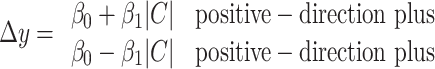(9)

or time of pulse

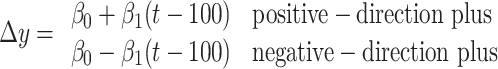(10)

where Δy is the change in LIP spike rate attributed to the pulse in the epochs defined above. If the effect of background motion pulse depends on motion strength or time, then β₁ > 0 in Equations 9 and 10, respectively. These effects were assessed by two-tailed t tests (H₀: β₁ = 0). The lines drawn in Figure 10 A reflect four individual applications of Equation 9, one to each combination of pulse direction and dot direction (i.e., we allowed β₀ and β₁ to vary freely for each line). The lines drawn in Figure 10 B reflect two individual applications of Equation 10, one for each pulse direction. The approximate mirror symmetry of the lines shown in Figure 10, A and B, supports the use of the pooled analyses described in Equations 9 and 10.

Simulation and analysis of a perfect integrator. We wanted to assess the degree to which bounded integration would limit the effectiveness of pulses and thus mimic the effect of integration leak. We also wanted to determine whether the magnitude of change in response in LIP spike rate is consistent with their effect on behavior (choices and RTs). As explained in Results, the presence of a decision bound limits the observed temporal persistence of pulse effects. Even in a perfect (lossless) integrator, the mean responses for both pulse conditions converge as they approach an asymptote at the decision bound. To tease apart the effects of the decision bound from those of true leak of the integrator, we measured the effects of pulses on a computer model that simulated LIP activity and the corresponding decision process as driven by the perfect temporal accumulation of sensory evidence to a decision bound. This model has been described previously (Mazurek et al., 2003) and has been shown to account for the major patterns of both psychophysical and physiological data observed in an unperturbed version of this reaction-time direction-discrimination task (Roitman and Shadlen, 2002). We extended the model to include time-varying motion stimuli. We then measured the effects of motion pulses on this model to assess the degree of temporal persistence one would expect to observe under the assumption that LIP spike rates reflect the perfect, but bounded, time integral of motion evidence.

The model assumes that LIP spikes rates are driven by the time integral of the time-varying difference between the spike rates of two opposing direction-selective pools of MT neurons. Briefly, the model has three stages: (1) “sensory,” representation of the motion evidence by simulated MT neurons; (2) “temporal integration,” accumulation of the evidence into a decision variable by simulated LIP neurons; and (3) “choice,” comparison of the accumulated decision variable (LIP spike rate) with a decision bound and subsequent behavioral response.

In the sensory stage, we simulate the responses of two opposed pools of direction-selective MT neurons to random dot motion of varying motion strengths and directions (e.g., left and right). Each neuron in the two pools produces a sequence of spikes with an expected rate proportional to the strength of motion (Britten et al., 1993). The expected rate throughout a trial (with no motion pulse) is a constant, beginning 100 ms after motion onset. Because the simulated neural discharge is variable, the averaged spike rates contain variability as a function of time. The averaged spike rate from the two pools furnishes the output of the sensory stage, which is passed on to the temporal integration stage.

In the temporal integration stage, we simulate the responses of two pools of LIP neurons. One of the LIP pools represents a plan to choose one choice target (e.g., corresponding to rightward motion), whereas the other represents the opposite plan (e.g., leftward). The expected firing rates of these neurons are determined by the evolving time integral of the difference in the output of the opposing MT pools. The expected LIP firing rate is calculated by integrating the time-varying difference in spike rate signals from MT. This integral is represented in LIP firing rate 125 ms later, consistent with our measurements (see below). The averaged spike rate from the two pools of LIP neurons furnishes a pair of decision variables on which the decision is made. The two ensemble average spike rates are smoothed using a first-order filter with time constant of 0.1 s. As noted by Mazurek et al. (2003), this smoothing is necessary because fluctuations in the simulated instantaneous spike rate in LIP would lead to early bound crossings, thereby dissociating choices from the sensory evidence in area MT. The choice of 0.1 s is chosen to approximate the smallest value that minimizes this discrepancy between mathematical integration of MT signals and representation of this integral by spiking LIP neurons. The presence of this smoothing step implies that the simulated LIP signals are noisier than the signals that ultimately control behavior. This smoothing step may stand in for the neural computations performed in other brain areas that are involved in this task but are not included in the model architecture (e.g., frontal eye field and superior colliculus). These smoothed LIP signals race against each other, reflecting the weight of evidence for their preferred choice direction.

In the choice stage, the simulated LIP responses are compared with a “decision bound,” a requisite level at which integration ends and a decision is rendered. The first LIP pool to reach its respective decision bound determines the target choice and the decision time. A random time is then added to mimic saccadic latency, noting that the total RT in a trial is the sum of decision time plus several nondecision time intervals (retina-MT visual latency, latency of decision-related activity in LIP, and saccadic latency, accounting for ∼300-400 ms nondecision time on average).

Although the model has several parameters, most were fixed by consulting previous results and by matching general characteristics of the LIP responses on trials with no pulses. The parameter values were similar to those used by Mazurek et al. (2003), but fine adjustments were made to provide a more precise match to the current set of stimulus conditions and results. It is important to note that, although some of the parameters were adjusted to fit various aspects of the data, they did not directly determine the degree of temporal persistence in the model: the model posits perfect, but bounded, integration. Specifically, the slope of the linear relationship between dot motion coherence and MT spike rate was adjusted to fit the slopes of the dependencies of choices and mean RTs on motion coherence. The dynamic range of the LIP responses was adjusted to fit the LIP responses we measured on no-pulse trials. The height of the decision bound (in units of LIP spikes per second) was adjusted to fit the observed psychophysical data on no-pulse trials. The equivalent strength of the motion pulse was adjusted to match the overall effects of pulses on choices and RTs. Finally, the postdecision saccadic latency was fit to account for the range of observed RTs. Table 1 shows all model parameter settings.

Table 1.

Parameters in LIP simulation

Parameter	Value	Justification
MT, baseline firing rate	8 spikes/s	Britten et al., 1993
MT, firing rate to 0% coherence	20 spikes/s	Britten et al., 1993
MT, latency	100 ms	Britten et al., 1993
MT, gain on preferred direction	0.36 spikes/s/%coh	Match to psychophysical data on no-pulse trials
MT, gain on null direction	−0.18 spikes/s/%coh	Match to psychophysical data on no-pulse trials
Magnitude of interneuronal correlation	r = 0.21	Bair et al., 2001
Timescale of interneural correlation	width of CCG at half-height = 9 ms	Bair et al., 2001
LIP, gain on MT signal	5.6	Match to LIP responses on no-pulse trials
LIP, baseline firing rate	48 spikes/s	Match to LIP responses on no-pulse trials
LIP, latency	125 ms	Match to LIP responses on no-pulse trials
Spike rate smoothing, MT	τ = 20 ms	Mazurek et al., 2003; for explanation, see Materials and Methods
Spike rate smoothing, LIP	τ = 100 ms	Mazurek et al., 2003; for explanation, see Materials and Methods
Height of decision bound	68 spikes/s	Match to psychophysical data on no-pulse trials
Effective pulse strength	10% motion coherence	Match to pulse effect on psychophysical data
Postdecision time	Mean = 150 ms	Match to psychophysical data on no-pulse trials

The table shows parameter settings for a simulated bounded integrator used to generate predictions in Figures 9 and 10. The “Justification” column indicates the source of data that was used to set the parameter. For simulation and analysis of a model perfect integrator, see Materials and Methods. For comparison of LIP activity with perfect integration to a decision bound for additional information, see Results. %coh, Percentage coherence; CCG, cross-correlogram. Format follows that for Mazurek et al. (2003).

We modeled the postdecision saccadic latency as an inverse Gaussian distribution to model some of the likely variability in nondecision components of the decision process (this contrasts with the simple diffusion-to-barrier model we used for the fits of the psychophysical data shown in Fig. 3, which did not need to consider variability to account for the mean RTs). We also assumed that the various nondecision latencies were additive, independent, and unaffected by the strength of motion or the decision outcome. Although there is evidence for anatomical connectivity between MT and LIP (Blatt et al., 1990), it is certainly possible that signals from MT pass through other areas before arriving at LIP (Schall et al., 1995).

With the model parameters set, we then simulated the range of conditions present in our experiments (motion coherence/direction, pulse direction, and pulse onset time) and investigated the effects of the brief motion pulses on the simulated LIP responses. To identify the degree of temporal persistence one would expect if LIP reflected the perfect integral of motion evidence, we randomly selected one model neuron and analyzed its spike times in exactly the same manner as we analyzed the real LIP data (see above).

Results

We recorded from 54 LIP neurons in two rhesus monkeys (55,014 trials; 35 neurons from monkey I, 19 neurons from monkey S) while they discriminated the direction of motion in a dynamic random dot display. As in previous studies, the stimuli were chosen randomly from a list that spanned a range of motion strengths in the two directions (Newsome and Paré, 1988). The monkeys were rewarded for choosing the correct direction of net motion, which they communicated by making a saccadic eye movement to a peripheral choice target. We used a reaction time version of this task in which we allowed the monkeys to initiate an eye-movement response whenever ready (Roitman and Shadlen, 2002). The RT measured on each trial allows us to infer the time period that the monkeys used to form each decision, complementing the measurement of the accuracy of each choice.

In this study, we briefly perturbed the strength of the motion while the monkeys formed their decisions by inserting 100-ms-long motion pulses into the background of the visual display. These brief perturbations allowed us test the hypotheses that decisions about motion are informed by the accumulation of motion evidence as a function of time, and that neurons in area LIP represent the time integral of the motion evidence. In the following four subsections, we (1) describe the effects of pulses on psychophysical performance, (2) describe the effects of pulses on LIP activity, (3) compare the observed temporal persistence of pulse effects on LIP activity with that of a simulated integrator that performs perfect integration to a decision bound, and (4) assess the additivity and time-shift invariance of the bounded integration evident in LIP.

Motion pulses affect perceptual choices and reaction times

The monkeys' choices and RTs depended systematically on the strength and direction of the moving dot display (Roitman and Shadlen, 2002; Ditterich et al., 2003; Palmer et al., 2005) and were further affected by the motion pulses. The positive and negative motion coherences correspond to dot motions in opposite directions. By convention, the positive direction is the one toward the eye movement target in RF of the LIP neuron (the preferred choice target). Strong motion in either direction led to near-perfect direction discrimination: almost all preferred-target choices for strong positive motions and almost no preferred-target choices for strong negative motions (i.e., all null-target choices). For the purely random noise dots (0% motion coherence, middle of graph), the monkeys distributed their responses approximately equally between preferred-target and null-target choices. At intermediate motion strengths, in which accuracy was neither perfect nor at chance, the monkeys made an increasing proportion of preferred-target and null-target choices with increasing positive and negative motions.

On two-thirds of trials, we inserted a 100 ms motion pulse into the dim random-pixel texture behind the dots. The pulse moved in either the same or opposite direction of dot motion and occurred at one of five possible times during the trial. Importantly, the monkeys were rewarded for choosing the correct direction of random dot motion and were thus encouraged to ignore the motion pulse. Nonetheless, motion pulses exerted systematic effects on both choices and RTs. The insertion of a positive-direction pulse increased the probability of the monkey making a preferred-target choice, and the presentation of a negative-direction pulse decreased the probability of a preferred-target choice (Fig. 3A, green and red points). The motion pulses caused the psychometric function to shift along the abscissa by an amount equivalent to ±1.6% coherent motion, as if the strength of the random dots were altered by this amount for the entire duration of the trial.

The motion pulses exerted a similar effect on RTs. On trials during which no motion pulse was presented, the monkeys' RTs also depended on the direction and strength of the moving dots (Fig. 3B, black points). At the strongest positive and negative motion strengths, the monkeys made their decisions relatively quickly, whereas at lower motion strengths, the monkeys took progressively longer to complete trials. Positive-direction pulses sped up RTs for preferred-target choices and slowed down RTs for null-target choices. Likewise, negative-direction pulses slowed down RTs for preferred-target choices and sped up RTs for null-target choices (Fig. 3B, green and red points). The fact that negative-direction pulses slowed down preferred-target choices (and that positive-direction pulses slowed down null-target choices) indicates that pulses could affect the decision process even when they did not determine the choice itself. Indeed, pulses shifted the RTs subtly but systematically, as if a small amount of motion from the pulse was added to, or subtracted from, the stream of motion information supplied by the dynamic random dots.

The solid curves in Figure 3, A and B, are fits of a diffusion model to the data (Eqs. 6, 7). They are derived from the premise that a common process underlies the choice and decision time on each trial. The key idea is that motion gives rise to a noisy quantity, termed the momentary evidence, in favor of one direction and against the other. The accumulation of this noisy momentary evidence resembles the diffusion of a particle. The diffusion is biased in the positive or negative direction, depending on the direction and strength of the motion. The process terminates when the accumulation reaches either a positive or negative bound, thereby determining the choice and decision time.

All of the curves shown in Figure 3, A and B, were jointly fit using a use a single diffusion model (Eqs. 6, 7). That is, for all motion strengths and for all pulse conditions, we assumed a common value for the height of the decision bounds (±A), the same constant of proportionality to convert from random dot motion strength to momentary evidence (k), and the same mean nondecision time (t̄_nd). The addition of a pulse was explained by adding or subtracting 1.6% motion coherence to the random dot motion (95% CI, 1.4-1.7% motion coherence). We allowed for the possibility that the background pulses might affect choice and RT by different amounts, but we failed to find evidence to support this (Eq. 7; δ = -0.05% motion coherence; no significant improvement in fit by likelihood ratio test, p = 0.70). Similar effects of the motion pulses on choices and RTs were observed in both of the monkeys, although the absolute magnitude of the pulse effect was stronger for one monkey than the other (Table 2). Together, these results suggest that both the speed and accuracy of decisions depended on a simple combination of random dot and texture motions.

Table 2.

Summary of fits to behavioral data

	Combined	Monkey I	Monkey S
k	0.426 (0.004)	0.411 (0.005)	0.500 (0.008)
A	22.811 (0.056)	22.358 (0.069)	22.63 (0.107)
tR	417 ms (2)	411 ms (2)	440 ms (3)
γ	1.60% (0.08%)	2.15% (0.10%)	0.89% (0.12%)
δ	−0.05% (0.13%)	−0.30% (0.17%)	0.29% (0.22%)

Table shows best-fit parameters of Equations 6 and 7 to choice and reaction time data for both monkeys (“Combined”, as shown in Fig. 3) and for both monkeys separately. SEs of fit parameters are in parentheses. The scaling term, k, and the pulse effect, γ, are common to both psychometric and chronometric function fits; k is in units [% coh]⁻¹; γ and δ are in units of percentage coherence. Note that δ appears only in the expression for the chronometric function. It allows for the possibility that the pulse effects on choices and RTs might differ, but it was not significantly different from 0 in all cases (likelihood ratio test, all p > 0.05).

We reasoned that, if temporal integration underlies the decision-making process, pulses should exert effects on choices even for decisions made long after the brief pulse had occurred. To examine this, we grouped trials based on the RT relative to the onset of the pulse. In each group, we quantified the effects of pulses on choices by estimating the motion coherence equivalent to a pulse (i.e., similar to the way we analyzed pulse effects on the aggregate choice data in Fig. 3A) (Eq. 8). As shown in Figure 4, pulses affected the choices that occurred ∼300 ms after pulse onset; trials in which saccadic responses were initiated earlier relative to the pulse showed no significant effect of the pulse. After this, however, the pulses had a persistent effect on choices. Trials in which responses were initiated from 300 to 900 ms after pulse onset showed a clear effect of the pulse on choice behavior. Thus, responses made up to 900 ms after a pulse still reflected effects of the pulse direction.

The time course of these effects also suggested that pulses exerted a similar effect on choices across a range of RTs, instead of preferentially affecting decisions made within a restricted time range, shortly after the pulse. Had the pulses precipitated choices in this manner, they would have distorted the shape of the RT distributions, shifting probability toward or away from the pulse time for preferred and null direction pulses, respectively. This observation is not borne out by an examination of the RT distributions. Positive and negative pulses simply scaled and shifted the RT distributions seen on no-pulse trials (Kolmogorov-Smirnov test, p > 0.6 for all pairwise comparisons of standardized RT distributions: ±pulse vs no-pulse, positive vs negative pulse).

The persistent effect of the pulses on choices is consistent with the existence of long-lasting temporal integration, or “memory,” of sensory events. Furthermore, the fact that the pulse effects persisted for hundreds of milliseconds enabled us to study the physiological mechanism underlying this temporal integration. In the following section, we describe how the latency and temporal persistence of the pulse effects on choices can be explained by the neural activity in area LIP.

Motion pulses affect LIP activity

Neural activity in area LIP depended on the strength and direction of random dot motion, as shown previously (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002), and was further perturbed by the motion pulses. On trials without a motion pulse, the average spike rate increased or decreased as a function of time, indicating whether the monkey would make a decision communicated by a saccade into or out of the RF of the neuron. These responses also depended on the dot direction, motion coherence, and amount of viewing time. These properties are apparent in the responses of the single neuron shown in Figure 5A. The responses are grouped by the monkey's choices (thick vs thin curves) and by the direction and strength of motion (indicated by shading).

Before the onset of random dot motion (Fig. 5A, vertical line), the mean spike rate for this neuron was ∼50 spikes/s because of the presence of one of the choice targets in the RF of the neuron. After the onset of the dots, there was a dip-and-rise in activity, followed by a ramp-like increase or decrease in activity that reflected the direction and strength of motion. Beginning 200-225 ms after onset of the random dot motion, the spike rate increased or decreased before preferred-target and null-target choices, respectively. The ramp-like responses then developed over several hundreds of milliseconds as the monkey formed its decision. The slopes of these ramping responses depended on the strength of the motion signal: stronger (or weaker) motions in the preferred direction corresponded to faster (or slower) rates of increase, and stronger (or weaker) motions in the null direction corresponded to faster (or slower) rates of decrease. Within the last 100 ms before a preferred-direction decision was made, the activity of this neuron reached a common level independent of motion coherence. This is made clear by aligning responses not to the onset of the dots but to the time of the saccade (Fig. 5B, vertical line). The direction-, coherence-, and time-dependent responses illustrated by this neuron are representative of the sample of 54 LIP neurons and are consistent with previous findings from our laboratory (Roitman and Shadlen, 2002). We note that the dynamic range of this sample neuron was higher than that of the population average.

To gauge the effect of the motion pulse, we examined the deviation in spike rate, as a function of time, from the neural response that would have occurred independent of the presence of a pulse. For each neuron, we estimated a response trace from each trial, defined as the time-varying spike rate from onset of random dot motion until 100 ms before saccade initiation (see Materials and Methods). We then grouped these response traces by choice and motion strength to form a set of time-dependent averages, which we term response templates. We used all trials to form these response templates regardless of whether a pulse was present or not. Thus, each response template represents our best estimate of the LIP spike rate as a function of time for a given motion strength, direction, and choice, absent any knowledge about the pulse. We then asked how trials with pulses differed from these response template averages. In short, we estimated for each trial the time-dependent residual from the corresponding spike rate response template. The procedure identifies the change in spike rate induced by the motion pulse, isolated from the effects of possible confounding factors (dot motion, monkey choice, and time).

Figure 6 shows the time course of pulse-induced changes in LIP activity, aligned to the onset of the motion pulse. The two curves show the average deviation in spike rate caused by positive and negative motion pulses across all trials for all 54 neurons. The effects of motion pulses became evident ∼225 ms after the onset of the pulse and persisted until ∼800 ms after the pulse. Thus, the 100-ms-long pulses affected LIP spike rates for ∼575 ms, indicating that LIP activity reflects sensory events that occurred over the previous half-second or more. This timescale is considerably longer than that observed in neural activity in sensory areas such as MT, in which fleeting sensory events cause only fleeting changes in spike rates for ∼120 ms (Bair et al., 1997; Bair and Movshon, 2004; Cook et al., 2004).

The lasting effect of the motion impulse on LIP activity is consistent with the hypothesis that LIP represents the time integral of relative motion evidence in favor of one choice alternative over another. Although it is tempting to interpret the diminishing effect of the pulse in Figure 6 as a sign of the time constant of the integrator, we will explain in a later section that such a gradual decline of pulse effects are expected even if signals were integrated perfectly, without substantial leak, to a bound. The important point here is that pulses exerted an effect on the LIP response over a duration that matched the timescale of the decision process in this task.

One possible concern about the analysis in Figure 6 is that the gradual and prolonged effect of pulses on the averaged data may not be present in single trials. In principle, motion pulses could affect neural activity briefly on any individual trial. To produce the averages in Figure 6, we might imagine that the motion pulse perturbs the firing rate briefly, at a variable latency just before the saccade. In principle, the averaged pulse effects could reflect the union of these brief events. To test this, we repeated the analysis in Figure 6 using only trials with RTs ≥ pulse onset time + 750 ms (Fig. 6, inset). An averaging artifact in this graph should delay the effect of pulses, but the time course looks very similar to the overall population average (Fig. 6, main panel). This demonstrates that the latencies and time courses of pulse effects were not closely linked to immediate behavioral responses and argues against the idea that the pulses tended to exert fleeting effects on individual trials.

Although the time course of pulse effects was difficult to appreciate in a single experimental session (typically ∼1000 trials per neuron), we confirmed that the changes in LIP spike rates exerted by motion pulses were a reliable characteristic of the 54 neurons we tested. For each neuron, we calculated the average change in spike rate caused by a positive or negative pulse in an epoch beginning 225 ms after pulse onset and ending either 800 ms after pulse onset or 100 ms before the saccadic eye movement (whichever came first). This is the period in which we observed pulse effects in the aggregate data (Fig. 6). LIP neurons typically discharged more on trials with positive-direction pulses than on trials with no pulse, and less on negative-direction pulse trials than on no-pulse trials (positive direction, +1.00 ± 0.21 spikes/s; negative-direction, -0.89 ± 0.22 spikes/s; mean ± SE) (Fig. 7A,B). These modulations of response after positive- and negative-direction pulses were significant across our sample of LIP neurons (F_(2,159) = 22.28; p < 10^-8, one-way ANOVA) and were individually significant in one-third (18) of the neurons studied (positive direction > negative direction; t test, p < 0.05; 13 of 35 in monkey I, 5 of 19 in monkey S). This analysis indicates that the population of LIP neurons reflects the combination of both dot and texture motions, and that the effect shown in the population average (Fig. 6) is representative of the effects in individual neurons.

The pulse effects we measured were subtle, and many of our analyses benefit from the power achieved by combining all our data across recording sessions and across monkeys. However, on some individual recording sessions, we were able to observe pulse effects similar to those seen in the population data. Figure 7C shows the pulse effects on the activity of a single LIP neuron, in the same format as the population data in Figure 6. Pulses affected the activity of this neuron on a timescale very similar to that of the population. Although such recording sessions were exceptional, this observation further supports the idea that the activity of at least some individual neurons can reflect substantial temporal integration similar to that shown in the population average. Likewise, pulse effects in the two monkeys were similar to the averaged data, although both the psychophysical and physiological pulse effects were slightly stronger in monkey I than monkey S (see above) (Table 2).

Finally, we note that we rewarded the monkeys for choosing the correct direction of dot motion, regardless of the pulse direction (see Materials and Methods). This reward scheme may indeed have motivated the monkeys to actively ignore the motion pulses present in the background texture, leaving open the possibility that the monkeys transiently attended to the background texture in an attempt to selectively “filter out” the motion pulse. However, the fact that pulses exerted direction-selective effects (increasing for positive direction, decreasing for negative direction) on both choices and neural responses cannot be accounted for by a time-varying increase in perceptual sensitivity or in neural activity associated with time-varying increases in attention at the time of a pulse (Ghose and Maunsell, 2002).

Comparison of LIP activity with perfect integration to a decision bound

As described above, our results demonstrate that both LIP spike rates and psychophysical choices reflect substantial temporal integration of visual motion: brief pulses of motion exert effects that persist for several hundreds of milliseconds. Although the effects of pulses on choices and LIP spike rates decline over time, this apparent “decay” will occur in even a perfect integrator so long as the noisy accumulation process stops when it reaches a decision bound.

This point can be made evident by numerically simulating the responses of a perfect integrator. Figure 8A shows simulated responses of a perfect integrator as it accumulates evidence in favor of a preferred-target choice. Green traces indicate trials with a positive-direction pulse, and red traces indicate trials with a negative direction pulse. The thin lines show the response of the perfect integrator on individual trials. Note that each individual path meanders because of noisy samples of sensory evidence acquired at each instant in time. This meandering accumulation process can be likened to a random walk or diffusion process. The thick lines show the average response: a ramp of activity bumped up or down after onset of a motion pulse. As a result of the perfect temporal integration, the effects of these brief perturbations persist as parallel offsets that continue over time.

Figure 8.

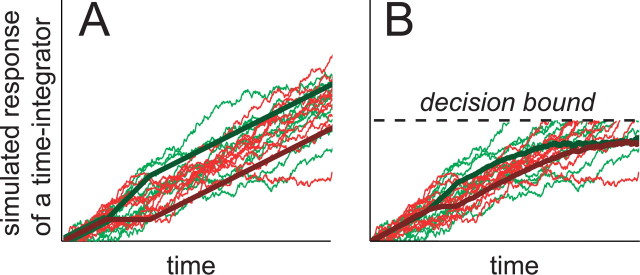
Presence of a decision bound limits the apparent degree of temporal persistence of pulse effects. Integration of noisy sensory signals can be described as a random walk or diffusion process. The thin traces in both panels show sample trajectories of such diffusion processes. They depict the accumulated sensory evidence associated with repeated trials using a relatively strong positive motion. The sensory signal gives rise to a sequence of random numbers drawn from a Gaussian distribution with mean μ (σ² =Δt). After 100 ms, the mean changes to μ±Δμ for 100 ms and then returns to μ. Each trace is the time integral of such a sequence of random numbers (green, +Δμ mimicking a positive-direction pulse; red, -Δμ mimicking a negative-direction pulse). The time integrals are themselves perfect: they do not introduce additional noise and there is no decay. Averages of these trajectories are shown by the thick lines. A, Unbounded case. The mean trajectories are straight lines with slope = μ, which is perturbed momentarily by ±Δμ. Under the assumption of perfect integration, the mean trajectories remain separated for all t. B, Bounded case. The mean trajectories begin as in A, but they approach an upper bound. The perturbation still causes a separation of the averaged trajectories, but this separation diminishes over time.

In our decision-making task, this integration does not continue on indefinitely. The decision-making period of each trial is thought to end when the monkey has accumulated a criterion amount of evidence in favor of one alternative over another. This idea is consistent with the observation that the firing rates of LIP neurons rise to a common value 70-100 ms before a behavioral response is made (Fig. 5B) [Roitman and Shadlen (2002) their Fig. 8]. Although the firing rates of many neurons may continue to change in the ensuing interval just before and during the saccade, none of these spikes are included in our analyses (Figs. 6, 7). Each trial contributes spikes only up to 100 ms before saccade initiation. Thus, to a first approximation, each of the trials leading to a preferred choice can be regarded as an integration path that terminates at the decision bound. As shown in Figure 8B (dashed lines), the average of these integration paths approaches an asymptote at the decision bound.

This same logic applies to trials in which the integrated evidence is perturbed by a positive or negative background pulse. Because these paths approach a common asymptote, they must converge over time, even if each individual trial reflects perfect integration. The thick lines in Figure 8B show the average of the integrated signals as they approach the decision bound. This simple illustration supports the idea that bounded, but otherwise perfect and linear, integration would give rise to the appearance of a diminishing pulse effect in time when one considers the average integration path over multiple trials.

To estimate the degree of temporal persistence one would expect to observe if LIP spike rates reflected the perfect temporal integration of evidence up to a decision bound, we replaced the schematic trajectories in Figure 8 with mean spike rates of simulated LIP responses. The model used to generate these simulated LIP responses posits that the firing rates of LIP neurons represents the (perfect) time integral of the difference between the firing rates of opposing, direction-selective pools of neurons in area MT. These direction-selective neurons are modeled with realistic levels of variability and covariance (Britten et al., 1993; Zohary et al., 1994; Shadlen and Newsome, 1998; Bair et al., 2001); they give rise to noisy accumulations. The spike discharge from each simulated LIP neuron is a noisy instantiation of these accumulations. We model two types of LIP neurons: those that represent the accumulated evidence for the positive direction and against the negative direction, and those that represent the opposite accumulation. The decision process terminates when the pooled activity from one of the LIP populations reaches a criterion level of firing rate. This model has been described in detail previously and was shown to account for the major psychophysical and physiological results in an unperturbed version of the RT direction-discrimination task (Mazurek et al., 2003) (see Materials and Methods).

We calibrated the model by approximating the dependencies of choice and mean RT on motion coherence, for unperturbed motion (Fig. 9A,B, black points). To do this, we adjusted four parameters of the model: (1) a scaling factor that governs the mean spike rate of MT neurons as a function of motion strength; (2) the bound height that governs the speed accuracy tradeoff (i.e., the number of excess spikes from rightward- vs leftward-preferring MT neurons needed to terminate the decision process with a “right” choice); (3) a scaling factor that converts the representation of this integrated difference to the averaged responses of our LIP neurons; and (4) a nondecision time that reflects the delay between LIP activity reaching the decision bound and the actual execution of the saccadic response. The model provides a coherent explanation of the monkeys' behavior and the LIP responses on trials without a pulse, on the assumption that LIP neurons represent the integral of the difference in firing rates between direction-selective neurons in MT. The quality of the fit does not prove this assumption true. Here we use the model to ask a simple question: what is the predicted change in LIP response to the pulses under the hypothesis of perfect, bounded integration?

Figure 9.

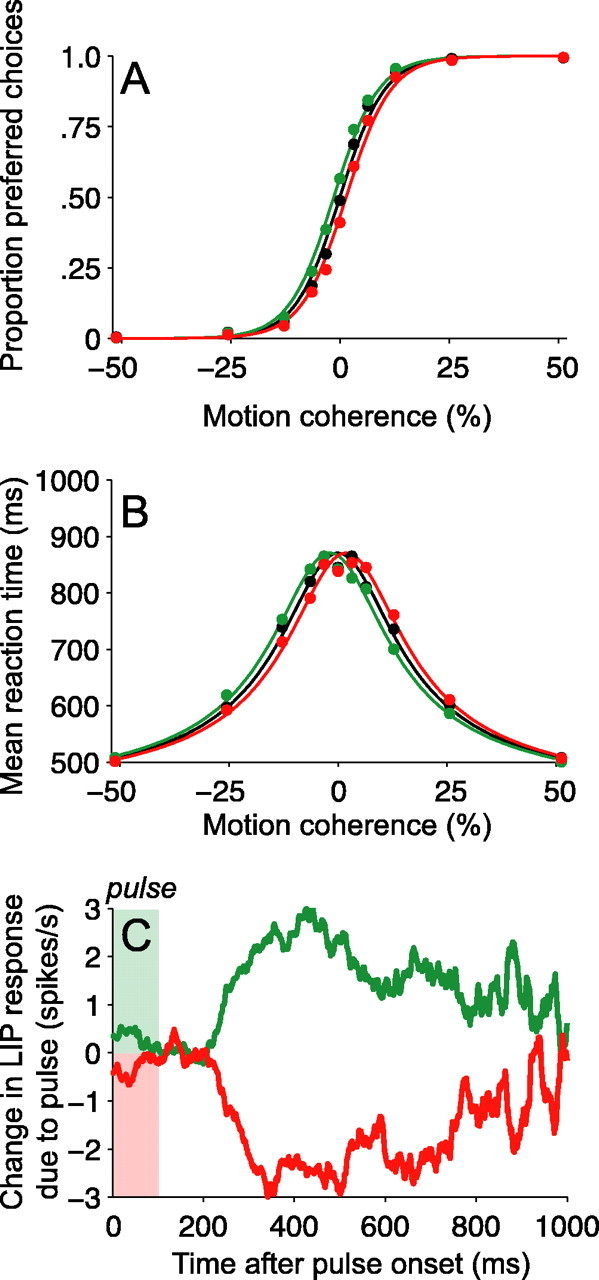
Simulated perfect integrator accounts for choices, RTs, and LIP activity. Results of simulations of a three-stage model. Stage 1 contains two pools of direction-selective neurons with properties like neurons in area MT. The pools prefer motion in the positive and negative directions, respectively. Their firing rates are proportional to motion coherence plus a constant plus noise, delayed by 100 ms relative to the motion stimulus. Stage 2 contains two pools of neurons, which are hypothesized to bear the following similarity to LIP neurons described in this paper. Their spike rates represent the integral of the difference in spike rates from opposing pools of the simulated MT neurons, delayed by 125 ms relative to the MT response. The pools integrate evidence for/against and against/for the positive direction of motion. Stage 3 is a threshold crossing detection that terminates the decision when the average response of one of the stage 2 pools reaches a bound. The pool reaching the bound first governs the choice; the behavioral response is initiated ∼150 ms later. Note that the averaging described above is over neurons in the pool, not over time. A, B, Calibration of the model using the behavioral results. Filled points show the same data as in Figure 3. The solid curves are averages from model simulations. The expected firing rates of stage 1 neurons to positive and negative motion were adjusted, along with the height of the decision bound in stage 3, to approximate the psychometric and chronometric functions on trials without motion pulses (black curves in A, B). The expected change in stage 1 firing rates accompanying the 100 ms background pulses was adjusted to approximate the observed shifts in choice and RT associated with positive- and negative-direction pulses (green and red curves, respectively). C, Model predictions for stage 2 neurons. The calibrated model was used to simulate the experiment, using the same motion strengths, directions, pulses, pulse times, and number of trials. The simulated responses (spikes) from stage 2 neurons were analyzed in the same way as the neural data (see Fig. 6). Positive-direction pulses induced positive deviations in spike rate from stage 2 neurons (red curve). Negative-direction pulses induced negative deviations in spike rate. The magnitude and time course of the pulse-induced deviations of stage 2 neurons is similar to real LIP neurons (Fig. 6).

To answer this question, we simulated trials with pulses by increasing or decreasing the expected firing rate of MT neurons for 100 ms. We used the same mixture of trial types (range of motion strengths, directions, pulse onset times, and pulse directions) as in our experiments. We adjusted one parameter: the change in MT firing rate was set to match the observed effect on behavior (a horizontal shift of the curves equivalent to ∼1.6% motion coherence) (Fig. 9A,B, colored curves). This was the only change we introduced to the model to accommodate the pulses.

We then assessed the change in activity in the simulated LIP neurons on the idea that these neurons represent the perfect time integral of MT signals. We applied the same analysis to the simulated LIP responses that was applied to the data: removing template responses to isolate the effect of the pulse. The latencies in the model ensure that the onset of a pulse (and the onset of motion) begins to affect the LIP firing rates 225 ms after onset. As shown in Figure 9C, the pulses caused an increase or decrease in simulated spike rate of 1.5-2.5 spikes/s. This difference diminished gradually over the ensuing ∼625 ms. In contrast to a perfect, unbounded integrator, which would show pulse effects that continue forever, the perfect, bounded integrator shows a gradual decline of pulse effects similar to that observed in the LIP data (compare with Fig. 6). The model exercise suggests that the size and time course of the pulse effects on LIP are consistent with integration to bound. However, the pulse effects in our data were somewhat smaller than predicted and not quite as persistent. We consider several explanations for this discrepancy in the following section.

More generally, this analysis demonstrates that our measurement of the temporal persistence of pulse effects does not furnish an estimate of the leak of the integration process. The presence of the decision bound explains the dramatic decline of pulse effects with time. Of course, there is not perfect agreement between model and data, but the relatively small remaining difference between the pulse effects seen in the LIP data and in the simulated integrator does not necessarily implicate a leaky integrator. Instead, there are several potential ways in which LIP could deviate from the ideal integration posited in our simulations. In the next section, we investigate two assumptions of linearity that underlie the ideal bounded integration process: additivity and time-shift invariance. In our experiment, additivity would correspond to pulses exerting equal effects across trials with different motion coherences, and time-shift invariance would correspond to pulses exerting equal effects regardless of when they were presented. These analyses identify a departure from time-shift invariance that may underlie the difference in pulse effects seen in LIP and the simulated perfect integrator.

Additivity and time-shift invariance of integration

In a perfectly linear integrator, the effect of a perturbation would not depend on the background value that the integration has attained up to the time of the perturbation, nor would it depend on the time that the perturbation is applied. In our experiments, we would expect a perfect integrator to respond to motion pulses identically, whether they are superimposed on strong or weak motion (additivity) and whether they are applied earlier or later during random dot motion viewing (time-shift invariance). In this section, we assess these characteristics in the LIP data and compare them with the output of the simulated perfect, bounded integrator introduced in the previous section. Analogous to the way that the bound limits the temporal persistence of measured pulse effects (Fig. 8), the decision bound also limits the range over which one would expect to observe additivity and time-shift invariance.

To assess additivity of the instantaneous pulse effects, we measured the average pulse effect over the 250-350 ms after a pulse. We restricted our analysis to the earliest pulse and to a short time window immediately after the pulse effect was evident. This allowed us to focus on responses that occurred relatively early during motion viewing and were thus were less likely to be affected by the presence of the decision bound.

The analysis shown in Figure 10A depicts pulse effects on LIP firing rate across the range of random dot motion strengths to which the pulses were added (Fig. 10A, left). There is a tendency for pulses to exert smaller effects when added to stronger motion strength (Eq. 9, β₁ = -2.5 spikes/s per 100% motion coherence; 95% CI, -4.6 to -0.3; p < 0.05, two-tailed t test). Interestingly, a similar trend is apparent in the model (Fig. 10A, right). This perfect, bounded integrator predicts a similar dependence on the strength of random dot motion (Fig. 10A, right) (β₁ = -1.5 spikes/s per 100% motion strength; 95% CI, -3.7 to 0.8; p = 0.18; same number of trials in simulation and data).

This analysis suggests that the immediate effect of a pulse on spike rates was approximately additive with the effects of dot motion coherence. The tendency for pulses to exert weaker effects on trials with higher motion coherences occurs because the accumulation on high coherence trials tends to be closer to the decision bound at the time of pulse onset. Deviations from additivity would be expected to become increasingly apparent for pulses that occurred later during the trial and for responses assessed longer after the pulse.

To assess time-shift invariance of the pulse effects, we measured the average pulse effect over the 250-350 ms after a pulse, for each pulse onset time separately. We focused this analysis on the two weakest motion strengths (0 and 3.2% coherence) because they typically result in longer RT. Nonetheless, because later pulses necessarily occur when the integration process is closer to the decision bound, one might expect that later pulses will be more affected by the presence of the decision bound.

The analysis shown in Figure 10B shows the average pulse effect as a function of the onset time of the pulse relative to the start of the moving dot stimulus. Pulses delivered later in the trial appear to influence the LIP response to a lesser degree than pulses delivered early in the trial (Fig. 10B, left). The regression fits point to a substantial departure from time-shift invariance. Pulse effects declined at a rate of -0.6 spikes/s per 100 ms of pulse onset time (95% CI, -0.9 to -0.3; p < 0.001, t test).

Not surprisingly, the simulated perfect, bounded integrator exhibits a departure from time-shift invariance (Fig. 10B, right). However, the regression demonstrates that the effect is considerably weaker than in the data (-0.1 spikes/s per 100 ms of pulse onset time; 95% CI, -0.4 to 0.1; p = 0.29). It appears that bounded integration is not sufficient to explain the weak impact of later pulses on the LIP responses. An attractive possibility is that the decision bound is not stationary but decreases over time (Ditterich, 2006). Equivalently, an “urgency” signal might be added to the accumulated evidence (Janssen and Shadlen, 2005). Time-varying effects of attention (Ghose and Maunsell, 2002) or neuronal responsivity (adaptation) might also play a role. Alternatively, the neural mechanism underlying the integration process itself might incorporate nonlinearities (e.g., attractor dynamics) that accelerate the rise of the LIP response in time (Wang, 2002). All of these potential nonlinearities would decrease the sensitivity to perturbations presented later in time.

The observed departure from time-shift invariance is less easily accounted for by leak of the integration process. Although leak can decrease the temporal persistence of pulse effects, it should not preferentially affect the strength of pulses that occur later in time. A more in-depth treatment of the linearity of various components of the integration mechanism will require additional experimentation. At present, our results demonstrate that LIP spike rates reflect substantial temporal integration.

Discussion

By presenting time-varying visual stimuli while monkeys performed a random dot direction-discrimination task, we tested the degree to which both decision-related activity in LIP and psychophysical decisions reflected temporal integration of sensory evidence. We observed that the effects of brief motion pulses on both LIP activity and choices persisted for several hundreds of milliseconds, consistent with temporal integration on the time-scale of decisions in our discrimination task. Computer simulation of LIP as a perfect, bounded integrator suggests that the temporal decline of pulse effects is not primarily caused by a short integration time constant (or leak) in the integration process itself. Rather, the time course of the pulse effects is consistent with the hypothesis that LIP reflects approximately linear integration that stops when the accumulation reaches a bound.

Previous experiments using dynamic random dot motion stimuli have indicated that discrimination accuracy improves as if dependent on the linear accumulation of signal plus variance (i.e., signal-to-noise ratio was proportional to 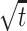) over several hundreds of milliseconds and sometimes over 1 s or more (Watamaniuk and Sekuler, 1992; Watamaniuk, 1993; Grzywacz et al., 1995; Gold and Shadlen, 2000; Burr and Corsale, 2001; Burr and Santoro, 2001). The accumulation inferred from psychophysics implies that the brain computes an integral with respect to time. It is worth noting that such integration does not hold for all visual tasks. In simple detection tasks, for example, linear accumulation of signal plus variance is often restricted to very short durations, under 80 ms (Watson, 1986). Moreover, improvement in detection associated with longer viewing exposures is not explained by temporal integration but rather by an increase in the number of opportunities to detect an extreme value among a series of brief, temporally independent, noncumulative observations, a process termed “probability summation over time” (Watson, 1979). We do not know why the visual system integrates in some cases but not others, although we suspect that the stochastic nature of the moving dot stimulus makes this beneficial.

Our findings provide direct support for this time-integral computation by demonstrating that brief perturbations of the stimulus have long-lasting effects on both decisions and neural activity. Although the pulses lasted only 100 ms, their effect on decisions was >0.5 s, lasting from 225 to 800 ms from the time of onset. Moreover, the effect of pulses on RTs suggests that they simply added or subtracted a fixed amount of momentary direction evidence, even when they did not determine the choice. This pattern of results requires a decision-making mechanism that maintains a persistent record of accumulated sensory evidence in favor of one alternative over the other until the end of the trial. A large class of decision-making models posit some form of temporal integration, including accumulator (LaBerge, 1962; Audley and Pike, 1965; Vickers, 1970), random walk (Stone, 1960; Link, 1975; Link and Heath, 1975; Laming, 1979), diffusion (Ratcliff, 1978; Ratcliff et al., 2003), and a variety of nonstationary and hybrid models (Smith, 1995, 2000; Usher and McClelland, 2001; Ditterich, 2005). Our results provide clear psychophysical and physiological support for such a temporal integration mechanism, and they are inconsistent with alternative mechanisms that do not rely on temporal integration. For example, it is possible in principle that the discrimination is performed on the basis of brief salient sensory events that either succeed of fail to induce a decision. Such memory-less mechanisms are supported in grating discrimination experiments (Watson, 1979) (but see Burr and Corsale, 2001). They are incompatible with the findings in our study because brief perturbations affect behavior and the neural response over a prolonged interval.

The motion pulses we inserted during the discrimination process serve as temporal “tags” that allow us to trace the time course of changes in the visual scene through neural activity and the behavioral response. The pulses first affected LIP activity ∼225 ms after onset and caused detectable changes in firing rate for another ∼575 ms (Fig. 6). The pulses affected choices over a similar range of times but lagged the LIP changes by ∼75-100 ms (Fig. 4). The order of these effects suggests that LIP activity does not reflect a postdecision feedback signal representing a choice that has already occurred but more likely reflects the ongoing computations during the formation of decisions. Although this temporal ordering does not guarantee causation, the temporal relationship between LIP activity and choices suggests that the signals in LIP are available to guide behavior.

The latency for motion information to affect LIP activity is long compared with the responses of LIP neurons to visual stimuli in their receptive fields (Bisley et al., 2004). However, it is important to realize that, in our experiments, the motion is not in the receptive field of the neuron; one of the choice targets is. This suggests that the decision-related activity in LIP, which is based on sensory information outside the LIP RF, might excite LIP neurons using a different pathway or different circuitry within area LIP.

As shown previously (Roitman and Shadlen, 2002) and as replicated in these experiments, the first 200-225 ms of the LIP response after the onset of the moving dots follows a stereotyped dip-and-rise that reflects neither the strength and direction of motion nor the monkey's choice. It was not clear from these previous observations whether the first 200-225 ms of visual motion information was ignored by LIP or was simply delayed in arriving at LIP. The finding here that motion pulses affect LIP response with a latency of 225 ms suggests that LIP does not ignore the first 200-225 ms of random dot motion but instead lags the visual stimulus by ∼225 ms.

Thus, we hypothesize that the first 225 ms of LIP activity (the dip-and-rise) reflects a “reset” of the integrator, after which temporal integration of the motion signals begins. Once LIP activity reaches a decision bound, another ∼100-150 ms are required to execute the motor response (Colby et al., 1996; Roitman and Shadlen, 2002). Interestingly, dip-and-rise response profiles with similar latencies have been reported in other tasks and brain areas (Sato and Schall, 2001; Leon and Shadlen, 2003) in which they also appear to signal the beginning of a cognitive process.

The end of the integration process is more mysterious. We do not know how the level of the decision bound set or how it is applied to level of integrated evidence. Human subjects are capable of adjusting the decision bound to implement a desired balance between speed and accuracy in the direction-discrimination task (Palmer et al., 2005). A recent theoretical study suggests that the superior colliculus and basal ganglia might play a role in both setting the bound level and detecting a bound crossing (Lo and Wang, 2004). Additional experiments will be needed to test this intriguing hypothesis.

Our experiments do not furnish a measurement of the integration time constant. The modeling exercise in Figures 8, 9, 10 demonstrate that an integrator with an infinite time constant (i.e., with no leak) will not show lasting effects of a motion perturbation if integration terminates at a bound. Nevertheless, in simple eye-movement tasks, LIP neurons can maintain persistently elevated firing rates during memory delays substantially longer than the timescale of decisions in our task (Gnadt and Andersen, 1988; Friedman and Goldman-Rakic, 1994; Li et al., 1999; Paré and Wurtz, 2001; Goldberg et al., 2002; Zhang and Barash, 2004). These observations suggest that the circuitry is not inherently leaky (Kaneko, 1999; Goldman et al., 2002; Major et al., 2004; Mensh et al., 2004), at least not over the timescale we considered in our experiments. Taking into account the sensory and motor latencies that constitute some portion of the monkeys' reaction times, the temporal persistence of our pulses provides direct support for neural integration on a timescale of at least ∼0.5 s. The capacity of LIP neurons to integrate beyond this time will need to be tested in a different behavioral paradigm.

Our experimental findings show that LIP neurons represent the time integral of motion evidence but lend little insight into the mechanism underlying the integration process. We do not know whether the neurons we studied actually perform the integration or whether they are relaying the result of a neural computation performed by other neurons in LIP or in another structure. If the latter, then they appear to mirror the computation with great fidelity, because the LIP responses bear an uncanny resemblance to the signals that govern choice and RT. Conversely, LIP may be part of a larger neural system involved in temporal integration. Indeed, it is likely that LIP works in concert with other areas that exhibit both persistent and decision-related activity, such as the prefrontal cortex and superior colliculus (Kim and Shadlen, 1999; Horwitz and Newsome, 2001a,b; Gold and Shadlen, 2003; Ratcliff et al., 2003). Whether the integration is performed in LIP or elsewhere, the LIP activity we measured shows small deviations from the mathematical idealization. The main deviation from ideal integration is explained by terminating integration once a bound or criterion is reached. Other departures from linearity that we observed (Fig. 10B) might be explained by emerging models of neural integration that depend on nonlinear mechanisms such as attractor dynamics (Wang, 2002; Machens et al., 2005) or hysteresis in input-output relationships (Koulakov et al., 2002; Goldman et al., 2003). Additional experiments using more complex perturbations (e.g., pulse pairs) are expected to shed light on these possibilities.

Our results suggest an analogy between the temporal integration by LIP of sensory evidence into a decision variable and the conversion by the brainstem oculomotor integrator of a transient velocity signal into a persistent position signal used to maintain a steady eye position (Cannon et al., 1983; Cannon and Robinson, 1987; Kaneko, 1997; Aksay et al., 2001; Major and Tank, 2004). Oculomotor integrator neurons are able to maintain graded levels of activity to represent different gaze positions, and much theoretical work has investigated how these neurons are able to maintain this continuum of persistent and steady levels of activity (Cannon et al., 1983; Cannon and Robinson, 1985; Arnold and Robinson, 1991; Seung, 1996; Seung et al., 2000; Koulakov et al., 2002; Goldman et al., 2003). Preliminary observations using a discrete and sequential presentation of evidence suggest that persistent activity in LIP can represent graded levels of accumulated evidence (Yang and Shadlen, 2004). It remains to be seen whether similar mechanisms underlie integration in the variety of brain regions that exhibit persistent activity, including those involved in other sensory-motor transformations (Romo et al., 1999; Machens et al., 2005). The observation that LIP appears to reflect integration to a bound may indicate it has different properties than the unbounded oculomotor integrator.

Previous studies of LIP responses in other tasks have identified signals that are not immediately linked to incoming sensory stimuli or to the execution of motor actions. Thus, LIP has been implicated in a variety of higher functions, including spatial working memory, motor planning, and the allocation of spatial attention (Gnadt and Andersen, 1988; Mazzoni et al., 1996; Snyder et al., 1997; Gottlieb et al., 1998; Ciaramitaro et al., 2001; Paré and Wurtz, 2001; Bisley and Goldberg, 2003; Zhang and Barash, 2004). Although our results do not immediately allow us to distinguish between competing accounts of LIP function, they do shed light on the neural computations reflected in LIP. For example, a common feature of LIP responses in many experimental contexts is a persistent change in neural activity that is triggered by a sensory cue but does not simply depend on the visual presence or absence of that cue. It is tempting to view the subsequent persistent activity as a sign of neural integration. For example, in simple memory guided saccades, an impulse of “evidence” about the location of a target is integrated to a step response.

Of course, time integration alone cannot account for a wide variety of functions ascribed to LIP, including the representation of prior probability (Platt and Glimcher, 1999), reward expectation (Platt and Glimcher, 1999), subjective value (Dorris and Glimcher, 2004; Sugrue et al., 2004), and elapsed time (Leon and Shadlen, 2003; Janssen and Shadlen, 2005). However, even in these contexts, temporal integration may facilitate the incorporation of these various types of information into neural computations that occur over a more flexible and extended time frame. The temporal integration we have identified may underlie the flexible combination or comparison of multiple pieces of sensory evidence that occur at different times but that are all relevant to a common decision or action.