Spike-Frequency Adaptation Separates Transient Communication Signals from Background Oscillations

Abstract

Spike-frequency adaptation is a prominent feature of many neurons. However, little is known about its computational role in processing behaviorally relevant natural stimuli beyond filtering out slow changes in stimulus intensity. Here, we present a more complex example in which we demonstrate how spike-frequency adaptation plays a key role in separating transient signals from slower oscillatory signals. We recorded in vivo from very rapidly adapting electroreceptor afferents of the weakly electric fish Apteronotus leptorhynchus. The firing-frequency response of electroreceptors to fast communication stimuli (“small chirps”) is strongly enhanced compared with the response to slower oscillations (“beats”) arising from interactions of same-sex conspecifics. We are able to accurately predict the electroreceptor afferent response to chirps and beats, using a recently proposed general model for spike-frequency adaptation. The parameters of the model are determined for each neuron individually from the responses to step stimuli. We conclude that the dynamics of the rapid spike-frequency adaptation is sufficient to explain the data. Analysis of additional data from step responses demonstrates that spike-frequency adaptation acts subtractively rather than divisively as expected from depressing synapses. Therefore, the adaptation dynamics is linear and creates a high-pass filter with a cutoff frequency of 23 Hz that separates fast signals from slower changes in input. A similar critical frequency is seen in behavioral data on the probability of a fish emitting chirps as a function of beat frequency. These results demonstrate how spike-frequency adaptation in general can facilitate extraction of signals of different time scales, specifically high-frequency signals embedded in slower oscillations.

Introduction

Many neurons will respond to the onset of a constant input with spike-frequency adaptation (i.e., a gradual reduction of the firing frequency). Neuronal adaptation is believed to underlie the commonly observed behavioral habituation of sensory systems to constant stimulation. There are numerous processes that can produce spike-frequency adaptation, including both intrinsic mechanisms and network interactions such as inhibition or synaptic depression. Recently, there has been much attention focused on possible functional implications of synaptic depression for computations such as gain control (Abbott et al., 1997), coincidence detection (Senn et al., 1998), and decorrelation (Goldman et al., 2002). Adaptation induced by slow intrinsic ionic currents of the spike generator is, however, also commonly observed in neurons and may enhance their response to high-frequency input (Nelson et al., 1997; French et al., 2001), mask low-intensity stimuli (Sobel and Tank, 1994; Wang, 1998), induce contrast adaptation (Sanchez-Vives et al., 2000), remove temporal correlations from the input (Wang et al., 2003), or affect network synchrony and rhythms (Crook et al., 1998; Ermentrout et al., 2001; van Vreeswijk and Hansel, 2001; Fuhrmann et al., 2002). Because adaptation usually operates within complex neural circuits and on many different time scales (Fairhall et al., 2001; Baccus and Meister, 2002; Kohn and Whitsel, 2002), it has been difficult to determine how these different cellular mechanisms contribute to network-level computations [e.g., sensory adaptation (Chung et al., 2002; Castro-Alamancos, 2004) or contrast adaptation (Sanchez-Vives et al., 2000; Fairhall et al., 2001; Kim and Rieke, 2003) in the visual system]. There are few studies on the functional role of adaptation or synaptic depression within a behavioral context (Sobel and Tank, 1994; Cook et al., 2003; Luksch et al., 2004; Ronacher and Hennig, 2004).

Here, we examine a sensory system that exhibits prominent spike-frequency adaptation to constant input and in which the functional role of adaptation can be investigated in the context of natural and behaviorally relevant stimuli. By means of a detailed phenomenological characterization of the observed spike-frequency adaptation, we conclude that the underlying mechanism includes adaptation of spike generation. Furthermore, we demonstrate that spike-frequency adaptation permits the detection of transient weak communication signals in the presence of strong low-frequency signals by enhancing the response to fast-stimulus components.

The weakly electric fish Apteronotus leptorhynchus (brown ghost knifefish) generates a quasi-sinusoidal electric organ discharge (EOD) in the 700-1000 Hz range, the amplitude of which is encoded in the discharge of fast-adapting electroreceptors (P-units) (Bastian, 1981; Nelson et al., 1997). The electrosensory system is used for the detection of objects and prey as well as for communication. In the latter case, the superposition of the electric fields of two fish results in a beat, an EOD amplitude modulation (AM) with a frequency that is given by the frequency difference, Δf, of the two fish. Low-frequency beats (|Δf| < 50 Hz) will evoke EOD modulations termed “chirps”: small chirps are agonistic communication signals in which the frequency of the EOD is increased transiently (Zupanc and Maler, 1993).

In this study, we present in vivo recordings from electroreceptors showing that chirps can evoke a response that is significantly enhanced compared with the response to slower beats. Furthermore, using a recently developed universal model of adaptation (Benda and Herz, 2003), we successfully predict the firing-frequency response of electroreceptors to chirps. Thus, understanding the dynamics of adaptation is essential for explaining the measured data. It is the cutoff frequency of the high-pass filter induced by adaptation that separates slow beats, transmitted with low gain, from fast chirps that are transmitted with a larger gain.

Materials and Methods

Chirp recordings. For recordings of chirps as shown in Figure 1, fish were placed in a mesh between the stimulation electrodes. The fish was stimulated with sine waves of different randomly ordered frequencies -12, -10,..., 10, 12 Hz above the fish's EOD frequency at 20% contrast (10 s long, 20 s pause). The spontaneously emitted chirps were detected as brief peaks >20 Hz above baseline EOD frequency.

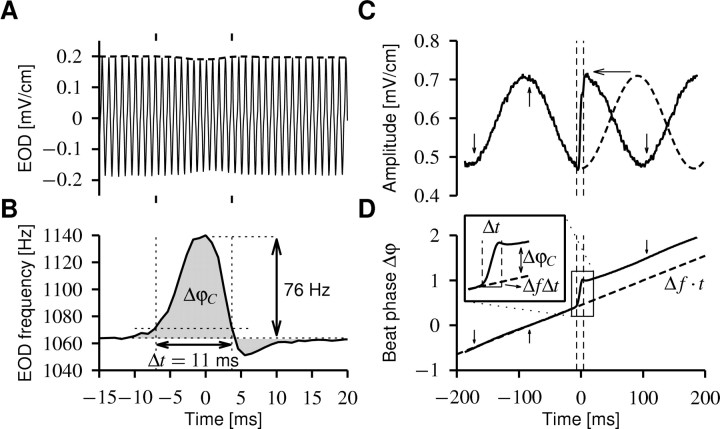
Figure 1.

Chirps. A, Looking at the EOD waveform (solid line), a small chirp (within the tic marks) is only visible as a small decrease in EOD amplitude (dashed line). This trace was recorded from the head-tail electrodes that do not pick up an additional stimulus field. B, Plotting the frequency of the EOD reveals the chirp, a transient (Δt = 11 ms) increase in EOD frequency (76 Hz) followed sometimes by a much smaller decrease in EOD frequency. This frequency excursion results in a phase shift Δφ_C relative to an EOD without a chirp, which is given by the integral over the EOD frequency minus its baseline frequency (gray area). Δφ_C is always positive, because a chirp always increases the EOD frequency. C, The presence of an EOD of a second fish creates a beat; here, with frequency Δf = 5 Hz. The chirp (with in the vertical dashed lines) has a huge impact on the beat pattern (envelope of the EOD, solid line). One-half of a cycle of the beat (dashed line) is compressed (horizontal arrow) within the chirp, thus resulting in a phase shift of the beat. The same chirp as in A is shown but recorded from the transdermal electrodes while applying an artificial EOD on the stimulus electrodes mimicking a second fish. D, The phase Δφ of the beat determines the position of peaks (upward arrow) and troughs (downward arrows) of the beat. Δφ is the difference between the phases of the two EODs. In the absence of chirps, the phases of the EODs φ₁ = f₁t and φ₂ = f₂t are determined by their respective frequencies, f₁ and f₂, and thus the phase of the beat is linearly increasing in time (dashed line; Δφ = φ₂ - φ₁ =Δft), as determined by the beat frequency Δf = f₂ - f₁. A chirp leads to a sudden increase in the phase of the beat (solid line), because the phase shift Δφ_C of the chirp is added to the phase shift of the beat ΔfΔt and thus accelerates the beat pattern for the duration Δt of the chirp. This is demonstrated by the inset that shows enlarged the time course of the beat phase during the chirp. Note also that the phase increase during the chirp is in good approximation linear.

Electrophysiology. Data from nine adult A. leptorhynchus (12-16 cm) are used in this study. For surgical exposure of the electrosensory lateral line lobe (ELL), fish were anesthetized (MS-222; Sigma-Aldrich, St. Louis, MO). After surgery, fish were immobilized (Flaxedil; Sigma) and transferred into a tank (28°C) where they were respired by a constant flow of oxygenated water through their mouth. Action potentials from single P-unit afferents were recorded routinely in vivo with sharp glass micropipettes (100 MΩ) that were advanced into the ELL with a piezo-electric microdrive (Inchworm IW-711; Burleigh, Fishers, NY). The potential between the micropipette and the reference electrode, which was placed in the fish's neck muscle, was amplified (Axoprobe 1A; Axon Instruments, Union City, CA), bandpass filtered (0.45-7 kHz, PC1; Tucker-Davis Technologies, Alachua, FL), and notch filtered at 60 Hz and the fish's EOD frequency (Ultra-Q Pro; Boehringer Mannheim, Willich, Germany). All experimental protocols were approved by the University of Ottawa Animal Care Committee.

The EOD unperturbed by the stimulus was recorded between the head and tail of the fish using two vertical carbon rods (11 cm long, 8 mm diameter). The transdermal voltage constituting the stimulus picked up by the P-units was estimated by two silver wires coated with nail polish, 1 cm apart, placed perpendicular to the side of the fish. Both EOD voltages were amplified and low-pass filtered at 5 kHz (2015F; Intronix, Bolton, Ontario, Canada). Stimuli were attenuated (PA4; TDT), isolated (model 2002; A-M Systems, Carlsborg, WA), and delivered by two stimulation electrodes (30-cm-long, 8-mm-diameter carbon rods) placed 10 cm on either side of the fish, parallel to its longitudinal axis. Two classes of stimuli were used: direct stimuli (sine waves to mimic the EOD of a second fish) and AMs. For the latter, the AM signal was multiplied with the fish's EOD (MT3; TDT). Note that with direct stimulation, the AMs measured from the EOD peaks are of the same size as the AMs measured from the EOD troughs: they equal the amplitude of the stimulus. In contrast, AM stimuli can result in unequally sized AMs if the EOD is asymmetric (often the peak is wider than the trough).

The extracellular potential, the EOD, the transdermal potential, and the attenuated stimulus were digitized at 20 kHz with a 12-bit Multi-IO board (PCI-MIO-16E-4; National Instruments, Austin, TX) on an Intel Pentium IV 1.8 GHz Linux personal computer. Spike and EOD detection, stimulus generation and attenuation, and preanalysis of the data were performed on-line during the experiment within our OEL (Online Electrophysiology Laboratory) software.

Protocols and data analysis. Identified P-units (Bastian, 1981) were stimulated with artificial sinusoidal EOD waveforms with frequencies 5, 10, 20, 30, and 60 Hz above the fish's own EOD frequency, resulting in the same positive beat frequencies, Δf. The amplitude of the artificial EOD was chosen to be ∼20% of the amplitude of the fish's own EOD. Ten identical chirps were included into each stimulus as a Gaussian increase in EOD frequency, such that they were separated by at least one complete beat cycle and would appear at 10 different positions within the beat. The width of the chirps at 10% height was 14 ms, and their size was 30, 60, 100, 122, or 153 Hz corresponding to phase advances Δφ_C = 0.25, 0.5, 0.8, 1.0, and 1.25 (throughout this report, phases are defined modulo one). Each such stimulus was presented 10-20 times. The actual position of a chirp within the beat was determined by measuring the phase shift between the stimulus and the fish's EOD, because even slight changes in the fish's EOD frequency make it impossible to accurately predict the position of the chirp within the beat cycle. Spike trains for the chirps were then sorted into 10 bins of different beat positions. The firing frequency was computed as the inverse interspike interval (ISI) averaged over the trials for every 0.5 ms. We computed the gain in firing frequency as the maximum modulation depth of the firing-frequency response during the chirp divided by the modulation depth during the beat. To minimize noise, we smoothed the firing frequency with a 0.05/|Δf| wide window before measuring the modulation depth during the beat. We also computed a gain for the stimulus as the modulation depth of the AM during the chirp divided by the modulation depth during the beat. The response gain shown in Figures 5 and 7 is the gain of the firing frequency divided by the gain of the stimulus. The latter was close to 1 in most cases.

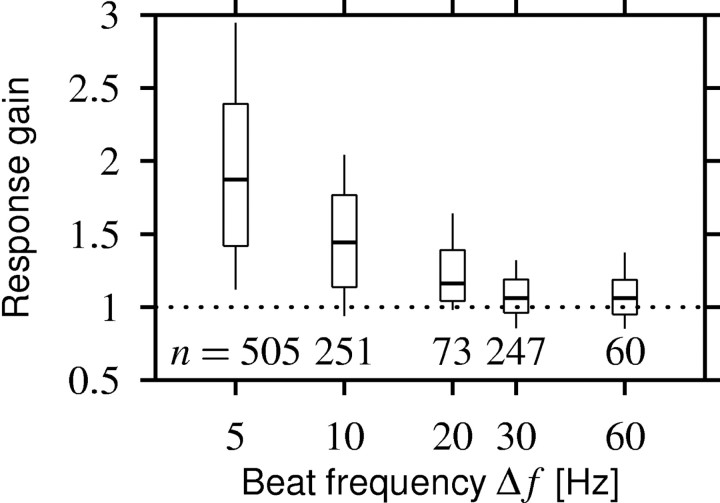
Figure 5.

Response gain as a function of beat frequency Δf for all 1208 chirp responses measured. The horizontal line within the boxes represents the median, the box includes the 2nd and 3rd quartiles, and the ends of the vertical lines mark the 1st and 9th deciles. Chirps evoke a response that is larger than the response to the beat (response gain >1) if the beat frequency is smaller than ∼30 Hz.

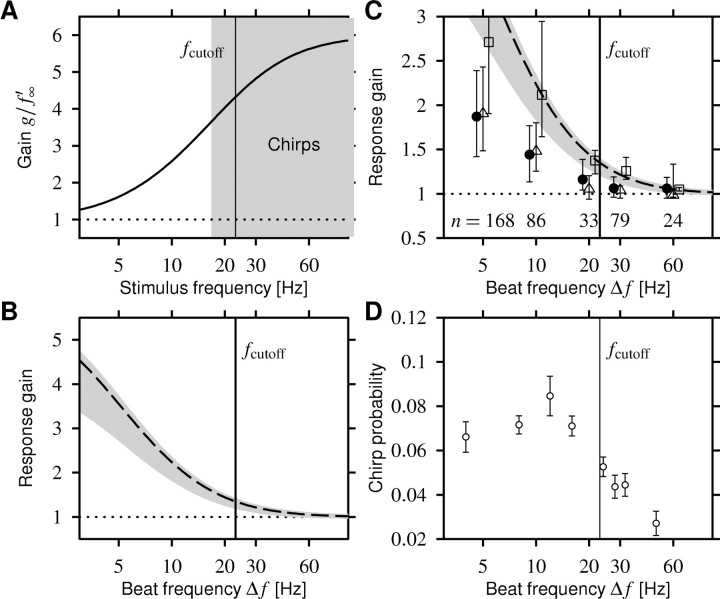
Figure 7.

Comparison of the response-gain data with model predictions and behavior. A, The gain Equation 3 of the high-pass filter generated by adaptation (solid line) as a function of stimulus frequency. The averaged value of the measured effective adaptation time constants sets the cutoff frequency f_cutoff of the gain function to 23 Hz (vertical line in all panels). Chirps are high-frequency signals (gray area) that are transmitted with a high gain. B, The response gain Equation 6 as a function of positive beat frequencies Δf estimated from the high-pass filter shown in A. The dashed line is the response gain for 14-ms-wide chirps that generate a phase shift of 1, and the gray area is for phase shifts ranging from 0.25 to 1.5. C, The response gain from B (dashed line and gray area) explains the decay of the observed response gain only qualitatively (filled circles; median with 2nd and 3rd quartiles). For the 18 cells in which f-I curves were measured, we computed the response gains as predicted by the models. Using the adaptation model Equation 1, thus taking the saturating f-I curves into account, does not improve the match (squares). However, the additional low-pass filter properties introduced by spikes, modeled using the perfect integrator Equation 4, reduce the predicted response gains significantly (triangles), resulting in a much better match to the actually observed data. The variability of the response-gain data can be mainly attributed to the different sized chirps (compare error bars to the width of the gray area). D, The probability of a male fish emitting chirps as a function of beat frequency as reported by Bastian et al. (2001), their Fig. 3A.

Stimuli for measuring f-I curves were composed of a 100-ms-long preadaptation part of amplitude I_pre immediately followed by a 150-ms-long test stimulus of amplitude I. While holding I_pre fixed, we varied I randomly such that each I was presented 6-16 times. The cells completely adapted to the preadaptation stimulus. Therefore, the response evoked by the test stimulus revealed the properties of the cell being in a fixed state of adaptation. As the steady-state response, we measured the mean firing frequency within the last 100 ms of the test stimulus. The onset firing frequency was determined as the largest deviation from the response preceding the test stimulus within the first 30 ms of the response smoothed with a running average of 3 ms width. To parameterize f-I curves, we fitted the Boltzmann function f(I) = f_max/(1 + exp(-k(I - I_1/2))) to the data. The slope of the linear part of the f-I curve is then given by s = f_maxk/4.

Adaptation model. Benda and Herz (2003) derived a general model for the dynamics of spike-frequency adaptation (Eq. 1) from the known kinetics of various adaptation mechanisms acting on the spike generator (“encoder adaptation”) [e.g., M-type currents, afterhyperpolarization (AHP)-type currents, and even slow recovery from inactivation of the fast sodium current]. If the dynamics of adaptation are slow compared with an ISI, then the much faster dynamics of the spike generator can be treated independently of the slower dynamics of the adaptation process. In the simplest case in which the stimulus is changing slowly within an ISI, the generation of spikes can be described by a simple mapping of the stimulus through the f-I curve f₀(I) of the neuron that returns the output firing frequency f(t) as a function of the input stimulus I(t) that varies with time t. Most mechanisms of encoder adaptation result in a change in an ionic current through the membrane of the neuron that is flowing in parallel with the ionic current I constituting the input. Therefore, adaptation is acting subtractively on the input. In contrast, a divisive effect on the stimulus would be expected if adaptation is attributable to depressing synapses (Abbott et al., 1997; Tsodyks et al., 1998).

The adaptation current can be approximated by its temporal average A, because we assumed it to be slow compared with the spike generation. Averaging the dominant slow process of the adaptation mechanism (gating of the M-type current, removal of intracellular calcium for AHP-type currents) yields the following dynamics of the firing frequency f(t):

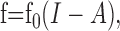1a

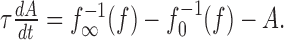1b

The onset f-I curve f₀(I) is the f-I curve of the unadapted neuron that one gets by measuring the onset response to step-like stimuli of various intensities, I. The averaged adaptation current is subtracted from the input in Equation 1a and therefore shifts f₀(I) to higher input intensities. Because adaptation currents are activated by the generated spikes, the dynamics of adaptation is driven by the output firing frequency. For an expression of the steady-state value of A, we used the steady-state f-I curve [see Fig. 6 for an example of f₀(I) and f_∞(I)]. In particular, the state of adaptation A(t) in Equation 1b is driven by the horizontal distance 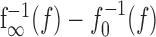between the onset and steady-state f-I curve at the firing frequency f.

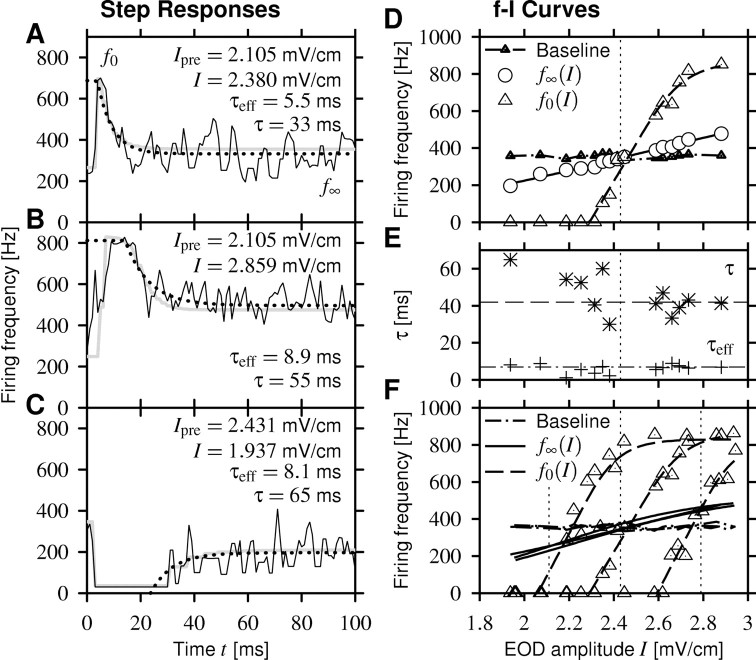
Figure 6.

Firing frequency-intensity curves (f-I curves) measured in the same cell as in Figure 4A-C. First, the cell was adapted to some EOD amplitude I_pre higher, lower, or equal to the EOD baseline amplitude (2.43 mV/cm) to prepare the cell in different states of adaptation. Then the stimulus was stepped to various amplitudes I at time t = 0. Three examples of the firing-frequency response to the second part of the stimulus are shown in A-C (black solid lines). An exponential fit (dotted line; clipped at the maximum response) measured the effective time constant of adaptation τ_eff, and a fit of the computed response of the adaptation model Equations 1 and 4 (gray line) yields the adaptation time constant τ. Note that fitting an exponential to the step responses describes the data sufficiently well but, in contrast to the adaptation model Equation 1, does not define a dynamics for arbitrary stimuli. A, Stimulus amplitudes I larger than I_pre evoke a strong onset response f₀, which rapidly adapts down to a steady-state value f_∞ slightly above baseline activity (357 Hz). B, For very large intensities, the response saturates at the EOD frequency.C, Decreasing the EOD amplitude may even cause cessation of firing. After a while, the cell recovers from adaptation and starts firing again, leveling out below the baseline activity. D, Onset f-I curve f₀(I) (triangles) and steady-state f-I curve f_∞(I) (circles) constructed from onset and steady-state responses for a particular preadaptation stimulus I_pre (here the EOD baseline amplitude; vertical dotted line). Fitting Boltzmann functions to both f-I curves describes the data reasonably well (solid and dashed lines; see Materials and Methods). The baseline firing frequency (triangles) as the response to the fish's own EOD was measured during 100 ms before applying the preadapting stimulus. E, The effective time constant τ_eff (+) and the adaptation time constant τ (^*) obtained from the measurement shown in D are independent of stimulus intensity I. The averaged time constants from all 18 cells are τ_eff = 7 ms (dashed dotted line) and τ = 42 ms (dashed line). F, Comparison of f-I curves measured for three values of I_pre (vertical dotted lines) of the preadaptation stimulus and thus three different states of adaptation. By definition, the steady-state f-I curves (solid lines) and the baseline firing frequencies (dashed dotted line) are independent of I_pre. In contrast, the onset f-I curves (triangles, data; dashed lines, fit) are shifted by adaptation along the intensity axis while keeping their shape.

Other plausible adaptation mechanisms, acting, for example, on the transduction of a physical stimulus in a receptor neuron (Gollisch and Herz, 2004), could be driven by the input stimulus I directly. In this case, the dynamics for A is governed by the following:

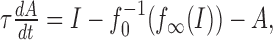2

where 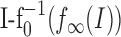is the distance of the two f-I curves at the steady-state firing frequency f_∞(I). In contrast to the corresponding term for output-driven adaptation in Equation 1b that depends on the actual firing frequency, this term is constant for a constant stimulus I.

In the special case of linear f-I curves, the model for output-driven adaptation Equation 1 is linear and constitutes a high-pass filter with gain as follows:

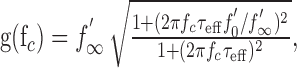3

where f′₀ and f′_∞ are the slopes of the f-I curves, and f_c is the frequency component of the stimulus I(t). The effective time constant of adaptation τ_eff = τf′_∞/f′₀ can be observed as the exponential decay of the firing frequency evoked by a step-like stimulus. It is smaller than the adaptation time constant τ describing the dynamics of the adaptation mechanism. Note that for input-driven adaptation, τ_eff equals the adaptation time constant τ in Equation 2.

Equations 1-3 describe the effect of adaptation only. However, if stimulus fluctuations are fast compared with an ISI (≈1/f), the low-pass filter effect of spikes has to be taken into account by specifying a model for spike generation (Benda and Herz, 2003). The perfect integrate-and-fire neuron,

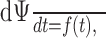4

requires no additional parameter and is the canonical model for the dynamics on a limit cycle, as emerging by suprathreshold stimulation. Whenever the phase Ψ reaches the value 1, Ψ is reset to zero, and a spike is elicited. From these spikes, a firing frequency can be calculated as 1/ISI and compared with the experimentally measured one.

The two models Equations 1 and 2 in combination with Equation 4 are fully described by the onset and steady-state f-I curves of the neuron, f₀(I) and f_∞(I), and by the adaptation time constant τ. Therefore, the firing-frequency responses of an adapting neuron to time-varying stimuli can be predicted after determining the f-I curves of the neuron and adaptation time constant with step stimuli.

Results

Chirps: signal characteristics

Small chirps (also known as type II chirps) are brief events in which a fish raises the frequency of its EOD by 30-150 Hz (the size of the chirp) for 10-20 ms (Hagedorn and Heiligenberg, 1985; Zupanc and Maler, 1993; Engler et al., 2000; Bastian et al., 2001); an example is shown in Figure 1, A and B. This frequency modulation advances the phase of the EOD by approximately one (0.25-1.5) EOD cycle (Δφ_C) (Fig. 1B, gray area). In the presence of an EOD of a second fish, this phase advance generated by the chirp is added to the phase Δφ of the resulting beat (Fig. 1C,D). This advance of the beat phase produces a fast change in EOD amplitude (Fig. 1C), as illustrated in Figure 2. Thus, the superposition of a second EOD transforms the frequency modulation of the EOD generated by a chirp into a rapid EOD AM that interrupts the beat. Note that the EOD amplitude during a chirp never exceeds the amplitudes during the beat, because the chirp just accelerates the beat waveform without changing it.

Figure 2.

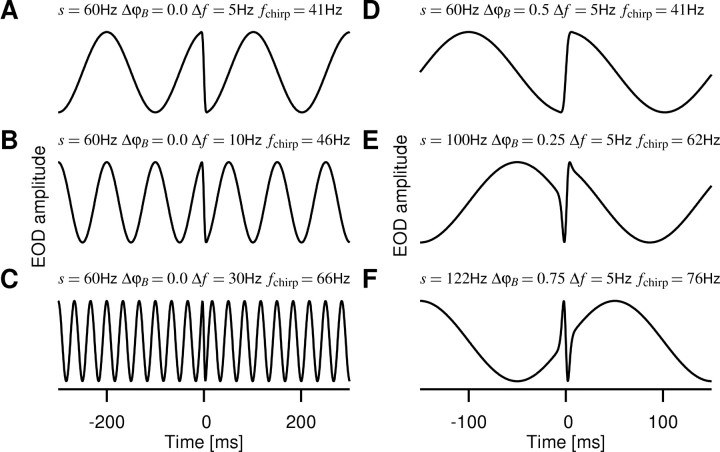
Stimuli generated by chirps. EOD AMs resulting from Δt = 14-ms-wide chirps of different peak frequency increases (size s of the chirp) centered around time 0 on various positions Δφ_B with in the beat of frequency Δf, as indicated, are shown. The traces were generated assuming a Gaussian frequency increase in the EOD during the chirp according to A(t) = cos(2πΔφ(t)), where 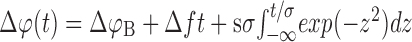is the phase of the beat as the time integral of the frequency difference of the two EODs and 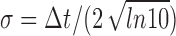. These artificial EOD AMs are very similar to AMs resulting from real chirps [compare with Zupanc and Maler (1993) and Fig. 1C]. f_chirp is an estimate of the stimulus frequency during the chirp as given in Equation 5. A-C, A 60 Hz chirp advancing the beat by one-half of a cycle (Δφ_C = 0.5) on different beat frequencies, Δf = 5, 10, and 30 Hz. The chirp is located at the peak of the beat and thus produces a sudden downstroke in EOD amplitude, which, however, is less salient at high beat frequencies (C). D, Same chirp as in A but one-half of a cycle later in the beat, therefore starting in the trough of the beat and producing an upstroke. E, A 100 Hz chirp advancing the beat by Δφ_C = 0.8 cycles at the zero-crossing of the beat-sine wave. F, After a 122 Hz chirp (Δφ_C = 1), the beat continues without a phase shift. The fish emit chirps on every position within the beat (data not shown).

There are two time scales in the EOD AMs. The rapid amplitude changes induced by chirps introduce a fast time scale, which is set by the chirp size and duration and, given the stereotyped nature of these signals, is approximately fixed. A variable time scale is set by the beat frequency that is given by the difference Δf of the EOD baseline frequencies of each fish. A fish could use differences in those two time scales to detect chirps within a beat.

For a quantitative estimation of the spectral characteristics of the EOD AM during a chirp, we assume that the phase of the beat Δφ is increased linearly by the chirp (Fig. 1D, compare inset). Therefore, the AM induced by a chirp can be characterized by a single frequency f_chirp that is determined by the slope of the beat phase at the chirp. The total change in beat phase during the chirp of width Δt is the phase shift ΔfΔt, attributable to the beat alone plus the phase shift Δφ_C of the chirp. Dividing by Δt yields the slope of Δφ and thus the characteristic frequency f_chirp of the AM during the chirp:

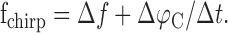5

The second term is in the order of ∼70 Hz (Δφ_C ≈ 1, Δt ≈ 14 ms); it ranges from 18 Hz (Δφ_C ≈ 0.25) to 110 Hz (Δφ_C ≈ 1.5). Therefore, as shown in Figure 2, chirp-induced AMs are faster than the beat AMs that typically elicit them (|Δf| < 50 Hz) (Bastian et al., 2001), but the relative difference in time scales is reduced for higher beat frequencies proportional to 1/|Δf| (Fig. 2C).

P-unit response

The response of a single P-unit stimulated with the superposition of the fish's own EOD and an artificial stimulus mimicking a second fish's EOD with chirps is shown in Figure 3A. As is known, the firing-frequency response (Fig. 3B) closely follows the slow beat (Bastian, 1981; Nelson et al., 1997). In the example shown, the response ranges from 50 Hz in the troughs to 250 Hz on the peaks, a 200 Hz firing frequency modulation. The chirp in this example produces one-half of an EOD cycle of phase advance in the trough of the beat, resulting in a fast upstroke in EOD amplitude (Fig. 3C). This signal evokes a clearly enhanced response of up to 420 Hz, overshooting the response to the beat peaks almost by a factor of 2.

Figure 3.

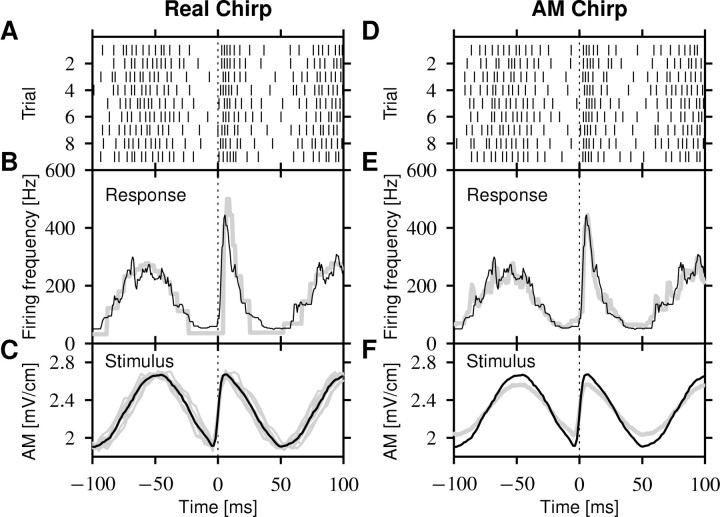
P-unit response to a chirp. The example shows a 60 Hz chirp at the trough of a Δf = 10 Hz beat. A, The spike trains evoked by the presentation of nine chirps at approximately the same beat position of a cell with p = 0.16 (141 Hz baseline firing rate divided by 881 Hz EOD frequency). B, The firing frequency computed as the averaged inverse ISI from the spikes in A (solid line). The gray line is the prediction of the spike-frequency adaptation model Equations 1 and 4. C, The relevant stimulus for the P-unit is the AM of the transdermal EOD. The gray lines are the individual realizations for each of the spike trains in A. The black line is the average stimulus. D-F, Each EOD AM in C was recorded and subsequently presented as a pure AM to confirm that the AM generated by the chirp is the only feature that is encoded by the P-units. D, The spike trains evoked by the AM stimuli. E, The corresponding firing frequency (gray line) is almost identical to the firing-frequency response to the real chirps (black line; same as in B). F, The averaged stimulus for the AMs (gray line) and the real chirps (black line; same as in B) differ in modulation depth because of the asymmetric EOD waveform (see Materials and Methods).

Chirps are frequency modulations produced by one fish that are converted into AMs by the superposition of the EOD of another fish. To confirm whether the enhanced response of the P-units to chirps is solely caused by the resulting AM, we additionally stimulated the fish with an AM similar to that generated by the chirp, but without the frequency modulation of a real chirp (see Materials and Methods) (Fig. 3D-F). The averaged mean difference between the firing-frequency response to the real chirp and the pure AM was 59 ± 50 Hz (n = 257 chirps), within ±50 ms around the chirp. This makes the two firing frequencies indistinguishable (χ² test; p = 0.66 ± 0.47).

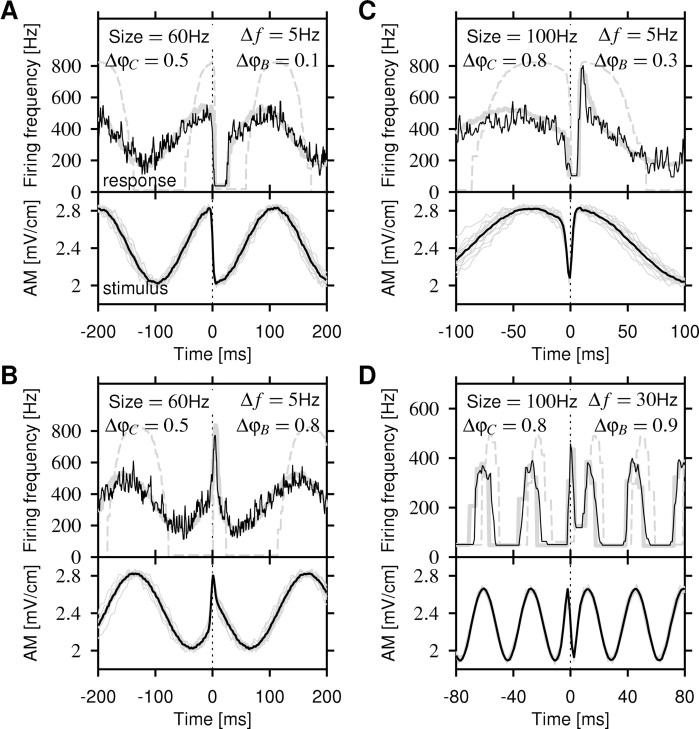
Additional examples of P-unit responses to chirps of different sizes at various beat positions and beat frequencies are shown in Figure 4. Chirp-induced downstrokes in EOD amplitude evoke a strongly reduced firing frequency or even a period of silence after the chirp (Fig. 4A,C). Upstrokes evoke strongly enhanced firing frequencies (Fig. 4B,C). Especially large chirps with phase shifts >0.5 produce both upstrokes and downstrokes (Fig. 2E,F), often resulting in a very low response followed by a very high response, as in Figure 4C, and vice versa. However, at higher beat frequencies, the response to chirps is just as large as the response to the beat (Fig. 4D).

Figure 4.

Firing-frequency responses (top panels; black line) to various-sized chirps generating a phase shift, Δφ_C, on a beat with frequency Δf at beat position Δφ_B as indicated. A-C, Recordings from a single P-unit with p = 0.42 (baseline firing rate, 346 Hz; EOD frequency, 826 Hz) are shown. The corresponding AMs of the transdermal EOD are shown in the bottom panels (individual stimuli, gray; averaged stimulus, black). The model prediction (top panels; gray solid line) closely follows the measured firing frequency (black line), whereas the prediction with the onset f-I curve alone does not describe the data (dashed gray line). A, A 60 Hz chirp occurring around the top of a 5 Hz beat generates a fast downstroke in EOD amplitude. This causes the neuron to entirely stop spiking. In contrast, the neuron still fires at the troughs of the beat. Note that the firing frequency cannot equal zero, because it is measured as the inverse ISI. Periods of silence appear as straight horizontal lines. B, Chirps at around the trough of the beat generate fast upstrokes, causing a much stronger response than the one during beat peaks. C, A larger 100 Hz chirp produces a downstroke immediately followed by an upstroke. This results in a short pause followed by a strong peak in the firing-frequency response. Note the enlarged time axis. D, A 100 Hz chirp on a faster 30 Hz beat recorded from a different unit (same unit as in Fig. 3). The response to the beat is almost as large as the response to the chirp.

We analyzed the responses of 36 P-units to 1208 chirps altogether. Each of these chirps had one of five different sizes (30, 60, 100, 122, and 153 Hz peak frequency increase corresponding to phase shifts of 0.25, 0.5, 0.8, 1.0, and 1.25) on five different beat frequencies (5, 10, 20, 30, and 60 Hz) and occurred on 10 different beat positions. Thus, only a small subset of all possible combinations of chirp sizes and beat frequencies was measured in each unit. On average, 13.5 trials were measured for each chirp. We assumed that the chirps are mainly coded by firing frequency and that the detectability of a chirp within a beat can be estimated by the response gain, which basically is the maximum modulation depth of the firing-frequency response during the chirp divided by its modulation depth during the beat (see Materials and Methods). The response gain did not show a significant dependence on chirp size (r = 0.03; p = 0.3; n = 1177) or beat position (r = 0.02; p = 0.5; n = 1208).

However, as suggested in Figure 4, beat frequency had a large effect on response gain (Fig. 5). For the 5 Hz beat, the response gain was, on average, 2.0 ± 0.7, thus enhancing the firing frequency twofold compared with the beat response. The response gain monotonically decreases as beat frequency increases. At 30 Hz, it is already down at 1.08 ± 0.20, meaning that the response to the beat is now as strong as the response to the chirp. These data suggest that there is a cutoff frequency in the system between 20 and 30 Hz that separates slow beats from chirps and fast beats, thus defining two ranges of signal time scales: slow beats on which chirps are detectable as an enhanced firing-frequency response and fast beats on which the P-unit firing-frequency response to chirps becomes invisible.

Spike-frequency adaptation and high-pass filtering

The data could be explained with a high-pass filter that transmits high-frequency stimuli such as chirps with a much larger gain than low-frequency stimuli such as beats. This may be accounted for by the known spike-frequency adaptation observed in P-units (Hagiwara and Morita, 1963; Bastian, 1981; Xu et al., 1996; Nelson et al., 1997). To test this hypothesis, we used a general model for the firing-frequency dynamics of an adapting neuron that was recently derived by Benda and Herz (2003) (see Materials and Methods). The model is completely characterized by the onset and steady-state f-I curves as well as the effective time constant of adaptation, all of which can be easily determined from the response of the neuron to step-like stimuli. Therefore, the model does not require any biophysical specification of the adaptation process. Adaptation of P-units, which are afferent fibers that innervate numerous tuberous electroreceptors (Bennett et al., 1989), might be attributable to adaptation of the transduction mechanism within the electroreceptors, depression of their synapses onto the afferents, or adaptation of the spike generator in the afferent. Within the model framework, these three fundamentally different adaptation mechanisms can be distinguished based on the step-response data.

We measured responses to step-like increases and decreases in the fish's EOD amplitude in 18 cells, using the AM-type stimulation as described in Materials and Methods. Figure 6A-C shows three examples of firing-frequency (f) responses to various intensities, I, of a constant stimulus switched on at t = 0. The initial onset-response f₀ of the firing frequency to the step stimulus reflects properties of the neuron in a fixed state of adaptation A. The steady-state response f_∞ reveals information about the maximum adaptation strength at a given stimulus intensity I. Measuring both quantities for different stimulus intensities results in the onset f-I curve f₀(I) and the steady-state f-I curve f_∞(I), as shown in Figure 6D. Both types of f-I curves are linear over a wide range of firing frequencies. Whereas the steady-state f-I curve spans the entire range of tested EOD amplitudes (more than ±20% of the EOD baseline amplitude), the onset f-I curve is much steeper and saturates at the EOD frequency at which the neuron fires a spike at each EOD cycle and goes to zero for lower amplitudes. This and saturating responses such as the one shown in Figure 6B is consistent with an adaptation process that must act at or before the generation of spikes in which the saturation is introduced.

Adaptation could have a subtractive or divisive effect on the onset f-I curve. To distinguish between these two possibilities, we measured the onset f-I curve for different levels of adaptation by increasing or decreasing the EOD amplitude to some value I_pre before measuring the response for different intensities, I. In all cells, the onset f-I curves for the different adaptation levels are only shifted along the intensity axis (Fig. 6F). Dividing the slopes of each pair of f-I curves of a cell, such that the slope of the f-I curve measured at the smaller preadaptation intensity I_pre is divided by the one at a larger preadaptation intensity, and averaging over all pairs results in 1.02 ± 0.21, which is indistinguishable from 1 (n = 22; p = 0.66; t test), showing that the adaptation process under investigation acts purely subtractively on the input. This suggests a weak influence of depressing synapses, because these would have a divisive effect on the input (Abbott et al., 1997; Tsodyks et al., 1998). Although, ultimately, only appropriate experiments can rule out the synapses as the locus of adaptation, the important finding is that adaptation in the electroreceptors is subtractive and not divisive.

The dynamics of adaptation can be driven either by the output spikes per firing frequency or the input stimulus directly (Eqs. 1, 2). The distinction between these different dynamics is more subtle, because for linear parts of the f-I curves, they result in exactly the same equations for the firing frequency. Knowing the onset and steady-state f-I curves (parameterized with a Boltzmann function), the only free parameter for both types of adaptation dynamics is the adaptation time constant τ. Fitting the models to the step-response data, we find for the output-driven model (Eq. 1) (Fig. 6A-C, gray lines) a slightly, although not significantly, better performance than for the input-driven model Equation 2. The root mean squared difference between the firing frequency of the models and the measured firing frequency is σ_diff = 31 ± 25 Hz for output-driven adaptation and σ_diff = 32 ± 36 Hz for input-driven adaptation (n = 639).

The negative correlation of ISIs that is observed in P-unit baseline activity (Hagiwara and Morita, 1963; Chacron et al., 2000; Ratnam and Nelson, 2000) can only be explained by spike-driven adaptation processes, because we already ruled out depressing synapses that also can induce negative ISI correlations (Goldman et al., 2002). The negative ISI correlations of the P-unit response can be easily reproduced by adding a simplified spike-driven adaptation current with a time constant of 42 ms (see below) to a perfect integrate-and-fire neuron [as proposed by Benda and Herz (2003), their Eq. 6.5] that is directly driven by the EOD with additive noise (data not shown). This additionally favors the hypothesis that the observed spike-frequency adaptation is caused by ionic currents acting on the spike generation, possibly mediated by Kv3.1 channels (Chacron et al., 2001). Thus, all of the characteristics of the adaptation model Equation 1 are met. Note that the model was originally derived for current stimuli that are directly applied to the spike generator, whereas here we only take the AM separated from the EOD as the stimuli. We show how to resolve this issue in the Appendix.

The adaptation time constants τ obtained by fitting the output-driven model Equation 1 to the step-response data are independent of stimulus intensity (r = -0.05 ± 0.54; p = 0.24 ± 0.31; mean ± SD from 38 cells with each 10-29 measured τ - I pairs) (Fig. 6E), thus confirming the assumption of the model of τ being constant. The time constants are also independent of the baseline firing rate of the P-units (r = -0.23; p = 0.17) or p value (baseline firing rate divided by EOD frequency; r = -0.14; p = 0.4) and averaged to 42 ± 17 ms (n = 38 cells).

The adaptation time constant describes the dynamics of the adaptation mechanism. It is usually larger than the effective time constant of adaptation that is obtained by fitting a single-exponential function [f(t) = (f₀ - f_∞) exp(-t/τ_eff) + f_∞] to the time course of the firing frequency evoked by step-like stimuli (Fig. 6A-C, dotted line), the reason being that in output-driven adaptation, the state of adaptation relaxes toward a value that is not constant and set by the stimulus but rather depends on the current firing frequency. The effective time constant of adaptation is independent of stimulus intensity (r = 0.01 ± 0.38; p = 0.38 ± 0.29; mean ± SD from 38 cells with each 5-28 successfully measured τ_eff - I pairs) (Fig. 6E) independent of the baseline firing frequency of the cells (r = -0.27; p = 0.09) or p value (r = -0.26; p = 0.12) and averages to 6.9 ± 2.0 ms (n = 38 cells), which is one-sixth of the value of τ. The two time constants τ and τ_eff are related by the relative slopes f′₀ and f′_∞ of the onset and steady-state f-I curves via τ_eff = τf′_∞/f′₀, if the f-I curves are approximately linear (Benda and Herz, 2003). Indeed, we find for the relative slopes f′₀/f′_∞ a value of 6.0 ± 1.6.

The high-pass filter Equation 3 induced by spike-frequency adaptation can be characterized by a cutoff frequency that separates slow stimuli that are transmitted with low gain from fast stimuli that are transmitted with a larger gain (Fig. 7A). The cutoff frequency f_cutoff = (2πτ_eff)^-1 is determined by the effective time constant of adaptation (Benda and Herz, 2003). From our data, we obtain f_cutoff = 23 ± 7 Hz. However, because the high-pass filter Equation 3 is just a single-pole filter, it has no sharp cutoff. The gain raises rather gradually from low to high values over the range of stimulus frequencies considered in this study.

Model prediction for beats and chirps

Having measured the onset f-I curve, the steady-state f-I curve, and the adaptation time constant for a given cell, the adaptation model Equation 1 is defined completely. In combination with the perfect integrator Equation 4 for simulating a spike generator (see below and Materials and Methods), we can now predict the firing-frequency response of the same cell to an entirely different set of stimuli, namely beats and chirps, without any additional parameter fitting. For this purpose, we feed the measured AM of the EOD evoked by the chirp as the stimulus I(t) into the model Equations 1 and 4. As Figures 3 and 4 show, the prediction of the model closely follows the firing-frequency response to the beats as well as the chirps (χ² test; p = 0.51 ± 0.49; n = 635). The root mean squared difference σ_diff between the predicted and the measured firing frequency within ±50 ms around each chirp is 56 ± 36 Hz, on average. Comparing this error to the modulation depth of the response during the beat results in a prediction error of 24 ± 8%. On the contrary, neglecting adaptation and just using the onset f-I curve [f = f₀(I)] obviously fails to predict the firing frequency (Fig. 4, dashed gray lines). The good performance of the adaptation model shows that spike-frequency adaptation is sufficient for explaining the firing-frequency response of the electroreceptors to chirps.

What happens is that the adaptation strength follows low-frequency beats (i.e., in terms of the model, the onset f-I curve is shifted according to the stimulus to lower and higher intensities, which results in firing frequencies that are close to the ones given by the steady-state f-I curve). An AM generated by a chirp, however, is too fast for the adaptation dynamics to follow; the onset f-I curve will practically stay where it was right before the chirp. If the chirp occurs at the peak of the beat, then the neuron is strongly adapted (i.e., the onset f-I curve is shifted to high stimulus intensities), and if the sudden downstroke of the produced AM easily gets below the threshold of the f-I curve, the neuron stops firing. If the chirp occurs during the trough of the beat, then the neuron is very sensitive, because its onset f-I curve is shifted to low stimulus intensities. The sudden upstroke caused by the chirp thus evokes very high firing frequencies that then rapidly adapt back to values given by the steady-state f-I curve.

Using the gain g(f_c) Equation 3 of the high-pass filter of the linearized adaptation model with the mean values τ_eff = 7 ms and 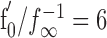, we can predict the response gain as the gain of the chirp divided by the gain of the beat, as follows:

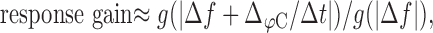6

where we used Equation 5 for an estimate of the AM frequency during a chirp. Chirps are high-frequency events with respect to the cutoff frequency of the high-pass filter. Therefore, their gain is maximal and approximately independent of the beat frequency Δf for positive Δf. Dividing by the gain of the beat results in a function that gradually decreases with increasing |Δf| (Fig. 7B). It reproduces the decay of the response gain data with increasing Δf qualitatively but drastically overestimates the observed gain (Fig. 7C, circles), especially at low beat frequencies.

In addition to the response gain estimate Equation 6, which assumes linear f-I curves, the model Equation 1 takes the saturation of the f-I curves into account. The response gain computed from the prediction of the model (Fig. 7C, squares) is, however, still very similar to the linear estimate.

The adaptation model Equation 1a maps the fast transients of the chirp stimulus directly into a firing frequency via the onset f-I curve. However, as pointed out by Benda and Herz (2003) (their Eq. 6.3), during each ISI, a suprathreshold-driven spike generator integrates over the stimulus along its limit cycle. This temporal averaging results in low-pass filtering that can have a substantial effect on the response to stimulus transients that are short compared with an ISI (especially at periods of silence as in Fig. 4A). For predicting the firing-frequency response, we already used the perfect integrate-and-fire neuron Equation 4 to generate spikes and thus to account in the simplest possible way for the low-pass filter effect. The response gain calculated from the predictions (Fig. 7C, triangles) indeed matches the observed values well (Fig. 7C, circles).

Discussion

The example we have presented here emphasizes the general functional role of high-pass filter properties that result from any kind of spike-driven adaptation. We have demonstrated how adaptation in electroreceptor afferents of the weakly electric fish A. leptorhynchus enhances the response to small but fast communication signals (i.e., the chirps) by temporally separating them from slower background signals (i.e., the beats). The stimuli generated by small chirps boil down to a sudden and short increase in AM frequency of the EOD by ∼18-110 Hz on top of a beat pattern of arbitrary frequency. From the effective time constant τ_eff = 7 ms, measured from the exponential decay of the firing-frequency response of the electroreceptor afferents to constant stimuli, we conclude that the cutoff frequency of the generated high-pass filter is at f_cutoff = 23 Hz. This cutoff frequency defines a time scale that separates slow from fast stimuli. Chirps on beat frequencies below that frequency give rise to an enhanced response, whereas on higher beat frequencies, the response to the beat is about as strong as the one to the chirp. Note that this result is independent of the phase shift (Fig. 1C, arrow) of the beat induced by the chirp.

In a behavioral study, Bastian et al. (2001) measured the probability of a fish emitting a small chirp (Fig. 7D). They observed a decrease in chirp probability with increasing beat frequency in a manner surprisingly similar to that reported here for the response gain of the electroreceptor afferents. Assuming that the fish emit chirps mainly at beat frequencies at which a conspecific fish would be able to detect the chirps, this match is consistent with our hypothesis that an enhanced firing-frequency response induced by a chirp is important for the detectability of a chirp. Although we are not able to make a causal connection between detectability of chirps in electroreceptor responses and behavior, and although it is not known from behavioral studies on which beat frequencies a fish is really able to detect a chirp, the single adaptation mechanism explaining our data could, in principle, account for a large part of the behavior. Moreover, this is consistent with the independence of the adaptation time constant from the electroreceptor p value (baseline activity divided by EOD frequency), because this guarantees a well defined cutoff frequency to the higher-level neurons.

The important concept of a high-pass filter and its cutoff frequency relies on the linearity of the system under investigation. Because of their high baseline activity of ∼140-450 Hz (Bastian, 1981), their nicely linear f-I curves around that baseline activity and the subtractive shift of the onset f-I curve by adaptation P-units are indeed well described by linear adaptation dynamics. Depressing synapses, on the other hand, exhibit similar signal transmission properties, in that they respond to changes in the input with strong transients (Abbott et al., 1997; Tsodyks and Markram, 1997; Tsodyks et al., 1998). However, depressing synapses are inherently nonlinear because of the fractional depletion of resources that differentiates them from the basically linear dynamics of spike-driven adaptation (Benda and Herz, 2003). Therefore, they might have more complex signal transmission properties.

The high-pass filter model introduced by Nelson et al. (1997) is equivalent to our model Equation 1 for the linear parts of the f-I curves (τ_a = τ_eff, G_a = f′₀ - f′_∞, G_b = 0, G_C = f′_∞). Longer adaptation time constants, as reported by Xu et al. (1996) and Nelson et al. (1997), do not play a role in encoding chirps, because the stimuli fluctuate symmetrically around the EOD baseline amplitude and usually contain frequencies >1 Hz. Furthermore, the additional threshold dynamics of an integrate-and-fire neuron introduced by Chacron et al. (2000) to explain negative ISI correlations (Hagiwara and Morita, 1963; Ratnam and Nelson, 2000) can be replaced by the adaptation dynamics of the high-pass filter that is added as an spike-activated adaptation current to a model for the spike generator. Thus, this single adaptation current of the electroreceptor afferents plays a threefold role in encoding behaviorally relevant stimuli. Because of negative ISI correlations, the spike-count variability to low-frequency stimuli is reduced, hence improving object detection (Ratnam and Nelson, 2000; Chacron et al., 2001). High-frequency stimuli including the transient induced by small chirps are transmitted with higher gain than low-frequency signals (Nelson et al., 1997; present study), and the negative ISI correlations additionally enhance the mutual information for high-frequency stimuli (Chacron et al., 2001).

Spike-driven adaptation and depressing synapses can produce many of the same input transformations. Both can account for negative ISI correlations in the output spike train (Goldman et al., 2002), and both respond to changes in the stimulus with strong transients. However, each depressing synapse filters its input individually, and the gain to each of the inputs of the neuron is therefore adjusted selectively (Abbott et al., 1997). In contrast, spike-driven adaptation acts on the overall input to the neuron and thus works like a master volume control. Spike-driven adaptation is observed in a wide range of neurons, and we propose that it may act to globally optimize detection of higher-frequency input. The combination of adaptation and synaptic depression may result in more complex computations. For example, avian wide-field tectal neurons (stratum griseum centrale cells) get input from retinal ganglion cells via depressing synapses. Together with an additional adaptation mechanism in the dendrites or soma, the cell performs spatiotemporal computations resulting in motion sensitivity independent of stimulus details (Luksch et al., 2004).

Appendix

EOD AM as a separately processed stimulus

The adaptation model Equation 1 was derived for currents directly stimulating the spike generator (Benda and Herz, 2003). However, in our study, we only used the AM as a stimulus, ignoring the fact that P-unit spikes are phase-locked to the EOD (Hagiwara et al., 1965) and that the spike generator therefore must be driven by the EOD. In other modeling studies of P-units, the EOD AM is processed independently from the EOD as well (Nelson et al., 1997; Chacron et al., 2000). Below, we show how the treatment of the EOD amplitude independent of the EOD carrier waveform could be justified.

The EOD waveform s(t) can be approximated by a sine wave with angular frequency ω, the amplitude of which is modulated by the stimulus I(t):

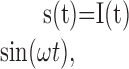7

[Note that in this notation, I(t), includes the baseline EOD amplitude]. The EOD is picked up by 20-40 receptor cells that synapse to a single nerve fiber (Zakon, 1987; Bennett et al., 1989). The transduction process and the transmission through the synapses might in its simplest case be described by a rectification of the stimulus, denoted by [·]₊, which cuts off the negative parts of the argument, so that we get for the current J(t) arriving at the spike generator:

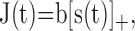8

where b = const is a proportionality factor. This current is converted into a series of spikes. Adopting the formalism of Benda and Herz (2003), the spike generation can be characterized by the firing frequency f(t) given by the onset f-J curve f̂₀(J):

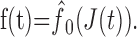9

Assume that a weight function, w(t), independent of I(t), exists such that replacing the input current J(t) in Equation 9 by its average

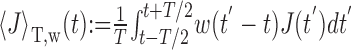10

over a single ISI T does not change the output firing frequency f for any I(t). Then we get the following:

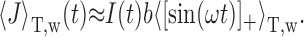11

Because T is usually greater than the period of the EOD, the average on the right can be approximated by a constant c. Absorbing b and c into the f-I curve, we finally get the following:

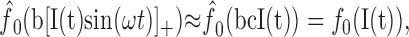12

justifying the separated treatment of the AM I(t) by the adaptation model Equation 1. Because our results obtained for AM stimuli are consistent with the model Equation 1, w(t) might likely exists. Thanks to the high baseline firing frequency of P-units of ∼140-450 Hz, the cutoff frequency of the low-pass filter (10) is much higher than the one of the high-pass filter induced by adaptation, so that it does not interfere with our results. In summary, because of the integration (averaging) of the stimulus by the spike generator during ISIs that are usually longer than an EOD period, the treatment of the EOD AM independent of the EOD is possible.