Abstract
Background: Functional magnetic resonance imaging (fMRI) provides non-invasive measures of neuronal activity using an endogenous Blood Oxygenation-Level Dependent (BOLD) contrast. This article introduces a nonlinear dimensionality reduction (Locally Linear Embedding) to extract informative measures of the underlying neuronal activity from BOLD time-series. The method is validated using the Leave-One-Out-Cross-Validation (LOOCV) accuracy of classifying psychiatric diagnoses using resting-state and task-related fMRI. Methods: Locally Linear Embedding of BOLD time-series (into each voxel’s respective tensor) was used to optimise feature selection. This uses Gauß’ Principle of Least Constraint to conserve quantities over both space and time. This conservation was assessed using LOOCV to greedily select time points in an incremental fashion on training data that was categorised in terms of psychiatric diagnoses. Findings: The embedded fMRI gave highly diagnostic performances (> 80%) on eleven publicly-available datasets containing healthy controls and patients with either Schizophrenia, Attention-Deficit Hyperactivity Disorder (ADHD), or Autism Spectrum Disorder (ASD). Furthermore, unlike the original fMRI data before or after using Principal Component Analysis (PCA) for artefact reduction, the embedded fMRI furnished significantly better than chance classification (defined as the majority class proportion) on ten of eleven datasets. Interpretation: Locally Linear Embedding appears to be a useful feature extraction procedure that retains important information about patterns of brain activity distinguishing among psychiatric cohorts.
Keywords: Nonlinear, dimensionality reduction, image processing, machine learning, kernel methods, optimization, least squares, neurophysiology, evidence-based medicine, (computer-assisted) diagnosis, fMRI, method of image charges, integration, oscillations, theorema egregium
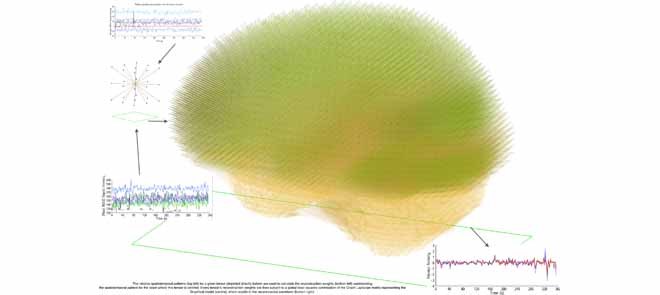
The relative spatiotemporal patterns (top left) for a given tensor (depicted directly below) are used to calculate the reconstruction weights (bottom left) summarising the spatiotemporal pattern for the voxel where this tensor is centred. Every tensor's reconstruction weights are then subject to a global least squares optimisation of the Graph Laplacian matrix representing the Graphical model (centre), which results in the reconstructed waveform (bottom right).
I. Introduction
Over a century ago, Charles Darwin alluded to an experimental paradigm that involved direct observation of the brain’s physical mechanisms (nervous matter) [14], where such observations [55] would serve as the physical basis for dichotomising species-specific behaviour. In the early 90s, an indirect and non-invasive measurement of mental activity over uniformly-spaced time points became possible through functional Magnetic Resonance Imaging (fMRI), which allows paramagnetic deoxyhemoglobin to act as an endogenous Blood Oxygenation-Level Dependent (BOLD) contrast [49]. This article pursues Darwin’s proposed experimental paradigm by Locally Linear Embedding (LLE) [54] the BOLD time-series to produce precise summaries of cerebral activity that may optimise the classification of different brain states, such as mental disorders.
Logothetis et al found that an increase in invasively-measured neural activity directly and monotonically reflects local BOLD signal increases and, for short stimulus presentations, there is a linear relationship between BOLD and neural responses [39]. This suggests the unobservable neural activity is spatially-localised in anatomical space. Locally Linear Embedding of fMRI data in space and time can, in principle [2], [20], [24] (see Appendix IV), summarise these local measurements of neuronal mass activity [40]–via the notion of analytic capacity [45]–to disclose information about global (i.e., whole-brain) activity patterns.
II. Methods: Testing Locally Linear Embedding (LLE) With Cross Validation
The discriminatory power of Locally Linear Embedding was compared to the original fMRI, both before and after applying Principal Component Analysis (PCA) [31] for artefact reduction [39]. This comparison was performed on eleven datasets containing cohorts with different mental disorders, using a combination of Leave One Out Cross Validation (LOOCV) on the training set, with greedy feature selection based on Fisher discriminability [17], [18]. The purpose of using LOOCV and feature selection is to find the time points that discriminate patients from controls on the respective dataset. The feature selection step initially starts with an empty candidate set of time points and proceeds to select the time point with the highest discriminatory power [63]. Then, time points that improve discrimination in conjunction with those already in the candidate set are added to this set in incremental fashion; this process is terminated when there are no more time points that can be added to the candidate set to improve discriminability. Note that the selection of time points is based upon cross validation and does not induce any biased sampling.
To illustrate the patterns that best discriminate between groups, a paired two-sample t-test between the patient and control groups is performed to both threshold and identify the statistically-significant differences (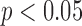 uncorrected) in space (at the time points identified by the greedy feature selection). Per Mill’s Methods of Induction (Method of difference), the functional differences (depicted by the statistically significantly-different regions) at the respective time point are therefore a necessary part of the cause of the phenomena that distinguish the subject groups [46], which in this case pertain to a neuropsychiatric disorder. Neuropsychiatric disorders are diagnosed using clinical assessments that include: evaluating the background demographics, collecting first and third party observations, and a structured psychiatric interview with the subject [53]. In detail:
uncorrected) in space (at the time points identified by the greedy feature selection). Per Mill’s Methods of Induction (Method of difference), the functional differences (depicted by the statistically significantly-different regions) at the respective time point are therefore a necessary part of the cause of the phenomena that distinguish the subject groups [46], which in this case pertain to a neuropsychiatric disorder. Neuropsychiatric disorders are diagnosed using clinical assessments that include: evaluating the background demographics, collecting first and third party observations, and a structured psychiatric interview with the subject [53]. In detail:
Every subject’s fMRI time-series is treated as a four-dimensional array 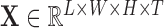 with
with 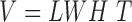 -dimensional voxel waveforms
-dimensional voxel waveforms 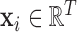 for
for 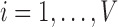 . Assume each subject scan
. Assume each subject scan 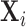 is associated with a binary-valued class label
is associated with a binary-valued class label 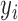 representing the diagnosis and that, for any subject scan, every voxel waveform
representing the diagnosis and that, for any subject scan, every voxel waveform 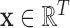 is generated by a vector
is generated by a vector 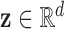 corresponding to a point on the manifold. Our approach to fMRI-based diagnosis involves two stages:
corresponding to a point on the manifold. Our approach to fMRI-based diagnosis involves two stages:
-
fMRI reconstruction takes the subject’s fMRI as input and outputs a reconstructed fMRI that is more informative than the original. Formally, this reconstruction is a mapping
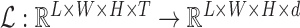 .
.In other words, Locally Linear Embedding reduces a time-series of length
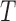 to a smaller number of spatial modes of dimensionality
to a smaller number of spatial modes of dimensionality 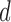 ; these modes contain all the information used for the subsequent step.
; these modes contain all the information used for the subsequent step. Classification builds a classifier that takes the subject’s reconstructed fMRI as input, and outputs a class label
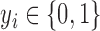 . The classifier is therefore a mapping
. The classifier is therefore a mapping 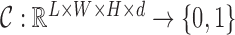 .
.
The reconstructed, or reduced, fMRI data produced from step 1 is hereon referred to as 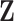 . All reconstructions initially vectorise the fMRI data to produce a two-dimensional array
. All reconstructions initially vectorise the fMRI data to produce a two-dimensional array 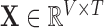 , and conclude by reshaping the resulting two-dimensional reconstruction
, and conclude by reshaping the resulting two-dimensional reconstruction 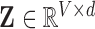 into a four-dimensional array
into a four-dimensional array 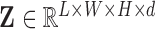 .
.
-
a)Principal Component Analysis (PCA) [5], [31]: reconstructs
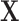 by finding an orthogonal rotation that minimises the reconstruction cost
by finding an orthogonal rotation that minimises the reconstruction cost
where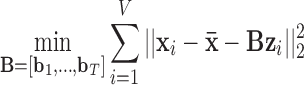
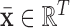 is the mean over all voxel waveforms, and
is the mean over all voxel waveforms, and 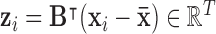 . To find the optimal
. To find the optimal 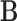 , compute the right-hand matrix for the singular value decomposition (SVD) of
, compute the right-hand matrix for the singular value decomposition (SVD) of 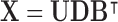 , which contains the
, which contains the 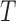 right-singular vectors of
right-singular vectors of 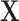 [26]. It follows that
[26]. It follows that 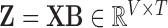 is the rotated matrix that minimises the reconstruction cost of the subject’s fMRI, where every column of
is the rotated matrix that minimises the reconstruction cost of the subject’s fMRI, where every column of 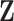 is a principal component. It is assumed the first
is a principal component. It is assumed the first 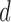 principal components (columns) of
principal components (columns) of 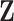 capture the “systematic structure,” where the confounding factors are relegated to the remaining
capture the “systematic structure,” where the confounding factors are relegated to the remaining 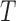 -
- 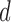 principal components, which produces the two-dimensional reconstructed fMRI
principal components, which produces the two-dimensional reconstructed fMRI 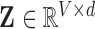 .
.Using PCA’s “systematic structure” for distinguishing humans with different neurological disorders has been met with caution [16], largely because PCA’s application to fMRI has some subjective components [1]. The main limitation behind the PCA reconstruction is that it assumes the lower-dimensional manifold is a linear subspace. We demonstrate that introducing the Cauchy stress tensor [9] on the Cartesian space with the Pythagorean distance metric enables three-dimensional measurements over time, thereby revealing the local (group) action in the physical system.
-
b)Locally Linear Embedding (LLE) [54], [56]: reconstructs
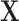 by constructing the Cauchy stress tensor [9] at every voxel
by constructing the Cauchy stress tensor [9] at every voxel 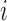 for
for 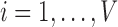 , which is achieved by minimising the reconstruction cost of its waveform
, which is achieved by minimising the reconstruction cost of its waveform 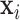 in terms of its spatially-adjacent neighbours:
in terms of its spatially-adjacent neighbours:
where the neighbourhood set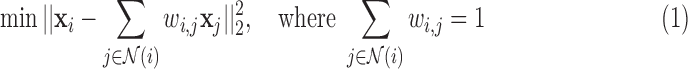
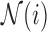 for voxel
for voxel 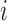 is the complement of its
is the complement of its 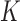 spatial neighbours on the surface of the sphere with radius
spatial neighbours on the surface of the sphere with radius 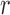 , and
, and 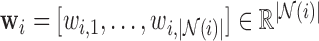 are the reconstruction weights containing the spatially-invariant geometric properties of the Cauchy stress tensor at voxel
are the reconstruction weights containing the spatially-invariant geometric properties of the Cauchy stress tensor at voxel 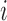 .
.
To determine the analytic capacity
[45] at every voxel location 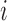 , LLE first subtracts the
, LLE first subtracts the 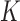 spatial patterns of the voxels on the boundary of the sphere centred around voxel
spatial patterns of the voxels on the boundary of the sphere centred around voxel 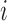 to determine the separation distance from the origin of the tensor at the respective voxel. Then, it computes the local (symmetric) spatiotemporal covariance matrix:
to determine the separation distance from the origin of the tensor at the respective voxel. Then, it computes the local (symmetric) spatiotemporal covariance matrix:
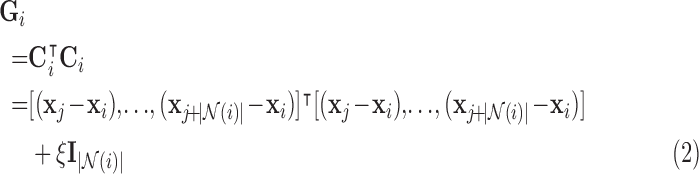 |
where 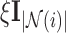 is a non-negative regularisation term to enforce positive-definiteness (for this study,
is a non-negative regularisation term to enforce positive-definiteness (for this study, 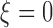 ). LLE calculates the reconstruction weights by finding the unique minimum-norm solution [50] to the constrained least-squares problem defined by:
). LLE calculates the reconstruction weights by finding the unique minimum-norm solution [50] to the constrained least-squares problem defined by:
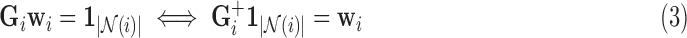 |
where 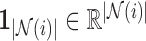 is a vector of ones and the
is a vector of ones and the 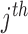 element of
element of 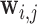 can be thought of as the average height of a curve representing the mean transit time of the indicator
[34] of voxel
can be thought of as the average height of a curve representing the mean transit time of the indicator
[34] of voxel 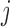 from voxel
from voxel 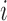 over the duration of the scan. Since
over the duration of the scan. Since 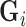 represents the squared distance of the surface forces from voxel
represents the squared distance of the surface forces from voxel 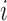 , the reconstruction weights
, the reconstruction weights 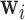 are Lebesgue measures [36] summarising the analytic capacity, or spatially-invariant geometry [25], of the space-filling curve [27], where the constraint ensures that the areas between the imaginary surface (acting as the origin that divides the body) and curves (defined by the stress vectors) are 1 in each of the
are Lebesgue measures [36] summarising the analytic capacity, or spatially-invariant geometry [25], of the space-filling curve [27], where the constraint ensures that the areas between the imaginary surface (acting as the origin that divides the body) and curves (defined by the stress vectors) are 1 in each of the 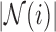 directions. In practice the weights can be brittle [65] due to any number of reasons. Modified Locally Linear Embedding (MLLE) therefore computes the
directions. In practice the weights can be brittle [65] due to any number of reasons. Modified Locally Linear Embedding (MLLE) therefore computes the 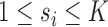 linearly-independent (orthogonal) vectors1
linearly-independent (orthogonal) vectors1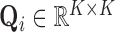 of
of 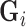 using the eigendecomposition
using the eigendecomposition 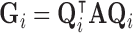 , thereby allowing the definition of multiple weight vectors for each voxel. Assuming the columns (eigenvectors)
, thereby allowing the definition of multiple weight vectors for each voxel. Assuming the columns (eigenvectors) 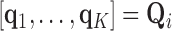 are sorted in descending order of their respective eigenvalues
are sorted in descending order of their respective eigenvalues 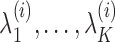 , MLLE uses the first
, MLLE uses the first 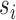 columns to compute multiple local weight vectors for a single voxel:
columns to compute multiple local weight vectors for a single voxel:
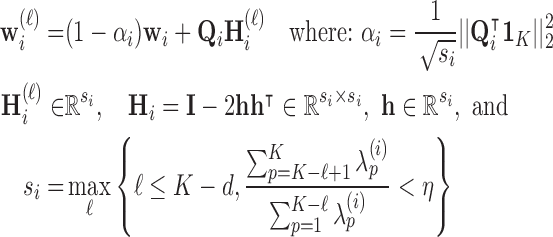 |
where 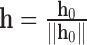 if
if 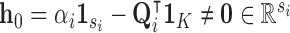 (else
(else 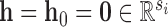 ),
), 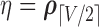 ,
, 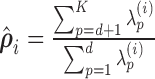 ,
, 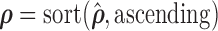 , and
, and 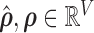 . Since every measure’s invariant properties are determined in a square-integrable space [58], LLE performs a global least-squares optimisation based on Gauß’ Principle of Least Constraint [23] to calculate the vectors
. Since every measure’s invariant properties are determined in a square-integrable space [58], LLE performs a global least-squares optimisation based on Gauß’ Principle of Least Constraint [23] to calculate the vectors 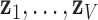 corresponding to points on the manifold:
corresponding to points on the manifold:
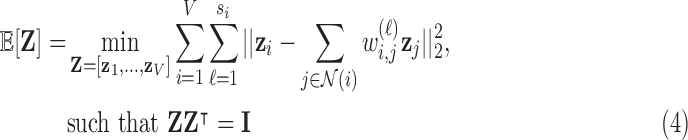 |
where 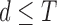 is the dimensionality parameter selected by the user and
is the dimensionality parameter selected by the user and 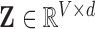 is the two-dimensional reconstructed fMRI. The global optimisation therefore calculates the points on the manifold [57], [59] that act as the four-dimensional orthogonal basis that best retains the geometry of the stress vectors. These represent the second order invariant properties of each voxel’s Cauchy stress tensor. A detailed explanation of this optimisation is provided below.
is the two-dimensional reconstructed fMRI. The global optimisation therefore calculates the points on the manifold [57], [59] that act as the four-dimensional orthogonal basis that best retains the geometry of the stress vectors. These represent the second order invariant properties of each voxel’s Cauchy stress tensor. A detailed explanation of this optimisation is provided below.
Define 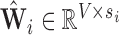 as the local sparse adjacency matrix, where:
as the local sparse adjacency matrix, where:
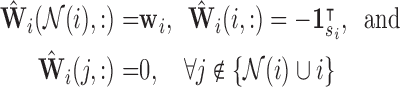 |
The optimisation in Equation 4 can be written as a minimisation of the expected reconstruction cost, or error:
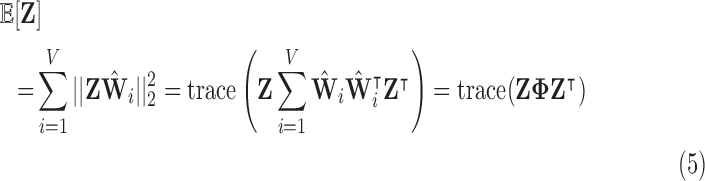 |
where 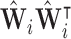 is the orthogonal projection for voxel
is the orthogonal projection for voxel 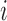 , and
, and 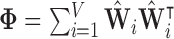 is the sparse, symmetric and positive-definite alignment matrix, and therefore admits the eigendecomposition [42]:
is the sparse, symmetric and positive-definite alignment matrix, and therefore admits the eigendecomposition [42]:
 |
where 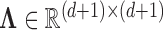 is the diagonal matrix containing the
is the diagonal matrix containing the 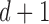 smallest eigenvalues of
smallest eigenvalues of 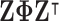 , and
, and 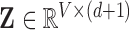 are the corresponding eigenvectors; Rayleigh’s variational principle [12], [52] enables calculation of these bottom
are the corresponding eigenvectors; Rayleigh’s variational principle [12], [52] enables calculation of these bottom 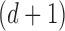 eigenvectors. Each eigenvector represents a degree of freedom in space and time, where the
eigenvectors. Each eigenvector represents a degree of freedom in space and time, where the 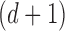 eigenvector is the global unit vector that fills three-dimensional space. The global unit vector is discarded to enforce the constraint that the manifolds have mean zero.
eigenvector is the global unit vector that fills three-dimensional space. The global unit vector is discarded to enforce the constraint that the manifolds have mean zero.
Note: To avoid degenerate solutions, LLE requires the manifolds to be centred around the origin in both space and time– i.e., 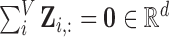 and
and 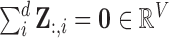 – and also have outer products with unit covariance– i.e.,
– and also have outer products with unit covariance– i.e., 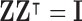 . Centring the manifolds about the origin ensures they are of the same scale, which is superficially similar to the common practice of signal, or count rate, normalisation [51]. The unit covariance constraint imposes the requirement that the reconstruction errors of the extracted manifolds are measured on the same scale.
. Centring the manifolds about the origin ensures they are of the same scale, which is superficially similar to the common practice of signal, or count rate, normalisation [51]. The unit covariance constraint imposes the requirement that the reconstruction errors of the extracted manifolds are measured on the same scale.
A. Feature & Parameter Selection
Hyper-parameter Selection involves selecting the algorithm parameters that will be used to generate the reconstructed fMRI from LLE and PCA, respectively. Both PCA and LLE require one to specify the number of reconstruction dimensions 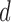 , where LLE’s additional hyper-parameter,
, where LLE’s additional hyper-parameter, 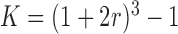 , selects the neighbouring voxels whose coordinates are on the boundary of a sphere with radius
, selects the neighbouring voxels whose coordinates are on the boundary of a sphere with radius 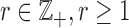 that is centred around the respective voxel. For both PCA and LLE, the number of reconstruction dimensions is bounded by the number of time points. In the case of PCA, the optimal
that is centred around the respective voxel. For both PCA and LLE, the number of reconstruction dimensions is bounded by the number of time points. In the case of PCA, the optimal 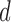 is often chosen by the proportion of variance captured by the first
is often chosen by the proportion of variance captured by the first 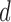 eigenvectors, expressed as
eigenvectors, expressed as 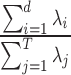 . For LLE, however, there is no analogous interpretation because the
. For LLE, however, there is no analogous interpretation because the 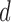 eigenvectors are uniformly spaced “time points” on the world line [47]. Thus cross-validation procedures are implemented (see following subsection for details) on the training data to systematically select the best hyper-parameters, iterating over
eigenvectors are uniformly spaced “time points” on the world line [47]. Thus cross-validation procedures are implemented (see following subsection for details) on the training data to systematically select the best hyper-parameters, iterating over 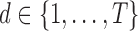 , where
, where 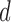 is generated on a log-scale from 1 to
is generated on a log-scale from 1 to 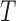 .
.
Sequential Forward Selection (SFS)2 [63]
is a nonparametric method for measurement (feature) selection that starts with an empty “candidate,” or near-optimal, set of “time points”. The method first finds the “time point,” defined as the second moment [6], with the highest classification accuracy and adds the corresponding image volume to the set. The method then finds an additional “time point” that strictly improves the classification accuracy in conjunction with the volume(s) whose “time points” are already in the “candidate” set, and terminates when no such volume can be found. Thus, SFS produces a near-optimal set of “time points” (volumes) that distinguish the subject groups with high classification accuracy, where this set is determined by adding “time points” to the near optimal set in a one-by-one fashion. It follows that the near-optimal set of “time points” represent points in time during the scan that enable discrimination of patients from controls with high classification accuracy. Note that SFS is only used on the training data (see Section II-C).
B. Classifier
A slight abuse of notation is introduced by redefining variable 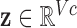 as the one-dimensional representation of the
as the one-dimensional representation of the 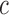 diagnostic volumes from the respective subject’s reconstructed fMRI
diagnostic volumes from the respective subject’s reconstructed fMRI 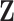 produced in the previous step. Here, it is assumed there are
produced in the previous step. Here, it is assumed there are 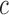 diagnostic time points and that
diagnostic time points and that 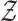 is a random variable containing the collection of cohorts’ reconstructed fMRI.
is a random variable containing the collection of cohorts’ reconstructed fMRI.
Fisher’s Linear Discriminant (LDA)3 [17], [18]
is a linear classification rule [26] that assumes both the patient and control class densities (at each voxel location) can be represented as multivariate Gaussians in three-dimensional space, each with some intrinsic curvature [21], [22]. Each class density is expressed as
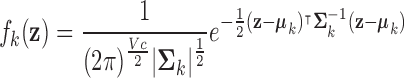 |
where it is assumed the 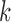 classes have a common covariance matrix– i.e.,
classes have a common covariance matrix– i.e., 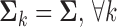 . This assumption allows the log ratio between the posterior distribution of each class to form a decision boundary that lies between patients (class 1) and controls (class 0), written as
. This assumption allows the log ratio between the posterior distribution of each class to form a decision boundary that lies between patients (class 1) and controls (class 0), written as  , which is linear in
, which is linear in 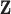 . LDA therefore calculates the
. LDA therefore calculates the 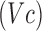 -dimensional hyperplane that best discriminates, or separates, the diagnostic volumes that have been determined using SFS with LOOCV on the respective dataset, for each class’ reconstructed fMRI. It follows these diagnostic volumes contain spatial locations with sufficiently different patient and control class densities, where statistically-significantly different regions possess the requisite margin between the class densities such that they are perceptible [51].
-dimensional hyperplane that best discriminates, or separates, the diagnostic volumes that have been determined using SFS with LOOCV on the respective dataset, for each class’ reconstructed fMRI. It follows these diagnostic volumes contain spatial locations with sufficiently different patient and control class densities, where statistically-significantly different regions possess the requisite margin between the class densities such that they are perceptible [51].
C. Evaluation Criteria
Each dataset was split such that the proportion of patients in the training partition was near-equal to the proportion of controls, and the holdout dataset contained at least 10 cohorts. In all but two cases, the aforementioned criteria could not be met because the datasets were unbalanced. For these situations, the training dataset was constructed such that it was a representative sample of the overall data, with the remaining cohorts being assigned to the holdout dataset. The holdout set therefore contained group proportions that could deviate from the training set. The cohorts used to define the training and holdout partition for each dataset are provided in Table 3 of the Supplementary Information.
Performance was compared to the original fMRI, both before and after applying PCA for artefact reduction [39], and chance, which is defined as the proportion of the majority class on the respective dataset. The performance of the reconstruction methods are evaluated using a combination of Leave-One-Out Cross Validation (LOOCV) and holdout data classification performance [26]. LOOCV is used on the training data to find both the best reconstruction parameter 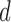 , and the diagnostic volumes that produce the highest accuracy for this
, and the diagnostic volumes that produce the highest accuracy for this 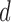 . The holdout data classification accuracies use the parameters found from performing LOOCV on the training data. Note: the cohorts in the holdout set are never involved in determining the optimal hyper-parameter
. The holdout data classification accuracies use the parameters found from performing LOOCV on the training data. Note: the cohorts in the holdout set are never involved in determining the optimal hyper-parameter 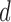 , or the diagnostic volumes produced from this
, or the diagnostic volumes produced from this 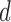 .
.
III. Results
A. Performance & Visualisation
Tables 1 and 2 demonstrate that Locally Linear Embedded fMRI can distinguish various mental disorders from healthy controls with high discriminatory power (> 80%); results for six additional resting-state datasets are provided in Table 2 of the Supplementary Information. The datasets contained healthy controls and patients with either Schizophrenia, Attention-Deficit Hyperactivity Disorder (ADHD), or Autism Spectrum Disorder (ASD). Ten of these datasets contained cohorts in the resting-state, with the remaining containing schizophrenic patients and healthy controls performing the Sternberg Item Recognition Paradigm (SIRP) task [61]. For a description of the data sources and technical details, please consult the appendix.
TABLE 1. Results.
| Dataset | Partition | Specificity | Sensitivity | Precision | Accuracy | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chance | Original | LLE | PCA | Chance | Original | LLE | PCA | Chance | Original | LLE | PCA | Chance | Original | LLE | PCA | ||
| Beijing (Peking_3) | Training | 100% | 73.3% ± 15.8% | 80% ± 14.3% | 66.7% ± 16.9% | 0% | 53.3% ± 17.9% | 93.3% ± 8.9% | 80% ± 14.3% | 0% | 66.7% ± 16.9% | 82.4% ± 13.6% | 70.6% ± 16.3% | 50% ± 17.9% | 63.3% ± 17.2% | 86.7% ± 12.2% | 73.3% ± 15.8% |
| Holdout | 100% | 75% | 87.5% | 25% | 0% | 100% | 50% | 25% | 0% | 66.7% | 66.7% | 14% | 67% | 83.3% | 75% | 25% | |
| COBRE | Training | 100% | 57.7% ± 13.6% | 92.3% ± 7.3% | 96.2% ± 5.3% | 0% | 60% ± 13.4% | 88% ± 8.9% | 52% ± 13.7% | 0% | 57.7% ± 13.6% | 91.7% ± 7.6% | 92.9% ± 7.1% | 51% ± 13.7% | 54.9% ± 13.7% | 90.2% ± 8.2% | 74.5% ± 6.1% |
| Holdout | 100% | 60% | 100% | 100% | 0% | 70% | 100% | 60% | 0% | 63.6% | 100% | 100% | 50% | 65% | 100% | 80% | |
| Mind Research Network (MRN) | Training | 100% | N/A | 88.2% ± 11.5% | 100% | 0% | N/A | 84.6% ± 12.9% | 23.1% ± 15.1% | 0% | N/A | 84.6% ± 12.9% | 100% | 56.7% ± 17.7% | N/A | 86.7% ± 12.2% | 66.7% ± 16.9% |
| Holdout | 100% | N/A | 67% | 100% | 0% | N/A | 71% | 14% | 0% | N/A | 63% | 100% | 56% | N/A | 68.8% | 62.5% | |
| Stanford | Training | 100% | 73.3% ± 15.8% | 80% ± 14.3% | 100% | 0% | 66.7% ± 16.9% | 86.7% ± 12.2% | 33.3% ± 16.9% | 0% | 71.4% ± 16.2% | 81.3% ± 14% | 100% | 50% ± 17.9% | 70% ± 16.4% | 83.3% ± 13.3% | 66.7% ± 16.9% |
| Holdout | 100% | 80% | 80% | 100% | 0% | 40% | 60% | 0% | 0% | 67% | 75% | 0% | 50% | 60% | 70% | 50% | |
| University of Michigan (UM_2) | Training | 100% | 69.2% ± 20.2% | 100% | 100% | 0% | 42.9% ± 21.7% | 71.4% ± 19.8% | 14.3% ± 15.3% | 0% | 42.9% ± 21.7% | 100% | 100% | 65% ± 20.9% | 60% ± 21.5% | 90% ± 13.1% | 70% ± 20.1% |
| Holdout | 100% | 66.6% | 100% | 83.3% | 0% | 25% | 50% | 0% | 0% | 20% | 100% | 0% | 60% | 30% | 80% | 50% | |
TABLE 2. Dataset Summary.
| Dataset | Experimental Design | Pulse Sequence | Patient Disorder | Source | Training Data total patients controls | Holdout Data total patients controls | fMRI Dimensionality (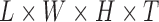 ) ) |
Parameters LLE 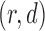 PCD PCD 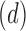
|
Age Range [min,mean,max] | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing (Peking_3) | resting-state | EPI | ADHD | ADHD200 | 30 | 15 | 15 | 12 | 4 | 8 | 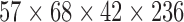 |
(2,236) | 236 | [11, 13.24, 16] |
| COBRE | resting-state | EPI | Schizophrenia | COBRE | 51 | 25 | 26 | 20 | 10 | 10 | 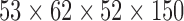 |
(2,150) | 150 | [18, 37.45, 65] |
| Mind Research Network (MRN) | block-design | EPI | Schizophrenia | MCIC | 30 | 13 | 17 | 16 | 7 | 9 | 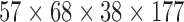 |
(2,177) | 177 | [18, 34.15, 60] |
| Stanford | resting-state | Spiral-IN/OUT EPI | Autism | ABIDE | 30 | 15 | 15 | 10 | 5 | 5 | 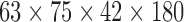 |
(2,60) | 60 | [7.52, 9.95, 12.93] |
| University of Michigan (UM_2) | resting-state | Spiral-IN EPI | Autism | ABIDE | 20 | 7 | 13 | 10 | 4 | 6 | 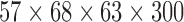 |
(2,222) | 222 | [13.1, 16.26, 28.8] |
Given that performance on the training partition uses Leave One Out Cross Validation (LOOCV) to individually predict each subject’s diagnosis, which is analogous to performing 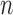 Bernoulli trials [4] (where
Bernoulli trials [4] (where 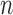 is the number of cohorts), the training data’s performance metrics can be interpreted as the mean of successes over
is the number of cohorts), the training data’s performance metrics can be interpreted as the mean of successes over 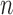 binomially-distributed observations. To calculate the error of these estimates, we follow Laplace’s approach of employing a normal distribution to estimate the error of binomially-distributed observations [33]. Given that discrimination performance on the holdout partition is determined in a one-time fashion, variance estimates are not applicable.
binomially-distributed observations. To calculate the error of these estimates, we follow Laplace’s approach of employing a normal distribution to estimate the error of binomially-distributed observations [33]. Given that discrimination performance on the holdout partition is determined in a one-time fashion, variance estimates are not applicable.
The Harvard-Oxford Subcortical/Cortical and Cerebellum atlases [30] are used to identify the statistically-significant differences between patients and controls in the diagnostic volumes for the respective dataset, shown in Figures 1, 2, and 3 (Figures 1, 2, 3, 4, 5, and 6 for datasets in the Supplementary Information). Each dataset’s figure contains six different views of the statistically-significant differences at the time reflected by the respective time point(s); the coloured voxels at these time points denote statistically significant (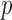 < 0.05 uncorrected) physical differences between the patient and control groups, where these groups include cohorts from both the training and holdout partitions. The proportion of significantly different voxels in each region, calculated by dividing the number of significantly different voxels by the total number of voxels in the respective region defined by the atlas, are provided in Tables 4 and 5 of the Supplementary Information.
< 0.05 uncorrected) physical differences between the patient and control groups, where these groups include cohorts from both the training and holdout partitions. The proportion of significantly different voxels in each region, calculated by dividing the number of significantly different voxels by the total number of voxels in the respective region defined by the atlas, are provided in Tables 4 and 5 of the Supplementary Information.
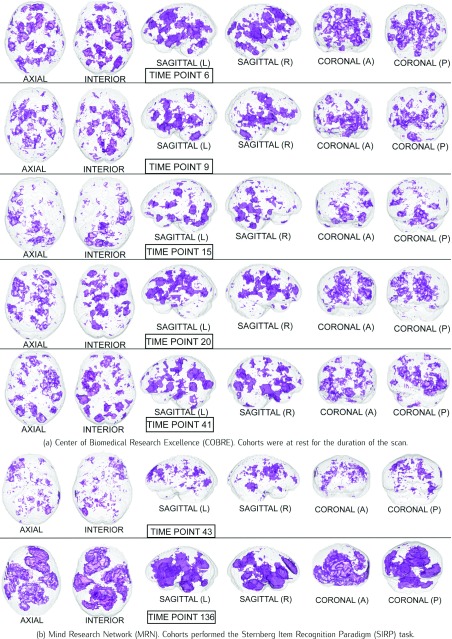
FIGURE 1.
Statistical maps illustrating the individual differences in mental activity (schizophrenic patients versus healthy controls) for the discriminative time points determined on the training partition.
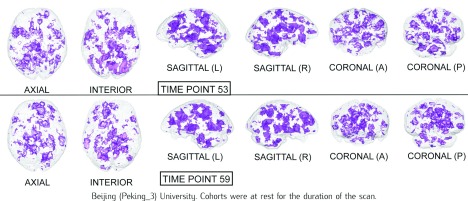
FIGURE 2.
Statistical maps illustrating the individual differences in mental activity (ADHD patients versus healthy controls) for the discriminative time points determined on the training partition.
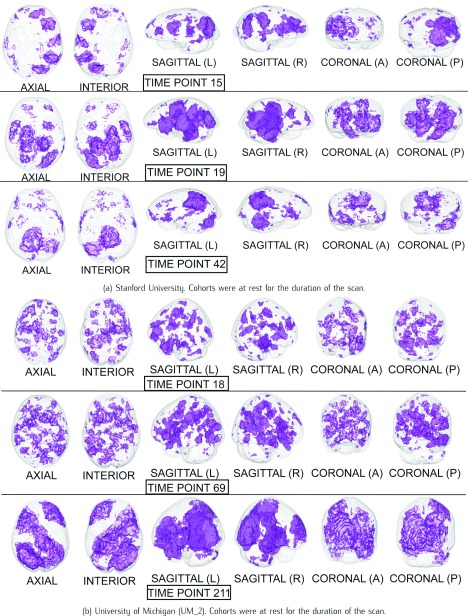
FIGURE 3.
The statistical maps illustrating the individual differences in mental activity (ASD patients versus healthy controls) for the discriminative time points determined on the training partition.
FIGURE 4.
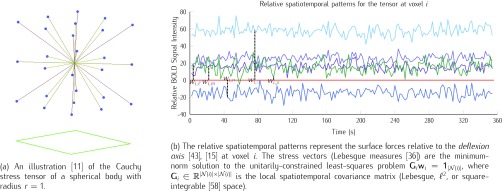
The local geometry of the Cauchy stress tensor and its relative spatiotemporal patterns on topology [7]
 , which is defined on the Cartesian space with the Pythagorean distance metric.
, which is defined on the Cartesian space with the Pythagorean distance metric.
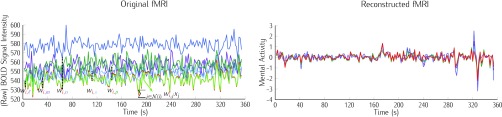
FIGURE 5.
Illustrating the reconstruction of the waveform at voxel 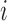 , located in the left cerebral cortex of a schizophrenic patient performing the Sternberg Item Recognition Paradigm (SIRP), as a linear combination of the Lebesgue measures [36]
, located in the left cerebral cortex of a schizophrenic patient performing the Sternberg Item Recognition Paradigm (SIRP), as a linear combination of the Lebesgue measures [36]
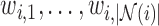 (defined on the Cauchy stress tensor) and the spatial patterns of the voxels on the boundary of the sphere, where spatial distance is defined using the Pythagorean distance metric; in this example,
(defined on the Cauchy stress tensor) and the spatial patterns of the voxels on the boundary of the sphere, where spatial distance is defined using the Pythagorean distance metric; in this example, 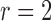 . For comprehension, only the five nearest voxel waveforms are shown.
. For comprehension, only the five nearest voxel waveforms are shown.
B. Neurobiological Interpretation
1). Schizophrenia
David Ingvar & Göran Franzèn found that healthy controls exhibit increased flows in the prefrontal regions and decreased flow in the post central regions, and schizophrenic patients exhibited the reversed pattern, with low flows prefrontally and high flows postcentrally [28]. Furthermore, they noticed that a lower flow in the premotor and frontal regions was associated with symptoms of indifference, activity and autism, and a higher postcentral flow over the temporo-occipito-parietal regions was associated with disturbed cognition [28]. Inspecting the statistical maps for the volumes in Figure 1, the significantly different areas seem to further substantiate Ingvar & Franzèn’s observations, as there are significant differences in the various temporo-occipital-parietal regions in all of the volumes.
The Sternberg Item Recognition Paradigm (SIRP) task evaluates cohorts’ short-term, or working, memory. Each of the seven tasks during the scan involves the subject memorising a set of objects, followed by presentation of a new object whose membership in this set is identified by a ‘yes’ or ‘no.’ The tasks therefore evaluate the hypothesised information processing differences between schizophrenics and healthy controls [16]. It has been shown that the prefrontal and medial temporal regions are involved in encoding information, and it is believed the interactions between these regions are central to retrieval of stored information [60]. Figure 1b, especially volume 136, illustrates significant differences in the areas associated with the prefrontal and medial temporal regions; this is further supported by the fact that the accuracy on the holdout data rose from 68.8% to 75% when using only volume 136. Thus, it is possible that schizophrenia indeed affects the physical mechanisms associated with retrieving stored information, as these mechanisms are central to the SIRP task. The reconstruction method therefore successfully reveals physical differences associated with task performance between patients and controls, which are different from the resting-state differences for the same subject groups.
2). Attention-Deficit Hyperactivity Disorder (ADHD)
Similar to the goals of Ingvar & Franzèn [28], previous work used PET scans to compare the regional cerebral blood flow of children with Attention-Deficit Hyperactivity Disorder (ADHD) to healthy controls, where it was found that the disorder was associated with hypoperfusion in the striatal and posterior periventricular regions [41]; these results provide biological evidence that is consistent with the canonical model for ADHD as a fronto-striatal deficient disorder. Figure 2 shows significant differences in the various occipital, striatal, cerebellar and ventral regions of the brain.
3). Autism Spectrum Disorder (ASD)
Similar to Ingvar & Franzèn’s observations that schizophrenic patients and healthy controls had normal hemisphere flows [28], studies using PET to compare the regional cerebral blood flow of Autism Spectrum Disorder (ASD) patients to healthy controls observed normal metabolism and blood flow. Hypoperfusion in the temporal lobes, centred in the associative auditory and adjacent multimodal cortex [66], was observed in autistic children. Furthermore, this temporal hypoperfusion was individually identifiable in 75% of autistic children [66]. Figure 3 illustrates statistical differences in many areas of the temporal lobe.
In summary, Locally Linear Embedding appears to have conserved spatiotemporal patterns in resting-state fMRI (and task-related responses) that are consistent with literature on regionally-specific abnormalities of cerebral activity in the psychiatric conditions used to assess classification performance.
IV. Discussion
The multidisciplinary nature of this work undoubtedly introduces difficulty when discussing its motivations, which is the deployment of this methodology in a clinical setting. Such a goal imposes some conditions. First, while the results support deployment, the methodology must be further evaluated by trained clinicians well-versed in the etymology of the disease under investigation. More importantly, however, experimental designs are compulsory when discovering biological markers for disease; that is, patients must be subject to the same stimulus presentation at the same time during the scan in order to homogenise comparisons. With respect to resting-state fMRI, it is felt that a consensus is required to glean neurobiological insight that can generalise, which makes further discussion more appropriate for future work.
This exposition focused on Locally Linear Embedding as a promising and effective form of dimensionality reduction as a pre-processing step for the analysis of fMRI time-series. The approaches and aims of this form of pre-processing share a close relationship with other approaches in imaging neuroscience. These approaches include Independent Component Analysis, the use of Support Vector Machines (and regression) to classification problems (and prediction), and algorithms based on adaptive smoothing. In future work, it will be interesting to explore the formal connections between other approaches and assess their relative sensitivity in the context of the classification problems considered above.
One hundred and fourty-eight years after Darwin ascertained that mental activity invokes physical mechanisms in the brain [14], the brain of man and ant alike are among the marvellous collection of atoms in the world.
Supplementary Material
Locally Linear Embedding and fMRI feature selection in psychiatric classification
29KB
Windows
The relative spatiotemporal patterns (top left) for a given tensor (depicted directly below) are used to calculate the reconstruction weights (bottom left) summarising the spatiotemporal pattern for the voxel where this tensor is centred. Every tensor's reconstruction weights are then subject to a global least squares optimisation of the Graph Laplacian matrix representing the Graphical model (centre), which results in the reconstructed waveform (bottom right).

Acknowledgements
This work is dedicated to the late Sam Roweis (1972–2010), Donald MacCrimmon MacKay (1922–1987) and his son David John Cameron MacKay (1967–2016). Additionally, many thanks to colleagues Ruitong Huang & Dr. Csaba Szepesvàri, Joshua T. Vogelstein, Dr. Vincent D. Calhoun, Dr. Neil Lawrence, Dr. Bert Vogelstein, Dr. Michael Milham, Dr. Karl J. Friston, Dr. Klaas Enno Stephan, Dr. Nikos K. Logothetis, Dr. Christof Koch, and Dr. Yifan Hu of AT&T Labs’ Information Visualisation department for his assistance with GraphViz, which was used to depict the Cauchy Stress Tensor in three dimensions.
Appendix. Locally Linear Embedding
fMRI contain 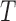 uniformly-spaced time points, where time point
uniformly-spaced time points, where time point 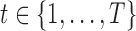 describes a three-dimensional space comprised of
describes a three-dimensional space comprised of 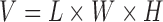 voxels (volumetric elements); this is the global description. Each voxel is a volumetric measurement of the brain’s physical mechanisms in both space and time– i.e., every voxel represents a measurement at spatial coordinates
voxels (volumetric elements); this is the global description. Each voxel is a volumetric measurement of the brain’s physical mechanisms in both space and time– i.e., every voxel represents a measurement at spatial coordinates 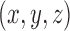 at time
at time 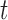 , which can also be expressed as a four-tuple
, which can also be expressed as a four-tuple 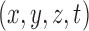 . The BOLD contrast over
. The BOLD contrast over 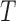 uniformly-spaced time points can be viewed as a random variable, or measurable function, [6] that is caused by local neuronal fluctuations. The terms global and local are only valid under a rigorous definition of three-dimensional space. A topological space requires specification of the relationships between points in a set and their respective open sets, which are defined as the sets that generalise the concept of an open interval in the real line while also providing a rigorous definition for nearness of points in this space [7].
uniformly-spaced time points can be viewed as a random variable, or measurable function, [6] that is caused by local neuronal fluctuations. The terms global and local are only valid under a rigorous definition of three-dimensional space. A topological space requires specification of the relationships between points in a set and their respective open sets, which are defined as the sets that generalise the concept of an open interval in the real line while also providing a rigorous definition for nearness of points in this space [7].
Locally Linear Embedding (LLE) [54] is a congruent transformation [13] that first extracts the local mathematical (geometric) structure of the data, and then performs a global optimisation that best conserves this local latent structure
[3], or extension
[38]. The application of LLE is challenging, primarily due to the implicit assumption that each data point and its neighbours lie on, or close to, a locally linear subspace [56]; earlier applications of LLE to fMRI discarded spatial properties of the data in the neighbourhood selection step [44], thereby failing to preserve the inherent spatial configuration. In contrast, specifying the topological space 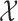 allows LLE to treat each data point’s open set as its neighbourhood, thereby forgoing the neighbourhood selection step entirely. It follows that the benefit of LLE depends on the suitability of the distance metric used in determining the neighbourhood of each data point. Figures 4 and 5 suggest that the physical reality represented by topological space
allows LLE to treat each data point’s open set as its neighbourhood, thereby forgoing the neighbourhood selection step entirely. It follows that the benefit of LLE depends on the suitability of the distance metric used in determining the neighbourhood of each data point. Figures 4 and 5 suggest that the physical reality represented by topological space 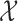 is a collection of locally-linear subspaces whose properties are subject to change at any time.
is a collection of locally-linear subspaces whose properties are subject to change at any time.
LLE uses the local description to construct the Cauchy stress tensor [9] at every voxel, which proceeds as follows: Initially, the spatial pattern of each voxel 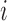 , given by
, given by 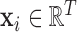 , is subtracted from both itself and the spatial patterns of its neighbours
, is subtracted from both itself and the spatial patterns of its neighbours 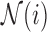 , thereby allowing its “zero waveform” (represented as
, thereby allowing its “zero waveform” (represented as 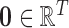 ) to serve as the imaginary plane, or deflexion axis
[15], [43], that divides the spherical body; the subtracted spatial patterns, given by (vector space)
) to serve as the imaginary plane, or deflexion axis
[15], [43], that divides the spherical body; the subtracted spatial patterns, given by (vector space) 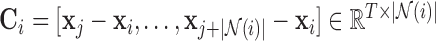 , represent the distances (over time) from the respective voxel’s spatial location.
, represent the distances (over time) from the respective voxel’s spatial location.
We then use the inner-product 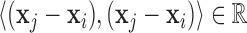 for
for 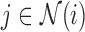 to compute the squared distances, which results in the real-symmetric positive-definite spatiotemporal covariance matrix
to compute the squared distances, which results in the real-symmetric positive-definite spatiotemporal covariance matrix 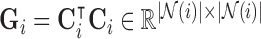 for every voxel
for every voxel  . Since the contact forces are inversely proportional to the squared differences represented in elements of
. Since the contact forces are inversely proportional to the squared differences represented in elements of 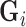 [48], we use the Moore-Penrose inverse [50] to solve for the minimum-norm solution (
[48], we use the Moore-Penrose inverse [50] to solve for the minimum-norm solution (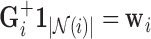 ) to the constrained least squares problem
) to the constrained least squares problem 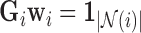 . Here,
. Here, 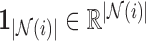 is the unit-length direction vector in each of the
is the unit-length direction vector in each of the 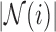 directions, and weights
directions, and weights 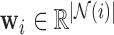 represent the stress vectors originating from voxel
represent the stress vectors originating from voxel 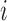 . By the spectral theorem, there exists an orthogonal basis
. By the spectral theorem, there exists an orthogonal basis 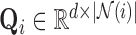 such that
such that 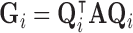 and
and 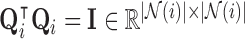 [62]; thus the stress vectors represented by
[62]; thus the stress vectors represented by 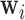 are shift, rotation, and translation invariant in the space defined on basis
are shift, rotation, and translation invariant in the space defined on basis 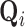 . The substantial overlap between spatially-adjacent voxels’ tensors precludes independently calculating orthogonal bases
. The substantial overlap between spatially-adjacent voxels’ tensors precludes independently calculating orthogonal bases 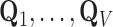 , as this defines each tensor’s basis on separate vector spaces.
, as this defines each tensor’s basis on separate vector spaces.
The stress vector 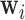 for each voxel’s Cauchy stress tensor,
for each voxel’s Cauchy stress tensor, 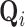 , represents the spatially-invariant properties of the three-dimensional forces applied over the duration of the scan in the respective subspace. LLE retains these spatially-local invariant properties by constructing the (global) adjacency matrix
, represents the spatially-invariant properties of the three-dimensional forces applied over the duration of the scan in the respective subspace. LLE retains these spatially-local invariant properties by constructing the (global) adjacency matrix 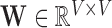 such that
such that  ; by construction
; by construction 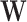 contains every voxel’s stress vectors, which were determined using the Cauchy stress tensor. Given that the stress vectors’ invariant properties are determined using squared distances, LLE then computes the squared distances between every voxel in the (global) normalised Laplacian matrix [10]
contains every voxel’s stress vectors, which were determined using the Cauchy stress tensor. Given that the stress vectors’ invariant properties are determined using squared distances, LLE then computes the squared distances between every voxel in the (global) normalised Laplacian matrix [10]
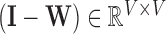 . This is expressed by
. This is expressed by 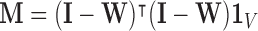 , where
, where 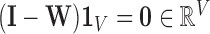 [35]. By construction,
[35]. By construction,  is symmetric and positive-definite, which means there exists an orthogonal basis
is symmetric and positive-definite, which means there exists an orthogonal basis 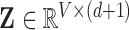 such that
such that 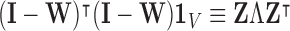 [42], where
[42], where 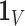 represents the global unit vector in three-dimensional space.4 Since the Cauchy stress tensor is of second order, LLE uses Rayleigh’s variational principle [12], [52] to calculate the resonance frequencies that best preserve the geometry of the deflexion axis at every voxel’s stress tensor. These are given by the bottom (d+1) eigenvectors, each of which represent one degree of freedom in space and time. LLE therefore uses a global optimisation to embed the relative measurements of every voxel’s Cauchy stress tensor [9] in a global coordinate system
represents the global unit vector in three-dimensional space.4 Since the Cauchy stress tensor is of second order, LLE uses Rayleigh’s variational principle [12], [52] to calculate the resonance frequencies that best preserve the geometry of the deflexion axis at every voxel’s stress tensor. These are given by the bottom (d+1) eigenvectors, each of which represent one degree of freedom in space and time. LLE therefore uses a global optimisation to embed the relative measurements of every voxel’s Cauchy stress tensor [9] in a global coordinate system 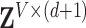 that conserves quantities over both space and time [19], where this coordinate system contains a mechanical system [32] in static equilibrium [8]. Applying LLE to fMRI data can therefore be viewed as using Carl Friedrich Gauß’ Principle of Least Constraint [23] to determine the true motion of the mechanical system defined on the topology
that conserves quantities over both space and time [19], where this coordinate system contains a mechanical system [32] in static equilibrium [8]. Applying LLE to fMRI data can therefore be viewed as using Carl Friedrich Gauß’ Principle of Least Constraint [23] to determine the true motion of the mechanical system defined on the topology 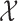 , where the Cauchy stress tensor [9] allows preservation of the intrinsic local Gaussian curvature [21], [22] in space and time.
, where the Cauchy stress tensor [9] allows preservation of the intrinsic local Gaussian curvature [21], [22] in space and time.
Footnotes
When using MLLE it is possible for 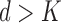 , thus the optimal number of weight vectors
, thus the optimal number of weight vectors 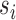 for each voxel
for each voxel 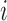 is determined by setting
is determined by setting 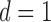 so that
so that 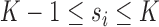 –i.e.,
–i.e., 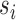 is set to span as large of a basis as possible. After this step the desired dimensionality
is set to span as large of a basis as possible. After this step the desired dimensionality 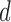 is then input to the eigensolver.
is then input to the eigensolver.
Implemented using MATLAB’s (R2013a) sequentialfs function
Implemented using MATLAB’s (R2013a) classify function with the ‘diaglinear’ argument to estimate the positive diagonal covariance matrix
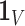 is also the
is also the 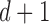 eigenvector of
eigenvector of 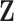 , which is discarded after the global optimisation.
, which is discarded after the global optimisation.
References
- [1].Andersen A. H., Gash D. M., and Avison M. J., “Principal component analysis of the dynamic response measured by fMRI: A generalized linear systems framework,” Magn. Reson. Imag., vol. 17, no. 6, pp. 795–815, 1999. [DOI] [PubMed] [Google Scholar]
- [2].Archibald R. C., “Time as a fourth dimension,” Bull. Amer. Math. Soc., vol. 20, no. 8, pp. 409–412, 1914. [Google Scholar]
- [3].Bacon F., Francisci De Verulamio, Summi Angliae Cancellarii, Instauratio Magna. London, U.K.: Apud Joannem Billium, Typographum Regium, 1620. [Google Scholar]
- [4].Bernoulli J., Ars Conjectandi. Basel, Switzerland: Impensis Thurnisiorum, Fraetum, 1713. [Google Scholar]
- [5].Bishop C. M., Pattern Recognition and Machine Learning. New York, NY, USA: Springer, 2006. [Google Scholar]
- [6].Billingsley P., Probability and Measure. Hoboken, NJ, USA: Wiley, 1979. [Google Scholar]
- [7].Bourbaki N., ´ Eléments de mathématique. Topologie algébrique. Berlin, Germany: Springer-Verlag, 2016, chs. 1–4. [Google Scholar]
- [8].Carathéodory C., “Untersuchungen über die grundlagen der thermodynamik,” Mathematische Annalen, vol. 67, no. 3, pp. 355–386, 1909. [Google Scholar]
- [9].Cauchy A. L., “De la pression ou tension dans un corps solide,” Exercices De Mathèmatiques, vol. 2, pp. 42–56, 1827. [Google Scholar]
- [10].Chung F. R. K., Spectral Graph Theory. Providence, RI, USA: American Mathematical Society, 1997. [Google Scholar]
- [11].Cormen T. H., Leiserson C. E., Rivest R. L., and Stein C., Introduction to Algorithms, 2nd ed. Cambridge, MA, USA: MIT Press, 2001. [Google Scholar]
- [12].Courant R., “Variational methods for the solution of problems of equilibrium and vibrations,” Bull. Amer. Math. Soc., vol. 49, no. 1, pp. 1–23, 1943. [Google Scholar]
- [13].Coxeter H. S. M., Introduction to Geometry, 2nd ed. Hoboken, NJ, USA: Wiley, 1989. [Google Scholar]
- [14].Darwin C., The Descent Man. London, U.K.: Murray, 1871. [Google Scholar]
- [15].Deeley E. M. and MacKay D. M., “Multiplication and division by electronic-analogue methods,” Nature, vol. 163, no. 4147, p. 650, Apr. 1949. [DOI] [PubMed] [Google Scholar]
- [16].Demirci O.et al. , “A review of challenges in the use of fMRI for disease classification / characterization and a projection pursuit application from a multi-site fMRI schizophrenia study,” Brain Imag. Behav., vol. 2, no. 3, pp. 207–226, Sep. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Fisher R. A., “The use of multiple measurements in taxonomic problems,” Ann. Eugenics, vol. 7, no. 2, pp. 179–188, 1936. [Google Scholar]
- [18].Fisher R. A., “The statistical utilization of multiple measurements,” Ann. Eugenics, vol. 8, no. 4, pp. 376–386, 1938. [Google Scholar]
- [19].Friston K., “The free-energy principle: A unified brain theory?” Nature Rev. Neurosci., vol. 11, no. 2, pp. 127–138, 2010. [DOI] [PubMed] [Google Scholar]
- [20].Garabedian P. R. and Schiffer M., “On existence theorems of potential theory and conformal mapping,” Ann. Math., vol. 52, no. 1, pp. 164–187, 1950. [Google Scholar]
- [21].Gauß C. F., Disquisitiones Generales Circa Superficies Curvas. Berlin, Germany: Typis Ditericianis, 1828. [Google Scholar]
- [22].Gauß C. F., Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium. Hamburg, Germany: Perthes et Besser, 1809. [Google Scholar]
- [23].Gauß C. F., “Über ein neues allgemeines grundgesetz der mechanik,” J. Für Die Reine Angewandte Mathematik, vol. 4, no. 4, pp. 232–235, 1829. [Google Scholar]
- [24].Gillespie R. J., “Fifty years of the VSEPR model,” Coordination Chem. Rev., vol. 252, nos. 12–14, pp. 1315–1327, Jul. 2008. [Google Scholar]
- [25].Gregory J., Geometriae Pars Universalis. Patavii, Italy: Typis heredum Pauli Frambotti, 1668. [Google Scholar]
- [26].Hastie T., Tibshirani R., and Friedman J., The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Springer Series in Statistics), 2nd ed. New York, NY, USA: Springer, 2009. [Google Scholar]
- [27].Hilbert D., “Ueber die stetige Abbildung einer Line auf ein Flächenstück,” Mathematische Annalen, vol. 3, no. 38, pp. 459–460, 1891. [Google Scholar]
- [28].Ingvar D. H. and Franzén G., “Distribution of cerebral activity in chronic schizophrenia,” Lancet, vol. 304, no. 7895, pp. 1484–1486, Dec. 1974. [DOI] [PubMed] [Google Scholar]
- [29].Ingvar D. H. and Lassen N. A., “Quantitative determination of regional cerebral blood-flow in man,” Lancet, vol. 278, no. 7206, pp. 806–807, Oct. 1961. [Google Scholar]
- [30].Jenkinson M., Beckmann C. F., Behrens T. E. J., Woolrich M. W., and Smith S. M., “FSL,” NeuroImage, vol. 62, no. 2, pp. 782–790, Aug. 2012. [DOI] [PubMed] [Google Scholar]
- [31].Jolliffe I., Principal Component Analysis. New York, NY, USA: Springer-Verlag, 2002. [Google Scholar]
- [32].Koch C. and Hepp K., “Quantum mechanics in the brain,” Nature, vol. 440, no. 7084, pp. 611–612, 2006. [DOI] [PubMed] [Google Scholar]
- [33].Laplace P., Théorie Analytique Des Probabilités. Paris, France: Courcier, 1812. [Google Scholar]
- [34].Lassen N. A., Ingvar D. H., Potchen E. J., and McCready V. R., Eds., “Radioisotopic assessment of regional cerebral blood flow,” Progress in Nuclear Medicine: Neuro-Nuclear Medicine, vol. 1 Baltimore, MD, USA: Univ. Park Press, 1972, pp. 376–409. [PubMed] [Google Scholar]
- [35].Lawrence N. D., “A unifying probabilistic perspective for spectral dimensionality reduction: Insights and new models,” J. Mach. Learn. Res., vol. 13, pp. 1609–1638, Jun. 2012. [Google Scholar]
- [36].Lebesgue H., “Leçons sur L’intégration et la recherche des fonctions primitives, professées au collège de France,” in Collection de Monographies Sur la Théorie des Fonctions. Paris, France: Gauthier-Villars, 1904. [Google Scholar]
- [37].Liddle P. F., Friston K. J., Frith C. D., Hirsch S. R., Jones T., and Frackowiak R. S. J., “Patterns of cerebral blood flow in schizophrenia,” Brit. J. Psychiatry, vol. 160, no. 2, pp. 179–186, 1992. [DOI] [PubMed] [Google Scholar]
- [38].Locke J., An Essay Concerning Human Understanding. Oxford, U.K.: Thomas Basset, 1690. [Google Scholar]
- [39].Logothetis N. K., Pauls J., Augath M., Trinath T., and Oeltermann A., “Neurophysiological investigation of the basis of the fMRI signal,” Nature, vol. 412, no. 6843, pp. 150–157, Jul. 2001. [DOI] [PubMed] [Google Scholar]
- [40].Logothetis N. K., “What we can do and what we cannot do with fMRI,” Nature, vol. 453, no. 7197, pp. 869–878, Jun. 2008. [DOI] [PubMed] [Google Scholar]
- [41].Lou H. C., Henriksen L., and Psych P. B. C., “Focal cerebral dysfunction in developmental learning disabilities,” Lancet, vol. 335, no. 8680, pp. 8–11, Jan. 1990. [DOI] [PubMed] [Google Scholar]
- [42].MacKay D. J. C., Information Theory, Inference and Learning Algorithms. Cambridge, U.K.: Cambridge Univ. Press, 2003. [Google Scholar]
- [43].MacKay D. M., “A high-speed electronic function generator,” Nature, vol. 159, no. 4038, pp. 406–407, Mar. 1947. [Google Scholar]
- [44].Mannfolk P., Wirestam R., Nilsson M., Ståhlberg F., and Olsrud J., “Dimensionality reduction of fMRI time series data using locally linear embedding,” Magn. Reson. Mater. Phys., Biol. Med., vol. 23, nos. 5–6, pp. 327–338, Dec. 2010. [DOI] [PubMed] [Google Scholar]
- [45].Mel’nikov M. S., “Analytic capacity: Discrete approach and curvature of measure,” Sbornik, Math., vol. 186, no. 6, pp. 827–846, 1995. [Google Scholar]
- [46].Mill J. S., A System of Logic, Ratiocinative and Inductive: Being a Connected View of the Principles of Evidence and the Methods of Scientific Investigation, vol. 1 London, U.K.: John W. Parker, 1843. [Google Scholar]
- [47].Minkowski H., “Raum und zeit,” Physikalische Zeitschrift, vol. 10, pp. 104–111, Feb. 1909. [Google Scholar]
- [48].Newton I., Philosophiae Naturalis Principia Mathematica. [Google Scholar]
- [49].Ogawa S., Lee T. M., Kay A. R., and Tank D. W., “Brain magnetic resonance imaging with contrast dependent on blood oxygenation,” Proc. Nat. Acad. Sci. USA, vol. 87, no. 24, pp. 9868–9872, 1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Penrose R., “A generalized inverse for matrices,” Math. Proc. Cambridge Phil. Soc., vol. 51, no. 3, pp. 406–413, Jul. 1955. [Google Scholar]
- [51].Popham M. G., Potchen E. J., and McCready V. R., Eds., “Numerical methods for the detection of abnormalities in radionuclide brain scans,” in Progress in Nuclear Medicine: Neuro-Nuclear Medicine, vol. 1 Baltimore, MD, USA: Univ. Park Press, 1972, pp. 117–141. [PubMed] [Google Scholar]
- [52].Rayleigh J. W. S., The Theory of Sound. London, U.K.: Macmillan, 1877. [Google Scholar]
- [53].Robins L. N. and Helzer J. E., “Diagnosis and clinical assessment: The current state of psychiatric diagnosis,” Annu. Rev. Psychol., vol. 37, no. 1, pp. 409–432, 1986. [DOI] [PubMed] [Google Scholar]
- [54].Roweis S. T. and Saul L. K., “Nonlinear dimensionality reduction by locally linear embedding,” Science, vol. 290, no. 5500, pp. 2323–2326, Dec. 2000. [DOI] [PubMed] [Google Scholar]
- [55].Roy C. S. and Sherrington C. S., “On the regulation of the blood-supply of the brain,” J. Physiol., vol. 11, nos. 1–2, pp. 85–158, Jan. 1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Saul L. K. and Roweis S. T., “Think globally, fit locally: Unsupervised learning of low dimensional manifolds,” J. Mach. Learn. Res., vol. 4, pp. 119–155, Dec. 2003. [Google Scholar]
- [57].Seung H. S. and Lee D. D., “The manifold ways of perception,” Science, vol. 290, no. 5500, pp. 2268–2269, 2000. [DOI] [PubMed] [Google Scholar]
- [58].Schmidt E., “Über die auflösung linearer gleichungen mit unendlich vielen unbekannten,” Rendiconti Circolo Matematico Palermo, vol. 25, no. 1, pp. 53–77, 1908. [Google Scholar]
- [59].Sherrington C. S., Man on His Nature—Gifford Lectures. Edinburgh, U.K.: Edinburgh Univ. Press, 1951. [Google Scholar]
- [60].Simons J. S. and Spiers H. J., “Prefrontal and medial temporal lobe interactions in long-term memory,” Nature Rev. Neurosci., vol. 4, no. 8, pp. 637–648, Aug. 2003. [DOI] [PubMed] [Google Scholar]
- [61].Sternberg S., “High-speed scanning in human memory,” Science, vol. 153, no. 3736, pp. 652–654, 1966. [DOI] [PubMed] [Google Scholar]
- [62].Sylvester J. J., “A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares,” London, Edinburgh, Dublin Philos. Mag. J. Sci., vol. 4, no. 23, pp. 138–142, 1852. [Google Scholar]
- [63].Whitney A. W., “A direct method of nonparametric measurement selection,” IEEE Trans. Comput., vol. C-20, no. 9, pp. 1100–1103, Sep. 1971. [Google Scholar]
- [64].Williams J. B. W.et al. , “The structured clinical interview for DSM-III-R (SCID): II. Multisite test-retest reliability,” Arch. Gen. Psychiatry, vol. 49, no. 8, pp. 630–636, Aug. 1992. [DOI] [PubMed] [Google Scholar]
- [65].Zhang Z. and Wang J., “MLLE: Modified locally linear embedding using multiple weights,” Adv. Neural Inf. Process. Syst., vol. 19, no. 19, pp. 1593–1600, Dec. 2007. [Google Scholar]
- [66].Zilbovicius M.et al. , “Temporal lobe dysfunction in childhood autism: A PET study,” Amer. J. Psychiatry, vol. 157, no. 12, pp. 1988–1993, 2000. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Locally Linear Embedding and fMRI feature selection in psychiatric classification
29KB
Windows
The relative spatiotemporal patterns (top left) for a given tensor (depicted directly below) are used to calculate the reconstruction weights (bottom left) summarising the spatiotemporal pattern for the voxel where this tensor is centred. Every tensor's reconstruction weights are then subject to a global least squares optimisation of the Graph Laplacian matrix representing the Graphical model (centre), which results in the reconstructed waveform (bottom right).